An adaptive direct multisearch method for black-box multi-objective optimization

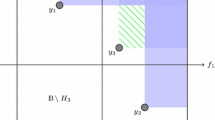
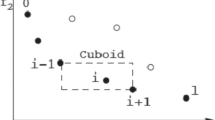
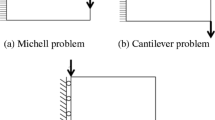
Abstract

At present, black-box and simulation-based optimization problems with multiple objective functions are becoming increasingly common in the engineering context. In many cases, the functional relationships that define the objective and constraints are only known as black-boxes, cannot be differentiated accurately, and may be subject to unexpected failures. Directional direct search techniques, in particular the direct multisearch (DMS) methodology, may be applied to identify Pareto fronts for such problems. In this work, we propose a mechanism for adaptively selecting search directions in the DMS framework, with the goal of reducing the number of black-box evaluations required during the optimization. Our method relies on the concept of simplex derivatives in order to define search directions that are optimal for a local, linear model of the objective function. We provide a detailed description of the resulting algorithm and offer several practical recommendations for efficiently solving the associated subproblems. The overall performance in an academic context is assessed via a standard benchmark. Through a realistic case study, involving the bi-objective design optimization of a mechatronic quarter-car suspension, the performance of the novel method in a multidisciplinary engineering setting is tested. The results show that our method is competitive with standard implementations of DMS and other state-of-the-art multi-objective direct search methods.

Technical results used in the proof of Theorem 2

The first step is to recognize that the distance function has the following subadditivity property.

Lemma 1

(Subadditivity of the distance function) Let ${\mathcal {W}}_1,{\mathcal {W}}_2 \subset {\mathbb {R}}^n$ be closed, and let $\mathbf {w} \in {\mathbb {R}}^n$ be an arbitrary vector. Then

$$\begin{aligned} {\text {dist}}\left( {\mathcal {W}}_1,{\mathcal {W}}_2\right) \le {\text {dist}}\left( \mathbf {w},{\mathcal {W}}_1\right) + {\text {dist}}\left( \mathbf {w},{\mathcal {W}}_2\right) . \end{aligned}$$

(40)

Proof

For arbitrary $\mathbf {w}_1 \in {\mathcal {W}}_1, \mathbf {w}_2 \in {\mathcal {W}}_2$, and $\mathbf {w} \in {\mathbb {R}}^n$ we have

$$\begin{aligned} {\text {dist}}\left( {\mathcal {W}}_1,{\mathcal {W}}_2\right)&\le ||\mathbf {w}_1-\mathbf {w}_2||\\&\le ||\mathbf {w}_1-\mathbf {w}|| + ||\mathbf {w}_2-\mathbf {w}|| \end{aligned}$$

by the triangle inequality. Since this holds for any $\mathbf {w}_1$ and $\mathbf {w}_2$, it must also be the case that

$$\begin{aligned} {\text {dist}}\left( {\mathcal {W}}_1,{\mathcal {W}}_2\right)&\le \min _{\mathbf {w}_1 \in {\mathcal {W}}_1} ||\mathbf {w}_1-\mathbf {w}|| + \min _{\mathbf {w}_2 \in {\mathcal {W}}_2}||\mathbf {w}_2-\mathbf {w}||\\&= {\text {dist}}\left( \mathbf {w},{\mathcal {W}}_1\right) + {\text {dist}}\left( \mathbf {w},{\mathcal {W}}_2\right) . \end{aligned}$$

$\square$

The next lemma is used to show that a specific hyperplane is supporting for a convex set.

Lemma 2

(Supporting hyperplane for convex sets) Let ${\mathcal {W}} \subset {\mathbb {R}}^n$ be closed and convex. Let $\mathbf {w}^*$ be the minimizer

$$\begin{aligned} \mathbf {w}^*= \arg \min _{\mathbf {w}\in {\mathcal {W}}}||\mathbf {w}||. \end{aligned}$$

Then, for arbitrary $\mathbf {w}\in {\mathcal {W}}$, the vector $\mathbf {w}^*$ defines a supporting hyperplane:

$$\begin{aligned} \mathbf {w}^T\mathbf {w}^*\ge \mathbf {w}^{*T}{\mathbf {w}}^*. \end{aligned}$$

Proof

Since the norm minimization is a convex problem, $\mathbf {w}^*$ exists and is a unique minimizer. By convexity, for any $\mathbf {w}\in {\mathcal {W}}$ and $\alpha \in [0,1]$ we have

$$\begin{aligned} \mathbf {w}^*+ \alpha (\mathbf {w}-\mathbf {w}^*) \in {\mathcal {W}}. \end{aligned}$$

The definition of $\mathbf {w}^*$ implies

$$\begin{aligned} ||\mathbf {w}^*||^2&\le ||\mathbf {w}^*+ \alpha (\mathbf {w}-\mathbf {w}^*)||^2 \\&= ||\mathbf {w}^*||^2 + 2\alpha \mathbf {w}^{*T}(\mathbf {w}-\mathbf {w}^*) + \alpha ^2||\mathbf {w}-\mathbf {w}^*||^2. \end{aligned}$$

Hence

$$\begin{aligned} 0 \le 2\mathbf {w}^{*T}(\mathbf {w}-\mathbf {w}^*) + \alpha ||\mathbf {w}-\mathbf {w}^*||^2 \end{aligned}$$

as long as $\alpha > 0$. Taking the limit $\alpha \rightarrow 0$, we find

$$\begin{aligned} \mathbf {w}^T\mathbf {w}^*\ge \mathbf {w}^{*T}\mathbf {w}^*. \end{aligned}$$

$\square$

Intuitively, one might expect the optimal separation of two convex sets to occur when they are diametrically opposed across the origin. Such a situation indeed achieves an equality of the Eq. (40), as the next lemma demonstrates.

Lemma 3

(Distance between diametrically opposed convex sets) Let ${\mathcal {W}}_1,{\mathcal {W}}_2 \subset {\mathbb {R}}^n$ be closed and convex. Let $\mathbf {w}_1^*$ and $\mathbf {w}_2^*$ be the respective minimizers

$$\begin{aligned} \mathbf {w}_1^*= \arg \min _{\mathbf {w}_1\in {\mathcal {W}}_1}||\mathbf {w}_1|| \quad \text {and} \quad \mathbf {w}_2^*= \arg \min _{\mathbf {w}_2\in {\mathcal {W}}_2}||\mathbf {w}_2||. \end{aligned}$$

Suppose $\mathbf {w}_1^*,\mathbf {w}_2^*\ne \mathbf {0}$ and that $\mathbf {w}_1^*= -\alpha \mathbf {w}_2^*$ with $\alpha > 0$. Then

$$\begin{aligned} {\text {dist}}\left( {\mathcal {W}}_1,{\mathcal {W}}_2\right) = {\text {dist}}\left( \mathbf {0},{\mathcal {W}}_1\right) + {\text {dist}}\left( \mathbf {0},{\mathcal {W}}_2\right) . \end{aligned}$$

Proof

For arbitrary $\mathbf {w}_1 \in {\mathcal {W}}_1, \mathbf {w}_2 \in {\mathcal {W}}_2$ we have

$$\begin{aligned} ||\mathbf {w}_1^*||\,||\mathbf {w}_1-\mathbf {w}_2||&\ge \mathbf {w}_1^{*T}(\mathbf {w}_1-\mathbf {w}_2) \qquad \qquad \text {Cauchy-Schwarz inequality} \\&= \mathbf {w}_1^{*T}\mathbf {w}_1+\alpha \mathbf {w}_2^{*T}\mathbf {w}_2 \qquad {\mathbf {w}_1^*= -\alpha \mathbf {w}_2^*} \\&\ge \mathbf {w}_1^{*T}\mathbf {w}_1^*+\alpha \mathbf {w}_2^{*T}\mathbf {w}_2^*\qquad {\text{Lemma}}\, 2, \alpha > 0 \\&= ||\mathbf {w}_1^*||^2+\alpha ||\mathbf {w}_2^*||^2. \end{aligned}$$

Therefore,

$$\begin{aligned} ||\mathbf {w}_1-\mathbf {w}_2|| \ge ||\mathbf {w}_1^*||+||\mathbf {w}_2^*|| = ||\mathbf {w}_1^*- \mathbf {w}_2^*||, \end{aligned}$$

since the minimizers are aligned in opposite directions. Because the inequality holds for arbitrary $\mathbf {w}_1$ and $\mathbf {w}_2$, and because of the definition of $\mathbf {w}_1^*$ and $\mathbf {w}_2^*$, we finally obtain

$$\begin{aligned} {\text {dist}}\left( {\mathcal {W}}_1,{\mathcal {W}}_2\right) = ||\mathbf {w}_1^*- \mathbf {w}_2^*|| = ||\mathbf {w}_1^*||+||\mathbf {w}_2^*|| = {\text {dist}}\left( \mathbf {0},{\mathcal {W}}_1\right) + {\text {dist}}\left( \mathbf {0},{\mathcal {W}}_2\right) . \end{aligned}$$

$\square$