Introduction

With the success on applications in ImageNet challenge, the deep neural networks (DNNs) have been extensively utilized in a wide variety of applications [1,2,3] and showed superiorities over other approaches. However, as the structure becomes deeper and larger, the number of network parameters would increase considerably, resulting in a dramatic escalation in computing cost during the utilization of DNNs. Therefore, DNN with relatively low computing cost yet high accuracy is urgently needed nowadays, which gives rise to the development of network pruning technique to simplify the structure and reduce the parameters. Pruning deep CNNs is an important direction for accelerating the network. Recent developments on pruning can be generally divided into two categories, namely weight pruning [4,5,6] and filter pruning [7,8,9,10, 60,61,62].

Fig. 1
figure 1

An illustration of the difference between the traditional single-task pruning method and our multi-task pruning method

Full size image

It is the objective of model pruning to compress the model size and accelerate the inference of the network. Weight-pruning methods remove connections in the filters or across different layers, thereby reducing the cost of memory cost. However, the main weakness of weight pruning is the unstructural operation manner. The unstructured sparsity of the filters makes weight pruning hard to deploy existing basic linear algebra subprograms (BLASs) libraries. Hence, weight pruning is not effective in reducing computational cost. In contrast, filter pruning allows models to be structured with sparsity, reducing the storage usage on devices and achieving practical acceleration.

It should be noted that most of the existing results regarding the network pruning mainly concentrates on single network structure, and few effort has been devoted to investigating the multi-task pruning due primarily to the difficulty brought by the cross-coupling of different tasks as well as increasing parameters. Moreover, different from traditional multi-task learning algorithms, the methods proposed in this paper of sharing information for different tasks should be designed with a trade-off between network size and performance. In addition, keeping the balance between different tasks is also a challenge for multi-task pruning.

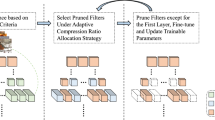
Very recently, it has been declared in [11] that the key of multi-task pruning is to reduce both intra-redundancy in single task and inter-redundancy between multiple tasks. However, the proposed algorithm cannot be applied directly for pruning because of depending on the results of network merging. Motivated by this, we intend to propose a unified Multi-task Filter Index Sharing (MFIS) framework which could systematically deal with both single-task and multi-task pruning. As illustrated in Fig. 1, we first establish a filter candidate box which contains all filters in both tasks. Different from traditional methods for single-task pruning, within our proposed framework, important filters are selected under certain criteria imposed on multi-task, which is converted into a many-objective optimization problem (MOP) [12]. Then, filter sharing (FS) strategy is developed to force each filter choosing one and only one important candidate to support. Filters that support the same candidate might be pruned, merged or remained according to FS strategy. Moreover, an index matrix is introduced by the pruning and merging results of multi-networks to keep the network structure and to regulate the information sharing in subsequent multi-task learning.

The main contributions of this paper can be highlighted as follows:

  1. i)

    Different from most traditional pruning techniques only applicable for single task, we propose a more general framework MFIS, which is able to deal with both multi-task pruning and single-network pruning.

  2. ii)

    The proposed FIS in different networks is capable of selecting important filters and determining the most suitable operation (pruning, merging, or remaining) for each filter. Meanwhile, the index matrix in FIS can keep the network structure in multi-task training.

  3. iii)

    Three criteria for selecting targeted important filters are put forward to further appropriately characterize the performance of MFIS that is subsequently optimized via the MOP method.

  4. iv)

    The proposed algorithm is quite flexible where two pruning rate strategies, namely adaptive rates for different tasks and fixed rate for individual task, are adopted to balance the learning speed and accuracy.

  5. v)

    Via extensive experiments, the effectiveness and efficiency of MFIS are demonstrated on different networks and databases. We prove that MFIS performs better compared with both single-task pruning methods and multi-task pruning methods.

The remainder of this paper is organized as follows. In Section 2, we introduce the related work of model pruning, multi-task learning and many-objective optimization problem. In Section 3, we describe our framework in detail. The experimental study and the corresponding analysis are presented in Section 4. Section 5 gives the conclusions of this paper.

Related Work

Model Pruning

Filter pruning removes the entire filters, which could reduce the memory cost, and meanwhile, shows effectiveness of promotion on the inference speed. In recent publications, some works (e.g., [13, 14]) have utilized the training data and filter activations to determine the pruned filters, while other methods (e.g., [15, 16]) have determined the importance of the filters by weights. Commonly, data-independent algorithms are more effective than the former because the utilizing of training data is always computation consuming. Among data-independent algorithms, researchers design criterions to prune unimportant filters. In most existing publications regarding the model compression task, only single model compression has been considered which means that most criterions are designed for single mission. Although there have been some initial results on corresponding multi-task case, the developed algorithms have certain limitations. For instance, in [17], the proposed MTZ framework has only been able to deal with compression without pruning. In [11], an RDNet has been first established by two pre-trained models with a threshold parameter \(\alpha\), but the technique of pruning, i.e., Variational Information Bottleneck (VIB), is borrowed from [18].

Multi-task Learning

As is well known, multi-task Learning aims to improve generalization performance and reduces the risk of overfitting by jointly learning multiple related tasks [19,20,21,22]. ML of DNNs has been applied nowadays in various applications, from scene understanding [23] to face detection [1], to name but a few. ML enables combined model to generalize better for all tasks by sharing representations from related original networks. Recently, many researchers have devoted efforts on issues of ‘what to share’ and ‘how to share’ among tasks, especially those relevant to deep neural networks. Some representative works can be summarized as follows. Yang et al. [24] have proposed an algorithm of learning cross-task sharing structure at each layer in a deep network. Cross-stitching networks developed in [25] have introduced cross-stitch units to learn shared representations. In [26], soft ordering approach of shared layers has been applied in multi-task learning which shows more effective sharing ability. Lu et al. has proposed an automatic approach in [27] for designing multi-task deep learning architectures, which starts with a thin multi-layer network that is dynamically widened during training. All the mentioned multi-task learning methods do not consider the network size and only focus on tasks highly related. The parameters even grow during training process, leading to opposite outcome for pruning. Hence, a new multi-task pruning algorithm should be designed for combining model pruning and multi-task learning.

Many-objective Optimization Problem

On another reach frontier, MOP has been attracting particular attention in machine learning due to the fact that many relevant optimization problems can be converted to MOPs [12]. The description of an MOP problem is illustrated by the following (1) with m objectives:

$$\begin{aligned} \begin{aligned} \min _{\varvec{\nu }}&\mathcal {F}(\varvec{\nu })\\&\mathcal {F}=\{\mathcal {F}_1(\varvec{\nu }),\mathcal {F}_2(\varvec{\nu }),\ldots ,\mathcal {F}_m(\varvec{\nu })\} \end{aligned} \end{aligned}$$
(1)

where \(\varvec{\nu }=(\nu _1,\nu _2,\ldots ,\nu _n)\) is a set of n decision variables; \(\mathcal {F}(\cdot )\) is the objective function.

In our proposed work, by borrowing the idea from many-objective optimization problem, we first convert the issues of selecting the important filters into an MOP and then solve the problem by evolutionary algorithm, which will be discussed later in detail.

Methodology

Criteria for Selection

Taking two tasks as example, filter set \(V_A\) and \(V_B\) contain the original filters in model A and B, respectively. Filter candidate set C is initialize with V. We should first obtain an important filter set \(C^E\) from C. For the purpose of converting the selection of important filters \(C^E\) into an MOP, we introduce a binary-valued hyperparameter \(\alpha _i\in \{0,1\}\) for each filter \(f_i\in C\). When \(\alpha _i=1\), it is said that \(f_i\) belongs to \(C^E\). Then, \(\varvec{\alpha }=(\alpha _1,\alpha _2,\ldots ,\alpha _m)\) is the set of decision variables. The objectives of MOP can be designed according to the following criteria.

Loss of Replacing

This criterion aims to assure that each filter in V has appropriately small \(\delta E\) with a candidate in \(C^E\):

$$\begin{aligned} \begin{aligned} \forall {f_i\in {V}}: \&\exists f_j\in {C^E},\\&\mathrm{s.t.} \ \delta E(i,j)< \epsilon \end{aligned} \end{aligned}$$
(2)

where \(\delta E(i,j)\) denotes the loss of replacing \(f_i\) with \(f_j\). Here, we calculate the loss of replacing \(f_i \in V\) with \(f_j \in C\) on task A by

$$\begin{aligned} \delta \hat{E^A}(i,j) = \left\{ \begin{array}{rcl} +\infty &{} &{}\alpha _j = 0 \wedge f_i\in V_A\\ \delta E^A(i,j)&{} &{}\alpha _j = 1 \wedge f_i\in V_A\\ 0&{} &{} f_i\in V_B \end{array} \right. \end{aligned}$$
(3)

Similarly, the loss of replacing \(f_i\) with \(f_j\) on task B is defined by

$$\begin{aligned} \delta \hat{E^B}(i,j) = \left\{ \begin{array}{rcl} +\infty &{} &{}\alpha _j = 0 \wedge f_i\in V_B\\ \delta E^B(i,j)&{} &{}\alpha _j = 1 \wedge f_i\in V_B\\ 0&{} &{} f_i\in V_A \end{array} \right. \end{aligned}$$
(4)

Then, the corresponding objective functions are defined as follows:

$$\begin{aligned} \mathcal {F}_1(\varvec{\alpha })=\sum _{f_i \in V}{\min _{f_j \in C}\{\delta \hat{E}^A(i,j)\}} \end{aligned}$$
(5)
$$\begin{aligned} \mathcal {F}_2(\varvec{\alpha })=\sum _{f_i \in V}{\min _{f_j \in C}\{\delta \hat{E}^B(i,j)\}} \end{aligned}$$
(6)

\(\mathcal {F}_1(\cdot )\) and \(\mathcal {F}_2(\cdot )\) describe the losses of replacing for network A and B, respectively. With limit on size of \(C^E\), \(\mathcal {F}_1(\cdot )\) and \(\mathcal {F}_2(\cdot )\) will get rid of inappropriate candidates from \(C^E\), thereby reducing the intra-redundancy in tasks and inter-redundancy between tasks at the minimum loss.

Fig. 2
figure 2

Filter sharing in networks

Full size image

The Diversity of Selected Candidates

This criterion is to keep the diversity of selected candidates in \(C^E\). To this end, we define the diversity of \(C^E\) as the sum of losses by replacing \(f_i\in C^E\) with all the other filters in \(C^E\), which is represented as follows:

$$\begin{aligned} \mathcal {D}=\sum ^{\alpha _i=1}_{i}\sum ^{\alpha _j=1}_{j}{\delta {E}(i,j)} \end{aligned}$$
(7)

Then, the corresponding objective function \(\mathcal {F}_3(\cdot )\) is defined by

$$\begin{aligned} \mathcal {F}_3(\varvec{\alpha })=-\mathcal {D} \end{aligned}$$
(8)

The Entropy of Weights

A filter without variation may be failed on capturing the important information from input data [28]. Here, entropy of layer is introduced to evaluate the variation of filters’ weights, which can be calculated as follows:

$$\begin{aligned} \mathcal {I}=-\sum ^n_{k=1}p_k\log p_k \end{aligned}$$
(9)

where n is the number of classes of sampling weights and \(p_k\) is the probability of classes k. High entropy of filters means high variation on weights. Then, the corresponding objective function \(\mathcal {F}_4(\cdot )\) is defined by

$$\begin{aligned} \mathcal {F}_4(\varvec{\alpha })=-\mathcal {I} \end{aligned}$$
(10)

Among aforementioned objectives, \(\mathcal {F}_1(\cdot )\) and \(\mathcal {F}_2(\cdot )\) control the intra-redundancy in tasks and inter-redundancy between tasks; \(\mathcal {F}_3(\cdot )\) ensures diversity and searches candidates which are more similar to the clustering centres, close to supporters but irreplaceable with each other; Criterion \(\mathcal {F}_4(\cdot )\) pays more attention to the contributions of candidates for preserving useful information. Each criterion conflicts with others and is chosen for different purpose. It is worth noting that though pruning with small \(L_2\) norm is a mainly used criterion for filter pruning [15, 16], ‘smaller-norm-less-important’ has been reconsidered in some literature [29]. For multi-task pruning, searching filters with similar information that can be shared (in multi-network) or replaced (in single-network) are more important for designing criteria.

Filter Sharing

As illustrated in Fig. 2, all filters in V should choose one and only one candidate in the important filter set \(C^E\). If \(f_{j^*}\in C^E\) satisfies

$$\begin{aligned} j^* = \mathop {\arg \min }_{j}\{\delta E(i,j)\}. \end{aligned}$$
(11)

we call \(f_i\) a supporter of candidate \(f_{j^*}\).

The key point of the proposed filter sharing (FS) strategy is to collect filters which share the same candidate, with the same shape of colours in Fig. 2. On the one hand, pruning filters working on the same task (e.g., filters with green in \(V_A\) or filters with blue in \(V_B\)) can help to reduce the parameters of networks and accelerate the inference. On the other hand, merging filters with different tasks (e.g., filters with cyan in \(V_A\) and \(V_B\)) can share information of two tasks. The orange and purple filters will be maintained in the new layers.

Then, we define \(C^E=\{C^E_A,C^E_B,C^E_S\}\) with

$$\begin{aligned} \left\{ \begin{aligned}&C^E_A = \{f_i|S_i \subseteq V_A\}\\&C^E_B = \{f_j|S_j \subseteq V_B\}\\&C^E_S = \{f_k|S_k \cap V_A\ne \emptyset \wedge S_k \cap V_B\ne \emptyset \}\\ \end{aligned} \right. \end{aligned}$$
(12)

where \(C^E_A\), \(C^E_B\) and \(C^E_S\) consist of filters attributed to, respectively, task A, task B and both tasks; \(S_\eta\) is comprised of supporters with the same candidate \(f_\eta\), which is defined by

$$\begin{aligned} S_\eta =\{f_i| \mathop {\arg \min }_{j} \ \delta \hat{E}(i,j)=\eta \}. \end{aligned}$$
(13)

Note that \(S_\eta \ne \emptyset\) because \(S_\eta\) contains at least \(f_\eta\), namely, \(f_\eta\) will support itself.

figure a

Pruning and Merging

Suppose that layer l has \(N_l\) filters. If a pruning rate \(P_l\) is set for layer in network A and B, we would not get \(P_l\times N_l\) filters pruned with \(N^E=(1-P_l)\times N_l\) for each network. Actually, the real sum of pruned filters is \(2\times P_l\times N_l-length(C^E_S)\) according to Algorithm 1.

Base on the aforementioned discussions, we have two strategies for pruning and merging step. Strategy one is to simply restrict the pruning rate P for the whole models and the real sum of reduced filters will be determined adaptively by FS strategy as well as the pruning rates on different tasks. Strategy two is to restrict the pruning rate for each network, under which we will prune additional \(length(C^E_S)\) with norm-based criterion (pruning filters with small \(L_p\) norm) after filter sharing. Then the real pruning rate can be confirmed for each network. These two strategies can be chosen under different situations. Strategy one does not need to decide the specific rates on tasks. However, the real pruning rates cannot be confirmed. In contrast, although the rate on every task should be manually decided when using strategy two, pruning on networks are strictly executed under the preset rates.

MOP Model for Multi-task Pruning

Consequently, the MOP model is established as

$$\begin{aligned} \begin{aligned} \min _{\alpha }&\mathcal {F}(\varvec{\alpha })\\&\mathcal {F}=\{\mathcal {F}_1(\varvec{\alpha }), \mathcal {F}_2(\varvec{\alpha }), \mathcal {F}_3(\varvec{\alpha }), \mathcal {F}_4(\varvec{\alpha })\} \end{aligned} \end{aligned}$$
(14)

In this paper, we shall use MOEA/D proposed in [30] to optimize the many-objective problem in (14). We provide the modified mutating strategy of MOEA/D as shown in Algorithm 2. Instead of randomly changing \(\varvec{\alpha }\), we impose a probabilistic constraint on the mutation of \(\varvec{\alpha }\) in the following way:

First, we remove the filter \(f_k\) from \(C^E_{cur}\) which is nearest to \(C^E_{cur}\):

$$\begin{aligned} \begin{aligned} k = \mathop {\arg \min }_{i}&\delta E(i,j)\\&\mathrm{s.t.} \ i\ne j \end{aligned} \end{aligned}$$
(15)

Then, we add a filter \(f_k\in {C \setminus C^E_{cur}}\) into \(C^E_{cur}\):

$$\begin{aligned} k = \mathop {\arg \max }_{i}\{\min _j\delta E(i,j)\}. \end{aligned}$$
(16)

Since the PF \(P=\{\varvec{\alpha }_1,\ldots ,\varvec{\alpha }_p\}\) obtained by MOP algorithm is not a single optimal solution, we should seek an optimal value for \(\varvec{\alpha }\). For instance, \(\varvec{\alpha ^*}\) can be chosen as follows:

$$\begin{aligned} \begin{aligned} \varvec{\alpha ^*} = \mathop {\arg \min }_{\varvec{\alpha }}&\sum f_i(\varvec{\alpha })\\&\mathrm{s.t.} \ \sum {\alpha _i}=N^E \end{aligned} \end{aligned}$$
(17)

where \(N^E\) is the limit size of \(C^E\).

figure b

How to Update Weights

Suppose \(\delta E(i,j)\) is the difference between the original output results of \(f_i\) and the corresponding results replaced by \(f_j\). We apply an alternative way introduced in [5, 31] to approximate the error function by Taylor series expansion as follows:

$$\begin{aligned} \begin{aligned} \delta E_{l}(i,j)&= E_l(j)-E_l(i)\\&=(\frac{\partial E_l}{\partial \theta _l})^T \delta \theta _l+\frac{1}{2}{\delta \theta _l}^T \mathbf {H}_l \delta \theta _l+ O(\Vert \delta \theta _l\Vert ^3) \end{aligned} \end{aligned}$$
(18)

where \(l=1,\ldots ,L\) is the number of layers; \(\delta \theta _l = \theta _{l,j}-\theta _{l,i}\) denotes the perturbation when \(f_i\) with parameter \(\theta _{l,i}\) changes to \(f_j\) with parameter \(\theta _{l,j}\); \(\mathbf {H}_l=\partial ^2 E_l/\partial \theta _l^2\) is the Hessian matrix which contains the whole second-order derivatives. The first term in (18) is vanished during training and higher-order terms \(O(\Vert \delta \theta _l\Vert ^3)\) can be regarded as 0 [5]. Hence, \(\delta E_l^A(i,j)\) for task A can be redefined by

$$\begin{aligned} \delta E_l^A(i,j) = \frac{1}{2}(\delta \theta _l^A)^T \cdot \mathbf {H}^A_l \cdot \delta \theta _l^A \end{aligned}$$
(19)

where \(\mathbf {H}^A_l\) is calculated by

$$\begin{aligned} \mathbf {H}^A_l = \frac{1}{n} \sum {x_l^A \cdot (x_l^A)^T } \end{aligned}$$
(20)

with \(x_l^A\) the input of layer l for task A.

Then, in order to merge filters with as less losses as possible, \(f_\eta\) can be updated by optimizing the following error function:

$$\begin{aligned} \begin{aligned} \min _{\delta \theta (1),\ldots ,\delta \theta (n)}&\sum _{f_i\in S_\eta }{\delta E(i,\eta )} \\ \mathrm{s.t.}&\ \delta \theta (1)+\theta (1)= \ldots =\delta \theta (n)+\theta (n) \end{aligned} \end{aligned}$$
(21)

where n is the number of filters in \(S_\eta\). By applying the method of Lagrange multipliers, the optimal result \(\theta (\eta )\) of \(f_\eta\) is obtained via the following formula:

$$\begin{aligned} \begin{aligned} \theta (\eta ) =&\delta \theta (n)+\theta (n)\\ =&(\mathbf {H}(1)+\ldots +\mathbf {H}(n))^{-1} \cdot (\mathbf {H}(1)(\theta (1)-\theta (n))+\\&\ldots +\mathbf {H}(n-1)(\theta (n-1)-\theta (n)))+\theta (n) \end{aligned} \end{aligned}$$
(22)

with \(\mathbf {H}(n)\) denoting the Hessian matrix of \(f_n\). Particularly, if all the filters have the same input, then \(\theta (\eta )\) can be computed by

$$\begin{aligned} \theta (\eta ) = \frac{1}{n}\sum _{f_i\in S_\eta }{\theta (i)} \end{aligned}$$
(23)

It should be mentioned that computing \(\mathbf {H}\) is still a tough work in some databases. Hence, we can calculate the distance instead (e.g., Euclidean distance) in the experiments:

$$\begin{aligned} \delta E(i,j) =dist(i,j) = \sum ^{N_{l-1}}\sum ^K\sum ^K \Vert \theta _i-\theta _j\Vert ^2 \end{aligned}$$
(24)

where \(N_{l-1}\) is the input channels of layer l; \(K\times K\) denotes the kernel size. When using Euclidean distance in (7), the selection under criterion \(\mathcal {F}_3(\cdot )\) is similar to judging filters by geometric median in [7].

figure c

Multi-task Filter Index Sharing Framework

Fig. 3
figure 3

The multi-task indexing steps

Full size image

We are now in a position to propose the MFIS framework. MFIS can be classified into the following two categories according to the number of tasks: single-task pruning FIS (SP-FIS) and multi-task pruning FIS (MP-FIS).

For SP-FIS, we only need to establish one network and prune the redundant filters by setting weights with 0. The MOP of SP-FIS is established according to (14) as follows,

$$\begin{aligned} \begin{aligned} \min _{\alpha }&\mathcal {F}(\varvec{\alpha })\\&\mathcal {F}=\{\mathcal {F}_1(\varvec{\alpha }), \mathcal {F}_3(\varvec{\alpha }), \mathcal {F}_4(\varvec{\alpha })\} \end{aligned} \end{aligned}$$
(25)

For MP-FIS, distinguishing from [17] and [11], index sharing is proposed for multiple networks to keep network structure where sharing index will be preserved along with an index matrix I, shown in Fig. 3. To be specific, we record the indices of each single filter pointing to pruning, merging or remaining. Then, new networks can be easily recovered and trained according to the index matrix. The importance of keeping network structure has been proved in Section 4.4.1. Finally, the MFIS framework is described in Algorithm 3. It should be noticed that if a filter \(f_i\in C^E_S\) is pruned in step 11 when using strategy two, it will be removed from \(C^E_S\) along with its shared filter in the other model.

In order to show the differences between MFIS framework and other methods more clearly, we compare with model compression methods, shown in Table 1.

Extending MFIS to Many-task Cases

MFIS can be easily extended to an M-task (\(M\ge 3\)) case which is illustrated in Fig. 4. Each network \(M_k\) can accept information from the other networks because FIS can determine each filter to be pruned, merged or remained for networks. In Fig. 4, original networks are presented with different color blocks in the bottom line. In the top block line, the grey blocks describe the unimportant filters selected by our algorithm and the color ones are the remained or merged filters for three tasks. Each filter may work for one to three tasks after pruning and merging.

Experiments

In this section, we shall examine our MFIS framework on single-task pruning and multi-task pruning on various benchmarks with different networks. We will further explore the influence of keeping network structure and the balance on different tasks with MFIS. Finally, the MFIS will be extended to more task case.

Table 1 The difference between MFIS and other methods
Full size table
Fig. 4
figure 4

The many-task case of MFIS

Full size image

Experimental Settings

Databases

In our experiments, the following databases are considered: MNIST database [32] is a small digital handwriting data set, which contains 60,000 images. CIFAR-10 and CIFAR-100 [33] contain 60,000 colour images in each database, in which 50,000 training images and 10,000 testing images are included. SVHN [34] is a real-world image dataset, which is obtained from house numbers in Google Street View images, with 73,257 digits for training and 26,032 digits for testing. ILSVRC-2012 [35] (ImageNet) is a large-scale dataset containing 1.28 million training images and 50,000 validation images of 1,000 classes.

Table 2 Comparison of single-task pruning of ResNet on CIFAR-10
Full size table
Table 3 Comparison of pruning ResNet-50 on ILSVRC-2012
Full size table
Table 4 Comparison of multi-task pruning of VGG-net on CIFAR-10 and CIFAR-100
Full size table

Training Settings

Two types of network structure are used in the following experiments: VGG-net [37] and ResNet [38]. VGG used here is a slight modified version in [39] without Dropout [40], which contains only 2 FC layers. Compared with VGG-16 [37], the modified VGG has much fewer parameters in the fully connected layers. Hence, it could be more challenging to do compression work on it. We train the pre-trained networks with optimizer (stochastic gradient descent algorithm, SGD), initial learning rate (0.1) for baseline, momentum (0.9), batch size (128) and weight decay (0.0005). For CIFAR, the learning rate is divided by \(5\times\) at epoch 60, 120 and 160 and the network is trained for 200 epochs in total. For ImageNet, the learning rate is divided by \(10\times\) after every 30 epochs and the total epoch is 100. The training schedule of learning rate is set following the work in [7].

Pruning Settings

For pruning the scratch model, we utilize the regular training schedule without additional fine-tuning. For pruning, the pre-trained model with fine-tuning, the learning rate is reduced to one-tenth of the original learning rate [7]. For MOEA/D, we set the scale of the optimization iteration to be 200 for ResNet-20, 32, 56, 110 and 1000 for VGG-net and ResNet-50. The probabilities of mating and mutating are set to be 0.5 and 0.7.

Performance Metric

To measure the network compression and testing performance, the following measurements are applied:

Acc. The accuracy of testing on database. Acc. \(\downarrow\) (%) is the accuracy drop between pruned and the baseline model. The smaller, the better. For CIFAR-10, top-1 accuracy is provided, while for ILSVRC-2012, both top-1 and top-5 accuracies are reported.

Params. In this paper, Params. \(\downarrow\) (%) indicates the percentage of reduced parameters in networks. Bigger Params. \(\downarrow\) (%) means larger compression ratio.

FLOPs The overall floating point operations (FLOPs) denote the computation cost of networks. We use FLOPs \(\downarrow\) (%) to describe the percentage of reduced FLOPs.

Table 5 Comparison of multi-task pruning of ResNet on CIFAR-10 and CIFAR-100
Full size table

Single-task Pruning

For CIFAR-10 dataset, we test our SP-FIS on ResNet with depth 20, 32, 56, 110 and show the results in Table 2. We compare SP-FIS with existing single-task acceleration algorithms, namely, PFEC [16], CP [13], MIL [36], SFP [15], NISP [10], FPGM [7] and HRank [8]. For CIFAR, we run each setting three times and report the “mean ± std”. In “Fine-tune?” column, “✓” and “✗” denote whether to use the pre-trained model as initialization or not, respectively. The experiment results validate the effectiveness of our method. Specifically, the best result of FPGM (FPGM-mix) on ResNet-110 accelerates the random initialized with an improvement of 0.17% on accuracy, but our SP-FIS achieves the results of 0.33% improvement with the same speedup ratio. Likewise, on ResNet-56, FPGM achieves the best result of 0.66% accuracy drop with FPGM-only, while our SP-FIS gains better result of only 0.32% accuracy drop. In comparison to SFP, our SP-FIS shows 0.49% accuracy drop which is better than 0.55% for SFP on ResNet-32, while the acceleration rate of 53.2% is also much better than 41.5% for SFP. To make the comparison more clearly, we also provide a result of 41.5% acceleration rate for SP-FIS, which gives an accuracy drop of only 0.18%. For pre-trained models, SP-FIS also achieve comparable results compared to other state-of-the-art methods. SP-FIS gives superior results because our method selects proper candidates for both pre-trained and randomly initialized networks by taking into account the three objectives mentioned earlier.

The proposed framework is also tested on ILSVRC-2012 with pre-trained ResNet-50. Following [7], we do not prune the projection shortcuts for simplification. The results are described in Table 3 and compared with six state-of-the-art methods.

Multi-task Pruning

In the experiments of MP-FIS, we first perform MP-FIS on VGG-net with pruning rate P on the whole models. Because few methods prune multi-task networks simultaneously, the following two methods are utilized for the comparison with our MP-FIS, namely, MTZ [17], a multi-task model compression method but without pruning, and PFEC [16], a pruning method for single task. All models use the same pre-trained networks. All models use the same pre-trained networks.

The experiment results are described in Table 4, where “ / ” denotes no result is provided. Considering that PFEC is a single-task method, we perform it on CIFAR-10 and CIFAR-100 separately with two types of compression ratio strategies: 49.90% parameters reduced on CIFAR-10 and 49.74% on CIFAR-100; 71.19% parameters reduced on CIFAR-10 and 27.41% on CIFAR-100. Note that MTZ does not accelerate the networks (no result on “FLOPs \(\downarrow\) (%)” column) because of lack of pruning step. In “Params. \(\downarrow\) (%)” column, the percentage of reduced parameters is given in three conditions: whole networks, network on CIFAR-10 and network on CIFAR-100, due to the existence of shared parameters in MTZ and MP-FIS. For MP-FIS, MP-FIS “with H” and “w/o H” describe computing \(\delta E\) by (19) or computing Euclidean distance instead. Obviously, it can be seen that the proposed MP-FIS performs much better in comparison to other methods.

The advantages of MP-FIS can be attributed to the fact that it allows access to relevant information in different tasks and limits redundant information in the same task, while traditional pruning methods only focus on one single task and do not take into account the facilitation of multi-task for learning. Although MTZ can deal with multiple tasks, it just simply forces one-to-one merging of filters between different tasks without pruning, which may lead to adverse outcome for tasks, especially when tasks are not strongly correlated, such as CIFAR-10 and CIFAR-100.

Then, we test our method with pruning rate P on each network of ResNet with depth 32, 56, and 110. The additional \(length \ (C^E_S)\) filters are pruned with norm-based criterion. As shown in shown in Table 5, we record the best accuracy results for two tasks, respectively, which means that filters in \(C^E_S\) are not forced to be shared for testing in this experiment. Likewise, as a single-task pruning method, FPGM is performed on CIFAR-10 and CIFAR-100 separately for comparison. The result also validates the effectiveness of our method.

Fig. 5
figure 5

The tendency TE of sharing filters from different tasks in the second FC layer with and without keeping layer structure

Full size image
Fig. 6
figure 6

The pruning rate of networks on different tasks in the last 6 layer

Full size image

More Explorations

Influence of Keeping Network Structure

For the purpose of proving the necessity of keeping network structure, we define TE to scale the tendency of sharing information from different tasks in the next layer as follows:

$$\begin{aligned} TE = \frac{1-(\delta E^A(A,B)+\delta E^B(B,A))}{1-(\delta E^A(A,A)+\delta E^B(B,B))} \end{aligned}$$
(26)

where \(\delta E^A(A,B)\) represents the average loss on model A of replacing filters in model A with those in model B. For pre-trained models, Lenet-300-100 network [32], which is a fully connected network with 2 FC hidden layers will be trained on MNIST database. We change the limit size in the first FC layer and then observe the variation of TE in the second FC layer. The results are shown in Fig. 5, from which we can observe that, without keeping network structure, the difference between filters becomes much bigger in two models. Such a phenomenon is mainly due to the fact that the filter similarity between two models has been influenced after breaking layer structure in the pruning step.

Balance on Tasks

With the hope of further showing that MFIS is able to prune the most appropriate filters between networks, we depict, in Fig. 6, the pruning rates of CIFAR-10 and CIFAR-100 in the last 6 layers of VGG-net. It is seen that the average pruning rate in CIFAR-100 is far smaller than that in CIFAR-10, as for VGG-net, network of CIFAR-10 has much more redundant filters compared with CIFAR-100. This has also been proved in Table 4 that PFEC achieves similar accuracies with 71.19% or 49.90% parameters reduced on CIFAR-10, while the performance is much worse with 49.74% or 27.41% parameters reduced on CIFAR-100.

Table 6 Pruning ResNet on more than two tasks
Full size table

Extending MFIS to Many-task Cases

We extend MFIS to a 3-task (CIFAR-10, CIFAR-100 and SVHN) case and give the results in Table 6. We can see that the results of the MP-FIS (\(M=3\)) are further improved compared to MP-FIS (\(M=2\)).

Conclusion

In this paper, a multi-task pruning algorithm MFIS has been provided by virtue of the filter index sharing approach. A filter sharing strategy has been proposed capable of automatically sharing filters of both inner networks (pruning) and external networks (merging). Through FIS, the proposed algorithm can determine the most suitable operation for filters. Three criteria have been developed to select important filters of multi-task networks. The proposed MFIS can deal with both multi-task pruning and single-network pruning by converting the optimization problem into MOP. In experiment parts, our proposed framework has shown much better performance in comparison to certain state-of-the-art methods via tests based on several benchmarks. It is has also been proved that MFIS works well on many-task case. However, there are still certain limitations of the developed MFIS. For instance, the criteria proposed in this paper for MFIS are only applicable for image classification task. In the future, some other type of tasks (e.g., semantic segmentation) should be considered in applications. One of the potential research topics might be taking more sorts of criteria into consideration and applying the framework into real-world applications [2, 3, 41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]