Quantum Control of Coherent π-Electron Dynamics in Aromatic Ring Molecules

1 Introduction

Recent progress in laser science and technology has facilitated the coherent control of ultrafast charge migration dynamics in molecular systems [1–21]. Controlled charge migration can generate unidirectional currents and current-induced magnetic fields, which can be used as a guiding principle for the next-generation ultrafast optoelectronic devices [22, 23]. Laser control of π-electron rotations in aromatic ring molecules is a typical example. Pioneering studies on the generation of coherent π-electron rotations in high-symmetry ring molecules such as Mg porphyrin having degenerate excited states have been reported by the Manz group [24–26]. π-Electron rotations were induced by degenerate electronic excited states, which were coherently created by circularly polarized ultraviolet (UV) lasers. The generation mechanism of the photon angular momentum involves the photon transfer from the circularly polarized UV lasers to the π-electrons, thereby the left- or right-handed circular polarization of the applied laser defines the rotational direction of the angular momentum [27]. In contrast in ring molecules with low-symmetry π-electrons cannot be rotated by using the circularly polarized lasers, due to the absence of electronic excited states degenerate, that would receive the photon angular momentum. Thus, it was commonly understood that coherent π-electron rotations could not be generated in low-symmetry aromatic ring molecules. However, Kanno et al. [28–31] have invalidated this long-established understanding by demonstrating that π-electrons in oriented chiral aromatic ring molecules can be rotated by the coherent excitation of a pair of quasi-degenerate π-electronic excited states using a linearly polarized UV/vis laser pulse with a properly designed photon polarization direction [28, 29]; the polarization direction of the pulse determines the initial direction of the π-electron rotation, whether right- or left-handed one. The duration of the unidirectional rotation is inversely proportional to the energy difference between the two quasi-degenerate excited states, and inverse rotation begins after the duration because the coherent state is not a nonstationary state rather than an eigenstate. Pump and dump laser pulses with their properly designed polarization directions for these lasers are applied to eliminate the reverse rotation. The number of unidirectional rotations during the duration can be estimated from the energy difference between the quasi-degenerate excited and ground states. This only applies to the ideal case in which any dephasing processes disturbing the electronic coherence are omitted. It is expected that unidirectional ring currents produce much stronger magnetic fields than traditional static magnetic fields [32, 33].

The concept of the conventional ring current has already been established previously and plays an important role in interpreting the magnetic properties and aromaticity of conjugated molecular systems [34, 35]. The molecules investigated based on the ring current are in the ground state, and the current densities for evaluation of the ring current are calculated using the first-order electronic wave function in the time-independent magnetic field and in a permanent magnetic dipole. Such a conventional ring current should be called an incoherent current.

In this article, we present the most recent results of our theoretical studies on the quantum control of coherent π˗electron rotations in low-symmetry aromatic ring molecules. Low-symmetry aromatic ring molecules are not rare, but rather common: high-symmetry aromatic molecules often become low-symmetry ones by substitution of a functional group, or under environment conditions. In the next section, the fundamental theory for the quantitative analysis of coherent π-electrons in a low-symmetry aromatic ring molecule is introduced. Here, the time-dependent coherent angular momentum, ring current, and ring current-induced magnetic field are analytically derived in a closed form in the quantum chemical MO theory. Time-evolutions of these quantities are derived by the density matrix method [36–39]. The temporal behavior of coherence is determined by the off-diagonal element of density matrix. Then, the Markov approximation is ultilized for considering the dephasing effects on the conherent angular momenta and ring currents. The magnitudes of the electronic angular momenta and ring currents are expressed as the summation of the expectation values of the corresponding one-electron operators in the aromatic rings. The bond current between the nearest neighbor carbon atoms, C_i and C_j, is defined as an electric current flowing through a half plane perpendicular to the C_i$-$C_j bond. The coherent bond current in an aromatic ring is defined as the average of all bond currents. The application of this theory to a nonplanar chiral aromatic molecule, (P)-2,2’-biphenol, is briefly described. (P)-2,2’-biphenol has four patterns of coherent π-electron rotations along with the two phenol rings because of its nonplanar geometrical structure [39, 40]. A sequence of the four rotational patterns can be controlled through a coherent excitation of two electronic states with two requirements: the symmetry of the two electronic states, and their relative phase. Quantum switching of coherent π-electron rotations is proposed [40]. In Section 3, the key points are summarized for the application of the quantum optimal control method for controlling coherent ring currents in polycyclic aromatic hydrocarbons (PAHs). These molecules exhibit several localization patterns of coherent π-electron rotations. Therefore, how to set up the target state for a desired localization pattern is crucial [41, 42]. However, we demonstrate that the target state can easily be set up using the Lagrange multiplier method. As examples, two types of current localizations for the simplest PAH, anthracene, are adopted [42]: current localization to the designated benzene ring, and the perimeter ring current. In Section 4, a convenient scenario involving unidirectional π-electron rotations in low-symmetry aromatic ring molecules is described [43]. The basic idea behind unidirectional electron rotations is to degenerate two nondegenerate excited states by utilizing dynamic Stark shifts. A degenerate state induced by dynamic Stark shifts is called a dynamic Stark-induced degenerate electronic state (DSIDES). Two linearly polarized continuous lasers with different frequencies and phases are used to form a DSIDES, where each laser is set to selectively interact with each electronic state through non-resonant excitation. As a result, the unidirectional π-electron rotation is driven by the lasers. This scenario was applied to toluene. The resulting angular momenta can be represented by a pulse train having an angular momentum. Each angular momentum pulse represents the unidirectional π-electrons rotation, which begins with acceleration and ends with deceleration.

2 Coherent π-electron Dynamics in Low-Symmetry Aromatic Ring Molecules

In this section we present the theoretical formalism for the coherent π-electrons in a low-symmetry aromatic ring molecule to derive analytical expressions for the coherent angular momentum, ring current and the current-induced magnetic field within the framework of the quantum chemical MO treatment [39, 40].

2.1 Equations of Motion for Coherent π-Electron Rotations Induced by Ultrashort UV/Vis Lasers

The expectation values of the coherent π−electron angular momentum and the ring current operators in an aromatic molecule are generally expressed as

Here, $\widehat{O}\left(r\right)$ is a single-electron operator for the angular momentum or current. $\Psi \left(t\right)$ is the wave function of the π−electrons in laser field F(t) at time t, n denotes the number of electrons, and ${\mathbf{r}}_i$ express the ith electron coordinates. Since the optically-allowed electronic excited states of the conjugated aromatic rings are of our interest, the electronic wave function can be expanded by the two electronic configurations, i.e., the ground configuration ${\mathbf{\Phi }}_0$, and the singly excited ones ${\mathbf{\Phi }}_{\alpha }$ as

where ${\mathbf{\Phi }}_0$ is defined by a single Slater determinant as ${\Phi }_0({\mathbf{r}}_1,\cdots ,{\mathbf{r}}_n)=\Vert {\varphi }_1\cdots {\varphi }_a\cdots {\varphi }_b\cdots {\varphi }_n\Vert$ with ${\varphi }_n\equiv {\varphi }_n\left({\mathbf{r}}_n\right)$. Here, ${\varphi }_a$ and ${\varphi }_b$ are the occupied orbitals, ${\Phi }_{\alpha }$ is the electronic wave function for a single electron excited configuration $\alpha :a\to a\prime$, i.e., the single electron transition from the occupied molecular orbital (MO) a to the unoccupied MO $a\prime$, when ${\Phi }_{\alpha }({\mathbf{r}}_1,\cdots ,{\mathbf{r}}_n)=\Vert {\varphi }_1\cdots {\varphi }_{a\text{'}}\cdots {\varphi }_b\cdots {\varphi }_n\Vert$.

The coherent and incoherent temporal behaviors of the electrons induced by a laser field $\mathbf{F}\left(t\right)$ can be obtained directly by solving the coupled electronic equations of motion expressed by the density matrix elements ${\rho }_{\alpha \beta }\left(t\right)$ under the initial population conditions ${\rho }_{00}\left(0\right)=1$ and ${\rho }_{\alpha \alpha }\left(0\right)=0$ for $\alpha \ne 0$ and ${\rho }_{\alpha \beta }\left(0\right)=0$ for $\alpha \ne \beta$, that is, there is no electronic coherence at the initial time such that

Here, ${\rho }_{\alpha \beta }\left(t\right)\equiv c_{\alpha }\left(t\right)c_{\beta }^{\ast }\left(t\right)$ is the density matrix element, and $V_{\alpha \gamma }\left(t\right)$ is the coupling matrix element between states α and γ via the molecule-laser interaction $\widehat{V}\left(t\right)=-\mathbf{\mu }\cdot \mathbf{F}\left(t\right)$, where $\mathbf{\mu }$ denotes the transition dipole moment operator, ${\gamma }_{\alpha \beta }\left(=\frac{1}{2}({\gamma }_{\alpha }+{\gamma }_{\beta })+{\gamma }_{\alpha \gamma }^{\left(d\right)}\right)$ are the dephasing constants in the Markov approximation [38, 39] and ${\omega }_{\beta \alpha }$is the frequency difference between the two electronic states α and β. Here, ${\gamma }_{\alpha }\left({\gamma }_{\beta }\right)$ is the non-radiative transition rate constant of the electronic state α(β), and ${\gamma }_{\alpha \beta }^{\left(d\right)}$ are the pure dephasing constants induced by the elastic interaction between the heat bath and molecule of interest.

Because we are interested in the coherent behaviors of dipole-allowed quasi-degenerate π-electronic excited states in the visible or UV region of an aromatic ring molecule, Eq. 1 can be rewritten in terms of singly excited configurations $\left\{{\Phi }_{\kappa }\right\}$ if $\kappa \ne 0$ as

where $O_{\alpha \beta }\left(r\right)=\langle {\Phi }_{\alpha }\left|\widehat{O}\left(r\right)\right|{\Phi }_{\beta }\rangle$.

In Eq. 4, the coherence between singly excited state configurations is considered, and the coherence between the ground state and the excited state is neglected because this coherence is much shorter compared to that between the singly excited state configurations. In this case, the coherence time is proportional to the inverse of the energy gap between the two electronic states.

The coherent π-electron angular momentum is formulated in the quantum chemical MO theory, and the π-orbital ${\varphi }_k$ associated with the optical transition is expanded in terms of a linear combination of atomic orbitals ${\chi }_i$ as

where ${\chi }_i$ denotes the atomic orbital, and $c_{k,i}$ indicates the molecular orbital coefficient.

Equation 4 can be expressed by using the Eq. 5 as

Here, the temporal behavior of the expectation value $\langle \widehat{O}\left(t\right)\rangle$ can be expressed using the off-diagonal density matrix element ${\rho }_{\beta \alpha }\left(t\right)$. The suffixes (a, a’) ((b, b’)) corresponds to the electronic configurations α(β), respectively.

2.2 Coherent π-Electron Angular Momentum

Consider the spatially fixed aromatic ring molecule with N aromatic rings. The electron angular momentum operator is defined as $\widehat{O}\left(\mathbf{r}\right)={\mathbf{l}}_Z={\displaystyle \sum _K{\widehat{O}}_K\left(\mathbf{r}\right)}$ with ${\widehat{O}}_K\left(\mathbf{r}\right)={\mathbf{l}}_{Z,K}=-i\hslash \left(x_K\partial /\partial y_K-y_K\partial /\partial x_K\right){\mathbf{n}}_{\perp ,K}$. Here ${\mathbf{l}}_{Z,K}$is the electronic angular momentum operator of the component perpendicular to ring K. Coordinates $x_K$ and $y_K$ are defined on the aromatic ring K, and ${\mathbf{n}}_{\perp ,K}$ is the unit vector perpendicular to the aromatic ring. The expectation value of Kth angular momentum operator is given in terms of a 2p_z carbon atomic orbitals (AOs) as

where n_e is the total number of electrons in the system.

Note that in Eq. 7 the dependence of the electron angular momentum on the laser intensity is reflected in the imaginary part of the off-diagonal density matrices $\mathrm{Im}{\rho }_{\beta \alpha }\left(t\right)$.

2.3 Coherent π-Electron Ring Current

From Eq. 6, the perpendicular component of the time-dependent electric current flowing through a surface S (SeeFigure 1) is generally defined as

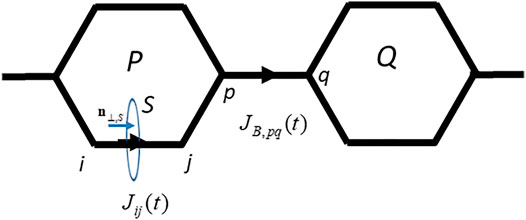
FIGURE 1. The interatomic bond current $J_{ij}\left(t\right)$ and bridge bond current $J_{B,pq}\left(t\right)$ are depicted. Here, i and j indicate the positions of two atomic sites in the bond C_i − C_j, and each carbon atom C_p, or C_q belongs to a different aromatic ring P or Q, which are in neighbors.

Here $\widehat{J}\left(\mathbf{r}\right)=\frac{e\hslash }{2m_{e}i}\left(\overrightarrow{\nabla }-\overleftarrow{\nabla }\right)$ is the current density operator. $\overrightarrow{\nabla }$($\overleftarrow{\nabla }$) is the nabla operating on the atomic orbital on the right-hand side (left-hand side).

Equation 8 can be expressed as

where

with

where ${\mathbf{n}}_{\perp ,S}$ is a unit vector perpendicular to a surface S, which is given as ${\mathbf{n}}_{\perp ,S}=\frac{{\mathbf{r}}_j-{\mathbf{r}}_i}{\left|{\mathbf{r}}_j-{\mathbf{r}}_i\right|}$, and the surface S is set at the center of the carbon bond C_i − C_j. The surface integrations in Eqs. 8, 10b are carried out over the half-plane S (seeFigure 1). Using Slater type AOs for $\left\{{\chi }_i\right\}$, $J_{ij}$ in Eq. 10b can be expressed in analytical form [40].

We introduce the bridge bond current$J_{B,pq}\left(t\right)$ which is a specific case of an interatomic bond current, and is defined as the current bridging two aromatic rings P and Q, passing from the nearest neighbor carbon atom at site p to q. Here, each carbon atom C_p, or C_q belongs to a different aromatic ring P or Q which are in the neighbors. (seeFigure 1).

The bridge bond current is given in terms of the interatomic current, $J_{pq}\left(t\right)$, as

Here, ${\theta }_d$ is the dihedral angle between the two rings P and Q [39].

We now define an averaged ring current along ring K, $J_K\left(t\right)$, which is defined by taking the average of all bond currents as

where $n_K$ is the number of bonds in ring K.

2.4 Application to Nonplanar (P)-2,2’-biphenol

(P)-2,2’-biphenol is one of the typical nonplanar chiral aromatic ring molecules, which has two aromatic rings connected through the C-C bridge bond. For convenience, hereafter, we denote L (R) for the left- (right-) hand side phenol ring of (P)-2,2’-biphenol. Figure 2A exhibits the geometrical structure of (P)-2,2’-biphenol with the transition dipole moments vectors between the ground and excited states. (P)-2,2’-biphenol was assumed to be fixed on a surface by a non-conjugated chemical bond or was oriented in the space by the molecular orientation techniques by laser [44–46]. The laboratory-fixed Y-axis was set parallel to the single chemical bond bridging two phenol molecules, and the rotational axis of the molecule belonging to point group C₂ was set along the laboratory-fixed Z-axis which was parallel to the surface normal. The ground state geometry of (P)-2,2’-biphenol was optimized using the DFT-B3LYP level theory with the 6-31G+(d,p) basis set in the GAUSSIAN09 code [47]. The dihedral angle ${\theta }_d$ between the two phenol rings, was found to be ${108.9}^{\circ }$ based on the density functional theory (DFT) calculations. The calculated geometrical structures are provided in Refs. [39, 40].

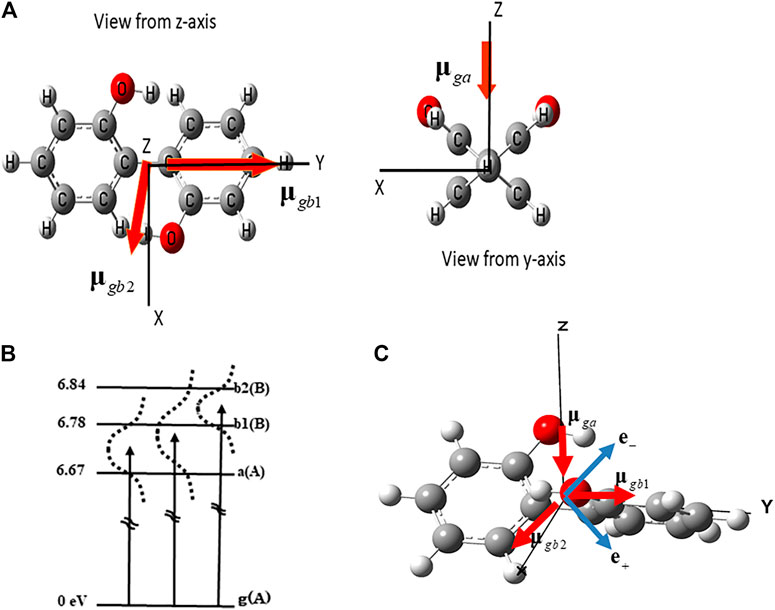
FIGURE 2. (A) Geometrical structure of (P)-2,2’-biphenol belonging to point group C₂ and the transition dipole moments between the ground state (g) and three excited states a, b₁ and b₂. (B) Three electronic excited states and the dipole allowed transitions used to create the coherent electronic states. A and B are the irreducible representations of point group C₂. Dotted lines indicate the laser band widths that cover the superpositions of two electronic excited states (a b₁), (a b₂) and (b₁ b₂) respectively. (C) Linearly polarized unit vector of laser e₊ (e₋) used to generate the in-phase superposition (a+b₁) (out-of-phase superposition (a-b₁)).

To create the coherent angular momenta and ring currents in (P)-2,2’-biphenol, we focused on the three dipole-allowed electronic excited states (a, b₁, and b₂) as shown in Figure 2B. The transition energies from the ground (g) to the a, b₁, and b₂ states, which were calculated under the optimized ground state geometry using the TD-DFT B3LYP level of theory [39, 40] were 6.67, 6.78, and 6.84 eV, respectively.

2.4.1 Generation of Two-state Electronic Coherence Using Linearly Polarized UV Pulses

For a creation of the coherent angular momentum and ring current using linearly polarized laser pulses, it is essential to prepare for an electronic coherence with a fixed relative phase between two electronic states, a and b₁, i.e., in-phase (a + b₁) or out-of-phase (a - b₁). The principle behind the preparation of the electronic coherence (a + b₁) ((a − b₁)) using a linearly polarized laser with polarization unit vector e₊ (e_-) is schematically demonstrated in Figure 2C [39, 40].

In the frame work of the three-excited state model, there are three types of two-electronic coherent states represented as $b_1\pm b_2$, $a\pm b_1$ and $a\pm b_2$, respectively. At the initial time each electronic coherence can be generated by applying a linearly polarized UV laser with a properly selected laser polarized direction. Because of the non-planar geometry of the molecule, the angular momentum is two-dimensional, and the two ring currents flow are on the two different planes, the direction of total angular momentum is dependent on the symmetry of the coherent state created by the laser: The Z-directional angular momentum (ring current) is generated for the created coherent state with the A-irreducible representation of the C₂ point group, while the X-directional angular momentum (ring current) is generated for the coherent state with B.

It is remarkable that even though the third excited state is located between the two excited states in the three-excited states system, the coherent electronic state can still be created if the applied linearly polarized lasers satisfy the following conditions. For example, for the (a ± b₂) electronic coherence, the conditions for the linearly polarized lasers with polarization vectors ${\mathbf{e}}_{\pm }$ are given as

or equivalently,

Thus, if the laser overlaps the electronic states a, b₁, and b₂, the (a + b₂) or (a – b₂) electronic coherent state can be created selectively.

2.4.2 Coherent Angular Momentum Quantum Beats and Bond Currents

Figure 3 exhibits the temporal behaviors of the angular momenta calculated for three types of electronic coherences, (b₁+b₂), (a + b₁) and (a + b₂), each of which is created by a linearly polarized UV laser pulse with a properly selected polarization direction of laser. For the (b₁+b₂) electronic coherence, the total angular momentum parallel to the Z-axis, l_Z, is created together with two ring components l_L = l_R, whereas for both the (a + b₁) and (a + b₂) electronic coherences, the total angular momenta parallel to the X-axis, l_X, are generated with l_L = $-$l_R, with a π-phase shift. Similarly, for out-of-phase electronic coherences, (b₁ − b₂), (a − b₁) and (a − b₂), the angular momentum can be given by the corresponding in-phase electronic coherence with a π-phase shift. The simple sinusoidal temporal behavior originates from the coherence of two electronic states with the oscillation period corresponding to a frequency difference between the two-electronic states. This is referred to as the angular momentum quantum beats, which are similar to the fluorescence quantum beats which originate from the vibronic coherence [48]. We note that π-electrons rotate a few times in a unidirectional manner within a half cycle of the oscillation. This unidirectional π-electron rotation can produce a unidirectional ring current and corresponding current-induced magnetic flux. In principle, this enables the design of ultrafast switching devices which consist of organic aromatic ring molecules.

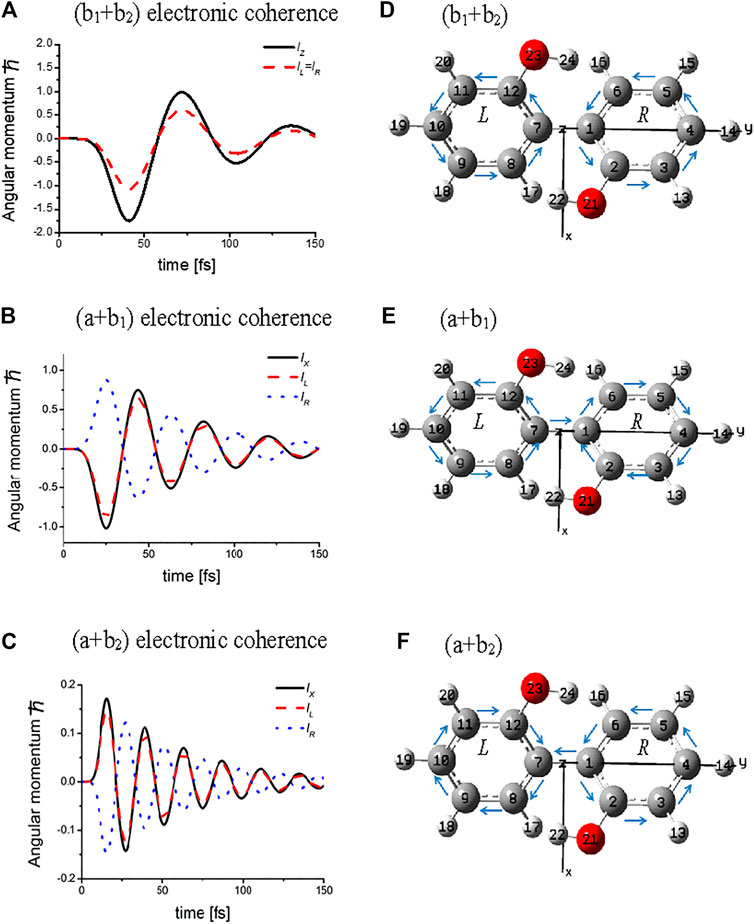
FIGURE 3. Temporal behaviors of the coherent angular momenta, total values l_Z (l_X), and components, l_L (l_R) of L (R) ring for three types of the electronic coherence and the directions of the bond currents at the initial time: upper panel for (b₁ + b₂) electronic coherence excited by laser pulse with amplitude of 0.19 TW/cm²; middle panel for (a + b₁) electronic coherence excited by laser pulse with amplitude of 0.83 TW/cm²; lower panel for (a + b₂) electronic coherence excited by the laser pulse with amplitude of 3.32 TW/cm². The dephasing constants were set as γ_b1b2 = γ_ab1= γ_ab2 = 0.01 eV (∼1/50 fs ⁻¹). The arrows above the C – C bonds indicate the initial directions of the currents. Note that the bridge bond current J_1,7 = 0 for the (b₁ +b₂) electronic coherence, while J_1,7$\ne$0 for the (a +b₁) and (a +b₂) electronic coherences. Reprinted with permission from Ref. [39] Copyright (2013) American Institute of Physics.

The angular momenta $l_Z\left(t\right)$ and $l_X\left(t\right)$, shown in Figure 3, are obtained by the summation of the angular momenta created in the L and R aromatic rings ${\mathbf{l}}_L\left(t\right)$ and ${\mathbf{l}}_R\left(t\right)$ using the following relationship $l_Z\left(t\right)=2{\mathbf{l}}_L\left(t\right)\cdot {\mathbf{e}}_Z\sin \frac{{\theta }_d}{2}$ with ${\mathbf{l}}_L\left(t\right)\cdot {\mathbf{e}}_Z={\mathbf{l}}_R\left(t\right)\cdot {\mathbf{e}}_Z$, and $l_X\left(t\right)=2{\mathbf{l}}_L\left(t\right)\cdot {\mathbf{e}}_X\cos \frac{{\theta }_d}{2}$ (where ${\mathbf{l}}_L\left(t\right)\cdot {\mathbf{e}}_X=-{\mathbf{l}}_R\left(t\right)\cdot {\mathbf{e}}_X$). Table 1 lists the angular momenta of (P)-2,2’-biphenol with the dihedral angle ${\theta }_d={108.9}^{\circ }$where the electronic coherence is maximum at time $t=t\ast$, i.e., when the magnitude of the imaginary part of the density matrix element is maximized ($\mathrm{Im}{\rho }_{\alpha \beta }(t\ast )=-\frac{1}{2}$) and dephasing effects are neglected. This results in $l_X(t\ast )>0$ or $l_X(t\ast )<0$ for the (a + b₁) and (a + b₂) electronic coherences, respectively, and in $l_Z(t\ast )<0$ for the (b₁ + b₂) electronic coherence.

TABLE 1. Angular momenta of the two phenol rings $l_L\equiv {\mathbf{l}}_L(t\ast )\cdot {\mathbf{n}}_L$ and $l_R\equiv {\mathbf{l}}_R(t\ast )\cdot {\mathbf{n}}_R$, and the resulting angular momenta l_X and l_Z at the maximum coherence time t = t^∗1).

The magnitudes of the bond current, $J_{ij}$ calculated at the maximum coherence time, are presented in detail in [40]. The magnitudes of the averaged ring current over the C-C bonds at the maximum coherence time, $\overline{J}$ are on the order of tens of μA, i.e., $\overline{J}=161$, 86.5 and 63.4 μA for (b₁ + b₂), (a + b₁), and (a + b₂) coherences, respectively.

Effects of dephasings on coherent π-electron angular momentum and ring currents were treated in the Markov approximation, and time-independent dephasing constants were used under the assumption of instantaneous interactions between the system and phonon baths. In a system such as condensed phases, the Markov approximation is broken down. Non-Markov response of coherent should be essential. Time evolution of coherent ring currents were calculated in a hierarchical master equation approach beyond the Markov approximation has been treated [49].

2.4.3 Ultrafast Quantum Switching of Angular Momentum

Consider the quantum control of $\pi$-electron rotations for two-dimensional angular momentum switching based on the results shown in Table 1. Here, two-dimensional quantum switching is defined as a sequential pulse of the electronic angular momentum with its constant sign (positive or negative) along the Z- or X-axis. Note that any quantum switching step should be completed before the reverse rotation of the $\pi$-electrons begins, because it may otherwise disturb the signal. Consider a sequential four-step control, which is expressed as $l_Z(-)$→$l_X(+)$→$l_Z(+)$→$l_X(-)$. This indicates the switching of rotational patterns in the order CC → AC → AA → CA, where the symbol C (A) means clockwise (anti-clockwise) direction, and for example, CA rotation means clockwise and anti-clockwise rotations along the phenol rings L and R, respectively. Here, $l_X(+)$ ($l_Z(-)$) means the $\pi$-electron angular momentum along the X- (Z-) axis with a positive (negative) sign, i.e., anti-clockwise (clockwise) rotation of $\pi$-electrons around the corresponding axis.

Figure 4A presents a 3D plot of the angular momentum as it switches based on the sequential four-step control scheme. From Figure 4A, we can see that the $\pi$-electron rotations are successfully manipulated by the pulses depicted in Figure 4B. That is, both the rotational axis parallel to the Z- or X-axis and the rotational directions around those axes, clockwise or anti-clockwise, are manipulated by the sequential four-step process. In Figure 4B, each switching step of control was performed using pump and dump pulses with specific polarization directions and phases. The laser pulse with an amplitude of 1.2 GV/m (= 1.9 × 10¹¹ W/cm²) was used in the second and fourth steps. The dynamic Stark shifts between electronic states a, b₁ and b₂ were on the order of 0.01 eV [39], indicating that the Stark effects could be omitted in Figure 4A.

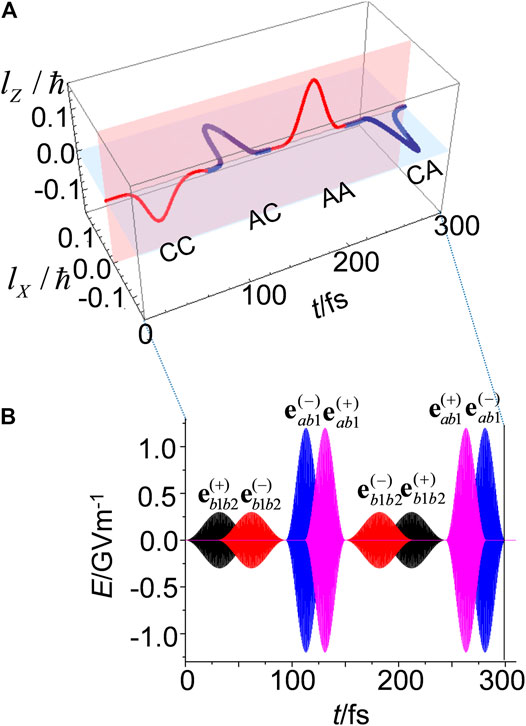
FIGURE 4. (A) Sequential four-step quantum switching of $\pi$-electron rotations in (P)-2,2’-biphenol. (B) The sequential overlapped pump and dump laser pulses. Reprinted with permission from Ref. [40] Copyright (2012) American Chemical Society.

The pulses shown in Figure 4B have two features. The first feature is that the pump (dump) pulse for each step has polarizations, ${\mathbf{e}}_{\alpha \beta }^{(-)}$(${\mathbf{e}}_{\alpha \beta }^{(+)}$) or ${\mathbf{e}}_{\alpha \beta }^{(+)}$ (${\mathbf{e}}_{\alpha \beta }^{(-)}$). Each pulse has an energy width that is large enough to coherently excite two quasi-degenerate electronic excited states, as shown in Figure 2. The second feature is that the pump and dump laser pulses partially overlap. In the creation of the CC rotation, for example, the electric field of the pump pulse was ${\mathit{E}}_{b1b2}^{(+)}\left(t\right)={\mathit{e}}_{b1b2}^{(+)}{E}_{b1b2}^0{\sin }^2(\pi t/T_{b1b2})\sin \left({\omega }_{c,b1b2}t\right)$, while the electric field of the dump pulse was ${\mathit{E}}_{b1b2}^{(-)}\left(t\right)={\mathit{e}}_{b1b2}^{(-)}{E}_{b1b2}^0{\sin }^2(\pi (t-t_{b1b2}^{pd})/T_{b1b2})\sin ({\omega }_{c,b1b2}t+\pi /2)$. Here, $T_{b1b2}$ (= 60.9 fs) indicates the oscillation period between b₁ and b₂ states, $E_{b1b2}^0$ is the amplitude of the laser pulse, ${\omega }_{c,b1b2}$ is the central frequency between the two excited states b₁ and b₂; and $t_{b1b2}^{pd}$ (the time interval between the pump and dump laser pulses) was set to $T_{b1b2}/2$ (Supporting information in Ref. [39]). The angle between the two polarization vectors, ${\mathbf{e}}_{b1b2}^{(+)}$ and ${\mathbf{e}}_{b1b2}^{(-)}$, was 113.5°.

With respect to ultrafast quantum switching, it is crucial to create the overlap of the pump and dump pulses, where the resulting electric field rotates as an elliptically polarized electric field in the overlapped time domain, and the dump laser pulse reverse the rotation that occurs during this region. As a result, the angular momentum of the $\pi$-electrons is nullified.

2.4.4 Coherent Ring Current-Induced Magnetic Field

There have been interesting reports on the evaluation of the magnetic fields of atoms and oriented heteronuclear diatomic molecules, AlCl and BeO [32, 50, 51]. Strong and unidirectional magnetic fields are generated from the degenerate electronic states of these atoms and molecules excited by circularly polarized intense laser pulses. We estimated the magnetic fields (magnetic field flux density) generated by the coherent ring currents of (P)-2,2’-biphenol. The results may provide fundamental information for designing ultrafast switching devices controlled by current-induced magnetic fields as well as coherent ring currents [52–54].

As an example, consider the magnetic field induced by the ring current for the (b₁ + b₂) electronic coherence. In Figure 5, $B_K(t\ast ,h)$ represents the current-induced magnetic field along the central axis perpendicular to ring K (L or R) as a function of the height h above the Z-axis at $t=t\ast$ under the maximum coherence condition (when $\mathrm{Im}{\rho }_{b_1{b}_2}(t\ast )=-1/2$). An expression for the magnetic field $B_K(t\ast ,h)$ was derived by taking into account the interatomic bond currents with the 2p_z Slater AOs [40]. Note that $B_L(t\ast ,h)=B_R(t\ast ,h)$ for the (b₁ + b₂) electronic coherence (Table 1). It is interesting to compare the behaviors of $B_K(t\ast ,h)$ with those calculated using

which was derived using a simple ring loop (SRL) model. Here, ${\mu }_0=4\pi \cdot {10}^{-7}\left[{\text{W}}_b/\left(\text{A}\cdot \text{m}\right)\right]$ is the magnetic constant, r (= r_ij) is the ring radius, and $\eta \left(={\sin }^{-1}\left(r/\sqrt{r^2+h^2}\right)\right)$ is defined as the angle between the Z-axis and a straight line depicted from the point on ring K that crosses the Z-axis. $B_K(t,0)$ at $\eta =\pi /2$ is the magnetic field measured at the center of ring K. The magnitude of $B_K(t\ast ,0)$ induced by $J_K(t\ast )$ = 100 μA is 448 mT at the center of the ring K with r = 0.14 nm. It can be found from Figure 5 that the magnitudes of $B_K^{SRL}(t\ast ,h)$ are overestimated near the aromatic ring plane $0\le h<1$Å, while the magnitudes are reasonable for $h>1$ Å, although slightly different results can be observed between the two magnetic fields for large values of h. At the center of the aromatic ring, $B_K(t\ast ,h=0)=0.66B_K^{SRL}(t\ast ,h=0)$. This can be understood from the result that the π-electron current density is densely distributed over the aromatic ring. A subtle difference between $B_K^{SRL}(t\ast ,h)$and $B_K(t\ast ,h)$ is observed for large h, although both magnetic fields $B_K^{SRL}(t\ast ,h\to \infty )=0$ and $B_K(t\ast ,h\to \infty )=0$ approach zero. This deviation originates from the approximation that the aromatic ring is not a considered to be a perfect ring.

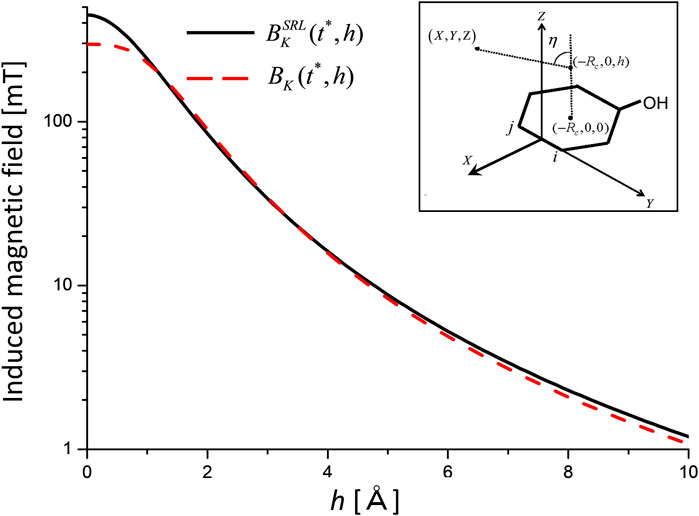
FIGURE 5. Induced magnetic fields for the (b₁ +b₂) electronic coherence as a function of height h measured from the center of aromatic ring K at the maximum coherence time $t=t\ast$. $B_K^{SRL}(t\ast ,h)$ and $B_K(t\ast ,h)$ represent the induced magnetic field calculated by a simple ring loop model, and the field calculated by the expression that explicitly takes into account the coherent ring currents, respectively. The inset panel defines the coordinate system for height h and angle η. R_c denotes the center of the phenol ring.

It is necessary to check whether the value of $B_K(t,0)$ is larger than the one corresponding to the magnetic field B_Laser induced by the applied laser field F when the induced magnetic fields are created during an ultrasfast laser pulse excitation at the early time regime. The magnitude of magnetic field B_Laser can be estimated from a simple formula |B_Laser | = |F|/c with c = 3.0 × 10⁸ ms⁻¹. The calculated magnitude of magnetic field B_Laser with |F| = 1.0 GV/m is approximately 7.4$B_K(t\ast ,h)$, which is on the same order as the field induced by the ring current J = 100 μA. This implies that we need a careful examination to observe the current-induced magnetic flux, or to use the electro-magnetic device as a switching control tool.

Thus far, we have taken into account the ring current-induced magnetic fields of the low-symmetry aromatic ring molecule (P)-2,2’-biphenol, in which nondegenerate two electronic excited states are coherently excited by the linearly polarized UV lasers. Here we briefly discuss the ring current-induced magnetic field for the degenerate electronic excited states of an aromatic molecule induced by the intense circularly polarized UV laser pulse. Yuan and Bandrauk [2, 33] have numerically demonstrated that the circularly polarized ultrashort pulses are generated from the molecular high-order harmonic generation using the intense linearly and circularly polarized laser pulses. This indicates a possibility for the ultrashort circularly polarized UV laser pulses to create the ring current-induced magnetic fields in high symmetric aromatic ring molecules. We can estimate the magnitude of the ring current-induced magnetic field of benzene within the SRL model using Eq. 15. Here, $J\left(t\right)$ is the electric ring current of the degenerated electronic state. The electronic spectrum of benzene is characterized by the dipole-allowed transition from the ground state to the third singlet electronic excited state (¹E_1u). For an equal population between the two states at $t=t\ast$, $B^{SRL}(t\ast ,0)=874\text{ mT}$ is obtained using the maximum value of the coherent ring current $J(t\ast )=195\text{ μA}$ evaluated under the π-electron approximation [40, 55]. For comparison, we obtained $B_K^{SRL}(t\ast ,0)=874\text{ mT}$ and $B_K(t\ast ,0)=579\text{ mT}$when $J(t\ast )=195\text{ μA}$for (P)-2,2’-biphenol. Note that the same magnitudes of the induced magnetic field $B_K^{SRL}(t\ast ,0)$ for (P)-2,2’-biphenol and $B^{SRL}(t\ast ,0)=874\text{ mT}$ for benzene were obtained in the SRL model because the two parameters in the SRL model, the radius of the ring r, and the ring current $J(t\ast )$ have the same values for both types of ring molecules. The same tendency in the magnitudes between $B_K^{SRL}(t\ast ,0)$ and $B_K(t\ast ,0)$ is also observed for benzene.

3 Current Localization in Polycyclic Aromatic Hydrocarbons

In this section we consider a localization of coherent ring current in polyatomic aromatic hydrocarbons (PAH) [41, 42]. There exist various current localization patterns in PAH simply because of their geometrical structures consisting of many benzene units. Quantum optimal control method is a general and reliable one to choose a desired current localization pattern from the various patterns using control lasers. The quantum control method has successfully been applied to manipulation of molecules such as coherent control of chemical reactions [56, 57]. After a brief introduction of quantum optimal control method [41, 42, 58], we demonstrate how the target state is set up for the designated ring current using the Lagrange multiplier method. Here, the π-electron ring current is expressed in terms of the interatomic bond currents between two adjoining C–C atoms. At final, the target states are derived for the two types of current localization: the localized ring current, which indicates that the ring current is localized to the designated aromatic ring in linear PAH, and the perimeter ring current in linear PAH [41, 42].

3.1 Quantum Optimal Control Approach

The objective functional to be maximized, is defined as [59–61].

where $H_0$ is a Hamiltonian in absence of field, and $\Psi \left(t\right)$ is the time-dependent wave function in the electric field $\mathbf{F}\left(t\right)$. Here, the target operator ${\widehat{O}}_T$ is expressed as ${\widehat{O}}_T=|{\Psi }_T><{\Psi }_T|$, where ${\Psi }_T$ is the target state wave function at the final time T, defined as ${\Psi }_T={\displaystyle \sum _a{c}_a\left(T\right){\Phi }_a}$, and is equal to $\Psi \left(T\right)$ under the optimal condition, ${\widehat{O}}_T=|{\displaystyle \sum _a{c}_a\left(T\right){\Phi }_a}\rangle \langle {\displaystyle \sum _b{c}_b\left(T\right){\Phi }_b}|$. The penalty factor ${\alpha }_0$ is introduced to suppress the magnitude of the electric field $\mathbf{F}\left(t\right)$. $\xi \left(t\right)$is the time-dependent Lagrange multiplier. The third term in Eq. 16 is added to decouple the boundary conditions of the equations for $\Psi \left(t\right)$ and $\xi \left(t\right)$ as indicated in Eq. 17. Taking the variational condition $\delta J\left[\mathbf{F}\right]=0$, the following coupled equations are obtained,

where

Here, $\Psi \left(t\right)$ satisfies the initial condition $\Psi \left(0\right)={\Phi }_0$, and $\xi \left(T\right)$ satisfies the condition, $\xi \left(T\right)={\widehat{O}}_T\Psi \left(T\right)$ at final time T. Note that by solving Eq. 17, we obtain the optimal solution $\Psi \left(T\right)$, which is equal to ${\Psi }_T$.

3.2 Setup of Target Operators

Consider the ring current localization to a designated ring $\chi$ in a PAH, as shown in Figure 6. From Eqs. 10a, 12, the ring current on ring κ at the target time T is expressed as

with $c_i\equiv c_i\left(T\right)$, and

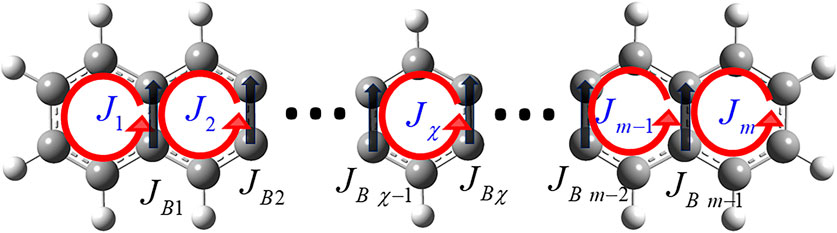
FIGURE 6. π-Electron ring currents $J_l$ and bridge bond currents $J_{B{l}^{\prime }}$ ($1\le l\le m,1\le l^{\prime }\le m-1$) in a linear planar polycyclic aromatic hydrocarbon (PAH). $J_{\chi }$ refers to the π-electron ring current localized on aromatic ring $\chi$.

Here, n is the number of electronic excited states. Hereafter, we write $c_{\alpha }\left(T\right)$ as $c_{\alpha }$ for simplicity.

The target state ${\Psi }_T={\displaystyle \sum _{\alpha }{c}_{\alpha }{\Phi }_{\alpha }}$ can be determined by applying the Lagrange multiplier method to the ring currents at the target time T in Eq. 18a, which provides the coupled equations in terms of the configuration interaction coefficients with {$\mathrm{Re}{c}_{\alpha }$,$\mathrm{Im}{c}_{\alpha }$}. The target operator is given as ${\widehat{O}}_T=|{\Psi }_T><{\Psi }_T|$.

The coupled equations for the ring current localization to aromatic ring $\chi$ can be expressed as

and

A brief derivation of Eq. 19 is summarized in Appendix A.

The coefficients $\left\{\mathrm{Re}{c}_{\alpha },\mathrm{Im}{c}_{\alpha }\right\}$with ${\lambda }_l$ included are numerically determined by applying the Newton-Raphson method to the coupled equations in Eq. 19. The target operator for the localization is obtained as ${\widehat{O}}_T=|{\displaystyle {\sum }_{\alpha }{c}_{\alpha }{\Phi }_{\alpha }}\rangle \langle {\displaystyle {\sum }_{\beta }{c}_{\beta }{\Phi }_{\beta }}|$.

Now consider the bridge bond currents $J_{B{l}^{\prime }}$ shown in Figure 6, and the perimeter ring current of a PAH with m aromatic rings, $J_P\equiv \frac{1}{m}{\displaystyle \sum _{l=1}^m{J}_l}$, which is defined as the average of the π-electron ring currents at each aromatic ring site. For the perimeter ring current, the bridge bond currents $J_{Bl\text{'}}$($1\le l^{\prime }\le m-1$) flowing among the nearest neighbor aromatic rings, should be zero at the target time. The target operators for the bridge bond currents, $J_{Bl\text{'}}$($1\le l^{\prime }\le m-1$), and perimeter ring current, $J_P$, can be derived from Eq. 19 by replacing $J_{\kappa ,\beta \alpha }$ with $J_{Bl\text{'},\beta \alpha }$ and $J_{P,\beta \alpha }$, respectively, because $J_{Bl\text{'}}$ and $J_P$ can be written in terms of $\left\{\mathrm{Re}{c}_{\alpha },\mathrm{Im}{c}_{\alpha }\right\}$ as

and

respectively.

Similar to Eq. 19, the coupled equations for the perimeter ring current are derived in Appendix B.

3.3 Application of Current Localization Control to Anthracene

We applied the quantum optimal control (QOC) method described in the preceding section to anthracene, one of the smallest PAHs [42]. Anthracene (D_2h) was assumed to be fixed on a surface (the XY plane), or oriented spatially by lasers The molecular geometry was optimized in the MP2/6-311+g(d,p) level theory using the GAUSSIAN09 code [47]. As demonstrated in Figure 7A, anthracene consists of three aromatic rings, which are called L-, M-, and R- rings respectively.

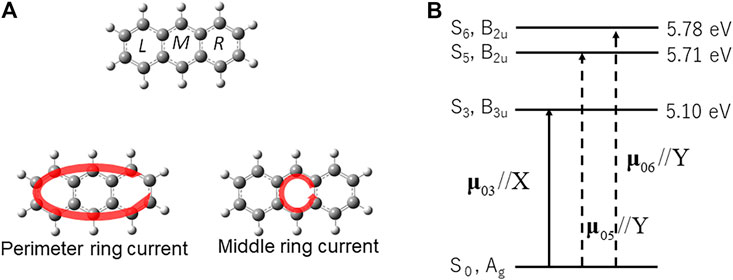
FIGURE 7. (A) Symmetry-adapted ring currents (B_1g) in anthracene, perimeter ring current, and middle ring current. (B) The electronic excited states adapted for laser control of π-electron ring in anthracene (D_2h), and the non-zero transition dipole moments between the ground/excited-excited states. The solid (dashed) arrows represent the transition dipole moments which are parallel to the X (Y) axis.

Consider the two types of π-electron localized ring currents of anthracene: the perimeter current flowing along the outside chemical bonds of anthracene, and the middle ring current localized to the M-ring. Both types of localized ring currents belong to the irreducible representation B_1g of the D_2h point group, which are symmetry-adapted. The excited states contributing to the two ring currents need to belong to the B_3u and B_2u representations, because each corresponding electronic coherence created by the two excited states belongs to the B_1g representation. The excited state for the localized ring current is S₃ with B_3u representation, and the other two excited states S₅ and S₆ with B_2u representation as shown in Figure 7B. This defines a “symmetry-adapted ring current” [41, 42].

The excited state energies in Figure 7B were calculated to be $E_3=5.10$ eV, $E_5=5.71$ eV, and $E_6=5.78$ eV. Here, S₄ (B_3u) with $E_4=5.13$ eV was excluded because the oscillator strength was negligibly small (f = 0.0013) in our numerical simulation. The non-zero transition dipole moments relevant to the coherent π-electron ring current control were calculated using the time-dependent density functional theory (TDDFT) method as, ${\mathbf{\mu }}_{\text{S0,S}3}=\left(-3.98,\mathrm{0,0}\right)$, ${\mathbf{\mu }}_{\text{S0,S}5}=\left(0,-0.64,0\right)$, and ${\mathbf{\mu }}_{\text{S0,S}6}=\left(0,-0.44,0\right)$(in a.u.) for the ground and excited states. The vapor absorption spectrum of anthracene shows the strongest absorption peak at 5.30 eV [62], which corresponds to $E_3=5.10$ eV in the TDDFT calculation.

Figure 8 shows the QOC results for the generation of an anti-clockwise perimeter ring current in anthracene. The target state is expressed from the results obtained using the Lagrange multiplier method as

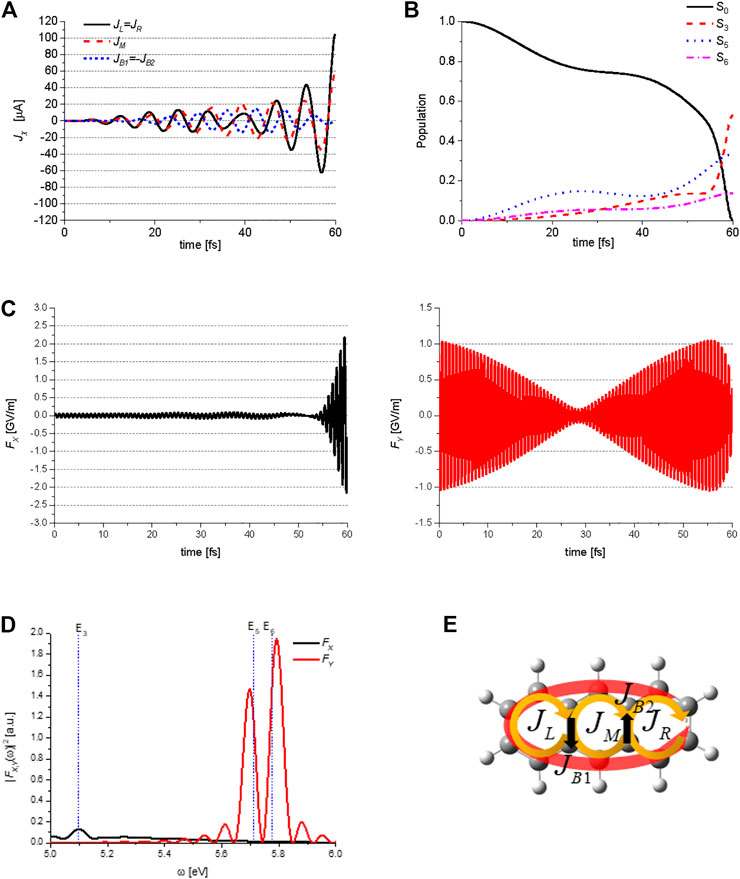
FIGURE 8. Quantum optimal control simulations for generation of the perimeter ring current in anthracene: (A) temporal behavior of the three ring currents $J_L\left(t\right)=J_R\left(t\right)$ (solid line), $J_M\left(t\right)$ (broken line), and those of the two bridge bond currents $J_{B1}\left(t\right)=-J_{B2}\left(t\right)$ (dotted line); (B) temporal behavior of the population in S₀, and those in the three excited states: S₃(B_2u), S₅(B_2u), and S₆(B_2u); (C) optimized X- polarized laser pulse field F_X(t) (left-hand side) and Y-polarized F_Y(t) (right-hand side); (D) Fourier transformed spectra of the two laser fields F_X(ω) and F_Y(ω); (E) five components of the perimeter ring current at an arbitrary time. Reprinted with permission from Ref. [40] Copyright (2012) American Chemical Society.

Here, the subscripts specifying the target state, for example, ACA for ${\Psi }_{\text{ACA}}$, indicates the anti-clockwise ring currents in two aromatic rings, L and R, and a clockwise ring current in aromatic ring M. It should be noted that the target state for a generation of any coherent ring current is expressed in terms of its complex form. The control target time was set to T = 60 fs. The matrix elements of π-electron ring currents $J_{\mathit{{\rm X}},\alpha \beta }$ (X = L, M, R) and the bond current $J_{Bi,\alpha \beta }$ (i = 1, 2), for two excited states α, β are presented in Table 2. Here the π-electron ring current flowing in an anticlockwise direction is defined as positive, whereas the bond current flowing toward the Y direction is defined as positive (SeeFigure 6). Figure 8A shows the temporal evolutions of the coherent ring currents $J_{\chi }$ for the three aromatic rings of anthracene, $\chi =L,M,R$, and those for B1 and B2. It can be observed from Figure 8A that the two bond currents $J_{B1,\alpha \beta }$ and $J_{B2,\alpha \beta }$ vanish at the target control time of T = 60 fs, and all ring currents in three aromatic rings exhibit positive. This indicates that the coherent π-electrons rotate clockwise along the outside (perimeter) of the aromatic ring. The laser-controlled π-electrons includes a ring current averaged over the three aromatic rings, $J_p\equiv (J_L+J_M+J_R)/3=89.0\text{ μA}$, which is the perimeter ring current.

TABLE 2. Matrix elements of the coherent π-electron ring currents for the three aromatic rings of anthracene, $J_{\mathit{x},\alpha \beta }$(X = L, M, R), and those of the coherent bond currents shared by the two adjacent aromatic rings, $J_{Bi,\alpha \beta }$ (i = 1, 2) (seeFigure 8E).

Figure 8B shows the temporal behavior of the ground state S₀, and three excited states S₃ (B_3u), S₅ (B_2u), and S₆ (B_2u) populations during the QOC process, which are induced by the two control lasers. Figure 8C shows the X and Y-components of the electric field $\mathbf{F}\left(t\right)$ generated by the control lasers, and Figure 8D shows the Fourier transformed spectra $F_X\left(\omega \right)$ and $F_Y\left(\omega \right)$ in the ultraviolet (UV) frequency domain. By analyzing the temporal behavior of the electric field $\mathbf{F}\left(t\right)$ of the control lasers in Figure 8C and the Fourier transformed spectra of the control laser fields in Figure 8D, the mechanisms of the laser-controlled ring currents in anthracene can be clarified. It is evident that from the modulation in Figure 8C the two linearly (Y-) polarized lasers with a relative phase zero induce the electronic coherence between the two excited states S₅ (B_2u) and S₆ (B_2u), and that the linearly polarized laser pulse parallel to the X-axis creates the perimeter ring current on the molecular plane.

Thus far, we have considered the QOC procedure for generating an anti-clockwise perimeter current. The QOC procedure for generating a clockwise perimeter current can be carried out in the same manner as described above (SeeEq. 21) by considering the target state,

We carry out the QOC procedure to generate the anticlockwise ring current localized to the middle ring of anthracene. The target state is expressed as

The target state for the middle ring current with the clockwise flow is given by the relationship ${\Psi }_{\text{0C0}}={\Psi }_{0\text{A}0}^{\ast }$. Figure 9 exhibits the QOC results, where Figure 9A displays the temporal evolutions of ring current localization control to the three aromatic rings, indicating that J_M is a ring current with 64.4 μA at the target control time of 60 fs, but on the other hand the ring currents J_L and J_R of the other two aromatic rings vanish. This indicates that the ring current localized to the middle aromatic ring is created by the control laser pulses presented in Figures 9C,D. The temporal behaviors of the populations shown in Figure 9B are nearly the same as those of the perimeter ring currents as shown in Figure 8B. As presented in Figure 9C, the two linearly (Y-) polarized lasers induce the electronic coherence between the two excited states S₅ and S₆ with a definite relative phase π, in contrast to the results presented in Figure 8C. In the mechanism of generation between the perimeter and the middle ring currents there is no difference except the phase difference between the two excited states S₅ and S_6, because the temporal behavior in both Figure 8B and Figure 9B and the temporal behavior in the X-polarized laser pulse in both Figure 8C and Figure 9C are similar to each other.

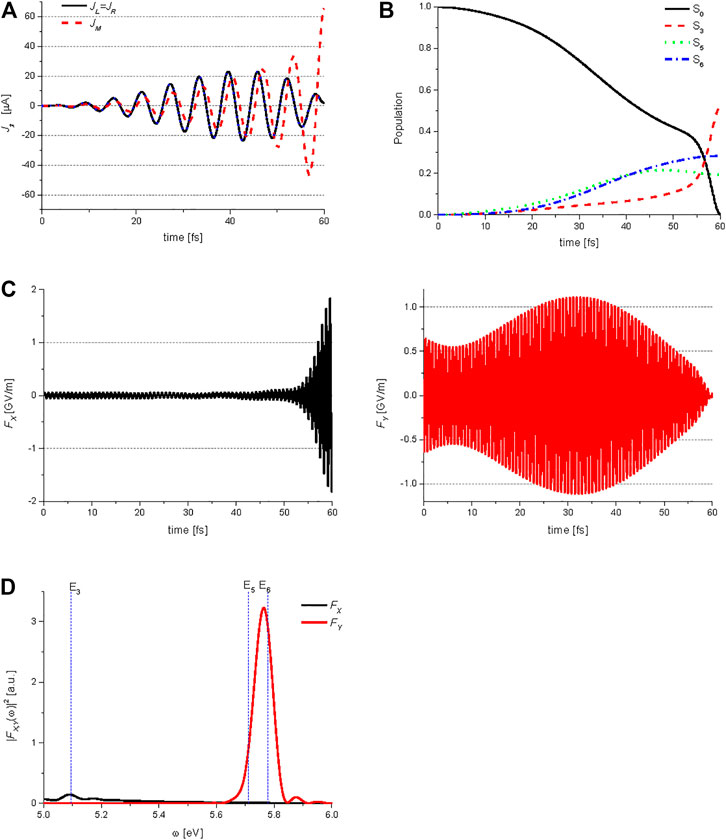
FIGURE 9. Quantum optimal control simulations for generation of the middle ring current in anthracene: (A) temporal behavior of the ring currents $J_L\left(t\right)=J_R\left(t\right)$ (solid line) and $J_M\left(t\right)$ (broken line); (B) temporal behavior of the S₀ population and those of the three excited state S₃(B_2u), S₅(B_2u) and S₆(B_2u) populations; (C) optimized X- and Y-polarized laser pulse fields F_X(t) (left-hand side) and F_Y(t) (right-hand side); (D) Fourier transformed spectra of the laser pulse fields F_X(ω) and F_Y(ω). Reprinted with permission from Ref. [42] Copyright (2017) American Institute of Physics.

Main difference between the temporal behaviors of the Y-polarized lasers in Figure 8C and Figure 9C can be explained briefly in the following. The two coherent states created by the Y-polarized lasers can be expressed as

and

For simplicity, the amplitudes of the two coherent states are assumed to have the same value, i.e., $F_{S5}=F_{S6}\equiv F_Y$. The above expressions can then be simplified to

and

Here, the frequency difference $|{\omega }_{S5}-{\omega }_{S6}|/2$ yields an oscillation beating period of 120 fs, which is nearly the same as that of the quantum beat frequency observed in Figure 8C and Figure 9C.

Having clarified the control mechanism of the coherent ring current generation, we can semi-quantitatively reproduce the above results in Figures 8, 9 by using an analytical method [42]. This indicates, in principle, that two types of ring current localizations, the perimeter ring current and the middle ring current in linear PAHs, can be generated in experiment using three coherent UV lasers without a sophisticated QOC device.

For QOC numerical simulations of the ring current localization control in anthracene, we have only considered the perimeter and the middle ring currents generations, which are symmetry-adapted, while we did not consider a ring current localization to the L- or R-ring of anthracene, which are created by a symmetry-broken procedure, as demonstrated for naphthalene in Ref. [41]. That is, other excited state(s) with gerade symmetry must be considered in addition to the excited states with ungerade symmetry as described in the previous subsection.

It is important to consider how to observe the ultrafast coherent ring currents in PAHs. We proposed a method to detect the direction of the atto-second coherent ring current by tracking the femtosecond molecular vibrational motions that can induce the nonadiabatic couplings [30]. Rodriguez and Mukamel [63] have proposed measuring the circular dichroism (CD) of the ring current using the pump-probe method. Recently, two methods have been proposed for the detection of the ultrafast coherent ring currents. One method, recently proposed by Yuan et al., Bandrauk’s group [64], is utilizing the atto-second detection method of the coherent electronic dynamics in molecules with the temporal and spatial resolutions using the circularly polarized ultrashort UV pump and X-ray probe laser pulses. The other method is to utilize the time-resolved scanning microscopy (STM) and the magnetic force microscopy (MFM) to detect the ring current-induced magnetic fields during the ultrashort time [65–67].

It is also expected that to apply our methods to planar or non-planar extended molecular systems, such as graphene sheets. In principle, our method can be extended to these large systems, by considering the symmetry of the molecular system and the constraints on the π-electron ring currents.

Using laser control, it is also essential to maintain the created ring current at the target region (path) at least during one vibrational period of the PAH [68]. Otherwise, the created ring current would dissipate quickly because of the vibronic interactions and/or the nonadiabatic couplings between the two electronic excited states [30, 69–71].

4 Dynamic Stark-Induced π-Electron Rotations in Low-Symmetry Aromatic Ring Molecules

In this section, we present a convenient method for inducing unidirectional π-electron rotations in aromatic ring molecules with low symmetry [43]. The basic idea behind the induction of unidirectional electron rotations is to degenerate two nondegenerate excited states by utilizing dynamic Stark shifts, as demonstrated in Figure 10. We refer to this as the dynamic Stark-induced degenerate electronic state (DSIDES) [43]. Two linearly polarized continuous lasers operating at different frequencies and phases are used to form DSIDES: Each laser is set to selectively interact with each electronic state through non-resonant excitation. The lower and higher excited states are shifted up and down with the same population, respectively, and the DSIDES is formed at the center between them. As a result, unidirectional π-electron rotation is driven by two lasers. In the laser control scenario, only one input parameter out of the four possible parameters (frequency and intensity for each laser), is required to induce the DSIDES formation.

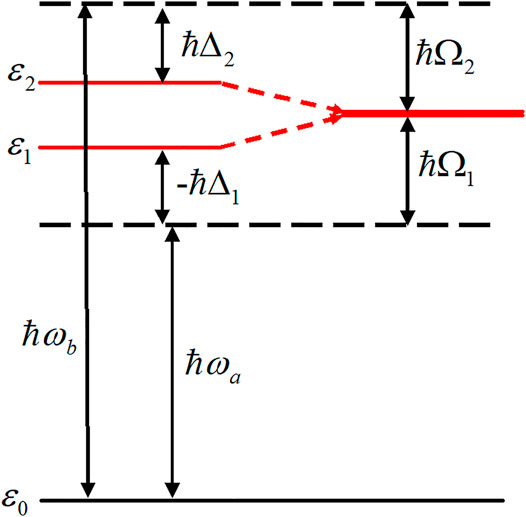
FIGURE 10. Dynamic Stark-induced degenerate state with the Rabi frequencies (Ω₁ and Ω₂) using two stationary linearly-polarized lasers with the frequencies, ${\omega }_a$ and ${\omega }_b$, and detuning frequencies ${\Delta }_1$ and${\Delta }_2$ respectively.

First, the DSIDES formation is described in a three-electronic state model under the fixed nuclei condition, and the time-dependent expectation value of the angular momentum operator of π-electrons is derived and analytically expressed. Next, to demonstrate the applicability of the control scenario, the results of the DSIDES treatment for toluene, which is a typical aromatic ring molecule of low symmetry belonging to Cs point group, are presented.

4.1 Formation of Dynamic Stark-Induced Degenerate Electronic State DSIDES and the Resulting Angular Momentum

Consider the coherent π-electron angular momentum in an aromatic ring molecule with low symmetry excited by non-resonant, stationary UV/visible lasers. The molecule of our interest is one oriented in a space or attached to a surface, as mentioned in the preceding sections. We adopt a three-electronic state model in the frozen nuclei approximation. The three electronic states including the ground state specified by the energy ${\epsilon }_0(\equiv \hslash {\omega }_0)$, and two excited states specified by ${\epsilon }_1(\equiv \hslash {\omega }_1)$ and ${\epsilon }_2(\equiv \hslash {\omega }_2)$, as shown in Figure 10. Here, DSIDES can be formed by two stationary linearly polarized lasers with detuning frequencies ${\Delta }_1={\omega }_a-{\omega }_{10}<0$ and ${\Delta }_2={\omega }_b-{\omega }_{20}>0$. The frequency difference between the two excited states is expressed as ${\omega }_{21}={\omega }_2-{\omega }_1$. The dynamic Stark shifts are denoted by the Rabi frequencies Ω₁ and Ω₂, as presented in Figure 10. The wave function of the total system in the stationary lasers is defined through laser-molecular interactions as

Here, the normalization condition for the coefficients $c_0\left(t\right)$, $c_1\left(t\right)$, and $c_2\left(t\right)$ are as follows,

The system Hamiltonian interacting with the electric fields is given as

where $H_0$ satisfies $H_0{\varphi }_i={\epsilon }_i{\varphi }_i$ for i =0, 1, and 2. In Eq. 29, the interaction Hamiltonian $V\left(t\right)$ between the system and the two electric fields is written as

Here $\mathbf{\mu }=-e\mathbf{r}$ is the electronic dipole moment operator, where $\mathbf{r}$ means the electron coordinate. ${\mathbf{F}}_{\alpha }=F_{\alpha }{\mathbf{e}}_{\alpha }$ ($\alpha =a,b$) is the electric field with amplitude $F_{\alpha }$ and photo-polarization vector ${\mathbf{e}}_{\alpha }$, ${\zeta }_{\alpha }$ is the initial phase, and ${\omega }_{\alpha }$ is the central frequency. In Eq. 30, the two electric fields denoted by a and b induce non-resonant transitions from the ground state to the two excited states. The selective transition conditions are set by the choice of the laser polarization vectors (${\mathbf{e}}_a$ and ${\mathbf{e}}_b$) satisfying ${\mathbf{\mu }}_{02}\perp {\mathbf{e}}_a$ and ${\mathbf{\mu }}_{01}\perp {\mathbf{e}}_b$, respectively.

The time-dependent Schrödinger equation can be written as

The coefficients must satisfy the coupled differential equation

where the interaction Hamiltonian,

is applied with $V_{01}^a\left(t\right)=<{\varphi }_0|\mathbf{\mu }\cdot {\mathbf{F}}_a|{\varphi }_1>\cos ({\omega }_{a}t-{\zeta }_a)exp(-i{\omega }_{10}t)$ and $V_{02}^b\left(t\right)=<{\varphi }_0|\mathbf{\mu }\cdot {\mathbf{F}}_b|{\varphi }_2>\cos ({\omega }_{b}t-{\zeta }_b)exp(-i{\omega }_{20}t)$.

Equation 32 can be rewritten in the rotating approximation (RWA) and solved under the following restriction conditions to obtain the analytical solutions for the time-dependent coefficients $\left\{c_i\left(t\right)\right\}$. For this purpose, we introduce three conditions that can be set experimentally:

And

where the transition magnitudes are $V_{01}^a\equiv -{\mathbf{\mu }}_{01}\cdot {\mathbf{F}}_a/\left(2\hslash \right)$, and $V_{02}^b\equiv -{\mathbf{\mu }}_{02}\cdot {\mathbf{F}}_b/\left(2\hslash \right)$.

In Eq. 34c, the two dressed states are assumed to have equal energies, i.e., $\Omega \equiv {\Omega }_1={\Omega }_2(=\sqrt{{\Delta }^2+2V^2})$, which is called the Rabi frequency [43]. The three conditions lead to a reduction of the input parameters of the two lasers, such that the two amplitudes (F_a and F_b), and two central frequencies (${\omega }_a$ and ${\omega }_b$) are reduced to one input parameter. We take F_a$\equiv$F hereafter. Analytical expressions for time-dependent coefficients $\left\{c_i\left(t\right)\right\}$ are given in Appendix C.

The time-dependent angular momentum defined as an expectation value of an angular momentum operator ${\widehat{L}}_Z=-i\hslash \frac{\partial }{\partial \phi }=\left(\hslash {\widehat{l}}_Z,{\widehat{l}}_Z=-i\frac{\partial }{\partial \phi }\right)$, can be expressed,

Here, $l_{Z,12}=<{\varphi }_1\left|{\widehat{l}}_Z\right|{\varphi }_2>=-<{\varphi }_2\left|{\widehat{l}}_Z\right|{\varphi }_1>=-l_{Z,21}$ and $l_{Z,12}=i\mathrm{Im}{l}_{Z,12}$.

4.2 Unidirectional π-Electron Rotations in Toluene

We calculate L_Z(t) (derived in the preceding subsection) in a real molecule, toluene. The simplest three-electronic state model is applied for toluene because the quasi-degenerate states S₃ (A") and S₄ (A′) in toluene (C_s) correspond to the doubly degenerate state S₃ (E_1u) in benzene (D_6h): Note that the S₃ (E_1u) state is a dipole-allowed excited state in benzene (D_6h), whereas the other two lower excited states, S₂(B_1u) and S₁(B_2u), are dipole-forbidden. The geometry optimization of toluene was carried out with the MP2 level of theory [43]. The C_S symmetry of toluene indicates that one of the hydrogen atoms belonging to the methyl group is perpendicular to an aromatic ring plane (Figure 11A).

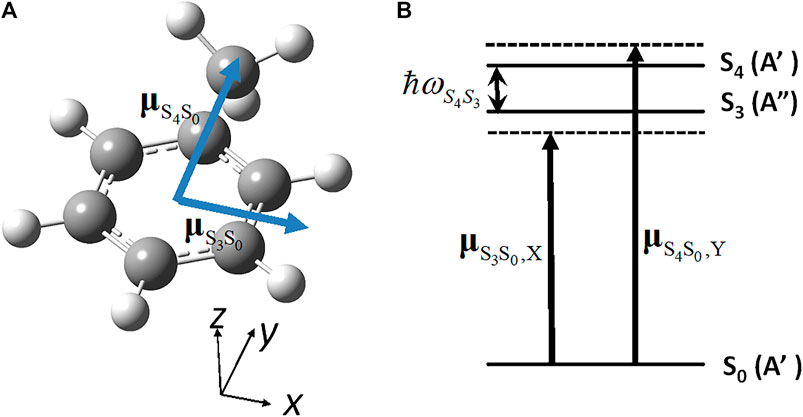
FIGURE 11. (A) Geometrical structure of toluene molecule (C_S) in the ground state (S₀) with the directions of the two electronic transition dipole moments; (B) Parameters for the three electronic states adopted to induce the unidirectional angular momentum: $\hslash {\omega }_{S_4{S}_3}=0.10$ eV as the energy difference between S₄ and S₃, ${\mu }_{S_3{S}_0,X}=5.27$ D, and ${\mu }_{S_4{S}_0,Y}=5.67$ D as the transition dipole moments, $E_{S_3}=8.2\text{ eV}$ and $E_{S_4}=8.3\text{ eV}$as the vertical transition energies. The angular momentum matrix element between S₃ and S₄, ${\ell }_{Z,S_3{S}_4}=0.672i$, is perpendicular to the aromatic ring.

Figure 12A shows the calculated time-dependent angular momentum expectation values L_Z(t) with respect to the relative phase ζ = −π/2 (ζ = +π/2) between the two lasers for the left (right) panel. These were calculated using Eq. 35 combined with Eq. 34. Here, the amplitude of the electric field F_a is adopted as the input parameter F (≡ F_a). Other parameters are shown in Table 3A, while Table 3B shows the time-dependent populations in the three electronic states.

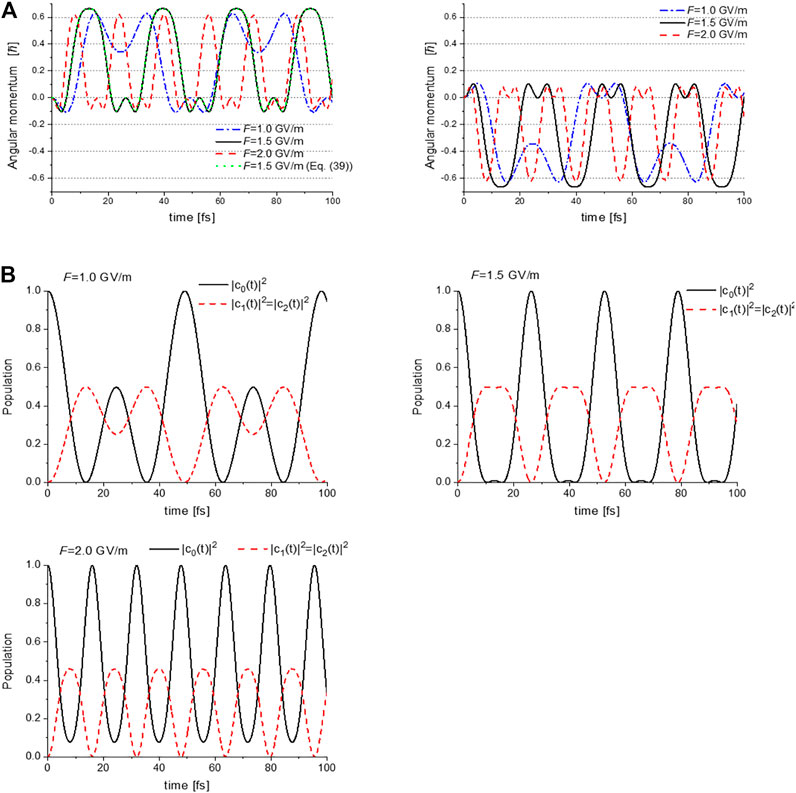
FIGURE 12. (A) Expectation values of the angular momentum operator L_Z(t) for toluene, calculated with the laser input parameter values F = 1.0, 1.5 and 2.0 GV/m. The left (right) panel shows L_Z(t) with respect to the relative phase between two lasers ζ = −π/2 (ζ = +π/2); (B) Temporal evolutions of the populations in S₀, S₃, and S₄ for F = 1.0, 1.5 and 2.0 GV/m. Reprinted with permission from Ref. [43] Copyright (2016) Royal Society of Chemistry.

TABLE 3A. Input parameter F (≡ F_a) and other parameters for a generation of unidirectional π-electron rotation in toluene.

Table 3B. Calculated physical properties of the unidirectional π-electron rotation in toluene.

The time-dependent angular momenta plotted in Figure 12A are comprised of angular momentum pulse trains of the same shape for each value of F. Each angular momentum pulse corresponds to the unidirectional π-electron rotation, which begins with acceleration and ends with deceleration. The direction of the π-electron rotations is determined by the relative phase ζ between the two lasers: clockwise rotation for ζ=+π/2, and anti-clockwise rotation for ζ=−π/2. Here we discuss how the unidirectional π-electron rotations are created. We first note that L_Z(t) can be rewritten under the two conditions, Eq. 34a and Eq. 34b, for Ω≈Δ as

Equation 36 expresses no unidirectional π-electron rotations. By introducing the third condition, Eq. 34c, which provides for the formation of the doubly degenerate dressed states with ζ = ±π/2, Eq. 36 can be expressed as

This indicates a unidirectional π-electron rotation whose direction is determined by the relative phase ζ, that is, L_Z(t) > 0 for ζ = −π/2 and L_Z(t) < 0 for ζ = +π/2, as demonstrated in Figure 12. The dotted line shown in Figure 12A represents $L_Z\left(t\right)$ for F = 1.5 GV/m as calculated by Eq. 37, which well reproduces $L_Z\left(t\right)$ curve calculated using Eq. 35 without the approximation of Ω≈Δ approximation. Thus, the unidirectional π-electron rotation originates from the DSIDES formed by the two non-resonant lasers with a definite relative phase of ±π/2.

As demonstrated in Figure 12A, the oscillation periods of the angular momentum pulses become shorter (higher Rabi frequency Ω), and those amplitudes decrease as F increases. These two behaviors result from the third restriction condition for degeneracy (Eq. 35c) used in the derivation of L_Z(t). This degeneracy condition should be satisfied for the two dressed states with equal energies to maintain their energies located at the center of the two excited states, even though the laser intensities of two lasers increase. This results in an increase in the detuning parameter Δ of the two lasers, that is, a decrease (increase) in ω_a (ω_b), as shown in Table 3A.

Figure 12A exhibits that the maximum magnitude of the angular momentum occurs in the vicinity of F = 1.5 GV/m. This can be explained by noting that the constant in Eq. 37, $V^2{\Delta }^2/{\Omega }^4$, with Rabi frequency of $\Omega =\sqrt{{\Delta }^2+2V^2}$, reaches its maximum at ${\Delta }^2=2V^2$, which in turn provides the maximum angular momentum. Using the relationship ${\Delta }^2=2V^2$for the dressed states with equal energies in Eq. 34c, the electric field F is estimated as $F=\sqrt{2}\hslash \Delta /{\left({\mathbf{\mu }}_{10}\right)}_X$ = 1.52 GV/m with Δ = 0.118 eV, which is close to the F = 1.5 GV/m value shown in Figure 12A.