Algorithm implementation and numerical analysis for the two-dimensional tempered fractional Laplacian

Abstract

Tempered fractional Laplacian is the generator of the tempered isotropic Lévy process. This paper provides the finite difference discretization for the two-dimensional tempered fractional Laplacian by using the weighted trapezoidal rule and the bilinear interpolation. Then it is used to solve the tempered fractional Poisson equation with homogeneous Dirichlet boundary condition and the error estimate is also derived. Numerical experiments verify the predicted convergence rates and effectiveness of the schemes.

Appendices

Appendix

Fig. 5

Division of the integral region for a fixed point (x, y)

Numerically calculating $(\varDelta +\lambda )^{\frac{\beta }{2}}$ performed on a given function

According to the equation $-(\varDelta +\lambda )^{\frac{\beta }{2}} u(x,y)=f(x,y)$, we can compute $-(\varDelta +\lambda )^{\frac{\beta }{2}} u(x,y)$ to get the source term f(x, y). Since the singularity and non-locality of $-(\varDelta +\lambda )^{\frac{\beta }{2}} u(x,y)$, one can’t directly approximate it by the trapezoidal rule. Now we provide the technique to calculate it. For a fixed point (x, y), we denote

$$\begin{aligned} \begin{aligned}&r_1=\sup _{\begin{array}{c} (\xi ,\eta )\in \partial \varOmega \end{array}}\max (|x-\xi |,|y-\eta |),\\&r_2=\inf _{\begin{array}{c} (\xi ,\eta )\in \partial \varOmega \end{array}}\sqrt{(x-\xi )^2+(y-\eta )^2}. \end{aligned} \end{aligned}$$

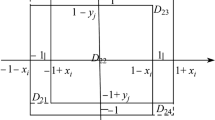
Without loss of generality, we set $\varOmega =(-1,1)\times (-1,1)$. For any $(x,y)\in \varOmega$, we denote $A_1$ as a square whose length is $2r_1$ and center point is (x, y) and $A_2$ as a square whose length is $2r_2$ and center point is (x, y). To compute the source term f(x, y), we divide the domain into four parts, i.e., ${\mathbb {R}}\times {\mathbb {R}}=({\mathbb {R}}\times {\mathbb {R}})\backslash A_1\bigcup (A_1\backslash \varOmega )\bigcup (\varOmega \backslash A_2)\bigcup A_2$, shown in Fig. 5.

For the term

$$\begin{aligned} \int \int _{({\mathbb {R}}\times {\mathbb {R}})\backslash (A_1)}\frac{u(\xi ,\eta )-u(x,y)}{e^{\lambda \sqrt{(x-\xi )^2+(y-\eta )^2}}\left( \sqrt{(x-\xi )^2+(y-\eta )^2}\right) ^{{2+\beta }}}d\xi d\eta , \end{aligned}$$

(A.1)

since $\mathbf{supp }~u(x,y)\subset \varOmega$, (A.1) can be rewritten as

$$\begin{aligned} -u(x,y)\int \int _{({\mathbb {R}}\times {\mathbb {R}})\backslash (A_1)}\frac{1}{e^{\lambda \sqrt{(x-\xi )^2+(y-\eta )^2}}\left( \sqrt{(x-\xi )^2+(y-\eta )^2}\right) ^{{2+\beta }}}d\xi d\eta . \end{aligned}$$

Next, we establish polar coordinates at point (x, y) and let $x-\xi =r\cos (\theta )$, $y-\eta =r\sin (\theta )$. Then, by simple calculations, we can obtain

$$\begin{aligned} \begin{aligned}&\int \int _{({\mathbb {R}}\times {\mathbb {R}})\backslash (A_1)}\frac{1}{e^{\lambda \sqrt{(x-\xi )^2+(y-\eta )^2}}\left( \sqrt{(x-\xi )^2+(y-\eta )^2}\right) ^{{2+\beta }}}d\xi d\eta \\&\quad =\int _{0}^{\frac{\pi }{4}}\int _{\frac{r_1}{\cos (\theta )}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta +\int _{\frac{\pi }{4}}^{\frac{2\pi }{4}}\int _{\frac{r_1}{\cos (\frac{\pi }{2}-\theta )}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta \\&\qquad +\int _{\frac{2\pi }{4}}^{\frac{3\pi }{4}}\int _{\frac{r_1}{\cos (\theta -\frac{\pi }{2})}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta +\int _{\frac{3\pi }{4}}^{\frac{4\pi }{4}}\int _{\frac{r_1}{\cos (\pi -\theta )}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta \\&\qquad +\int _{\frac{4\pi }{4}}^{\frac{5\pi }{4}}\int _{\frac{r_1}{\cos (\theta -\pi )}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta +\int _{\frac{5\pi }{4}}^{\frac{6\pi }{4}}\int _{\frac{r_1}{\cos (\frac{3\pi }{2}-\theta )}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta \\&\qquad +\int _{\frac{6\pi }{4}}^{\frac{7\pi }{4}}\int _{\frac{r_1}{\cos (\theta -\frac{3\pi }{2})}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta +\int _{\frac{7\pi }{4}}^{\frac{8\pi }{4}}\int _{\frac{r_1}{\cos (2\pi -\theta )}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta \\&\quad =8\int _{0}^{\frac{\pi }{4}}\int _{\frac{r_1}{\cos (\theta )}}^{\infty }\frac{1}{r^{1+\beta }e^{\lambda r}}dr d\theta . \end{aligned} \end{aligned}$$

(A.2)

When $\lambda =0$ for (A.2), we have

$$\begin{aligned} \begin{aligned} 8\int _{0}^{\frac{\pi }{4}}\int _{\frac{r_1}{\cos (\theta )}}^{\infty }\frac{1}{r^{1+\beta }}dr d\theta =\frac{8}{\beta }\int _{0}^{\frac{\pi }{4}}\left( \frac{r_1}{\cos (\theta )}\right) ^{-\beta }d\theta . \end{aligned} \end{aligned}$$

We just approximate it by the trapezoidal rule in a finite interval. When $\lambda \ne 0$, we approximate (A.2) by the function ‘integral2.m’ in MATLAB.

For the term

$$\begin{aligned} \int \int _{A_2}\frac{u(\xi ,\eta )-u(x,y)}{e^{\lambda \sqrt{(x-\xi )^2+(y-\eta )^2}}\left( \sqrt{(x-\xi )^2+(y-\eta )^2}\right) ^{{2+\beta }}}d\xi d\eta , \end{aligned}$$

using its symmetry leads to

$$\begin{aligned} \begin{aligned}&\int \int _{A_2}\frac{u(\xi ,\eta )-u(x,y)}{e^{\lambda \sqrt{(x-\xi )^2+(y-\eta )^2}}\left( \sqrt{(x-\xi )^2+(y-\eta )^2}\right) ^{{2+\beta }}}d\xi d\eta \\&\quad =\int _{-r_2}^{r_2}\int _{-r_2}^{r_2}\frac{u(x+\xi ,y+\eta )-u(x,y)}{e^{\lambda \sqrt{\xi ^2+\eta ^2}}\left( \sqrt{\xi ^2+\eta ^2}\right) ^{{2+\beta }}}d\xi d\eta \\&\quad =\int _{0}^{r_2}\int _{0}^{r_2}\frac{u(x+\xi ,y+\eta )+u(x-\xi ,y-\eta )+u(x+\xi ,y-\eta )+u(x-\xi ,y+\eta ) -4u(x,y)}{e^{\lambda \sqrt{\xi ^2+\eta ^2}}\left( \sqrt{\xi ^2+\eta ^2}\right) ^{{2+\beta }}}d\xi d\eta . \end{aligned} \end{aligned}$$

(A.3)

Because of the weak singularity, we try to compute it in polar coordinates. Let $\xi =r\cos (\theta )$, $\eta =r\sin (\theta )$. Then (A.3) can be rewritten as

$$\begin{aligned} \begin{aligned}&\int \int _{A_2}\frac{u(\xi ,\eta )-u(x,y)}{e^{\lambda \sqrt{(x-\xi )^2+(y-\eta )^2}}\left( \sqrt{(x-\xi )^2+(y-\eta )^2}\right) ^{{2+\beta }}}d\xi d\eta \\&\quad =\int _{0}^{\frac{\pi }{4}}\int _{0}^{\frac{r_2}{\cos (\theta )}}(u(x+r\cos (\theta ),y+r\sin (\theta ))+u(x-r\cos (\theta ),y+r\sin (\theta ))\\&\qquad +u(x+r\cos (\theta ),y-r\sin (\theta ))+u(x-r\cos (\theta ),y-r\sin (\theta ))\\&\qquad -4u(x,y))r^{-1-\beta }e^{-\lambda r}dr d\theta \\&\qquad +\int _{\frac{\pi }{4}}^{\frac{2\pi }{4}}\int _{0}^{\frac{r_2}{\cos (\frac{\pi }{2}-\theta )}}\left( u(x+r\cos (\theta ),y+r\sin (\theta ))+u(x-r\cos (\theta ),y+r\sin (\theta ))\right. \\&\qquad +u(x+r\cos (\theta ),y-r\sin (\theta ))+u(x-r\cos (\theta ),y-r\sin (\theta ))\\&\qquad -4u(x,y))r^{-1-\beta }e^{-\lambda r}dr d\theta . \end{aligned} \end{aligned}$$

(A.4)

In (A.4), for some special function, such as $u(x,y)=(1-x^2)^2(1-y^2)^2$, we can expand it as

$$\begin{aligned} \begin{aligned}&(u(x+r\cos (\theta ),y+r\sin (\theta ))+u(x-r\cos (\theta ),y+r\sin (\theta ))\\&\qquad +u(x+r\cos (\theta ),y-r\sin (\theta ))+u(x-r\cos (\theta ),y-r\sin (\theta ))-4u(x,y))r^{-1-\beta }e^{-\lambda r}\\&\quad =4 r^{1-\beta }e^{-\lambda r} (r^6 \sin ^4(\theta ) \cos ^4(\theta )+6 r^4 x^2 \sin ^4(\theta ) \cos ^2(\theta )+6 r^4 y^2 \sin ^2(\theta ) \cos ^4(\theta )\\&\qquad -2 r^4 \sin ^2(\theta ) \cos ^4(\theta )\\&\qquad -2 r^4 \sin ^4(\theta ) \cos ^2(\theta )+r^2 x^4 \sin ^4(\theta )+36 r^2 x^2 y^2 \sin ^2(\theta ) \cos ^2(\theta )-2 r^2 x^2 \sin ^4(\theta )\\&\qquad -12 r^2 x^2 \sin ^2(\theta ) \cos ^2(\theta )+r^2 y^4 \cos ^4(\theta )-2 r^2 y^2 \cos ^4(\theta )-12 r^2 y^2 \sin ^2(\theta ) \cos ^2(\theta )\\&\qquad +r^2 \sin ^4(\theta )+r^2 \cos ^4(\theta )+4 r^2 \sin ^2(\theta ) \cos ^2(\theta )\\&\qquad +6 x^4 y^2 \sin ^2(\theta )-2 x^4 \sin ^2(\theta )+6 x^2 y^4 \cos ^2(\theta )\\&\qquad -12 x^2 y^2 \sin ^2(\theta )-12 x^2 y^2 \cos ^2(\theta )+4 x^2 \sin ^2(\theta )\\&\qquad +6 x^2 \cos ^2(\theta )-2 y^4 \cos ^2(\theta )+6 y^2 \sin ^2(\theta )\\&\qquad +4 y^2 \cos ^2(\theta )-2 \sin ^2(\theta )-2 \cos ^2(\theta )). \end{aligned} \end{aligned}$$

For (A.4), the inner integration about r can be calculated analytically when $\lambda =0$, so we approximate the outer integration about $\theta$ by the trapezoidal rule; when $\lambda \ne 0$, we can transform the inner integration about r to a nonsingular numerical integration by virtue of integration by parts.

For another two terms,

$$\begin{aligned} \int \int _{(A_1\backslash \varOmega )\bigcup (\varOmega \backslash A_2)}\frac{u(\xi ,\eta )-u(x,y)}{e^{\lambda \sqrt{(x-\xi )^2+(y-\eta )^2}}\left( \sqrt{(x-\xi )^2+(y-\eta )^2}\right) ^{2+\beta }}d\xi d\eta , \end{aligned}$$

we get them by the trapezoidal rule directly.

Weights of approximating tempered fractional Laplacian

$$\begin{aligned} w_{i,j}=-c_{2,\beta }\left\{ \begin{aligned}&-4\left( \frac{\frac{k_\gamma }{4}G_{0,0}+W^1_{1,1}+W^2_{1,1}+W^3_{1,1}}{e^{\lambda \sqrt{\xi _1^2+\eta _1^2}}\left( \sqrt{\xi _1^2+\eta _1^2}\right) ^\gamma }\right. \\&~~~~~~ +\frac{\frac{k_\gamma }{4}G_{0,0}+W^1_{1,0}}{e^{\lambda \sqrt{\xi _1^2+\eta _0^2}}\left( \sqrt{\xi _1^2+\eta _0^2}\right) ^\gamma }+\frac{\frac{k_\gamma }{4}G_{0,0}+W^1_{0,1}}{e^{\lambda \sqrt{\xi _0^2+\eta _1^2}}\left( \sqrt{\xi _0^2+\eta _1^2}\right) ^\gamma }\\&~~~~~~ +\sum _{i=2}^{N-1}\frac{W^1_{i,0}+W^2_{i,0}}{e^{\lambda \sqrt{\xi _i^2+\eta _0^2}}\left( \sqrt{\xi _i^2+\eta _0^2}\right) ^\gamma }+\sum _{j=2}^{N-1}\frac{W^1_{0,j}+W^3_{0,j}}{e^{\lambda \sqrt{\xi _0^2+\eta _j^2}}\left( \sqrt{\xi _0^2+\eta _j^2}\right) ^\gamma }\\&~~~~~~ +\sum _{i=1}^{N-1}\frac{W^3_{i,N}+W^4_{i,N}}{e^{\lambda \sqrt{\xi _i^2+\eta _{N}^2}}\left( \sqrt{\xi _i^2+\eta _{N}^2}\right) ^\gamma }+\sum _{j=1}^{N-1}\frac{W^2_{N,j}+W^4_{N,j}}{e^{\lambda \sqrt{\xi _{N}^2+\eta _j^2}}\left( \sqrt{\xi _{N}^2+\eta _j^2}\right) ^\gamma }\\&~~~~~~+\sum _{i=1,j=1; (i,j)\ne (1,1)}^{i=N-1,j=N-1}\frac{W^1_{i,j}+W^2_{i,j}+W^3_{i,j}+W^4_{i,j}}{e^{\lambda \sqrt{\xi _{i}^2+\eta _j^2}}\left( \sqrt{\xi _{i}^2+\eta _j^2}\right) ^\gamma }\\&~~~~~~ +\frac{W^3_{0,N}}{e^{\lambda \sqrt{\xi _0^2+\eta _{N}^2}}\left( \sqrt{\xi _0^2 +\eta _{N}^2}\right) ^\gamma }+\frac{W^2_{N,0}}{e^{\lambda \sqrt{\xi _{N}^2+\eta _0^2}}\left( \sqrt{\xi _{N}^2+\eta _0^2}\right) ^\gamma }\\&~~~~~~\left. +\frac{W^4_{N,N}}{e^{\lambda \sqrt{\xi _{N}^2+\eta _{N}^2}}\left( \sqrt{\xi _{N}^2+\eta _{N}^2}\right) ^\gamma }+G^\infty \right) ,&i=0,j=0,\\&\frac{\frac{k_\gamma }{4}G_{0,0}+W^1_{1,1}+W^2_{1,1}+W^3_{1,1}}{e^{\lambda \sqrt{\xi _1^2+\eta _1^2}}\left( \sqrt{\xi _1^2+\eta _1^2}\right) ^\gamma },&i=1,j=1,\\&2\frac{\frac{k_\gamma }{4}G_{0,0}+W^1_{1,0}}{e^{\lambda \sqrt{\xi _1^2+\eta _0^2}}\left( \sqrt{\xi _1^2+\eta _0^2}\right) ^\gamma },&i=1,j=0,\\&2\frac{\frac{k_\gamma }{4}G_{0,0}+W^1_{0,1}}{e^{\lambda \sqrt{\xi _0^2+\eta _1^2}}\left( \sqrt{\xi _0^2+\eta _1^2}\right) ^\gamma },&i=0,j=1,\\&2\frac{W^1_{i,0}+W^2_{i,0}}{e^{\lambda \sqrt{\xi _i^2+\eta _0^2}}\left( \sqrt{\xi _i^2+\eta _0^2}\right) ^\gamma ,}&1<i<N,j=0,\\&2\frac{W^1_{0,j}+W^3_{0,j}}{e^{\lambda \sqrt{\xi _0^2+\eta _j^2}}\left( \sqrt{\xi _0^2+\eta _j^2}\right) ^\gamma },&i=0, 1<j<N,\\&\frac{W^3_{i,N}+W^4_{i,N}}{e^{\lambda \sqrt{\xi _i^2+\eta _{N}^2}}\left( \sqrt{\xi _i^2+\eta _{N}^2}\right) ^\gamma },&1\le i<N,j=N,\\&\frac{W^2_{N,j}+W^4_{N,j}}{e^{\lambda \sqrt{\xi _{N}^2+\eta _j^2}}\left( \sqrt{\xi _{N}^2+\eta _j^2}\right) ^\gamma },&i=N, 1\le j<N,\\&2\frac{W^3_{0,N}}{e^{\lambda \sqrt{\xi _{0}^2+\eta _{N}^2}}\left( \sqrt{\xi _{0}^2+\eta _{N}^2}\right) ^\gamma },&i=0,j=N,\\&2\frac{W^2_{N,0}}{e^{\lambda \sqrt{\xi _{N}^2+\eta _0^2}}\left( \sqrt{\xi _{N}^2+\eta _0^2}\right) ^\gamma },&i=N,j=0,\\&\frac{W^4_{N,N}}{e^{\lambda \sqrt{\xi _{N}^2+\eta _{N}^2}}\left( \sqrt{\xi _{N}^2+\eta _{N}^2}\right) ^\gamma },&i=N,j=N,\\&\frac{W^1_{i,j}+W^2_{i,j}+W^3_{i,j}+W^4_{i,j}}{e^{\lambda \sqrt{\xi _{i}^2+\eta _j^2}}\left( \sqrt{\xi _{i}^2+\eta _j^2}\right) ^\gamma },&\mathrm{otherwise}. \end{aligned} \right. \end{aligned}$$

(B.1)