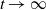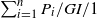1. Introduction
In almost all queueing models, the impact of initial conditions dissipates as time evolves. Thus, for stationary models interest usually centers on the steady-state distribution and convergence to it for various initial conditions. The asymptotic loss of memory (appropriately defined) is also anticipated in queueing models with time-varying arrival rates, as evidenced by results for the time-varying ![]() $G_t/M_t/s_{t}+GI_{t}$ many-server fluid model in [Reference Liu and Whitt29] and the weak ergodicity results for nonhomogeneous Markov chains in [Reference Isaacson and Madsen26, Chapter V]. In contrast, here we consider a queueing model in which the long-run behavior of the arrival process depends critically on the early history of the arrival process.
$G_t/M_t/s_{t}+GI_{t}$ many-server fluid model in [Reference Liu and Whitt29] and the weak ergodicity results for nonhomogeneous Markov chains in [Reference Isaacson and Madsen26, Chapter V]. In contrast, here we consider a queueing model in which the long-run behavior of the arrival process depends critically on the early history of the arrival process.
Such a stochastic process is said to exhibit path-dependent behavior. There has long been substantial interest in systems with path-dependent behavior, as can be seen from [Reference Arthur1, Reference Arthur, Ermoliev and Kanjovski2] and the citations of them. The classic example is the familiar Pólya urn model discussed in [Reference Feller14], first studied in [Reference Pólya and Eggenberger34]. There is an urn containing r red balls and b blue balls. At each step, we select one ball from the urn at random and then return that ball and one new ball of the selected color to the urn. The proportion of balls of any given color has a path-dependent limit, converging almost surely to a random limit, which has the beta distribution, depending on the parameters r and b. The different converging paths depending on the early history are shown in [Reference Arthur, Ermoliev and Kanjovski2, Figure 1]. (Figure 1 in Section 2 here is an analog.)
It is natural for queues to arise in the allocation of scarce resources in systems with path-dependent behavior. Thus we are motivated to consider a queue with a path-dependent arrival process. Hence we consider the ![]() $\sum_{i=1}^{n} P_i/GI/1$ queue, which is a single-server queue with unlimited waiting space, the first-come first-served service discipline and independent and identically distributed (i.i.d.) service times with a general distribution, with arrivals according to the superposition of n i.i.d. Pólya point processes. A Pólya point process can be represented as a limit of Pólya urn models as indicated in [Reference Feller14, p. 480]. Theorem 1 shows that the Pólya point process is a stationary point process, while Theorem 3 shows that it satisfies a non-ergodic law of large numbers (LLN), which we use as our definition of path dependence. Proposition 3 (from [Reference Cha and Badia8]) shows that the superposition process is a special generalized Pólya process as considered by [Reference Cha7, Reference Konno27], which inherits those properties.
$\sum_{i=1}^{n} P_i/GI/1$ queue, which is a single-server queue with unlimited waiting space, the first-come first-served service discipline and independent and identically distributed (i.i.d.) service times with a general distribution, with arrivals according to the superposition of n i.i.d. Pólya point processes. A Pólya point process can be represented as a limit of Pólya urn models as indicated in [Reference Feller14, p. 480]. Theorem 1 shows that the Pólya point process is a stationary point process, while Theorem 3 shows that it satisfies a non-ergodic law of large numbers (LLN), which we use as our definition of path dependence. Proposition 3 (from [Reference Cha and Badia8]) shows that the superposition process is a special generalized Pólya process as considered by [Reference Cha7, Reference Konno27], which inherits those properties.
We establish several results for queues with Pólya point process arrival processes. Our main contribution here is Theorem 5, which establishes a heavy-traffic limit that provides, via Corollary 6, a tractable description of the transient queue length distribution in the ![]() $\sum_{i=1}^{n} P_i/GI/1$ queueing model when the service-time distribution has finite second moment, exposing the performance impact of the path-dependent behavior of the arrival process. That follows from Theorem 4, which establishes a functional central limit theorem (FCLT) for the
$\sum_{i=1}^{n} P_i/GI/1$ queueing model when the service-time distribution has finite second moment, exposing the performance impact of the path-dependent behavior of the arrival process. That follows from Theorem 4, which establishes a functional central limit theorem (FCLT) for the ![]() $\sum_{i=1}^{n} P_i$ superposition process, showing that the limit is a Gaussian Markov process with stationary increments (
$\sum_{i=1}^{n} P_i$ superposition process, showing that the limit is a Gaussian Markov process with stationary increments (![]() $\Psi$-GMP, where
$\Psi$-GMP, where ![]() $\Psi$ is a mnemonic for SI to denote stationary increments) studied in [Reference Fendick16].
$\Psi$ is a mnemonic for SI to denote stationary increments) studied in [Reference Fendick16].
In Section 2 we place our superposition process in the context of generalized Pólya processes, as developed in [Reference Cha7, Reference Cha and Badia8, Reference Konno27]. In Theorems 1 and 2 we identify generalized Pólya processes that are stationary point processes and show how this class can be used to represent any generalized Pólya process. In Section 3 we establish the FCLT for the superposition process and state various consequences. In Section 4 we establish the FCLT with an extra drift and exhibit some striking properties of the ![]() $\Psi$-GMP with drift, further exposing the path-dependent behavior. In Section 5 we establish the associated heavy-traffic limit for the
$\Psi$-GMP with drift, further exposing the path-dependent behavior. In Section 5 we establish the associated heavy-traffic limit for the ![]() $\sum_{i=1}^{n} P_i/GI/1$ queue.
$\sum_{i=1}^{n} P_i/GI/1$ queue.
Afterwards, we provide additional results and discussion. In Section 6 we obtain stability results for the single-server queue and then establish steady-state results for queues with Pólya arrival processes when either (i) there are infinitely many servers or (ii) there is a single server with an adaptive rate-matching service-rate control in the spirit of [Reference Whitt37]. In Section 7 we present some remaining technical details. In Section 8 we present conclusions and discussion.
We conclude this introduction by discussing related work. First, we note that queues with Pólya arrival processes have been previously considered as a way to capture exceptional variability [Reference Mirtchev31, Reference Mirtchev and Goleva32, Reference Mirtchev and Ganchev33]; we discuss that earlier work in Remark 2. Second, the heavy-traffic limit of the ![]() $\sum_{i=1}^{n} P_i/GI/1$ queue can be regarded as a Gaussian queue with a net input process that is a
$\sum_{i=1}^{n} P_i/GI/1$ queue can be regarded as a Gaussian queue with a net input process that is a ![]() $\Psi$-GMP with drift. Thus, this paper is related to the large literature on Gaussian queues, which can be seen from [Reference Debicki and Rolski10, Reference Debicki, Kosinski and Mandjes11]. The FCLT here yields a
$\Psi$-GMP with drift. Thus, this paper is related to the large literature on Gaussian queues, which can be seen from [Reference Debicki and Rolski10, Reference Debicki, Kosinski and Mandjes11]. The FCLT here yields a ![]() $\Psi$-GMP with positive dependence, i.e. in which the increments over disjoint intervals are positively correlated; see Corollary 4. As we indicate in Section 8, similar limits hold for processes with negative dependence. That leads to convergence of empirical processes to the Brownian bridge and related queueing heavy-traffic limits as in [Reference Hajek22, Reference Honnappa, Jain and Ward25].
$\Psi$-GMP with positive dependence, i.e. in which the increments over disjoint intervals are positively correlated; see Corollary 4. As we indicate in Section 8, similar limits hold for processes with negative dependence. That leads to convergence of empirical processes to the Brownian bridge and related queueing heavy-traffic limits as in [Reference Hajek22, Reference Honnappa, Jain and Ward25].
2. Generalized Pólya point process with stationary increments:  $\Psi$-GPP
$\Psi$-GPP
The Pólya point process has been extended to the generalized Pólya process (GPP) [Reference Cha7, Reference Konno27]. A GPP ![]() $N \equiv \{N(t)\,{:}\, t \ge 0\}$ is a Markov point process with stochastic intensity (defined in terms of the internal histories
$N \equiv \{N(t)\,{:}\, t \ge 0\}$ is a Markov point process with stochastic intensity (defined in terms of the internal histories ![]() $\mathcal{H}_{t}$; see, e.g., [Reference Baccelli and Bremaud3, Section 1.8]) by
$\mathcal{H}_{t}$; see, e.g., [Reference Baccelli and Bremaud3, Section 1.8]) by
where ![]() $N(0) = 0$,
$N(0) = 0$, ![]() $\gamma$ and
$\gamma$ and ![]() $\beta$ are positive constants,
$\beta$ are positive constants, ![]() $\kappa (t)$ is a positive integrable real-valued function and
$\kappa (t)$ is a positive integrable real-valued function and ![]() $\equiv$ denotes equality by definition. The classical Pólya point process is the special case of (1) with
$\equiv$ denotes equality by definition. The classical Pólya point process is the special case of (1) with ![]() $\beta = 1$ and
$\beta = 1$ and
Many properties of the GPP were deduced in [Reference Cha7] by exploiting the restarting property.
Proposition 1. (The restarting property [Reference Cha7]) If N is a GPP with parameter triple ![]() $(\kappa (t), \gamma, \beta)$, then the conditional future process
$(\kappa (t), \gamma, \beta)$, then the conditional future process ![]() $N_u (t) \equiv N(u+t) - N(u)$ given
$N_u (t) \equiv N(u+t) - N(u)$ given ![]() $N(u) = n$ and the history up to time u is itself a GPP with parameter triple
$N(u) = n$ and the history up to time u is itself a GPP with parameter triple ![]() $(\kappa (u + t), \gamma, \beta + n \gamma)$.
$(\kappa (u + t), \gamma, \beta + n \gamma)$.
Theorem 1 of [Reference Cha7] establishes the joint distribution of a GPP by exploiting the restarting property. As a consequence, the marginal distribution of a GPP starting at ![]() $N(0) = 0$ has a simple form.
$N(0) = 0$ has a simple form.
Proposition 2. (Negative binomial marginal distribution [Reference Cha7]) If N is a GPP with parameter triple ![]() $(\kappa (t), \gamma, \beta)$, then N(t) has a negative binomial distribution with probability mass function
$(\kappa (t), \gamma, \beta)$, then N(t) has a negative binomial distribution with probability mass function ![]() $\mathbb{P}(N(t) = k) \equiv f(k;\ r, p(t)) = C(\beta, \gamma, k) (1-p(t))^r p(t)^k$,
$\mathbb{P}(N(t) = k) \equiv f(k;\ r, p(t)) = C(\beta, \gamma, k) (1-p(t))^r p(t)^k$, ![]() $k = 0,1, 2, \ldots$, where
$k = 0,1, 2, \ldots$, where ![]() $r = \beta/\gamma$,
$r = \beta/\gamma$, ![]() $p(t) = 1 - \exp\!\{-\gamma K (t)\}$,
$p(t) = 1 - \exp\!\{-\gamma K (t)\}$, ![]() $K(t) \equiv \int_{0}^{t} \kappa (s) \, \mathrm{d} s$,
$K(t) \equiv \int_{0}^{t} \kappa (s) \, \mathrm{d} s$, ![]() $t \ge 0$, and
$t \ge 0$, and ![]() $C(\beta, \gamma, k) = \Gamma ((\beta/\gamma) + k)/\Gamma ((\beta/\gamma)) k!$, with
$C(\beta, \gamma, k) = \Gamma ((\beta/\gamma) + k)/\Gamma ((\beta/\gamma)) k!$, with ![]() $\Gamma$ being the gamma function, so N(t) has mean and variance
$\Gamma$ being the gamma function, so N(t) has mean and variance
For a general function ![]() $\kappa (t)$ the time-varying behavior can be complicated, but it simplifies for the classical Pólya point process and closely related processes (allowing
$\kappa (t)$ the time-varying behavior can be complicated, but it simplifies for the classical Pólya point process and closely related processes (allowing ![]() $\beta \not= 1$). Indeed, for
$\beta \not= 1$). Indeed, for ![]() $\kappa (t)$ in (2) the GPP is a (strictly) stationary point process, i.e. the joint distribution of any k increments is independent of time shifts, as we show next. In the spirit of [Reference Fendick16], we thus call the GPP with triple
$\kappa (t)$ in (2) the GPP is a (strictly) stationary point process, i.e. the joint distribution of any k increments is independent of time shifts, as we show next. In the spirit of [Reference Fendick16], we thus call the GPP with triple ![]() $(\kappa (t), \gamma, \beta)$ for
$(\kappa (t), \gamma, \beta)$ for ![]() $\kappa (t)$ in (2) a
$\kappa (t)$ in (2) a ![]() $(\beta,\gamma)$
$(\beta,\gamma)$ ![]() $\Psi$-GPP (again, with
$\Psi$-GPP (again, with ![]() $\Psi$ as a mnemonic for SI).
$\Psi$ as a mnemonic for SI).
Theorem 1. (A stationary point process: ![]() $\Psi$-GPP) Consider a GPP with parameter triple
$\Psi$-GPP) Consider a GPP with parameter triple ![]() $(\kappa (t), \gamma, \beta)$. If
$(\kappa (t), \gamma, \beta)$. If ![]() $\kappa (t)$ is given by (2), then
$\kappa (t)$ is given by (2), then ![]() $1 - p(t) = \kappa (t)$,
$1 - p(t) = \kappa (t)$,
Moreover, the joint distribution of k increments, ![]() $N(s_i+t_i+h) - N(s_i+h)$,
$N(s_i+t_i+h) - N(s_i+h)$, ![]() $1 \le i \le k$, is independent of
$1 \le i \le k$, is independent of ![]() $h > 0$ for all h, so that N is a stationary stochastic point process with
$h > 0$ for all h, so that N is a stationary stochastic point process with
Proof. For ![]() $\kappa$ in (2),
$\kappa$ in (2),
so that ![]() $1 - p(t) = \mathrm{e}^{-\gamma K(t)} = \kappa (t)$. Then the conclusion about the distribution of a single increment follows from the displayed distribution of an increment in [Reference Cha7, Theorem 1(ii)]. For the covariance in (4), write
$1 - p(t) = \mathrm{e}^{-\gamma K(t)} = \kappa (t)$. Then the conclusion about the distribution of a single increment follows from the displayed distribution of an increment in [Reference Cha7, Theorem 1(ii)]. For the covariance in (4), write ![]() $\mathrm{Var}(N(t-s)) = \mathrm{Var}(N(t)-N(s)) = \mathrm{Var}(N(t)) + \mathrm{Var}(N(s))-2 \mathrm{Cov}(N(s),N(t))$, where the first equality follows from stationary increments, to obtain
$\mathrm{Var}(N(t-s)) = \mathrm{Var}(N(t)-N(s)) = \mathrm{Var}(N(t)) + \mathrm{Var}(N(s))-2 \mathrm{Cov}(N(s),N(t))$, where the first equality follows from stationary increments, to obtain ![]() $\mathrm{Cov}(N(s), N(t)) = [\mathrm{Var}(N(t)) + \mathrm{Var}(N(s)) - \mathrm{Var}(N(t-s))]/2$, and then use the variance formula in (3).
$\mathrm{Cov}(N(s), N(t)) = [\mathrm{Var}(N(t)) + \mathrm{Var}(N(s)) - \mathrm{Var}(N(t-s))]/2$, and then use the variance formula in (3).
For the joint distribution of k increments, we first observe that, without loss of generality, we can assume that the k increments are disjoint and contiguous, so that they represent a partition of a fixed interval ![]() $(s,s+t]$ into finitely many subintervals. (We are thus initially adding intervals and determining the joint distribution for more intervals.) We then apply [Reference Cha7, Theorem 3 and Remark 3] to conclude that the conditional distribution for the sequence of times when N increases on
$(s,s+t]$ into finitely many subintervals. (We are thus initially adding intervals and determining the joint distribution for more intervals.) We then apply [Reference Cha7, Theorem 3 and Remark 3] to conclude that the conditional distribution for the sequence of times when N increases on ![]() $(s,s+t]$ given that
$(s,s+t]$ given that ![]() $N(s + t) - N(s)=k$ is, first, independent of s, and second, is itself the same as that of the order statistics of k i.i.d. random variables, each with probability density function
$N(s + t) - N(s)=k$ is, first, independent of s, and second, is itself the same as that of the order statistics of k i.i.d. random variables, each with probability density function
assuming ![]() $s = 0$. If
$s = 0$. If ![]() $\kappa (t)$ is given by (2), then
$\kappa (t)$ is given by (2), then ![]() $f(x)=1/t$; i.e. the probability density function (PDF) of the uniform distribution. That in turn implies that the joint distribution of the k disjoint and contiguous increments
$f(x)=1/t$; i.e. the probability density function (PDF) of the uniform distribution. That in turn implies that the joint distribution of the k disjoint and contiguous increments ![]() $N(s_i+t_i+h) - N(s_i+h)$,
$N(s_i+t_i+h) - N(s_i+h)$, ![]() $1 \le i \le k$, all within some larger interval
$1 \le i \le k$, all within some larger interval ![]() $(s+h, s + t + h)$, is independent of
$(s+h, s + t + h)$, is independent of ![]() $h > 0$ for all h. That follows because the conditioning event that
$h > 0$ for all h. That follows because the conditioning event that ![]() $N(s + t+ h) - N(s + h) =k$ has a distribution that is independent of h, and then the conditional distribution of the points within the interval given that
$N(s + t+ h) - N(s + h) =k$ has a distribution that is independent of h, and then the conditional distribution of the points within the interval given that ![]() $N(s + t+ h) - N(s + h) =k$ is also independent of h. Finally, we go from the case of contiguous intervals to the original case by integrating out in order to obtain the desired marginal distribution; e.g. when we let the probability that one interval is
$N(s + t+ h) - N(s + h) =k$ is also independent of h. Finally, we go from the case of contiguous intervals to the original case by integrating out in order to obtain the desired marginal distribution; e.g. when we let the probability that one interval is ![]() $\le \infty$, then that interval drops out.
$\le \infty$, then that interval drops out.
We now show that any GPP with general ![]() $\kappa (t)$ in (1) can be expressed as a unique deterministic time-transformation of a
$\kappa (t)$ in (1) can be expressed as a unique deterministic time-transformation of a ![]() $\Psi$-GPP based on (2). As a consequence, limits established for
$\Psi$-GPP based on (2). As a consequence, limits established for ![]() $\Psi$-GPPs will extend to GPPs by the continuous mapping theorem. Let
$\Psi$-GPPs will extend to GPPs by the continuous mapping theorem. Let ![]() $\stackrel{\rm d}{=}$ denote equality in distribution, including for stochastic processes.
$\stackrel{\rm d}{=}$ denote equality in distribution, including for stochastic processes.
Theorem 2. (Characterization of GPP) Let ![]() $\hat{N}$ be the GPP with parameter triple
$\hat{N}$ be the GPP with parameter triple ![]() $(\kappa (t), \gamma, \beta)$ satisfying (1); let N be the
$(\kappa (t), \gamma, \beta)$ satisfying (1); let N be the ![]() $\Psi$-GPP with parameter triple
$\Psi$-GPP with parameter triple ![]() $(\kappa (t), \gamma, \beta)$ satisfying (1) and (2); and let
$(\kappa (t), \gamma, \beta)$ satisfying (1) and (2); and let
where ![]() $\mu$ is a continuous positive function on
$\mu$ is a continuous positive function on ![]() $[0, \infty)$. Then
$[0, \infty)$. Then ![]() $\{\hat{N}(t)\,{:}\, t \ge 0\} \stackrel{\rm d}{=} \{N(M(t))\,{:}\, t \ge 0\}$ if and only if
$\{\hat{N}(t)\,{:}\, t \ge 0\} \stackrel{\rm d}{=} \{N(M(t))\,{:}\, t \ge 0\}$ if and only if
Proof. The stochastic intensity of N can be interpreted as
where ![]() $\{\mathcal{H}_t\,{:}\, t \ge 0\}$ is the family of histories associated with N. Let
$\{\mathcal{H}_t\,{:}\, t \ge 0\}$ is the family of histories associated with N. Let ![]() $C(t) = N(M(t))$,
$C(t) = N(M(t))$, ![]() $t \ge 0$, be the composition process and let
$t \ge 0$, be the composition process and let ![]() $\lambda_{C} (t)$ be its stochastic intensity function. Let
$\lambda_{C} (t)$ be its stochastic intensity function. Let ![]() $\{\mathcal{C}_t\,{:}\, t > 0\}$ be the histories associated with C. Because of (5),
$\{\mathcal{C}_t\,{:}\, t > 0\}$ be the histories associated with C. Because of (5), ![]() $\mathcal{C}_t = \mathcal{N}_{M(t)}$,
$\mathcal{C}_t = \mathcal{N}_{M(t)}$, ![]() $t \ge 0$. Then,
$t \ge 0$. Then,
 \begin{align*}\lambda_{C} (t) & \equiv \lambda_{C} (t \mid \mathcal{C}_{t-})\equiv \lim_{h \rightarrow 0}{\frac{\mathbb{P}(C(t+h) - C(t) = 1 \mid \mathcal{C}_{t-})}{h}} \nonumber \\[3pt]& = \lim_{h \rightarrow 0}{\frac{\mathbb{P}(N(M(t+h)) - N(M(t)) = 1 \mid \mathcal{N}_{M(t)-})}{h}} \nonumber \\[3pt]& = \lim_{h \rightarrow 0}{\frac{\mathbb{P}(N(M(t) + \delta(h))) - N(M(t)) = 1 \mid \mathcal{N}_{M(t)-}))}{\delta(h)}\frac{\delta(h)}{h}},\end{align*}
\begin{align*}\lambda_{C} (t) & \equiv \lambda_{C} (t \mid \mathcal{C}_{t-})\equiv \lim_{h \rightarrow 0}{\frac{\mathbb{P}(C(t+h) - C(t) = 1 \mid \mathcal{C}_{t-})}{h}} \nonumber \\[3pt]& = \lim_{h \rightarrow 0}{\frac{\mathbb{P}(N(M(t+h)) - N(M(t)) = 1 \mid \mathcal{N}_{M(t)-})}{h}} \nonumber \\[3pt]& = \lim_{h \rightarrow 0}{\frac{\mathbb{P}(N(M(t) + \delta(h))) - N(M(t)) = 1 \mid \mathcal{N}_{M(t)-}))}{\delta(h)}\frac{\delta(h)}{h}},\end{align*}
where ![]() $\delta \equiv \delta(h) \equiv M(t + h) - M(t) = \mu (t) h + o(h)$ as
$\delta \equiv \delta(h) \equiv M(t + h) - M(t) = \mu (t) h + o(h)$ as ![]() $h \downarrow 0$. Hence,
$h \downarrow 0$. Hence,
where we use the specific form of ![]() $\kappa (t)$ in (2) because N is a
$\kappa (t)$ in (2) because N is a ![]() $\Psi$-GPP.
$\Psi$-GPP.
Now let ![]() $\hat{\lambda} (t)$ be the stochastic intensity associated with
$\hat{\lambda} (t)$ be the stochastic intensity associated with ![]() $\hat{N}$. Then
$\hat{N}$. Then ![]() $\hat{\lambda} (t) = (\gamma \hat{N} (t) + \beta) \kappa (t)$,
$\hat{\lambda} (t) = (\gamma \hat{N} (t) + \beta) \kappa (t)$, ![]() $t \ge 0$. Under the condition that
$t \ge 0$. Under the condition that ![]() $\hat{N} (t) = N(M(t))$, we have
$\hat{N} (t) = N(M(t))$, we have ![]() $\gamma \hat{N} (t) + \beta = \gamma N((M(t)) + \beta$. Hence,
$\gamma \hat{N} (t) + \beta = \gamma N((M(t)) + \beta$. Hence, ![]() $\lambda_{C} (t) = \hat{\lambda} (t)$ for all
$\lambda_{C} (t) = \hat{\lambda} (t)$ for all ![]() $t \ge 0$ if and only if
$t \ge 0$ if and only if
Integrating both sides of (7), we get (6), as claimed. In closing, we mention two alternative proofs. The first can be based on the martingale characterization of the stochastic intensity as in [Reference Baccelli and Bremaud3, Section 1.8]. Then ![]() $\lambda (t) \equiv \lambda (t \mid \mathcal{H}_t)$ is the stochastic intensity of N in (1) if
$\lambda (t) \equiv \lambda (t \mid \mathcal{H}_t)$ is the stochastic intensity of N in (1) if
for all intervals (a, b]. The second is to directly show that the finite-dimensional distributions are the same.
Remark 1. (Index of dispersion) To better understand the impact of the variability as a function of time in an arrival process on the performance of a queueing model, we have shown in [Reference Fendick and Whitt17, Reference Whitt and You.38, Reference Whitt and You.39] that it is often helpful to look at the index of dispersion for counts, which for a ![]() $(\beta,\gamma)$
$(\beta,\gamma)$ ![]() $\Psi$-GPP is
$\Psi$-GPP is
From this equation, we see that the variability increases without bound as t increases by this measure, consistent with Theorem 3. The index of dispersion for counts is also considered in [Reference Mirtchev31, Reference Mirtchev and Goleva32, Reference Mirtchev and Ganchev33] under the name ‘peakedness’, which is often used to describe traffic variability, but more commonly in a different way; see [Reference Li and Whitt28] and references therein.
We next apply Theorem 1 to characterize the nature of the path-dependent behavior for a ![]() $(\beta,\gamma)$
$(\beta,\gamma)$ ![]() $\Psi$-GPP. We do that by the following non-ergodic LLN; see, e.g., [Reference Gregoire20, Section 5.1] and references therein.
$\Psi$-GPP. We do that by the following non-ergodic LLN; see, e.g., [Reference Gregoire20, Section 5.1] and references therein.
Theorem 3. (Non-ergodic LLN) If N(t) is a ![]() $(\beta, \gamma)$
$(\beta, \gamma)$ ![]() $\Psi$-GPP, then
$\Psi$-GPP, then ![]() $t^{-1}N(t) \rightarrow L(\gamma, \beta)$ as
$t^{-1}N(t) \rightarrow L(\gamma, \beta)$ as ![]() $t \rightarrow \infty$ with probability 1, where L has a gamma distribution with shape
$t \rightarrow \infty$ with probability 1, where L has a gamma distribution with shape ![]() $\beta/\gamma$ and rate
$\beta/\gamma$ and rate ![]() $1/\gamma$, and thus mean
$1/\gamma$, and thus mean ![]() $\mathbb{E}[L] = \beta$ and variance
$\mathbb{E}[L] = \beta$ and variance ![]() $\mathrm{Var}(L) = \beta \gamma$.
$\mathrm{Var}(L) = \beta \gamma$.
Proof. Because the increments ![]() $N(n) - N(n-1)$,
$N(n) - N(n-1)$, ![]() $n \ge 1$, form a stationary sequence, we can apply the Birkhoff ergodic theorem as in [Reference Breiman6, Theorem 6.2.1] to establish the almost sure convergence of
$n \ge 1$, form a stationary sequence, we can apply the Birkhoff ergodic theorem as in [Reference Breiman6, Theorem 6.2.1] to establish the almost sure convergence of ![]() $N(n)/n$ as
$N(n)/n$ as ![]() $n \rightarrow \infty$. The almost sure convergence of
$n \rightarrow \infty$. The almost sure convergence of ![]() $N(t)/t$ as
$N(t)/t$ as ![]() $t \rightarrow \infty$ is an easy consequence, e.g. using
$t \rightarrow \infty$ is an easy consequence, e.g. using ![]() $N(\lfloor nt \rfloor) \le N(t) \le N(\lfloor nt \rfloor + 1)$ for
$N(\lfloor nt \rfloor) \le N(t) \le N(\lfloor nt \rfloor + 1)$ for ![]() $\lfloor nt \rfloor \le t < \lfloor nt \rfloor + 1$. Next, from (3), we see that
$\lfloor nt \rfloor \le t < \lfloor nt \rfloor + 1$. Next, from (3), we see that ![]() $\mathbb{E}[N(t)/t] = \beta$ for all
$\mathbb{E}[N(t)/t] = \beta$ for all ![]() $t > 0$ and
$t > 0$ and ![]() $\mathrm{Var}(N(t)/t) = \beta(1 + \gamma t)/t \rightarrow \beta \gamma$ as
$\mathrm{Var}(N(t)/t) = \beta(1 + \gamma t)/t \rightarrow \beta \gamma$ as ![]() $t \rightarrow \infty$. The limiting gamma distribution for
$t \rightarrow \infty$. The limiting gamma distribution for ![]() $N(t)/t$ is obtained by taking the limit as
$N(t)/t$ is obtained by taking the limit as ![]() $t \rightarrow \infty$ of the characteristic function
$t \rightarrow \infty$ of the characteristic function ![]() $\phi_{N(t)/t} (s) = \phi_{N(t)} (s/t)$. In particular, using Taylor-series asymptotics in the last step, we obtain
$\phi_{N(t)/t} (s) = \phi_{N(t)} (s/t)$. In particular, using Taylor-series asymptotics in the last step, we obtain
 \begin{eqnarray*} \phi_{t^{-1} N(t)} (s) & = & \left(\frac{1 - p(t)}{1 - p(t)\mathrm{e}^{is/t}}\right)^{\beta/\gamma} = \left(\frac{1}{1 + [p(t)/(1 - p(t))](1 - \mathrm{e}^{is/t})}\right)^{\beta/\gamma} \nonumber \\ & = & \left(\frac{1}{1 + \gamma t (1 - \mathrm{e}^{is/t})}\right)^{\beta/\gamma} = \left(\frac{1}{1 + \gamma t (1 - (1 + (is/t) + O(1/t^2))}\right)^{\beta/\gamma} \nonumber \\ & \rightarrow & \left(\frac{1}{1 - is \gamma}\right)^{\beta/\gamma} \quad\mbox{as}\quad t \rightarrow \infty.\end{eqnarray*}
\begin{eqnarray*} \phi_{t^{-1} N(t)} (s) & = & \left(\frac{1 - p(t)}{1 - p(t)\mathrm{e}^{is/t}}\right)^{\beta/\gamma} = \left(\frac{1}{1 + [p(t)/(1 - p(t))](1 - \mathrm{e}^{is/t})}\right)^{\beta/\gamma} \nonumber \\ & = & \left(\frac{1}{1 + \gamma t (1 - \mathrm{e}^{is/t})}\right)^{\beta/\gamma} = \left(\frac{1}{1 + \gamma t (1 - (1 + (is/t) + O(1/t^2))}\right)^{\beta/\gamma} \nonumber \\ & \rightarrow & \left(\frac{1}{1 - is \gamma}\right)^{\beta/\gamma} \quad\mbox{as}\quad t \rightarrow \infty.\end{eqnarray*}
Finally, we recognize the limit as the characteristic function of the claimed gamma distribution. Convergence of characteristic functions then applies the convergence in distribution by [Reference Feller15, Theorem XV.2].
Theorem 3 implies that the pure birth process N has a limiting rate as ![]() $t \rightarrow \infty$, but that rate is random.
$t \rightarrow \infty$, but that rate is random.
Corollary 1. (Asymptotically Poisson with a random rate.) If N(t) is a ![]() $(\beta, \gamma)$
$(\beta, \gamma)$ ![]() $\Psi$-GPP, with stochastic intensity
$\Psi$-GPP, with stochastic intensity ![]() $\lambda (t)$ in (1), then
$\lambda (t)$ in (1), then ![]() $\lambda (t) \rightarrow L(\gamma, \beta)$ as
$\lambda (t) \rightarrow L(\gamma, \beta)$ as ![]() $t \rightarrow \infty$ with probability 1, where L is the gamma random variable from Theorem 3 with shape
$t \rightarrow \infty$ with probability 1, where L is the gamma random variable from Theorem 3 with shape ![]() $\beta/\gamma$ and rate
$\beta/\gamma$ and rate ![]() $1/\gamma$. Hence, asymptotically as
$1/\gamma$. Hence, asymptotically as ![]() $t \rightarrow \infty$ the point process behaves as a Poisson process at random rate
$t \rightarrow \infty$ the point process behaves as a Poisson process at random rate ![]() $L(\gamma, \beta)$.
$L(\gamma, \beta)$.
Proof. Multiply and divide by t in (1) and observe that the numerator converges to ![]() $\gamma L$ by Theorem 3, while the denominator converges to
$\gamma L$ by Theorem 3, while the denominator converges to ![]() $\gamma$.
$\gamma$.
Remark 2. (Instability of the ![]() $P/GI/1$ queue.) Theorem 3 and Corollary 1 imply that the queue length process is not stable in the
$P/GI/1$ queue.) Theorem 3 and Corollary 1 imply that the queue length process is not stable in the ![]() $P/GI/1$ queue with a Pólya arrival process; i.e. there does not exist a random variable Q with
$P/GI/1$ queue with a Pólya arrival process; i.e. there does not exist a random variable Q with ![]() $\mathbb{P}(Q < \infty) = 1$ such that
$\mathbb{P}(Q < \infty) = 1$ such that ![]() $Q(t) \Rightarrow Q$ as
$Q(t) \Rightarrow Q$ as ![]() $t \rightarrow \infty$, where
$t \rightarrow \infty$, where ![]() $\Rightarrow$ denotes convergence in distribution. That contradicts various conclusions about steady-state performance in [Reference Mirtchev31, Reference Mirtchev and Goleva32, Reference Mirtchev and Ganchev33]. We elaborate on stability and discuss ways to stabilize performance in queues with Pólya arrival processes in Section 6, but our main goal is to obtain a tractable approximation for transient performance in a class of
$\Rightarrow$ denotes convergence in distribution. That contradicts various conclusions about steady-state performance in [Reference Mirtchev31, Reference Mirtchev and Goleva32, Reference Mirtchev and Ganchev33]. We elaborate on stability and discuss ways to stabilize performance in queues with Pólya arrival processes in Section 6, but our main goal is to obtain a tractable approximation for transient performance in a class of ![]() $P/GI/1$ models. That is established by Theorem 5 and Corollary 6.
$P/GI/1$ models. That is established by Theorem 5 and Corollary 6.
We illustrate Theorem 3 by showing the results of a simulation experiment. Figure 1 plots the empirical distribution of ![]() $N(100)/100$ based on 50,000 i.i.d. samples (left) and 25 individual sample paths of
$N(100)/100$ based on 50,000 i.i.d. samples (left) and 25 individual sample paths of ![]() $N(t)/t$ over [0, 200] for a stationary Pólya point process with parameter pair
$N(t)/t$ over [0, 200] for a stationary Pólya point process with parameter pair ![]() $(\beta, \gamma) = (1, 1)$, assuming that (2) holds (right).
$(\beta, \gamma) = (1, 1)$, assuming that (2) holds (right).

Figure 1: Display of the empirical distribution of ![]() $N(100)/100$ (left) and 25 individual sample paths of
$N(100)/100$ (left) and 25 individual sample paths of ![]() $N(t)/t$ over [0, 200] (right) for a stationary Pólya point process N with
$N(t)/t$ over [0, 200] (right) for a stationary Pólya point process N with ![]() $(\beta, \gamma) = (1, 1)$.
$(\beta, \gamma) = (1, 1)$.
Figure 1 shows that much of the uncertainty about the long-run average disappears after an initial time t, e.g. ![]() $t = 50$, but the process
$t = 50$, but the process ![]() $N_u (t) \equiv N(t + u) - N(u)$,
$N_u (t) \equiv N(t + u) - N(u)$, ![]() $t \ge 0$, given that
$t \ge 0$, given that ![]() $N(u) = m$, is itself a new GPP by the restart property in Proposition 1. Additional results about this conditional process are given in [Reference Cha7]. We now apply [Reference Cha7] to further quantify the impact of starting at time u. The following result is elementary to prove, but the relations are revealing.
$N(u) = m$, is itself a new GPP by the restart property in Proposition 1. Additional results about this conditional process are given in [Reference Cha7]. We now apply [Reference Cha7] to further quantify the impact of starting at time u. The following result is elementary to prove, but the relations are revealing.
Corollary 2. (Impact of starting later) If ![]() $N_u (t) \equiv N(u + t) - N(u)$ conditioned on
$N_u (t) \equiv N(u + t) - N(u)$ conditioned on ![]() $N(u) = m$, where N is the
$N(u) = m$, where N is the ![]() $\Psi$-GPP with parameter triple
$\Psi$-GPP with parameter triple ![]() $(\kappa (t),\beta, \gamma)$ for
$(\kappa (t),\beta, \gamma)$ for ![]() $\kappa (t)$ in (2), then
$\kappa (t)$ in (2), then ![]() $N_u$ is a new
$N_u$ is a new ![]() $\Psi$-GPP with parameter triple
$\Psi$-GPP with parameter triple ![]() $(\kappa_{u} (t),\beta_{u}, \gamma_{u})$ for
$(\kappa_{u} (t),\beta_{u}, \gamma_{u})$ for ![]() $\kappa_{u} (t) = \kappa (u + t)$,
$\kappa_{u} (t) = \kappa (u + t)$, ![]() $\beta_u \equiv \beta + m \gamma$ and
$\beta_u \equiv \beta + m \gamma$ and ![]() $\gamma_u \equiv \gamma$. Consequently,
$\gamma_u \equiv \gamma$. Consequently, ![]() $N_{u} (t)$ has a negative binomial distribution for each
$N_{u} (t)$ has a negative binomial distribution for each ![]() $t \ge 0$ with
$t \ge 0$ with
where
so that ![]() $\mathbb{E}[N_u (t)] \le \mathbb{E}[N (t)]$ if and only if
$\mathbb{E}[N_u (t)] \le \mathbb{E}[N (t)]$ if and only if ![]() $(m/u) \le \gamma$. Moreover, for
$(m/u) \le \gamma$. Moreover, for ![]() $0 \le s \le t$,
$0 \le s \le t$,
 \begin{align*} \mathrm{Cov}(N_{u} (s), N_{u} (t)) & = (\beta_{u}\eta_u/\gamma_u) s(1 + \eta_{u} t) = \mathbb{E}[N_{u} (s)](1 + \eta_{u} t) , \nonumber \\[3pt] I_{u} (t) & \equiv \frac{\mathrm{Var}(N_u (t))}{\mathbb{E}[N_{u} (t)]} = 1 + \eta_{u} t,\end{align*}
\begin{align*} \mathrm{Cov}(N_{u} (s), N_{u} (t)) & = (\beta_{u}\eta_u/\gamma_u) s(1 + \eta_{u} t) = \mathbb{E}[N_{u} (s)](1 + \eta_{u} t) , \nonumber \\[3pt] I_{u} (t) & \equiv \frac{\mathrm{Var}(N_u (t))}{\mathbb{E}[N_{u} (t)]} = 1 + \eta_{u} t,\end{align*}
where ![]() $\eta_{u}$ is strictly decreasing in u with
$\eta_{u}$ is strictly decreasing in u with ![]() $\eta_{0} = \gamma$ and
$\eta_{0} = \gamma$ and ![]() $\eta_{u} \rightarrow 1$ as
$\eta_{u} \rightarrow 1$ as ![]() $u \rightarrow \infty$.
$u \rightarrow \infty$.
Proof. This result mostly follows from the restart property from [Reference Cha7] stated here in Proposition 1. We also apply the explicit distribution of ![]() $N_{u} (t)$ given in [Reference Cha7, (20)]. The stationarity property follows from essentially the same proof as for Theorem 1.
$N_{u} (t)$ given in [Reference Cha7, (20)]. The stationarity property follows from essentially the same proof as for Theorem 1.
We close this section by comparing the ![]() $\Psi$-GPP to another self-exciting process.
$\Psi$-GPP to another self-exciting process.
Remark 3. (Comparison to the Hawkes process.) The nondegenerate limit in Theorem 2 makes the ![]() $\Psi$-GPP quite different from the widely applied Hawkes [Reference Hawkes23, Reference Hawkes24] process and most of its variants. For the basic Hawkes process in [Reference Hawkes23, (8)], instead of (1) we have
$\Psi$-GPP quite different from the widely applied Hawkes [Reference Hawkes23, Reference Hawkes24] process and most of its variants. For the basic Hawkes process in [Reference Hawkes23, (8)], instead of (1) we have
where N is defined over the entire real line and g is a nonnegative kernel satisfying ![]() $\eta \equiv \int_{0}^{\infty} g(u) \, \mathrm{d} u < 1$, so that the stationary rate is
$\eta \equiv \int_{0}^{\infty} g(u) \, \mathrm{d} u < 1$, so that the stationary rate is ![]() $\nu/(1 - \eta)$. Hawkes processes are alternative self-exciting processes, but they are stationary and ergodic point processes [Reference Bacray, Delattre, Hoffman and Muzy4]. Thus, Hawkes processes are not path dependent. For applications of Hawkes processes to queues, see [Reference Daw and Pender9, Reference Gao and Zhu18].
$\nu/(1 - \eta)$. Hawkes processes are alternative self-exciting processes, but they are stationary and ergodic point processes [Reference Bacray, Delattre, Hoffman and Muzy4]. Thus, Hawkes processes are not path dependent. For applications of Hawkes processes to queues, see [Reference Daw and Pender9, Reference Gao and Zhu18].
3. Convergence to a  $\Psi$-GMP
$\Psi$-GMP
We now show that a properly scaled sequence of the superpositon of i.i.d. ![]() $\Psi$-GPPs in Section 2 converges to a
$\Psi$-GPPs in Section 2 converges to a ![]() $\Psi$-GMP, the Gaussian Markov process with stationary increments studied in [Reference Fendick16]. (In fact, [Reference Fendick16] focuses on a multivariate
$\Psi$-GMP, the Gaussian Markov process with stationary increments studied in [Reference Fendick16]. (In fact, [Reference Fendick16] focuses on a multivariate ![]() $\Psi$-GMP.) We obtain all possible univariate
$\Psi$-GMP.) We obtain all possible univariate ![]() $\Psi$-GMPs exhibiting positive dependence, as we explain in Section 8.
$\Psi$-GMPs exhibiting positive dependence, as we explain in Section 8.
For ![]() $n \ge 1$, let
$n \ge 1$, let
be the sum of n i.i.d. GPPs each with parameter triple ![]() $(\kappa (t), \gamma, \beta)$. We first note that our superposition process is another GPP.
$(\kappa (t), \gamma, \beta)$. We first note that our superposition process is another GPP.
Proposition 3. (Superposition, Theorem 1 of [Reference Cha and Badia8].) The superposition of two independent GPPs with parameter triples ![]() $(\kappa (t), \gamma, \beta_i)$,
$(\kappa (t), \gamma, \beta_i)$, ![]() $i = 1,2$, is itself a GPP with parameter triple
$i = 1,2$, is itself a GPP with parameter triple ![]() $(\kappa (t), \gamma, \beta_1 + \beta_2)$. If each GPP is a
$(\kappa (t), \gamma, \beta_1 + \beta_2)$. If each GPP is a ![]() $\Psi$-GPP, then so is the superposition process. Then the superposition process satisfies the non-ergodic LLN in Theorem 3.
$\Psi$-GPP, then so is the superposition process. Then the superposition process satisfies the non-ergodic LLN in Theorem 3.
We now apply the usual FCLT spatial scaling, but without scaling time by n (as in [Reference Whitt36, (2.1) on p. 226 or (8.4) on p. 320]). In particular, for ![]() $n \ge 1$, let
$n \ge 1$, let
Let ![]() $\Rightarrow$ denote convergence in distribution and let
$\Rightarrow$ denote convergence in distribution and let ![]() $D \equiv D[0, \infty)$ be the usual function space of right-continuous real-valued functions [Reference Billingsley5, Reference Whitt36].
$D \equiv D[0, \infty)$ be the usual function space of right-continuous real-valued functions [Reference Billingsley5, Reference Whitt36].
Theorem 4. (FCLT for the superposition process.) Consider the scaled superposition process ![]() $A_n (t)$ in (9). For
$A_n (t)$ in (9). For ![]() $\kappa (t)$ in (2), so that in (8)
$\kappa (t)$ in (2), so that in (8) ![]() $N^1$ is a
$N^1$ is a ![]() $(\beta, \gamma)$
$(\beta, \gamma)$ ![]() $\Psi$-GPP while
$\Psi$-GPP while ![]() $A^n$ is an
$A^n$ is an ![]() $(n\beta, \gamma)$
$(n\beta, \gamma)$ ![]() $\Psi$-GPP,
$\Psi$-GPP,
where A is a ![]() $\Psi$-GMP, i.e. a zero-mean Gaussian Markov process with stationary increments and covariance function
$\Psi$-GMP, i.e. a zero-mean Gaussian Markov process with stationary increments and covariance function
The limit A also satisfies the stochastic differential equation
where ![]() $A(0) \equiv 0$, B is standard Brownian motion,
$A(0) \equiv 0$, B is standard Brownian motion,
Proof. For the limit in (10), we apply Hahn’s [Reference Hahn21] FCLT for sums of processes in [Reference Whitt36, Theorem 7.2.1]. We verify the moment inequality conditions in that theorem in Section 7. The stochastic differential equation characterization in (12) and (13) follows from [Reference Fendick16, Theorem 3]. A Gaussian process with that covariance kernel is a Markov process by [Reference Doob12, Theorem 8.1, p. 233].
Remark 4. (Parameters.) Even though (11) shows identical structure in the covariance functions of the ![]() $\Psi$-GPP
$\Psi$-GPP ![]() $N^1$ in (8) and the
$N^1$ in (8) and the ![]() $\Psi$-GMP A in (10), the conventions here for the parameters are not the same as in [Reference Fendick16]. When
$\Psi$-GMP A in (10), the conventions here for the parameters are not the same as in [Reference Fendick16]. When ![]() $N^1$ is a
$N^1$ is a ![]() $(\beta, \gamma)$
$(\beta, \gamma)$ ![]() $\Psi$-GPP, A is an
$\Psi$-GPP, A is an ![]() $(\alpha^*, \beta^*) = (\beta, -\beta \gamma)$
$(\alpha^*, \beta^*) = (\beta, -\beta \gamma)$ ![]() $\Psi$-GMP in [Reference Fendick16].
$\Psi$-GMP in [Reference Fendick16].
Remark 5. (Structural analogs.) Many properties of the ![]() $\Psi$-GMP were established in [Reference Fendick16]. Properties can also be deduced as a consequence of Theorem 4. Lemma 4 of [Reference Fendick16] established an analog of the restarting property in Proposition 1. A variant of the proof of Theorem 3 shows that the
$\Psi$-GMP were established in [Reference Fendick16]. Properties can also be deduced as a consequence of Theorem 4. Lemma 4 of [Reference Fendick16] established an analog of the restarting property in Proposition 1. A variant of the proof of Theorem 3 shows that the ![]() $\Psi$-GMP also satisfies a non-ergodic LLN, with a Gaussian limit instead of a gamma distribution. Additional properties of a
$\Psi$-GMP also satisfies a non-ergodic LLN, with a Gaussian limit instead of a gamma distribution. Additional properties of a ![]() $\Psi$-GMP with drift are established in the next section.
$\Psi$-GMP with drift are established in the next section.
4. Convergence to a  $\Psi$-GMP with drift
$\Psi$-GMP with drift
For stable queueing models, there tends to be a negative drift in the potential net input process. Hence, in this section we consider a modification of the FCLT in Theorem 4 to produce a drift in the ![]() $\Psi$-GMP limit process. For that purpose, let
$\Psi$-GMP limit process. For that purpose, let ![]() $\{\mu_n\,{:}\, n \ge 1\}$ be a sequence of real numbers that satisfies
$\{\mu_n\,{:}\, n \ge 1\}$ be a sequence of real numbers that satisfies
We are primarily interested in the case ![]() $\mu < 0$. Let
$\mu < 0$. Let ![]() $A^{d,n} (t) = A^n (\mu_n t)$ and
$A^{d,n} (t) = A^n (\mu_n t)$ and
Let ![]() $e \equiv e(t) = t$,
$e \equiv e(t) = t$, ![]() $t \ge 0$, be the identity function in D, and let
$t \ge 0$, be the identity function in D, and let ![]() $D^k$ be the usual k-fold product space.
$D^k$ be the usual k-fold product space.
Corollary 3. (FCLT with a drift.) If (14) holds in addition to the assumptions of Theorem 4, then ![]() $A^{d}_n \Rightarrow A + \omega e$ in D as
$A^{d}_n \Rightarrow A + \omega e$ in D as ![]() $n \rightarrow \infty$ for
$n \rightarrow \infty$ for ![]() $A^{d}_n$ in (15) and
$A^{d}_n$ in (15) and ![]() $\omega \equiv \beta \mu$.
$\omega \equiv \beta \mu$.
Proof. We apply the continuous mapping argument for composition with centering as in [Reference Whitt36, Section 13.3]. For that purpose, let ![]() $(\bar{M}_n (t), M_n (t)) \equiv \left(\mu_n t, \sqrt{n}(\mu_n - 1)t\right)$. Note that
$(\bar{M}_n (t), M_n (t)) \equiv \left(\mu_n t, \sqrt{n}(\mu_n - 1)t\right)$. Note that ![]() $A^{d}_n = A_n \circ \bar{M}_n + \beta M_n$, where
$A^{d}_n = A_n \circ \bar{M}_n + \beta M_n$, where ![]() $\circ$ denotes the composition map. It is elementary that
$\circ$ denotes the composition map. It is elementary that ![]() $(\bar{M}_n , M_n ) \rightarrow (e, \mu e)$ in
$(\bar{M}_n , M_n ) \rightarrow (e, \mu e)$ in ![]() $D^2$ as
$D^2$ as ![]() $n \rightarrow \infty$. Then apply [Reference Whitt36, Theorem 11.4.5] with Theorem 4 above to get the joint convergence
$n \rightarrow \infty$. Then apply [Reference Whitt36, Theorem 11.4.5] with Theorem 4 above to get the joint convergence ![]() $(A_n, \bar{M}_n , M_n) \Rightarrow (A, e, \mu e)$ in
$(A_n, \bar{M}_n , M_n) \Rightarrow (A, e, \mu e)$ in ![]() $D^3$. Then the limit preservation in [Reference Whitt36, Theorem 13.3.1] yields
$D^3$. Then the limit preservation in [Reference Whitt36, Theorem 13.3.1] yields ![]() $A^{d}_n = (A_n \circ \bar{M}_n + \beta M_n) \Rightarrow A + \mu \beta e$ in D as
$A^{d}_n = (A_n \circ \bar{M}_n + \beta M_n) \Rightarrow A + \mu \beta e$ in D as ![]() $n \rightarrow \infty$.
$n \rightarrow \infty$.
We now state three properties of a GMP with drift. The first two provide additional characterization of the path-dependent behavior.
Proposition 4. (Conditional mean, Lemma 4 from [Reference Fendick16].) If ![]() $A^d \equiv A + \omega e$ as in Corollary 3, where A is a
$A^d \equiv A + \omega e$ as in Corollary 3, where A is a ![]() $\Psi$-GMP satisfying (11) in Theorem 4, then
$\Psi$-GMP satisfying (11) in Theorem 4, then ![]() $\mathbb{E}[A^d (s + t) - A^d (s) \mid A^d(u), 0 \le u \le s] = \omega (s) t$ for all
$\mathbb{E}[A^d (s + t) - A^d (s) \mid A^d(u), 0 \le u \le s] = \omega (s) t$ for all ![]() $s, t \ge 0$, where
$s, t \ge 0$, where ![]() $\omega (s) \equiv \omega + \gamma (1 + \gamma s)^{-1} (A^d (s) - s \omega)$.
$\omega (s) \equiv \omega + \gamma (1 + \gamma s)^{-1} (A^d (s) - s \omega)$.
Proposition 4 shows that conditioning on the history induces the process to have a new constant drift.
Let ![]() $\mathrm{Cor}(X,Y) \equiv \mathrm{Cov}(X,Y)/\sqrt{\mathrm{Var}(X)\mathrm{Var}(Y)}$ be the correlation function.
$\mathrm{Cor}(X,Y) \equiv \mathrm{Cov}(X,Y)/\sqrt{\mathrm{Var}(X)\mathrm{Var}(Y)}$ be the correlation function.
Corollary 4. (Correlation between non-overlapping time intervals, Proposition 2 of [Reference Fendick16].) For ![]() $A^d$ as in Proposition‘ 4,
$A^d$ as in Proposition‘ 4,
for all ![]() $t \ge 0$ and
$t \ge 0$ and ![]() $u \ge s \ge 0$.
$u \ge s \ge 0$.
Corollary 4 concludes that the correlation between increments over non-overlapping intervals of equal lengths depends on the length of the intervals (s here) but not at all on the separation between the intervals (u here). The following corollary gives the limiting distribution. Let ![]() $\Phi (x) \equiv \mathbb{P}(N(0,1) \le x)$ be the standard normal cumulative distribution function (CDF) and let
$\Phi (x) \equiv \mathbb{P}(N(0,1) \le x)$ be the standard normal cumulative distribution function (CDF) and let ![]() $\Phi^c (x) \equiv 1 - \Phi (x)$.
$\Phi^c (x) \equiv 1 - \Phi (x)$.
Corollary 5. (Asymptotics for the CDF.) For ![]() $A^d$ as in Proposition 4,
$A^d$ as in Proposition 4,
for all x and all ![]() $t \ge 0$. Moreover,
$t \ge 0$. Moreover,
 \begin{align} \begin{split} \lim_{x \rightarrow -\infty} \lim_{t \rightarrow \infty}{\mathbb{P}(A^d (t) \le x)} & = \Phi(-\omega/\sqrt{\beta\gamma}) , \\ \lim_{x \rightarrow +\infty} \lim_{t \rightarrow \infty}{\mathbb{P}(A^d (t) > x)} & = \Phi^{c}(-\omega/\sqrt{\beta\gamma}). \end{split}\end{align}
\begin{align} \begin{split} \lim_{x \rightarrow -\infty} \lim_{t \rightarrow \infty}{\mathbb{P}(A^d (t) \le x)} & = \Phi(-\omega/\sqrt{\beta\gamma}) , \\ \lim_{x \rightarrow +\infty} \lim_{t \rightarrow \infty}{\mathbb{P}(A^d (t) > x)} & = \Phi^{c}(-\omega/\sqrt{\beta\gamma}). \end{split}\end{align}
Proof. To get the first result we can directly take the limit in the Gaussian distribution of ![]() $A^d (t)$, which is
$A^d (t)$, which is
from which (16) follows directly.
Corollary 5 can be understood by recognizing that the standard deviation is the same order t as the mean, i.e. ![]() $\mathbb{E}[A^d (t)] = \omega t$ and
$\mathbb{E}[A^d (t)] = \omega t$ and ![]() $t^{-1}\sqrt{\mathrm{Var}(A^d (t))} \rightarrow \sqrt{\beta \gamma}$ as
$t^{-1}\sqrt{\mathrm{Var}(A^d (t))} \rightarrow \sqrt{\beta \gamma}$ as ![]() $t \rightarrow \infty$. Thus,
$t \rightarrow \infty$. Thus, ![]() $\mathbb{P}(A^d (t) > 0)$ does not approach 0 or 1 as t increases.
$\mathbb{P}(A^d (t) > 0)$ does not approach 0 or 1 as t increases.
5. Heavy-traffic limit for the  $\sum_{i=1}^{n} P_i/GI/1$ queue
$\sum_{i=1}^{n} P_i/GI/1$ queue
We now consider the single-server queue with arrival process ![]() $A^{d,n} (t) = A^{n} (\mu_n t)$ defined before (15). We assume that the service times are independent of the arrival process, mutually i.i.d. with a general distribution having mean
$A^{d,n} (t) = A^{n} (\mu_n t)$ defined before (15). We assume that the service times are independent of the arrival process, mutually i.i.d. with a general distribution having mean ![]() $1/\beta$ and squared coefficient of variation (variance divided by the square of the mean)
$1/\beta$ and squared coefficient of variation (variance divided by the square of the mean) ![]() $c_s^2$, where the service times are independent of the arrival times. We work with the associated renewal counting process C(t). Since we center with
$c_s^2$, where the service times are independent of the arrival times. We work with the associated renewal counting process C(t). Since we center with ![]() $\beta n t$ in (15), we assume that the rate of this renewal process is also
$\beta n t$ in (15), we assume that the rate of this renewal process is also ![]() $\beta$. Let the scaled service process be
$\beta$. Let the scaled service process be
As in [Reference Whitt36, Section 9.3], for the service process we only require a standard FCLT. Thus, that part of the following theorem can easily be generalized.
Let ![]() $X_n \equiv A^{d}_n - S_n$,
$X_n \equiv A^{d}_n - S_n$, ![]() $n \ge 1$, and let
$n \ge 1$, and let
where ![]() $\{Q^n (t)\,{:}\, t \ge 0\}$ is the queue length (number in system) process in the system with initial queue length
$\{Q^n (t)\,{:}\, t \ge 0\}$ is the queue length (number in system) process in the system with initial queue length ![]() $Q^n (0)$, arrival process
$Q^n (0)$, arrival process ![]() $\{A^{d}_n (t)\,{:}\, t \ge 0\}$ defined before (15) and scaled service renewal counting process
$\{A^{d}_n (t)\,{:}\, t \ge 0\}$ defined before (15) and scaled service renewal counting process ![]() $\{S_{n} (t)\,{:}\, t \ge 0\}$ defined in (17).
$\{S_{n} (t)\,{:}\, t \ge 0\}$ defined in (17).
With those definitions, we apply the one-dimensional reflection map in [Reference Whitt36, Section 13.5]. Let ![]() $\phi\,{:}\, D \times R \rightarrow D$ be the reflection map mapping a net input function x with
$\phi\,{:}\, D \times R \rightarrow D$ be the reflection map mapping a net input function x with ![]() $x(0) = 0$ and an initial queue length q(0) with
$x(0) = 0$ and an initial queue length q(0) with ![]() $q(0) \ge 0$ into q(t) for
$q(0) \ge 0$ into q(t) for ![]() $t > 0$ by
$t > 0$ by
The reflection map in (19) is a continuous function on its domain.
Theorem 5. (Heavy-traffic FCLT for the ![]() $\sum_{i = 1}^{n} P_i/GI/1$ queue.) Consider a sequence of
$\sum_{i = 1}^{n} P_i/GI/1$ queue.) Consider a sequence of ![]() $\sum_{i = 1}^{n} P_i/GI/1$ queues indexed by n, where the nth arrival process is the scaled superposition process
$\sum_{i = 1}^{n} P_i/GI/1$ queues indexed by n, where the nth arrival process is the scaled superposition process ![]() $A^{d}_n (t)$ in (15) and (8), while the scaled service process is the scaled renewal counting process
$A^{d}_n (t)$ in (15) and (8), while the scaled service process is the scaled renewal counting process ![]() $S_n (t)$ in (17). We make the following assumptions about the initial conditions: let the arrival process after time 0 be independent of
$S_n (t)$ in (17). We make the following assumptions about the initial conditions: let the arrival process after time 0 be independent of ![]() $Q_n (0)$; let the remaining service time in the process at time 0, if any, have finite mean; let all customers enter service in order of arrival from the service renewal counting process. If
$Q_n (0)$; let the remaining service time in the process at time 0, if any, have finite mean; let all customers enter service in order of arrival from the service renewal counting process. If ![]() $n^{(-1/2)}Q^{n}(0) = Q_{n}(0)$ as
$n^{(-1/2)}Q^{n}(0) = Q_{n}(0)$ as ![]() $n \rightarrow \infty$ and
$n \rightarrow \infty$ and ![]() $X_n \equiv A^{d}_n - S_n$, then
$X_n \equiv A^{d}_n - S_n$, then ![]() $(A^{d}_n, S_n, X_n, Q_n) \Rightarrow (A + \omega e,S,X,Q)$ in
$(A^{d}_n, S_n, X_n, Q_n) \Rightarrow (A + \omega e,S,X,Q)$ in ![]() $D^4$ as
$D^4$ as ![]() $n \rightarrow \infty$, where
$n \rightarrow \infty$, where ![]() $\omega \equiv \mu \beta$ and A is a
$\omega \equiv \mu \beta$ and A is a ![]() $\Psi$-GMP, while
$\Psi$-GMP, while ![]() $S = \beta^{3/2} c_s B$ with B being standard Brownian motion,
$S = \beta^{3/2} c_s B$ with B being standard Brownian motion, ![]() $X \equiv Y + \omega e$,
$X \equiv Y + \omega e$, ![]() $Y \equiv A - S$ and
$Y \equiv A - S$ and ![]() $Q \equiv \phi(X, Q(0))$ for
$Q \equiv \phi(X, Q(0))$ for ![]() $\phi$ in (19). In particular, Y is a
$\phi$ in (19). In particular, Y is a ![]() $\Psi$-GMP with
$\Psi$-GMP with ![]() $\mathbb{E}[Y(s)Y(t)] = \beta s(1 + \gamma t) + \beta^3 c_s^2 s$ and
$\mathbb{E}[Y(s)Y(t)] = \beta s(1 + \gamma t) + \beta^3 c_s^2 s$ and ![]() $\mathrm{Var}(Y(t)) = \beta t(1 + \gamma t) + \beta^3 c_s^2 t$ for
$\mathrm{Var}(Y(t)) = \beta t(1 + \gamma t) + \beta^3 c_s^2 t$ for ![]() $0 \le s \le t$, and so parameter pair
$0 \le s \le t$, and so parameter pair ![]() $(\alpha^*, \beta^*) = (\beta + \beta^3 c_s^2, -\beta \gamma)$ in the terminology of [Reference Fendick16], while X is a
$(\alpha^*, \beta^*) = (\beta + \beta^3 c_s^2, -\beta \gamma)$ in the terminology of [Reference Fendick16], while X is a ![]() $\Psi$-GMP with
$\Psi$-GMP with ![]() $\mathrm{Var}(X(t)) = \mathrm{Var}(Y(t))$ and deterministic drift
$\mathrm{Var}(X(t)) = \mathrm{Var}(Y(t))$ and deterministic drift ![]() $\omega \equiv \mu \beta$.
$\omega \equiv \mu \beta$.
Proof. We apply the standard methodology for establishing a heavy-traffic FCLT for a single-server queue. We apply Donsker’s FCLT for the service times in [Reference Whitt36, Section 4.3] and the inverse equivalence in [Reference Whitt36, Theorem 7.3.2], in particular [Reference Whitt36, Corollary 7.3.2 on p. 236], to obtain ![]() $S_n \Rightarrow \beta^{3/2} c_s B$ in D as
$S_n \Rightarrow \beta^{3/2} c_s B$ in D as ![]() $n \rightarrow \infty$, where B is a standard Brownian motion. Then we can apply Corollary 3 to obtain the limit
$n \rightarrow \infty$, where B is a standard Brownian motion. Then we can apply Corollary 3 to obtain the limit ![]() $A^{d}_n \Rightarrow A + \omega e$ in D. Joint convergence for
$A^{d}_n \Rightarrow A + \omega e$ in D. Joint convergence for ![]() $(A^{d}_n, S_n)$ then follows from independence and [Reference Whitt36, Theorem 11.4.4]. We can then apply [Reference Whitt36, Theorems 9.3.3, 9.3.4, 9.8.2].
$(A^{d}_n, S_n)$ then follows from independence and [Reference Whitt36, Theorem 11.4.4]. We can then apply [Reference Whitt36, Theorems 9.3.3, 9.3.4, 9.8.2].
Remark 6. (Other processes) As indicated in [Reference Whitt36, Theorems 9.3.3 and 9.3.4], we can also obtain a heavy-traffic limit for other processes, including the workload and departure process, jointly with the limit above, by the same argument.
By the continuous mapping theorem with the projection map, we have the following corollary providing a limit for the marginal distributions. Theorem 5 of [Reference Fendick16] provides the explicit form of the marginal distribution of the limit process, so that it can provide useful numerical results. Let the PDF of the joint limiting distribution be denoted by ![]() $f(x_{s}, q_{s},q_{s + t}) \equiv f_{X(s), Q(s), Q(s + t)} (x_{s}, q_{s},q_{s + t})$, and similarly for the associated marginal PDFs and conditional PDFs. We express the limiting distribution in terms of the exponential function and the standard normal CDF
$f(x_{s}, q_{s},q_{s + t}) \equiv f_{X(s), Q(s), Q(s + t)} (x_{s}, q_{s},q_{s + t})$, and similarly for the associated marginal PDFs and conditional PDFs. We express the limiting distribution in terms of the exponential function and the standard normal CDF ![]() $\Phi (x) \equiv \mathbb{P}(N(0,1) \le x)$ and PDF
$\Phi (x) \equiv \mathbb{P}(N(0,1) \le x)$ and PDF ![]() $\phi (x)$. Let the associated CDF of
$\phi (x)$. Let the associated CDF of ![]() $N(m, \sigma^2) \stackrel{\rm d}{=} m + \sigma N(0,1)$ be denoted by
$N(m, \sigma^2) \stackrel{\rm d}{=} m + \sigma N(0,1)$ be denoted by ![]() $\Phi (x;\ m, \sigma^2)$, and similarly for the others. To connect with [Reference Fendick16], let
$\Phi (x;\ m, \sigma^2)$, and similarly for the others. To connect with [Reference Fendick16], let
where
as in Remark 4. Let ![]() $\delta (\!\cdot\!)$ be the Dirac delta function and let
$\delta (\!\cdot\!)$ be the Dirac delta function and let ![]() $\textbf{1}_A$ be the indicator function, equal to 1 on A and 0 elsewhere.
$\textbf{1}_A$ be the indicator function, equal to 1 on A and 0 elsewhere.
Corollary 6. (Marginal limiting distributions.) Under the conditions of Theorem 5, ![]() $(X_n (s), Q_n (s), Q_n (s + t)) \Rightarrow (X (s), Q(s), Q(s+t))$ in
$(X_n (s), Q_n (s), Q_n (s + t)) \Rightarrow (X (s), Q(s), Q(s+t))$ in ![]() ${\mathbb R}^3$ as
${\mathbb R}^3$ as ![]() $n \rightarrow \infty$, where X(s) is a (mean-
$n \rightarrow \infty$, where X(s) is a (mean-![]() $\omega s$, variance
$\omega s$, variance ![]() $s(\alpha^* - \beta_{s}^* s))$ Gaussian random variable for
$s(\alpha^* - \beta_{s}^* s))$ Gaussian random variable for ![]() $\beta_{s}^*$ in (20), while the joint limiting distribution has joint PDF
$\beta_{s}^*$ in (20), while the joint limiting distribution has joint PDF
where, assuming ![]() $\mathbb{P}(Q(0) = q_0) = 1$,
$\mathbb{P}(Q(0) = q_0) = 1$,
 \begin{align*} f(x_{s}) & \equiv \phi(x_s;\ \omega s, s(\alpha^* - \beta^* s)) = \frac{1}{\sqrt{s(\alpha^* - \beta^{*} s)}\,} \phi\left( \frac{x_s - \omega s}{\sqrt{s(\alpha^* - \beta^* s)}\,}\right)\!, \\[3pt] f(q_{s} \mid x_{s}) & \equiv \left(1 - \mathrm{e}^{\{-2q_{s}(q_{s} - x_s)/(\alpha^*s) \}}\right)(\delta(q_s - q_{0} - x_s)\textbf{1}_{\{q_s \ge 0\}} + \textbf{1}_{\{q_s - q_0 - x_s \ge 0\}}\delta(q_s)) \\[3pt] & \quad + \left(\frac{(4 q_s - 2 x_s)\mathrm{e}^{\{- 2q_s( q_s - x_s)/(\alpha^* s)\}}}{\alpha^* s}\right) \textbf{1}_{\{q_{s} - q_0 - x_s \ge 0\}}\textbf{1}_{\{q_s \ge 0\}}, \\[3pt] f(q_{s + t} \mid x_{s}, q_{s}) & \equiv \frac{1}{\sqrt{t(\alpha^* - \beta_{s}^{*} t)}\,}\phi\left( \frac{q_{s+t} - q_{s} - \omega_{s} t}{\sqrt{t(\alpha^* - \beta_{s}^* t)}\,}\right) \\[3pt] & \quad + \mathrm{e}^{\{-2 q_{s+t}(\beta_{s}^* q_{s + t} - \alpha^* \omega_s)/\alpha^{* 2}\}} (A_1 + A_2) \end{align*}
\begin{align*} f(x_{s}) & \equiv \phi(x_s;\ \omega s, s(\alpha^* - \beta^* s)) = \frac{1}{\sqrt{s(\alpha^* - \beta^{*} s)}\,} \phi\left( \frac{x_s - \omega s}{\sqrt{s(\alpha^* - \beta^* s)}\,}\right)\!, \\[3pt] f(q_{s} \mid x_{s}) & \equiv \left(1 - \mathrm{e}^{\{-2q_{s}(q_{s} - x_s)/(\alpha^*s) \}}\right)(\delta(q_s - q_{0} - x_s)\textbf{1}_{\{q_s \ge 0\}} + \textbf{1}_{\{q_s - q_0 - x_s \ge 0\}}\delta(q_s)) \\[3pt] & \quad + \left(\frac{(4 q_s - 2 x_s)\mathrm{e}^{\{- 2q_s( q_s - x_s)/(\alpha^* s)\}}}{\alpha^* s}\right) \textbf{1}_{\{q_{s} - q_0 - x_s \ge 0\}}\textbf{1}_{\{q_s \ge 0\}}, \\[3pt] f(q_{s + t} \mid x_{s}, q_{s}) & \equiv \frac{1}{\sqrt{t(\alpha^* - \beta_{s}^{*} t)}\,}\phi\left( \frac{q_{s+t} - q_{s} - \omega_{s} t}{\sqrt{t(\alpha^* - \beta_{s}^* t)}\,}\right) \\[3pt] & \quad + \mathrm{e}^{\{-2 q_{s+t}(\beta_{s}^* q_{s + t} - \alpha^* \omega_s)/\alpha^{* 2}\}} (A_1 + A_2) \end{align*}
for
 \begin{align*} A_1 & \equiv \left(\frac{4 \beta_{s}^* q_{s + t} - 2 \alpha^* \omega_s}{\alpha^{*2}}\right) \Phi\left( \frac{\left(2 \beta_{s}^* q_{s+t} - \alpha^* \omega_{s}\right)t - \alpha^*(q_{s+t} + q_{s})} {\alpha^* \sqrt{t(\alpha^* - \beta_{s}^* t)}}\right) , \\[3pt] A_2 & \equiv \left(\frac{\alpha^* - 2 \beta_{s}^* t}{\alpha^*\sqrt{t(\alpha^* - \beta_{s}^* t)}\,}\right)\phi\left( \frac{\left(2 \beta_{s}^* q_{s+t} - \alpha^* \omega_{s}\right)t - \alpha^*(q_{s+t} + q_{s})}{\alpha^* \sqrt{t(\alpha^* - \beta_{s}^* t)}}\right) , \end{align*}
\begin{align*} A_1 & \equiv \left(\frac{4 \beta_{s}^* q_{s + t} - 2 \alpha^* \omega_s}{\alpha^{*2}}\right) \Phi\left( \frac{\left(2 \beta_{s}^* q_{s+t} - \alpha^* \omega_{s}\right)t - \alpha^*(q_{s+t} + q_{s})} {\alpha^* \sqrt{t(\alpha^* - \beta_{s}^* t)}}\right) , \\[3pt] A_2 & \equiv \left(\frac{\alpha^* - 2 \beta_{s}^* t}{\alpha^*\sqrt{t(\alpha^* - \beta_{s}^* t)}\,}\right)\phi\left( \frac{\left(2 \beta_{s}^* q_{s+t} - \alpha^* \omega_{s}\right)t - \alpha^*(q_{s+t} + q_{s})}{\alpha^* \sqrt{t(\alpha^* - \beta_{s}^* t)}}\right) , \end{align*}
![]() $q_s, q_{s+t} \ge 0$. As a consequence, the associated conditional CDF, for
$q_s, q_{s+t} \ge 0$. As a consequence, the associated conditional CDF, for ![]() $q_{s+t} \ge 0$, is
$q_{s+t} \ge 0$, is
 \begin{align} \mathbb{P}(Q(s + t) \le q_{s+t} \mid X(s) &= x_s, Q(s) = q_{s}) = \Phi\left( \frac{q_{s+t} - q_{s} - \omega_{s} t}{\sqrt{t(\alpha^* - \beta_{s}^* t)}}\right)\nonumber\\[3pt] &\quad - \mathrm{e}^{\left(\frac{ -2 q_{s+t}(\beta_{s}^* q_{s + t} - \alpha^* \omega_s)}{\alpha^{* 2}}\right)}\Phi\left(\frac{(2 \beta_{s}^* q_{s+t} - \alpha^* \omega_{s})t- \alpha^*(q_{s+t} + q_{s})}{\alpha^*\sqrt{t(\alpha^* - \beta_{s}^* t)}}\right) \end{align}
\begin{align} \mathbb{P}(Q(s + t) \le q_{s+t} \mid X(s) &= x_s, Q(s) = q_{s}) = \Phi\left( \frac{q_{s+t} - q_{s} - \omega_{s} t}{\sqrt{t(\alpha^* - \beta_{s}^* t)}}\right)\nonumber\\[3pt] &\quad - \mathrm{e}^{\left(\frac{ -2 q_{s+t}(\beta_{s}^* q_{s + t} - \alpha^* \omega_s)}{\alpha^{* 2}}\right)}\Phi\left(\frac{(2 \beta_{s}^* q_{s+t} - \alpha^* \omega_{s})t- \alpha^*(q_{s+t} + q_{s})}{\alpha^*\sqrt{t(\alpha^* - \beta_{s}^* t)}}\right) \end{align}
and, for ![]() $q_t \ge 0$,
$q_t \ge 0$,
 \begin{multline*} \mathbb{P}(Q(t) \le q_{t}) = \Phi\left( \frac{q_{t} - q_{0}- \omega t}{\sqrt{t(\alpha^* - \beta^* t)}\,}\right) \\[3pt] - \mathrm{e}^{\left(\frac{ -2 q_{t}(\beta^* q_{t} - \alpha^* \omega)}{\alpha^{* 2}}\right)}\Phi\left(\frac{(2 \beta^* q_{t} - \alpha^* \omega)t- \alpha^*(q_{t} + q_{0})}{\alpha^*\sqrt{t(\alpha^* - \beta^* t)}}\right)\!.\end{multline*}
\begin{multline*} \mathbb{P}(Q(t) \le q_{t}) = \Phi\left( \frac{q_{t} - q_{0}- \omega t}{\sqrt{t(\alpha^* - \beta^* t)}\,}\right) \\[3pt] - \mathrm{e}^{\left(\frac{ -2 q_{t}(\beta^* q_{t} - \alpha^* \omega)}{\alpha^{* 2}}\right)}\Phi\left(\frac{(2 \beta^* q_{t} - \alpha^* \omega)t- \alpha^*(q_{t} + q_{0})}{\alpha^*\sqrt{t(\alpha^* - \beta^* t)}}\right)\!.\end{multline*}
Proof. We give a brief overview of the proof in [Reference Fendick16] (appearing on the last two pages), which draws heavily on [Reference Hajek22]. We focus on ![]() $X(t) \equiv Y(t) + \omega t$, where Y is an
$X(t) \equiv Y(t) + \omega t$, where Y is an ![]() $(\alpha^*,\beta^*)$
$(\alpha^*,\beta^*)$ ![]() $\Psi$-GMP for
$\Psi$-GMP for ![]() $(\alpha^*,\beta^*) = (\beta + \beta^3 c_s^2, - \beta \gamma)$ and
$(\alpha^*,\beta^*) = (\beta + \beta^3 c_s^2, - \beta \gamma)$ and ![]() $\omega t$ is the drift, as in Theorem 5. We exploit known results for the Brownian bridge by looking at increments from the past conditioned on later process values. For that purpose, let
$\omega t$ is the drift, as in Theorem 5. We exploit known results for the Brownian bridge by looking at increments from the past conditioned on later process values. For that purpose, let ![]() $X^{(s)} (t) \equiv X(s + t) - X(s)$ for some (s, t) with
$X^{(s)} (t) \equiv X(s + t) - X(s)$ for some (s, t) with ![]() $0 \le s \le t$. We observe that conditioning
$0 \le s \le t$. We observe that conditioning ![]() $X^{(s)}$ on both
$X^{(s)}$ on both ![]() $X(s) = x_s$ and
$X(s) = x_s$ and ![]() $Q(s) = q_s$ results in a new
$Q(s) = q_s$ results in a new ![]() $(\alpha^*,\beta_{s}^*)$
$(\alpha^*,\beta_{s}^*)$ ![]() $\Psi$-GMP for
$\Psi$-GMP for ![]() $\beta_{s}^*$ in (20) that depends on
$\beta_{s}^*$ in (20) that depends on ![]() $x_s$ but not
$x_s$ but not ![]() $q_s$. Further conditioning it on
$q_s$. Further conditioning it on ![]() $X^{(s)} (t) = x^{(s)}_t$ for some
$X^{(s)} (t) = x^{(s)}_t$ for some ![]() $t\ge s$ results in yet another
$t\ge s$ results in yet another ![]() $(\alpha^*, t^{-1} \alpha^*)$
$(\alpha^*, t^{-1} \alpha^*)$ ![]() $\Psi$-GMP with drift
$\Psi$-GMP with drift ![]() $t^{-1} x^{(s)}_t$ on [0, t] (which no longer depends on
$t^{-1} x^{(s)}_t$ on [0, t] (which no longer depends on ![]() $\beta_{s}^*$). That process depends on
$\beta_{s}^*$). That process depends on ![]() $x^{(s)}_t$ but on neither
$x^{(s)}_t$ but on neither ![]() $q_s$ nor
$q_s$ nor ![]() $x_s$. Therefore, the process obtained by conditioning
$x_s$. Therefore, the process obtained by conditioning ![]() $\{Q(u)\,{:}\, s \le u \le s + t\}$ on
$\{Q(u)\,{:}\, s \le u \le s + t\}$ on ![]() $X(s) = x_s$,
$X(s) = x_s$, ![]() $Q(s) = q_s$ and
$Q(s) = q_s$ and ![]() $X^{(s)} (t) = x^{(s)}_t$ begins at state
$X^{(s)} (t) = x^{(s)}_t$ begins at state ![]() $q_s$ at time s and evolves according to a net input process that is an
$q_s$ at time s and evolves according to a net input process that is an ![]() $(\alpha^*, t^{-1} \alpha^*)$
$(\alpha^*, t^{-1} \alpha^*)$ ![]() $\Psi$-GMP on the interval [0, t]. That process is a scaled Brownian bridge, for which the distribution of the queue length was previously obtained by [Reference Hajek22]. The result in (23) is obtained from that conditional queue length distribution using the law of total probability. We remark that
$\Psi$-GMP on the interval [0, t]. That process is a scaled Brownian bridge, for which the distribution of the queue length was previously obtained by [Reference Hajek22]. The result in (23) is obtained from that conditional queue length distribution using the law of total probability. We remark that ![]() $f(q_s \mid x_s)$ in (22) is the density of the CDF
$f(q_s \mid x_s)$ in (22) is the density of the CDF
as derived by [Reference Hajek22]. It suffices to apply the product rule for differentiation in this equation.
Some further insight can be gained from further Gaussian LLN limits for the limit process. For that purpose, let ![]() $X_s (t) \equiv (X(s + t) \mid X(s)= x_s)$ and
$X_s (t) \equiv (X(s + t) \mid X(s)= x_s)$ and ![]() $Q_s (t) \equiv (Q(s + t) \mid X(s) = x_s,Q(s) = q_s)$. Let
$Q_s (t) \equiv (Q(s + t) \mid X(s) = x_s,Q(s) = q_s)$. Let ![]() $N(m, \sigma^2)$ denote a normal random variable with mean m and variance
$N(m, \sigma^2)$ denote a normal random variable with mean m and variance ![]() $\sigma^2$, and let
$\sigma^2$, and let ![]() $(x)^{+} \equiv \max{\{x, 0\}}$, so that
$(x)^{+} \equiv \max{\{x, 0\}}$, so that ![]() $\mathbb{P}(N(m, \sigma^2)^{+} = 0) = \mathbb{P}(N(m, \sigma^2) \le 0)$.
$\mathbb{P}(N(m, \sigma^2)^{+} = 0) = \mathbb{P}(N(m, \sigma^2) \le 0)$.
Corollary 7. (LLN limit for the limit process.) Given the ![]() $\Psi$-GMP limit in Theorem 4 and the associated heavy-traffic limit in Theorem 5 and Corollary 6, we have the following limit:
$\Psi$-GMP limit in Theorem 4 and the associated heavy-traffic limit in Theorem 5 and Corollary 6, we have the following limit:
as ![]() $t \rightarrow \infty$ for some constant
$t \rightarrow \infty$ for some constant ![]() $s > 0$ and
$s > 0$ and ![]() $(\omega_{s}, \beta^{*}_{s})$ in (21), where
$(\omega_{s}, \beta^{*}_{s})$ in (21), where ![]() $(N_1, N_2)$ is a random vector in
$(N_1, N_2)$ is a random vector in ![]() ${\mathbb R}^2$ with Gaussian one-dimensional marginal distributions.
${\mathbb R}^2$ with Gaussian one-dimensional marginal distributions.
Proof. For the first three processes, we exploit the distribution as a function of t as in the proof of Corollary 5. For the next two processes, note that ![]() $\mathbb{P}(X(t) \le xt) \rightarrow \Phi((x - \omega)/\sqrt{\beta \gamma})$ as
$\mathbb{P}(X(t) \le xt) \rightarrow \Phi((x - \omega)/\sqrt{\beta \gamma})$ as ![]() $t \rightarrow \infty$ as just described, and
$t \rightarrow \infty$ as just described, and
 \begin{eqnarray*}\mathbb{P}(Q (t) \le t q \mid X(t) = tx) & = & (1 - \mathrm{e}^{-(2t^2q(q-x))/\alpha^* s})\textbf{1}_{\{tq - tx \ge q_0\}}\textbf{1}_{\{q \ge 0\}} \nonumber \\ & = & (1 - \mathrm{e}^{-(2t^2q(q-x))/\alpha^* s})\textbf{1}_{\{t \ge q_0/(q-x)\}}\textbf{1}_{\{q - x > 0\}}\textbf{1}_{\{q \ge 0\}} \nonumber \\ & \rightarrow & \textbf{1}_{\{q - x > 0\}}\textbf{1}_{\{q \ge 0\}} \qquad \text{ as } t \rightarrow \infty.\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}(Q (t) \le t q \mid X(t) = tx) & = & (1 - \mathrm{e}^{-(2t^2q(q-x))/\alpha^* s})\textbf{1}_{\{tq - tx \ge q_0\}}\textbf{1}_{\{q \ge 0\}} \nonumber \\ & = & (1 - \mathrm{e}^{-(2t^2q(q-x))/\alpha^* s})\textbf{1}_{\{t \ge q_0/(q-x)\}}\textbf{1}_{\{q - x > 0\}}\textbf{1}_{\{q \ge 0\}} \nonumber \\ & \rightarrow & \textbf{1}_{\{q - x > 0\}}\textbf{1}_{\{q \ge 0\}} \qquad \text{ as } t \rightarrow \infty.\end{eqnarray*}
The joint PDF for the two limits is therefore
The joint PDF for the limits of the last two processes is similarly obtained.
Figure 2 illustrates the heavy-traffic limits established in this section by plotting results of simulations of the scaled queue-length process in the ![]() $\sum_{i = 1}^{n} P_i/D/1$ queue.
$\sum_{i = 1}^{n} P_i/D/1$ queue.
We consider the ![]() $(\beta,\gamma)$
$(\beta,\gamma)$ ![]() $\Psi$-GPP with parameters
$\Psi$-GPP with parameters ![]() $\beta = \gamma = 1$ as a function of the number n of processes superposed. We introduce a negative drift in the limit process by using (14) with
$\beta = \gamma = 1$ as a function of the number n of processes superposed. We introduce a negative drift in the limit process by using (14) with ![]() $\mu = 1$. We let the service times initially have mean (and fixed value) 1, but that becomes
$\mu = 1$. We let the service times initially have mean (and fixed value) 1, but that becomes ![]() $1/n$ with the scaling in (17). We look at n ranging from 4 to 200. We consider two values of T: 25 and 500. The similarity of the plots supports Corollary 7. The convergence as n increases supports Corollary 6. Numerical study indicates errors roughly of order
$1/n$ with the scaling in (17). We look at n ranging from 4 to 200. We consider two values of T: 25 and 500. The similarity of the plots supports Corollary 7. The convergence as n increases supports Corollary 6. Numerical study indicates errors roughly of order ![]() $1/\sqrt{n}$.
$1/\sqrt{n}$.
Remark 7. (Insights from Corollary 7) Contrary to the usual queueing behavior, the limits are continuous functions of the drift constant ![]() $\omega$, showing that the usual critical level for stability does not apply to the limit process. We elaborate on this property in Section 6.1. The limit for the last two components in Corollary 7 shows that the limit as
$\omega$, showing that the usual critical level for stability does not apply to the limit process. We elaborate on this property in Section 6.1. The limit for the last two components in Corollary 7 shows that the limit as ![]() $t \rightarrow \infty$ is not independent of fixed s. Corollary 7 also quantifies the growing variability in all processes except for the service-time process as t increases. The conditional random variable
$t \rightarrow \infty$ is not independent of fixed s. Corollary 7 also quantifies the growing variability in all processes except for the service-time process as t increases. The conditional random variable ![]() $Q_s (t)$ is highly variable as t increases for any given conditioning event
$Q_s (t)$ is highly variable as t increases for any given conditioning event ![]() $(X(s), Q(s)) = (x_s, q_s)$.
$(X(s), Q(s)) = (x_s, q_s)$.
6. Steady-state results for queues with  $\Psi$-GPP arrivals
$\Psi$-GPP arrivals
This section is something of a departure from Sections 3–5, because we no longer consider FCLTs or heavy-traffic limits. In this section we present further results for queues with ![]() $\Psi$-GPP arrivals. In Section 6.1 we obtain some elementary stability results and show that we can obtain both positive and negative results from a sample-path version of Little’s law. In Section 6.2 we show that stability can be achieved when there are infinitely many servers. In Section 6.3 we show that it is also possible to devise adaptive service policies that stabilize performance in a single-server queue with
$\Psi$-GPP arrivals. In Section 6.1 we obtain some elementary stability results and show that we can obtain both positive and negative results from a sample-path version of Little’s law. In Section 6.2 we show that stability can be achieved when there are infinitely many servers. In Section 6.3 we show that it is also possible to devise adaptive service policies that stabilize performance in a single-server queue with ![]() $\Psi$-GPP arrivals. We use new (but similar) notation in this section.
$\Psi$-GPP arrivals. We use new (but similar) notation in this section.
6.1. Stability and Little’s law
We first discuss the implications of the LLN in Theorem 3 for the ![]() $P/GI/1$ queue with a Pólya arrival process. For this purpose, let the service times have mean 1. Given Theorem 3, the following is a standard heavy-traffic law of large numbers for overloaded queues, as in [Reference Whitt36, Theorem 5.3.2].
$P/GI/1$ queue with a Pólya arrival process. For this purpose, let the service times have mean 1. Given Theorem 3, the following is a standard heavy-traffic law of large numbers for overloaded queues, as in [Reference Whitt36, Theorem 5.3.2].
Corollary 8. (Explosion.) Let Q(t) be the queue length process, starting with ![]() $Q(0) = 0$, in the
$Q(0) = 0$, in the ![]() $P/GI/1$ queue with a
$P/GI/1$ queue with a ![]() $(\beta, \gamma)$
$(\beta, \gamma)$ ![]() $\Psi$-GPP arrival process, where
$\Psi$-GPP arrival process, where ![]() $0 < \beta < \infty$ and
$0 < \beta < \infty$ and ![]() $0 < \gamma < \infty$, and i.i.d. service times with mean 1. Then
$0 < \gamma < \infty$, and i.i.d. service times with mean 1. Then ![]() $t^{-1} Q(t) \rightarrow \max{\{L(\beta, \gamma) - 1, 0\}}$ as
$t^{-1} Q(t) \rightarrow \max{\{L(\beta, \gamma) - 1, 0\}}$ as ![]() $t \rightarrow \infty$ with probability 1, so that
$t \rightarrow \infty$ with probability 1, so that ![]() $\mathbb{P}(Q(t) \rightarrow \infty \text{ as } t \rightarrow \infty) = \mathbb{P}(L(\gamma,\beta) >1)$, where
$\mathbb{P}(Q(t) \rightarrow \infty \text{ as } t \rightarrow \infty) = \mathbb{P}(L(\gamma,\beta) >1)$, where ![]() $0 < \mathbb{P}(L(\gamma, \beta)\break > 1) < 1$.
$0 < \mathbb{P}(L(\gamma, \beta)\break > 1) < 1$.
We illustrate the less critical role of the usual traffic intensity by showing the results of a simulation experiment. Figure 3 plots the 25 individual sample paths of ![]() $Q(t)/t$ over [0, 250], starting empty, for a
$Q(t)/t$ over [0, 250], starting empty, for a ![]() $P/D/1$ queue with parameter pairs
$P/D/1$ queue with parameter pairs ![]() $(\beta, \gamma) = (0.5, 1)$ (left) and
$(\beta, \gamma) = (0.5, 1)$ (left) and ![]() $(\beta, \gamma) = (1.5, 1)$ (right). These plots only clearly display the paths that tend to be unstable by time
$(\beta, \gamma) = (1.5, 1)$ (right). These plots only clearly display the paths that tend to be unstable by time ![]() $t = 250$. There are 3 of these in the 25 plots for
$t = 250$. There are 3 of these in the 25 plots for ![]() $\beta = 0.5$ on the left, but about 12 in the 25 plots for
$\beta = 0.5$ on the left, but about 12 in the 25 plots for ![]() $\beta = 1.5$ on the right. However, Corollary 2 implies that we cannot draw a firm conclusion about ultimate stability by what we see over the interval [0, 250].
$\beta = 1.5$ on the right. However, Corollary 2 implies that we cannot draw a firm conclusion about ultimate stability by what we see over the interval [0, 250].

Figure 3: Display of 25 individual sample paths of ![]() $Q(t)/t$ for
$Q(t)/t$ for ![]() $0 \le t \le 250$, starting empty, for a
$0 \le t \le 250$, starting empty, for a ![]() $P/D/1$ queue with parameter pairs
$P/D/1$ queue with parameter pairs ![]() $(\beta, \gamma) = (0.5, 1)$ (left) and
$(\beta, \gamma) = (0.5, 1)$ (left) and ![]() $(\beta, \gamma) = (1.5, 1)$ (right).
$(\beta, \gamma) = (1.5, 1)$ (right).
Nevertheless, there is a version of Little’s law in this setting that can accommodate quite general initial conditions, but for simplicity assume that the system starts empty. Let ![]() $W_k$ be the waiting time of customer k, and let
$W_k$ be the waiting time of customer k, and let
Corollary 9. (Little’s law.) Consider the ![]() $P/GI/1$ queue with a
$P/GI/1$ queue with a ![]() $(\beta, \gamma)$
$(\beta, \gamma)$ ![]() $\Psi$-GPP arrival process starting with
$\Psi$-GPP arrival process starting with ![]() $Q(0) = 0$ as above, where
$Q(0) = 0$ as above, where ![]() $0 < \beta < \infty$ and
$0 < \beta < \infty$ and ![]() $0 < \gamma < \infty$.
$0 < \gamma < \infty$.
![]() $(\textit{a})$ If
$(\textit{a})$ If ![]() $W^*$ in (25) is well defined and finite and if
$W^*$ in (25) is well defined and finite and if ![]() $L(\beta,\gamma) < 1$, which occurs with positive probability, then
$L(\beta,\gamma) < 1$, which occurs with positive probability, then ![]() $L^*$ in (25) is well defined and
$L^*$ in (25) is well defined and ![]() $L^* = \lambda^* W^* < \infty$.
$L^* = \lambda^* W^* < \infty$.
![]() $(\textit{b})$ If
$(\textit{b})$ If ![]() $L(\beta, \gamma) > 1$, as occurs with positive probability, then
$L(\beta, \gamma) > 1$, as occurs with positive probability, then ![]() $L^*$ in (25) is well defined but
$L^*$ in (25) is well defined but ![]() $L^* = \infty$. Moreover,
$L^* = \infty$. Moreover, ![]() $W^*$ is then also well defined and
$W^*$ is then also well defined and ![]() $W^* = L^* = \infty$.
$W^* = L^* = \infty$.
Proof. For part (a), we apply the sample-path version of Little’s law from [Reference Stidham35]. For part (b), we apply Corollary 8 together with [Reference Wolff and Yao40, (6)]. Sufficient conditions for more results are also given in [Reference Wolff and Yao40].
6.2. The  $\Psi$-GPP/GI/
$\Psi$-GPP/GI/ $\infty$ queue
$\infty$ queue
We next consider the ![]() $\Psi$-GPP/GI/
$\Psi$-GPP/GI/![]() $\infty$ infinite-server queue. We show that bounded service times ensure reaching steady state in finite time. Let
$\infty$ infinite-server queue. We show that bounded service times ensure reaching steady state in finite time. Let ![]() $\stackrel{\rm d}{=}$ denote equality in distribution.
$\stackrel{\rm d}{=}$ denote equality in distribution.
Theorem 6. (Infinite-server queue with bounded service times.) For an infinite-server queue with a ![]() $(\beta, \gamma)$
$(\beta, \gamma)$ ![]() $\Psi$-GPP arrival process, if the service times are (i) independent of the arrival process, (ii) mutually i.i.d., each distributed as a random variable V, and (iii)
$\Psi$-GPP arrival process, if the service times are (i) independent of the arrival process, (ii) mutually i.i.d., each distributed as a random variable V, and (iii) ![]() $\mathbb{P}(V \le \zeta) = 1$ for some
$\mathbb{P}(V \le \zeta) = 1$ for some ![]() $\zeta < \infty$, then the number of busy servers Q(t) reaches steady state by time
$\zeta < \infty$, then the number of busy servers Q(t) reaches steady state by time ![]() $\zeta$, i.e.
$\zeta$, i.e.
Proof. We apply a useful device from [Reference Glynn and Whitt19, Section 2]. We note that if the service times are deterministic with ![]() $\mathbb{P}(V = d) = 1$, then
$\mathbb{P}(V = d) = 1$, then
Because the ![]() $\Psi$-GPP arrival process has stationary increments, the distribution of Q(t) in (27) is independent of t for
$\Psi$-GPP arrival process has stationary increments, the distribution of Q(t) in (27) is independent of t for ![]() $t \ge d$, and so has reached steady state by time d.
$t \ge d$, and so has reached steady state by time d.
We next observe that Q(t) also reaches steady state in finite time when the service time distribution has finite support within the interval ![]() $[0, \zeta]$. Hence, suppose that
$[0, \zeta]$. Hence, suppose that ![]() $P(V = d_i) = q_i$,
$P(V = d_i) = q_i$, ![]() $1 \le i \le n$. Now we can classify the arrivals by ‘type’ according to their service time, where this type assignment is done independently of the arrival process. Thus, the distribution of Q(t) is the sum of the number of each type in the system at time t, so that we can write
$1 \le i \le n$. Now we can classify the arrivals by ‘type’ according to their service time, where this type assignment is done independently of the arrival process. Thus, the distribution of Q(t) is the sum of the number of each type in the system at time t, so that we can write
where ![]() $T_i (t, d_i)$ is the proportion of the
$T_i (t, d_i)$ is the proportion of the ![]() $N(t) - N(t - d_i)$ arrivals in
$N(t) - N(t - d_i)$ arrivals in ![]() $[t - d_i, t]$ that are of type i, i.e. have service times
$[t - d_i, t]$ that are of type i, i.e. have service times ![]() $d_i$, which has a multinomial distribution.
$d_i$, which has a multinomial distribution.
We then observe that the distribution of Q(t) is independent of t, because the random vector ![]() $(N(t) - N(t - d_i)\,{:}\, 1\le i \le n)$ is independent of t in
$(N(t) - N(t - d_i)\,{:}\, 1\le i \le n)$ is independent of t in ![]() ${\mathbb R}^n$ for all
${\mathbb R}^n$ for all ![]() $t \ge \max{\{d_i\,{:}\, 1 \le i \le n\}}$.
$t \ge \max{\{d_i\,{:}\, 1 \le i \le n\}}$.
The joint distribution of ![]() $(T_i (t, d_i)\,{:}\, 1 \le i \le n)$ is somewhat complicated, but we can directly deduce that it has property (26) and we can write down the mean:
$(T_i (t, d_i)\,{:}\, 1 \le i \le n)$ is somewhat complicated, but we can directly deduce that it has property (26) and we can write down the mean:
 \begin{eqnarray*} \mathbb{E}[Q (t)] & = & \sum_{i = 1}^{n} \mathbb{E}[Q_i (t)] = \sum_{i = 1}^{n} \mathbb{E}[N(t) - N(t - d_i)] \mathbb{E}[T_i (t, d_i)] \nonumber \\& = &\sum_{i = 1}^{n} \beta d_i \mathbb{E}[T_i (t, d_i)] = \beta \mathbb{E}[V].\end{eqnarray*}
\begin{eqnarray*} \mathbb{E}[Q (t)] & = & \sum_{i = 1}^{n} \mathbb{E}[Q_i (t)] = \sum_{i = 1}^{n} \mathbb{E}[N(t) - N(t - d_i)] \mathbb{E}[T_i (t, d_i)] \nonumber \\& = &\sum_{i = 1}^{n} \beta d_i \mathbb{E}[T_i (t, d_i)] = \beta \mathbb{E}[V].\end{eqnarray*}
Since the probability distributions with finite support in ![]() $[0, \zeta]$ are dense in the space of all probability distributions with support in
$[0, \zeta]$ are dense in the space of all probability distributions with support in ![]() $[0, \zeta]$, we obtain the general results by taking a limit. To obtain the limit, note that we can express Q(t) in terms of the arrival times
$[0, \zeta]$, we obtain the general results by taking a limit. To obtain the limit, note that we can express Q(t) in terms of the arrival times ![]() $T_i$ associated with the arrival process N(t) and service times
$T_i$ associated with the arrival process N(t) and service times ![]() $V_i$ by
$V_i$ by ![]() $Q(t) = \sum_{i = 1}^{N(t)} \textbf{1}_{\{T_i + V_i > t\}}$, which representation implies that Q(t) is almost surely a continuous function of the service times with respect to the limit process, so that we can apply the generalized continuous mapping theorem from [Reference Whitt36, Theorem 3.4.4]. In particular, we see that Q(t) is almost surely a continuous function of the service times except when
$Q(t) = \sum_{i = 1}^{N(t)} \textbf{1}_{\{T_i + V_i > t\}}$, which representation implies that Q(t) is almost surely a continuous function of the service times with respect to the limit process, so that we can apply the generalized continuous mapping theorem from [Reference Whitt36, Theorem 3.4.4]. In particular, we see that Q(t) is almost surely a continuous function of the service times except when ![]() $T_i + V_i = t$ for some i. For any CDF of V, that almost surely does not occur because
$T_i + V_i = t$ for some i. For any CDF of V, that almost surely does not occur because
by (3). We see that the probability is 0 by letting ![]() $\varepsilon \downarrow 0$. Hence we can apply the generalized continuous mapping theorem to deduce that the distribution of Q(t) is almost surely a continuous function of the distribution of V in this setting.
$\varepsilon \downarrow 0$. Hence we can apply the generalized continuous mapping theorem to deduce that the distribution of Q(t) is almost surely a continuous function of the distribution of V in this setting.
6.3. Adaptive service processes to enforce stability
Suppose that we let the service rate at time t depend on the history of the arrival process up to that time. In particular, let the arrival-history-dependent service rate be
The proposed control is a variant of the rate-matching service-rate control in [Reference Ma and Whitt30, Reference Whitt37]. The following is an analog of [Reference Whitt37, Theorem 3.1].
Theorem 7. If the arrival-history-dependent service process in (28) with ![]() $\rho < 1$ is used in the single-server queue with
$\rho < 1$ is used in the single-server queue with ![]() $Q(0) = 0$ and the GPP arrival process having parameter triple
$Q(0) = 0$ and the GPP arrival process having parameter triple ![]() $(\kappa (t), \gamma, \beta)$ with
$(\kappa (t), \gamma, \beta)$ with ![]() $\kappa$ in (2), then the pair of rates satisfies the joint limit
$\kappa$ in (2), then the pair of rates satisfies the joint limit
where ![]() $L(\gamma, \beta)$ is the gamma random variable in Theorem 3. Moreover, the queue length process
$L(\gamma, \beta)$ is the gamma random variable in Theorem 3. Moreover, the queue length process ![]() $\{Q(t)\,{:}\, t \ge 0\}$ is distributed the same as in an
$\{Q(t)\,{:}\, t \ge 0\}$ is distributed the same as in an ![]() $M/M/1$ queue in a random environment, so that
$M/M/1$ queue in a random environment, so that
as in the ![]() $M/M/1$ queue with traffic intensity (arrival rate divided by the maximum potential service rate)
$M/M/1$ queue with traffic intensity (arrival rate divided by the maximum potential service rate) ![]() $\rho$.
$\rho$.
Proof. First, the joint limit in (29) follows easily from Corollary 1 and (28). For the connection to ![]() $M/M/1$, we start by representing the counting processes N(t) and S(t) in terms of Poisson processes, using the martingale representation for point processes as in [Reference Baccelli and Bremaud3, Section 1.8]. Let
$M/M/1$, we start by representing the counting processes N(t) and S(t) in terms of Poisson processes, using the martingale representation for point processes as in [Reference Baccelli and Bremaud3, Section 1.8]. Let ![]() $\Pi_1 (t)$ and
$\Pi_1 (t)$ and ![]() $\Pi_{2} (t)$ be two independent rate-1 Poisson counting processes. Then the counting process N can be represented as
$\Pi_{2} (t)$ be two independent rate-1 Poisson counting processes. Then the counting process N can be represented as ![]() $\Pi_1 (\Lambda (t))$,
$\Pi_1 (\Lambda (t))$, ![]() $t \ge 0$, where
$t \ge 0$, where ![]() $\Lambda (t)$ is the cumulative rate function associated with
$\Lambda (t)$ is the cumulative rate function associated with ![]() $\lambda (t)$ and the compensator of the point process, i.e.
$\lambda (t)$ and the compensator of the point process, i.e. ![]() $\Lambda (t) \equiv \int_{0}^{t} \lambda (s) \, \mathrm{d} s$,
$\Lambda (t) \equiv \int_{0}^{t} \lambda (s) \, \mathrm{d} s$, ![]() $t \ge 0$. Because of (28), we thus have
$t \ge 0$. Because of (28), we thus have ![]() $\{(N(t), S(t))\,{:}\, t \ge 0\} \stackrel{\rm d}{=} \{(\Pi_{1} (\Lambda (t)), \Pi_{2} (\rho^{-1} \Lambda (t)))\,{:}\, t \ge 0\}$; see, e.g., [Reference Ethier and Kurtz13, Theorem 6.4.1]. Then the queue length process Q(t) can be expressed as the reflection map applied to the net-input process
$\{(N(t), S(t))\,{:}\, t \ge 0\} \stackrel{\rm d}{=} \{(\Pi_{1} (\Lambda (t)), \Pi_{2} (\rho^{-1} \Lambda (t)))\,{:}\, t \ge 0\}$; see, e.g., [Reference Ethier and Kurtz13, Theorem 6.4.1]. Then the queue length process Q(t) can be expressed as the reflection map applied to the net-input process ![]() $Y(t) \equiv N(t) - S(t)$. Let
$Y(t) \equiv N(t) - S(t)$. Let ![]() $\tilde{Q} (t)$ and
$\tilde{Q} (t)$ and ![]() $\tilde{Y} (t)$ be the corresponding processes in an
$\tilde{Y} (t)$ be the corresponding processes in an ![]() $M/M/1$ queue with arrival rate 1 and service rate
$M/M/1$ queue with arrival rate 1 and service rate ![]() $1/\rho$, i.e.
$1/\rho$, i.e. ![]() $\tilde{Y} (t) \equiv \Pi_{1} (t) - \Pi_{2} (\rho^{-1} t)$. With this representation we have
$\tilde{Y} (t) \equiv \Pi_{1} (t) - \Pi_{2} (\rho^{-1} t)$. With this representation we have ![]() $\{Y(t), Q(t)\,{:}\, t \ge 0\} \stackrel{\rm d}{=} \{(\tilde{Y} (\Lambda (t)), \tilde{Q} (\Lambda (t)))\,{:}\, t \ge 0\}$, where
$\{Y(t), Q(t)\,{:}\, t \ge 0\} \stackrel{\rm d}{=} \{(\tilde{Y} (\Lambda (t)), \tilde{Q} (\Lambda (t)))\,{:}\, t \ge 0\}$, where ![]() $\{\Lambda (t)\,{:}\, t \ge 0\}$ is independent of
$\{\Lambda (t)\,{:}\, t \ge 0\}$ is independent of ![]() $\{(\tilde{Y} (t), \tilde{Q} (t))\,{:}\, t \ge 0\}$. Because
$\{(\tilde{Y} (t), \tilde{Q} (t))\,{:}\, t \ge 0\}$. Because ![]() $\Lambda (t) \rightarrow \infty$ as
$\Lambda (t) \rightarrow \infty$ as ![]() $t \rightarrow \infty$ with probability 1, we have the claimed representation and convergence in (30).
$t \rightarrow \infty$ with probability 1, we have the claimed representation and convergence in (30).
7. Completing the proof of Theorem 4
We complete the proof of Theorem 4 by verifying the two inequality conditions in Hahn’s theorem [Reference Hahn21] as in [Reference Whitt36, Theorem 7.2.1]. To do so, we prove convergence in D[0, 1], as in [Reference Hahn21], but we note that essentially the same arguments show convergence in D[0, T] for any ![]() $T>0$ and therefore implies convergence in
$T>0$ and therefore implies convergence in ![]() $D[0,\infty)$; see [Reference Whitt36, Section 12.9].
$D[0,\infty)$; see [Reference Whitt36, Section 12.9].
By Theorem 1, ![]() $\mathbb{E}[A_1(s)A_1(t)]= \beta s(1+\gamma t)$ when
$\mathbb{E}[A_1(s)A_1(t)]= \beta s(1+\gamma t)$ when ![]() $A_1$ is the centered process defined in (9). First, for
$A_1$ is the centered process defined in (9). First, for ![]() $0\le t_1\le t_2\le 1$,
$0\le t_1\le t_2\le 1$,
 \begin{align*} \mathbb{E}\left[(A_1(t_2)-A_1(t_1))^2\right] &=\beta \left(t_2-t_1\right)\left(1+\gamma \left(t_2-t_1\right)\right) \nonumber \\& = \beta \left(t_2+\gamma t_2^2\right)-\beta \left(t_1+\gamma t_1^2\right)-2\beta \gamma t_1\left(t_2-t_1\right)\nonumber \\& \le \beta \left(t_2+\gamma t_2^2\right)-\beta \left(t_1+\gamma t_1^2\right) , \end{align*}
\begin{align*} \mathbb{E}\left[(A_1(t_2)-A_1(t_1))^2\right] &=\beta \left(t_2-t_1\right)\left(1+\gamma \left(t_2-t_1\right)\right) \nonumber \\& = \beta \left(t_2+\gamma t_2^2\right)-\beta \left(t_1+\gamma t_1^2\right)-2\beta \gamma t_1\left(t_2-t_1\right)\nonumber \\& \le \beta \left(t_2+\gamma t_2^2\right)-\beta \left(t_1+\gamma t_1^2\right) , \end{align*}
so that condition (2.3) of [Reference Whitt36, Theorem 7.2.1] is met. We will also show that
for ![]() $0\le t_1\le t\le t_2\le 1$ and a constant c, so that condition (2.4) of [Reference Whitt36, Theorem 7.2.1] will be met as well.
$0\le t_1\le t\le t_2\le 1$ and a constant c, so that condition (2.4) of [Reference Whitt36, Theorem 7.2.1] will be met as well.
To do the explicit calculations, we again apply [Reference Cha7, Theorem 3 and Remark 3], as in the proof of Theorem 1. That applies for any GPP ![]() $N^1$, the conditional distribution for the sequence of times when
$N^1$, the conditional distribution for the sequence of times when ![]() $N^1$ increases on
$N^1$ increases on ![]() $\left(0,1\right)$ given that
$\left(0,1\right)$ given that ![]() $N^1\left(1\right)=k$ is the same as that of the order statistics of k i.i.d. random variables, each with probability density function
$N^1\left(1\right)=k$ is the same as that of the order statistics of k i.i.d. random variables, each with probability density function
For a ![]() $\Psi$-GPP,
$\Psi$-GPP, ![]() $f(x)=1$. Hence, the conditional distribution for the ordered sequence of times when the
$f(x)=1$. Hence, the conditional distribution for the ordered sequence of times when the ![]() $\Psi$-GPP
$\Psi$-GPP ![]() $N^1$ increases on
$N^1$ increases on ![]() $\left(0,1\right)$ given that
$\left(0,1\right)$ given that ![]() $N^1\left(1\right)=k$ is the same as that of the order statistics of i.i.d. uniform random variables
$N^1\left(1\right)=k$ is the same as that of the order statistics of i.i.d. uniform random variables ![]() $U_j$ on [0, 1].
$U_j$ on [0, 1].
Following the proof of [Reference Billingsley5, Theorem 14.3], let ![]() $p_1=t-t_1$,
$p_1=t-t_1$, ![]() $p_2=t-t_2$; let
$p_2=t-t_2$; let ![]() $V_j$ be
$V_j$ be ![]() $\left(1-p_1\right)$ or
$\left(1-p_1\right)$ or ![]() $- p_1$ as
$- p_1$ as ![]() $U_j$ lies in
$U_j$ lies in ![]() $\left[t_1,t\right)$ or not; let
$\left[t_1,t\right)$ or not; let ![]() $W_j$ be
$W_j$ be ![]() $\left(1-p_2\right)$ or
$\left(1-p_2\right)$ or ![]() $- p_2$ as
$- p_2$ as ![]() $U_j$ lies in
$U_j$ lies in ![]() $\left[t,t_2\right]$ or not. Also, let
$\left[t,t_2\right]$ or not. Also, let ![]() $V=\overset k{\underset{j=1}{\sum }}V_j$,
$V=\overset k{\underset{j=1}{\sum }}V_j$, ![]() $W=\overset k{\underset{j=1}{\sum }}W_j$,
$W=\overset k{\underset{j=1}{\sum }}W_j$, ![]() $\tilde{V}= \left(N^{1}(1) - \beta\right)p_1$ and
$\tilde{V}= \left(N^{1}(1) - \beta\right)p_1$ and ![]() $\tilde{W} =\left(N^{1}(1) - \beta\right)p_2$. Then
$\tilde{W} =\left(N^{1}(1) - \beta\right)p_2$. Then
 \begin{align}&\mathbb{E}\left[\left(A_1(t)-A_1\left(t_1\right)\right)^2\left(A_1\left(t_2\right)-A_1(t)\right)^2 \mid N^1\left(1\right)=k\right] \nonumber \\[2pt]
& \quad= \mathbb{E}\left[\left(\overset k{\underset{j=1}{\sum }}\left(V_j+\frac{\left(k-\beta\right)p_1} k\right)\right)^2\left(\overset k{\underset{j=1}{\sum}}\left(W_j+\frac{ \left(k-\beta\right)p_2} k\right)\right)^2 \Bigg| N^1\left(1\right)=k\right] \nonumber \\[2pt]
&\quad = \mathbb{E}\left[(V + \tilde{V})^2(W + \tilde{W})^2 \mid N^1(1) = k\right] \nonumber \\[2pt]&\quad = \mathbb{E}\left[\left((VW + V\tilde{W}) +W\tilde{V} + \tilde{V}\tilde{W}\right)^2 \mid N^1(1) = k\right] \nonumber \\[2pt]&\quad \le 4 \mathbb{E}\left[(VW)^2 + (V\tilde{W})^2 + (W\tilde{V})^2 + (\tilde{V}\tilde{W})^2 \mid N^1(1) = k\right],\end{align}
\begin{align}&\mathbb{E}\left[\left(A_1(t)-A_1\left(t_1\right)\right)^2\left(A_1\left(t_2\right)-A_1(t)\right)^2 \mid N^1\left(1\right)=k\right] \nonumber \\[2pt]
& \quad= \mathbb{E}\left[\left(\overset k{\underset{j=1}{\sum }}\left(V_j+\frac{\left(k-\beta\right)p_1} k\right)\right)^2\left(\overset k{\underset{j=1}{\sum}}\left(W_j+\frac{ \left(k-\beta\right)p_2} k\right)\right)^2 \Bigg| N^1\left(1\right)=k\right] \nonumber \\[2pt]
&\quad = \mathbb{E}\left[(V + \tilde{V})^2(W + \tilde{W})^2 \mid N^1(1) = k\right] \nonumber \\[2pt]&\quad = \mathbb{E}\left[\left((VW + V\tilde{W}) +W\tilde{V} + \tilde{V}\tilde{W}\right)^2 \mid N^1(1) = k\right] \nonumber \\[2pt]&\quad \le 4 \mathbb{E}\left[(VW)^2 + (V\tilde{W})^2 + (W\tilde{V})^2 + (\tilde{V}\tilde{W})^2 \mid N^1(1) = k\right],\end{align}
where the last inequality follows from the Cauchy–Schwartz inequality.
It follows from [Reference Cha7, Theorem 1(i)] that ![]() $N\equiv N^1\left(1\right)$ has a negative binomial distribution with moment-generating function
$N\equiv N^1\left(1\right)$ has a negative binomial distribution with moment-generating function
where ![]() $r=\beta /\gamma $ and
$r=\beta /\gamma $ and ![]() $\theta =\left(1+\gamma \right)^{-1}$. Then,
$\theta =\left(1+\gamma \right)^{-1}$. Then,
which implies that
 \begin{align} \begin{split} \mathbb{E}[N] & = \beta, \\[2pt] \mathbb{E}\left[N^2\right] & = \beta \gamma +\beta ^2+\beta , \\[2pt] \mathbb{E}\left[N^3\right] & = \beta (2\gamma ^2+3\beta \gamma +3\gamma +\beta ^2+3\beta +1) , \\[2pt] \mathbb{E}\left[N^4\right] & = \beta (6\gamma ^3+11\beta \gamma ^2+12\gamma ^2+6\beta ^2\gamma +18\beta \gamma +7\gamma +\beta^3+6\beta ^2+7\beta +1). \end{split}\end{align}
\begin{align} \begin{split} \mathbb{E}[N] & = \beta, \\[2pt] \mathbb{E}\left[N^2\right] & = \beta \gamma +\beta ^2+\beta , \\[2pt] \mathbb{E}\left[N^3\right] & = \beta (2\gamma ^2+3\beta \gamma +3\gamma +\beta ^2+3\beta +1) , \\[2pt] \mathbb{E}\left[N^4\right] & = \beta (6\gamma ^3+11\beta \gamma ^2+12\gamma ^2+6\beta ^2\gamma +18\beta \gamma +7\gamma +\beta^3+6\beta ^2+7\beta +1). \end{split}\end{align}
By [Reference Billingsley5, (14.10)], ![]() $\mathbb{E}\big[\left(VW\right)^2 \mid N^1\left(1\right)=k\big]\le 6\ k^2p_1p_2$, so that
$\mathbb{E}\big[\left(VW\right)^2 \mid N^1\left(1\right)=k\big]\le 6\ k^2p_1p_2$, so that
Similarly,
 \begin{align*}\mathbb{E}\left[\left(V\tilde{W}\right)^2\right] & = \mathbb{E}\left[Np_1\left(1-p_1\right)\left(\left(N-\beta\right)p_2\right)^2\right], \\[2pt] \mathbb{E}\left[\left(\tilde{V} W\right)^2\right] & = \mathbb{E}\left[Np_2\left(1-p_2\right)\left(\left(N-\beta\right)p_1\right)^2\right],\end{align*}
\begin{align*}\mathbb{E}\left[\left(V\tilde{W}\right)^2\right] & = \mathbb{E}\left[Np_1\left(1-p_1\right)\left(\left(N-\beta\right)p_2\right)^2\right], \\[2pt] \mathbb{E}\left[\left(\tilde{V} W\right)^2\right] & = \mathbb{E}\left[Np_2\left(1-p_2\right)\left(\left(N-\beta\right)p_1\right)^2\right],\end{align*}
and
Using Macsyma for algebraic simplification, we find first, by (32),
 \begin{align*} &\mathbb{E}[\left(A_1(t)-A_1\left(t_1\right)\right)^2 \left(A_1\left(t_2\right)-A_1(t)\right)^2] \\[2pt] &\quad \le \Omega \equiv 4\left(\mathbb{E}\left[\left(VW\right)^2\right]+\mathbb{E}\left[\left(V\tilde{W}\right)^2\right]+\mathbb{E}\left[\left(\tilde{V} W\right)^2\right]+ \mathbb{E}\left[\left(\tilde{V}\tilde{W}\right)^2\right]\right)\!.\end{align*}
\begin{align*} &\mathbb{E}[\left(A_1(t)-A_1\left(t_1\right)\right)^2 \left(A_1\left(t_2\right)-A_1(t)\right)^2] \\[2pt] &\quad \le \Omega \equiv 4\left(\mathbb{E}\left[\left(VW\right)^2\right]+\mathbb{E}\left[\left(V\tilde{W}\right)^2\right]+\mathbb{E}\left[\left(\tilde{V} W\right)^2\right]+ \mathbb{E}\left[\left(\tilde{V}\tilde{W}\right)^2\right]\right)\!.\end{align*}
Then, by (33)–(35), we find that
 \begin{align*} \Omega & = 4\beta\left(6 \gamma^3 p_1p_2 + 3\beta\gamma^2 p_1 p_2 + 8\gamma^2 p_1p_2 +4\beta \gamma p_1p_2+ \gamma p_1p_2 +\beta p_1p_2 - p_1p_2 + 2 \gamma^2 p_2 \right. \\[2pt] & \left. \quad + \, \beta \gamma p_2 + 3\gamma p_2+\beta p_2+ p_2 +2\gamma^2 p_1 + \beta \gamma p_1 + 3 \gamma p_1 + \beta p_1 + p_1 + 6\gamma + 6\beta + 6\right)p_1 p_2 \\[2pt] & \le 4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)p_1p_2 \\[2pt] & = 4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)\left(t-t_1\right)\left(t_2-t\right) \\[2pt] & \le 4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)\left(t_2-t_1\right)^2.\end{align*}
\begin{align*} \Omega & = 4\beta\left(6 \gamma^3 p_1p_2 + 3\beta\gamma^2 p_1 p_2 + 8\gamma^2 p_1p_2 +4\beta \gamma p_1p_2+ \gamma p_1p_2 +\beta p_1p_2 - p_1p_2 + 2 \gamma^2 p_2 \right. \\[2pt] & \left. \quad + \, \beta \gamma p_2 + 3\gamma p_2+\beta p_2+ p_2 +2\gamma^2 p_1 + \beta \gamma p_1 + 3 \gamma p_1 + \beta p_1 + p_1 + 6\gamma + 6\beta + 6\right)p_1 p_2 \\[2pt] & \le 4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)p_1p_2 \\[2pt] & = 4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)\left(t-t_1\right)\left(t_2-t\right) \\[2pt] & \le 4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)\left(t_2-t_1\right)^2.\end{align*}
Thus, we conclude that condition (2.4) of [Reference Whitt36, Theorem 7.2.1] holds for ![]() $c=4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)$. Under those conditions, [Reference Whitt36, Theorem 7.2.1] shows that
$c=4\beta (6 \gamma^3 +3\beta\gamma^2 + 12 \gamma^2 + 6\beta\gamma +13 \gamma + 9\beta + 7)$. Under those conditions, [Reference Whitt36, Theorem 7.2.1] shows that ![]() $A_n\Rightarrow A$, where A is a zero-mean Gaussian process with the same covariance kernel as
$A_n\Rightarrow A$, where A is a zero-mean Gaussian process with the same covariance kernel as ![]() $A_1$.
$A_1$.
Remark 8. (Easier proof of Theorem 3 fails.) A candidate easier proof of Theorem 4 for sums of Markov processes is provided by [Reference Whitt36, Theorem 7.2.2], but conditions (2.9) and (2.10) there are not satisfied in our case. The proof of Theorem 4 shows that the expectation in (32) conditional on ![]() $N=N^1(1)$ does not have a uniform bound of the form of the right-hand side of (31). The uniform bound in (31) is obtained from the conditional expectation only after accounting for the distribution of N. Therefore, the candidate easier proof for sums of Markov processes fails in our case.
$N=N^1(1)$ does not have a uniform bound of the form of the right-hand side of (31). The uniform bound in (31) is obtained from the conditional expectation only after accounting for the distribution of N. Therefore, the candidate easier proof for sums of Markov processes fails in our case.
8. Conclusions
In this paper we have helped expose the performance consequence on a single-server queue of having a path-dependent arrival process. Our first main result is Theorem 4, which shows that a superposition of ![]() $\Psi$-GPPs, which is itself a
$\Psi$-GPPs, which is itself a ![]() $\Psi$-GPP, converges to a
$\Psi$-GPP, converges to a ![]() $\Psi$-GMP as studied in [Reference Fendick16]; i.e. the limit process is a Gaussian Markov process with stationary increments. Our second main result is the consequence for queueing models in Theorem 5. Corollaries 6 and 7 provide explicit performance approximations for the queueing processes. Such explicit representations are unusual in the theory of Gaussian queues.
$\Psi$-GMP as studied in [Reference Fendick16]; i.e. the limit process is a Gaussian Markov process with stationary increments. Our second main result is the consequence for queueing models in Theorem 5. Corollaries 6 and 7 provide explicit performance approximations for the queueing processes. Such explicit representations are unusual in the theory of Gaussian queues.
In the process of establishing the results above, we also clarified the role of ![]() $\Psi$-GPPs within the larger class of GPPs in Theorems 1 and 2. The
$\Psi$-GPPs within the larger class of GPPs in Theorems 1 and 2. The ![]() $\Psi$-GPP and the limiting
$\Psi$-GPP and the limiting ![]() $\Psi$-GMP exhibit positive dependence, but the class of
$\Psi$-GMP exhibit positive dependence, but the class of ![]() $\Psi$-GMPs considered in [Reference Fendick16] also include processes exhibiting negative dependence. We close by observing that it is possible to obtain all possible
$\Psi$-GMPs considered in [Reference Fendick16] also include processes exhibiting negative dependence. We close by observing that it is possible to obtain all possible ![]() $\Psi$-GMPs considered in [Reference Fendick16] by limits like that in Theorem 4. Indeed, all possible limits are obtained by considering linear combinations of uniform empirical processes and superpositions of
$\Psi$-GMPs considered in [Reference Fendick16] by limits like that in Theorem 4. Indeed, all possible limits are obtained by considering linear combinations of uniform empirical processes and superpositions of ![]() $\Psi$-GPPs. That is natural because both processes can be regarded as superposition processes. The case of negative dependence connects with previous heavy-traffic limits for queues in [Reference Hajek22, Reference Honnappa, Jain and Ward25]. In fact, the proof of the explicit form of the distribution of the reflected
$\Psi$-GPPs. That is natural because both processes can be regarded as superposition processes. The case of negative dependence connects with previous heavy-traffic limits for queues in [Reference Hajek22, Reference Honnappa, Jain and Ward25]. In fact, the proof of the explicit form of the distribution of the reflected ![]() $\Psi$-GMP in Corollary 6 already drew on the structure of the Brownian bridge, as can be seen from our sketch of that proof.
$\Psi$-GMP in Corollary 6 already drew on the structure of the Brownian bridge, as can be seen from our sketch of that proof.
Additional insight into the steady-state performance of queues with path-dependent arrival processes was provided by the results in Section 6. We showed how Little’s law can be stated in this context, and we provided conditions under which there is stability for a queue with a Pólya arrival process.