Skip to main content
SpringerLink
Log in

Riemann–Hilbert problem for the Kundu-type nonlinear Schrödinger equation with \(N\) distinct arbitrary-order poles

  • Research Articles
  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

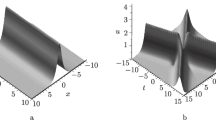
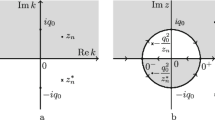
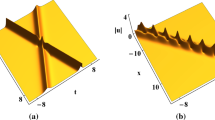
We use the Riemann–Hilbert (RH) method to study the Kundu-type nonlinear Schrödinger (Kundu–NLS) equation with a zero boundary condition in the case where the scattering coefficient has \(N\) distinct arbitrary-order poles. We perform a spectral analysis of the Lax pair and consider the asymptotic property, symmetry, and analyticity of the Jost solution. Based on these results, we formulate the RH problem whose solution allows solving the considered Kundu–NLS equation. In addition, using graphic analysis, we study the characteristics of soliton solutions of some particular cases of the problem with \(N\) distinct arbitrary-order poles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

References

  1. G. P. Agrawal, Nonlinear Fiber Optics, Acad. Press, San Diego (2001).

    MATH  Google Scholar 

  2. D. J. Benney, “A general theory for interactions between short and long waves,” Stud. Appl. Math., 56, 81–94 (1976).

    Article  MathSciNet  MATH  Google Scholar 

  3. T. Kakutani and K. Michihiro, “Marginal state of modulational instability: Note of Benjamin–Feir instability,” J. Phys. Soc. Japan., 52, 4129–4137 (1983).

    Article  ADS  Google Scholar 

  4. H. Bailung and Y. Nakamura, “Observation of modulational instability in a multi-component plasma with negative ions,” J. Plasma Phys., 50, 231–242 (1993).

    Article  ADS  Google Scholar 

  5. Y. S. Kivshar and G. P. Agrawal, Optical Solitons: From Fibers to Photonic Crystals, Acad. Press, New York (2003).

    Google Scholar 

  6. B. A. Malomed, D. Mihalache, F. Wise, and L. Torner, “Spatiotemporal optical solitons,” J. Opt. B, 7, R53–R72 (2005).

    Article  ADS  Google Scholar 

  7. L. Pitaevskii and S. Stringari, Bose–Einstein Condensation and Superfluidity (Intl. Ser. Monogr. Phys., Vol. 164), Oxford Univ. Press, Oxford (2016).

    Book  MATH  Google Scholar 

  8. G. Fanjoux, J. Michaud, H. Maillotte, and T. Sylvestre, “Cascaded Raman slow light and optical spatial solitons in Kerr media,” Phys. Rev. A., 87, 033838 (2013).

    Article  ADS  Google Scholar 

  9. M. Li, J.-H. Xiao, W.-J. Liu, P. Wang, B. Qin, and B. Tian, “Mixed-type vector solitons of the \(N\)-coupled mixed derivative nonlinear Schrödinger equations form optical fibers,” Phys. Rev. E, 87, 032914 (2013).

    Article  ADS  Google Scholar 

  10. F. G. Mertens, N. R. Quintero, and A. R. Bishop, “Nonlinear Schrödinger solitons oscillate under a constant external force,” Phys. Rev. E, 87, 032917 (2013).

    Article  ADS  Google Scholar 

  11. J. T. Cole and Z. H. Musslimani, “Band gaps and lattice solitons for the higher-order nonlinear Schrödinger equation with a periodic potential,” Phys. Rev. A, 90, 013815 (2014).

    Article  ADS  Google Scholar 

  12. A. Kundu, “Landau–Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations,” J. Math. Phys., 25, 3433–3438 (1984).

    Article  ADS  MathSciNet  Google Scholar 

  13. A. Kundu, “Integrable hierarchy of higher nonlinear Schrödinger type equations,” SIGMA, 2, 078 (2006).

    MathSciNet  MATH  Google Scholar 

  14. X.-B. Wang and B. Han, “The Kundu-nonlinear Schrödinger equation: Breathers, rogue waves, and their dynamics,” J. Phys. Soc. Japan, 89, 014001 (2020).

    Article  ADS  Google Scholar 

  15. C. Zhang, C. Li, and J. He, “Darboux transformation and rogue waves of the Kundu-nonlinear Schrödinger equation,” Math. Methods Appl. Sci., 38, 2411–2425 (2015).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. X.-B. Wang and B. Han, “Inverse scattering transform of an extended nonlinear Schrödinger equation with nonzero boundary conditions and its multisoliton solutions,” J. Math. Anal. Appl., 487, 123968 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  17. X.-W. Yan, “Riemann–Hilbert method and multi-soliton solutions of Kundu-nonlinear Schrödinger equation,” Nonlinear Dynam., 102, 2811–2819 (2020).

    Article  Google Scholar 

  18. M. J. Ablowitz and P. A. Clarkson, Solutions, Nonlinear Evolution Equations, and Inverse Scattering (London Math. Soc. Lect. Note Ser., Vol. 149), Cambridge Univ. Press, Cambridge (1991).

    Book  MATH  Google Scholar 

  19. V. B. Matveev and M. A. Salle, Darboux Transformations and Solitons (Springer Ser. Nonlin. Dyn., Vol. 5), Springer, Berlin (1991).

    Book  MATH  Google Scholar 

  20. R. Hirota, The Direct Method in Soliton Theory (Cambridge Tracts Math., Vol. 155), Cambridge Univ. Press, Cambridge (2004).

    Book  MATH  Google Scholar 

  21. G. W. Bluman and S. Kumei, Symmetries and Differential Equations (Appl. Math. Sci., Vol. 81), Springer, New York (1989).

    Book  MATH  Google Scholar 

  22. C. S. Gardner, J. M. Greene, M. D. Kruskal, and R. M. Miura, “Method for solving the Korteweg–de Vries equation,” Phys. Rev. Lett., 19, 1095–1097 (1967).

    Article  ADS  MATH  Google Scholar 

  23. E. Noether, “Invariante Variationsprobleme,” Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl., 2, 235–275 (1918).

    MATH  Google Scholar 

  24. C. J. Papchristou and B. K. Harrison, “A method for constructing a Lax pair for the Ernst equation,” Electron. J. Theor. Phys., 6, 29–40 (2009); http://www.ejtp.com/articles/ejtpv6i22p29.pdf (2009).

    Google Scholar 

  25. M. J. Ablowitz, D. J. Kaup, A. C. Newell, and H. Segur, “Nonlinear-evolution equations of physical significance,” Phys. Rev. Lett., 31, 125–127 (1973).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. M. J. Ablowitz, D. J. Kaup, A. C. Newell, and H. Segur, “The inverse scattering transform–Fourier analysis for nonlinear problems,” Stud. Appl. Math., 53, 249–315 (1974).

    Article  MathSciNet  MATH  Google Scholar 

  27. R. Y. Chiao, E. Garmire, and C. H. Townes, “Self-trapping of optical beams,” Phys. Rev. Lett., 13, 479–481 (1965).

    Article  ADS  Google Scholar 

  28. V. E. Zakharov, “Stability of periodic waves of finite amplitude on the surface of a deep fluid,” J. Appl. Mech. Tech. Phys., 9, 190–194 (1968).

    Article  ADS  Google Scholar 

  29. A. Hasegawa and F. Tappert, “Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers,” Appl. Phys. Lett., 23, 142–144 (1973).

    Article  ADS  Google Scholar 

  30. V. E. Zakharov, S. V. Manakov, S. P. Novikov, and L. P. Pitaevskii, Theory of Solitons: Inverse Problem Method [in Russian], Nauka, Moscow (1980); English transl.: S. P. Novikov, S. V. Manakov, L. P. Pitaevskii, and V. E. Zakharov, Theory of Solitons: The Inverse Scattering Method, Consultants Bureau, New York (1984).

    MATH  Google Scholar 

  31. G. Biondini and G. Kovačič, “Inverse scattering transform for the focusing nonlinear Schrödinger equation with nonzero boundary conditions,” J. Math. Phys., 55, 031506 (2014).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. X. Zhou, “The Riemann–Hilbert problem and inverse scattering,” SIAM J. Math. Anal., 20, 966–986 (1989).

    Article  MathSciNet  MATH  Google Scholar 

  33. M. Kashiwara, “The Riemann–Hilbert problem for holonomic systems,” Publ. Res. Inst. Math. Sci., 20, 319–365 (1984).

    Article  MathSciNet  MATH  Google Scholar 

  34. A. S. Fokas and V. E. Zakharov, “The dressing method and nonlocal Riemann–Hilbert problems,” J. Nonlinear Sci., 2, 109–134 (1992).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  35. D.-S. Wang, D.-J. Zhang, and J. Yang, “Integrable properties of the general coupled nonlinear Schrödinger equations,” J. Math. Phys., 51, 023510 (2010).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. S.-F. Tian, “The mixed coupled nonlinear Schrödinger equation on the half-line via the Fokas method,” Proc. Roy. Soc. London Ser. A, 472, 20160588 (2016).

    ADS  MATH  Google Scholar 

  37. X. Geng and J. Wu, “Riemann–Hilbert approach and \(N\)-soliton solutions for a generalized Sasa–Satsuma equation,” Wave Motion, 60, 62–72 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  38. S.-F. Tian, “Initial-boundary value problems of the coupled modified Korteweg–de Vries equation on the half-line via the Fokas method,” J. Phys. A: Math. Theor., 50, 395204 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  39. S.-F. Tian, “Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method,” J. Differ. Equ., 262, 506–558 (2017).

    Article  ADS  MATH  Google Scholar 

  40. W.-X. Ma, “Riemann–Hilbert problems and \(N\)-soliton solutions for a coupled mKdV system,” J. Geom. Phys., 132, 45–54 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. Y. Zhang, J. Rao, Y. Cheng, and J. He, “Riemann–Hilbert method for the Wadati–Konno–Ichikawa equation: \(N\) simple poles and one higher-order pole,” Phys. D, 399, 173–185 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  42. W. Peng, S. Tian, X. Wang, T. Zhang, and Y. Fang, “Riemann–Hilbert method and multi-soliton solutions for three-component coupled nonlinear Schrödinger equations,” J. Geom. Phys., 146, 103508 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  43. J.-J. Yang, S.-F. Tian, and Z.-Q. Li, “Riemann–Hilbert approach to the inhomogeneous fifth-order nonlinear Schrödinger equation with non-vanishing boundary conditions,” arXiv:2001.08597v1 [nlin.SI] (2020).

  44. P. Zhao and E. Fan, “Finite gap integration of the derivative nonlinear Schrödinger equation: A Riemann–Hilbert method,” Phys. D, 402, 132213 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  45. C. Zhang, C. Li, and J. He, “Rogue waves of the Kundu-nonlinear Schrödinger equation,” Open. J. Appl. Sci., 3, 94–98 (2013).

    Article  ADS  Google Scholar 

  46. A. S. Fokas, “A unified transform method for solving linear and certain nonlinear PDEs,” Proc. Roy. Soc. London Ser. A, 453, 1411–1443 (1997).

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors sincerely thank the editor and referees for their valuable comments.

Funding

This research was supported by the National Natural Science Foundation of China (Grant No. 11975306), the Natural Science Foundation of Jiangsu Province (Grant No. BK20181351), the Six Talent Peaks Project in Jiangsu Province (Grant No. JY-059), and the Fundamental Research Fund for the Central Universities (Grant Nos. 2019ZDPY07 and 2019QNA35).

Author information

Authors and Affiliations

  1. School of Mathematics and Institute of Mathematical Physics, China University of Mining and Technology, Xuzhou, China

    Zi-Yi Wang, Shou-Fu Tian & Xiao-Fan Zhang

Authors
  1. Zi-Yi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shou-Fu Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiao-Fan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shou-Fu Tian.

Ethics declarations

The authors declare no conflicts of interest.

Additional information

Translated from Teoreticheskaya i Matematicheskaya Fizika, 2021, Vol. 207, pp. 23-43 https://doi.org/10.4213/tmf10015.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, ZY., Tian, SF. & Zhang, XF. Riemann–Hilbert problem for the Kundu-type nonlinear Schrödinger equation with \(N\) distinct arbitrary-order poles. Theor Math Phys 207, 415–433 (2021). https://doi.org/10.1134/S0040577921040024

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040577921040024

Keywords

Search

Navigation