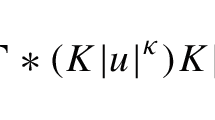Abstract
We construct an exactly solvable model of a linear harmonic oscillator with a coordinate-dependent mass in a uniform gravitational field. This model is placed in an infinitely deep potential well with the width \(2a\) and corresponds to the exact solution of the angular part of the Schrödinger equation with one of the Hautot potentials. The wave functions of the oscillator model are expressed in terms of Jacobi polynomials. In the limit \(a\to\infty\), the equation of motion, wave functions, and energy spectrum of the model correctly reduce to the corresponding results of the ordinary nonrelativistic harmonic oscillator with a constant mass. We obtain a new asymptotic relation between the Jacobi and Hermite polynomials and prove it by two different methods.
Similar content being viewed by others
References
D. J. BenDaniel and C. B. Duke, “Space-charge effects on electron tunneling,” Phys. Rev., 152, 683–692 (1966).
P. M. Mathews and M. Lakshmanan, “On a unique nonlinear oscillator,” Quart. Appl. Math., 32, 215–218 (1974).
O. von Roos, “Position-dependent effective masses in semiconductor theory,” Phys. Rev. B, 27, 7547–7552 (1983).
J.-M. Lévy-Leblond, “Position-dependent effective mass and Galilean invariance,” Phys. Rev. A, 52, 1845–1849 (1995).
A. R. Plastino, A. Rigo, M. Casas, F. Garcias, and A. Plastino, “Supersymmetric approach to quantum systems with position-dependent effective mass,” Phys. Rev. A, 60, 4318–4325 (1999).
J. F. Cariñena, M. F. Rañada, and M. Santander, “One-dimensional model of a quantum nonlinear harmonic oscillator,” Rep. Math. Phys., 54, 285–293 (2004).
A. D. Alhaidari, “Solution of the Dirac equation with position-dependent mass in the Coulomb field,” Phys. Lett. A, 322, 72–77 (2004).
C. Quesne and V. M. Tkachuk, “Deformed algebras, position-dependent effective masses, and curved spaces: An exactly solvable Coulomb problem,” J. Phys. A: Math. Gen., 37, 4267–4281 (2004); arXiv:math-ph/0403047v1 (2004).
H. Rajbongshi and N. N. Singh, “Generation of exactly solvable potentials of the \(D\)-dimensional position-dependent mass Schrödinger equation using the transformation method,” Theor. Math. Phys., 183, 715–729 (2015).
H. Rajbongshi, “Exactly solvable potentials and the bound-state solution of the position-dependent mass Schrödinger equation in \(D\)-dimensional space,” Theor. Math. Phys., 184, 996–1010 (2015).
J. F. Cariñena, M. F. Rañada, and M. Santander, “Quantization of Hamiltonian systems with a position dependent mass: Killing vector fields and Noether momenta approach,” J. Phys. A: Math. Theor., 50, 465202 (2017).
G. Bastard, Wave Mechanics Applied to Semiconductor Heterostructure, Les Éditions de Physique, Les Ulis Cedex, France (1988).
M. Barranco, M. Pi, S. M. Gatica, E. S. Hernández, and J. Navarro, “Structure and energetics of mixed \(^4\)He–\(^3\)He drops,” Phys. Rev. B, 56, 8997–9003 (1997).
P. Harrison, Quantum Wells, Wires, and Dots, John Wiley and Sons, New York (2000).
M. Lozada-Cassou, S.-H. Dong, and J. Yu, “Quantum features of semiconductor quantum dots,” Phys. Lett. A, 331, 45–52 (2004).
S.-H. Dong and M. Lozada-Cassou, “Exact solutions of the Schrödinger equation with the position-dependent mass for a hard-core potential,” Phys. Lett. A, 337, 313–320 (2005).
E. Schrödinger, “An undulatory theory of the mechanics of atoms and molecules,” Phys. Rev., 28, 1049–1070 (1926).
P. A. M. Dirac, Principles of Quantum Mechanics, Oxford Univ. Press, Oxford (1982).
O. Klein, “Quantentheorie und fünfdimensionale Relativitätstheorie,” Z. Phys., 37, 895–906 (1926).
W. Gordon, “Der Comptoneffekt nach der Schrödingerschen Theorie,” Z. Phys., 40, 117–133 (1926).
V. G. Kadyshevsky, R. M. Mir-Kasimov, and N. B. Skachkov, “Quasi-potential approach and the expansion in relativistic spherical functions,” Nuovo Cimento Ser. A, 55, 233–257 (1968).
S. M. Nagiyev and K. S. Jafarova, “Relativistic quantum particle in a time-dependent homogeneous field,” Phys. Lett. A, 377, 747–752 (2013).
P. M. Morse, “Diatomic molecules according to the wave mechanics: II. Vibrational levels,” Phys. Rev., 34, 57–64 (1929).
G. Pöschl and E. Teller, “Bemerkungen zur Quantenmechanik des anharmonischen Oszillators,” Z. Phys., 83, 143–151 (1933).
L. Hulthén, “Über die Eigenlösungen der Schrödinger–Gleichung des Deuterons,” Ark. Mat. Astron. Fys., 28A, No. 5, 1–12 (1942).
R. D. Woods and D. S. Saxon, “Diffuse surface optical model for nucleon–nuclei scattering,” Phys. Rev., 95, 577–578 (1954).
H. Hartmann, “Die Bewegung eines Körpers in einem ringförmigen Potentialfeld,” Theoret. Chim. Acta, 24, 201–206 (1972).
A. Hautot, “Exact motion in noncentral electric fields,” J. Math. Phys., 14, 1320–1327 (1973).
Sh. M. Nagiyev and A. I. Ahmadov, “Exact solution of the relativistic finite-difference equation for the Coulomb plus a ring-shaped-like potential,” Internat. J. Modern Phys. A, 34, 1950089 (2019).
A. F. Nikiforov and V. B. Uvarov, Special Functions of Mathematical Physics [in Russian], Nauka, Moscow (1984); English transl., Birkhäuser, Basel (1988).
H. Bateman and A. Erdélyi, Higher Transcendental Functions, Vol. 2, McGraw-Hill, New York (1953).
R. Koekoek, P. A. Lesky, and R. F. Swarttouw, Hypergeometric Orthogonal Polynomials and Their \(q\)-Analogues, Springer, Berlin (2010).
G. Ghosh, T. K. Roy, and R. Gangopadhyay, “Dynamical symmetry and exact solvability,” Phys. Rev. A, 36, 1449–1451 (1987).
Y. Alhassid, F. Gürsey, and F. Iachello, “Potential scattering, transfer matrix, and group theory,” Phys. Rev. Lett., 50, 873–876 (1985).
E. I. Jafarov, S. M. Nagiyev, and A. M. Jafarova, “Quantum-mechanical explicit solution for the confined harmonic oscillator model with the von Roos kinetic energy operator,” Rep. Math. Phys., 86, 25–37 (2020).
A. P. Prudnikov, Yu. A. Brychkov, and O. I. Marichev, Integrals and Series [in Russian], Vol. 2, Special Functions [in Russian], Nauka, Moscow (1983); English transl., Gordon and Breach, New York (1986).
R. C. Miller, A. C. Gossard, D. A. Kleinman, and O. Munteanu, “Parabolic quantum wells with the GaAs-Al\(_x\)Ga\(_{1-x}\)As system,” Phys. Rev. B, 29, 3740–3743 (1984).
R. C. Miller, D. A. Kleinman, and A. C. Gossard, “Energy-gap discontinuities and effective masses for GaAs-Al\(_x\)Ga\(_{1-x}\)As quantum wells,” Phys. Rev. B, 29, 7085–7087 (1984).
R. C. Miller, A. C. Gossard, and D. A. Kleinman, “Band offsets from two special GaAs-Al\(_x\)Ga\(_{1-x}\)As quantum well structures,” Phys. Rev. B, 32, 5443–5446 (1985).
A. C. Gossard, R. C. Miller, and W. Wiegmann, “MBE growth and energy levels of quantum wells with special shapes,” Surf. Sci., 174, 131–135 (1986).
Funding
The research of E. I. Jafarov is supported by the Science Foundation of the State Oil Company of the Azerbaijan Republic 2019–2020 (Grant No. 13LR-AMEA) and the Science Development Fund under the President of the Republic of Azerbaijan (Grant No. EIF-KETPL-2-2015-1(25)-56/01/1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare no conflicts of interest.
Additional information
Translated from Teoreticheskaya i Matematicheskaya Fizika, 2021, Vol. 207, pp. 58-71 https://doi.org/10.4213/tmf9960.
Rights and permissions
About this article
Cite this article
Jafarov, E.I., Nagiyev, S.M. Angular part of the Schrödinger equation for the Hautot potential as a harmonic oscillator with a coordinate-dependent mass in a uniform gravitational field. Theor Math Phys 207, 447–458 (2021). https://doi.org/10.1134/S0040577921040048
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0040577921040048