FFT phase-field model combined with cohesive composite voxels for fracture of composite materials with interfaces

Abstract

A framework for damage modelling based on the fast Fourier transform (FFT) method is proposed to combine the variational phase-field approach with a cohesive zone model. This combination enables the application of the FFT methodology in composite materials with interfaces. The composite voxel technique with a laminate model is adopted for this purpose. A frictional cohesive zone model is incorporated to describe the fracture behaviour of the interface including frictional sliding. Representative numerical examples demonstrate that the proposed model is able to predict complex fracture behaviour in composite microstructures, such as debonding, frictional sliding of interfaces, crack deviation and coalescence of interface cracking and matrix cracking.

1 Introduction

Variational phase field modelling is gaining popularity by virtue of its efficiency in predicting complex fracture initiation and propagation, see e.g. [1,2,3,4,5,6,7] among many others. By introducing a diffuse regularisation to the sharp crack surface, the variational approach [8] bridges the classical continuum damage mechanics with Griffith’s fracture theory. When it comes to simulations of composite materials, it is essential to properly take into account interface failure between the constituents. The interface failure is commonly modelled with the traction–separation law of cohesive zone (CZ) theory [9]. The combination of the CZ theory and phase-field fracture models was first proposed by Verhoosel and De Borst [10], by defining an auxiliary field related to the cohesive crack opening. A more robust phase-field formulation has since been proposed by Nguyen et al. [3], taking into account both bulk damage and interface fracture. In their work, by analogy to the phase field method, the interface was regularised throughout the whole computation domain according to a level set function. This idea of interface regularisation was also incorporated by Zhang et al. [11] based on the unified phase field model of [7] for cohesive fracture problems. Hansen-Dörr et al. [12] proposed a phase field model, in which the adhesive interface is assigned a fracture toughness within a finite width. Different from the regularised interface representation of [3, 11], Paggi and Reinoso [13] proposed a general framework integrating a local CZ model into the phase field formulation. This model relies upon interface finite elements that are compatible with the phase field approach. It has been proven to be able to deal with the interaction of bulk damage and interface failure with both high and low interface stiffness, and for a brittle interface, it produces results consistent with linear elastic fracture mechanics derived by He and Hutchinson [14].

All the aforementioned phase-field models have been solved with the finite element (FE) method, which is a powerful and versatile numerical solver. Although massive parallel implementations and large-scale FE simulations have been developed, e.g. [15,16,17], it is still not straightforward to generalise the methodologies to nonlocal damage models. The method based on the fast Fourier transform (FFT) has been proposed as an efficient alternative to conventional FE methods [18] to speed up the solution of composite problems in the context of homogenisation theory. The FFT methods provide advantages especially for image-based modelling since it intrinsically uses regular structured grids for the discretisation. This image-like discretisation, on the one hand, avoids the cumbersome meshing procedure of FE, on the other hand, makes it possible to apply efficiently, through the use of standard FFT libraries, a Green operator in Fourier space that solves the polarisation problem (Lippmann–Schwinger equation) related to the local equilibrium with periodic boundary conditions. The derivations involved in the equilibrium problem become local operations in Fourier space, making the algorithm relatively simple to parallelise over high performance computing systems [19]. It should be noted that the periodicity of boundary conditions of the FFT methods, which is usually considered as an advantage for homogenisation computation, can be a drawback for structure computation though recent attempts have been made with realistic pseudo-periodic microstructures [19, 20].

After a steady development over two decades, the basic scheme of [18] has been improved in terms of accuracy and computation efficiency. Eyre and Milton [21] proposed an accelerated scheme to achieve a faster convergence rate. Accounting for the increasing computation cost at each iteration, Michel et al. [22] introduced an augmented Lagrangian scheme for problems with infinite elastic contrasts. To deal with infinite elastic contrasts while keeping the simplicity of the basic scheme, Brisard and Dormieux [23] reformulated the FFT methods from a variational framework, and Willot [24] introduced a modified discrete Green operator. Conjugate gradient algorithms have also been used to accelerate the FFT methods, see [23, 25, 26]. In the mathematical understanding of the FFT methods, contributions have been made by several research groups, e.g. [27,28,29,30] among others, demonstrating that the FFT methods can actually be derived from a standpoint of the classical FE method using Galerkin formulation. For application to heterogeneous materials, the idea of accounting for the heterogeneity within interface voxels (composite voxels) was first raised in the work of Brisard and Dormieux [23]. Composite voxel techniques were then proposed for both linear elastic [31,32,33] and nonlinear material behaviours [34, 35]. As demonstrated by the aforementioned works, the composite voxel technique reduces the spurious oscillations related to the sharp elastic discontinuity at the interface.

A recent trend in the development of FFT methods is the extension to fracture and damage problems. Li et al. [36] proposed an FFT solver for an integral-type nonlocal damage model. Wang et al. [37] applied FFT methods to a local anisotropic damage model for fibre composites. An FFT solver has been proposed for gradient-type nonlocal damage models by Boeff et al. [38]. More recently, FFT solvers have been proposed for phase-field fracture models [39,40,41]. In [41], an FFT solver for higher order partial differential equations was proposed, so now a broader range of phase-field fracture models can be solved with FFT methods accounting for damage anisotropy. Within the framework of FFT methods, interface failure has been addressed only very recently. A volumetric representation of the interface has been adopted by Sharma et al. [42] to regularise the interface within a small vicinity (artificial interface thickness), and this approach has been further extended to multi-dimensional problems [43] in the context of crystal plasticity. Within their anisotropic FFT phase field model, Ma and Sun [41] explicitly defined the grain boundaries with a set of voxels that were assigned an anisotropic tensor to describe the transverse isotropy with respect to the interface normal direction. In contrast to the idea of volumetric representation of interface, the fracture behaviour of the interface could also be modelled in a local fashion, as usually adopted by conventional FE models. In conventional FE methods, the interface geometry can be explicitly described with cohesive elements of a conformal mesh. However, the FFT methods intrinsically use image-type discretisation grids, for which the voxel/pixel interface elements would lead to strong biases. Therefore, some specific treatments are necessary to incorporate cohesive zone models into the interface behaviour for FFT methods. The composite voxel technique has the potential to accomplish this task. Nevertheless, although a framework for inelastic problems has been proposed, see e.g. [35], to the knowledge of the authors, the use of the composite voxel technique in interface fracture has not yet been reported, although the latter is essential for simulations of many composite materials, particularly fibre-reinforced composites, as well as polycrystalline and polygranular materials.

The present work proposes an FFT based approach coupling a phase-field (PF) fracture model with a frictional cohesive zone (CZ) model, and aims to provide a first proof-of-concept investigation that uses the composite voxel technique to solve the coupled problem. The basic idea of the composite voxel technique is to make use of a mixture rule (Reuss, Voigt or laminate) to compute a homogenized property of each voxel that contains more than one material. In the case of interface fracture and sliding, a laminate mixture rule is a better approximation, since it is able to take into account the strong anisotropy that is related to the interface orientation in both elastic and damaged regimes. In the present paper, a 3-layer laminate model is used to insert into the composite voxel either the elastic or the inelastic (including fracture and sliding) behaviour of the interphase. The phase-field model of [6] is used to model the damage behaviour in the bulk, and the interphase fracture and sliding are modelled by the cohesive zone model of [44] with friction taken into account. A semi-explicit staggered scheme is used to solve the problems of bulk damage, cohesive interphase damage, stress/strain fields, separately. Let us note that the term “interphase” herein refers to as a volumetric representation of the interface. This is a numerical consideration to incorporate the CZ model within the composite voxel technique. This choice of volumetric representation (interphase), instead of surface representation (interface), allows us to directly benefit from the original composite voxel concept that has been already implemented in the literature. The present development has been based on its implementation over the platform AMITEX [31, 45].

The paper is organised as follows. Section 2 introduces the coupled problem, as well as the composite voxel technique with the 3-layer laminate mixture rule. Section 3 presents the numerical implementation with an FFT solver. Finally, representative results are discussed in Sect. 4 to show the efficiency and some limitations of the proposed method. For the mathematical symbols, we use simple letters (e.g. $a$) to represent scalars, under-bar (e.g. $\underline {a}$) for vectors and bold letters (e.g. ${\varvec{a}}$) for second-order matrices.

2 Phase-field: cohesive zone model (PF-CZ)

2.1 Phase-field damage model with interface

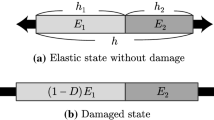
Let us consider a solid body Ω with two bulk constituents and an interface (with negligible thickness) between them (Fig. 1). Dissociating the fracture of the bulk materials and that of the interface, two types of internal discontinuities exist in this system: (1) bulk crack surface Γ^b that can evolve as the external loading changes, (2) interface between bulk constituents Γ^I, whose mechanical behaviour is assumed to be elastic and damageable, and whose position is assumed to be known and fixed. The damage level of the interface is described by a variable $d^{I}$ ($0 \le d^{I} \le 1$), with $d^{I} = 0$ for intact interface and $d^{I} = 1$ for fully fractured interface.

Fig. 1

Schematic illustration of a composite body containing crack surface Γ^b and interface Γ^I between two materials

The energy functional of such a cracked solid with interfacial fracture is written as

$$ {\Pi } = \mathop \int \limits_{{{\Omega }\backslash \left( {{\Gamma }^{b} \cup {\Gamma }^{I} } \right)}}^{{}} \psi \left( {{\varvec{\varepsilon}}\left( {\underline {x} } \right)} \right)d{\Omega } + \mathop \int \limits_{{{\Gamma }^{b} }}^{{}} G_{c}^{b} \left( {\underline {x} } \right)d{\Gamma } + \mathop \int \limits_{{{\Gamma }^{I} }}^{{}} D^{I} \left( {{\varvec{\varepsilon}}\left( {\underline {x} } \right),d^{I} \left( {\underline {x} } \right)} \right)d{\Gamma } $$

(1)

where $\psi$ is the elastic energy density in bulk material, $G_{c}^{b}$ is the crack resistance in the bulk material, and $D^{I}$ is the energy dissipation function for interface fracture that follows cohesive zone formulation. Here we use a volumetric representation of the interface, referred to as interphase, whose thickness is assumed to be negligibly small so that its deformation does not contribute to the stored elastic energy. In what follows, the coordinate variable $\underline {x}$ will be omitted, yet it should be kept in mind that all parameters will be allowed to be heterogeneous.

We follow the idea of the phase-field fracture models [5, 46] to regularise the crack surface in the bulk. By introducing a crack surface density $\gamma$ that is dependent on a damage variable $d$ and its gradient in a quadratic form $\gamma = \frac{1}{{2l_{c} }}d^{2} + \frac{{l_{c} }}{2}\left| {\nabla d} \right|^{2}$, with $l_{c}$ a characteristic length that controls the width of the smeared crack, the energy functional can be written in a semi-regularised form with the interface remaining as a sharp surface:

$$ {\Pi } = \mathop \int \limits_{{{\Omega }\backslash {\Gamma }^{I} }}^{{}} g\left( d \right)\psi \left( {\varvec{\varepsilon}} \right)d{\Omega } + \mathop \int \limits_{{{\Omega }\backslash {\Gamma }^{I} }}^{{}} G_{c}^{b} \cdot \left( {\frac{1}{{2l_{c} }}d^{2} + \frac{{l_{c} }}{2}\left| {\nabla d} \right|^{2} } \right)d{\Omega } + \mathop \int \limits_{{{\Gamma }^{I} }}^{{}} D^{I} \left( {{\varvec{\varepsilon}},d^{I} } \right)d{\Gamma } $$

(2)

where $g\left( d \right)$ is a degradation function that verifies $g\left( 0 \right) = 1$, $g\left( 1 \right) = 0$, $g^{\prime}\left( 1 \right) = 0$ and $g^{\prime}\left( d \right) < 0$, see e.g. [47]. We choose the simplest quadratic polynomial for the degradation function:

$$ g\left( d \right) = \left( {1 - d} \right)^{2} + \kappa $$

(3)

where $\kappa$ is a numerical parameter close to zero. The quadratic form of crack surface density function $\gamma$ is usually referred to as AT2 (Ambrosio–Tortorelli) formulation, which differs from the AT1 formulation using a linear form of crack density function [48].

In order to distinguish the tensile and compressive fracture behaviour, a common treatment is to split the strain energy function $\psi$ into a tensile part $\psi^{ + }$ and a compressive part $\psi^{ - }$ with degradation applying only on the tensile part. This yields the following functional:

$$ {\Pi } = \mathop \int \limits_{{{\Omega }\backslash {\Gamma }^{I} }}^{{}} g\left( d \right)\psi_{ + } \left( {\varvec{\varepsilon}} \right) + \psi_{ - } \left( {\varvec{\varepsilon}} \right)d{\Omega } + \mathop \int \limits_{{{\Omega }\backslash {\Gamma }^{I} }}^{{}} G_{c}^{b} \cdot \left( {\frac{1}{{2l_{c} }}d^{2} + \frac{{l_{c} }}{2}\left| {\nabla d} \right|^{2} } \right)d{\Omega } + \mathop \int \limits_{{{\Gamma }^{I} }}^{{}} D^{I} \left( {{\varvec{\varepsilon}},d^{I} } \right)d{\Gamma } $$

(4)

Different strain energy splitting strategies have been proposed in the literature, among which we mention two widely adopted ones: volumetric–deviatoric decomposition, see e.g. [49], and spectral decomposition see e.g. [6]. In the present work, we follow Miehe’s approach so that

$$ \psi_{ \pm } = \frac{\lambda }{2}\langle tr\left( {\varvec{\varepsilon}} \right)\rangle_{ \pm }^{2} + \mu \left( {{\varvec{\varepsilon}}_{ \pm } :{\varvec{\varepsilon}}_{ \pm } } \right),\quad {\text{with}}\;{\varvec{\varepsilon}}_{ \pm } = \mathop \sum \limits_{i = 1}^{3} \langle \varepsilon_{i}\rangle_{\pm } \underline {n}_{i} \otimes \underline {n}_{i} $$

(5)

where $\lambda$ and $\mu$ are Lamé coefficients, $\langle * \rangle_{ \pm } = \left( {* \pm \left| * \right|} \right)/2$, and $\varepsilon_{i}$ and $\underline {n}_{i}$ are the eigenvalues and eigenvectors of the strain tensor.

To take into account the irreversibility of damage evolution, a history field is introduced by Miehe et al. [6] ${\mathcal{H}}\left( {\varvec{\varepsilon}} \right) = \max_{{\tau \in \left[ {0,t} \right]}} \psi_{ + } \left( {{\varvec{\varepsilon}},t} \right)$, leading to a new energy functional:

$$ {\Pi } = \mathop \int \limits_{{{\Omega }\backslash {\Gamma }^{I} }}^{{}} g\left( d \right) \cdot {\mathcal{H}}\left( {\varvec{\varepsilon}} \right) + \psi_{ - } \left( {\varvec{\varepsilon}} \right)d{\Omega } + \mathop \int \limits_{{{\Omega }\backslash {\Gamma }^{I} }}^{{}} G_{c}^{b} \cdot \left( {\frac{1}{{2l_{c} }}d^{2} + \frac{{l_{c} }}{2}\left| {\nabla d} \right|^{2} } \right)d{\Omega } + \mathop \int \limits_{{{\Gamma }^{I} }}^{{}} D^{I} \left( {{\varvec{\varepsilon}},d^{I} } \right)d{\Gamma } $$

(6)

It should be noted that the use of the history field in Eq. 6 makes the resulting model different from the original formulation of Frankfort and Marigo [8], see e.g. [50, 51]. Although it has not yet been mathematically proven to be sufficient for irreversibility enforcement, various examples have shown its robustness in the context of cyclic loadings [52, 53], therefore it is widely adopted in the literature. Other irreversibility treatments have been proposed within the original variational framework by directly forcing non-increasing damage evolution in time when solving the minimisation problem. The readers are referred to [54, 55] for using relaxed constraints via a notion of crack set, [56] for augmented Lagrangian method, [57] for primal–dual active set method and [51] for penalty formulation, to name a few. In the present work, we choose to use the history field irreversibility treatment, but the proposed framework can be easily adjusted to other techniques based on alternating minimisation (staggered scheme).

By minimizing the above functional (Eq. 6), the equilibrium equation can be obtained,

$$ \nabla \cdot {\varvec{\sigma}} = \underline {0} $$

(7)

where ${\varvec{\sigma}}\left( {\underline {x} } \right)$ is the local stress tensor dependent on the local deformation ${\varvec{\varepsilon}}\left( {\underline {x} } \right)$ and damage variable $d\left( {\underline {x} } \right)$ for $\underline {x} \in {\Omega }\backslash {\Gamma }^{I}$ and $d^{I} \left( {\underline {x} } \right)$ for $\underline {x} \in {\Gamma }^{I}$. The constitutive law for the isotropic bulk material is

$$ {\varvec{\sigma}} = \left( {1 - d} \right)^{2} \left[ {\lambda \langle tr\left( {\varvec{\varepsilon}} \right)\rangle_{ + } {\varvec{I}} + 2\mu {\varvec{\varepsilon}}_{ + } } \right] + \left[ {\lambda \langle tr\left( {\varvec{\varepsilon}} \right)\rangle_{ - } {\varvec{I}} + 2\mu {\varvec{\varepsilon}}_{ - } } \right]\;{\text{for}}\;\underline {x} \in {\Omega }\backslash {\Gamma }^{{\text{I}}} $$

(8)

where ${\varvec{I}}$ is a 3 × 3 identity matrix.

As for the interphase, a frictional cohesive zone model is used to describe the constitutive behaviour:

$$ {\varvec{\sigma}}\left( {\underline {x} } \right) = {\varvec{\sigma}}_{CZM} \left( {{\varvec{\varepsilon}}\left( {\underline {x} } \right),d^{I} \left( {\underline {x} } \right)} \right) \quad {\text{for}}\;\underline {x} \in {\Gamma }^{I} $$

(9)

which will be presented later in Sect. 2.3. The interphase damage variable is assumed as local and its evolution can be explicitly determined according to the deformation state at a given time step.

The evolution equation of the bulk damage variable $d\left( {\underline {x} } \right)$ can also be derived from the energy functional as

$$ \frac{{G_{c}^{b} }}{{l_{c} }}d - G_{c}^{b} l_{c} {\Delta }d - \left( {\nabla \cdot \left( {G_{c}^{b} l_{c} } \right)} \right)\nabla d = 2\left( {1 - d} \right){\mathcal{H}}\left( {\varvec{\varepsilon}} \right) $$

(10)

Following an approximation already used for heterogeneous materials in the literature [39, 41, 58,59,60,61], the last term of the left-hand side is omitted, which leads to

$$ \frac{{G_{c}^{b} }}{{l_{c} }}\left[ {d - l_{c}^{2} {\Delta }d} \right] = 2\left( {1 - d} \right){\mathcal{H}}\left( {\varvec{\varepsilon}} \right) $$

(11)

A discussion on such an approximation in the context of FFT methods was given by Ma and Sun [41]. As a collocation approach, FFT methods consider the material parameters as piece-wise constant, leading to the assumption that the gradient of $G_{c}^{b}$ and $l_{c}$ are zero at each material point. As a consequence, the last term of the left-hand side in Eq. 10 vanishes. Otherwise, we note an alternative method proposed by Ernesti et al. [40] to circumvent this issue, by solving multiple damage fields, with each associated with a homogeneous domain of a constitutive material. Further investigations (both theoretical and numerical) are required to verify whether the approximation incorporated herein (as many other works) leads to discrepancies, yet this is beyond the scope of the present work.

2.2 Local homogenisation at interface voxels

FFT methods intrinsically use image-type (regular uniform) discretisation, whereas the interface ${\Gamma }^{I}$ can have any arbitrary geometry in the computation domain. To deal with this geometry-discretisation mismatch, the composite voxel technique is used. The thickness of the interphase is assumed to be always sufficiently small, so that a 3-layer laminate model can be used whatever the voxel size is. Figure 2 illustrates a composite voxel of three laminate layers, representing two bulk phases and an interphase between them.

Fig. 2

Illustration of a composite voxel with three laminate layers. The interface coordinate system is described by a normal vector $\underline{{e_{n} }}$ and two tangential vectors $\underline{{e_{t1} }}$ and $\underline{{e_{t2} }}$. The principal tangential vector $\underline{{e_{t} }}$ is in the same plane of $\underline{{e_{t1} }}$ and $\underline{{e_{t2} }}$ and it depends on the strain state of the interphase $\tilde{\varvec{\varepsilon }}^{I}$

The laminate model will be expressed within the interface coordinates ($\underline{{e_{n} }} , \underline{{e_{t1} }} ,\underline{{e_{t2} }}$ see Fig. 2). The stress and strain tensors ($\tilde{\varvec{\sigma }}$ and $\tilde{\varvec{\varepsilon }}$) in the interface coordinates and the global unit-cell coordinates can be easily calculated with the rotation matrix ${\varvec{Q}} = \left[ {\underline{{e_{n} }} ,\underline{{e_{t1} }} ,\underline{{e_{t2} }} } \right]^{T}$ as

$$ \tilde{\varvec{\sigma }} = {\varvec{Q}}^{T} \varvec{\sigma Q}\quad \tilde{\varvec{\varepsilon }} = {\varvec{Q}}^{T} \varvec{\varepsilon Q} $$

(12)

Within the interface coordinates, the equilibrium and continuity conditions of the laminate structure are:

$$ \langle \tilde{\varvec{\sigma }}^{AP}\rangle = \tilde{\varvec{\sigma }}^{AP,1} = \tilde{\varvec{\sigma }}^{AP,2} = \tilde{\varvec{\sigma }}^{AP,I} $$

(13a)

$$ \langle \tilde{\varvec{\sigma }}^{IP} \rangle = f_{v1} \cdot \tilde{\varvec{\sigma }}^{IP,1} + f_{v2} \cdot \tilde{\varvec{\sigma }}^{IP,2} + f_{vI} \cdot \tilde{\varvec{\sigma }}^{IP,I} $$

(13b)

$$ \langle \tilde{\varvec{\varepsilon }}^{AP}\rangle = f_{v1} \cdot \tilde{\varvec{\varepsilon }}^{AP,1} + f_{v2} \cdot \tilde{\varvec{\varepsilon }}^{AP,2} + f_{vI} \cdot \tilde{\varvec{\varepsilon }}^{AP,I} $$

(13c)

$$ \langle \tilde{\varvec{\varepsilon }}^{IP}\rangle = \tilde{\varvec{\varepsilon }}^{IP,1} = \tilde{\varvec{\varepsilon }}^{IP,2} = \tilde{\varvec{\varepsilon }}^{IP,I} $$

(13d)

where $f_{v1}$, $f_{v2}$, $f_{vI}$ are the volume fractions of the three phases in the composite voxel, verifying $f_{v1} + f_{v2} + f_{vI} = 1$. The brackets $\langle * \rangle$ denote the overall value of $*$ within a composite voxel. The superscripts $*^{AP}$ and $*^{IP}$ represent the anti-plane and in-plane components of stress or strain tensor:

$$ \varvec{*}^{AP} = \left( {\begin{array}{*{20}c} {*_{nn} } & {*_{nt1} } & {*_{nt2} } \\ {*_{nt1} } & 0 & 0 \\ {*_{nt2} } & 0 & 0 \\ \end{array} } \right)\quad {\text{and}}\quad \varvec{*}^{IP} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {*_{t1t1} } & {*_{t1t2} } \\ 0 & {*_{t1t2} } & {*_{t2t2} } \\ \end{array} } \right) $$

(14)

such that $\tilde{\varvec{\sigma }} = \tilde{\varvec{\sigma }}^{AP} + \tilde{\varvec{\sigma }}^{IP}$ and $\tilde{\varvec{\varepsilon }} = \tilde{\varvec{\varepsilon }}^{AP} + \tilde{\varvec{\varepsilon }}^{IP}$. This laminate model is then completed with the constitutive laws, Eq. 8 for the bulk and Eq. 9 for the interphase, with the latter described in the next section. As the interphase is assumed to have negligibly small thickness, its in-plane resistance can be considered as null $\tilde{\varvec{\sigma }}^{IP,I} = 0$.

In practice, the volume fractions of the three phases ($f_{v1}$, $f_{v2}$, $f_{vI}$) are calculated at each composite voxel when generating the microstructural unit cells. First, we determine the intersection plane between the interface (without thickness) at each composite voxel. Then two preliminary volume fractions ($\tilde{f}_{v1}$ and $\tilde{f}_{v2}$) of the two bulk phases are calculated from the volumes of the 3D polygons cut from the voxel by the interface plane, with $\tilde{f}_{v1} + \tilde{f}_{v2} = 1$. Finally, the volume fraction of the interphase $f_{vI}$ is subtracted from the maximum of $\tilde{f}_{v1}$ and $\tilde{f}_{v2}$:

$$ f_{vi} = \left\{ {\begin{array}{*{20}l} {\tilde{f}_{vi} - f_{vI} } \hfill & {\quad if \; \tilde{f}_{vi} = \mathop {\max }\limits_{j = 1,2} \tilde{f}_{vj} } \hfill \\ {\tilde{f}_{vi} } \hfill & {\quad otherwise} \hfill \\ \end{array} ,} \right.\quad {\text{with}}\;i = 1,2 $$

(15)

such that the condition $f_{v1} + f_{v2} + f_{vI} = 1$ is satisfied. In the present study, $f_{vI}$ is set to a constant value for all composite voxels, though it can be more precisely calculated from the intersection area between the interface plane and the voxel, associated with an arbitrary thickness. It will be shown in the next section that the simulation result can be insensitive to $f_{vI}$ due to a reasonable simplification.

2.3 Cohesive zone model for interphase behaviour

Cohesive zone models describe the relationship between the displacement jump (i.e. separation) and traction between the two crack faces, whereas the original concept of the composite voxel technique is expressed with strain and stress (Eq. 13). Therefore, we need first to convert the strain tensor $\tilde{\varvec{\varepsilon }}^{AP,I}$ to a displacement vector $\underline {s} = \left( {s_{n} ,s_{t1} ,s_{t2} } \right)^{T}$, then the traction vector $\underline {t} = \left( {t_{n} ,t_{t1} ,t_{t2} } \right)^{T}$ to the stress tensor $\tilde{\varvec{\sigma }}^{I} = \tilde{\varvec{\sigma }}^{AP,I}$.

2.3.1 Interphase strain tensor to interface displacement vector

The contribution of an interface displacement jump $\underline {s}$ to the overall strain of the composite voxel can be expressed as $\left( {\begin{array}{*{20}c} {s_{n} } & {s_{t1} } & {s_{t2} } \\ {s_{t1} } & 0 & 0 \\ {s_{t2} } & 0 & 0 \\ \end{array} } \right) \cdot S/V$, with S the surface area of the interface within the composite voxel and $V = h^{3}$ the voxel volume. Combining Eq. 13c that corresponds to a classical laminate with an interphase, we obtain

$$ f_{vI} \cdot \tilde{\varvec{\varepsilon }}^{AP,I} = \left( {\begin{array}{*{20}c} {s_{n} } & {s_{t1} } & {s_{t2} } \\ {s_{t1} } & 0 & 0 \\ {s_{t2} } & 0 & 0 \\ \end{array} } \right) \cdot S/V $$

(16)

A simplification is then made by assuming that $S = h^{2}$, which leads to

$$ \left( {\begin{array}{*{20}c} {s_{n} } \\ {s_{t1} } \\ {s_{t2} } \\ \end{array} } \right) = f_{vI} h\left( {\begin{array}{*{20}c} {\tilde{\varepsilon }_{nn}^{I} } \\ {\tilde{\varepsilon }_{nt1}^{I} } \\ {\tilde{\varepsilon }_{nt2}^{I} } \\ \end{array} } \right) $$

(17)

If we substitute Eq. 16 into Eq. 13c, and assuming that the in-plane components of the interphase stress $\tilde{\varvec{\sigma }}^{IP,I}$ equal zero, the volume fraction of interphase $f_{vI}$ vanishes from the 3-layer laminate system, though its insignificant effect remains in changing the ratio between $f_{v1}$ and $f_{v2}$ (see Eq. 15). A numerical analysis will be conducted in Sect. 4.2.3, confirming the insensitivity to the choice of $f_{vI}$.

In addition, CZMs are usually expressed in 2D, so we need to determine the principal shear direction $\underline{{e_{t} }}$ in 3D space:

$$ \underline{{e_{t} }} = \left[ {0,s_{t1} /s_{t} ,s_{t2} /s_{t} } \right]^{T} \quad {\text{with}}\;s_{t} = \sqrt {s_{t1}^{2} + s_{t2}^{2} } $$

(18)

so that 2D CZMs can be applied to 3D problems with the 2D displacement vector $\underline {s}^{2D} = \left( {s_{n} , s_{t} } \right)^{T}$, associated with a 2D traction vector $\underline {t}^{2D} = \left( {t_{n} ,t_{t} } \right)^{T}$. For the sake of simplicity, the superscript $*^{2D}$ will be omitted hereafter.

2.3.2 Frictional CZ model

In this work, we incorporate the CZ model of [44], which assumes that an elementary interface area A can be decomposed into damaged and undamaged parts, so that the traction vectors and the displacement jumps follow a mixture rule and a continuity condition, respectively:

$$ \begin{aligned} \underline {t} & = \left( {1 - d^{I} } \right) \cdot \underline {t}^{u} + d^{I} \cdot \underline {t}^{d} \\ \underline {s} & = \underline {s}^{u} = \underline {s}^{d} \\ \end{aligned} $$

(19)

where $\underline {t}^{u}$ and $\underline {t}^{d}$ represent the tractions of the undamaged and damaged parts, respectively, and $\underline {s}^{u}$ and $\underline {s}^{d}$ the corresponding displacement jumps.

On the undamaged part of the interface, the traction $\underline {t}^{u}$ follows a linear relationship with the displacement jump:

$$ \underline {t}^{u} = \left[ {\begin{array}{*{20}c} {K_{n} } & 0 \\ 0 & {K_{t} } \\ \end{array} } \right] \cdot \underline {s}^{u} $$

(20)

where $K_{n}$ and $K_{t}$ are the stiffness in mode I and mode II loads, respectively.

On the damaged part, the traction vector $\underline {t}^{d}$ is determined by a linear relationship of the elastic part of displacement jump $\underline {s}^{de}$, and combined with a unilateral condition in the normal direction:

$$ \underline {t}^{d} = \left[ {\begin{array}{*{20}c} {\left( {1 - H\left( {s_{n} } \right)} \right)K_{n} } & 0 \\ 0 & {K_{t} } \\ \end{array} } \right] \cdot \underline {s}^{de} $$

(21)

where $H\left( {s_{n} } \right)$ denotes the Heaviside function evaluated for $s_{n}$, so that the unilateral condition in the normal direction is taken into account. The elastic part $\underline {s}^{de}$ can be calculated from

$$ \underline {s}^{de} = \underline {s}^{d} - \underline {s}^{di} $$

(22)

where $\underline {s}^{di} = \left[ {s_{n}^{di} ,s_{t}^{di} } \right]^{T}$ is the inelastic part of the displacement jump, describing the interpenetration in the normal direction (mode I direction), and the frictional sliding in the tangential direction (mode II direction). Interpenetration is excluded from the present model, so $s_{n}^{di} = 0$; the frictional sliding displacement $s_{t}^{di}$ is determined by

$$ s_{t}^{di} = \left( {s_{t}^{di} } \right)^{{t_{n - 1} }} + {\Delta }\lambda \frac{{t_{t}^{d} }}{{\left| {t_{t}^{d} } \right|}} $$

(23)

where the superscript $*^{{t_{n - 1} }}$ denotes the quantity from the previous time step. ${\Delta }\lambda$ is used to introduce the Kuhn–Tucker conditions for friction:

$$ {\Delta }\lambda \ge 0, \mu^{I} t_{n}^{d} + \left| {t_{t}^{d} } \right| \le 0,\quad {\Delta }\lambda \left( {\mu^{I} t_{n}^{d} + \left| {t_{t}^{d} } \right|} \right) = 0 $$

(24)

where $\mu^{I}$ denotes the friction coefficient of the fractured interface. In practice, a trial quantity of $\mu^{I} t_{n}^{d,el} + \left| {t_{t}^{d,el} } \right|$ is first calculated, with $t_{n}^{d,el} = \left( {1 - H\left( {s_{n} } \right)} \right)K_{n} s_{n}$ and $t_{t}^{d,el} = K_{t} \left( {s_{t} - \left( {s_{t}^{di} } \right)^{{t_{n - 1} }} } \right)$. If $\mu^{I} t_{n}^{d,el} + \left| {t_{t}^{d,el} } \right| \le 0$, then no sliding occurs, i.e. ${\Delta }\lambda = 0$ and $t_{t}^{d} = t_{t}^{d,el}$; otherwise, a new equilibrium [44] needs to be found, leading to

$$ {\Delta }\lambda = \frac{1}{{K_{t} }}\left( {\mu^{I} t_{n}^{d,el} + \left| {t_{t}^{d,el} } \right|} \right)\quad {\text{and}}\quad t_{t}^{d} = - \mu^{I} t_{n}^{d,el} \frac{{t_{t}^{d,el} }}{{\left| {t_{t}^{d,el} } \right|}} $$

(25)

For the damage evolution, a bilinear traction–separation law (Fig. 3) is used. By satisfying a mixed-mode criterion of $\frac{{G_{n} }}{{G_{cI} }} + \frac{{G_{t} }}{{G_{cII} }} = 1 \left( {G_{i} = \mathop \int \limits_{0}^{ + \infty } t_{i} {\text{ds}}_{{\text{i}}} } \right)$, the damage variable $d^{I}$ at each composite voxel is calculated as:

$$ d^{I} = \max \left\{ {0,\min \left( {0,\frac{1}{\eta }\left( {\frac{\beta }{1 + \beta }} \right)} \right)} \right\}\quad {\text{with}}\;\beta = \sqrt {\left( {\frac{{ \langle s_{n}\rangle{+} }}{{s_{0n} }}} \right)^{2} + \left( {\frac{{s_{t} }}{{s_{0t} }}} \right)^{2} } - 1 $$

(26)

Fig. 3

Traction–separation relations for mode I (a) and mode II (b) fractures of the CZ model used for describing interfacial damage behaviour. Five parameters are chosen to characterise the CZ model: the critical stresses ($t_{01} ,t_{02}$), the fracture energies $\left( {G_{cI} , G_{cI} } \right)$ and the shape ratio $\eta = 1 - \frac{{s_{01 } }}{{S_{c1} }} = 1 - \frac{{s_{02 } }}{{S_{c2} }}$

where $s_{0n}$ and $s_{0t}$ are the critical displacement jumps corresponding to the peak traction values of mode I and mode II fractures, respectively. The parameter $\eta$ is defined as $\eta = 1 - \frac{{s_{0n} }}{{s_{cn} }} = 1 - \frac{{s_{0t} }}{{s_{ct} }}$, which allows the initial stiffness to be tuned without changing the two physical parameters: critical stress $t_{0*}$ and fracture energy $G_{c*}$. In fact, as shown in Fig. 4, the three parameters together determine the shape of the bi-linear traction separation law. The irreversibility of interface damage evolution is enforced numerically, i.e. the damage variable $d^{I}$ is forced to be monotonically increasing at each loading step.

Fig. 4

Effect of the model parameters ($\eta$, $t_{01}$ and $G_{cI}$) on the bi-linear traction–separation law (example of pure mode I fracture)

2.3.3 Interface traction vector to interphase stress tensor

Once the traction $\underline {t}$ is calculated according to the above cohesive zone model, the stress tensor in the interphase is calculated by:

$$ \tilde{\varvec{\sigma }}^{I} = \tilde{\varvec{\sigma }}^{AP,I} = \left( {\begin{array}{*{20}c} {t_{n} } & {t_{t} s_{t1} /s_{t} } & {t_{t} s_{t2} /s_{t} } \\ {t_{t} s_{t1} /s_{t} } & 0 & 0 \\ {t_{t} s_{t2} /s_{t} } & 0 & 0 \\ \end{array} } \right) $$

(27)

where the in-plane terms have been set to zero.

3 FFT solver for the PF-CZ model with composite voxel technique

3.1 Overall algorithm

The FFT solver proposed by [39] for a PF model without interface fracture is now extended to solve the present PF-CZ model. A staggered scheme is used to separately solve the two governing equation systems (Eqs. 7 and 11), both using the FFT method with fixed-point iteration algorithm. The overall algorithm is illustrated in Fig. 5.

Fig. 5

Overall algorithm for solving the PF-CZ model with FFT method

The mechanical problem at each load increment is solved using the basic scheme of [18] together with a modified Green operator [24] and Anderson’s convergence acceleration technique [19]. Within this fixed-point loop, the bulk and interphase damage ($d$ and $d^{I}$) are considered as unchanged. The bulk voxels (homogenous) follow an isotropic elastic constitutive law (Eq. 8), while the interphase voxels (composite) are governed by the 3-layer laminate model (Eq. 13). The numerical solution of the laminate model will be summarised later in Sect. 3.2.

The evolutions of the damage variables $d$ and $d^{I}$ are determined with the stress fields being unchanged. The governing equation of the bulk damage (Eq. 11) is solved with the fixed-point algorithm of [39], as it remains essentially the same as the PF model without interface fracture, except for the composite voxels. For the latter, we choose to calculate the average material parameters ($l_{c} , G_{c}^{b}$), as well as the driving force ${\mathcal{H}}\left( {\varvec{\varepsilon}} \right)$, according to the volume fractions of each bulk phase:

$$ G_{c}^{b} = \frac{{f_{v1} G_{c}^{b1} + f_{v2} G_{c}^{b2} }}{{f_{v1} + f_{v2} }};\quad l_{c} = \frac{{f_{v1} l_{c1} + f_{v2} l_{c2} }}{{f_{v1} + f_{v2} }};\quad {\mathcal{H}}\left( {\varvec{\varepsilon}} \right) = \frac{{f_{v1} {\mathcal{H}}_{1} + f_{v2} {\mathcal{H}}_{2} }}{{f_{v1} + f_{v2} }} $$

(28)

As for the interphase, its damage $d^{I}$ is determined by a closed form of Eq. 26 from the anti-plane stresses and strains of the interphase layer. In order to ensure the laminate model is well conditioned, the bulk and interphase of composite voxels $\underline {x}^{I}$ are forbidden to be simultaneously fully damaged. In practice, a numerical parameter $k,$ with $k$ smaller than but close to 1, is introduced: if both the bulk damage $d$ and the interphase damage $d^{I}$ at the same composite voxel $\underline {x}^{I}$ reach a value higher than $k$, the bulk damage variable is set to $d = k$. The choice of the parameter $k$ does not affect the prediction as will be shown in Sect. 4.2.5. This ad-hoc treatment helps the algorithm achieve convergence for some critical composite voxels, especially for those where the crack deflects from the interface to the bulk or vice-versa.

Once the damage variables are updated, the algorithm moves forwards to the next loading step. As an explicit algorithm, it relies on the time step being sufficiently small to obtain converged results, as will be shown in Sect. 4.2.2. We note that alternative algorithms have been proposed to address this issue, see e.g. [40] and [61].

3.2 Numerical solution of the 3-layer laminate model

At each composite voxel, the overall stress response $\langle{\varvec{\sigma }}\rangle$ to a prescribed overall strain $\langle \tilde{\varvec{\varepsilon }}\rangle$ is computed using the 3-layer laminate model of Eq. 13, in which the in-plane strain components ($\tilde{\varvec{\varepsilon }}^{AP,1}$, $\varvec{ \tilde{\varepsilon }}^{AP,2}$, $\varvec{ \tilde{\varepsilon }}^{AP,I}$) of each phase are the variables to be determined. Now we re-cast the laminate equations into a system of residual equations that will be solved by Newton–Raphson’s method, as proposed and implemented by [45]. Using phase 1 as reference, and substituting Eqs. 13c and 13d into the anti-plane equilibrium condition (Eq. 13a), one obtains the following residual equations:

$$ \begin{aligned} {\mathbf{\varvec{\mathcal{R}}}} & : = \left( {\begin{array}{*{20}c} {\tilde{\varvec{\sigma }}^{AP,I} \left( {\tilde{\varvec{\varepsilon }}^{AP,I} } \right) - \tilde{\varvec{\sigma }}^{AP,1} \left( {\tilde{\varvec{\varepsilon }}^{1} } \right)} \\ {\tilde{\varvec{\sigma }}^{AP,2} \left( {\tilde{\varvec{\varepsilon }}^{2} } \right) - \tilde{\varvec{\sigma }}^{AP,1} \left( {\tilde{\varvec{\varepsilon }}^{1} } \right)} \\ \end{array} } \right) = \mathbf{0} \\ &\quad \;{\text{with}}\;\tilde{\varvec{\varepsilon }}^{1} = \tilde{\varvec{\varepsilon }}^{IP,1} + \frac{{\langle \tilde{\varvec{\varepsilon }}^{AP}\rangle - f_{vI} \tilde{\varvec{\varepsilon }}^{AP,I} - f_{v2} \tilde{\varvec{\varepsilon }}^{AP,2} }}{{f_{v1} }}\;{\text{and}}\;\tilde{\varvec{\varepsilon }}^{2} = \tilde{\varvec{\varepsilon }}^{IP,2} + \tilde{\varvec{\varepsilon }}^{AP,2} \\ \end{aligned} $$

(29)

Note that the anti-plane stress components $\tilde{\varvec{\sigma }}^{AP,I}$ of the interphase are only dependent upon the anti-plane strain components $\tilde{\varvec{\varepsilon }}^{AP,I}$ via the cohesive zone model described in Sect. 2.3.2, whereas those of phase 1 and phase 2 are dependent, through the constitutive relation of Eq. 8, on the whole strain tensors $\tilde{\varvec{\varepsilon }}^{1}$ and $\tilde{\varvec{\varepsilon }}^{2}$, respectively. Combining the continuity equation (Eq. 13d), the unknowns in this system become the anti-plane strains of phase 2 and interphase $\tilde{\varvec{\varepsilon }}^{AP,2}$, $\tilde{\varvec{\varepsilon }}^{AP,I}$.

Let us note that the system of Eq. 29 is non-linear, due to the unilateral condition of the bulk phases, as well as the frictional sliding of the interphase, despite the damage variables being constant during the numerical resolution of the laminate model. The unknowns and the equations (Eq. 29) are explicitly expressed within vector form:

$$ \begin{aligned} & \widetilde{{\underline {\varepsilon } }}^{AP} = \left[ {\tilde{\varepsilon }_{nn}^{I} ,\tilde{\varepsilon }_{nt1}^{I} ,\tilde{\varepsilon }_{nt2}^{I} ,\tilde{\varepsilon }_{nn}^{2} ,\tilde{\varepsilon }_{nt1}^{2} ,\tilde{\varepsilon }_{nt2}^{2} } \right]^{T} \\ & \underline {{\mathfrak{R}}} : = \left[ {\tilde{\sigma }_{nn}^{I} - \tilde{\sigma }_{nn}^{1} , \tilde{\sigma }_{nt1}^{I} - \tilde{\sigma }_{nt1}^{1} , \tilde{\sigma }_{nt2}^{I} - \tilde{\sigma }_{nt2}^{1} ,\tilde{\sigma }_{nn}^{2} - \tilde{\sigma }_{nn}^{1} , \tilde{\sigma }_{nt1}^{2} - \tilde{\sigma }_{nt1}^{1} , \tilde{\sigma }_{nt2}^{2} - \tilde{\sigma }_{nt2}^{1} } \right]^{T} = \underline {0} \\ \end{aligned} $$

(30)

The solution procedure consists in iteratively calculating the following equations:

$$ \left\{ {\begin{array}{*{20}l} {\left( {\frac{{\partial \underline{{\mathcal{R}}}}}{{\partial \underline{{\tilde{\varepsilon }}}^{AP} }}} \right)^{i - 1} :\left( {\Delta \widetilde{{\underline {\varepsilon } }}^{AP} } \right)^{i} = - \underline{{\mathcal{R}}}\left( {\left( {\widetilde{{\underline {\varepsilon } }}^{AP} } \right)^{i - 1} } \right)} \hfill \\ {\left( {\underline{{\tilde{\varepsilon }}}^{AP} } \right)^{i} = \left( {\underline{{\tilde{\varepsilon }}}^{AP} } \right)^{i - 1} + \left( {\Delta \underline{{\tilde{\varepsilon }}}^{AP} } \right)^{i} } \hfill \\ {i = i + 1 } \hfill \\ \end{array} } \right. $$

(31)

where the superscripts $\left( * \right)^{i - 1}$ and $\left( * \right)^{i}$ represent the quantities at the $\left( {i - 1} \right)$-th and $i$-th iterations. The anti-plane components of the overall strain $\langle \underline{{\tilde{\varepsilon }}}^{AP}\rangle$ are used as the initial guess of the unknown vector $\left( {\underline{{\tilde{\varepsilon }}}^{AP} } \right)^{i = 0}$. The tangent stiffness matrix, denoted by $\frac{{\partial \underline{{\mathcal{R}}} }}{{\partial \underline{{\tilde{\varepsilon }}}^{AP} }}$, for Newton–Raphson’s algorithm is calculated numerically with a simple perturbation method:

$$ \left( {\frac{{\partial \underline{{\mathcal{R}}} }}{{\partial \underline{{\tilde{\varepsilon }}}^{AP} }}} \right)_{pq} \approx \frac{1}{\epsilon }\left( {{\mathcal{R}}_{p} \left( {\tilde{\varepsilon }_{q}^{AP} + \varepsilon } \right) - {\mathcal{R}}_{p} \left( {\tilde{\varepsilon }_{q}^{AP} } \right)} \right),\quad {\text{for}}\;p,q = 1,2, \ldots ,6 $$

(32)

where $\epsilon$ represents a small perturbation to each component $\tilde{\varepsilon }_{q}^{AP}$ of the unknown vector $\underline{{\tilde{\varepsilon }}}^{AP}$. In the numerical examples of the present paper, this value is chosen equal to $10^{ - 8}$.

3.3 Modified Laplacian operator for the phase-field problem

In our previous FFT solver [39], the Laplacian operator involved in the phase-field problem (Eq. 11) was calculated by a simple multiplication of the frequency vectors in Fourier space. This induces some local oscillations of the damage field as shown in Fig. 7b of [39]. To alleviate this issue, inspired by the idea of a discrete frequency vector (e.g. [24, 62], we incorporate here a modified Laplacian operator deduced from discrete Fourier transform of the finite difference operator:

$$ {\varvec{\xi}}^{2} = \frac{{2\left( {\cos \left( {\frac{{2\pi \left( {i - 1} \right)}}{{n_{x} }}} \right) - 1} \right)}}{{h^{2} }} + \frac{{2\left( {\cos \left( {\frac{{2\pi \left( {j - 1} \right)}}{{n_{y} }}} \right) - 1} \right)}}{{h^{2} }} + \frac{{2\left( {\cos \left( {\frac{{2\pi \left( {k - 1} \right)}}{{n_{z} }}} \right) - 1} \right)}}{{h^{2} }} $$

(33)

where $i,j,k$ are the integer indices along the three axes, and $n_{x} , n_{y} , n_{z}$ the corresponding dimensions. A similar strategy has also been adopted by [41] in their higher-order phase-field models.

The benefits of this modified Laplacian operator are demonstrated in Fig. 6 for a single-edge notched specimen under tension. The simulations have been conducted using the phase-field model without interface fracture [39]. The modified Laplacian operator clearly reduces the spurious oscillations of the damage field, and it also makes the stress–strain curve smoother, i.e. removing the abnormal decrease of stress as pointed out by the black arrow in Fig. 6b.

Fig. 6

Single-edge notched tensile test: a geometry used in the test; b stress–strain curves obtained with and without the modified Laplacian operator; c and d damage field around the crack tip for both simulations at the beginning of fracture process [indicated by the black diamond on the stress–strain curves in (b)]

4 Numerical examples

First, we validate the implementation of the frictional CZM with one single composite voxel. Then, we choose to use a single-edge notched specimen with an inclined interface as a benchmark to investigate the performance of the proposed FFT solver for the PF-CZ model, as well as the effects of some model parameters on the convergence rate and prediction results. Finally, fibre-matrix systems are tested to check the applicability to curved interfaces and complex fracture behaviours. We note that the stresses and strains shown in the present paper are homogenised values over the whole computation domain. Also, as we focus on numerical aspects and aim to give some illustrative numerical examples, some of the material parameters have been chosen following the literature, and some have been chosen in a way that complex fracture scenarios can be obtained with competing multi-phase cracks.

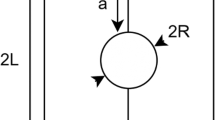
4.1 One-voxel shear test

Cyclic shear and constant compression ($\sigma_{yy} = - 10$ MPa) are applied to a single composite voxel with voxel size $h = 0.1$ mm. The volume fractions of different phases are $f_{v1} = 0.25, \;f_{vI} = 0.5, \;f_{v2} = 0.25$. This large $f_{vI}$ has been chosen only for the specific purpose of verifying the implementation of the CZ model, and it must be kept in mind that $f_{vI}$ should be small in normal usage of the model. The CZM parameters for the interphase are the same as those used by Alfano and Sacco [44]: $t_{0n} = t_{0t} = 3$ MPa, $G_{cI} = G_{cII} = 0.3$ N/mm and $\eta = 0.9$ with the friction coefficient $\mu^{I} = 0.5$. According to the conversion process presented in Sect. 2.3 (strain tensor to displacement vector and traction vector to stress tensor), the effective stiffness of the interphase can be evaluated as

$$ E_{*}^{I} = f_{vI} hK_{*} \quad {\text{with}}\;* = n,t $$

(34)

Hence, the elastic modulus of the interphase is $E_{*}^{I} = 1.5 \times 10^{ - 3}$ MPa, whereas those of the bulk are set to be much higher with $\lambda = 10^{6}$ MPa and $\mu = 10^{6} { }$ MPa. Also, only the interphase damage is activated in this test, by setting the fracture energy of the bulk materials to a very large value $g_{c} = 10^{12}$ N/mm, with the characteristic length $l_{c} = 0.01$ mm. Therefore, the total strain of the composite voxel can be approximately related to the shear displacement of the interphase via its thickness ($f_{vI} h = 0.05$ mm in the present case).

The stress–strain curve is shown in Fig. 7, and compared to the result of [44]. The very good agreement suggests that the CZM has been correctly implemented with the composite voxel technique.

Fig. 7

Stress–strain curve of a composite voxel under cyclic mode II shear. The dashed black curve has been obtained by dividing the displacement values of [44] by the interphase thickness (0.05 mm)

4.2 Single-edge notched specimen with inclined interface

The geometry of the single-edge notched tensile specimen with an inclined interface is depicted in Fig. 8. Both the crack notch and the interface are described by the laminate composite voxels. Macroscopic tension is applied to the computation domain in the vertical direction (Y-axis) by incrementally increasing $\varepsilon_{YY}$ and keeping $\sigma_{ZZ} , \sigma_{XX} , \sigma_{XY} ,\sigma_{XZ} ,\sigma_{YZ}$ to be zero. The subscript $*_{YY}$ of the loading strain will be omitted hereafter for the sake of simplicity.

Fig. 8

a Geometry of the single edge notched tensile specimen, with an inclination angle of θ = 30° between the interface and the predefined crack. A marginal layer of void with zero elastic constants has been added to the right-side border of the unit cell, so that the lateral surfaces are free of stresses. b A zoom-in of the unit-cell grid (h = 0.002 mm for this example), the location of the interface is shown by the red line

The material parameters are given in Table 1. The parameters of the bulk materials are the same as used in [6]. The CZM parameters of the interface voxels have been chosen such that the crack first propagates along the interface and then deviates into the bulk matrix. The critical stresses $t_{0n}$ and $t_{0t}$ and the shape ratio $\eta$ of the crack notch voxels are set to be very small so that its initial stiffness is much lower than those of the interface and bulk materials. In addition, its damage variable $d^{I}$ has been set to $\left( {1 - 10^{ - 9} } \right)$ from the first loading increment. This parameter setting of the crack notch makes the corresponding composite voxels behave approximately like a crack with free displacement discontinuity, i.e. a realistic crack. The friction coefficient is set to zero for all the simulations presented in this section (Sect. 4.2). The volume fraction of interphase and the CZM shape ratio of the crack notch voxels are fixed as $f_{vI} = 10^{ - 4}$ and $\eta = 0.1$, respectively; whereas those of the interface voxels are $f_{vI} = 10^{ - 4}$ and $\eta = 0.99$ for most of the tests except the tests on the effect of the corresponding parameter (Sect. 4.2.3 and Sect. 4.2.4). The numerical parameter k (see Sect. 3.1 for definition) is set to 0.999 for all tests except those in Sect. 4.2.5.

Table 1 Material parameters used for the benchmark study with single-edge notched tensile specimen

With this benchmark geometry, we will investigate the mesh dependency and the effects of some model parameters: the loading increment, the volume fraction of interphase $f_{vI}$, the shape ratio η of the CZM model, and the numerical parameter k.

4.2.1 Mesh dependency

Simulations with four different voxel sizes ($h = 0.005$ mm, $0.002$ mm, $0.001$ mm, $0.0005$ mm) are performed, with the CZM shape ratio $\eta = 0.99$ for the interface voxels. The incremental load is conducted with two stages: first ${\Delta }\varepsilon = 4 \times 10^{ - 5}$ for the elastic stage until $\varepsilon = 4 \times 10^{ - 3}$, and then ${\Delta }\varepsilon = 1 \times 10^{ - 6}$ until the final facture. The macroscopic stress–strain curves are shown in Fig. 9a for different voxel sizes. This result shows a convergence of the predicted behaviour as the voxel size decreases. It is worth noting that the condition on the voxel size for a converged prediction is more restrictive than $h < \frac{1}{2}l_{c}$ [6], which is presumably due to the use of CZ model. The numbers of iterations for the mechanical problem are also given in Fig. 9b, suggesting that more iterations are required when the crack starts to grow. Figure 9c and d shows the crack patterns at two different loading steps. The crack first initiates at the interface and then deviates into the bulk matrix. The bulk crack exhibits a straight path and its orientation seems affected by the existence of the interface.

Fig. 9

a Stress–strain curves of the single-edge notched tensile test with different voxel sizes; b Number of iterations with respect to the macroscopic strain for different voxel sizes. c and d Crack patterns at two loading steps [as indicated in (a) by the diamond symbols], showing interface and bulk cracking: results from the simulation with h = 0.002 mm. The bulk damage variable in the composite voxels is hidden to visualise the interface, but they have similar values as their neighbouring bulk voxels

Figure 10 shows the effect of the voxel size on the computation time per each fixed-point iteration and on the total number of iterations. The computation time per iteration has been calculated by the total computation time divided by the total number of iterations of the simulation. For both mechanical and phase-field problems, the computation time per iteration (Fig. 10a) exhibits a linear dependency on the number of voxels in the unit cell. Figure 10b shows that the total numbers of iterations for both mechanical and phase-field problems increase with the number of voxels in the unit-cell at logarithmic rates. These observations suggest that the proposed FFT solver is appropriate for large-scale simulations.

Fig. 10

Effect of voxel size (expressed by the number of voxels ~ 1/h² on the X-axis of both graphs) on a the average computation time per iteration and b the total number of iterations undertaken by each simulation

4.2.2 Effect of loading increment

The unit cell with $h = 0.002$ mm is used to test the effect of loading increment. The CZM shape ratio is $\eta = 0.99$ for the interface voxels. Three different increments ($\Delta\upvarepsilon = 10^{ - 5} ,\; \Delta\upvarepsilon = 5 \times 10^{ - 6} , \;\Delta\upvarepsilon = 10^{ - 6} ,\;\Delta\upvarepsilon = 5 \times 10^{ - 7}$) are applied to the second loading stage (after the elastic regime until $\varepsilon = 5 \times 10^{ - 3}$), giving the stress–strain curves shown in Fig. 11a. When the loading increment is large, the predicted fracture is retarded; whereas when it becomes small enough (${\Delta }\upvarepsilon = 10^{ - 6}$ for the present example), the predicted behaviour becomes relatively insensitive to the loading increment. The crack patterns from different loading increment are compared in Fig. 11b and c. A large increment produces a shorter interface crack, while the predicted crack length tends to stabilise as the increment decreases to small enough (${\Delta }\varepsilon = 10^{ - 6}$ in the present case).

Fig. 11

a stress–strain curves of the single-edge notched specimen under tension, with different loading increments ${\Delta }\varepsilon$ for the second loading stage. b–c crack patterns of the simulations with ${\Delta }\varepsilon = 10^{ - 5}$, ${\Delta }\varepsilon = 10^{ - 6}$ and $\Delta \varepsilon = 5 \times 10^{ - 7}$

We note that selecting loading increment is not always straightforward for displacement-controlled staggered scheme (used in the present work). Compromise must be found between accuracy and computation time. Ideally, it would be useful to find a criterion that helps determine the maximum loading increment for arbitrary configurations without performing preliminary calculations. In this regard, techniques of automatic loading step control have been explored in several previous contributions. Interested readers are referred to [63,64,65,66] for more details. Alternatively, a fracture-controlled (instead of displacement-controlled) staggered scheme has been proposed by Singh et al. [67], which inherits the property of its underlying monolithic scheme, thus simplifying the choice of loading increment.

4.2.3 Effect of the volume fraction of interphase $f_{vI}$

Four simulations are conducted with different volume fractions of interphase: $f_{vI} = 10^{ - 1} , 10^{ - 2} , 10^{ - 3} , 10^{ - 4}$. The voxel size is $h = 0.002$ mm. The CZM shape ratio is $\eta = 0.99$ for the interface voxels. Tensile load is applied with ${\Delta }\varepsilon = 10^{ - 6}$ for the stage after the elastic regime. The results are shown in Fig. 12, suggesting that $f_{vI}$ has no effect on either the predicted stress–strain curves or the time consumed for each fixed-point iteration. Within the staggered scheme, $f_{vI}$ is not involved in the phase-field problem, so it is legitimate for it to have no effect on the solution process. For the mechanical problem, $f_{vI}$ is involved in the composite voxels, yet as mentioned in Sect. 2.3.1, $f_{vI}$ vanishes across the numerical solution of the laminate model, consequently, it does not affect the solution of the laminate model, which is here confirmed by Fig. 12b. This insensitivity to $f_{vI}$ is rather a promising property of the model, since $f_{vI}$ is just a numerical parameter associated with the volumetric representation of interface. However, to avoid numerical issues it is still recommended to use an appropriate value of $f_{vI}$ that makes the volume fraction of any phase in most of the composite voxels not too small (e.g. $\ge 10^{ - 4}$).

Fig. 12

Effect of $f_{vI}$ for the single edge notched specimen test. Four simulations have been performed with different values of $f_{vI}$: a stress–strain curves; b the effect of $f_{vI}$ on the average time consumed by each fixed-point iteration for either the mechanical or the phase-field problem

4.2.4 Effect of the shape ratio η of the CZM

The benchmark problem is now tested with different values of the CZM shape ratio η for the interface voxels. As mentioned in Sect. 2.3 (Fig. 4a), a smaller η leads to a lower initial stiffness of the cohesive traction–separation law. This effect can also be seen in Fig. 13a, where a smaller η leads to a lower elastic stiffness in the stress–strain curves. Moreover, this parameter also has a clear effect on the crack growth path, as shown in Fig. 13b–d. A lower initial stiffness of the interphase leads to a full debonding at the interphase, whilst a higher initial stiffness makes the crack deviate into the bulk at the very beginning of the interphase debonding. This clear effect of the shape ratio η on the simulation result shows that the proposed model is able to predict different fracture situations: pure interphase or bulk fracture and both. However, it is not the focus of the present work to determine which value of η should be used for a specific interface.

Fig. 13

Effect of the CZM shape ratio η: a stress–strain curves; b–d crack patterns from η = 0.9999, 0.99, 0.5, respectively

4.2.5 Effect of the numerical parameter k

Finally, we test the effect of the numerical parameter k using three different values $k = 0.5, 0.9, 0.999$. By definition this parameter should be smaller than but close to 1. The stress–strain curves and the evolution of number of iterations shown in Fig. 14 suggest that it has no effect on the prediction result even though a small value of k is used. This is not surprising because this parameter exerts its effect only on a small number of composite voxels in the very specific case that both d and $d^{I}$ exceed k.

Fig. 14

Effect of the numerical parameter k: a stress–strain curves from simulations with different values of k; b number of iterations for the solution of mechanical problem at all strain levels. The curves and markers are superimposed for all simulations with different k

4.3 Frictional behaviour of an interface under compressive shear

Here we test the capability of the model in predicting the sliding behaviour of an interface. Figure 15a depicts the geometry of the unit cell, with mesh size $h = 0.005$ mm. It is subjected to a cyclic shear load in positive and negative range, whilst a constant compression of 300 MPa in the Y-axis is maintained. The material parameters for the bulk materials are $\lambda = 121.15 \times 10^{3}$ MPa, $\mu = 80.77 \times 10^{3}$ MPa, $l_{c} = 0.02$ mm, $G_{c}^{b} = 2.7 \times 10^{3}$ N/mm. The CZM parameters for the interface voxels are $t_{0n} = 1000$ MPa, $t_{0t} = 1000$ MPa, $G_{cI} = G_{cII} = 1$ N/mm, $\eta = 0.99$, $\mu^{I} = 0.5$. The predefined crack notch is also described by a set of composite voxels with the same CZM parameters as the interphase voxels, except that the initial damage variable is set to be $d^{I} = 1 - 10^{ - 9}$, such that the composite voxels undergo pure frictional stress when shear sliding takes place.

Fig. 15

Frictional sliding of interface: a geometry of the unit cell, subjected to a constant compression and a cyclic shear load; b the simulated stress–strain curve; c shear strain map at different loading steps and the corresponding interphase damage

The stress response is shown in Fig. 15b. After a quasi-linear increase of shear stress, a brittle fracture occurs at the interface. Because of the compression in the Y-axis, the stress drops to a non-zero value (150 MPa) and interfacial sliding takes place as the shear strain continues to increase. Then the shear strain is unloaded and reloaded in the opposite direction. In this unload-reload process, the shear stress first linearly decreases, and then reaches the sliding stress (− 150 MPa) in the opposite direction. Let us note that the magnitude of the sliding stress (150 MPa) corresponds well to the friction coefficient 0.5. Maps of shear strains are given in Fig. 15c together with the interphase damage at different loading steps. Due to the periodic boundary conditions intrinsically imposed by the FFT method, the interphase damage initiates from two ends at step 1. Strong strain localisation occurs in the notch and the fractured section of the interphase. The interphase is fully fractured at step 2 and the damage variable remains throughout the cyclic load confirming the irreversibility. Localised strains at the interphase and notch increase as the shear load increases in the positive direction until step 3. When the shear increment changes its direction but the apparent load remains positive (step 4), the localised strains remain positive due to the residual inelastic strains accumulated during the previous frictional sliding at the interphase and notch. These residual strains gradually decrease to zero and increase in the negative direction as the negative shear increases from step 4 to step 5.

4.4 Application to curved interface: fibre-matrix system

4.4.1 Single-fibre system

With the geometry depicted in Fig. 16, we test our model over a single fibre-matrix system under transverse tension. A marginal layer of void (null elastic constants) has been added to the right-hand side of the unit cell to make the left and right borders free of stress. As indicated in Fig. 16, different positions for the fibre centre are tested. Macroscopic tension in the Y-axis is applied to the unit cell with a constant loading increment ${\Delta }\varepsilon = 10^{ - 6}$ until final failure. The elastic parameters correspond to glass fibre and epoxy matrix [68]: $\lambda_{i} = 22.80$ GPa, $\mu_{i} = 29.02$ GPa and $\lambda_{m} = 2.04$ GPa, $\mu_{m} = 1.05$ GPa. For both fibre and matrix, the fracture energy is set to $G_{c}^{b} = 0.005$ N/mm and the characteristic length is $l_{c} = 0.001$ mm. The interface has the parameters: $t_{0n} = t_{0t} = 0.02$ GPa, $G_{cI} = G_{cII} = 0.001$ N/mm and $\eta = 0.99$, with friction coefficient $\mu^{I} = 0$.

Fig. 16

Geometry and voxel discretisation of a single fibre embedded in matrix. The fibre-matrix interface is described by a set of composite voxels, in which the orientation (normal direction of the interface) and the volume fractions of fibre are specified by the arrows and the colours, respectively. Different offsets along the Y-axis are tested on the centre of the fibre: a = 0, 0.2 h, 0.4 h, 0.5 h, 0.6 h, 0.8 h, h, with h the voxel size

With the voxel size $h = 0.0002$ mm, we test the mesh sensitivity in terms of relative position of the discretisation grid with respect to the curved interface. Different position offsets of the fibre along the Y-axis are tested, and the simulation results are shown in Fig. 17. For all the simulations, interface debonding first takes place, and the damage field remains symmetric until before the deviation of the crack into the matrix. For the matrix cracking, a repeatable variation of the predicted crack pattern is observed with a periodicity of one voxel. When the fibre centre lies on a voxel centre ($a = 0, h$), the structure is perfectly symmetric in the Y-axis, leading to two cracks symmetrically growing at the two sides (top and bottom) of the fibre. When the offset of the fibre centre with respect to voxel centre is non-zero, a slight asymmetry on the discretisation grid is introduced, which produces one single crack growing either on the top or the bottom side of the fibre. The transition is found to occur when the offset is half voxel $a = 0.5h$. Moreover, the macroscopic responses are identical for the offsets that are symmetric to half voxel: $a = \left\{ {0, h} \right\}, \left\{ {0.2h, 0.8h} \right\}, \left\{ {0.4h, 0.6h} \right\}$. A small discrepancy is observed on the predicted peak load of the stress–strain curves. To verify whether this mesh effect is secondary compared to that of microstructural heterogeneities, a double-fibre system is studied in Appendix 1. The results show that the position offsets of the fibres induce just a slight effect on the crack pattern and the macroscopic stress–strain curve, and it seems that the microstructural heterogeneity is the major factor influencing the fracture process.

Fig. 17

Simulation results (stress–strain curve and crack pattern) with different offsets of fibre position

Using the offset $a = 0.2h$, we verify the effect of voxel size on the prediction result of the single-fibre system. The stress–strain curves for the simulations with different voxel sizes are shown in Fig. 18, suggesting that as the voxel becomes small enough (e.g. ~ 1/100 of fibre diameter), the prediction result converges to the same behaviour.

Fig. 18

Stress–strain curves for the inclusion-matrix system under tension with different voxel sizes

4.4.2 Multiple-fibre system: transverse load

As shown in Fig. 19, a periodic unit cell containing 30 fibres embedded in a matrix is used in this test. The voxel size is $h = 0.002$ mm. A tensile strain is incrementally applied to the unit cell in the X-axis, with a constant step of ${\Delta }\varepsilon = 10^{ - 5}$. The elastic moduli for fibres and matrix are E^fibre = 40 GPa, ν^fibre = 0.33 and E^matrix = 4 GPa, ν^matrix = 0.4. The characteristic length and fracture energy are set to $l_{c} = 0.0075$ mm and $G_{c}^{{\text{b}}} = 0.3$ N/mm for both fibres and matrix. The CZM parameters for interface voxels are $t_{0n} = t_{0t} = 10$ N/mm², $G_{cI} = G_{cII} = 0.3$ N/mm, $\eta = 0.99$, $\mu^{I} = 0$. The total computation time of this simulation with 2.5 × 10⁵ voxels (6017 composite voxels) took about 3.5 h over a workstation with 8-core Intel(R) Xeon(R) CPU 2.00 GHz.

Fig. 19

Unit cell of multiple-fibre system with periodicity in X and Y directions, 30 fibres are arbitrarily placed inside the domain

The simulation results are shown in Fig. 20. The macroscopic stress–strain curve first exhibits a marked decrease of stress (Fig. 20a), and then a gradual slowing-down of the rate of stress decrease is observed, which is related to the effect of the heterogeneous microstructure on the crack growth. As shown in Fig. 20b, the numbers of iterations for both the mechanical solution and the phase-field solution increase as the damage starts to develop, and these numbers remain at a high level even after the marked decrease of the macroscopic stress. This is due to the complex crack propagation path induced by the heterogeneous microstructure, which continuously challenges the algorithm. The complex cracking process is shown in Fig. 20c, suggesting that the fracture starts with fibre-matrix debonding, and then the crack deviates into the matrix. The matrix crack can also coalesce with neighbouring fibre-matrix debondings.

Fig. 20

a Stress–strain curve of the multiple-fibre system under transverse tension, and the corresponding numbers of iterations at each time step for the solution of either mechanical or phase-field problem. b Crack patterns at different loading steps marked on the stress–strain curve in (a)

4.4.3 Multiple-fibre system: longitudinal load

The last numerical example is a 3D fibre-matrix system, whose geometry is shown in Fig. 21a. The volume fractions of fibres and pores are 50% and 5%, respectively. In addition, a small notch is added to localise the crack initiation. With a voxel size of $h = 0.0005$ mm, the unit cell contains 2.1 million voxels with 1.9 × 10⁵ composite voxels. Longitudinal tension is applied to the unit cell with a constant loading step of ${\Delta }\varepsilon = 2 \times 10^{ - 5}$. SiC fibres and SiC matrix are considered in this test with representative elastic parameters of E^fibre = 365 GPa, E^matrix = 444 GPa and ν^fibre = ν^matrix = 0.2. The characteristic length and fracture energy are $l_{c}^{{{\text{fibre}}}} = 0.001$ mm, $l_{c}^{{{\text{matrix}}}} = 0.002$ mm and $G_{c}^{{{\text{fibre}}}} = 0.1$ N/mm, $G_{c}^{{{\text{matrix}}}} = 0.039$ N/mm. The CZM parameters of the interphase are $G_{cI} = G_{cII} = 0.0001$ N/mm, $\eta = 0.999$, $\mu^{I} = 0$.2. In order to study the effect of the strength of interphase, two critical values are tested: $t_{0n} = t_{0t} = 100$ MPa and $t_{0n} = t_{0t} = 500$ MPa.

Fig. 21

Simulations of a multiple-fibre system under longitudinal tension: a geometry of the periodic unit cell; b macroscopic stress–strain curves using two different interphase properties and the corresponding crack patterns

The simulation results are shown in Fig. 21b, indicating the typical effect of the interface strength for ceramic matrix composites: a strong interface ($t_{0n} = t_{0t} = 500$ MPa) does not allow the deflection of matrix crack whereas a weak interface does ($t_{0n} = t_{0t} = 100$ MPa). In the case of the weak interface, the phenomenon of multiple cracking has also been reproduced by the simulation.

In terms of total computation time, the weak-interface simulation is much slower than the strong-interface one: ~ 49 h versus ~ 9 h both running on a workstation with 8-core Intel(R) Xeon(R) CPU 2.00 GHz. This is because the interphase fracture described by the laminate model is more computationally expensive than the fracture of fibres and matrix described by the phase-field model. Moreover, convergence could not be achieved when the crack starts to grow in the fibres (see the result for $t_{0n} = t_{0t} = 100$ MPa in Fig. 21b). Different from the examples shown in the previous sections, the simulation of weak interface herein involves a more complex cracking scenario with fracture occurring in all the three phases (matrix, interphase and fibres). The oscillations observed on the hardening part of the stress–strain curve may be due to the frictional cohesive law at interphase that becomes unstable in the staggered scheme facing the complex fracture scenario. Further investigations are required to understand and/or improve the performance of the proposed model in these situations.

5 Conclusions

An FFT based PF-CZ model has been proposed to predict the fracture behaviour of composite materials with interfaces. The coupled problem has been deduced from the variational approach, with interface failure described by a frictional cohesive zone model. The grid-geometry mismatch has been tackled by the composite voxel technique with a 3-layer laminate mixture rule. A volumetric representation of interface (referred to as interphase) has been chosen, which made it necessary to introduce a volume fraction $f_{vI}$, whose effect on the simulation result has been proven negligible. Yet, it should be kept in mind that a surface representation of the interface is also possible, by re-formulating the laminate model with cohesive displacement jumps as the variables in the interface layer. As for the FFT solver of the phase-field problem, a modified Laplacian operator is incorporated, which reduces the spurious oscillations of the damage field. The proposed model exhibits a clear numerical convergence with respect to the voxel size. It is able to predict complex fracture behaviours, such as the debonding and frictional sliding of interface, the interaction between bulk and interface fractures in both single-fibre and multiple-fibre systems. The present work demonstrates the possibility of using the composite voxel technique in fracture problems.

Some limitations remain to be addressed. First, a slight dependency has been observed on the relative position of voxelised grid and interface geometry (Fig. 17). Although it is only a secondary effect, further investigations are still required to improve the model for high-fidelity simulations. Second, the use of the laminate model requires the local orientation to be determined prior to the simulations. This could be a difficult process for materials with complex interface geometries. To alleviate this particular difficulty, the regularisation approach of [3] might outperform the present model, however, the frictional sliding could be difficult to take into account in that approach. Thirdly, although convergence is ensured for most of the numerical examples, it may still be an issue in some situations involving complex multi-phase cracking (Sect. 4.4.3).

Apart from the above-mentioned limitations, further investigations may also discuss the interaction between build damage and interface damage. In the present work, we have used a discrete formulation to combine the nonlocal phase-field model and the local cohesive zone model. The coupling between the two has been carried out via the equilibrium of the laminate composite voxel system. Direct interaction between bulk damage and cohesive damage has not been considered in the present formulation. Paggi et al. [13] proposed a formulation that makes the CZM energy release rates dependent on the adjacent bulk damage variable. This can be considered as a one-way interaction, as only the CZM equation is affected by bulk damage, but the phase-field equation is still independent of cohesive damage. As also mentioned by Paggi et al. further investigations are required to properly discuss this issue. A two-way interaction formulation may be established by adding mutual dependency of bulk damage and interface damage into their respective evolution equations. However, such mutual dependency must be supported by experimental or/and theoretical arguments, which may be significantly different from one material to another, and which itself can be a complex research topic.

Appendix 1: Test of mesh sensitivity with a double-fibre system

To check the effect of the relative position of interface and voxelised grid in competition with microstructural non-symmetry, we use a unit cell depicted in Fig. 22, where two fibres are embedded in a matrix. The relative position between the two fibres are fixed, and we change their Y-axis positions with different offsets: $0, 0.2h,0.4h, 0.6h, 0.8h, h$, with $h = 0.0002$ mm. The material parameters are the same as those used for the single-fibre system in Sect. 4.4.1.

Fig. 22

Geometry of the unit cell used for testing the mesh sensitivity with microstructural non-symmetry

The simulation results are gathered in Fig. 23. Both the stress–strain curves and the crack patterns exhibit a very slight effect from the offsets of the positions of the fibres, demonstrating that the mesh related bias shown in Fig. 17 should be secondary compared to the effect of microstructural heterogeneity.

Fig. 23

Simulation results of the double-fibre system with different offsets of the Y-axis positions of the fibres: a stress–strain curves; b crack patterns