Graphical Modelling of Hoop Force Distribution for Equilibrium Analysis of Masonry Domes

Abstract

The behaviour of axisymmetric masonry shells can be simulated by a system of forces constituted by meridian forces acting in the vertical planes, and by hoop forces acting circumferentially. A crucial component for the assessment of these structures using the Modified Thrust Line Method (MTLM) is the determination of hoop forces, whose computation is strenuous, limiting the practical application of MTLM. Working around this limitation, the current research introduces a strategy to manipulate the hoop forces by graphically implementing a function describing their distribution. The adaptiveness of this distribution function not only allows the application of MTLM for the analysis of a range of geometries, but also enables the simulation of membrane behaviour, arch behaviour and their combination, for considering partially cracked structures. Taking this into account, the approach is applied in the case studies illustrated within the current research.

Introduction

Avant-garde structures built during recent decades, such as Ambika P3 (Parascho et al. 2020) or Armadillo Vault pavilion (Block et al. 2018), testify to the progress and the new focus on the research in the field of masonry. Although the roots of the theory of plasticity were laid by Drucker (1950) and Kooharian (1952), only Heyman (1966) applied the limit analyses for masonry structures. Three assumptions are at the base of his theory: (i) masonry has no tensile strength, (ii) stresses are so low that masonry has effectively an unlimited compressive strength and (iii) sliding failure does not occur. According to Heyman’s work, the geometry assumes a crucial role in guaranteeing the equilibrium for masonry structures, and indeed his formulation provided the roots for thriving research (Varma and Ghosh 2016; De Chiara et al. 2019; Iannuzzo et al. 2019; Fraddosio et al. 2020).

The relation between geometry and structural behaviour of a masonry arch has been recognised starting from the works of Robert Hooke in 1670 (Huerta 2008) (Fig. 1a) but the first exhaustive formulation of the curve of pressure which correlates form and force was published by Thomas Young in 1817 (Huerta 2010a). The curve of pressure is the locus of the application points of the resultant internal forces. It is uniquely defined and describes the actual state of the investigated structure. Moreover, to guarantee the balance, the curve of pressure must be entirely contained within the arch’s thickness (Mosley 1833) (Fig. 1).

Fig. 1

Structural behaviour of an Arch. a Hooke’s analogy between an arch and a hanging chain; b Superposition of the Catenary and the arch by R. Pedreschi and Hooke’s analogy (Hensel and Menges 2008)

Although the concept of the curve of pressures was known since the early French studies on arches (De La Hire 1729), its derivation remained unknown through the nineteenth century (Mosley 1833). Following this, during the twentieth century, the spreading of elasticity theory (Timoshenko and Goodier 1951) led to the abandonment of methods of assessment involving the pressure curve.

Only after Heyman’s work (1966) were the approaches relying on the curve of pressure re-discovered, and the focus posed on determining the line of thrust, i.e., one of the possible paths on which internal forces in a structure transport external loads to the supports. The ‘line of thrust’ does not describe the actual state of the structure as the curve of pressure does, but only one among the infinite possibilities. Despite this, the state of masonry structures can be assessed through the Safe Theorem (Heyman 1966); e.g., referring to an arch, if at least one line of thrust lies entirely within the section of the structure, then that structure is in equilibrium. In recent decades, inspired by the membrane formulation, researchers have extended the idea of the line of thrust, adapting it to double-curved structures (Angelillo et al. 2014; Block and Ochsendorf 2007) and developing the historical graphic statics (GS) methods. This adaptation is seen in the case of the slicing technique formulated by Frézier (1737), today widely adopted by several researchers (Huerta 2007; Cennamo et al. 2019), thrust network analysis (Block and Ochsendorf 2007) whose roots can be found in Maxwell’s structural reciprocity idea of 1864 (Baker et al. 2013), or the research conducted on the Durand-Claye method (Aita et al. 2017).

The GS method investigated here is derived from Eddy’s work (1878). His formulation was the first dedicated to the analysis of masonry spherical domes. Indeed, the method allows the simulations of these structures through a system of forces constituted by meridian forces acting in the vertical planes and by hoop forces acting circumferentially.

A development of Eddy’s method was published by Wolfe (1921), in which, as shown in Fig. 2b), a larger variety of geometry can be analysed. Both approaches are extremely conservative; they evaluate the line of thrust located in correspondence to the median radius of domes. Recently Eddy’s work has been described analytically in (Galassi et al. 2017), but the first review of the work of Eddy and Wolfe is provided by Cipriani and Lau (2006), who developed the Modified Thrust Line Method (MTLM).

Fig. 2

MTLM in historical formulations. a Eddy’s method (1878) relative to a hemispherical dome; b Wolfe’s method (1921), which considers the lack of tensile strength of masonry

MTLM allows assessing the state of axisymmetric structures by tracing the line of thrust within the entire thickness of the structure investigated. Here, Wolfe’s and Eddy’s conservative constraints have been removed, and for solving the static indeterminacy of domes, the hoop forces are estimated through an optimisation algorithm (Lau 2006).

This present research presents the development of the MTLM. Here considerations on the hoop forces are exposed and, through adoption of a distribution function for hoop forces, they are estimated. The formulation does not violate Heyman’s hypotheses (i) (ii) (iii); and relies on the observation of the visible crack patterns seen on existing masonry domes, such as the dome of the Pantheon in Rome (Terenzio 1933). Similar to the curve of pressure, the actual distribution of hoop forces cannot be determined, but to counter this, a restricted domain in which searching for the distribution of hoop forces is proposed. Therefore, through the distribution function and the bounded domain, the hoop forces can be determined graphically and a line of thrust traced for assessing the state of the structure. The authors do not aim to propose a new GS tool but rather to increase the efficiency of the existing MTLM; indeed, one reason why this method is not widely applied is the difficulty of determining the hoop forces (Lau 2006), which is addressed through the present research.

An exhaustive formulation is provided in Sect. 2, where the process on which MTLM is based is described. In particular, the equilibrium of blocks is set forth in Sect. 2.1, while considerations on hoop forces and the definition of the distribution function are addressed in Sect. 2.2. In Sect. 3, two different case studies are illustrated. The purpose of these sections is to provide two examples of how to apply the formulation proposed and also highlight the unconventional applications. The conclusions are discussed in the last Sect. 4 (Fig. 2).

Modified Thrust Line Method

The slicing technique is a powerful GS method for estimating the structural state of domes, which Poleni (1748) applied to investigate the equilibrium of St. Peter’s dome in Rome (Heyman and Poleni 1988). The slicing technique makes it possible to evaluate the state of the dome by dividing the structure into equal slices; however, it neglects the action of the hoop forces and for that reason, it is an extremely conservative method.

Due to spatial geometries, vaults, domes, and shells exhibit quite different behaviour compared to one-dimensional structures such as arches. According to the membrane theory, the three-dimensional geometries provide additional resources to withstand loads, thus slicing techniques cannot simulate their structural behaviour. In contrast, MTLM and thrust network analysis can describe the mechanics of doubly-curved structures. In particular, with thrust network analysis, the state of doubly-curved shells is examined exploiting the advantages of reciprocal polygons (force polygon and form polygon) (Maxwell 1870); thus, accounting for hoop forces. Due to the possibility of graphically manipulating the form and the force polygons, thrust network analysis is widely used for the design of masonry structures (Davis et al. 2012).

MTLM combines membrane theory and slicing technique; it recognises the influence of the hoop forces but relies on a fixed form polygon. In addition to Heyman’s hypotheses (i), (ii) and (iii), MTLM requires one more assumption: (iv) loads and geometry analysed must be axisymmetric. Due to this additional assumption (iv), the set of structures that can be analysed through MTLM is limited, and for this reason, it is scarcely applied for the design of new shells. Despite that, as Sect. 3 points out, the method is suitable for estimating the state of historical domes (Zessin et al. 2010).

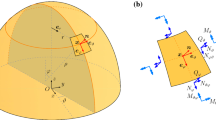
MTLM relies on an iterative procedure, analogous to the slicing technique. Indeed, as in the slicing technique, the shell that is the object of the investigation is cut radially into equal portions called lunes; due to the symmetry, only one lune needs to be analysed (Fig. 3a). Then, the representative section of the lune (section A–A) is examined by the estimation of the line of thrust. Due to Safe Theorem and symmetry of the structure analysed, the balanced state of the whole structure is guaranteed if a line of thrust can be traced that lies entirely within the cross-section of the lune (Heyman 1967).

Fig. 3

Representation of an axisymmetric masonry structure. a Sectional view: representative section of a lune (top); plan view: structure divided into lunes (bottom). b Representation of the section A–A, the rigid bodies (blocks) and relative centroids enumerated

For the purpose of tracing the line of thrust, the investigated lune is divided into rigid bodies, also called blocks. These are enumerated starting from the bottom to the crown of the shell; that is, blocks index $i=0$ corresponds to the one placed at the spring, and the $i=n$ to the uppermost one (Fig. 3b). Then, relying on the lune’s actual geometry, centroids ${{\varvec{C}}}_{i}=\left( {x}_{ci} , {z}_{ci}\right)$ and relative weights ${{\varvec{w}}}_{i}$ for each block are defined (Fig. 3).

The shape of the line of thrust is traced by the interpolation of the points ${{\varvec{P}}}_{i}=\left( {x}_{i} , {z}_{i}\right)$, whose individuation involves geometrical and physical entities. All points ${{\varvec{P}}}_{i}$ belong to the plane of the section analysed, and are determined as expressed by the condition in Eq. 1, i.e., referring to a ith block, the position of point ${{\varvec{P}}}_{i}$ is the intersection of the vertical line passing the centroid ${{\varvec{C}}}_{i}$ and the line of action of the thrust on the ith block passing through the point ${{\varvec{P}}}_{i+1}$.

$$ {\varvec{P}}_{i} := {\varvec{P}}_{i} \in \left\{ {z = x_{ci} \wedge z = tan\left( {\gamma_{i + 1} } \right)\left( {\frac{{x - x_{ci + 1} }}{{z_{i + 1} }}} \right)} \right\} $$

(1)

In Eq. 1 the angle ${\gamma }_{i+1}$ represents the inclination of the thrust acting on the ith block, and the distance ${z}_{i+1}$ the ordinate of ${{\varvec{P}}}_{i+1}$, thus the position of all points ${{\varvec{P}}}_{i}$ are defined knowing the angle ${\gamma }_{i+1}$ of the thrust and by solving Eq. 1 starting from the point whose index $i=n$, i.e., the one relative to uppermost block. Unlike all other points ${{\varvec{P}}}_{i}$, the position of the last point ${{\varvec{P}}}_{n}$ is arbitrarily imposed (Fig. 4).

Fig. 4

Determination of point ${{\varvec{P}}}_{n}$. The point ${{\varvec{P}}}_{i}$ has the same abscissa of centroid C_i and is determined by the intersection of the line t_i and the vertical line s_i

As already mentioned, the line of thrust is traced by interpolating the set of points ${{\varvec{P}}}_{i}$ and to be acceptable, this curve must lie within the thickness of the dome. To accomplish this the condition in Eq. 1 alone is not sufficient. Therefore, denoting the entire surface of the section by $\Sigma$ (Fig. 3a), an additional condition is placed. Equation 2 constrains the position of ${{\varvec{P}}}_{i}$ within the section analysed:

$$ \forall { P}_{i} \in \Sigma $$

(2)

Equations 1 and 2 together determine the restricted set in which points ${{\varvec{P}}}_{i}$ must be included to achieve the balanced state. These two equations do not involve the forces directly, but only entities associated to them, such as the inclination ${\gamma }_{i+1}$. Thus, for determining the set of points ${{\varvec{P}}}_{i}$, equilibrium equations must be written and solved.

Equilibrium of Blocks

Referring to the ith block drawn in Fig. 5b, the nodal equations of equilibrium involve all the forces acting on it: the thrust ${{\varvec{T}}}_{i+1}$, which is the resultant of the upper portion of the lune, the reaction ${-{\varvec{T}}}_{i}$, the weight ${{\varvec{w}}}_{i}$, and the hoop forces ${\boldsymbol{\Delta }{\varvec{H}}}_{i}$. The equilibrium along the z-direction is expressed by Eq. 3: the reaction ${-{\varvec{T}}}_{i}$ balances the weight ${{\varvec{w}}}_{i}$ and the thrust ${{\varvec{T}}}_{i+1}$. In this direction, there is no contribution to the hoop forces ${\boldsymbol{\Delta }{\varvec{H}}}_{i}$; in fact, they act on a plane horizontal and parallel to the normal of the lateral face of the block (Fig. 5a), thus, as Eq. 4 states, they affect the balance in the x-direction. In the last direction, the one perpendicular to the section plane, the only forces involved are the hoop forces ${\boldsymbol{\Delta }{\varvec{H}}}_{i}$ Nevertheless, since the sail is symmetrical and symmetrically loaded, their sum is always null, given by the Eq. 5 (Fig. 5).

$$ T_{i + 1}^{z} + w_{i} = T_{i}^{z} $$

(3)

$$ T_{i + 1}^{x} + 2\Delta H_{i}^{x} = T_{i}^{x} $$

(4)

$$ \Delta H_{i}^{y} = \Delta H_{i}^{y} $$

(5)

Fig. 5

Equilibrium of block. a Equilibrium of the ith block, plan view, x–y plane (top) and elevation, z-x plane (bottom) and relative polygon of forces. The forces applied to the point ${{\varvec{P}}}_{i}$ are: the thrusts (red), the weight of the block (blue) and the hoop forces (green); b Spatial representation of the forces acting on the ith block; c Equilibrium of the nth block, the abscissa of the point ${{\varvec{P}}}_{n}$ is arbitrarily chosen respecting Eq. 2 (Color figure online)

Equations 3, 4 and 5 describe the balanced state of point ${{\varvec{P}}}_{i}$ along the X, Y and Z directions. In these equations, all forces involved are decomposed into their components by the relations given by Eqs. 6, 7, 8 and 9.

$$ T_{i}^{x} = \left\| {{\varvec{T}}_{i} } \right\|\cos \gamma_{i} $$

(6)

$$ T_{i}^{z} = \left\| {{\varvec{T}}_{i} } \right\|\sin \gamma_{i} $$

(7)

$$ \Delta H_{i}^{x} = \left\| {{\Delta H}_{i} } \right\|\sin \vartheta $$

(8)

$$ {\Delta }H_{i}^{y} = \left\| {{\Delta H}_{i} } \right\|\cos \vartheta $$

(9)

The angle ϑ indicates the inclination of the hoop forces ${\boldsymbol{\Delta }{\varvec{H}}}_{i}$ with respect to the axis X. For each point ${{\varvec{P}}}_{i}$ Eqs. 3 and 4 allow the calculation of the inclination of the thrust γ_i by Eq. 10. Thus, their resolution allows the determination of the points ${{\varvec{P}}}_{i}$ by Eq. 1.

$$ \gamma_{i} = \arctan \frac{{T_{i}^{y} }}{{T_{i}^{x} }} $$

(10)

However, due to the static indeterminacy, to solve the nodal equation of equilibrium other hypotheses are needed. Referring to the $i={n}^{th}$ block, the balance equations Eqs. 3 and 4 become:

$$ + w_{n} = T_{n}^{z} $$

(11)

$$ 2\Delta H_{n}^{x} = T_{n}^{x} $$

(12)

The z-component of thrust ${{\varvec{T}}}_{i}$ is obtained by Eq. 11, but neither the inclination of the thrust γ_n nor the x-component of the thrust ${{\varvec{T}}}_{i}$ are defined, hence Eq. 12 can be only solved by estimating the hoop force ${\boldsymbol{\Delta }{\varvec{H}}}_{n}$. The assumption of these two entities (${\boldsymbol{\Delta }{\varvec{H}}}_{n}$ and γ_n) permits individuating the point ${{\varvec{P}}}_{i=n-1}$ and proceeds towards the following iteration $i=n-1$, where, again, Eq. 4 can be solved only after the estimation of ${\boldsymbol{\Delta }{\varvec{H}}}_{n-1}$.

On Hoop Forces

As detailed in Sect. 2.1, the knowledge of the hoop forces is necessary to find the position of points ${{\varvec{P}}}_{i}$, and therefore it is needed for evaluating the state of the lune. Due to the assumption (iv), the direction of hoop forces is known; they act normally about each block’s lateral face, as seen in Fig. 5a. Further, consistent with Heyman’s hypothesis (i), they induce only compressive stresses. Here, only their magnitude $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{i}\Vert$ unknown, but due to the static indeterminacy it is not possible to identify the actual value. In fact, as long as no kinematic mechanism appears, infinite lines of thrust states are admissible. Despite that, by examining the crack patterns of existing domes, it is plausible to state a few observations on the hoop forces.

The cause of cracks could depend on several factors: excessive load, thermal alteration, etc. Among the several causes, the increasing of the span due to settling of the supports is one of the most common phenomena that leads to cracks (Masi et al. 2018; Pavlovic et al. 2016). Under these conditions, hemispherical or axisymmetric domes manifest cracks which start from the base, open along the meridian direction, and stop near the crown of the dome (Heyman 1967). This crack pattern is illustrated in Fig. 6a, and can be observed in the dome of Pantheon in Rome (Mark and Hutchinson 1986), in the dome of San Pietro in Rome (Como 2018), and even in that of Santa Maria del Fiore in Florence (Ottoni et al. 2010).

Fig. 6

Crack patterns of historic domes. a Heyman’s (1966) scheme of a dome’s crack pattern due to the increase of span; b Terenzio’s (1933) survey of the crack pattern of the Pantheon; c Possible distribution of the Pantheon’s hoop forces (green lines) based on Terenzio’s survey; d Crack pattern of the octagonal dome of Santa Maria del Fiore Cathedral (Ottoni et al. 2010); e Crack pattern of the hemispherical dome of San Pietro Cathedral (Rome, 1748 survey by Poleni); f Crack pattern of the ellipsoidal dome of Santuario della Natività di Maria Basilica (Cuneo, 1962 survey by Garro); g Crack pattern of the hemispherical dome of Santa Maria Assunta in Carignano (Genoa, 1907 survey by De Gaspari) (Bacigalupo et al. 2013)

Whatever the cause, for ordinary structures the cracks appear in correlation to the tensile stresses. Furthermore, according to membrane theory, tensile stresses manifest in the lower portions of axisymmetric shells (Timoshenko and Woinowsky-Krieger 1959). Thus, in general terms, at the base of domes, meridian cracks open and no compressive hoop forces exist. Similarly to a set of juxtaposed arches, shells display a one-dimensional behaviour, at least in the cracked portion. Near the crown, even cracked domes exhibit a double-curved behaviour that is needed to achieve a balanced state. Here, hoop forces can manifest (Fig. 6c).

Consistent with the description above, and considering positive compressive forces, it is assumed that the magnitude of the hoop forces is maximum near the dome’s crown and decreases along the z-direction. Thus, the minimum value, even a null one, is reached in proximity of the base of the structure. This assumption is compatible with the observation on the hoop forces described by Heyman (1966), as well as with membrane theory where the compressive forces decrease until they become tensile forces below a latitude of 51.82°. Therefore, the condition in Eq. 13 expresses the relationship that all hoop forces must satisfy:

$$ \left\| {{\Delta H}_{i + 1} } \right\| \ge \left\| {{\Delta H}_{i} } \right\| \forall i $$

(13)

For each point P_i, the magnitude of its related hoop force $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{i}\Vert$ is greater the following one $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{i-1}\Vert$. Thus, Eq. 13 highlights the existence of a correlation among hoop forces: their magnitude does not vary randomly but decreases as they go from the crown to the base.

According to Eq. 13, to solve the nodal equations of equilibrium a function which describes the distribution of hoop forces is introduced. This function, termed Dh, expresses the distribution of hoop forces in relation to a new variable k, providing the magnitude of all hoop forces required to assess the state of the structures (Fig. 7).

Fig. 7

Determining of the hoop forces through Dh. Three different distribution functions Dh (top), their respective thrust lines in red (center), and relative hoop forces ${\boldsymbol{\Delta }{\varvec{H}}}_{i}$ in green (bottom) (Color figure online)

Referring to the same section displayed in Fig. 7, several equilibrated states can be identified, each determined by a different hoop forces’ distribution, Dh. Similar to the thrust line, the Dh are not uniquely defined; only when the structure is statically determined is the distribution function Dh unique.

The variable k is related to the index i of blocks by Eq. 14. Further, the value of function Dh provides the hoop forces’ magnitude of the n-1 block, i.e., if variable k is equal to 1, the index $i=n-1$ and value of Dh(k) corresponds to the magnitude of $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{i-1}\Vert$.

$$ k = n - i $$

(14)

The distribution functions Dh are defined by the conditions in Eqs. 15, 16 and 17. Hence the distribution functions Dh are bounded (Eq. 16) and monotonic decreasing (Eq. 17). Their upper bound M is arbitrarily defined; in contrast, the lower limit is not determined a priori, but in keeping with the behaviour of existing shells, it cannot assume tensile values.

$$ Dh :\left\{ {k \in {\mathbb{N}}{|} I := 1 \le k \le n} \right\} \mapsto {\mathbb{R}}_{0}^{ + } $$

(15)

$$ k_{1} < k_{2} \to Dh\left( {k_{1} } \right) \ge Dh\left( {k_{2} } \right)\quad \forall k \in I $$

(16)

$$ Dh\left( k \right) \le M \forall\quad k \in I $$

(17)

All distribution functions Dh implemented within the present research respect the conditions in Eqs. 15, 16 and 17. However, by observation of a different crack pattern, different conditions could be assumed. Indeed, the procedure could be adapted to a solution that respects the different crack patterns.

The implementation adopted for performing the analyses makes it possible to write functions Dh analytically and then manipulate them graphically. Hence, in this formulation of MTLM the hoop forces are estimated in real time by manipulating the distribution functions. Therefore, the introduction of the distribution function Dh and the choice of the position ${{\varvec{P}}}_{n}$ (see Sect. 2) make it possible to solve the nodal equations of equilibrium and to define points ${{\varvec{P}}}_{i}$ and hence trace the line of thrust to assess the state of the lune.

Case Studies

To demonstrate the method described in Sect. 2, two historic masonry structures are analysed. The first one is the dome of the Pantheon in Rome built between 120 and 135 CE (MacDonald 2002). The second case study corresponds to the dome of Santa Maria in Ciel d’Oro in Montefiascone (Viterbo): this masonry shell is a self-balanced structure, i.e., due to the use of cross herringbone technique, it was built without the aid of any temporary support (Paris et al. 2020).

These two quite different structures are chosen for their peculiarities and in the analyses performed these features are included. For the case study of Pantheon’s dome, the presence of the relevant crack pattern is accounted for within simulations, while in the case of the dome of Santa Maria in Ciel d’Oro, due to the construction without scaffolding, several construction stages are examined along with the completed dome.

The Dome of the Pantheon

The Pantheon’s dome, with a diameter of 43.30 m, is the largest hemispherical dome in the world, its thickness decreases from 5.90 m at the base to 1.5 m at the crown (Aliberti et al. 2015; Fletcher 2019) (Fig. 8). The dome, constructed in unreinforced concrete with coffering on the intrados (Aliberti and Alonso-Rodríguez 2017), is composed of different layers of aggregate; the one near the support has the highest specific weight (16.00 kN/m³) and, like the thickness, it decreases with height (from 16.00 to 13.50 kN/m³) (Masi et al. 2018).

Fig. 8

Sectional view of the Pantheon’s dome. The two lines of thrust drawn are relative to the two structural behaviours: the continuous line to a full membrane behaviour (I), while dash line to a partially cracked dome (II)

For this case study, two different structural behaviours are simulated using MTLM. In the first simulation (I), the presence of meridional cracks is neglected, thus a full membrane behaviour is assumed. The second simulation (II) represents the actual configuration of the Pantheon’s dome, with the presence of the meridional cracks being considered. In keeping with the crack pattern visible on the dome (see Fig. 6b), only above the latitude of 56°, the hoop forces are not null, and below this the dome exhibits an arch behaviour.

The two structural behaviours (I) and (II) are reported respectively in Figs. 10 and 11. For both simulations, the dome is sliced into 32 equal lunes and the central section of one lune is examined. Following the steps reported in Sect. 2, the lune was subdivided into 87 blocks for determining the set of points ${{\varvec{P}}}_{i}$.

Two different distribution functions Dh were considered, one for each structural behaviour (I) and (II), but for both the functions Dh were defined with the purpose of tracing the safest line of thrust, i.e., the line of thrust which lies close to the median curve of the investigated section (Huerta 2010b). For this, and to differentiate these two distributions functions with others adopted in the following analyses they are denominated as Safe Dh.

In simulations (I) the Safe Dh is the linear function illustrated in Fig. 9 (continuous line). Its maximum is 10.25; thus, the maximum magnitude of the x-component of hoop forces $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{n=87}^{x}\Vert$ is 10.25 kN, and as stated by Eq. 8, the hoop force correspondent is $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{87}\Vert$ = 104.57 kN. Further, in (I) simulation, the hoop forces are never null; their magnitude decreases until reaching the minimum values of $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{1}\Vert$ = 60.11 kN at the dome’s base. With this Dh, the line of thrust lies close to the section’s median curve (see Fig. 8). Thus, the dome exhibits a balanced state with a high safety factor (Huerta 2010b).

Fig. 9

MTLM analyses for simulation (I). (Top) Dh function assumed; (centre) sectional view of the dome and lines of thrust; (bottom), plan view of the lune analysed and the hoop forces applied on it; (right) polygon of forces

The presence of meridional cracks, simulation (II), leads to a variation of the magnitude of hoop forces. In fact, in simulation (II), the Safe Dh adopted has Dh(0) = $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{n=87}^{x}\Vert$  = 12.00 kN as maximum and becomes zero from k = 25, that is i = 62 or latitude equal to φ_i = 56°. The magnitude of the hoop forces rapidly decreases from the maximum $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{87}\Vert$ = 122.43 kN to the value of 82.56 kN when index i = 72. After that, the hoop forces remain constant up until block 63. The geometry of the line of thrust traced using this function is close to the median curve of the section up until a latitude of φ = 56°, and then the absence of hoop forces, move the line of thrust toward the intrados (Fig. 9).

For both structural behaviours, a few investigations about the relation between the distribution function and the line of thrust were carried out. For each behaviour (I) and (II), two distribution functions were assumed: a constant function denoted with Constant Dh, and an impulse function indicated as Impulse Dh. These analyses were performed searching for the minimum and the maximum hoop forces at the uppermost blocks (i = 87). The minimum magnitude was computed assuming a Constant Dh and placing point P₈₇ close to the extrados of the dome, while the maximum magnitude occurs considering the Impulse Dh, whose peak occurs for k = 0.

For both structural behaviours (I) and (II), the Impulse Dh does not lead to a balanced state. Thus, in both simulations, the Impulse Dh has a minimum constant value different from zero for any k, and leads to define constant hoop forces, whose magnitude is $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{0-86}\Vert$ = 29.13 kN for (I) and $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{63-86}\Vert$ = 46.65 kN for (II). With these Impulse Dh and under the assumption placed in Sect. 2.2, the x-component of the thrust at the base of the dome is =  ${{\varvec{T}}}_{1}^{x}$771.12 kN for (I) and 514.89 kN for (II), and the lines of thrust traced correspond to the minimum line of thrust. As reported in Table 1 and displayed in Figs. 10 and 11, unlike Impulse Dh, the Constant Dh functions do not give any significant line of thrust.

Table 1 Forces calculated by MTLM for the two structural behaviours (I) and (II)

Fig. 10

MTLM analyses for simulation (II). (Top) Dh function assumed; (centre) sectional view of the dome and lines of thrust; (bottom) plan view of the lune analysed and the hoop forces applied on it; (right) polygon of forces (right)

Fig. 11

Geometry of Santa Maria in Ciel d’Oro dome. (Top) B–B and C–C sectionals views of the dome; (bottom) the bottom-up view of two lunes

Concerning the uppermost block, the two distribution functions (Constant Dh and Impulse Dh) are determined in order to define respectively the minimum and the maximum magnitude of the hoop forces. The minimum corresponds to $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{87}\Vert$ = 78.30 kN for simulation (I) and $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{87}\Vert$ = 87.74 kN in simulation (II). Thus, any distribution of hoop forces with maximum magnitude lower than one estimated with the Constant Dh would lead to an unbalanced state. In contrast, in the case of Impulse Dh, higher magnitudes than $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{87}\Vert$ = 1428.32 kN for full membrane behaviour and $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{87}\Vert$ = 1226.83 kN in simulation with the presence of cracks (II) lead to collapse (Fig. 10).

It should be noted that the range of admissible magnitude of hoop forces $\Vert \boldsymbol{\Delta }{{\varvec{H}}}_{87}\Vert$ relative to simulation (I) is larger than that of simulation (II). The cause of this is attributable to the presence of cracks, and consequently the absence of hoop forces, which reduce the domain of equilibrated solutions. Denoting the ratio between the maximum and the minimum hoop forces with α_i, the difference between the two simulations is highlighted. Indeed, in simulation (I) the ratio α₈₇ is equal to 18.24, and 13.98 for simulation (II), i.e., the presence of crack leads to a reduction of the admissible range of 23.35%.

The Dome of Santa Maria in Ciel d’Oro

The dome of Santa Maria in Ciel d’Oro is an octagonal masonry dome whose diagonal measures 13.52 m (Docci 2011), and whose thickness varies from 0.82 to 0.32 m with the height. The dome also carries the weight of a small lantern and part of the roof. Further, the intrados of the dome is not plastered, and the masonry layout is exposed, along with several other restoration and maintenance interventions conducted in concrete. Thus, for all analyses executed, a concentrated load is applied in correspondence of the oculus and equal to 140.00 kN; and a specific weight equal to 18.00 kN/m³ is assumed.

The use of the distinctive building technology—the cross-herringbone—enabled the construction of the dome without falsework. Hence, the balanced state must be achieved even during the construction work. For this reason, two different construction stages and the completed structure are examined. The first construction stage is simulated by evaluating the geometry of the dome up to the latitude of φ = 30.6°, therefore each lune is constituted by 34 blocks, while in the analyses concerning the second construction stage the number of the blocks is 59, and the portion of the dome is arrested at a latitude of φ = 53.1°. Finally, in the completed dome 84 blocks compose each lune. As in the case study of the Pantheon’s dome, the blocks are obtained by radial divisions, starting from the dome’s centre and with an inclination changing at a uniform 0.9° angle in all three cases, thus allowing the comparison between the different construction stages.

For all simulations performed, the dome was divided into 16 lunes, and in order to address the absence of axial symmetry of the geometry two of them were analysed. These two lunes are reported in Fig. 11. The first one contains section B–B, i.e., the section obtained by the intersection of the dome and the vertical radial plane whose projection onto the XY plane passes through the midpoint of the edge of the dome itself. The second one includes the diagonal of the octagon and is indicated by C–C.

The balanced state of the dome is guaranteed only if both the lunes are in equilibrium, but they are adjacent to each other and thus have a common interface through which exchange forces. Thus, the equilibrium can be achieved only if the hoop forces determined for the two lunes are the same. For this reason, the two lines of thrust illustrated in Fig. 11 were estimated assuming the same Dh, despite the fact that, due to the lune’s different geometries, the two lines of thrust are different. The variation in term of z-components $\Vert {{\varvec{T}}}_{i}^{z}\Vert$ is relevant. Indeed, the lune related to section C–C weights 12% more than the other one; nevertheless, the horizontal thrust $\Vert {{\varvec{T}}}_{i}^{x}\Vert$ evaluated in correspondence of section C–C is 31.93 kN, while for section B-B it is $\Vert {{\varvec{T}}}_{i}^{x}\Vert$= 32.18kN. Therefore, the variation of the horizontal component of the thrust is only 0.25 kN, equal to 0.7% of the $\Vert {{\varvec{T}}}_{i}^{x}\Vert$ of section B-B, which makes it possible to ascertain that the hoop forces acting on the two lunes are the same. Indeed, even if the Dh adopted for the two analyses is the same, due to the difference in the geometry of the two lunes and thus of the blocks, the hoop forces change slightly. Despite that they have same distribution and their sums the $\Vert {{\varvec{T}}}_{i}^{x}\Vert$ are almost identical, and therefore it is possible to affirm that the two lunes balance each other (Fig. 11).

Even if the analyses were always carried out on both the lunes, for clarity in what follows the results reported will refer only to the section B-B.

Table 2 summarises the values of forces estimated in the three different simulations related to different construction stages. In particular, the analysis highlights the fact that the maximum hoop forces required to achieve an equivalent condition of balance are about 13 times larger in the completed dome than during construction. Indeed, the maximum magnitude of hoop forces at completed construction works is $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{84}\Vert$ = 33.75 kN while in the other cases $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{59}\Vert$ = 2.56 kN for second construction stage and $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{35}\Vert$ = 2.56 kN for the first stage. The reason for this should be attributable to the concentrated load derived by the lantern, and by removing this added load and maintaining the same line of thrust, it can be seen that the hoop forces decrease to the value of $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{84}\Vert$ = 3.08 kN, returning back to the same order of the construction stages.

Table 2 Forces calculated by MTLM for the three construction stages

This characteristic is readable even in the shape of the Dh functions: the two Dh related to the first and second construction stages (Fig. 13b, c) are quite similar, while the function associated to the completed dome reaches a peak and then decreases rapidly to a value of 0.15, becoming linear and reaching the zero values for k = 82. Thus, in case of completed dome, the hoop forces related to the firsts blocks are zero, while the magnitude of hoop forces for the other two construction stages it does not reach zero, they are $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{1}\Vert$ = 0.34 kN for second construction stages and $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{1}\Vert$ = 0.02 kN for the first one (Fig. 12).

Fig. 12

MTLM analyses for the dome of Santa Maria in Ciel d’Oro. a Completed construction stage; b second construction stage; c first construction stage

Concerning a generic ith block, the hoop forces decrease during the construction works, e.g., for a latitude of φ₃₄ = 30.6° their magnitude $\Vert {\varvec{\Delta}}{{\varvec{H}}}_{34}\Vert$ starts from 2.56 kN in the first stage and reaches 0.18 kN at completed dome. This behaviour is exhibited even if the concentrated load is not considered. These analyses highlight the stabilising action of the load coming from the blocks placed above the one examined, i.e., in terms of sliding failure, the most dangerous stage occurs during the placing operation (D’Ayala and Tomasoni 2011).

Other simulations were carried out to examine the variation of the hoop forces during the construction works. The entire construction process was investigated through ten other simulations, and a distribution function was defined for each one. As in the previous analyses, these were conducted defining functions Dh lead to the same shape of the line of thrust, therefore all Dh determined are similar, and their variation is almost regular. In the early stages of construction, i.e., up to the angle φ = 20°, linear functions describe the distribution of hoop forces, then the distribution changes slightly becoming superlinear.

The spatial surface displayed in Fig. 13 is derived by interpolating all distribution functions determined for the different construction stages, and for the final one, which corresponds to the completed dome, however, here the concentrated load is not considered. The surface describes the variation of the distribution of hoop forces during the construction works, for this reason, it is denoted by the term surface of distribution of hoop forces (ζ). The three axes which describe the ζ correspond to the distribution functions Dh, in the Z direction, and to the construction stages and the index i, in the XY plane. Thus, the surface ζ is interpolated by monotonically increasing function, and it has a minimum and a maximum, which respectively correspond to 0.11 and 1.20. For what is observed, all functions Dh relative to all construction stages can be derived. For example, the two distribution functions illustrated in Fig. 13a, b relative to the first and second construction analysed previously can be derived through the intersection of vertical planes and the surface itself. Furthermore, the surfaces confirm what has already been highlighted: during the construction the hoop forces needed to reach a fixed balanced state change. Considering a block, the maximum hoop forces are recorded during the placing of the block itself. Figure 13 also reports the function Dh in case of the completed dome and considering the concentrated load added due to the lantern. In this simulation the distribution function is different and the surface ζ exhibits discontinuity to the previous one (Fig. 13).

Fig. 13

Spatial surface interpolated by the distribution function relative to the different construction stages. The two axes in the plane XY represent the progression of the construction works, and the blocks, this one denoted by index i. The third axis describes the variation of distribution function Dh

Conclusion

The actual structural state of a masonry dome or shell cannot be known; however, its stability can be assessed within the limit analysis and with the aid of the Safe Theorem (Heyman 1966). In this study a new formulation of MTLM is presented. The introduction of the distribution function Dh allows estimating the hoop forces needed to solve the equilibrium through an automatically iterative process.

The two cases studies presented in Sects. 3.1 and 3.2, testify to the wide range of application of the MTLM combined with the use of distribution function Dh. These applications include structures whose geometries are different from the axisymmetric ones, but which present axes that converge to a point, e.g., regular polygons in plan. In these cases, further assumptions must be considered, for example, as shown in Sect. 3.2, an octagonal dome is analysed by studying two different lunes and assuming a unique distribution function. Hence, with careful observations, regular polygons can be investigated. As also proven by the analyses on Santa Maria in Ciel d’Oro, the use of Dh allows to carry out simulations on the variation of the structural state during the different construction stages. Indeed, even from this trivial analysis, an exciting remark on the variation of the dome’s structural state can be concluded by inspecting the surface ζ. This surface exhibits neither discontinuities nor gaps, which occur due to unexpected variation of loads (concentrated load due to the lantern) or sudden alterations in the geometry. Thus, knowing the structural state of a dome and relative Dh function for two different construction stages, it is possible to estimate other states using the surface of the distribution of hoop forces.

Studies on the variation of the structural state during the construction works can provide in-depth knowledge of architectural heritage, e.g., helping understand the evolution of construction technologies, and the reasons behind the architectural design. Furthermore, the evaluation of the structural state variation could be applied to different research fields. For example, the concept of the surface of distribution ζ could be used to define the best process of construction of new self-balancing masonry shells, i.e., built without any temporary supports or centring.

Therefore, the introduction of the distribution function Dh widens the range of the application of MTLM, facilitating the estimation of the structural state of historical masonry domes or shells. The use of distribution function Dh also places the basis for evaluating the variation of the structural state during the construction works. In this direction, the MTLM can provide a useful contribution to the development and construction of the avant-garde masonry shells.