Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T04:28:24.025Z Has data issue: false hasContentIssue false
  • English
  • Français

DERIVED HECKE ALGEBRA AND COHOMOLOGY OF ARITHMETIC GROUPS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  23 December 2019

AKSHAY VENKATESH
AKSHAY VENKATESH*
Affiliation:
Institute for Advanced Study, Princeton, NJ 08540; akshay@ias.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe a graded extension of the usual Hecke algebra: it acts in a graded fashion on the cohomology of an arithmetic group 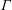$\unicode[STIX]{x1D6E4}$. Under favorable conditions, the cohomology is freely generated in a single degree over this graded Hecke algebra.

From this construction we extract an action of certain 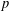$p$-adic Galois cohomology groups on 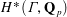$H^{\ast }(\unicode[STIX]{x1D6E4},\mathbf{Q}_{p})$, and formulate the central conjecture: the motivic 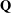$\mathbf{Q}$-lattice inside these Galois cohomology groups preserves 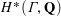$H^{\ast }(\unicode[STIX]{x1D6E4},\mathbf{Q})$.

MSC classification

Primary: 11F75: Cohomology of arithmetic groups 11F80: Galois representations
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 7 , 2019 , e7
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2019

References

Allen, P., Le Hung, B., Caraiani, A., Calegari, F., Gee, T., Helm, D., Newton, J., Taylor, R., Thorne, J. and Scholze, P., ‘Potential automorphy over CM fields’, Preprint, http://math.uchicago.edu/ fcale/papers/Ramanujan.pdf.Google Scholar
Bloch, S. and Kato, K., ‘ L-functions and Tamagawa numbers of motives’, inThe Grothendieck Festschrift, Vol. I, Progress in Mathematics, 86 (Birkhäuser Boston, Boston, MA, 1990), 333–400.Google Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups’, Ann. Sci. École Norm. Sup. (4) 7 (1974), 235–272.Google Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups. II’, inManifolds and Lie groups (Notre Dame, Ind., 1980), Progress in Mathematics, 14 (Birkhäuser, Boston, MA, 1981), 21–55.Google Scholar
Borel, A. and Wallach, N., Continuous Cohomology, Discrete Subgroups, and Representations of Reductive Groups, 2nd edn, Mathematical Surveys and Monographs, 67 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Brown, K. S., Cohomology of Groups, Graduate Texts in Mathematics, 87 (Springer, New York, 1994), Corrected reprint of the 1982 original.Google Scholar
Buzzard, K. and Gee, T., ‘The conjectural connections between automorphic representations and Galois representations’, inAutomorphic Forms and Galois Representations, Vol. 1, London Mathematical Society Lecture Note Series, 414 (Cambridge University Press, Cambridge, 2014), 135–187.Google Scholar
Calegari, F. and Emerton, M., ‘Completed cohomology—a survey’, inNon-abelian Fundamental Groups and Iwasawa Theory, London Mathematical Society Lecture Note Series, 393 (Cambridge University Press, Cambridge, 2012), 239–257.Google Scholar
Calegari, F. and Geraghty, D., ‘Modularity lifting beyond the Taylor-Wiles method’, Invent. Math. 211(1) (2018), 297–433.Google Scholar
Calegari, F. and Venkatesh, A., ‘A torsion Jacquet–Langlands correspondence’, Asterisque 409 (2019), https://arxiv.org/abs/1212.3847.Google Scholar
Caraiani, A., Gulotta, D. R., Hsu, C.-Y., Johansson, C., Mocz, L., Reinecke, E. and Shih, S.-C., ‘Shimura varieties at level $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations’, Preprint, https://arxiv.org/abs/1804.00136.Google Scholar
Chriss, N. and Khuri-Makdisi, K., ‘On the Iwahori-Hecke algebra of a p-adic group’, Int. Math. Res. Not. IMRN (2) (1998), 85–100.Google Scholar
Clozel, L., Harris, M. and Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations’, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.Google Scholar
Galatius, S. and Venkatesh, A., ‘Derived Galois deformation rings’, Adv. Math. 327 (2018), 470–623.Google Scholar
Gee, T., ‘Modularity lifting theorems’, Preprint, http://wwwf.imperial.ac.uk/∼tsg/index_files/ArizonaWinterSchool2013.pdf.Google Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., ‘Equivariant cohomology, Koszul duality, and the localization theorem’, Invent. Math. 131(1) (1998), 25–83.Google Scholar
Harris, M. and Venkatesh, A., ‘Derived Hecke algebra for weight one forms’, Exp. Math. 28(3) (2019), 342–361.Google Scholar
Huber, A. and Kings, G., ‘A cohomological Tamagawa number formula’, Nagoya Math. J. 202 (2011), 45–75.Google Scholar
Kahn, B., ‘On the Lichtenbaum-Quillen conjecture’, inAlgebraic K-Theory and Algebraic Topology (Lake Louise, AB, 1991), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 407 (Kluwer Academic Publishers, Dordrecht, 1993), 147–166.Google Scholar
van der Kallen, W., ‘Homology stability for linear groups’, Invent. Math. 60(3) (1980), 269–295.Google Scholar
Khare, C. B. and Thorne, J. A., ‘Potential automorphy and the Leopoldt conjecture’, Amer. J. Math. 139(5) (2017), 1205–1273.Google Scholar
Langlands, R. P., ‘Automorphic representations, Shimura varieties, and motives. Ein Märchen’, inAutomorphic Forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977) Part 2, Proceedings of Symposia in Pure Mathematics, XXXIII (American Mathematical Society, Providence, R.I., 1979), 205–246.Google Scholar
Murre, J. P., ‘On the motive of an algebraic surface’, J. Reine Angew. Math. 409 (1990), 190–204.Google Scholar
Ollivier, R. and Schneider, P., ‘A canonical torsion theory for pro-p Iwahori-Hecke modules’, Adv. Math. 327 (2018), 52–127.Google Scholar
Prasanna, K. and Venkatesh, A., ‘Automorphic cohomology, motivic cohomology and the adjoint $L$ -function’, Preprint, 2016, https://arxiv.org/abs/1609.06370.Google Scholar
Quillen, D., ‘On the cohomology and K-theory of the general linear groups over a finite field’, Ann. of Math. (2) 96 (1972), 552–586.Google Scholar
Ronchetti, N., ‘A satake homomorphism for the mod $p$ Hecke algebra’, Preprint, 2018,https://arxiv.org/abs/1808.06512.Google Scholar
Schneider, P., ‘Smooth representations and Hecke modules in characteristic p ’, Pacific J. Math. 279(1-2) (2015), 447–464.Google Scholar
Scholl, A. J., ‘Integral elements in K-theory and products of modular curves’, inThe Arithmetic and Geometry of Algebraic Cycles (Banff, AB, 1998), NATO Sci. Ser. C Math. Phys. Sci., 548 (Kluwer Academic Publ., Dordrecht, 2000), 467–489.Google Scholar
Scholze, P., ‘On torsion in the cohomology of locally symmetric varieties’, Ann. of Math. (2) 182(3) (2015), 945–1066.Google Scholar
Sella, Y., ‘Comparison of sheaf cohomology and singular cohomology’, Preprint, 2016,arXiv:1602.06674.Google Scholar
Soulé, C., ‘ K-théorie des anneaux d’entiers de corps de nombres et cohomologie étale’, Invent. Math. 55(3) (1979), 251–295.Google Scholar
Srinivas, V., Algebraic K-theory, Modern Birkhäuser Classics, 2nd edn , (Birkhäuser Boston, Inc., Boston, MA, 2008).Google Scholar
Treumann, D., ‘Smith theory and geometric Hecke algebras’, Math. Ann. 375 (2019), https://arxiv.org/abs/1107.3798.Google Scholar
Venkatesh, A., ‘Cohomology of arithmetic groups and periods of automorphic forms’, Jpn. J. Math. 12(1) (2017), 1–32.Google Scholar
Weibel, C., ‘Étale Chern classes at the prime 2’, inAlgebraic K-Theory and Algebraic Topology (Lake Louise, AB, 1991), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 407 (Kluwer Acad. Publ., Dordrecht, 1993), 249–286.Google Scholar
Yoneda, N, ‘Note on products in Ext’, Proc. Amer. Math. Soc. 9 (1958), 873–875.Google Scholar