Heat Transfer Analysis of 3-D Viscoelastic Nanofluid Flow Over a Convectively Heated Porous Riga Plate with Cattaneo-Christov Double Flux

Loganathan, K.; Alessa, Nazek; Kayikci, Safak

doi:10.3389/fphy.2021.641645

ORIGINAL RESEARCH article

Front. Phys., 20 August 2021
Sec. Statistical and Computational Physics
Volume 9 - 2021 | https://doi.org/10.3389/fphy.2021.641645

Heat Transfer Analysis of 3-D Viscoelastic Nanofluid Flow Over a Convectively Heated Porous Riga Plate with Cattaneo-Christov Double Flux

K. Loganathan¹*

Nazek Alessa² www.frontiersin.org

Safak Kayikci³

¹Research and Development Wing, Live4Research, Tiruppur Tamilnadu, India
²Department of Mathematical Sciences, Faculty of Science, Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia
³Department of Computer Engineering, Bolu Abant Izzet Baysal University, Bolu, Turkey

The impact of heat-absorbing viscoelastic nanofluidic flow along with a convectively heated porous Riga plate with Cattaneo-Christov double flux was analytically investigated. The Buongiorno model nanofluid was implemented with the diversity of Brownian motion and thermophoresis. Making use of the transformations; the PDE systems are altered into an ODE system. We use the homotopy analysis method to solve these systems analytically. The reaction of the apposite parameters on fluid velocity, fluid temperature, nanoparticle volume fraction skin friction coefficients (SFC), local Nusselt number and local Sherwood number are shown with vividly explicit details. It is found that the fluid velocities reflect a declining nature for the development of viscoelastic and porosity parameters. The liquid heat becomes rich when escalating the radiation parameter. In addition, the nanoparticle volume fraction displays a declining nature towards the higher amount of thermophoresis parameter, whereas the inverse trend was obtained for the Brownian motion parameter. We also found that the fluid temperature is increased in viscoelastic nanofluid compared to the viscous nanofluid. When we change the fluid nature from heat absorption to heat generation, the liquid temperature also rises. In addition, the fluid heat is suppressed when we change the flow medium from a stationary plate to a Riga plate for heat absorption/generation cases.

1 Introduction

Many industries depend on fluids, because they play an indispensable role in the heating and cooling process. Regular fluids like oil, ethylene, water, and glycol normally have scant heat transfer (HT) attributes because of their lesser thermal conductivity. So enhancing the fluid thermal conductivity is essential to cut down the work time process and extend equipment work life. Adding metallic nanosized (1–100 mm) particles, like Cu, Fe, Ti, Ag, or their oxides to regular fluids can reinforce their thermal conductivity. Rana and Bhargava [1] conducted HT analysis of a nanofluidic flow over a non-linear stretching surface (SS). They detected that fluid heat develops in huge quantities in the Brownian motion (BM) parameter. Khan and Pop [2] formed a mathematical model of 2D boundary layer flow of a nanofluidic flow over an SS. They learned that the mass transfer gradient depresses when the thermophoresis values enlarge. Bachok et al. [3] studied the flow of nanofluid on a moving semi-infinite plate and discovered that there was a larger energy rate when the Prandtl number was smaller. Viscoelastic nanofluidic flow with velocity slip with the finite element method was scrutinized by Goyal and Bhargava [4]. They observed that fluid heat enriches with the rising values of velocity slip. Hassani et al. [5] derived the series solution of a nanofluid over an SS. It is identified that a smaller mass transfer rate is obtained in higher values of the BM parameter. The recent developments for this direction are found in the referenced works [6–9].

Recently, several researchers have tried to prevent the reduction of mechanical energy. One of the simplest ways is to reduce the drag force, which helps to increase the mechanical energy. A Riga plate (RP) is one of the external agents used to curtail the drag force and control the fluid flow. This phenomenon is adopted in many production processes, like, MHD power generators, solar energy devices, heat exchangers, thermal nuclear reactors, and energy recovery, etc. The Blasius fluid flow past an RP was inspected by Magyari and Pantokratoras [10]. The impact of thermophoresis and Brownian parameters of a nanofluidic flow at an RP was addressed by Adeel et al. [11]. They identified that skin friction coefficient (SFC) diminishes with a developing modified Hartmann number (MHN). Zero normal wall mass flux of tangent hyperbolic nanofluidic flow on an RP, including partial slip, thermal radiation, and a chemical reaction along with activation energy was inspected by Nayak et al. [12]. New attempts for the above concept are included in the referenced works [13–16].

Many researchers are interested in examining the importance of convective boundary condition, because many engineering processes are based on these conditions. A few examples are, nuclear plants, thermal energy storage, transpiration cooling, geothermal energy extraction, laser pulse heating, petroleum processing, textile drying, and many others. Ahmad et al. [17] numerically examined nanofluidic flow on an RP with a convective heating (CH) condition. Their results speculate that temperature gradient reflects an inciting nature for strengthening the Biot number. Ramzan et al. [18] studied a radiative Williamson nanofluid on an RP with CH. They discovered that fluid heat develops when the value of the Biot number increases. Zaib et al. [19]. elucidated the flow of a blended convective micropolar fluid occupied by water/kerosene based Ti O ₂ nanoparticles on a Riga surface. The impact of CH of a third-grade nanofluid flow over an SS with entropy features was discussed by Loganathan et al. [20]. They proved that entropy rate increases when the Biot number increases. Nanofluidic flow over a convectively heated surface was portrayed by Makinde and Aziz [21]. Their results show that the thermal boundary layer thickness becomes thicker when the Biot number increases. Notable studies of convective boundary conditions are seen in the referenced works [22–24].

The aforementioned inspection reveals that many authors are willing to divulge the analysis of HT and MT using the Cattaneo-Christov theory with different physical configurations. But nobody yet has investigated the above analysis with porous RP. So we investigate the viscoelastic nanofluidic flow over a convectively heated porous RP. The homotopy method was implemented for solving the physical governing equations and the computational results are reported via graphs and tables. In petroleum engineering, pore space is essential for finding the permeability and porosity of a reservoir rock. So, this property is necessarily needed for storage capacity and flow motion. Further, the fluid needs to have heat generating and absorbing characteristics because this property can change the temperature gradient in the flow field. Potential applications of this effect are semi-conductor wafers, electronic chips, and combustion modeling. Also, these analyses are very useful in thermal engineering for designing thermal systems. Some other different computational methods and their utilizations are obtained in the referenced works [27–31].

2 Mathematical Formulation

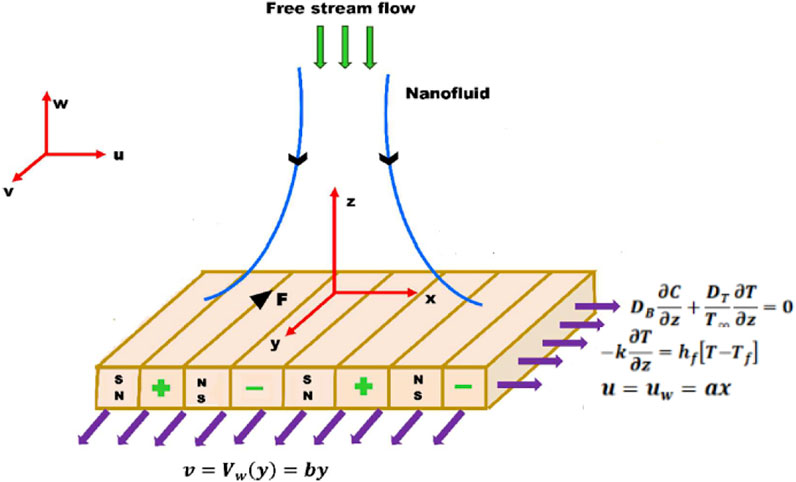
We now look into the 3D flow of VENF flow in a stretchy RP at z = 0. The plate is fixed at z = 0 and the flow is restrained to z ≥ 0. Let u_w (x, y) = ax and v_w (x, y) = by be the plate velocity in x & y directions. The plate has an invariable temperature T_w and nanoparticle concentration C_w. When z → ∞, the free stream value of temperature and nanoparticle concentration is denoted by T_∞ and C_∞. The HT and MT attributes are inspected along with CCDF. The base of the plate is convectively heated with hot fluid along with temperature T_f and this generates a HT coefficient h_c, see Figure 1. The ruling boundary layer equations are taken from [25].

FIGURE 1

FIGURE 1. Physical model of the given system.

\begin{matrix} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 \end{matrix} (1)

\begin{matrix} \frac{\partial u}{\partial x} u + \frac{\partial u}{\partial y} v + \frac{\partial u}{\partial z} \hat{w} = ν \frac{\partial^{2} u}{\partial z^{2}} \\ - β [\frac{\partial^{3} u}{\partial x \partial z^{2}} u + \frac{\partial^{3} u}{\partial z^{3}} w - \frac{\partial^{2} u}{\partial z^{2}} \frac{\partial u}{\partial x} - \frac{\partial^{2} w}{\partial z^{2}} \frac{\partial u}{\partial z} - 2 \frac{\partial^{2} u}{\partial x \partial z} \frac{\partial u}{\partial z} - 2 \frac{\partial^{2} u}{\partial z^{2}} \frac{\partial w}{\partial z}] \\ + \frac{π J_{0} M_{0}}{8 ρ} exp (\frac{- π y}{a}) - \frac{ν}{k_{1}} u \end{matrix} (2)

\begin{matrix} \frac{\partial v}{\partial x} u + \frac{\partial v}{\partial y} v + \frac{\partial v}{\partial z} w = ν \frac{\partial^{2} v}{\partial z^{2}} \\ - β [\frac{\partial^{3} v}{\partial y \partial z^{2}} v + \frac{\partial^{3} v}{\partial z^{3}} w - \frac{\partial^{2} v}{\partial z^{2}} \frac{\partial v}{\partial y} - \frac{\partial^{2} w}{\partial z^{2}} \frac{\partial v}{\partial z} - 2 \frac{\partial^{2} v}{\partial y \partial z} \frac{\partial v}{\partial z} - 2 \frac{\partial^{2} v}{\partial z^{2}} \frac{\partial w}{\partial z}] - \frac{ν}{k_{1}} v \end{matrix} (3)

with

\begin{matrix} u = u_{w} (x) = a x, v = v_{w} (y) = b y, w = 0 a t z = 0 \\ u \to 0, v \to 0 a s z \to \infty \end{matrix} (4)

The energy and concentration expressions are taken from [31].

\begin{matrix} \frac{\partial T}{\partial x} u + \frac{\partial T}{\partial y} v + \frac{\partial T}{\partial z} w + Ω_{T} = α (1 + \frac{16 σ * T_{\infty}}{3 K K *}) \frac{\partial^{2} T}{\partial z^{2}} \\ + τ [D_{B} \frac{\partial T}{\partial z} \frac{\partial C}{\partial z} + \frac{D_{T}}{T_{\infty}} {(\frac{\partial T}{\partial z})}^{2}] + \frac{Q}{ρ C_{p}} (T - T_{\infty}) \end{matrix} (5)

\begin{matrix} \frac{\partial C}{\partial x} u + \frac{\partial C}{\partial y} v + \frac{\partial C}{\partial z} w + Ω_{C} = D_{B} \frac{\partial^{2} C}{\partial z^{2}} + \frac{D_{T}}{T_{\infty}} (\frac{\partial^{2} T}{\partial z^{2}}) \end{matrix} (6)

where

\begin{matrix} Ω_{T} = \frac{\partial^{2} T}{\partial x^{2}} u^{2} + \frac{\partial^{2} T}{\partial y^{2}} v^{2} + \frac{\partial^{2} T}{\partial z^{2}} w^{2} + (\frac{\partial u}{\partial x} u + \frac{\partial u}{\partial y} v + \frac{\partial u}{\partial z} w) \frac{\partial T}{\partial x} \\ + (\frac{\partial \hat{v}}{\partial x} u + \frac{\partial v}{\partial y} v + \frac{\partial v}{\partial z} w) \frac{\partial T}{\partial \hat{y}} + (\frac{\partial w}{\partial x} u + \frac{\partial w}{\partial y} v + \frac{\partial w}{\partial z} w) \frac{\partial T}{\partial z} \\ + 2 \frac{\partial^{2} T}{\partial x \partial y} u v + 2 \frac{\partial^{2} T}{\partial y \partial z} v w + 2 \frac{\partial^{2} T}{\partial x \partial z} u w \end{matrix} (7)

\begin{matrix} Ω_{C} = \frac{\partial^{2} C}{\partial x^{2}} u^{2} + \frac{\partial^{2} C}{\partial y^{2}} v^{2} + \frac{\partial^{2} C}{\partial z^{2}} w^{2} + (\frac{\partial u}{\partial x} u + \frac{\partial u}{\partial y} v + \frac{\partial u}{\partial z} w) \frac{\partial C}{\partial x} \\ + (\frac{\partial v}{\partial x} u + \frac{\partial v}{\partial y} v + \frac{\partial v}{\partial z} w) \frac{\partial C}{\partial y} + (\frac{\partial w}{\partial x} u + \frac{\partial w}{\partial y} v + \frac{\partial w}{\partial z} w) \frac{\partial C}{\partial z} \\ + 2 \frac{\partial^{2} C}{\partial x \partial y} \hat{u} v + 2 \frac{\partial^{2} C}{\partial y \partial z} v w + 2 \frac{\partial^{2} C}{\partial x \partial z} u w \end{matrix} (8)

with

\begin{matrix} - k \frac{\partial T}{\partial z} = - h_{c} (T - T_{f}), \frac{D_{T}}{T_{\infty}} \frac{\partial T}{\partial z} + D_{B} \frac{\partial C}{\partial z} = 0 a t z = 0 \\ T \to T_{\infty}, C \to C_{\infty} a s z \to \infty \end{matrix} (9)

u, v, & w are the “fluid speed components,” x, y & z are the “direction co-ordinates,” ν is the “kinematic viscosity,” β is the “material parameter of fluid,” k₁ is the “permeability of the porous medium,” a is the“ width of magnets and electrodes,” J₀ is the “applied current density of the electrodes,” M₀ is the “magnetization of the permanent magnets,” ρ is the “fluid density,” T is the “fluid temperature,” Ω_T Ω_C are the “relaxation time of heat and mass fluxes,” α is the “thermal diffusivity,” C_p is the “specific heat capacity,” σ* is the “Stefan Boltzmann constant,” k is the “fluid thermal conductivity,” k* is the “mean absorption coefficient,” Q is the “heat absorption/generation coefficient,” D_B is the “mass diffusivity,” C is the “fluid concentration,” τ is the “ratio of the effective heat capacity of the nanoparticle material and the base fluid,” T_∞ & C_∞ are the “free stream temperature and concentration,” and D_T is the “thermophoretic diffusion coefficient.”

The instigation of dimensionless are taken from [31].

\begin{matrix} u = f^{'} (η) x a, v = g^{'} (η) y a, w = - \sqrt{ν a} (g (η) + f (η)) \\ η = \sqrt{\frac{a}{ν}} z, θ (η) = \frac{T - T_{\infty}}{T_{f} - T_{\infty}}, ϕ (η) = \frac{C - C_{\infty}}{C_{w} - C_{\infty}} \end{matrix} (10)

\begin{matrix} f^{'''} + g f^{''} + f f^{''} - {[f^{'}]}^{2} + K g f^{i v} + K f f^{i v} - K g^{''} f^{''} + K f^{''} f^{''} - 2 K g^{'} f^{'''} - 2 K f^{'} f^{'''} \\ - Λ f^{'} + H a e^{- β η} = 0 . \end{matrix} (11)

\begin{matrix} g^{'''} + g g^{''} + f g^{''} - {[g^{'}]}^{2} + K g g^{i v} + K f g^{i v} + K g^{''} g^{''} - K \bar{f^{''}} g^{''} - 2 K g^{'} g^{'''} - 2 K f^{'} g^{'''} \\ - Λ g^{'} = 0 . \end{matrix} (12)

\begin{matrix} θ^{''} (1 + \frac{4}{3} R d) + P r g θ^{'} + P r f θ^{'} - P r Γ {θ^{''} {[g + f]}^{2} + θ^{'} [g + f] [g^{'} + f^{'}]} + P r N_{b} ϕ^{'} θ^{'} \\ + P r N_{t} θ^{2} + P r H g θ = 0, \end{matrix} (13)

\begin{matrix} ϕ^{''} + S c g ϕ^{'} + S c f ϕ^{'} - S c Γ_{c} {ϕ^{''} {[g + f]}^{2} + ϕ^{'} [g + f] [g^{'} + f^{'}]} + \frac{N_{t}}{N_{b}} θ^{''} = 0 . \end{matrix} (14)

with the condition that

\begin{matrix} f (0) = 0, f^{'} (0) = 1, g (0) = 0, g^{'} (0) = c, \\ θ^{'} (0) = - B i [1 - θ (0)], N b ϕ^{'} (0) + N t θ^{'} (0) = 0, \\ f^{'} (\infty), g^{'} (\infty), θ (\infty), ϕ (\infty) \to \infty \end{matrix} (15)

where $K = \frac{β a}{ν}$ is the “viscoelastic parameter” (VEP), $Λ = \frac{ν}{k_{1} a}$ is the “porosity parameter,” $H m = \frac{π J_{0} M_{0}}{8 ρ a^{2} x}$ is the “modified Hartmann number” (MHN), $R d = \frac{4 σ_{0}^{*} T_{\infty}^{* 3}}{k^{*} k}$ is the “radiation parameter” $P r = \frac{ν}{α}$ is the “Prandtl number,” Γ = Ω_Ta is the “non-dimensional thermal relaxation time parameter,” Γ_c = Ω_Ca is the “non-dimensional nanoparticle relaxation time parameter,” $H g = \frac{Q}{ρ C_{p} a}$ is the “heat generation/absorption parameter,” $S c = \frac{ν}{D_{B}}$ is the “Schmidt number,” $c = \frac{b}{a}$ is the “stretching ratio,” $N b = \frac{τ D_{B} (C_{w} - C_{\infty})}{ν}$ is the “Brownian motion parameter” (BM), $N t = \frac{τ D_{T} (T_{f} - T_{\infty})}{ν T_{\infty}}$ is the “thermophoresis parameter,” and $B i = \frac{h_{c} \sqrt{\frac{ν}{a}}}{k}$ is the “Biot number.”

Then, the dimensionless form of the skin friction coefficients $(C_{f_{x}} & C_{f_{y}})$ , local Nusselt number (Nu), and local Sherwood number (Sh) are defined as

τ_{w x} = ν \frac{\partial u}{\partial z} + k_{1} {[u \frac{\partial u}{\partial x \partial z} + v \frac{\partial u}{\partial y \partial z} + w \frac{\partial u}{\partial z^{2}} + \frac{\partial u}{\partial z} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial z} \frac{\partial v}{\partial x} + 2 \frac{\partial w}{\partial z} \frac{\partial w}{\partial x} - \frac{\partial w}{\partial z} \frac{\partial u}{\partial z}]}_{z = 0} (16)

τ_{w y} = ν \frac{\partial v}{\partial z} + k_{1} {[u \frac{\partial v}{\partial x \partial z} + v \frac{\partial v}{\partial y \partial z} + w \frac{\partial v}{\partial z^{2}} + \frac{\partial u}{\partial z} \frac{\partial u}{\partial y} + \frac{\partial v}{\partial z} \frac{\partial v}{\partial y} + 2 \frac{\partial w}{\partial z} \frac{\partial w}{\partial y} - \frac{\partial w}{\partial z} \frac{\partial v}{\partial z}]}_{z = 0} (17)

N u = \frac{x k_{T} {[\frac{\partial T}{\partial z}]}_{Z = 0}}{k_{T} (T_{w} - T_{\infty})} [- \frac{4 σ_{0}}{3 k^{*}} {(\frac{\partial T^{4}}{\partial z})}_{z = 0}] (18)

S h = - \frac{x {[\frac{\partial c}{\partial z}]}_{Z = 0}}{(c_{w} - c_{\infty})} (19)

\begin{matrix} C_{f_{x}} \sqrt{R e} & = & f^{″} (0) + 2 K f^{″} (0) f^{'} (0) - K g (0) f^{'''} (0) - K f (0) f^{'''} (0) + K g^{'} (0) f^{″} (0) + K f^{'} (0) f^{″} (0), \\ C_{f_{y}} \sqrt{R e} & = & g^{″} (0) + 2 K g^{″} (0) g^{'} (0) - K g (0) g^{'''} (0) - K f (0) g^{'''} (0) + K g^{'} (0) g^{″} (0) + K f^{'} (0) g^{″} (0), \\ N u / \sqrt{R e} & = & - (1 + \frac{4}{3} R d) [θ^{'} (0)], \\ S h / \sqrt{R e} & = & - [ϕ^{'} (0)] . \end{matrix}

3 Homotopy Analysis Method Solutions

The initial assumptions are f₀(η) = 1 − e^−η, $g_{0} (η) = c (1 - e^{- η})$ , $θ_{0} (η) = \frac{B i e^{- η}}{1 + B i}$ , and $ϕ_{0} (η) = - \frac{N t B i e^{- η}}{N b (1 + B i)}$ .

The linear operators are L_f = $f^{'''} - f^{'}$ , L_g = $g^{'''} {- g}^{'}$ , L_θ = $θ^{''}$ −θ, and L_ϕ = $ϕ^{''}$ − ϕ.with the properties.

\begin{matrix} L_{f} [ω_{1} + ω_{2} e^{η} + ω_{3} e^{- η}] = 0 \end{matrix} (20)

\begin{matrix} L_{g} [ω_{4} + ω_{5} e^{η} + ω_{6} e^{- η}] = 0 \end{matrix} (21)

\begin{matrix} L_{θ} [ω_{7} e^{η} + ω_{8} e^{- η}] = 0 \end{matrix} (22)

\begin{matrix} L_{ϕ} [ω_{9} e^{η} + ω_{10} e^{- η}] = 0 \end{matrix} (23)

in which, ω_i, (i = 1–10) denote the arbitrary constants.

Finally, the general solution of equations (52)-(55) can be written as.

\begin{matrix} f_{m} (η) = f_{m}^{*} (η) + ω_{1} + ω_{2} e^{η} + ω_{3} e^{- η} \end{matrix} (24)

\begin{matrix} g_{m} (η) = g_{m}^{*} (η) + ω_{4} + ω_{5} e^{η} + ω_{6} e^{- η} \end{matrix} (25)

\begin{matrix} θ_{m} (η) = θ_{m}^{*} (η) + ω_{7} e^{η} + ω_{8} e^{- η} \end{matrix} (26)

\begin{matrix} ϕ_{m} (η) = ϕ_{m}^{*} (η) + ω_{9} e^{η} + ω_{10} e^{- η} \end{matrix} (27)

here particular solutions are denoted as $f_{m}^{*} (η)$ , $g_{m}^{*} (η)$ , $θ_{m}^{*} (η)$ , and $ϕ_{m}^{*} (η)$ .

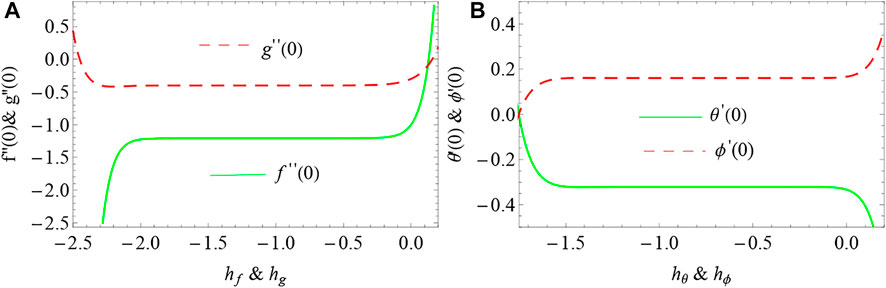
The use of control variables (h_f, h_g, h_θ, h_ϕ) play a significant role in the convergence of the series. Hence Figures 1A,B displays the h-curves. It is observed that the acceptable values of $(h_{f}$ , $h_{\bar{g}}$ , $h_{\bar{θ}}$ , $h_{ϕ})$ are −1.8 ≤ h_f, h_g ≤ −0.5, −1.4 ≤ h_θ, and h_ϕ ≤ −0.2, see Figures 2A,B. For a more accurate solution, we choose −1 as the h_f & h_g values and −0.8 for h_θ & h_ϕ. The HAM order of approximation is portrayed in Table 1 and we proved that the 15th order is enough for all profiles. Table 2 shows the evaluation of − f′′(0) for different c values from Qayyum et al. [25] and Li et al. [26]. From this table, we conclude that our outcomes have high accuracy.

FIGURE 2

FIGURE 2. h− graph of $\hat{f^{''} (0)}$ , $\hat{g^{''}} (0)$ , $\hat{θ^{'} (0)}$ , and $\hat{ϕ^{'} (0)}$ .

TABLE 1

TABLE 1. Homotopy Analysis Method order.

TABLE 2

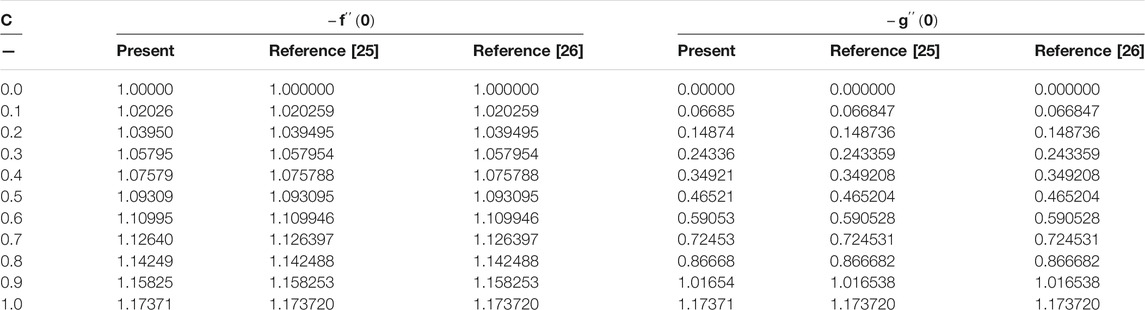
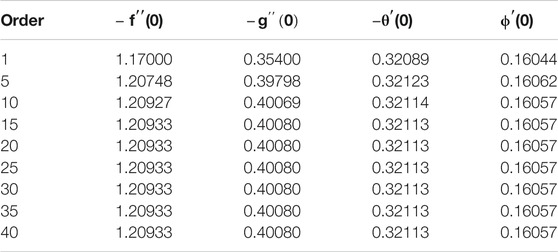
TABLE 2. Illustrating the disparity of $- f^{''} (0)$ and $- g^{''} (0)$ with c when K = Q = Λ = 0.0 from Qayyum et al. [25] and Li et al. [26].

4 Correlation Analysis

To analyze the performance of the thermal system design, correlation equations are crucial. The obtained numerical values are used to derive the correlation equations with the help of linear regression analysis. The correlation equations of the Nusselt number and Sherwood number are derived as

\begin{matrix} N u / \sqrt{R e} & = & 0.349019 + 0.010508 * H a - 0.011297 * Λ + 0.324013 * R d \\ S h / \sqrt{R e} & = & 0.084673 + 0.001545 * H a - 0.001669 * Λ - 0.013826 * R d \end{matrix}

here Ha ∈{0, 0.3}, Λ ∈ [0, 0.4], and R ∈ [0, 1] with maximum error is 0.0076.

5 Results and Discussion

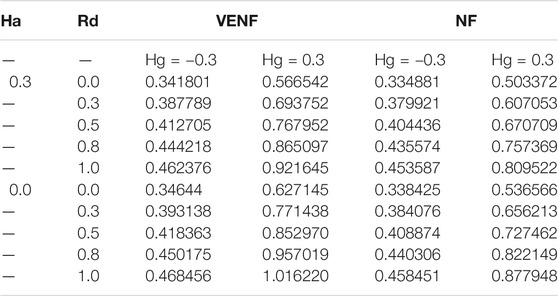
The impact of the distinguished variables on the velocities, temperature, NPVF, SFCs, LNN, and LSN are interpreted in this section. Table 3 establishes the significance of K, Ha, and Λ on $C f_{x}$ , $C f_{y}$ , $N u / \sqrt{R e}$ , and $S h / \sqrt{R e}$ . It is found that the SFCs, LNN, and LSN become smaller with higher values of K and Λ. In addition, the HT and MT gradients form an enhancing behavior and SFCs form a decaying behavior with the rising values of MHN. The significance of fluid temperature (θ(η)) for various combinations of Ha, Rd, and Hg is exhibited in Table 4. We noted that fluid heat heightens as the value of Rd increases for all cases. The maximum fluid temperature is attained with a heat generating VENF on an SP with a high presence of radiation. Also we found that fluid temperature decreases in RP with a heat absorbing NF and the absence of radiation. In the RP and VENF case, we change the fluid nature from heat absorption to heat generation; the minimum increase percentage (66%) is attained at Rd = 0 and the maximum enhancing percentage (99%) is obtained at Rd = 1. This analysis clearly shows that radiation plays an important role in rising fluid temperature. In the SP and VENF fluid case, (81%) and (117%) are the smallest and highest enhance percentage of fluid heat with the absence and presence of radiation, respectively. In the RP and NF case, we change the fluid nature from heat absorption to heat generation, the lowest increase percentage (50%) is attained at Rd = 0 and the maximum rising percentage (79%) is obtained at Rd = 1. In the SP and NF case, (59%) and (92%) are the smallest and highest enhance percentage of fluid heat with the absence and presence of radiation, respectively. In the above observation, fluid is quickly heated in VENF compared to NF with an increasing radiation parameter. In addition, fluid temperature is suppressed when we change the flow medium from SP to RP for heat absorption/generation cases.

TABLE 3

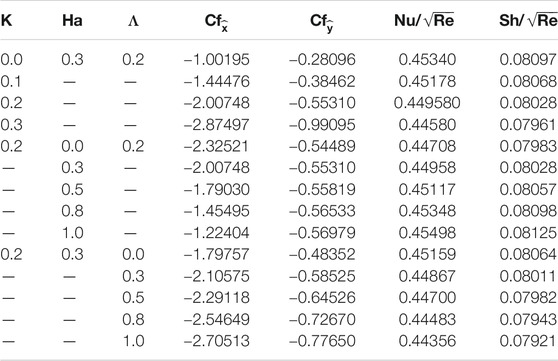
TABLE 3. Skin friction coefficients, local Nusselt number, and Local Sherwood number for different values of K, Q, and Λ.

TABLE 4

TABLE 4. Variation of θ(η) for various combinations of Ha, R, and Hg for VENF and NF.

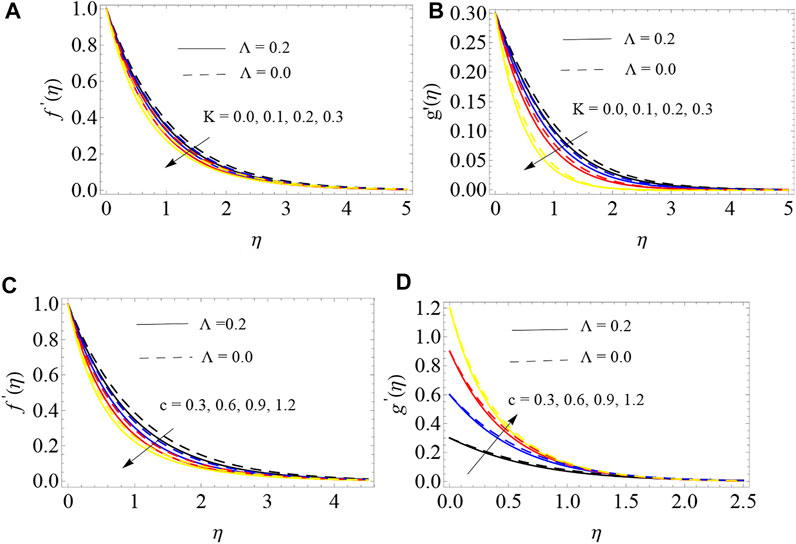
The consequences of a viscoelastic parameter, porosity parameter, and stretching ratio parameter on both velocity profiles over a porous and non-porous RP are shown in Figures 3A–F. We proved that both direction velocities become smaller when escalating the values of K. Physically, a stronger viscoelastic effect creates a stronger resistive force and this force opposes fluid motion. Thereby the fluid velocity and its associative boundary layer (BL) thickness diminishes when the values of K are raised. In addition, the thickness of the momentum BL is high in viscous fluid (K = 0.0) compared to the viscoelastic fluid K ≠ 0, see Figures 3A,B. We found that x−direction velocity declines against a higher quantity of c whereas the opposite behavior was attained for y−direction velocity. From these figures, we also found that the larger momentum BL thickness is obtained in NPRP for the x−direction and in PRP for the y−direction, see Figures 3C,D.

FIGURE 3

FIGURE 3. The impact of “K” and “c” on both velocity profiles.

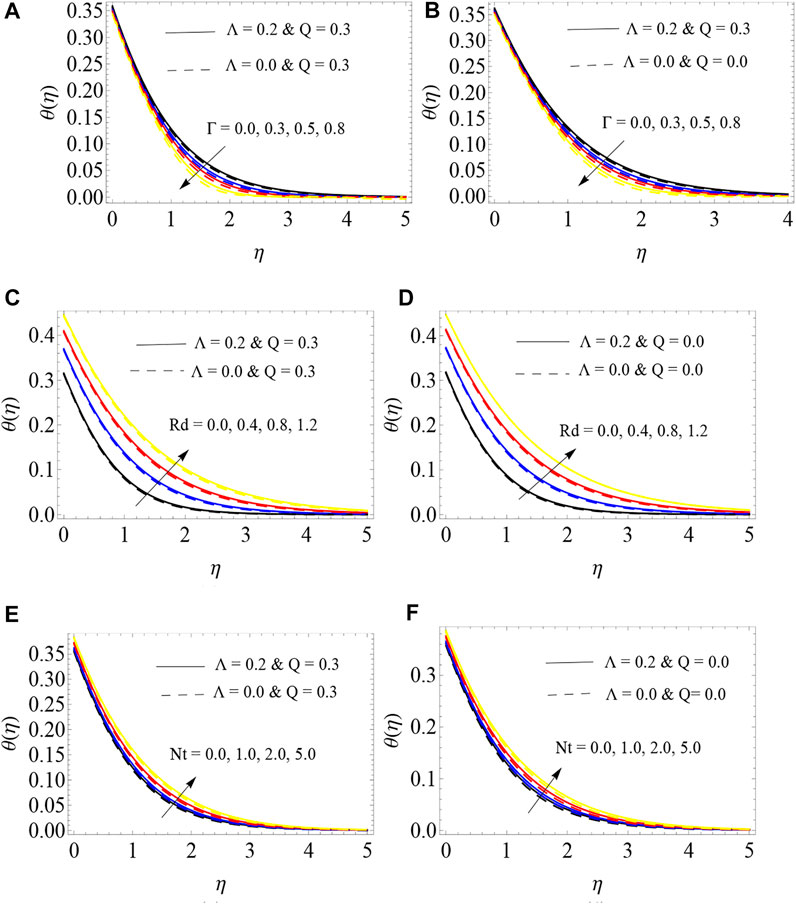
Figures 4A–F indicate the variations of temperature profile for distinct values of Γ, Rd, and Nt for PRP, NPRP, PSP, and NPSP. We detected that fluid heat decreases with larger values of Γ. Higher thermal BL thickness in both plates was attained only in the presence of porous medium, see Figures 4A,B. We noticed that the fluid temperature increases with rising values of Rd (Figures 4C,D). Physically, a larger quantity of the radiation parameter generates more heat in the fluid and enhances the thickness of thermal BL. The thickness of the thermal BL is almost the same for RP and SP. Also, we found that a lower fluid temperature occurs in the non-porous plate for both cases. In Figures 4A,E,F larger thermophoresis parameter relates to higher fluid thermal conductivity and this causes an increase in the temperature of the fluid. Also, we noted that a smaller thermal BL thickness was apparent in the non-porous plate for both cases.

FIGURE 4

FIGURE 4. The impact of “Q,” “Λ,” “Γ,” “Rd,” and “Nt” on temperature profiles.

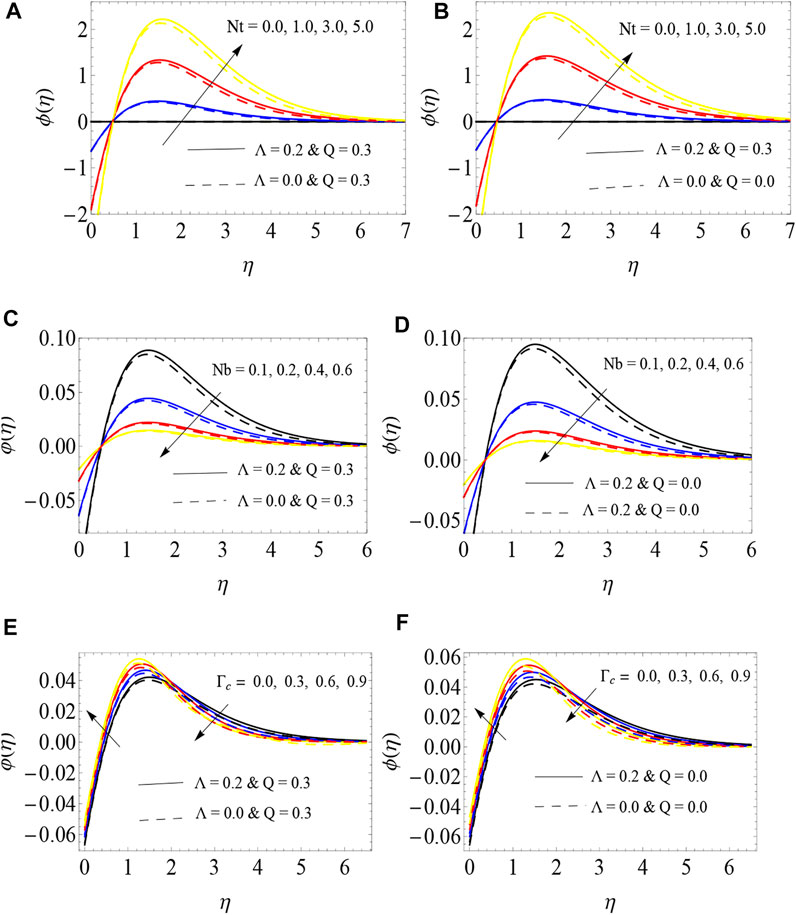
Figures 5A–F describe the impact of Nt, Nb, and Γ_c on NPVF profile for PRP, NPRP, PSP, and NPSP. In Figures 5A,B, we see that the large values of Nt lead to the enhancement of the NPVF. Also, we proved that the NPVF is a non-developing function of Nb (5 (c-d)). From Figures 5E,F, we report higher values of Γ_c as the NPVF increases near the plate, which decreases further away from the surface. In the above cases, BL thickness of the NPVF becomes thinner in the non-porous plate for both cases. The SFC (x− direction) for various values of c and Λ is displayed in Figures 6A,B. We noticed that the SFC is suppressed with improving values of c and Λ. We also note that a larger SFC is attained in RP compared to the SP. An opposite situation was obtained for y− direction SFC, see Figures 6C,D. Only small variations were found between RP and SP.

FIGURE 5

FIGURE 5. The impact of “Nt,” “Nb,” and “Γ_c” on nanoparticle volume fraction profile.

FIGURE 6

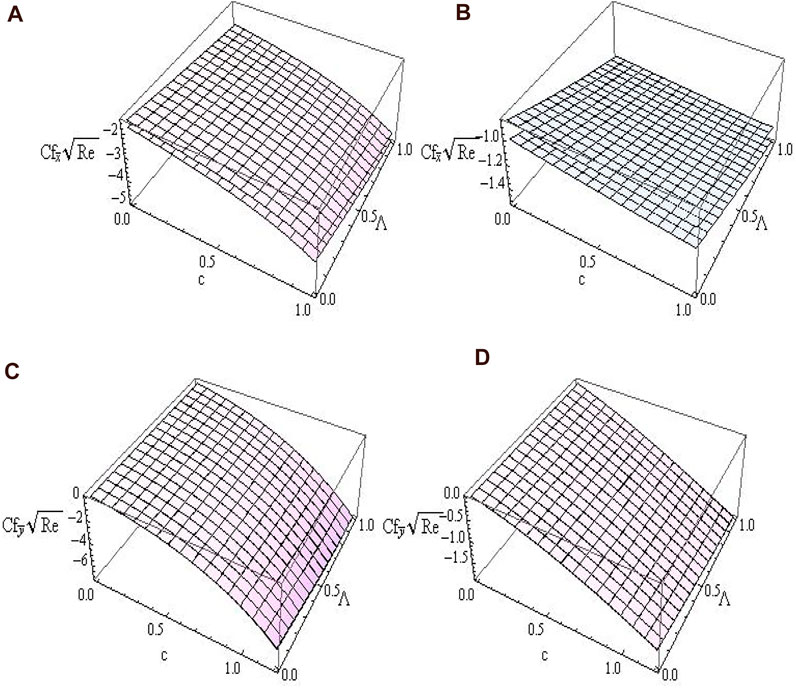
FIGURE 6. The variations of “ $C f_{\hat{x}}$ ” on c and Λ for (A) upper plate K = 0.2, Q = 0.3 and lower plate K = 0.2, Q = 0.0, (B) upper plate K = 0.0, Q = 0.3 and lower plate K = 0.0, Q = 0.0, “ $C f_{\hat{y}}$ ” on c and Λ for (C) lower plate K = 0.2, Q = 0.3 and upper plate K = 0.2, Q = 0.0, and (D) lower plate K = 0.0, Q = 0.3 and upper plate K = 0.0, Q = 0.0.

Figures 7A–D portray the variations of LNN for various combinations of Rd, Ha, Γ, Hg, Bi, and Λ. From Figures 7A,B, we noticed that the fluid temperature gradient was suppressed with enhancing values of Rd, Hg, and Λ. In the convective heating case, the rate of change of HT rate is enhanced with a small quantity of Rd and is suppressed with a higher quantity of Rd, see Figure 7C. On the other hand, the decreasing rate of the HT gradient is small for a small amount of Rd and is high for a larger amount of Rd, see Figure 7D. Figures 8A–D demonstrate the influence of Rd, Ha, Γ, Hg, Bi, and Λ on LSN. We found that the LSN is depressed with the increasing values of Rd, Hg, and Λ and is boosted with the escalating values of Γ. In both HT and MT gradients, the RP plays a significant role.

FIGURE 7

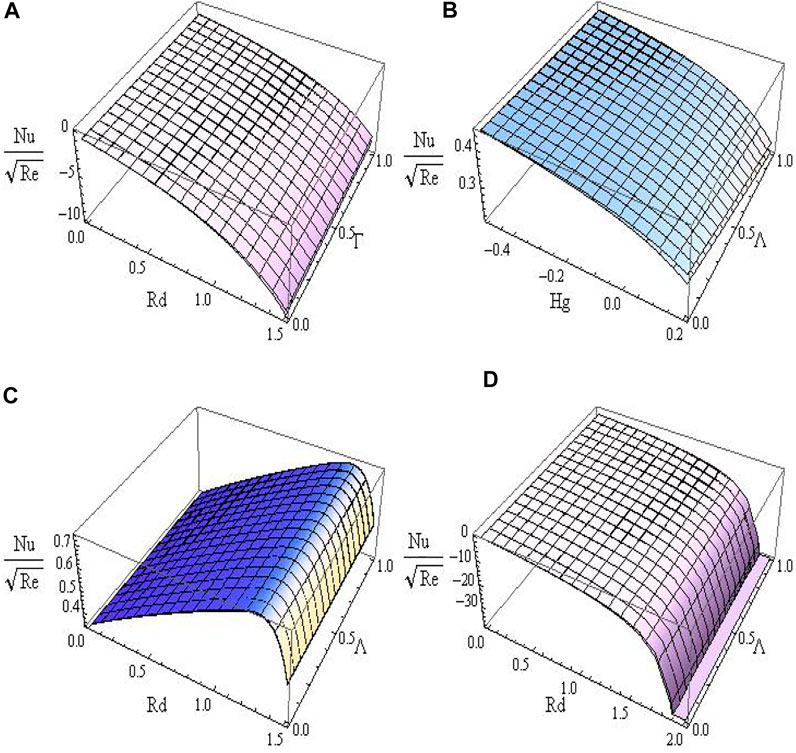
FIGURE 7. The variations of “Nu” for various combinations of Rd, Γ, Λ, and Hg with (A) lower plate (Λ = 0.2) and upper plate (Λ = 0.0), (B) lower plate (Q = 0.3) and upper plate (Q = 0.0), (C) lower plate (Q = 0.0 & Bi = 0.5) and upper plate (Q = 0.3 & Bi = 0.5), and (D) lower plate (Q = 0.0 & Bi = −0.5) and upper plate (Q = 0.3 & Bi = −0.5).

FIGURE 8

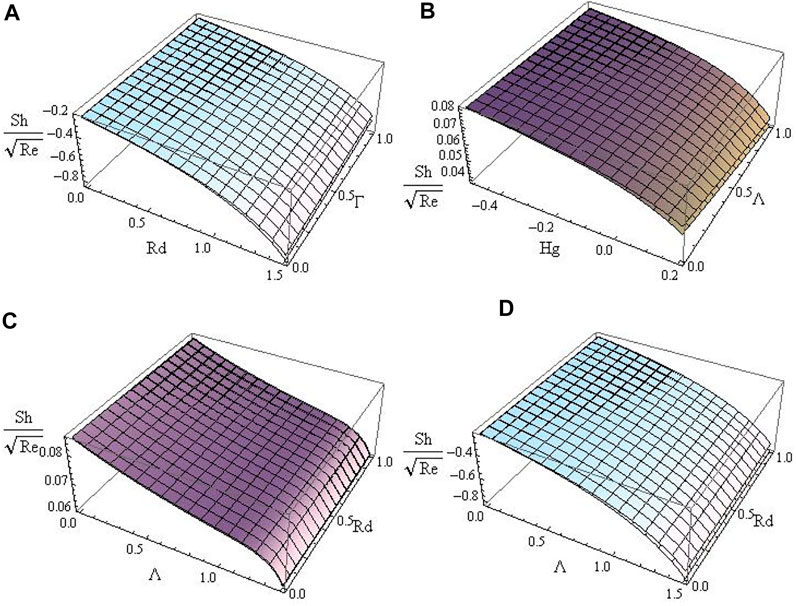
FIGURE 8. The variations of “Sh” for various combinations of Rd, Γ, Λ, and Hg with (A) lower plate (Λ = 0.2) and upper plate (Λ = 0.0), (B) lower plate (Q = 0.3) and upper plate (Q = 0.0), (C) lower plate (Q = 0.0 & Bi = 0.5) and upper plate (Q = 0.3 & Bi = 0.5), and (D) lower plate (Q = 0.0 & Bi = −0.5) and upper plate (Q = 0.3 Bi = −0.5).

6 Conclusion

The outcomes of the BL flow of a heat-absorbing viscoelastic nanofluid with CCDF and convective heating has been considered and the obtained key points are as follows:

• The momentum BL thickness becomes small with the presence of the viscoelastic parameter

• The thermal BL thickness increases with larger values of the thermal relaxation time parameter

• The NPVF is highly negatively correlated with the presence of the Brownian motion parameter

• The skin friction coefficient declined with a higher modified Hartmann number

• An increase in Hg gives a reduction in the mass transfer gradient

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University through the Fast-track Research Funding Program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rana P, Bhargava R. Flow and Heat Transfer of a Nanofluid over a Nonlinearly Stretching Sheet: A Numerical Study. Commun Nonlinear Sci Numer Simulation (2012) 17:212–26. doi:10.1016/j.cnsns.2011.05.009

ORIGINAL RESEARCH article

Heat Transfer Analysis of 3-D Viscoelastic Nanofluid Flow Over a Convectively Heated Porous Riga Plate with Cattaneo-Christov Double Flux

1 Introduction

2 Mathematical Formulation

3 Homotopy Analysis Method Solutions

4 Correlation Analysis

5 Results and Discussion

6 Conclusion

Data Availability Statement

Author Contributions

Funding

Conflict of Interest

Publisher’s Note

References

Glossary

This article is part of the Research Topic

People also looked at