Abstract
Since marine seismic studies are relatively sparse and unevenly distributed, detailed tomographic images of the Moho geometry under large parts of the world’s oceans and marginal seas are not yet available. Marine gravity data is, therefore, often used to detect the Moho depth in these regions. Alternatively, Airy’s isostatic theory can be applied for this purpose. In this study, we compare different isostatic and gravimetric methods for a Moho recovery under the oceanic crust and continental margins, particularly focusing on a numerical performance of Airy, Vening Meinesz–Moritz (VMM), direct gravity inversion, and generalized (for the Earth’s spherical approximation) Parker–Oldenburg methods. Numerical experiments are conducted to estimate the Moho depth beneath the Indian Ocean. Results reveal that, among these investigated methods, the VMM model is probably the most suitable for a gravimetric Moho recovery beneath the oceanic crust and continental margins, when taking into consideration the lithospheric mantle density information. This method could to some extent model realistically a Moho geometry beneath mid-oceanic spreading ridges, oceanic subductions, most of oceanic volcanic formations, and marine sediment deposits. Nonetheless, this model still cannot fully reproduce a gradual Moho deepening caused by a conductive cooling and a subsequent isostatic rebalance of the oceanic lithosphere, which can functionally be described by a Moho deepening with the increasing ocean-floor age. Results also indicate that the Airy method typically overestimates the Moho depth under oceanic volcanic formations, while the direct gravity inversion and generalized Parker–Oldenburg methods could not reproduce more detailed features in the Moho geometry. Since Pratt’s theory better describes a large-scale isostatic mechanism of the oceanic lithosphere by means of compensation density variations, but does not account for additional changes in compensation depth (i.e., Moho depth) that are caused by these density changes, we tested a possibility of combining Pratt and Airy’s isostatic theories in order to estimate the Moho depth under the oceanic crust. Even this combined model cannot fully reproduce a gradual Moho deepening with the increasing ocean-floor age.

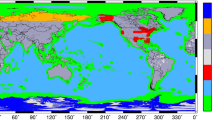
taken from Rathnayake et al. (2019). Black dotted lines indicate tectonic margins




















Similar content being viewed by others
References
Airy GB (1855) On the computation of the effect of the attraction of mountain-masses, as disturbing the apparent astronomical latitude of stations in geodetic surveys. Philos Trans R Soc Lond 145:101–104
Aghaei O, Nedimović MR, Carton H, Carbotte SM, Canales JP, Mutter JC (2014) Crustal thickness and Moho character of the fast-spreading East Pacific Rise from 9°42′N to 9°57′N from poststack-migrated 3D MCS data. Geochem Geophys Geosyst 15:634–657
Andriampenomanana F, Nyblade AA, Wysession ME, Durrheim RJ, Tilmann F, Julià J, Martin JP, Rambolamanana G, Aleqabi G, Shore RT (2017) The structure of the crust and uppermost mantle beneath Madagascar. Geophys J Int 210(3):1525–1544
Arabelos DN, Mantzios G, Tsoulis D (2006) Moho Depths in the Indian Ocean Based on the Inversion of Satellite Gravity Data. Adv Geoscie 9:41–52
Ashalatha B, Subrahmanyam C, Singh RN (1991) Origin and compensation of Chagos-Laccadive Ridge, Indian Ocean, from admittance analysis of gravity and bathymetry data. Earth Planet Sci Lett 105(1–3):47–54
Bagherbandi M, Sjöberg LE (2012) Non-isostatic effects on crustal thickness: A study using CRUST2.0 in Fennoscandia. Phys Earth Planet Inter 200–201:37–44
Bagherbandi M, Tenzer R, Sjöberg LE, Novák P (2013) Improved global crustal thickness modeling based on the VMM isostatic model and non-isostatic gravity correction. J Geodyn 66:25–37
Bowie W (1924) Gravity observations on the Indian Ocean and the results of their isostatic reduction. Nature 114:930–931
Bown JW, White RS (1994) Variation with spreading rate of oceanic crustal thickness and geochemistry. Earth Planet Sci Lett 121:435–449
Brune J, Singh D (1986) Continent-like crustal thickness beneath the Bay of Bengal sediments. Bull Seismol Soc Am 76(1):191–203
Carlson RL, Raskin GS (1984) Density of the ocean crust. Nature 311:555–558
Carmichael R (1989) Practical Handbook of Physical Properties of Rocks and Minerals CRC Press, Faccenda M, Bressan G, Burlini L (2007) Seismic properties of the upper crust in the central Friuli area (northeastern Italy) based on petrophysical data. Tectonophysics 445:210–226
Chakraborty K, Agarwal B (1992) Mapping of crustal discontinuities by wavelength filtering of the gravity FIELD1. Geophys Prospect 40(7):801–822
Chand S, Radhakrishna M, Subrahmanyam C (2001) India and East Antarctica conjugate margins: gravity and isostasy. Earth Planet Sci Lett 185:225–236
Chand S, Subrahmanyam C (2001) Gravity and isostasy along a sheared margin—Cauvery basin, Eastern Continental Margin of India. Geophys Res Lett 28:2273–2276
Chand S, Subrahmanyam C (2003) Rifting between India and Madagascar—mechanism and isostasy. Earth Planetary Science Letters 210:317–332
Charvis P, Laesanpura A, Gallart J, Hirn A, Lépine JC, de Voogd B, Minshull TA, Hello Y, Pontoise B (1999) Spatial distribution of hotspot material added to the lithosphere under La Reunion, from wide-angle seismic data. J Geophys Res 104(B2):2875–2893
Chen W, Tenzer R, Gu X (2014) Sediment stripping correction to marine gravity data. Mar Geod 37(4):419–439
Chen W, Tenzer R (2015) Harmonic coefficients of the Earth’s Spectral Crustal Model 180 - ESCM180. Earth Sci Inf 8(1):147–159
Chen W, Tenzer R (2017a) Moho modelling in spatial domain: a case study under Tibet. Advances in Space Research 59(12): 2855–2869
Chen W, Tenzer R (2017b) Moho modelling using FFT technique. Pure Appl Geophys 174(4):1743–1757
Chen W, Tenzer R (2020) Reformulation of Parker-Oldenburg’s method for Earth’s spherical approximation. Geophys J Int 222(2):1046–1073
Chen Y (1992) Oceanic crustal thickness versus spreading rate. Geophys Res Lett 19:753–756
Christensen NI, Mooney WD (1995) Seismic velocity structure and composition of the continental crust: A global view. Journal of Geophysical Research: Solid Earth 100(B6):9761–9788
Coffin MF, Pringle MS, Duncan RA, Gladczenko TP, Storey M, Muller RD, Gahagan LA (2002) Kerguelen hotspot magma output since 130 Ma. J Petrol 43:1121–1139
Cogley JG (1984) Continental margins and the extent and number of the continents. Rev Geophys 22:101–122
Corchete V (2017) Three-dimensional imaging of the S-velocity structure for the crust and the upper mantle beneath the Arabian Sea from Rayleigh wave analysis. Int J Earth Sci 106:1123–1131
Curray J, Emmel F, Moore D, Raitt R (1982) Structure, tectonics, and geological history of the northeastern Indian Ocean. In The ocean basins and margins :399–450
Cutnell JD, Kenneth WJ (1995) Physics, 3rd edn. Wiley, New York
Debayle E, Lévêque J-J, Cara M (2001) Seismic evidence for a deeply rooted low-velocity anomaly in the upper mantle beneath the northeastern Afro/Arabian continent. Earth Planet Sci Lett 193:423–436
Divins DL (2003) Total sediment thickness of the world’s oceans and marginal seas, NOAA Natl Geophys Data Cent, Boulder, Colorado
Divins DL, Rabinowitz PD (1990) Thickness of sedimentary cover for the South Atlantic, in International Geological-Geophysical Atlas of the Atlantic Ocean, edited by GB Udintsev GB, pp 126–127, Intergovernmental Oceanographic Commission, Moscow
Dofal A, Fontaine F, Michon L, Barruol G, Hrvoje T (2018) Crustal structure variation across the southwestern Indian Ocean from receiver functions determined at Ocean-Bottom Seismometers. in Proceedings of the AGU Fall Meeting, 2018AGUFM.T43G0497B, AGU
Dreiling J, Tilmann F, Yuan X, Haberland C, Seneviratne SWM (2020) Crustal structure of Sri Lanka derived from joint inversion of surface wave dispersion and receiver functions using a Bayesian approach. Journal of Geophysical Research: Solid Earth. doi: https://doi.org/10.1029/2019JB018688
Drinkwater M, Floberghagen R, Haagmass R, Muzi D, Papescu A (2003) GOCE: ESA’s first Earth explorer core mission. Space Sci Rev 00:1–14
Eckhardt DH (1983) The gains of small circular, square and rectangular filters for surface waves on a sphere. Bull Geod 57:394–409
Eshagh M (2016) A theoretical discussion on Vening Meinesz-Moritz inverse problem of isostasy. Geophys J Int 207:1420–1431
Eshagh M, Hussain M, Tenzer R, Romeshkani M (2016) Moho density contrast in central Eurasia from GOCE gravity gradients. Remote Sensing 8(418):1–18
Eshagh M (2017) On the approximations in formulation of the Vening Meinesz-Moritz inverse problem of isostasy. Geophys J Int 210:500–508
Floberghagen R, Fehringer M, Lamarre D, Muzi D, Frommknecht B, Steiger C, Piñeiro J, Costa A (2011) Mission design, operation and exploitation of the Gravity field and steady-state Ocean Circulation Explorer mission. J Geodesy 85(11):749–758
Fontaine FR, Barruol G, Tkalčić H, Wölbern I, Rümpker G, Bodin T, Haugmard M (2015) Crustal and uppermost mantle structure variation beneath La Réunion hotspot track. Geophys J Int 203:107–126
Forsyth SW, Ehrenbarda RL, Chapin S (1987) Anomalous upper mantle beneath the Australian-Antarctic discordance. Earth Planet Sci Lett 84:471–478
Fourno JP, Roussel J (1994) Imaging of the Moho depth in Madagascar through the inversion of gravity data: geodynamic implications. Terra Nova 6:512–519
Förste C, Bruinsma SL, Abrikosov O, Lemoine JM, Marty JC, Flechtner F, Balmino G, Barthelmes F, Biancale R (2014) EIGEN-6C4-The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Services Tapley BD, Bettadpur S, Watkins M
Francis TJG, Shor GG (1966) Seismic refraction measurements in the northwest Indian ocean. J Geophys Res 71:427–449
French SW, Romanowicz B (2015) Broad plumes rooted at the base of the Earth’s mantle beneath major hotspots. Nature 525:95–99
Furumoto AS, Wiebenga WA, Webb JP, Sutton GH (1973) crustal structure of the Hawaiian archipelago, northern Melanesia, and the central pacific basin by seismic refraction methods. Tectonophysics 20:153–164
Gaedicke C, Schlüter H-U, Roeser HA, Prexl A, Schreckenberger B, Meyer H, Reichert C, Clift P, Amjad S (2002) Origin of the northern Indus Fan and Murray Ridge, Northern Arabian Sea: interpretation from seismic and magnetic imaging. Tectonophysics 355:127–143
Ghosh A, Thyagarajulu G, Steinberger B (2017) The importance of upper mantle heterogeneity in generating the Indian Ocean Geoid Low. Geophys Res Lett 44(19):9707–9715
Gladkikh V, Tenzer R (2011) A mathematical model of the global ocean saltwater density distribution. Pure Appl Geophys 169(1–2):249–257
Gomez-Oritz D, Agarwal BNP (2005) 3DINVER.M: a MATLAB program to invert the gravity anomaly over a 3D horizontal density interface by Parker Oldenburg’s algorithm. Geosci 31:13–520
Gómez-Ortiz D, Agarwal BNP, Tejero R, Ruiz J (2011) Crustal structure from gravity signatures in the Iberian Peninsula. Geolog Soc Amer Bull 123(7–8):1247–1257
Grevemeyer I, Flueh ER, Reichert C, Bialas J, Kläschen D, Kopp C (2001) Crustal architecture and deep structure of the Ninetyeast Ridge hotspot trail from active-source ocean bottom seismology. Geophys J Int 144(2):414–431
Gu X, Tenzer R, Gladkikh V (2014) Empirical models of the ocean-sediment and marine sediment-bedrock density contrasts. Geoscie J 18(4):439–447
Gupta S, Mishra S, Rai SS (2010) Magmatic underplating of crust beneath the Laccadive Island. NW Indian Ocean Geophys J Int 183(2):536–542
Hammond JOS, Kendall JM, Collier JS, Rümpker G (2013) The extent of continental crust beneath the Seychelles. Earth Planet Sci Lett 381:166–176
Hartmann J, Moosdorf N (2012) The new global lithological map database GLiM: A representation of rock properties at the Earth surface, Geochemistry, Geophysics, Geosystems, vol. 13, no. 12
Hayes DE, LaBrecque JL (1991) Sediment isopachs: Circum-Antarctic to 30S. In: Marine Geological and Geophysical Atlas of the Circum-Antarctic to 30S, edited by Hayes DE. Antarc Res Ser 54: 29–35
Hayford JF (1909) Geodesy: The figure of the earth and isostasy from measurements in the United States (No 82), US Government Printing Office
Hayford J, Bowie W (1912) Geodesy: Effect of topography and isostatic compensation upon the intensity of gravity special publication No. 10, U.S. Coast and Geodetic Survey
Jin Y, McNutt MK, Zhu Y (1994) Evidence from gravity and topography data for folding of Tibet. Nature 371(6499):669–674
Hazarika N (2008) Ph D thesis, Tezpur University, Assam, India
Heiskanen WH, Moritz H (1967) Physical geodesy. Freeman WH and Co, San Francisco
Heiskanen WA, Vening Meinesz FA (1958) The Earth and its gravity field. McGraw-Hill Book Company, Inc
Hinze WJ (2003) Bouguer reduction density, why 2.67? Geophys 68(5): 1559–1560
Hirt C, Rexer M (2015) Earth 2014: 1 arc-min shape, topography, bedrock and ice-sheet models - available as gridded data and degree-10,800 spherical harmonics. Int J Appl Earth Obs Geoinf 39:103–112
Ihnen SM, Whitcomb JH (1983) The Indian Ocean gravity low: Evidence for an isostatically uncompensated depression in the upper mantle. Geophys Res Lett 10:421–423
Jackson J, Haines J, Holt W (1995) The accommodation of Arabia-Eurasia plate convergence in Iran. J Geophys Res 15:205–15219
Kahle H, Naini BR, Talwani M, Eldholm O (1981) Marine geophysical study of the Comorin ridge, north central Indian basin. J Geophys Res 86:3807–3814
Kiamehr R, Gomes-Ortiz D (2009) A new 3D Moho depth model for Iran based on the terrestrial gravity data and EGM2008 model. EGU General Assembly, 11, EGU2009–321–1, Vienna, Austria (Abstract)
Knapmeyer-Endrun B, Krüger F, Group TPW (2014) Moho depth across the Trans-European Suture Zone from P-and S-receiver functions. Geophys J Int 197(2):1048–1075
Kornfeld RP, Arnold BW, Gross MA, Dahya NT, Klipstein WM, Gath PF, Bettadpur S (2019) GRACE-FO: The gravity recovery and climate experiment follow-on mission. J Spacecr Rocket 56:3. https://doi.org/10.2514/1.A34326
Kopp H, Klaeschen D, Flueh ER, Bialas J, Reichert C (2002) Crustal structure of the Java margin from seismic wide-angle and multichannel reflection data. J Geophys Res 107: B2ETG 1–1-ETG 1–24
Krishna KS, Neprochnov YP, Gopala Rao D, Grinko BN (2001) Crustal structure and tectonics of the Ninetyeast Ridge from seismic and gravity studies. Tectonics 20(3):416–433
Kumar N, Zeyen H, Singh AP, Singh B (2013) Lithospheric structure of southern Indian shield and adjoining oceans: integrated modelling of topography, gravity, geoid and heat flow data. Geophys J Int 194(1):30–44
Kumar S, Chaubey, AK, Shankar U (2019) Volume and Mass of Sediments and Crystalline Crust Beneath the Arabian Basin, North-West Indian Ocean, American Geophysical Union, Fall Meeting 2019, abstract #T23C-0457
Kunnummal P, Anand SP, Haritha C, Rama RP (2017) Moho depth variations over the Maldive Ridge and adjoining Arabian & Central Indian basin, Western Indian Ocean, from three-dimensional inversion of gravity anomalies. J Asian Earth Sci 156:316–330
Kunnummal P, Anand SP, Haritha C, Rao RP (2018) Moho depth variations over the Maldive Ridge and adjoining Arabian and Central Indian Basins, Western Indian Ocean, from three-dimensional inversion of gravity anomalies. J Asian Earth Sci 156:316–330
Kunnummal P, Anand SP (2019) Qualitative appraisal of high-resolution satellite derived free air gravity anomalies over the Maldive Ridge and adjoining ocean basins, western Indian Ocean. J Asian Earth Sci 169:199–209
Kusznir NJ, Alvey A (2010) Alpha Ridge: Oceanic or Continental Crust? Constraints from Crustal Thickness Mapping using Gravity Inversion. American Geophysical Union, Fall Meeting 2010, abstract id. T31A-2149
Laske G, Masters G, Ma Z, Pasyanos ME (2013) Update on CRUST1.0 - A 1-degree global model of Earth’s crust. Geophys Res Abstr 15, p 2658
Leahy G, Collins JA, Wolfe CJ, Laske G, Solomon SC (2010) Underplating of the Hawaiian Swell: Evidence from teleseismic receiver functions. Geophys J Int 183:313–329
Lefort JP, Agarwal BNP (2000) Gravity and geomorphological evidence for a large crustal bulge cutting across Brittany (France): a tectonic response to the closure of the Bay of Biscay. Tectonophys 323(3):149–162
Le Pichon X, Talwani M (1969) Regional gravity anomalies in the Indian Ocean. Deep-Sea Res Oceanogr Abstr 16(3):263–266
Ludwig WJ, Houtz RE (1979) Isopach map of the sediments in the Pacific Ocean Basin, color map with text, Am Assoc Pet Geol, Tulsa, OK
Matthias PK, Rabinowitz PD, Dipiazza N (1988) Sediment thickness map of the Indian Ocean, Map 505, Am Assoc Pet Geol, Tulsa, OK
Melluso L, Morra V (2000) Petrogenesis of Late Cenozoic mafic alkaline rocks of the Nosy Be archipelago (northern Madagascar): relationships with the Comorean magmatism: J Volcan Geotherm Res 96: 129–142
Mishra DC, Kumar VV, Rajasekhar RP (2006) Analysis of airborne magnetic and gravity anomalies of peninsular shield, India integrated with seismic and magneto telluric results and gravity anomalies of Madagascar, Sri Lanka and East Antarctica. Gondwana Res 10(1–2):6–17
Mishra DC, Kumar MR (2012) Long and short wavelengths of Indian Ocean geoid and gravity lows: Mid-to-upper mantle sources, rapid drift and seismicity of Kachchh and Shillong plateau, India. J Asian Earth Sci 60:212–224
Mitra S, Priestley K, Gaur VK, Rai SS, Haines J (2006) Variation of Rayleigh wave group velocity dispersion and seismic heterogeneity of the Indian crust and uppermost mantle. Geophys J Int 164:88–98
Mitra S, Priestley K, Acton C, Gaur VK (2009) The Bay of Bengal crust and upper mantle (unpublished)
Montagner J-P, Jobert N (1988) Vectorial tomography—II. Application to the Indian Ocean. Geophys J Int 94:309–344
Mooney WD, Laske G, Masters TG (1998) CRUST 5.1: A global crustal model at 5× 5. J Geophys Res 103(B1): 727–747
Moritz H (1990) The figure of the Earth. Wichmann, H, Karlsruhe
Mukherjee P, Borah K, Bora DK (2020) Nature of crust beneath Sri Lanka using teleseismic receiver function. Journal of Asian Earth Sciences 187
Müller RD, Royer JY, Lawver LA (1993) Revised plate motions relative to the hotspots from combined Atlantic and Indian Ocean hotspot tracks. Geology 21(3):275–278
Müller RD, Gaina C, Clark S (2000) Seafloor spreading around Australia" Billion-year Earth history of Australia and neighbours in Gondwanaland. North Ryde, NSW: Gemoc Press: 18–28
Munschy M, Schlich R (1989) The Rodriguez Triple Junction (Indian Ocean): structure and evolution for the past one million years. Mar Geophys Res 11(1):1–14
Naini BR, Talwani M (1982) Structural Framework and the Evolutionary History of the Continental Margin of Western India. Studies in Continental Margin Geology, JS Watkins, CL Drake
Nair N, Anand SP, Rajaram M (2015) A relook into the crustal architecture of Laxmi Ridge, northeastern Arabian Sea from geopotential data. J Earth Syst Sci 124:613–630
Oldenburg DW (1974) The inversion and interpretation of gravity anomalies. Geophysics 39(4):526–536
Operto S, Charvis P (1996) Deep structure of the southern Kerguelen Plateau (southern Indian Ocean) from ocean bottom seismometer wide-angle seismic data. Journal of Geophysical Research Atmospheres 1012(B11):25077–25104
Parker RL (1972) The rapid calculation of potential anomalies. Geophys J Roy Astronom Soc 31:447–455
Parkin CJ, White RS (2008) Influence of the Iceland mantle plume on oceanic crust generation in the North Atlantic. Geophys J Int 173:168–188
Pasyanos ME, Nyblade AA (2007) A top to bottom lithospheric study of Africa and Arabia. Tectonophysics 444:27–44
Pasyanos ME, Masters TG, Laske G, Ma Z (2014) LITHO1.0: An updated crust and lithospheric model of the Earth. J Geophys Res 119(3): 2153–2173
Pathak A, Kumar MR, Sarkar D (2006) Seismic structure of Sri Lanka using receiver function analysis: A comparison with other high-grade Gondwana terrains. Gondwana Res 10(1):198–202
Paul JD, Eakin CM (2017) Mantle upwelling beneath Madagascar: evidence from receiver function analysis and shear wave splitting. J Seismolog 21:1–12
Phillips L (1962) A technique for the numerical solution of certain integral equations of the first kind. J Assoc Comput Mach 9(1):84–97
Prasanna W, Chen HMI, İz HB (2013) High resolution local Moho determination using gravity inversion: A case study in Sri Lanka. J Asian Earth Sci 74:62–70
Pratt JH (1855) On the attraction of the Himalaya Mountains, and of the elevated regions beyond them, upon the plumb-line in India. Phil Trans Roy Soc London 145:53–100
Radhakrishna MR, Verma RK, Purushotham AK (2002) Lithospheric structure below the eastern Arabian Sea and adjoining west coast of India based on Integrated analysis of gravity and seismic data. Mar Geophys Res 23:25–42
Rai A, Gaur VK, Rai SS, Priestley K (2009) Seismic signatures of the Pan-African orogeny: Implications for southern Indian high-grade terranes. Geophys J Int 176(2):518–528
Rajaomazava F (1992) Etude de la subsidence du bassin sédimentaire de Morondava (Madagascar) dans le cadre de l’évolution géodynamique de la marge Est-Africaine. PhD thesis, Univ. Montpellier, France
Rakotondrainibe (1977) Contribution à l'étude de la séismicité de Madagascar. PhD Thesis, Univ. Antananarivo, Madagascar
Rakotondraompiana SA, Albouy Y, Piqué A (1999) Lithospheric model of the Madagascar island (western Indian Ocean): a new interpretation of the gravity data. J Afr Earth Sci 28:961–973
Rambolamanana G, Suhadolc P, Panza GF (1997) Simultaneous inversion of hypocentral parameters and structure velocity of the central region of Madagascar as a premise for the mitigation of seismic hazard in Antananarivo. Pure Appl Geophys 149:707–730
Rathnayake S, Tenzer R (2019) Optimum choice of parameters and numerical schemes for a regional gravimetric Moho recovery. Geodesy and Geodynamics 10(6):417–429
Rathnayake S, Tenzer R, Eshagh M, Pitoňák M (2019) Gravity maps of the lithospheric structure beneath the Indian Ocean. Surveys in Geophysics; doi: https://doi.org/10.1007/s10712-019-09564-6
Reid I, Jackson HR (1981) Oceanic spreading rate and crustal thickness. Mar Geophys Res 5:165–172
Reigber C, Bock R, Forste C, Grunwaldt L, Jakowski N, Lühr H, Schwintzer P, Tilgner C (1996) CHAMP phase B executive summary, GFZ Potsdam, Germany, STR96/13
Reigber C, Lühr H, Schwintzer P (2002) CHAMP mission status. Adv Space Res 30:129–134
Reigber C, Schwintzer P, Lühr H (1999) The CHAMP geopotential mission. Bollettino Di Geofisica Teorica e Applicata 40:285–289
Reiss MC, Rümpker G, Tilmann F, Yuan X, Giese J, Rindraharisaona EJ (2016) Seismic anisotropy of the lithosphere and asthenosphere beneath southern Madagascar from teleseismic shear wave splitting analysis and waveform modeling. J Geophys Res. https://doi.org/10.1002/2016JB013020
Reguzzoni M, Sampietro D (2014) GEMMA: An Earth crustal model based on GOCE satellite data. Int J Appl Earth Obs Geoinf 35:31–43
Reiss A, Thomas C, Driel J, Heyn B (2017) A hot midmantle anomaly in the area of the Indian Ocean geoid low. Geophys Res Lett 44:6702–6711
Rindraharisaona EJ, Tilmann F, Yuan X, Rümper G, Giese J, Rambolamanana G, Barruol G (2017) Crustal structure of southern Madagascar from receiver functions and ambient noise correlation: implications for crustal evolution. J Geophys Res 122(2):1179–1197
Royer JY, Sandwell DT (1989) Evolution of the eastern Indian Ocean since Late Cretaceous: constraints from Geosat altimetry. J Geophys Res 94:13755–13782
Sampietro D, Capponi M (2019) Practical tips for 3D regional gravity inversion. Geosciences 9(8):351
Singh DD (1988) Quasicontinental-oceanic structure beneath the Arabian Fan sediments from the observed surface wave dispersion studies. Bull Seismol Soc Am 78:1510–1521
Singh DD (1990) Q-structure beneath the north and central Indian Ocean from the inversion of observed Love and Rayleigh wave attenuation data. Phys Earth Planet Inter 59:243–258
Singh DD (1999) Surface wave tomography studies beneath the Indian subcontinent. J Geodyn 28:291–301
Singh SC (2011) Crustal reflectivity (oceanic) and magma Chamber. Encyclopedia of Solid Earth Geophysics. Springer, Netherlands, pp 78–89
Singh SC, Carton H, Chauhan AS, Androvandi S, Davaille A, Dyment J, Cannat M, Hananto ND (2011) Extremely thin crust in the Indian Ocean possibly resulting from Plume - Ridge Interaction. Geophys J Int 184(1):29–42
Singh M, Kaviani A, Rümpker G (2016) The crustal structure beneath Mauritius from teleseismic P receiver functions: Oceanic or continental?: The Crustal Structure Beneath Mauritius Geophysical research letters 43 (18): 9636–9643
Sinha MC, Louden KE, Parsons BB (1981) The crustal structure of the Madagascar Ridge. Geophys J Roy Astron Soc 66(1981):351–377
Sheng M, Shaw C, Vaníček P, Kingdon R, Santos M, Foroughi I (2019) Formulation and validation of a global laterally varying topographical density model. Tectonophys 762:45–60
Shin YH, Choi KS, Xu H (2006) Three-dimensional forward and inverse models for gravity fields based on the Fast Fourier Transform. Comput Geosci 32(6):727–738
Shin YH, Xu H, Braitenberg C, Fang J, Wang Y (2007) Moho undulations beneath Tibet from GRACE integrated gravity data. Geophys J Int 170:971–985
Sjöberg LE (2009) Solving Vening Meinesz-Moritz inverse problem in isostasy. Geophys J Int 179(3):1527–1536
Suo Y, Li S, Li X, Guo L, Wang Y (2016) Crustal thickness anomalies in the Indian Ocean inferred from gravity analysis. Geol J 51:634–643
Sreejith KM, Radhakrishna M, Krishna KS, Majumdar TJ (2011) Development of the negative gravity anomaly of the 85°E Ridge, northeastern Indian Ocean - A process-oriented modelling approach. Journal of Earth System Science. Indian Academy of Sciences 120(4): 605–616
Sreejith KM, Rajesh S, Majumdar TJ, Rao GS, Radhakrishna M, Krishna KS, Rajawat AS (2013) High-resolution residual geoid and gravity anomaly data of the northern Indian Ocean – an input to geological understanding. J Asian Earth Sci 62:616–626
Sreejith KM, Unnikrishnan P, Radhakrishna M (2019) Isostasy and crustal structure of the Chagos-Laccadive Ridge, Western Indian Ocean: Geodynamic implications. J Earth Syst Sci: 128–157
Straume EO, Gaina C, Medvedev S, Hochmuth K, Gohl K, Whittaker JM, Abdul Fattah R, Doornenbal JC, Hopper JR (2019) GlobSed: Updated total sediment thickness in the world’s oceans. Geochem Geophys Geosyst 20:1756–1772
Szwillus W, Afonso JC, Ebbing J, Mooney WD (2019) Global crustal thickness and velocity structure from geostatistical analysis of seismic data. J Geophys Res -Solid Earth 124:1626–1652
Tapley BD, Bettadpur S, Watkins M, Reigber C (2004) The gravity recovery and climate experiment: Mission overview and early results. Geophys Res Lett 31(9):L09607
Tedla GE, Meijde M, Meer NAA, FD, (2011) A crustal thickness map of Africa derived from a global gravity field model using Euler deconvolution. Geophys J Int 187:1–9
Tenzer R, Hamayun VP (2008) Global map of the gravity anomaly corrected for complete effects of the topography, and of density contrasts of global ocean, ice, and sediments. Contributions to Geophysics and Geodesy 38(4):357–370
Tenzer R, Hamayun, Vajda P (2009a) Global maps of the CRUST2.0 components stripped gravity disturbances. J Geophys Res (Solid Earth), 114, B05408
Tenzer R, Vajda P, Hamayun, (2009) Global atmospheric corrections to the gravity field quantities. Contributions to Geophysics and Geodesy 39(3):221–236
Tenzer R, Hamayun, Vajda P (2009c) A global correlation of the step-wise consolidated crust-stripped gravity field quantities with the topography, bathymetry, and the CRUST 2.0 Moho boundary. Contributions to Geophysics and Geodesy 39(2): 133–147
Tenzer R, Abdalla A, Vajda P, Hamayun, (2010) The spherical harmonic representation of the gravitational field quantities generated by the ice density contrast. Contributions to Geophysics and Geodesy 40(3):207–223
Tenzer R, Novák P, Gladkikh V (2011) On the accuracy of the bathymetry-generated gravitational field quantities for a depth-dependent seawater density distribution. Stud Geophys Geodaet 55(4):609–626
Tenzer R, Novák P, Vajda P, Gladkikh V, Hamayun, (2012a) Spectral harmonic analysis and synthesis of Earth’s crust gravity field. Comput Geoscie 16(1):193–207
Tenzer R, Gladkikh V, Vajda P, Novák P (2012b) Spatial and spectral analysis of refined gravity data for modelling the crust-mantle interface and mantle-lithosphere structure. Surv Geophys 33(5):817–839
Tenzer R, Novák P, Gladkikh V (2012c) The bathymetric stripping corrections to gravity field quantities for a depth-dependent model of the seawater density. Mar Geod 35:198–220
Tenzer R, Novák P, Hamayun VP (2012d) Spectral expressions for modelling the gravitational field of the Earth’s crust density structure. Stud Geophys Geod 56(1):141–152
Tenzer R, Bagherbandi M, Gladkikh V (2012e) Signature of the upper mantle density structure in the refined gravity data. Comput Geoscie 16(4):975–986
Tenzer R, Hamayun, Novák P, Gladkikh V, Vajda P (2012e) Global crust-mantle density contrast estimated from EGM2008, DTM2008, CRUST2.0, and ICE-5G. Pure Appl Geophys 169(9): 1663–1678
Tenzer R, Chen W (2014a) Regional gravity inversion of crustal thickness beneath the Tibetan plateau. Earth Sci Inf 7:265–276
Tenzer R, Chen W (2014b) Expressions for the global gravimetric Moho modeling in spectral domain. Pure Appl Geophys 171(8):1877–1896
Tenzer R, Gladkikh V (2014) Assessment of density variations of marine sediments with ocean and sediment depths. Sci World J 823296:9
Tenzer R, Chen W, Tsoulis D, Bagherbandi M, Sjöberg LE, Novák P, Jin S (2015a) Analysis of the refined CRUST1.0 crustal model and its gravity field. Surv Geophys 36(1): 139–165
Tenzer R, Chen W, Jin S (2015b) Effect of the upper mantle density structure on the Moho geometry. Pure Appl Geophys 172(6):1563–1583
Tenzer R, Foroughi I, Pitoňák M, Šprlák M (2017) Effect of the Earth’s inner structure on the gravity in definitions of height systems. Geophys J Int 209(1):297–316
Tenzer R, Chen W (2019) Mantle and sub-lithosphere mantle gravity maps from the LITHO1.0 global lithospheric model. Earth Sci Rev 194:38–56
Tikhonov AN (1963) Solution of incorrectly formulated problems and the regularization method. Soviet Math Dokl 5:1035–1038
Tikhonov AN, Arsenin VI (1977) Solutions of Ill-Posed Problems 14. Winston, Washington, DC
Torsvik TH, Amundsen H, Hartz EH, Corfu F, Kusznir N, Gaina C, Doubrovine PV, Steinberger B, Ashwal LD, Jamtveit B (2013) A Precambrian microcontinent in the Indian Ocean. Nat Geoscie. https://doi.org/10.1038/NGEO1736
Tugume F, Nyblade A, Julià J, Meijde M (2013) Precambrian crustal structure in Africa and Arabia: evidence lacking for secular variation. Tectonophys 609:250–266
Turcotte D, Schubert G (2014) Geodynamics, 3rd edn. Cambridge University Press
Udinstev GB (2003) International Geological-Geophysical Atlas of the Pacific Ocean, p 192, Intergovernmental Oceanographic Commission, Moscow-Saint Petersburg
Vening Meinesz FA (1931) Une nouvelle me´thode pour la re´duction isostatique re´gionale de l’intensite´ de la pesanteur. Bull Geod 29:33–51
Vernant P, Nilforoushan F, Hatzfeld D, Abassi MR, Vigny C, Masson F, Nankali H, Martinod J, Ashtiani M, Bayer R, Tavakoli F, Chéry J (2004) Present-day crustal deformation and plate kinematics in the Middle East constrained by GPS measurements in Iran and northern Oman. Geophys J Int 157:381–398
Walford HL, White NJ, Sydow JC (2005) Solid sediment load history of the Zambezi Delta. Earth Planet Sci Lett 238:49–63
Watts AB, Ten Brink US, Buhl P, Brocher TM (1985) A multichannel seismic study of lithospheric flexure across the Hawaiian-Emperor seamount chain. Nature 315(6015):105–111
West TR, Shakoor A (2018) Geology applied to engineering. Second Edition, Waveland Press, Inc, ISBN 13: 978–1–4786–3500–0, p 575
White RS, McKenzie D, O’Nions RK (1992) Oceanic crustal thickness from seismic measurements and rare Earth element inversions. J Geophys Res 97:19683–19715
Wölbern I, Jacob AWB, Blake TA, Kind R, Li X, Yuan X, Duennebier F, Weber M (2006) Deep origin of the Hawaiian tilted plume conduit derived from receiver functions. Geophys J Int 166:767–781
Wölbern I, Rümpker G (2016) Crustal thickness beneath Central and East Java (Indonesia) inferred from P receiver functions. J Asian Earth Sci 115:69–79
Ye Z, Tenzer R, Liu L (2017) Comparison of spectral and spatial methods for a Moho recovery from gravity and vertical gravity-gradient data. Stud Geophys Geod 61(3):469–496
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Direct Gravity Inversion Method—Functional Relation Between the Moho Depth and Gravity Data
The gravitational contribution generated by a Moho geometry can be expressed as follows (Tenzer and Chen 2014a; 2014b):
where the Moho depths \(D_{M}\) are measured relative to the geoid surface and \({\text{D}}_{{0}}\) is the mean Moho depth.
The spectral representation of the radial derivative of the reciprocal spatial distance \(\partial \,l^{ - 1} /\partial \,r\) for the external convergence domain \(r \ge r^{^{\prime}}\) reads (e.g., Heiskanen and Moritz 1967)
Substitution from Eq. (A.2) to Eq. (A.1) yields
Defining the radial integral on the right-hand side of Eq. (A.3) as
and combing Eqs. (A.4) and (A.3), we arrive at
The expression in Eq. (A.5) is a nonlinear Fredholm integral equation of the first kind (e.g., Sjöberg 2009). Its linearization is done by applying a Taylor series with respect to a mean Moho depth \({\text{D}}_{{0}}\), while disregarding the higher than first-order terms. We then write
It can readily be shown that \(K\left( {r,t,{\text{D}}_{{0}} } \right) = 0\). Hence, after inserting from Eq. (A.6) back to Eq. (A.5), we get
where \(dD = D_{M} - {\text{D}}_{{0}}\).
We further define
Denoting \(\tau = \left( {{\text{R}} - {\text{D}}_{{0}} } \right)/r\), the spectral representation of the integral kernel \({\text{T}}(r,t,{\text{D}}_{{0}} )\) is rewritten as
To find the spatial form of \({\text{T}}\left( {t,\tau } \right)\), we first separate its spectral representation into zero- and higher-order terms (with respect to \({\text{P}}_{{\text{n}}}\)) as follows:
and further rearrange Eq. (A.10) into the following form
with
and
where
Combining Eqs. (A.9)–(A.14), the closed form of \({\text{T}}\left( {t,\tau } \right)\) is found to be
The functional relation between the (complete) Bouguer gravity disturbances \(\delta g^{B}\) and the unknown Moho depth corrections \(dD^{^{\prime}} = D_{M} - {\text{D}}_{{0}}\) in Eq. (A.7) is defined by means of the integral convolution of \({\text{T}}\left( {t,\tau } \right)\) and \(\Delta \rho^{{\text{c/m}}}\). The discretization of the integral in Eq. (A.7) is done by means of dividing the entire surface integration domain into a finite number of surface elements. The most convenient way is to apply discretization on a regular grid of geographical coordinates. Introducing the surface elements \(\Delta \Omega_{{\text{j}}}^{^{\prime}} = \;\;\cos \varphi_{{\text{j}}}^{^{\prime}} \,\Delta \varphi_{{\text{j}}}^{^{\prime}} \;\Delta \lambda_{{\text{j}}}^{^{\prime}}\) (where \(\Delta \varphi^{\prime}\) and \(\Delta \lambda^{\prime}\) are discretization steps in latitude and longitude, respectively), the integral equation in Eq. (A.7) becomes
where \(I\) is the total number of input gravity data and \(J\) is the total number of discretization elements. In our discrete model, we assume that \(I = J\). When \(I > J\), the Moho depths can be determined by applying a least-squares analysis. The Moho density contrast values \(\left\{ {\,\Delta {\uprho }_{j}^{{\text{c/m}}} :\;j = 1,\,2,\,...,\,J} \right\}\;\) are considered within each of the discretized surface elements \(\left\{ {\,\Delta \Omega^{\prime}_{{\text{j}}} :\;j = 1,\,2,\,...,\,J} \right\}^{{}}\).
Since the surface integral in Eq. (A.16) does not have a closed analytical form in terms of geographical coordinates, it is solved (for each surface element) numerically. Applying the simplest numerical scheme, Eq. (A.16) becomes
where a surface integral for each individual surface element is evaluated from
For \(i \ne j\), the kernel \({\text{T}}_{{\text{i,j}}}\) in Eq. (A.18) is computed as
For \(i = j\), \(t_{i,j} = 1\), after some algebra, the kernel \({\text{T}}_{{\text{i,i}}}\) simplifies to
The integral kernel \({\text{T}}\) has a singularity for \(\tau \to 1 \wedge t \to 1\). However, this singularity does not occur in the numerical solution because a minimum crustal thickness is everywhere at least a few kilometers below the geoid surface.
Appendix B: Generalized Parker–Oldenburg Method—Functional Relation Between the Moho Depth and Gravity Data
The disturbing potential generated by a Moho geometry can be expressed as follows (Chen and Tenzer, 2017b):
The spectral representation of a reciprocal spatial distance \(l^{ - 1}\) for the external convergence domain \(r \ge r^{^{\prime}}\) reads (e.g., Heiskanen and Moritz 1967),
Using the addition theorem, the Legendre polynomial \({\text{P}}_{{\text{n}}}\) can be expressed as follows:
Combining Eqs. (B.1)–(B.3), we arrive at
The disturbing potential coefficients \({\text{T}}_{{{\text{nm}}}}^{B}\) (corrected for gravitational contributions of topography and crustal density heterogeneities) in Eq. (B.4) are given by
where \({\text{M}} = \;\frac{4}{3}{{\uppi \overline{\uprho }}}^{{{\text{Earth}}}} {\text{R}}^{3}\) is the Earth’s total mass.
The radial integral in Eq. (B.5) is formally divided into two parts (e.g., Sjöberg 2009)
The radial integral kernels of two constituents on the right-hand side of Eq. (B.6) read
where \(\tau_{0} = - {\text{D}}_{{0}} /{\text{R}}\) and \(\tau = - D_{M} \left( {\Omega^{^{\prime}} } \right)/{\text{R}}.\)
Inserting from Eqs. (B.6) and (B.7) back to Eq. (B.5), we arrive at
Now, we define
Moreover, we introduce the following relation:
The expression in Eq. (B.10) is further rewritten as
Since both sides of Eq. (B.11) comprise the term \((\Delta \rho \tau )_{nm}\), the solution is carried out iteratively.
Rights and permissions
About this article
Cite this article
Rathnayake, S., Tenzer, R., Chen, W. et al. Comparison of Different Methods for a Moho Modeling Under Oceans and Marginal Seas: A Case Study for the Indian Ocean. Surv Geophys 42, 839–897 (2021). https://doi.org/10.1007/s10712-021-09648-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-021-09648-2