Skip to main content
SpringerLink
Log in

On the method of reflections

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

This paper aims at reviewing and analysing the method of reflections, which is an iterative procedure designed for solving linear boundary value problems set in multiply connected domains. Being based on a decomposition of the domain boundary, this method is particularly well-suited to numerical solvers relying on boundary integral representation. For both the sequential and parallel forms of the method appearing in the literature, we interpret the procedure in terms of projection operators. Using a Hilbert space setting and orthogonality, we prove the unconditional convergence of the sequential form and propose a modification of the parallel one that makes it unconditionally converging. Several examples of boundary value problems that enter such a framework are given, an alternative proof of convergence is provided in a case which does not. A few numerical tests conclude the study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. One can for instance check the Ref. [10], in which different solution methods are used depending on the nature of the considered one-object problem.

  2. One may consider the first kind of boundary condition for the Laplace equation to be Dirichlet’s, the second, Neumann’s, and the third, Robin’s.

  3. The algorithm presented here is a reformulation of the method analysed in [47], as the auxiliary fields do not appear explicitly in the reference.

  4. The version of the method presented in Chapter 6 of [32] differs slightly from the above procedure by focusing on one specific object. The reflections with respect to this object are then computed as in the sequential form of the method, whereas the reflections with respect to the other \(N-1\) objects are computed as in the parallel form.

  5. In the same work, a sufficient condition for convergence, depending on the frequency, the diameters and the areas of the sub-scatterers, as well as the respective distances between the sub-scatterers, is established.

  6. To see this, one can compare the hierarchy of different levels of approximation given in [11], ranging from the Born approximation to the Foldy–Lax model, with the sequence of approximations produced by the method of reflections.

  7. The mapping T is said to be nonexpansive on the normed space H if it is a function from H to itself such that

    $$\begin{aligned} \forall (u,v)\in H^2,\ \Vert Tu-Tv\Vert _H\le \Vert u-v\Vert _H. \end{aligned}$$

  8. The mapping T is said to be asymptotically regular on the normed space H if it is a function from H to itself such that

    $$\begin{aligned} \forall u\in H,\ \lim _{k\rightarrow +\infty }\Vert T^{k+1}u-T^ku\Vert _H=0. \end{aligned}$$

  9. Indeed, one has trivially that \(M\subset {\text {Fix}}T\), while the converse follows from the idempotence and the self-adjointness of the orthogonal projectors.

  10. This result remains valid for the more general sum \(\sum _{j=1}^N\gamma _j\,P_{M_j}\), where the scalars \(\gamma _i\), with i in \(\{1,\dots ,N\}\), are the weights of a convex combination (that is, such that, \(\forall i\in \{1,\dots ,N\}\), \(\gamma _i>0\), and \(\sum _{j=1}^n\gamma _j=1\)).

  11. Some authors say the sequence converges uniformly (see [4]).

  12. According to the definition of Friedrichs [26], if \(M_i\) and \(M_j\) are closed subspaces in a Hilbert space H, the angle between \(M_i\) and \(M_j\) is the angle in \([0,\frac{\pi }{2}]\) whose cosine is defined by

    Another notion is that of the minimal angle between \(M_i\) and \(M_j\), given by Dixmier in [24], which is the angle in \([0,\frac{\pi }{2}]\) whose cosine is defined by

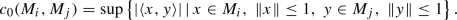
    These two definitions are different if \(M_i\cap M_j\ne \{0\}\), and they both coincide with (different) principal angles (as introduced by Jordan [39]) if \(H=\mathbb {C}^n\).

  13. For \(N=2\), it is known (see [19] for instance) that \(c(M_1,M_2)<1\), where \(c(M_1,M_2)\) denotes the cosine of the angle between the subspaces \(M_1\) and \(M_2\), if and only if \(M_1+M_2\) is closed, if and only if \({M_1}^\bot +{M_2}^\bot \) is closed, if and only if \((M_1\cap (M_1\cap M_2)^\bot )+(M_2\cap (M_1\cap M_2)^\bot )\) is closed. For \(N\ge 3\), a generalization of the Friedrichs angle to several subspaces is introduced in [4] and it is shown in the same paper that the method converges linearly if and only if \(c(M_1,\dots ,M_N)<1\), which is a weaker condition (see Example 4.5 in [4]) than the sufficient one, based on Theorems 2.1 in [21] and 4.1 in [4], that one of the cosines \(c_{ij}=c_0(M_i\cap (\cap _{\ell =1}^N M_\ell )^\bot ,M_j\cap (\cap _{\ell =1}^N M_\ell )^\bot )\) of the Dixmier angles involving two subspaces \(M_i\) and \(M_j\) is strictly less than one.

  14. We recall that the Green function G is such that

    $$\begin{aligned} \forall (x,y)\in \varOmega \times \varOmega ,\ x\ne y,\ G(x,y)=\varPhi (y-x)-\varphi _x(y), \end{aligned}$$

    the function \(\varPhi \) being the fundamental solution of the Laplace equation and \(\varphi _x\) being a corrector function which, for a fixed x in \(\varOmega \), satisfies \(\varDelta \varphi _x=0\) in \(\varOmega \) and \(\varphi _x=\varPhi (\cdot -x)\) on \(\partial \varOmega \).

  15. For instance, for suspensions sedimenting in a uniform gravitational field, one has \(F_{O_i}=m_{O_i}\varvec{G}\), where \(m_{O_i}\) is the mass of the particle adjusted for buoyancy and \(\varvec{G}\) is the gravitational acceleration, and \(\tau _{O_i}=0\).

  16. Integral Equation Solver (http://www.mathworks.com/matlabcentral/fileexchange/34241) by Alexandre Munnier and Bruno Pinçon, MATLAB Central File Exchange. Retrieved February 15, 2016.

  17. This fact can be commonly observed in practice (see [12] for instance) and is theoretically proved for \(N=2\) in [52].

References

  1. Amrouche, C., Girault, V., Giroire, J.: Dirichlet and Neumann exterior problems for the \(n\)-dimensional Laplace operator. An approach in weighted Sobolev spaces. J. Math. Pures Appl. 76(1), 55–81 (1997). https://doi.org/10.1016/S0021-7824(97)89945-X

    Article  MathSciNet  MATH  Google Scholar 

  2. Aronszajn, N.: Theory of reproducing kernels. Trans. Am. Math. Soc. 68(3), 337–404 (1950). https://doi.org/10.1090/S0002-9947-1950-0051437-7

    Article  MathSciNet  MATH  Google Scholar 

  3. Auslender, A.: Optimisation: méthodes numériques. Masson, Paris (1976)

    MATH  Google Scholar 

  4. Badea, C., Grivaux, S., Müller, V.: The rate of convergence in the method of alternating projections. St. Petersb. Math. J. 23(3), 413–434 (2012). https://doi.org/10.1090/S1061-0022-2012-01202-1

    Article  MathSciNet  MATH  Google Scholar 

  5. Balabane, M.: Boundary decomposition for Helmholtz and Maxwell equations 1: disjoint sub-scatterers. Asymptot. Anal. 38(1), 1–10 (2004)

    MathSciNet  MATH  Google Scholar 

  6. Balabane, M., Tirel, V.: Décomposition de domaine pour un calcul hybride de l’équation de Helmholtz. C. R. Acad. Sci. Paris Sér. I Math. 324(33), 281–286 (1997). https://doi.org/10.1016/S0764-4442(99)80361-9

    Article  MathSciNet  MATH  Google Scholar 

  7. Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38(3), 367–426 (1996). https://doi.org/10.1137/S0036144593251710

    Article  MathSciNet  MATH  Google Scholar 

  8. Bauschke, H.H., Deutsch, F., Hundal, H.: Characterizing arbitrarily slow convergence in the method of alternating projections. Int. Trans. Oper. Res. 16(4), 413–425 (2009). https://doi.org/10.1111/j.1475-3995.2008.00682.x

    Article  MathSciNet  MATH  Google Scholar 

  9. Bauschke, H.H., Deutsch, F., Hundal, H., Park, S.H.: Accelerating the convergence of the method of alternating projections. Trans. Am. Math. Soc. 355(9), 3433–3461 (2003). https://doi.org/10.1090/S0002-9947-03-03136-2

    Article  MathSciNet  MATH  Google Scholar 

  10. Boyer, F., Gossiaux, P.B., Jawad, B., Lebastard, V., Porez, M.: Model for a sensor inspired by electric fish. IEEE Trans. Robot. 28(2), 492–505 (2012). https://doi.org/10.1109/TRO.2011.2175764

    Article  Google Scholar 

  11. Cassier, M., Hazard, C.: Multiple scattering of acoustic waves by small sound-soft obstacles in two dimensions: mathematical justification of the Foldy–Lax model. Wave Motion 50(1), 18–28 (2013). https://doi.org/10.1016/j.wavemoti.2012.06.001

    Article  MathSciNet  MATH  Google Scholar 

  12. Censor, Y., Chen, W., Combettes, P.L., Davidi, R., Herman, G.T.: On the effectiveness of projection methods for convex feasibility problems with linear inequality constraints. Comput. Optim. Appl. 51(3), 1065–1088 (2012). https://doi.org/10.1007/s10589-011-9401-7

    Article  MathSciNet  MATH  Google Scholar 

  13. Chen, S.B., Keh, H.J.: Electrophoresis in a dilute dispersion of colloidal spheres. AIChE J. 34(7), 1075–1085 (1988). https://doi.org/10.1002/aic.690340704

    Article  Google Scholar 

  14. Ciaramella, G., Gander, M.J.: Analysis of the parallel Schwarz method for growing chains of fixed-size subdomains: part I. SIAM J. Numer. Anal. 55(3), 1330–1356 (2017). https://doi.org/10.1137/16M1065215

    Article  MathSciNet  MATH  Google Scholar 

  15. Ciaramella, G., Gander, M.J., Halpern, L., Salomon, J.: Methods of reflections: relations with Schwarz methods and classical stationary iterations, scalability and preconditioning. SMAI J. Comput. Math. 5, 161–193 (2019). https://doi.org/10.5802/smai-jcm.46

    Article  MathSciNet  MATH  Google Scholar 

  16. Cimmino, G.: Calcolo approssimato per le soluzioni dei sistemi di equazioni lineari. La Ricerca Scientifica 9, 326–333 (1938)

    MATH  Google Scholar 

  17. Coatléven, J., Joly, P.: Operator factorization for multiple-scattering problems and an application to periodic media. Commun. Comput. Phys. 11(2), 303–318 (2012). https://doi.org/10.4208/cicp.231109.090710s

    Article  MathSciNet  MATH  Google Scholar 

  18. Dautray, R., Lions, J.L.: Mathematical Analysis and Numerical Methods for Science and Technology. Integral Equations and Numerical Methods, vol. 4. Springer, Berlin (2000). https://doi.org/10.1007/978-3-642-61531-3

    Book  MATH  Google Scholar 

  19. Deutsch, F.: Rate of convergence of the method of alternating projections. In: Brosowski, B., Deutsch, F. (eds.) Parametric Optimization and Approximation, International Series of Numerical Mathematics, vol. 72, pp. 96–107. Birkhäuser-Verlag, Basel (1985)

    Chapter  Google Scholar 

  20. Deutsch, F.: The method of alternating orthogonal projections. In: Singh, S.P. (ed.) Approximation Theory, Spline Functions and Applications, NATO ASI Series, vol. 356, pp. 105–121. Springer, Dordrecht (1992). https://doi.org/10.1007/978-94-011-2634-2_5

    Chapter  Google Scholar 

  21. Deutsch, F., Hundal, H.: The rate of convergence for the method of alternating projections. II. J. Math. Anal. Appl. 205(2), 381–405 (1997). https://doi.org/10.1006/jmaa.1997.5202

    Article  MathSciNet  MATH  Google Scholar 

  22. Deutsch, F., Hundal, H.: Slow convergence of sequences of linear operators II: arbitrarily slow convergence. J. Approx. Theory 162(9), 1717–1738 (2010). https://doi.org/10.1016/j.jat.2010.05.002

    Article  MathSciNet  MATH  Google Scholar 

  23. Dhont, J.K.G.: An Introduction to Dynamics of Colloids, Studies in Interface Science, vol. 2. Elsevier, Amsterdam (1996)

    Google Scholar 

  24. Dixmier, J.: Étude sur les variétés et les opérateurs de Julia, avec quelques applications. Bull. Soc. Math. France 77, 11–101 (1949)

    Article  MathSciNet  Google Scholar 

  25. Foldy, L.L.: The multiple scattering of waves. I. General theory of isotropic scattering by randomly distributed scatterers. Phys. Rev. 67(3–4), 107–119 (1945). https://doi.org/10.1103/PhysRev.67.107

    Article  MathSciNet  MATH  Google Scholar 

  26. Friedrichs, K.: On certain inequalities and characteristic value problems for analytic functions and for functions of two variables. Trans. Am. Math. Soc. 41(3), 321–364 (1937). https://doi.org/10.1090/S0002-9947-1937-1501907-0

    Article  MathSciNet  MATH  Google Scholar 

  27. Gander, M.J.: Schwarz methods over the course of time. Electron. Trans. Numer. Anal. 31, 228–255 (2008)

    MathSciNet  MATH  Google Scholar 

  28. Ganesh, M., Hawkins, S.C.: A high-order algorithm for multiple electromagnetic scattering in three dimensions. Numer. Algor. 50(4), 469–510 (2009). https://doi.org/10.1007/s11075-008-9238-z

    Article  MathSciNet  MATH  Google Scholar 

  29. Golusin, G.M.: Auflösung einiger ebenen Grundaufaben der mathematischen Physik im Fall der Laplaceschen Gleichung und mehrfachzusammenhängender Gebiete, die durch Kreise begrenzt sind. Mat. Sb. 41(2), 246–276 (1934)

    MATH  Google Scholar 

  30. Grisvard, P.: Elliptic Problems in Nonsmooth Domains. Pitman, London (1985)

    MATH  Google Scholar 

  31. Halperin, I.: The product of projection operators. Acta Sci. Math. (Szeged) 23(1–2), 96–99 (1962)

    MathSciNet  MATH  Google Scholar 

  32. Happel, J., Brenner, H.: Low Reynolds Number Hydrodynamics with Special Applications to Particulate Media, Mechanics of Fluids and Transport Processes, vol. 1. Martinus Nijhoff publishers, Leiden (1983). https://doi.org/10.1007/978-94-009-8352-6

    Book  Google Scholar 

  33. Höfer, R.: Sedimentation of inertialess particles in Stokes flows. Commun. Math. Phys. 360(1), 55–101 (2018). https://doi.org/10.1007/s00220-018-3131-y

    Article  MathSciNet  MATH  Google Scholar 

  34. Höfer, R.M., Velázquez, J.J.L.: The method of reflections, homogenization and screening for Poisson and Stokes equations in perforated domains. Arch. Rational Mech. Anal. 227(3), 1165–1221 (2018). https://doi.org/10.1007/s00205-017-1182-4

    Article  MathSciNet  MATH  Google Scholar 

  35. Hruslov, E.J.: The method of orthogonal projections and the Dirichlet problem in domains with a fine-grained boundary. Math. USSR-Sb. 17(1), 37–59 (1972). https://doi.org/10.1070/SM1972v017n01ABEH001490

    Article  MathSciNet  Google Scholar 

  36. Ichiki, K., Brady, J.F.: Many-body effects and matrix inversion in low-Reynolds-number hydrodynamics. Phys. Fluids 13(1), 350–353 (2001). https://doi.org/10.1063/1.1331320

    Article  MATH  Google Scholar 

  37. Jabin, P.E., Otto, F.: Identification of the dilute regime in particle sedimentation. Commun. Math. Phys. 250(2), 415–432 (2004). https://doi.org/10.1007/s00220-004-1126-3

    Article  MathSciNet  MATH  Google Scholar 

  38. Jones, R.B.: Hydrodynamic interaction of two permeable spheres I: the method of reflections. Phys. A 92(3–4), 545–556 (1978). https://doi.org/10.1016/0378-4371(78)90150-4

    Article  Google Scholar 

  39. Jordan, C.: Essai sur la géométrie à \(n\) dimensions. Bull. Soc. Math. France 3, 103–174 (1875)

    Article  MathSciNet  Google Scholar 

  40. Kayalar, S., Weinert, H.L.: Error bounds for the method of alternating projections. Math. Control Signals Syst. 1(1), 43–59 (1988). https://doi.org/10.1007/BF02551235

    Article  MathSciNet  MATH  Google Scholar 

  41. Kim, S., Karrila, S.J.: Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann, Oxford (1991)

    Google Scholar 

  42. Kynch, G.J.: The slow motion of two or more spheres through a viscous fluid. J. Fluid Mech. 5(2), 193–208 (1959). https://doi.org/10.1017/S0022112059000155

    Article  MathSciNet  MATH  Google Scholar 

  43. Lax, M.: Multiple scattering of waves. Rev. Mod. Phys. 23(4), 287–310 (1951). https://doi.org/10.1103/RevModPhys.23.287

    Article  MathSciNet  MATH  Google Scholar 

  44. Lax, M.: Multiple scattering of waves. II. The effective field in dense systems. Phys. Rev. 85(4), 621–629 (1952). https://doi.org/10.1103/PhysRev.85.621

    Article  MathSciNet  MATH  Google Scholar 

  45. Li, T.: A class of non-local boundary value problems for partial differential equations and its applications in numerical analysis. J. Comput. Appl. Math. 28, 49–62 (1989). https://doi.org/10.1016/0377-0427(89)90320-8

    Article  MathSciNet  MATH  Google Scholar 

  46. Lions, J.L., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications. Volume I, Grundlehren der mathematischen Wissenschaften, vol. 181. Springer, Berlin (1972). https://doi.org/10.1007/978-3-642-65161-8

    Book  Google Scholar 

  47. Luke, J.H.C.: Convergence of a multiple reflection method for calculating Stokes flow in a suspension. SIAM J. Appl. Math. 49(6), 1635–1651 (1989). https://doi.org/10.1137/0149099

    Article  MathSciNet  MATH  Google Scholar 

  48. Mettot, C., Lauga, E.: Energetics of synchronized states in three-dimensional beating flagella. Phys. Rev. E 84(6), 061905 (2011). https://doi.org/10.1103/PhysRevE.84.061905

    Article  Google Scholar 

  49. von Neumann, J.: On rings of operators. Reduction theory. Ann. Math. (2) 50(2), 401–485 (1949). https://doi.org/10.2307/1969463

    Article  MathSciNet  MATH  Google Scholar 

  50. Niethammer, B., Schubert, R.: A local version of Einstein’s formula for the effective viscosity of suspensions. SIAM J. Math. Anal. 52(3), 2561–2591 (2020). https://doi.org/10.1137/19M1251229

  51. Pierra, G.: Decomposition through formalization in a product space. Math. Program. 28(1), 96–115 (1984). https://doi.org/10.1007/BF02612715

    Article  MathSciNet  MATH  Google Scholar 

  52. Reich, S., Zalas, R.: The optimal error bound for the method of simultaneous projections. J. Approx. Theory 223, 96–107 (2017). https://doi.org/10.1016/j.jat.2017.08.005

    Article  MathSciNet  MATH  Google Scholar 

  53. Schuster, G.T.: A hybrid BIE+Born series modeling scheme: generalized Born series. J. Acoust. Soc. 77(3), 865–879 (1985). https://doi.org/10.1121/1.392055

    Article  MathSciNet  MATH  Google Scholar 

  54. Showalter, R.E.: Hilbert Space Methods for Partial Differential Equations, Monographs and Studies in Mathematics, vol. 1. Pitman, London (1977)

    Google Scholar 

  55. Smirnov, V.I.: A Course of Higher Mathematics. Volume 4, International Series of Monographs in Pure and Applied Mathematics, vol. 61. Pergamon, Oxford (1964). https://doi.org/10.1016/C2013-0-06630-3

    Book  Google Scholar 

  56. Smith, K.T., Solomon, D.C., Wagner, S.L.: Practical and mathematical aspects of the problem of reconstructing objects from radiographs. Bull. Am. Math. Soc. 83(6), 1227–1270 (1977). https://doi.org/10.1090/S0002-9904-1977-14406-6

    Article  MathSciNet  MATH  Google Scholar 

  57. Smoluchowski, M.: Über die Wechselwirkung von Kugeln, die sich in einer zähen Flüssigkeit bewegen. Bull. Int. Acad. Sci. Cracovie, Cl. Sci. Math. Nat., Sér. A Sci. Math. pp. 28–39 (1911)

  58. Traytak, S.D.: Convergence of a reflection method for diffusion-controlled reactions on static sinks. Phys. A Stat. Mech. Appl. 362(2), 240–248 (2006). https://doi.org/10.1016/j.physa.2005.03.061

    Article  Google Scholar 

  59. Vishik, M.I.: The method of orthogonal and direct decomposition in the theory of elliptic differential equations (Russian). Mat. Sb. 25(67), 189–234 (1949)

    Google Scholar 

  60. Wang, H., Liu, J.: On decomposition method for acoustic wave scattering by multiple obstacles. Acta Math. Sci. 33(1), 1–22 (2013). https://doi.org/10.1016/S0252-9602(12)60191-X

    Article  MathSciNet  MATH  Google Scholar 

  61. Weyl, H.: The method of orthogonal projection in potential theory. Duke Math. J. 7(1), 411–444 (1940). https://doi.org/10.1215/S0012-7094-40-00725-6

    Article  MathSciNet  MATH  Google Scholar 

  62. Wilson, H.J.: Stokes flow past three spheres. J. Comput. Phys. 245, 302–316 (2013). https://doi.org/10.1016/j.jcp.2013.03.020

    Article  MathSciNet  MATH  Google Scholar 

  63. Xu, J., Zikatanov, L.: The method of alternating projections and the method of subspace corrections in Hilbert space. J. Am. Math. Soc. 15(3), 573–597 (2002). https://doi.org/10.1090/S0894-0347-02-00398-3

    Article  MathSciNet  MATH  Google Scholar 

  64. Zaremba, S.: Sur un problème toujours possible comprenant, à titre de cas particulier, le problème de Dirichlet et celui de Neumann. J. Math. Pures Appl. 9(6), 127–164 (1927). https://doi.org/10.1090/S0894-0347-02-00398-3

    Article  MATH  Google Scholar 

Download references

Acknowledgements

Philippe Laurent would like to thank Frédéric Boyer for introducing him to the method of reflections. Guillaume Legendre would like to thank Christophe Hazard for pointing him to the relevant paper [5], and Mikhael Balabane himself for an interesting discussion on the topic. Julien Salomon would like to thank Gabriele Ciaramella, Olivier Glass and Alexandre Munnier for helpful discussions. Finally, the authors collectively thank the anonymous reviewers whose comments and suggestions helped improve the manuscript.

Author information

Authors and Affiliations

  1. Institut de Recherche en Communications et Cybernétique de Nantes, CNRS, UMR 6597, École des Mines de Nantes, 4, rue Alfred Kastler, 44307, Nantes, France

    Philippe Laurent

  2. CEREMADE, UMR CNRS 7534, Université Paris-Dauphine, PSL Research University, Place du Maréchal De Lattre De Tassigny, 75775, Paris Cedex 16, France

    Guillaume Legendre

  3. INRIA Paris, ANGE Project-Team, 75589, Paris Cedex 12, France

    Julien Salomon

  4. CNRS, Laboratoire Jacques-Louis Lions, Sorbonne Université, 75005, Paris, France

    Julien Salomon

Authors
  1. Philippe Laurent
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guillaume Legendre
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Julien Salomon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Julien Salomon.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work has been supported by the Agence Nationale de la Recherche (ANR), Projet Blanc Cine-Para ANR-15-CE23-0019-01.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Laurent, P., Legendre, G. & Salomon, J. On the method of reflections. Numer. Math. 148, 449–493 (2021). https://doi.org/10.1007/s00211-021-01207-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-021-01207-6

Mathematics Subject Classification

Search

Navigation