Abstract
In this paper, we have considered a deterministic epidemic model with logistic growth rate of the susceptible population, non-monotone incidence rate, nonlinear treatment function with impact of limited hospital beds and performed control strategies. The existence and stability of equilibria as well as persistence and extinction of the infection have been studied here. We have investigated different types of bifurcations, namely Transcritical bifurcation, Backward bifurcation, Saddle-node bifurcation and Hopf bifurcation, at different equilibrium points under some parametric restrictions. Numerical simulation for each of the above-defined bifurcations shows the complex dynamical phenomenon of the infectious disease. Furthermore, optimal control strategies are performed using Pontryagin’s maximum principle and strategies of controls are studied for two infectious diseases. Lastly using efficiency analysis we have found the effective control strategies for both cases.
Similar content being viewed by others
1 Introduction
The main objective of mathematical epidemiology is to study of the mechanism that obsesses the disease transmission and controls its impact in the population [1, 2]. Mathematical modeling becomes an important tool to investigate the dynamical evolution of infectious disease and effective measures as needed to reduce the influence of the disease [3,4,5]. Using mathematical models, researchers can identify trends of the disease, analyze epidemiological surveys and make general forecasts about the disease. First classical model for smallpox spreading was designed and analyzed by Bernoulli in 1760 [6]. Thereafter, many researchers have used various types of mathematical models to express the dynamical changes in the population due to influence of the disease and to prevent its impact. Among them, in 1927 Kermack and Mckendrick’s compartmental SIR model is a milestone for deterministic process in theory of epidemiology [7].
Population birth rate and disease transmission rate play important role in behavioral change of disease dynamics. Two types of birth rates, namely constant birth rate [8,9,10] and logistic growth rate [11], are used to formulate compartmental model. Constant birth rate is not more realistic for large populated countries. To prevent huge number of spreading infection, logistic type of birth rate is considered in mathematical modeling for limited medical resources, long-lasting disease, disease with high death rate and large number of the population [3, 5]. Various types of disease incidence rates are considered in mathematical modeling to describe the disease spreading. Bilinear disease transmission rate (\(\beta x y\)) is used based on mass action property where \(\beta \) is the rate of disease transmission per contact and x and y represent density of susceptible and infected individual, respectively [12]. For largely populated countries, consideration of bilinear incidence rate is not realistic as rate of disease transmission increases with the increase in susceptible population. So for largely populated countries standard form of incidence is used in the form\(\dfrac{\beta x y}{N}\) where N is total number of population [13, 14]. For standard incidence rate, disease transmission rate does not tend to infinity with number of susceptible increases. In case of bilinear and standard incidence rate, we get simple dynamical behavior of the model system. To get rich dynamics, nonlinear incidence rates are used in mathematical modeling. Yorke and London [15] used the incidence rate in the form \(\beta (1 - c y) x y\) to describe measles outbreak and also Levin and Iwasa [16] considered in the form \(\lambda x^{p} y^{q}\). For concerning inhibition effect of susceptible population and crowding effect of infected population, saturated type of incidence rate was first used by Capasso and Serio [17] in the form \(\dfrac{\beta x y}{1 + \alpha y}\) where \(\beta y\) is the force of infection and \(\dfrac{1}{1 + \alpha y}\) is inhibition effect due to change in behavior of susceptible population and also crowding effect of the infected individuals. At first, disease transmission increases with the increase in infected population, and for huge number of infected individuals it ultimately tends to \(\dfrac{\beta }{\alpha }x\) which indicates for social awareness of susceptible population, disease transmission gradually decreases [18, 19]. Later on for describing disease dynamics of some short-term but highly infectious diseases such as SARS, influenza Xiao and Ruan [20] proposed non-monotone type of incidence rate in the form \(\dfrac{\beta x y}{1 + \alpha y^{2}}\). Here, at the beginning due to lack of knowledge about the infection, the disease spreads among the people in short time. After some days, when the disease is spreading highly among the people, then due to social awareness and other psychological factors people take necessary actions to control the infection, and then, the rate of infection will start to decrease. The above-defined incidence rate increases first with y and reaches the maximum value when \( y=\frac{1}{\sqrt{\alpha }}\) then starts to decrease and tends to zero as \( t\rightarrow \infty \). Further, Ruan and Wang [21], Lu and Ruan [8] studied different types of nonlinear incidence rates, namely \(\dfrac{k x y^{2}}{1 + \alpha y^{2}}\), \(\dfrac{k x y^{2}}{1 + \beta y + \alpha y^{2}}\), respectively, to get more complicated dynamical phenomenon of the disease such as periodic oscillations, multiple peaks of the infection, different types of bifurcations. Generalized type of nonlinear transmission rate \(\dfrac{\beta x y^{p}}{1 + \alpha y^{q}}\) where \( \beta , p, q>\) 0 and \(\alpha \) is suppression effect co-efficient is investigated by Liu [22], Hethcote and Driessche [23] to observe the effect of behavioral changes.
To get recovery from infectious disease, treatment is an important method. Treatment has effective role to prevent and control the spreading of the disease. Several researchers studied different types of treatment functions such as vaccination, quarantine, isolation and medicine. Proper and timely treatment can reduce the effect of the spreading disease. In classical epidemic model, rate of treatment is assumed as proportional to the number of infected individuals. But this type of treatment function is not realistic for large populated countries since treatment is generally based on medical resources such as medicines, doctors, hospital beds, vaccines and isolation places. Every country has a limited capacity in medical resources, and due to this limitation there can be delayed in getting the treatment, so it is very important to adopt a suitable recovery function. Wang and Ruan [24] introduced a constant recovery function T(y) into epidemic model which is in the form \(T\left( y \right) \) = \( {\left\{ \begin{array}{ll} r,\ y>0 \\ 0, \ y=0 \end{array}\right. }\) maximum medical resources is used here to cure the disease. Further, Wang [25] proposed a piecewise linear recovery function in the form \(T\left( y \right) \) = \( {\left\{ \begin{array}{ll} k y,\ 0\leqslant y \leqslant y_{0} \\ k y_{0},\ \ \ \ y > y_{0} \end{array}\right. }\) where recovery rate is proportional to number of infected population before reaching its maximum capacity. Later, Zhang and Liu [26] considered a saturated type recovery function in the form T(y) = \(\dfrac{r y}{1+ k y}\) where delay in receiving treatment and limited medical resources are included. Consideration of this type of saturated treatment function has an advantage that T(y) has linear type characteristic when the number of infected population is very low, whereas it tends to a constant limit \(\dfrac{r}{k}\) for higher value of infected population. They established that the system experiences Backward bifurcation in the presence of saturated type treatment. Additionally, Zhou and Fan [27] modified this type of treatment function by introducing in the form \(T(I) = \dfrac{\alpha y}{\omega + y}\) and studied existence, stability of equilibria, Backward bifurcation and also Hopf bifurcation. Later on, obeying the report of World Health Organization (WHO) Statistical Information System, health planners used hospital bed population ratio (HBPR), number of hospital beds available per 10,000 population as a method for estimating medical resource ability to the public. Considering WHO’s rationale, Shan and Zhu [28] introduced removal rate as a function of hospital beds (b) and number of infected individuals y in the form
where \(\mu _{0}\) \(\left( > 0 \right) \) is the minimum per capita recovery rate and \(\mu _{1}\) \(\left( > 0 \right) \) is the maximum per capita recovery rate. They have established that the system with standard incidence and limited bed recovery rate shows rich and interesting dynamical phenomenon such as Saddle-node bifurcation, Backward bifurcation, Hopf bifurcation and Bogdanov–Takens bifurcation of co-dimension 2 and 3. In [29], Abdelrazec studied recovery rate \(\mu \left( b,y \right) \) to investigate available medical resources as spreading and controlling dengue fever which is helpful for health planners to allocate resources for controlling dengue transmission. Recently, the limitation of hospital beds is highly applicable for providing treatment to the COVID-19-infected population.
On the other hand, use of optimal control strategy in epidemic model is an important mathematical tool. Using optimal control in epidemic model the health planners can find out the best strategy which is more effective to reduce the disease spreading among the population with minimum cost [30]. Sometimes, only vaccination is applied to control the disease [31, 32], whereas only treatment is also used to reduce the influence of the infection [33]. Both vaccination and treatment are used in [34] to minimize the impact of the infection as well as reduce the cost of implementation due to applying treatment and vaccination to the individuals. Our intention will be fulfilled if a number of infective individuals are reduced by applying optimal control strategies taking the best effective preventive measures for controlling the disease.
The proposed model in this paper is extension of the work of Xiao and Ruan [20], Shan and Zhu [28]. We have extended the model considering the nonlinear incidence rate \(\beta \left( y \right) \) = \(\dfrac{\beta y}{1+ \alpha y^{2}}\) and treatment function as \(\mu \left( b,y \right) \) = \(\mu _{0}\) + \(\left( \mu _{1}-\mu _{0} \right) \dfrac{b}{b+y} \) in the presence of logistic type birth rate for susceptible population. We have studied different types of bifurcations such as Transcritical, Backward, Saddle-node and Hopf bifurcations and finally investigate the optimal control policy and efficiency analysis of the applied controls.
The rest of the paper is organized as follows : In Sect. 2, we have formulated the proposed model and discussed the basic properties of the solutions. Then, we have analyzed different cases for existence of equilibria and obtained basic reproduction number in Sect. 3. Next in Sect. 4, we have examined the necessary and sufficient conditions for local stability of disease-free equilibrium and endemic equilibrium point. In Sect. 5, we have studied persistence and extinction of the infectious disease under some suitable conditions. We have investigated bifurcations such as Transcritical bifurcation, Backward bifurcation, Saddle-node bifurcation and Hopf bifurcation in Sect. 6. In Sect. 7, we have formulated optimal control of the problem and used Pontryagin’s maximum principle for obtaining necessary conditions for optimality. Finally, in Sect. 8 we have summarized the results and given epidemiological significance for number of limited hospital beds and interpreted strategies for controlling the emerging disease.
2 Model formulation and boundedness
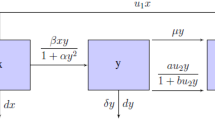
We assume that the total population is divided into three classes, namely susceptible, infected and recovered classes. Let, x(t), y(t) and z(t) represent density of the susceptible, infected and recovered population at any time t, respectively. Let the susceptible population have logistic growth rate with two types of death rates, namely normal death and disease-induced death. The rate of incidence is non-monotonic type in the form \( \dfrac{\beta x y}{1 + \alpha y^{2}} \), and the treatment rate is of the form \(\mu (b,y)=\left( \mu _{0} + \left( \mu _{1}-\mu _{0} \right) \dfrac{b}{b+y}\right) \). Based on the above discussion, we have proposed the deterministic epidemic model in the following form:
satisfying initial conditions \(x(0) \geqslant 0\), \(y(0) \geqslant 0\), \(z(0) \geqslant 0\) for all \(t \geqslant 0\). The model parameters of the system (1) are enlisted in Table 1.
In the proposed epidemic model, we assume that the total population remains constant or approaches asymptotically a constant which is reasonable for quickly spreading disease or rarely death-caused disease [28]. Since the third equation of (1) is independent from the other two, for stability analysis purpose we omit the last equation, but to investigate the optimal control problem we will consider all the three equations.
with initial conditions \(x(0) \geqslant 0\), \(y(0) \geqslant 0\) for all \(t \geqslant 0\). In the next sub-section, we shall investigate the basic properties such as positivity and boundedness of the solutions of the reduced model system (2).
2.1 Basic properties of the model
First, we shall show that all solutions of model system (2) satisfying the initial conditions \(x(0) \geqslant 0\), \(y(0) \geqslant 0\) are non-negative for all \(t \geqslant 0\), and then, we shall prove that the solutions are bounded for all \(t \geqslant 0\).
Theorem 1
All solutions (x(t), y(t)) of model system (2) satisfying the non-negative initial conditions are non-negative for any value of \( t (> 0)\).
Proof
First, we show x(t) is non-negative for all values of t. To prove this, we proceed with first equation of model system (2)
where M = \(max \left\{ \dfrac{y}{1 + \alpha y^2}\right\} = \dfrac{1}{2 \sqrt{\alpha }}\)
Integrating and simplifying, we get
Thus, we have established \( x(t)> 0 \, \forall \, t > 0 \), i.e., the susceptible populations are always positive. Similarly, we can show that \(y(t) \ge 0 \) \( \ \forall \ t > 0 \).
This completes proof of the theorem. \(\square \)
Next we show solutions of model system (2) are uniformly bounded for all \(t \geqslant 0\). We establish our result in the following theorem :
Theorem 2
The set \( \sum = \left\{ (x,y)\in \mathbb {R} _{+}^{2} : 0<\, x + y \le \dfrac{K(r - u_{1})^{2}}{4 r d} \right\} \) is a positively invariant attracting region for the epidemic model given by the system (2) in \( \mathbb {R}_{+}^{2} \).
Proof
Adding both equations of model system (2), we get
i.e.,
Integrating and taking limit as \(t \longrightarrow \infty \), we get
Thus, \( 0< x + y \leqslant \dfrac{K(r - u_{1})^{2}}{4 r d}\, \, \forall t \geqslant 0 \) with \(x(0)\geqslant 0, y(0)\geqslant 0\). Using this result and the result of Theorem 1, we can state that the solution of the model (2) is positively bounded in the region \(\sum \). \(\square \)
3 Existence of equilibria and basic reproduction number
In this section, we shall discuss the existence of different equilibrium points and basic reproduction number (\(R_0\)) of model system (2). Basic reproduction number \(\left( R_{0} \right) \) is the average number of secondary infections produced by an infective during an entire period of infection. The model system (2) has always a trivial equilibrium point \( E_{00}(0,0) \) and a disease-free equilibrium point \( E_{0} \) = \(\left( \dfrac{K \left\{ r - (d + u_{1}) \right\} }{r} , 0 \right) \) will exist when \( r > d + u_1 \). Hence, \( R_{0}\) can be calculated using next-generation matrix approach [35]. In the following theorem, we compute basic reproduction number using Driessche and Watmough’s [35] technique.
Theorem 3
Basic reproduction number of the model system (2) is \(R_{0}\) = \(\dfrac{\beta K \left\{ r - (d + u_{1}) \right\} }{r \left( d + \mu + \delta + \mu _{1} \right) }\).
Proof
The model system (2) has only one infected component, namely y. Let \(\mathscr {F}\) and \(\mathscr {V}\) be the new infection terms and remaining terms, respectively, then \(\mathscr {F} = \Bigg ( \dfrac{\beta x y}{1 + \alpha y^2}\Bigg )_{1\times 1}\)and \(\mathscr {V} = \Bigg ((d+\mu +\delta )y + \left( \mu _{0} + \left( \mu _{1}-\mu _{0} \right) \dfrac{b}{b+y} \right) y\Bigg )_{1\times 1}.\) Let \(F= \frac{d\mathscr {F}}{dy} \) and \(V= \frac{d\mathscr {V}}{dy} \), then the next-generation matrix is \(\mathscr {K}\) = \(F V^{- 1}\) = \(\Bigg ( \dfrac{\beta K \left\{ r - (d + u_{1}) \right\} }{r (d+\mu +\delta + \mu _{1})}\Bigg )_{1\times 1}\). Therefore, basic reproduction number of the model system (2) is given by
\(\square \)
The components of endemic equilibrium point \(E(x^{*},y^{*})\) of the system (2) are \( x^{*}\) = \(\dfrac{1 + \alpha y{^{*}}^2}{\beta } \left[ (d+\mu +\delta ) + \left( \mu _{0} + \left( \mu _{1}-\mu _{0} \right) \dfrac{b}{b+y^*} \right) \right] > 0 \) and \( y^{*} \) is positive root of p(y) = 0
and \( A_{5} = \alpha ^{2} r (d + \mu + \delta + \mu _{0}), A_{4} = \alpha ^{2} b r (d + \mu + \delta + \mu _{1}), A_{3} = \alpha r (d + \mu + \delta + \mu _{1})(1 - R_{0}) + \alpha r(d + \mu + \delta + \mu _{0})(1 - \Delta _{2}), A_{2} = \alpha b r (d + \mu + \delta + \mu _{1}) + K \beta ^{2} + \alpha b (d + \mu + \delta + \mu _{1}) (1 - R_{0}), A_{1} = r (d + \mu + \delta + \mu _{1})(1 - R_{0}) + K b \beta ^{2} (1 - \Delta _{1}), A_{0} = b r (d + \mu + \delta + \mu _{1})(1 - R_{0}) \).
Since \( p(y) = 0 \) is a fifth-order equation, it is very difficult to find the expressions of positive roots of the equation explicitly in terms of \( R_0 \). Using the Descartes’ rules of signs, we can get idea about the number of positive roots of Eq. (3) which is summarized in Table 2 in terms of \(R_{0}\) and the thresholds \(\Delta _{1} = \dfrac{r(\mu _{1} - \mu _{0})}{K b \beta ^{2}}\) and \(\Delta _{2} = \dfrac{(\mu _{1} - \mu _{0})}{(d + \mu + \delta + \mu _{0})}\).
Considering \(b = 0.57, \, r = 0.58, \, \mu _{1} = 1.2\) and keeping all other parameters fixed as shown in Table 3, we are varying the disease transmission rate \(\beta \) (consequently \( R_{0} \) will vary) and have drawn the solution curve for infected population (i.e., for existence of endemic equilibria) with respect to \( R_{0} \) (see Fig. 1). The number of equilibrium points for different values of \( R_{0}\) is summarized in the following lemma:
Lemma 1
-
(1)
Model system (2) always has a trivial equilibrium point \(E_{00}\) and a disease-free equilibrium point \(E_{0}\).
-
(2)
For \(R_{0} < 1\), model system (2) may have no, one coincident or two endemic equilibrium points.
-
(3)
For \(R_{0} > 1\), model system (2) may have one, two with one coincident or three endemic equilibrium points.
4 Local stability analysis
To investigate the nature of the equilibrium points, we first need to compute Jacobian matrix of model system (2) at any equilibrium point E(x, y) which is given by
Theorem 4
Trivial equilibrium point \(E_{00}(0,0)\) is stable if \( r< (d + u_{1}) \) and saddle point if \( r>(d + u_{1})\).
Proof
The Jacobian matrix (4) at the trivial equilibrium point \(E_{00}(0,0)\) is:
Eigenvalues of the above Jacobian matrix are given by \(r -(d+ u_{1})\) and \(-(d+ \mu +\delta + \mu _{1})\). Clearly, one eigenvalue is negative and other will be negative if \(r< (d + u_{1})\), and hence, under this restriction \( E_{00}(0,0) \) is stable. If \(r> (d + u_{1})\) holds, then one eigenvalue is positive and other value is negative; consequently, \( E_{00}(0,0) \) is a saddle point.
In biological point of view, \( r< (d + u_{1}) \) means birth rate of susceptible is less than sum of vaccination rate and death rate of the susceptible population. Two cases may arise: (i) high vaccination (i.e., \( u_1 \) is nearer to r such that \( (u_1+d)>r \)) and (ii) high death rate. The first case implies most of the people are vaccinated to get recovery from a particular disease. As for example for preventing polio, tuberculosis disease, etc., vaccination is given step by step from the childhood. As a result, these types of diseases are eliminated now from the population. The second case is totally impossible because in this case all susceptible population will die out in the community. On the other hand, \(r> (d + u_{1})\) means birth rate of the population is higher than sum of vaccination and death rate of population which is realistic. \(\square \)
Theorem 5
If \(R_{0} < 1\), then the disease-free equilibrium point \(E_{0}\) is locally asymptotically stable, and for \(R_{0} > 1\) it is unstable. For \(R_{0} = 1\), disease-free equilibrium point \(E_{0}\) is a saddle-node of co-dimension 1 if \(\dfrac{\beta ^2 K}{r} \ne \dfrac{\mu _{1} - \mu _{0}}{b}\) and a semi-hyperbolic attracting node of co-dimension 2 if \(\dfrac{\beta ^2 K}{r} = \dfrac{\mu _{1} - \mu _{0}}{b}\).
Proof
Jacobian matrix of the system (2) at the disease-free equilibrium point \(E_{0}\) is
Eigenvalues of \( J_{E_{0}} \) are \(- \left\{ r -(d+ u_{1})\right\} \) and \((d+ \mu +\delta + \mu _{1})(R_{0} - 1)\). If \(R_{0} < 1\), then both the eigenvalues are negative, and hence, \( E_0 \) is stable and is unstable(saddle) for \(R_{0} > 1\).
For \(R_{0} = 1\), one of the above eigenvalues vanishes, and hence, the disease-free equilibrium point \(E_{0}\) is a non-hyperbolic equilibrium point. Use center manifold theorem to determine the nature of equilibrium point \(E_{0}\).
First we translate disease-free equilibrium point \(E_{0}\left( \dfrac{K \left\{ r - (d + u_{1})\right\} }{r}, 0 \right) \) to origin using the transformation \(S = x - \dfrac{K \left\{ r - (d + u_{1})\right\} }{r}\), \(I = y\); then, the model system (2) takes the following form:
Introducing the transformation \( S = - \ \dfrac{\beta K}{r} x + y, I = x \), the System (5) becomes :
It is clear from (6) that if \(\dfrac{\beta ^2 K}{r} \ne \dfrac{\mu _{1} - \mu _{0}}{b}\), then disease-free equilibrium point \(E_{0}\) is a saddle-node of co-dimension 1 [36]. Now, if \(\dfrac{\beta ^2 K}{r} = \dfrac{\mu _{1} - \mu _{0}}{b}\), then use center manifold theorem [36] for investigating nature of the disease-free equilibrium point \(E_{0}\).
Let the local center manifold of the system is given by \(W^c(0) = \Big \lbrace (x,y)\in R^2 : y = h(x) = a_{1} x^2 + a_{2} x^3 + a_{3} x^4 + a_{4} x^5, |x|< \delta ^{'} \Big \rbrace \) satisfying \(h(0) = 0, Dh(0) = 0\) where \(\delta ^{'}\) is sufficiently small and Dh is the derivative of h with respect to x. Using the conditions, we get \(a_{1} = 0\), \(a_{2} = \dfrac{\alpha \beta K}{r}\).
Thus, local manifold of the system is given by \(y = h(x) = \dfrac{\alpha \beta K}{r}x^3 \), and then, the system (6) reduces to
From system (7), it is clear that disease-free equilibrium point \(E_{0}\) is a semi-hyperbolic attracting node of co-dimension 2 if \(\dfrac{\beta ^2 K}{r} = \dfrac{\mu _{1} - \mu _{0}}{b}\). Hence, the theorem is proved. \(\square \)
Next we shall establish the local stability of the endemic equilibrium \(E(x^*,y^*)\) in the following theorem:
Theorem 6
The characteristic endemic equilibrium \(E(x^*,y^*)\) is locally asymptotically stable if \(\dfrac{b(\mu _{1} - \mu _{0})}{b + y^*} < min \Big \lbrace \dfrac{r x^*}{K}+\dfrac{2 \alpha \beta x^* y^*{^2}}{(1 + \alpha y^*{^2})^2}+\dfrac{b^2 (\mu _{1} \!-\! \mu _{0})}{(b + y^*)^2}, \dfrac{2 \alpha \beta x^* y^* (b + y^*)}{(1 + \alpha y^*{^2})^2}+ \dfrac{K\beta ^2 (1 - \alpha y^*{^2})(b + y^*)}{r(1 + \alpha y^*{^2})^3} \Big \rbrace \) and is unstable otherwise.
Proof
Jacobian matrix of the model system (2) at the endemic equilibrium \(E(x^*,y^*)\) is
The corresponding characteristic equation is
where \(a_1 = - tr(J_E) \) and \(a_0 = det(J_E)\).
Roots of the above equation will have negative real part if \(a_1 = - tr(J_{E}) > 0 \) and \(a_0 = det(J_{E}) > 0 \).
Now, \(tr(J_{E}) {=} - \dfrac{r x^*}{K} {-} \dfrac{2 \alpha \beta x^* y^*{^2}}{(1 {+} \alpha y^*{^2})^2} {+} \dfrac{b (\mu _{1} - \mu _{0})}{(b {+} y^*)} - \dfrac{b^2 (\mu _{1} - \mu _{0})}{(b + y^*)^2} < 0 \) if \( \dfrac{r x^*}{K}+\dfrac{2 \alpha \beta x^* y^*{^2}}{(1 + \alpha y^*{^2})^2}+\dfrac{b^2 (\mu _{1} - \mu _{0})}{(b + y^*)^2} > \dfrac{b (\mu _{1} - \mu _{0})}{b + y^*}\) and \( det(J_{E})\) = \( \dfrac{r x^*}{K} \left\{ \dfrac{ 2 \alpha \beta x^* y^*{^2} }{(1 + \alpha y^*{^2})^2} - \dfrac{ b y^* (\mu _{1} - \mu _{0})}{(b + y^*)^2} \right\} + \dfrac{\beta ^2 x^* (1 - \alpha y^*{^2})y^*}{(1 + \alpha y^*{^2})^3} > 0 \) if \(\dfrac{2 \alpha \beta x^* y^*{^2}}{(1 + \alpha y^*{^2})^2}+ \dfrac{K\beta ^2 (1 - \alpha y^*{^2})y^*}{r(1 + \alpha y^*{^2})^3} > \dfrac{ b y^* (\mu _{1} - \mu _{0})}{(b + y^*)^2}\).
That means \(a_1 = - tr(J_{E}) > 0 \) and \(a_0 = det(J_{E}) > 0 \) if \(\dfrac{b(\mu _{1} - \mu _{0})}{b + y^*} < min \Big \lbrace \dfrac{r x^*}{K}+\dfrac{2 \alpha \beta x^* y^*{^2}}{(1 + \alpha y^*{^2})^2}+\dfrac{b^2 (\mu _{1} - \mu _{0})}{(b + y^*)^2},\ \ \dfrac{2 \alpha \beta x^* y^* (b + y^*)}{(1 + \alpha y^*{^2})^2}+ \dfrac{K\beta ^2 (1 - \alpha y^*{^2})(b + y^*)}{r(1 + \alpha y^*{^2})^3} \Big \rbrace \).
Hence, endemic equilibrium \(E(x^*,y^*)\) is locally asymptotically stable if \(\dfrac{b(\mu _{1} - \mu _{0})}{b + y^*} < min \Big \lbrace \dfrac{r x^*}{K}+\dfrac{2 \alpha \beta x^* y^*{^2}}{(1 + \alpha y^*{^2})^2}+\dfrac{b^2 (\mu _{1} - \mu _{0})}{(b + y^*)^2},\ \ \dfrac{2 \alpha \beta x^* y^* (b + y^*)}{(1 + \alpha y^*{^2})^2}+ \dfrac{K\beta ^2 (1 - \alpha y^*{^2})(b + y^*)}{r(1 + \alpha y^*{^2})^3} \Big \rbrace \) and is unstable otherwise. Thus, we arrive at our desired result. \(\square \)
5 Persistence and extinction of the infection
Basic reproduction number is playing a crucial role in dynamical change of infection. In this section, we shall establish the eradication and persistence of disease is dependent on the value of \(R_0\). Eradication and persistence of the disease can be determined by stability of disease-free equilibrium point \( E_{0}\left( \dfrac{K \left\{ r - (d + u_{1}) \right\} }{r} , 0 \right) \) and the endemic equilibrium \( E(x^*, y^*)\). First we shall show the disease-free equilibrium point \( E_{0}\) is globally stable when \( R_{0} \) less than a threshold value then infection will be eradicated from the system. In the following theorem, we shall prove the global stability of disease-free equilibrium point \(E_{0}\).
Theorem 7
Disease-free equilibrium point \(E_{0}\) is globally stable if \(R_{0} < (1 - R_{0}^{*})\) where \(R_{0}^{*} = \dfrac{ K (\mu _{1} - \mu _{0})(r - u_{1})^2}{(d +\mu +\delta + \mu _{1})\left\{ 4brd + K (r - u_{1})^2 \right\} } \).
Proof
Using Lyapunov’s stability theorem [37, 38], we shall establish the global stability of disease-free equilibrium point.
Let, V : \(\chi \) \(\longrightarrow \) R where \(\chi = \Big \lbrace (x,y) \in R^2 : x> 0, y> 0 \Big \rbrace \) defined by \( V(x,y) = y \) is a Lyapunov function as it is positive definite.
Then, \(\dfrac{\mathrm{d}V}{\mathrm{d}t} = \dfrac{\mathrm{d}y}{\mathrm{d}t} = \dfrac{\beta x y}{1 + \alpha y^2}-(d+\mu +\delta )y - \left\{ \mu _{0} + \dfrac{(\mu _{1} - \mu _{0}) b}{b + y}\right\} y \).
i.e., \(\dfrac{\mathrm{d}V}{\mathrm{d}t} = \ \Bigg [ \dfrac{\beta x}{1 + \alpha y^2} -(d+\mu +\delta ) - \Bigg \lbrace \mu _{0} + \dfrac{(\mu _{1} - \mu _{0}) b}{b + y} \Bigg \rbrace \Bigg ] y \)
i.e., \(\dfrac{\mathrm{d}V}{\mathrm{d}t} \leqslant \ \bigg [ \dfrac{\beta K \lbrace r -(d + u_{1})\rbrace }{r} - (d +\mu +\delta + \mu _{1}) - \bigg \lbrace \mu _{0} + \dfrac{(\mu _{1} - \mu _{0}) b}{b + \dfrac{(r - u_{1})^2 K}{4rd}} - \mu _{1} \bigg \rbrace \bigg ] . \ y \)
i.e., \(\dfrac{\mathrm{d}V}{\mathrm{d}t} \leqslant \ (d +\mu +\delta + \mu _{1}) \Bigg [ R_{0} - \Bigg \lbrace 1 - \dfrac{ K (\mu _{1} - \mu _{0})(r - u_{1})^2}{(d +\mu +\delta + \mu _{1})\lbrace 4brd + K (r - u_{1})^2 \rbrace } \Bigg \rbrace \Bigg ] . \ y \)
i.e., \(\dfrac{\mathrm{d}V}{\mathrm{d}t} \leqslant \ (d +\mu +\delta + \mu _{1}) \left\{ R_{0} - (1 - R_{0}^{*}) \right\} . \ y \)
Therefore, \(\dfrac{\mathrm{d}V}{\mathrm{d}t} < 0\) if \(R_{0} < (1 - R_{0}^{*})\) where \(R_{0}^{*} = \dfrac{K (\mu _{1} - \mu _{0})(r - u_{1})^2}{(d +\mu +\delta + \mu _{1})\left\{ 4brd + K (r - u_{1})^2 \right\} } \).
So, by Lyapunov’s Stability Theorem [37, 38] one can conclude that \(E_{0}\) is globally stable if \(R_{0} < (1 - R_{0}^{*})\). \(\square \)
The above result is epidemiologically most important because if the value of \(R_{0}\) is less than a threshold quantity, then the disease will be eliminated from the population. Therefore, to control the influence of the infection, our target is to adopt proper preventive policies such that value of \(R_{0}\) is less than that threshold value.
Now we shall prove global stability of endemic equilibrium point \(E(x^*,y^*)\). For discussing global stability of endemic equilibrium point, use Dulac criterion [25, 36]. In the following theorem, we shall establish the condition of global stability of the endemic equilibrium point.
Theorem 8
For \( R_{0} > 1\), endemic equilibrium point \(E(x^*,y^*)\) is globally asymptotically stable if \(\dfrac{r(d + \mu + \delta + \mu _{1})}{K(r - (d +u_{1}))}< \beta < \dfrac{r}{K(1 + \alpha b^2)}\) satisfied.
Proof
We write our model system (2) as given below:
To show global stability of endemic equilibrium \(E(x^*,y^*)\), we use Dulac function criterion [25, 36] of stability analysis. Considering Dulac function as \(D(x,y) = \dfrac{b + y}{x y}\), we have
Again \( R_{0} > 1\) implies \(\beta >\dfrac{r(d + \mu + \delta + \mu _{1})}{K(r - (d +u_{1}))}\).
Combining the above two conditions, we get \(\dfrac{\partial }{\partial x}(DF) + \dfrac{\partial }{\partial y}(DG) < 0\) if \( \dfrac{r(d + \mu + \delta + \mu _{1})}{K(r - (d +u_{1}))}< \beta < \dfrac{r}{K(1 + \alpha b^2)}\).
Thus, by Dulac criterion we can conclude that system (2) has no closed orbit that means endemic equilibrium point \(E(x^*,y^*)\) is globally stable for \(R_{0} > 1\) under the conditions stated in the theorem. \(\square \)
we have shown in the above theorem that for \(R_{0} > 1\) there exist a certain region of the model parameter \(\beta \) where endemic equilibrium \(E(x^*,y^*)\) is globally asymptotically stable that means infection persists in the system. If new infection produced by single susceptible during its entire infectious period is greater than one, then there exist a certain number of infected individuals. Therefore, the number of infected individuals gradually diminishes if new infection produced by single susceptible during lifespan less than one. Thus, the necessary condition to eliminate or persist of infection is to maintain the value of basic reproduction number less or greater than one, respectively.
6 Bifurcation analysis and epidemiological interpretation
In this section, we shall discuss various types of bifurcations about different equilibrium points considering different model parameters as the bifurcation parameters and interpret the biological consequences of the results at the corresponding bifurcation values of the model parameters. We have studied Transcritical bifurcation with respect to maximum number of per capita recovery rate \((\mu _1)\), and it gives the upper limit of \(\mu _1 \) above which disease will eliminate from the system and below which disease will persist. Again Backward bifurcation is studied with respect to \( R_0 \). We have found the threshold number of available hospital beds (b) below which the system shows Backward bifurcation, i.e., disease eradication not only depends on values of \( R_0 \) but also on initial number of infection. If the value of intrinsic growth rate r passes through its critical value \(r^{*}\), then new endemic equilibrium points are created and destroyed through Saddle-node bifurcation. Thus, we get different stability criteria for controlling the spreading of the disease. The endemic equilibrium point \(E_{1}\) may lose its stability through Hopf bifurcation when number of available hospital beds (b) passes through its critical value. Thus, we have shown the condition for persistence of the disease may change through Hopf bifurcation.
6.1 Transcritical bifurcation
Theorem 9
The model system (2) experiences Transcritical bifurcation at the disease-free equilibrium \(E_{0}\left( \dfrac{ K \left( r - (d + u_{1})\right) }{r},0 \right) \) as the recovery parameter \(\mu _{1}\) passes through the critical value \(\mu _{1}^{*}\) if \(\beta ^2 \ne \dfrac{r(\mu _1^* - \mu _0)}{K b}\) where \(\mu _{1}^{*} = \dfrac{\beta K}{r} \lbrace r - ( d + u_{1} ) \rbrace - ( d + \mu +\delta )\).
Proof
Since at \( R_0=1\), i.e., \( \mu _1=\mu ^*_1\), one of the eigenvalues of \( J_{E_0} \) is zero and other is negative, to investigate the nature of the solution at \( E_0 \), we have to use Sotomayor’s theorem [36, 39]. For this purpose, we construct a function with two components given by \(f(x,y) = \left( \begin{array}{ccc} f_{1}(x,y) \\ f_{2}(x,y) \end{array} \right) \) where
Let corresponding to zero eigenvalue \(J_{E_{0}}(\mu _{1}^{*})\) and \(J_{E_{0}}^{T}(\mu _{1}^{*})\) have eigenvectors V and W, respectively, where \( V = \left( \begin{array}{ccc} - \ \dfrac{\beta K}{r} \\ 1 \end{array} \right) \) and \( W = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) . \) From (10) we have \(f_{\mu _{1}}(x,y) = \left( \begin{array}{ccc} 0 \\ - \ \dfrac{b y}{b + y} \end{array} \right) \), \(Df_{\mu _{1}}(x,y) = \left( \begin{array}{ccc} 0 &{} 0 \\ 0 &{} - \ \dfrac{b^2 }{(b + y)^2} \end{array} \right) \) and \( D^2f(E_{0};\mu _{1}^{*}) (V,V)\) = \(\left( \begin{array}{ccc} 0 \\ - \dfrac{2 \beta ^2 K}{r} + \dfrac{2(\mu _{1} - \mu _{0})}{b}\end{array} \right) .\)
Therefore,
Hence, the model system (2) satisfies all conditions of Sotomayor’s theorem for Transcritical bifurcation with respect to parameter \(\mu _{1}\). Thus, model system (2) experiences Transcritical bifurcation in the neighborhood of the critical value of the maximum value of the recovery parameter \(\mu _{1} = \mu _{1}^{*}\). \(\square \)
6.1.1 Significance of \(\mu _{1}\) as a Transcritical bifurcation parameter
Here, numerically we shall interpret significance of the maximum value of the per capita recovery rate ( \(\mu _{1}\)) as the Transcritical bifurcation parameter for lower and upper value of the rate of infection(\( \beta \)). We consider the lower value as \( \beta =0.09 \) and the upper value as \( \beta =0.9 \).
6.1.2 (a) For lower value of disease transmission rate \(\left( \beta \right) \)
For \(\beta = 0.09\) and other parameter values are described as shown in Table-3 with \(b = 1.24, \, r = 0.98\), we get the critical value of Transcritical bifurcation parameter as \(\mu _{1}^{*} = 1.689795918\). \(\left( i \right) \) For \(\mu _{1} = 1.63 < \mu _{1}^{*}\), one saddle disease-free equilibrium point \(E_{0}\) and one stable endemic equilibrium point \(E_{1}\) exist (see the corresponding phase portrait in Fig. 2a). \(\left( ii \right) \) for \(\mu _{1}^{*} < \mu _{1}= 1.75 \), there exist one stable disease-free equilibrium point \(E_{0}\) and two endemic equilibrium points \(E_{1}\) and \(E_{2}\) where \(E_{1}\) is saddle point and \(E_{2}\) is stable spiral (see the phase portrait in Fig. 2b). Thus, when \(\mu _{1}\) passes from left side to right side through its critical value \(\mu _{1}^{*}\), then the disease-free equilibrium point \(E_{0}\) and the endemic equilibrium point \(E_{1}\) exchange their stability through Transcritical bifurcation with creation of one stable endemic equilibrium point. \(\left( iii \right) \) If we take value of \(\mu _{1}\) far from the transcritical value in right side of \(\mu _{1}^{*}\) say \( \mu _{1}= 5 \), then only a stable disease-free equilibrium point exists (see the phase portrait in Fig. 2c).
It is clear from the above discussion that there exists a critical value of the maximum value of treatment rate \((\mu _{1})\) below which the disease will persist in the system for any initial population density. But for the values of \(\mu _{1} \) greater than the critical value persistence of the disease will depend on the population density of the initial spreading. In this situation, two stable equilibrium points exist: one is disease-free equilibrium and other is with disease. In this case, initial population density plays a crucial role for persistence or elimination of the disease. Again for higher value of the maximum value of cure rate, disease is eradicated from the system which indicates applying high level of treatment disease can be eradicated from the population. Therefore, population density and treatment both have vital role in disease controlling.
6.1.3 (b) For higher value of disease transmission rate \(\left( \beta \right) \)
For \(\beta = 0.9\) and other parameter values are given in Table 3 with \(b = 1.24, \, r = 0.98\), we get the critical value of the maximum cure rate as \(\mu _{1}^{*} = 24.99795918\). Now, for \( \mu _{1}=28 > \mu _{1}^*\), only one stable disease-free equilibrium point exists, i.e., disease will not persist in the system (see the phase portrait in Fig. 3a) and for \( \mu _{1}=20 < \mu _{1}^*\), there exist a unstable (saddle) disease-free equilibrium point and one unstable endemic equilibrium point with a stable limit cycle (see the phase portrait in Fig. 3b, the red curve is stable limit cycle). Taking the value of \(\mu _{1}\) more in the left side of \( \mu _{1}^{*}\), say \( \mu _{1}(= 4) < \mu _{1}^{*}\), there exist one unstable disease-free equilibrium point and one endemic equilibrium point which is stable spiral (see the phase portrait in Fig. 3c). Hence, for higher values of the disease transmission rate, the transcritical value of maximum cure rate is also high; then, the disease will be eradicated from the system for higher amount of treatment. For investigating disease dynamics, we observe the behavioral change of equilibrium point in left side as well as right side of \(\mu _{1}^{*}\).
From the above, we have seen that for higher treatment rate disease can be eradicated from the population. In just left side of \( \mu _{1}^{*}\), i.e., for \(\mu _{1}(= 20) < \mu _{1}^{*}\), disease will persist in the system with oscillatory population density, and for very lower value of \( \mu _1 \), i.e., for \( \mu _{1}(= 4) < \mu _{1}^{*}\) disease will persist in the system with steady state. Thus, the treatment has important role in controlling disease transmission.
Therefore, it is clear from the above analysis that for lower rate of the infection if we take proper action, i.e., apply moderate or high medical facility, then disease can be easily eradicated from the system, but if the rate of the infection is higher, then to eliminate the disease, we need to apply high medical facility to control the disease. If we provide lower medical facility, then disease will persist in the system either it oscillates or in steady state.
6.2 Backward bifurcation
Theorem 10
The model system (2) experiences Backward bifurcation if \( b < \dfrac{r(\mu _{1} - \mu _{0})}{K \beta ^*{^2}}\) when \(R_{0}\) crosses the critical value \(R_{0} = 1\) and Forward bifurcation if \( b > \dfrac{r(\mu _{1} - \mu _{0})}{K \beta ^*{^2}}.\)
Proof
To determine the condition for Backward bifurcation of the model system (2), we use the methodology as developed in [40]. Let us consider \(\beta \) as the bifurcation parameter and \(R_0 = 1\) implies \(\beta = \dfrac{r(d + \mu + \delta + \mu _{1})}{K \left\{ r - (d + u_{1})\right\} }\) \(\left( = \beta ^{*} \, \text {say} \right) \), and for this value of \(R_0\) one of the eigenvalues of \(J_{E_0}\) vanishes. Let \( W = \left( \begin{array}{ccc} - \ \dfrac{\beta ^{*} K}{r} \\ 1 \end{array} \right) \) and \( V = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \) be the right eigen vector and left eigen vector, respectively, of \( J_{E_{0}} \) corresponding to the eigenvalue \(\lambda =0\). In order to apply Castillo–Chavez and Song’s bifurcation theorem [40], we need to compute the value of \(\phi \) and \(\psi \) which are given by
Thus, the model system (2) experiences Backward bifurcation at \(R_{0} = 1\) if \(\phi > 0\), i.e., \(b < \dfrac{r(\mu _{1} - \mu _{0})}{K \beta ^*{^2}}\), and for \(b > \dfrac{r(\mu _{1} - \mu _{0})}{K \beta ^*{^2}}\) bifurcation is forward. \(\square \)
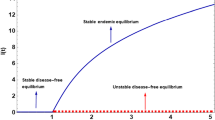
In Fig. 4, we have plotted the bifurcation diagram with respect to \(R_{0}\) varying the disease transmission rate \( \beta \). It is clear from the figure that there is a critical value of \(R_{0}\), say \(R_{0}^{*}\), such that in \(0< R_{0}< R_{0}^{*}\) there exists only one stable disease-free equilibrium point, for \(R_{0}^{*}< R_{0} < 1\), there exist two endemic equilibrium points along with the stable disease-free equilibrium point, and for \(R_{0} > 1\) one stable endemic equilibrium point with unstable disease-free equilibrium point exists. Among the two endemic equilibrium points, the equilibrium with lower infected level is saddle, but point with higher infected level is stable, which means for \(R_{0}^{*}<R_{0} < 1\), one stable disease-free equilibrium point as well as one stable endemic equilibrium point exist. Epidemiologically this result is highly significant because eradication of disease from the system depends on values of \(R_{0}\) as well as on initial infection density also. At the same time for \(0< R_{0}< R_{0}^{*}\), only stable disease-free equilibrium point exists which indicates disease eradicates from the system. For \(R_{0} > 1\), we see that disease-free equilibrium point is unstable and endemic equilibrium point is stable (see Fig. 4). It is clear from theoretical analysis that there is a critical value of the number of hospital beds (b) below which this type of phenomenon occurs. Hence, to eliminate the disease from any system we have to increase the number of hospital beds, i.e., the treatment facility.
Backward bifurcation diagram with respect to \( R_{0} \) varying the disease transmission rate \( \beta \), and other parameters are given in Table 3 with \(r = 0.58, \, b = 0.57, \, \mu _{1} = 1.2\), the blue line corresponds to stable branch and red line is for unstable branch
6.3 Saddle-node bifurcation
In this subsection, we shall examine the Saddle-node bifurcation with respect to the intrinsic growth rate (r). Let for the critical value \(r = r^{*}\) the equation (3) has a coincident root.
Theorem 11
The model system (2) experiences a Saddle-node bifurcation at the coincident endemic equilibrium point \(E(x^*,y^*)\) for \(r = r^{*}\) if the conditions stated in the text are satisfied.
Proof
It can be shown that for \(r = r^{*}\) one of the eigenvalues of \(J_{E}\) vanishes and other one is negative real, these occur if \(det(J_E)| _{r = r^{*}} = 0\) and \(tr(J_E)| _{r = r^{*}} > 0\). We have to check the transversality conditions for Saddle-node bifurcation using Sotomayor’s theorem [36, 39]. Let V and W be the eigen vectors corresponding to the zero eigenvalue for the matrices \(J_{E}\) and \(J^{T}_{E}\), respectively, then \( V = \left( \begin{array}{ccc} \frac{\beta \left( 1 - \alpha y^*{^2} \right) }{\left( 1+\alpha y^*{^2} \right) ^2} \\ - \dfrac{ r^{*}}{K} \end{array} \right) \) and \( W = \ \left( \begin{array}{ccc} \dfrac{\beta y^*}{1 + \alpha y^*{^2}} \\ \dfrac{ r^{*} \ x^*}{K} \end{array} \right) \).
Now, \(f_{r}(E(x^*,y^*) ; r^{*}) = \left( \begin{array}{ccc} x^* \left( 1 - \dfrac{x^*}{K} \right) \\ 0 \end{array} \right) \) and  Therefore, \(W^T f_{r}(E(x^*,y^*) ; r_{0})\) = \(\dfrac{\beta x^* y^* \left( 1 - \dfrac{x^*}{K}\right) }{1 + \alpha \ y^*{^2}} \ne 0. \) and \(W^T \left[ D^2f(E(x^*,y^*) ; r^{*})(V, V)\right] = \dfrac{2 \alpha \beta x^* y^* {r^*}^2 (3 - \alpha y^*{^2})}{K^2(1 + \alpha y^*{^2})^3}\left[ r^{*} \left( 1\! -\! \dfrac{2 x^*}{K} \right) \!-\! (d + u_{1} ) \right] - \dfrac{2 {r^*}^2 \beta ^2 x^*(1 - \alpha y^*{^2})^2}{K^2(1 + \alpha y^*{^2})^4} + \ \ \dfrac{2 {r^*}^3 b^2 x^*(\mu _{1} - \mu _{0})}{K^3(b + y^*)^3} \ \ \) \(\ne 0\) if \(\dfrac{\alpha \beta y^* (3 - \alpha y^*{^2})}{(1 + \alpha y^*{^2})^3}\left[ r^{*} \left( 1 - \dfrac{2 x^*}{K} \right) - (d + u_{1} ) \right] + \ \ \dfrac{ r^* b^2 (\mu _{1} - \mu _{0})}{K(b + y^*)^3} \ne \dfrac{ \beta ^2 (1 - \alpha y^*{^2})^2}{(1 + \alpha y^*{^2})^4} \)
Therefore, \(W^T f_{r}(E(x^*,y^*) ; r_{0})\) = \(\dfrac{\beta x^* y^* \left( 1 - \dfrac{x^*}{K}\right) }{1 + \alpha \ y^*{^2}} \ne 0. \) and \(W^T \left[ D^2f(E(x^*,y^*) ; r^{*})(V, V)\right] = \dfrac{2 \alpha \beta x^* y^* {r^*}^2 (3 - \alpha y^*{^2})}{K^2(1 + \alpha y^*{^2})^3}\left[ r^{*} \left( 1\! -\! \dfrac{2 x^*}{K} \right) \!-\! (d + u_{1} ) \right] - \dfrac{2 {r^*}^2 \beta ^2 x^*(1 - \alpha y^*{^2})^2}{K^2(1 + \alpha y^*{^2})^4} + \ \ \dfrac{2 {r^*}^3 b^2 x^*(\mu _{1} - \mu _{0})}{K^3(b + y^*)^3} \ \ \) \(\ne 0\) if \(\dfrac{\alpha \beta y^* (3 - \alpha y^*{^2})}{(1 + \alpha y^*{^2})^3}\left[ r^{*} \left( 1 - \dfrac{2 x^*}{K} \right) - (d + u_{1} ) \right] + \ \ \dfrac{ r^* b^2 (\mu _{1} - \mu _{0})}{K(b + y^*)^3} \ne \dfrac{ \beta ^2 (1 - \alpha y^*{^2})^2}{(1 + \alpha y^*{^2})^4} \)
Hence, all the conditions for Saddle-node bifurcation are satisfied for \(r = r^{*}\) at the coincident endemic equilibrium point \(E(x^*, y^*)\) of the model system (2). So by Sotomayor’s theorem for Saddle-node bifurcation, we can conclude that model system (2) experiences a Saddle-node bifurcation at the coincident endemic equilibrium point \(E(x^*, y^*)\) when the intrinsic growth rate crosses its critical value. \(\square \)
In Fig. 5, we have presented the one parameter bifurcation diagram of infected individuals considering r as the bifurcation parameter for the proposed model. It is clear from the figures that for lower value of \(\beta \) one Saddle-node bifurcation point exists, say \(r^*\), and for higher value of disease transmission rate \((\beta )\) there exist two Saddle-node bifurcation points, say \(r_{1}^{*}\) and \(r_{2}^{*}\).
Bifurcation diagram with respect to r considering different values of \(\beta \) and other parameters are given in Table 3 with \(b = 0.57, \, \mu _{1} = 1.2\)
6.3.1 Effect of population birth rate \(\left( r\right) \) and disease transmission rate \(\left( \beta \right) \) on model dynamics
In this subsection, numerically we shall show that population birth rate (r) and rate of infection \((\beta )\) are playing crucial role in disease spreading dynamics where other parameters are fixed as shown in Table 3 with \(b = 0.57, \, \mu _{1} = 1.2\). First, we investigate the dynamics considering the lower value of disease transmission rate \(\left( \beta \right) \) then for higher value of \(\beta \) and finally compare the results.
6.3.2 (a) For lower value of disease transmission rate \(\left( \beta \right) \)
First, we consider \(\beta = 0.091\) keeping other parameters fixed for Saddle-node bifurcation as given in Table 3 with \(b = 0.57, \, \mu _{1} = 1.2\). For \(\beta = 0.091\), we get only one critical value of r which is \(r^{*} = 0.5835215509\) (see Fig. 5a). To interpret biological significance of the results, we consider following cases. \(\left( i \right) \) First, consider \(r(= 0.50) < r^{*}\); in this case, there exists only one stable disease-free equilibrium point and no endemic equilibrium point exists (see the phase portrait in Fig. 6a). \(\left( ii \right) \) For \(r = r^{*}\), one stable disease-free equilibrium point and one saddle endemic equilibrium point exist (see the phase portrait in Fig. 6b). \(\left( iii \right) \) Next, we consider \(r^{*} < r(= 0.62);\) then, one stable disease-free equilibrium point exists along with two endemic equilibrium points. Among them, one endemic equilibrium point is saddle and another one is stable (see the phase portrait in Fig. 6c).
Thus, we observe that the number of endemic equilibrium point changes from zero to two through Saddle-node bifurcation as bifurcation parameter r passes through its critical point \(r^{*}\) from left side to right side. Here always one stable disease-free equilibrium point exists. That means in this case disease can be eradicated from the population for lower value of r, whereas for higher value of r disease persists in the system. So, we need to take necessary actions such that values of intrinsic birth rate \(\left( r\right) \) become lower to control the infection in the population. Here we observe that for lower value of disease transmission rate the influence of the disease spreading can be decreased; moreover, disease can be eliminated from the population.
6.3.3 (b) For higher value of disease transmission rate \(\left( \beta \right) \)
Secondly, we take \(\beta = 0.91\) and other parameter values are described in Table 3 with \(b = 0.57, \, \mu _{1} = 1.2\). For \(\beta = 0.91\), we get two critical values of population birth rate; those are \(r_{1}^{*} = 1.164851284\) and \(r_{2}^{*} = 1.283695472\) (from Fig. 5b, we see that two critical values of r exist for higher value of \(\beta \)). Now we consider three cases \(\left( i \right) \) \(r < r_{1}^{*}\) \(\left( ii \right) \) \(r_{1}^{*}< r < r_{2}^{*}\) and \(\left( iii \right) \) \(r_{2}^{*} < r\). In each of the above three cases, we find the number of equilibrium points and their behavior. \(\left( i \right) \) For \(r(= 1.10) < r_{1}^{*}\), the system contains two equilibrium points: one is disease-free equilibrium point \((E_{0})\) and other one is endemic equilibrium point \((E_{1})\). Disease-free equilibrium point is saddle, whereas endemic equilibrium point is stable spiral (see the phase portrait in Fig. 7a). For \(r = r_{1}^{*}\), saddle disease-free equilibrium point \(E_{0}\) and two endemic equilibrium points exist among which one is stable and other one is saddle (see the phase portrait in Fig. 7b). \(\left( ii \right) \) \(r_{1}^{*}< r(= 1.22) < r_{2}^{*}\) saddle disease-free equilibrium point and three endemic equilibrium points \(E_{1}\), \(E_{2}\), \(E_{3}\) exist where \(E_{1}\), \(E_{3}\) are stable spiral and \(E_{2}\) is saddle. In this case, two more endemic equilibrium points arise through Saddle-node bifurcation among them one is saddle and another one stable endemic equilibrium point when r crosses \(r = r_{1}^{*}\) from left side to right side (see the phase portrait in Fig. 8a). For \(r = r_{2}^{*}\), saddle disease-free equilibrium, one stable endemic equilibrium and one saddle endemic equilibrium point exist (see the phase portrait in Fig. 8b). \(\left( iii \right) \) Now for \(r_{2}^{*} < r(= 1.35)\) saddle disease-free equilibrium point and one stable endemic equilibrium point \(E_{1}\) exist. Here two endemic equilibrium points diminish through the Saddle-node bifurcation when r crosses \(r = r_{2}^{*}\) from left side to right side (see the phase portrait in Fig. 8c).
From the above three cases, we observe that when r passes from left side to right side through critical value \(r_{1}^{*}\), the number of endemic equilibrium points increases, and when r crosses left side to right side through critical value \(r_{2}^{*}\), the number of endemic equilibrium points decreases through Saddle-node bifurcation. Moreover, we see that for higher values of disease transmission rate \(\left( \beta \right) \), there always exists a stable endemic equilibrium point. It is also clear from the analysis that if values of disease transmission rate \(\left( \beta \right) \) increases, then the threshold value of population birth rate \(\left( r\right) \) for Saddle-node bifurcation also increases. That means for higher value of r one stable endemic equilibrium point exists which indicates disease always persists in this case.
6.4 Hopf bifurcation
To investigate Hopf bifurcation of the model system (2) about the endemic equilibrium point \( E(x^*,y^*) \), we choose b as the bifurcation parameter fixing other model parameters. Let us suppose that roots of the equation (8) become purely imaginary at \( b=b^*\). Suppose there exists a \(\epsilon -\) neighborhood (\(\epsilon >0\)) \( (b^*-\epsilon , b^*+\epsilon ) \) of \( b^* \) in which roots of the equation (8) are of the form \( \lambda =F\pm iG \) with \( F(b^*)=0 \) where \(F = - \dfrac{a_1}{2}, G = \dfrac{\sqrt{4 a_0 - a_1^2}}{2}\). Now putting values of \( \lambda \) in equation (8) and separating the real and imaginary parts we get
Differentiating (11) with respect to b and putting \( b=b^* \), we get
Eliminating \( \dfrac{\mathrm{d}G(b^*)}{\mathrm{d}b} \) from the above two equations, we obtain
Summarizing the above results, we have the following theorem:
Theorem 12
A necessary and sufficient condition for model system (2) will experience Hopf bifurcation at the endemic equilibrium point \(E(x^*, y^*)\) is that there exists \(b = b^*\) such that
(i) \(Re(\lambda (b^*)) = 0\) and (ii) \(\left[ \dfrac{d Re(\lambda (b))}{db}\right] _{b = b^*} \ne 0.\)
where \(\lambda \) is complex root of Eq. (8).
6.5 Direction of Hopf bifurcation
In the above, we have derived the necessary and sufficient condition for which model system (2) experiences Hopf bifurcation. Now we deduce the normal form of Hopf bifurcation to investigate the sufficient conditions for stability of Hopf bifurcated periodic solutions [41,42,43] and direction of Hopf bifurcation.
Theorem 13
If \(F'(b^*) = \left[ \dfrac{\mathrm{d} Re(\lambda (b))}{\mathrm{d}b}\right] _{b = b^*} \ne 0\), then the model system (2) undergoes through Hopf bifurcation about the endemic equilibrium point \(E(x^*, y^*)\) when the number of bed (b) crosses the critical value \(b = b^*\). Furthermore, (i) If \( c_{1}(b^*) < 0 \), then periodic solution is stable; therefore, Hopf bifurcation is supercritical, and
(ii) \( c_{1}(b^*) > 0 \), then periodic solution is unstable; therefore, Hopf bifurcation is subcritical where \( c_{1}(b^*) \) is defined in the text.
Proof
First, we translate the origin to the endemic equilibrium point \(E(x^*, y^*)\) of the system (2) using the transformation \( X = x - x^*\), \(Y = y - y^* \) which gives
By Taylor’s series expansion about \((x^*, y^*)\), from (13) we get
where \(A=\left[ \begin{array}{cc} a_{10} &{} a_{01} \\ b_{10} &{} b_{01} \end{array} \right] \), \( \phi _{1}(X, Y) = a_{20} X^2 + a_{11} X Y + a_{02} Y^2 + a_{12} X Y^2 + a_{03} Y^3 \) and \( \phi _{2}(X, Y) = b_{11} X Y + b _{02} Y^2 + b_{12} X Y^2 + b_{03} Y^3\) with \(a_{10} = - \dfrac{r x^*}{K}\), \(a_{01} = - \dfrac{\beta x^*(1 - \alpha {y^*}^2)}{(1 + \alpha {y^*}^2)^2},\) \(b_{10} = \dfrac{\beta y^*}{1 + \alpha {y^*}^2},\) \(b_{01} = - \dfrac{2 \alpha \beta x^* {y^*}^2}{(1 + \alpha {y^*}^2)^2} + \dfrac{(\mu _1 - \mu _0)b y^*}{(b + y^*)^2}\), \(a_{20}\) = \(\left( - \ \dfrac{r }{K}\right) \), \(a_{11}\) = \(-\dfrac{\beta ( 1 - \alpha y^*{^2} ) }{(1+\alpha y^*{^2} )^2 }\), \(a_{02}\) = \(\dfrac{\alpha \beta x^* y^* ( 3 - \alpha y^*{^2} ) }{( 1+\alpha y^*{^2})^ 3 }\), \(a_{12}\) = \(\dfrac{2 \alpha \beta y^*}{(1 + \alpha y^*{^2})^2} - \ \dfrac{\alpha \beta ( 3 \alpha y^*{^2} - 1 ) }{( 1+\alpha y^*{^2} )^ 3 }\) , \(a_{03}\) = \(\dfrac{\alpha \beta x^* ( \alpha ^2 y^*{^4} - 6 \alpha y^*{^2} + 1 ) }{( 1+\alpha y^*{^2} )^ 4 },\) \(b_{11}\) = \(\dfrac{\beta ( 1 - \alpha y^*{^2} ) }{( 1+\alpha y^*{^2} \ )^2 }\) , \(b_{02}\) = \( \dfrac{(\mu _{1} - \mu _{0}) b^2_{0}}{( b_{0} + y^*)^3}- \dfrac{ \alpha \beta x^* y^*( 3 - \alpha y^*{^2})}{(1+ \alpha y^*{^2})^3 }\), \(b_{12}\) = \( \ - \ \dfrac{ \alpha \beta y^*( 3 - \alpha y^*{^2} )}{(1+ \alpha y^*{^2} )^3 }\), \(b_{03}\) = \( \ \dfrac{\alpha \beta x^* ( 6 \alpha y^*{^2} - \alpha ^2 y^*{^4} - 1 )}{( 1+\alpha y^*{^2} \ )^ 4 } \ - \ \dfrac{(\mu _{1} - \mu _{0}) b^2_{0}}{( b_{0} + y^*) ^4 \ } \).
The characteristic roots of A are in the form \(F \pm i G\) in the neighborhood of \( b = b^* \). The eigen vector corresponding to the eigenvalue \(\lambda = F + i G \) is \( X = \left[ \begin{array}{c} 1 \\ N - i P \end{array} \right] \) where \( N = \left( F + \dfrac{r x^*}{K} \right) \dfrac{\beta x^* (\alpha {y^*}^2 - 1) (1 + \alpha {y^*}^2)^2}{G^2 (1 + \alpha {y^*}^2)^4 + \beta ^2 {x^*}^2 (1 - \alpha {y^*}^2)^2}\) and P = - \(\left( F + \dfrac{r x^*}{K} \right) \dfrac{G (1 + \alpha {y^*}^2)^4 }{G^2 (1 + \alpha {y^*}^2)^4 + \beta ^2 {x^*}^2 (1 - \alpha {y^*}^2)^2}\).
Using the transformation \(\left[ \begin{array}{c} X \\ Y \end{array} \right] = C \left[ \begin{array}{c} u \\ v \end{array} \right] \) where \(C = \left[ \begin{array}{cc} 1 &{} 0 \\ N &{} P \end{array} \right] \) which gives \( X = u,\) \(Y = u N + v P\).
Under the above transformation the system (14) reduces to
where \( f(u, v) = (a_{20}+N a_{11} + N^2 a_{02}) u^2 + (P a_{11} + 2 N P a_{02})uv + P^2 a_{02} v^2 + (N^2 a_{12} + N^3 a_{03})u^3 + (2 N P a_{12} + 3 N^2 P a_{03})u^2 v + (3 N P^2 a_{03} + P^2 a_{12})u v^2 + P^3 a_{03} v^3 \)
System (15) can be written in the polar form using the methodology developed in [41,42,43]
which is the normal form of Hopf bifurcation.
Expanding by Taylor’s series expansion about \(b = b^*,\) from (16) we get
where
with \(f_{uuu}(0,0,b^*) = a_{12} N^2 + a_{03} N^3,\) \(f_{uvv}(0,0,b^*) = 3 N P^2 a_{03} + P^2 a_{12},\)
\(g_{uuv}(0,0,b^*) = \dfrac{3 P N b_{12} + 3 P N^2 b_{03} - (3 N^2 P a_{03} + 2N P a_{12})N}{P},\) \(g_{vvv}(0,0,b^*) = \dfrac{P^3 b_{03} - NP^3 a_{03}}{P},\)
\(f_{uv}(0,0,b^*) = P a_{11} + 2 a_{02} N P,\) \(f_{uu}(0,0,b^*)= a_{20} + a_{11} N + a_{02}N^2,\) \(f_{vv}(0,0,b^*) = P^2 a_{02},\)
\(g_{uv}(0,0,b^*) = \dfrac{P b_{11} + 2 NP b_{02} - N(2 N P a_{02}+ P a_{11})}{P},\)
\(g_{uu}(0,0,b^*) = \dfrac{N^2 b_{02}+ N b_{11} - (N^2 a_{02} + N a_{11} + a_{20})N}{P},\)
\(g_{vv}(0,0,b^*)= \dfrac{P^2 b_{02} - N P^2 a_{02}}{P}.\)
Thus, for existence of the periodic solution we must have [43]
Again if \( c_{1}(b^*)\ne 0\), then the system follows a surface of periodic solution in the center manifold [41, 43], the periodic solution is stable \( c_{1}(b^*) < 0 \) and unstable for \( c_{1}(b^*) > 0 \).
This completes proof of the theorem. \(\square \)
Bifurcation diagram with respect to parameter b and other parameter values given in Table 3 with \(\beta = 0.2, \, r = 0.5, \, \mu _{1} = 1.8\)
In Fig. 9, we have presented the bifurcation diagram with respect to the number of available hospital beds (b). It is clear from the figures that switching of instability occurs here. We see from the figures that the system losses stability at \(P_{1}\) (for \(b = b_{1}^{*} = 0.3608114828 \)) through supercritical Hopf bifurcation about the endemic equilibrium point. Again at \(P_{2}\) (for \(b = b_{2}^{*} = 1.185564499)\), the system becomes stable through subcritical Hopf bifurcation.
6.5.1 Significance of b as a Hopf bifurcation parameter
For the parameter values given in Table 3 with \(\beta = 0.2, \, r = 0.5, \, \mu _{1} = 1.8\), we get two critical values of the bifurcation parameter b namely \(b_{1}^{*} = 0.3608114828\) and \(b_{2}^{*} = 1.185564499\) for which \(tr(J_{E}) = 0\) with \(det(J_{E}) > 0\). The considered system experiences Hopf bifurcation at these two critical points. To investigate the dynamics for different values of b, we consider the following three cases: (i) \(b < b_{1}^{*}\) (ii) \(b_{1}^{*}< b < b_{2}^{*}\) (iii) \( b> b_{2}^{*}.\) In the first case, for \(b = 0.3\), the system contains one saddle disease-free equilibrium point and a stable endemic equilibrium point (see the phase portrait in Fig. 10a). For the second case, we consider \(b = 0.75\); then, the endemic equilibrium point becomes unstable and a stable limit cycle arises around the endemic equilibrium point, whereas the disease-free equilibrium point remains same (see the phase portrait in Fig. 10b, the red curve is the stable limit cycle). In the third case for \(b = 1.25\), the endemic equilibrium point again becomes stable and the disease-free equilibrium point remains same (see the phase portrait in Fig. 10c).
For \(b < b_{1}^{*}\), disease-free equilibrium point is saddle and endemic equilibrium point is stable which indicates disease persists in this case. For \(b_{1}^{*}< b < b_{2}^{*}\), disease-free equilibrium point is saddle and endemic equilibrium point is unstable which gives stable limit cycle that means disease oscillates within and on the limit cycle, so disease cannot be eradicated here. Further, for \(b_{2}^{*} < b\), disease-free equilibrium point is saddle and endemic equilibrium point is stable which means disease also persists in this case.
7 Optimal control technique and its application
In this section, our aim is to find the best policy among vaccination and treatment for controlling the disease as well as minimizing the cost using the technique of optimal control theory. To minimize the disease transmission, generally vaccination and treatment are performed to susceptible and infected individuals, respectively. But if constant rate of vaccination and treatment are taken into consideration for eradication of the disease, then cost for implementation of vaccine and treatment may be very high. So for eradication of the disease with minimum cost in a finite time, we need to consider control variable as a function of time t. The main purpose for applying optimal control strategy is to reduce the number of susceptible and infected individuals with minimum cost for vaccination and treatment [30]. In the proposed model, we have considered vaccination to the susceptible individuals and treatment to the infected individuals as disease controlling variable. Now we need to formulate an optimal control problem for minimizing the implemented cost for vaccine and treatment and also at same time to reduce susceptible and infected individuals.
7.1 Formulation of optimal control problem
In model system (2), we consider the treatment rate \(\psi (b, y) = \left\{ \mu _{0} + (\mu _{1} - \mu _{0})\dfrac{b}{b + y}\right\} \) as a function of limited hospital resources that means in terms of available number of hospital beds \(\left( b\right) \). We have already seen that the value of per capita cure rate lies between \(\mu _{0}\) and \(\mu _{1}\), whereas the value of b is finite. In order to consider the effect of treatment control, we are reconstructing treatment rate introducing new control variable \(u_2\) in the form \(\prod (u_{2}) = \left\{ \mu _{0} + (\mu _{1} - \mu _{0}) \dfrac{b u_{2}}{b + u_{2} y}\right\} \) which has minimum and maximum value \(\mu _{0}\) and \(\mu _{1}\) corresponding to \(u_{2}\) = 0 and \(u_{2}\) = 1 with large number of infected individuals, respectively. Thus, the control variable \(u_{2}\) is bounded in the function \(\prod (u_{2})\). To formulate optimal control problem, we are considering the control variables \(u_{1}(t)\) and \(u_{2}(t)\) as function of t.
The problem is to minimize objective functional given by
subject to the system of equations
satisfying \(x(0) \geqslant 0\), \(y(0) \geqslant 0\), \(z(0) \geqslant 0\) and the controls \(u_{1}(t)\) and \(u_{2}(t)\) are Lebesgue measurable functions such that control constraint U is given by
In the optimal objective functional, constants \(A_{1}(> 0)\) and \(A_{2}(> 0)\) are the weighted cost for minimizing total number of susceptible and infected individuals, whereas \(A_{3}(> 0)\) and \(A_{4}(> 0)\) are weighted cost associated with vaccination and treatment function. We use quadratic term of the control variable in objective functional to reflect severity of side effects of treatment and vaccination for giving too much amount to an individual [44]. Our intention is to reduce susceptible and infected individuals, at the same time to maximize recovered individuals with minimize cost due to implementation of vaccine and treatment on a finite interval [0, T]. In optimal constraint U, vaccinated and treated percentage of susceptible and infected individuals per unit time is represented by control variable \((u_{1}(t), u_{2}(t)) \in U \). Thus, we seek an optimal control pair \(\left( u_{1}^*, u_{2}^* \right) \) such that
where U is defined in (20).
7.2 Existence and uniqueness of optimal control
Theorem 14
For optimal control problem (18) subject to the condition (19), there exist an optimal control pair \((u_{1}^{*}, u_{2}^{*})\) and corresponding optimal state variables \((x^{*}, y^{*}, z^{*})\) which minimize objective functional \( M(u_{1}, u_{2})\) over set of optimal constraint \(U = \lbrace \left( u_{1}(t), u_{2}(t) \right) | \ 0 \leqslant u_{1}(t) \leqslant 1 , 0 \leqslant u_{2}(t) \leqslant 1, t \in [0, T] \rbrace \) such that
Proof
The existence of optimal control problem can be verified using the result of Filippove–Cesari theorem [46]. The control and corresponding state variables are non-negative and non-empty. Control variables \(u_{1}, u_{2} \in U \) are closed and bounded. Compactness of control variables is needed for existence of optimal control. The control constraint set U is also convex set and the state variables (x, y, z) are also bounded. Furthermore, integrand of the objective functional \(M(u_{1}, u_{2})\) is also convex with respect to control variables \(u_{1}, u_{2}\). Finally, we can obtain \(w_{1}, w_{2} > 0\) and \(\rho \) such that integrand of objection functional \(M(u_{1}, u_{2})\) satisfies
Therefore, all conditions for existence of optimal control problem are satisfied and uniqueness property are guaranteed by Lipschitz property of the state variables x, y, z. Hence, the theorem is proved. \(\square \)
7.3 Characterization of optimal control problem
Theorem 15
Given optimal control pair \((u_{1}^{*}, u_{2}^{*})\) and corresponding optimal state variables \((x^{*}, y^{*}, z^{*})\) of state system (18) and (19) which minimize \(M(u_{1}, u_{2})\) over U, there exist adjoint variables \(\lambda _{1}, \lambda _{2}\) and \(\lambda _{3}\) satisfying
with transversality condition
and the optimal control pair \(u^{*}(t)\) = \((u_{1}^{*}(t), u_{2}^{*}(t))\) is given by
where \(\overline{u}_{2}\) is the non-negative root of the equation \(A_{4}u_{2} ( b + u_{2} y^{*} ) ^2 = b^{2}y^{*}(\lambda _{2} - \lambda _{3}) (\mu _{1} - \mu _{0}).\)
Proof
To characterize the optimal control, we use Pontryagin’s Maximum Principle [45]. First we define Lagrangian of optimal control problem (18) as
and Hamiltonian H as
satisfies adjoint equations
with transversality condition \(\lambda _{i}(T) = 0, i = 1, 2, 3 \)
Solving equations in (26), we see that adjoint variables \(\lambda _{1}, \lambda _{2}, \lambda _{3}\) satisfy the following equations :
with \(\lambda _{1}(T) = \lambda _{2}(T) = \lambda _{3}(T) = 0\).
Now using optimality conditions \(\dfrac{\partial H}{\partial u_{1}} = 0\) and \(\dfrac{\partial H}{\partial u_{2}} = 0 \) at \(u_{1}(t) = u_{1}^{*}(t)\), \(u_{2}(t) = u_{2}^{*}(t)\), we get
where \( \overline{u}_{2}\) is non-negative root of the equation \(A_{4}u_{2} ( b + u_{2} y^{*} )^2 = b^{2} y^{*}(\lambda _{2} - \lambda _{3}) (\mu _{1} - \mu _{0})\). It is clear that \(\dfrac{\partial ^{2} H}{\partial u_{1}^{2}} > 0\), \(\dfrac{\partial ^{2} H}{\partial u_{2}^{2}} > 0\) and \(\dfrac{\partial ^{2} H}{\partial u_{1}^{2}}\).\(\dfrac{\partial ^{2} H}{\partial u_{2}^{2}}\) > \( \left( \dfrac{\partial ^{2} H}{\partial u_{1} \partial u_{2}} \right) ^2 \) at \((u_{1}^{*}, u_{2}^{*})\).
Therefore, optimal control problem is minimum at \(u^{*}(t)\) = \((u_{1}^{*}(t), u_{2}^{*}(t))\). \(\square \)
We have solved the optimal control problem numerically using forward–backward sweep method which combines forward application of fourth-order Runge–Kutta method of the system (19) with backward application of fourth-order Runge–Kutta method of the system (22) satisfying the condition (23). For model simulation purpose, we take the vaccination and treatment time interval as [0, 20] (where unit of time may be day or week depending on nature of the disease), i.e., vaccination and treatment continue up to 20 units of time, and after this time, both policy will automatically stop. To study the effect of control strategies here we are considering two infectious disease like influenza (low rate of infection) and COVID-19 (high rate of infection). We observe from the literature that the rate of infection (\(\beta \)), natural death rate of human (d) and disease-induced death rate of human (\(\delta \)) of populations are in the following range:
-
(i)
For influenza: \(\beta \in [5 \times 10^{-5},0.7]\), \(d\in [0.0143,0.0167],\) and \(\delta \in [0.06,0.09]\) [47,48,49, 53].
-
(ii)
For COVID-19: \(\beta \in [0.75,1]\), \(d\in [0.0143,0.0167],\) and \(\delta \in [0.03712,0.0572]\)[50,51,52,53].
For model simulation purpose, we consider value of other model parameters and weight functions \(A_{i}, i = 1,2,3,4\) as given in Table 4 with initial population \(x(0) = 100000\), \(y(0) = 10000\), \(z(0) = 0\).
In Figs. 11 and 12, we have presented the time series of susceptible, infected, recovered individuals and control strategies in presence and absence of controls for \(\beta = 0.1\) (for Influenza) with \(d = 0.0147,\) \(\delta = 0.07\) and \(\beta = 0.9\) (for COVID-19) with \(d = 0.0147\), \(\delta = 0.038\), respectively. It is clear from first three figures of both cases that in the presence of control, density of infected population is lower compared to the absence of controls. In Figs. 11d, e and 12d, e we have presented the time series of control variables. It is clear from Fig. 11d, e that full strength of vaccination will continue up to 18.98 unit and full strength of treatment policy is not required for lower rate of infection (i.e., \(\beta = 0.1\)). The controls will reduce following the path as shown in Fig. 11d, e and it will stop after 20 unit time. But for high rate of infection (see Fig. 12d, e) the full strength vaccination and treatment policy will continue up to 18.48 unit and from 1.03 unit to 4.43 unit, respectively, and it will stop after 20 unit time. If same control parameters are used beyond t = 20 unit time, then also the density of infected individuals will reduce in both cases. Thus, it is clear from the above analysis that the vaccination policy is more or less same for both lower and higher rate of infection, but higher rate of treatment is necessary for higher rate of infection.
7.4 Efficiency analysis
In our study, we have used two types of control parameter \(u_{1}\) and \(u_{2}\) where \(u_{1}\) is applied for susceptible individuals, whereas \(u_{2}\) is used for infected individuals. If we want to apply only one type of control among vaccination and treatment to reduce cost as well as time, one question arises ’which one will better among them to reduce the infection?’ When two or more than two control are used in mathematical models, to know best efficient policy among them to reduce the infection, then we perform efficiency analysis. In efficiency analysis, efficiency index (E.I.) is given by the formula E.I.= \(\left( 1 - \dfrac{A^{c}}{A^{0}} \right) \times 100\) where \(A^{c}\) and \(A^{0}\) are cumulative number of infective with and without control parameter, respectively. Higher value of efficiency index (E.I.) number is the best strategy [54].
Two types of controls \(u_{1}\) and \(u_{2}\) are used in our model system. Now three cases may arise. (i) When we use only vaccination for susceptible, but we do not use treatment for infected individuals, i.e., \(u_{1} \ne 0\) but \(u_{2} = 0\), and (ii) when we use only treatment for infected individuals, but we do not use any vaccination for susceptible, i.e., \(u_{1} = 0\) but \(u_{2} \ne 0\). (iii) When we use both vaccination for susceptible and treatment for infected individuals. We rename these three cases as strategy 1, strategy 2 and strategy 3, respectively. So strategy 1 is \(u_{1} \ne 0\) but \(u_{2} = 0\), strategy 2 is \(u_{1} = 0\), but \(u_{2} \ne 0\) and strategy 3 is \(u_{1} \ne 0\) but \(u_{2} \ne 0\). Now to evaluate the value of efficiency index number (E.I.), we first calculate the values of \(A^{0}\) and \(A^{c}\). We compute the value of \(A^{0}\), cumulative number of infected individuals without control during time t, \(t \in [0,20]\) by \(A^{0} = \int _{0}^{20} y(t) dt\) using Simpson’s \(\dfrac{1}{3}\) rule. For \(\beta = 0.1\), \(A^{0} = 38.2155\) and values of \(A^{c}\) and efficiency index (E.I.) are given in Table 5. For \(\beta = 0.9\), \(A^{0} = 96.5638\) and values of \(A^{c}\) and efficiency index (E.I.) are given in Table 6. From Tables 5 and 6, it is clear that between strategy 1 and strategy 2, strategy 1 is better than strategy 2 for both cases. In view of epidemiology, vaccination for susceptible is more efficient than using treatment to infected individuals to reduce the influence of infection. But strategy 3 is more effective among three strategies for both cases. So in biological sense of view, if both vaccination and treatment are applied in the community, then the number of infected individuals is more reduced.
8 Conclusion
In this paper, we have proposed an epidemic model with logistic growth rate of susceptible population, non-monotone incidence rate and nonlinear treatment rate with the effect of limited hospital beds. We have carried out stability and bifurcation analysis of the system in the neighborhood of different equilibrium points with respect to different model parameters. For \( R_{0} < 1 \), the disease-free equilibrium point is locally stable, and for \( R_{0} > 1 \) the endemic equilibrium point is always locally stable. Using center manifold theorem, we have established that the disease-free equilibrium point shows two types of behaviors: one is saddle-node point of co-dimension one and other is an attracting node of co-dimension 2 for the threshold value \( R_{0} = 1 \). We have studied different types of bifurcations, namely Transcritical bifurcation, Backward bifurcation, Saddle-node bifurcation and Hopf bifurcation for different parameter values. Numerically we have shown bifurcation diagrams and the corresponding phase portraits for each type of bifurcation. We have shown that for lower values of both the rate of infection and birth rate of susceptible population, disease will be eradicated from the system, but in this situation if the birth rate becomes higher, then disease will persist in the system. On the hand for higher value of the rate of infection, disease persists in the system with more infected population density. We have also shown that for higher influence of disease transmission, disease cannot be eradicated from the system even higher level of treatment provided. According to our study, we see that there exists two endemic equilibrium points for \(R_{0} < 1\), smaller one is unstable, whereas bigger one is stable which shows that \(R_{0}\) is not enough to conclude the dynamical behavior of the model system. To diminish the impact of the disease spreading, we need to control the density of the population. For our proposed model, multi-stable state, stable limit cycle, stable spiral arise which indicates to control the disease, we should take necessary actions such that initial infected population is at lower level. We observed that rich dynamical behavior not only depends on \(R_{0}\), it also depends on the number of hospital beds, vaccination, inhibitory factors of susceptible, crowding effect of infected population etc. Therefore, to control or eradicate the disease, we should combined government intervention policies as well as hospitalized condition. Optimal control strategies and efficiency analysis are performed to find out the best policy to minimize the impact of the disease. Improving medical techniques and investing large number of medical resources such as medicines, doctors, isolation places and quarantine, disease can be controlled in the community.
Data availability
Data of this study will be made available from the corresponding author on reasonable request.
References
Cai, Y., Kang, Y., Banerjee, M., Wang, W.: A stochastic SIRS epidemic model with infectious force under intervention strategies. J. Differ. Equ. 259, 7463–7502 (2015)
Yu, P., Zhang, W.: Complex dynamics in a unified SIR and HIV disease model: a bifurcation theory approach. J. Nonlinear Sci. 29, 2447–2500 (2019)
Bailey, N.T.J.: The Mathematical Theory of Infectious Diseases and Its applications, 2nd edn. Hafner Press, New York (1975)
Brauer, F., Castillo-Chavez, C.: Mathematical Models in Population Biology and Epidemiology. Springer, Berlin (2011)
Anderson, R.M., May, R.M.: Infectious Diseases of Humans: Dynamics and control. Oxford University Press, Oxford (1992)
Bernoulli, D.: An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it, reprint. Rev. Med. Virol. 14, 275–288 (2004)
Kermack, W., Mckendrick, A.: A contribution to mathematical theory of epidemics. Proc. R. Soc. Lond. A 115, 700–721 (1927)
Lu, M., Huang, J., Ruan, S., Yu, P.: Bifurcation analysis of an SIRS epidemic model with a generalized non-monotone and saturated incidence rate. J. Differ. Equ. 267, 1859–1898 (2019)
Liu, J., Wang, K.: Hopf bifurcation of a delayed SIQR epidemic model with constant input and nonlinear incidence rate. Adv. Differ. Equ. 168, (2016)
Nwagwo, A., Bakare, E.A.: Stability analysis of an SIR epidemic model and effect of control strategies with constant recruitment. Appl. Math. Sci. (2014)
Li, J., Teng, Z., Wang, G., Zhang, L., Hu, C.: Stability and bifurcation analysis of an SIR epidemic model with logistic growth and saturated treatment. Chaos Solitons Fractals 99, 63–71 (2017)
Wang, J., Zhang, J., Jin, Z.: Analysis of an SIR model with bilinear incidence rate. Nonlinear Anal. RWA 11, 2390–2402 (2010)
Hu, Z.Y., Chang, L.L., Teng, Z.D., Chen, X.: Bifurcation analysis of a discrete SIRS epidemic model with standard incidence rate. Adv. Differ. Equ. 155 (2016)
Martcheva, M.: An Introduction to Mathematical Epidemiology. Springer, New York (2015)
Yorke, J., London, W.: Recurrent outbreaks of measles, chickenpox and mumps. Am. J. Epidemiol. 98, 469–482 (1973)
Liu, W., Levin, S., Iwasa, Y.: Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J. Math. Biol. 23, 187–204 (1986)
Capasso, V., Serio, G.: A generalization of the Kermack–Mckendric deterministic epidemic model. Math. Biosci. 42, 43–61 (1978)
Jana, S., Nandi, S.K., Kar, T.K.: Complex dynamics of an SIR epidemic model with saturated incidence rate and treatment. Acta Biotheor. 84(1), 65–84 (2016)
Khan, M.A., Khan, Y., Islam, S.: Complex dynamics of an SEIR epidemic model with saturated incidence rate and treatment. Phys. A 493, 210–227 (2018)
Xiao, D., Ruan, S.: Global analysis of an epidemic model with non-monotone incidence rate. Math. Biosci. 208, 419–429 (2007)
Ruan, S., Wang, W.: Dynamical behavior of an epidemical model with a nonlinear incidence rate. J. Differ. Equ. 188, 135–163 (2003)
Liu, W., Hethcote, H., Levin, S.: Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 25, 359–380 (1987)
Hethcote, H., Driessche, P.: Some epidemiological models with nonlinear incidence. J. Math. Biol. 29, 271–287 (1991)
Wang, W., Ruan, S.: Bifurcation in an epidemic model with constant removal rate of the infectives. J. Math. Anal. Appl. 291, 775–793 (2004)
Wang, W.: Backward bifurcation of an epidemic model with treatment. Math. Biosci. 201, 58–71 (2006)
Zhang, X., Liu, X.N.: Backward bifurcation of an epidemic model with saturated treatment function. J. Math. Anal. Appl. 348, 433–443 (2008)
Zhou, L., Fan, M.: Dynamics of an SIR epidemic model with limited medical resources revisited. Nonlinear Anal. Real World Appl. 13, 312–324 (2012)
Shan, C., Zhu, H.: Bifurcations and complex dynamics of an SIR model with the impact of the number of hospital beds. J. Differ. Equ. 257, 1662–1688 (2014)
Abdelrazec, A., Belair, J., Shan, C., Zhu, H.: Modeling the spread and control of dengue with limited public health resources. Math. Biosci. 271, 136–145 (2016)
Lenhart, S., Workman, J.T.: Optimal control applied to biological model. Mathematical and Computational Biology Series. Chapman and Hall/CRC, Boca Raton (2007)
Kar, T.K., Jana, S.: A theoretical study on mathematical modelling of an infectious disease with application of optimal control. Biosystems 111(1), 37–50 (2013)
Zaman, G., Kang, Y., Jung, J.: Stability analysis and optimal vaccination of an SIR epidemic model. Biosystems 93, 240–249 (2008)
Zaman, G., Kang, Y.H., Jung, J.H.: Optimal treatment of an SIR epidemic model with time delay. Biosystems 98(1), 43–50 (2009)
Gaff, H., Schaefer, E.: Optimal control applied to vaccination and treatment strategies for various epidemiological models. Math. Biosci. Eng. 469–492 (2009)
van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease trans-mission. Math. Biosci. 180, 29–48 (2002)
Wiggins, S.: Introduction to Applied Nonlinear Dynamical System and Chaos. Text in applied Mathematics, Vol. 2, Springer-Verlag, New York (2003)
Liapunov, A.M.: Stability of motion, with a contribution by V. A. Pliss and an introduction by V. P. Basov. Translated from the Russian by Flavian Abramovici and Michael Shimshoni. Mathematics in Science and Engineering. 30, Academic Press, New York (1966)
Shuai, Z., van den Driessche, P.: Global stability of infectious disease models using Lyapunov functions. SIAM J. Appl. Math. 73, 1513–1532 (2013)
Perko, L.: Differential Equations and Dynamical Systems, vol. 7. Springer, Berlin (2000)
Castillo-Chavez, C., Song, B.: Dynamical model of tuberculosis and their applications. Math. Biosci. Eng. 1(2004), 361–404 (2004)
Marsden, J.E., McCracken, M.: The Hopf Bifurcation and Its Applications, Applied Mathematical Sciences, vol. 19. Springer-Verlag, Berlin (1976)
Nayfeh, A.H., Balachandran, B.: Applied Nonlinear Dynamics: Analytical. WILEY-VCH Verlag, Computational and Experimental Methods (1995)
Han, M., Hu, P.: Normal Forms. Applied Mathematical Sciences, Springer-Verlag, Melnikov Functions and Bifurcations of Limit Cycles (2012)
Sharomi, O., Malik, T.: Optimal control in epidemiology. Ann. Oper. Res. (2015). https://doi.org/10.1007/s10479-015-1834-4
Pontryagin, L.S., Boltyanskii, V.G., Gamkrelidze, R.V., Mishchenko, E.F.: The Mathematical Theory of Optimal Processes. Wiley, New Jersey (1962)
Nababan, S.: A Filippov-type lemma for functions involving delays and its application to time delayed optimal control problems. Optim. Theory Appl. 27(3), 357–376 (1979)
Vaidya, N.K., Morga, M., Jones, T., Miller, L., Lapin, S., Schwartz, E.J.: Modelling the epidemic spread of an H1N1 influenza outbreak in a rural university town. Epidemiol. Infect. 143, 1610–1620 (2015)
Prieto, K., Ibarguen-Mondragon, E.: Parameter estimation, sensitivity and control strategies analysis in the spread of influenza in Mexico. J. Phys. Conf. Ser. 1408, 012020 (2019). https://doi.org/10.1088/1742-6596/1408/1/012020
Kim, Y., Barber, A.V., Lee, S.: Modeling influenza transmission dynamics with media coverage data of the 2009 H1N1 outbreak in Korea. PLoS ONE 15(6), e0232580 (2020). https://doi.org/10.1371/journal.pone.0232580
Biswas, S.K., Ghosh, J.K., Sarkar, S., Ghosh, U.: COVID-19 pandemic in India: a mathematical model study. Nonlinear Dyn. (2020). https://doi.org/10.1007/s11071-020-05958-z
Khajanchi, S., Sarkar, K.: Forecasting the daily and cumulative number of cases for the COVID-19 pandemic in India. Chaos (2020). https://doi.org/10.1063/5.0016240
Carcione, J.M., Santos, J.E., Bagaini, C., and Jing, B.: A simulation of a COVID-19 epidemic based on a deterministic SEIR model. Front. Public Health. 8 (2020)
Pinho, S.T.R., Ferreira, C.P., Esteva, L., Barreto, F.R., Silva, V.C.M., Teixeira, M.G.L.: Modelling the dynamics of dengue real epidemics. Philos. Trans. R. Soc. A 368, 5679–5693 (2010)
Carvalho, S.A., Silva, S.O., Cunha I.C.: Mathematical modeling of dengue epidemic: control methods and vaccination strategies. arXiv: 1508.00961 (2015)
Acknowledgements
The authors would like to thank the reviewers and the editor for the valuable comments and suggestions. The first author would also like to thank UGC, Government of India, for the financial assistance under Junior Research Fellowship Scheme (UGC Ref. No.: 1222/(CSIR-UGC NET JUNE 2019)) toward this research work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors of this paper declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Saha, P., Ghosh, U. Global dynamics and control strategies of an epidemic model having logistic growth, non-monotone incidence with the impact of limited hospital beds . Nonlinear Dyn 105, 971–996 (2021). https://doi.org/10.1007/s11071-021-06607-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06607-9