On interrelations between strongly, weakly and chord separated set-systems (a geometric approach)

Abstract

We consider three types of set-systems that have interesting applications in algebraic combinatorics and representation theory: maximal collections of the so-called strongly, weakly, and chord separated subsets of a set $[n]=\{1,2,\ldots ,n\}$. These collections are known to admit nice geometric interpretations; namely, they are, respectively, in bijection with rhombus tilings on the zonogon Z(n, 2), combined tilings on Z(n, 2), and fine zonotopal tilings (or “cubillages”) on the 3-dimensional zonotope Z(n, 3). We describe interrelations between these three types of set-systems in $2^{[n]}$, working in terms of their geometric models. In particular, we characterize the sets of rhombus and combined tilings properly embeddable in a fixed 3-dimensional cubillage and give efficient methods of extending a given rhombus or combined tiling to a cubillage, etc.

1 Introduction

For a positive integer n, the set $\{1,2,\ldots ,n\}$ is denoted by [n]. We deal with three types of binary relations on subsets of [n].

• Sets $A,B\subseteq [n]$ are called strongly separated (from each other) if there are no three elements $i<j<k$ of [n] such that one of $A-B$ and $B-A$ contains i, k, and the other contains j.

• Sets $A,B\subseteq [n]$ are called chord separated if there are no elements $i<j<k<\ell$ of [n] such that one of $A-B$ and $B-A$ contains i, k, and the other contains $j,\ell$.

• Sets $A,B\subseteq [n]$ are called weakly separated if they are chord separated and, in addition, if there are three elements $i<j<k$ of [n] such that $i,k\in A-B$ and $j\in B-A$ (resp. $i,k\in B-A$ and $j\in A-B$), then $|A|\le |B|$ (resp. $|B|\le |A|$).

Accordingly, a collection ${{\mathcal {A}}}\subseteq 2^{[n]}$ of subsets of [n] is called strongly (weakly, chord) separated if any two members of ${{\mathcal {A}}}$ are strongly (resp. weakly, chord) separated.

Hereinafter, for sets $A,B\subseteq [n]$, we write |A| for the size (the number of elements) of A,  $A-B$ for the set difference $\{i:A\ni i\notin B\}$, and $A<B$ if the maximal element $\max (A)$ of A is smaller than the minimal element $\min (B)$ of B, letting $\min (\emptyset ):=\infty$ and $\max (\emptyset ):=-\infty$. Also, we say that A surrounds B if $\min (A-B)<\min (B-A)$ and $\max (A-B)>\max (B-A)$. (In particular, when A, B are weakly separated, A surrounds B, and $B-A\ne \emptyset$, it follows that $|A|\le |B|$.)

Recall that the notions of strong and weak separations were introduced by Leclerc and Zelevinsky in [8], and the notion of chord separation is due to Galashin [5] (who justified this term by the observation that if n points labeled $1,2,\ldots ,n$ are disposed on a circumference O, in this order cyclically, then O has a chord separating $A-B$ from $B-A$.)

For brevity, we refer to strongly, weakly, and chord separated collections as s-, w-, and c-collections, respectively. In the hierarchy of these collections, any s-collection is a w-collection, and any w-collection is a c-collection, but the converse need not hold. Such collections are encountered in interesting applications. In particular, s-, and w-collections appeared in [8] in connection with a characterization of quasi-commuting flag minors of a quantum matrix. Weak separation for subsets of a fixed size also arises in the study of the cluster structure on the Grassmannian coordinate ring [12]. Also, they admit impressive geometric representations, which will be discussed later.

An important fact is that these three sorts of collections possess the property of purity. More precisely, let us say that a set-system (domain) ${\mathcal {D}}\subseteq 2^{[n]}$ is s-pure (w-pure, c-pure) if all inclusion-wise maximal s-collections (resp. w-collections, c-collections) in ${\mathcal {D}}$ have the same cardinality, which in this case is called the s-rank (resp. w-rank, c-rank) of ${\mathcal {D}}$. We will rely on the following results on the full domain $2^{[n]}$, where $s_n$ denotes $\left( {\begin{array}{c}n\\ 2\end{array}}\right) + \left( {\begin{array}{c}n\\ 1\end{array}}\right) +\left( {\begin{array}{c}n\\ 0\end{array}}\right)$ ($=\frac{1}{2} n(n+1)+1$)).

• (1.1) [8]  $2^{[n]}$ is s-pure and its s-rank is equal to $s_n$.

• (1.2) [1]  $2^{[n]}$ is w-pure (and its w-rank is equal to $s_n$ as well, in view of a result in [8]).

• (1.3) [5]  $2^{[n]}$ is c-pure and its c-rank is equal to $\left( {\begin{array}{c}n\\ 3\end{array}}\right) +\left( {\begin{array}{c}n\\ 2\end{array}}\right) + \left( {\begin{array}{c}n\\ 1\end{array}}\right) +\left( {\begin{array}{c}n\\ 0\end{array}}\right)$.

(The phenomenon of w-purity has also been established for some other interesting domains, see [2, 10, 11]; however, those results are beyond our paper.)

As is seen from (1.1) to (1.3), the c-rank of $2^{[n]}$ is O(n) times larger that its s- and w-ranks, and we address the following issue: given a maximal c-collection $C\subset 2^{[n]}$, what can one say about the sets $\mathbf{S}(C)$ and ${\mathbf{W}}(C)$ of inclusion-wise maximal s-collections and w-collections, respectively, contained in C?

It turns out that a maximal c-collection C need not be s-pure or w-pure in general, as we show in Sect. 3.1. Nevertheless, the sets of s-collections and w-collections contained in C and having the maximal possible size $s_n$, denoted as $\mathbf{S}^*(C)$ and ${\mathbf{W}}^*(C)$, respectively, have nice structural properties, as is shown in this paper.

For this purpose and wider, we essentially use known geometric constructions for s-, w-, and c-collections. From results in [8], it follows that each maximal s-collection in $2^{[n]}$ corresponds to the vertex set of a rhombus tiling on the n-zonogon in the plane, and vice versa. A somewhat more sophisticated planar structure, namely the so-called combined tilings, or combies, on the n-zonogon are shown to represent the maximal w-collections in $2^{[n]}$, see [2]. As to the maximal c-collections, Galashin [5] recently showed that they are in bijection with subdivisions of the 3-dimensional cyclic zonotope Z(n, 3) into parallelotopes, the so-called fine zonotopal tilings. For brevity, we refer to such subdivisions as cubillages (following terminology in [7]), and to the parallelotopes forming cubillages as cubes.

In this paper, we first discuss interrelations between strongly and chord separated set-systems. A brief outline is as follows. (Note that a theoretical ground of constructions mentioned in (a),(b) below goes back to results on higher Bruhat orders in Manin and Schechtman [9] and their geometric interpretations in Kapranov and Voevodsky [7] and Ziegler [14]. See also [3] for a survey.)

(a) For a maximal c-collection $C\subset 2^{[n]}$, let $Q=Q(C)$ be its associated cubillage (where the elements of C correspond to the 0-dimensional cells, or vertices, of Q regarded as a complex). Then, for each $S\in \mathbf{S}^*(C)$, its associated rhombus tiling T(S) is viewed (up to a piecewise linear deformation) as a 2-dimensional subcomplex of Q, called an s-membrane in it. Furthermore, these membranes (and therefore the members of $\mathbf{S}^*(C)$) constitute a distributive lattice with the minimal and maximal elements formed by the “front side” ${Z^{{\,\mathrm fr}}}$ and “rear side” ${Z^{{\,\mathrm rear}}}$ of the boundary subcomplex of Z(n, 3), respectively. This lattice is “dense,” in the sense that any two s-collections whose s-membranes are neighboring in the lattice are obtained from each other by a standard flip, or mutation (which involves a hexagon, or, in terminology of Leclerc and Zelevinsky [8], is performed “in the presence of six witnesses”).

(b) It is natural to raise a “converse” issue: given a maximal s-collection $S\subset 2^{[n]}$, what can one say about the set ${\mathbf{C}}(S)$ of maximal c-collections containing S? One can efficiently construct an instance of such c-collections, by embedding the tiling T(S), as an s-membrane M, into the “empty” zonotope Z(n, 3) and then by growing, step by step (or cube by cube), a required cubillage containing M. In fact, the set of cubillages for ${\mathbf{C}}(S)$ looks like a “direct product” of two sets ${\mathbf{Q}}^-(M)$ and ${\mathbf{Q}}^+(M)$, where the former (latter) is formed by partial cubillages consisting of “cubes” filling the volume of Z(n, 3) between the surfaces ${Z^{{\,\mathrm fr}}}$ and M (resp. between M and ${Z^{{\,\mathrm rear}}}$).

A somewhat similar program is fulfilled for w-collections, and on this way, we obtain the main results of this paper. We consider a maximal c-collection $C\subset 2^{[n]}$ and cut each cube of the cubillage Q associated with C into two tetrahedra and one octahedron, forming a subdivision of Z(n, 3) into smaller pieces, denoted as $Q^\equiv$ and called the fragmentation of Q. We show that each combi K(W) associated with a maximal by size w-collection $W\subset {\mathbf{W}}^*(C)$ is related to one or more 2-dimensional subcomplexes of $Q^\equiv (C)$, called w-membranes. Like s-membranes, the set of all w-membranes of $Q^\equiv$ are shown to form a distributive lattice with the minimal element ${Z^{{\,\mathrm fr}}}$ and the maximal element ${Z^{{\,\mathrm rear}}}$, and any two neighboring w-membranes in the lattice are linked by either a tetrahedral flip or an octahedral flip (the latter corresponds to a mutation of a w-collection “in the presence of four witnesses,” in terminology of [8]). As to the “converse direction,” we consider a fixed maximal w-collection $W\subset 2^{[n]}$ and develop an efficient geometric method to construct a cubillage on Z(n, 3) containing (as a 2-dimensional subcomplex) the combi K(W).

This paper is organized as follows. Section 2 recalls definitions of rhombus and combined tilings on a zonogon and cubillages on a 3-dimensional zonotope, and reviews their relations to maximal s-, w-, and c-collections in $2^{[n]}$. Section 3 starts with an example of a maximal c-collection in $2^{[n]}$ that is neither s-pure nor w-pure. Then, it introduces s-membranes in a cubillage, discusses their relation to rhombus tilings, and describes transformations of cubillages on Z(n, 3) to ones on $Z(n-1,3)$ and back that are needed for further purposes. Section 4 studies the structure of the set of s-membranes in a fixed cubillage and, as a consequence, describes the lattice $\mathbf{S}^*(C)$. Section 5 discusses a method of constructing a cubillage containing one or two prescribed rhombus tilings. Then, we start studying interrelations between maximal w- and c-collections. Section 6 introduces w-membranes in the fragmentation $Q^\equiv$ of a fixed cubillage Q, explains that they form a lattice, demonstrates a relationship to combined tilings, and more. The concluding Sect. 7 is devoted to the problem of extending a given combi to a cubillage, which results in an efficient algorithm of finding a maximal c-collection in $2^{[n]}$ containing a given maximal w-collection.

2 Background

In this section, we recall the geometric representations for s-, w-, and c-collections that we are going to use. For disjoint subsets A and $\{a,\ldots ,b\}$ of [n], we use the abbreviated notation $Aa\ldots b$ for $A\cup \{a,\ldots ,b\}$, and write $A-c$ for $A-\{c\}$ when $c\in A$. An interval in [n] is a set of the form $\{a,a+1,\ldots ,b\}\subseteq [n]$, denoted as [a..b] (so $[n]=[1..n]$).

2.1 Rhombus tilings

Let $\Xi =\{\xi _1,\ldots ,\xi _n\}$ be a system of n non-collinear vectors in the upper hyperplane ${\mathbb {R}}\times {\mathbb {R}}_{\ge 0}$ that follow in this order clockwise around (0, 0). The zonogon generated by $\Xi$ is the 2n-gon that is the Minkowski sum of segments $[0,\xi _i]$, $i=1,\ldots ,n$, i.e., the set

$$\begin{aligned} Z=Z(\Xi ):=\{\lambda _1\xi _1+\ldots + \lambda _n\xi _n\,:\lambda _i\in {\mathbb {R}},\; 0\le \lambda _i\le 1,\; i=1,\ldots ,n\}; \end{aligned}$$

we also may denote it as Z(n, 2) (not fixing the choice of $\Xi$). A tiling that we deal with is a subdivision T of Z into tiles, each being a parallelogram of the form $\sum _{k\in X} \xi _k +\{\lambda \xi _i+\lambda '\xi _j\,:0\le \lambda ,\lambda '\le 1\}$ for some $i<j$ and some subset $X\subseteq [n]-\{i,j\}$. In other words, the tiles are not overlapping (have no common interior points) and their union is Z. A tile determined by X, i, j as above is called an ij-tile and denoted as $\lozenge (X|ij)$.

We identify each subset $X\subseteq [n]$ with the point $\sum _{i\in X} \xi _i$ in Z (assuming, w.l.o.g., that the generators $\xi _i$ are ${\mathbb {Z}}_2$-independent, i.e., all 0,1-combinations of these are different). Depending on the context, we also may think of T as a 2-dimensional complex and associate to it the planar directed graph $(V_T,E_T)$ in which each vertex is labeled by the corresponding subset of [n] and each edge that is a parallel translation of $\xi _i$ for some i is called an i-edge, or an edge of type (or color) i. In particular, the left boundary of the zonogon is the directed path $(v_0,e_1,v_1,\ldots ,e_n,v_n)$ in which each vertex $v_i$ is the interval [i] (and $e_i$ is an i-edge), whereas the right boundary of Z is the directed path $(v'_0,e'_1,v'_1,\ldots , e'_n,v'_n)$ with $v'_i=[n]-[i]$ (and $e'_i$ being an $(n-i+1)$-edge).

The vertex set $V_T$ regarded as a set-system in $2^{[n]}$ is called the spectrum of T. In fact, the graphic structure of T (and therefore its spectrum) does not depend on the choice of generating vectors $\xi _i$ (by keeping their ordering clockwise). In the literature, one often takes vectors of the same Euclidean length, in which case each tile becomes a rhombus and T is called a rhombus tiling. In what follows, we will liberally use this term whatever generators $\xi _i$ are chosen.

One easily shows that for any $1\le i<j\le n$, there exists a unique ij-tile, or ij-rhombus, in T. The correspondence between maximal s-collections and commutation classes of reduced words for permutations established by Leclerc and Zelevinsky in [8, Th. 1.6] leads to the following central property of rhombus tilings:

• (2.1) the correspondence $T\mapsto V_T$ gives a bijection between the set $\mathbf{RT}_n$ of rhombus tilings on Z(n, 2) and the set $\mathbf{S}_n$ of maximal s-collections in $2^{[n]}$.

Then, each maximal s-collection S determines a unique rhombus tiling T with $V_T=S$, and this T is constructed easily: each pair of vertices of the form X, Xi is connected by (straight line) edge from X to Xi; the resulting graph is planar and all its faces are just rhombi, giving T. Two rhombus tilings play especial roles. The spectrum of one of them, called the standard tiling and denoted as ${T^{\mathrm{st}}}_n$, is formed by all intervals in [n], including the “empty interval” $\emptyset$. The other one, called the anti-standard tiling and denoted as ${T^{\mathrm{ant}}}_n$, has the spectrum consisting of all co-intervals, i.e., the complements $[n]-I$ of intervals I. These two tilings for $n=4$ are illustrated on the picture.

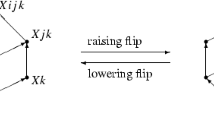
Next, from results in [8] it follows that $\mathbf{RT}_n$ is endowed with a poset structure. In this poset, $T^{\mathrm{st}}_n$ and $T^{\mathrm{ant}}_n$ are the unique minimal and maximal elements, respectively, and a tiling T immediately precedes a tiling $T'$ if $T'$ is obtained from T by one strong (or hexagonal) raising flip (and in turn T is obtained from $T'$ by one strong lowering flip). This means that

• (2.2) there exist $i<j<k$ and $X\subseteq [n]-\{i,j,k\}$ such that: T contains the vertices X, Xi, Xj, Xk, Xij, Xjk, Xijk, and the set $V_{T'}$ is obtained from $V_T$ by replacing Xj by Xik.

(This transformation is called in [8] a “mutation in the presence of six witnesses,” namely X, Xi, Xk, Xij, Xjk, Xijk.) See the picture.

We denote the corresponding hexagon in T as $H=H(X|ijk)$ and say that H has Y-configuration ($\Lambda$-configuration) if the three rhombi subdividing H are as illustrated in the left (resp. right) fragment of the above picture.

2.2 Combined tilings

For tilings of this sort, the system $\Xi$ generating the zonogon is required to satisfy the additional condition of strict concavity, namely: for any $1\le i<j<k\le n$,

$$\begin{aligned} \xi _j=\lambda \xi _i+\lambda '\xi _k,\quad \text{ where } \lambda ,\lambda '\in {\mathbb {R}}_{>0} \text{ and } \lambda +\lambda '>1. \end{aligned}$$

(1)

Besides, we use vectors $\epsilon _{ij}:=\xi _j-\xi _i$ for $1\le i<j\le n$. A combined tiling, or simply a combi, is a subdivision K of $Z(\Xi )$ into certain polygons specified below. Like the case of rhombus tilings, a combi K may be regarded as a complex and we associate to it a planar directed graph $(V_K,E_K)$ in which each vertex corresponds to some subset of [n] and each edge is now a parallel translation of either $\xi _i$ or $\epsilon _{ij}$ for some i, j. In the latter case, we say that the edge has type ij. We call $V_K$ the spectrum of K.

There are three sorts of tiles in T: $\Delta$-tiles, $\nabla$-tiles, and lenses. A $\Delta$-tile ($\nabla$-tile) is a triangle with vertices $A,B,C\subseteq [n]$ and edges (B, A), (C, A), (B, C) (resp. (A, C), (A, B), (B, C)) of types j, i and ij, respectively, where $i<j$. We denote this tile as $\Delta (A|ji)$ (resp. $\nabla (A|ij)$), call (B, C) its base edge and call A its top (resp. bottom) vertex. See the left and middle fragments of the picture.

In a lens $\lambda$, the boundary is formed by two directed paths $U_\lambda$ and $L_\lambda$, with at least two edges in each, having the same beginning vertex $\ell _\lambda$ and the same end vertex $r_\lambda$; see the right fragment of the above picture. The upper boundary $U_\lambda =(v_0,e_1,v_1,\ldots ,e_p,v_p)$ is such that $v_0=\ell _\lambda$, $v_p=r_\lambda$, and $v_k=Xi_k$ for $k=0,\ldots ,p$, where $p\ge 2$, $X\subset [n]$ and $i_0<i_1<\cdots <i_p$ (so k-th edge $e_k$ is of type $i_{k-1}i_k$). And the lower boundary $L_\lambda =(u_0,e'_1,u_1,\ldots ,e'_q,u_q)$ is such that $u_0=\ell _\lambda$, $u_q=r_\lambda$, and $u_m=Y-j_m$ for $m=0,\ldots ,q$, where $q\ge 2$, $Y\subseteq [n]$ and $j_0>j_1>\cdots >j_q$ (so m-th edge $e'_m$ is of type $j_mj_{m-1}$). Then, $Y=Xi_0j_0=Xi_pj_q$, implying $i_0=j_q$ and $i_p=j_0$, and we say that the lens $\lambda$ has type $i_0j_0$. Note that X as well as Y need not be a vertex in K; we refer to X and Y as the lower and upper root of $\lambda$, respectively. Due to condition (1), each lens $\lambda$ is a convex polygon of which vertices are exactly the vertices of $U_\lambda \cup L_\lambda$.

Remark 1

In the definition of a combi introduced in [2], the generators $\xi _i$ are assumed to have equal Euclidean lengths. However, taking arbitrary (cyclically ordered) generators subject to (1) does not affect, in essence, the structure of the combi and its spectrum, and in what follows, we may vary the generators when needed. Next, to simplify visualizations, it is convenient to think of edges of type i as “almost vertical,” and of edges of type ij as “almost horizontal”; we refer to the former edges as V-edges, and to the latter ones as H-edges (following terminology of [2]). Note that any rhombus tiling turns into a combi without lenses in a natural way: each rhombus $\lozenge$ is subdivided into two “semi-rhombi” $\Delta$ and $\nabla$ by drawing the “almost horizontal” diagonal in it.

The picture below illustrates a combi K having one lens $\lambda$ for $n=4$; here the V-edges and H-edges are drawn by thick and thin lines, respectively.

We will rely on the following central result on combies shown in [2]:

• (2.4) the correspondence $K\mapsto V_K$ gives a bijection between the set $\mathbf{K}_n$ of combined tilings on Z(n, 2) and the set $\mathbf{W}_n$ of maximal w-collections in $2^{[n]}$.

In particular, each maximal w-collection W determines a unique combi K with $V_K=W$, and [2] explains how to construct this K efficiently.

By results in [1, 2], the set $\mathbf{K}_n$ forms a poset in which ${T^{\mathrm{st}}}_n$ and $T^{\mathrm{ant}}_n$ are the unique minimal and maximal elements, respectively, and a combi K immediately precedes a combi $K'$ if $K'$ is obtained from K by one weak raising flip (and in turn K is obtained from $K'$ by one weak lowering flip). This means that

• (2.5) there are $i<j<k$ and $X\subseteq [n]-\{i,j,k\}$ such that: K contains the vertices Xi, Xj, Xk, Xij, Xjk, and $V_{K'}$ is obtained from $V_K$ by replacing Xj by Xik.

(Using terminology of [8], one says that $V_K$ and $V_{K'}$ are linked by a “mutation in the presence of four witnesses,” namely Xi, Xk, Xij, Xjk.)

2.3 Cubillages

Now we deal with the zonotope generated by a “cyclic configuration” $\Theta$ of vectors in the space ${\mathbb {R}}^3$ with coordinates (x, y, z). It consists of n vectors $\theta _i=(1,y_i,z_i)$, $i=1,\ldots ,n$, with the following strict convexity condition:

• (2.6) $y_1<y_2<\cdots <y_n$, and $z_i=f(y_i)$, $i\in [n]$, where f is a strictly convex function.

An example with $n=5$ is illustrated in the picture (where $z_i=y_i^2$ and $y_i=-y_{6-i}$). Hereinafter, we think of x, y, z as “vertical,” “left-to-right,” and “to-depth” coordinates in ${\mathbb {R}}^3$, respectively.

The zonotope Z generated by $\Theta$, also denoted as Z(n, 3), is the Minkowski sum of segments $[0,\theta _i]$, $i=1,\ldots ,n$. A cubillage (also known as a fine zonotopal tiling in the literature) is a subdivision Q of Z into parallelotopes of which any two are either disjoint or share a face, and each face of the boundary of Z is contained in one of these parallelotopes. This implies that each parallelotope is of the form $\sum _{p\in X}\theta _p +\{\lambda \theta _i+\lambda '\theta _j+ \lambda ''\theta _k\,:0\le \lambda ,\lambda ',\lambda ''\le 1\}$ for some $i<j<k$ and $X\subseteq [n]-\{i,j,k\}$. For brevity, we liberally refer to parallelotopes as cubes. (For a survey on cubillages of any dimensions generated by cyclic configurations, see, e.g., [3].)

Depending on the context, we also may think of a cubillage Q as a polyhedral complex or as a set of cubes. In particular, (in the former case) by a vertex, edge, rhombus in Q we mean, respectively (the closure of) a 0-, 1-, 2-dimensional cell of this complex, and (in the latter case) when writing $\zeta \in Q$, we mean that $\zeta$ is a cube of Q.

Like the case of zonogons and rhombus tilings, each subset $X\subseteq [n]$ is identified with the point $\sum _{i\in X}\theta _i$ in Z (assuming, w.l.o.g., that the generators $\theta _i$ are ${\mathbb {Z}}_2$-independent). Accordingly, we may refer to an edge, rhombus, and cube in Q as an i-edge, ij-rhombus, ijk-cube (where $i<j<k$), or as an edge, rhombus, cube of type i, ij, ijk, respectively. The edges are directed according to the generating vectors. An ij-rhombus (ijk-cube) with the bottom vertex X is denoted as $\lozenge (X|ij)$ (resp. $\zeta (X|ijk)$). As a specialization to $d=3$ of a well-known property of cubillages on zonotopes Z(n, d), there holds:

• (2.7) for any $1\le i<j<k\le n$, a cubillage Q has exactly one ijk-cube.

The directed graph formed by the vertices and edges occurring in Q is denoted by $G_Q=(V_Q,E_Q)$ and we call the vertex set $V_Q$ regarded as a set-system in $2^{[n]}$ the spectrum of Q. The following property shown in [5] is of importance for us:

• (2.8) the correspondence $Q\mapsto V_Q$ gives a bijection between the set $\mathbf{Q}_n$ of cubillages on Z(n, 3) and the set $\mathbf{C}_n$ of maximal c-collections in $2^{[n]}$.

Next, when studying interrelations of s- and c-collections, we will use the projection $\pi :{\mathbb {R}}^3\rightarrow {\mathbb {R}}^2$ along the third coordinate vector, i.e., given by $\pi (x,y,z):=(x,y)$. Then, $\pi (Z)$ is the zonogon generated by the vectors $\pi (\theta _1),\ldots , \pi (\theta _n)$ (which lie in the “upper half-plane” and follow clockwise, in view of (2.6)).

For a compact set $S\subset {\mathbb {R}}^3$, let $S^{\mathrm{fr}}$ ($S^\mathrm{rear}$) denote the subset of S “seen” in the direction of the third coordinate vector $e_{3}$ (resp. $-e_{3}$) of ${\mathbb {R}}^3$, i.e., formed by the points $(x,y,z)\in S$ such that there is no $(x,y,z')\in S$ with $z'<z$ (resp. $z'>z$). We call $S^{\mathrm{fr}}$ ($S^{\mathrm{rear}}$) the front (resp. rear) side of S.

In particular, the boundary ${\mathrm{bd}}(Z)$ of Z is the union ${Z^{{\,\mathrm fr}}}\cup {Z^{{\,\mathrm rear}}}$ of the front (“seen”) and rear (“unseen”) sides of the zonotope Z. Then, ${Z^{{\,\mathrm rim}}}:={Z^{{\,\mathrm fr}}}\cap {Z^{{\,\mathrm rear}}}$ is the closed piecewise linear curve, called the rim of Z, being the union of two directed paths connecting the vertices $\emptyset$ and [n] in $G_Q$. Condition (2.6) provides that

• (2.9) the maximal affine sets in ${Z^{{\,\mathrm fr}}}$ and ${Z^{{\,\mathrm rear}}}$ are the rhombi projected by $\pi$ to elements of the standard and anti-standard tilings on the zonogon $\pi (Z)$, respectively (whose spectra are formed by the intervals and co-intervals in [n], see Sect. 2.1).

3 S-membranes

This section starts with an example of cubillages whose spectra are neither s-pure nor w-pure. Next, we consider a fixed cubillage Q on Z(n, 3), introduce a class of 2-dimensional subcomplexes in it, called s-membranes, explain that each of them is isomorphic to a rhombus tiling T on Z(n, 2) such that $V_T\subset V_Q$, and vice versa (thus obtaining a geometric description of $\mathbf{S}^*(V_Q)$), and demonstrate some other properties.

3.1 An example of non-purity

Consider the zonotope $Z=Z(4,3)$. The vertices of its boundary ${\mathrm{bd}}(Z)$ are the intervals and co-intervals on the set [4] (cf. (2.9)), and there are exactly two subsets of [4] that are neither intervals nor co-intervals, namely 13 and 24. So 13 and 24 are exactly those “points” in $2^{[4]}$ that are contained in the interior of Z. Since they are not chord separated, there are exactly two cubillages on Z: one containing 13 and the other containing 24 (taking into account that the vertices of ${\mathrm{bd}}(Z)$ belong to any cubillage and that each cubillage is determined by its spectrum, by (2.8)).

Lemma 1

For the cubillage Q on Z(4, 3) that contains 13, the set $V_Q$ is neither s-pure nor w-pure, i.e., there are $S\in {\mathbf{S}}(V_Q)$ and $W\in {\mathbf{W}}(V_Q)$ with $|S|,|W| < s_4$.

Proof

Let $R,V_1,V_2$ be the vertices in the rim, front side, and rear side of Z(4, 3), respectively (for definitions, see the paragraph before (2.9)). Then, R consists of the eight intervals of the form [i] or $[4]-[i]$ ($0\le i\le 4$); $V_1$ is R plus the intervals 2, 3, 23; and $V_2$ is R plus the co-intervals 14, 124, 134. Note that the vertices (intervals) of the rim of a zonotope Z(n, 3) are strongly separated from any subset of [n].

Consider the set $S:=R\cup \{2,124\}$. It is a subset of

$$\begin{aligned} V_Q=V_1\cup V_2\cup \{13\}= R\cup \{2,3,23,14,124,134,13\}. \end{aligned}$$

We observe that S is an s-collection (since $2\subset 124$) but not an s-collection of maximum size in $2^{[4]}$ (since $|S|=10$ but $|V_1|=s_4=11$). At the same time, 124 surrounds both 3 and 23 but $|124|>|3|,|23|$; and each of 14, 134, 13 surrounds 2 but $|14|,|134|,|13|>|2|$. This implies that S is simultaneously a maximal s-collection and a maximal w-collection in $V_Q$, yielding the result. $\square$

(In fact, using results on s- and w-membranes given later, one can strengthen the above lemma by showing that for $n\ge 4$, the spectrum $V_Q$ of any cubillage Q on Z(n, 3) is neither s-pure nor w-pure; we omit a proof here.)

3.2 S-membranes

The definitions of the front and rear sides of a set given in Sect. 2.3 can be used when we deal with a subcomplex of a cubillage on $Z=Z(n,3)$.

Example. In view of (2.6), for a cube $\zeta =\zeta (X|ijk)$ (where $i<j<k$),  $\zeta ^{{\,\mathrm fr}}$ is formed by the rhombi $\lozenge (X|ij), \lozenge (X|jk), \lozenge (Xj|ik)$, while $\zeta ^{{\,\mathrm rear}}$ is formed by $\lozenge (X|ik), \lozenge (Xi|jk), \lozenge (Xk|ij)$. See the picture.

Definition

A connected 2-dimensional subcomplex M of a cubillage Q is called an s-membrane if $\pi$ bijectively sends M to a rhombus tiling on the zonogon Z(n, 2). In other words, $M=M^{{\,\mathrm fr}}=M^{{\,\mathrm rear}}$ and M is a disk whose boundary is ${Z^{{\,\mathrm rim}}}$.

In particular, both ${Z^{{\,\mathrm fr}}}$ and ${Z^{{\,\mathrm rear}}}$ are s-membranes. Therefore, up to a piecewise linear deformation, we may think of M as a rhombus tiling whose spectrum is contained in $V_Q$. So the vertex set $V_M$ of M belongs to $\mathbf{S}^*(V_Q)$. Moreover, the following sharper property holds. It can be deduced from general results on higher Bruhat orders and their geometric models in [3, 7, 9, 14], yet we prefer to give a direct proof, which makes our description more self-contained.

Theorem 1

The correspondence $M\mapsto V_M$ gives a bijection between the s-membranes M in a cubillage Q on Z(n, 3) and the set $\mathbf{S}^*(V_Q)$ of maximum by size s-collections contained in $V_Q$.

In light of explanations above, it suffices to prove the following

Proposition 1

For any rhombus tiling T on Z(n, 2) with $V_T\subset V_Q$, there exists an s-membrane M in Q isomorphic to T.

This proposition will be proved in Sect. 3.4, based on a more detailed study of structural features of cubillages and operations on them given in the next subsection.

3.3 Pies in a cubillage

Given a cubillage Q on $Z=Z(n,3)$ and $i\in [n]$, let $\Pi _i=\Pi _i(Q)$ be the part of Z covered by cubes of Q having edges of color i, or, let us say, i-cubes. When it is not confusing, we also think of $\Pi _i$ as the set of i-cubes or as the corresponding subcomplex of Q. We refer to $\Pi _i$ as the i-pie of Q. When $i=n$ or 1, the pie structure becomes rather transparent, which will enable us to apply some useful reductions.

To clarify the structure of $\Pi _n$, we first consider the set U of n-edges lying in the boundary ${\mathrm{bd}}(Z)$. Since the tilings on the sides ${Z^{{\,\mathrm fr}}}$ and ${Z^{{\,\mathrm rear}}}$ of Z are isomorphic to ${T^{\mathrm{st}}}_n$ and $T^{\mathrm{ant}}_n$, respectively (cf. (2.9)), one can see that

• (3.1) the beginning vertices of edges of U are precisely those contained in the cycle $C=P'\cup P''$, where $P'$ is the subpath of left path of ${Z^{{\,\mathrm rim}}}$ from the bottom vertex $\emptyset$ to $[n-1]$, and $P''$ is the path in ${Z^{{\,\mathrm fr}}}$ passing the vertices $\emptyset$ and $[i..(n-1)]$ for $i=n-1,n-2,\ldots ,1$; in other words, C is the rim of the zonotope $Z(n-1,3)$ generated by $\theta _1,\ldots ,\theta _{n-1}$.

Accordingly, the end vertices of edges of U lie on the cycle $C':=C+\theta _n$; this $C'$ is viewed as the rim of the zonotope $Z(n-1,3)$ shifted by $\theta _n$. The area of ${\mathrm{bd}}(Z)$ between C and $C'$ is subdivided into $2(n-2)$ rhombi whose types include color n; we call this the belt of $\Pi _n$. See the picture with $n=5$.

Now fix an n-edge $e=(X,Xn)$ not on ${\mathrm{bd}}(Z)$ and consider the set S of cubes in $\Pi _n$ containing e. Each cube $\zeta \in S$ is the (Minkowski) sum of some rhombus $\lozenge =\lozenge (X'|ij)$ and the segment $[0,\theta _n]$, and $n>i,j$ implies that $\lozenge$ belongs to the front side $\zeta ^{{\,\mathrm fr}}$ of $\zeta$. Gluing together such rhombi $\lozenge$, we obtain a disk $\delta$ lying on the front side of ${\widehat{S}}:=\cup (\zeta \in S)$ and containing X as an interior point; this ${\widehat{S}}$ is just the sum of $\delta$ and $[0,\theta _n]$. Based on this local behavior, one can realize that

• (3.2) $\Pi _n$ is the Minkowski sum of a disk D and the segment $[0,\theta _n]$; this disk lies in $\Pi ^{{\,\mathrm fr}}_n$ and its boundary is formed by the cycle C as in (3.1).

Then $D':=D+\theta _n$ is the disk in $\Pi ^{\mathrm{rear}}_n$ whose boundary is the cycle $C'=C+\theta _n$.

The facts that $D^{\mathrm{fr}}=D$ and $C={Z^{{\,\mathrm rim}}}(n-1,3)$ imply that D is subdivided into rhombi which (being projected by $\pi$) form a rhombus tiling on $Z(n-1,2)$. And similarly for $D'$.

In what follows, we write: $\Pi ^-_n$ for D;  $\Pi ^+_n$ for $D'$;  $Z^-_n$ ($Z^+_n$) for the (closed) region of Z between the front side of $Z':=Z(n-1,3)$ and $\Pi ^-_n$ (resp. between $\Pi ^+_n$ and the rear side of $Z'+\theta _n$); and $Q^-_n$ ($Q^+_n$) for the portion (partial cubillage) of Q lying in $Z^-_n$ (resp. $Z^+_n$). One can see that

• (3.3) the edges (of the graph $G_Q$) of Q connecting $Z^-_n$ and $Z^+_n$ are directed from the former to the latter and are exactly the n-edges of Q; each vertex of $Q^-_n$ is in $[n-1]$ and each vertex of $Q^+_n$ is of the form Xn, where $X\subseteq [n-1]$.

The following two operations (converse to each other) are of importance.

n-Contraction. Shrink $\Pi _n$ into the disk $\Pi ^-_n$, and accordingly shift the region $Z^+_n$ together with the cubillage $Q^+_n$ filling it by the vector $-\theta _n$. As a result, the disks $\Pi ^-_n$ and $\Pi ^+_n$ merge and we obtain a cubillage on the zonotope $Z(n-1,3)$; it is denoted as $Q^{\mathrm{con}}_n$ and called the contraction of Q by (the color) n, or the n-contraction.

Note that $\Pi ^-_n$ becomes an s-membrane of $Q^{\mathrm{con}}_n$. Also the following is obvious:

• (3.4) each cube $\zeta =\zeta (X|ijk)$ of Q with $k<n$ (i.e., not contained in $\Pi _n$) one-to-one corresponds to a cube $\zeta '$ of $Q^{\mathrm{con}}_n$; this $\zeta '$ is of the form $\zeta (X|ijk)$ if $\zeta \in Q^-_n$, and $\zeta (X-n|ijk)$ if $\zeta \in Q^+_n$.

n-Expansion. Let M be an s-membrane in a cubillage $Q'$ on the zonotope $Z'=Z(n-1,3)$. Define $Z^-(M)$ ($Z^+(M)$) to be the region of $Z'$ between $(Z')^{\mathrm{fr}}$ and M (resp. between M and $(Z')^{\mathrm{re}}$) and define $Q^-(M)$ ($Q^+(M)$) to be the subcubillage of $Q'$ contained in $Z^-(M)$ (resp. $Z^+(M)$). The n-expansion operation for (Q, M) consists in shifting $Z^+(M)$ together with $Q^+(M)$ by $\theta _n$ and filling the “region between” M and $M+\theta _n$ by the corresponding set of n-cubes, denoted as $Q^0_n(M)$. More precisely, each rhombus $\lozenge (X|ij)$ in M generates the cube $\zeta (X|ijn)$ of $Q^0_n(M)$. A fragment of the operation is illustrated in the picture.

Since $M^{{\,\mathrm fr}}=M$ and the boundary cycle of M is the rim of $Z'$, we obtain that

• (3.5) taken together, the cubes in $Q^-(M)$, $Q^0_n(M)$ and $\{\zeta +\theta _n\,:\zeta \in Q^+(M)\}$ form a cubillage on $Z=Z(n,3)$.

We denote this cubillage as $Q_n(Q',M)$ and call it the n-expansion of $Q'$ using M. There is a natural relation between the n-contraction and n-expansion operations, as follows (a proof is straightforward and left to the reader)

Proposition 2

The correspondence $(Q',M)\mapsto Q_n(Q',M)$, where $Q'$ is a cubillage on $Z(n-1,3)$ and M is an s-membrane in $Q'$, gives a bijection between the set of such pairs $(Q',M)$ and the set of cubillages on Z(n, 3). Under this correspondence, $Q'$ is the n-contraction of $Q=Q_n(Q',M)$ and M is the image of the n-pie in Q under the n-contraction operation. $\square$

We will also take advantage of handling the 1-pie of a cubillage Q on Z(n, 3) and applying the corresponding 1-contraction and 1-expansion operations, which are symmetric to those concerning the color n as above. More precisely, if we make a mirror reflection of $\Theta$ by replacing each generator $\theta _i=(1,y_i,z_i)$ by $\theta '_{n+1-i}:=(1,-y_i,z_i)$, then the 1-edges of Q turn into n-edges of the corresponding cubillage $Q'$ on $Z(\theta '_1,\ldots ,\theta '_n)$, and the 1-pie of Q turns into the n-pie of $Q'$. This leads to the corresponding counterparts of (3.1)–(3.5) and Proposition 2. (Note that in this paper we do not need to consider i-pies, i-contractions and i-expansions when $1<i<n$.)

3.4 Applications of the contraction and expansion operations

One useful application of such operations is as follows.

Proposition 3

Let Q be a cubillage on $Z=Z(n,3)$.

• (i) If Q contains vertices X and Xi, then it has the edge (X, Xi).

• (ii) If Q contains vertices X, Xi, Xj, Xij ($i<j$), then it has the rhombus $\lozenge (X|ij)$.

• (iii) If Q contains a set S of eight vertices X, Xi, Xj, Xk, Xij, Xik, Xjk, Xijk ($i<j<k$), then it has the cube $\zeta (X|ijk)$.

Proof

We use induction on n. Let us prove (iii), denoting by $Q'$ the cubillage on $Z(n-1,3)$ that is the n-contraction of Q. Three cases are possible.

(a) Let $k<n$ and $n\notin X$. Then, S belongs to the vertex set of the subcubillage $Q^-_n$ (cf. (3.3)) and, therefore, to the vertex set of $Q'$. By induction, $Q'$ contains the cube on S, namely $\zeta =\zeta (X|ijk)$. From (3.5) and Proposition 2, it follows that under the n-expansion operation for $Q'$ using the s-membrane $M:=\Pi ^-_n$, $\zeta$ becomes a cube in Q, as required.

(b) Let $n\in X$. Then, $k<n$ and S belongs to the vertex set of $Q^+_n$. Therefore, $S':=\{Y-n\,:Y\in S\}$ is included in $V_{Q'}$ and, moreover, in the vertex set of the subcubillage $Q^+(M)$ of $Q'$ (where M is as in (a)). By induction, $Q^+(M)$ contains the cube $\zeta '=\zeta (X-n|ijk)$. The n-expansion operation for $Q'$ using M transfers $\zeta '$ to the desired cube $\zeta (X|ijk)$ in Q.

(c) Now let $n\notin X$ and $k=n$. Then, the set $S^-:=\{X,Xi,Xj,Xij\}$ belongs to $\Pi ^-_n$, and the set $S^+:=\{Xn,Xin,Xjn,Xijn\}$ to $\Pi ^+_n$. The n-contraction operation shifts $S^+$ by $-\theta _n$ and merges it with $S^-$ (which lies in M). By induction, $Q'$ contains the rhombus $\lozenge =\lozenge (X|ij)$. The n-expansion operation for $Q'$ using M transforms $\lozenge$ into the cube $\zeta (X|ijn)$ in $Q^0_n(M)\subset Q$ (cf. (3.5)), as required.

Assertions in (i) and (ii) are shown in a similar fashion (even easier). $\square$

Based on this proposition, we now prove Proposition 1.

Let Q be a cubillage on Z(n, 3), and T a rhombus tiling on Z(n, 2) with $V_T\subset V_Q$ (regarding vertices as subsets of [n]). For each rhombus $\lozenge =\lozenge (X|ij)$ in T, the vertices of the form X, Xi, Xj, Xij are contained in Q as well, and by (ii) in Proposition 3, Q has rhombus $\lozenge '$ on these vertices. Then, $\lozenge =\pi (\lozenge ')$. Combining such rhombi $\lozenge '$ in Q determined by the rhombi $\lozenge$ on T, we obtain a 2-dimensional subcomplex M in Q which is bijectively mapped by $\pi$ onto T. Hence, M is an s-membrane in Q isomorphic to T, yielding Proposition 1 and Theorem 1.

4 The lattice of s-membranes

As mentioned in the Introduction, the set $\mathbf{S}^*(C)$ of maximal by size strongly separated collections $S\subset 2^{[n]}$ that are contained in a fixed maximal chord separated collection $C\subset 2^{[n]}$ has nice structural properties. Due to (2.1), (2.8) and Theorem 1, it is preferable to deal with equivalent geometric objects, by considering a cubillage Q on the zonotope $Z=Z(n,3)$ and the set ${\mathcal {M}}(Q)$ of s-membranes in Q.

Using notation as in Sect. 3.3, for an s-membrane $M\in {\mathcal {M}}(Q)$, we write $Z^-(M)$ ($Z^+(M)$) for the region of Z bounded by the front side ${Z^{{\,\mathrm fr}}}$ of Z and M (resp. by M and the rear side ${Z^{{\,\mathrm rear}}}$)) and write $Q^-(M)$ ($Q^+(M)$) for the set of cubes of Q contained in $Z^-(M)$ (resp. $Z^+(M)$). The sets $Q^-(M)$ and $Q^+(M)$ are important in our analysis and we call them the front heap and the rear heap of M, respectively.

Consider two s-membranes $M,M'\in {\mathcal {M}}(Q)$ and form the sets $N:=(M\cup M')^{\mathrm{fr}}$ and $N':=(M\cup M')^{\mathrm{rear}}$. Then, both $N,N'$ are in bijection with Z(n, 2) via $\pi$. Also one can see that for any rhombus $\lozenge$ in M, if some interior point of $\lozenge$ belongs to N ($N'$), then the entire $\lozenge$ lies in N (resp. $N'$), and similarly for $M'$. These observations imply that:

(4.1)

• (i) both N and $N'$ are s-membranes in Q;

• (ii) the front heap $Q^-(N)$ of N is equal to $Q^-(M)\cap Q^-(M')$, and the front heap $Q^-(N')$ of $N'$ is equal to $Q^-(M)\cup Q^-(M')$.

(Accordingly, the rear heaps of N and $N'$ are $Q^+(N)=Q^+(M)\cup Q^+(M')$ and $Q^+(N')=Q^+(M)\cap Q^+(M')$.) By (4.1), the front heaps of s-membranes constitute a distributive lattice, which gives rise to a similar property for the s-membranes themselves.

Proposition 4

The set ${\mathcal {M}}(Q)$ of s-membranes in Q is endowed with the structure of distributive lattice in which the meet and join operations for $M,M'\in {\mathcal {M}}(Q)$ produce the s-membranes $M\wedge M'$ and $M\vee M'$ such that $Q^-(M\wedge M')=Q^-(M)\cap Q^-(M')$ and $Q^-(M\vee M')=Q^-(M)\cup Q^-(M')$. $\square$

It is useful to give an alternative description for this lattice, which reveals an intrinsic structure and a connection with flips in rhombus tilings. It is based on a natural partial order on Q defined below. Recall that for a cube $\zeta$, the front side $\zeta ^{{\,\mathrm fr}}$ and the rear side $\zeta ^{{\,\mathrm rear}}$ are formed by the rhombi as indicated in the Example in Sect. 3.2.

Definition

For $\zeta ,\zeta '\in Q$, we say that $\zeta$ immediately precedes $\zeta '$ if $\zeta ^{{\,\mathrm rear}}$ and $(\zeta ')^{\mathrm{fr}}$ share a rhombus.

The following property is of importance:

• (4.2) the directed graph $\Gamma _Q$ whose vertices are the cubes of Q and whose edges are the pairs $(\zeta ,\zeta ')$ such that the cube $\zeta$ immediately precedes $\zeta '$ is acyclic.

This (as well as the corollary below) follows from properties of higher Bruhat orders established in [9, Th. 3]; cf. also [13, Prop. 2.1]. A far generalization of  (4.2), involving all cubes within a cyclic zonotope, is given in [3, Th. D.1].

Corollary 1

The graph $\Gamma _Q$ induces a partial order $\prec$ on the cubes of Q. Moreover, the ideals of $(Q,\prec )$ (i.e., the subsets $Q'\subseteq Q$ satisfying $\zeta \in Q',\; \zeta '\prec \zeta \Longrightarrow \zeta '\in Q')$ are exactly the front heaps $Q^-(M)$ of s-membranes $M\in {\mathcal {M}}(Q)$. $\square$

Using this, we now explain a relation to strong flips in rhombus tilings. For convenience we identify an s-membrane $M\in {\mathcal {M}}(Q)$ with the rhombus tiling $\pi (M)$ on Z(n, 2). In particular, the minimal s-membrane ${Z^{{\,\mathrm fr}}}$ is identified with the standard tiling ${T^{\mathrm{st}}}_n$, and the maximal s-membrane ${Z^{{\,\mathrm rear}}}$ with the anti-standard tiling $T^{\mathrm{ant}}_n$.

Let $M\in {\mathcal {M}}(Q)$ be different from ${T^{\mathrm{st}}}_n$. Then, the heap $J:=Q^-(M)$ is nonempty. Since $\Gamma _Q$ is acyclic, J has a maximal element $\zeta =\zeta (X|ijk)$ (i.e., there is no $\zeta '\in J$ with $\zeta \prec \zeta '$). Then, M contains all rear rhombi of $\zeta$, namely $\lozenge (X|ik),\; \lozenge (Xi|jk),\; \lozenge (Xk|ij)$. They span the hexagon H(X|ijk) having $\Lambda$-configuration and we observe that

• (4.3) for $M,\,J,\, \zeta$ as above, the set $J':=J-\{\zeta \}$ is an ideal of $(Q,\prec )$ as well, and the s-membrane (rhombus tiling) $M'$ with $Q^-(M')=J'$ is obtained from M by replacing the rhombi of $\zeta ^{{\,\mathrm rear}}$ by the rhombi forming $\zeta ^{{\,\mathrm fr}}$ (namely $\lozenge (X|ij),\; \lozenge (X|jk),\;\lozenge (Xj|ik)$), or, in other words, by the lowering flip involving the hexagon H(X|ijk) (see the picture in the end of Sect. 2.1).

(Of an especial interest are principal ideals of $(Q,\prec )$; each of them is determined by a cube $\zeta \in Q$ and consists of all $\zeta '\in Q$ from which $\zeta$ is reachable by a directed path in $\Gamma _Q$. The s-membrane corresponding to such an ideal admits only one lowering flip within Q, namely that determined by the rhombi of $\zeta$. Symmetrically: considering $M\in {\mathcal {M}}(Q)$ different from $T^{\mathrm{ant}}_n$ and its rear heap $R:=Q^+(M)$, and choosing an element $\zeta \in R$ that admits no $\zeta '\in R$ with $\zeta '\prec \zeta$, we can make the raising flip by replacing in M the rhombi of $\zeta ^{{\,\mathrm fr}}$ by the ones of $\zeta ^{{\,\mathrm rear}}$. When R is formed by some $\zeta \in Q$ and all $\zeta '\in Q$ reachable from $\zeta$ by a directed path in $\Gamma _Q$, then M admits only one raising flip within Q, namely that determined by the rhombi of $\zeta$.)

In terms of maximal s-collections, (4.3) together with Proposition 4 implies the following.

Corollary 2

Let C be a maximal chord separated collection in $2^{[n]}$. The set $\mathbf{S}^*(C)$ of maximal by size s-collections in C is a distributive lattice with the minimal element ${\mathcal {I}}_n$ and the maximal element co-${\mathcal {I}}_n$ (being the set of intervals and the set of co-intervals in [n], respectively) in which $S\in \mathbf{S}^*(C)$ immediately precedes $S'\in \mathbf{S}^*(C)$ if and only if $S'$ is obtained from S by one raising flip (“in the presence of six witnesses”).

Remark 2

The set of all maximal s-collections in $2^{[n]}$ forms a poset, which is exactly the higher Bruhat order B(n, 2), in terminology of [9]. However, in contrast to $\mathbf{S}^*(C)$, this poset is not a lattice for $n\ge 6$, as is shown in Ziegler [14].

Note also that a triple $\tau$ of rhombi in an s-membrane $M\in {\mathcal {M}}(Q)$ that spans a hexagon need not belong to one cube of Q (in contrast to (iii) in Proposition 3 where Q contains a cube if all eight vertices of this cube belong to $V_Q$). In this case, $(M,\tau )$ determines a flip in the set of all rhombus tilings on Z(n, 2) but not within ${\mathcal {M}}(Q)$.

5 Embedding rhombus tilings in cubillages

In this section, we study cubillages on Z(n, 3) containing one or more fixed s-membranes.

5.1 Extending an s-membrane to a cubillage

We start with the following issue. Given a maximal strongly separated collection $S\subset 2^{[n]}$, let ${\mathbf{C}}(S)$ be the set of maximal chord separated collections containing S. How to construct explicitly one instance of such c-collections? A navíe method consists in growing, step by step, a c-collection C including S, by enumerating subsets $X\subseteq [n]$ and adding a new X to a current C whenever $\{X\}\cup C$ is chord separated. However, this method is expensive as it may take exponentially many (w.r.t. n) steps.

An efficient approach, which is relatively simple logically, is based on geometric interpretations as above and uses flips in s-membranes. More precisely, in the “empty” zonotope $Z=Z(n,3)$, we build the abstract s-membrane M with $V_M=S$, by embedding S (as the corresponding set of points) in Z and forming the rhombus $\lozenge (X|ij)$ for each quadruple of the form $\{X,Xi,Xj,Xij\}$ in S; this gives the desired M. Next, we construct a cubillage Q containing M (thus obtaining $S\subset V_Q\in {\mathbf{C}}(S)$, as required).

This is performed in two stages. At the first stage, assuming that M is different from ${Z^{{\,\mathrm fr}}}$ (equivalently, $\pi (M)\ne {T^{\mathrm{st}}}_n$), we grow, step by step, a partial cubillage $Q'$ filling the region $Z^-(M)$ between ${Z^{{\,\mathrm fr}}}$ and M, starting with $Q':=\emptyset$. At each step, the current $Q'$ is such that $(Q')^{\mathrm{rear}}=M$ and $(Q')^{\mathrm{fr}}$ forms an s-membrane $M'$. If $M'={Z^{{\,\mathrm fr}}}$, we are done. Otherwise $\pi (M')\ne {T^{\mathrm{st}}}_n$ implies that $M'$ contains at least one triple of rhombi spanning a hexagon having $\Lambda$-configuration (see the end of Sect. 2.1). We choose one hexagon $H=H(X|ijk)$ of this sort, add to $Q'$ the cube $\zeta =\zeta (X|ijk)$ determined by H, and update $M'$ accordingly, by replacing the rhombi of H by the other three rhombi in $\zeta$ (forming $\zeta ^{{\,\mathrm fr}}$); we say that the updated $M'$ is obtained from the previous membrane by the lowering flip using $\zeta$. And so on until we reach ${Z^{{\,\mathrm fr}}}$.

At the second stage, acting in a similar way, we construct a partial cubillage $Q''$ filling the region $Z^+(M)$ between M and ${Z^{{\,\mathrm rear}}}$. Namely, a current $Q''$ is such that $(Q'')^{\mathrm{fr}}=M$, and $(Q'')^{\mathrm{rear}}$ forms an s-membrane $M''$. Unless $M''={Z^{{\,\mathrm rear}}}$, we choose in $M''$ a hexagon H having Y-configuration, add to $Q''$ the cube $\zeta$ determined by H and update $M''$ accordingly, thus making the raising flip using $\zeta$. And so on.

The resulting $Q:=Q'\cup Q''$ becomes a complete cubillage in Z containing M, as required. Since $Q'$ and $Q''$ are constructed independently, we obtain that

• (5.1) the set ${\mathbf{Q}}(M)$ of cubillages on $Z=Z(n,3)$ containing a fixed s-membrane M is represented as the “direct product” of the sets ${\mathbf{Q}}^-(M)$ and ${\mathbf{Q}}^+(M)$ of partial cubillages filling $Z^-(M)$ and $Z^+(M)$, respectively, i.e., ${\mathbf{Q}}(M)=\{Q'\cup Q''\,:Q'\in {\mathbf{Q}}^-(M),\; Q''\in {\mathbf{Q}}^+(M)\}$.

Remark 3

When $M={Z^{{\,\mathrm fr}}}$ ($M={Z^{{\,\mathrm rear}}}$),  ${\mathbf{Q}}^+(M)$ (resp. ${\mathbf{Q}}^-(M)$) becomes the set ${\mathbf{Q}}_n$ of all cubillages on Z(n, 3). The latter set is connected via local transformations (flips) changing subcubillages within sub-zonotopes of the form Z(4, 3). A similar connectedness takes place for cubillages on zonotopes of any dimension, as a consequence of results in [9] (for details, see also [3, Sec. 8]).

5.2 Cubillages for two s-membranes

One can address the following issue. Suppose we are given two abstract s-membranes $M,M'$ properly embedded in $Z=Z(n,3)$. When does there exist a cubillage Q on Z containing both M and $M'$? The answer is clear: if and only if the set $V_M\cup V_{M'}$ is chord separated. However, one can ask: how to construct such a Q efficiently?

For simplicity, consider the case of “non-crossing” s-membranes, assuming that M is situated in Z before $M'$, i.e., M lies in $Z^-(M')$.

A partial cubillage $Q'$ filling $Z^-(M)$ and a partial cubillage $Q''$ filling $Z^+(M')$ always exist and can be constructed by the method as in Sect. 5.1. So the only problem is to construct a partial cubillage ${\widetilde{Q}}$ filling the space between M and $M'$, i.e., $Z(M,M'):=Z^+(M)\cap Z^-(M')$; then $Q:=Q'\cup {\widetilde{Q}}\cup Q''$ is as required. Conditions when a required ${\widetilde{Q}}$ does exist are expounded in the proposition below.

We need some definitions. Consider a rhombus tiling T on the zonogon $Z'=Z(n,2)$ and a color $i\in [n]$. For each i-edge e in T, let m(e) be the middle point on e, and for each $j\in [n]-\{i\}$, let $c(\lozenge$) be the central point of the rhombus $\lozenge$ with edges of colors i, j in T (it is the ij-rhombus when $i<j$, and the ji-rhombus when $j<i$). For such a $\lozenge$ and the i-edges in it, say, e and $e'$, connect $c(\lozenge )$ by straight-line segments with both points m(e) and $m(e')$. One easily shows that the concatenation of these segments over all j produces a non-self-intersecting piecewise linear curve connecting the middle points of the two i-edges on the left and right boundaries of $Z'$; denote it as $D_i$ and call i-th (undirected) dual path for T. (The set $\{D_1,\ldots , D_n\}$ matches a pseudo-line arrangement, in a sense.)

Definitions. Let $1\le i<j<k\le n$ and let $\lozenge$ be the ik-rhombus in T. The triple ijk is called normal if $\lozenge$ lies above $D_j$, and an inversion if $\lozenge$ lies below $D_j$. The set of inversions for T is denoted by $\mathrm{Inv}(T)$. Also, we say that a triple ijk in T is elementary if the rhombi of types ij, ik and jk in it span a hexagon (which has Y-configuration if ijk is normal, and $\Lambda$-configuration if ijk is an inversion).

See the picture where a normal triple (an inversion) ijk is illustrated in the left (resp. right) fragment, the corresponding dual paths are drawn by dotted lines, and the ik-rhombus is marked by a circle.

Proposition 5

Let $M,M'$ be two s-membranes in $Z=Z(n,3)$ such that $M\subset Z^-(M')$. Then, a partial cubillage ${\widetilde{Q}}$ filling $Z(M,M')$ (and therefore a cubillage on Z containing both $M,M'$) exists if and only if $\mathrm{Inv}(M)\subseteq \mathrm{Inv}(M')$. Such a ${\widetilde{Q}}$ consists of $|\mathrm{Inv}(M')|-|\mathrm{Inv}(M)|$ cubes and can be constructed efficiently.

One direction in this proposition is easy. Indeed, suppose that a partial cubillage ${\widetilde{Q}}$ filling $Z(M,M')$ does exist. Take a minimal (w.r.t. the order $\prec$ as in Sect. 4) cube $\zeta =\zeta (X|ijk)$ in ${\widetilde{Q}}$. Then, the front side $\zeta ^{{\,\mathrm fr}}$ lies in M and forms the hexagon $H=H(X|ijk)$ having Y-configuration. Hence, the triple ijk in M is normal and elementary. By making the flip in M using $\zeta$, we obtain an s-membrane in which ijk becomes an inversion, and the fact that ijk is elementary implies that no other triple $i'j'k'$ changes its status under the flip. Also the new s-membrane becomes closer to $M'$. Applying the procedure $|{\widetilde{Q}}|$ times, we reach $M'$. This shows “only if” part.

As to “if” part in Proposition 5, its proof is less trivial and relies on a result by Felsner and Weil. Answering an open question raised by Ziegler in [14], they proved the following assertion (stated in [4] in equivalent terms of pseudo-line arrangements).

Theorem 2

[4] Let $T,T'$ be rhombus tilings on Z(n, 2) and let $\mathrm{Inv}(T)\subset \mathrm{Inv}(T')$. Then, T has an elementary triple occurring in $\mathrm{Inv}(T')-\mathrm{Inv}(T)$.

(This is a 2-dimensional analog of the well-known fact that for two permutations $\sigma ,\sigma '\in S_n$ with $\mathrm{Inv}(\sigma )\subset \mathrm{Inv}(\sigma ')$, $\sigma$ has a transposition in $\mathrm{Inv}(\sigma ')-\mathrm{Inv}(\sigma )$. Ziegler [14] showed that the corresponding assertion in dimension 3 or more is false.)

Now Theorem 2 implies that if $M,M'$ are s-membranes with $\mathrm{Inv}(M)\subset \mathrm{Inv}(M')$, then there exists a cube $\zeta =\zeta (X|ijk)$ such that $\zeta ^{{\,\mathrm fr}}\subset M$ and $ijk\in \mathrm{Inv}(M')-\mathrm{Inv}(M)$. The flip in M using $\zeta$ produces an s-membrane closer to $M'$ and having the set of inversions $\mathrm{Inv}(M)\cup \{ijk\}$. This enables us to recursively construct a partial cubillage filling $Z(M,M')$ starting with $\zeta$, and “if” part of Proposition 5 follows.

Remark 4

One can check that the above definition of inversions of an (abstract) s-membrane M in $Z=Z(n,3)$ (equivalently, of the rhombus tiling $\pi (M)$) is consistent with the notion of inversions in higher Bruhat orders introduced by Manin and Schechtman [9], and its geometric interpretation given in [7, 14]. According to the latter, the set $\mathrm{Inv}(M)$ consists of the types ijk of cubes of a partial cubillage $Q'$ filling $Z^-(M)$ (which does not depend on $Q'$).

6 W-membranes and quasi-combies

In this section, we deal with a maximal c-collection C in $2^{[n]}$ and its associated cubillage Q on the zonotope $Z=Z(n,3)$ (i.e., with $V_Q=C$), and consider the class ${\mathbf{W}}^*(C)$ of maximal by size weakly separated collections contained in C. (Recall that C need not be w-pure, by Lemma 1.) Since each $W\in {\mathbf{W}}^*(C)$ is the spectrum of a combi on the zonogon $Z'=Z(n,2)$ (cf. )(2.4), a reasonable question is how a combi K with $V_K\subset V_Q$ (regarding vertices as subsets of [n]) relates to the structure of Q. We have seen that maximal by size s-collections in C and their associated rhombus tilings on $Z'$ are represented by s-membranes, which are special 2-dimensional subcomplexes in Q. In case of weak separation, we will represent combies via w-membranes, which are subcomplexes of a certain subdivision, or fragmentation, of Q. Also, along with a combi K with $V_K\subset V_Q$, we will be forced to deal with the set of so-called quasi-combies accompanying K, which were introduced in [2] and have a nice geometric interpretation in terms of Q as well.

6.1 Fragmentation of a cubillage and quasi-combies

The fragmentation $Q^\equiv$ of a cubillage Q on $Z=Z(n,3)$ is the complex obtained by cutting Q by the horizontal planes through the vertices of Q, i.e., the planes $x=h$ for $h=1,\ldots ,n-1$ (where x is the “vertical” coordinate in ${\mathbb {R}}^3$). This subdivides each cube $\zeta =\zeta (X|ijk)$ into three pieces: the lower tetrahedron $\zeta ^\nabla$, the middle octahedron $\zeta ^\square$, and the upper tetrahedron $\zeta ^\Delta$, called the $\nabla$-, $\square$-, and $\Delta$-fragments of $\zeta$, respectively. Depending on the context, we also may think of $Q^\equiv$ as the set of such fragments over all cubes of Q. We say that a fragment has height $h+\frac{1}{2}$ if it lies between the planes $x=h$ and $x=h+1$.

It is convenient to visualize faces of $Q^\equiv$ as though looking at them from the front and slightly from below, i.e., along a vector $(\epsilon ,0,1)$, and accordingly use the projection $\pi ^\epsilon : {\mathbb {R}}^3\rightarrow {\mathbb {R}}^2$ defined by $\pi ^\epsilon (x,y,z)=(x-\epsilon z,y)$ for a sufficiently small $\epsilon >0$. (Compare $\pi ^\epsilon$ with $\pi$ defined in Sect. 2.3.) One can see that $\pi ^\epsilon$ transforms the generators $\theta _1, \ldots ,\theta _n$ for Z as in (2.6) into generators for $Z'=Z(n,2)$) which are adapted for combies, i.e., satisfy the strict concavity condition (1).

For a closed set $S\subseteq Z$, let $S^{\,\epsilon ,{\mathrm{fr}}}$ ($S^{\,\epsilon ,{\mathrm{rear}}}$) denote the set of points of S seen from the front (from the rear) in the direction related to $\pi ^\epsilon$, i.e., the points $(x,y,z)\in S$ such that there is no $(x',y',z')\in S$ with $\pi ^\epsilon (x',y',z')=\pi ^\epsilon (x,y,z)$ and $z'<z$ (resp. $z'>z$). We call it the $\epsilon$-front (resp. $\epsilon$-rear) side of S. Note that when replacing the projection $\pi$ by $\pi ^\epsilon$, all facets (triangles) of the fragments of a cube become fully seen from the front or rear; see the picture.

Thus, all 2-dimensional faces in $Q^\equiv$ are triangles, and we conditionally refer to those of them that lie in horizontal sections $x=h$ as horizontal triangles, and to the other ones (halves of rhombi in Q) as vertical ones. Horizontal triangles $\tau$ are divided into two groups. Namely, $\tau$ is called upper (lower) if it has vertices of the form Xi, Xj, Xk (resp. $Y-k,Y-j,Y-i$) for $i<j<k$, and therefore its “obtuse” vertex Xj (resp. $Y-j$) is situated above the edge (Xi, Xk) (resp. below the edge $(Y-k,Y-i)$), called the longest edge of $\tau$ (which is not confusing when $\epsilon$ is small). Equivalently, an upper (lower) horizontal $\tau$ belongs to an $\nabla$-fragment (resp. $\Delta$-fragment) of $Q^\equiv$.

Accordingly, we refer to the edges in horizontal sections as horizontal ones, or H-edges, and to the other edges as vertical ones, or V-edges (adapting terminology for combies from Sect. 2.2).

For $h\in [n]$, let $S_h(Q)$ denote the section of Q at height h, regarded as a triangulation consisting of horizontal triangles which are partitioned into upper and lower ones. (A nice property of $S_h(Q)$ pointed out in [5] is that its spectrum (the set of vertices regarded as subsets of [n]) constitutes a maximal w-collection in $\left( {\begin{array}{c}[n]\\ h\end{array}}\right)$.) For example, if Q is the cubillage on Z(4, 3) formed by four cubes $\zeta (\emptyset |123),\; \zeta (\emptyset |134),\; \zeta (1|234),\; \zeta (3|124)$, then the triangulations $S_1(Q), S_2(Q), S_3(Q)$ are as illustrated in the picture, where the sections of these cubes are labeled by a, b, c, d, respectively.

6.2 W-membranes

Definition

A 2-dimensional subcomplex M of the fragmentation $Q^\equiv$ is called a w-membrane if M is bijectively projected by $\pi ^\epsilon$ onto Z(n, 2). Equivalently, $M=M^{\,\epsilon ,{\mathrm{fr}}}=M^{\,\epsilon ,{\mathrm{rear}}}$ and the boundary of M is the rim ${Z^{{\,\mathrm rim}}}$ of $Z=Z(n,3)$ and .

Arguing as in Sect. 4 for s-membranes, one shows that the set ${\mathcal {M}}(Q^\equiv )$ of w-membranes in $Q^\equiv$ constitutes a distributive lattice.

More precisely, associate with a w-membrane M: (a) the part $Z^-(M)$ ($Z^+(M)$) of Z between ${Z^{{\,\mathrm fr}}}$ and M (resp. between M and ${Z^{{\,\mathrm rear}}}$); and (b) the subcomplex $Q^{-}(M)$ ($Q^{+}(M)$) of $Q^\equiv$ contained in $Z^-(M)$ (resp. $Z^+(M)$), called the front heap (resp. rear heap) of M when it is regarded as the corresponding set of $\nabla$-, $\square$-, and $\Delta$-fragments.

Then, for any two w-membranes $M,M'\in {\mathcal {M}}(Q^\equiv )$, we have (cf. (4.1)):

(6.1)

• (i) both $N:=(M\cup M')^{\,\epsilon ,\mathrm{fr}}$ and $N':=(M\cup M')^{\,\epsilon ,\mathrm{rear}}$ are w-membranes;

• (ii) $Q^{-}(N)=Q^{-}(M)\cap Q^{-}(M')$ and $Q^{-}(N')=Q^{-}(M)\cup Q^{-}(M')$.

Proposition 6

${\mathcal {M}}(Q^\equiv )$ is a distributive lattice in which operations $\wedge$ and $\vee$ applied to $M,M'\in {\mathcal {M}}(Q^\equiv )$ produce w-membranes $M\wedge M'$ and $M\vee M'$ such that $Q^{-}(M\wedge M')=Q^{-}(M)\cap Q^{-}(M')$ and $Q^{-}(M\vee M')=Q^{-}(M)\cup Q^{-}(M')$. $\square$

Next, for fragments $\phi ,\phi '$ in $Q^\equiv$, we say that $\phi$ immediately precedes $\phi '$ if $\phi ^{\,\epsilon ,{\mathrm{rear}}}\cap (\phi ')^{\,\epsilon ,\mathrm fr}$ consists of a (vertical or horizontal) triangle. Accordingly, we define the directed graph $\Gamma _{Q^\equiv }$ whose vertices are the fragments in $Q^\equiv$ and whose edges are the pairs $(\phi ,\phi ')$ such that $\phi$ immediately precedes $\phi '$.

Lemma 2

The graph $\Gamma _{Q^\equiv }$ is acyclic.

Proof

Consider a directed path $P=(\phi _0,e_1,\phi _1,\ldots ,e_p,\phi _p)$ in $\Gamma _{Q^\equiv }$. We show that P is not a cycle as follows.

If consecutive fragments $\phi =\phi _{i-1}$ and $\phi '=\phi _i$ share a horizontal triangle $\sigma$ of height h (i.e., lying in the plane $x=h$), then the construction of $\pi ^\epsilon$ together with the equality $\sigma =\phi ^{\,\epsilon ,{\mathrm{rear}}}\cap (\phi ')^{\,\epsilon ,\mathrm fr}$ implies that $\phi$ lies below and $\phi '$ lies above the plane $x=h$. On the other hand, if $\phi$ and $\phi '$ share a vertical triangle, then both $\phi ,\phi '$ have the same height.

Thus, it suffices to show that P is not a cycle if all fragments $\phi _i$ in P have the same height. This assertion follows from (4.2) and the observation that if fragments $\phi ,\phi '$ of $Q^\equiv$ share a vertical triangle $\sigma$, and $\phi$ immediately precedes $\phi '$, then the cubes $\zeta ,\zeta '$ of Q containing these fragments (respectively) share the rhombus $\lozenge$ including $\sigma$ and such that $\lozenge =\zeta ^{{\,\mathrm rear}}\cap (\zeta ')^{\mathrm{fr}}$. $\square$

Corollary 3

The graph $\Gamma _{Q^\equiv }$ induces a partial order $\prec$ on the fragments of $Q^\equiv$. The ideals of $(Q^\equiv ,\prec )$ are exactly the front heaps $Q^{-}(M)$ of w-membranes $M\in {\mathcal {M}}(Q^\equiv )$. $\square$

When a w-membrane M is different from the minimal membrane ${Z^{{\,\mathrm fr}}}$, the ideal $F:=Q^{-}(M)$ has at least one maximal element, i.e., a fragment $\phi \in F$ such that there is no $\phi '\in F-\{\phi \}$ with $\phi \prec \phi '$. Equivalently, the $\epsilon$-rear side $\phi ^{\,\epsilon ,{\mathrm{rear}}}$ is entirely contained in M. The lowering flip in M using $\phi$ replaces the triangles of $\phi ^{\,\epsilon ,{\mathrm{rear}}}$ by the ones of $\phi ^{\,\epsilon ,{\mathrm{fr}}}$, producing a w-membrane $M'$ closer to ${Z^{{\,\mathrm fr}}}$, namely such that $Q^{-}(M')=F-\{\phi \}$. Note that this flip preserves the set of vertices (i.e., $V_{M'}=V_M$) if $\phi$ is a $\nabla$- or $\Delta$-fragment, in which case we refer to this as a tetrahedral (lowering) flip. See the picture.

In contrast, if $\phi$ is a $\square$-fragment, then the set of vertices does change, namely $V_{M'}=(V_M-\{Xik\})\cup \{Xj\}$, where $\phi$ is contained in the cube $\zeta (X|ijk)$; we refer to such a flip as octahedral or essential. See the picture.

Symmetrically, when $M\ne {Z^{{\,\mathrm rear}}}$, its rear heap $R:=Q^{+}(M)$ has at least one minimal fragment $\phi$, i.e., such that there is no $\phi '\in R-\{\phi \}$ with $\phi '\prec \phi$. Equivalently, $\phi ^{\,\epsilon ,{\mathrm{fr}}}$ is entirely contained in M. The raising flip in M using $\phi$ produces a w-membrane $M'$ closer to ${Z^{{\,\mathrm rear}}}$. Such flips, referred to as tetrahedral and octahedral (or essential) as before, are illustrated in the above two pictures as well.

Making all possible lowering or raising tetrahedral flips starting with a given w-membrane M, we obtain a set of w-membranes with the same spectrum $V_M$, denoted as ${\mathcal {E}}(M)$ and called the escort of M. Of an especial interest is a w-membrane $L\in {\mathcal {E}}(M)$ that has the maximum number of V-edges. Such an L admits neither a $\nabla$-fragment $\phi$ with $\phi ^{\,\epsilon ,{\mathrm{rear}}}\subset L$, nor a $\Delta$-fragment $\phi '$ with $(\phi ')^{\,\epsilon ,\mathrm fr}\subset L$, since a lowering flip in the former case and a raising flip in the latter case would increase the number of V-edges. We call L a fine w-membrane.

We shall see later that the w-membranes one-to-one correspond to the so-called non-expensive quasi-combies, and the fine w-membranes to the combies which are compatible with $Q^\equiv$. The following auxiliary statement will be of use.

(6.2)

• (i) Let $Q^\equiv$ contain a vertical $\Delta$-triangle $\tau$ and a lower horizontal triangle $\sigma$ sharing an edge e that is the longest edge of $\sigma$ (and the base edge of $\tau$). Then, $\tau$ and $\sigma$ belong to the same $\Delta$-fragment $\phi$ of $Q^\equiv$ (thus forming $\phi ^{\,\epsilon ,{\mathrm{fr}}}$).

• (ii) Symmetrically, if a vertical $\nabla$-triangle $\tau$ and an upper horizontal triangle $\sigma$ share an edge that is the longest edge of $\sigma$, then $\tau \cup \sigma = \phi ^{\,\epsilon ,{\mathrm{rear}}}$ for some $\nabla$-fragment $\phi$ of $Q^\equiv$.

Indeed, let $\lozenge$ be the rhombus in Q containing the triangle $\Delta$ as in (i). This $\lozenge$ is a facet of one or two cubes of Q and $\sigma$ lies in the section of one of them, $\zeta$ say, by the horizontal plane containing e. Since $\sigma$ is lower, the only possible case is when $\Delta$ and $\sigma$ form the $\epsilon$-front side of the $\Delta$-fragment of $\zeta$, as required. The case (ii) is symmetric.

A useful consequence of (6.2) is that

• (6.3) for any horizontal triangle $\sigma$ of a fine w-membrane L, the longest edge of $\sigma$ belongs to one more (lower or upper) horizontal triangle of L.

Indeed, if $\sigma$ is lower, then its longest edge belongs to neither a vertical $\nabla$-triangle (since $\pi ^\epsilon$ is injective on L), nor a vertical $\Delta$-triangle (otherwise $\sigma \cup \Delta$ would be as in (6.2)(i) and one could make a lowering flip increasing the number of V-edges). When $\sigma$ is upper, the argument is similar (using (6.2)(ii)).

6.3 Quasi-combies and w-membranes

We assume that the zonogon $Z':=Z(n,2)$ is generated by the vectors $\xi _i=\pi ^\epsilon (\theta _i)$, $i=1,\ldots ,n$, where the $\theta _i$ are as in (2.6); then the $\xi _i$ satisfy (1). Speaking of combies and etc., we use terminology and notation as in Sect 2.2.

A quasi-combi on $Z'$ is defined in the same way as a combi, with the only difference that the requirement that for any lens $\lambda$, the lower boundary $L_\lambda$, as well as the upper boundary $U_\lambda$, has at least two edges is now withdrawn; so one of $L_\lambda$ and $U_\lambda$ is allowed to have only one edge. When all vertices of $\lambda$ are contained in $L_\lambda$, and therefore $U_\lambda$ has a unique edge, namely $(\ell _\lambda ,r_\lambda )$, we say that $\lambda$ is a lower semi-lens. Symmetrically, when all vertices of $\lambda$ belong to $U_\lambda$, $\lambda$ is called an upper semi-lens. An important special case of a semi-lens $\lambda$ is a (lower of upper) triangle.

We refer to the $\Delta$- and $\nabla$-tiles of a quasi-combi K as vertical ones, and to the lenses and semi-lenses in it as horizontal tiles. This is justified by the fact that all vertices A of a horizontal tile have the same size, or lie in the same level $h=|A|$.

A quasi-combi is called fully triangulated if all its tiles are triangles. An immediate observation is that

• (6.4) $\pi ^\epsilon$ maps any w-membrane M of $Q^\equiv$ to a fully triangulated quasi-combi (regarding M as a 2-dimensional complex).

In what follows, we liberally identify M with $\pi ^\epsilon (M)$ and may speak of a w-membrane as a quasi-combi. A property converse to (6.4), in a sense, is valid in a more general situation. Before stating it, we introduce four simple operations on a quasi-combi K.

(S) Splitting a horizontal tile. For a lens $\lambda$ of K and non-adjacent vertices u, v in $L_\lambda$ or in $U_\lambda$, the operation cuts $\lambda$ into two pieces (either one lens and one semi-lens or two semi-lenses) by connecting u, v by the line segment [u, v]. When $\lambda$ is a lower (upper) semi-lens and u, v is a pair of non-adjacent vertices in $L_\lambda$ (resp. $U_\lambda$), the operation acts similarly.

(M) Merging two horizontal tiles. Suppose that $\lambda '$ and $\lambda ''$, which are either two semi-lenses or one lens and one semi-lens, have a common edge e that is the longest edge of at least one of them, $\lambda '$ say, i.e., $e=(\ell _{\lambda '},r_{\lambda '})$. The operation merges $\lambda ',\lambda ''$ into one piece $\lambda :=\lambda '\cup \lambda ''$.

One can see that both operations result in correct quasi-combies. Two examples are illustrated in the picture.

The next two operations involve semi-lenses and vertical triangles and resemble, to some extent, tetrahedral flips in w-membranes. Here by a lower (upper) fan in a quasi-combi K we mean a sequence of $\nabla$-tiles $\nabla _r=\nabla (X|i_{r-1}i_r)$ (resp. $\Delta$-tiles $\Delta _r=\Delta (Y|i_{r-1}i_r)$, $r=1,\ldots ,p$, where $i_0<\cdots <i_p$ (resp. $i_0>\cdots >i_p$), i.e., these triangles have the same bottom vertex X (resp. the same top vertex Y) and two consecutive triangles share a vertical edge.

(E) Eliminating a semi-lens. Suppose that the longest edge $e=(\ell _\lambda ,r_\lambda )$ of a lower semi-lens $\lambda$ belongs to a $\Delta$-tile $\Delta =\Delta (Y|ji)$ ($j>i$). Then, e is the base edge $(Y-j,Y-i)$ of $\Delta$, and $\lambda$ has the upper root just at Y. The operation of eliminating $\lambda$ replaces $\lambda$ and $\Delta$ by the corresponding upper fan $(\Delta _r\,:r=1,\ldots ,p)$, where each $\Delta _r$ has the top vertex Y and its base edge is r-th edge in $L_\lambda$. Symmetrically, if an upper semi-lens $\lambda$ and a $\nabla$-tile $\nabla$ share an edge e (which is the longest edge of $\lambda$ and the base edge of $\nabla$), then the operation replaces $\lambda$ and $\nabla$ by the corresponding lower fan $(\nabla _r\,:r=1,\ldots ,p)$, where the base edge of $\nabla _r$ is r-th edge in $U_\lambda$.

(C) Creating a semi-lens. This operation is converse to (E). It deals with a lower or upper fan of vertical triangles and replaces them by the corresponding pair consisting of either an upper semi-lens and a $\nabla$-tile, or a lower semi-lens and a $\Delta$-tile.

Again, it is easy to check that (E) and (C) result in correct quasi-combies. These operations are illustrated in the picture (where $p=3$).

Definition

For a quasi-combi K, the set $\Omega (K)$ of all quasi-combies $K'$ on $Z'$ with the same spectrum $V_K$ is called the escort of K.

(Compare with the definition of the escort ${\mathcal {E}}(M)$ of a w-membrane M.)

Lemma 3

(i)  $\Omega (K)$ contains exactly one combi. (ii)  $\Omega (K)$ is the set of quasi-combies that can be obtained from K by use of operations (S),(M),(E),(C). In particular, $V_K$ is a maximal w-collection in $2^{[n]}$.

Proof

Choosing an arbitrary quasi-combi $K'\in \Omega (K)$ and applying to $K'$ a series of operations (M) and (E), one can produce $K^*$ having no semi-lenses at all (since each application of (M) or (E) decreases the number of semi-lenses). Therefore, $K^*$ is a combi with $V_{K^*}=V_K=:S$. Moreover, $K^*$ is the unique combi with the given spectrum S, by (2.4) (see also [2, Th. 3.5]). This gives (i). In its turn, (i) implies (ii) (since any $K'\in \Omega (K)$ can be obtained from $K^*$ using (S) and (C), which are converse to (M) and (E)). $\square$

As a consequence of (6.4) and Lemma 3, we obtain

Corollary 4

The spectrum of any w-membrane is a maximal w-collection in $2^{[n]}$.

Definition

A quasi-combi K is called compatible with a cubillage Q if each edge of K is (the image by $\pi ^\epsilon$ of) an edge of $Q^\equiv$. (In particular, $V_K\subset V_Q$.)

Proposition 7

Let K be a quasi-combi on $Z'=Z(n,2)$ compatible with a cubillage Q on Z(n, 3). Then, the horizontal tiles (lenses and semi-lenses) of K can be triangulated so as to turn K into (the image by $\pi ^\epsilon$ of) a w-membrane in $Q^\equiv$.

Proof

Let $\tau$ be a $\Delta$- or $\nabla$-tile in K; then the edges of $\tau$ belong to $Q^\equiv$. Arguing as in the proof of Proposition 3 (using induction on n and considering the n-contraction of Q and its fragmentation), one can show that $\tau$ is a facet (a vertical triangle) of $Q^\equiv$. Now consider a lens or semi-lens $\lambda$ of K lying in level h, say. Since all edges of $\lambda$ belong to $Q^\equiv$, the polygon $\lambda$ must be subdivided into a set of triangles in the section $S_h(Q)$ of $Q^\equiv$ by the plane $x=h$. Combining such sets and vertical triangles $\tau$ as above, we obtain a disk bijective to $Z'$ by $\pi ^\epsilon$, yielding a w-membrane M in $Q^\equiv$ with $V_K\subset V_M$. Now the fact that both $V_M$ and $V_K$ are maximal w-collections implies $V_K=V_M$, and the result follows. $\square$

Definition

A quasi-combi K is called non-expensive if all semi-lenses in it are triangles (while admitting arbitrary lenses) and there are no semi-lens $\lambda$ whose longest edge $(\ell _\lambda ,r_{\lambda })$ is simultaneously either an edge of a lens or the longest edge of another semi-lens.

A special case of non-expensive quasi-combies is a combi. Proposition 7 and (6.4) imply that each w-membrane M one-to-one corresponds (via $\pi ^\epsilon$) to a fully triangulated quasi-combi compatible with Q and having the same spectrum $V_M$. One more correspondence following from Proposition 7 concerns non-expensive quasi-combies.

Corollary 5

Any w-membrane M of a cubillage Q one-to-one corresponds to a non-expensive quasi-combi K compatible with Q and such that $V_K=V_M$. Two non-expensive quasi-combies with the same escort have the same set of lenses.

Indeed, for a non-expensive quasi-combi K, the corresponding w-membrane M is obtained by subdividing each lens of K into triangles of $Q^\equiv$. We also use the fact that each application of operation (E) matches a tetrahedral flip in the corresponding w-membrane (since each semi-lens is a triangle), and a series of such operations results in a combi with the same set of lenses.

A sharper version of above results is stated by weakening the requirement of compatibility.

Theorem 3

For any maximal by size w-collection W contained in the spectrum $V_Q$ of a cubillage Q, there exists a w-membrane M in $Q^\equiv$ with $V_M=W$.

Proof

Let K be the combi with $V_K=W$. In light of the reasonings in the proof of Proposition 7, it suffices to show that

• (6.5) each vertical triangle $\tau$ of K can be extended to a rhombus of Q (and therefore $\tau$ is a face of $Q^\equiv$).

To see this, we rely on the following fact (which is interesting in its own right).

Claim

Let a set $Y\subset [n]$ be chord separated from each of X, X1, Xn for some $X\subseteq [n]-\{1,n\}$. Then, Y is chord separated from the set X1n as well.

Proof of the Claim

Let $1,\ldots ,n$ be disposed in this order on a circumference O. Let $Y':=Y-X$ and $X':=X-Y$. One may assume that $1,n\notin Y'$ (otherwise the chord separation of Y and X1n immediately follows from that of Y, X, X1, Xn).

If Y and X1n are not chord separated, then there are elements $x,x'\in X'1n$ and $y,y'\in Y'$ such that the corresponding chords $e=[x,x']$ and $e'=[y,y']$ “cross” each other. Then, $\{x,x'\}\ne \{1,n\}$ (since 1, n are neighboring in O). So one may assume that $x\in X'$ (and $x'\in X'1n$). But in each possible case $(x'\in X'$ or $x'=1$ or $x'=n$), the chord e crossing $e'$ connects two elements of either $X'$ or $X'1$ or $X'n$, yielding a contradiction. $\square$

Next consider a $\nabla$-tile $\nabla (X|ij)$ of K (having the vertices X, Xi, Xj with $i<j$). If $\{i,j\}=\{1,n\}$, then, by the Claim (and (2.8)), Xij is chord separated from all vertices of Q, and the maximality of $V_Q$ implies that Xij is a vertex of Q as well. Hence, by Proposition 3(ii), Q contains the rhombus $\lozenge (X|ij)$, as required.

So we may assume that at least one of $j<n$ and $1<i$ takes place. Assuming the former, we use induction on n and argue as follows.

Let $Q'$ be the n-contraction of Q, and M the s-membrane in $Q'$ that is the image of the n-pie in Q (for definitions, see Sect. 3.3). Besides $Q'$, we need to consider the reduced set $W':=\{A\subseteq [n-1]\,:A$ or An or both belong to $W\}$. Then, $W'$ is a maximal w-collection in $2^{[n-1]}$, and as is shown in [2],

• (6.6) if $\tau$ is a vertical triangle of K having type ij with $j<n$ and vertices A, B, C, and if $K'$ is the combi on $Z(n-1,2)$ with $V_{K'}=W'$, then $K'$ has a vertical triangle with the vertices either A, B, C or $A-n,\,B-n,\,C-n$.

Now consider two cases: $n\notin X$ and $n\in X$.

If $n\notin X$, then X, Xi, Xj are vertices of $Q'$ and simultaneously vertices of the reduced combi $K'$. By (6.6), $K'$ has the tile $\nabla '=\nabla (X|ij)$. By induction, the vertices of $\nabla '$ are extended to a rhombus $\lozenge '$ of $Q'$. This $\lozenge '$ is lifted to Q, as required.

If $n\in X$, then $Q'$ and $K'$ contain the vertices $X',X'i,X'j$ for $X':=X-n$,  $K'$ has the triangle $\nabla '=\nabla (X'|ij)$ (by (6.6)), the vertices of $\nabla '$ are extended to a rhombus $\lozenge '$ of $Q'$, and $\lozenge '$ is lifted to the desired rhombus $\lozenge (X|ij)$ in Q.

The case of a $\Delta$-tile $\Delta =\Delta (Y|ji)$ of K with $i<j<n$ is symmetric.

Finally, if $1<i<j=n$, we act in a similar fashion, but applying to Q the 1-contraction operation, rather than the n-contraction one (this is just the point where we use the 1-contraction mentioned in Sect. 3.3); the details are left to the reader.

This completes the proof of the theorem. $\square$

7 Extending a combi to a cubillage

The purpose of this section is to explain how to efficiently extend a fixed maximal w-collection in $2^{[n]}$ to a maximal c-collection, by working with their geometric interpretations: combies and cubillages. Our construction will imply the following

Theorem 4

Given a maximal weakly separated collection $W\subset 2^{[n]}$, one can find, by applying $O(n^3)$ flips, a maximal chord separated collection $C\subset 2^{[n]}$ including W.

Proof

It is convenient to work with an arbitrary fully triangulated quasi-combi K with $V_K=W$. The goal is to construct a cubillage Q on $Z=Z(n,3)$ whose fragmentation $Q^\equiv$ contains K as a w-membrane. (Note that it is routine to construct the (unique) combi with the spectrum W (see [2] for details), and in order to form K we subdivide each lens of the combi into the pair of upper and lower semi-lenses and then triangulate them arbitrarily. The resulting cubillage Q will depend on the choice of such triangulations.)

We start with properly embedding K (as an abstract w-membrane) into the “empty” zonotope Z, and our method consists of two phases. At the first (second) phase, we construct a partial fragmentation $F^-$ (resp. $F^+$) consisting of $\nabla$-, $\square$-, and $\Delta$-fragments of some cubes $\zeta (X|ijk)$ (where, as usual, $i<j<k$ and $X\subseteq [n]-\{i,j,k\}$) filling the region $Z^-(K)$ of Z between ${Z^{{\,\mathrm fr}}}$ and K (resp. the region $Z^+(K)$ between K and ${Z^{{\,\mathrm rear}}}$). For definitions, see Sect. 6.1. Then, $F:=F^+ \cup F^-$ is a subdivision of Z into such fragments, and it is not difficult to realize that F is just the fragmentation $Q^\equiv$ of some cubillage Q; so $Q^\equiv$ is as required for the given K.

Let us describe the first phase. At each step in it, we deal with an additional w-membrane M such that

$(*)$:

M lies in $Z^-(K)$, and there is a partial fragmentation $F'$ filling the region Z(M, K) between M and K (i.e., $F'$ is a subdivision of Z(M, K) into $\nabla$-, $\square$-, and $\Delta$-fragments).

If M (regarded as a fully triangulated quasi-combi) has no horizontal triangle (semi-lens), then M is, in essence, a rhombus tiling in which each rhombus $\lozenge (X|ij)$ is cut into two vertical triangles, namely $\nabla (X|ij)$ and $\Delta (Xij|ji)$. So M can be identified with the corresponding s-membrane, and we can construct a partial cubillage $Q'$ filling the region $Z^-(M)$ (between ${Z^{{\,\mathrm fr}}}$ and M) by acting as in Sect. 5.1. Combining $Q'$ and $F'$, we obtain the desired fragmentation $F^-$ filling $Z^-(K)$.

Now assume that M has at least one semi-lens, and let h be the minimum level such that the set ${\mathcal {L}}$ of semi-lenses in this level is nonempty. Choose $\lambda \in {\mathcal {L}}$ such that no edge in its lower boundary $L_\lambda$ belongs to another semi-lens. (The existence of such a $\lambda$ is provided by the acyclicity of the directed graph whose vertices are the elements of ${\mathcal {L}}$ and whose edges are the pairs $(\lambda ,\lambda ')$ such that $U_\lambda$ and $L_{\lambda '}$ share an edge, which can be shown, e.g., by use of (4.2).) Two cases are possible.

Case 1: $\lambda$ is an upper triangle, i.e., $L_\lambda$ consists of a single edge, namely $e=(\ell _\lambda ,r_\lambda )$. Let $U_\lambda$ have vertices Xi, Xj, Xk (where $i<j<k$, $Xi=\ell _\lambda$ and $Xk=r_\lambda$). Then, e belongs to a $\nabla$-tile in M, namely $\nabla =\nabla (X|ik)$. Form the $\nabla$-fragment $\phi =\zeta ^\nabla (X|ijk)$ (the lower tetrahedron with the vertices X, Xi, Xj, Xk). We add $\phi$ to $F'$ and accordingly make the lowering flip in M using $\phi$, which replaces the triangles $\lambda$ and $\nabla$ (forming $\phi ^{\,\epsilon ,{\mathrm{rear}}}$) by $\nabla (X|ij)$ and $\nabla (X|jk)$ (forming $\phi ^{\,\epsilon ,{\mathrm{fr}}}$); see an illustration in Sect. 6.2. The updated M is a correct fully triangulated quasi-combi (embedded as a w-membrane in Z), which is closer to ${Z^{{\,\mathrm fr}}}$.

Case 2: $\lambda$ is a lower triangle. Then, $L_\lambda$ consists of two edges: $e=(\ell _\lambda =Y-k,Y-j)$ and $e'=(Y-j,Y-i=r_\lambda )$, where $i<j<k$. Also by the choice of h and $\lambda$, the edges $e,e'$ belong to $\nabla$-tiles of M, namely ones of the form $\nabla =\nabla (X|jk)$ and $\nabla '=\nabla (X'|ij)$, respectively, where $X:=Y-\{j,k\}$ and $X':=Y-\{i,j\}$. See the left fragment of the picture.

Let $A:=Y-j$ ($=Xk=X'i$). Note that the “angle” between the edges (X, A) and $(X',A)$ is filled by an upper fan $(\Delta _1,\ldots ,\Delta _p)$, where $\Delta _r=\Delta (A|i_{r-1}i_r)$ and $k=i_0>i_1>\cdots >i_p=i$ (cf. Sect 6.2). Consider two possibilities.

Subcase 2a: $p=1$, i.e., the fan consists of only one tile, namely $\Delta =\Delta (A|ki)$. From the octahedron containing the vertices $X,X',Xj,X'j,A$, namely $\phi =\zeta ^\square (\widetilde{X}|ijk)$, where ${\widetilde{X}}$ is $X-i=X'-k$. Observe that the triangles $\lambda ,\nabla ,\nabla ',\Delta$ form the $\epsilon$-rear side of $\phi$. We add $\phi$ to $F'$ and accordingly make the octahedral flip in M using $\phi$, which replaces $\phi ^{\,\epsilon ,{\mathrm{rear}}}$ by the $\epsilon$-front side $\phi ^{\,\epsilon ,{\mathrm{fr}}}$ (formed by four triangles shared the new vertex $A':={\widetilde{X}}j$). See the middle fragment of the above picture where $\phi ^{\,\epsilon ,{\mathrm{fr}}}$ is indicated by solid lines. The updated M is a correct w-membrane, which is closer to ${Z^{{\,\mathrm fr}}}$. (Note that under the flip, the semi-lens $\lambda$ is replaced by an upper semi-lens $\lambda '$ in level $h-1$; this $\lambda '$ has the longest edge $(X,X')$ and the top $A'$.)

Subcase 2b: $p>1$. Then, X and $X'$ are connected in M by the path P that passes the vertices $X=A-i_0,A-i_1,\ldots , A-i_p=X'$. We make two transformations. First we connect X and $X'$ by line segment ${\widetilde{e}}$. Note that ${\widetilde{e}}$ lies in the region $Z^-(M)$ (by the convexity condition (2.6)). From the truncated polyhedral cone $\Sigma$ with the top vertex A and the base polygon B bounded by $P\cup {\widetilde{e}}$. See the right fragment of the above picture (where $p=3$). We arbitrarily subdivide B into $p-1$ triangles $\sigma _1,\ldots ,\sigma _{p-1}$ (having vertices on P) and extend each $\sigma _r$ to tetrahedron $\phi _r$ with the top A. These $\phi _1,\ldots ,\phi _{p-1}$ subdivide $\Sigma$ into $\Delta$-fragments (each being of the form $\zeta ^\Delta (A|i_\alpha i_\beta i_\gamma )$ for some $0\le \alpha<\beta <\gamma \le p$). Observe that the $\epsilon$-rear side $\Sigma ^{\,\epsilon ,\mathrm rear}$ of $\Sigma$ is formed by the fan $(\Delta _1,\ldots ,\Delta _p)$, whereas $\Sigma ^{\,\epsilon ,\mathrm fr}$ consists of the lower horizontal triangles $\sigma _1,\ldots ,\sigma _{p-1}$ plus one vertical triangle with the top A and the base ${\widetilde{e}}$, denoted as ${\widetilde{\Delta }}$.

We add the fragments $\phi _1,\ldots ,\phi _{p-1}$ to $F'$ and accordingly update M by replacing the triangles of $\Sigma ^{\,\epsilon ,\mathrm rear}$ by the ones of $\Sigma ^{\,\epsilon ,\mathrm fr}$ (as though making $p-1$ lowering tetrahedral flips). The new w-membrane has the upper fan at A consisting of a single $\Delta$-tile, namely ${\widetilde{\Delta }}$, and now we make the second transformation, by applying the octahedral flip as in Subcase 2a (involving the triangles $\lambda ,\nabla ,\nabla ',{\widetilde{\Delta }}$ on the vertices $X,X',Xj,X'j,A$).

Doing so, we eventually get rid of semi-lenses in the current M; then M becomes an s-membrane in essence, which enables us to extend the current $F'$ to the desired fragmentation $F^-$ filling $Z^-(K)$ (as mentioned above).

At the second phase, we act “symmetrically,” starting with $M:=K$ and moving toward ${Z^{{\,\mathrm rear}}}$, in order to obtain a fragmentation $F^+$ filling $Z^+(K)$.

Note that each tetrahedral or octahedral fragment $\phi$ uniquely determines the cube within Z to which $\phi$ belongs. Moreover, one can see that each triple of vertices in a section (at height 1 or 2) of a cube determines this cube. Using this, one can conclude that $F:=F^-\cup F^+$ is the fragmentation of a cubillage Q on Z, and M is a w-membrane in Q. The number of fragments in F is $3\left( {\begin{array}{c}n\\ 3\end{array}}\right)$, implying the theorem. (In fact, one can see that the algorithm behind the above proof takes polynomial time.) $\square$