Selection of third party reverses logistic providers: an approach of BCF-CRITIC-MULTIMOORA using Archimedean power aggregation operators

Abstract

One of the most powerful tools to operate imprecision is bipolar complex fuzzy sets (BCFSs), which is an enlargement of bipolar fuzzy sets (BFSs) as well as complex fuzzy sets (CFSs). This paper deals with an integrated MULTIMOORA (multi-objective optimization on the basis of ratio analysis plus full multiplicative form) framework as a generalization of fuzzy MULTIMOORA procedure to assess the multi-criteria decision-making (MCDM) problems with BCFSs. We develop BCF-Archimedean power weighted (ordered weighted) arithmetic and geometric aggregation operators (AOs) and discuss their properties from this point of view. The proposed Archimedean power-weighted AOs can eliminate the influence of extreme evaluating criteria values from some biased experts with different preference attitudes under the BCF setting. Afterward, we put forward an integrated MULTIMOORA algorithm based on the proposed AOs, where criteria weights are estimated using the CRITIC (criteria importance through inter-criteria correlation) method, which is a well-known objective weighting method based on aggregated score values of options, intensity contrast of every criteria and conflict among attributes. In the proposed methodology, criteria values are aggregated based on the MULTIMOORA method that involves three sub-methods: the ‘ratio system’, the ‘reference point’ and the ‘full multiplicative form’ and thus takes less computational time, minimum mathematical evaluations and bears good stability. In the following, third-party reverse logistics providers' (3PRLP) selection problem is brought into consideration to manifest the sufficiency of the developed methodology. At the end of this study, we draw attention to a comparison between the proposed decision-making approach with the corresponding BCF-CRITIC-TOPSIS and BCF-CRITIC-WASPAS methods.

Introduction

To begin with reverse logistics (RLs), it is uniformly essential to distinguish what RL is and how it functions. Council of Logistics Management (CLM) illustrates ‘RLs’ as “to achieve the purpose of recycling value and proper disposal, a process from the point of consumption to the starting point in an efficient and economical way that plans, implements, and controls raw materials, semi-finished inventory, finished goods and related information [70].” In other words, RL is defined as the procedure of planning, executing, and controlling the efficient, cost-effective flow of raw materials, in-process stock, finished merchandise, and associated information from the point of expenditure to origin for the goal of suitable disposal [10]. Using rendering profit with second-hand products reinstatement and protecting the environment through reprocessing and appropriate disposal [68, 99], the RLs might show the avenue of a stable and compatible parity in between environmental and economic affairs.

The inherent behavior of RLs shows its viable effort [90]. The viability based components are covered up by RLs through reduction of prices economically, keeping save the atmosphere with 3R (reduce, reuse, recycle), disposal and other practices as an environmental aspect, and lastly, providing security to resources obtained from nature thinking about future generations socially [50, 69]. Consequently, RLs turn into an inexorable policy for production-based industries in the modern period [1]. Thus far, using this policy requires a skilled support panel, in addition, formation of both design and plan of a robust network together with mending and charging professionals for keeping the network operational, owing to the complications associated with RLs performance [88, 99]. On account of quantifying difficulty, very often some of the criteria from a considerable large set of criteria, affects fixing the plan and design of a network, particularly reverse logistic in nature resulting it to become complicated and gradually becomes a vital job in case of any organization. As a result, several companies engaged themselves in outsourcing these logistics functions into learned third-party reverse logistics providers (3PRLPs) that in turn effectively reducing price and upraise the efficiency of regaining of second-hand products that are already dispatched for creating competition towards the advantages [34, 74]. In addition, a vital role by the 3PRLPs is being played to assist the organizations for the development and proper execution of the reverse supply chains on account of returns. Thus, the 3PRLP assessment decision can be a strategic critical partnering problem handled by processes and reverse supply chain executives’ sustaining managerial strategic competitive advantage. Accordingly, it is difficult for the companies to choose the most accessible 3PRLP among a set of provider alternatives by considering the desired evaluation criteria. Hence, the evaluation and selection of a desirable 3PRLPs is a multi-faceted and complex decision-making task due to multiple qualitative and quantitative attributes [74]. The criteria involved in this process may fluctuate based on the type of considered item and often conflict with each other [59].

In recent times, the assessment of the 3PRLPs selection process has received great attention from the researchers. Numerous scholarly articles on the selection of the best 3PRLP alternative have been presented in the literature. However, more studies are required to manage the preferences of different expertise, different backgrounds, and knowledge levels on reverse logistics with considering social, environmental, and economic aspects simultaneously. Consequently, the present study is concentrated on introducing a novel decision-making method for 3PRLP selection under uncertain contexts. The concept of bipolar complex fuzzy sets (BCFSs) [7] is pioneered as an innovative tool to describe the bipolar nature in the lack of sureness and periodicity semantics by applying the BFSs range in the domain of complex geometry. In BCFSs theory, the amplitude term corresponding to membership (non-membership) degree gives the extent of belongingness (non-belongingness) of an object, and the phase term associated with membership (non-membership) degree gives the additional information, generally related with periodicity. BFS theory deals with only one dimension at a time, which results in information loss in some instances. On the other hand, CFS theory deals with the two-dimensional information of an object. However, in day-to-day life, we come across complex natural phenomena where it becomes essential to consider the two-dimensional and the bipolar information (positive and negative information) of an object. BCFSs [7] can efficiently deal with this situation. To illustrate the significance of BCFS, consider the example (adapted from [7]: "As indicated by Chinese devotees, all universe articles can be seen from the perspective of Yin and Yang components [23]. Many factors with the viewpoint of bipolarity have affected simultaneously with types of food Yin and Yang to have a fair body like our everyday exercises sitting actually is Yin, practice is Yang, our current circumstance a chilly climate atmosphere and a sleepy country town is more Yin,a more blazing atmosphere and busy city is Yang, and our level of profound mindfulness and change. Cousens [23] introduced that "the level of otherworldly mindfulness and change influences how much our brain is moved by the yin and yang energy of foods in a fairly unexpected manner in comparison to different elements influencing yin and yang". These kinds of data convey the bipolarity of uncertainty (food types) and the bipolarity of periodicity (day-by-day exercises, climate, or level of otherworldly mindfulness and change). The present circumstance can't be displayed precisely utilizing CFS and BFS theory as none of them can deal with two factors at the same time used to find the ideal body balance in the Yin and Yang food framework. An ideal approach to speak to this is BCFS theory. Thus BCFS is more general compared to FS [97], BFS [103] and CFS [72]. At present, very few scholars have focused their attention on BCFSs. Based on its unique amenities, in this paper, our discussion encompasses the BCFSs environment. It is clear from the literature that there has been no study on developing the integrated MCDM tool associating the CRITIC and MULTIMOORA approaches with BCF information. Also, there has been no study in the literature regarding the developed hybrid approach, namely BCF-CRITIC-MULTIMOORA, in assessing the 3PRLP selection process. The novel contributions are as follows:

• BCF-Archimedean power AOs have been developed and their basic characteristics are surveyed.

• Novel integrated BCF-CRITIC-MULTIMOORA methodology has been developed to deal with MCDM problems.

• To illustrate the feasibility and usefulness of BCF-CRITIC-MULTIMOORA approach, an empiric case study of 3PRLP selection has been studied in the BCFSs setting.

• A comparative discussion has been deployed to show the strength of the introduced approach.

We summarize the remaining paper as follows: In “Literature review”, we give a concise literature review. In “Prerequisites”, we recall the definition of a BCFN and some related concepts such as score, accuracy value, ranking rules of the BCFNS, Archimedean operational laws for BCFNs and the definition of the power aggregation (PA) operator. In “BCF-Archimedean power weighted aggregation operators”, we develop some BCF Archimedean power-weighted AOs, such as BCFAPWAA, BCFAPOWAA, BCFAPWGA, and BCFAPOWGA. Also, we discuss the essential postulates of proposed operators. In “BCF-CRITIC-MULTIMOORA methodology for decision-making”, we develop a novel BCF-CRITIC-MULTIMOORA framework with CRITIC method and the proposed AOs where the criteria values take the form of BCFNs. In “Case study: 3PRLPs selection”, we deploy a case study on 3PRLP selection to gloss the developed method. “Comparative study” deals with the comparative discussion to affirm the prevalence of the developed technique. In the end, in “Conclusions”, we make some conclusions upon this entire study and give an outline of future prospects.

Literature review

Here, a comprehensive review related to this study is presented.

Bipolar complex fuzzy sets

The doctrine of FSs, pioneered by Zadeh [97], has received huge interest from several authors in handling uncertainty in diverse fields. However, FSs cannot deal with complex problems as they only have a belongingness degree (BD). Next, Atanassov [9] developed the idea of IFSs, which is considered BD and non-belongingness degree (ND). Over the last few decades, various authors have initiated several kinds of algorithms to solve the MCDM problems by using the FSs and IFSs theories, but it has been observed commonly for the data assessment of an element that analogous to each postulate, there exists some counter postulate. To conquer this issue, Zhang [103, 104] pioneered BFSs, which consists of positive BD and negative BD. The positive BD lies in [0, 1] and the negative BD lies in [− 1, 0]. Zhang and Zhang [106] put forth the notion of bipolar logic and fuzzy logic to represent how quantum fields are merged with neural biology networks, equilibrium combines with bipolar disorder, and gets to know how especial hypothesis get united with brain and behavior. Alghamdi et al. [5] suggested MCDM techniques by reporting the BF concept. Akram and Arshad [2] initiated BF linguistic variables and BF numbers as a generalization of BFSs. The notion of BFSs has widely been applied in medical diagnosis, bipolar disorder, decision making, optimization, and others [3, 4, 40, 77, 78, 105, 15].

Ramot et al. [72] pioneered the concept of CFSs, characterized by a BD, whose limit is expanded to a circle with a unit radius in the complex plane in place of [0, 1]. The concept of extending the span of FS to a broader limit of CFS lies in its capacity to collect the semantics comprising the uncertainty and periodicity news altogether. Ramot et al. [71] gave an additional term named the phase term to handle the enigma in transforming some complex-valued functions on physical expressions to human language and vice versa. In Cartesian and polar structures, the membership grade for complex fuzzy may be expressed with two fuzzy components [85]. As a potent trick to establish the notion of BCFSs [7], the phase term of complex numbers (CNs) is taken into consideration.

The new idea of BCFS may be deployed to illustrate the imprecision and difficulty in periodicity of bipolar fuzzy messages in complex geometry in a combined manner. Firstly, Singh [79] suggested the bipolar complex fuzzy lattice ideas by its possible infliction to circumnavigate or decompose the BCFSs and their semantics by utilizing a demonstrative example. Alkouri et al. [7] studied the mathematical structure of BCFS and its applications. Al-Husban et al. [6] presented an overview of BCFS and its basic concepts.

CRITIC methods

In the process of MCDM, determining the criteria weights is a significant concern for DEs. The criteria weight determination approaches are divided into objective and subjective weights [65]. The CRITIC model, propounded by Diakoulaki et al. [25], is one of the weighting tools to determine the objective criteria weights. In this approach, with the help of the contradictory intensity of each criterion, known as standard deviation, criteria’s significance can be judged. In contrast, it is treated the controversy in between the criteria as the correlation coefficient among them. The basis of the CRITIC approach is the intensity of the contrast in the construction of decision-making issues [25]. Recently, few hybrid methods have been developed by combining CRITIC and many other MCDM approaches under uncertain environments. For example, Ghorabaee et al. [30] suggested an integrated model with CRITIC and WASPAS approaches to assess the third-party logistics providers. Ghorabaee et al. [29] designed a hybrid fuzzy MCDM framework based on the CRITIC, SWARA and EDAS methods. Peng et al. [67] presented an integrated Pythagorean fuzzy CRITIC and CoCoSo based methodology for 5G industry evaluation. Wei et al. [92] studied an integrated method by combining GRA and CRITIC approaches to evaluate and select the desired location for electric vehicle charging stations under probabilistic uncertain linguistic term sets the context. Peng and Huang [66] proposed a combined methodology by integrating CRITIC and CoCoSo approaches for financial risk evaluation. Liang [54] gave an MCDM method with the CRITIC and EDAS methods to gradually compute the attribute weights and the favor ordering of the alternatives.

MULTIMOORA method

An MCDM, a part of decision theory, is an act of selecting an ideal choice from a given set of decision variants. Due to the wide-spread changes and the development of socio-economic environment, real-world decision-making issues are becoming more and more complex. Over the last few decades, many new approaches have been proposed to deal with real-life MCDM problems, where each of them has its own advantages and limitations. The MOORA model, propounded by Brauers and Zavadskas [18], is an efficient and renowned MCDM method consisting of RS and RP models. To increase the robustness of MOORA model, Brauers and Zavadskas [19] pioneered the MULTIMOORA approach, which consists of three aggregation models with different functions: the RS method, the RP model, and FMF procedure. In comparison with AHP, TOPSIS, VIKOR, PROMETHEE, LINMAP, and ELECTRE, the MULTIMOORA approach has more superiority, easy mathematical expressions, less computation time, and strong robustness [17]. Due to its unique advantages over other MCDM methods, the classical MULTIMOORA method has been employed for various MCDM concerns [80, 94].

Further, to tackle uncertain information arises in MCDM problems, several extensions of MULTIMOORA have been introduced under diverse uncertain environments (see Table 1).

Table 1 Literature on MULTIMOORA approach in different environments

The 3PRLPs selection

A variety of criteria are involved in the evaluation of 3PRLPs selection procedure; accordingly, this selection process can be observed as an MCDM problem. Existing studies on the 3PRLP selection problem confirm the emergent interest of scholars and manufacturers. Over the last few years, copious MCDM models have been established in the setting of 3PRLP assessment problem. Realistic reverse logistics outsourcing assessments are commonly prepared under imprecise and vague environment due to multiple indicators, like as partial ignorance, imprecise estimation, partial or inaccessible decision information [16, 27]. Consequently, crisp values are usually unsuitable for modelling such types of practical decision conditions.

The FSs theory and their extensions have proven to be suitable tools to handle uncertain and vague information in realistic MCDM settings. Efendigil et al. [27] designed a two-way method by integrating fuzzy logic and artificial neural networks to assess an ideal 3PRLP option. A structured procedure with AHP on FSs was developed by Kannan [43] for evaluating the 3PRLP selection problem. Govindan and Murugesan [33] used the fuzzy extent assessment approach for choosing the desirable 3PRLP for a battery manufacturing industry. Senthil et al. [76] suggested a combined model with AHP and TOPSIS approaches for evaluating an ideal reverse logistics contractor. In a further study by Tajik et al. [84], a hybrid fuzzy decision-making framework was introduced for choosing the most suitable 3PRLP alternative by considering all three aspects of sustainability. Later, Uygun et al. [91] planned and selected an outsourcing provider for a telecommunications business by employing DEMATEL and fuzzy ANP approaches. In another study, Tavana et al. [87] suggested a conceptual analytic network model to thoroughly model the complex behavior of interactions among the 3PRLPs assessment elements. Mavi et al. [59] presented the SWARA method for weighting the assessment criteria of 3PRLP in the plastics industry and further ranked the sustainable 3PRLP alternatives through MOORA model within FSs context. Tavana et al. [86] suggested a combined method with the integration of ANP and grey superiority and inferiority methods on intuitionistic fuzzy sets to assess the 3PRLPs selection process. Li et al. [51] used a combined cumulative prospect doctrine with hybrid-information MCDM methodology to evaluate 3PRLPs from sustainability perspectives. Zarbakhshnia et al. [98] weighted the assessment criteria through fuzzy-SWARA method and ranked the sustainable 3PRLPs by employing COPRAS method under fuzzy environment. Liu et al. [57] suggested an innovative IVPHF-BWM to research the selection of 3PRLPs. Bai and Sarkis [11] pioneered multi-stage, multi-method, and MCDM tool with TOPSIS, VIKOR and neighborhood rough set for the evaluation of 3PRLP selection decision. Zhang and Su [107] introduced a dominance-score dependent heterogeneous linguistic model to assess the best sustainable 3PRLP for a car manufacture industry. Mishra et al. [62] introduced a hybrid approach using the CoCoSo method and discrimination measure on HFSs to deal with the 3PRLP assessment problem. Mishra et al. [63] presented an integrated model with CRITIC and evaluation based on distance from average solution (EDAS) models for Fermatean fuzzy sets (FFSs) to tackle with the S3PRLP assessment. To select the optimal S3PRLP, Mishra and Rani [61] initiated a hybrid approach with combined compromise solution (CoCoSo) and CRITIC approaches on single-valued neutrosophic sets (SVNSs). Chen et al. [22] gave a projection model to analyze, rank, evaluate and select the optimal 3PRLPs on IVIFSs.

Prerequisites

In this section, we present the definition, score and accuracy value, ranking rules, distance measure, and Archimedean operations of BCFNs. At the end, we recall the definition of power AO.

Definition 1

[7] Let U denotes a universe set (finite). Then a BCFS $\tilde{A}$ on U is expressed by

$$ \tilde{A} = \left\{ {\left( {u,\left\langle {\mu_{{\tilde{A}}}^{ + } (u),\mu_{{\tilde{A}}}^{ - } (u)} \right\rangle } \right):\,u \in U} \right\}, $$

where the terms $\mu_{{\tilde{A}}}^{ + } (u)\,\,and\,\,\mu_{{\tilde{A}}}^{ - } (u)$ are known as complex-valued positive BD and complex valued negative BD of the object $u \in U$. The values of $\mu_{{\tilde{A}}}^{ + } (u)\,\,and\,\,\mu_{{\tilde{A}}}^{ - } (u)$ lie within the unit disc $D = \{ z \in C:\,\left| z \right| \le 1\,\}$ (C denotes the set of all complex numbers). So, without loss of generality, we may accept that $\mu_{{\tilde{A}}}^{ + } (u) = \alpha (u){\text{e}}^{{\left( {i\omega \delta (u)} \right)}}$ and $\mu_{{\tilde{A}}}^{ - } (u) = \beta (u){\text{e}}^{{\left( {i\omega \vartheta (u)} \right)}} ,$ where $\alpha (u),\,\,\delta (u) \in [0,1]$ and $\beta (u),\,\,\vartheta (u) \in [ - 1,0]$ for any $u \in U$ and $i = \sqrt { - 1}$. $\omega \,( \in (0,2\pi ])$ is called the scaling factor and it is utilized to restrict the elucidation of phases inside the unit disk and the interval $(0,2\pi ]$. $\delta (u)$ and $\vartheta (u)$ are known as positive and negative phase values of the object $u \in U$. Without these phase values, the BCFS $\tilde{A}$ is reduced to a traditional BFS. Moreover if we set $\beta (u) = 0$$\forall \,\,u \in U,$ then BCFS reduces to a traditional CFS.

Thus the BCFS $\tilde{A}$ can be rewritten as $\tilde{A} = \left\{ {\left( {u,\left\langle {\alpha (u){\text{e}}^{{\left( {i\omega \delta (u)} \right)}} ,\beta (u){\text{e}}^{{\left( {i\omega \vartheta (u)} \right)}} } \right\rangle } \right):\,u \in U} \right\}.$ For any $u \in U,$ the pair $\left\langle {\alpha (u){\text{e}}^{{\left( {i\omega \delta (u)} \right)}} ,\beta (u){\text{e}}^{{\left( {i\omega \vartheta (u)} \right)}} } \right\rangle$ is termed as a bipolar complex fuzzy number (BCFN). For easiness, the symbol $\xi = \left\langle {\alpha {\text{e}}^{{\left( {i\omega \delta } \right)}} ,\beta {\text{e}}^{{\left( {i\omega \vartheta } \right)}} } \right\rangle$ is used to denote a BCFN. The set of all BCFN on U is signified as $BCFN^{U} .$

Definition 2

[56] Let $\xi = \left\langle {\alpha \times {\text{e}}^{{\left( {i\omega \delta } \right)}} ,\beta \times {\text{e}}^{{\left( {i\omega \vartheta } \right)}} } \right\rangle \in BCFN^{U}$. Then the score value of $\xi$ is defined as $S(\xi ) = \frac{1}{4}\left( {2 + \alpha + \,\delta + \beta + \,\vartheta } \right).$

Clearly, $0 \le S(\xi ) \le 1$. It is observed that the score function can’t be effectively used to discriminate various BCFNs in several specific cases. For instance, if $\xi_{1} = \left\langle {0.5 \times {\text{e}}^{{\left( {0.7i\pi } \right)}} , - 0.3 \times {\text{e}}^{{\left( { - 0.7i\pi } \right)}} } \right\rangle$ and $\xi_{2} = \left\langle {0.6 \times {\text{e}}^{{\left( {0.5i\pi } \right)}} , - 0.3 \times {\text{e}}^{{\left( { - 0.6i\pi } \right)}} } \right\rangle ,$ then $S(\xi_{1} ) = S(\xi_{2} )$ (taking $\omega = \pi$). To tackle this scenario, the notion of accuracy value of a BCFN was proposed by Liu et al. [56].

Definition 3

[56] Let $\xi = \left\langle {\alpha \times {\text{e}}^{{\left( {i\omega \delta } \right)}} ,\beta \times {\text{e}}^{{\left( {i\omega \vartheta } \right)}} } \right\rangle \in BCFN^{U}$. Then the accuracy value of $\xi$ is defined as $AC(\xi ) = \frac{1}{4}\left( {\alpha - \,\delta + \beta - \,\vartheta } \right)$.

Clearly, $0 \le AC(\xi ) \le 1$.

Corresponding to the score and accuracy values of BCFNs, a comparative process of BCFNs is described as.

Definition 4

[56]: Let $\xi_{1} ,$ $\xi_{2} \in BCFN^{U}$. Then:

(I) If $S(\xi_{1} ) > S(\xi_{2} )$, then $\xi_{1} \succ \xi_{2} \,\,\,({\text{or}}\,\,\xi_{2} \prec \xi_{1} )$.

(II) If $S(\xi_{1} ) = S(\xi_{2} )$, then.

(i) if $AC(\xi_{1} ) > AC(\xi_{2} )$, then $\xi_{1} \succ \xi_{2} \,\,\,({\text{or}}\,\,\xi_{2} \prec \xi_{1} )$.

(ii) if $AC(\xi_{1} ) = AC(\xi_{2} )$, then $\xi_{1} = \xi_{2}$.

Based on Archimedean operational laws [46], Liu et al. [56] introduced Archimedean operational laws for BCFNs which are presented by.

Definition 5

[56]: Let $\xi_{1} = \left\langle {\alpha_{1} e^{{(i\omega \delta_{1} )}} ,\beta_{1} e^{{(i\omega \vartheta_{1} )}} } \right\rangle ,\xi_{2} = \left\langle {\alpha_{2} e^{{(i\omega \delta_{2} )}} ,\beta_{2} e^{{(i\omega \vartheta_{2} )}} } \right\rangle$ $\in BCFN^{U}$. Then the Archimedean operational laws of BCFNs are:

• (i) $\xi_{1} \tilde{ \oplus }\xi_{2} = \left\langle {(g^{ - 1} (g(\alpha_{1} ) + g(\alpha_{2} ))){\text{e}}^{{(\omega i(g^{ - 1} (g(\delta_{1} ) + g(\delta_{2} ))))}} ,\,\, - (h^{ - 1} (h(\left| {\beta_{1} } \right|) + h(\left| {\beta_{2} } \right|))){\text{e}}^{{( - \omega i(h^{ - 1} (h(\left| {\vartheta_{1} } \right|) + h(\left| {\vartheta_{2} } \right|))))}} } \right\rangle$

• (ii) $\xi_{1} \tilde{ \otimes }\xi_{2} = \left\langle {(h^{ - 1} (h(\alpha_{1} ) + h(\alpha_{2} ))){\text{e}}^{{(\omega i(h^{ - 1} (h(\delta_{1} ) + h(\delta_{2} ))))}} ,\,\, - (g^{ - 1} (g(\left| {\beta_{1} } \right|) + g(\left| {\beta_{2} } \right|))){\text{e}}^{{( - \omega i(g^{ - 1} (g(\left| {\vartheta_{1} } \right|) + g(\left| {\vartheta_{2} } \right|))))}} } \right\rangle$

• (iii) $\lambda * \xi_{1} = \left\langle {(g^{ - 1} (\lambda g(\alpha_{1} ))){\text{e}}^{{(\omega i(g^{ - 1} (\lambda g(\delta_{1} ))))}} ,\,\, - (h^{ - 1} (\lambda h(\left| {\beta_{1} } \right|))){\text{e}}^{{( - \omega i(h^{ - 1} (\lambda h(\left| {\vartheta_{1} } \right|))))}} } \right\rangle \,\,{(\lambda > 0)}$

• (iv) $\lambda \circ \xi_{1} = \left\langle {(h^{ - 1} (\lambda h(\alpha_{1} ))){\text{e}}^{{(\omega i(h^{ - 1} (\lambda h(\delta_{1} ))))}} ,\,\, - (g^{ - 1} (\lambda g(\left| {\beta_{1} } \right|))){\text{e}}^{{( - \omega i(g^{ - 1} (\lambda g(\left| {\vartheta_{1} } \right|))))}} } \right\rangle \,\,{(\lambda > 0)}$

Here, g and h is an Archimedean t-norm and t-conorm, respectively [46].

Definition 6

[96] Let $a_{1} ,a_{2} ,\,.......,a_{n}$ are considered as accumulation of crisp numbers. Then the power average (PA) operator associated to aggregation of these numbers is given by

$$ PA(a_{1} ,a_{2} ,\,...,a_{n} ) = \frac{{\sum\nolimits_{i = 1}^{n} {(1 + \Delta (a_{i} ))a_{i} } }}{{\sum\nolimits_{i = 1}^{n} {(1 + \Delta (a_{i} ))} }}\;{\text{where}}\;\Delta (a_{i} ) = \sum\limits_{j = 1,j \ne i}^{n} {{\text{Supp}}(a_{i} ,a_{j} )} . $$

Here, ${\text{Supp}}(a_{i} ,a_{j} )$ denotes the support for $a_{i}$ from $a_{j}$ and has three postulates as

• (i) $0 \le {\text{Supp}}(a_{i} ,a_{j} ) \le 1$

• (ii) ${\text{Supp}}(a_{i} ,a_{j} ) = {\text{Supp}}(a_{j} ,a_{i} ).$

• (iii) ${\text{Supp}}(a_{i} ,a_{j} ) \ge {\text{Supp}}(a_{k} ,a_{r} )$ provided $\left| {a_{i} - a_{j} } \right| < \left| {a_{k} - a_{r} } \right|$ where $i,j,k,r \in N_{n}$.

BCF-Archimedean power weighted aggregation operators

In this current section, we build up some BCF-Archimedean power-weighted AOs with the help of the Archimedean operations of BCFNs.

BCF-Archimedean power weighted arithmetic AOs:

Here, we propose BCFAPWAA and BCFAPOWAA operators and study their properties.

Definition 7

Suppose $\xi_{j} = \left\langle {\alpha_{j} {\text{e}}^{{\left( {i\omega \delta_{j} } \right)}} \beta_{j} {\text{e}}^{{\left( {i\omega \vartheta_{j} } \right)}} } \right\rangle \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right).$ Then the BCFAPWAA operator a function ${\text{BCFAPWAA}}:{\text{BCFN}}^{U} \to {\text{BCFN}}^{U}$ given by:

$$ {\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{n} \,) = \mathop {\tilde{ \oplus }}\nolimits_{j = 1}^{n} \frac{{(1 + \Delta (\xi_{j} ))w_{j} }}{{\sum\nolimits_{j = 1}^{n} {w_{j} (1 + \Delta (\xi_{j} ))} }} \times \xi_{j} , $$

where $w_{j} > 0\,\,(j \in N_{n} )$ is the weight of $\xi_{j}$ with $\sum\nolimits_{j = 1}^{n} {w_{j} } = 1$.

Here $\Delta (\xi_{i} ) = \sum\nolimits_{j = 1,j \ne i}^{n} {{\text{Supp}}(\xi_{i} ,\xi_{j} )}$.

Next, the theorem given below follows from Definition 7.

Theorem 1

The aggregated value ${\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{n} \,)$ is also a BCFN and

$$ \begin{aligned}& {\text{BCFAPWAA}}(\xi _{1} \,,\xi _{2} \,,\xi _{3} \,,...,\xi _{n} \,) \hfill \\ &\quad = \left\langle {\left( {g^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} g(\alpha _{j} )} } \right)} \right)\text{e} ^{{\left( {\omega i\left( {g^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} g\left( {\delta _{j} } \right)} } \right)} \right)} \right)}} ,\,\,} \right. \\ &\quad\quad\times \left. {\left( { - h^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} h(\left| {\beta _{j} } \right|)} } \right)} \right)\text{e} ^{{\left( { - \omega i\left( {h^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} h\left( {\left| {\vartheta _{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle , \hfill \\ \end{aligned} , $$

(1)

where $\theta_{j} = \frac{{(1 + \Delta (\xi_{j} ))w_{j} \,}}{{\sum\nolimits_{i = 1}^{n} {w_{j} \,(1 + \Delta (\xi_{j} ))} }}\,\,\,(j \in N_{n} )$.

Proof is given in Appendix.

Theorem 2

(Shift invariance) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} ( \ne \xi_{j} ) \in {\text{BCFN}}^{U}$. Then ${\text{BCFAPWAA}}(\xi_{0} \tilde{ \oplus }$ $\xi_{1} \,,\xi_{0} \tilde{ \oplus }\xi_{2} \,,\,......,\xi_{0} \tilde{ \oplus }\xi_{n} ) = \xi_{0} \tilde{ \oplus }{\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} )$.

Proof is given in Appendix.

Theorem 3

(Idempotency) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} \in {\text{BCFN}}^{U}$ such that $\xi_{j} \, = \xi_{0} \,\,\,\forall \,j$. Then we have,${\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) = \xi_{0} \,.$

Proof is given in Appendix.

Theorem 4

(Boundedness) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right).$ Then, $\xi^{ - } \prec {\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,$$........,\xi_{n} ) \prec \xi^{ + } \,$ where $\xi^{ - } = \left\langle {\varphi^{ + } {\text{e}}^{{\left( {i\omega \eta^{ + } } \right)}} \,,} \right.\left. {\Phi^{ - } {\text{e}}^{{\left( {i\omega \psi^{ - } } \right)}} } \right\rangle \,\,{\text{and}}\,\,\xi^{ + } = \left\langle {\alpha^{ + } {\text{e}}^{{\left( {i\omega \delta^{ + } } \right)}} \,,} \right.\left. {\beta^{ - } {\text{e}}^{{\left( {i\omega \vartheta^{ - } } \right)}} } \right\rangle$.

Theorem 5

(Monotonicity) Suppose $\xi_{j} ,\xi^{\prime}_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ satisfying $\alpha_{j} \le \alpha^{\prime}_{j} ,\delta_{j} \le \delta^{\prime}_{j} ,\beta_{j} \ge \beta^{\prime}_{j} ,\vartheta_{j} \ge \vartheta^{\prime}_{j}$ where $\xi^{\prime}_{j} = \left\langle {\alpha^{\prime}_{j} {\text{e}}^{{\left( {i\omega \delta^{\prime}_{j} } \right)}} ,\beta^{\prime}_{j} {\text{e}}^{{\left( {i\omega \vartheta^{\prime}_{j} } \right)}} } \right\rangle$.Then we have,

$$ {\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec {\text{BCFAPWAA}}(\xi^{\prime}_{1} \,,\xi^{\prime}_{2} ,\xi^{\prime}_{3} ,..........,\xi^{\prime}_{n} ). $$

Proof is given in Appendix.

Next, based on ${\text{BCFAPWAA}}$ operator, we develop the ${\text{BCFAPOWAA}}$ operator as follows:

Definition 8

Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right).$ Then the BCFAPOWAA is a function ${\text{BCFAPOWAA}}:{\text{BCFN}}^{U} \to {\text{BCFN}}^{U}$ which is defined as follows:

$$ {\text{BCFAPOWAA}}(\xi_{1} ,\xi_{2} ,\xi_{3} \,,...,\xi_{n} \,) = \mathop {\tilde{ \oplus }}\limits_{j = 1}^{n} \left( {\theta_{j} \times \xi_{\sigma (j)} } \right), $$

where $(\sigma (1),\sigma (2),\sigma (3),...,\sigma (n))$ is an arrangement of $\xi_{j}$ with $\xi_{\sigma (j - 1)} \ge \xi_{\sigma (j)}$$\forall \,j \in N_{n} .$

The following theorem follows from Definition 8.

Theorem 6

The aggregated value ${\text{BCFAPOWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{n} \,)$ is also a BCFN and

$$ \begin{aligned} &{\text{BCFAPOWAA}}(\xi _{1} \,,\xi _{2} \,,\xi _{3} \,,...,\xi _{n} \,) \hfill \\ &\quad= \left\langle {\left( {g^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} g(\alpha _{{\sigma (j)}} )} } \right)} \right)\text{e} ^{{\left( {\omega i\left( {g^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} g\left( {\delta _{{\sigma (j)}} } \right)} } \right)} \right)} \right)}} ,\,\,} \right. \\ &\quad\quad\times \left. {\left( { - h^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} h(\left| {\beta _{{\sigma (j)}} } \right|)} } \right)} \right)\text{e} ^{{\left( { - \omega i\left( {h^{{ - 1}} \left( {\sum\limits_{{j = 1}}^{n} {\theta _{j} h\left( {\left| {\vartheta _{{\sigma (j)}} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle . \hfill \\ \end{aligned} . $$

(2)

In particular, if $w_{j} = \frac{1}{n}\,\,\forall \,j \in N_{n} ;$, then the BCFAPOWAA reduces to the BCFAPWAA.

Theorem 7

(Shift invariance) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} ( \ne \xi_{j} )\, \in {\text{BCFN}}^{U} .$ Then ${\text{BCFAPOWAA}}(\xi_{0} \tilde{ \oplus }$$\xi_{1} \,,\xi_{0} \tilde{ \oplus }\xi_{2} \,,\,......,\xi_{0} \tilde{ \oplus }\xi_{n} ) = \xi_{0} \tilde{ \oplus }{\text{BCFAPOWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} )$.

Theorem 8

(Idempotency) Suppose $\xi_{j} \in BCFN^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} \, \in {\text{BCFN}}^{U}$ satisfying $\xi_{j} \, = \xi_{0} \,\,\,\forall \,j$. Then we have,${\text{BCFAPOWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) = \xi_{0} \,.$

Theorem 9

(Boundedness) Suppose $\xi_{j} \in BCFN^{U} \,\left( {j \in N_{n} } \right).$ Then,

$$ \xi^{ - } \prec BCFAPOWAA(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec \xi^{ + } \, $$

where $\xi^{ - } = \left\langle {\varphi^{ + } {\text{e}}^{{\left( {i\omega \eta^{ + } } \right)}} \,,} \right.\left. {\Phi^{ - } {\text{e}}^{{\left( {i\omega \psi^{ - } } \right)}} } \right\rangle \,\,{\text{and}}\,\,\xi^{ + } = \left\langle {\alpha^{ + } {\text{e}}^{{\left( {i\omega \delta^{ + } } \right)}} \,,} \right.\left. {\beta^{ - } {\text{e}}^{{\left( {i\omega \vartheta^{ - } } \right)}} } \right\rangle$.

Theorem 10

(Monotonicity) Suppose $\xi_{j} ,\xi^{\prime}_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ such that $\alpha_{j} \le \alpha^{\prime}_{j} ,\delta_{j} \le \delta^{\prime}_{j} ,\beta_{j} \ge \beta^{\prime}_{j} ,\vartheta_{j} \ge \vartheta^{\prime}_{j}$ where $\xi^{\prime}_{j} = \left\langle {\alpha^{\prime}_{j} {\text{e}}^{{\left( {i\omega \delta^{\prime}_{j} } \right)}} ,\beta^{\prime}_{j} {\text{e}}^{{\left( {i\omega \vartheta^{\prime}_{j} } \right)}} } \right\rangle$. Then, we have ${\text{BCFAPOWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec {\text{BCFAPOWAA}}(\xi^{\prime}_{1} \,,\xi^{\prime}_{2} ,\xi^{\prime}_{3} ,..........,\xi^{\prime}_{n} ).$

Proofs are similar to above.

BCF-Archimedean power weighted geometric AOs

In this sub-section, we propose BCF Archimedean power-weighted geometric AO (BCFAPWGA) and BCF Archimedean power ordered weighted geometric AO (BCFAPOWGA)).

Definition 9

Suppose $\xi_{j} \in BCFN^{U} \,\left( {j \in N_{n} } \right).$ Then the BCFAPWGA is a function $BCFAPWGA:BCFN^{U} \to BCFN^{U}$ which is defined as follows:

$$ {\text{BCFAPPWGA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{n} \,) = \mathop {\tilde{ \otimes }}\nolimits_{j = 1}^{n} \frac{{(1 + \Delta (\xi_{j} ))w_{j} }}{{\sum\nolimits_{j = 1}^{n} {w_{j} (1 + \Delta (\xi_{j} ))} }} \circ \xi_{j} \,, $$

where $w_{j} > 0$ is the weight of $\xi_{j}$ with $\sum\nolimits_{j = 1}^{n} {w_{j} } = 1$.

Here $\Delta (\xi_{j} ) = \sum\nolimits_{j = 1,j \ne i}^{n} {{\text{Supp}}(\xi_{i} ,\xi_{j} )} .$

The given theorem follows the Definition 9.

Theorem 11

The aggregated value ${\text{BCFAPWGA}} (\xi_{1}, \xi_{2},\break \xi_{3} \,,........,\xi_{n} \,)$ is also a BCFN and

$$ \begin{aligned} &{\text{BCFAPWGA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,...,\xi_{n} \,) \hfill \\ & \quad= \left\langle {\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\alpha_{j} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\left| {\beta_{j} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle\hfill \\ \end{aligned} , $$

(3)

where $\theta_{j} = \frac{{(1 + \Delta (\xi_{j} ))}}{{\sum\nolimits_{j = 1}^{n} {(1 + \Delta (\xi_{j} ))} }}w_{j} \,\,(j \in N_{n} )$.

Theorem 12

(Shift invariance) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} \,( \ne \xi_{j} ) \in {\text{BCFN}}^{U} .$ Then ${\text{BCFAPWGA}}$$(\xi_{0} \tilde{ \otimes }\xi_{1} \,,\xi_{0} \tilde{ \otimes }\xi_{2} \,,\,......,\xi_{0} \tilde{ \otimes }\xi_{n} ) = \xi_{0} \tilde{ \otimes }{\text{BCFAPWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} )$.

Theorem 13

(Idempotency) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} \, \in {\text{BCFN}}^{U}$ such that $\xi_{j} \, = \xi_{0} \,\,\,\forall \,j$. Then we have,${\text{BCFAPWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) = \xi_{0} \,.$

Theorem 14

(Boundedness) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right).$ Then,

$$ \xi^{ - } \prec {\text{BCFAPWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec \xi^{ + } \, $$

where $\xi^{ - } = \left\langle {\varphi^{ + } {\text{e}}^{{\left( {i\omega \eta^{ + } } \right)}} \,,} \right.\left. {\Phi^{ - } {\text{e}}^{{\left( {i\omega \psi^{ - } } \right)}} } \right\rangle \,\,{\text{and}}\,\,\xi^{ + } = \left\langle {\alpha^{ + } {\text{e}}^{{\left( {i\omega \delta^{ + } } \right)}} \,,} \right.\left. {\beta^{ - } {\text{e}}^{{\left( {i\omega \vartheta^{ - } } \right)}} } \right\rangle$, ${\text{such that }}\,\varphi^{ + } = \mathop {\min }\nolimits_{j} \{ \alpha_{j} \} ,\,\eta^{ + } = \mathop {\min }\nolimits_{j} \{ \delta_{j} \} ,\Phi^{ - } = \mathop {\max }\nolimits_{j} \{ \beta_{j} \} ,\psi^{ - } = \mathop {\max }\nolimits_{j} \{ \vartheta_{j} \} ,\alpha^{ + } = \mathop {max}\nolimits_{j} \{ \alpha_{j} \} ,\,\delta^{ + } = \mathop {max}\nolimits_{j} \{ \delta_{j} \} , \hfill \beta^{ - } = \mathop {min}\nolimits_{j} \{ \beta_{j} \} ,\vartheta^{ - } = \mathop {\min }\nolimits_{j} \{ \vartheta_{j} \} . \hfill$

Theorem 15

(Monotonicity) Suppose $\xi_{j} ,\xi^{\prime}_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ such that $\alpha_{j} \le \alpha^{\prime}_{j} ,\delta_{j} \le \delta^{\prime}_{j} ,\beta_{j} \ge \beta^{\prime}_{j} ,\vartheta_{j} \ge \vartheta^{\prime}_{j}$ where $\xi^{\prime}_{j} = \left\langle {\alpha^{\prime}_{j} {\text{e}}^{{\left( {i\omega \delta^{\prime}_{j} } \right)}} ,\beta^{\prime}_{j} {\text{e}}^{{\left( {i\omega \vartheta^{\prime}_{j} } \right)}} } \right\rangle .$ Then, we have ${\text{BCFAPWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec {\text{BCFAPWGA}}(\xi^{\prime}_{1} \,,\xi^{\prime}_{2} ,\xi^{\prime}_{3} ,..........,\xi^{\prime}_{n} )$.

Next, based on ${\text{BCFAWPGA}}$ operator, we shall develop the ${\text{BCFAOWPGA}}$ as follows:

Definition 10

Consider a collection $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right).$ Then the BCFAPOWGA is a function ${\text{BCFAPOWGA}}:{\text{BCFN}}^{U} \to {\text{BCFN}}^{U}$ which is defined as follows:

$$ {\text{BCFAOWPGA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,...,\xi_{n} \,) = \mathop {\tilde{ \otimes }}\limits_{j = 1}^{n} \left( {\theta_{j} \circ \xi_{\sigma (j)} \,} \right), $$

where $(\sigma (1),\sigma (2),\sigma (3),...,\sigma (n))$ is an arrangement of $\xi_{j} \,$ satisfying $\xi_{\sigma (j - 1)} \ge \xi_{\sigma (j)}$$\forall \,j \in N_{n}$.

Next, the mentioned theorem follows from Definition 10.

Theorem 16

The aggregated value ${\text{BCFAPOWGA}}(\xi_{1} \,,\xi_{2},\break \xi_{3} \,,........,\xi_{n} \,)$ is also a BCFN and

$$ \begin{aligned} &{\text{BCFAPOWGA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,...,\xi_{n} \,) \hfill \\ & \quad= \left\langle {\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\alpha_{\sigma (j)} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\delta_{\sigma (j)} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\left| {\beta_{\sigma (j)} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\left| {\vartheta_{\sigma (j)} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle\hfill \\ \end{aligned} . $$

(4)

If $w_{j} = \frac{1}{n}\,\,\forall \,j \in N_{n} ;$ then the BCFAPOWGA reduces to the BCFAPWGA.

Theorem 17

(Shift invariance) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} \,( \ne \xi_{j} ) \in {\text{BCFN}}^{U} .$ Then ${\text{BCFAPOWGA}}$$(\xi_{0} \tilde{ \otimes }\xi_{1} \,,\xi_{0} \tilde{ \otimes }\xi_{2} \,,\,......,\xi_{0} \tilde{ \otimes }\xi_{n} ) = \xi_{0} \tilde{ \otimes }{\text{BCFAPOWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} )$.

Theorem 18

(Idempotency) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ and $\xi_{0} \, \in {\text{BCFN}}^{U}$ such that $\xi_{j} \, = \xi_{0} \,\,\,\forall \,j$. Then we have,${\text{BCFAPOWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) = \xi_{0} \,.$

Theorem 19

(Boundedness) Suppose $\xi_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right).$ Then,

$$ \xi^{ - } \prec {\text{BCFAPOWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec \xi^{ + } \, $$

where $\xi^{ - } = \left\langle {\varphi^{ + } {\text{e}}^{{\left( {i\omega \eta^{ + } } \right)}} \,,} \right.\left. {\Phi^{ - } {\text{e}}^{{\left( {i\omega \psi^{ - } } \right)}} } \right\rangle \,\,{\text{and}}\,\,\xi^{ + } = \left\langle {\alpha^{ + } {\text{e}}^{{\left( {i\omega \delta^{ + } } \right)}} \,,} \right.\left. {\beta^{ - } {\text{e}}^{{\left( {i\omega \vartheta^{ - } } \right)}} } \right\rangle$ ${\text{such that }}\varphi^{ + } = \mathop {\min }\nolimits_{j} \{ \alpha_{j} \} ,\,\eta^{ + } = \mathop {\min }\nolimits_{j} \{ \delta_{j} \} ,\Phi^{ - } = \mathop {\max }\nolimits_{j} \{ \beta_{j} \} ,\psi^{ - } = \mathop {\max }\nolimits_{j} \{ \vartheta_{j} \} ,\alpha^{ + } = \mathop {max}\nolimits_{j} \{ \alpha_{j} \} ,\,\delta^{ + } = \mathop {max}\nolimits_{j} \{ \delta_{j} \} ,$ $\beta^{ - } = \mathop {min}\nolimits_{j} \{ \beta_{j} \} ,\vartheta^{ - } = \mathop {\min }\nolimits_{j} \{ \vartheta_{j} \} .$

Theorem 20

(Monotonicity) Suppose $\xi_{j} ,\xi^{\prime}_{j} \in {\text{BCFN}}^{U} \,\left( {j \in N_{n} } \right)$ satisfying $\alpha_{j} \le \alpha^{\prime}_{j} ,\delta_{j} \le \delta^{\prime}_{j} ,\beta_{j} \ge \beta^{\prime}_{j} ,\vartheta_{j} \ge \vartheta^{\prime}_{j}$ where $\xi^{\prime}_{j} = \left\langle {\alpha^{\prime}_{j} {\text{e}}^{{\left( {i\omega \delta^{\prime}_{j} } \right)}} ,\beta^{\prime}_{j} {\text{e}}^{{\left( {i\omega \vartheta^{\prime}_{j} } \right)}} } \right\rangle$. Then, we have,${\text{BCFAPOWGA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec {\text{BCFAPOWGA}}(\xi^{\prime}_{1} \,,\xi^{\prime}_{2} ,\xi^{\prime}_{3} ,..........,\xi^{\prime}_{n} ).$

BCF-CRITIC-MULTIMOORA methodology for decision-making

In this present section, an integrated CRITIC-MULTIMOORA approach with BCF data in view of the introduced AOs is developed.

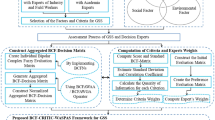
To solve a MCGDM problem comprising m different alternatives A₁, A₂, …, A_m in which the alternatives are assessed by DEs D₁, D₂, …, D_l in BCF environment over a set of n distinct attributes C₁, C₂, …, C_n, we develop an integrated BCF-CRITIC-MULTIMOORA methodology as follows (see Fig. 1):

Fig. 1

The flowchart of BCF-CRITIC-MULTIMOORA framework

Step 1: Consider the BCF-matrices representing the initial assessments of DEs.

Suppose $\wp_{k} = \left[ {d_{rj}^{k} } \right]_{m \times n} = \left[ {\left\langle {\alpha_{rj}^{k} {\text{e}}^{{\left( {i\omega \delta_{rj}^{k} } \right)}} \,,} \right.\left. {\beta_{rj}^{k} {\text{e}}^{{\left( {i\omega \vartheta_{rj}^{k} } \right)}} } \right\rangle } \right]_{m \times n}$ represents the initial assessment of the DE D_k.

Step 2: Normalize the BCF-matrices $\wp_{k} = \left[ {d_{rj}^{k} } \right]_{m \times n} \,\,(k \in N_{l} )$.

The normalized BCF-matrices are $\left[ {\tilde{d}_{rj}^{k} } \right]_{m \times n} = \left[ {\left\langle {\tilde{\alpha }_{rj}^{k} {\text{e}}^{{(i\omega \tilde{\delta }_{rj}^{k} )}} \,,} \right.\left. {\tilde{\beta }_{rj}^{k} {\text{e}}^{{(i\omega \tilde{\vartheta }_{rj}^{k} )}} } \right\rangle } \right]_{m \times n}$ where

$$ \left\langle {\tilde{\alpha }_{rj}^{k} {\text{e}}^{{(i\omega \tilde{\delta }_{rj}^{k} )}} \,,} \right.\left. {\tilde{\beta }_{rj}^{k} {\text{e}}^{{(i\omega \tilde{\vartheta }_{rj}^{k} )}} } \right\rangle = \left\{ {\begin{array}{*{20}c} {\left\langle {\alpha_{rj}^{k} {\text{e}}^{{(i\omega \delta_{rj}^{k} )}} \,,} \right.\left. {\beta_{rj}^{k} {\text{e}}^{{(i\omega \vartheta_{rj}^{k} )}} } \right\rangle ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,C_{j} \in Q_{B} } \\ {\left\langle {(1 - \alpha_{rj}^{k} ){\text{e}}^{{(i\omega (1 - \delta_{rj}^{k} ))}} \,,} \right.\left. {( - 1 - \beta_{rj}^{k} ){\text{e}}^{{(i\omega ( - 1 - \vartheta_{rj}^{k} ))}} } \right\rangle ,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\,C_{j} \in Q_{C} } \\ \end{array} } \right. $$

(5)

Step 3: Find out the supports ${\text{Supp}}(\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} )\,\,(k,s \in N_{l} ;\,k \ne l)$, using the below expression

$$ {\text{Supp}}(\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} ) = 1 - D(\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} )\,\,(k,s \in N_{l} ;\,k \ne l) $$

(6)

where $D(\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} )$ is the distance between BCFNs $\tilde{d}_{rj}^{k}$ and $\tilde{d}_{rj}^{s}$ given by Eq. (7).

$$ D(\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} ) = \frac{1}{3}\left( {\left| {\tilde{\alpha }_{rj}^{k} - \tilde{\alpha }_{rj}^{s} } \right| + \left| {\tilde{\delta }_{rj}^{k} - \tilde{\delta }_{rj}^{s} } \right| + \left| {\tilde{\beta }_{rj}^{k} - \tilde{\beta }_{rj}^{s} } \right| + \left| {\tilde{\vartheta }_{rj}^{k} - \tilde{\vartheta }_{rj}^{s} } \right|} \right). $$

(7)

It is easy to verify that Eq. (7) satisfies all the conditions of distance measures of BCFSs [7].

Step 4: Obtain the values $\Delta (\tilde{d}_{rj}^{k} )$ and $\theta_{rj}^{k}$ utilizing Eqs. (8) and (9) respectively.

$$ \Delta (\tilde{d}_{rj}^{k} ) = \sum\limits_{s = 1,k \ne s}^{l} {{\text{Supp}}(\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} )} , $$

(8)

$$ \theta_{rj}^{k} = \frac{{\varpi_{k} (1 + \Delta (\tilde{d}_{rj}^{k} ))}}{{\sum\nolimits_{k = 1}^{l} {\varpi_{k} (1 + \Delta (\tilde{d}_{rj}^{k} ))} }}\,\,\,\,(r \in N_{m} ;\,j \in N_{n} ;\,k \in N_{l} ). $$

(9)

Here $\varpi_{k} \,(k \in N_{l} )$ are weights of DEs $D_{k} \,(k \in N_{l} )$. Clearly, $\sum\nolimits_{k = 1}^{l} {\theta_{rj}^{k} } = 1$.

Step 5: Obtain the aggregated BCF matrix.

We use the proposed BCFAPWAA (or BCFAPWGA) operator to get the aggregated BCF matrix $\left[ {d_{rj}^{{}} } \right]_{m \times n}$ as follows:

$$\begin{aligned} & d_{rj}^{{}} \, = {\text{BCFAPWAA}}(\tilde{d}_{rj}^{1} ,\tilde{d}_{rj}^{2} ,...,\tilde{d}_{rj}^{l} )\, \hfill \\ & \quad= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} g(\tilde{\alpha }_{rj}^{k} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} g\left( {\tilde{\delta }_{rj}^{k} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - h^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} h(\left| {\tilde{\beta }_{rj}^{k} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} h\left( {\left| {\tilde{\vartheta }_{rj}^{k} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned}. $$

(10)

or

$$\begin{aligned} d_{rj}^{{}} & = {\text{BCFAPWGA}}(\tilde{d}_{rj}^{1} ,\tilde{d}_{rj}^{2} ,...,\tilde{d}_{rj}^{l} )\, \\ & = \left\langle {\left( {h^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} h(\tilde{\alpha }_{rj}^{k} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {h^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} h\left( {\tilde{\delta }_{rj}^{k} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - g^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} g(\left| {\tilde{\beta }_{rj}^{k} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {g^{ - 1} \left( {\sum\limits_{k = 1}^{l} {\theta_{rj}^{k} g\left( {\left| {\tilde{\vartheta }_{rj}^{k} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned}. $$

(11)

Suppose the aggregated BCF matrix is $\left[ {d_{rj}^{{}} } \right]_{m \times n} = \left[ {\left\langle {\alpha_{rj}^{{}} {\text{e}}^{{{(i\omega \delta_{rj}{}} )}} \,,} \right.\left. {\beta_{rj}^{{}} {\text{e}}^{{{(i\omega \vartheta_{rj}{}} )}} } \right\rangle } \right]_{m \times n} .$

Step 6: Computations of criteria weights.

Let $w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}$ such that $\sum\nolimits_{j = 1}^{n} {w_{j} = 1} ,$ $\,w_{j} \in \left[ {0,\,\,1} \right]$ be weight values for the criterion set. The indispensable attribute weights could uncover abundant data connecting in each of them, which is known as “objective weight”. The CRITIC is a methodology for processing the objective weights of the considered criteria. The weights inferred by this methodology associated both intensity contrast of every criteria and conflict among attributes. Intensity contrast of attribute is esteemed to standard deviation (SD) and conflict among them is calculated by the correlation coefficient (CRC). In this step, we implement this methodology into BCFNs.

Step 6.1: Utilizing the score values of BCFNs $d_{rj}^{{}} ,$ we construct the score matrix $\tilde{S} = \left[ {S(d_{rj}^{{}} )} \right]_{m \times n} ,$ where $S(d_{rj}^{{}} )$ = score value of the BCFN $d_{rj}^{{}}$ where

$$ S\left( {d_{rj}^{{}} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{{2 + \alpha_{rj} + \delta_{rj} + \beta_{rj} + \vartheta_{rj} }}{4},\,\,\,{\text{if}}\,\,C_{j} \in Q_{B} } \\ {\frac{{2 + (1 - \alpha_{rj} ) + (1 - \delta_{rj} ) + ( - 1 - \beta_{rj} ) + ( - 1 - \vartheta_{rj} )}}{4},\,\,\,{\text{if}}\,\,C_{j} \in Q_{C} } \\ \end{array} } \right. $$

(12)

Step 6.2: Convert the score matrix $\tilde{S}$ into the standard BCF-matrix $\hat{S} = \left( {\tilde{\zeta }_{rj} } \right)_{m\, \times \,n}$ where

$$ \tilde{\zeta }_{rj} = \left\{ \begin{aligned} \frac{{S(d_{rj} ) - \zeta_{j}^{ - } }}{{\zeta_{j}^{ + } - \zeta_{j}^{ - } }},\,\,\,\,\,{\text{if}}\,\,C_{j} \in Q_{B} \hfill \\ \frac{{\zeta_{j}^{ + } - S(d_{rj} )}}{{\zeta_{j}^{ + } - \zeta_{j}^{ - } }},\,\,\,\,\,\,{\text{if}}\,\,C_{j} \in Q_{C} \hfill \\ \end{aligned} \right.\, $$

(13)

where $\zeta_{j}^{ + } = \mathop {\max }\nolimits_{r} S(d_{rj} )$ and $\zeta_{j}^{ - } = \mathop {\min }\nolimits_{r} S(d_{rj} ).$

Step 6.3: Compute the attribute SDs by Eq. (14):

$$ \sigma_{j} = \sqrt {\frac{{\sum\nolimits_{r = 1}^{m} {\left( {\tilde{\zeta }_{rj} - \overline{\zeta }_{j} } \right)^{2} } }}{m}} ,\;{\text{where}}\;\overline{\zeta }_{j} = \frac{1}{m}\sum\limits_{r = 1}^{m} {\tilde{\zeta }_{rj} } . $$

(14)

Step 6.4: Estimate the correlation coefficient (CRC) utilizing Eq. (4):

$$ r_{jy} = \frac{{\sum\nolimits_{r = 1}^{m} {\left( {\tilde{\zeta }_{rj} - \overline{\zeta }_{j} } \right)\left( {\tilde{\zeta }_{ry} - \overline{\zeta }_{y} } \right)} }}{{\sqrt {\sum\nolimits_{r = 1}^{m} {\left( {\tilde{\zeta }_{rj} - \overline{\zeta }_{j} } \right)^{2} \sum\nolimits_{r = 1}^{m} {\left( {\tilde{\zeta }_{ry} - \overline{\zeta }_{y} } \right)^{2} } } } }}. $$

(15)

Step 6.5: Analyze the amount of information of each attribute as

$$ c_{j} = \sigma_{j} \,\sum\limits_{y = 1}^{n} {\left( {1 - r_{jy} } \right)} . $$

(16)

Step 6.6: Obtain the criteria weights using:

$$ w_{j} = \frac{{c_{j} }}{{\sum\nolimits_{j = 1}^{n} {c_{j} } }}. $$

(17)

Step 7: Obtain the best-suited alternative by the RS approach.

In the following sub steps it may be explored the choice of the best alternative and the ranking order of the alternatives with this approach in the suggested BCF-CRITIC-MULTIMOORA method.

Step 7.1: Compute $Y_{r}^{ + }$ and $Y_{r}^{ - }$ by utilizing the BCFAWAA operator [56] as given below:

$$\begin{aligned} & Y_{r}^{ + } \, = {\text{BCFAWAA}}(d_{r1} ,d_{r2} ,...,d_{rn} )\,\hfill \\ & \quad = \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} g(\alpha_{rj} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} g\left( {\delta_{rj} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - h^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} h(\left| {\beta_{rj} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} h\left( {\left| {\vartheta_{rj} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned}, $$

(18)

$$\begin{aligned} & Y_{r}^{ - } \, = {\text{BCFAWAA}}(d_{r1} ,d_{r2} ,...,d_{rn} )\hfill \\ & \quad = \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} g(\alpha_{rj} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} g\left( {\delta_{rj} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - h^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} h(\left| {\beta_{rj} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} h\left( {\left| {\vartheta_{rj} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle\hfill \\ \end{aligned} , $$

(19)

where $Y_{r}^{ + }$ and $Y_{r}^{ - }$ represent the alternative’s ($A_{r}$) significance that are achieved subject to the respective benefit and cost criteria. Clearly, $Y_{r}^{ + }$ and $Y_{r}^{ - }$ are BCFNs.

Step 7.2: Compute the score values of the BCFs $Y_{r}^{ + }$ and $Y_{r}^{ - }$$(r \in N_{m} )$ by using Definition 2.

Step 7.3: Compute the overall significance for each alternative using the formula:

$$ \Omega_{r}^{{}} = S(Y_{r}^{ + } ) - S(Y_{r}^{ - } )\;(r \in N_{m} ). $$

(20)

Step 7.4: Selection of the best alternative is to be performed after of their ranking. Similar to the RS approach underlying the ordinary MULTIMOORA method, the process of giving the ranking order can be entertained at this step.

Step 8: Obtain the ranking order of alternatives based on the RP approach.

Step 8.1: Compute the RP. Here, each coordinate $r_{j}^{*}$$(j\, = \,1\,,2,....,n)$ of the RP $r^{*} = \left\{ {r_{1}^{*} ,r_{2}^{*} ,...,r_{n}^{*} } \right\}$ is a BCFN that are calculated by the following way:

$$ r_{j}^{*} = \,\left\{ \begin{aligned} \,\left\langle {\mathop {\max }\limits_{r} \alpha_{rj} \times {\text{e}}^{{\left( {i\omega \mathop {\max }\limits_{r} \delta_{rj} } \right)}} \,,} \right.\left. {\mathop {\min }\limits_{r} \beta_{rj} \times {\text{e}}^{{\left( {i\omega \mathop {\min }\limits_{r} \vartheta_{rj} } \right)}} } \right\rangle ,\,\,{\text{for}} \,j \in \,Q_{B} \hfill \\ \left\langle {\mathop {\min }\limits_{r} \alpha_{rj} \times {\text{e}}^{{\left( {i\omega \mathop {\min }\limits_{r} \delta_{rj} } \right)}} \,,} \right.\left. {\mathop {\max }\limits_{r} \beta_{rj} \times {\text{e}}^{{\left( {i\omega \mathop {\max }\limits_{r} \vartheta_{rj} } \right)}} } \right\rangle ,\,\,{\text{for}} \,j \in \,Q_{C} \hfill \\ \end{aligned} \right.. $$

(21)

Step 8.2: Distance between RPs and each alternative is to be calculated using the condition:

$$ D_{rj} = w_{j} \times D\left( {d_{rj} ,r_{j}^{*} } \right), $$

(22)

in which $D_{rj}$ represents the alternative’s ($A_{r}$) distance which is determined on the basis of evaluation criterion $C_{j}$ obtained by Eq. (7).

Step 8.3: Using the following relation, each alternative’s highest distance is to be measured.

$$ d_{r} = \mathop {\max }\nolimits_{j} D_{rj} \,\,\left( {r \in N_{m} } \right) $$

(23)

Step 8.4: Selection of the best alternative is to be performed after their ranking. Similar to the RP approach underlying the ordinary MULTIMOORA method, the process of giving the ranking order can be entertained at this step.

Step 9: Obtain the ranking order of alternatives based on the FMF procedure.

Step 9.1: Utilizing the BCFAWGA operator [56], calculate $\Gamma_{r}$ and $\Phi_{r}$ as follows:

$$ \begin{aligned} &\Gamma_{r} \, = {\text{BCFAWGA}}(d_{r1} ,d_{r2} ,...,d_{rn} )\, \hfill \\ & \quad= \left\langle {\left( {h^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} h(\alpha_{rj} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {h^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} h\left( {\delta_{rj} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - g^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} g(\left| {\beta_{rj} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {g^{ - 1} \left( {\sum\limits_{{j \in Q_{B} }}^{{}} {w_{j} g\left( {\left| {\vartheta_{rj} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned} , $$

(24)

$$\begin{aligned} \Phi_{r} \, &= \,{\text{BCFAWGA}}(d_{r1} ,d_{r2} ,...,d_{rn} )\, , \\ &= \left\langle {\left( {h^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} h(\alpha_{rj} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {h^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} h\left( {\delta_{rj} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - g^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} g(\left| {\beta_{rj} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {g^{ - 1} \left( {\sum\limits_{{j \in Q_{C} }}^{{}} {w_{j} g\left( {\left| {\vartheta_{rj} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle , \end{aligned}$$

(25)

where $\Gamma_{k}$ and $\Phi_{k}$ are BCFNs representing the multiplicative forms corresponding to benefit-type and cost-type attributes, respectively.

Step 9.2: Estimate the score values of the BCFNs $\Gamma_{r}$ and $\Phi_{r}$ using Definition 2.

Step 9.3: The overall effectiveness value for each alternative by FMF method is calculated by:

$$ \eta_{r} = \frac{{\Gamma_{r} }}{{\Phi_{r} }}\,\,\,(r \in N_{m} ). $$

(26)

Step 9.4: Select the best alternative after getting the ranking order.

Step 10: Determine the final ranking order of the alternatives.

The overall assessment value of alternative by improved Borda Rule [93] is obtained by

$$ I_{{{\text{IBR}}}} (A_{r} ) = \tilde{\Omega }_{r}^{{}} \times \frac{{m - \rho (\tilde{\Omega }_{k}^{{}} ) + 1}}{(m(m + 1)/2)} - \tilde{d}_{r}^{{}} \times \frac{{\rho (\tilde{d}_{r}^{{}} )}}{(m(m + 1)/2)} + \tilde{\eta }_{r} \times \frac{{m - \rho (\tilde{\eta }_{r} ) + 1}}{(m(m + 1)/2)}\,\,\,\,\,\,\,\,\,\,\left( {r \in N_{m} } \right), $$

(27)

where $\tilde{\Omega }_{r}^{{}} ,\tilde{d}_{r}^{{}} ,\tilde{\eta }_{r}$ are the normalized score values and $\rho (\tilde{\Omega }_{k}^{{}} ),$ $\rho (\tilde{d}_{k}^{{}} ),$ $\rho (\tilde{\eta }_{k} ),$ are the final ranks of the alternative $A_{r}$ by RS, RP and FMF approaches, respectively. The best alternative has the maximum value of $I_{{{\text{IBR}}}} \left( {A_{r} } \right)$.

Case study: 3PRLPs selection

Problem description

In order to reveal the application of the developed framework, an illustrative case study of Chinese electronics’ company has been presented. The preferred company was established in the early 21st era and placed in the southwestern province of China to rise into an enterprise leader in computer manufacturing. At the moment, the company has an annual manufacturing capacity in excess of 2.5 million computers. However, the end-of-life (EOL) products generated a large volume of waste largely generating plastics and metal waste which had environmental effects and even polluted the water and land. Taking into consideration the increasing public awareness on environmental issues, increase in charge of raw materials, and compulsory green legislation in China, this manufacturer has decided to create a sustainable closed-loop supply chain with recycle the green products in forms of energy conservation. Consequently, the executives had arrived at a contract in implementation of a reverse logistics structure to efficiently organize and evoke the worth of reverse flow by reuse, recycling, reproducing, and eco-friendly disposal. On the other hand, the company considered in this study has a lack of experience and accessible organization capacity for RLs, and therefore decided to outsource RLs execution to 3PRLPs. After the open bidding, ten 3PRLPs displayed their curiosity in offering services. On the basis of preliminary analysis and discussions with experts, the company identified five potential 3PRLPs (A₁, A₂, A₃, A₄, A₅). A group of experts has been invited to evaluate the present 3PRLPs selection problem over fifteen identified criteria. The details of the criteria are depicted in Table 2.

Table 2 List of Assessment criteria for 3PRLPs selection

Problem solution

To solve the problem described above we take $\omega = \pi$. To reduce the shape and size of each table and for the purpose of simplistic presentation of each entry, in this sub-section, the notation $(\alpha ,\delta ;\beta ,\vartheta )$ is used to signify a BCFN $\left\langle {\alpha e^{(i\pi \delta )} ,\,\beta e^{(i\pi \vartheta )} } \right\rangle$.

Step 1: In this step, the decision experts will assess the five options $A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5}$ in relation to considered attributes $C_{j} \,(j \in N_{15} )$. The initial assessment results are given in the form of the matrices $\left[ {d_{rj}^{k} } \right]_{5 \times 15} \,\,( = \left[ {d_{jr}^{k} } \right]_{15 \times 5} )\,\,(k \in N_{3} )$ is given in the form of Table 3 (taking $\omega = \pi$):

Table 3 Initial decision matrix

Steps 2–3: We normalize the matrices $\left[ {d_{rj}^{k} } \right]_{5 \times 15} \,\,( = \left[ {d_{jr}^{k} } \right]_{15 \times 5} )\,\,(k \in N_{3} )$ by making use of Eq. (5). Then we calculate the supports ${\text{Supp(}}\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} )\,\,(r \in N_{5} ;\,j \in N_{15} ;\,\,k,s \in N_{3} ;\,k \ne s)$, based on Eqs. (6) and (7) and we represent them as $S^{(ks)} \,(\,k,s \in N_{3} ;\,k \ne s)$. These are presented in Table 4.

Table 4 Values of ${\text{Supp}}(\tilde{d}_{rj}^{k} ,\tilde{d}_{rj}^{s} )\,\,(r \in N_{5} ;\,j \in N_{15} ;\,\,k,s \in N_{3} ;\,k \ne s)$

Step 4: Utilizing Eqs. (8) and (9), values of $\theta_{rj}^{k} \,(r \in N_{5} ;\,j \in N_{15} ;\,\,k \in N_{3} )$ are obtained (Table 5) by taking $\varpi_{1} = 0.35,\,\,\varpi_{2} = 0.25,\varpi_{3} = 0.40$.

Table 5 Values of $\theta_{rj}^{k} \,(r \in N_{5} ;\,j \in N_{15} ;\,\,k \in N_{3} )$

Step 5: Utilizing Eq. (10) and taking $h(t) = - \ln t\,\,\,(where\,\,t \in (0,1])$, we get the aggregated BCF matrix (Table 6).

Table 6 Aggregated BCF-matrix

Step 6: Here, CRITIC method is implemented to calculate the criteria weight value. First, using Eq. (12) and Table 6, we calculate the score values of aggregated BCF matrix. Switch the score matrix $S = \left( {\zeta_{ij} } \right)_{m\, \times \,n}$ into the standard BCF-matrix $\tilde{S} = \left( {\tilde{\zeta }_{ij} } \right)_{m\, \times \,n}$ by utilizing the Eq. (13). Next, by applying Eqs. (14)–(16), the standard deviation, correlation coefficient and quantity of information of each factor are computed and depicted in Table 7. The criteria weights are computed by using Eq. (17) and are depicted in the final column of Table 7.

Table 7 The standard BCF-matrix, SD, amount of information and criteria weights using CRITIC

Step 7: The overall importance and rank of the alternative using RS method using Eqs. (18), (19) and (20) and taking $h(t) = - \ln t\,\,\,(where\,\,t \in (0,1])$ are given in Table 8.

Table 8 Overall importance and rank of the alternative based on RS technique

Step 8: The reference points $r_{j}^{*} \,(j = 1,2,....,15)$ are computed using Eq. (21) and are given by:

$$ r_{1}^{*} \, = < 0.{686673872} \times e^{{\left( {0.810622539{\text{i}}} \right)}} , - 0.{647148423} \times e^{{\left( { - 0.750635151{\text{i}}} \right)}} > , $$

$r_{2}^{*} \,$ =  < 0.630747981 × $e^{{\left( {0.791276869{\text{i}}} \right)}}$, − 0.481311088 × $e^{{\left( { - 0.57688361{\text{i}}} \right)}}$ > ,

$r_{3}^{*} \,$ =  < 0.295691311 × $e^{{\left( {0.163487059{\text{i}}} \right)}}$, − 0.271312913 × $e^{{\left( { - 0.272904272{\text{i}}} \right)}}$ > ,

$r_{4}^{*} \,$ =  < 0.767096534 × $e^{{\left( {0.870258995{\text{i}}} \right)}}$, − 0.665506341 × $e^{{\left( { - 0.7103762{\text{i}}} \right)}}$ > ,

$r_{5}^{*} \,$ =  < 0.639349863 × $e^{{\left( {0.693125864{\text{i}}} \right)}}$, − 0.760180273 × $e^{{\left( { - 0.770749938{\text{i}}} \right)}}$ > ,

$r_{6}^{*} \,$ =  < 0.691723482 × $e^{{\left( {0.818116623{\text{i}}} \right)}}$, − 0.431668642 × $e^{{\left( { - 0.533942955{\text{i}}} \right)}}$ > ,

$r_{7}^{*} \,$ =  < 0.25965885 × $e^{{\left( {0.249700265{\text{i}}} \right)}}$, − 0.23482627 × $e^{{\left( { - 0.220334061{\text{i}}} \right)}}$ > ,

$r_{8}^{*} \,$ =  < 0.635180188 × $e^{{\left( {0.775736758{\text{i}}} \right)}}$, − 0.569030413 × $e^{{\left( { - 0.677697106{\text{i}}} \right)}}$ > ,

$r_{9}^{*} \,$ =  < 0.734764713 × $e^{{\left( {0.855967702{\text{i}}} \right)}}$, − 0.750936934 × $e^{{\left( { - 0.752943443{\text{i}}} \right)}}$ > ,

$r_{10}^{*} \,$ =  < 0.654960339 × $e^{{\left( {0.778172555{\text{i}}} \right)}}$, − 0.760180273 × $e^{{\left( { - 0.770749938{\text{i}}} \right)}}$ > ,

$r_{11}^{*} \,$ =  < 0.57326954 × $e^{{\left( {0.632781179{\text{i}}} \right)}}$, − 0.611341863 × $e^{{\left( { - 0.615991472{\text{i}}} \right)}}$ > ,

$r_{12}^{*} \,$ =  < 0.730943836 × $e^{{\left( {0.831633305{\text{i}}} \right)}}$, − 0.46515778 × $e^{{\left( { - 0.56561423{\text{i}}} \right)}}$ > ,

$r_{13}^{*} \,$ =  < 0.705745217 × $e^{{\left( {0.852557965{\text{i}}} \right)}}$, − 0.688555132 × $e^{{\left( { - 0.656988502{\text{i}}} \right)}}$ > ,

$r_{14}^{*} \,$ =  < 0.499084649 × $e^{{\left( {0.645368466{\text{i}}} \right)}}$, − 0.62304841 × $e^{{\left( { - 0.728076504{\text{i}}} \right)}}$ > ,

$r_{15}^{*} \,$ =  < 0.739902529 × $e^{{\left( {0.869951265{\text{i}}} \right)}}$, − 0.411981496 × $e^{{\left( { - 0.514521399{\text{i}}} \right)}}$ > .

Next, using Eq. (22), we estimate the distance from each alternative to all coordinates of the RPs and present them in Table 9.

Table 9 Distance from each alternative to the RPs

Finally the maximum distance of the alternative using RP method using Eq. (23) are derived and are given by

$d_{1}^{{}}$ = 0.032322726, $d_{2}^{{}}$ = 0.037651253, $d_{3}^{{}}$ = 0.037404686,$d_{4}^{{}}$ = 0.028443613, $d_{5}^{{}}$ = 0.040699801.

Step-9: The overall importance of the alternative using FMF method using Eqs. (24), (25) and (26) are given in Table 10.

Table 10 Overall importance of the alternative using FMF method

Step 10: The overall assessment values and ranks of the alternatives obtained by Eq. (27) are given in Table 11.

Table 11 Overall assessment values and rank of the alternatives

Hence, the priority order of the options is: $A_{3} > A_{1} > A_{4} > A_{5} > A_{2}$ where the sign “$>$” signifies “superior to”. Therefore, the most suitable sustainable supplier is $A_{3}$.

Comparative study

To validate our result, we compare our proposed BCF-CRITIC-MULTIMOORA method with the corresponding BCF-CRITIC-TOPSIS and BCF-CRITIC-WASPAS approaches.

(a) TOPSIS model, introduced by Hwang and Yoon [42] focuses on relative closeness to the optimal solution. In other words, according to the TOPSIS method, the selected alternatives should maintain the minimum and maximum geometric distance from the PIS and the NIS, respectively. Actually, for comparative study, we made original extensions of TOPSIS by combining it with the CRITIC technique in BCF setting. The algorithm for this extended TOPSIS method, i. e., BCF-CRITIC-TOPSIS method is given below:

Steps 1–6: Same as discussed in Sect. 6

At the end of step 6, we get the aggregated decision matrix $\left[ {d_{rj}^{{}} } \right]_{m \times n} = \left[ {\left\langle {\alpha_{rj}^{{}} {\text{e}}^{{{(i\omega \delta_{rj}{}} )}} \,,} \right.\left. {\beta_{rj}^{{}} {\text{e}}^{{{(i\omega \vartheta_{rj}{}} )}} } \right\rangle } \right]_{m \times n}$.

Step 7: Construct the weighted aggregated decision matrix $\left[ {d_{rj}^{W} } \right]_{m \times n} = \left[ {\left\langle {\alpha_{rj}^{W} e^{{(i\omega \delta_{rj}^{W} )}} \,,} \right.\left. {\beta_{rj}^{W} {\text{e}}^{{(i\omega \vartheta_{rj}^{W} )}} } \right\rangle } \right]_{m \times n}$ by using the BCFAWAA operator [56] as follows:

$$\begin{aligned} & d_{rj}^{W} = BCFAWAA(d_{r1} ,d_{r2} ,...,d_{rn} )\, \hfill \\ & \quad= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {w_{j} g(\alpha_{rj} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {w_{j} g\left( {\delta_{rj} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {w_{j} h(\left| {\beta_{rj} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {w_{j} h\left( {\left| {\vartheta_{rj} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned} . $$

(28)

Step 8: Define the PIS and the NIS, respectively by

$$ \Delta_{j}^{ + } = \left\{ {\begin{array}{*{20}c} {\left\langle {\mathop {\max }\limits_{1 \le r \le m} \alpha_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\max }\limits_{1 \le r \le m} \delta_{rj}^{W} } \right)}} \,,} \right.\left. {\mathop {\min }\limits_{1 \le r \le m} \beta_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\min }\limits_{1 \le r \le m} \vartheta_{rj}^{W} } \right)}} } \right\rangle ,\,\,\,{\text{if}}\,\,j \in Q_{B} } \\ {\left\langle {\mathop {\min }\limits_{1 \le r \le m} \alpha_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\min }\limits_{1 \le r \le m} \delta_{rj}^{W} } \right)}} \,,} \right.\left. {\mathop {\max }\limits_{1 \le r \le m} \beta_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\max }\limits_{1 \le r \le m} \vartheta_{rj}^{W} } \right)}} } \right\rangle ,\,\,\,{\text{if}}\,\,j \in Q_{C} } \\ \end{array} } \right. $$

and

$$ \Delta_{j}^{ - } = \left\{ {\begin{array}{*{20}c} {\left\langle {\mathop {\min }\limits_{1 \le r \le m} \alpha_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\min }\limits_{1 \le r \le m} \delta_{rj}^{W} } \right)}} \,,} \right.\left. {\mathop {\max }\limits_{1 \le r \le m} \beta_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\max }\limits_{1 \le r \le m} \vartheta_{rj}^{W} } \right)}} } \right\rangle ,\,\,\,{\text{if}}\,\,j \in Q_{B} } \\ {\left\langle {\mathop {\max }\limits_{1 \le r \le m} \alpha_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\max }\limits_{1 \le r \le m} \delta_{rj}^{W} } \right)}} ,} \right.\left. {\mathop {\min }\limits_{1 \le r \le m} \beta_{rj}^{W} {\text{e}}^{{\left( {i\omega \mathop {\min }\limits_{1 \le r \le m} \vartheta_{rj}^{W} } \right)}} } \right\rangle ,\,\,\,{\text{if}}\,\,j \in Q_{C} } \\ \end{array} } \right. $$

Let us take $\Delta_{j}^{ + } = \left\langle {\alpha_{j}^{ + } {\text{e}}^{{(i\omega \delta_{j}^{ + } )}} \,,} \right.\left. {\beta_{j}^{ + } {\text{e}}^{{(i\omega \vartheta_{j}^{ + } )}} } \right\rangle$ and $\Delta_{j}^{ - } = \left\langle {\alpha_{j}^{ - } {\text{e}}^{{(i\omega \delta_{j}^{ - } )}} \,,} \right.\left. {\beta_{j}^{ - } {\text{e}}^{{(i\omega \vartheta_{j}^{ - } )}} } \right\rangle$.

Step 9: Estimate the BCF-distances $D(d_{rj}^{W} ,\,\Delta_{j}^{ + } )$ and $D(d_{rj}^{W} ,\,\Delta_{j}^{ - } )\,\,(r \in N_{5} ;\,j \in N_{15} )$ where the values $D(d_{rj}^{W} ,\,\Delta_{j}^{ + } )\,$ and $D(d_{rj}^{W} ,\,\Delta_{j}^{ - } )\,$ are calculated using Eqs. (29) and (30).

$$ D(d_{rj}^{W} ,\,\Delta_{j}^{ + } )\, = \frac{1}{3} \left(\left| {\alpha_{rj}^{W} - \alpha_{j}^{ + } } \right| + \left| {\delta_{rj}^{W} - \delta_{j}^{ + } } \right| + \left| {\beta_{rj}^{W} - \beta_{j}^{ + } } \right| + \left| {\vartheta_{rj}^{W} - \vartheta_{j}^{ + } } \right| \right) $$

(29)

$$ D(d_{rj}^{W} ,\,\Delta_{j}^{ - } )\, = \frac{1}{3}(\left| {\alpha_{rj}^{W} - \alpha_{j}^{ - } } \right| + \left| {\delta_{rj}^{W} - \delta_{j}^{ - } } \right| + \left| {\beta_{rj}^{W} - \beta_{j}^{ - } } \right| + \left| {\vartheta_{rj}^{W} - \vartheta_{j}^{ - } } \right|) $$

(30)

Step 10: The distances of the alternatives from the PIS and the NIS are calculated as:

$\mho_{r}^{ + } = \sum\nolimits_{j = 1}^{n} {D(d_{rj}^{W} ,\,\Delta_{j}^{ + } )\,}$ and $\mho_{r}^{ - } = \sum\nolimits_{j = 1}^{n} {D(d_{rj}^{W} ,\,\Delta_{j}^{ - } )\,} \,\,\,\,\,\,{\text{for}}\,\,\,r \in N_{5} .$

Step 11: Obtain the closeness index values of all alternatives by utilizing the formula given below:

$$ \rlap{--} \lambda_{r} = \frac{{\mho_{r}^{ + } }}{{\mho_{r}^{ + } + \mho_{r}^{ - } }}\,\,\,\,\,\,(\,r \in N_{5} ) $$

Step 12: Alternatives are ranked according to their closeness index values $\rlap{--} \lambda_{r} \,\,(\,r \in N_{5} )$.

In Table 12, we depict the distances of alternatives from PIS and NIS. The closeness index of all alternatives and their final ranks are also given in Table 12.

Table 12 Result by BCF-CRITIC-TOPSIS method

Thus using BCF-CRITIC-TOPSIS method, the ranking order becomes $A_{3} \succ A_{1} \succ A_{5} \succ A_{2} \succ A_{4}$. On the other hand, our developed BCF-CRITIC-MULTIMOORA method suggests a slightly different ranking order which is $A_{3} \succ A_{1} \succ A_{4} \succ A_{5} \succ A_{2}$. However, both the methods favored $A_{3}$ as the best alternative, which means that the ranking result suggested by the BCF-CRITIC-MULTIMOORA method is validated and credible.

(b) WASPAS model developed by Zavadskas et al. [101] has the utility to determine the optimal alternative that is very close to the optimal solution. WASPAS, an integration of WSM and WPM, is the emphatic new MCDM procedure. WASPAS model is more accurate compare to WSM and WPM. Moreover, WASPAS technique enables us to meet the highest accuracy of estimation. For the purpose of comparison, we consider BCF-CRITIC-WASPAS method [56] which is an original extension of WASPAS by combining it with CRITIC technique in BCF setting. We apply this in the case study considered earlier and the final score values of $A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5}$ are respectively 0.798277, 0.763399, 0.848130, 0.845793, 0.756968 according to which the ranking order is $A_{3} \succ A_{4} \succ A_{1} \succ A_{2} \succ A_{5}$ and the best 3PRLP is $A_{3}$. This also means that the ranking result suggested by the BCF-CRITIC-MULTIMOORA method is validated and credible.

The above results are summarized in Fig. 2.

Fig. 2

Final preference values of alternatives based on different methods

Next, to illustrate the strengths of the developed approaches, we also apply the existing methods [3, 7, 16, 30, 35, 59] to the same numerical example discussed earlier. The results are summarized in Table 13. Table 13 clearly demonstrates the superiority of the proposed method over the existing methods [3, 7, 16, 30, 35, 39].

Table 13 Comparative study: proposed with existing methods

Conclusions

In today’s complex environment, selecting an appropriate 3PRLP becomes more significant for most companies to accomplish the objectives of sustainable development and environmental safety. This process involves quantitative and qualitative criteria to choose the most desirable provider. Several methods have already been propounded by numerous researchers to get the best 3PRLP provider. We know that uncertainty is one of the widespread and major problems arising in the procedure of MCDM because of time-bound, a dearth of information, or larger complexity of socio-economic conditions. In this context, the more versatile and flexible BCFSs, as the successive extension of FSs, BFSs and CFSs, can be exploited to tackle the incertitude of real-world decisive problems as BCFSs mainly can negotiate with erratic and periodic bipolar fuzzy data in complex geometry. This present paper deals with an authentic integrated BCF-CRITIC-MULTIMOORA approach developed through the BCF-Archimedean power weighted AOs to achieve aggregated results, CRITIC Method to compute criteria weights and MULTIMOORA method to pick out the optimal option under the BCF environment. Next, we consider a 3PRLP selection problem in the regime of BCF to ensure the effectiveness of the method developed in this study. Afterward, a comparison is studied with the introduced and corresponding related BCF-CRITIC-TOPSIS and BCF-CRITIC-WASPAS methods that validate the outcomes. The outcomes implicate that the proposed BCF-CRITIC-MULTIMOORA approach is serviceable and well-consistent.

The proposed BCF-CRITIC-MULTIMOORA method has the following advantages:

• As BCFSs are extended versions of FSs and CFSs, so they can deal more dubious complex data that exists in practical decision-making problems. Thus, our developed method is more general.

• The proposed Archimedean weighted AOs can eliminate the influence of extreme evaluating criteria values from some biased DEs with different preference attitudes under the BCF setting. In other words, BCF-Archimedean weighted can reduce the impact of extreme assessment criteria values from some biased decision-experts with various inclination perspectives. Thus, the inclusion of these operators in the decision-making process makes the process more reasonable.

• To develop the BCF-power weighted AOs, we have used Archimedean operations (Archimedean norm and conorm) between BCFNs because Archimedean operations are flexible and decision-makers can adopt the suitable functions depending on the risk preferences. Thus our proposed AOs are much flexible.

• Our proposed method determines the criteria weights by using the CRITIC method which is a well-known objective method. This framework is based on aggregated score values of options, intensity contrast of every criteria and conflict among attributes. Intensity contrast of attribute is esteemed to standard deviation (SD) and conflict among them is calculated by the correlation coefficient (CRC). Thus, the inclusion of CRITIC technique makes the decision-making problem more realistic.

• Our proposed approach is based on MULTIMOORA approach which is one of the most renowned MCDM tools to enhance the MOORA model. MULTIMOORA framework involves three sub-methods, that is, the RS procedure, the RP procedure, and the FMF procedure.

A characteristic comparison between MULTIMOORA method and other MCDM methods can be found in Table 14 presented as follows:

Table 14 Comparative assessment of MCDM models [17]

As mentioned above, the proposed BCF-CRITIC-MULTIMOORA methodology has several advantages. But it has certain drawbacks too as mentioned below:

• It is based on Archimedean power aggregation operators on the bipolar complex fuzzy environment and thus cannot consider the interrelationships among criteria.

• It does not consider both the subjective and objective weights of experts.

• It is not suitable when the number of experts is more than 11 because in that case, the problem becomes a large-scale group decision-making problem.

To overcome the drawbacks, in the future, other AOs namely Bonferroni mean operators, Hamy mean operators, Maclaurin symmetric mean operators, and others can be developed with BCFSs, new decision models with integrated approaches like integrated MARCOS method, integrated TODIM method and others can be developed for providing a practical solution to decision problems, namely-cluster analysis, pattern recognition, charging station’s site selection for electric vehicle, treatment technology selection for medical waste, technological forecasting method selection, cloud vendor selection problem etc. Further, information measures such as divergence measures and uncertain measures for BCFSs can be developed for the determination of criteria weights. Moreover, based on consistency harmonious weight coefficient and similarity between DEs preferences, subjective and objective weights of DEs can be formulated. Lastly, a consensus-based behavioral TOPSIS method can be developed with BCF information if the number of experts exceeds 11. It is pertinent to mention that the proposed methodology can be extended to bipolar complex Pythagorean fuzzy and bipolar complex q-rung orthopair fuzzy environments.

Appendix: Proof of the Theorems

Proof of Theorem 1

The first result holds immediately from definition 7. Now to show the rest part, we use the method of mathematical induction on n which are summarized as follows:

For n = 1, the result is obvious. For n = 2, we have,

$$ \begin{aligned} {\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ) &= (\theta_{1} * \xi_{1} )\tilde{ \oplus }(\theta_{2} * \xi_{2} ) \\ &= \left\langle (g^{ - 1} (\theta_{1} g(\alpha_{1} )))e^{{(\omega i(g^{ - 1} (\theta_{1} g(\delta_{1} ))))}} \,,\right.\\ &\left. - (h^{ - 1} (\theta_{1} h(\left| {\beta_{1} } \right|)))e^{{(\omega i(h^{ - 1} (\theta_{1} h(\left| {\vartheta_{1} } \right|))))}} \right\rangle \\ &\,\,\,\,\tilde{ \oplus }\left\langle (g^{ - 1} (\theta_{2} g(\alpha_{2} )))e^{{(\omega i(g^{ - 1} (\theta_{2} g(\delta_{2} ))))}} \,,\right.\\ &\left. - (h^{ - 1} (\theta_{2} h(\left| {\beta_{2} } \right|)))e^{{(\omega i(h^{ - 1} (\theta_{2} h(\left| {\vartheta_{2} } \right|))))}} \right\rangle \\ &= \left\langle (g^{ - 1} (\theta_{1} g(\alpha_{1} ) + \theta_{2} g(\alpha_{2} )))\right.\\ & e^{{(\omega i(g^{ - 1} (\theta_{1} g(\delta_{1} ) + \theta_{2} g(\delta_{2} ))))}} , \\ &\,\,\, \, - (h^{ - 1} (\theta_{1} h(\left| {\beta_{1} } \right|) + \theta_{2} h(\left| {\beta_{2} } \right|)))\\ &\left. e^{{( - \omega i(h^{ - 1} (\theta_{1} h(\left| {\vartheta_{1} } \right|) + \theta_{2} h(\left| {\vartheta_{2} } \right|))))}} \right\rangle \\ \end{aligned} $$

Thus Eq. (1) holds good for n = 2. Let us assume that Eq. (1) holds for n = r. Then,

$$ \begin{aligned} &{\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{r} \,) \hfill \\&\quad = \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} g(\alpha_{j} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { \left( { - h^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned} $$

Now for n = r + 1, we have,

$$ \begin{aligned} &{\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{r + 1} \,) \hfill \\ &\quad= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} g(\alpha_{j} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \left. { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ &\,\,\,\,\tilde{ \oplus }\left\langle {\left( {g^{ - 1} \left( {\theta_{r + 1} g(\alpha_{r + 1} )} \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {\theta_{r + 1} g\left( {\delta_{r + 1} } \right)} \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \left. { - \left( {h^{ - 1} \left( {\theta_{r + 1} h(\left| {\beta_{r + 1} } \right|)} \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {\theta_{r + 1} h\left( {\left| {\vartheta_{r + 1} } \right|} \right)} \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned} $$

$$ \begin{aligned} &= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} g(\alpha_{j} )} + \theta_{r + 1} g(\alpha_{r + 1} )} \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} g\left( {\delta_{j} } \right) + \theta_{r + 1} g\left( {\delta_{r + 1} } \right)} } \right)} \right)} \right)}} ,} \right. \hfill \\ &\,\,\,\,\left. { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} h(\left| {\beta_{j} } \right|)} + \theta_{r + 1} h(\left| {\beta_{r + 1} } \right|)} \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{r} {\theta_{j} h\left( {\left| {\zeta_{j} } \right|} \right) + \theta_{r + 1} h\left( {\left| {\vartheta_{r + 1} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ &= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r + 1} {\theta_{j} g(\alpha_{j} )} } \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{r + 1} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \left. { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{r + 1} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{r + 1} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned} $$

Thus, Eq. (1) holds good for n = r + 1 also. Hence, by the Principle of induction, we conclude that Eq. (1) is true for all natural numbers n.

Proof of Theorem 2

Suppose $\xi_{0} = \left\langle {\alpha_{0}^{{}} e^{{\left( {i\omega \delta_{0} } \right)}} ,\beta_{0}^{{}} e^{{\left( {i\omega \vartheta_{0} } \right)}} } \right\rangle$.

Since $\xi_{0} \tilde{ \oplus }\xi_{j}$

$$ \begin{aligned} & = \left\langle \left( g^{ - 1} \left( {g(\alpha_{0} ) + g(\alpha_{j} )} \right) \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {g\left( {\delta_{0} } \right) + g\left( {\delta_{j} } \right)} \right)} \right)} \right)}} , \right.\\ & \qquad\left. { - \left( {h^{ - 1} \left( {h(\left| {\beta_{0} } \right|) + h(\left| {\beta_{j} } \right|)} \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {h\left( {\left| {\vartheta_{0} } \right|} \right) + h\left( {\left| {\vartheta_{j} } \right|} \right)} \right)} \right)} \right)}} } \right\rangle \end{aligned} $$

Then we have by Eq. (1), ${\text{BCFAPWAA}}(\xi_{0} \tilde{ \oplus }\xi_{1} \,,\xi_{0} \tilde{ \oplus }\xi_{2} \,,\,......,\xi_{0} \tilde{ \oplus }\xi_{n} )$.

$$ \begin{aligned} &= \left\langle \left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} (g(\alpha_{0} ) + g(\alpha_{j} ))} } \right)} \right)\right.\\ &e^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} \left( {g\left( {\delta_{0} } \right) + g\left( {\delta_{j} } \right)} \right)} } \right)} \right)} \right)}} , \\ & - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} \left( {h(\left| {\beta_{0} } \right|) + h(\left| {\beta_{j} } \right|)} \right)} } \right)} \right)\\ &\left. e^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} \left( {h\left( {\left| {\vartheta_{0} } \right|} \right) + h\left( {\left| {\vartheta_{j} } \right|} \right)} \right)} } \right)} \right)} \right)}} \right\rangle \\ &= \left\langle \left( g^{ - 1} \left( {g(\alpha_{0} ) + \sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right) \right)\right.\\ & e^{{\left( {\omega i\left( {g^{ - 1} \left( {g\left( {\delta_{0} } \right) + \sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\, \\ & \,\, - \left( {h^{ - 1} \left( {h(\left| {\beta_{0} } \right|) + \sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right)\\ &\left. e^{{\left( { - \omega i\left( {h^{ - 1} \left( {h\left( {\left| {\vartheta_{0} } \right|} \right) + \sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} \right\rangle \\ \end{aligned} $$

Next ccutilizing the proposed operations and using Eq. (1), we get,

$$ \begin{aligned} & \xi_{0} \tilde{ \oplus }{\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \\ &= \left( \left\langle {\alpha_{0} {\text{e}}^{{\left( {i\omega \delta_{0} } \right)}} ,\beta_{0} {\text{e}}^{{\left( {i\omega \vartheta_{0} } \right)}} } \right\rangle \right)\\ & \tilde{ \oplus }\left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,} \right.\\ & \left. { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \\ &= \left\langle {\left( {g^{ - 1} \left( {g(\alpha_{0} ) + \sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {g\left( {\delta_{0} } \right) + \sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,} \right.\\ & \left. { - \left( {h^{ - 1} \left( {h(\left| {\beta_{0} } \right|) + \sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {h\left( {\left| {\vartheta_{0} } \right|} \right) + \sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned} $$

Hence, ${\text{BCFAPWAA}}(\xi_{0} \tilde{ \oplus }$ $\xi_{1} \,,\xi_{0} \tilde{ \oplus }\xi_{2} \,,\,......,\xi_{0} \tilde{ \oplus }\xi_{n} ) = \xi_{0} \tilde{ \oplus }{\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} )$.

Proof of Theorem 3

Suppose $\xi_{0} = \left\langle {\alpha_{0}^{{}} e^{{\left( {i\omega \delta_{0} } \right)}} ,\beta_{0}^{{}} e^{{\left( {i\omega \vartheta_{0} } \right)}} } \right\rangle$.

Since $\xi_{j} \, = \xi_{0} \,\,\,\forall \,j$, we have, $\alpha_{0} = \alpha_{j} ,\delta_{0} = \delta_{j} ,\beta_{0} = \beta_{j} ,\vartheta_{0} = \vartheta_{j} \,\,\,\forall \,j = 1,2,3,......,n.$. Then from Eq. (1), we get,

$$ \begin{aligned} &{\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{n} \,) \hfill \\ &\quad= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \left. { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \, \hfill \\ &= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{0} )} } \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{0} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \left. { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{0} } \right|)} } \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{0} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ \end{aligned} $$

$$ \begin{aligned}& {\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{n} \,) \hfill \\ &\quad= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \left. {- \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \, \hfill \\ &\quad= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{0} )} } \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{0} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{0} } \right|)} } \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{0} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle \hfill \\ &\quad= \left\langle {\left( {g^{ - 1} \left( {g(\alpha_{0} )\sum\limits_{j = 1}^{n} {\theta_{j} } } \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {g\left( {\delta_{0} } \right)\sum\limits_{j = 1}^{n} {\theta_{j} } } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad\times \left. { - \left( {h^{ - 1} \left( {h(\left| {\beta_{0} } \right|)\sum\limits_{j = 1}^{n} {\theta_{j} } } \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {h\left( {\left| {\vartheta_{0} } \right|} \right)\sum\limits_{j = 1}^{n} {\theta_{j} } } \right)} \right)} \right)}} } \right\rangle \hfill \\ &\quad= \left\langle {\left( {g^{ - 1} \left( {g(\alpha_{0} )} \right)} \right)e^{{\left( {\omega i\left( {g^{ - 1} \left( {g\left( {\delta_{0} } \right)} \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \left. { - \left( {h^{ - 1} \left( {h(\left| {\beta_{0} } \right|)} \right)} \right)e^{{\left( { - \omega i\left( {h^{ - 1} \left( {h\left( {\left| {\vartheta_{0} } \right|} \right)} \right)} \right)} \right)}} } \right\rangle \hfill \\ &\quad= \left\langle {\alpha_{0} e^{{\left( {i\omega \delta_{0} } \right)}} , - \left| {\beta_{0} } \right|e^{{\left( { - i\omega \left| {\vartheta_{0} } \right|} \right)}} } \right\rangle = \left\langle {\alpha_{0} e^{{\left( {i\omega \delta_{0} } \right)}} ,\beta_{0} e^{{\left( {i\omega \vartheta_{0} } \right)}} } \right\rangle = \xi_{0} . \hfill \\ \end{aligned} $$

Proof of Theorem 4

For any $j \in \{ 1,2,3,......,n\}$, we have, $\mathop {\min }\nolimits_{j} \{ \alpha_{j} \} \le \alpha_{j} \le \mathop {\max }\nolimits_{j} \{ \alpha_{j} \}$ and $\mathop {\min }\nolimits_{j} \{ \delta_{j} \} \le \delta_{j} \le \mathop {\min }\nolimits_{j} \{ \delta_{j} \}$. Since $g\,{\text{and}}$ $g^{ - 1}$ are increasing functions, we get,

$$ \begin{aligned} &\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\min }\nolimits_{j} \{ \alpha_{j} \} } \right)} \le \sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} \le \sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\max }\nolimits_{j} \{ \alpha_{j} \} } \right)}\\ &{\text{and}}\,\,\,\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\min }\nolimits_{j} \{ \delta_{j} \} } \right)} \le \sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)}\\ & \le \sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\max }\nolimits_{j} \{ \delta_{j} \} } \right)} \, \\&\quad \Rightarrow g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\min }\nolimits_{j} \{ \alpha_{j} \} } \right)} } \right) \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right)\\ & \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\max }\nolimits_{j} \{ \alpha_{j} \} } \right)} } \right) \\ &\quad{\text{and}}\,\,g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\min }\nolimits_{j} \{ \delta_{j} \} } \right)} } \right) \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)\\ & \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\mathop {\max }\nolimits_{j} \{ \delta_{j} \} } \right)} } \right) \\ &\quad\Rightarrow g^{ - 1} \left( {g\left( {\mathop {\min }\nolimits_{j} \{ \alpha_{j} \} } \right)\sum\limits_{j = 1}^{n} {\theta_{j} } } \right) \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right)\\ & \le g^{ - 1} \left( {g\left( {\mathop {\max }\nolimits_{j} \{ \alpha_{j} \} } \right)\sum\limits_{j = 1}^{n} {\theta_{j} } } \right) \\ &\quad{\text{and}}\,\,g^{ - 1} \left( {g\left( {\mathop {\min }\nolimits_{j} \{ \delta_{j} \} } \right)\sum\limits_{j = 1}^{n} {\theta_{j} } } \right) \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)\\ & \le g^{ - 1} \left( {g\left( {\mathop {\max }\nolimits_{j} \{ \delta_{j} \} } \right)\sum\limits_{j = 1}^{n} {\theta_{j} } } \right) \hfill \\ \end{aligned} $$

$$ \begin{aligned} &\Rightarrow \mathop {\min }\nolimits_{j} \{ \alpha_{j} \} \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right) \le \mathop {\max }\nolimits_{j} \{ \alpha_{j} \} \,\,{\text{and}}\,\,\mathop {\min }\nolimits_{j} \{ \delta_{j} \} \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right) \le \mathop {\max }\nolimits_{j} \{ \delta_{j} \} \hfill \\ &\quad\Rightarrow \varphi^{ + } \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right) \le \alpha^{ + } \,\,{\text{and}}\,\,\,\eta^{ + } \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right) \le \delta^{ + } . \hfill \\ \end{aligned} $$

Similarly, we can show that $\Phi^{ - } \le - h^{ - 1} \left( {\sum\nolimits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right) \le \beta^{ - } \,\,{\text{and}}\,\,\psi^{ - } \le - h^{ - 1} \left( {\sum\nolimits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right) \le \vartheta^{ - }$.

Now $S(\xi^{ - } )$

$$ \begin{aligned} & = \frac{1}{4}\left( {2 + \varphi^{ + } + \,\eta^{ + } + \Phi^{ - } + \,\psi^{ - } } \right) \\ & \le \frac{1}{4}\left( 2 + g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right) + \left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)\right.\\ &\left. - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right) - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right) \right) \\ & = S({\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} )) \hfill \\ \end{aligned} $$

Again, $S({\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ))$

$$ \begin{aligned} & = \frac{1}{4}\left( 2 + g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right) + \left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)\right.\\ &\left. - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right) - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right) \right) \hfill \\ \le \frac{1}{4}\left( {2 + \alpha^{ + } + \delta^{ + } + \beta^{ - } + \vartheta^{ - } } \right) \hfill \\ = S(\xi^{ + } ) \hfill \\ \end{aligned} $$

Combining these two results, we get, $S(\xi^{ - } ) \le S({\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} )) \le S(\xi^{ + } )$.

Hence, by ranking rules of BCFNs, we get, $\xi^{ - } \prec {\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec \xi^{ + } \,$.

Proof of Theorem 5

We have from Theorem 1,

$$ \begin{aligned} &{\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} \,,\xi_{3} \,,........,\xi_{n} \,) \hfill \\ &\quad= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \times\left. { \left( { - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle , \hfill \\ &{\text{BCFAPWAA}}(\xi^{\prime}_{1} \,,\xi^{\prime}_{2} \,,\xi^{\prime}_{3} \,,........,\xi^{\prime}_{n} \,) \hfill \\ &= \left\langle {\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha^{\prime}_{j} )} } \right)} \right){\text{e}}^{{\left( {\omega i\left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta^{\prime}_{j} } \right)} } \right)} \right)} \right)}} ,\,\, } \right. \\ &\quad\quad \times\left. {\left( { - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta^{\prime}_{j} } \right|)} } \right)} \right){\text{e}}^{{\left( { - \omega i\left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta^{\prime}_{j} } \right|} \right)} } \right)} \right)} \right)}} } \right\rangle . \hfill \\ \end{aligned} $$

Given that, for any $j \in \{ 1,2,3,......,n\}$, we have, $\alpha_{j} \le \alpha^{\prime}_{j}$ and $\delta_{j} \le \delta^{\prime}_{j}$. Since $g\,{\text{and}}$ $g^{ - 1}$ are increasing functions, we get,

$$ g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right) \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha^{\prime}_{j} )} } \right)\,\,{\text{and}}\,\,g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right) \le g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta^{\prime}_{j} } \right)} } \right). $$

Again, given that for any $j \in \{ 1,2,3,......,n\}$, we have, $\beta_{j} \ge \beta^{\prime}_{j}$ and $\vartheta_{j} \ge \vartheta^{\prime}_{j}$. Since $h\,\,{\text{and}}$ $h^{ - 1}$ are decreasing functions, we get,

$$ - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right) \le - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta^{\prime}_{j} } \right|)} } \right)\,\,{\text{and}}\,\,\, - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right) \le - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta^{\prime}_{j} } \right|} \right)} } \right). $$

Now $S({\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ))$

$$ \begin{aligned} &= \frac{1}{4}\left( {2 + g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha_{j} )} } \right) + \left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta_{j} } \right)} } \right)} \right)} \right. \\ &\left. \quad { - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta_{j} } \right|)} } \right)} \right) - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta_{j} } \right|} \right)} } \right)} \right) \\ & \le \frac{1}{4}\left( 2 + g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g(\alpha^{\prime}_{j} )} } \right) + \left( {g^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} g\left( {\delta^{\prime}_{j} } \right)} } \right)} \right)\right.\\ &\left. - \left( {h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h(\left| {\beta^{\prime}_{j} } \right|)} } \right)} \right) - h^{ - 1} \left( {\sum\limits_{j = 1}^{n} {\theta_{j} h\left( {\left| {\vartheta^{\prime}_{j} } \right|} \right)} } \right) \right) \hfill \\ & \quad= {\text{BCFAPWAA}}(\xi^{\prime}_{1} \,,\xi^{\prime}_{2} ,\xi^{\prime}_{3} ,..........,\xi^{\prime}_{n} ) \\ \end{aligned} $$

Thus, ${\text{BCFAPWAA}}(\xi_{1} \,,\xi_{2} ,\xi_{3} ,..........,\xi_{n} ) \prec {\text{BCFAPWAA}}(\xi^{\prime}_{1} \,,\xi^{\prime}_{2} ,\xi^{\prime}_{3} ,..........,\xi^{\prime}_{n} )$.