A new theoretical approach to the strain dependence of magnetic crystal-field anisotropy

Abstract

We report on the derivation of analytical equations for ab-initio calculations of the strain dependence of crystal-electric-field (CEF) parameters for arbitrary deformations. The calculation is based on the fundamental assumption that the charge distribution deforms in the same way as the crystal. Based on this deformed-charge model, simple formulas for the practical usage are given for various site symmetries of cubic lattices under uniform strain. These formulas can be used to predict the change of the magnetic crystal-field anisotropy under strain, which is important for the design of magnetic materials and devices. As an example for the power of the method, we present a calculation of the magnetic contribution to the thermal expansion in some rare-earth-based materials.

1 Introduction

The strain dependence of magnetic anisotropy is of great importance in the design of novel materials and needs to be tuned to achieve technological applications of magnetic materials. For example, advanced ultrathin spintronic nanodevices with customized electronic and magnetic properties will need a local-strain engineering [1]. Historically, this problem has been recognized in investigations of magnetoelastic parameters in rare-earth materials [2,3,4]. Some recent research with focus on transition-metal oxides has been using cluster methods [5] and spin-polarized bandstructure calculations [6]. However, a full understanding and quantitative prediction of the strain dependence of magnetic interactions is missing.

Research on this matter started with the theoretical analysis of magnetoelastic constants [2,3,4]. Since then, the huge problem of calculating reliable crystal-electric-field (CEF) and exchange parameters in magnetic materials by ab-initio methods have been in the focus of research for many years.

In many studies of magnetoelastic effects, the comparison of theory and experiment involved the fitting of one or more magnetoelastic parameters to the data [7, 8].

In this work, we make an attempt to calculate the strain dependence of the magnetic crystal-field anisotropy for an arbitrary deformation. In many cases, these single-ion effects play an essential role in the description of the anisotropic elastic behavior. Other anisotropies, such as those of the magnetic exchange (e.g., dipolar or Dzyaloshinskii–Moriya interactions, higher-order coupling effects), are not considered here. However, these can be additionally included using the analysis of the distortion dependence of the exchange parameters. Thus, it is in principle possible to investigate changes in physical properties caused by a symmetry breaking, such as elimination of lattice-induced magnetic frustrations. Macroscopic magnetic anisotropies, such as shape or surface anisotropy, are outside the scope of our microscopic considerations. For example, the considered magnetic deformations can be induced in magnetic devices by (i) external tensile or (ii) compressive strain or by (iii) chemical pressure. Experimentally, the effect on the anisotropy can be measured by high-sensitivity magnetization and other bulk techniques or spectroscopic methods [9]. Moreover, we show how the strain dependence of magnetic anisotropy may be used to predict the magnetic contribution to the thermal expansion.

This paper is made up as follows: In Sect. 2, we give a thorough introduction to the formulas important for the magnetoelastic coupling. We use different representations of the strain tensor to derive explicit formulas of the thermal expansion for various strain modes. In Sect. 3, we give the main result of this paper: the strain-derivative of a quantity closely related to the CEF parameters. From this quantity, the change of the CEF parameters under strain may easily be calculated. We evaluate the main formula for all possible strain modes in Sect. 4. Finally, we show the calculated CEF volume striction of several compounds in Sect. 5. We close with an outlook and a summary of the results in Sects. 6 and 7.

2 A recapitulation of the theory

The strain $\varvec{\mathsf {\epsilon }}$ is a $3\times 3$ matrix, a second-rank tensor, that represents the deformation of a crystal. In the following, we consider only homogeneous strain, i.e., the strain is constant in all of the samples. We use two different ways to represent the strain tensor. On the one hand, we decompose $\varvec{\mathsf {\epsilon }}$ in irreducible representations of the space group of the crystal and we denote the components of the strain tensor as $\epsilon ^{\varGamma j}_i$. Here, $\varGamma$ denotes the irreducible representation of the space group of the crystal, the index j differentiates between multiple representations of the same type $\varGamma$, and the index i denotes the different components of the (multi-dimensional) irreducible representation. In this decomposition, the elastic energy takes on a simple form. On the other hand, we decompose $\varvec{\mathsf {\epsilon }}$ in terms of irreducible tensors, i.e., irreducible representations of the rotation group, that transform into each other via a simple law under rotations. We denote the components with $\epsilon _{JM}$, with J and M denoting the irreducible representation and its $2J+1$ components, respectively; these are analogous to the angular momentum formalism in quantum mechanics. Since the strain tensor is symmetric, both these representations have six components.

The simplest possible expression of the harmonic elastic energy of a unit cell is given by [2, 3, 10]:

$$\begin{aligned} E_\mathrm {el}(\varvec{\mathsf {\epsilon }}) = \frac{V}{2} \sum _{mnkl} c_{mnkl} \epsilon _{mn}, \epsilon _{kl}, \end{aligned}$$

(1)

where $\epsilon _{mn}$ are the Cartesian components of the strain tensor $\varvec{\mathsf {\epsilon }}$, $c_{mnkl}$ are the Cartesian components of the elasticity tensor characteristic of each compound and obey certain symmetries depending on the lattice; V is the volume of a unit cell of the crystal. Depending on the lattice symmetry, we can rewrite the elastic energy in terms of strains adapted to the lattice symmetry $\epsilon ^{\varGamma ,j}_i$ [2]:

$$\begin{aligned} E_\mathrm {el}= \frac{V}{2} \sum _{\varGamma j j' i} c^\varGamma _{jj'} \epsilon ^{\varGamma ,j}_i \epsilon ^{\varGamma ,j'}_i. \end{aligned}$$

(2)

The $c^\varGamma _{jj'}$ are the elastic constants of the symmetry-adapted strain modes $\epsilon ^{\varGamma ,j}_i$ of the ith component of the jth one-, two- or three-dimensional irreducible representation $\varGamma$; these strain modes are given for each lattice symmetry in the classic paper [2]. In particular, the elastic energies of the cubic and hexagonal crystal with the conventional superscripts are given by [3]:

$$\begin{aligned} E_\mathrm {el}^c&= \frac{V}{2} \Big ( c^\alpha \epsilon ^\alpha \epsilon ^\alpha + c^\gamma (\epsilon ^\gamma _1 \epsilon ^\gamma _1 + \epsilon ^\gamma _2 \epsilon ^\gamma _2) \end{aligned}$$

(3)

$$\begin{aligned}&\quad + c^\epsilon (\epsilon ^\epsilon _1 \epsilon ^\epsilon _1 + \epsilon ^\epsilon _2 \epsilon ^\epsilon _2 + \epsilon ^\epsilon _3 \epsilon ^\epsilon _3) \Big ), \end{aligned}$$

(4)

$$\begin{aligned} E_\mathrm {el}^h&= \frac{V}{2} \Big ( (c^\alpha _{11} \epsilon ^{\alpha ,1} \epsilon ^{\alpha ,1} + 2c^\alpha _{12} \epsilon ^{\alpha ,1} \epsilon ^{\alpha ,2} + c^\alpha _{22} \epsilon ^{\alpha ,2} \epsilon ^{\alpha ,2}) \end{aligned}$$

(5)

$$\begin{aligned}&\quad + c^\epsilon (\epsilon ^\epsilon _1 \epsilon ^\epsilon _1 + \epsilon ^\epsilon _2 \epsilon ^\epsilon _2) + c^\zeta (\epsilon ^\zeta _1 \epsilon ^\zeta _1 + \epsilon ^\zeta _2 \epsilon ^\zeta _2) \Big ). \end{aligned}$$

(6)

Besides the elastic energy, we use the CEF energy to investigate magnetoelastic coupling in this work. Below the ordering temperature of a magnetic compound (if existing), exchange effects are dominating the magnetoelastic behavior of a compound. However, also in that region the CEF-striction mechanism is contributing; however, only above the ordering temperature and at zero field, the CEF striction can be isolated from exchange striction. The CEF Hamiltonian ${\hat{H}}_\mathrm {CEF}$ of one unit cell projected on the J-manifold of the ground state of the free rare-earth ion up to first order in the symmetrized strains $\epsilon ^{\varGamma ,j}_i$ is given by:

$$\begin{aligned} {\hat{H}}_\mathrm {CEF}&= \sum _{flm} {B}^{l}_{m}(f,\varvec{\mathsf {\epsilon }}_f(\varvec{\mathsf {\epsilon }})) {\hat{O}}^l_m(J_f) \end{aligned}$$

(7)

$$\begin{aligned}&= \sum _{flm} {B}^{l}_{m}(f,\varvec{\mathsf {0}}) {\hat{O}}^l_m(J_f)\end{aligned}$$

(8)

$$\begin{aligned}&\quad + \sum _{flm} \left( \sum _{\varGamma j i} \partial _{\epsilon ^{\varGamma ,j}_i} {B}^{l}_{m}(f,\varvec{\mathsf {\epsilon }}_f(\varvec{\mathsf {\epsilon }})) \epsilon ^{\varGamma ,j}_i \right) {\hat{O}}^l_m(J_f)\end{aligned}$$

(9)

$$\begin{aligned}&\quad + {\mathcal {O}}((\epsilon ^{\varGamma ,j}_i)^2), \end{aligned}$$

(10)

where ${B}^{l}_{m}(f,\varvec{\mathsf {\epsilon }}_f(\varvec{\mathsf {\epsilon }}))$ and ${\hat{O}}^l_m(J_f)$ are Stevens parameters and operators of the fth ion in the unit cell under the strain $\varvec{\mathsf {\epsilon }}_f$ in the local coordinate system at that position, respectively. The operators ${\hat{O}}^l_m(J_f)$ are represented in the angular-momentum operators of the local coordinate system at the fth ion. The first term on the right is the CEF Hamiltonian of the undeformed crystal and the second term is the magnetoelastic coupling Hamiltonian. The coupling constants are, therefore, $\partial _{\epsilon ^{\varGamma ,j}_i} {B}^{l}_{m}(f,\varvec{\mathsf {\epsilon }}_f(\varvec{\mathsf {\epsilon }}))$, the strain dependence of the CEF parameters, the quantity we are interested in.

The components of $\varvec{\mathsf {\epsilon }}_f$ are related to the components of the global strain $\varvec{\mathsf {\epsilon }}$ via rotation matrices. The latter is the strain in the global reference frame parallel to the symmetry axes of the crystal and the former is $\varvec{\mathsf {\epsilon }}$ represented in the local coordinate system used for the CEF Hamiltonian. To get simple transformation laws between the components of the strain tensor, we avoid using the Cartesian standard basis and instead use irreducible tensors as basis. The components in this basis are denoted with $\epsilon ^f_{JM}$ and they relate to the components $\epsilon _{JM'}$ in the global coordinate system via:

$$\begin{aligned} \epsilon ^f_{JM'} = \sum ^{+J}_{M=-J} \epsilon _{JM} D^J_{M,M'}(\alpha _f,\beta _f,\gamma _f), \end{aligned}$$

(11)

where $D^J_{M',M}(\alpha _f,\beta _f,\gamma _f)$ denotes the Wigner-D-matrix of the rotation of Euler angles $\alpha _f$, $\beta _f$ and $\gamma _f$ between the local and global coordinate system [11]. The strain tensor, being a symmetric tensor, is made up of the six components with $J=0$, $M=0$ and $J=2$, $M=-2,-1,\dots ,2$. The irreducible tensors in Cartesian coordinates are given in the appendix. Hence, the derivative of the CEF parameter ${B}^{l}_{m}$ at ion f can be written as:

$$\begin{aligned}&\partial _{\epsilon ^{\varGamma ,j}_i} {B}^{l}_{m}(f,\varvec{\mathsf {\epsilon }}_f(\varvec{\mathsf {\epsilon }})) = \partial _{\varvec{\mathsf {\epsilon }}_f} {B}^{l}_{m}(f,0) \cdot \partial _{\varvec{\mathsf {\epsilon }}} \varvec{\mathsf {\epsilon }}_f \cdot \partial _{\epsilon ^{\varGamma ,j}_i} \varvec{\mathsf {\epsilon }}\nonumber \\&\quad = \sum _{J M M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{J M'}} \frac{\partial \epsilon ^f_{J M'}}{\partial \epsilon _{JM}} \frac{\partial \epsilon _{J M}}{\partial \epsilon ^{\varGamma j}_{i}}\nonumber \\&\quad = \sum _{J M M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{J M'}} D^J_{M,M'}(\alpha _f,\beta _f,\gamma _f) \frac{\partial \epsilon _{J M}}{\partial \epsilon ^{\varGamma j}_{i}},\nonumber \\ \end{aligned}$$

(12)

where $\alpha _f$, $\beta _f$ and $\gamma _f$ are the Euler angles that rotate the global reference frame to the local reference frame at ion f. For convenience in the following formulas, we use $\frac{\partial \epsilon ^f_{J M'}}{\partial \epsilon ^{\varGamma j}_{i}} = \sum _{M} D^J_{M,M'}(\alpha _f,\beta _f,\gamma _f) \frac{\partial \epsilon _{J M}}{\partial \epsilon ^{\varGamma j}_{i}}$. Note that $D^0_{0,0}(\alpha _f,\beta _f,\gamma _f) = 1$ for all angles, which leads to simple evaluation of the uniform strain mode.

For high symmetry lattices such as cubic, hexagonal, trigonal and tetragonal lattices, the symmetrized strains of the lattice coincide with the irreducible tensors, i.e., the last factor in Eq. (12) is one or zero. For the other lattices, simple linear relations between the symmetrized strains of the lattice and the irreducible tensor components can be found by decomposing the first in terms of the latter, as shown in the Appendix A.

Before calculating the strain dependence of the CEF parameters, we show how it can be used to calculate the equilibrium strain. The elastic energy and the CEF energy change with deformation and compete with each other. In equilibrium, the free energy is minimized, i.e., the derivative of the free energy with respect to $\epsilon ^{\varGamma j}_i$ vanishes [2, 3, 10]. The strain-dependent part of the free energy is simply the sum of the CEF energy and the elastic energy:

$$\begin{aligned} F(\varvec{\mathsf {\epsilon }}) = \sum _f \sum _{lm} {B}^{l}_{m}(f,\varvec{\mathsf {\epsilon }}_f(\varvec{\mathsf {\epsilon }})) \langle {\hat{O}}^l_m(f) \rangle + E_\mathrm {el}(\varvec{\mathsf {\epsilon }}),\qquad \end{aligned}$$

(13)

where $\langle {\hat{O}}^l_m\rangle$ denotes the thermal average of the expectation value of the operator ${\hat{O}}^l_m$. The equilibrium condition yields a system of linear equations in $\epsilon ^{\varGamma ,j}_i$ [2]. For example, for the cubic lattice (omitting the index $j = 1$):

$$\begin{aligned} \epsilon ^{\alpha }&= \frac{1}{Vc^\alpha } \sum _{flm} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{00}} \langle {\hat{O}}^l_m(f) \rangle , \end{aligned}$$

(14)

$$\begin{aligned} \epsilon ^{\gamma }_i&= \frac{1}{Vc^\gamma } \sum _{flm} \sum _{M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{2M'}} \frac{\partial \epsilon ^f_{2 M'}}{\partial \epsilon ^{\gamma }_{i}} \langle {\hat{O}}^l_m(f) \rangle , i=1,2, \end{aligned}$$

(15)

$$\begin{aligned} \epsilon ^{\epsilon }_i&= \frac{1}{Vc^\epsilon } \sum _{flm} \sum _{M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{2M'}} \frac{\partial \epsilon ^f_{2 M'}}{\partial \epsilon ^{\gamma }_{i}} \langle {\hat{O}}^l_m(f) \rangle , i=1,2,3, \end{aligned}$$

(16)

and for the hexagonal lattice with $\varDelta = c^\alpha _{11}c^\alpha _{22} - c^\alpha _{12} c^\alpha _{12}$:

$$\begin{aligned} \epsilon ^{\alpha ,1}&= \frac{1}{V\varDelta } \Bigg ( - c^\alpha _{22} \sum _{flm} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{00}} \langle {\hat{O}}^l_m(f) \rangle \end{aligned}$$

(17)

$$\begin{aligned}&\quad + c^\alpha _{12} \sum _{flm} \sum _{M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{2M'}} \frac{\partial \epsilon ^f_{2 M'}}{\partial \epsilon ^{\alpha ,2}_{i}} \langle {\hat{O}}^l_m(f) \rangle \, \Bigg ), \end{aligned}$$

(18)

$$\begin{aligned} \epsilon ^{\alpha ,2}&= \frac{1}{V\varDelta } \Bigg ( c^\alpha _{12} \sum _{flm} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{00}} \langle {\hat{O}}^l_m(f) \rangle \end{aligned}$$

(19)

$$\begin{aligned}&\quad - c^\alpha _{11} \sum _{flm} \sum _{M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{2M'}} \frac{\partial \epsilon ^f_{2 M'}}{\partial \epsilon ^{\alpha ,2}_{i}} \langle {\hat{O}}^l_m(f) \rangle \Bigg ), \end{aligned}$$

(20)

$$\begin{aligned} \epsilon ^{\epsilon }_i&= \frac{1}{Vc^\epsilon } \sum _{flm} \sum _{M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{2M'}} \frac{\partial \epsilon ^f_{2 M'}}{\partial \epsilon ^{\gamma }_{i}} \langle {\hat{O}}^l_m(f) \rangle , i=1,2, \end{aligned}$$

(21)

$$\begin{aligned} \epsilon ^{\zeta }_i&= \frac{1}{Vc^\zeta } \sum _{flm} \sum _{M'} \frac{\partial {B}^{l}_{m}(f,0)}{\partial \epsilon ^f_{2M'}} \frac{\partial \epsilon ^f_{2 M'}}{\partial \epsilon ^{\zeta }_{i}} \langle {\hat{O}}^l_m(f) \rangle , i=1,2. \end{aligned}$$

(22)

Having given the explicit formulas of the equilibrium strain, we now come to the evaluation of the strain derivative of the CEF parameters, which will be given in the next section hosting the main result of this paper.

3 Strain derivative of the CEF parameters

The CEF parameters ${B}^{l}_{m}(f)$ are linear functions of ${\omega }^{l}_{m}(f)$, which are expressed by:

$$\begin{aligned} {\omega }^{l}_{m}(f) = \frac{1}{2l+1} \int \mathrm {d}^3R\frac{\rho _f(\varvec{R}) {Y}^{l}_{m}(\varOmega _{\varvec{R}})}{\epsilon _0 |\varvec{R}|^{l+1}}, \end{aligned}$$

(23)

where $\rho _f$ is the charge distribution in the crystal centered on the fth ion in the unit cell in the local frame of reference, ${Y}^{l}_{m}$ denotes the spherical harmonics, $\varOmega _{\varvec{R}}$ the solid angle and $\varvec{R}$ the position vector. The ${B}^{l}_{m}$ are defined by the tesseral (i.e., real spherical) harmonics and related to ${\omega }^{l}_{m}$ via:

$$\begin{aligned} {B}^{l}_{m}= {\beta }^{l}_{m} \left\{ \begin{array}{ll} \frac{i}{\sqrt{2}} ({\omega }^{l}_{m} - (-1)^m {\omega }^{l}_{-m}), &{} \quad \text {if}\ m< 0,\\ {\omega }^{l}_{0}, &{} \quad \text {if}\ m=0,\\ \frac{1}{\sqrt{2}} ({\omega }^{l}_{-m} + (-1)^m {\omega }^{l}_{m}), &{} \quad \text {if}\ m> 0, \end{array} \right. \nonumber \\ \end{aligned}$$

(24)

where ${\beta }^{l}_{m} = -|e| {p}^{l}_{m} \langle r_{4f}^l \rangle \varTheta _l$. In order to go transform back and forth between ${B}^{l}_{m}$ and ${\omega }^{l}_{m}$, we also need the inverse relation:

$$\begin{aligned} {\omega }^{l}_{m}= \left( {\beta }^{l}_{m} \right) ^{-1} \left\{ \begin{array}{ll} \frac{1}{\sqrt{2}} ({B}^{l}_{|m|} - i {B}^{l}_{-|m|}), &{} \quad \text {if}\ m< 0,\\ {B}^{l}_{0}, &{} \quad \text {if}\ m=0,\\ \frac{(-1)^m}{\sqrt{2}}({B}^{l}_{|m|} + i{B}^{l}_{-|m|}),&{} \quad \text {if}\ m> 0. \end{array} \right. \nonumber \\ \end{aligned}$$

(25)

The main assumption of our model is that the charge distribution deforms in the same way as the lattice. This assumption seems natural and is usually justified a posteriori. In the vicinity of structural phase transitions, this assumption may be violated, for example near the variant conversion transition in magnetic shape memory systems such as RCu$_2$ [12]. For the general formulas, we derive here, we parametrize the specific strain modes by the linear expansion $\epsilon = \varDelta l/l$ such that the tensor $\varvec{\mathsf {\epsilon }}= \varvec{\mathsf {M}}\epsilon$, where $\varvec{\mathsf {M}}$ is a constant $3\times 3$ matrix. To take full advantage of the formalism of spherical harmonics in [11], we will represent the components of the tensor $\varvec{\mathsf {\epsilon }}$ in the spherical basis [11] and not Cartesian; in this basis, we use the indices $\sigma$ and $\sigma '$ for $\epsilon$ and the matrix $\varvec{\mathsf {M}}$. Suppose the lattice deformation in the local reference frame is given by the matrix $\varvec{\mathsf {O}}= \varvec{\mathsf {E}}+ \epsilon ^f \varvec{\mathsf {M}}$ with $\varvec{\mathsf {E}}$ the $3\times 3$ unit matrix and $\varvec{\mathsf {M}}$ a symmetric matrix. Then, we assume that the deformed charge distribution $\rho '_f$ is related to the undeformed charge distribution $\rho _f$ with the deformation matrix $\varvec{\mathsf {O}}^{-1}$ via:

$$\begin{aligned} \rho _f'(\varvec{R}) = \det (\varvec{\mathsf {O}}^{-1}) \rho _f(\varvec{\mathsf {O}}^{-1} \varvec{R}), \end{aligned}$$

(26)

where the factor $\det (\varvec{\mathsf {O}}^{-1})$ is needed to ensure the invariance of the total charge: $\int \rho _f' \mathrm {d}^3R= \int \rho _f \mathrm {d}^3R$.

$$\begin{aligned}&{\omega }^{l}_{m}(f,\epsilon ^f) = {\omega }^{l}_{m}(f,0) - \epsilon ^f (l+1)\nonumber \\&\qquad \sum _{m',\mu ,\sigma ,\sigma '} M_{\sigma '\sigma } C^{lm}_{(l+1) \mu 1 \sigma } C^{l m'}_{(l+1) \mu 1 \sigma '} {\omega }^{l}_{m'}(f,0) \nonumber \\&\quad + \epsilon ^f \sqrt{\frac{(l+1)(l+2)}{(2l+1)(2l + 5)}} \nonumber \\&\qquad \sum _{m',\mu ,\sigma ,\sigma '} M_{\sigma '\sigma } C^{lm}_{(l+1) \mu 1 \sigma } C^{l+2 m'}_{(l+1) \mu 1 \sigma '} {W}^{l}_{m'}(f,0),\nonumber \\ \end{aligned}$$

(27)

$$\begin{aligned}&\quad \text {where} \qquad {W}^{l}_{m'}(f,0) = \int \mathrm {d}^3R'\frac{\rho _f(\varvec{R'})}{\epsilon _0 |\varvec{R'}|^{l+1}} {Y}^{l+2}_{m'}\,\nonumber \\ \end{aligned}$$

(28)

Using fundamental identities of integral transformations, the approximation $\varvec{\mathsf {O}}^{-1} = \varvec{\mathsf {E}}- \epsilon \varvec{\mathsf {M}}$ and the Clebsch–Gordan expansion of products of spherical harmonics, we obtain the main result of this paper, Eq. (27); the derivation is given in the Appendix B. In Eq. (27), $C^{c\gamma }_{a \alpha b \beta }$ denote the Clebsch–Gordan coefficients [11] and the matrix $\varvec{\mathsf {M}}$ is represented in the spherical basis with components $M_{\sigma \sigma '}$; the indices $\sigma$ and $\sigma '$ may take values $\pm 1$ and 0. To study arbitrary deformations, we decompose them in the specific deformation modes $\epsilon ^f_{JM}$ and study their effects individually. For a given set of CEF parameter ${B}^{l}_{m}$, the strain dependence may be calculated via casting the ${B}^{l}_{m}$ to ${\omega }^{l}_{m}$ using Eq. (25), then calculating the strain dependence of the ${\omega }^{l}_{m}$ with Eq. (27) and recasting the ${\omega }^{l}_{m}$ to ${B}^{l}_{m}$ using Eq. (24).

In the case of a general deformation, the linear expansion of ${\omega }^{l}_{m}(\epsilon )$ includes three parts:

• (a) ${\omega }^{l}_{m}(f,0)$ as zero order approximation,

• (b) a sum that mixes contributions of ${\omega }^{l}_{m'}(f,0)$ into ${\omega }^{l}_{m}(f,0)$, depending on the specific deformation,

• (c) a sum that mixes contributions of a quantity similar to ${\omega }^{l}_{m}$ but of a higher multipolar order of maximal order 8.

In general, not all necessary quantities can be obtained from the unperturbed system. Especially, the last term makes evaluation for small arbitrary deformations difficult. For the special case of the volume changing mode $\epsilon ^f_{00}$, however, evaluation is simple. Yet, it is only in systems with cubic lattice symmetry, that the volume changing mode does not couple to other modes when considering the equilibrium strain. Therefore, even though we give explicit formulas for all modes $\epsilon ^f_{JM}$, the calculated example afterwards is focused on the volume changing mode $\epsilon ^f_{00}$ in cubic systems.

4 Explicit formulas

In this section, we evaluate the previous formula for the different $\epsilon _{JM}$ with their specific $\varvec{\mathsf {M}}$ in spherical coordinates using the Kronecker delta function $\delta _{nm}$. We start with the simplest deformation mode:

$$\begin{aligned}&\varvec{\mathsf {\epsilon }}^f_{00}:\quad M_{\sigma ' \sigma } = \frac{1}{\sqrt{3}} \delta _{\sigma ' \sigma }, \end{aligned}$$

(29)

$$\begin{aligned}&{\omega }^{l}_{m}(f,\epsilon _{00}) = {\omega }^{l}_{m}(f,0) - \epsilon _{00} \frac{l + 1}{\sqrt{3}} {\omega }^{l}_{m}(f,0), \end{aligned}$$

(30)

where the formula follows from straightforward evaluation or the identity $\sum _{\alpha \beta } C^{c \gamma }_{a \alpha b \beta } C^{c' \gamma '}_{a \alpha b \beta } = \delta _{cc'}\delta _{\gamma \gamma '}$ [11], since the second term in Eq. (27) reduces to $\epsilon _{00} (l+1)/\sqrt{3} {\omega }^{l}_{m}$ and the third term vanishes. For the other $\varvec{\mathsf {\epsilon }}^f_{JM}$, evaluation of the Clebsch–Gordan coefficients is straightforward [11] and yields Eqs. (31)–(40).

$$\begin{aligned}&\varvec{\mathsf {\epsilon }}^f_{20}: M_{\sigma ' \sigma } = \frac{1}{\sqrt{6}} (3\delta _{\sigma ' 0} \delta _{\sigma 0} - \delta _{\sigma '\sigma }), \end{aligned}$$

(31)

$$\begin{aligned}&{\omega }^{l}_{m}(f, \epsilon ^f_{20}) = {\omega }^{l}_{m}(0) - \frac{\epsilon ^f_{20}}{\sqrt{6} (2l+3)}\left( (l^2 + 1 - 3m^2) {\omega }^{l}_{m}(0) - 3 \sqrt{\frac{(l+1+m)(l+1-m)(l+2+m)(l+2-m)}{(2l+1)(2l + 5)}} {W}^{l}_{m} \right) ,\end{aligned}$$

(32)

$$\begin{aligned}&\varvec{\mathsf {\epsilon }}^f_{21}: M_{\sigma '\sigma } = \frac{1}{\sqrt{2}} (\delta _{\sigma ' 0} \delta _{\sigma -1} - \delta _{\sigma ' 1} \delta _{\sigma 0}),\end{aligned}$$

(33)

$$\begin{aligned}&{\omega }^{l}_{m}(f,\epsilon ^f_{21}) = {\omega }^{l}_{m}(f,0) - \frac{\epsilon ^f_{21}}{\sqrt{2}} \frac{\sqrt{l+1+m}}{2l+3} \Bigg ( \frac{-1}{\sqrt{2}} \sqrt{(l-m)} (1+2m) {\omega }^{l}_{m+1}(f,0) + \sqrt{\frac{(l+1-m)(l+2+m)(l+3+m)}{(2l+1)(2l + 5)}} {W}^{l}_{m+1}(f,0) \Bigg ),\end{aligned}$$

(34)

$$\begin{aligned}&\varvec{\mathsf {\epsilon }}^f_{2-1}: M_{\sigma '\sigma } = \frac{1}{\sqrt{2}} (\delta _{\sigma ' 0} \delta _{\sigma 1} - \delta _{\sigma ' -1} \delta _{\sigma 0}),\end{aligned}$$

(35)

$$\begin{aligned}&\quad {\omega }^{l}_{m}(f,\epsilon ^f) = {\omega }^{l}_{m}(f,0) - \frac{\epsilon ^f_{2-1}}{\sqrt{2}} \frac{\sqrt{l+1-m}}{2l+3} \Bigg ( \frac{-1}{\sqrt{2}} \sqrt{(l+m)} (1-2m) {\omega }^{l}_{m-1}(f,0) + \sqrt{\frac{(l+1+m)(l+2-m)(l+3-m)}{(2l+1)(2l + 5)}} {W}^{l}_{m-1}(f,0) \Bigg ),\end{aligned}$$

(36)

$$\begin{aligned}&\varvec{\mathsf {\epsilon }}^f_{22}: M_{\sigma '\sigma } = (\delta _{\sigma ' 1} \delta _{\sigma -1}),\end{aligned}$$

(37)

$$\begin{aligned}&{\omega }^{l}_{m}(f,\epsilon ^f_{22}) = {\omega }^{l}_{m}(f,0) - \epsilon ^f_{22} \frac{\sqrt{(l+1+m)(l+2+m)}}{2(2l+3)} \Bigg ( \sqrt{(l-1-m)(l-m)} {\omega }^{l}_{m+2}(f,0) + \sqrt{\frac{(l+3+m)(l+4+m)}{(2l+1)(2l + 5)}} {W}^{l}_{m+2}(f,0) \Bigg ),\end{aligned}$$

(38)

$$\begin{aligned}&\varvec{\mathsf {\epsilon }}^f_{2-2}: M_{\sigma '\sigma } = (\delta _{\sigma ' -1} \delta _{\sigma 1}),\end{aligned}$$

(39)

$$\begin{aligned}&{\omega }^{l}_{m}(f,\epsilon ^f_{2-2}) = {\omega }^{l}_{m}(f,0) - \epsilon ^f_{2-2} \frac{\sqrt{(l+1-m)(l+2-m)}}{2(2l+3)} \Bigg ( \sqrt{(l-1+m)(l+m)} {\omega }^{l}_{m-2}(f,0) + \sqrt{\frac{(l+3-m)(l+4-m)}{(2l+1)(2l + 5)}} {W}^{l}_{m-2}(f,0)\Bigg ). \end{aligned}$$

(40)

From the linearization of ${\omega }^{l}_{m}$, we can obtain the linearization of ${B}^{l}_{m}$ via Eq. (24), for example, for the mode $\varvec{\mathsf {\epsilon }}^f_{00}$ in cubic crystals:

$$\begin{aligned} {B}^{l}_{m}(f,\varvec{\mathsf {\epsilon }}^f_{00})&= {B}^{l}_{m}(f,0) - \epsilon ^f_{00} \frac{l + 1}{\sqrt{3}} {B}^{l}_{m}(f,0)\end{aligned}$$

(41)

$$\begin{aligned} {\hat{H}}_\mathrm {CEF}&= \sum _{flm} {B}^{l}_{m}(f,\epsilon ^f_{00}) {\hat{O}}^l_m(f)\end{aligned}$$

(42)

$$\begin{aligned}&= \sum _{flm} \left( 1 - \epsilon ^f_{00} \frac{l + 1}{\sqrt{3}} \right) {B}^{l}_{m}(f,0){\hat{O}}^l_m(f). \end{aligned}$$

(43)

Depending on the CEF symmetry at the relevant rare-earth site, only few Stevens parameters are non-zero. For the mode $\varvec{\mathsf {\epsilon }}^\alpha$, we now also give the equilibrium strain, which is particularly simple to express, because $\varvec{\mathsf {\epsilon }}_\alpha = \sqrt{3} \varvec{\mathsf {\epsilon }}^f_{00} = \sqrt{3} \varvec{\mathsf {\epsilon }}_{00}$ independent of the local coordinate system at position f. Hence, the equilibrium strain in an arbitrary CEF symmetry and for a cubic Bravais lattice reads:

$$\begin{aligned} \epsilon ^\alpha&= \frac{1}{Vc^\alpha } \sum _f \sum _{lm} (l+1) {B}^{l}_{m}(f,0) \langle {\hat{O}}^l_m(f) \rangle \end{aligned}$$

(44)

$$\begin{aligned}&= \frac{N}{Vc^\alpha } \sum _{lm} (l+1) {B}^{l}_{m}(1,0) \langle {\hat{O}}^l_m(1) \rangle , \end{aligned}$$

(45)

where N is the number of rare-earth ions in the unit cell and ${B}^{l}_{m}(1,0)$ and $\langle {\hat{O}}^l_m(1) \rangle$ are evaluated for the first ion as representation of all others in the unit cell. Thus, we see that for the calculation of volume expansion in cubic crystals, the knowledge of the CEF parameters is sufficient. However, the Stevens parameters have very complicated influence on the expansion because they are not only explicitly used in the formulas but also implicitly contained in the CEF levels and wave functions used for thermal average $\langle {\hat{O}}^l_m\rangle$. The formulas of the Hamiltonians and expansions for the several important point symmetries are given in Table 1.

Table 1 CEF Hamiltonians for rare-earth ions in various site symmetries

We want to mention the effects of anisotropic deformations that are not important for the case of zero field and the paramagnetic state in cubic crystals; following [2] for symmetry reasons the anisotropic modes vanish. However, if behavior in field, axial stress (as in recently available strain cells) or the thermal expansion of crystals with lower symmetry than cubic are considered also the anisotropic modes $\varvec{\mathsf {\epsilon }}_{2M}$ with $M = 0, \pm 1, \pm 2$ will become relevant and the according expressions above may be used. For example, the hexagonal, trigonal and tetragonal Bravais lattices have one more symmetry conserving mode $\varvec{\mathsf {\epsilon }}^{\gamma ,1}$ that decomposes in irreducible tensors of type $\varvec{\mathsf {\epsilon }}_{2M}$ with $M = 0, \pm 1, \pm 2$.

Coming back to the case of the thermal CEF volume striction of cubic crystals, we use Eq. (45) in the examples in the next section.

5 Example: CEF parameters and CEF volume striction of pyrochlore titanates

In this section, to illustrate the theoretical part, we show how to apply the derived equations from the last section, to calculate the CEF volume striction given only the CEF parameters, the elastic constants and the lattice parameters. The thermal averages of the expectation values of the Stevens operators $\langle {\hat{O}}^l_m\rangle$ are calculated with McPhase[13]. We show how to derive the CEF parameters for members of an isostructural series when the CEF parameters of one of them is known and the lattice parameters of the whole series is known. The calculated CEF is then used to calculate the CEF volume striction for all compounds of the isostructural series. We use the isostructural series of rare-earth titanate pyrochlores as an example, crystallizing in the cubic space group $Fd{\bar{3}}m$ (Nr. 227).

The CEF parameters of rare-earth compounds are calculated via [10]:

$$\begin{aligned} {B}^{l}_{m} = -|e| {p}^{l}_{m} {\gamma }^{l}_{m} \langle r_{4f}^l \rangle \varTheta _l , \end{aligned}$$

(46)

where $-|e| {p}^{l}_{m}$ is a factor independent of the rare-earth ion and the lattice, ${\gamma }^{l}_{m}$ are the coefficients of the multipole expansion of the charge distribution $\rho$ and a linear combination of the ${\omega }^{l}_{m}$ so that the same behavior under volume change applies that we have derived earlier; $\langle r_{4f}^l \rangle \varTheta _l$ is a factor dependent only on the ground state and the kind of the rare-earth ion. $\varTheta _l$ is $\alpha _J$, $\beta _J$ or $\gamma _J$ for $l=2,4,6$, respectively, and tabulated, cf. [10]. If the substiitution of the rare-earth ion R by another rare-earth ion R’ in a compound does not change the lattice symmetry but only the lattice parameter, then there are two parts contributing to changes of the Stevens parameters: First, the linear expansion or contraction of the lattice influences the CEF parameters according to Eq. (41), with $\epsilon = \sqrt{3} \epsilon ^f_{00}$. And second, the substitution of the rare-earth ion has a large influence shown in Eq. (46). Putting both together, we get:

$$\begin{aligned} {B}^{l}_{m}(R')&= {B}^{l}_{m}(R')|_\epsilon \end{aligned}$$

(47)

$$\begin{aligned}&= \left( 1 - \epsilon (l+1) \right) {B}^{l}_{m}(R')|_0\end{aligned}$$

(48)

$$\begin{aligned}&= \left( 1 - \epsilon (l+1) \right) \frac{\langle r_{4f}^l(R') \rangle \varTheta _l(R')}{\langle r_{4f}^l(R) \rangle \varTheta _l(R)} {B}^{l}_{m}(R)|_0. \end{aligned}$$

(49)

In the following example, we use this formula to calculate the CEF parameters of compounds in the same isostructural series and using these we calculate the CEF volume striction.

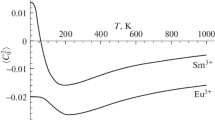
The rare-earth ion resides at Wyckoff position 16d with local CEF symmetry $D_{3d}$. The cubic crystal structure is stable for the relevant temperature range. Using Eq. (45) in the special case of a point symmetry $D_{3d}$ (cf. Table 1), we can calculate the contribution of the CEF to the thermal expansion. For all rare-earth titanate pyrochlores, the CEF parameters of the rare-earth ions were calculated from the ones of Ho$_2$Ti$_2$O$_7$[14] using Eq. (49). The values compare very well to the ones given in [14] and were then used to calculate the CEF volume striction shown in Fig. 1.

We calculate the CEF volume striction with McPhase using the lattice parameters from [15] and an estimate of the elastic parameter $c^\alpha = {568}\hbox { GPa}$ measured for Ho$_2$Ti$_2$O$_7$ [16]. Figure 1 shows that the CEF has a significant contribution to the thermal expansion between $\varDelta L/L = \epsilon _{CEF} = 4\times 10^{-4}$ for Tb$_2$Ti$_2$O$_7$ and $7.5\times 10^{-4}$ for Tm$_2$Ti$_2$O$_7$ between 0 and ${500}\,K$. Compared to phononic thermal expansion in the order of $3\times 10^{-3}$, this would be a measurable effect. Essentially, the order of magnitude is the same for all titanate pyrochlores and largest for Tm$_2$Ti$_2$O$_7$.

Fig. 1

CEF contribution to the thermal expansion of the pyrochlore titanates due to the thermal population of the CEF levels computed with McPhase using Eq. (45) with lattice parameters from [15] and a $c^\alpha = {568}\,\hbox {GPa}$ (measured for Ho$_2$Ti$_2$O$_7$ [16]) as estimate for all compounds.

6 Outlook

Several possible ways to work with the results presented in this paper come to mind.

First, for high-symmetry crystals, an intensive study of Eq. (28) might allow evaluation of arbitrary homogeneous deformations. The authors expect many of these values to vanish for high-symmetry crystals. Second, an investigation of low-symmetry crystals seems promising, since significantly larger CEF striction effects can be expected from our model. The reason for this is that the elastic constants, especially shear elastic constants are considerably softened in non-centrosymmetric crystals [17]. Third, an extension of the theory to the strain dependence of the exchange parameters would also be possible. This would take a thorough investigation of the symmetry of the two quantum states of neighboring atoms and is a natural next step to consider. Important theoretical work has already been done in the review [18]. Finally, our formulas may be used as an equation-of-state for numerical simulations: Strictly speaking, a crystal is an object that is invariant under some (discrete) translation group; inhomogeneous deformations would break this translation invariance, as would statistically distributed defects. However, given that the quantum state at a specific atom in the crystal is influenced only by a small region surrounding it, the local symmetry of that environment at the position of the atom needs to be considered. That symmetry group may change within the crystal to allow symmetry breaking by defects or non-homogeneous deformations, as possible in non-centrosymmetric crystals [19]. However, the solution of such a problem in general is not accessible with analytic methods and one needs to use numerical methods.

7 Summary

In this paper, we have shown new formulas of the effect of a deformation on the CEF parameters associated with Stevens operators. We started from a so-called deformed charge model, where the lattice deformation affects the charge distribution one-to-one and even charge clouds are deformed. This ansatz allowed us to derive an analytical formula of the change of the CEF parameters for small deformation $\epsilon$. We applied this formula to different deformation modes and found in the simplest case of a pure volume changing mode a simple formula. The resulting formulas can be used to calculate the change of the CEF parameters in new strain experiments on bulk materials as well as thin films. We also gave a recapitulation of the general theory of CEF striction with explicit formulas for cubic and hexagonal crystals. With these formulas, it is easy to expand the theory given in this paper if the formulas of the strain derivative of the Stevens parameters can be evaluated. Finally, we used the formulas for several cases of current scientific interest, such as the rare earth pyrochlores including the spin-ice compounds Dy$_2$Ti$_2$O$_7$ and Ho$_2$Ti$_2$O$_7$.

Appendices

Irreducible tensors in Cartesian coordinates

The irreducible tensors in Cartesian coordinates are given for the convenience of the reader and may be found in literature [11]:

$$\begin{aligned} \varvec{\mathsf {\epsilon }}_{00}&= \frac{1}{\sqrt{3}}\left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{array} \right) ,&\quad \varvec{\mathsf {\epsilon }}_{20}&= \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{}-2 \end{array} \right) , \end{aligned}$$

(50)

$$\begin{aligned} \varvec{\mathsf {\epsilon }}_{21}&= \frac{1}{2} \left( \begin{array}{ccc} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} i\\ 1 &{} i &{} 0 \end{array} \right) ,&\quad \varvec{\mathsf {\epsilon }}_{2-1}&= \frac{1}{2} \left( \begin{array}{ccc} 0 &{} 0 &{}-1\\ 0 &{} 0 &{} i\\ -1 &{} i &{} 0 \end{array} \right) ,\end{aligned}$$

(51)

$$\begin{aligned} \varvec{\mathsf {\epsilon }}_{22}&= \frac{1}{2} \left( \begin{array}{ccc} -1 &{} -i &{} 0\\ -i &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) ,&\quad \varvec{\mathsf {\epsilon }}_{2-2}&= \frac{1}{2} \left( \begin{array}{ccc} -1 &{} i &{} 0\\ i &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) .\nonumber \\ \end{aligned}$$

(52)

The $N \times N$ square matrices form an $N^2$-dimensional vector space. Together with the Frobenius inner product as scalar product, we can project out components of matrices in the same way as components of vectors. The Frobenius inner product of two $N \times N$ matrices $\varvec{\mathsf {A}}$ and $\varvec{\mathsf {B}}$ is given by $\varvec{\mathsf {A}}\cdot \varvec{\mathsf {B}}= \sum _{ij} \bar{A_{ij}} B_{ij}$. With this scalar product, the irreducible tensors above form an orthonormal basis for the subspace of symmetric matrices like the strain tensor. We can use this basis to uniquely decompose arbitrary symmetric $N \times N$ matrices. To illustrate the procedure of decomposing a matrix into its irreducible components, we perform this on the symmetric matrix:

$$\begin{aligned} \varvec{\mathsf {M}}= \left( \begin{array}{ccc} 1 &{} 2 &{} 3\\ 2 &{} 4 &{} 5\\ 3 &{} 5 &{} 6 \end{array} \right) . \end{aligned}$$

(53)

For example, we project out the $\varvec{\mathsf {\epsilon }}_{00}$ component of the tensor $\varvec{\mathsf {M}}$ like this:

$$\begin{aligned} (\varvec{\mathsf {\epsilon }}_{00} \cdot \varvec{\mathsf {M}}) = \frac{1 + 4 + 6}{\sqrt{3}}. \end{aligned}$$

(54)

Projecting out the other components of $\varvec{\mathsf {M}}$ we get the decomposition of $\varvec{\mathsf {M}}$ in the symmetric irreducible tensors $\varvec{\mathsf {\epsilon }}_{JM}$:

$$\begin{aligned} \varvec{\mathsf {M}}= & {} \left( \begin{array}{ccc} 1 &{} 2 &{} 3\\ 2 &{} 4 &{} 5\\ 3 &{} 5 &{} 6 \end{array} \right) = \frac{11}{\sqrt{3}} \varvec{\mathsf {\epsilon }}_{00} + \frac{-7}{\sqrt{6}} \varvec{\mathsf {\epsilon }}_{20} + \frac{6 - 10i}{2} \varvec{\mathsf {\epsilon }}_{21} \nonumber \\&+\frac{-6 - 10i}{2} \varvec{\mathsf {\epsilon }}_{2-1} + \frac{3 + 4i}{2} \varvec{\mathsf {\epsilon }}_{22} + \frac{3 - 4i}{2} \varvec{\mathsf {\epsilon }}_{2-2}.\nonumber \\ \end{aligned}$$

(55)

For the sake of completeness: To decompose arbitrary $N \times N$ matrices or antisymmetric tensors, which we do not need to do in this paper, the irreducible tensors $\varvec{\mathsf {\epsilon }}_{11}$ and $\varvec{\mathsf {\epsilon }}_{1-1}$ are needed, as well.

Derivation of the crystal field parameters

Our goal is to expand ${\omega }^{l}_{m}(\epsilon )$ linearly for small deformations $\epsilon$ of the charge distribution $\rho '$ with deformation matrix $\varvec{\mathsf {O}}= \varvec{\mathsf {E}}+ \epsilon \varvec{\mathsf {M}}$.

$$\begin{aligned} {{\omega }^{l}_{m}}'&= \frac{1}{2l+1} \int \mathrm {d}^3R\frac{\rho '(\varvec{R}){Y}^{l}_{m}(\varOmega _{\varvec{R}})}{\epsilon _0 |\varvec{R}|^{l+1}}, \rho '(\varvec{R}) = \det {\varvec{\mathsf {O}}^{-1}} \rho (\varvec{\mathsf {O}}^{-1} \varvec{R}) \end{aligned}$$

(56)

$$\begin{aligned}&= \frac{1}{2l+1} \int \mathrm {d}^3R\frac{\det {\varvec{\mathsf {O}}^{-1}}\rho (\varvec{\mathsf {O}}^{-1} \varvec{R}) {Y}^{l}_{m}(\varOmega _{\varvec{R}})}{\epsilon _0 |\varvec{R}|^{l+1}}, \varvec{R'}= \varvec{\mathsf {O}}^{-1} \varvec{R}\end{aligned}$$

(57)

$$\begin{aligned}&= \frac{1}{2l+1} \int \mathrm {d}^3R'\frac{\rho (\varvec{R'}) {Y}^{l}_{m}(\varOmega _{\varvec{\mathsf {O}}\varvec{R'}})}{\epsilon _0 |{\varvec{\mathsf {O}}\varvec{R'}}|^{l+1}}\end{aligned}$$

(58)

$$\begin{aligned}&= \frac{1}{2l+1} \int \mathrm {d}^3R'\frac{\rho (\varvec{R'})}{\epsilon _0} \left( \frac{{Y}^{l}_{m}(\varOmega _{\varvec{R'}})}{|\varvec{R'}|^{l+1}} + \nabla \left[ \frac{{Y}^{l}_{m}(\varOmega _{\varvec{R'}})}{|\varvec{R'}|^{l+1}} \right] \right. \nonumber \\&\quad \left. \cdot (\varvec{\mathsf {M}}\varvec{R'}) \epsilon \right) , \quad \nabla \left[ \frac{{Y}^{l}_{m}(\varOmega _{\varvec{R'}})}{|\varvec{R'}|^{l+1}} \right] = \sqrt{(l+1)(l+2)} \frac{{\varvec{Y}}^{l+1}_{lm}}{|\varvec{R'}|^{l+2}} \end{aligned}$$

(59)

$$\begin{aligned}&= {\omega }^{l}_{m}(0) + \epsilon \sqrt{\frac{l+1}{2l+1}} \int \mathrm {d}^3R'\frac{\rho (\varvec{R'})}{\epsilon _0} \left( \frac{{\varvec{Y}}^{l+1}_{lm}}{|\varvec{R'}|^{l+2}} \cdot (\varvec{\mathsf {M}}\varvec{R'}) \right) \ \end{aligned}$$

(60)

$$\begin{aligned}&= {\omega }^{l}_{m}(0) + \epsilon \sqrt{\frac{l+1}{2l+1}} \int \mathrm {d}^3R'\frac{\rho (\varvec{R'})}{\epsilon _0 |\varvec{R'}|^{l+1}}\nonumber \\&\quad \sum _{\mu ,\sigma ,\sigma '} M_{\sigma '\sigma } \sqrt{\frac{4\pi }{3}} \left( C^{lm}_{(l+1) \mu 1 \sigma } {Y}^{l+1}_{\mu } {Y}^{1}_{\sigma '} \right) \end{aligned}$$

(61)

$$\begin{aligned}&= {\omega }^{l}_{m}(0) - \epsilon (l+1) \sum _{m'} \left( {\omega }^{l}_{m'} \sum _{\mu ,\sigma ,\sigma '} M_{\sigma '\sigma } C^{lm}_{(l+1) \mu 1 \sigma } C^{l m'}_{l+1 \mu 1 \sigma '} \right) \end{aligned}$$

(62)

$$\begin{aligned}&\quad +\epsilon \sqrt{\frac{(l+1)(l+2)}{(2l+1)(2l + 5)}} \sum _{m'} \left( \int \mathrm {d}^3R'\frac{\rho (\varvec{R'})}{\epsilon _0 |\varvec{R'}|^{l+1}} {Y}^{l+2}_{m'}\right. \nonumber \\&\left. \quad \sum _{\mu ,\sigma ,\sigma '} M_{\sigma '\sigma } C^{lm}_{(l+1) \mu 1 \sigma } C^{l+2 m'}_{l+1 \mu 1 \sigma '} \right) . \end{aligned}$$

(63)

This is achieved in the derivation in Eqs. (56)–(63). While the first steps are simple insertions of definitions the last steps need some more explanation that is given in the following. In Eq. (60), ${\varvec{Y}}^{l+1}_{lm}$ denotes the vector spherical harmonics [11]; if represented in spherical basis, these read: ${\varvec{Y}}^{l+1}_{lm} = \sum _{\mu ,\sigma } C^{lm}_{(l+1) \mu 1 \sigma } {Y}^{l+1}_{\mu } (\varOmega _R) \varvec{e}_\sigma$. To evaluate the scalar product in Eq. (60), we also expand $\varvec{R'}= |\varvec{R'}| \sqrt{\frac{4\pi }{3}} \sum _{\sigma '} {Y}^{1}_{\sigma '} \varvec{e}^{\sigma '}$ in the spherical basis [11]. The effect of $\varvec{\mathsf {M}}$ on the spherical basis is given by: $\varvec{\mathsf {M}}\varvec{e}^{\sigma '} = \sum _{\mu '} \varvec{e}^{\mu '} M_{\sigma '\mu '}$. Hence, we can evaluate Eq. (60) using $\varvec{e}^{\mu '}\varvec{e}_{\sigma } = \delta _{\mu '\sigma }$. We further simplify Eq. (61) using the Clebsch–Gordan expansion of the product of two spherical harmonics

$$\begin{aligned} {Y}^{l_1}_{m_1}{Y}^{l_2}_{m_2} = \sum _{LM} \sqrt{\frac{(2l_1 + 1)(2l_2 + 1)}{4\pi (2L + 1)}} C^{L0}_{l_1 0 l_2 0} C^{L M}_{l_1 m_1 l_2 m_2} {Y}^{L}_{M}.\nonumber \\ \end{aligned}$$

(64)

So considering the product ${Y}^{l+1}_{\mu }{Y}^{1}_{\sigma '}$ there are three possible $L=l,l+1,l+2$ of which only $L=l$ or $L=l+2$ contribute since $C^{L0}_{l+1 0 1 0}$ is zero for odd L. As l is even, we get

$$\begin{aligned}&{Y}^{l+1}_{\mu }{Y}^{1}_{\sigma '} = - \sqrt{\frac{3}{4\pi }}\sum _{m'} \sqrt{\frac{l+1}{2l + 1}} C^{l m'}_{l+1 \mu 1 \sigma '} {Y}^{l}_{m'}\nonumber \\&\quad +\sqrt{\frac{3}{4\pi }} \sum _{m'} \sqrt{\frac{l+2}{2l + 5}} C^{l+2 m'}_{l+1 \mu 1 \sigma '} {Y}^{l+2}_{m'}. \end{aligned}$$

(65)

Inserting this into Eq. (61), we obtain Eq. (63), the main result of this paper. This formula is used in the main text to calculate the change of the CEF parameters during a deformation of the lattice.