Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-27T02:40:00.363Z Has data issue: false hasContentIssue false
  • English
  • Français

GEOMETRIC QUADRATIC CHABAUTY

Part of: Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  17 June 2021

Bas Edixhoven Open the ORCID record for Bas Edixhoven [Opens in a new window]  and
Guido Lido
Bas Edixhoven
Affiliation:
Mathematisch Instituut Universiteit Leiden, Postbus 9512, 2300 RA Leiden, The Netherlands (edix@math.leidenuniv.nl, guidomaria.lido@gmail.com)
Guido Lido
Affiliation:
Mathematisch Instituut Universiteit Leiden, Postbus 9512, 2300 RA Leiden, The Netherlands (edix@math.leidenuniv.nl, guidomaria.lido@gmail.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Since Faltings proved Mordell’s conjecture in [16] in 1983, we have known that the sets of rational points on curves of genus at least 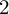$2$ are finite. Determining these sets in individual cases is still an unsolved problem. Chabauty’s method (1941) [10] is to intersect, for a prime number p, in the p-adic Lie group of p-adic points of the Jacobian, the closure of the Mordell–Weil group with the p-adic points of the curve. Under the condition that the Mordell–Weil rank is less than the genus, Chabauty’s method, in combination with other methods such as the Mordell–Weil sieve, has been applied successfully to determine all rational points in many cases.

Minhyong Kim’s nonabelian Chabauty programme aims to remove the condition on the rank. The simplest case, called quadratic Chabauty, was developed by Balakrishnan, Besser, Dogra, Müller, Tuitman and Vonk, and applied in a tour de force to the so-called cursed curve (rank and genus both 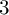$3$ ).

This article aims to make the quadratic Chabauty method small and geometric again, by describing it in terms of only ‘simple algebraic geometry’ (line bundles over the Jacobian and models over the integers).

Keywords

rational pointscurvesChabautynonabelianquadraticgeometric

MSC classification

Primary: 14G05: Rational points
Secondary: 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 1 , January 2023 , pp. 279 - 333
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Atiyah, M. F. and Macdonald, I. G., Introduction to Commutative Algebra (Addison–Wesley Publishing Co., Reading, MA, 1969)Google Scholar
Balakrishnan, J., Besser, A., Bianchi, F. and Müller, J. S., ‘Explicit quadratic Chabauty over number fields’, Preprint, 2019, https://arxiv.org/abs/1910.04653.Google Scholar
Balakrishnan, J., Bianchi, F., Cantoral-Farfán, V., Çiperiani, M. and Etropolski, A., Chabauty–Coleman experiments for genus 3 hyperelliptic curves, in Research Directions in Number Theory , Association for Women in Mathematics Series, 19, pp. 67–90 (Springer, New York, US, 2019).CrossRefGoogle Scholar
Balakrishnan, J. and Dogra, N., Quadratic Chabauty and rational points, I: p-adic heights, Duke Math. J. 167(11) (2018), 1981–2038. With an appendix by J. S. Müller.CrossRefGoogle Scholar
Balakrishnan, J., Dogra, N., Müller, J. S., Tuitman, J. and Vonk, J., Explicit Chabauty-Kim for the split Cartan modular curve of level 13, Ann. of Math. (2) 189(3) (2019), 885–944.CrossRefGoogle Scholar
Bertrand, D. and Edixhoven, B., ‘Pink’s conjecture on unlikely intersections and families of semi-abelian varieties’, J. Éc. polytech. Math. 7 (2020), 711–742, https://jep.centre-mersenne.org/item/JEP_2020__7__711_0/.Google Scholar
Besser, A., p-adic Arakelov theory, J. Number Theory 111(2) (2005), 318—371.CrossRefGoogle Scholar
Betts, A., ‘The motivic anabelian geometry of local heights on abelian varieties’, Preprint, (2017), https://arxiv.org/abs/1706.04850.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models , Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 21 (Springer-Verlag, Berlin, 1990).CrossRefGoogle Scholar
Chabauty, C., Sur les points rationnels des courbes algébriques de genre supérieur àl'unité (French), C. R. Acad. Sci. Paris 212 (1941), 882–885.Google Scholar
Coleman, R. and Gross, G., $p$ -adic heights on curves: Algebraic number theory, Adv. Stud. Pure Math. 17 (1989), 73–81.CrossRefGoogle Scholar
Costa, E., Mascot, N., Sijsling, J. and Voight, J., Rigorous computation of the endomorphism ring of a Jacobian, Math. Comp. 88(317) (2019), 1303–1339.CrossRefGoogle Scholar
Coupek, P., Lilienfeldt, D., Xiao, L. and Yao, Z., ‘Geometric quadratic Chabauty over number fields’, Unpublished notes, 2020, http://www.math.mcgill.ca/lilien/Chabauty-Part1.pdf.Google Scholar
Dogra, N., ‘Unlikely intersections and the Chabauty-Kim method over number fields’, Preprint, 2019, https://arxiv.org/abs/1903.05032.Google Scholar
Edixhoven, B., ‘Geometric quadratic Chabauty’, Lectures at the Arizona Winter School, 2020, http://swc.math.arizona.edu/index.html.Google Scholar
Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. Math. 73(3) (1983), 349–366.CrossRefGoogle Scholar
Flynn, V., A flexible method for applying Chabauty’s theorem, Compos. Math. 105(1) (1997), 79–94.CrossRefGoogle Scholar
Hasegawa, Y., Table of quotient curves of modular curves ${X}_0(N)$ with genus $2$ , Proc. Japan Acad. Ser. A Math. Sci. 71(10) (1995), 235–239.CrossRefGoogle Scholar
Hashimoto, S., ‘Cartoon guide to finding $\mathbb{Q}$ -points with geometric quadratic Chabauty’, Unpublished notes, 2020, https://github.com/sachihashimoto/cartoon-guide-gqc.Google Scholar
Honda, T., On the theory of commutative formal groups, J. Math. Soc. Japan 22(2) (1970), 213–246, https://projecteuclid.org/euclid.jmsj/1259942752.Google Scholar
Katz, N. and Mazur, B., Arithmetic Moduli of Elliptic Curves , Annals of Mathematics Studies, 108 (Princeton University Press, Princeton, NJ, 1985).CrossRefGoogle Scholar
Liu, Q., Algebraic Geometry and Arithmetic Curves , Oxford Graduate Texts in Mathematics, 6 (Oxford University Press, Oxford, UK, 2002).Google Scholar
Mazur, B. and Tate, J., Canonical height pairings via biextensions, in Arithmetic and Geometry, Vol. I , Progress in Mathematics, 35, pp. 195–237 (Birkhäuser Boston, Boston, MA, 1983).CrossRefGoogle Scholar
McCallum, W. and Poonen, B., The method of Chabauty and Coleman, in Explicit Methods in Number Theory, Panoramas et Synthèses, 36, pp. 99–117 (Société mathématique de France, Paris, 2012).Google Scholar
Moret-Bailly, L., Métriques permises, in Seminar on Arithmetic Bundles: The Mordell Conjecture (Paris, 1983/84), Astérisque, 127, pp. 29–87 (Soc.\ Math.\ France, Paris, 1985), http://www.numdam.org/article/AST_1985__127__29_0.pdf.Google Scholar
Moret-Bailly, L., Pinceaux de variétés abéliennes, Astérisque 129 (1985).Google Scholar
Müller, S., Applying the Mordell-Weil sieve, Appendix to [4].Google Scholar
Raynaud, M., Spécialisation du foncteur de Picard, Publ. Math. Inst. Hautes Études Sci. 38 (1970), 27–76.CrossRefGoogle Scholar
Groupes de monodromie en géométrie algébrique. I. Séminaire de Géométrie Algébrique du Bois-Marie 1967–1969 (SGA 7 I). Dirigé par A. Grothendieck. Avec la collaboration de M. Raynaud et D.S. Rim. Lecture Notes in Mathematics, Vol 288. Springer–Verlag, Berlin–New York, 1972.Google Scholar
Spelier, P., A Geometric Approach to Linear Chabauty , Master’s thesis, Universiteit Leiden, 2020.Google Scholar
Stoll, M., ‘Finite coverings and rational points’, Oberwolfach lecture, 2005, http://www.mathe2.uni-bayreuth.de/stoll/workshop2005/oberwolfach2005.pdf.Google Scholar
Zarhin, Y., Neron coupling and quasicharacters, Izv. Akad. Nauk SSSR Ser. Mat. 36 (1972), 497–509.Google Scholar