Modelling of Love Waves in a Heterogeneous Medium Demarcated by Functionally Graded Piezoelectric Layer and Size-Dependent Micropolar Half-Space

Abstract

Purpose

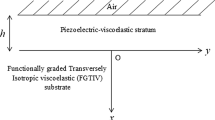
This article is concerned with the analysis of Love-type waves in a three-layer medium consisting of a functionally graded piezoelectric layer loaded on a heterogeneous solid layer above a size-dependent micropolar half-space. The intermediate layer is heterogeneous due to exponential type variation in rigidity and density.

Methods

Separation of variable method has been used to compute the displacement components, potential function and microrotational vectors of the composite layered structure. For electrically open circuit and short circuit cases, the closed form expression of the generalized frequency equation has been obtained in terms of the Bessel functions from the condition of constructive interference.

Results

Extractions of this theoretical study are in perfect agreement with the standard results. An extensive analysis for the propose model is carried out through numerical computation and graphical demonstration to explore the presence of piezoelectricity, heterogeneity and micropolarity in the frequency equation.

Conclusions

This study also reveals that the material parameters associated with upper layer, constrained layer and half-space, thickness parameter of the layers has a remarkable effect on phase and damped velocities of the Love waves propagation under considered geometrical structure.

Appendices

Appendices

Appendix A

$$\begin{aligned} a_{11} & = \left( {\overline{\varsigma }_{44} + \tau \overline{e}_{15} } \right)\left\{ {\frac{f}{2}\sin \varsigma (h + H) + \varsigma \cos \varsigma (h + H)} \right\}e^{f(h + H)} , \,\,a_{12} = \left( {\overline{\varsigma }_{44} + \tau \overline{e}_{15} } \right)\left\{ {\varsigma \sin \varsigma (h + H) - \frac{f}{2}\cos \varsigma (h + H)} \right\}e^{f(h + H)} ,\\ a_{13} & = q_{1} \,\overline{e}_{15} \,e^{{\,\left( {\frac{f}{2} - q_{1} } \right)\,(h + H)}} ,\,\, a_{14} = q_{2} \,\overline{e}_{15} \,e^{{\,\left( {\frac{f}{2} - q_{2} } \right)\,(h + H)}},\,\, a_{1\,j} = 0\,,\,\,j = 5 - 10\,;\, a_{21} = e^{\frac{fH}{2}} \sin \varsigma H\,,\, a_{22} = - e^{\frac{fH}{2}} \,\cos \varsigma H,\, \\ a_{23} & = a_{2\,4} = \,0,\, a_{25} = J_{l} \left( {\frac{kc}{{\delta c_{2} }}e^{\delta H} } \right)e^{{\frac{{m_{h} H}}{2}}} \,, a_{26} = Y_{l} \left( {\frac{kc}{{\delta c_{2} }}e^{\delta H} } \right)e^{{\frac{{m_{h} H}}{2}}} \,, a_{2j} = 0\,,\,\,j = 7 - 10\,;\, \\ a_{31} & = \left( {\overline{\varsigma }_{44} + \tau \overline{e}_{15} } \right)\left\{ {\frac{f}{2}\sin \varsigma H + \varsigma \cos \varsigma H} \right\}e^{fH} , a_{32} = \left( {\overline{\varsigma }_{44} + \tau \overline{e}_{15} } \right)\left\{ { - \frac{f}{2}\cos \varsigma H + \varsigma \sin \varsigma H} \right\}e^{fH} ,\,a_{33} = \overline{e}_{15} \,q_{1} \,e^{{\left( {\frac{f}{2} - q_{1} } \right)H}} ,\\ a_{34} & = \overline{e}_{15} \,q_{2} \,e^{{\left( {\frac{f}{2} - q_{2} } \right)H}} ,\,a_{35} = \overline{\mu }_{2} \,e^{{ - \frac{{m_{h} H}}{2}}} \left\{ {\frac{{m_{h} }}{2}J_{l} \left( {\frac{kc}{{\delta c_{2} }}e^{\delta H} } \right) + \frac{kc}{{c_{2} }}\,e^{\delta H} \,J^{\prime}_{l} \left( {\frac{kc}{{\delta c_{2} }}e^{\delta H} } \right)} \right\}, a_{36} = \overline{\mu }_{2} \,e^{{ - \frac{{m_{h} H}}{2}}} \left\{ {\frac{{m_{h} }}{2}Y_{l} \left( {\frac{kc}{{\delta c_{2} }}e^{\delta H} } \right) + \frac{kc}{{c_{2} }}\,e^{\delta H} \,Y^{\prime}_{l} \left( {\frac{kc}{{\delta c_{2} }}e^{\delta H} } \right)} \right\}, \end{aligned}$$

$$\begin{aligned}a_{3j} & = 0\,,\,\,j = 7 - 10\,;\, a_{4j} = 0\,,\,\,j = 1 - 4\,,\, a_{45} = J_{l} \left( {\frac{kc}{{\delta c_{2} }}} \right)\,,\, \\ a_{46} &= Y_{l} \left( {\frac{kc}{{\delta c_{2} }}} \right)\,,\, a_{47} = 0\,,\,a_{48} = - M\,,\, a_{49} = - N\,,\, a_{410} = 0\,; a_{5j} = 0\,,\,\,j = 1 - 4,\\ a_{55} &= - \overline{\mu }_{2} \left\{ {\frac{{m_{h} }}{2}J_{l} \left( {\frac{kc}{{\delta c_{2} }}} \right) + \frac{kc}{{c_{2} }}J^{\prime}_{l} \left( {\frac{kc}{{\delta c_{2} }}} \right)} \right\}, \\ a_{56} &= - \overline{\mu }_{2} \left\{ {\frac{{m_{h} }}{2}Y_{l} \left( {\frac{kc}{{\delta c_{2} }}} \right) + \frac{kc}{{c_{2} }}Y^{\prime}_{l} \left( {\frac{kc}{{\delta c_{2} }}} \right)} \right\}\,, a_{57} = ik\kappa_{3} \,,\, a_{58} = P\left( {M\mu_{3} - \kappa_{3} } \right),\\ a_{59} & = Q\left( {N\mu_{3} - \kappa_{3} } \right)\,,\,\,\,a_{510} = 0\,; \,\,a_{6j} = 0\,,\,\,j = 1 - 6\,,\,a_{67} = R^{2} \left( {\alpha_{3} + \beta_{3} + \gamma_{3} } \right) - k^{2} \alpha_{3} \,,\, a_{68} = ikP\left( {\beta_{3} + \gamma_{3} } \right)\,,\, a_{69} = ikQ\left( {\beta_{3} + \gamma_{3} } \right)\,,\, a_{610} = 0\,; a_{7j} = 0\,,\,\,j = 1 - 6,\\ a_{77} & = - ikR\left( {\beta_{3} + \gamma_{3} } \right)\,,a_{78} = k^{2} \beta_{3} + P^{2} \gamma_{3} \,,\,a_{79} = k^{2} \beta_{3} + Q^{2} \gamma_{3} \,,\,a_{710} = 0;\\ a_{81} & = - e^{\frac{fH}{2}} \,\tau \,\sin \varsigma H\,,\, a_{82} = e^{\frac{fH}{2}} \,\tau \,cos\varsigma H\,,\,a_{83} = e^{{ - q_{1\,} H}} \,,\, a_{84} = e^{{ - q_{2\,} H}} \,,\,a_{8j} = 0\,,\,\,j = 5 - 10\,; \\ a_{91} & = - e^{{\frac{f(h + H)}{2}}} \,\tau \,sin\varsigma (h + H)\,,\, a_{92} = e^{{\frac{f(h + H)}{2}}} \,\tau \,\cos \varsigma (h + H)\,,\,a_{93} = e^{{ - \,q_{1} \,(h + H)}} \,,\,a_{94} = e^{{ - \,q_{2} \,(h + H)}} \,,\, a_{9j} = 0\,,\,\,j = 5 - 10\,; \end{aligned}$$

$$\begin{aligned}a_{101} & = a_{10\,2} = 0\,,\, a_{103} = q_{1} \,\overline{\eta }_{11} \,e^{{ - \,(f + q_{1} )\,(h + H)}} \,,\, a_{104} = q_{2} \,\overline{\eta }_{11} \,e^{{ - \,(f + q_{2} )\,(h + H)}} \,,\, a_{10j} = 0\,,\,\,j = 5 - 9\,,\,a_{1010} = \eta_{a} \,k\,e^{ - \,k\,(h + H)} \,;\\ \,\, a_{111}& = - \tau \,e^{{\frac{f(h + H)}{2}}} \,\sin \varsigma (h + H)\,,\, a_{112} = \tau \,e^{{\,\frac{f(h + H)}{2}}} \,\cos \varsigma (h + H)\,,\,a_{113} = e^{{ - \,q_{1} (h + H)}} \,,\, a_{114} = e^{{ - \,q_{2} (h + H)}} \,,\, a_{11j} = 0\,,\,\,j = 5 - 9\,,\, a_{1110} = - e^{ - \,k(h + H)} \,.\end{aligned}$$

Also $a_{\,p\,q}^{0} = a_{\,p\,q} ,\,\,p = 1 - 8,\,q = 1 - 10\,\,\& \,\,a_{\,p\,q}^{0} = a_{\,p + 1\,\,q} \,,\,p = 9,10\,,\,q = 1 - 10$ and $a_{\,p\,q}^{s} = a_{\,p\,q} \,;\,p,q = 1 - 9.$

Appendix B

Define $b_{6\,j} = 0\,,\,\,j = 1 - 6\,,\,$ $b_{6\,7} = R\,,\,$ $b_{6\,7} = R\,,\,$$b_{6\,8} = ik,$ $b_{6\,9} = ik,$ $b_{\,6\,10} = 0\,;$ $b_{7\,j} = 0\,,\,\,j = 1 - 6\,,\,$ $b_{7\,7} = ik\,,\,$ $b_{7\,8} = - P\,,\,$ $b_{7\,9} = - Q\,,\,$ $b_{\,7\,10} = 0\,.$

Thus for $p = 1 - 5\,\& \,8 - 10\,,\,\,\overline{a}_{\,p\,q}^{0} = a_{\,p\,q}^{0} ;\,q = 1 - 10$ and for $p = 6\,\& \,7\,,\,\,\overline{a}_{\,p\,q}^{0} = b_{\,p\,q} \,;\,q = 1 - 10\,.$

Also for $p = 1 - 5\,{\text{and}}\,8 - 9\,,\,\,\overline{a}_{\,p\,q}^{s} = a_{\,p\,q}^{s}$ and for $p = 6\,{\text{and}}\,7\,,\,\,\overline{a}_{\,p\,q}^{s} = b_{\,p\,q} \,;\,q = 1 - 9\,.$