On the Maximal Colorings of Complete Graphs Without Some Small Properly Colored Subgraphs

Abstract

Let $\mathrm{pr}(K_{n}, G)$ be the maximum number of colors in an edge-coloring of $K_{n}$ with no properly colored copy of G. For a family ${\mathcal {F}}$ of graphs, let $\mathrm{ex}(n, {\mathcal {F}})$ be the maximum number of edges in a graph G on n vertices which does not contain any graphs in ${\mathcal {F}}$ as subgraphs. In this paper, we show that $\mathrm{pr}(K_{n}, G)-\mathrm{ex}(n, \mathcal {G'})=o(n^{2}),$ where $\mathcal {G'}=\{G-M: M \text { is a matching of }G\}$. Furthermore, we determine the value of $\mathrm{pr}(K_{n}, P_{l})$ for sufficiently large n and the exact value of $\mathrm{pr}(K_{n}, G)$, where G is $C_{5}, C_{6}$ and $K_{4}^{-}$, respectively. Also, we give an upper bound and a lower bound of $\mathrm{pr}(K_{n}, K_{2,3})$.

1 Introduction

We call a subgraph of an edge-colored graph rainbow, if all of its edges have different colors. While a subgraph is called properly colored (also can be called locally rainbow), if any two adjacent edges receive different colors. The anti-Ramsey number of a graph G in a complete graph $K_{n}$, denoted by $\mathrm{ar}(K_{n}, G)$, is the maximum number of colors in an edge-coloring of $K_{n}$ with no rainbow copy of G. Namely, $\mathrm{ar}(K_{n}, G)+1$ is the minimum number k of colors such that any k-edge-coloring of $K_{n}$ contains a rainbow copy of G. In this paper, we let $\mathrm{pr}(K_{n}, G)$ be the maximum number of colors in an edge-coloring of $K_{n}$ with no properly colored copy of G. Namely, $\mathrm{pr}(K_{n}, G)+1$ is the minimum number k of colors such that any k-edge-coloring of $K_{n}$ contains a properly colored copy of G.

Given a family ${\mathcal {F}}$ of graphs, we call a graph G an ${\mathcal {F}}$-free graph, if G contains no graph in ${\mathcal {F}}$ as a subgraph. The Turán number $\mathrm{ex}(n, {\mathcal {F}})$ is the maximum number of edges in a graph G on n vertices which is ${\mathcal {F}}$-free. Such a graph G is called an extremal graph, and the set of extremal graphs is denoted by $\mathrm{EX}(n, {\mathcal {F}})$. The celebrated result of Erdős-Stone-Simonovits Theorem [7, 9] states that for any ${\mathcal {F}}$ we have

$$\begin{aligned} \mathrm{ex}(n, {\mathcal {F}})=\left( \frac{p-1}{2p}+o(1)\right) n^{2}, \end{aligned}$$

(1.1)

where $p=\Psi ({\mathcal {F}})=\min \{\chi (F): F\in {\mathcal {F}}\}-1,$ is the subchromatic number.

The anti-Ramsey number was introduced by Erdős, Simonovits and Sós in [8]. There they showed that $\mathrm{ar}(K_{n}, G)\ge \mathrm{ex}(n, {\mathcal {G}})+1$, where ${\mathcal {G}}=\{G-e: e\in E(G)\}$ and by (1.1), they showed that $\mathrm{ar}(K_{n}, G)=(\frac{d-1}{2d}+o(1))n^{2}$, where $d=\Psi ({\mathcal {G}})$. This determined $\mathrm{ar}(K_{n}, G)$ asymptotically when $\Psi ({\mathcal {G}})\ge 2.$ In the case $\Psi ({\mathcal {G}})= 1$, the situation is more complex. Already the cases when G is a tree or a cycle are nontrival. For a path $P_{k}$ on k vertices, Simonovits and Sós [20] proved $\mathrm{ar}(K_{n}, P_{2t+3+\epsilon })=tn-\left( {\begin{array}{c}t+1\\ 2\end{array}}\right) +1+\epsilon$, for large n, where $\epsilon =0$ or 1. Jiang [11] showed $\mathrm{ar}(K_{n}, K_{1,p})=\lfloor \frac{n(p-2)}{2}\rfloor +\lfloor \frac{n}{n-p+2}\rfloor$ or possibly this value plus one if certain conditions hold. For a general tree T of k edges, Jiang and West [12] proved $\frac{n}{2}\lfloor \frac{k-2}{2}\rfloor +O(1)\le \mathrm{ar}(K_{n}, T)\le \mathrm{ex}(n, T)$ for $n\ge 2k$ and conjectured that $ar(K_{n}, T)\le \frac{k-2}{2}n+O(1).$ For cycles, Erdős, Simonovits and Sós [8] conjectured that for every fixed $k\ge 3$, $\mathrm{ar}(K_{n}, C_{k})=(\frac{k-2}{2}+\frac{1}{k-1})n+O(1)$, and proved that for $k=3$. Alon [1] proved this conjecture for $k=4$ and gave some upper bounds for $k\ge 5$. Finally, Montellano-Ballesteros and Neumann-Lara [18] completely proved this conjecture, that is, for $n\ge k\ge 3$ and $n\equiv r_{k} \pmod {(k-1)}$, where $0\le r_{k}\le k-2$,

$$\begin{aligned} ar(K_{n}, C_{k})=\left\lfloor \frac{n}{k-1}\right\rfloor \left( {\begin{array}{c}k-1\\ 2\end{array}}\right) +\left( {\begin{array}{c}r_{k}\\ 2\end{array}}\right) +\left\lceil \frac{n}{k-1}\right\rceil -1. \end{aligned}$$

(1.2)

For cliques, Erdős, Simonovits and Sós [8] showed $\mathrm{ar}(K_{n}, K_{p+1})=\mathrm{ex}(n, K_{p})+1$ for $p\ge 3$ and sufficiently large n. Montellano-Ballesteros and Neumann-Lara [17] and independently Schiermeyer [19] showed that $\mathrm{ar}(K_{n}, K_{p+1})=\mathrm{ex}(n, K_{p})+1$ holds for every $n\ge p\ge 3$. For complete bipartite graphs, Axenovich and Jiang [2] showed that $\mathrm{ar}(K_{n}, K_{2,t})=\mathrm{ex}(n, K_{2,t-1})+O(n)$, where $t\ge 2$. Krop and York [13] showed that $\mathrm{ar}(K_{n}, K_{s,t})=\mathrm{ex}(n, K_{s,t-1})+O(n)$, where $t\ge s\ge 2$. Also, there are many other results about anti-Ramsey numbers. We mention the excellent survey by Fujita, Magnant and Ozeki [10] for more conclusions on this topic.

The maximum number of colors in an edge-colored complete graph without some properly colored subgraphs was first studied by Manoussakis, Spyratos, Tuza and Voigt in [15]. For cliques, they [15] obtained the approximate value of $\mathrm{pr}(K_{n}, K_{t})$.

Theorem 1

[15] For $t\ge 3$, let $b=\left\lfloor \frac{t-1}{2}\right\rfloor$, we have $\mathrm{pr}(K_{n}, K_{t})=\left( \frac{b-1}{2b}+o(1)\right) n^2.$

For paths and cycles, they [15] showed that $\mathrm{pr}(K_{n}, P_{n})=\left( {\begin{array}{c}n-3\\ 2\end{array}}\right) +1$ for large n and $\mathrm{pr}(K_{n}, C_{n})=\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) +1$. Also, they gave a conjecture about cycles as follows.

Conjecture 1

[15] Let $n>l\ge 4$. Assume that $K_{n}$ is colored with at least k colors, where

$$\begin{aligned} k= {\left\{ \begin{array}{ll} \frac{1}{2}l(l+1)+n-l+1, \, \text {if} \,\, n < \frac{10l^{2}-6l-18}{6(l-3)};\\ \frac{1}{3}ln-\frac{1}{18}l(l+3)+2, \, \text {if}\,\, n\ge \frac{10l^{2}-6l-18}{6(l-3)},\\ \end{array}\right. } \end{aligned}$$

then $K_{n}$ admits a properly colored cycle of length $l+1$.

In this paper, we generalize Theorem 1 to an arbitrary graph G which shows that $\mathrm{pr}(K_{n}, G)$ is related to the Turán number like the anti-Ramsey number.

Theorem 2

Let G be a graph and $\mathcal {G'}=\{G-M: M \text { is a matching of }G\}$, then $\mathrm{pr}(K_{n}, G)\ge \mathrm{ex}(n, \mathcal {G'})+1$ and $\mathrm{pr}(K_{n}, G)=\left( \frac{d-1}{2d}+o(1)\right) n^2,$ where $d=\Psi (\mathcal {G'})$.

We will prove Theorem 2 in Sect. 2 by the method used in the proof of Theorem 1 in [15]. Theorem 2 determines $pr(K_{n}, G)$ asymptotically when $\Psi (\mathcal {G'})\ge 2$. As the anti-Ramsey number, the case $\Psi (\mathcal {G'})= 1$ is more complex.

In Sect. 3, we will determine $\mathrm{pr}(K_{n}, P_{l})$ for large n by proving the following theorem.

Theorem 3

Let $P_{l}$ be a path on l vertices and $l\equiv r_{l}\pmod 3$, where $0\le r_{l}\le 2$. For $n\ge 2l^{3}$, we have

$$\begin{aligned} \mathrm{pr}(K_{n}, P_{l})= \left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) n-\left( {\begin{array}{c}\left\lfloor \frac{l}{3}\right\rfloor \\ 2\end{array}}\right) +1+r_{l}. \end{aligned}$$

For cycles, we slightly improve the lower bound of Conjecture 1 (See Proposition 4). Also, We modify Conjecture 1 as follows.

Conjecture 2

Let $C_{k}$ be a cycle on k vertices and $(k-1)\equiv r_{k-1}\pmod 3$, where $0\le r_{k-1}\le 2$. For $n\ge k,$

$$\begin{aligned} \mathrm{pr}(K_{n}, C_{k})=\max \left\{ \left( {\begin{array}{c}k-1\\ 2\end{array}}\right) +n-k+1, \left\lfloor \frac{k-1}{3} \right\rfloor n-\left( {\begin{array}{c}\left\lfloor \frac{k-1}{3} \right\rfloor +1\\ 2\end{array}}\right) +1+r_{k-1}\right\} . \end{aligned}$$

It is easy to see that $\mathrm{pr}(K_{n}, C_{3})=\mathrm{ar}(K_{n}, C_{3})=n-1$. Also, by Proposition 4 and (1.2), one can check that for $n\ge 3$,

$$\begin{aligned} \mathrm{pr}(K_{n},C_{n})=\mathrm{ar}(K_{n},C_{n})&=\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) +1, \end{aligned}$$

(1.3)

$$\begin{aligned} \mathrm{pr}(K_{n+1},C_{n})=\mathrm{ar}(K_{n+1},C_{n})&=\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) +2. \end{aligned}$$

(1.4)

Li, Broersma and Zhang [14], and later Xu, Magnant and Zhang [21] showed that for $n\ge 4$, $\mathrm{pr}(K_{n}, C_{4})=n$. We obtain the exact value of $\mathrm{pr}(K_{n}, C_{5})$ and $\mathrm{pr}(K_{n}, C_{6})$ in Sect. 4.

Theorem 4

For $n\ge 5$, $\mathrm{pr}(K_{n}, C_{5})=n+2$.

Theorem 5

For $n\ge 6$, $\mathrm{pr}(K_{n}, C_{6})=n+5$.

Let $K_{4}^{-}$ be the diamond, the graph obtained from $K_4$ by deleting an edge. We obtain the exact value of $\mathrm{pr}(K_{n}, K_{4}^{-})$ in Sect. 5.

Theorem 6

For $n\ge 3$, $\mathrm{pr}(K_{n}, K_{4}^{-})= \left\lfloor \frac{3(n-1)}{2}\right\rfloor .$

We also give a lower bound and an upper bound of $\mathrm{pr}(K_{n}, K_{2,3})$ in Section 5.

Theorem 7

For $n\ge 5$, $\frac{7}{4}n+O(1)\le \mathrm{pr}(K_{n}, K_{2,3})\le 2n-1.$

Notations: Let G be a simple undirected graph. For $x\in V (G)$, we denote the neighborhood and the degree of x in G by $N_G(x)$ and $d_G(x)$, respectively. The maximum degree of G is denoted by $\Delta (G)$. The common neighborhood of $U\subset V(G)$ is the set of vertices in $V(G){{\setminus }} U$ that are adjacent to each vertex of U. We will use $G- x$ to denote the graph that arises from G by deleting the vertex $x\in V (G)$. For a vertex set $X \subset V (G)$, G[X] is the subgraph of G induced by X and $G -X$ is the subgraph of G induced by $V (G){{\setminus }} X$. Given a graph $G= (V, E)$, for any (not necessarily disjoint) vertex sets $A, B\subset V$, we let $E_{G}(A, B):=\{uv\in E(G)| u\ne v, u\in A, v\in B\}$. We use ${\overline{G}}$ to denote the complement of G. Given two vertex disjoint graphs $G_{1}$ and $G_{2}$, we denote by $G_{1}+G_{2}$ the join of graphs $G_{1}$ and $G_{2}$, that is the graph obtained from $G_{1}\cup G_{2}$ by joining each vertex of $G_{1}$ with each vertex of $G_{2}$.

Given an edge-coloring c of $K_{n}$, we denote the color of an edge uv by c(uv). For any vetex $v\in V(G)$, let $C(v):=\{c(vw):\, w\in V(K_{n}){{\setminus }}\{v\}\}$ and $d_{c}(v):=|C(v)|.$ A color a is starred (at x) if all the edges with color a induce a star $K_{1,r}$ (centered at the vertex x). We let $d^{c}(v)=|\{a\in C(v) : a \text { is starred at }~ v\}|$. For a subgraph H of G, we denote $C(H)=\{c(uv):\, uv\in E(H)\}$. A representing subgraph of an edge-colored $K_n$ is a spanning subgraph containing exactly one edge of each color. The weak representing subgraph of an edge-colored $K_{n}$ is consisting of all the edges whose color appears only once in $K_{n}$. Note that an edge xy is the unique edge with color a in $K_{n}$ if and only if the color a is stared at both x and y. Thus, if G is the weak representing subgraph of an edge-colored $K_{n}$, then we have

$$\begin{aligned} |E(G)|\ge \sum _{v\in V(K_{n})} d^{c}(v)-|C(K_{n})|. \end{aligned}$$

(1.5)

2 The Proof of Theorem 2

In this section, we will prove Theorem 2 by a similar argument used in the proof of Theorem 1 in [15].

Theorem 2

Let G be a graph and $\mathcal {G'}=\{G-M: M \text { is a matching of }G\}$, then $\mathrm{pr}(K_{n}, G)\ge \mathrm{ex}(n, \mathcal {G'})+1$ and $\mathrm{pr}(K_{n}, G)=\left( \frac{d-1}{2d}+o(1)\right) n^2,$ where $d=\Psi (\mathcal {G'})$.

Proof

Let F be a graph in $\mathrm{EX}(n, \mathcal {G'})$. We color the edges of $K_{n}$ as follows. Take a subgraph F of $K_{n}$, and assign distinct colors to all of E(F) and a new color $c_{0}$ to all the remaining edges. Suppose there is a properly colored G, then $M=\{e\in E(G), e \text { is colored with } c_{0}\}$ is a matching of G, and $G-M\subset F$. By the definition of $\mathcal {G'}$, we have $G-M \in \mathcal {G'}$, and this is a contradiction with F being $\mathcal {G'}$-free. Thus we have $\mathrm{pr}(K_{n}, G)\ge \mathrm{ex}(n, \mathcal {G'})+1=(\frac{d-1}{2d}+o(1))n^2$ by (1.1).

Let $G_{0}=G-M_{p}$, where $M_{p}$ is a p-matching of G and $\chi (G_{0})=d+1$. We prove that for every fixed $\varepsilon > 0$, and for n large enough with respect to $n_{0}=|V(G)|$ and $\varepsilon$, there is a properly colored copy of G in any $(\frac{d-1}{2d}+\varepsilon )n^2$-edge-coloring of $K_{n}$. In a representing subgraph of $K_{n}$ with $(\frac{d-1}{2d}+\varepsilon )n^2$ edges, for an arbitrarily fixed s, and for n sufficiently large, by (1.1), there exists a complete $(d+1)$-partite subgraph $K_{s,s,\ldots ,s}$ with s vertices in each class. We take $s=2^{n_{0}+d+1}.$

Denote by V the vertex set of $K_{s, s, \ldots , s}$ and by $V_{1}, V_{2}, \ldots , V_{d+1}$ its vertex classes. We apply the following procedure.

For each $i=1, 2, \ldots , d+1$ do sequentially the following:

• (1) Select arbitrarily $2^{n_{0}+d+1-i}$ pairwise disjoint pairs $\{u_{ij}, v_{ij}\}$ in $V_{i}$, $j= 1,2,\ldots , 2^{n_{0}+d+1-i}.$

• (2) For $j=1, 2, \ldots , 2^{n_{0}+d+1-i}$, delete from $K_{s, s, \ldots , s}$ the (at most one) vertex $z\in V{{\setminus }} V_{i}$ for which either $c(zu_{ij})=c(u_{ij}v_{ij})$ or $c(zv_{ij})=c(u_{ij}v_{ij})$, and if z has already been selected in a previous pair $\{u_{i'j'}, v_{i'j'}\}$, for some $i'<i$, then also delete the other member of its pair.

Claim 1

The above procedure can be executed smoothly and there are at least $2^{n_{0}}$ pairs remains undeleted in each $V_{i}$ at the end of the execution.

The Proof of Claim 1

In the beginning, each $V_{i}$ contains $2^{n_{0}+d+1}$ vertices, $i=1, 2, \ldots , d+1$. In the first iteration, $i=1$, we can carry out (1) and (2) easily. Suppose we have carried out up to the $(i-1)$-st iteration. Before executing the i-th iteration observe that at most $\sum _{1\le j\le i-1}2^{n_{0}+d+1-j}= 2^{n_{0}+d+1}-2^{n_{0}+d+2-i}$ vertices have been deleted from $V_{i}$. Thus, $V_{i}$ contains at least $2^{n_{0}+d+2-i}$ vertices and it is enough to execute instruction (1) in the ith iteration.

On the other hand, for any $i=1, 2, \ldots , d$, from the $(i+1)$-st iteration up to the end, due to instructions of type (2), at most $\sum _{i+1\le j\le d+1}2^{n_{0}+d+1-j}=2^{n_{0}+d+1-i}-2^{n_{0}}$ pairs in $V_{i}$ have been deleted and thus at least $2^{n_{0}}$ pairs in $V_{i}$ remains undeleted. Note also that $V_{d+1}$ contains $2^{n_{0}}$ pairs of vertices and there is no deletion of pair in $V_{d+1}$. $\square$

For $1\le i\le d+1$, let $\{x_{ij}y_{ij}: 1\le j\le 2^{n_{0}}\}$ be the $2^{n_{0}}$ pairs in $V_{i}$ which remain undeleted and $V'_{i}=\{x_{ij}, y_{ij}: 1\le j\le 2^{n_{0}}\}$. Let H be the graph obtained by adding the edge set $\{x_{ij}y_{ij}: 1\le i\le d+1, 1\le j\le 2^{n_{0}}\}$ to the graph $K_{s, s, \ldots , s}[V'_{1}\cup \cdots \cup V'_{d+1}]$. Then H is properly colored by Claim 1. Since $G_{0}= G-M_{p}$ and $\chi (G_{0})=d+1$, we have $H\supset G$. Thus $\mathrm{pr}(K_{n}, G)\le (\frac{d-1}{2d}+o(1))n^2$. $\square$

3 Paths

In this section, we study the maximum number of colors in an edge-colored complete graph without properly edge-colored paths, and prove Theorem 3. Before doing so, we determine $\mathrm{pr}(K_{n}, P_{l})$ for some small values of l.

Proposition 1

• (a) $\mathrm{pr}(K_{n}, P_{3})=1,$ for $n\ge 3$.

• (b) $\mathrm{pr}(K_{n}, P_{4})=2,$ for $n\ge 4$.

• (c) $\mathrm{pr}(K_{n}, P_{5})=3,$ for $n\ge 5$.

Proof

• (a) The conclusion holds trivially.

• (b) Choose a vertex v of $K_{n}$, color all edges incident to v with color $c_{1}$ and color all the remaining edges with color $c_{2}$. We use two colors and there is no properly colored $P_{4}$. Hence $\mathrm{pr}(K_{n}, P_{4})\ge 2$.

For $n\ge 5$, we have $\mathrm{pr}(K_{n}, P_{4})\le \mathrm{ar}(K_{n}, P_{4})=2$ (see [3]). For $n=4$, let $V(K_{4})=\{u, v, x, y\}$. Given a 3-edge-coloring of $K_{4}$, there exists at least one edge in $E(\{u,v\}, \{x,y\})$, we say ux, such that $c(ux)\ne c(uv)$ and $c(ux)\ne c(xy)$. Thus vuxy is a properly colored $P_{4}$ and $\mathrm{pr}(K_{n}, P_{4})\le 2$.

• (c) Choose two vertices u and v of $K_{n}$, assign one color $c_{1}$ to all edges incident with u, one new color $c_{2}$ to all edges incident with v (except the edge uv) and the other new color $c_{3}$ to all the remaining edges. We use three colors and there is no properly colored $P_{5}$. Hence $\mathrm{pr}(K_{n}, P_{5})\ge 3$.

Let $n\ge 5$. Given a 4-edge-coloring of $K_{n}$, there is always a rainbow $P_{4}=u_{1}u_{2}u_{3}u_{4}$ since $\mathrm{ar}(K_{n}, P_{4})=2$ (see [3]). Since $|C(P_{4})|=|E(P_{4})|=3$, there is a color $c_{0}\in C(K_{n}){{\setminus }} C(P_{4})$. Suppose there is no properly colored $P_{5}$ in the 4-edge-coloring of $K_{n}$. Then for all $u\in V(K_{n})\backslash V(P_{4})$, it must be $c(uu_{1})=c(u_{1}u_{2})$, $c(uu_{4})=c(u_{3}u_{4})$, $c(uu_2)\in \{c(u_1u_2),c(u_2u_3)\}$ and $c(uu_3)\in \{c(u_2u_3),c(u_3u_4)\}$. If $c(u_{1}u_{4})=c_{0},$ then $uu_{1}u_{4}u_{3}u_{2}$ is a properly colored $P_{5}$, a contradiction. If $c(u_{1}u_{3})=c_{0}$ or $c(u_{2}u_{4})=c_{0}$, say $c(u_{1}u_{3})=c_{0}$, then $u_{4}uu_{1}u_{3}u_{2}$ is a properly colored $P_{5}$, a contradiction. So we may assume that there are two vertices $x,y\in V(K_{n}){{\setminus }} V(P_{4})$ such that $c(xy)=c_{0}$. In this case, $u_{4}yxu_{2}u_{1}$ or $u_{4}yxu_{2}u_{3}$ is a properly colored $P_{5}$, a contradiction. Hence $\mathrm{pr}(K_{n}, P_{5})\le 3$. $\square$

Here, we give the lower bound of $pr(K_{n}, P_{l})$ by the following proposition.

Proposition 2

Let $P_{l}$ be a path on l vertices and $l\equiv r_{l} \pmod 3$, where $0\le r_{l}\le 2$. For $n\ge l$, we have

$$\begin{aligned} \mathrm{pr}(K_{n}, P_{l})\ge \max \left\{ \left( {\begin{array}{c}l-3\\ 2\end{array}}\right) +1, \left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) n-\left( {\begin{array}{c}\left\lfloor \frac{l}{3}\right\rfloor \\ 2\end{array}}\right) +1+ r_{l}\right\} . \end{aligned}$$

Proof

We color the edges of $K_{n}$ as follows. For the first lower bound, we choose a $K_{l-3}$ and color it rainbow, and use one extra color for all the remaining edges. In such way, we use exactly $\left( {\begin{array}{c}l-3\\ 2\end{array}}\right) +1$ colors and do not obtain a properly colored $P_{l}$.

For the second lower bound, we partition $K_{n}$ into two graphs $K_{\lfloor \frac{l}{3}\rfloor -1}+{\overline{K}}_{n-\lfloor \frac{l}{3}\rfloor +1}$ and $K_{n-\lfloor \frac{l}{3}\rfloor +1}$. First we color $K_{\lfloor \frac{l}{3}\rfloor -1}+{\overline{K}}_{n-\lfloor \frac{l}{3}\rfloor +1}$ rainbow. Then we color $K_{n-\lfloor \frac{l}{3}\rfloor +1}$ by $(1+ r_{l})$ new colors without producing a properly colored $P_{3+ r_{l}}$ (See the proof of Proposition 3.1). In such way, we use exactly $\left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) n-\left( {\begin{array}{c}\left\lfloor \frac{l}{3}\right\rfloor \\ 2\end{array}}\right) +1+ r_{l}$ colors and do not obtain a properly colored $P_{l}$. $\square$

The proof of the following proposition is trivial. We will use it to prove Theorem 3.

Proposition 3

Let $P_{l}$ be a path with l vertices, and $l\equiv r_{l} \pmod 3$, where $0\le r_{l}\le 2$. If an edge-colored $K_{n}$ contains a rainbow copy of $K_{\lfloor \frac{l}{3}\rfloor -1, 2\lfloor \frac{l}{3}\rfloor +3}$ but does not contain a properly colored $P_{l}$. We denote by Q the vertices of $K_{n}-K_{\lfloor \frac{l}{3}\rfloor -1, 2\lfloor \frac{l}{3}\rfloor +3}$, by X the smaller class of $K_{\lfloor \frac{l}{3}\rfloor -1, 2\lfloor \frac{l}{3}\rfloor +3}$ and by Y the other one. Then $|C(K_{n}[Y])|\le 1+r_{l}$. Furthermore, we have $|C(K_{n}[Y])\cup C(E_{K_{n}}(Y, Q))|\le 1+r_{l}$ and $|C(K_{n}[Y\cup Q])|\le 1+r_{l}$. We get the most colors if the colors of all the edges between X and $Y\cup Q$ and all the edges in X are different, they differ from all the other edges and we use exactly $1+r_{l}$ colors in $Y\cup Q$ such that there is no properly colored $P_{3+r_{l}}$ in $Y\cup Q$. Then the number of colors is

$$\begin{aligned} \left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) n-\left( {\begin{array}{c}\left\lfloor \frac{l}{3}\right\rfloor \\ 2\end{array}}\right) +1+r_{l}. \end{aligned}$$

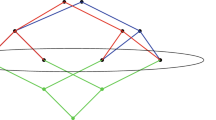
Now, we will prove Theorem 3, and the idea comes from [20] (Fig. 1).

Theorem 3

Let $P_{l}$ be a path on l vertices and $l\equiv r_{l}\pmod 3$, where $0\le r_{l}\le 2$. For $n\ge 2l^{3}$, we have

$$\begin{aligned} \mathrm{pr}(K_{n}, P_{l})= \left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) n-\left( {\begin{array}{c}\left\lfloor \frac{l}{3}\right\rfloor \\ 2\end{array}}\right) +1+r_{l}. \end{aligned}$$

Proof

We just need prove the upper bound for $l\ge 6$. We shall use the following famous results of Erdős and Gallai (see [5]): for $n\ge r\ge 2$,

$$\begin{aligned} \mathrm{ex}(n, P_{r})&\le \frac{r-2}{2}n,\end{aligned}$$

(3.1)

$$\begin{aligned} \mathrm{ex}(n,\{C_{r+1}, C_{r+2},\ldots \} )&\le \frac{r(n-1)}{2}. \end{aligned}$$

(3.2)

Let c be an edge-coloring of $K_{n}$ using $\mathrm{pr}(K_{n}, P_{l})$ colors without producing a properly colored $P_{l}$. Take a longest properly colored path $P_{s}=v_{1}v_{2}\cdots v_{s}$, where $s\le l-1.$ Denote by G the graph obtained by choosing one edge from each remaining color such that the number of edges joining $P_{s}$ to the remaining $n-s$ vertices is as large as possible. We would partition $V(G)\backslash V(P_{s})$ into three sets $U_{1}, U_{2}$ and $U_{3}$ as follows:

• (a) $U_{1}$ is the vertex set of $V(K_{n})\backslash V(P_{s})$ not jointed to $P_{s}$ at all: neither by edges nor by paths;

• (b) $U_{2}$ is the set of isolated vertices of $V(K_{n})\backslash V(P_{s})$ jointed to $P_{s}$ by edges;

• (c) $U_{3}=V(K_{n})\backslash (V(P_{s})\cup U_{1}\cup U_{2}).$

Claim 1

For any vertex $u\in U_{1}\cup U_{2}\cup U_{3}$, we have $c(uv_{1})=c(v_{1}v_{2})$ and $c(uv_{s})=c(v_{s-1}v_{s})$. Moreover, $E_{G}(U_{2}\cup U_{3}, \{v_{1}, v_{2}, v_{s-1}, v_{s}\})=\emptyset .$

Proof of Claim 1

It is obvious that $c(uv_{1})=c(v_{1}v_{2})$ and $c(uv_{s})=c(v_{s-1}v_{s})$ for any vertex $u\in U_{1}\cup U_{2}\cup U_{3}$ by the maximality of $P_{s}$, thus we have $E_{G}(U_{2}\cup U_{3}, \{v_{1}, v_{s}\})=\emptyset$. Suppose that there is a vertex $u\in U_{2}\cup U_{3}$ such that $uv_{2}\in E(G)$ or $uv_{s-1}\in E(G)$, we say $uv_{2}\in E(G)$. Notice that $c(uv_{1})=c(v_{1}v_{2})\ne c(uv_{2})$ by the definition of G, it follows that $v_{1}uv_{2}\cdots v_{s}$ is a properly colored path of order $s+1$, a contradiction to the maximality of $P_{s}$. $\square$

Fig. 1

The structure of graph G

Claim 2

$G[U_{1}]$ contains no $P_{\lfloor \frac{s}{2}\rfloor }$.

Proof of Claim 2

Suppose $P_{\lfloor \frac{s}{2}\rfloor }=u_{1}u_{2}\ldots u_{\lfloor \frac{s}{2}\rfloor }$ is a path in $G[U_{1}]$. By the definition of G, the colors of $C(G[U_{1}])$ can not appear in any edges between $U_{1}$ and $V(P_{s})$. Thus, $c(u_{1}v_{\lceil \frac{s}{2}\rceil })\ne c(u_{1}u_{2})$, $c(u_{\lfloor \frac{s}{2}\rfloor }v_1)\ne c(u_{\lfloor \frac{s}{2}\rfloor }u_{\lfloor \frac{s}{2}\rfloor -1})$ and $c(u_{\lfloor \frac{s}{2}\rfloor }v_s)\ne c(u_{\lfloor \frac{s}{2}\rfloor }u_{\lfloor \frac{s}{2}\rfloor -1})$. Since $c(v_{\lceil \frac{s}{2}\rceil -1}v_{\lceil \frac{s}{2}\rceil })\ne c(v_{\lceil \frac{s}{2}\rceil }v_{\lceil \frac{s}{2}\rceil +1})$, at most one of $c(v_{\lceil \frac{s}{2}\rceil -1}v_{\lceil \frac{s}{2}\rceil })$ and $c(v_{\lceil \frac{s}{2}\rceil }v_{\lceil \frac{s}{2}\rceil +1})$ is the same as $c(u_{\lceil \frac{s+1}{2}\rceil }v_{\lceil \frac{s}{2}\rceil })$. So at least one of $v_{1}v_{2}\ldots v_{\lceil \frac{s}{2}\rceil }u_{1}u_{2}\ldots u_{\lfloor \frac{s}{2}\rfloor } v_{s}$ and $v_{s}v_{s-1}\ldots v_{\lceil \frac{s}{2}\rceil }u_{1}u_{2}\ldots u_{\lfloor \frac{s}{2}\rfloor } v_{1}$ is a properly colored path of order at least $s+1$, a contradiction to the maximality of $P_{s}$. Hence, $G[U_{1}]$ contains no $P_{\lfloor \frac{s}{2}\rfloor }$. $\square$

By Claim 2 and (3.1), we have

$$\begin{aligned} |E(G[U_{1}])|\le \frac{1}{2}\left( \left\lfloor \frac{s}{2}\right\rfloor -2\right) |U_{1}|\le \left( \frac{1}{2}\left\lfloor \frac{l-1}{2}\right\rfloor -1\right) |U_{1}|. \end{aligned}$$

(3.3)

Claim 3

For any vertex $u\in U_{2}\cup U_{3}$ and any three consecutive vertices $v_{i}, v_{i+1}, v_{i+2}\in V(P_{s})$, we have $|E_{G}(u, \{v_{i}, v_{i+1}, v_{i+2}\})|\le 1.$

Proof of Claim 3

Suppose there exist a vertex $u\in U_{2}\cup U_{3}$ and three consecutive vertices $v_{i}, v_{i+1}, v_{i+2}\in V(P_{s})$ such that $|E_{G}(u, \{v_{i}, v_{i+1}, v_{i+2}\})|\ge 2$, that is at least two of $uv_{i}, uv_{i+1}, uv_{i+2}$ are edges of G, then whatever $c(vv_{i})$ is, at least one of $v_{1}\ldots v_{i}uv_{i+1}v_{i+2}\ldots v_{s}$ and $v_{1}\ldots v_{i}v_{i+1}uv_{i+2}\ldots v_{s}$ is a properly colored path of order $s+1$, a contradiction to the maximality of $P_{s}$. $\square$

By Claims 1 and 3, we have $|E_{G}(u, P_{s})|\le \left\lceil \frac{s-4}{3}\right\rceil \le \left\lceil \frac{l-5}{3}\right\rceil =\left\lfloor \frac{l}{3}\right\rfloor -1$ for all $u\in U_2$. Thus, we have

$$\begin{aligned} |E_{G}(U_{2}, P_{s})|\le \left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) |U_{2}|. \end{aligned}$$

(3.4)

Let H be any component of $G[U_{3}]$ and r be the length of the longest cycle in H. If H contains no cycles, then we write $r=2$. By (3.2), we have

$$\begin{aligned} |E(H)|\le \frac{r|V(H)|-r}{2}. \end{aligned}$$

(3.5)

Now we will estimate the number of edges between V(H) and $V(P_{s})$ in G by the following two claims.

Claim 4

For any vertex $u\in V(H)$, we have

$$\begin{aligned} E_{G}(u, \{v_{1},\ldots , v_{2r+1}, v_{s-2r},\ldots , v_{s}\})=\emptyset . \end{aligned}$$

(3.6)

Proof of Claim 4

Since H is connected and the length of the longest cycle in H is r, we can always find a path $P_{r}\subset H$ starting from u in H. Let $P_{r}=u_{1}u_{2}\ldots u_{r}$ be such a path, where $u_{1}=u$. By an argument very similar to the one in Claim 1, we have $E_{G}(u, \{v_{1},\ldots , v_{r+1}, v_{s-r},\ldots , v_{s}\})=\emptyset .$ By the symmetry, we just need to show that there is no edge between u and $\{v_{r+2},\ldots , v_{2r+1}\}$. If there exists $v_i\in \{v_{r+2},\ldots , v_{2r}\}$ such that $uv_{i}\in E(G)$, we have $i\ge r+2\ge 4$. By the definition of G, we have $c(u_{r}v_{\lfloor \frac{i}{2}\rfloor })\ne c(u_{r-1}u_{r})$. Since $c(v_{\lfloor \frac{i}{2}\rfloor -1}v_{\lfloor \frac{i}{2}\rfloor })\ne c(v_{\lfloor \frac{i}{2}\rfloor }v_{\lfloor \frac{i}{2}\rfloor +1})$, at most one of $c(v_{\lfloor \frac{i}{2}\rfloor -1}v_{\lfloor \frac{i}{2}\rfloor })$ and $c(v_{\lfloor \frac{i}{2}\rfloor }v_{\lfloor \frac{i}{2}\rfloor +1})$ is the same as $c(u_{r}v_{\lfloor \frac{i}{2}\rfloor })$. Thus at least one of $v_{1}v_{2}\ldots v_{\lfloor \frac{i}{2}\rfloor }u_{s}\ldots u_{1}v_{i}v_{i+1}\ldots v_{s}$ and $v_{i-1}v_{i-2}\ldots v_{\lfloor \frac{i}{2}\rfloor }u_{s}\ldots u_{1}v_{i}v_{i+1}\ldots v_{s}$ is a properly colored path of order at least $s+1$, a contradiction to the maximality of $P_{s}$. If $uv_{2r+1}\in E(G)$, then we have $c(uv_{2r})\ne c(v_{2r}v_{2r+1})$, otherwise $v_{1}v_{2}\cdots v_{2r}uv_{2r+1}v_{2r+2}\cdots v_{s}$ is a properly colored path of order $s+1$, a contradiction to the maximality of $P_{s}$. Also, we have $c(uv_{2r})\ne c(uu_{2})$. By an argument similar to the above, one can find a properly colored path of order at least $s+1$, a contradiction to the maximality of $P_{s}$. $\square$

Claim 5

For any six consecutive vertices $v_{i}, v_{i+1}, v_{i+2}, v_{i+3}, v_{i+4}, v_{i+5}\in V(P_{s})$, all edges between $\{v_{i}, v_{i+1}, v_{i+2}, v_{i+3}, v_{i+4}, v_{i+5}\}$ and V(H) of G induce a star.

Proof of Claim 5

If not, suppose $xv_{i}$ and $yv_{j}$ are two independent edges between V(H) and $\{v_{i}, v_{i+1}, v_{i+2}, v_{i+3}, v_{i+4}, v_{i+5}\}$ in G, where $x, y\in V(H)$ and $j\in \{i+1, i+2, i+3, i+4, i+5\}$. Let $P_{xy}$ be a path of H which connect x and y. If $j\in \{i+1, i+2, i+3\}$, then whatever $c(xv_{i+1})$ is, at least one of $v_{1}\ldots v_{i}xv_{i+1} \cdots v_{s}$ and $v_{1}\ldots v_{i}v_{i+1}xP_{xy}yv_{j}\ldots v_{s}$ is a prorperly colored path of order at least $s+1$, a contradiction to the maximality of $P_{s}$. If $j=i+4$, then we have $c(xv_{i+3})=c(v_{i+2}v_{i+3})$ and $c(yv_{i+1})=c(v_{i+1}v_{i+2})$, otherwise, $v_{1}v_{2}\ldots v_{i+3}xP_{xy}yv_{i+4}\ldots v_{s}$ or $v_{1}v_{2}\ldots v_{i+1}yP_{yx}xv_{i+3}\ldots v_{s}$ is a properly colored path of order at least $s+2$, a contradiction to the maximality of $P_{s}$. It follows that $v_{1}\ldots v_{i+1}yP_{yx}xv_{i+3}\ldots v_{s}$ is a properly colored path of order at least $s+1$, a contradiction to the maximality of $P_{s}$. If $j=i+5$, by a similar argument of the former case, we have $c(xv_{i+3})=c(yv_{i+2})=c(v_{i+2}v_{i+3})$ and $v_{1}v_{2}\ldots v_{i+2}yP_{yx}xv_{i+3}\ldots v_{s}$ is a properly colored path of order at least $s+2$, a contradiction to the maximality of $P_{s}$. $\square$

By Claim 3, for any six consecutive vertices $v_{i}, v_{i+1}, v_{i+2}, v_{i+3}, v_{i+4}, v_{i+5}\in V(P_{s})$ and any vertex $u\in V(H)$, we have $|E_{G}(u,\{v_{i}, v_{i+1}, v_{i+2}, v_{i+3}, v_{i+4}, v_{i+5}\})|\le 2$. Thus, by Claim 5, we have

$$\begin{aligned} |E_G(V(H),\{v_{i}, v_{i+1}, v_{i+2}, v_{i+3}, v_{i+4}, v_{i+5}\})|\le \max \{2, |V(H)|\}\le |V(H)|. \end{aligned}$$

(3.7)

Combining (3.6) and (3.7), we have

$$\begin{aligned} |E_G(V(H),V(P_{s}))|\le \left\lceil \frac{s-2(2r+1)}{6}\right\rceil |V(H)|. \end{aligned}$$

(3.8)

Combining (3.5) and (3.8), we have

$$\begin{aligned} \begin{aligned} |E_{G}(V(H), V(P_{s}))|+|E(H)|&\le \left\lceil \frac{s-2(2r+1)}{6}\right\rceil |V(H)|+\frac{r|V(H)|-r}{2}\\&\le \left( \left\lceil \frac{s-4r-2}{6}\right\rceil +\frac{r}{2}\right) |V(H)|\\&\le \left( \left\lceil \frac{s-4r-2}{6}+\frac{r+1}{2}\right\rceil \right) |V(H)|\\&\le \left\lceil \frac{s-1}{6}\right\rceil |V(H)| \end{aligned} \end{aligned}$$

The last inequality holds since $r\ge 2$. Note that $|E_{G}(V(H), V(P_{s}))|+|E(H)|\le \left\lceil \frac{s-1}{6}\right\rceil |V(H)|$ holds for each component H of $G[U_{3}]$. Thus, we have

$$\begin{aligned} |E_{G}(U_{3}, P_{s})|+|E(G[U_{3}])|\le \left\lceil \frac{s-1}{6}\right\rceil |U_{3}|\le \left\lceil \frac{l-2}{6}\right\rceil |U_{3}|. \end{aligned}$$

(3.9)

By (3.3), (3.4) and (3.9), we have

$$\begin{aligned} \begin{aligned} \mathrm{pr}(K_{n}, P_{l})&=|C(K_{n})| \le |C(P_{s})|+ |E(G)|\\&\le \left( {\begin{array}{c}s\\ 2\end{array}}\right) +|E(G[U_{1}])|+|E_{G}(U_{2}, P_{s})|+|E_{G}(U_{3}, P_{s})|+|E(G[U_{3}])|\\&\le \left( {\begin{array}{c}s\\ 2\end{array}}\right) +\left( \frac{1}{2}\left\lfloor \frac{l-1}{2}\right\rfloor -1\right) |U_{1}|+\left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) |U_{2}|+\left\lceil \frac{l-2}{6}\right\rceil |U_{3}|.\end{aligned}\end{aligned}$$

Note that $\frac{1}{2}\left\lfloor \frac{l-1}{2}\right\rfloor -1\le \left\lfloor \frac{l}{3}\right\rfloor -1-\frac{1}{2}$ for $l\ge 6$ and $\left\lceil \frac{l-2}{6}\right\rceil \le \left\lfloor \frac{l}{3}\right\rfloor -1-\frac{1}{2}$ for all $l\ge 12$. When $l\le 11$, we have $s\le 10$, by Claim 4, $U_{3}=\emptyset$. Let $U^{*}=\{u\in U_{2}: d_{G}(u)=\left\lfloor \frac{l}{3}\right\rfloor -1\}.$ Then we have

$$\begin{aligned} \mathrm{pr}(K_{n},P_{l})\le \left( {\begin{array}{c}s\\ 2\end{array}}\right) +\left( \left\lfloor \frac{l}{3}\right\rfloor -1-\frac{1}{2}\right) (n-s-|U^{*}|)+\left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) |U^{*}|. \end{aligned}$$

(3.10)

Since $n\ge 2l^{3}$, by Proposition 2, we have

$$\begin{aligned} \mathrm{pr}(K_{n},P_{l})\ge \left( \left\lfloor \frac{l}{3}\right\rfloor -1\right) n-\left( {\begin{array}{c}\left\lfloor \frac{l}{3}\right\rfloor \\ 2\end{array}}\right) +1+r_{l}. \end{aligned}$$

(3.11)

Combining (3.10) and (3.11), since $n\ge 2l^{3}$, we have $|U^{*}|\ge l^{3}$. By Claims 1 and 3, there are at most $\left( {\begin{array}{c}s-4-2(\lfloor \frac{l}{3}\rfloor -1-1)\\ \lfloor \frac{l}{3}\rfloor -1\end{array}}\right)$ distinct $(\lfloor \frac{l}{3}\rfloor -1)$-subset of $V(P_{s})$ can be the neighborhood of some vertex in $U^{*}$. Since $s\le l-1$ and $6\le l\le 3\left\lfloor \frac{l}{3}\right\rfloor +2$, we have

$$\begin{aligned} \left( {\begin{array}{c}s-4-2(\lfloor \frac{l}{3}\rfloor -1-1)\\ \lfloor \frac{l}{3}\rfloor -1\end{array}}\right) \le \left( {\begin{array}{c}l-1-2\lfloor \frac{l}{3}\rfloor \\ \lfloor \frac{l}{3}\rfloor -1\end{array}}\right) \le \left( {\begin{array}{c}\lfloor \frac{l}{3}\rfloor +1\\ \lfloor \frac{l}{3}\rfloor -1\end{array}}\right) = \left( {\begin{array}{c}\lfloor \frac{l}{3}\rfloor +1\\ 2\end{array}}\right) \le \frac{l^{2}}{9}. \end{aligned}$$

Note that $|U^{*}|\ge l^{3}>\frac{l^{2}}{9}(2\lfloor \frac{l}{3}\rfloor +3)$, by Pigeonhole Principle, $U^{*}$ contains at least $2\lfloor \frac{l}{3}\rfloor +3$ vertices which have a common neighborhood of size $\lfloor \frac{l}{3}\rfloor -1$ in G. That is, we find a rainbow $K_{\lfloor \frac{l}{3}\rfloor -1, 2\lfloor \frac{l}{3}\rfloor +3}$. By Proposition 3, the proof is complete.

$\square$

4 Cycles

The lower bound of $\mathrm{pr}(K_{n}, C_{k})$ was given roughly by Manoussakis, Spyratos, Tuza and Voigt in [15]. Here we prove the lower bound precisely again.

Proposition 4

Let $C_{k}$ be a cycle on k vertices and $(k-1)\equiv r_{k-1} \pmod 3,$ where $0\le r_{k-1}\le 2$. For $n\ge k,$

$$\begin{aligned} \mathrm{pr}(K_{n}, C_{k})\ge \max \left\{ \left( {\begin{array}{c}k-1\\ 2\end{array}}\right) +n-k+1, \left\lfloor \frac{k-1}{3} \right\rfloor n-\left( {\begin{array}{c}\left\lfloor \frac{k-1}{3}\right\rfloor +1\\ 2\end{array}}\right) +1+r_{k-1}\right\} . \end{aligned}$$

Proof

We color the edges of $K_{n}$ as follows. For the first lower bound, we choose a $K_{k-1}$ and color it rainbow, and use one extra color for all the remaining edges. In such way, we use exactly $\left( {\begin{array}{c}k-1\\ 2\end{array}}\right) +1$ colors and do not obtain a properly colored $C_{k}$.

For the second lower bound, we partition $K_{n}$ into two graphs $K_{\lfloor \frac{k-1}{3}\rfloor }+{\overline{K}}_{n-\lfloor \frac{k-1}{3}\rfloor }$ and $K_{n-\lfloor \frac{k-1}{3}\rfloor }$. First we color $K_{\lfloor \frac{k-1}{3}\rfloor }+{\overline{K}}_{n-\lfloor \frac{k-1}{3}\rfloor }$ rainbow. Then we color $K_{n-\lfloor \frac{k-1}{3}\rfloor }$ by $(1+ r_{k-1})$ new colors without producing a properly colored $P_{3+ r_{k-1}}$ (See the proof of Proposition 3.1). In such way, we use exactly $\lfloor \frac{k-1}{3}\rfloor n-\left( {\begin{array}{c}\lfloor \frac{k-1}{3}\rfloor +1\\ 2\end{array}}\right) +1+ r_{k-1}$ colors and do not obtain a properly colored $C_{k}$. $\square$

Conjecture 3

Let $C_{k}$ be a cycle on k vertices and $(k-1)\equiv r_{k-1}\pmod 3$, where $0\le r_{k-1}\le 2$. For $n\ge k,$

$$\begin{aligned} \mathrm{pr}(K_{n}, C_{k})=\max \left\{ \left( {\begin{array}{c}k-1\\ 2\end{array}}\right) +n-k+1, \left\lfloor \frac{k-1}{3} \right\rfloor n-\left( {\begin{array}{c}\left\lfloor \frac{k-1}{3} \right\rfloor +1\\ 2\end{array}}\right) +1+r_{k-1}\right\} . \end{aligned}$$

Now we prove Conjecture 2 holds for $C_{5}$ and $C_{6}$, respectively.

Theorem 4

For $n\ge 5$, $\mathrm{pr}(K_{n}, C_{5})=n+2$.

Proof

By Proposition 4, we have $\mathrm{pr}(K_{n}, C_{5})\ge n+2$ for $n\ge 5$. We will prove $\mathrm{pr}(K_{n}, C_{5})\le n+2$ by induction on n. The base cases $n=5$ and $n=6$ follow from (1.3) and (1.4), respectively. For $n\ge 7$, assume that the conclusion holds for order less than n. Let c be an $(n+3)$-edge-coloring of $K_{n}$. If there is a vertex v such that $d^{c}(v)\le 1$, then $|C(K_{n}-v)|\ge n+3-1=(n-1)+3$ and there is a properly colored $C_{5}$ by the induction hypothesis. Thus we assume that $d^{c}(v)\ge 2$, for all $v\in V(K_{n})$. Let G be the weak representing subgraph of $K_{n}$. By (1.5), we have $|E(G)|\ge 2n-(n+3)=n-3\ge 4$. Thus, G contains a 2-matching. Let $\{xy, zw\}$ be a 2-matching of G. Choose a vertex $u\in V(K_{n}){{\setminus }} \{x, y, z, w\}$. We consider the following two cases.

Case 1. There are at least two edges of $\{ux, uy, uz, uw\}$ are colored with distinct colors.

In this case, there are at least one edge of $\{ux, uy\}$, we say ux, and at least one edge of $\{uz, uw\}$, we say uz, such that $c(ux)\ne c(uz)$. By the definition of G, we have $c(ux)\ne c(xy)$, $c(uz)\ne c(zw)$ and $c(xy)\ne c(yw)\ne c(zw)$. Thus, uxywzu is a properly colored $C_{5}$.

Case 2. The four edges ux, uy, uz and uw are colored with the same color.

If c(ux) is starred at u, since $d^{c}(u)\ge 2$, there exists a vertex $v\in V(K_{n}){{\setminus }} \{x, y, z, w, u\}$ such that c(uv) is starred at u and $c(uv)\ne c(ux)$. Also, we have $c(ux)\ne c(xz) \ne c(zw)$ and $c(zw)\ne c(vw)\ne c(uv)$. Thus, uxzwvu is a properly colored $C_{5}$. If c(ux) is not starred at u, since $d^{c}(u)\ge 2$, there exists two vertices $v_{1}, v_{2}\in V(K_{n}){{\setminus }} \{x, y, z, w, u\}$ such that $c(uv_{1})$ and $c(uv_{2})$ are starred at u and $c(uv_{1})\ne c(uv_{2})$. Also, we have $c(uv_{1})\ne c(v_{1}x)\ne c(xy)$ and $c(uv_{2})\ne c(v_{2}z)\ne c(xy)$. Thus, $uv_{1}xyv_{2}u$ is a properly colored $C_{5}$.

$\square$

For $C_{6}$, we consider more cases to prove it.

Theorem 5

For $n\ge 6$, $\mathrm{pr}(K_{n}, C_{6})=n+5$.

Proof

By Proposition 4, we have $\mathrm{pr}(K_{n}, C_{6})\ge n+5$ for $n\ge 6.$ We will prove $pr(K_{n}, C_{6})\le n+5$ by induction on n. The base cases $n=6$ and $n=7$ follow from (1.3) and (1.4), respectively. For $n\ge 8$, assume that the conclusion holds for order less than n. Let c be an $(n+6)$-edge-coloring of $K_{n}$. If there is a vertex v such that $d^{c}(v)\le 1$, then $|C(K_{n}-v)|\ge n+6-1=(n-1)+6$ and there is a properly colored $C_{6}$ by the induction hypothesis. Thus we assume that $d^{c}(v)\ge 2$ for all $v\in V(K_{n})$. Let G be the weak representing subgraph of $K_{n}$. By (1.5), we have $|E(G)|\ge 2n-(n+6)=n-6\ge 2$.

Case 1. $\Delta (G)\ge 2$.

In this case, G contains a path of order 3. Let $P_{3}=xyz$ be such a path of G and $U=V(K_{n}){{\setminus }} \{x, y, z\}.$ Let H be a subgraph $K_{n}$ obtained by choosing one edge from the colors which are starred at some vertex of U such that the number of edges between $\{x,y,z\}$ and U is as large as possible.

Case 1.1 $|E(H[U])|\ge 2$.

Let $u_{1}u_{2}, v_{1}v_{2}\in E(H[U])$. If $u_{1}u_{2}$ and $v_{1}v_{2}$ have a common end vertex, we say $u_2=v_1$, then $c(xu_1)\ne c(u_1v_1)$ and $c(zv_2)\ne c(v_1v_2)$ by the choice of H. Thus $xyzv_2v_1u_1x$ is a properly colored $C_{6}$. Now we may assume that $\{u_1u_2, v_1v_2\}$ is a 2-matching of H. Assume that $c(u_{1}u_{2})$ and $c(v_{1}v_{2})$ are starred at $u_{1}$ and $v_{1}$ respectively. Thus $c(u_{2}v_{2})\ne c(u_{1}u_{2})$ and $c(u_{2}v_{2})\ne c(v_{1}v_{2})$. By the choice of H, we have $c(xu_{1})\ne c(u_{1}u_{2})$ and $c(yv_{1})\ne c(v_{1}v_{2})$. Thus, $xyv_{1}v_{2}u_{2}u_{1}x$ is a properly colored $C_{6}$.

Case 1.2 $|E(H[U])|=1.$

Assume $uv\in E(H[U])$ and c(uv) is starred at u. Then we have $c(xu)\ne c(uv)$. Also, $c(vz)\ne c(uv)$. Take a vertex $w\in U{{\setminus }}\{u, v\}$. Since $d^{c}(w)\ge 2$, we have $|E_{H}(w,\{x, y ,z\})|\ge 2$. There is at least one of $\{x, z\}$, say x, such that c(wx) is starred at w and $c(wx)\ne c(wy)$. Also, we have $c(wx)\ne c(ux)$. Thus wxuvzyw is a properly colored $C_{6}$.

Case 1.3 $E(H[U])=\emptyset .$

For all $v\in U$, since $d^{c}(v)\ge 2$, we have $|E_{H}(v, \{x, y, z\})|\ge 2$. Notice that $|U|\ge n-3\ge 5.$ If there are three vertices in U, say $u_{1}, u_{2}, u_{3}\in U$, such that they have a common neighborhood $\{x, z\}$ in H, then at least one of $\{u_{1}x, u_{1}z\}$, say $u_{1}x$, such that $c(u_{1}y)\ne c(u_{1}x)$. Also, at most one edge of $\{u_{2}x, u_{2}z, u_{3}x, u_{3}z\}$ has the same color as $c(u_{2}u_{3})$. Thus, at least one of $xu_{1}yzu_{3}u_{2}x$ and $xu_{1}yzu_{2}u_{3}x$ is a properly colored $C_{6}$.

Now we may assume that there are at least two vertices in U, say $u_{1}, u_{2}$, such that they have a common neighborhood $\{x, y\}$ or $\{y,z\}$ in H, say $\{x, y\}$. If there is a vertex $u_{3}\in U{{\setminus }} \{u_{1}, u_{2}\}$ such that $u_{3}y, u_{3}z \in E(H)$, we have $c(zx)\notin \{c(xu_{1}), c(xu_{2}), c(zu_{3})\}$ and at most one edge of $\{u_{1}x, u_{1}y, u_{2}x, u_{2}y\}$ has the same color as $c(u_{1}u_{2})$. Thus, at least one of $xu_{1}u_{2}yu_{3}zx$ and $xu_{2}u_{1}yu_{3}zx$ is a properly colored $C_{6}$. If there is a vertex $u_{3}\in U{{\setminus }} \{u_{1}, u_{2}\}$ such that $u_{3}x, u_{3}z \in E(H)$, at least one of $xu_{1}u_{2}yzu_{3}x$ and $xu_{2}u_{1}yzu_{3}x$ is a properly colored $C_{6}$. Now we may assume that U has a common neighborhood $\{x, y\}$ in H. Take four distinct vertices $u_{1}, u_{2}, u_{3}, u_{4}\in U$. At most one edge of $\{u_{1}x, u_{1}y, u_{2}x, u_{2}y\}$ has the same color as $c(u_{1}u_{2})$ and at most one edge of $\{u_{3}x, u_{3}y, u_{4}x, u_{4}y\}$ has the same color as $c(u_{3}u_{4})$. Thus the graph induced by the edges set $\{u_{1}u_{2}, u_{3}u_{4}, xu_{i}, yu_{i}: 1\le i\le 4\}$ contains a a properly colored $C_{6}$.

Case 2. $\Delta (G)=1.$

Note that if G has three independent edges, then we can find a properly colored $C_{6}$. Recall that $|E(G)|\ge n-6\ge 2$. Now we may assume that $n=8$ and $|E(G)|=2$. Let $E(G)=\{xy, zw\}$ and $U=V(K_{8}){{\setminus }} \{x, y, z, w\}=\{u_{1}, u_{2}, u_{3}, u_{4}\}.$

Case 2.1 There is an edge $u_{i}u_{j}$ such that $c(u_{i}u_{j})$ is starred at $u_{i}$, say $c(u_{1}u_{2})$ is starred at $u_{1}$.

If there is one vertex in $\{x, y, z, w\}$, say x, such that $c(u_{1}x)\ne c(u_{1}u_{2})$, then $u_{1}xyzwu_{2}u_{1}$ is a properly colored $C_{6}$. We assume that $c(u_{1}x)=c(u_{1}y)=c(u_{1}z)=c(u_{1}w)=c(u_{1}u_{2}).$ Since $d^{c}(u_{1})\ge 2$, we can assume that $c(u_{1}u_{3})$ is starred at $u_{1}$ and $c(u_{1}u_{3})\ne c(u_{1}u_{2}).$ Thus $u_{1}xyzwu_{3}u_{1}$ is a properly colored $C_{6}$.

Case 2.2 For all edge $u_{i}u_{j}$, $c(u_{i}u_{j})$ is not starred at $u_{i}$ or $u_{j}$.

Since $d^{c}(u_{1})\ge 2$ and $d^{c}(u_{2})\ge 2$, we can find two distinct vertices $v_{1}, v_{2}\in \{ x, y, z, w\}$ such that $c(u_{1}v_{1})$ is starred at $u_{1}$ and $c(u_{2}v_{2})$ is starred at $u_{2}$. If $v_{1}=x$ and $v_{2}=y$, then $u_{1}xzwyu_{2}u_{1}$ is a properly colored $C_{6}$. If $v_{1}=x$ and $v_{2}=z$, then $u_{1}xywzu_{2}u_{1}$ is a properly colored $C_{6}$. $\square$

5 $K_{4}^{-}$ and $K_{2,3}$

In this section, we will prove Theorems 6 and 7. First, we determine the exact value of $\mathrm{pr}(K_{n}, K_{4}^{-})$.

Theorem 6

For $n\ge 4$, $\mathrm{pr}(K_{n}, K_{4}^{-})= \left\lfloor \frac{3(n-1)}{2}\right\rfloor .$

Proof

The lower bound: Consider an edge-coloring of $K_{n}$ as follows. Take a triangle $C_{3}=xyz$ of $K_{n}$ and a maximum matching $M=\{x_{1}y_{1}, x_{2}y_{2}, \ldots , x_{\lfloor \frac{n-3}{2}\rfloor }y_{\lfloor \frac{n-3}{2}\rfloor }\}$ of $K_{n}-\{x,y,z\}$. There is one vertex w in $V(K_{n}){{\setminus }} (V(M)\cup \{x,y,z\})$ when n is even. For $1\le i\le \lfloor \frac{n-3}{2}\rfloor$, color all the edges of $\{ux_{i} :u\in \{x, y, z, x_{1}, y_{1}, x_{2}, y_{2}, \ldots , x_{i-1}, y_{i-1}\}\}$ with color $c_{1i}$ and all the edges of $\{uy_{i} :u\in \{x, y, z, x_{1}, y_{1}, x_{2}, y_{2}, \ldots , x_{i-1}, y_{i-1}\}\}$ with color $c_{2i}$. If n is even, color all edges of $\{uw: u\in V(K_{n}-w)\}$ with a new color. Finally, assign distinct new colors to all edges of $C_{3}\cup M$. In such a coloring, there is no properly colored $K_{4}^{-}$, and the number of colors is $\lfloor \frac{3(n-1)}{2}\rfloor$.

The upper bound: We will prove that for any $\lfloor \frac{3n-1}{2}\rfloor$-edge-coloring of $K_{n}$, there is a properly colored $K_{4}^{-}$ by induction on n. The base case $n=4$ is trivial. For $n\ge 5$, assume that the conclusion holds for order less than n. Let c be a $\left\lfloor \frac{3n-1}{2}\right\rfloor$-edge-coloring of $K_{n}$. If there is a vertex v such that $d^{c}(v)\le 1$, then $|C(K_{n}-v)|\ge \left\lfloor \frac{3n-1}{2}\right\rfloor -1\ge \left\lfloor \frac{3(n-1)-1}{2}\right\rfloor$, and there is a properly colored $K_{4}^{-}$ in $K_{n}-v$ by the induction hypothesis. We may assume that $d^{c}(v)\ge 2$ for all $v\in V(K_{n})$. Let G be the weak representing subgraph of $K_{n}$. By (1.5), we have $|E(G)|\ge 2n-\left\lfloor \frac{3n-1}{2}\right\rfloor =\left\lceil \frac{n+1}{2}\right\rceil$, which implies there is a path $P_{3}=xyz$ in G. By the construction of G, if $e=uv\in E(G)$, the c(e) is starred at u and v. We consider the following two cases.

Case 1. $xz\notin E(G)$.

In this case, c(xz) is not starred at x or z, say x. Since $d^{c}(x)\ge 2$, there is a vertex $w\not \in \{ x, y, z\}$ such that c(xw) is starred at x. Then $c(xz), c(yw)\notin \{c(xy), c(yz), c(xw)\}$ and the edge set $\{xy, yz, xz, xw, yw\}$ induces a properly colored $K_{4}^{-}$.

Case 2. $xz\in E(G)$.

In this case, we can assume $c(ux)=c(uy)=c(uz)$ for all $u\in V(K_{n}){{\setminus }}\{x, y ,z\}$; otherwise we easily have a properly colored copy of $K_{4}^{-}$ in $K_{n}[x, y, z, u]$. Thus we have

$$\begin{aligned} |C(K_{n}-\{x,y\})|\ge \left\lfloor \frac{3n-1}{2}\right\rfloor -3=\left\lfloor \frac{3(n-2)-1}{2}\right\rfloor . \end{aligned}$$

If $n=5$, then $3=|E(K_{5}-\{x,y\})|\ge |C(K_{5}-\{x,y\})|\ge 4$, a contradiction. Thus we may assume that $n\ge 6$, there is a properly colored $K_{4}^{-}$ in $K_{n}-\{x, y\}$ by the induction hypothesis. $\square$

Now we prove the lower bound and upper bound of $\mathrm{pr}(K_{n}, K_{2,3})$. We conjecture that the exact value is closer to the lower bound.

Theorem 7

For $n\ge 5$, $\frac{7}{4}n+O(1)\le \mathrm{pr}(K_{n}, K_{2,3})\le 2n-1.$

Proof

The lower bound: Let $n=4k+r$, where $1\le r\le 4$. Set $V(K_n)=V_1\cup \cdots \cup V_k\cup V_{k+1}$ such that $V_i\cap V_j=\emptyset$ for $i\not =j$, $|V_i|=4$ for $1\le i\le k$ and $|V_{k+1}|=r$. We color the edges with end-vertices in the same set with $6k+\left( {\begin{array}{c}r\\ 2\end{array}}\right)$ distinct colors and color the remaining edges with k addition colors $c_{1}, c_{2}, \ldots , c_{k}$ such that all edges between $V_{i}$ and $V_{j}$ are colored with $c_{\min \{i, j\}}$, where $i\ne j$. The total number of colors is $\frac{7}{4}n+O(1)$ and there is no properly colored $K_{2,3}$.

The upper bound: We will prove that for any 2n edge-coloring of $K_{n}$, there is a properly colored $K_{2,3}$ by induction on n. The base case $n=5$ is trivial. For $n\ge 6$, assume that the conclusion holds for order less than n. Let c be a 2n-edge-coloring of $K_{n}$. If there is a vertex v such that $d^{c}(v)\le 2$, then $|C(K_{n}-v)|\ge 2n-2$ and there is a properly colored $K_{2,3}$ in $K_{n}-v$ by the induction hypothesis. We may assume that $d^{c}(v)\ge 3$ for all $v\in V(K_{n})$. Let G be the weak representing subgraph of $K_{n}$. By (1.5), we have $|E(G)|\ge 3n-2n=n.$ Note that for $n\ge 4, \mathrm{ex}(n, P_{4})\le n$ and the equality holds for the graph of disjoint copies of $C_{3}$ (see [5]). So we will consider the following two cases.

Case 1. G contains a $P_{4}=xyzw$.

If $G[V(P_{4})]\cong K_{4}$, then we can assume $c(ux)=c(uy)=c(uz)=c(uw)$ for all $u\in V(K_{n}){{\setminus }}\{x,y,z,w\};$ otherwise we easily have a properly colored copy of $K_{2,3}$. Therefore

$$\begin{aligned} |C(K_{n}-\{x, y, z\})|\ge 2n-6=2(n-3). \end{aligned}$$

If $n=6$, then $3=|E(K_{6}-\{x,y,z\})|\ge |C(K_{6}-\{x,y,z\})|\ge 6$, a contradiction. If $n=7$, then $6=|E(K_{6}-\{x,y,z\})|\ge |C(K_{6}-\{x,y,z\})|\ge 8$, a contradiction. Thus we may assume that $n\ge 8$, there is a properly colored $K_{2,3}$ in $K_{n}-\{x, y, z\}$ by the induction hypothesis.

Now we consider the case $G[V(P_{4})]\not \cong K_{4}$. Since $d^{c}(x)\ge 3$ and $d^{c}(w)\ge 3$, there is a vertex $u\in V(K_{n}){\setminus }\{x,y,z,w\}$ such that c(xu) or c(wu), say c(xu) is starred at x and $c(xu)\notin \{c(xy), c(xw)\}$. Therefore, the edges between $\{x,z\}$ and $\{y,u,w\}$ induce a properly colored $K_{2,3}$.

Case 2. G is the graph of disjoint copies of $C_{3}$.

Let $T_{1}=xyzx$ be a triangle of G. Since $d^{c}(x)\ge 3$, there is a vertex $u\in V(K_{n}){\setminus }\{x,y,z\}$ such that c(xu) is starred at x and $c(xu)\notin \{c(xy), c(xz)\}$. Suppose u belong to the triangle $T_{2}=uvwu$ of G. Therefore, the edges between $\{y,u\}$ and $\{x,z,v\}$ induce a properly colored $K_{2,3}$.

$\square$

6 Conclusion

In this paper, we obtain the relationship of $\mathrm{pr}(K_{n}, G)$ and $\mathrm{ex}(n, \mathcal {G'})$ by Theorem 2. We also determine the value of $\mathrm{pr}(K_{n}, G)$ for some small graphs. Since the lower bound of $\mathrm{pr}(K_{n}, C_{k})$ is very similar to the paths, we expect that the idea of the proof of Theorem 3 would be helpful to prove Conjecture 2 for large n.

Another interesting open problem is determining the behavior of $\mathrm{pr}(K_{n},K_{4}).$ Theorem 1 shows that $\mathrm{pr}(K_{n},K_{4})=o(n^{2})$ and Theorem 2 shows that $\mathrm{pr}(K_{n},K_{4})\ge \mathrm{ex}(n,C_{4})+1$. Since $\mathrm{ex}(n,C_{4})= \frac{1}{2}n^{3/2}+o(n^{3/2})$ (See [4, 6]), one can prove that $\mathrm{pr}(K_{n},K_{4})=O(n^{3/2})$. The main idea is that for an edge-coloring of $K_{n}$, if the weak representing subgraph contains a $C_{4}$, then there exists a properly colored $K_{4}$ in $K_{n}$.