Beyond graph neural networks with lifted relational neural networks

Abstract

We introduce a declarative differentiable programming framework, based on the language of Lifted Relational Neural Networks, where small parameterized logic programs are used to encode deep relational learning scenarios through the underlying symmetries. When presented with relational data, such as various forms of graphs, the logic program interpreter dynamically unfolds differentiable computation graphs to be used for the program parameter optimization by standard means. Following from the declarative, relational logic-based encoding, this results into a unified representation of a wide range of neural models in the form of compact and elegant learning programs, in contrast to the existing procedural approaches operating directly on the computational graph level. We illustrate how this idea can be used for a concise encoding of existing advanced neural architectures, with the main focus on Graph Neural Networks (GNNs). Importantly, using the framework, we also show how the contemporary GNN models can be easily extended towards higher expressiveness in various ways. In the experiments, we demonstrate correctness and computation efficiency through comparison against specialized GNN frameworks, while shedding some light on the learning performance of the existing GNN models.

1 Introduction

This paper concerns the problem of learning neural networks from relational representations. Although virtually all the standard models have been traditionally limited to data in the form of fixed-size tensors, there are also relational data, omnipresent in the interlinked structures of the Internet and relational databases, inducing machine learning tasks such as molecule toxicity modeling, social network analysis, knowledge-base completion, protein function prediction, and others. While learning from relational representations has been traditionally dominated by approaches rooted in relational logic (Muggleton and De Raedt 1994) and their probabilistic extensions (Kersting and De Raedt 2001; Richardson and Domingos 2006; De Raedt et al. 2007), the neural networks offer highly efficient latent representation learning, which is beyond capabilities of the symbolic systems. The neural models, on the other hand, have traditionally been limited to the fixed tensor representations, which cannot explicitly capture the unbounded, dynamic and irregular nature of the relational data. Consequently, there has been a continuous research in combining relational logic with neural networks to address learning from increasingly complex relational data (Uwents et al. 2011; Šourek et al. 2015; Kazemi and Poole 2018; Hohenecker and Lukasiewicz 2020) by exploiting the symmetries of the underlying domains (Kimmig et al. 2015).

Meanwhile, Graph Neural Networks (GNNs) (Scarselli et al. 2008) introduced an important paradigm shift by moving from fixed neural architectures to dynamically constructed computation graphs, directly following the structural bias and symmetries presented by the differently structured input data. As opposed to the approaches mapping all the samples into fixed-size tensors, this enabled to exploit the structural properties of the data more efficiently, as they are simply directly encoded into the very structure of the model itself, similarly to lifted graphical models (Kimmig et al. 2015). Consequently, these models recently achieved remarkable successes in a wide range of tasks (Zhou et al. 2018).

Currently, we are seeing an unprecedented expansion of the GNN model class, with hundreds of new GNN modifications being proposed under variety of names. However, similarly to some of the previous rapid topic growths in deep learning, this progress is so far mostly empirical, lacking a more grounded and unified view. Given the pace of the progress, it is then difficult to recognize the commonalities between the proposed models, leading to a lot of rediscoveries of the same ideas and architectures under different names.

In this paper, we offer one such unified view on the GNN model class from the perspective of the previous work on deep relational learning, concerned with combining relational logic with neural networks. There, in the same fashion of how graphs form a special case of relational logic models,¹ the GNNs can be seen as a special case of relational neural networks. As demonstrated throughout the paper, this view then offers a unified approach to a variety of existing GNN modelling constructs, as well as a very direct way to generalize them towards higher expressiveness, which is one of the core subjects of the contemporary GNN research.

1.1 Deep relational learning

It has been recently proposed by several authors that incorporating relational logic capabilities into neural networks is crucial to achieve more powerful AI systems (Marcus 2020; De Raedt et al. 2020; Lamb et al. 2020). Indeed, we see a rising interest in enriching deep learning models with certain facets of symbolic AI, ranging from logical entailment (Evans et al. 2018), rule learning (Evans and Grefenstette 2018), and solving combinatorial problems (Palm et al. 2018; Bengio et al. 2020; Prates et al. 2019; Cameron et al. 2020), to proposing differentiable versions of the whole Turing machine (Graves et al. 2014, 2016). However, similarly to the Turing-completeness of recurrent neural networks, the expressiveness of these advanced neural architectures is not easily translatable into actual learning performance, as their optimization tends to be often prohibitively difficult (Lipton et al. 2015).

There has also been a long stream of research in neural-symbolic integration (Bader and Hitzler 2005; Garcez et al. 2019), traditionally focused on emulating logic reasoning within static neural networks (Towell and Shavlik 1994; Smolensky 1990; Botta et al. 1997; Ding and Liya Ding 1995). The efforts eventually evolved from propositional (Towell and Shavlik 1994; Garcez and Zaverucha 1999) into full first order logic settings, mapping logic constructs and semantics into respective tensor spaces and optimization constraints (Serafini and d’Avila Garcez 2016; Dong et al. 2019; Marra et al. 2020).

While targeting integration of relational logic and deep learning, one of the core desired properties for an integrated system is to keep expressiveness of both the worlds as a special case. Although much focus has been traditionally devoted to keep the expressiveness of the logic reasoning, considerably less attention was put on the neural models themselves.² Consequently, modeling the existing modern advances in deep learning architectures, such as the GNNs, is out of scope of these integrated systems.³

1.1.1 Contributions

In contrast to the classic efforts of approximating complex relational logic reasoning within standard neural networks, in this paper we show how to use simple relational logic programs to capture advanced neural architectures -- in a tightly integrated and exact manner. Particularly, we use the language of Lifted Relational Neural Networks (LRNNs) (Šourek et al. 2018) and demonstrate that a wide range of neural models, ranging from simple MLPs and CNNs to complex contemporary GNNs, can be elegantly captured under the unified formalism of the LRNNs, directly exposing the underlying principles and symmetries of the models. Importantly, we present the unification not only from the theoretical perspective of (relational) model expressiveness, but directly from the practical point of view, as the relational logic-based encodings of the neural models’ principles are also directly runnable.⁴

The main focus of this paper is then on encoding of the GNN models. We show how to elegantly capture the core information propagation principles of GNNs with relational logic, extend it into some of the most complex GNN architectures and, importantly, beyond. We also directly compare against specialized GNN frameworks of PyTorch Geometric and Deep Graph Library. Additionally, we shed some more light on the generalization performance of some advanced state-of-the-art GNN models, as compared to basic GNNs, through measurements under a unified protocol over a large collection of datasets.

The paper is structured as follows. Firstly, we introduce the necessary preliminaries of logic and deep learning in Sect. 2. In Sect. 3, we introduce the language of LRNNs, which we use throughout the paper. Subsequently, we illustrate the LRNNs on a range of example models in Sect. 4. Capturing and extending GNNs is then detailed in Sect. 5. In Sect. 6, we demonstrate practicality and computation efficiency of the approach. We then discuss related works in Sect. 7 and conclude in Sect. 8.

2 Background

In this section we introduce the necessary preliminaries of relational logic (programming) and (graph) neural networks, which we seek to integrate towards a more unified view and generalization of the latter.

2.1 Logic

Mathematical logic is the core language of the symbolic AI approaches, and while there are also other representation formalisms for structured data, knowledge and processes (e.g. UML, ERM, SQL, RDF, etc.), specific to different application domains, mathematical logic still servers as the lingua franca for studying their expressiveness and relationships (Gallaire et al. 1989; Kuhlmann and Gogolla 2012). In this paper, we then target relational logic, which limits the classic first-order logic representation to contain no function symbols other than constants,⁵ however note that the relational logic formalism already covers the widest range of existing learning domains with structured data sources, such as the graphs, networks, knowledge-bases, and relational databases (Gallaire et al. 1989).

2.1.1 Syntax

Syntax specifies the structure, or grammar, of the logic language, which is formed from formulas. A relational logic theory is a set of such formulas. Formulas are formed from a set of constants, a set of variables, a set of n-ary predicates for $n\in {\mathbb {N}}$, and the propositional connectives $\vee$, $\wedge$ and $\lnot$ (Smullyan 1995). Constant symbols represent objects in the domain of interest (e.g. $\textit{hydrogen}_1$) and will be written in lower-case. Variables range over the objects in the domain and, to prevent confusion, will be written with a capitalized first letter (e.g. $\textit{X}$). Predicates represent relations among objects in the domain, or their attributes. A term is a constant or a variable. An atom⁶ is an n-ary predicate symbol, for some $n\in {\mathbb {N}}$, applied to a tuple of n terms (e.g. $\textit{bond}(X,\textit{hydrogen}_1)$). A ground atom, also called a proposition, is an atom which only has constants as arguments (e.g. $\textit{bond}(\textit{oxygen}_1,\textit{hydrogen}_1)$). A literal $\phi$ is an atom or negation of an atom. A clause $\alpha$ is a universally quantified disjunction of literals.⁷ A clause with exactly one positive literal is a definite clause. A definite clause with no negative literals (i.e. consisting of just one literal) is called a fact. A definite clause $h \vee \lnot b_1 \vee \dots \vee \lnot b_k$ can also be written as an implication $h \leftarrow b_1 \wedge \dots \wedge b_k$. The literal h is then called head and the conjunction $b_1 \wedge \dots \wedge b_k$ is called body. We will often call definite clauses, which are not facts, rules. A set of such rules is then commonly called a logic program.

2.1.2 Semantics

Semantics is an assignment of “meaning” to the, syntactically valid, logical sentences, which forms foundation for the logical entailment and model computation. The Herbrand base of a set of first-order formulas ${\mathcal {P}} = \{\alpha _1,\dots ,\alpha _m\}$ is the set of all ground atoms which can be constructed using the constants and predicates that appear in this set (while respecting the arity of each predicate). A Herbrand interpretation of ${\mathcal {P}}$, also called a possible world $\omega$, is a mapping that assigns a truth value to each element from ${\mathcal {P}}$’s Herbrand base. This can also be seen simply as a set of ground atoms (those which are true). We say that a possible world $\omega$ satisfies a ground atom a, written $\omega \models a$, if $a\in \omega$. The satisfaction relation is then generalized from ground atoms to arbitrary ground formulas through the standard interpretation of the $\vee$, $\wedge$ and $\lnot$ connectives (Smullyan 1995). A set of ground formulas is satisfiable if there exists at least one possible world in which all formulas from the set are true; such a possible world is called a Herbrand model. Each set of definite clauses has a unique Herbrand model that is minimal w.r.t. the subset relation $\subset$, called its least Herbrand model. The least Herbrand model of a finite set of ground definite clauses can be constructed in a finite number of steps using the immediate-consequence operator (Van Emden and Kowalski 1976). This immediate consequence operator is a mapping $T_p : {\mathcal {I}} \rightarrow {\mathcal {I}}$ from Herbrand interpretations to Herbrand interpretations, defined for a set of ground definite clauses ${\mathcal {P}}$ as $T_p(\omega ) = \{h \,|\, (h \leftarrow b_1 \wedge \dots \wedge b_k) \in {\mathcal {P}}, \{b_1,\ldots , b_k\} \subseteq \omega \}$.

Now consider a set of non-ground definite clauses ${\mathcal {P}}$. A substitution $\theta$ is a mapping from variables to terms. For a clause $\alpha$, we write $\alpha \theta$ for the clause $\{\phi \theta \,|\, \phi \in \alpha \}$, where $\phi \theta$ is obtained by replacing each occurrence in $\phi$ of a variable v by the corresponding term $\theta (v)$. A grounding substitution is then a substitution in which each variable is mapped to a constant. Clearly, if $\theta$ is a grounding substitution, then for any literal $\phi$ it holds that $\phi \theta$ is ground. The grounding of a clause $\alpha$ from ${\mathcal {P}}$ is the set of ground clauses $G(\alpha ) = \{\alpha \theta _1,\ldots ,\alpha \theta _n\}$ where $\theta _1,\ldots ,\theta _n$ is the set of all possible substitutions, each mapping the variables occurring in $\alpha$ to constants appearing in ${\mathcal {P}}$. Note that if $\alpha$ is already ground, its grounding is a singleton. The grounding of ${\mathcal {P}}$ is given by $G({\mathcal {P}}) = \bigcup _{\alpha \in {\mathcal {P}}} G(\alpha )$. The least Herbrand model of ${\mathcal {P}}$ is then defined as the least Herbrand model of $G({\mathcal {P}})$.

In practice, most of the rules in the grounding $G({\mathcal {P}})$ will be irrelevant, as their body can never be satisfied. The restricted grounding limits the grounding to those rules which are “active”, i.e. whose body is satisfied⁸ in the least Herbrand model ${\mathcal {H}}$. It is defined by $G^R({\mathcal {P}}) = \{h\theta \leftarrow b_1\theta \wedge \dots \wedge b_k\theta \,|\, (h \leftarrow b_1 \wedge \dots \wedge b_k) \in {\mathcal {P}} \text{ and } \{ h\theta , b_1\theta , \dots , b_k\theta \} \subseteq {\mathcal {H}} \}$.

2.2 Logic programming

Logic programming is a declarative programming paradigm for computation with logic programs ${\mathcal {P}} = \{\alpha _1,\dots ,\alpha _m\}$, which are used to encode data and knowledge about a given (relational) domain. Syntactically, the rules $h \leftarrow b_1 \wedge \dots \wedge b_k$ in the program ${\mathcal {P}}$ are commonly written as

where each comma “, ” stands for conjunction, and “:-” replaces the logical implication, which now reads right-to-left. Recall that facts are definite clauses consisting of a single atom, i.e. rules with no body. Note that such (ground) facts may be conveniently used to represent structured data, such as, but not limited to, various graphs.⁹

Example 1

For graph structured data, we can simply define a binary predicate edge/2 with a set of atoms edge(X, Y) for all adjacent nodes X, Y in the graph, while also retaining the orientation of each edge (given by the order of the terms). Additionally, we may also use other propositions to assign attributes to the nodes such as red(X) etc.¹⁰ An example of such encoding of graphs within logic is displayed in Fig. 1-left.

Fig. 1

An example of a graph structure encoded in relational logic (left), with two possible proof trees of the query path(d, a) derived from it (right)

The computation in logic programming is then generally carried out by the means of the logical entailment. This paradigm is particularly expressive with relational programs ${\mathcal {P}}$ containing (sets of) interconnected non-ground clauses, where the entailment needs to be resolved (recursively) by the means of substitution(s) (Sect. 2.1.2), enabling to compose general and reusable programming patterns to target structured data problems.

Example 2

Following up on the example with graph structured data (Example 1), we can, e.g., define (recursive) patterns in ${\mathcal {P}}$ such as

which then automatically binds to a (possibly) multitude of substructures in the graph(s) via different substitutions ${\mathcal {P}}\theta$ for the variables $\{X,Y,Z\}$ upon execution of ${\mathcal {P}}$ (Fig. 1).

Particularly, to target the assumed relational logic setting, we consider the language of Datalog (Unman 1989) -- a restricted function-free subset of Prolog (Bratko 2001). In contrast with Prolog, Datalog is a truly declarative language,¹¹ where the order of clauses and their literals does not influence execution, and it is also guaranteed to terminate. This allows for separation of the programs ${\mathcal {P}}$ from the underlying execution engine (Bancilhon et al. 1985), which leads to two different, albeit equivalent, semantics.

2.2.1 Model-theoretic semantics

Here, the semantics of a Datalog program ${\mathcal {P}}$ is defined by the means of its unique minimal model $\omega$. As outlined in Sect. 2.1.2, this minimal model can be constructed in a finite number of repeated applications of the immediate consequence operator $T_p$. The operator $T_p$ then expands the current set of true atoms, i.e. the current Herbrand interpretation ${\mathcal {I}}$, with their immediate consequences as prescribed by the rules in ${\mathcal {P}}$. It is initially applied to an empty interpretation ${\mathcal {I}}=\varnothing$, iteratively adding the head atoms of each ground rule instance $\alpha \theta$, the body of which is satisfied by the current interpretation ${\mathcal {I}}_i$ as

• 1: ${\mathcal {I}}_1$ = $T_p(\varnothing )$

• 2: ${\mathcal {I}}_2$ = $T_p(T_p(\varnothing ))$

• $\dots$

• n: ${\mathcal {I}}_n$ = $T_p^n(\varnothing )$

The minimal model ${\mathcal {I}}_n = \omega$ of ${\mathcal {P}}$ then corresponds to the least fixed-point n of $T_p$, where no more facts are being added to ${\mathcal {I}}_{i=n}$. For instance, following up on the Example 2 (Fig. 1), such ${\mathcal {I}}_{i=2}$ model will contain an atom path(., .) for all the paths in the graph (with length 1 and 2).

This simple bottom-up method is called “naive evaluation”, but with some additional optimizations it is actually being used in practice. Likewise, we follow this approach, with some optimizations, in the proposed framework (Sect. 3).

2.2.2 Proof-theoretic semantics

Similarly to querying a standard (non-deductive) database with SQL, in logic programming one may also provide a query atom q to drive the evaluation engine towards a logical proof of a specific target q. For instance, following up again on the Example 2, we can ask a query:

While this can be achieved by computing the minimal model $\omega$ of ${\mathcal {P}}$ in the bottom-up fashion (Sect. 2.2.1) and checking whether $q \subseteq \omega$, if all we need is to find any derivation of q from ${\mathcal {P}}$, that might be inefficient. Consequently, it is common to employ a top-down “proving” strategy, which starts at the query atom q, and searches through the rules in ${\mathcal {P}}$ for a rule $h \leftarrow b_1,\dots ,b_n$ for which there is some $\theta$ such that $h\theta =q$. This search then continues recursively for the (possible) body atoms $b_1\theta ,\dots ,b_n\theta$ of the rule that now need to be derived from ${\mathcal {P}}$. Ultimately, the atoms to be proved can be found directly as facts in ${\mathcal {P}}$, forming the leaves of the induced recursive proof-tree of q from ${\mathcal {P}}$, if successful. This procedure is visualized for the two possible derivations of path(d, a) in Fig. 1 - right.

This top-down, backward rule-chaining approach is then commonly used in Prolog and theorem provers.¹² We note that in the supervised learning setting, we do evaluate LRNN programs w.r.t. a target query atom. However, since the LRNN semantics¹³ requires evaluation of all possible derivations of each such query, we ultimately found it more efficient to employ (an optimized version of) the bottom-up approach from Sect. 2.2.1.

2.3 Deep learning

Deep learning is a machine learning approach commonly characterized by the use of multi-layered neural networks. Similarly to other (supervised) machine learning models, a neural network is a mapping $X \underset{\small {\mathcal {W}}}{\rightarrow } Y$ from the input sample space (attribute-value) representations X to the output target labels Y, parameterized by some ${\mathcal {W}}$. In the multi-layered networks, this mapping can be seen as a hierarchical composition of (nonlinear) activation functions which, following the pattern of the composition, can be conveniently represented as a computational graph.

A computational graph $\text {G}=({\mathcal {N}},{\mathcal {E}},{\mathcal {F}})$, composed of nodes ${\mathcal {N}}$, edges ${\mathcal {E}}$ and the activation functions ${\mathcal {F}}$, is a general way to represent nested mathematical functions using the language of graph theory. The graphs are directed with the information flowing from the children nodes to parent nodes, where the children of a node $N \in {\mathcal {N}}$ are naturally defined as all those nodes M such that $(M,N) \in {\mathcal {E}}$, and analogically for the parents. The neural networks are then commonly conveyed by the means of differentiable, parameterized, data-flow computation graphs $\text {G}=({\mathcal {N}},{\mathcal {E}},{\mathcal {F}},{\mathcal {W}})$, associated also with a set of learnable parameters ${\mathcal {W}}$, commonly called weights. Here, the data flowing through the directed edges $e \in {\mathcal {E}}$ are being successively transformed by the differentiable activation functions $f \in {\mathcal {F}}$ associated with the nodes $N \in {\mathcal {N}}$, commonly referred to as “neurons”. As discussed in the introduction, the data are then commonly restricted to the numeric vectors (or tensors) $\varvec{x}$. The term neural “layer” k is then used to refer to a set of neurons $\{N~|~\mathsf {depth}_\text {G}(\textit{N})= k\}$ residing at the same depth k in $\text {G}$.¹⁴ An input layer $k=0$ is then commonly used to represent the feature values $\varvec{x}$ of the input data samples $(\varvec{x}_i,\varvec{y}_i)$ themselves. An output layer $k=\mathsf {depth}(\text {G})$ then corresponds to the target values $\varvec{y}$. A “deep” neural network is a graph with multiple layers in between, i.e. with $\mathsf {depth}(\text {G})>3$.

By adapting the weights $w \in {\mathcal {W}}$, commonly associated with the edges ${\mathcal {E}} \rightarrow {\mathcal {W}}$, the model $X \underset{\small {\mathcal {W}}}{\rightarrow } Y$ can be trained to approximate some target function $t : X \rightarrow Y$, representing the original (deterministic) system S. This is done, as usual, via minimization of some given cost function $({\mathcal {W}};{\mathcal {D}}_{train}) \rightarrow {\mathbb {R}}$ capturing the discrepancy between the model and t over some set of training data samples $(x_i,t(x_i)) \in {\mathcal {D}}_{train}$. Owing to the differentiability of the used activation functions $f \in {\mathcal {F}}$, the parameters $w \in {\mathcal {W}}$ of a graph $\text {G}$ can be effectively adapted by gradient-descent routines, which is a distinguishing feature of all successful deep learning architectures.

Dynamic Computation Graphs: In standard neural models, the structure of the computation graph $\text {G}$ is static, and only the values $\varvec{x_i}=(x_i^1,\dots ,x_i^m)$ forming input to the leave nodes $\{N_1,\dots ,N_m\} \subset {\mathcal {N}}$ are used to encode particularities of individual learning samples $\varvec{x_i} \in {\mathcal {D}}$. These input nodes are then associated with identity functions $f^j(x_i)=x_i^j$. In contrast, many of the advanced relational neural models we assume in this paper are based on dynamic computation graphs, mapping each $x_i$ onto a new $\text {G}_i$ to exploit particular structural properties of each input sample. Consequently, the leave nodes in these dynamic $\text {G}_i$’s are associated with constant functions $f_i^j=x_i^j$, outputting the associated input sample values (if any). This enables to train neural models directly from structured data such as trees, graphs and databases.

2.3.1 Neural architectures

Due to the increasingly complex nature of the computation graphs $\text {G}$ and the operations ${\mathcal {F}}$ utilized in their nodes ${\mathcal {N}}$, the field has been recently also referred to as differentiable programming.¹⁵ The term neural architecture is then often used to refer to common programming patterns used in creation of these programs, reflected also in the structure of the underlying computation graphs. Each such pattern then reflects some common principle, stemming from the features of its typical application. Here, we briefly overview the main ideas behind some of the most common and successful neural architectures used in deep learning. Each of the outlined architectures is then later described in more detail together with its encoding as a differentiable LRNN program in Sect. 4.

Perhaps the most common design pattern is a fully-connected layer (Schmidhuber 2015). The main idea behind such a transformation is then in “representation learning” of the input data, often referred to as embedding, where one can think of outputs of the individual layers as transformed representations of the input, each extracting gradually more expressive information w.r.t. the output learning target.

Other very common patterns are the convolutional and pooling layers from Convolutional Neural Networks (CNNs) (LeCun et al. 1998). The main idea behind the convolution operation is exploitation of translation symmetries in the domain. This is done via application of the same parameterized filter over different sub-regions of the input, inducing equivariance w.r.t. the filter transformation. This enables to abstract away common patterns out of different sub-parts of the input representation. The main idea behind the pooling operation is then to further enforce invariance w.r.t. translation in the input.

Another successful pattern often used for problems with underlying sequential dynamics are layers from Recurrent Neural Networks (Schmidhuber 2015). These are designed to capture symmetries in sequential (time series) data. The main idea behind recurrent patterns is that the hidden representation can store a form of memory or state of the computation.

A generalization from sequential to regularly tree-structured data was then popularized with Recursive Neural Networks (Socher et al. 2013b). The important idea behind recursive networks is that neural learning can be extended towards structured data by generating a dynamic computation graph for each individual example. The design pattern then exploits the convolution (parameter sharing) principle to discover the underlying compositionality of the learning representations in recursive structures.

2.3.2 Graph neural networks

Graph Neural Networks (GNN) (Wu et al. 2020)¹⁶ can be seen as a further extension of the CNN principles to completely irregular graph structures $x_i = \{{\mathcal {N}}_i,{\mathcal {E}}_i\}$. For that purpose, they dynamically unfold each computational graph $\text {G}_i$ from each input structure $x_i$, similarly to the recursive networks. However, a GNN is a multi-layered feed-forward neural architecture, where the structure of each layer k exactly follows the structure of the whole input graph $x_i$. Every node $N_{x_i}$ in each input graph $x_i$ can now be associated with a feature vector (embedding), forming the input layer representation h in the computation graph $\text {G}_i$ as $h(N_{\text {G}_i})^{(0)} = features(N_{x_i})$.¹⁷

For computation of the next layer $k+1$ representations of the nodes in $\text {G}_i$, each node N calculates its own value h(N) by aggregating A (“pooling”) the values of the nodes $M : (N,M) \in {\mathcal {E}}_{i}$ adjacent in the input graph $x_i$ (“message passing”), transformed by some parametric function $C_{W_1}$ (“convolution”), which is being reused with the same parameterization $W_1^k$ within each layer k as:

$$\begin{aligned} {\tilde{h}}(N)^{(k)} = A^{(k)}(\{C^{(k)}_{W_1^k}(h(M)^{(k-1)}) | M : (N,M) \in {\mathcal {E}}_i \}) \end{aligned}$$

(1)

The ${\tilde{h}}^{(k)}(N)$ can be further combined through another $C_{W_2}$ with the central node’s N representation from the previous layer $k-1$ to obtain the final updated value $h^{(k)}(N)$ for layer k as:

$$\begin{aligned} h(N)^{(k)} = C_{W_2^k}^{(k)} (h(N)^{(k-1)}, {\tilde{h}}(N)^{(k)}) \end{aligned}$$

(2)

Note that in contrast to recursive networks, a different parameterization is typically used at each layer. This general “aggregate and combine” (Xu et al. 2018a) computation scheme covers a wide variety of the popular GNN models, which then reduces to the choice of particular aggregations A and transformations $C_{W}$. For instance in GraphSAGE (Hamilton et al. 2017), the operations are

$$\begin{aligned} {\tilde{h}}(N)^{(k)} = max \{ReLU(W \cdot h^{(k-1)}(M)) | M : (N,M) \in {\mathcal {E}}_i \} \end{aligned}$$

and

$$\begin{aligned} h(N)^{(k)} = W_f \cdot [(h(N)^{(k-1)}, act^{(k)}(N)] \end{aligned}$$

while in the popular Graph Convolutional Networks (Kipf and Welling 2017), these can be even merged into a single step as

$$\begin{aligned} h^{(k)}(N) = ReLU(W^k \cdot avg\{ h^{(k-1)}(M) | M : (N,M) \in {\mathcal {E}}_i \cup \{N\}\}) \end{aligned}$$

and the same generic principle applies to many other GNN works (Xu et al. 2018b; Gilmer et al. 2017; Xu et al. 2018a).

GNNs can be directly utilized for both graph-level as well as node-level classification tasks. For output prediction on the level of individual nodes, we simply apply some activation function on top of its last layer representation, e.g. $query(N) = \sigma (h(N)^{(d)})$. For predictions on the level of the whole graph $\text {G}$, all the node representations need to be aggregated by some pooling operation such as $query(\text {G}) = \sigma (avg\{h^{(d)}(N) | N \in \text {G}\})$.

By following the same pattern at each layer k, the computation will produce increasingly more aggregated representations, since at layer k each node N effectively aggregates representations from its “k-hops” neighborhood. Intuitively, the GNN inference can thus be seen as a continuous version of the popular Weisfeiler-Lehman algorithm (Weisfeiler and Lehman 1968) for calculating graph fingerprints used for refutation checking in graph isomorphism testing.

A large number of different variants of the original GNNs (Scarselli et al. 2008) have been proposed, recently achieving state-of-the-art empirical performance in many tasks (Wu et al. 2020; Zhou et al. 2018). In essence, each introduced GNN variant came up with a certain combination of common activation and aggregation functions, and/or proposed extending the architecture with additional connections (Xu et al. 2018b) or layers borrowed from other neural architectures (Veličković et al. 2017; Li et al. 2015), nevertheless they all share the same introduced idea of successive aggregation of node representations. For a general overview, we refer to Wu et al. (2020); Zhou et al. (2018).¹⁸

Knowledge Base Embeddings (KBEs) are a set of approaches designed for the task of knowledge base completion (KBC) (Kadlec et al. 2017), i.e. predicting existing (missing) edges in large knowledge graphs. Particularly, these methods approach the task through learning of a distributed representation (embedding) for the nodes. In multi-relational graphs, a representation of the edge (relation) can also be added, forming a commonly used triplet representation of (object, relation, subject). To predict the probability of a given edge in the knowledge graph, KBEs then choose one of a plethora of functions designed to combine¹⁹ the three embeddings from the underlying triplet (Kadlec et al. 2017).

3 The language of lifted relational neural networks

We follow up on the work of Lifted Relational Neural Networks (LRNNs) (Šourek et al. 2018) which have been introduced as a framework for templated modeling of diverse neural architectures (Sect. 2.3.1) oriented to relational data, based on the underlying symmetries. In this paper, we show that it can also be understood as a differentiable version of simple Datalog programming (Sect. 2.2), where the templates, encoding various neuro-relational learning architectures, take the form of parameterized Datalog programs. During learning, when presented with relational data, such as various forms of graphs, the program interpreter dynamically unfolds differentiable computational graphs to be used for the program parameter optimization by standard (gradient descent) means. This differs from the commonly used frameworks, such as PyTorch or Tensorflow, in the declarative, relational nature of the encoding, enabling one to abstract further away from the procedural details of the underlying computation graphs. In turn, this allows to reveal the common principles and symmetries of the neural models, simplifying their extensions and generalizations. We explain principles of this abstraction in the following subsections.

3.1 Syntax: weighted logic programs

The syntax of LRNNs is derived directly from the Datalog (Unman 1989) language (Sect. 2.2), which we further extend with numerical parameters. Note that this has been exploited in many previous works, where the parameters can signify values associated with facts (Bistarelli et al. 2008) or rules (Eisner and Filardo 2010). Such extensions are typically designed to integrate standard statistical (or probabilistic (De Raedt et al. 2007)) modelling techniques with the high expressiveness of relational representation and reasoning (Getoor and Taskar 2007).

In this work we seek to integrate Datalog with deep learning, for which we allow each literal in each clause of the logic program to be associated with a tensor weight. A parameterized program, formed by a multitude of such weighted rules, then declaratively encodes all computations to be performed in a given learning scenario. For clarity of correspondence with standard (neural) learning scenarios, we here further split²⁰ the program into unit clauses (facts), constituting the learning examples, and definite clauses (rules), constituting the learning template.

3.1.1 Learning examples

The learning examples contain factual description of a given world. For their representation we use weighted ground facts. A learning example is then a set ${E} = \{(V_1, e_1),\dots ,(V_m,e_m)\}$, where each $V_i$ is a real-valued tensor and each $e_i$ is a ground fact, i.e. expression of the form

where $p_1,\dots ,p_m$ are predicates with corresponding arities ${l_1},\dots ,{l_m}$, and $c_i^j$ are arbitrary constants. Note that the actual values, predicates, and constants at different indices may actually be the same (i.e. shared).

Standard logical representation is then a special case where each ${V_i} = 1$.²¹ One can either write 1::$carbon(c_1$) or omit the weight and write, e.g., $bond(c_1,o_2)$. The values do not have to be binary and can represent a “degree of truth” to which a certain fact holds, such as 0.4::$aromatic(c_1$). The values are also not necessarily restricted to (0, 1), and can thus naturally represent numerical features, such as 6::$atomicNumber(c_1)$ or 2.35::$ionEnergy(c_1,level_2$). Finally the values are not necessarily restricted to scalars, and can thus have the form of feature vectors (tensors), such as ${[1.0, -7, \dots , 3.14]}$::$features(c_1)$.

Ground facts in examples are also not restricted to unary predicates, and can thus describe not only properties of individual objects, but values of arbitrary relational properties. For example, one can assign feature values to edges in graphs, such as describing a bond between two atoms ${[2.7, -1]}$::$bond(c_1,o_2)$.

There is no syntactical restriction on how these representations can be mixed together, and one can thus select which parts of the data are better modelled with (sub-symbolic) distributed numerical representations, and which parts yield themselves to be represented by purely logical means, and move continuously along this dimension as needed.

Query: Queries (Sect. 2.2.2) represent the classification labels or regression targets associated with an example for supervised learning. They again utilize the same weighted fact representation such as 1::class or 4.7::$target(c_1)$. Note that the target queries again do not have to be unary, and one can thus use the same format for different tasks. For example, for knowledge-graph completion, we would use queries such as 1.0::coworker(alice, bob).

3.1.2 Learning template

The weighted logic programs written in LRNNs are then often referred to as templates. Syntactically, a learning template ${\mathcal {T}}$ is a set of weighted rules ${\mathcal {T}} = \{(\alpha _i, \{W^{i}_j\})\} = \{(W^i_0, h^i) \leftarrow (W_1^i, b_1^i), \dots , (W_k^i, b_k^i)\}$ where each $\alpha _i$ is a definite clause and each $W_j^i$ is some real-valued tensor, i.e. expressions of the form

where h$^i$’s and b$^i_j$’s are predicates forming positive literals, and ${W^i_j}$’s are the associated tensors. The treatment of constants within the literals is then the same as in the learning examples (Sect. 3.1.1), however note that there may also be logic variables in their place. Note also again that the actual predicates, constants, variables and weights can be commonly reused (shared) in different places in the template. Intuitively, the template constitutes roughly what neural architecture means in deep learning²² -- i.e. it does not (necessarily) encode a particular model or knowledge of the problem, but rather a generic mode of computation.

Example 3

Consider a simple template for learning with molecular data, encoding a generic idea that the (distributed) representation (h(.)) of a chemical atom (e.g. $o_1$) is dependent on the chemical atoms adjacent to it. Given that a molecule can be represented by the set of contained atoms (a(.))²³ and bonds (b(. , .)) between them (see left part of Fig. 2), we can encode this idea by the following rule

Moreover, one might be interested in using the representation of all atoms (h(X)) for deducing the representation of the whole molecule, for which we can write

to derive a single ground query atom (q), which can be associated with the learning target of the whole molecule. The concrete semantics of this template then follows in the next section.

3.2 Semantics: computational graphs defined by LRNNs

To explain the correspondence between a relational template ${\mathcal {T}}$ and a “neural architecture” (Sect. 2.3.1), we now describe the mapping that takes the template and a given example description and produces a standard neural model. Here, “standard neural model” refers to a specific differentiable computational graph (Section 2.3).

First, let ${\mathcal {N}}_l$ be the set of rules and facts obtained from the template and a learning example ${\mathcal {N}}_l = {\mathcal {T}} \cup E_l$ by removing all the tensor weights. For instance, if we had a weighted rule W::$h~{:-}~{W_1}$:$b_1 , {W_2}$:$b_2$ , we would obtain $h~{:-}~b_1, b_2$. Then we construct the least Herbrand model $\overline{{\mathcal {N}}_l}$ of ${\mathcal {N}}_{l}$ (Sect. 2.1.2), which can be done using separate, efficient grounding (theorem proving) techniques.²⁴

One option we employ is the bottom-up grounding strategy,²⁵ repeatedly applying the immediate consequence operator²⁶ (Sect. 2.2.1). We note that for the consequent neural learning, the target query atom q associated with $E_l$ must be logically entailed by ${\mathcal {N}}_{l}$, i.e. present in $\overline{{\mathcal {N}}_l}$.²⁷

Having the least Herbrand model $\overline{{\mathcal {N}}_l}$ containing q, we can construct a neural computational graph $G_l$. Intuitively, the structure of the graph contains all the logical derivations of the target query literal q from the example evidence ${E}_l$ through the template ${\mathcal {T}}$. Now, we formally define the transformation mapping from ${\mathcal {N}}_l$ to a computational graph:

• For each weighted ground fact $(V_i,e)$ occurring directly in ${E}_l$, there is a node $F_{(V_i,e)}$ in the computational graph, called a fact node.

• For each ground atom h occurring in $\overline{{\mathcal {N}}_l} \setminus {E}_l$, there is a node $A_{h}$ in the computational graph, called an atom node.

• For every rule $c \leftarrow b_1 \wedge \dots \wedge b_k \in {{\mathcal {T}}}$ and every grounding substitution $c\theta = h \in \overline{{\mathcal {N}}_l}$, there is a node $\textit{G}_{(c \leftarrow b_1 \wedge \dots \wedge b_k)}^{c\theta =h}$ in the computational graph, called an aggregation node.

• For every ground rule $\alpha _i\theta = (c\theta \leftarrow b_1\theta \wedge \dots \wedge b_k\theta )$ which is active in $\overline{{\mathcal {N}}_l}$, there is a node $R_{(c\theta \leftarrow b_1\theta \wedge \dots \wedge b_k\theta )}$ in the computational graph, called a rule node.

Table 1 Correspondence between the logical ground model and computational graph

An overview of the correspondence between the logical and the neural model, together with the used notation, is reviewed in Table 1.

The nodes of the computational graph that we defined above are then interconnected so as to follow the derivation of the logical facts by the immediate consequence operator starting from ${E}_l$, i.e. starting from the fact nodes $F_{(V_i,e)}$ which have no antecedent inputs in the computational graph and simply output their associated values as $out(F_{(V_i,e)}) = V_i$. The fact nodes are commonly used to represent information from the input examples or background knowledge.

The fact nodes are then connected into rule nodes $R_{\alpha \theta }$, particularly a node $F_{(V_i,e)}$ will be connected into every node $R_{\alpha \theta } = R_{(c\theta \leftarrow b_1\theta \wedge \dots \wedge b_k\theta )}$ where $e=b_i\theta$ for some i. We note that an efficient $\theta$-subsumption engine from (Kuželka and Železný 2008)²⁸ is used in the process of finding all such valid substitutions $R_{\alpha \theta }$ in $\overline{{\mathcal {N}}}$. Having all the inputs, corresponding to the body literals of the associated ground rule, connected, the rule node will output a value calculated as

$$\begin{aligned} out(R_{\alpha \theta }) = g_{\wedge }\big (W_1^{\alpha }\cdot out(F_{(V_1,b_1\theta )}),\dots , W_k^{\alpha }\cdot out(F_{(V_i,b_k\theta )})\big ). \end{aligned}$$

The rule node’s activation function $g_{\wedge }$ is up to user’s choice. For scalar inputs, it can be for example set to mimic conjunction from Lukasiewicz logic, as in our previous work (Šourek et al. 2018). However, one can also choose to ignore the fuzzy-logical interpretation and use completely distributed semantics and activations utilized commonly in deep learning. In this case, the computation follows the common (matrix) calculus by firstly aggregating the node’s input values into its activation value

$$\begin{aligned} \underset{(l \times 1)}{{act(R_{\alpha \theta })}} = \underset{(l \times n)}{W_1^\alpha } \cdot \underset{(n \times 1)}{{out(F_1)}} + \cdots + \underset{(l \times m)}{W_j^\alpha } \cdot \underset{(m \times 1)}{{out(F_k)}}, \end{aligned}$$

followed by an element-wise application of any differentiable function, such as logistic sigmoid

$$\begin{aligned} \underset{(l \times 1)}{{out(R_{\alpha \theta })}} = \sigma (\underset{(l \times 1)}{{act(R_{\alpha \theta })}}) = \sigma \big (act(R_{\alpha \theta })_1, \dots , act(R_{\alpha \theta })_l\big ). \end{aligned}$$

In general, the rule nodes are used to represent (conjunctive) patterns to be repeatedly matched in the input (or transformed) data while reusing the same parameterization, such as the convolutional filters in CNNs.²⁹

Fig. 2

A simple LRNN template with 2 rules described in Example 1. Upon receiving 2 example molecules, 2 neural computation graphs get created, as prescribed by the semantics (Sect. 3.2)

The rule nodes are then connected into aggregation nodes. Particularly, a rule node $R_{(c\theta \leftarrow b_1\theta \wedge \dots \wedge b_k\theta )}$ is connected into the aggregation node ${G}_{(c \leftarrow b_1 \wedge \dots \wedge b_k)}^{c\theta =h}$ that corresponds to the same ground head literal ${c\theta }$. Having all the inputs, corresponding to different grounding substitutions $\theta _i$ of the rule $c \leftarrow (b_1 \wedge \dots \wedge b_k)$ with the same ground head $h = c\theta _1 = \cdots = c\theta _q$, connected, the aggregation node will output the value

$$\begin{aligned} out(G_{\alpha }^c\theta =h) = g_*\big (out(R_{\alpha \theta _1}^{c\theta _1=h}),\dots ,out(R_{\alpha \theta _q}^{c\theta _q=h})\big ). \end{aligned}$$

where $g_*$ is some aggregation function, such as avg or max. The aggregation nodes effectively aggregate all the different ways by which a literal h can be derived from a single rule $\alpha$. The aggregation $g_*$ is then applied in each dimension of the input values as

$$\begin{aligned}\underset{l \times 1}{{out(G_{\alpha }^h)}} &= g_*(\underset{l \times 1}{out(R_1)}, \dots , \underset{l \times 1}{out(R_q)}) = \Big ( g_*\big (out(R_1)^1, \dots , out(R_q)^1\big ), \dots , \\&\quad \quad \dots , g_*\big (out(R_1)^l, \dots , out(R_q)^l\big ) \Big ). \end{aligned}$$

Note that since all the input values are derived from a single rule $\alpha$, their dimensionalities are necessarily the same. Intuitively, the aggregation nodes are used to aggregate values from the pattern matches of the underlying rule nodes, such as the pooling operation used in CNNs.$^{29}$

The aggregation nodes are then connected into atom nodes. In particular, an aggregation node $G_{\alpha }^h$ will be connected into the atom node $A_{h}$ that is associated with the same atom h. The inputs of the atom node represent all the possible rules $\alpha _i$ through which the same atom h can be derived. Having them all connected, $A_{h}$ will output the value

$$\begin{aligned} out(A_{h}) = g_{\vee }\big (W_1^c \cdot out(\textit{G}_{\alpha _1}^{h}), \dots , W_m^c \cdot out(\textit{G}_{\alpha _m}^{h})\big ). \end{aligned}$$

Apart from the choice of activation function $g_{\vee }$, the computation of the atom node’s output follows exactly the same scheme as for the rule nodes. However, the atom nodes are used to combine the aggregated values (pattern matches) from different rules (such as the combine operation in GNNs (Sect. 2.3.2)).

Finally, the atom nodes are connected into rule nodes in exactly the same fashion as fact nodes, i.e. $A_{h}$ will be connected into every $R_{(c\theta \leftarrow b_1\theta \wedge \dots \wedge b_k\theta )}$ where $h=b_i\theta$ for some i, and the whole process continues recursively. Note that only the restricted grounding (Sect. 2.1) of ${{\mathcal {N}}_l}$ is involved in the process, keeping the resulting models complete,³⁰ yet minimal in size. Note also that this process of transforming a learning example into a computational graph is performed only once, as the subsequent neural training can only change the values of the parameters but not the structure of the graphs.

Example 4

Let us follow up on the Example 1 by extending the described template with two example molecules of hydrogen and water. The template will then be used to dynamically unfold two computation graphs, one for each molecule, as depicted in Fig. 2. Note that the computational graphs have different structures, following from the different Herbrand models derived from each molecule’s facts, but share parameters in a scheme determined by the lifted structure of the joint template.

4 Examples of common neural architectures

We now demonstrate flexibility of the declarative LRNN paradigm, stemming from the abstraction power of Datalog, by encoding a variety of common neural architectures (Sect. 2.3.1) into very simple differentiable logic programs. For completeness, we start from simple neural models, where the advantages of templating are not so apparent, but continue to advanced deep learning architectures, where the expressiveness of relational templating stands out more clearly. Note that all the templates in this paper are actual programs that can be run and trained with the LRNN interpreter.

4.1 Feed-forward neural networks

A multi-layered perceptron (MLP) is the original and most common neural architecture. It encodes a directed feed-forward graph, where the interconnections between nodes in subsequent layers k and $k+1$ follow the “fully-connected” pattern where for all $N^k,N^{k+1} : (N^k,N^{k+1}) \in {\mathcal {E}}$, i.e. a complete bipartite graph. Moreover, each edge is associated with a unique weight as ${\mathcal {E}} \overset{\small 1:1}{\longrightarrow } {\mathcal {W}}$. Consequently, assuming the common vector form of the input data sample $\varvec{x}$ (features), the computational graph can be efficiently reduced to a linear series of full (dense) matrix $W_k^{k+1}$ multiplications, each followed by an element-wise application of a non-linear function $f^{k+1}$, such as the common logistic “sigmoid” ($\sigma$), hyperbolic tangent ($\tanh$) or rectified linear unit (ReLU).

Encoding: MLPs form the most simple case where the weighted logic template is restricted to propositional clauses, and its single Herbrand model thus directly corresponds to a single neural model (Sect. 3.2). In this setting, the input example information can thus be encoded merely in the values of their associated tensors, which is the standard (static) deep learning scenario. In the vector form, we can associate each example $E_i$ with a fact proposition ${[v_1^i,\dots ,v_n^i]}$::$features^{(0)}$, forming the input (0-th) node of the neural model. Each labeled example is further associated with a target query value ${v_q^i}$::q.

In particular, an MLP with 3 layers, i.e. input layer$^{(0)}$, 1 hidden layer$^{(1)}$, and output layer$^{(2)}$, with the corresponding weight matrices $[{\underset{m \times n}{W}^{(1)}}, {\underset{1 \times m}{W}^{(2)}}]$ can be directly modelled with the following rule

Naturally, we can extend it to a deeper MLP by stacking more rules as

Once the template gets transformed into the corresponding neural model (Sect. 3.2), its computational graph will consist of a linear chain of nodes corresponding to standard fully-connected layers $1,\dots ,k$ with associated weight matrices $[{W}^{(1)},{W}^{(2)}\dots ,{W}^{(k)}]$, and activation functions of the user’s choice. We note that it is also possible to specify the activation functions with each rule (layer) separately, e.g. as

Fig. 3

Demonstration of the pruning technique on a sample MLP model unfolded from a 2-rule template of $\alpha _1 = {W_1}{{:}{:}} h_1 {:-} f.$ and $\alpha _2 = {W_2}{{:}{:}} h_2 {:-} h_1$

Note also that not all the weights need to be specified, and one can thus also write, e.g., either of

While each of these rules still encodes in essence a 3-layer MLP, either only the hidden (right) or only the output (left) layer will carry learnable parameters, respectively. Moreover, following the exact semantics (Sect. 3.2) for neural model creation, an aggregation node will be created on top of a rule node, representing the hidden layer. Since there is no need for aggregation in MLPs, i.e. only a single rule node ever gets created from each propositional rule, this introduces unnecessary operations in the graph. Since such nodes arguably do not improve learning of the model, we prune them out, as depicted in Fig. 3. The technique is further described in more detail in the appendix Sect. A.1.1. Note that we assume application of pruning, where applicable, in the remaining examples described in this paper.

4.2 Convolutional neural networks

A Convolutional Neural Network (CNN) is also a feed-forward architecture, yet not fully connected as the MLP. The interconnection patterns in one or more sub-parts of its computation graph $\text {G}$ are characterized by utilizing the particular operations of “convolution” (filtering) and “pooling” (Sect. 2.3.1). Given a vector input $\varvec{x}$ of size n, the convolutional filter (kernel) will also be represented by a vector $\varvec{c}$ of some size $c < n$. Scalar products of the filter and all the c-length subsequences of the input vector $\varvec{x}$ are then successively calculated to produce $n-c+1$ scalar values. The resulting values are commonly referred to as “feature-maps”. The second operation is the pooling, which aggregates values from predefined spatial sub-regions of the input values (feature-maps) into a single output through application of some (non-parameterized) aggregation function, such as the commonly used mean (avg) or maximum (max). The layers of these operations can then be mixed together with the previously introduced layers from MLPs in various combinations.

Encoding: The CNNs can no longer be represented with a propositional template. To emulate the additional parts w.r.t. the MLPs, i.e. the convolutional filters and pooling (Section 2.3), we need to move to relational rules (Sect. 2.1). Note that there is a natural, close relationship between convolutions and relational rules (or relational patterns in general), where the point of both is to exploit symmetries in some form of equivariance in the data. Moreover, the point of both the aggregation nodes and the pooling layers is to further enforce invariance. Let us demonstrate this relationship with the following example.

For clarity of presentation, consider a simplistic one-dimensional “image” consisting of 5 pixels $i=1,\ldots ,5$. While the regular grid structure of the image pixels is inherently assumed in CNN, we will need to encode it explicitly. Considering the 1-dimensional case, it is enough to define a linear ordering of the pixels such as $next(1,2),\dots ,next(4,5)$. The (gray-scale) value $v_i$ of each pixel i can then be encoded by a corresponding weighted fact ${v_i}: f(i)$. Next we encode a convolution filter of size [1, 3], i.e. vector which combines the values of each three ([left,middle,right]) consecutive pixels, and a (max/avg)-pooling layer that aggregates all the resulting values. This computation can be encoded using the following template

Fig. 4

Left: core part of a standard CNN architecture with sparse layer composed of sequential applications of a convolutional filter (h), creating a feature-map layer, followed by a pooling operator. Right: the corresponding computation graph derived from a LRNN template

A visualization of the CNN and the corresponding computation graph derived from the logic model of the template presented with some example pixel values $[v_1,\dots ,v_5]$ is shown in Fig. 4. Note that we exclude the purely logical (boolean) atoms (next(., .)) from the computation graphs for clarity, as they simply correspond to constant-valued (fact) nodes, which do not contribute to the learning capacity of the model.³¹

While this does not seem like a convenient way to represent learning with CNNs from images, the important insight is that convolutions in neural networks correspond to weighted relational rules (patterns). The efficiency of normal CNN encoding is due to the inherent assumptions that are present in CNNs w.r.t. topology of their application domain, i.e. grids of pixel values, and similarly complete, ordered structures. While with LRNNs we need to state all these assumptions explicitly, it also means that we are not restricted to them -- an advantage which will become clearer in the subsequent sections.

4.3 Recursive and recurrent neural networks

4.3.1 Recursive networks

A Recursive Neural Network (RNN)³² is a neural architecture which differs significantly from the previous in that it is based on the dynamic computation graphs (Sect. 2.3), i.e. the exact form of the computation graph is not given in advance. Instead, the computation graph structure $\text {G}_i$ directly follows the structure of each input example $x_i$, which takes the form of a $k-$regular tree. This enables to learn neural networks directly from differently-structured regular tree examples $x_i$, as opposed to the fixed-size tensors $\varvec{x}$ (which can also be seen as graphs with completely regular grid topologies).

The leaf nodes $N_j^0$ in each input sample tree $x_i$ can be associated with feature vector values (embeddings) $\varvec{x_i^j}$. Every c leaf nodes ${x^j,\dots ,x^{j+c}}$ with the same parent node $N_j^1$ in the respective computation tree $\text {G}_i$ are consequently combined by a given $\varvec{c}$-parameterized operation $\mathsf {c}$, such as a $\varvec{c}$-weighted dot-product, to compute the representation of the parent $N_j^1$. This combining operation $\mathsf {c}$ then continues recursively for all the interior nodes, until the representation for the root node $N^{k=depth(\text {G}_i)}$ is computed, which forms the output of the model for $x_i$. Similarly to the convolution in CNNs, the parameterized combining operation $\mathsf {c}$ over the children nodes remains the same over the whole tree (Socher et al. 2013a).³³

Encoding:

The dynamically changing structure of the input examples prevents us from creating fixed computation schemes, such as in the CNNs. Instead, we need to resort to a general convolutional pattern that can be applied over any k-regular tree. For that purpose, we again utilize the expressiveness of relational logic. Firstly, we encode the k-regular tree structure itself by providing a fact connecting each parent node in the tree to its child-nodes, i.e. $parent(node^{i+1}_j,node^{i}_l,\dots ,node^{i}_{l+k})$. Secondly, we associate all the leaf nodes in the tree with their embedding vectors ${[v_1^i,\dots ,v_n^i]}:: n(\textit{leaf}_i)$. Finally, a single relational rule can then be used to encode the recursive composition of representations in the, for instance 3-regular, tree as

which directly forms the whole learning template. Given a particular example tree, this rule translates to a computation graph recursively combining the children node representations (n(C)) into respective parent node representations, until the root node is reached. The root node representation (n(root)) could then be, e.g., fed into a standard MLP rule (Sect. 4.1) to output the value for a given target query associated with the whole tree example.

Fig. 5

Simple recurrent (left) and recursive (right) neural structures encoded through LRNNs

4.3.2 Recurrent networks

The basic form of the commonly known Recurrent Neural Networks (Lipton et al. 2015) can then be seen as a “restriction” of the idea to sequential structures, i.e. linear chains of input nodes.³⁴ The computation graph $\text {G}$ in the form of a linear chain is then successively unfolded along the input sequence to compute the hidden representation for each node $N_i$ based on the previous node’s $N_{i-1}$ representation and the current node features $\varvec{x_i}$ (current input).

Encoding: A simple recurrent neural network unfolded over a linear (time) structure can then be modelled in a simpler manner, where only a single (vector) input is given at each step and a linear chain of hidden nodes (h(X)) replaces the prescribed tree hierarchy. Assuming encoding of the ordinal example structure with predicate next(X, Y) as before, such a model can then be written simply as

The final hidden representation (h(k)) could then again be fed into a MLP for a whole sequence-level prediction. Neural architectures of both these templated models are displayed in Fig. 5.

5 Graph neural networks in LRNNs

Graph Neural Networks (GNNs) (Sect. 2.3.2) can be seen as a generalization of the introduced neural architectures (Sect. 4) to arbitrary graphs, for which they combine the principles of latent representation learning (Sect. 4.1), convolution (Sect. 4.2), and dynamic model structure (Sect. 4.3).

While modelling CNNs in the weighted logic formalism was somewhat cumbersome (because we had to explicitly represent the pixel grid), the encoding of GNNs is very straightforward. This is due to the underlying general graph representation with no additional assumptions of its structure, which yields itself very naturally to relational logic. The computation of the layer i update in GNNs can then be represented by a single rule as follows

where edge/2 is the binary relation of the given input graphs. With the choice of activation functions as $g_* = avg, g_\wedge = ReLU$, this simple rule already models the popular Graph Convolutional Neural Networks (GCN) (Kipf and Welling 2017).³⁵ The exact same rule (up to parameterization) is then used at each layer. For the final output query (q) representing the whole graph we simply aggregate representations of all the nodes as

A noticeable shortcoming of GCNs is that the representation of the “central” node (V) itself is not used in the representation update. While this can be done by extending the graph (edge/2) with self-loops, a novel³⁶ GNN model called GraphSAGE (g-SAGE) (Hamilton et al. 2017) was proposed to address this explicitly. To follow the architecture of g-SAGE, we thus split the template into 2 rules accordingly

Fig. 6

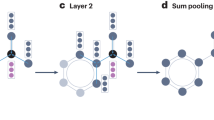
A computation graph of a sample (g-SAGE) GNN as encoded in LRNNs. Given an input graph of 4 (fact) nodes (F$_{n_1}\dots$F$_{n_4}$), neighbors of each node are firstly weighted and aggregated with rule and aggregation nodes, respectively (reduced in size in picture). The result is then combined with representation of the (central) node from the preceding layer, to form a new layer of 4 atom nodes, copying the structure of the input graph. After n such layers, each with the same structure but different parameters, a global readout (aggregation) node aggregates all the node representations, passing to the final query (atom) node’s transformation

and choose $g_\wedge = ReLU, g_* = max, g_\vee = identity$ for the very model (g-SAGE), the depiction of which can be seen in Fig. 6.

Another popular extension taken from neural architectures for image recognition are residual (skip) connections, where one effectively adds links to preceding layers at arbitrary depth (instead of just the preceding layer), i.e. we simply add one or more rules in the form

This technique is also used in the Graph Isomorphism Network (GIN) (Xu et al. 2018a), which is a theoretically substantiated GNN based on the expressive power of the Weisfeiler-Lehman test (WL) (Weisfeiler and Lehman 1968). Firstly, the GIN model differs in that it adds residual connections from all the preceding layers to the final layer (which the authors refer to as “jumping knowledge” (Xu et al. 2018b)). Secondly, the particularity of GIN is to add a 2-layered MLP on top of each aggregation to harvest its universal approximation power. Particularly, update formula derived from the WL-correspondence (Xu et al. 2018a) is

$$\begin{aligned} h^{(i)}(v) = MLP^{(i)}\big ((1+\epsilon ^{(i-1)}) \cdot h^{(i-1)}(v) + \sum _{u \in {\mathcal {N}}(v)} h^{(i-1)}(u)\big ) \end{aligned}$$

where MLP is the 2-layered MLP (Sect. 4.1). To accommodate the extra MLP layer, we thus extend the template as follows 

Note that, considering that such a single rule actually already models a 2-layer³⁷ MLP (as described in Sect. 4.1), a very similar computation can be carried out even simpler with

corresponding to a GIN version without the special ${(1+\epsilon ^{(i)})}$ coefficient, which the authors refer to as “GIN-0” (Xu et al. 2018a) and actually find performing better.³⁸ Finally they choose $g_*=sum$ as the function to aggregate the neighborhood representations. The authors proved the GIN model to belong to the most “powerful” class of GNN models, i.e. no other GNN model is more expressive than GIN, and demonstrated the GIN-0 model to provide state-of-the-art performance in various graph classification and completion tasks (Xu et al. 2018a).

5.1 Extending GNNs

While the GIN model presents the most “powerful” version of the basic GNN idea, there is a large number of ways in which the GNN approach can be extended. We discuss some of the direct, natural extensions in this subsection.

5.1.1 Edge representations

Originally aimed at single-relation graphs, GNNs do not adequately utilize the information about the possibly different types of edges. While it is straightforward to associate edges with scalar weights in the adjacency matrix, instead of using just binary edge indicators (Kipf and Welling 2017), extending to richer edge representations is not so direct, and has only been explored recently (Kipf et al. 2018; Gong and Cheng 2019; Kim et al. 2019).

In the templating approach, addressing edges is very simple, since we do not operate directly with the graph but with the ground logical model, where each edge ($edge(n_1,n_2)$) forms an atom in exactly the same way as the actual nodes ($node(n_1)$) in the graph itself (similarly to an extra transformation introduced in line-GNNs (Chen et al. 2017)). We can thus directly associate edges corresponding to different relations with arbitrary features (${[v_1,\dots ,v_n]}{{:}{:}}~edge(n_1,n_2)$), learn their distributed representations, and predict their properties (or existence), just like GNNs do with the nodes. For basic learning with edge representations, there is no need to change anything in the previously introduced templates. However, one might want to associate extra transformations for edge and node representation learning (Gong and Cheng 2019), in which case we would simply write

A large number of structured data then come in the form of multi-relational graphs, where the edges can take on different types. A straightforward extension is to learn a separate node representation of the nodes for each of the relations, e.g. as

and to choose from the different representations depending on context, such as in multi-sense word embeddings (Li and Jurafsky 2015), or simply directly combine (Schlichtkrull et al. 2018) these representations in the template.

5.1.2 Heterogeneous graphs

The majority of current GNNs assume homogeneous graphs, and learning from heterogeneous graphs has just been marked as one of the future directions for GNNs (Wu et al. 2020). In LRNNs, various heterogeneous graphs (Wang et al. 2019b) can be directly covered without any modification, since there is no restriction to the types of nodes and relations to be used in the same template (and so we do not have to e.g. split the graphs (Zhu et al. 2019) or perform any extra operation (Liu et al. 2018) for such a task). In the context of heterogeneous information networks, a similar “templating” idea has already become popular as defining “meta-paths” (Dong et al. 2017; Huang and Mamoulis 2017), which can be directly covered by a single LRNN rule and, importantly, differentiated through.

We can further represent the relations as actual objects to be operated by logical means, by reifying them into logical constants as

where variable E represents the edge object and h(E) is its hidden representation. The learned embeddings of the nodes and relations can then be directly used for predicting triplets of (Object,Relation,Subject) in KBC (Sect. 2.3.2), again with a simple template extension, e.g. for an MLP-based KBE (Dong et al. 2014), as

5.1.3 Hypergraphs

Naturally, the GNN idea can be extended to hypergraphs, too, as was recently also proposed (Feng et al. 2019). While extending to hypergraphs from the adjacency matrix form used for simple graphs can be somewhat cumbersome, in the relational Datalog, hypergraphs are first-class citizens, so we can just directly write

and possibly directly combine with all the other extensions.

There are many other simple ways in which GNNs can be extended towards higher expressiveness and there is a wide variety of emerging works in this area. While reaching beyond the standard, single adjacency matrix format, each of the novel extensions typically requires extra transformations (and libraries) to create their necessary intermediate representations (Chen et al. 2017; Dong et al. 2017). Many of these extensions are often deemed complex from the graph (GNN) point of view, but are rather trivial template modifications with LRNNs, as indicated in the preceding examples (and further in Sect. 5.2). This is due to the adopted declarative relational abstraction, as opposed to the procedural manipulations on ground graphs, defined often on a per-case basis.

5.2 Beyond GNN architectures

Previously, we discussed possible ways of direct extensions of GNNs. In this subsection, we introduce some more substantial generalizations that break beyond the core principles of current GNNs. Virtually all the GNNs are based on some form of the “message passing” idea (the WL label propagation (Weisfeiler and Lehman 1968)), where the nodes are restricted to “communicate” with neighbors through the existing edges. Obviously, there is no such restriction in LRNNs, and we can design templates for arbitrary information propagation schemes, corresponding to more complex and expressive convolutional filters, beyond the basic WL scheme. For instance, consider a simple extension beyond the immediate neighborhood aggregation by defining edges as weighted paths of length 2 (introduced as “soft edges” in Šourek et al. (2018)):

We can also easily compose the edges into small subgraph patterns of interest (also known as “graphlets” or “motifs” used in, e.g., social network analysis (Šourek et al. 2013)), such as triangles and other small cliques (alternatively conveniently representable by the hyper-edges (Sect. 5.1.3)), and operate on the level of these instead:

Since both nodes and edges can be treated uniformly as logic atoms, we can easily alter the GNN idea to hierarchically propagate latent representations of the edges, too. In other words, each edge can aggregate representations of “adjacent” edges from previous layers:

Naturally, this can be further combined with the standard learning of the latent node representations (as we do in experiments in Sect. 6).

Moreover, the messages do not have to spread homogeneously through the graph and a custom logic can drive the diffusion scheme. This can be, for instance, naturally put to work in the heterogeneous graph environments (Sect. 5.1.2) with explicit types, which can then be used to control communication and representation learning of the nodes:

Besides being able to represented the types explicitly as objects (as opposed to the vector embeddings), we can actually induce new types, for instance into latent hierarchical categories (such as in Šourek et al. 2016):

Importantly, there is no need to directly follow the input graph structure in each layer. We can completely abstract away from the graph representation in the subsequent layers and reason on the level of the newly invented, logically derived, entities, such as, e.g., the various graphlets, latent types, and their combinations:

Finally, the models can be directly extended with external relational background knowledge. Note that such knowledge can be specified declaratively, with the same expressiveness as the templates themselves, since they are consequently simply merged together, for instance³⁹:

Note that this is very different from the standard GNNs, where one can only input ground information in the form of numerical feature vectors along with the actual nodes (and possibly edges). Nevertheless this does not mean that LRNNs cannot work with numerical representations. On the contrary, besides the standard neural means, one can also directly interact with it by the logical means, e.g. by arithmetic predicates to define learnable numerical transformations (such as in Šourek et al. 2018) over some given (or learned) node similarities:

6 Experiments

The preceding examples were meant to demonstrate high expressiveness and encoding efficiency of the declarative LRNN templating. The main purpose of the experiments is to assess correctness and efficiency of the actual learning. For that purpose, we select GNNs as the most general and flexible of the commonly used neural architectures, since they encompass building blocks of all the other introduced architectures. Given the focus on GNNs, we compare against two most popular⁴⁰ GNN frameworks of Pytorch Geometric (PyG) (Fey and Lenssen 2019) and Deep Graph Library (DGL) (Wang et al. 2019a). Both these frameworks contain reference implementations of many popular GNN models, which makes them ideal for such a comparison. Note also that both these frameworks are highly contemporary and were specifically designed and optimized for creation and training of GNNs.

6.1 Datasets

For clarity of presentation, we restrict ourselves to the task of graph classification, but perform experiments across a large number of datasets to obtain statistically significant results. Particularly, we assembled a collection of 78 popular molecular datasets, ranging from small instances, such as the infamous Mutagenesis (Lodhi and Muggleton 2005), to medium-sized, such as the Predictive Toxicology Challenge (Helma et al. 2001), and large, particularly various datasets from the National Cancer Institute NCI (Milne et al. 1994).⁴¹ Note that these include popular datasets such as NCI1 (Xu et al. 2018a; Morris et al. 2019; Neumann et al. 2016) or NCI109 (Neumann et al. 2016; Niepert et al. 2016; Simonovsky and Komodakis 2017) that are commonly picked by GNN authors (but we also include the 70 others). The tasks with these are generally to recognize molecules w.r.t. their mutagenicity, toxicity or ability to inhibit growth of different types of tumors. On average, each of these datasets contains app. 3000 samples, each with app. 24 atoms and 51 bonds. Note we only use the basic (Mol2 (Tripos 2007)) types of atoms and bonds without extra chemical features.

While in this paper we only report experiments on the task of graph classification, we note that the LRNN framework is by no means limited to this setting, and can also be used for learning in all the standard settings,⁴² such as knowledge-base completion (link-prediction), too, as briefly explained in the appendix Sect. A.2.1.

6.2 Modern GNN frameworks

While popular deep learning frameworks such as TensorFlow or Pytorch provide ways for efficient acceleration of standard neural architectures such as MLPs and CNNs, implementing GNNs is more challenging due to the irregular, dynamic, and sparse structure of the input graph data. Nevertheless, following the success of vectorization of the classic neural architectures, both PyG and DGL adopt the standard (sparse) tensor representation of all the data to leverage vectorized operations upon these. This includes the graphs themselves, which are then represented by their sparse adjacency matrices $G_i^i$. Further, each node index i can be associated with a feature vector (${[f_1,\dots ,f_j]}_i$) through an additional matrix $F_i^j$ associated with each input graph.

Following the standard procedural differentiable programming paradigm, both frameworks then represent model computations explicitly through a predefined graph of tensor transformations applied directly to the input graph matrices, creating an updated feature tensor $F_i^{j^{(k)}}$ at each step k. The same tensor transformations are then applied to each input graph.

Both frameworks are then based on similar ideas of message passing between the nodes (neighborhood aggregation) and its respective acceleration through optimized sparse tensor operations and batching (gather-scatter). DGL then seems to support a wider range of operations (and backends), with high-level optimizations directed towards larger scale data and models (and a larger overhead), while PyG utilizes more efficient low-level optimizations stemming from its tighter integration with Pytorch.

6.3 Model and training correspondence

Firstly, note that the formal correctness of the GNN model encodings (Sect. 5) w.r.t. their mathematical definitions (Sect. 2.3.2) follows directly from the semantics of the LRNN compilation (Sect. 3.2) as detailed, for instance, in Examples 3 and 4 (Fig. 2).

Here, we further also empirically evaluate the actual learning correspondence between the GNN encodings in LRNNs and their reference implementations in PyG and DGL. For that, we select some of the most popular GNN models introduced in previous sections, particularly the original GCN (Kipf and Welling 2017), highly used GraphSAGE (g-SAGE) (Hamilton et al. 2017) and the “most powerful” GIN (Xu et al. 2018a) (particularly GIN-0). Each of the models comes with a slightly different aggregate-combine scheme and particular aggregation/activation functions (detailed in Sects. 2.3.2 and 5). Moreover, we keep original GCN and g-SAGE as 2-layered models, while we adopt 5-layers for GIN (as proposed by the authors).⁴³ We further use the same latent dimension $d=10$ for all the weights in all the models. Finally we set average-pooling operation, followed by a single linear layer, as the final graph-level readout for prediction in each of the models.

Fig. 7

Alignment of training errors of the 3 models (GCN, g-SAGE, GIN), as implemented in the 3 different frameworks (LRNNs, DGL, PyG), over first 5 (alphabetically) datasets

While the declarative templating takes a very different approach from the procedural GNN frameworks, for the specific case of GNN templates it is easy to align their computations, as they are mostly simple sequential applications of the (i) neighborhood aggregation, (ii) weighting, and (iii) non-linear activation, which can be covered altogether by a single rule (Sect. 5).⁴⁴

For the comparison, we use the same 10-fold crossvalidation splits for all the models. We further use Glorot initialization scheme (Glorot and Bengio 2010) where possible, and optimize using ADAM with a learning rate of $lr=1.5e^{-5}$ (betas and epsilon kept the usual defaults) against binary crossentropy over 2000 epochae. Note that some other works propose a more radical training scheme with $lr=0.01$ and exponential decay by 0.5 every 50 epochae (Xu et al. 2018a), however we find GNN training in this setting highly unstable,⁴⁵ and thus unsuitable for the alignment of the different implementations. We then display the actual training errors (as opposed to accuracy) as the most consistent evaluation metric for the alignment purpose in Fig. 7 over the first 5 datasets for demonstration.⁴⁶ Additionally, we report aggregated Mahalanobis⁴⁷ pair-wise distances (Nagino and Shozakai 2006) between the training errors of the respective frameworks and models calculated over all the datasets in Table 2.

Table 2 Average distances between the training errors of the respective models and frameworks over all the datasets

While it is very difficult to align the training perfectly due to the underlying stochasticity, we can see that the performances are tightly aligned within a margin of standard deviation calculated over the folds and datasets. The differences are generally highest for the most complex GIN model, which also exhibits most unstable performance over the folds. Importantly, the differences between LRNNs and the other frameworks is generally not greater than between PyG and DGL themselves, which both utilize the exact same PyTorch modules and operations.

6.4 Computing performance

The main aim of the declarative LRNN framework is quick prototyping of models aiming to integrate deep and relational learning capabilities, for which it generally provides more expressive constructs than that of GNNs (Sect. 5.2) and does not contain any specific optimizations for computation over graph data. Additionally, it introduces a startup model compilation overhead as the particular models are not specified directly by the user but rather automatically induced by the theorem prover. Moreover, it implements the neural training in a rather direct (but flexible) fashion of actual traversal over each network (such as in Dynet Neubig et al. 2017), and does so without batching, efficient tensor multiplication or GPU support.⁴⁸ Nevertheless, we show that the increased expressiveness still does not come at the cost of computation performance.

Table 3 Training times per epocha across the different models and frameworks. Additionally, the startup model creation time (theorem proving) overhead of LRNNs is displayed

We evaluate the training times of a GCN over 10 folds of a single dataset (containing app. 3000 molecules) over the different models. We set Pytorch as the DGL backend (to match PyG), and train on CPU⁴⁹ with a vanilla SGD (i.e. batch size=1) in all the frameworks. From the results in Table 3, we see that LRNNs surprisingly train significantly faster than PyG, which in turn runs significantly faster than DGL. While the performance edge of PyG over DGL generally agrees with Fey and Lenssen (2019),⁵⁰ the (app. 10x) edge of LRNN seems unexpected. It holds even accounting for the startup (theorem proving) overhead of LRNNs, required for creation of the logical and neural models from all the samples in each dataset first (giving PyG a head start of app. 10 epochae).

We account the superior performance of LRNNs to the rather sparse, irregular, small, dynamic graphs for which the common vectorization techniques, repeatedly transforming the tensors there and back, often create more overhead than speedup, making it more efficient to traverse the actual spatial graph representations (Neubig et al. 2017). Additionally, LRNNs are implemented in Java, removing the Python overhead, and contain some generic novel computation compression (Šourek et al. 2021) techniques (providing about 3x speedup for the GNN templates).

Note we also prevented the frameworks from batching over several graphs, which they do by embedding the adjacency matrices into a block-diagonal matrix. While (mini) batching has been shown to deteriorate model generalization (Masters and Luschi 2018; Wilson and Martinez 2003),⁵¹ it still remains the main source of speedup in deep learning frameworks (Keskar et al. 2016), and is a highlighted feature of PyG, too. We show the additional PyG speedup gained by batching on the GCN⁵³ model in Fig. 8. While batching truly boosts the PyG performance significantly, it still lacks behind the non-batched LRNNs.⁵⁴ For illustration, we additionally include an inflated version of the GCN model by a 10x increase of all the tensor dimensionalities. In this setting, we can finally observe a performance edge from mini-batching, due to vectorization and GPU,⁵⁵ over the non-batched LRNNs.⁵⁶

A Note on the Startup Overhead Recall that in the LRNNs workflow, the computation graphs are only created once for each of the learning samples during startup (Sect. 3.2). The subsequent training times are thus completely independent of reported the startup overhead stemming from the involved theorem proving (grounding) and neural network creation. An estimate of the total learning time can thus be obtained by $time_{startup} + 2000 \cdot time_{epocha}$, rendering the overhead practically negligible in all the reported experiments. Some further details on the theorem proving overhead can then be found in the appendix Sect. A.2.

Fig. 8

Improving the computing performance of PyG via mini-batching and model size blow-up. The actual GCN model ($10\times 10$ parameter matrices) and 10$\times$ inflated version ($100\times 100$ parameter matrices) as run on CPU and GPU. Compared to a non-batched (batch=1) LRNN run on CPU, denoted by the horizontal lines (corresponding to the first two columns from the left)

6.5 Model generalization

Finally we evaluate learning performances of the different models. We select the discussed GNN models of GCN, g-SAGE and GIN (we keep only the PyG implementation for clarity), and we further include some example relational templates (implemented in LRNNs) for demonstration. Particularly, we extend GIN with edge (bond) representations and associate all literals in all rules with learnable matrices (Sect. 5), denoted as “gin*”. In a second template we add a layer of graphlets (motifs) of size 3, aggregating jointly representations of three neighboring nodes, on top of GIN, denoted as “graphlets”. Lastly, we introduce latent bond learning (Sect. 5.2) into GIN, where bond (edge) representations are also aggregated into latent hierarchies, denoted as “latent_bonds”. Note that we restrict these new relational templates to the same tensor dimensionalities and number of layers as GIN. For statistical soundness, we increase the number of datasets to the first 10 (alphabetically). We run all the models on the same 10-fold crossvalidation splits with a 80:10:10 (train:val:test) ratio, and keep the same, previously reported, training hyperparameters. We display the aggregated training errors in Fig. 9, and the cross-validated test errors, corresponding to the best validation errors in each split, in Fig. 10.

Fig. 9

Comparison of train accuracies of selected models across 10 datasets

Fig. 10

Comparison of test accuracies of selected models across 10 datasets

We can observe that the training performance follows intuition about capacity of each model, where the more complex models generally dominate the simpler ones. However, the increased capacity does not seem to consistently translate to better test performance (contrary to the intuition stated in Xu et al. 2018a). While we could certainly pick a subset of datasets to support the same hypothesis on test sets, we can generally see that none of the models actually performs consistently better than another, and even the simplest models (e.g. GCN) often outperform the “powerful” ones (GIN and its modifications), and the test performances are thus generally inconclusive.⁵⁷ While this is in contrast with the self-reported results accompanying the diverse GNN proposals on similar-sized graph datasets, it is in agreement with another (much larger) recent benchmark (Dwivedi et al. 2020).

Additionally, we include results of an old LRNN template reported in Šourek et al. (2015), denoted as “lrnn(2015)”. It was based on small graphlets of size 3, similarly to the “graphlets” template (and similarly to some other recent works (Tu et al. 2019; Sankar et al. 2017)), however it only contained a single layer of learnable parameters for the atom and bond representations. Note that we use results from the original paper (Šourek et al. 2015) experiments, which were run with different hyperparameters and splits. Nevertheless, we can see that it is again generally on par with performance of the more recent, deeper, and bigger GNN models.

7 Related works

This work can actually be seen as a simple extension of the Lifted Relational Neural Networks (Šourek et al. 2015) language by increasing the amount of (tensor) parameterization. In turn LRNNs were inspired by lifted graphical models (Kimmig et al. 2015) such as Bayesian Logic Programs (Kersting and De Raedt 2001) or Markov Logic Networks (Richardson and Domingos 2006), working in a probabilistic setting. From another viewpoint, LRNNs can also be seen roughly as a lifting of the old Knowledge-Based Neural Networks (Towell and Shavlik 1994) idea into the relational setting. The most closely related works naturally comprise of other differentiable programming languages with relational expressiveness (De Raedt et al. 2020).⁵⁸

There is a number of works targeting similar abilities by extending logic programming with numerical parameters. The most prominent framework in this category is the language of Problog (De Raedt et al. 2007), where the parameters and values further posses probabilistic interpretation. The extension of Deep-Problog (Manhaeve et al. 2018) then incorporates “neural predicates” into Problog programs. Since probabilistic logic programs can be differentiated (Fadja et al. 2017) and trained as such, the gradients can be passed from the logic program to the neural modules and trained jointly. While this is somewhat similar to LRNNs, Deep-Problog introduces a clear separation line between the neural and logical parts of the program, which communicate merely through the gradient values (and so any gradient-based learner could be used instead). The logical part with relational expressiveness is thus completely oblivious of structure of the gradient-ingesting learner and vice versa, and it is thus impossible to model complex convolutional patterns (i.e. relational patterns in the neural part) as demonstrated in this paper. On the other hand LRNNs do not have probabilistic interpretation, which is elegantly incorporated in Deep-Problog. Related is also a recent extension of kProblog (Orsini et al. 2017), proposing integration of algebraic expressions into logic programs towards more general tensor-algebraic and ML algorithms.

Neural Theorem Provers (NTPs) (Rocktäschel and Riedel 2017) share very similar idea by the use of a relational logic template with a theorem prover to derive ground computation graphs, which are differentiable under certain semantics inspired by fuzzy logic. The use of parameterization differs between the frameworks, where NTPs are focused on learning embeddings of constants and LRNNs on embeddings of whole relational constructs.⁵⁹ Nevertheless NTPs represent all constants as embedding vectors, for which the theorem prover cannot perform standard unification, and NTPs thus resort to “soft-unification”. While nicely relaxing classic unification,⁶⁰ this leads to effectively trying all possible constant combinations in the inference process, preventing from using NTPs for explicit modelling of the exemplified convolutional neural architectures. Also, it severely limits NTP’s scalability, where the latter has been partially addressed by some recent NTP extensions (Minervini et al. 2018; Weber et al. 2019). LRNNs are more flexible in this sense as one can use the parameterization to specify which parts of the program keep the logical structure and which parts should succumb themselves to the exhaustive numerical optimization (and to combine them arbitrarily), enabling to find a more fine-grained neural-symbolic trade-off.

Another line of work is focused on inducing Datalog programs with the help of numerical relaxation. While such a task has traditionally been addressed by the means of Inductive Logic Programming (ILP) (Muggleton and De Raedt 1994), extending the rules with weights can help to relax the combinatorial search into a gradient descent optimization, while providing robustness to noise. An example of such an approach is $\delta$ILP (Evans and Grefenstette 2018). Similarly to LRNNs, Datalog programs are unfolded by chaining the rules, where the associated parameters are trained against given target to be solved by the program. The parameterization in these approaches is used differently as its purpose is to determine the right structure of the template. This is typically done by exhaustive enumeration from some restricted set of possible literal combinations (particularly 2 literals with arity at most 2 and no constants for $\delta$ILP), where each combination is then associated with a weight to determine its appropriateness for the program via gradient descent. The differentiability is again based on replacing the logical connectives with fuzzy logic operators (particularly product t-norm). Similarly, programs in a restricted subset of Datalog are learned in a system called TensorLog (Cohen 2016; Yang et al. 2017), which is a differentiable probabilistic database based on belief propagation (limited to tree-like factor graphs). Another recently proposed related system is called Difflog (Raghothaman et al. 2019), where the candidate rules are also exhaustively generated w.r.t. a more narrow language bias, thanks to which it seem to scale beyond previous systems. While we explicitly address only parameter learning in this paper, we note that structure learning of the LRNN programs can also be done (Šourek et al. 2017).

Other class of approaches targets full first order logic by providing mapping of all the logical constructs into numerical (tensor) spaces (“tensorization” Garcez et al. 2019). For instance, one can cast constants to vectors, functions terms to vector functions of the corresponding dimensionality, and similarly predicates to tensors of the corresponding arity-dimension (Rocktäschel et al. 2015; Diligenti et al. 2017). Again adopting a fuzzy logic interpretation of the logical connectives, the learning problem can then be cast as a constrained numerical optimization problem, including works such as Logic Tensor Networks (Serafini and d’Avila Garcez 2016) or LYRICS (Marra et al. 2019). While the distributed representation of the logical constructs is the subject of learning, in contrast with the discussed Datalog program structure learning approaches, the weight (strength) of each rule needs to be specified apriori -- a limitation which was recently addressed in Marra et al. (2020). Other recent works based on the idea of fully dissolving the logic into tensors, moving even further from the logical interpretation, include e.g. Neural Logic Machines (Dong et al. 2019). While these frameworks are theoretically more expressive than LRNNs (lacking the function terms and non-definite clauses), the whole logic interpretation is only approximate and completely dissolved in the tensor weights in these frameworks. Consequently, they lack the capability of precise relational logic inference chaining, based on the underlying theorem prover, which we use to explicitly model the advanced convolutional neural structures, such as GNNs, in this paper.

Alternatively, LRNNs can be seen as a (significant) extension of the GNNs, as discussed throughout this paper. From the graph-level perspective, the most similar idea to the introduced relational templating has become popular in the knowledge discovery community as “meta-paths” (Dong et al. 2017; Huang and Mamoulis 2017) defined on the schema-level of a heterogeneous information network. A meta-path is simply a sequence of types, the concrete instantiations of which are then searched for in the ground graphs. Such ground sequences can then be used to define node similarities (Sun et al. 2011; Shang et al. 2016), random walks (Dong et al. 2017) as well as node embeddings (Shi et al. 2018; Fu et al. 2017). An extension from paths to small DAGs was then proposed as “meta-graph” (or “meta-structure”) (Huang et al. 2016; Sun et al. 2018). We note that any meta-path or meta-graph can be understood as conjunctive a rule in a LRNN template. Naturally, we can stack multiple meta-graphs to create deep hierarchies and, importantly, differentiate them through to jointly learn all the parameters, and provide further extensions towards relational expressiveness, as exemplified in this paper.

8 Conclusions

We introduced a differentiable declarative programming approach to specification of advanced deep (relational) learning architectures, based on the language of Lifted Relational Neural Networks (LRNNs) (Šourek et al. 2018). We demonstrated how simple parameterized logic programs, also called templates, can be efficiently used for declaration and training of complex convolutional models, with a particular focus on Graph Neural Networks (GNNs). In contrast with the commonly used procedural (Python) frameworks, LRNNs abstract away the creation of the computational graphs, which are dynamically unfolded from the template by an underlying theorem prover. As a result, creating a diverse class of complex neural architectures reduces to rather trivial modifications of the templates, distilling only the very principles and symmetries of each architecture. We illustrated versatility of the approach on a number of examples, ranging gradually from simple neural models to complex GNNs, including very recent GNN models and their extensions. Finally we showed how the existing models can be easily generalized to even higher relational expressiveness.

In the experiments, we then demonstrated correctness and computation efficiency by the means of comparison against modern deep learning frameworks. We showed that while LRNNs are designed with the main focus on expressiveness, flexibility and abstraction, they do not suffer from computation inefficiencies for the simpler (GNN) models, as one might expect. On the contrary, we demonstrated that for a range of existing GNN models and their practical parameterizations, LRNNs actually outperform the existing frameworks optimized specifically for GNNs.

While there is a number of related works targeting the integration of deep and relational learning, to our best knowledge, capturing advanced convolutional neural architectures in an exact manner, as exemplified in this paper, would not be possible with these. The proposed relational upgrades can then be understood as proper extensions of the existing, arguably popular, GNN models.

Additional, we showed that the generalization performance of the various state-of-the-art GNN models is somewhat peculiar, as they actually performed with rather insignificant test error improvements, when measured uniformly over a large set of medium-sized, molecular structure-property prediction datasets, which is in agreement with another recent benchmark (Dwivedi et al. 2020).

Appendix

1.1 Technical differences from LRNNs (Šourek et al. 2018)

The framework introduced in this paper closely follows the original LRNNs (Šourek et al. 2018). In fact, the main semantic difference is “merely” in the parameterization of the rules, where one can now include the weights within the bodies (conjunctions), too, e.g.

$$\begin{aligned} w^{(2)}_1 {:}{:} {neuron^{(2)}_1(X)} \leftarrow w^{(1)}_1 \cdot neuron^{(0)}_1(X) \wedge w^{(1)}_2 \cdot neuron^{(0)}_2(X) \end{aligned}$$

We note that this could be in essence emulated in the original LRNNs through the use of auxiliary predicates, such as in Šourek et al. (2018), as follows

$$\begin{aligned} w^{(2)}_1&{:}{:} {neuron^{(2)}_1(X)} \leftarrow ~~ neuron^{(1)}_1(X) \wedge neuron^{(1)}_2(X)&\\ w^{(1)}_1&{:}{:} {neuron^{(1)}_1(X)} \leftarrow ~~ neuron^{(0)}_1(X)&\\ w^{(1)}_2&{:}{:} {neuron^{(1)}_2(X)} \leftarrow ~~ neuron^{(0)}_2(X)&\end{aligned}$$

which might be more appropriate in scenarios where the neurons correspond to actual logical concepts under fuzzy logic semantics,⁶¹ while the second representation is arguably more suitable to exploit the correspondence with standard deep learning architectures.

Another difference is that we now also allow tensor weights and values. While these could be modeled in LRNNs, too, for instance in the “soft-clustering” (embedding) construct (Šourek et al. 2015) used for atom representation learning:

$$\begin{aligned} w_{o_1}&{:}{:} \textit{gr}_1(X) \leftarrow {O}(X)&\ldots&w_{h_1}&{:}{:} \textit{gr}_1(X) \leftarrow {H}(X)\\ w_{o_2}&{:}{:} \textit{gr}_2(X) \leftarrow {O}(X)&\ldots&w_{h_2}&{:}{:} \textit{gr}_2(X) \leftarrow {H}(X) \end{aligned}$$

the explicit tensor-valued weights offer an arguably more elegant representation of the same construct:

$$\begin{aligned} {[w_{o_1},w_{o_2}]}~{:}{:}{} \textit{gr}(X)~~~{:-}~~~{O}(X)&\quad \quad ~~~\ldots&{[w_{h_1},w_{h_2}]}{:}{:}~\textit{gr}(X)~~~{:-}~~~{H}(X)\\ \end{aligned}$$

In general, with the new representation we can merge scalar weights of individual neurons into tensors used by the nodes (prev. referred to as “neurons”) in the computation graph. Note that we can process any ground LRNN network into this form, i.e. turn individual neurons into matrix layers, in a similar manner, as outlined in Algorithm 1.

Being heavily utilized in deep learning, such transformation can significantly speed up the training of the networks. However by reducing the number of rules, effectively merging together semantically equivalent rules which do not differ up to their (scalar) parameterization, we can also alleviate much of the complexity during model creation, i.e. calculation of the least Herbrand model, by avoiding repeated calculations. This results in a significant speedup during the model creation process.

1.1.1 Network pruning

Following the computational graph creation procedure from Sect. 3.2, we might end up with unnecessary trivial neural transformations through auxiliary predicates in cases, where the original rules have only a single literal in body and are unweighted. For mitigation, we can apply a straightforward procedure for detection and removal of linear chains of these trivial operations, as described in Algorithm 2. While such an operation arguably changes the inference and logical semantics of the original model, these structures do not contribute to learning capacity of the model and, on the contrary, cause gradient diminishing. This technique is thus particularly suited for improving training performance in correspondence with standard deep learning architectures. While this form of pruning can be theoretically performed directly in the template, it is easier to do as a post-processing step in the resulting neural networks.

Finally, the new LRNN framework (called “NeuraLogic”) presents a completely new implementation⁶² of the idea, with the whole functionality build from scratch, while aiming at flexibility and modularity.

1.2 A note on the theorem proving complexity

Naturally, the performance of the theorem prover (grounder) depends heavily on the complexity of the template, and can theoretically lead to excessively large models. Nevertheless, for LRNNs we only need to construct the least Herbrand model, which is typically small for the real-world (sparse) templates, such as in the GNN computation schemes (Sect. 5). Also, excessively large models would be translated into computation graphs too large to be trainable in practice, anyway. Consequently, the overhead of the theorem prover (grounder) is commonly negligible w.r.t. the overall learning time for practical neural model classes.

1.2.1 Learning with large knowledge graphs

Note that the same also applies for large input graphs, such as knowledge-bases, which can be learned from with LRNNs, too (as shown, e.g., in Šourek et al. 2016). The only difference in this learning setting is that there is but a single (large) input graph, instead of many small graphs, with a number of corresponding queries, instead of a single query per each input graph used in the graph classification setting (Sect. 3.1.1).

While the framework is again not explicitly optimized for this task, the computation performance is still decent. For instance, the grounding and network creation overhead of (multi-relational) GNN models combining 1 layer of GNN with KBE (reported in Šourek et al. 2021 ⁶³) on the knowledge-base completion datasets of Nations, Kinships and UMLS (Kok and Domingos 2007) takes 1s, 8s and 22s, corresponding to Herbrand models with app. 14314, 281552, and 845511 atoms, translated into 11681, 42196, and 27506 neurons, leading to train epocha times of app. 1.2s, 0.440s, and 0.660s, respectively.