1 Introduction

In the last few decades, robots have been used in operating rooms to assist surgeons in performing minimally invasive surgery, improving the precision of surgeons and the recovery time of patients (Mack 2001; Vidovszky et al. 2006). At present, surgeons use a console to tele-operate patient-side manipulators. One long-term goal of research in surgical robotics is the development of robot systems capable of executing a surgical operation, or at least a part of it, with minimal supervision of a human expert (Camarillo et al. 2004; Moustris et al. 2011). Such robot systems can boost safety, optimize resource usage, and reduce patient recovery time, surgeon fatigue, and hospital costs (Yang et al. 2017). The complexity of surgical scenarios makes it difficult to encode comprehensive domain knowledge or provide many labeled training examples. Hence, autonomy requires the robot to reason with incomplete commonsense domain knowledge, and adapt automatically to variations in the surgical scenario and individual patients. In Ginesi et al. (2020) we proposed a framework for surgical task execution that integrated logic-based reasoning about task-level actions with adaptive motion planning and control. This task-level reasoning was based on Answer Set Programming (ASP), a non-monotonic logic programming paradigm (Gebser et al. 2012). Logic programming can encode high-level specifications and constraints extracted from expert knowledge on the behavior of the robot system, in order to provide reliable operation in dynamic domains. Moreover, the non-monotonic logical reasoning capability of ASP, i.e., the ability to retract previously held beliefs, is important in robotics applications. A key limitation of our prior framework was that it assumed comprehensive knowledge of the task and domain in terms of domain attributes (e.g., object properties) and axioms governing domain dynamics (e.g., constraints, and action preconditions and effects). This is not feasible in practical robotics domains, especially in surgical scenarios that are characterized by high variability in the patient’s anatomy.

In this paper, we focus on the problem of learning previously unknown task-level knowledge from a small number of example executions of a benchmark surgical training task, the ring transfer task, executed with the Vinci\(^{\circledR }\) robot from Intuitive Surgical. We build on our recent proof of concept exploration of the use of inductive logic programming (ILP) to learn previously unknown axioms governing domain dynamics in answer set semantics (Meli et al. 2020). In that work, learned axioms represented action preconditions and executability constraints, and learning was based on four example executions. In this paper, we significantly extend this idea to consider temporal relations between domain attributes, learning previously unknown axioms representing the delayed effects of actions. To do so, we reformulate the axioms in Ginesi et al. (2020) using the principles of event calculus, a state of the art temporal logic formalism to represent a system’s reaction to events (Kakas and Michael 1995; Kowalski and Sergot 1989). This integration of ILP and event calculus supports fast learning with standard hardware resources.

The remainder of this paper is organized as follows. Section 2 reviews the state of the art in surgical process modeling and learning of domain knowledge. Next, Sect. 3 describes the ring transfer task and its original hand-written ASP encoding, introducing the new event calculus formalism for the effects of actions. Section 4 formalizes the ILP task under the answer-set semantics. Section 5 presents the results of evaluating our approach for learning axioms in simulated scenarios requiring coordination of different action sequences. Finally, Sect. 6 describes the conclusions and future research directions.

2 Related work

Building a surgical process model (SPM) requires the designer to choose the level of granularity at which the task is to be analyzed. We use the definition of granularity (for surgical processes) provided in Lalys and Jannin (2014) and shown in Fig. 1. Learning an SPM for tasks involving motion is challenging since surgical gestures present high variability (Neumuth et al. 2006). Hence, statistical methods such as Markov models (Loukas and Georgiou 2013; Tao et al. 2012; Lalys and Jannin 2014) are typically used to infer a motion-level SPM.

Fig. 1
figure 1

Standard granularity levels of surgical processes, as described in Lalys and Jannin (2014)

Full size image

In this paper, we focus on learning SPMs at a coarser granularity, i.e. at the level of relations between activities (or actions) that constitute a surgical step or phase. An action is an elementary motion associated with semantics; it specifies, for example, the arm and the surgical tool to be used to perform this action. The sequence of actions is affected by the variations in the anatomical conditions. Bayesian networks (BNs) represent the state of the art for learning SPMs at this granularity (Blum et al. 2008; Charrière et al. 2017). Recurrent (deep) neural networks have also been explored, exhibiting improvement in the accuracy at the expense of increased computational effort during training (Dergachyova et al. 2018). Since surgical tasks typically involve a transition between a sequence of states, a hidden Markov model has been used to model the surgical training task of ring transfer, which involves cooperation between a human and a robot (Berthet-Rayne et al. 2016). However, even a simplified version of this training tasks required 80 labeled human executions for training, making scalability to more complex tasks challenging. Another key limitation of many statistical methods is that they generate black-box models that do not provide any guarantees in terms of correctness and soundness, affecting the reliability of the surgical system. On the other hand, logic-based formalisms for representing and reasoning with domain knowledge inherently provide correctness guarantees (Neumuth et al. 2006), and they make the underlying reasoning more transparent. However, such logic-based formalisms for the ring transfer task have required comprehensive domain knowledge to be encoded a priori (Ginesi et al. 2020; Hong and Rozenblit 2016), which is difficult to do in more complex surgical scenarios.

There are many methods in AI for learning domain knowledge. Examples include the incremental revision of action operators represented in first-order logic (Gil 1994), the expansion of a theory of actions to revise or inductively learn ASP system descriptions (Balduccini 2007), and the combination of non-monotonic logical reasoning, inductive learning, and relational reinforcement learning to incrementally acquire previously unknown actions and their preconditions and effects (Sridharan and Meadows 2018). Previously unknown axioms governing domain dynamics have also been learned using decision tree induction in a framework that combines ASP-based non-monotonic logical reasoning with deep learning for scene understanding (Mota and Sridharan 2019, 2020). These approaches may be viewed as instances of interactive task learning, a general framework for acquiring domain knowledge using labeled examples or reinforcement signals obtained from domain observations, demonstrations, or human instructions (Laird et al. 2017).

Our framework for learning domain knowledge uses ILP to learn previously unknown domain axioms represented as ASP programs. ILP was developed to support learning from a limited set of labeled examples (Muggleton 1991). It has been used by an international research community in different domains, e.g., to identify a driver’s cognitive stress and distraction (Mizoguchi et al. 2015); for event recognition in city transport (Katzouris et al. 2015a); and to learn logic programs in robotics (Cropper and Muggleton 2019). ILP has also been successfully applied to the learning of programs based on the paradigm of event calculus (Moyle and Muggleton 1997), but providing the event calculus specification of any non-trivial task or domain can be challenging. Methods have been developed for automated, scalable, and incremental learning of event calculus definitions (Alrajeh et al. 2006; Katzouris et al. 2019). ILP has also been used to support learning in non-monotonic logic programs (Law et al. 2018) and probabilistic logic programs (De Raedt and Kersting 2008). In complex domains such as surgical robotics, learning with probabilistic logics is computationally challenging (Ng and Subrahmanian 1992), but non-monotonic logical reasoning is still necessary. We thus choose to build on ILASP, an implementation of ILP for learning domain axioms under answer set semantics (Law 2018). ILASP provides key advantages in comparison with other ILP-based approaches for learning axioms. For example, it supports faster learning than Inspire (Schüller and Benz 2018), another system based on answer set semantics, because it has fewer hyper-parameters. Although ILASP (by itself) does not support Inspire’s ability to automatically create and generalize predicates to obtain shorter axioms, this limitation can be partially overcome with an iterative version of ILASP. In addition, it has been shown (Law 2018) that ILASP is more general than XHAIL (Ray 2009), a state of the art tool for inductive learning of event calculus-based axioms, and its competitor ILED (Katzouris et al. 2015b). It also guarantees some appealing properties that are discussed in Sect. 4.

3 Original ASP encoding of the ring transfer task

Figure 2 shows the setup for the illustrative surgical training task of ring transfer. The objective is to place colored rings on pegs of the corresponding color using the two patient-side manipulators (PSM1 and PSM2) of the Vinci\(^{\circledR }\) robot. Each PSM can grasp any reachable ring and place it on any reachable peg; reachability is determined by the relative position of rings and pegs with respect to the center of the base. Pegs can be occupied by other rings and must be freed before placing the desired ring on it. Also, rings may be on pegs or on the base in the initial state, i.e., some rings may need to be extracted before being moved.

Fig. 2
figure 2

Setup for the ring transfer task. The dashed line marks the reachability regions for the two PSMs of the Vinci\(^{\circledR }\) robot

Full size image

We describe the ring transfer task in an established format for answer set programming (ASP) (Calimeri et al., 2020). ASP is a declarative language that can represent recursive definitions, defaults, causal relations, and constructs that are difficult to express in classical logic formalisms (Gebser et al. 2012). It encodes concepts such as default negation (negation by failure) and epistemic disjunction, e.g., unlike “\(\lnot\)a”, which implies that “a is believed to be false”, “not a” only implies “a is not believed to be true”, i.e., each literal can be true, false or unknown. ASP supports non-monotonic logical reasoning, i.e., adding a statement can reduce the set of inferred consequences. Modern ASP solvers support efficient reasoning with large knowledge bases or incomplete knowledge, and are used by an international research community (Erdem and Patoglu 2018).

A domain’s description in ASP comprises a system description \({\mathscr {D}}\) and a history \({\mathscr {H}}\). \({\mathscr {D}}\) comprises a sorted signature \(\Sigma\) and axioms. \(\Sigma\) comprises basic sorts arranged hierarchically; statics, i.e., domain attributes whose values do not change over time; fluents, i.e., domain attributes whose values can be changed; and actions. Domain attributes and actions are defined in terms of the sorts of their arguments. Fluents can be inertial (i.e., those that obey inertia laws and whose values are changed directly by actions) or defined (i.e., those that do not obey inertia laws and whose values are not changed directly by actions). Variables and object constants are terms; terms with no variables are ground. A predicate of terms is an atom; it is ground if all its terms are ground. An atom or its negation is a literal. For the ring transfer task, statics include location (including instance center), object (with sub-sorts ring and peg), the robot’s arm (with instances psm1 and psm2), the color of each ring and peg (can take values: red, green, blue, yellow, grey), and time for temporal reasoning; and fluents include reachable(arm, object, color), in_hand(arm, ring, color), on(ring, color, peg, color), at(arm, center), closed_gripper(arm), and at(arm, object, color). Actions include move(arm, object, color), move(arm, center, color), grasp(arm, ring, color), extract(arm, ring, color) and release(arm). Given this \(\Sigma\), axioms describing domain dynamics are first specified as statements in an action language, e.g., \(AL_d\) (Gelfond and Inclezan 2013), and then translated to ASP statements. Axioms define causal laws (i.e., action effects and preconditions), state constraints, and executability conditions (i.e., conditions under which certain actions are forbidden); some examples are provided later in this section. The domain’s history \({\mathscr {H}}\) is a record of statements encoding the observation of the values of particular fluents, and the execution of particular actions, at particular time steps.

To reason with domain knowledge, we construct the ASP program \(\Pi ({\mathscr {D}}, {\mathscr {H}})\) that includes the signature, axioms of \({\mathscr {D}}\), inertia axioms, reality checks, closed world assumptions for actions, observations and actions from \({\mathscr {H}}\), and helper statements (e.g., for goal definition, planning, and diagnostics). Planning, diagnostics, and inference can then be reduced to computing answer sets of \(\Pi\). An answer set (AS) describes a possible world in terms of the beliefs of an agent associated with \(\Pi\). We use the Clingo solver (Gebser et al. 2008) to generate answer set(s) of ASP program(s). For the ring transfer task, we are primarily interested in atoms of actions, and a subset of the fluents and statics; for simplicity, we will only focus on these atoms in our description of \(\Pi ({\mathscr {D}}, {\mathscr {H}})\) and its answer sets below. In our description, we will denote variables of specific sorts using capital letters (e.g., O for object, R for ring, P for peg, C for color, and A for arm), while constant values (e.g., specific instances of color or location) will be represented in lower case (e.g., center or red). The axioms of the ring transfer task are described next.

3.1 Preconditions of actions

Preconditions are statements that need to hold true for the corresponding actions to be have the desired effect(s), i.e., they help define causal laws. We define preconditions and guess executed actions of the domain with the following statement:

$$\begin{aligned}&{ \texttt {0 \{move(A, O, C, t) : reachable(A, O, C, t);}} \nonumber \\ {}&{ \texttt {move(A, center, \_, t) : in\_hand(A, R, C, t);}}\nonumber \\&{ \texttt {extract(A, R, C, t) : in\_hand(A, R, C, t);}}\nonumber \\&{ \texttt {grasp(A, R, C, t) : at(A, R, C, t);}}\nonumber \\&{ \texttt {release(A, t) : in\_hand(A, R, \_, t)\} 1.}} \end{aligned}$$
(1)

where 0 {a : b} 1 is an aggregate rule forcing the ASP solver to compute an answer set with at most one element a, given that b holds. Capital letters represent variables, “\(\_\)” is a placeholder for unused variables in the rules, and “t” refers to a discrete time step. Adding “t” as an additional argument is short hand that the corresponding action (fluent) occurs (holds) at a particular time step, e.g., grasp(A, R, C, t) instead of occurs(grasp(A, R, C), t) implies that the robot arm A grasps ring R of color C at time t; a precondition for this action is that the arm should be at same position as ring R of color C. In a similar manner, we will use in_hand(A, R, C, t) interchangeably with holds(in_hand(A, R, C), t) to imply that arm A has ring R or color C at time t. We will also denote atoms with the argument t as atom\(_t\).

The use of an aggregate rule to define preconditions of actions, i.e., a statement such as \({ \texttt {0 \{ Action: Pre-condition \} 1}}\), constrains the number of elements that can be selected from a set. In this case, only one action can be executed at a time step, resulting in a sequential execution of actions. Since the robot has two arms, we also consider parallel execution of an action by each arm at each time step, revising Statement 1 as follows:

$$\begin{aligned} { \texttt {0 \{Action: Pre-condition\} 1 :- arm(A).}} \end{aligned}$$
(2)

It is possible to combine the execution strategies, e.g., executing move(A, center, _, t) executes a motion primitive that moves both arms in parallel to transfer a ring from one arm to another.

3.2 Executability conditions

Executability conditions for the ring transfer task include the following:

$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A1, P, \_, t), in\_hand(A1, R, C, t),}}\nonumber \\&{ \texttt {in\_hand(A2, R, C, t), A1 != A2.}} \end{aligned}$$
(3a)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A, center, \_, t), in\_hand(A, R, C, t),}} { \texttt { on(R, C, P, \_, t).}} \end{aligned}$$
(3b)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A, P, \_, t), in\_hand(A, R, C, t), on(R, C, P, \_, t).}} \end{aligned}$$
(3c)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A, R, \_, t), closed\_gripper(A, t).}} \end{aligned}$$
(3d)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A, P, C, t), on(R, \_, P, C, t).}} \end{aligned}$$
(3e)

where \({\texttt {:-}}\equiv \ \leftarrow\), and each statement can be viewed as having a \(\bot\) in the head, i.e., atoms on the right hand side of each statement cannot hold at the same time. These statements thus describe conditions under which certain actions should not be considered for execution. Statement 3a implies that neither arm can move if they are both holding the same ring (during transfer); Statements 3b,c implies that a ring which is still on a peg cannot be moved; Statement 3d implies that an arm cannot move to a ring if the gripper is closed; and Statement 3e specifies that an arm cannot move to an occupied peg—this does not prevent an arm from moving to a ring that is on a peg by executing move(A, R, C, t). The objective of the ring transfer task is to have all visible (i.e., reachable by any arm) rings on pegs of matching color; this is expressed as the following constraint:

$$\begin{aligned}&{\texttt {:-}}{ \texttt {reachable(\_, R, C, t), reachable(\_, P, C, t), not on(R, C, P, C, t).}} \end{aligned}$$

3.3 Effects of actions

In our previous work, we assumed the effects of actions to be “instantaneous”, i.e., that they hold immediately after the action is executed and that these effects cease to hold at the subsequent time step (Ginesi et al. 2020). Here we consider a more realistic scenario by making the fluents inertial. Then, the inertia axioms ensure that fluents continue to hold their value until these values are changed explicitly, e.g., by action execution or a specific termination condition:

$$\begin{aligned}&{\texttt {holds(F, t+1)}} :- { \texttt {holds(F, t)}}, { \texttt {not}} \lnot { \texttt {holds(F, t+1).}} \\& \lnot { \texttt {holds(F, t+1)}} :- \lnot { \texttt {holds(F, t)}}, { \texttt {not holds(F, t+1).}} \end{aligned}$$

where F is an inertial fluent. In our illustrative ring transfer domain, effects are explicitly related to the corresponding actions as follows:

$$\begin{aligned}&{ \texttt {in\_hand(A, R, C, t) :- grasp(A, R, C, t-1).}} \nonumber \\& { \texttt {in\_hand(A, R, C, t) :- in\_hand(A, R, C, t-1), not release(A, t-1).}} \nonumber \\& { \texttt {closed\_gripper(A, t) :- \ grasp(A, R, \_, t-1).}} \nonumber \\& { \texttt {closed\_gripper(A, t) :- closed\_gripper(A, t-1), not\ release(A, t-1).}}\nonumber \\& { \texttt {on(R, C1, P, C2, t) :- in\_hand(A, R, C1, t-1),}}\nonumber \\& { \texttt {at(A, P, C2, t-1), release(A, t-1).}} \nonumber \\& { \texttt {on(R, C1, P, C2, t) :- on(R, C1, P, C2, t-1), not\ extract(\_, R, C1, t-1).}}\nonumber \\& { \texttt {at(A, R, C, t) :- move(A, R, C, t-1).}}\nonumber \\& { \texttt {at(A, P, C, t) :- move(A, P, C, t-1).}}\nonumber \\& { \texttt {at(A, center, t) :- move(A, center, \_, t-1)}}\nonumber \\& { \texttt {at(A, O, C, t) :- at(A, O, C, t-1), not\ move(A, O, C, t-1).}}\nonumber \\& { \texttt {at(A, O, C, t) :- at(A, O, C, t-1), not\ move(A, center, t-1).}}\nonumber \\& { \texttt {at(A, center, t) :- at(A, center, t-1), not\ move(A, O, C, t-1).}}\nonumber \\& { \texttt {at(A, center, t) :- at(A, center, t-1), not\ move(A, center, t-1).}} \end{aligned}$$
(4)

However, this formulation is challenging for ILP since it includes many default negations. To reduce the number of such default negation statements, we introduce relations inspired by work in event calculus. Event calculus was developed to represent and reason about events and their effects in a logic programming framework (Kowalski and Sergot 1989). An event calculus program relates the properties of a domain to triggering events. In our case, we introduce two relations, initiated and terminated, to encode the initiating and terminating conditions (respectively) for each fluent. We then reformulate the inertia axioms as follows:

$$\begin{aligned}&{ \texttt {holds(F, t) :- initiated(F, t).}} \nonumber \\&{ \texttt {holds(F, t) :- holds(F, t-1), not terminated(F, t).}} \end{aligned}$$
(5)

Next, we use these new relations to describe the effects of actions in the ring transfer domain as follows:

$$\begin{aligned}&{ \texttt {initiated(in\_hand(A, R, C), t) :- grasp(A, R, C, t-1).}} \nonumber \\&{ \texttt {initiated(closed\_gripper(A), t) :- grasp(A, R, \_, t-1).}} \nonumber \\&{ \texttt {initiated(on(R, C1, P, C2), t) :- in\_hand(A, R, C1, t-1),}}\nonumber \\&{ \texttt {at(A, P, C2, t-1), release(A, t-1).}} \nonumber \\&{ \texttt {initiated(at(A, R, C), t) :- move(A, R, C, t-1).}}\nonumber \\&{ \texttt {initiated(at(A, P, C), t) :- move(A, P, C, t-1).}}\nonumber \\&{ \texttt {initiated(at(A, center), t) :- move(A, center, \_, t-1).}} \end{aligned}$$
(6)
$$\begin{aligned}&{ \texttt {terminated(in\_hand(A, R, C), t) :- release(A, t-1),}}\nonumber \\&{ \texttt {in\_hand(A, R, C, t-1).}} \end{aligned}$$
(7a)
$$\begin{aligned}&{ \texttt {terminated(closed\_gripper(A), t) :- release(A, t-1).}} \end{aligned}$$
(7b)
$$\begin{aligned}&{ \texttt {terminated(on(R, C1, P, C2), t) :- extract(\_, R, C1, t-1),}}\nonumber \\&{ \texttt {color(C2), C1 != C2.}} \end{aligned}$$
(7c)
$$\begin{aligned}&{ \texttt {terminated(at(A, R, C), t) :- move(A, R, C1, t-1), color(C), C1 != C.}} \nonumber \\&{ \texttt {terminated(at(A, R, C), t) :- move(A, P, \_, t-1), color(C).}} \end{aligned}$$
(7d)
$$\begin{aligned}&{ \texttt {terminated(at(A, R, C), t) :- move(A, center,\_, t-1), color(C).}} \end{aligned}$$
(7e)
$$\begin{aligned}&{ \texttt {terminated(at(A, P, C), t) :- move(A, P, C1, t-1), color(C), C != C1.}} \end{aligned}$$
(7f)
$$\begin{aligned}&{ \texttt {terminated(at(A, P, C), t) :- move(A, R, \_, t-1), color(C).}} \end{aligned}$$
(7g)
$$\begin{aligned}&{ \texttt {terminated(at(A, P, C), t) :- move(A, center, \_, t-1), color(C).}} \end{aligned}$$
(7h)
$$\begin{aligned}&{ \texttt {terminated(at(A, center), t) :- move(A, O, \_, t-1).}} \end{aligned}$$
(7i)

As stated in Sect. 3.1, two actions can be executed in parallel under some conditions. For example, the execution of move(A, center, C) causes a different motion primitive to be executed concurrently on the two arms; the main arm A is eventually at the transfer location center, while the other arm is eventually at the grasping location of ring C. Two additional axioms are added to encode this effect:

$$\begin{aligned}&{ \texttt {initiated(at(A1, R, C), t) :- move(A2, center, C, t-1), A2 != A1, arm(A1).}}\nonumber \\& { \texttt {terminated(at(A1, center), t) :- move(A2, center, \_, t-1), A2 != A1, arm(A1).}} \end{aligned}$$
(8)

4 ILP task under AS semantics

The task of learning the system description under AS semantics has been formulated as an ILP by other researchers; please see Law et al. (2018) for details. Here, we provide the relevant definitions suitably adapted to our work and domain. A generic ILP problem \(\mathscr {T}\) under the AS semantics is defined as the tuple \(\mathcal {T} = \langle B, S_M, E \rangle\), where B is the background knowledge, i.e. a set of axioms in ASP syntax; \(S_M\) is the search space, i.e. the set of candidate ASP axioms that can be learned; and E is a set of examples. The goal of \(\mathcal {T}\) is to find a subset \(H \subseteq S_M\) such that \(H \cup B \models E\).

We use the iterative version of ILASP2 algorithm, ILASP2i, in the ILASP tool (Law 2018) to learn axioms inductively from ASP-syntax examples. This algorithm optimizes the search process by focusing on incrementally satisfying only those examples which are not covered by B and the current partial hypothesis (Law et al. 2016). In ILASP, examples are considered to be partial interpretations defined as follows.

Definition 1

(Partial interpretation) Let P be an ASP program. Any set of grounded atoms that can be generated from axioms in P is an interpretation of P. Given an interpretation I of P, we say that a pair of subsets of grounded atoms \(e = \langle e^{inc}, e^{exc} \rangle\) is a partial interpretation extended by interpretation I if \(e^{inc} \subseteq I\) and \(e^{exc} \cap I = \emptyset\).

Given this definition, ILASP solves a learning task defined as follows.

Definition 2

(ILASP learning task) The ILASP learning task \(\mathcal {T} = \langle B, S_M, E \rangle\) is a tuple of background knowledge B, search space \(S_M\) and examples \(E = \langle E^+, E^- \rangle\) such that \(E^+\) (\(E^-\)) is the subset of positive (negative) examples. The goal of \(\mathcal {T}\) is to find \(H \subseteq S_M\) such that \(\forall e \in E\), e is a partial interpretation of the ASP program \(B \cup H\). If AS is an answer set of the ASP program \(H \cup B\), the following must hold:

$$\begin{aligned} \begin{array}{lcl} \forall e \in E^+ \ \exists AS \ s.t. \ B \cup H \models AS : \ e \text { is extended by } AS \\ \forall e \in E^- \ \not \exists AS \ s.t. \ B \cup H \models AS : \ e \text { is extended by } AS \end{array} \end{aligned}$$

The above definition introduces two different categories of examples: positive examples, which must be extended by at least one answer set of \(B \cup H\), and negative examples, which cannot be extended by any of the answer sets. In this sense, we say that ILASP bravely induces positive examples, and cautiously induces negative examples (Sakama and Inoue 2009). ILASP can learn action preconditions and effects from positive examples, and executability conditions from negative examples. In particular, we exploit the ability of ILASP to learn from context-dependent examples (partial interpretations), as explained in Law et al. (2016).

Definition 3

(Context-dependent partial interpretation (CDPI)) A CDPI of an ASP program P with an interpretation I is a tuple \(e_c = \langle e, C \rangle\), where e is a partial interpretation, and C is an ASP program called context. I is said to extend \(e_c\) if \(e^{inc} \cup C \subseteq I\) and \((e^{exc} \cup C) \cap I = \emptyset\).

Definition 4

(ILASP task with CDPIs) An ILASP learning task with CDPIs is a tuple \(\mathcal {T} = \langle B, S_M, E \rangle\), where \(E = \langle E^+, E^- \rangle\) is a set of CDPIs with context C. We say that \(H \subseteq S_M\) is a solution to \(\mathcal {T}\) if the following hold:

$$\begin{aligned} \begin{array}{lcl} \forall e \in E^+ \ \exists AS \ s.t. \ B \cup H \cup C \models AS : \ e \text { is extended by } AS \\ \forall e \in E^- \ \not \exists AS \ s.t. \ B \cup H \cup C \models AS : \ e \text { is extended by } AS \end{array} \end{aligned}$$

All examples (for ILASP learning task) considered in this paper are tuples of the form \(e = \langle e^{inc}, e^{exc}, C \rangle\). This allows us to relate environmental fluents to actions when learning axioms for the task, thus capturing the dynamic nature of the illustrative ring transfer task.

ILASP allows to define the search space \(S_M\) with compact syntax, using mode bias to specify the atoms that can occur in the body and head of axioms (right- and left-hand side of an axiom respectively). In this paper, we consider two different kinds of learning tasks: one for preconditions and executability conditions and one for effects of actions. The specification of the mode bias for the two learning tasks will be presented in the next section. Another feature of ILASP is that it is designed to find the minimal H in the search space \(S_M\). To explain this feature, we first define the length of an axiom.

Definition 5

(Length of an axiom) Let \(\mathcal {R}\) be an axiom in an ASP program. The length of \(\mathcal {R}\), \(|\mathcal {R}|\), is defined as the number of atoms that appear in it. For an aggregate rule, i.e. a rule with an aggregate \(l \ \{a_1; a_2; \dots ; a_n\} \ u\) in the head, the length of the head is defined as \(\sum _{i=l}^{u}i \cdot n\).

The minimal set H is then the set of rules in \(S_M\) with minimal length that satisfy the goal of ILASP task.

5 Experiments in the ring transfer domain

In this section, we describe the experimental setup and the results of experimentally evaluating the capabilities of our approach in the context of the ring transfer task. In our experiments, we focused primarily on the ability to learn previously unknown axioms describing actions’ preconditions (e.g., Statement 1) and effects (e.g., Statement 4), and executability conditions (Statement 3). In order to restrict the search space and improve the computational efficiency, separate ILASP tasks for each action are defined to learn the different types of axioms. Also, separate ILASP tasks are defined for each domain fluent, one each for the initiated and the terminated conditions respectively.

We begin by defining the background knowledge and the search space for ILASP tasks (Sect. 5.1), and describe how the training examples were generated (Sect. 5.2). We then discuss the results of comparing the learned axioms with the ground truth information provided by the designer (Sect. 5.3). In the first experiment, we used the length of axioms and the computational time required by ILASP as the evaluation measures; we hypothesized that the learned axioms would closely match the ground truth information. In the next experiment, we considered 1000 simulated scenarios that mimic challenging conditions for the ring transfer task, including both sequential and parallel execution of actions. In each scenario, we conducted paired trials with the learned and ground truth axioms respectively. In these trials, we used planning time and plan length as the evaluation measures (with plans computed using the Clingo ASP solver).

5.1 Background knowledge and search space

In our experimental trials, we considered action preconditions and executability conditions in one set and the action effects in another set. Below, we describe the initial set up for these two sets of axioms.

5.1.1 Preconditions and executability conditions

For the experiment that focused on learning action preconditions and executability conditions, the background knowledge of each ILASP learning task (one per action) included the definitions of sorts and helper axioms describing the difference between two different arms or colors:

$$\begin{aligned}&{ \texttt {different(A1, A2) :- arm(A1), arm(A2), A1 != A2.}}\\& { \texttt {different(C1, C2) :- color(C1), color(C2), C1 != C2.}} \end{aligned}$$

The search space for each ILASP task was defined using mode bias for compactness. Specifically, for the task of learning preconditions and executability conditions for any given action, we defined the search space such that the action can only occur in the head of an aggregate rule (to capture preconditions) or in the body of axioms (for executability conditions). In ILASP syntax, this corresponded to the statements #modeha(action) and #modeb(1, action), respectively; #modeb(1, action) specifies that action can appear in the body of an axiom only once. We also specified that each environmental (i.e., domain) fluent presented in Sect. 3 may appear in the body of axioms, by adding the mode bias statement #modeb(1, fluent). Similarly, we added the statement #modeb(1, different). When defining the search space, arguments of atoms which are variables or constants must be clearly stated in ILASP. Axioms with more variables generally require more computational effort. For the task of learning preconditions and executability constraints, only arm and color were defined as variables in atoms. Finally, the length of the body of axioms is limited to three atoms using a specific ILASP flag from command line, to reduce the dimension of the problem.

5.1.2 Effects of actions

To learn the effects of action, we set up two ILASP learning tasks per environmental fluent, one each for the axioms associated with the initiated and terminated relations. The background knowledge for these learning tasks contained the same ASP statements presented in the previous section, and the laws of inertia (Statement 5). Moreover, since effects are delayed with respect to actions, we included the concept of temporal sequence:

$$\begin{aligned}&{ \texttt {delay(1..N).}}\\& { \texttt {prev(T1, T2, D) :- time(T1), time(T2), delay(D), T2 = T1+D.}} \end{aligned}$$

where delay is a variable constrained to the set 1..N and N is an estimate of the maximum delay between actions and effects in the domain; N can be increased until ILASP is able to find a suitable hypothesis with the minimum temporal delay. For the ring transfer task, ILASP found the minimum value of N=1. We then defined the search space using the mode bias #modeh(initiated(fluent, t)) or #modeh(terminated(fluent, t)), which specified the head of candidate normal axioms. Moreover, for each environmental fluent f and each action action of the task, we stated #modeb(1, f\(_t\)), #mode(1, action\(\_t\)) to allow them in the body of candidate rules. Also #modeb(1, prev) was included in the mode bias. Note that the inertia laws (Statement 5) imply that fluent\(\_t\) :- initiated(fluent, t), which would lead ILASP to learn the trivial axiom:

$$\begin{aligned} { \texttt {initiated(fluent, t) :- fluent}}\_t \end{aligned}$$

As a result, in the ILASP task to learn initiated conditions for a specific fluent, we omitted the mode bias #modeb(1, fluent\(\_t\)). ILASP variables included color, arm, and time, and delay was defined as a constant #constant(delay, 1..N) to reduce the size of the search space. The maximum body length of axioms is limited to three.

5.2 Experimental setup: generation of examples

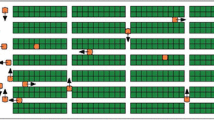
The training and testing examples were extracted from videos of a human or the robot performing the target task; we used similar videos in our prior work (Ginesi et al. 2020). When a human performed the task, all four rings were on grey pegs, and had to be transferred between the two arms before being placed on suitable colored pegs. Hence, all actions mentioned in Sect. 3 appeared in the videos. Figure 3 shows screenshots of the initial states of the task, when performed by the robot, focusing on scenarios that are useful to learn previously unknown knowledge about the task and the domain. For example, in Fig. 3a the transfer of the blue ring failed, and PSM2 had to re-open its gripper before moving to the blue ring again; this scenario can be used to learn the constraint encoded by Statement 3c. In a similar manner, the blue and red pegs were occupied in Fig. 3b and one of these pegs had to be freed to complete the task; this scenario can be used to learn the axiom encoded by Statement 3d. Finally, Fig. 3c corresponds to the scenario that requires concurrent (i.e., parallel) movement of the two arms.

Fig. 3
figure 3

Screenshots of initial states of surgical robot executing action sequences; information extracted from the corresponding images were used for experimental evaluation

Full size image

From each video, we extracted geometric features from each image (i.e., frame) of the videos using standard (color and shape) image segmentation algorithms. We matched these features semantically to the corresponding fluents; this is the same approach used in our previous work (Ginesi et al. 2020). In this process, we also exploited known transforms between frames of the PSMs and the RGB-D cameral these transforms were obtained from the calibration method described in Roberti et al. (2020). We then labeled each frame in the video with the recognized fluents and action being executed. This process was repeated in all the videos to generate the set of labeled examples that serves as the input to our approach to learn previously unknown axioms corresponding to executability conditions (Statement 3), action preconditions (Statement 1), and action effects (Statement 4). The target axioms define logical relations between atoms describing actions and domain fluents; the corresponding examples will only contain these atoms. We next describe the setup for these types of axioms.

5.2.1 Action preconditions and executability conditions

Since all atoms in the axioms corresponding to the preconditions and executability conditions of actions refer to the same timestep t (Sects. 3.1, 3.2), we omitted the timestep in the literals to reduce the number of variables in the search space and speed up learning. For each timestep, we defined the positive examples as CDPIs of the form \(\langle e^{inc}, e^{exc}, C \rangle\), where \(e^{inc}\) was the executed action, C contained the atoms of the fluents describing the environmental state, and \(e^{exc} = \emptyset\). We also specified actions that could not occur at each timestep, simulating knowledge from an expert designer analyzing the video under consideration. We then defined negative examples with forbidden actions in \(e^{inc}\) and \(e^{exc} = \emptyset\). Although it is possible to add forbidden actions in the set \(e^{exc}\) in the positive examples, the fact that ILASP learns through brave induction from positive examples (see Sect. 4) implies there is no guarantee that actions in \(e^{exc}\) will always be excluded by the solution hypothesis. On the contrary, negative examples are cautiously entailed by adding executability conditions to the hypothesis set to ensure that the learned axioms are reliable. As an illustrative example, consider the scene in Fig. 3a. The first action moves PSM1 towards the red ring, providing a positive example:

$$\begin{aligned} { \texttt {\#pos}}&{ \texttt {\{ex1, \{move(psm1,R,red)\}, \{\},}}\\&{ \texttt {\{reachable(psm1,R,red), reachable(psm2,R,blue),}}\\&{ \texttt {reachable(psm1,P,red), reachable(psm1,P,blue),}}\\&{ \texttt {reachable(psm2,P,green), reachable(psm2,P,yellow),}}\\&{ \texttt {reachable(psm1,P,grey), reachable(psm2,P,grey),}}\\&{ \texttt {on(R,red,P,grey)\}\}}} \end{aligned}$$

At the same time, it is not possible to move PSM1 to the blue ring, providing the negative example:

$$\begin{aligned} { \texttt {\#neg}}&{ \texttt {\{ex2, \{move(psm1,R,blue)\}, \{\},}}\\&{ \texttt {\{reachable(psm1,R,red), reachable(psm2,R,blue),}}\\&{ \texttt {reachable(psm1,P,red), reachable(psm1,P,blue),}}\\&{ \texttt {reachable(psm2,P,green), reachable(psm2,P,yellow),}}\\&{ \texttt {reachable(psm1,P,grey), reachable(psm2,P,grey),}}\\&{ \texttt {on(R,red,P,grey)\}\}}} \end{aligned}$$

To reduce the complexity of the learning task, we omitted redundant examples, i.e., examples that only differ in the grounding of variables in the atoms. For example, in the scenario in Fig. 3c, both arms moved to a ring (PSM1 moved to blue ring, PSM2 moved to yellow one) at t=1. This generated two examples that differ not in context but only in the grounding of move(A, R, C); only one example was added. Overall, we generated 8 positive examples and 8 negative examples for move(A, P, C); 9 positive examples and 20 negative examples for move(A, R, C); 2 positive examples and 1 negative example for move(A, center, C); 11 positive examples for grasp(A, R, C); 10 positive examples and 4 negative examples for release(A); and 1 positive example for extract(A, R, C).

5.2.2 Action effects

Since atoms in axioms corresponding to action effects do not share the same timestep (Sect. 3.3), examples for these axioms must account for the temporal aspects. Since our formulation includes predicates inspired by event calculus, we generated two examples for each fluent for each task execution, one each for the initiated and the terminated axioms of this fluent. Only positive examples were considered since they would not be used to learn executability conditions (see above). Examples were CDPIs of the form \(\langle e^{inc}, e^{exc}, C \rangle\), where \(e^{inc}\) was the set of initiated (or terminated) conditions at all timesteps, while \(e^{exc}\) was the set of initiated (or terminated) conditions that did not hold at all timesteps. The context C was the task history, i.e., the set of atoms corresponding to actions and fluents that were true at all timesteps. The set \(e^{exc}\) was needed to guarantee that only relevant causal laws were learned, given that positive examples are subject to brave induction—see Definition 2. Consider the scene in Fig. 3b as an illustrative example. For the fluent at(A, R, C, t), the positive example (considering only the initiated condition for simplicity) is shown below, with the atoms corresponding to the set \(e^{exc}\) underlined:

$$\begin{aligned}&{ \texttt {\#pos}}{ \texttt {\{ex3,}}\\&\quad{ \texttt {\{initiated(at(psm1,R,red,2)),initiated(at(psm1,R,blue,7)),...\},}}\\&\quad\underline{{ \texttt {\{initiated(at(psm1,R,blue,2)),initiated(at(psm1,R,red,7)),...\},}}}\\&\quad{ \texttt {\{reachable(psm1,R,red,\_), reachable(psm2,R,blue,\_),}}\\&\quad{ \texttt {reachable(psm1,P,red,\_), reachable(psm1,P,blue,\_),}}\\&\quad{ \texttt {reachable(psm2,P,green,\_), reachable(psm2,P,yellow,\_),}}\\&\quad{ \texttt {reachable(psm1,P,grey,\_), reachable(psm2,P,grey,\_),}}\\&\quad{ \texttt {on(R,red,P,blue,1), on(R,blue,P,red,1), ...\}\}}} \end{aligned}$$

As before, we omit redundant examples for action effects. Overall, we generated 1 example for the initiated (equivalently, terminated) condition for closed_gripper(A); 2 examples for in_hand(A, R, C); 1 example for at(A, center); 2 examples for on(R, C1, P, C2); and 3 examples for at(A, O, C).

5.3 Experimental results

Next, we describe and discuss the experimental resultsFootnote 1; these results were obtained on a PC with 2.6 GHz Intel Core i7 processor and 16 GB RAM.

5.3.1 Preconditions and executability conditions

We begin by describing the results for learning the action preconditions and executability conditions. The learned action preconditions are as follows:

$$\begin{aligned}&{ \texttt {0 \{move(A, O, C, t) : reachable(A, O, C, t);}}\nonumber \\&{ \texttt {move(A, center, C, t) : in\_hand(A, R, C, t);}}\nonumber \\&{\texttt {extract(A, R, C, t) : in\_hand(A, R, C, t);}}\nonumber \\&{ \texttt {grasp(A, R, C, t) : at(A, R, C, t);}}\nonumber \\&{ \texttt {release(A, t) : in\_hand(A, R, C, t)\} 1 :- arm(A).}} \end{aligned}$$
(12)

arm(A) is needed only for parallel execution of the task, see Sect. 3.1.

Statement 12 matches the action preconditions in Statement 1. Note that the ILASP learning task for any given action only provides the aggregate rule for the precondition of that action, e.g., 0 {move(A, R, C) : reachable(A, R, C)} 1. In Statement 12, the preconditions for all the actions are compacted into a single aggregate rule, which allows the agent to choose at most one of the available actions when solving the task planning problem. Moreover, the temporal variable is manually added to all atoms.

Next, the learned executability constraints obtained from the ILASP learning tasks for all actions are as follows:

$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A, P, C2, t), in\_hand(A, R, C, t), on(R, C, P, C1, t).}} \end{aligned}$$
(13a)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(\_, P, \_, t), in\_hand(A, R, C, t), not\ reachable(A, P, C, t).}} \end{aligned}$$
(13b)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A, center, C, t), on(R, C, P, C1, t).}} \end{aligned}$$
(13c)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {move(A, R, C, t), closed\_gripper(A, t).}} \end{aligned}$$
(13d)
$$\begin{aligned}&{\texttt {:-}}{ \texttt {on(R, C1, P, C, t), move(A, P, C, t).}} \end{aligned}$$
(13e)

Note that the timestep variable is added to each atom after it is learned. Statements 13a–c represent the same conditions as in Statements 3c, 3a and 3b respectively; forbidding motion when both arms hold the same ring is equivalent to forbidding motion when the arm which cannot reach the peg is holding the ring after transfer. Statements 13d,e match the constraints in Statements 3d,e. Note that Statement 13b contains placeholders in the action atom. In fact, executability conditions are learned through a separate ILASP learning task for each action, considering only examples that are relevant to that action. This results in the following executability condition without the action fluent (of moving to a peg):

$$\begin{aligned} {\texttt {:-}}{ \texttt {in\_hand(A, R, C, t), not\ reachable(A, P, C, t).}} \end{aligned}$$

This condition cannot be satisfied when combined with the set of axioms for the other actions. Hence, we add the action atom with placeholders to relate this condition to the action of moving to a peg. These placeholders help ensure the generality of the learned conditions.

Table 1 Quantitative results of the ILASP task for preconditions and executability conditions
Full size table

Table 1 shows the time taken to learn the preconditions and executability conditions for each action, and compares the length of the learned axioms with the original ASP encoding of the domain. Action move(A, P, C) has the largest learning time, the largest axiom length, and the largest number of variables in the axioms; more time is hence needed to search the set of hypotheses and find the correct one. Performance is also influenced by the number and type (i.e., positive, negative) of examples, e.g., the learning time for the release action is more than that of the grasp action that has more variables because release has four negative examples while grasp has none. An overall reduction from 26 to 24 is obtained in the length of the axioms using the ILASP-based approach. This reduction is based on the ability of ILASP to find shorter axioms connecting actions and environmental conditions, discovering logical relations that are not intuitive for a human manually encoding the domain and the task.

5.3.2 Effects of actions

The learned axioms corresponding to the effects of actions, after replacing prev(T1, T2, 1) with the more compact representation of the temporal variable in Clingo’s syntax, includes the following axioms related to the initiated relation:

$$\begin{aligned}&{ \texttt {initiated(in\_hand(A, R, C), t) :- grasp(A, R, C, t-1).}} \end{aligned}$$
(14a)
$$\begin{aligned}&{ \texttt {initiated(closed\_gripper(A), t) :- grasp(A, R, \_, t-1).}} \end{aligned}$$
(14b)
$$\begin{aligned}{ \texttt {initiated(on (R, C1, P, C2),t) :- in\_hand (A, R, C1, t-1),}}\\{ \texttt {at(A, P, C2, t-1), release(A, t-1).}} \end{aligned}$$
(14c)
$$\begin{aligned}&{ \texttt {initiated(at(A, R, C), t) :- move(A, R, C, t-1).}} \end{aligned}$$
(14d)
$$\begin{aligned}{ \texttt {initiated(at (A1, R, C),t) :- move (A2, center, C, t-1),}}\\{ \texttt {different(A1, A2).}} \end{aligned}$$
(14e)
$$\begin{aligned}&{ \texttt {initiated(at(A, P, C), t) :- move(A, P, C, t-1).}} \end{aligned}$$
(14f)
$$\begin{aligned}&{ \texttt {initiated(at(A, center), t) :- move(A, center, \_, t-1).}} \end{aligned}$$
(14g)

Note that ILASP initially finds the following axiom corresponding to the initiated relation for fluent closed_gripper(A):

$$\begin{aligned} { \texttt {initiated(closed\_gripper(A), t) :- in\_hand(A, R, C, t).}} \end{aligned}$$
(15)

This axiom is found because the execution of a grasp action sets the value of both of these fluents to be true. So we split any such axioms such that the fluents are related to the corresponding actions, as shown in Statement 14a and Statement 14b. Another point of interest is that Statement 14c is learnt using intermediate predicate invention. In fact, the ILASP2i algorithm used in this paper returns the partial hypothesis after evaluation of each example, particularly when it is unable to find a valid hypothesis for all examples at the first try; this is due to the constraint we imposed on the length of body of axioms to limit the search space for computational efficiency. In this case, the partial hypothesis is:

$$\begin{aligned} { \texttt {initiated(on(R, C, P, C), t) :- release(A, t-1), at(A, P, C, t-1).}} \end{aligned}$$

This hypothesis only covers examples in which a ring is placed on the same-colored peg, but it does not cover scenarios in which a ring has to be placed on a grey peg (Figure 3b). We add this partial hypothesis as an axiom in the background knowledge:

$$\begin{aligned} { \texttt {flag(A, C, T1, T2) :- release(A, T1), at(A, P, C, T1), prev(T1, T2, 1).}} \end{aligned}$$
(16)

and we modify the mode bias to include flag in the search space. ILASP is then able to find the correct axiom. Notice that increasing the maximum axiom length in the hyper-parameters would lead to the same result without intermediate predicate invention, though increasing the search space.

Note that the axioms learned also include statements corresponding to the terminated relation:

$$\begin{aligned}&{ \texttt {terminated(in\_hand(A, R, C), t) :- release(A, t-1),}}\nonumber \\&{ \texttt {in\_hand(A, R, C, t-1).}} \end{aligned}$$
(17a)
$$\begin{aligned}&{ \texttt {terminated(closed\_gripper(A), t) :- release(A, t-1).}} \end{aligned}$$
(17b)
$$\begin{aligned}&{{ \texttt{terminated(on(R, C1, P, C2), t) :- in\_hand(A, R, C1, t-1),}}}\\ &\quad \texttt{on(R, C1, P, C2, t-1).} \end{aligned}$$
(17c)
$$\begin{aligned}&{ \texttt {terminated(at(A, R, C), t) :- extract(A, R, C, t-1).}} \end{aligned}$$
(17d)
$$\begin{aligned}{ \texttt {terminated(at(A1, R, C), t)}} :- { \texttt {at(A1, P, C, t)}}, { \texttt {at(A2, center, t),}}{ \texttt {release(A1, t).}} \end{aligned}$$
(17e)
$$\begin{aligned}&{ \texttt {terminated(at(A, P, C), t) :- at(A, P, C, t-1), grasp(A, R, C1, t).}} \end{aligned}$$
(17f)
$$\begin{aligned}{ \texttt {terminated(at(A1, center), t) :- at(A1, center,\_),}} { \texttt {move(A2, R, C, t), grasp(A1, R, C, t).}} \end{aligned}$$
(17g)

Recall that Sect. 5.2.2 had highlighted the need to include non-observed fluents while learning causal laws. As an example, consider the initiated condition for the fluent at(A, R, C). Excluding non-occurring fluents from examples generates the following initiating axiom:

$$\begin{aligned} { \texttt {initiated(at(A, R, C), t) :- in\_hand(A, R, C, t+1).}} \end{aligned}$$

which does not always hold and inverts the causal relation between body and head of a rule.

Table 2 Quantitative results for axioms of action effects in the context of initiated
Full size table
Table 3 Quantitative results for axioms of action effects in the context of terminated
Full size table

5.3.3 Validation of learned axioms

We validated the learned axioms in simulated scenarios that mimic challenging environmental conditions for the ring transfer task. We generated 1000 scenarios by considering all possible combinations of four rings on the peg base, with the constraint that all rings need to be placed on a peg at the beginning. For each scenario, both sequential and parallel execution of the task were executed; overall, all available actions in the domain are included in the dataset of executions for proper validation of all axioms. We set a maximum limit of 200s for plan computation. This is because plan computation can take a long time with the manually-encoded original set of axioms shown in Sect. 3. The learned axioms provide a better encoding; once learned, they were used to replace the corresponding axioms from the original set.

Including the learned axioms discussed in the last few sections does not automatically support the computation of a plan in all the simulated scenarios; some knowledge may be missing in certain scenarios depending on the learning examples presented. So, we identified the axioms that affect the plan computation, iteratively omitting axioms for each domain fluent (effects of actions) and each action (preconditions and executability constraints). We found that Statements 17b-e-f were the bottleneck for plan computation. Hence, we ran a new ILASP task for corresponding fluents, i.e., at(A, O, C) and on(R, C1, P, C2), removing Statements 17b-e-f from the search space. This resulted in the following final set of axioms related to the terminated relation (with the new axioms underlined), which then allowed plans to be computed for all the simulated scenarios:

$$\begin{aligned}&{ \texttt {terminated(in\_hand(A, R, C), t) :- release(A, t-1),}}\nonumber \\&{ \texttt {in\_hand(A, R, C, t-1).}} \end{aligned}$$
(18a)
$$\begin{aligned}&{ \texttt {terminated(closed\_gripper(A), t) :- release(A, t-1).}} \end{aligned}$$
(18b)
$$\begin{aligned}&{{ \texttt {\underline{terminated(on(R, C1, P, C2), t) :- on(R, C1, P, C2, t-1),}} \texttt {\underline{extract(A, R, C1, t-1).}}}} \end{aligned}$$
(18c)
$$\begin{aligned}&{ \texttt {terminated(at(A, R, C), t) :- extract(A, R, C, t-1).}} \end{aligned}$$
(18d)
$$\begin{aligned}&\underline{{ \texttt {terminated(at(A, R, C), t) :- at(A, R, C, t-1), release(A, t-1).}}} \end{aligned}$$
(18e)
$$\begin{aligned}&{{ \texttt {\underline{terminated(at(A, R, C), t) :- at(A, R, C, t-1),}}} \texttt {\underline{move(A, center, C, t-1).}}} \end{aligned}$$
(18f)
$$\begin{aligned}&\underline{{ \texttt {terminated(at(A, P, C), t) :- at(A, P, C, t-1), at(A, R, C1, t).}}} \end{aligned}$$
(18g)
$$\begin{aligned}{{ \texttt {terminated(at(A1, center), t) :- at(A1, center, \_),}}}&~~~~{ \texttt {move(A2, R, C, t), grasp(A1, R, C, t).}} \end{aligned}$$
(18h)

Tables 2, 3 show the learning performances for initiated (Statements 14) and the new set of terminated axioms. For the closed_gripper(A) fluent, the learning time was the same as that for in_hand(A, R, C) because of the semantic equivalency between them—see discussion of Statement 15. For fluents on(R, C1, P, C2), at(A, O, C), and at(A, center), the initiating and terminating axioms required most of the overall learning time because the target hypothesis for these axioms was bigger than that of the other axioms. Another observation was that the original ASP encoding for the preconditions, executability conditions, and effects contains more axioms than learned ones, e.g., the condition for terminating at(A, P, C) is significantly shorter. In fact, a comparison of Statements 18g and 7f-h indicates that ILASP finds a single axiom describing the terminated condition, connecting fluents instead of actions, which is different from the statements encoded by a human designer.

Figures 4 and 5 show the comparison between learned and original ASP programs for the sequential and parallel task execution respectively. We specifically compared the size of the plans returned by the two ASP programs, and the plan computational time, in the simulated scenarios. To generate these figures, data collected from these simulated scenarios were processed first. We sorted all scenarios according to the size of the plan generated by the original ASP encoding, with plan size measured in terms of the number of actions in the plan; this resulted in several clusters of scenarios. For each scenario, we computed the size of the plan generated with the learned ASP encoding. Then the mean and standard deviation of plan length with the learned ASP encoding were computed for each cluster of scenarios, and compared with the plan length with the original ASP encoding (top part of Figs. 4, 5). We also computed the mean and standard deviation of planning time for each cluster of scenarios, both for original and learned ASP encoding, to obtain one pair of points in the bottom part of Figs. 4, 5. The results indicated that for scenarios that considered only the sequential execution of actions, plans computed with the learned ASP program are of similar length to those with the original ASP program. With scenarios that considered the parallel execution of actions, plans computed with the learned ASP program were slightly longer than those with the original ASP program.

Next, when we compared the planning time, the mean and standard deviation were significantly lower with the learned ASP program (and sequential action execution) in comparison with the original ASP program. This was mainly due to the shorter axioms found by ILASP. For example, the average planning time for the sixth, ninth and twelfth clusters was reduced by 100s; such a reduction is important for practical use of logic programming to surgery scenarios. Such a reduction was not observed in the scenarios with parallel execution of actions. We think this may be because the planning time (with parallel execution) was significantly lower than with sequential execution of actions, both for the learned and original ASP programs—see the relaxed choice encoded by Statement 2. Also, the computational time was similar for the original and learned ASP programs in this case. Note that one cluster of six scenarios had null (i.e., empty) plan size with sequential action execution and the original ASP program; this was because it was not possible to compute a plan within the maximum allowed time; the corresponding planning time was set to a maximum value of 600s, which was higher than the maximum allowed planning time, for visualization convenience. With the learned program, the plan could not be found in only one execution; the corresponding average planning time in the bottom part of Fig. 4-bottom is thus high but not as high as that with the original ASP program. The starting cluster of the failed attempts to compute the plan determines the initial apparent decrease in the plan computation time for sequential action execution. For the scenarios involving parallel action execution, the computational time rose with the plan size after the first cluster. This is reasonable since longer plans are generated in more complex conditions (e.g., colored pegs are occupied or more transfer of rings).

Fig. 4
figure 4

Comparison between learned and original axioms in simulation for scenarios that involve sequential execution of actions

Full size image
Fig. 5
figure 5

Comparison between learned and original axioms in simulation for scenarios that involve parallel execution of actions

Full size image

6 Conclusion

In this paper, we have presented an ILP-based approach for surgical task knowledge learning. Our method can cope with multiple issues of interest in surgical scenarios, such as the unavailability of large training datasets and the need for explainable surgical task description. We have used a benchmark task for training surgeons, the ring transfer executed with the Vinci\(^{\circledR }\) robot, as the illustrative task. Given a set of only four incomplete executions of the task from the human and the robot, we have shown that it is possible to fast learn the axioms in ASP syntax encoding actions and their relations with the environment, using inductive learning based on the ILASP tool. In addition, we have separated the learning tasks for different parts of the ASP encoding, and proposed a systematic learning approach that can be extended to other robot tasks. This separation of parts of the encoding supports incremental refinement of the knowledge (i.e., axioms) and the associated search space.

We evaluated our approach in the context of simulated scenarios of challenging conditions for the ring transfer task; we considered both sequential and parallel action execution. With the learned ASP encoding, performance is comparable or only slightly worse than that with the original ASP encoding in terms of the size of the plans found. We also examined the plan computation time, which affects the real-time execution on a physical robot in the surgery domain. The experimental results indicated the ability to discover semantic relations (between atoms) that were not in the original ASP encoding provided by the human designer; this results in shorter axioms and also significantly reduces the planning time in certain scenarios. There are some differences in performance between scenarios that involve sequential action execution and those that involve parallel action execution; these differences will be explored further in future work. The validation on an extensive set of simulated scenarios has also evidenced the need for refinement of initially learned axioms. This shows that initially provided examples were not “good” enough to learn adequate ASP axioms for complex instances of the ring transfer task.

A disadvantage of our method is the need for labeled executions of the target task, which may limit the scalability of this approach to more complex surgical procedures. Our ongoing research is focused on the unsupervised segmentation of actions and fluents from videos and kinematic recordings (Meli and Fiorini 2021), which is an open problem in the surgical domain (Krishnan et al. 2017; van Amsterdam et al. 2019). We are also integrating the framework for automated task execution presented in Ginesi et al. (2020) with our ILASP-based framework, following an approach similar to Calo et al. (2019). This will allow an expert human to supervise the learning system, defining the positive and negative examples in real-time for online refinement of ASP task knowledge.