Brownian motors arranged on nontrivial networks to achieve fast transport

Abstract

A method of calculating velocity, efficiency as well as coefficient of performance of the refrigerator in terms of complex generating functions is presented for a Brownian motor that operates between two heat baths. Based on the analytic method developed by Goldhirsch and Gefen (Phys Rev A 33:2583, 1986, Phys Rev A 35:1317, 1987), first the dependence for the velocity V, the efficiency $\eta$ as well as the coefficient of performance of the refrigerator $P_{\text {ref}}$ on model parameters is explored. Not only the previously known results are reconfirmed for a single Brownian engine but also the thermodynamic feature of M Brownian ratchets that are arranged in a complex network is investigated. The results that are shown in this paper depict that a proper arrangement of the motors on the network may achieve fast transport. It is shown that at a quasistatic limit, Carnot efficiency or Carnot refrigerator is attainable as long as the heat exchange via kinetic energy is omitted. For all cases, far from the quasistatic limit, the efficiency and the coefficient of performance of the refrigerator are far lower than Carnot efficiency or Carnot refrigerator. Moreover, a way of transporting a Brownian particle to a desired location in a network with many dangling bonds and loops is presented.

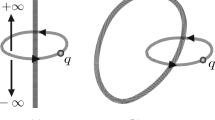
Graphic abstract

Appendix A: Derivation of velocity for three Brownian ratchets arranged perpendicularly in two-dimensional lattice

Let us now consider three Brownian ratchet potentials (each potential has a similar arrangement as Fig. 2) that are arranged as shown in Fig. 7. The generating function for the MFPT (From A to C) for the walker along the segment AC is given as [1, 2]

$$\begin{aligned} G_{{AC}}(\phi )= G_{{AE}}(\phi )R_{{E}}T_{{EC}}, \end{aligned}$$

(36)

where $G_{{AE}}$ the generating function for the MFPT towards the right direction for the walker that starts its journey at a point A and arrives at E. From Eq. (9), we get

$$\begin{aligned} G_{{AE}}(\phi )= {X_{1-P_{1}}T_{{AE}}\over 1-X_{1-P_{1}}Q_{{AE}}}, \end{aligned}$$

(37)

where

$$\begin{aligned} X_{1-P_{1}}= {1\over 1-(1-P_{1})e^{i\phi }}. \end{aligned}$$

(38)

On the other hand,

$$\begin{aligned} T_{{AE}}= P_{1}e^{i\phi }P_{3}e^{i\phi }, \end{aligned}$$

(39)

is the $\phi$ probability for the walker to leave the site A and to reach site B in the right direction without returning to site A, while

$$\begin{aligned} Q_{{AE}}= P_{1}e^{i\phi }P_{2}e^{i\phi }, \end{aligned}$$

(40)

is defined as the $\phi$ probability for the walker to leave site A and returns to A without touching E. The term

$$\begin{aligned} T_{{EC}}= P_{4}e^{i\phi }P_{2}e^{i\phi } \end{aligned}$$

(41)

denotes the $\phi$ probability for the walker to leave the site E and to reach site C in the right direction without returning to site E, while $Q_{{EC}}$ is defined as the $\phi$ probability for the walker to leave site E and returns back to E without touching C. The vertex normalization term $R_{{E}}$ [1, 2] is given by

$$\begin{aligned} R_{{E}}= {Q'_{{E}}\over 1-Q'_{{E}}S_{{B}}}, \end{aligned}$$

(42)

where $Q'_{{E}}$ is a term that related to the $\phi$ probability for the walker to leave site E and returns back to E without touching A, B, and C. After some algebra, we find

$$\begin{aligned} Q'_{{E}}= {X_{1-3P_{4}}\over 1-X_{1-3P_{4}}(Q_{{EB}}+Q_{{EC}}+Q_{{EA}})}, \end{aligned}$$

(43)

where

$$\begin{aligned} Q_{{EB}}= & {} Q_{{EC}}= Q_{{EA}} \nonumber \\= & {} P_{4}e^{i\phi }P_{3}e^{i\phi }. \end{aligned}$$

(44)

The terms $Q_{{EB}}$, $Q_{{EC}}$ and $Q_{{EA}}$ denote the $\phi$ probability for the walker to leave site E and returns back to E without touching A, B and C, respectively. On the other hand,

$$\begin{aligned} S_{B}= T_{{AE}}T_{{EA}}V_{A}+T_{{EB}}T_{{BE}}V_{{B}} \end{aligned}$$

(45)

denotes the $\phi$ probability for the walker to leave site E and returns to E after reaching A or B. For clarity, let us present the terms

$$\begin{aligned}&X_{1-3P_{4}}= {1\over 1-(1-3P_{4})e^{i\phi }}, \end{aligned}$$

(46)

$$\begin{aligned}&V_{A}= {X_{1-P_{1}}\over 1-X_{1-P_{1}}Q_{{AE}}}, \end{aligned}$$

(47)

$$\begin{aligned}&V_{B}= {X_{1-P_{5}}\over 1-X_{1-P_{5}}Q_{{BE}}}, \end{aligned}$$

(48)

$$\begin{aligned}&Q_{{BE}}= P_{5}e^{i\phi }P_{2}e^{i\phi }, \end{aligned}$$

(49)

$$\begin{aligned}&X_{1-P_{5}}= {1\over 1-(1-P_{5})e^{i\phi }}, \end{aligned}$$

(50)

$$\begin{aligned}&T_{{EA}}= T_{EB}=P_{4}e^{i\phi }P_{2}e^{i\phi }, \end{aligned}$$

(51)

and

$$\begin{aligned} T_{{BE}}= P_{5}e^{i\phi }P_{3}e^{i\phi }. \end{aligned}$$

(52)

When sites A and B are coupled with the hot bath as shown in Fig. 7, then $P_1=P_5$. Analyzing the generating functions for the MFPT, after some algebra, the MFPT from site A to C is calculated as

$$\begin{aligned} t^{+}&= {d G_{AC}(\Phi )^{+}\over d (i\phi )}|_{\phi =0} \nonumber \\&\!=\!\frac{P_1 P_2 P_3 (P_1\!-\!P_1 P_2\!-\!3 (\!-\!1\!+\!P_1 P_2\!+\!P_1 (\!-\!2\!+\!P_3)\!+\!P_3) P_4)}{(3 (P_1\!-\!P_1 P_2) (\!-\!1\!+\!P_3)\!+\!2 P_1P_2 P_3)^2 P_4}\nonumber \\&=12+6e^{{E\over T_{\text {c}}}}+12e^{{E\over T_{\text {h}}}}. \end{aligned}$$

(53)

For the case where sites A and B are coupled with the hot bath, following the above steps, the MFPT from C to A is given as

$$\begin{aligned} t^{-}=12+14e^{{E\over T_{\text {c}}}}+4e^{{E\over T_{\text {h}}}}. \end{aligned}$$

(54)

Here, throughout this section, we assume $f=0$. Since the segment AC is 4d long, the average velocity

$$\begin{aligned} V=(4d/t^{+} -4d/t^{-}). \end{aligned}$$

(55)

When only site A is coupled with the hot bath while site B is coupled with the cold bath. In this case, ignoring the rigorous mathematical steps, the MFPT towards the right direction along the AC segment is calculated as

$$\begin{aligned} t^{+}=12+10e^{{E\over T_{\text {c}}}}+8e^{{E\over T_{\text {h}}}}, \end{aligned}$$

(56)

while the MFPT from C to A is given as

$$\begin{aligned} t^{-}=12+18e^{{E\over T_{\text {c}}}}. \end{aligned}$$

(57)

The average velocity $V=(4d/t^{+} -4d/t^{-})$.