1 INTRODUCTION

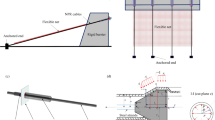
As has been shown in recent communications [1, 2] devoted to the intensification of fine air filtration, it is promising to create filters composed of submicron fibers coated with coaxial highly porous permeable shells (layers) consisting of nanofibers, including so-called nanowhiskers or nanoneedles oriented perpendicularly to the fiber surface (Fig. 1). Filters assembled of such modified fibers exhibit a noticeably higher particle collection efficiency than those composed of shell-free fibers. Therewith, the additional drag of the shells to a flow is low. It is reasonable to use such filters for fine air purification from submicron particles at low flow velocities of nearly several centimeters per second. Moreover, these filters may be useful for collecting larger particles when taking aerosol samples at high velocities. In this case, the deposition inside the shells occurs due to the sieve effect, and, if a particle has not penetrated into a shell and is only in contact with the point of a needle, it can be blown away, and the question as to the inefficient adhesion of particles requires special attention.

Fig. 1.
figure 1

The simulation cell for the problem of a Stokes flow around fibers coated with needles (whiskers). The arrow denotes the flow direction.

Full size image

The blowing of deposited particles out of filters was studied from the very beginning of developing the fine gas purification. The works carried out in this field have been reviewed in [3], where it has been shown that only micron-sized particles are prone to be blown away at flow velocities one or two orders of magnitude higher than the velocities at which submicron aerosols undergo HEPA filtration. It should be noted that the blowing of particles from a surface under the action of a turbulent air jet has recently been studied in detail, and approximately the same results have been obtained [4, 5]. In [6, 7], the doubts expressed in [8] about the efficient collection of nanoparticles subjected to intense Brownian motion have been excluded. In [6, 7], it has been shown that particles are not adhered to a surface, when the Stokes inertia criterion exceeds a critical value, which is not realized in the practice of fine filtration. The absence of nanoparticle rebound, including that at a high temperature, has recently been confirmed experimentally [9]. Thus, it may be stated that inefficient collection is excluded for submicron particles, and this fact has been confirmed in practice: high-efficiency HEPA filters reduce particle concentrations by several orders of magnitude. However, this cannot always be realizable for modified filters recommended in [2], because the small area of the contact between thin sharp needles grown on fibers and collected particles may appear to be a reason for inefficient adhesion. The deposition of particles coated with thin needles may also be inefficient.

In this communication, we shall estimate the van der Waals attractive force between a spherical particle and the point of a needle located on a fiber and compare it with the Stokes force applied to the particle at the contact point. Moreover, we shall consider the condition of the balance between the Stokes force applied to a moving spherical particle coated with radially directed needles and the van der Waals force of attraction to a smooth fiber. The analysis of the force balance with account of the hydrodynamic flow field at the points of the “particle–needle” and “needle–fiber” contacts will enable us to determine the conditions for inefficient particle collection.

2 DEPOSITION OF AEROSOL PARTICLES ONTO A FIBER WITH A SHELL COMPOSED OF NANONEEDLES

Sphere–Cylinder van der Waals Interaction

The equation for the force of the van der Waals interaction between an infinitely long cylinder and a macroscopic spherical particle with no regard to the retardation effect was, for the first time, derived in [10] under the additive approximation by summing pair potentials. This equation has an awkward form and is not presented here. To determine the adhesion of a particle brought in contact with a fiber, we use the following simple equation derived within the framework of the Derjaguin approximation [11]:

$${{F}_{{{\text{vw}}}}} = - \left( {{{{{A}_{6}}r} \mathord{\left/ {\vphantom {{{{A}_{6}}r} {6{{d}^{2}}}}} \right. \kern-0em} {6{{d}^{2}}}}} \right){{\left[ {{a \mathord{\left/ {\vphantom {a {\left( {a + r} \right)}}} \right. \kern-0em} {\left( {a + r} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$$
(1)

where \({{A}_{6}}\) is the Hamaker constant (10–12–10–13 erg), \(r\) is the particle radius, \(a\) is the cylinder radius, and \(d\) is the smallest distance between the surfaces of the cylinder and the sphere. In addition, Eq. (1) can be derived by expanding the equation obtained in [10] in terms of small parameter d. Below, we shall suppose that the gap between two bodies at the point of their contact is equal to a value corresponding to the minimum of the Lenard-Jones pair potential, \(d\) = 0.4 nm.

Estimates performed using Eq. (1) have shown that the particle–fiber attractive force substantially exceeds the viscous drag force calculated for a particle moving at a velocity on the order of several centimeters per second by the Stokes equation:

$${{F}_{{{\text{St}}}}} = 6\pi \mu ru{\kern 1pt} {\text{*}}{{C}^{{ - 1}}},$$
(2)

where \(u{\kern 1pt} {\text{*}}\) is the local flow velocity, with the asterisks denoting that the value is dimensional; μ = 1.84 × 10–4 P is the air viscosity under normal conditions; and С is the Cunningham–Milliken correction to the Stokes force [12], \(C = 1 + {\text{1}}{\text{.246K}}{{{\text{n}}}_{{\text{p}}}}\) + \({\text{0}}{\text{.42K}}{{{\text{n}}}_{{\text{p}}}}\exp \left( { - {{{\text{0}}{\text{.87}}} \mathord{\left/ {\vphantom {{{\text{0}}{\text{.87}}} {{\text{K}}{{{\text{n}}}_{{\text{p}}}}}}} \right. \kern-0em} {{\text{K}}{{{\text{n}}}_{{\text{p}}}}}}} \right),\) which takes into account the gas slip at a particle surface (\({\text{K}}{{{\text{n}}}_{{\text{p}}}} = {\lambda \mathord{\left/ {\vphantom {\lambda r}} \right. \kern-0em} r}\) is the Knudsen number of the particle). For example, a particle with radius \(r\) = 1 µm and a low value of the Hamaker constant, \({{A}_{{\text{6}}}}\) = 10–13 erg, is attracted to a fiber with a radius of 1 µm at a contact point with force \({{F}_{{{\text{vw}}}}}\) = –7.4 × 10–4 dyne, while the Stokes force for such a particle at \(u{\text{*}}\) = 5 cm/s is \({{F}_{{{\text{St}}}}}\) = 1.7 × 10–6 dyne. Taking into account that, near a fiber surface, the velocity is several times lower than the average velocity in a filter, the blowing away is, all the more, impossible.

Equation (1) is applicable at interaction distances that are small as compared with the characteristic length of the absorption spectrum λ0 ~ 100 Å. When calculating the particle–fiber van der Waals interaction at larger distances, it is necessary to take into account the electromagnetic retardation [13]. The expression for the sphere–cylinder interaction with allowance for the retardation effect was obtained under the additive approximation in [14]. This expression has an cumbersome form and is not presented here. In [14], it has been noted that, at \(r < a\), a simpler equation is applicable to the sphere–plane interaction [15]:

$$F_{{{\text{vw}}}}^{{{\text{ret}}}} = - \frac{{8{{A}_{7}}{{r}^{3}}\left( {d + r} \right)}}{{15{{d}^{3}}{{{\left( {d + 2r} \right)}}^{3}}}},$$
(3)

where \({{A}_{7}}\) is the constant of the van der Waals interaction between the condensed bodies with account of the retardation effect. Estimates carried out by Eq. (3) have shown that, when the distance between a particle and a fiber is equal to the needle length, the van der Waals force of attraction to the fiber turns out to be negligible. If a particle has not entered into the shell, but rather is located near the point of a needle, it may be blown out with a flow, all the more so because the flow velocity near the external boundary of the porous shell (at the needle points) is markedly higher than the velocity near a smooth core fiber (Fig. 2). This statement primarily concerns large particles. For short needles, the contribution of attractive force (3) may, on the contrary, appear to be essential.

Fig. 2.
figure 2

Profiles of dimensionless tangential flow velocity along the axis perpendicular to the vertices of (1, 2) conical and (3, 4) cylindrical whiskers located on a fiber at \(\theta \) = 90° as depending on the local \(z\) coordinate originating from the top of a whisker: \({{a}_{{\text{w}}}}\) = 0.05, \(2\phi \) = (1) 6° and (2) 90° (“pencil-shaped” needle), \({{a}_{{\text{w}}}}\) = (3) 0.01 and (4) 0.05; \({{h}_{{\text{w}}}}\) = 1, \({{y}_{0}}\) = 0.2, \(b\) = 0.2, and \(a\) = 1 µm.

Full size image

Van der Waals Interaction of a Particle with the Point of a Conical Needle

The attractive force between a needle and a planar surface at a contact point is determined by the gap between them and the shape of the needle apex. When the area of the hypothetic contact corresponds to a point, the force will depend only on the aperture angle of the needle apex [16]:

$${{F}_{{{\text{vw}}}}} = - \frac{{{{A}_{6}}{{H}^{3}}}}{6}\frac{{{\text{ta}}{{{\text{n}}}^{{\text{2}}}}\phi }}{{d{{{\left( {d + H} \right)}}^{3}}}},$$

where \(\phi \) is a half of the aperture angle of the cone, \(H = {{a}_{{\text{w}}}}{\text{cotg}}\phi \) is the cone height, and \({{a}_{{\text{w}}}}\) is the radius of the cone base. To take into account the surface curvature of a submicron particle contacting with the needle point (Fig. 1), let us find the interaction energy between a conical needle and a spherical particle by integrating the energy of atom–macroparticle interaction over the cone volume (with no account of the retardation) [14]. In the limiting case of small gap \(d\), the obtained expression yields the force of the van der Waals interaction between the cone vertex and the particle at the contact point:

$${{F}_{{{\text{vw}}}}} = - \frac{{{{A}_{6}}}}{{6d}}f{\text{ta}}{{{\text{n}}}^{2}}\phi ,$$

where

$$\begin{gathered} f = 1 + \frac{{11d}}{{2r}} - \frac{{3d}}{H} - \frac{{3d}}{{H + 2r}} + \frac{{4d{{r}^{2}}}}{{3{{{\left( {H + 2r} \right)}}^{3}}}} \\ - \,\,\frac{{3d}}{r}\ln \left( {\frac{H}{d}\frac{{2r}}{{\left( {d + 2r} \right)}}} \right). \\ \end{gathered} $$

The computations have shown that, at \(d\) = 0.4 nm, the interaction force between the particle and the needle point is comparable with the Stokes force. Even for a needle with large aperture angle 2\(\phi \) = 90° of the conical vertex, the attractive force is as weak as \({{F}_{{{\text{vw}}}}}\) = –4 × 10–7 dyne, thereby being comparable with the viscous force applied to a particle with radius \(r\) = 0.3 µm at a low velocity.

The Stokes force of a particle near a fiber is weak, because the local tangential flow velocity is low. However, the flow velocity increases with the distance from the fiber surface. Further, to calculate the viscous drag force by the methods of computational hydrodynamics, let us find the 3D flow velocity field in a row of fibers with needles.

Flow Velocity on the Surface of a Porous Shell Covering a Fiber

As an example, we calculated the velocity field of the Stokes flow around a row of fibers with surface layers consisting of radial needles. The method for calculating the flow field in a system of fibers with shells composed of nanocylinders has been presented in our previous work [2]. The simulation cell is shown in Fig. 1. Dimensionless stationary Stokes equations [17]

$${\text{grad}}p = \Delta {\mathbf{u}},\,\,\,\,{\text{div}}{\mathbf{u}} = 0,$$
(6)

where \(p = {{p{\text{*}}a} \mathord{\left/ {\vphantom {{p{\text{*}}a} {U\mu }}} \right. \kern-0em} {U\mu }}\) is the pressure and \({\mathbf{u}} = (u,{v},w)\) is the flow velocity vector, were solved under no-slip boundary conditions imposed on the streamlined fiber surface with needles, \(u = {v} = w = 0.\) Here and below, the linear and velocity scales are fiber radius a and flow velocity U before a filter. The conditions of constant velocity u =1 and the absence of viscous stresses were used at the inlet and outlet of the calculation cell, respectively. The conditions of symmetric components of velocities and stresses were imposed on the cell faces.

Figure 2 shows the calculated profiles of the dimensionless (in the units of U) tangential flow velocities at the points of needles having the shapes of cones with aperture angle \(2\phi \) = 6°, dimensionless base radius \({{a}_{{\text{w}}}}\), and height \({{h}_{{\text{w}}}}\) (curve 1); the shapes of “sharpened pencils” (circular cylinders with radius \({{a}_{{\text{w}}}}\) having conical vertices with \(2\phi \) = 90°) (curve 2); and the shapes of circular cylinders with radius \({{a}_{{\text{w}}}}\) (curves 3, 4). The profiles have been plotted as depending on the \(z\) coordinate at \(\theta = {\pi \mathord{\left/ {\vphantom {\pi {2,}}} \right. \kern-0em} {2,}}\) i.e., for the case of the maximum tangential velocity. The parameters of the row of fibers (Fig. 1) are as follows: \({{y}_{0}}\) = 0.2 is the distance between the layers of nanowhiskers on a fiber and \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}\) = 0.2, where \(2h\) is the distance between the axes of neighboring fibers. As is seen in Fig. 2, the velocity near a nanoneedle point is comparable with the average velocity in the model filter.

Condition for Blowing a Particle from a Nanoneedle Located on a Fiber

In this work, we do not consider the problem of the contact interaction, which takes into account the contact time, humidity, temperature, and deformation. We are interested in the question whether a particle moving in a flow is deposited after touching a needle point. To answer this question, let us compare the attractive force and the viscous drag force applied to a particle in a flow near the point of a needle on a fiber. Obviously, it becomes more difficult to blow a particle away as the particle radius, needle length, and local flow velocity at the contact point decrease. Comparing the van der Waals attractive force \({{F}_{{{\text{vw}}}}}\) calculated by Eq. (5) for a spherical particle with radius \(r\) with the Stokes force \({{F}_{{{\text{St}}}}}\) (2) at the contact point, we can determine flow velocity U before the filter, above which a particle that has approached the needle point at the minimum distance will not be deposited onto the fiber:

$${\text{|}}{{F}_{{{\text{vw}}}}}{\text{|}} < {{F}_{{{\text{St}}}}}.$$
(7)

Calculated flow velocities \(U,\) at which particles with \(r\) < 1 µm can be blown away from the point of a conical needle, are shown in Fig. 3. It follows from this figure that forces \({\text{|}}{{F}_{{{\text{vw}}}}}{\text{|}}\) and \({{F}_{{{\text{St}}}}}\) for submicron particles become equal already at gas flow velocities typical for HEPA filtration. It should however be noted that we have not taken into account a possible displacement of the particle along the needle, when the adhesion force of the contact between the particle and a lateral surface of the needle is several orders of magnitude stronger than the Stokes force, and the particle is not blown away. In addition, the blowing away becomes more difficult with an increase in angle \(2\phi .\) Moreover, a particle cannot be blown away from the planar top of a cylindrical whisker at flow velocities typical of fine filtration. In this case, the van der Waals force of particle attraction to the cylinder with radius \(a\) is calculated by an equation, which is easy to derive under the additive approximation by integrating the energy of atom–spherical particle interaction [14] over the cylinder volume:

$${{F}_{{{\text{vw}}}}} = - \frac{{4{{A}_{6}}{{a}^{2}}{{r}^{3}}}}{{3{{d}^{3}}{{{\left( {d + 2r} \right)}}^{3}}}}.$$
(8)

The forces of the cylinder–particle interaction calculated by this equation have an order the same as have those calculated by Eq. (5) and much exceed Stokes force (2).

Fig. 3.
figure 3

Flow velocity \(U\) before a filter above which a particle is not deposited on the point of a conical needle with \(2\phi \) = 90° located on a fiber at \(\theta \) = 90° as depending on particle radius: \({{A}_{6}}\) = 10–13 erg, \({{a}_{{\text{w}}}}\) = 0.05, \(b\) = 0.2, \({{y}_{0}}\) = 0.2, \({{h}_{{\text{w}}}}\) = 1, and \(a\) = 1 µm.

Full size image

All of the aforementioned refers to solid particles. When particles are not solid, as, e.g., particles of the biological origin, blowing away is, all the more, impossible. This has been confirmed in [18], where efficient collection of MS2 viruses was observed at flow velocities up to 26 cm/s in a filter consisting of fibers coated with a dense layer of very thin aluminum nanoneedles having diameter \(2{{a}_{{\text{w}}}}\) < 4 nm. (After droplets of deionized water containing viruses with a diameter of 28 nm were evaporated, the diameter of suspended particles was up to 400 nm.) Moreover, particles cannot be blown away from their deposit resulting from a long-term operation of a filter. Hence, only large solid particles can be blown away from a point, when the shell of a fiber consists of a large number of solid and sharp nanoneedles and the particles cannot penetrate into a shell.

3 DEPOSITION OF AEROSOL PARTICLES WITH SHELLS CONSISTING OF NANONEEDLES

Let us show that the deposition of needle-coated particles onto smooth fibers may also be inefficient. Such needles may be seen in micrographs of submicron particles of metal oxides, such as zinc oxide [12] or biological particles, such as spores and viruses (including coronaviruses).

Surface needles affect the efficiency of particle deposition, because they increase the drag of particles moving in air. In this case, particle diffusion coefficient and, hence, collection efficiency decrease. This was noted in review [20], where experimental data that were incomprehensible at that time were discussed. In particular, a discrepancy was noted between the theory and experimental data on filtration of aerosols of T-1 bacteriophage with a size of 0.1 µm through Whatman GF/A filters. At low and high flow velocities of aerosols through a filter, the measured collection efficiencies were lower and higher than the theoretical one, respectively. This finding was explained by the fact that, in the suspended state, the particles had larger sizes, and it was assumed that the droplets containing Т-1 had no time to evaporate. However, it was not known at that time that T-1 phage has a long tail appendix, whose size is comparable with the size of the phage. At a low velocity, this appendix decreased the diffusion coefficient of the particles, and the collection efficiency had to be lower, while, at a high velocity, the role of the interception effect increased and the efficiency was enhanced. The matter is that the collection efficiency of nonspherical particles is calculated using their maximum size because of their Brownian rotation. Thus, the existence of the long appendices explains the observed discrepancy between the experiments and the theory. Note that almost the same quantitative data were recently presented in [21] on the efficiency of collection of phages by GF/A filters (with the penetration on the order of \({n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}\) ~ 10–5). The attention should be focused on the fact that the matter concerns the measured multiplicity of air purification equal to 105 times; therefore, the question about blowing away is out of place. (In this case, after the phage was brought in contact, the flexible filament adhered to a fiber, thereby increasing the contact area.) Hence, it may be concluded that biological particles with flexible filaments or needles must not be blown away from a filter. However, when particles with rigid needles are deposited, the situation is ambiguous (see below).

Viscous Drag Force of a Sphere with a Shell Consisting of Needles

Let us estimate correction \(f\) to the Stokes drag force of a spherical particle for the additional drag of its highly porous shell (Fig. 4):

$$F = {\text{6}}\pi \mu rUf.$$
(9)

The drag force of a particle with needles is found from the numerical solution of Stokes 3D equations (6) by integrating the projection of the local total stress onto the flow direction over the particle surface area [17]:

$$F = \int\limits_S {{{T}_{x}}dS} ,$$

where \({\mathbf{T}} = \left( { - p{\text{I}} + \sigma {\kern 1pt} '} \right){\mathbf{n}},\) \(\sigma {\kern 1pt} '\) is the viscous stress tensor for an incompressible liquid, \({\text{I}}\) is the unit tensor, \({\mathbf{n}}\) is the vector of the external normal to the surface, and \(dS\) is an element of the surface. Here, the linear and velocity scales are particle radius r and velocity U, respectively.

Fig. 4.
figure 4

The simulation cell for the problem of a Stokes flow around a particle coated with a layer of needles.

Full size image

Since the motion of a particle in a resting medium is equivalent to a flow around a quiescent particle, let us consider the latter case by placing a particle into a cylindrical simulation cell (Fig. 4). Taking into account the symmetry of the problem, the calculations were performed for a fourth fraction of the particle in a cylinder sector (see Fig. 4). The length and radius of the cell were increased until a solution was found for the model problem of the flow around a needle-free particle and, analogously, in the case of a particle with needles. The condition of a uniform flow, \(u = 1,\) was imposed on the calculation cell inlet, while the condition of the absence of viscous stresses was used at its outlet. The condition of symmetric components of velocities and stresses was imposed on the cell faces. The no-slip condition was used for velocity components on the particle surface. The gas slip effect on needles was not taken into account, because it markedly complicates the solution of the problem.

Figure 5 shows the dependences of correction \(f = {F \mathord{\left/ {\vphantom {F {{{F}_{0}}}}} \right. \kern-0em} {{{F}_{0}}}}\) (9) to the Stokes force on thickness \({{h}_{{\text{w}}}}\) of the porous shell (needle length) for different numbers N of the needles in the shell (curve 1). Here, F is the drag force of a sphere with needles and \({{F}_{0}} = {\text{6}}\pi \mu rU\) is the drag force of the core (needle-free sphere). In this example, the radially directed needles were approximated by prolate ellipsoids (Fig. 4) with dimensionless axes 2\(a\) = 2\(c\) = 0.032 and \(2b = {{h}_{{\text{w}}}}.\) In addition, Fig. 5 shows analogous dependences of the drag force normalized with respect to F0 for a composite particle excluding the drag of the porous shell (the core screened with a shell, curve 2) and for an impermeable sphere with a radius equal to the radius of the porous shell (limiting case of an impermeable shell, curve 3).

Fig. 5.
figure 5

Ratios of drag forces of (1) a particle with a shell of needles, (2) a core particle screened with a shell of needles, and (3) an impermeable sphere with a radius equal to external radius \(1 + {{h}_{{\text{w}}}}\) of the porous shell to Stokes drag force F0 of a needle-free particle as depending on the thickness of the layer of needles. The numbers of needles in the shells are \(N\) = (a) 14, (b) 64, and (c) 256.

Full size image

As follows from this figure, the shell of the needles markedly increases the total drag of a particle only at relatively large values of N and \({{h}_{{\text{w}}}}.\) At the same time, the porous layer screens the core particle, thereby markedly decreasing its drag. Note that the character of the dependence of the drag force on the radius and permeability of the porous shell with no account of the gas slip coincides with the analytical solution obtained for a sphere with a uniform permeable porous shell in terms of the classical approach based on the combined solution of the Stokes and Brinkman equations [19].

Conditions for Nanoneedle-Coated Particle Blowing Away from Smooth Fiber

To determine the velocity at which force \(F\) is comparable with the force of rigid needle adhesion to a smooth fiber, let us consider a particle at contact point \(\rho = 1 + {{h}_{w}} + {r \mathord{\left/ {\vphantom {r a}} \right. \kern-0em} a}\) in the axial line behind a fiber at \(\theta = \pi \) (Fig. 6), where \(\rho \) and \(\theta \) are polar coordinates.

Fig. 6.
figure 6

Particle, which is coated with a porous shell composed of needles and brought in contact with a fiber flowed around by a Stokes flow (row of fibers with \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}\) = 0.2).

Full size image

In this case, force balance (6) can be exactly calculated, because the Stokes force and the van der Waals attractive force are directed oppositely along the same line. The Stokes drag force of the particle is calculated by the equation for the dimensionless radial component of the velocity near the fiber in the Kuwabara cell at packing density of fibers \(\alpha = {1 \mathord{\left/ {\vphantom {1 {36}}} \right. \kern-0em} {36}}\) [22]:

$$\begin{gathered} {{u}_{\rho }} = - \cos \theta \left\{ {A + B\frac{1}{{{{\rho }^{2}}}} + C\ln \rho - D{{\rho }^{2}}} \right\}, \\ A = - 0.67 + \frac{{2.51{\text{Kn}}}}{{1 + 3.66{\text{Kn}}}},\,\,\,\,B = \frac{{0.692 - 2.51{\text{Kn}}}}{{1 + 3.69{\text{Kn}}}}, \\ C = \frac{{1.43 - 1.72{\text{Kn}}}}{{1 + 4.3{\text{Kn}}}},\,\,\,\,D = \frac{{0.022 - 0.00801{\text{Kn}}}}{{1 + 1.44{\text{Kn}}}}, \\ \end{gathered} $$
(10)

where \({\text{Kn}} = {\lambda \mathord{\left/ {\vphantom {\lambda a}} \right. \kern-0em} a}\) is the Knudsen number for the fiber. Figures 7 and 8 show the flow velocities, at which particles with porous shells composed of needles can be blown away, as depending on the height of the needles in the shell of the particle and the fiber radius. These velocities are calculated by Eqs. (7) and (10). Here, we use approximate equation

$$F = 6\pi \mu rU\left( {1 + 0.066{{h}_{{\text{w}}}} + 0.587h_{{\text{w}}}^{2} - 0.201h_{{\text{w}}}^{{\text{3}}}} \right),$$
(11)

for the Stokes force with the correction for the drag of the porous shell. This equation was proposed on the basis of the results of calculations carried out within a range of \({{h}_{{\text{w}}}} = 0{\kern 1pt} - {\kern 1pt} 1\) for a particle with a shell consisting of N = 64 thin ellipsoids.

Fig. 7.
figure 7

Flow velocity before a filter above which particles with a layer of needles are blown away from the surface of a smooth fiber at \(\theta = \pi \) (axial line is behind the fiber flowed around) as depending on the height of conical needles with \(2\phi \) = (1) 15°, (2) 30°, and (3) 60°; \(2{{a}_{{\text{w}}}} = 0.032,\) \(r\) = 0.2 µm, \(a\) = 1 µm, and \({{A}_{6}}\) = 10–13 erg.

Full size image
Fig. 8.
figure 8

Flow velocity at the inlet of a filter above which particles with a layer of conical needles with \(2\phi \) = 30° at \(\theta = \pi \) are blown away as depending on the radius of a smooth fiber. (1) Assessment on the basis of drag force (10) of a particle with ellipsoidal needles; (2) assessment by Eq. (2) with no account of the contribution from the shell of ultrathin whiskers to the drag: \(2{{a}_{{\text{w}}}} = 0.032,\) \({{h}_{{\text{w}}}} = r = 0.2\) µm, and \({{A}_{6}}\) = 10–13 erg.

Full size image

The calculations have shown that, as the needle height decreases, the influence of retarded van der Waals force (3) of attraction between the particle and the fiber begins to manifest itself, thereby enhancing the attraction. In this case, the particle is blown away at a higher flow velocity (Fig. 7). It is obvious that the velocity of blowing away decreases with a reduction in the aperture angle of the conical needle vertex, i.e., with a decrease in the van der Waals attraction to the fiber. As height \(h{}_{{\text{w}}}\) of the ultrathin needles increases, the particle passes into the region where the local flow velocity and, hence, the Stokes force are enhanced. This explains the descending character of the curves in Fig. 7. When considering ultrathin needles having a radius comparable with the mean free path of air molecules, it is reasonable to assume that their contribution to the total drag of a particle is negligible. In this case, the drag of a particle located at distance \(\rho = {{(a + d + h_{{\text{w}}}^{*} + r)} \mathord{\left/ {\vphantom {{(a + d + h_{{\text{w}}}^{*} + r)} a}} \right. \kern-0em} a}\) from a fiber may be determined by Eq. (2) for the Stokes force with the Cunningham correction (Fig. 8, curve 2). It also follows from Fig. 8 that, as the fiber radius decreases, the velocity of blowing away also decreases, because the effect of the gas slip at submicron fibers develops, and the local flow velocity at the fiber increases.

Thus, the performed estimations have shown that there are conditions under which particles with shells consisting of needles are not adhered to fibers. This is possible at flow velocities typical of the fine filtration. In subsequent studies, the elastic properties of nanowhiskers; the role of external conditions, such as humidity and temperature; and the effect of the gas slip at ultrathin whiskers should be taken into account, and the reported results should be experimentally verified.

4 CONCLUSIONS

The influence of highly porous surface layers formed from radially oriented nanoneedles on filter fibers or particles on the efficiency of gas filtration has been studied at small Reynolds numbers. The three-dimensional field of velocities has been calculated for a system of fibers with highly porous layers of needless flowed around by a Stokes flow. The balance of the viscous and van der Waals forces applied to a particle occurring in contact with a fiber has been used to predict the conditions, under which the deposition of submicron particles onto fibers with the shells consisting of the heedless is inefficient. It has been shown that, at a flow velocity typical of fine filtration, solid undeformable particles are not blown away from the lateral surfaces of thin rigid needles, because the force of particle adhesion to the needles is several orders of magnitude greater than the Stokes force. It may be believed that, at low flow velocities, deformable particles cannot, all the more, be blown away, because their deformation increases the contact area. It has been shown that blowing away is possible only when a solid particle is brought in contact with a needle point. For example, large solid particles may remain uncollected by a porous shell with a high packing density of solid sharp needles. In this connection, it should be noted that it is reasonable to form highly porous shells with a high permeability, owing to which, their efficiency and the quality criterion of a filter increase [2].

The collection of needle-coated aerosol particles in filters has also been considered. Drag forces have been calculated for such particles moving in a Stokes flow. It has been noted that biological and polymer particles with flexible needles must not be blown away from even thin submicron fibers. However, it has been shown that rigid particles may remain uncollected because of a low adhesion of a rigid needle to a fiber. This effect should be taken into account when taking samples and calculating the collection efficiency of aerosols.