Non-intersecting Brownian Bridges in the Flat-to-Flat Geometry

Abstract

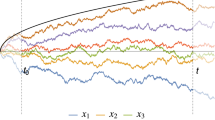
We study N vicious Brownian bridges propagating from an initial configuration $\{a_1< a_2< \ldots < a_N \}$ at time $t=0$ to a final configuration $\{b_1< b_2< \ldots < b_N \}$ at time $t=t_f$, while staying non-intersecting for all $0\le t \le t_f$. We first show that this problem can be mapped to a non-intersecting Dyson’s Brownian bridges with Dyson index $\beta =2$. For the latter we derive an exact effective Langevin equation that allows to generate very efficiently the vicious bridge configurations. In particular, for the flat-to-flat configuration in the large N limit, where $a_i = b_i = (i-1)/N$, for $i = 1, \ldots , N$, we use this effective Langevin equation to derive an exact Burgers’ equation (in the inviscid limit) for the Green’s function and solve this Burgers’ equation for arbitrary time $0 \le t\le t_f$. At certain specific values of intermediate times t, such as $t=t_f/2$, $t=t_f/3$ and $t=t_f/4$ we obtain the average density of the flat-to-flat bridge explicitly. We also derive explicitly how the two edges of the average density evolve from time $t=0$ to time $t=t_f$. Finally, we discuss connections to some well known problems, such as the Chern–Simons model, the related Stieltjes–Wigert orthogonal polynomials and the Borodin–Muttalib ensemble of determinantal point processes.

Appendices

Appendix A: Derivation of Eq. (43)

We recall the definition of characteristic polynomial (42) and formulate its “non-averaged” version

$$\begin{aligned} \tilde{\Omega }_N(y) = \prod _{i=1}^N \left( e^y-x_i \right) . \end{aligned}$$

The positions $x_i$ evolve according to the Langevin equation (36) which is rewritten as the following stochastic differential equation (hereafter SDE)

$$\begin{aligned} dx_i = \frac{1}{N t_f} \sum _{j(\ne i)} \frac{x_i^2}{x_i - x_j} d \theta + \frac{1+\theta }{t_f} x_i dW_i \;, \end{aligned}$$

(A1)

where the Wiener process is defined by $dW_i dW_j = \delta _{ij} \frac{1}{N} d\theta$. We compute the evolution equation for $\tilde{\Omega }_N(y)$ under the stochastic motion (A1). To this end, we use Ito’s lemma

$$\begin{aligned} d\tilde{\Omega }_N = \sum _i \frac{\partial \tilde{\Omega }_N}{\partial x_i} dx_i + \frac{1}{2} \sum _{i,j} \frac{\partial ^2 \tilde{\Omega }_N}{\partial x_i\partial x_j} dx_i dx_j \;. \end{aligned}$$

(A2)

We compute the derivatives as

$$\begin{aligned} \frac{\partial \tilde{\Omega }_N}{\partial x_i}&= - \frac{\tilde{\Omega }_N}{e^y-x_i} \;, \\ \frac{\partial ^2 \tilde{\Omega }_N}{\partial x_i \partial x_j}&= 0 \;, \\ \end{aligned}$$

and find

$$\begin{aligned}&\sum _i \frac{\partial \tilde{\Omega }_N}{\partial x_i} dx_i = - \tilde{\Omega }_N \left( \frac{N-1}{Nt_f} d\theta \sum _i \frac{x_i}{e^y-x_i} + \frac{1}{Nt_f} d\theta \sum _{j(\ne i)} \frac{x_i x_j}{(e^y-x_i)(x_i - x_j)}\right. \nonumber \\&\quad \left. + \frac{1+\theta }{Nt_f} \sum _i \frac{x_i dW_i}{e^y-x_i} \right) , \nonumber \\&\sum _{i,j} \frac{\partial ^2 {\tilde{\Omega }}_N}{\partial x_i\partial x_j} dx_i dx_j = 0 \;. \end{aligned}$$

(A3)

To obtain a closed equation, each term in the above expression ought to be expressed in terms of $\tilde{\Omega }_N$. To this end, we compute first partial results

$$\begin{aligned} \partial _y \tilde{\Omega }_N&= e^y \tilde{\Omega }_N \sum _i \frac{1}{e^y-x_i},\\ \partial _{yy} \tilde{\Omega }_N -\partial _y \tilde{\Omega }_N&= \tilde{\Omega }_N \sum _{i\ne j} \frac{e^{2y}}{(e^y-x_i)(e^y-x_j)}, \end{aligned}$$

and use them to get

$$\begin{aligned}&\sum _i \frac{x_i}{e^y-x_i} = -N + e^y \sum _i \frac{1}{e^y-x_i} = - N + \frac{\partial _y \tilde{\Omega }_N}{\tilde{\Omega }_N}, \end{aligned}$$

(A4)

$$\begin{aligned}&\sum _{i\ne j} \frac{x_i x_j}{(e^y-x_i)(x_i - x_j)} = \frac{N(N-1)}{2} + e^y(N-1) \sum _i \frac{1}{x_i - e^y} \nonumber \\&+ \frac{e^{2y}}{2} \sum _{i\ne j} \frac{1}{(x_i - e^y)(x_j - e^y)} \nonumber \\&\quad = \frac{N(N-1)}{2} - (N-1) \frac{\partial _y \tilde{\Omega }_N}{\tilde{\Omega }_N} + \frac{\partial _{yy} \tilde{\Omega }_N}{2\tilde{\Omega }_N} - \frac{\partial _{y} \tilde{\Omega }_N}{2\tilde{\Omega }_N} \;, \end{aligned}$$

(A5)

which are plugged back into Eq. (A3) and (A2) to yield

$$\begin{aligned} d\tilde{\Omega }_N =&\frac{N-1}{2t_f}\tilde{\Omega }_N d\theta + \frac{1}{2Nt_f} \left( \partial _y \tilde{\Omega }_N - \partial _{yy} \tilde{\Omega }_N \right) d\theta - \frac{1+\theta }{Nt_f} \tilde{\Omega }_N \sum _i \frac{x_i dW_i}{e^y-x_i}. \end{aligned}$$

This is a closed equation for ${\tilde{\Omega }}_N$ and the stochastic part is proportional to $dW_i$. This thus drops out when looking at the averaged characteristic polynomial $\langle \tilde{\Omega }_N\rangle = \Omega _N$, i.e.,

$$\begin{aligned} \partial _\theta \Omega _N = \frac{N-1}{2t_f}\Omega _N + \frac{1}{2Nt_f} \left( \partial _y \Omega _N - \partial _{yy} \Omega _N \right) , \end{aligned}$$

which is exactly the Eq. (43) given in the text.

Appendix B: Derivation of Eq. (68)

We start from the Sochocki–Plemejl formula relating the particle density and the e-Green’s function H

$$\begin{aligned} \rho ^{(x)} (x,\theta ) = -\frac{t_f}{\pi } \lim _{\epsilon \rightarrow 0_+} \text {Im} \left[ \frac{1}{w} \ln H(w;\theta ) \right] _{w = x-i\epsilon } \;. \end{aligned}$$

(B1)

We use the complex logarithm formula

$$\begin{aligned} \ln (H(x-i\epsilon )) = \ln |H(x-i\epsilon )| + i \arg H(x-i\epsilon )) + 2k\pi i \;, \end{aligned}$$

where k enumerates the branch cuts of the logarithm and where the real and imaginary parts are clearly separated. We also expand $1/(x-i\epsilon ) = \frac{x+i\epsilon }{x^2+\epsilon ^2}$, plug these two formulas into Eq. (B1) and find

$$\begin{aligned} \rho ^{(x)} (x,\theta ) = -\frac{t_f}{\pi } \lim _{\epsilon \rightarrow 0_+} \left[ \frac{\epsilon \ln |H(x-i\epsilon )|}{x^2+\epsilon ^2} + \frac{x}{x^2+\epsilon ^2} ( \arg H(x-i\epsilon )+2k\pi ) \right] \;. \end{aligned}$$

We assume that $\frac{\epsilon \ln |H(x-i\epsilon )|}{x^2+\epsilon ^2} \rightarrow 0$ as $\epsilon \rightarrow 0$ and we are left with

$$\begin{aligned} \rho ^{(x)} (x,\theta ) = -\frac{t_f}{\pi } \lim _{\epsilon \rightarrow 0_+} \left[ \frac{x}{x^2+\epsilon ^2} ( \arg H(x-i\epsilon )+2k\pi ) \right] \;. \end{aligned}$$

We choose the branch $k=0$ to make the resulting density normalizable (i.e. not divergent) and for $x>0$ the term $x/(x^2+\epsilon ^2)$ is regular and can be safely taken out of the limit which finally gives Eq. (68).

Appendix C: Calculation of the Moments of the average density for $t=t_f/2$.

In this Appendix we compute the moments of the densities $\rho ^{(x)}$ in Eq. (73) and $\rho ^{(\lambda )}$ in Eq. (74). We start with $\rho ^{(x)}$ and set $w_\pm ^{(1)} = x_\pm$ in Eq. (73). The k-th moment of the average density, using Eq. (73), is then given by

$$\begin{aligned} m^{(x)}_{k,\theta =1} = \int _{x_-}^{x_+} dx\, x^k \rho ^{(x)}(x;\theta =1) = \frac{t_f}{\pi } \int _{x_-}^{x_+} dx \, x^{k-1} \arctan \left[ \frac{\sqrt{4x-(1 + xT )^2}}{1+xT}\right] \;. \end{aligned}$$

(C1)

We perform a change of variables $x = \frac{1}{T} \left( \frac{2}{T} \left( 1+ \sqrt{1-T}p \right) - 1 \right)$, $dx = \frac{2\sqrt{1-T}}{T^2} dp$ resulting in

$$\begin{aligned} m^{(x)}_{k,\theta =1} = \frac{2t_f \sqrt{1-T}}{\pi T^{2k}} \int _{-1}^1 dp \left( 2p\sqrt{1-T} + 2-T \right) ^{k-1} \arctan \left( \frac{\sqrt{1-T}\sqrt{1-p^2}}{1+\sqrt{1-T}p} \right) . \end{aligned}$$

We continue with integration by parts. Since by normalization the zeroth moment is unity $m_{0,\theta =1}^{(x)} = 1$, we continue with $k \ge 1$ for which the following formula holds:

$$\begin{aligned} m^{(x)}_{k,\theta =1} = - \frac{t_f(2\sqrt{1-T})^{k-1}}{k\pi T^{2k}} \sum _{n=0}^{k-1} \left( {\begin{array}{c}k-1\\ n\end{array}}\right) \left( \! \frac{2-T}{2\sqrt{1-T}} \!\right) ^{k-1\!-\!n} \left[ (T\!-\!1) J_n \!-\! \sqrt{1-T} J_{n+1} \right] , \end{aligned}$$

where $J_n = \int _{-1}^1 dp p^n/\sqrt{1-p^2}$. These integrals are expressible via Catalan numbers $C_n = \frac{1}{n+1} \left( {\begin{array}{c}2n\\ n\end{array}}\right)$ since $J_0 = \pi$, $J_{2n} = \frac{2\pi (2n-1)}{4^n} C_{n-1}$ and $J_{2n-1} = 0$ for $n>0$:

$$\begin{aligned} m^{(x)}_{k,\theta =1}&= \frac{t_f (1-T)(2-T )^{k-1}}{kT^{2k}} + \frac{2t_f(1-T)^2(2-T)^{k-3}}{k T^{2k}}\nonumber \\&\quad \sum _{n=0}^{\lfloor \frac{k-1}{2} \rfloor -1} \left( {\begin{array}{c}k-1\\ 2n+2\end{array}}\right) \left( \frac{\sqrt{1-T}}{2-T} \right) ^{2n} (2n+1) C_{n} + \nonumber \\&\quad + \frac{t_f(1-T)(2-T)^{k-2}}{k T^{2k}} \sum _{n=0}^{\lfloor \frac{k}{2}-1 \rfloor } \left( {\begin{array}{c}k-1\\ 2n+1\end{array}}\right) \left( \frac{\sqrt{1-T}}{2-T} \right) ^{2n} (2n+1) C_{n} \;. \end{aligned}$$

(C2)

Thus, interestingly, the Catalan numbers also appear here.

An alternative formulation of these moments in terms of the modified Bessel function is possible with the use of an identity $\int _{-1}^1 dp \frac{e^{-\alpha p}}{\sqrt{1-p^2}} = \pi I_0(\alpha )$ applied to the integrals $J_n = (-1)^n \lim \limits _{\alpha \rightarrow 0} \frac{\partial ^n}{\partial \alpha ^n} \int _{-1}^1 dp \frac{e^{-\alpha p}}{\sqrt{1-p^2}}$. We find:

$$\begin{aligned} m_{k,\theta =1}^{(x)}&= \frac{t_f a (-2)^{k-1}}{k T^{2k}} \frac{\partial ^{k-1}}{\partial \alpha ^{k-1}} \left[ e^{-\frac{\alpha (2-T)}{2} } \left( a I_0(\alpha a) - I_1 (\alpha a) \right) \right] _{\alpha =0}, \qquad k \ge 1, \end{aligned}$$

where $a = \sqrt{1-T}$ and $I_i(x)$ is the modified Bessel function.

Using the relation (39) between particle densities in x and $\lambda$ spaces, we translate the moments find

$$\begin{aligned} m^{(\lambda )}_{k,\theta =1}&= \int _{\lambda _-}^{\lambda _+} d\lambda \lambda ^k \rho ^{(\lambda )}(\lambda ;\theta =1)\\&= \frac{t_f}{\pi } \left( \frac{t_f}{2} \right) ^k \int _{x_-}^{x_+} \frac{dx}{x} (\log x )^k \arctan \left( \frac{\sqrt{4x-(1+xT)^2}}{1+xT} \right) . \end{aligned}$$

We again change the variables:

$$\begin{aligned} m^{(\lambda )}_{k,\theta =1} = \frac{t_f a}{2\pi (k+1)} \left( \frac{t_f}{2} \right) ^k \int _{-1}^1 dp \frac{(c + \log (ap + b))^{k+1} (a+p) }{(ap+b)\sqrt{1-p^2}}, \end{aligned}$$

with $a = \sqrt{1-T}, b = 1-T/2, c = \log 2 + 2/t_f$. Now with the identity $\int _{-1}^1 dp \frac{1}{(ap+b)^\alpha \sqrt{1-p^2}} = \frac{\pi }{\sqrt{b^2-a^2}^\alpha } P_\alpha \left( \frac{b}{\sqrt{b^2-a^2}}\right)$ where $P_\alpha$ is a Legendre function, the moments in $\lambda$ space are given by:

$$\begin{aligned} m_{k,\theta =1}^{(\lambda )} = \frac{t_f(-1)^{k+1}}{2 (k+1)} \left( \frac{t_f}{2} \right) ^k \frac{\partial ^{k+1}}{\partial \alpha ^{k+1}}\left[ T^\alpha \left( P_{\alpha -1} \left( \frac{2-T}{T} \right) - P_{\alpha } \left( \frac{2-T}{T} \right) \right) \right] _{\alpha = 0}. \end{aligned}$$

As a last step, we propose a general identity (found only in special case $n=2$ in eq. 1.9 of [52] but checked by us numerically in Mathematica for n up to 5):

$$\begin{aligned} \frac{\partial ^n}{\partial \alpha ^n} \left[ P_{\alpha -1} \left( x \right) - P_{\alpha } \left( x \right) \right] _{\alpha = 0} = {\left\{ \begin{array}{ll} 0, &{} n \text { is even}\\ -2 \frac{\partial ^n}{\partial \alpha ^n} P_\alpha (x)_{\alpha =0}, &{} n \text { is odd}, \end{array}\right. }, \end{aligned}$$

which renders the final expression:

$$\begin{aligned} m_{k,\theta =1}^{(\lambda )} = \frac{t_f}{(k+1)} \left( -\frac{t_f}{2} \right) ^k \sum _{l=0}^{\left\lfloor \frac{k+1}{2} \right\rfloor } \left( {\begin{array}{c}k+1\\ l\end{array}}\right) (\log T)^{k-2l} \frac{\partial ^{2l+1}}{\partial \alpha ^{2l+1}}\left( P_{\alpha } \left( \frac{2-T}{T} \right) \right) _{\alpha = 0} \;. \end{aligned}$$

(C3)

Although the expression for the moments in the x-space in (C2) is easy to evaluate numerically, evaluating explicitly the moments in the $\lambda$-space from Eq. (C3) is difficult due to the apparent lack of explicit formulae for the derivatives of the Legendre function with respect to its degree (see e.g. [52]).

Appendix D: Computation of the Support for the $\beta =2$ Dyson’s Brownian Motion

We consider the Dyson’s Brownian motion with $\beta =2$ where the positions $\lambda _i(t)$ of N particles evolve in time via Eq. (5), starting from the initial positions $\vec {a}$ at $t=0$. One defines the Green’s function $G_N(z,t)$

$$\begin{aligned} G_N(z;t) = \frac{1}{N} \sum _{i=1}^N \frac{1}{z-\lambda _i(t)} \;. \end{aligned}$$

(D1)

The average density can be obtained via the Sochocki–Plemelj formula

$$\begin{aligned} \rho (\lambda ;t) = \frac{1}{\pi } \,\mathrm{Im}\,G_N(z - i 0^+;t) \;. \end{aligned}$$

(D2)

In the large N limit, this converges to

$$\begin{aligned} G(z;t) = G_\infty (z,t) = \int \frac{\rho (\lambda ;t)}{z-\lambda } \, d\lambda \;, \end{aligned}$$

(D3)

where $\rho (\lambda ;t)$ is the average density at time t. Thus the initial condition for G(z; t) reads

$$\begin{aligned} G(z;t=0) = G_0(z) = \int \frac{\rho (\lambda ;0)}{z-\lambda } \, d\lambda \;, \end{aligned}$$

(D4)

where $\rho (\lambda ;0)$ is the initial density. In the large N limit, one can show that G(z, t) satisfies the inviscid Burgers’ equation [38,39,40,41]

$$\begin{aligned} \partial _t G(t) + G(z,t) \partial _z G(z,t) = 0 \;. \end{aligned}$$

(D5)

The solution can be obtained in the parametric form by the method of characteristics, as discussed in Sect. 3. It reads

$$\begin{aligned} G(z;t) = G_0(\xi ) \;, \end{aligned}$$

(D6)

where $\xi$ and z are related by

$$\begin{aligned} z = \xi + t \,G_0(\xi ) \;. \end{aligned}$$

(D7)

Given z and t, we need to solve Eq. (D7) for $\xi$ and then substitute in Eq. (D6) to obtain G(z; t).

Let us first discuss some general properties of the Green’s function G(z; t). Consider first G(z; t) as a function of z along the positive real axis. An exactly similar analysis can be done on the negative real axis. From the definition in Eq. (D1), it is clear that as $z \rightarrow \infty$, $G(z;t) \simeq 1/z$ since $\rho (\lambda ;t)$ is normalized to 1. As z decreases from $+\infty$, G(z; t) typically increases with decreasing z. However, this does not go on for ever since we expect that there will be a cut along the real axis where G(z; t) acquires a nonzero imaginary part, which gives rise to a nonzero density via Eq. (D2). Let $z_{\mathrm{edge}}(t)$ denote this value of z below which G(z; t) is imaginary. Clearly, this is also the upper edge of the support of the density. Thus in the range $[z_{\mathrm{edge}}(t), +\infty )$, G(z; t) is a monotonically decreasing function of z. Similarly, the function $G_0(\xi )$ is, generically, a monotonically decreasing function of $\xi$ for $\xi \in [\xi _{\mathrm{edge}}, +\infty )$ and decays for large $\xi$ as $G_0(\xi ) \simeq 1/\xi$. Note that, for simplicity, we have presented only the behavior for the upper edge of the support of the density. A similar analysis can be done for the lower edge of the support, for which we need to analyse the Green’s function G(z; t) on the negative real axis in the complex z-plane.

Given z and t, we now want to find the solution for $\xi$ from Eq. (D7). Suppose that we plot z as a function of $\xi$ for $\xi > \xi _{\mathrm{edge}}$. The rhs of (D7) is the sum of two terms: the first one increases linearly with $\xi$ while the second term, for fixed t, is a decreasing function of $\xi$. Hence their sum, when plotted as a function of $\xi$ will first decrease with increasing $\xi$, achieves a minimum at $\xi _c(t)$ and then increases monotonically with $\xi$ (see Fig. 9). For a given z and t, this equation (D7) has typically two solutions $\xi _1(z) < \xi _2(z)$. Here, $\xi _2(z)$ is a monotonically increasing function of z, while $\xi _1(z)$ is a monotonically decreasing function of z (see Fig. 9). The correct solution is actually given by $\xi _2(z)$. This is because from Eq. (D6) we see that since G(z; t) is a monotonically decreasing function of z and $G_0(\xi )$ is also a monotonically decreasing function of $\xi$, hence z must be a monotonically increasing function of $\xi$. This justifies the fact that $\xi _2(z)$ is the correct root. Note however that $\xi _2(z)$ exists only if $z \ge z_c(t)$ where $z_c(t)$ is the value of $z(\xi ) = \xi + t \, G_0(\xi )$ at the minimum located at $\xi = \xi _c(t)$ (see Fig. 9). This minimum is obtained by setting

$$\begin{aligned} \frac{dz}{d\xi } = 1 + t \, G_0'(\xi ) = 0 \;. \end{aligned}$$

(D8)

Fig. 9

Plot of $z(\xi )$ in Eq. (D7) for $G_0(\xi ) = 1/\xi$ and $t=1/2$

This gives the value $\xi _c(t)$ and consequently

$$\begin{aligned} z_c(t) = \xi _c(t) + t \, G_0(\xi _c(t)) \;. \end{aligned}$$

(D9)

Therefore we see that the real solution exists only for $z \ge z_c(t)$. Thus we identify

$$\begin{aligned} z_{\mathrm{edge}}(t) = z_c(t) \;. \end{aligned}$$

(D10)

As an example, let us consider the simple case where all the particles start at the origin, i.e. $\rho (\lambda ;0) = \delta (\lambda )$. In this case, from Eq. (D4) we have $G_0(\xi ) = 1/\xi$. In this case $\xi _{\mathrm{edge}} = 0$. Consequently, from Eq. (D8), we get

$$\begin{aligned} \xi _c(t) = \sqrt{t} \;. \end{aligned}$$

(D11)

Note that $\xi _c(t)$ has nothing to do with $\xi _{\mathrm{edge}}$. Here we are considering the positive side of the support, hence we choose the positive root in (D11). Similarly, when analyzing the lower edge of the support, we should instead choose the negative root $\xi _c(t) = - \sqrt{t}$. From Eq. (D9) one gets for the positive side

$$\begin{aligned} z_c(t) = \sqrt{4\,t} \;. \end{aligned}$$

(D12)

This result tells us how the upper support of the average density evolves with time t. Indeed, in this case, one can solve for $\xi$ from the quadratic equation $z = \xi + t/\xi$, which gives two roots: $\xi _1(z) = (z - \sqrt{z^2-4})/2$ and $\xi _2(z) = (z + \sqrt{z^2-4t})/2$. As argued earlier, we choose the second branch as the correct one, i.e., $\xi = (z + \sqrt{z^2-4t})/2$. Consequently, from Eq. (D6) one gets

$$\begin{aligned} G(z;t) = G_0(\xi ) = \frac{2}{z + \sqrt{z^2-4t}} = \frac{1}{2t} \left( z - \sqrt{z^2-4t} \right) \;. \end{aligned}$$

(D13)

Therefore, from the relation (D2), the average density at time t is given by the semi-circular form

$$\begin{aligned} \rho (\lambda ;t) = \frac{1}{2\pi t} \sqrt{4t - \lambda ^2} \;. \end{aligned}$$

(D14)

Hence we see that the density is supported over the interval $[-\sqrt{4t},+\sqrt{4t}]$ and indeed the upper support $\sqrt{4t}$ coincides with the value of $z_c(t)=z_{\mathrm{edge}}(t)$ in Eqs. (D10) and (D12).