1 Introduction

Cooperative relaying utilizes additional relay nodes to assist information delivery between sources and destinations and thus can enlarge wireless communication coverage, combat channel fading and enhance received signal strength [1, 2]. In recent years, much attention has concentrated on a three-node cooperative relaying scenario, also called as bidirectional relaying (BDR) [3], where two sources want to deliver information to each other via a cooperative relay node. Initially, BDR is developed to enhance the spectrum efficiency and throughput of the two sources. With the continuously rapid growth of wireless communication services, however, energy conservation has turned into the primary considerations for modern wireless communications [3]. Therefore, in the research community, a great deal of research attention has been paid to developing effective physical-layer relaying and transmission techniques for achieving energy efficiency (EE).

Generally, a BDR system (BDRS) can employ either an amplify-and-forward (AF) relay or a decode-and-forward (DF) relay and adopt the time division broadcast (TDBC) or the multiple-access broadcast (MABC) transmission styles [4]. In case that an AF relay node is employed, the MABC transmission style would be adopted because it requires less number of channel uses for one cycle information delivery between the two sources. On the other hand, if a DF relay node is used, the TDBC transmission style is preferred since the sources’ transmitted signals are separated by different time slots or frequency bands and thus benefits the decoding at the relay sides.

One valid physical-layer method for enhancing EE of wireless communications is the utilization of power adaptation techniques [5,6,7], whereby a transmitter can frequently adapt its transmit-power level in the light of the wireless channel states as well as the quality-of-service (QoS) requirements of receivers. It is well known that a transmitter should use the channel knowledge so as to implement power adaptation. Generally, there exist two kinds of channel knowledge, i.e., instantaneous and statistical channel knowledge [8]. To acquire channel knowledge, a transmitter should first transmit training signals to its receiver. Then, the receiver assesses the channel based on the received training signals and next delivers the channel knowledge back to the transmitter through a feedback channel. It should be noted that instantaneous channel knowledge is a representation of the real-time properties of a channel, while statistical channel knowledge is just a long-term description of a channel. It is worth mentioning that in a time-division-duplex setting, a transmitter can acquire statistical channel knowledge by a long-term observation without any feedback transmissions from the receiver.

Another effective physical-layer approach to enhancing EE is the utilization of relay selection techniques. Generally speaking, there exist two kinds of relay selection techniques, i.e., centralized and decentralized techniques [5]. In view of cost saving, decentralized relay selection techniques are more preferred in practical implementations since centralized techniques always need much overhead to be exchanged between sources and relays [5]. Moreover, it is known that wireless relay nodes are usually battery-powered, and their overall energy to be available is limited. Therefore, from a practical implementation viewpoint, energy saving is very important for BDRSs.

2 Related works

Recently, the principles of power adaptation and relay selection have already been investigated for BDRSs, giving various physical-layer relaying and transmission techniques [5]-[12]. The authors of [5] took a BDRS using an AF relay into consideration and proposed a joint power adaptation and relay selection technique, minimizing the total transmit power. By using the statistical channel knowledge, a joint power adaptation and relay location algorithm was developed in [6] to reduce the total transmit power of an AF relay-assisted BDRS while guaranteeing the QoS requirement of the system. In [7], a DF relay-assisted BDRS with a fixed packet rate was investigated, leading to three power adaptation algorithms, minimizing the system, the relay and the source energy consumption, respectively. Then, the authors of [7] combined the optimized algorithms for minimizing the system and relay energy consumption into a generalized one, and it is demonstrated that the generalized algorithm is not only energy efficient for the desired packet rate but also rate optimal for the consumed energy. The authors of [9] investigated the relationship between spectrum efficiency and EE for AF relaying, DF relaying and compress-and-forward relaying systems. In addition, the investigation of spectrum efficiency and EE trade-off for BDRSs can be found in [10] and references therein. The authors of [11] considered a BDRS using digital network coding and proposed a set of transmission styles with the goal of minimizing the energy consumption by computing the optimal fraction of resources allocated to each style. The authors of [12] compared the energy consumption of BDRSs with different coding schemes, i.e., physical-layer network coding, digital network coding and superposition coding. It is demonstrated that digital network coding outperforms superposition coding in terms of total average energy consumption, and digital network coding performs better than physical-layer network coding if the required packet rate is low and worse otherwise.

It should be noted that most of the studies mentioned earlier focus only on single-carrier systems. Currently, various physical-layer relaying and transmission techniques have been extended to orthogonal frequency division multiplexing (OFDM) modulated systems. The authors of [13] considered an OFDM modulated BDRS using digital network coding and proposed a joint resource allocation algorithm minimizing the total transmission completion time under individual power constraints. Considering a DF relay-assisted system, the authors of [14] developed a simultaneous wireless information and power transfer scheme. In [15], an overhearing-based interference cancellation scheme and a power allocation algorithm were developed for a non-concurrent BDRS with the aim of maximizing the system sum rate. The authors of [16] proposed a resource management scheme controlling the transmit-power levels of the nodes and assigning the bit rates among different subcarriers so as to minimize the total transmit power of the system, while ensuring the target rates of the two sources. In [17], a multiple AF relays-assisted BDRS was investigated, leading to a joint implementation algorithm of subcarrier pairing and allocation, relay selection and transmit-power allocation. In [18], the system outage performance was studied for an OFDM modulated BDRS using a nonlinear AF relaying scheme. Our investigations show that EE techniques for BDRSs have not been well studied in the literature, especially in the case that the system has a QoS requirement and different kinds of resource management techniques are considered together under an OFDM modulated setting. Most recently, there are emerging some new concepts and techniques in the wireless communication community, e.g., full-duplex relaying [19], non-orthogonal multiple-access [20], wireless-powered information transmissions [21] and energy harvesting [22], which have been received much attention.

In this paper, we consider an AF relay-assisted BDRS utilizing the MABC transmission style. Unlike the existing studies, our goal is to develop a holistic resource management algorithm for joint implementation of relay selection, power adaptation and bit-rate management so as to maximize the system EE under a system QoS constraint. First, a general EE problem concerning the resource management is formulated. In order to solve the EE problem, a three-stage approach is proposed. At stage 1 (stage of power management), a per-subcarrier energy efficient problem is addressed, leading to a power adaptation algorithm for maximizing the system EE and ensuring the required level of the system QoS. Within the framework of the power adaptation algorithm and by exploiting spatial diversity of multiple-relay channels, distributed relay selection is investigated at stage 2 (stage of relay management). Next, we tackle at stage 3 the bit-rate management problem, namely assigning bit rate to different subcarriers to maximize the system EE further. Finally, summarizing the results achieved at the three stages, a novel EE technology combined with bit-rate assignment, power adaptation and relay selection is developed for optimal EE.

3 Method

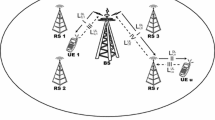
We consider a BDRS consisting of two sources and \(M\) relay nodes, each of which is equipped with a single antenna. As demonstrated in Fig.1, two sources A and B want to deliver information to each other via the \(m{\text{ - th}}\) half-duplex AF relay \({\text{R}}_{m}\), \(m \in \left\{ {1,2 \cdots ,M} \right\}\). Here, \({\text{R}}_{m}\) is chosen based on a pre-designed criterion. We use \({\mathbf{s}}_{u} \triangleq \left[ {s_{u} \left( 1 \right),s_{u} \left( 2 \right), \cdots ,s_{u} \left( K \right)} \right]^{{\text{T}}}\) and \({\mathbf{P}}_{u} \triangleq {\text{diag}}\left\{ {p_{u} \left( 1 \right), \cdots ,p_{u} \left( K \right)} \right\}\) to, respectively, denote the OFDM symbol and the transmit power of the source \(u\), where \(u \in \left\{ {{\text{A}},{\text{B}}} \right\}\), \(K\) is the number of subcarriers, and \(p_{u} \left( k \right)\), \(k \in \left\{ {1,2, \cdots ,K} \right\}\), stands for the transmit power of the node for the \(k{\text{ - th}}\) subcarrier. Likewise, \({\mathbf{P}}_{{{\text{R}},m}} \triangleq {\text{diag}}\left\{ {p_{{{\text{R}},m}} \left( 1 \right), \cdots ,p_{{{\text{R}},m}} \left( K \right)} \right\}\) is used to denote the transmit power of the \(m{\text{ - th}}\) relay node, where \(p_{{{\text{R,}}m}} \left( k \right)\) is the transmit power of the relay for the \(k{\text{ - th}}\) subcarrier. Suppose that \(s_{u} \left( k \right)\) has an unit energy and no direct link exists between A and B. We use \({\mathbf{G}}_{{u{\text{R}},m}} \triangleq {\text{diag}}\left\{ {g_{{u{\text{R}},m}} \left( 1 \right), \cdots ,g_{{u{\text{R}},m}} \left( K \right)} \right\}\) to denote the channel gain from the source \(u\) to the \(m{\text{ - th}}\) relay node, where \(g_{{u{\text{R}},m}} \left( k \right)\) represents the corresponding path gain for the \(k{\text{ - th}}\) subcarrier. In the paper, a propagation paradigm [3] is used to model \(g_{{u{\text{R}},m}} \left( k \right)\) as \(g_{{u{\text{R}},m}} \left( k \right) \triangleq {{h_{{u{\text{R}},m}} } \mathord{\left/ {\vphantom {{h_{{u{\text{R}},m}} } {\sqrt {d_{{u{\text{R}},m}}^{\alpha } } }}} \right. \kern-\nulldelimiterspace} {\sqrt {d_{{u{\text{R}},m}}^{\alpha } } }}\), where \(d_{{u{\text{R}},m}}\) and \(h_{{u{\text{R}},m}}\), respectively, denote the distance and the large-scale behavior of the path gain between the source \(u\) and the \(m{\text{ - th}}\) relay node, and \(\alpha\) is the corresponding path-loss coefficient. Without loss of generality, it is assumed that \(h_{{u{\text{R}},m}}\) is a complex Gaussian random variable and obeys \({\mathcal{C}\mathcal{N}}\left( {0,1} \right)\), and the channels are reciprocal and quasi-static. We use \({\mathbf{w}}_{u}\) and \({\mathbf{w}}_{{{\text{R}},m}}\) to denote the additive white Gaussian noises (AWGNs) at the source \(u\) and the \(m{\text{ - th}}\) relay node, respectively. Suppose that all the elements of AWGNs obey i.i.d. \({\mathcal{C}\mathcal{N}}\left( {0,1} \right)\).

As demonstrated in Fig. 1, one-cycle information delivery between A and B includes two phases, i.e., the multiple-access (MAC) and broadcast (BRC) phases. At the MAC phase, A and B, respectively, deliver \({\mathbf{s}}_{{\text{A}}}\) and \({\mathbf{s}}_{{\text{B}}}\) to all the relay nodes. Then, the chosen relay node receives

$${\mathbf{y}}_{{{\text{R}},m}} = {\mathbf{G}}_{{{\text{AR}},m}} \sqrt {{\mathbf{P}}_{{\text{A}}} } {\mathbf{s}}_{{\text{A}}} + {\mathbf{G}}_{{{\text{BR}},m}} \sqrt {{\mathbf{P}}_{{\text{B}}} } {\mathbf{s}}_{{\text{B}}} + {\mathbf{w}}_{{{\text{R}},m}} .$$
(1)

At the BRC phase, the relay node first scales each subcarrier of the received signal by a factor \({\mathbf{F}}_{m} \triangleq {\text{diag}}\left\{ {f_{m} \left( 1 \right), \cdots ,f_{m} \left( K \right)} \right\}\), where

$$f_{m} \left( k \right) = \frac{1}{{\sqrt {p_{{\text{A}}} \left( k \right)\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|^{2} + p_{{\text{B}}} \left( k \right)\left| {g_{{{\text{BR}}.m}} \left( k \right)} \right|^{2} + 1} }}.$$
(2)

Next, the relay node forwards the resulting signal to A and B. At the end of the BRC phase, the source \(u\) receives

$${\mathbf{y}}_{u} = {\mathbf{F}}_{m} \left( {\underbrace {{{\mathbf{G}}_{{u{\text{R}},m}} {\mathbf{G}}_{{u{\text{R}},m}} \sqrt {{\mathbf{P}}_{u} {\mathbf{P}}_{{{\text{R}},m}} } {\mathbf{s}}_{u} }}_{{{\text{self}} - {\text{int}} {\text{erference}}}} + {\mathbf{G}}_{{u{\text{R}},m}} {\mathbf{G}}_{{v{\text{R}},m}} \sqrt {{\mathbf{P}}_{v} {\mathbf{P}}_{{{\text{R}},m}} } {\mathbf{s}}_{v} + {\mathbf{G}}_{{u{\text{R}},m}} \sqrt {{\mathbf{P}}_{{{\text{R}},m}} } {\mathbf{w}}_{{{\text{R}},m}} } \right) + {\mathbf{w}}_{u} ,$$
(3)

where \(u,v \in \left\{ {{\text{A}},{\text{B}}} \right\}\) and \(u \ne v\). Armed with perfect channel knowledge, the source \(u\) can perform self-interference removal [16] and then acquire

$${\mathbf{y}}_{u}^{^{\prime}} = {\mathbf{F}}\left( {{\mathbf{G}}_{{u{\text{R}},m}} {\mathbf{G}}_{{v{\text{R}},m}} \sqrt {{\mathbf{P}}_{v} {\mathbf{P}}_{{{\text{R}},m}} } {\mathbf{s}}_{v} + {\mathbf{G}}_{{u{\text{R}},m}} \sqrt {{\mathbf{P}}_{{{\text{R}},m}} } {\mathbf{w}}_{{{\text{R}},m}} } \right) + {\mathbf{w}}_{u} .$$
(4)

As such, at the end of the BRC phase, the mutual information achieved by the source \(u\) can be expressed as [16],

$$I_{u} = \sum\limits_{k = 1}^{K} {I_{u} \left( k \right)} = \sum\limits_{k = 1}^{K} {\frac{1}{2}\log_{2} \left[ {1 + SNR_{u} \left( k \right)} \right]}$$
(5)

where \(I_{u} \left( k \right)\) and \(SNR_{u} \left( k \right)\) are the mutual information and the received SNR for the \(k{\text{ - th}}\) subcarrier and can be expressed as the following.

$$I_{u} \left( k \right) = \frac{1}{2}\log_{2} \left[ {1 + SNR_{u} \left( k \right)} \right]$$
(6)
$$SNR_{u} \left( k \right) = \frac{{p_{v} \left( k \right)p_{{\text{R}}} \left( k \right)\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|^{2} \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|^{2} }}{{\left[ {p_{u} \left( k \right) + p_{{\text{R}}} \left( k \right)} \right]\left| {g_{{u{\text{R}},m}} \left( k \right)} \right|^{2} + p_{v} \left( k \right)\left| {g_{{v{\text{R}},m}} \left( k \right)} \right|^{2} + 1}}$$
(7)

Here, energy-efficient techniques for the considered BDRS are studied. The aim is to maximize the delivered information bit per unit of energy of the BDRS. To achieve this goal, enabling techniques for EE, such as bit-rate management, power adaptation and relay selection, are investigated. Our idea is to develop a holistic algorithm for joint implementation of relay selection, power adaptation and bit-rate management so as to maximize the system EE. As such, a general optimization problem concerning the EE problem can be formulated as

$$\left[ {{\mathbf{P}}_{{\text{A}}}^{*} ,{\mathbf{P}}_{{\text{B}}}^{*} ,{\mathbf{P}}_{{{\text{R}},m^{*} }}^{*} ,r^{*} \left( k \right),m^{*} } \right] = \arg \mathop {\max }\limits_{{{\mathbf{P}}_{{\text{A}}} ,{\mathbf{P}}_{{\text{B}}} ,{\mathbf{P}}_{{{\text{R}},m}} ,r\left( k \right),m}} \frac{r}{{P_{{{\text{total}}}} }}$$
(8a)
$${\text{subject to Pr}}\left[ {{\text{min}}\left( {I_{{\text{A}}} ,I_{{\text{B}}} } \right) \le r} \right] \le Q_{{{\text{out}}}}$$
(8b)
$$\sum\limits_{k = 1}^{K} {r\left( k \right) = r}$$
(8c)
$$r\left( k \right) \ge 0$$
(8d)
$${\mathbf{P}}_{{\text{A}}} ,{\mathbf{P}}_{{\text{B}}} ,{\mathbf{P}}_{{{\text{R}},m}} \ge {\mathbf{0}}$$
(8e)
$$m \in \left\{ {1,2, \cdots ,M} \right\}$$
(8f)

where \(r\) is the target rate of A and B, \(P_{{{\text{total}}}}\) is the total energy consumption of the system, \(r\left( k \right)\) is the assigned bit rate for the \(k{\text{ - th}}\) subcarrier, \({\text{Pr}}\left[ {{\text{min}}\left( {I_{{\text{A}}} ,I_{{\text{B}}} } \right) \le r} \right]\) is recognized as the system outage probability, and \(Q_{{{\text{out}}}}\) is the desired QoS level of the system.

It is observed that a closed-form solution exists for problem (8) if only a single subcarrier is used. Therefore, in order to solve the main optimization problem (8), a three-stage approach is proposed. At stage 1 (stage of power management), a per-subcarrier power-adaptation problem maximizing the system EE is addressed. Here, the \(m\)-th relay node is assumed to have been selected, which is equivalent to a single-relay BDRS. Then, a power adaptation algorithm is proposed to maximize the EE of a single-relay BDRS while ensuring the required level of system QoS. Within the framework of the power adaptation algorithm and by exploiting spatial diversity of multiple-relay channels, distributed relay selection is investigated at stage 2 (stage of relay management). The idea is to choose the best relay node such that the system EE is further enhanced. Next, we tackle at stage 3 the bit-rate management problem, namely assigning bit rate to different subcarriers to maximize the system EE. Finally, summarizing the results achieved at the three stages, a novel EE technology combined with bit-rate assignment, power adaptation and relay selection is developed for optimal EE.

4 Problem solution

As described earlier, in this section, the three-stage approach is used to solve problem (8), leading to a novel EE technology for joint implementation of relay selection, bit-rate management and power adaptation.

4.1 Power management (Stage 1)

Here, it is assumed that the \(m\)-th relay node has been selected, namely a single-relay BDRS system. Then, a per-subcarrier optimization problem is considered. Thus, the optimization problem at stage 1 can be written as

$${\text{Stage}}\;1:\left[ {p_{{\text{A}}}^{m} \left( k \right),p_{{\text{B}}}^{m} \left( k \right),p_{{{\text{R}},m}}^{m} \left( k \right)} \right] = \mathop {\arg \max }\limits_{{p_{{\text{A}}} \left( k \right),p_{{\text{B}}} \left( k \right),p_{{{\text{R}},m}} \left( k \right)}} \frac{r\left( k \right)}{{p_{{\text{A}}} \left( k \right) + p_{{\text{B}}} \left( k \right) + p_{{{\text{R}},m}} \left( k \right)}}$$
(9a)
$${\text{subject to Pr}}\left\{ {{\text{min}}\left[ {I_{{\text{A}}} \left( k \right),I_{{\text{B}}} \left( k \right)} \right] \le r\left( k \right)} \right\} \le Q_{{{\text{out}}}}$$
(9b)
$$p_{{\text{A}}} \left( k \right),p_{{\text{B}}} \left( k \right),p_{{{\text{R}},m}} \left( k \right) \ge 0$$
(9c)

where \(r\left( k \right)\) is the data rate of the two sources on the \(k{\text{ - th}}\) subcarrier.

It can be observed that problem (9) is actually a special case of problem (9) in [5]. So the solution of (9) is given in the following proposition without proof.

Proposition 1

For an AF relay-assisted BDRS, the solution to the power adaptation problem (9) can be classified as the following two cases.

  • Case 1: \({1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} + {1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} \le {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} {\sqrt {Q_{{{\text{out}}}} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {Q_{{{\text{out}}}} } }}\). The solution can be given by

    $$p_{{\text{A}}}^{m} \left( k \right) = \frac{{\upsilon \left( k \right)\left[ {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right| + \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|} \right]}}{{\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|^{2} \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|}}$$
    (10)
    $$p_{{\text{B}}}^{m} \left( k \right) = \frac{{\upsilon \left( k \right)\left[ {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right| + \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|} \right]}}{{\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|^{2} }}$$
    (11)
    $$p_{{{\text{R}},m}}^{m} \left( k \right) = \frac{{\upsilon \left( k \right)\left[ {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right| + \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|} \right]^{2} + \left| {g_{{{\text{AR}},m}} \left( k \right)} \right|\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|}}{{\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|^{2} \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|^{2} }}$$
    (12)

    where \(\upsilon \left( k \right) = 2^{2r\left( k \right)} - 1\).

  • Case 2: \({1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} + {1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} > {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} {\sqrt {Q_{{{\text{out}}}} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {Q_{{{\text{out}}}} } }}\). The solution is given by \(\left[ {p_{{\text{A}}}^{m} \left( k \right),p_{{\text{B}}}^{m} \left( k \right),p_{{{\text{R}},m}}^{m} \left( k \right)} \right] = \left( {0,0,0} \right)\) indicating an occurring of an outage event. In this case, the two sources should stay silent without performing any operations.

Here, \(\eta_{{{\text{AR}},m}} \left( k \right)\) and \(\eta_{{{\text{BR}},m}} \left( k \right)\) are the expectations of \({1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|^{2} }}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|^{2} }}\) and \({1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|^{2} }}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|^{2} }}\), respectively.

Remarks

It is worth mentioning that the power-checking method proposed in [5] is employed in the above power-adaptation algorithm, namely a threshold \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\) is set for the total transmit power of the three nodes. It means that the total transmit power of the three nodes is kept below \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\). According to the solution achieved in [5], \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\), here, can be given by

$$\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right) = \frac{{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} }}{{Q_{{{\text{out}}}} }}.$$
(13)

The corresponding power adaptation technique is detailed below. First, power adaptation is conducted to enable perfect decoding at the two sources and the corresponding individual transmit-power levels are given by (10), (11) and (12). Next, \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\) is imposed on the total transmit power of the three nodes. If the total transmit power of the three nodes is less than or equal to \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\), the three nodes will use (10), (11) and (12) as their transmit-power levels for information delivery; otherwise, the system stays silent leading to an outage event. In order to satisfy the initial QoS requirement of the system,

$$\Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)} \right] \le Q_{{{\text{out}}}}$$
(14)

must be satisfied, where \(p_{{\text{T}}}^{m} \left( k \right)\) denotes the total transmit power of the three nodes and is the summation of the individual transmit powers given by (10), (11) and (12). It can be observed that with increasing the value of \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\), \(\Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)} \right]\) decreases, while the less value of \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\) we impose on the three nodes, the less energy the system will consume. Therefore, in view of energy saving, (14) is set to hold with equality. In addition, deriving a closed-form expression of \(\Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)} \right]\) is mathematically intractable. To overcome this difficulty, a closed-form upper bound of \(\Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)} \right]\) is used to determine \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\). Actually, the real probability of \(\Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)} \right]\) can be kept below \(Q_{{{\text{out}}}}\) if its upper bound is set to be less than \(Q_{{{\text{out}}}}\). Based on the above discussion, (14) leads to the closed-form expression of the threshold \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\) as given in (13). Then, using the inequality \(\left( {{1 \mathord{\left/ {\vphantom {1 x}} \right. \kern-\nulldelimiterspace} x}{ + }{1 \mathord{\left/ {\vphantom {1 y}} \right. \kern-\nulldelimiterspace} y}} \right) \ge {4 \mathord{\left/ {\vphantom {4 {xy}}} \right. \kern-\nulldelimiterspace} {xy}}\) for \(x > 0\) and \(y > 0\) in [5], \(p_{{\text{T}}}^{m} \left( k \right)\) can be upper-bounded by \(p_{{\text{T}}}^{m} \left( k \right) \le \left[ {2\upsilon \left( k \right) + 0.25} \right]\left( {\frac{1}{{\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} + \frac{1}{{\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|}}} \right)^{2}\). Substituting the upper bound of \(p_{{\text{T}}}^{m} \left( k \right)\) and (13) into \(p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\) leads to

$$p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right) \Rightarrow \frac{1}{{\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} + \frac{1}{{\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|}} > \frac{{\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} }}{{\sqrt {Q_{{{\text{out}}}} } }}.$$
(15)

As depicted in Proposition 1, if \(p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\) holds, the system would be in outage. So the system outage probability, namely the probability that \(p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)\) holds, is less than or equal to the probability that (15) holds. Thus, if the probability that (15) holds can be kept below \(Q_{{{\text{out}}}}\), the actual system outage probability can be ensured. Thus, if (15) holds, the three nodes stay silent leading to an outage event; otherwise, the three nodes will use (10), (11) and (12) as their’ transmit-power levels for information delivery.

4.2 Relay management (Stage 2)

In this subsection, we turn to the 2nd stage of choosing the best relay node so as to further enhance the system EE. Suppose that there are \(M\) relay nodes willing to forward messages for A and B. As such, the optimization problem at stage 2 can be written as

$${\text{Stage}}\;2:m^{*} = \mathop {\arg \max }\limits_{m} \frac{r\left( k \right)}{{p_{{\text{A}}}^{m} \left( k \right) + p_{{\text{B}}}^{m} \left( k \right) + p_{{{\text{R}},m}}^{m} \left( k \right)}}$$
(16a)
$${\text{subject to }}m \in \left\{ {1,2, \cdots ,M} \right\}$$
(16b)

where \(\left[ {p_{{\text{A}}}^{m} \left( k \right),p_{{\text{B}}}^{m} \left( k \right),p_{{{\text{R}},m}}^{m} \left( k \right)} \right]\) is the solution of (9). It can be observed that \(r\left( k \right)\) is fixed. So problem (16) reduces to choosing the relay node that can result in the minimum transmit power of the system. It should be noted that the relay selection framework is based on the power adaptation technique presented in Proposition 1. Therefore, the total system transmit power is the summation of the individual transmit powers given by (10), (11) and (12). Thus, the relay selection criterion can be given by

$$m^{*} = \mathop {\arg \min }\limits_{{m \in \mathcal{M}}} \frac{{2\upsilon \left( k \right)\left[ {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right| + \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|} \right]^{2} + \left| {g_{{{\text{AR}},m}} \left( k \right)} \right|\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|}}{{\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|^{2} \left| {g_{{{\text{BR}},m}} \left( k \right)} \right|^{2} }},$$
(17)

where \(\mathcal{M}\) is a set including all the subscripts of the relay nodes satisfying \({1 \mathord{\left/ {\vphantom {1 {g_{{{\text{AR}},m}} \left( k \right)}}} \right. \kern-\nulldelimiterspace} {g_{{{\text{AR}},m}} \left( k \right)}} + {1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} \le {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} {Q_{{{\text{out}}}}^{\frac{1}{2M}} }}} \right. \kern-\nulldelimiterspace} {Q_{{{\text{out}}}}^{\frac{1}{2M}} }}\). It should be noted that in case that no relay node can satisfy \({1 \mathord{\left/ {\vphantom {1 {g_{{{\text{AR}},m}} \left( k \right)}}} \right. \kern-\nulldelimiterspace} {g_{{{\text{AR}},m}} \left( k \right)}} + {1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}} \le {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} {Q_{{{\text{out}}}}^{\frac{1}{2M}} }}} \right. \kern-\nulldelimiterspace} {Q_{{{\text{out}}}}^{\frac{1}{2M}} }}\), \(\mathcal{M}\) is empty.

Remarks

It is worth mentioning that since the relay selection framework is based on the power adaptation technique given in Proposition 1, a transmit-power threshold should be imposed on the system, namely performing a power checking as presented in Proposition 1. Here, in order to reduce the complexity, we propose that such a power checking is performed at all the relay nodes and before the relay selection process. To be specific, for the \(m{\text{ - th}}\) relay node, if inequality \({1 \mathord{\left/ {\vphantom {1 {\left| {g_{AR,m} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{AR,m} \left( k \right)} \right|}} + {1 \mathord{\left/ {\vphantom {1 {\left| {g_{AR,m} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{AR,m} \left( k \right)} \right|}} \le\) \({{\left[ {\sqrt {\eta_{AR,m} \left( k \right)} + \sqrt {\eta_{BR,m} \left( k \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sqrt {\eta_{AR,m} \left( k \right)} + \sqrt {\eta_{BR,m} \left( k \right)} } \right]} {\sqrt {Q_{{{\text{out}}}} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {Q_{{{\text{out}}}} } }}\) holds, it will attend the relay selection process later; otherwise, it will not engage in the relay selection. In case that no relay node can attend the relay selection process, the two sources should stay silent without performing any operations, leading to an outage event. It should be noted that if the threshold used in the signal-relay case is adopted here, we have

$$\Pr \left\{ {\min \left[ {p_{{\text{T}}}^{m} \left( k \right)} \right] > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right),m \in \left\{ {1,2, \cdots ,M} \right\}} \right\} = \left\{ {\Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)} \right]} \right\}^{M} \le Q_{{{\text{out}}}}^{M} .$$
(18)

It is observed by (18) that the resulting outage probability is less than \(Q_{{{\text{out}}}}\). If the resulting outage probability is set to be equal to \(Q_{{{\text{out}}}}\), the power-checking threshold can be obtained by solving \(\Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > \mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)} \right] = Q_{{{\text{out}}}}^{\frac{1}{M}}\). It means that the power-checking threshold in a multiple-relay setting can be achieved by replacing \(Q_{{{\text{out}}}}\) with \(Q_{{{\text{out}}}}^{\frac{1}{M}}\) in a single relay setting. Specifically, for the \(m{\text{ - th}}\) relay node, if \({1 \mathord{\left/ {\vphantom {1 {g_{{{\text{AR}},m}} \left( k \right)}}} \right. \kern-\nulldelimiterspace} {g_{{{\text{AR}},m}} \left( k \right)}} + {1 \mathord{\left/ {\vphantom {1 {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|}}\) \(\le {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]} {Q_{{{\text{out}}}}^{\frac{1}{2M}} }}} \right. \kern-\nulldelimiterspace} {Q_{{{\text{out}}}}^{\frac{1}{2M}} }}\) holds, it will attend the relay selection process; otherwise, it will not engage in the relay selection. Moreover, it should be noted that once the best relay node is chosen, the optimal transmit-power levels of the three nodes denoted by \(\left[ {p_{{\text{A}}}^{{m^{*} }} \left( k \right),p_{{\text{B}}}^{{m^{*} }} \left( k \right),p_{{{\text{R}},m^{*} }}^{{m^{*} }} \left( k \right)} \right]\) can be readily acquired by substituting \(m^{*}\) into (10), (11) and (12). Moreover, as (17) demonstrates, in order to perform power checking, all the relay nodes should know the target rate of the sources for the \(k\)-subcarrier. To address this issue, we propose that the value of \(r\left( k \right)\) is included in the training signals.

4.3 Bit-rate management (Stage 3)

At stage 3, we tackle the problem of bit-rate management. The objective is to assign bit rates to different subcarriers so as to maximize the system EE. Therefore, the corresponding optimization problem can be written as

$${\text{Stage}}\;3:r^{*} \left( k \right) = \arg \mathop {\max }\limits_{r\left( k \right)} \frac{{\sum\limits_{k = 1}^{K} {r\left( k \right)} }}{{\sum\limits_{k = 1}^{K} {p_{{\text{T}}}^{{m^{*} }} \left( k \right)} }}$$
(19a)
$${\text{subject to }}\sum\limits_{k = 1}^{K} {r\left( k \right) = r}$$
(19b)
$$r\left( k \right) \ge 0$$
(19c)

where \(p_{{\text{T}}}^{{m^{*} }} \left( k \right)\) is the total transmit power of the system with the power adaptation and relay selection techniques proposed earlier and can be obtained by substituting \(m^{*}\) into (10), (11) and (12) and then computing theirs summation. Here, \(m^{*}\) is the subscript of the chosen best relay node.

It should be noted that at the bit-rate management stage, namely at stage 3, statistical channel knowledge is used to assign bit rates among all the subcarriers. Using Eq. (26) in [5], we can conclude that \({{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} } \mathord{\left/ {\vphantom {{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} } {\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)}}} \right. \kern-\nulldelimiterspace} {\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right)}} \ge Q_{{{\text{out}}}}\) must be satisfied so as to ensure the QoS requirement of the system. It means that \(\mathcal{T}_{{{\text{thr}}}}^{m} \left( k \right) \le {{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} } \mathord{\left/ {\vphantom {{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} } {Q_{{{\text{out}}}} }}} \right. \kern-\nulldelimiterspace} {Q_{{{\text{out}}}} }}\) must hold. Then, using \({{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} } \mathord{\left/ {\vphantom {{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} } {Q_{{{\text{out}}}} }}} \right. \kern-\nulldelimiterspace} {Q_{{{\text{out}}}} }}\) as an upper bound of \(p_{{\text{T}}}^{m} \left( k \right)\) and then substituting it into (19) lead to

$${\text{Stage}}\;3:r^{*} \left( k \right) = \arg \mathop {\max }\limits_{r\left( k \right)} \frac{r}{{\sum\limits_{k = 1}^{K} {\left[ {\frac{{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} }}{{Q_{{{\text{out}}}} }}} \right]} }}$$
(20a)
$${\text{subject to }}\sum\limits_{k = 1}^{K} {r\left( k \right) = r}$$
(20b)
$$r\left( k \right) \ge 0$$
(20c)

By the observation of (20), we find that \(r\) and \(M\) are all fixed. Thus, (20) reduces to finding the minimum summation of the system transmit power. As such, (19) is equivalent to the following optimization problem.

$$r^{*} \left( k \right) = \arg \mathop {\min }\limits_{r\left( k \right)} \sum\limits_{k = 1}^{K} {\frac{{\left[ {2\upsilon \left( k \right) + 0.25} \right]\left[ {\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} } \right]^{2} }}{{Q_{{{\text{out}}}} }}}$$
(21a)
$${\text{subject to }}\sum\limits_{k = 1}^{K} {r\left( k \right) = r}$$
(21b)
$$r\left( k \right) \ge 0$$
(21c)

In order to solve (21), we first neglect inequality constraint (21c). Then, using the Lagrangian method and employing the Karush–Kuhn–Tucker condition, we can obtain the following equation

$$\left\{ \begin{gathered} r\left( k \right) - r\left( {k + 1} \right) = \log_{2} \frac{{\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} }}{{\sqrt {\eta_{{{\text{AR}},m}} \left( {k + 1} \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( {k + 1} \right)} }} \hfill \\ \sum\limits_{k = 1}^{K} {r\left( k \right) - r} = 0 \hfill \\ \end{gathered} \right.$$
(22)

Further, (22) can be written as \({\mathbf{Xy}} = {\mathbf{c}}\)

$$\left( {\begin{array}{*{20}c} 1 & { - 1} & 0 & 0 & \cdots & 0 & 0 \\ 0 & 1 & { - 1} & 0 & \cdots & 0 & 0 \\ 0 & 0 & 1 & { - 1} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & { - 1} & 0 \\ 0 & 0 & 0 & 0 & \cdots & 1 & { - 1} \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right)\left[ {\begin{array}{*{20}c} {r\left( 1 \right)} \\ {r\left( 2 \right)} \\ {r\left( 3 \right)} \\ \vdots \\ {r\left( K \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {c\left( 1 \right)} \\ {c\left( 2 \right)} \\ \vdots \\ {c\left( {K - 1} \right)} \\ r \\ \end{array} } \right],$$
(23)

where \(c\left( k \right) = \log_{2} \frac{{\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} }}{{\sqrt {\eta_{{{\text{AR}},m}} \left( {k + 1} \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( {k + 1} \right)} }}\),\(k \in \left\{ {1,2, \cdots ,K - 1} \right\}\) . It is clear that linear system (23) can be solved by computing the inverse matrix of \({\mathbf{X}}\). The inverse matrix of \({\mathbf{X}}\) can be computed as

$${\mathbf{X}}^{ - 1} = \left( {\begin{array}{*{20}c} {\frac{K - 1}{K}} & {\frac{K - 2}{K}} & {\frac{K - 3}{K}} & {\frac{K - 4}{K}} & \cdots & {\frac{{K - \left( {K - 1} \right)}}{K}} & \frac{1}{K} \\ { - \frac{1}{K}} & {\frac{K - 2}{K}} & {\frac{K - 3}{K}} & {\frac{K - 4}{K}} & \cdots & {\frac{{K - \left( {K - 1} \right)}}{K}} & \frac{1}{K} \\ { - \frac{1}{K}} & { - \frac{2}{K}} & {\frac{K - 3}{K}} & {\frac{K - 4}{K}} & \cdots & {\frac{{K - \left( {K - 1} \right)}}{K}} & \frac{1}{K} \\ { - \frac{1}{K}} & { - \frac{2}{K}} & { - \frac{3}{K}} & {\frac{K - 4}{K}} & \cdots & {\frac{{K - \left( {K - 1} \right)}}{K}} & \frac{1}{K} \\ \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots \\ { - \frac{1}{K}} & { - \frac{2}{K}} & { - \frac{3}{K}} & { - \frac{4}{K}} & \cdots & {\frac{{K - \left( {K - 1} \right)}}{K}} & \frac{1}{K} \\ { - \frac{1}{K}} & { - \frac{2}{K}} & { - \frac{3}{K}} & { - \frac{4}{K}} & \cdots & { - \frac{{\left( {K - 1} \right)}}{K}} & \frac{1}{K} \\ \end{array} } \right).$$
(24)

Then, according to \({\mathbf{y}} = {\mathbf{X}}^{ - 1} {\mathbf{c}}\), we can straightforwardly obtain the solution of equation (22) as presented in the following proposition.

Proposition 3

For an AF relay-assisted BDRS, the optimal solution to the bit-rate-assignment problem (21) without inequality constraint (21c) can be classified as the following two cases.

  • Case 1 : \(k = 1\) or \(k = K\). The solution can be given by (25) or (26).

    $$r^{*} \left( 1 \right) = \frac{r}{K} + \sum\limits_{i = 1}^{K - 1} {\frac{{\left( {K - i} \right)\vartheta \left( i \right)}}{K}}$$
    (25)
    $$r^{*} \left( K \right) = \frac{r}{K} - \sum\limits_{j = 1}^{K - 1} {\frac{j\vartheta \left( j \right)}{K}}$$
    (26)

  • Case 2: \(k \in \left\{ {2,3, \cdots ,K - 1} \right\}\). The solution can be given by

    $$r^{*} \left( k \right) = \frac{r}{K} - \sum\limits_{j = 1}^{k - 1} {\frac{j\vartheta \left( j \right)}{K}} + \sum\limits_{i = k}^{K - 1} {\frac{{\left( {K - i} \right)\vartheta \left( i \right)}}{K}} .$$
    (27)

Here, \(\vartheta \left( i \right)\), \(i \in \left\{ {1,2, \cdots ,K - 1} \right\}\), is defined as

$$\vartheta \left( i \right) \triangleq \log_{2} \frac{{\sqrt {\eta_{{{\text{AR}},m}} \left( {k + 1} \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( {k + 1} \right)} }}{{\sqrt {\eta_{{{\text{AR}},m}} \left( k \right)} + \sqrt {\eta_{{{\text{BR}},m}} \left( k \right)} }}.$$
(28)

Discussion: Since the assigned bit rates for each subcarrier must be positive, we need to check the value of \(r^{*} \left( k \right)\), \(k \in \left\{ {1,2, \cdots ,K} \right\}\) given in Proposition 3. If \(r^{*} \left( k \right) \ge 0\) holds for \(k \in \left\{ {1,2, \cdots ,K} \right\}\), they are considered as the final solution to problem (21). Otherwise, the subcarrier assigned the minimum bit rates will not be used. Next, the target rate will be reassigned among the remaining subcarriers until all the bit rates assigned are positive. Based on Proposition 3, we present a bit-rate management algorithm which is given below.


Algorithm 1. Optimal bit-rate management

  • Step 1. Set \({\mathbb{Z}} \triangleq {\mathbb{K}}\), where \({\mathbb{K}} \triangleq \left\{ {1,2, \cdots ,K} \right\}\). Here, \({\mathbb{K}}\) is a set containing all the subscripts of the \(K\) subcarriers.

  • Step 2. Compute the assigned bit rates according to Proposition 3.

  • Step 3. Check \(r^{*} \left( z \right)\), \(z \in {\mathbb{Z}}\). For any \(z \in {\mathbb{Z}}\), \(r^{*} \left( z \right) \ge 0\) holds, go to step 4. Otherwise, give up the subcarrier with the minimum assigned bit rate, namely setting \({\mathbb{Z}} = {{\mathbb{Z}} \mathord{\left/ {\vphantom {{\mathbb{Z}} t}} \right. \kern-\nulldelimiterspace} t}\), where \(t\) is the subscript of the subcarrier with the minimum assigned bit rate, and then, go to Step 2.

  • Step 4. End of the algorithm.

4.4 Joint resource management

Based on the above discussion, a holistic algorithm for joint implementation of relay selection, power adaptation and bit-rate management is proposed as given in the following.


Algorithm 2: Joint implementation of relay selection, power adaptation and bit-rate management

  • Step 1. Set \({\mathbb{M}} \triangleq \left\{ {1,2, \cdots ,M} \right\}\). Here, \({\mathbb{M}}\) is a set containing all the subscripts of the \(M\) relay nodes.

  • Step 2. The two sources A and B send out training signals to all the relay nodes.

  • Step 3. All the relay nodes hear training signals, based on which channel knowledge between the relays and A and B is acquired.

  • Step 4. Each relay node performs power checking for each subcarrier. For the \(m\)-th relay node, if

    $$\frac{1}{{\left| {g_{AR,m} \left( k \right)} \right|}} + \frac{1}{{\left| {g_{BR,m} \left( k \right)} \right|}} > \frac{{\sqrt {\eta_{AR,m} \left( k \right)} + \sqrt {\eta_{BR,m} \left( k \right)} }}{{\sqrt {1 - \left( {1 - Q_{{{\text{out}}}}^{\frac{1}{M}} } \right)^{\frac{1}{K}} } }}$$
    (29)

    holds for any \(k \in \left\{ {1,2, \cdots ,K} \right\}\), the m-th relay node will not attend the relay selection process, namely removing \(m\) from \({\mathbb{M}}\), leading to \({\mathbb{M}}_{m} = {{{\mathbb{M}} } \mathord{\left/ {\vphantom {{{\mathbb{M}} } m}} \right. \kern-\nulldelimiterspace} m}\). It is noticed that each relay node needs to acquire not only the instantaneous channel knowledge, but also the statistical channel knowledge between itself and the two sources A and B, in addition to the required system QoS \(Q_{{{\text{out}}}}\) and the number of the relay nodes \(M\). Here, the instantaneous channel knowledge is obtained at Step 3, and the statistical channel knowledge can be acquired through a long-term observation of the channels. The required system QoS \(Q_{{{\text{out}}}}\) and the number of the relay nodes \(M\) are the two system parameters that are known to all the nodes in the system.

  • Step 5. If \({\mathbb{M}}_{m}\) is empty, a system outage occurs and then go to step 9.

  • Step 6. The relay node denoted by \(R_{s}\), where \(s \in {\mathbb{M}}_{m}\), performs the optimal bit-rate management algorithm (i.e., Algorithm 1) to assign the target rate of the sources to the subcarriers whose subscripts are included in set \({\mathbb{K}}_{s}\). According to Algorithm 1 and Proposition 3, here, only the statistical channel knowledge between the relay nodes and the two sources A and B is used. As mentioned earlier, this channel knowledge can be acquired through a long-term observation of the channels.

  • Step 7. The relay nodes whose subscripts are included in \({\mathbb{M}}_{m}\) compute the priorities that are proportional to the summation of the three nodes’ transmit power at all the used subcarriers. Then, each relay whose subscript is included in \({\mathbb{M}}_{m}\) starts a timer [5]. The timer of the relay with the best priority, namely having the minimum total transmit power, will expire first. Then, that relay transmits a flag packet to occupy the channel. It should be noted that in order to compute its priority, each relay node must know the instantaneous channel knowledge between itself and A and B, and the assigned bit rates on the used subcarriers, which are obtained at Steps 3 and 6, respectively

  • Step 8. The sources and the selected relay node compute their optimal transmit-power levels according to (10), (11) and (12) and then conduct information delivery. According to (10), (11) and (12), A, B and the selected \(m{\text{ - th}}\) relay node need to know \(\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|\), \(\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|\) and \(r\left( k \right)\) so as to find the optimal transmit-power levels. For the selected \(m{\text{ - th}}\) relay, \(\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|\), \(\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|\) and \(r\left( k \right)\) are known. In order to let A and B know these information, it is proposed that the values of \(\left| {g_{{{\text{AR}},m}} \left( k \right)} \right|\), \(\left| {g_{{{\text{BR}},m}} \left( k \right)} \right|\) and \(r\left( k \right)\) are included in the flag packet of the selected \(m{\text{ - th}}\) relay node.

  • Step 9. End of the algorithm.

Remark: It should be noted that the power checking is performed at the relay sides, namely each relay node check whether (28) holds for \(k \in \left\{ {1,2, \cdots ,K} \right\}\). As discussed earlier, for the m-th relay node and the two sources composed system, the outage probability can be written as

$$\begin{aligned} P_{{{\text{out}}}}^{m} &= 1 - \Pr \left[ {p_{{\text{T}}}^{m} \left( 1 \right) \le {\mathcal{T}}_{{{\text{thr}}}}^{m} \left( 1 \right), \cdots ,p_{{\text{T}}}^{m} \left( k \right) \le {\mathcal{T}}_{{{\text{thr}}}}^{m} \left( k \right), \cdots ,p_{{\text{T}}}^{m} \left( K \right) \le {\mathcal{T}}_{{{\text{thr}}}}^{m} \left( K \right)} \right]\\ &= 1 - \left\{ {\left[ {1 - \Pr p_{{\text{T}}}^{m} \left( k \right){ \mathcal{T}}_{{{\text{thr}}}}^{m} \left( {\text{k}} \right)} \right]} \right\}^{{\text{K}}}\end{aligned}$$
(30)

Taking all the relay nodes into consideration, the system outage probability can be expressed as

$$\begin{aligned} P_{{{\text{out}}}} &= \left\{ {1 - \Pr \left[ {p_{{\text{T}}}^{m} \left( k \right){ } \le {\mathcal{T}}_{{{\text{thr}}}}^{m} \left( k \right),\;{\text{for\,any}}k \in \left\{ {1,2, \cdots ,K} \right\}} \right]} \right\}^{M} \\ &= \left( {1 - \left\{ {1 - \Pr \left[ {p_{{\text{T}}}^{m} \left( k \right) > {\mathcal{T}}_{{{\text{thr}}}}^{m} \left( k \right)} \right]} \right\}^{K} } \right)^{M} .\end{aligned}$$
(31)

Here, \(P_{{{\text{out}}}} \le Q_{{{\text{out}}}}\) should be ensured. As mentioned earlier, in view of energy saving, \(P_{{{\text{out}}}} \le Q_{{{\text{out}}}}\) is set to hold with equality. Then, we have

$$\Pr \left[ {p_{T}^{m} \left( k \right)>{\mathcal{T}}_{{thr}}^{m} \left( k \right)} \right] = 1 - \left( {1 - Q_{{out}}^{{\frac{1}{M}}} } \right)^{{\frac{1}{K}}} .$$
(32)

It can be observed by (32) and (15) that for the M relay case, the power-checking threshold can be achieved by replacing \(Q_{{{\text{out}}}}\) with \(1 - \left( {1 - Q_{{{\text{out}}}}^{\frac{1}{M}} } \right)^{\frac{1}{K}}\) in a single relay case; namely, replacing \(Q_{{{\text{out}}}}\) with \(1 - \left( {1 - Q_{{{\text{out}}}}^{\frac{1}{M}} } \right)^{\frac{1}{K}}\) in (15) will arrive at (29).

It can be observed that Algorithm 2 includes nine steps, and at Step 6, the bit-rate management algorithm (i.e., Algorithm 1) is performed, where an iteration is needed. For the other eight steps, however, no iteration is needed and the execution is straightforward. For Algorithm 1, up to \(K\) iterations would be conducted in addition to a few simple algebraic manipulations that are used to find the optimal assigned bit rates of each subcarrier, as described in Proposition 3. Actually, the value of \(K\) is quite limited, e.g., \(K\) is set to 2048 for the fourth generation of mobile wireless networks. Overall, the computational complexity of Algorithm 2 is very low.

5 Simulation results and discussion

In this section, simulation results are presented to evaluate the performance of the proposed EE techniques. Here, it is assumed that the relay nodes are located on the line between the two sources A and B, and \(d_{{{\text{AB}}}} = 1\). It means that \(0 < d_{{{\text{AR}},m}} ,d_{{{\text{BR}},m}} < 1\) and \(d_{{{\text{AR}},m}} + d_{{{\text{BR}},m}} = 1\). The path-loss coefficient \(\alpha\) is set to 4 to model radio propagation in urban areas [23]. In the simulation experiments, \(Q_{{{\text{out}}}}\) is set to 0.01, a typical value for high-quality personal communications systems [23], and transmit-power levels are obtained by finding the mean of the transmit power. It is worth mentioning that in the figures presented below, “Algorithm 2” means using the developed holistic resource management algorithm for joint implementation of relay selection, power adaptation and bit-rate management; “equal bit-rate assignment” means that the relay selection and power adaptation techniques proposed in the paper are still employed, while the bit rates of the sources are equally assigned among all the subcarriers.

Figure 2 shows the total transmit power of the system and the system outage probability versus \(d_{{{\text{AR}}}}\) for the compared two kinds of EE techniques, where \(r = 10{\text{bit/s.Hz}}\) and \(K = 16\). Figure 2a demonstrates that the proposed resource management algorithm as presented in Algorithm 2 performs better than the “equal bit-rate assignment” algorithm and can reduce the system transmit power significantly. It is shown that the more number of relay nodes attend the relay selection process, the more energy can be saved. However, it can be observed that with increasing the number of relay nodes, the improvement in terms of saved energy decreases. Taking the complexity into account, the optimal number of relay node is 2 or 3. Figure 2b shows the corresponding system outage probabilities of the schemes employed in Fig. 2a. Figure 2b shows that all the schemes employed in Fig. 2a can ensure the QoS requirement of the system, verifying the correctness of our proposed techniques. Moreover, Fig. 2 shows that for any employed schemes, \(d_{{{\text{AR}}}} = 0.5\) can result in the lowest total transmit power and the system outage probability, meaning that the relay node is optimally located at the middle of the line between the two sources.

Fig. 1
figure 1

Bidirectional relaying system model

Full size image
Fig. 2
figure 2

Total transmit power and outage probability versus \(d_{{{\text{AR}}}}\), where \(r = 10{\text{bit/s/Hz}}\), \(K = 16\) and \(Q_{{{\text{out}}}} = 0.01\).

Full size image

Figures 3, 4, 5 show the total transmit power of the system and the system outage probability versus the sources’ target rate \(r\) for the compared two kinds of EE techniques, where \(K = 16\). Here, Figs. 3, 4, 5 correspond to three kinds of channels, namely symmetric channel \(d_{{{\text{AR}}}} = 0.5\), asymmetric channel \(d_{{{\text{AR}}}} = 0.3\) and strongly asymmetric channel \(d_{{{\text{AR}}}} = 0.1\), respectively. It is shown that the proposed resource management algorithm as presented in Algorithm 2 performs well across the whole range of \(r\), and all the schemes employed here can ensure the QoS requirement of the system, verifying the correctness of our proposed techniques. Moreover, it can be observed in Figs.3a, 4a and 5a that with increasing the target rate \(r\), the total transmit power increases as well, and the increment in terms of the transmit power reduces. This is because of the fact that there exist a number of subcarriers and all the available subcarriers can be used to deliver the target bit rates. Furthermore, Figs.3b, 4b and 5b show that the symmetric channel, i.e., \(d_{{{\text{AR}}}} = 0.5\), can result in the lowest system outage probability, meaning that the relay node is optimally located at the middle of the line between the two sources from a QoS point of view.

Fig. 3
figure 3

Total transmit power and outage probability versus \(r\), where \(d_{{{\text{AR}}}} = 0.5\), \(K = 16\) and \(Q_{{{\text{out}}}} = 0.01\).

Full size image
Fig. 4
figure 4

Total transmit power and outage probability versus \(r\), where \(d_{{{\text{AR}}}} = 0.3\), \(K = 16\) and \(Q_{{{\text{out}}}} = 0.01\).

Full size image
Fig. 5
figure 5

Total transmit power and outage probability versus \(r\), where \(d_{{{\text{AR}}}} = 0.1\), \(K = 16\) and \(Q_{{{\text{out}}}} = 0.01\).

Full size image

Figure 6 shows the total transmit power of the system and the system outage probability versus the number of subcarriers \(K\) for the compared two kinds of EE techniques, where \(r = 10{\text{bit/s/Hz}}\) and \(d_{{{\text{AR}}}} = 0.5\). Figure 6 demonstrates that the proposed resource management algorithm as presented in Algorithm 2 performs better than the “equal bit-rate assignment” algorithm and can reduce the system transmit power significantly. It is shown that the more subcarriers we use, the more transmit power we can save. However, the improvement in terms of the saved transmit power decreases with increasing the number of subcarriers. It is known that more subcarriers that are used will incur more complexity for practical implementation. Therefore, the actual value of the sources’ target rate should be taken into consideration when determining how many subcarriers that will be used. Figure. 2b shows that all the schemes employed in Fig. 2a can ensure the QoS requirement of the system, further verifying the correctness of our proposed techniques.

Fig. 6
figure 6

Total transmit power and outage probability versus \(K\), where \(r = 10{\text{bit/s/Hz}}\), \(d_{{{\text{AR}}}} = 0.5\) and \(Q_{{{\text{out}}}} = 0.01\).

Full size image

6 Conclusions

In this paper, we have investigated energy-efficient techniques for an AF relay-assisted BDRS under a QoS requirement constraint. As a result, a holistic resource management algorithm for joint implementation of relay selection, power adaptation and bit-rate management is developed for optimal EE. Simulation results validated the correctness and the efficiency of the proposed algorithm. It was demonstrated that with the proposed algorithm, the total transmit power of the system can be significantly reduced. With increasing the number of relay nodes and/or the number of subcarriers, the saved energy increases as well. However, the increment in terms of the saved energy decreases. Taking the complexity into account, the optimal number of relay node is 2 or 3, while the optimal number of subcarriers is related to the actual value of the sources’ target rate.