Transmission of Microwaves through the Composite Material with Fe–Si–Nb–Cu–B Alloy Particles

Abstract

The transmission of electromagnetic waves through the samples of the composite material containing Fe–Si–Nb–Cu–B alloy particles with a size of up to 50 µm was studied. The dependences of the transmission and reflection ratio on the magnetic field were measured at frequencies from 12 to 38 GHz. The dependence of the effective magnetic permeability on the magnetic field was determined, and the complex refractive index was calculated. The frequency dependence of maximum values was investigated for the real and imaginary parts of this index.

INTRODUCTION

Due to the possibility of adjusting the required electrical properties, oxidation stability, and easy preparation, composites with a metallic filler are used as materials for electromagnetic shielding and electrostatic protection [1]. The high-frequency properties of a composite with magnetic particles can be changed by means of an external magnetic field [2]. The problem of studying the microwave magnetic losses in composites [3] is of interest to researchers. The microwave electrical properties of composites were studied in [4, 5]. The effect of the magnetic field on the frequency dispersion of the magnetic permeability of composites was investigated in [5, 6]. Naturally, the shape of metallic particles and the concentration of magnetic particles have an important effect on high-frequency electromagnetic properties. An increased capability for electromagnetic shielding was revealed in the composites with lamellar particles [7, 8]. In the frequency range from 2 to 18 GHz, good absorbing properties were obtained for the composites with Fe₁₆Ni₈₂Mo₂ alloy particles in an epoxide matrix [9].

The composite samples studied in this work were manufactured from Fe–Si–Nb–Cu–B “finemet” alloy particles in an epoxy amine matrix. The particles have a size of no more than 50 µm. The matrix was selected due to its moderate dielectric permittivity, high strength, and corrosion stability. The transmission of microwaves was selected as a basic experimental method [11]. As a rule, the microwave properties of magnetic composites are studied within a frequency range to 20 GHz. The expansion of this frequency range makes it possible to observe and study the phenomenon of magnetic antiresonance in a composite [10].

The frequency dependence of the ratio of transmission through a composite material plate was measured in this study within a range from 12 to 38 GHz alongside the dependence of the transmission ratio on the magnetic field. Resonance phenomena were studied in detail.

EXPERIMENTAL METHODS AND SAMPLES

In the studied composite samples, Fe–Si–Nb–Cu–B “finemet” alloy particles were used with an approximate composition (%): Fe, 77; Si, 8.5; Nb, 8.4; Cu, 1.1; B, 1.2; Cr, 0.2. The particles were shaped as lamellae with a maximum size to 50 µm. The composite was synthesized in an epoxy amine matrix at a filling with metallic lamellae of 15 vol %. The composite structure photo was taken on a Vega3 Tescan electron microscope at an accelerating voltage of 20 kV (Fig. 1). The composite surface fragment can be seen to contain light metallic particles distributed over the epoxy amine matrix. Visually, no direct contacts between metallic particles are observed. This is also confirmed by a high (above 2 MΩ cm) resistance of the composite material.

Fig. 1.

Electron microscopic photo of the composite structure.

Microwave measurements were carried out within a frequency range from 12 to 38 GHz via the transmission of waves through a studied material sample shaped as a plate [9]. A sample was placed into a rectangular waveguide cross section so as to completely overlap it (Fig. 2). The waveguide operated on the TE₁₀ mode, and its dimensions were dictated by the range of working frequencies: 16 × 8 mm for 12–17 GHz, 11.5 × 5 mm for 17–26 GHz, and 7.2 × 3.4 mm for 27–38 GHz. The sample thickness was 2 mm. The modules of the transmission ratio D and reflection ratio R and their dependences on the frequency and intensity of an external magnetic field were measured by a standing wave and reflection ratio meter. The relative change of the transmission ratio module was determined as ${{d}_{m}} = {{\left( {\left| {D\left( H \right)} \right| - \left| {D\left( 0 \right)} \right|} \right)} \mathord{\left/ {\vphantom {{\left( {\left| {D\left( H \right)} \right| - \left| {D\left( 0 \right)} \right|} \right)} {\left| {D\left( 0 \right)} \right|}}} \right. \kern-0em} {\left| {D\left( 0 \right)} \right|}},$ where $\left| {D\left( 0 \right)} \right|$ is the transmission ratio module in the magnetic field H. Similarly, the relative change of the reflection coefficient was determined as ${{r}_{m}} = {{\left( {\left| {R\left( H \right)} \right| - \left| {R\left( 0 \right)} \right|} \right)} \mathord{\left/ {\vphantom {{\left( {\left| {R\left( H \right)} \right| - \left| {R\left( 0 \right)} \right|} \right)} {\left| {R\left( 0 \right)} \right|}}} \right. \kern-0em} {\left| {R\left( 0 \right)} \right|}},$ where $\left| {R\left( 0 \right)} \right|$ is the reflection ratio module in the magnetic field H. The constant magnetic field lies in the plate plane and is oriented perpendicularly to the superhigh-frequency magnetic field ${{{\mathbf{H}}}_{\sim }},$ ${\mathbf{H}} \bot {{{\mathbf{H}}}_{\sim }}.$ All microwave measurements were carried out at room temperature. The measurements of the frequency dependence of the transmission ratio were used to determine the complex dielectric permittivity ${{\varepsilon }_{{ef}}} = \varepsilon {\kern 1pt} ' - i\varepsilon ''$ by the method [5].

Fig. 2.

Arrangement of a sample in the waveguide.

RESULTS OF MICROWAVE MEASUREMENTS

The results of dielectric permittivity measurements are shown in Fig. 3. The frequency dependence of the real part ε' has a maximum at a frequency f = 21 GHz. At higher frequencies, ε' decreases and further attains a nearly constant value of nearly 5.5. The dependence of the imaginary part ε'' contains a discontinuity at 17 GHz. The existence of this discontinuity is associated with the fact that the measurements were carried out in waveguides of different cross sections and wave resistance. The maximum of ε' seems to be produced by relaxation properties of the composite governed by the concentration and sizes of metallic particles. To clarify the reason for the appearance of this maximum requires additional study. To calculate the refractive index, it is necessary to perform the numerical calculations of the complex dielectric permittivity. The data of Fig. 3 give us some grounds to believe that the composite may be considered an imperfect lossy dielectric without an external magnetic field at frequencies of the considered centimeter- and millimeter-wave bands.

Fig. 3.

Real (colored) and imaginary (uncolored) parts of the dielectric permittivity versus frequency.

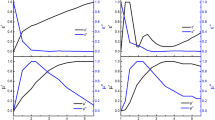
Let us consider the transmission and reflection of electromagnetic waves in a magnetic field. The field dependences of the transmission ratio are shown in Fig. 4a for the frequency range of 12–17.2 GHz and Fig. 5a for the frequency range of 26–38 GHz. The results of reflection ratio measurements are shown in Figs. 4b and 5b. The most pronounced singularity in Figs. 4a and 4b is a minimum in the transmission and reflection ratios. The field of this minimum shifts towards stronger fields with increasing wave frequency. This minimum is produced by the absorption of waves under ferromagnetic resonance (FMR) conditions. The field of resonance in the region of magnetic saturation is determined by the Kittel formula [11]

$$\frac{\omega }{\gamma } = \prod\limits_{j = \left\{ {x,y} \right\}} {\sqrt {H + ({{N}_{j}} - {{N}_{z}}){{M}_{{\text{s}}}}} } ,$$

(1)

where $\omega = 2\pi f$ is the angular frequency, γ the gyromagnetic ratio, M_s is the saturation magnetization, N_i is the components of the diagonalized tensor of demagnetizing factors, and $i = \left\{ {x,y,z} \right\}$ is the Cartesian coordinates. It is implied that the magnetization field H is oriented along the axis z. The components N_i depend on the shape and orientation of magnetic metallic particles. The difference between N_i for differently oriented lamellae leads to a broad FMR band.

Fig. 4.

(a) Transmission and (b) reflection ratios of microwaves versus magnetic field for a composite sample at frequencies from 12 to 17.2 GHz.

Fig. 5.

(a) Transmission and (b) reflection ratios of microwaves versus magnetic field for a composite sample at frequencies from 26 to 38 GHz.

In the frequency band of 17–26 GHz, the ratios D and R demonstrate the same character of their field dependences as shown in Fig. 4, but resonance is attained in stronger fields. At much higher frequencies of 26–38 GHz, the ratios are also observed to have a minimum produced by ferromagnetic resonance, as shown in Fig. 5. Let us note that the transmission ratio changes at a minimum of 50%, and it is of interest for practical applications. At frequencies above 32 GHz, the reflection ratio also has a maximum in addition to the minimum produced by ferromagnetic resonance (Fig. 5b). This maximum is attained in the fields below the FMR field and exists only at frequencies above a certain value. According to [10, 11], all the mentioned features correspond to ferromagnetic antiresonance (FMAR).

In the antiresonance field ${{H}_{2}}$, the real part of the effective magnetic permittivity μ_eff becomes zero, i.e., $\mu _{{{\text{eff}}}}^{'}$ = 0. According to [11], the frequency dependence of the field H₂ is specified by the relationship

$${{H}_{2}} = \sqrt {{{{\left( {\frac{\omega }{\gamma }} \right)}}^{2}} + {{{\left( {2\pi {{M}_{{\text{s}}}}} \right)}}^{2}}} - 2\pi {{M}_{{\text{s}}}}.$$

(2)

For the frequency $f = 35$ GHz, the estimation of the field ${{H}_{2}}$ by Eq. (2) at the saturation magnetization M_s = 900 G gives ${{H}_{2}}$ ≈ 8.1 kOe, which is much higher than the field of maximum reflection ratio at this frequency (Fig. 5b). This difference is not surprising, as Eq. (2) was written for a plate of a homogeneous ferromagnetic material and, in our case, the strongly heterogeneous composite with randomly oriented ferromagnetic lamellae is considered.

MICROWAVE REFRACTIVE INDEX

Knowing the FMR band width from Figs. 4a and 5a, it is possible to calculate components of the dynamic magnetic permeability tensor by the method [11]. Using the diagonal μ and nondiagonal μ_a permeability tensor components, it is possible to find the effective magnetic permeability μ_eff as

$${{\mu }_{{{\text{eff}}}}} = \mu - \frac{{\mu _{a}^{2}}}{\mu }.$$

(3)

The result of calculation of the effective magnetic permeability for the frequency $f = 12$ GHz is shown in Fig. 6a. The imaginary-part maximum corresponds to FMR. Below the FMR field, the real permeability part is negative and does not become zero. This means that no FMAR occurs at this frequency according to the experimental data of Fig. 4.

Fig. 6.

Real and imaginary (a) microwave magnetic permeability and (b) microwave refractive index parts versus magnetic field at a frequency of f = 12 GHz.

Knowing the magnetic permeability and using the effective dielectric permittivity data, it is possible to calculate the complex refractive index as

$$n = n{\kern 1pt} ' - in'' = \sqrt {{{\varepsilon }_{{{\text{eff}}}}}{{\mu }_{{{\text{eff}}}}}} ,$$

(4)

where $n{\kern 1pt} '$ is the refractive index, and $n''$ is the decay factor. The result of calculation for the real and imaginary parts of the refractive index is shown in Fig. 6b. The FMR field approximately corresponds to maximum imaginary part of the refractive index.

The frequency dependences of the field corresponding to the maximum in the dependences of several parameters on the magnetic field are shown in Fig. 7a. The dependence determined from experimental data is shown with uncolored symbols. The microwave dissipation maximum field is taken as a FMR field. The dissipation Δ is calculated from the ratios D(H) and R(H) as

$$\Delta \left( H \right) = 1 - {{\left| {D\left( H \right)} \right|}^{2}} - {{\left| {R\left( H \right)} \right|}^{2}}.$$

(5)

Fig. 7.

Resonance field and fields of maximum (a) real and imaginary refractive index parts and (b) resonance amplitude versus frequency and (c) maximum real and imaginary refractive index parts versus frequency.

The parameter Δ expresses the power fraction that is absorbed and dissipated in a sample.

The calculation is performed as follows. The transmission D(H) and reflection R(H) ratios are expressed by the formulas [9]

$$D = \frac{2}{{2\cosh{{\beta }_{2}}d + \left( {\xi + {{\xi }^{{ - 1}}}} \right)\sinh{{\beta }_{2}}d}},$$

(6)

$$R = \frac{{\left( {\xi - {{\xi }^{{ - 1}}}} \right)\sinh{{\beta }_{2}}d}}{{2\cosh{{\beta }_{2}}d + \left( {\xi + {{\xi }^{{ - 1}}}} \right)\sinh{{\beta }_{2}}d}}.$$

(7)

In these formulas, d is the sample thickness, a is the size of the larger wall of a rectangular waveguide, ${{\beta }_{2}} = \beta _{2}^{'} - i\beta _{2}^{{''}}$ is the constant of TE₁₀ wave propagation in a sample, and $\xi = {{{{Z}_{2}}} \mathord{\left/ {\vphantom {{{{Z}_{2}}} {{{Z}_{1}}}}} \right. \kern-0em} {{{Z}_{1}}}}$ is the ratio of equivalent resistances for the waveguide areas, among which one is filled with a sample (Z₂) and the other is not filled with a sample (Z₁). The equivalent resistances are calculated by the following formulas:

$${{Z}_{1}} = \frac{b}{a}\frac{{{\text{60}}{{\pi }^{2}}}}{{\sqrt {1 - {{{\left( {\frac{c}{{2af}}} \right)}}^{2}}} }};\,\,\,\,{{Z}_{2}} = \frac{b}{a}\frac{{{\text{60}}{{\pi }^{2}}{{\mu }_{{{\text{eff}}}}}}}{{\sqrt {{{\varepsilon }_{{{\text{eff}}}}}{{\mu }_{{{\text{eff}}}}} - {{{\left( {\frac{c}{{2af}}} \right)}}^{2}}} }}.$$

(8)

The effective magnetic permeability μ_ef is calculated through the components of magnetic permeability tensor by Eq. (3). The propagation constant β₂ can be calculated by Eq. (9)

$${{\beta }_{2}} = \sqrt {{{{\left( {\frac{\omega }{c}} \right)}}^{2}}{{\varepsilon }_{{{\text{eff}}}}}{{\mu }_{{{\text{eff}}}}} - {{{\left( {\frac{\pi }{a}} \right)}}^{2}}} .$$

(9)

For the waveguide area without a sample, it is necessary to set ε_eff = 1 and μ_eff = 1 in Eqs. (8) and (9). After calculating D(H) and R(H) by Eqs. (6) and (7), it is possible to determine the maxima of the dissipation Δ according to Eq. (5) (dark points in Fig. 7a). The calculated and experimental dissipation dependences are close to each other.

Afterwards, Eq. (4) was used to calculate the field dependences of the refractive index n. The positions of maxima in the field dependence of n' and n'' are also shown in Fig. 7a. Both the dissipation Δ and the imaginary refractive index part n'' are related to the absorption of microwave energy, so it may be expected that the maxima of these parameters in their frequency dependence (Fig. 7a) will be close to each other. The contribution to the dissipation Δ is made by several sources of losses, including decay in the dielectric subsystem of the material, decay in its magnetic subsystem, and dissipation in the nonhomogeneous composite. The two last sources of losses depend on the magnetic field. In the considered region of frequencies, the wavelength in the composite is $\lambda = {c \mathord{\left/ {\vphantom {c {\left( {f\sqrt \varepsilon } \right)}}} \right. \kern-0em} {\left( {f\sqrt \varepsilon } \right)}}$ ~ 3 mm, which is much longer than the maximum size of 50 µm for nanocomposite heterogeneities. Dissipation occurs in the Rayleigh region for this reason. It is quite probable that the difference between the dependences of the dissipation maximum and the maximum of n'' is produced by the dissipation of microwaves. The real part n' must have a maximum in higher fields, as shown in Fig. 7a.

The amplitude-frequency dependence for the maximum of the resonance band Δ is shown in Fig. 7b. As usual, the magnitude grows with increasing frequency. The discontinuities in this dependence at 17 and 26 GHz appear due to the fact that, according to Eqs. (6) and (7), the transmission and reflection ratios depend on the equivalent waveguide resistance. At these frequencies, one waveguide is replaced by the waveguide with a different cross section and, therefore, with a different wave resistance, thus leading to discontinuities.

The frequency characteristics of calculated maximum values for the real n' and imaginary n'' parts of the complex refractive index are shown in Fig. 7c. The discontinuities in these curves appear for the same reason. It can be seen from Fig. 7c that the maximum values of the real and imaginary parts of the complex refractive index near FMR conditions in the lower region of the considered frequency range have the same order of magnitude. In zero external magnetic field, n' and n'' have the values typical of an imperfect dielectric. For example, at a frequency f = 12 GHz, H = 0, and M = 0, we have n' = 2.72 and n'' = 0.62. However, it can be seen from Fig. 6b that the real and imaginary parts of the refractive index in a magnetic field below the FMR field are of the same order, i.e., n'' ≈ n'.

Let us consider the amplitude change ΔA for a wave transmitted through a sample in a strong magnetic field. In our experiments, this is a field with an intensity of 12 kOe. It can be seen from Figs. 4 and 5 that, at some frequencies, the amplitude of a transmitted wave in a field above 12 kOe is higher than in zero field.

The reason for this change is that both the real and imaginary parts of the effective magnetic permeability are decreased in the field above the FMR field. The calculation performed by Eq. (6) at a frequency f = 21 GHz has confirmed the possibility of such an explanation. The experimental and calculated field dependences are compared in Fig. 8a. Although no quantitative correspondence has been attained, the calculation confirms that the amplitude tends to grow in a strong magnetic field. The change in the amplitude of a transmitted wave in a field of 12 kOe as a frequency function is illustrated in Fig. 8b. The discontinuities in this curve and the change in its character at frequencies of 17 and 26 GHz point to the importance of change in the wave resistance upon the change of a waveguide cross section. Therefore, the value of changes in a strong magnetic field is governed not only by the change in the material parameters of a sample, but also by the method of experiment. Negative values of ΔA at frequencies of 32 GHz and higher (Fig. 8b) are due to the absorption of a wave near the FMR condition.

Fig. 8.

(a) Comparison of the experimental and calculated dependences of the transmission ratio on the magnetic field at a frequency of 21 GHz and (b) frequency dependence of the difference between the transmission ratios in maximum and zero magnetic fields.

CONCLUSIONS

The microwave properties of a composite material containing Fe–Si–Nb–Cu–B alloy lamellae in an epoxide matrix were studied. The transmission and reflection ratios and their dependences on the magnetic field were measured within a frequency range from 12 to 38 GHz. The effective dielectric permittivity of the composite was determined. The field dependences of the transmission and reflection ratios have a minimum produced by ferromagnetic resonance. The measured field dependences of the reflection ratio at frequencies above 32 GHz contain a maximum produced by magnetic antiresonance.

The complex refractive index was calculated, and its dependence on the magnetic field was plotted. This composite material with Fe–Si–Nb–Cu–B alloy lamellae exhibits insulator properties at a constant current, as the concentration of lamellae is below the percolation threshold, and there is no direct contact between them. At microwave frequencies without external magnetic field, the composite is an imperfect lossy dielectric. In magnetic fields below the FMR field, the real and imaginary parts of the complex refractive index have the same order of magnitude. For example, n' ≈ n'' at a frequency f = 12 GHz in a field of nearly 0.5 kOe.