Permutable SOS (symmetry operational similarity)

Abstract

Based on symmetry consideration, quasi-one-dimensional (1D) objects, relevant to numerous observables or phenomena, can be classified into eight different types. We provide various examples of each 1D type and discuss their symmetry operational similarity (SOS) relationships, which are often permutable. A number of recent experimental observations, including current-induced magnetization in polar or chiral conductors, non-linear Hall effect in polar conductors, spin-polarization of tunneling current to chiral conductors, and ferro-rotational domain imaging with linear gyration are discussed in terms of (permutable) SOS. In addition, based on (permutable) SOS, we predict a large number of new phenomena in low symmetry materials that can be experimentally verified in the future.

Introduction

The concept of SOS (symmetry operational similarity)^1,2 between specimen constituents (periodic crystallographic or magnetic lattices in an external magnetic field, electric fields or stress, and also their time evolution) and measuring probes/quantities (observables such as transmitting electrons, phonons, magnons, photons in various polarization states, including electrons or photons with spin or orbital angular momentum, bulk magnetization or polarization, and also experimental setups to measure, e.g., Hall-type effects) in relation to broken symmetries is powerful to understand and predict observable physical phenomena in low symmetry materials³. Precisely speaking, this SOS relationship means that specimen constituents have identical or more (but not less) broken symmetries, compared with measuring probes/quantities. In other words, in order to have an SOS relationship, specimen constituents cannot have higher symmetries than measuring probes/quantities do. The power of the SOS approach lies in providing readily understandable views of otherwise complex and unintuitive phenomena in low-symmetry materials.

In conjunction with the earlier publications, we here discuss (quasi-)one-dimensional objects (simply referred to as 1D objects): objects can be specimen constituents (periodic lattices in the presence of external perturbations) or measuring probes/quantities (observables), and (quasi-)1D refers objects that have a certain rotation symmetry around the 1D direction, and all rotational symmetry, possibly except C₂ symmetry, is broken around any directions perpendicular to the 1D direction. Note that periodic crystallographic or magnetic lattices can have two, three, four, or sixfold rotational symmetries (C₂, C₃, C₄, or C₆ symmetries in the standard crystallographic notations, respectively), 1D specimen constituents must have at least, C₂ or C₃ symmetry around the 1D direction, and broken all of C₃, C₄, and C₆ symmetries around any directions perpendicular to the 1D direction. One example of 1D objects is cycloidal spins having SOS with polarization (P), and cycloidal spins do have C₂ symmetry around P, but no rotation symmetry, including C₂, around any direction perpendicular to the P direction¹.

Herein, we use these symmetry operation notations: R = twofold rotation with the rotation axis perpendicular to the 1D object direction, R = twofold rotation with the rotation axis along the 1D object direction, I = space inversion, M = mirror reflection with the mirror perpendicular to the 1D object direction, M = mirror reflection with the mirror plane containing the 1D object direction, T = time reversal. In the standard crystallographic notations, “R, R, I, M, M, and T” are C_2⊥, C_2||, $\overline 1$, m_⊥, m_||, 1′, respectively¹. Our notations are natural and intuitive to consider 1D objects. Emphasize that since we consider 1D objects, translational as well as rotational symmetry operations along the 1D object direction are freely allowed¹. For example, T symmetry in a simple 1D antiferromagnet is considered to be not broken since translation is freely allowed. In addition, if the symmetry is preserved after a symmetry operation followed by a rotation around the 1D object direction, then we say that the symmetry is not broken.

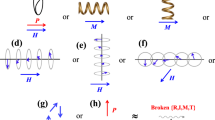
Hlinka has proposed that there exist eight kinds of vectorlike physical quantities in terms of their invariance under spatiotemporal symmetry operations⁴. In fact, our 1D objects are similar to the vectorlike physical quantities in terms of symmetry, so there are eight kinds of 1D objects. We will call them as ${\boldsymbol{\mathscr{D}}},\, {\boldsymbol{\mathscr{C}}},\, {\boldsymbol{\mathscr{P}}},$ ${\boldsymbol{\mathscr{a}}},$ ${\boldsymbol{\mathscr{D}}}^{\prime},\, {\boldsymbol{\mathscr{C}}}^{\prime},\, {\boldsymbol{\mathscr{P}}}^{\prime},$ ${\boldsymbol{\mathscr{a}}}^{\prime}$. Here ${\boldsymbol{\mathscr{D}}}, {\boldsymbol{\mathscr{C}}}, {\boldsymbol{\mathscr{P}}}$, and ${\boldsymbol{\mathscr{a}}}$ refer to the director, chirality, polarization, and rotational axial (electric toroidal) vector, respectively, and ′ refers to the time-reversal broken version. All left-hand-side 1D objects (${\boldsymbol{\mathscr{D}}},\, {\boldsymbol{\mathscr{C}}},\, {\boldsymbol{\mathscr{D}}}^{\prime},\, {\boldsymbol{\mathscr{C}}}^{\prime}$) in Fig. 1 have not-broken R (i.e., they are director-like) and all right-hand-side 1D objects (${\boldsymbol{\mathscr{P}}},\, {\boldsymbol{\mathscr{R}}},\, {\boldsymbol{\mathscr{P}}}^{\prime},\, {\boldsymbol{\mathscr{R}}}^{\prime}$) have broken R (i.e., they are vector-like).

Fig. 1: Eight types of 1D objects.

Each type has a particular set of broken symmetries: ${\boldsymbol{\mathscr{D}}}$; no broken symmetry, ${\boldsymbol{\mathscr{C}}}$; broken {I, M, M}, ${\boldsymbol{\mathscr{D}}}^{\prime}$; broken {T}, ${\boldsymbol{\mathscr{C}}}^{\prime}$; broken {I, M, M, T}, ${\boldsymbol{\mathscr{P}}}$; broken {R, I, M}, ${\boldsymbol{\mathscr{a}}}$; broken {R, M}, ${\boldsymbol{\mathscr{P}}}^{\prime}$; broken {R, I, M, T}, ${\boldsymbol{\mathscr{a}}}^{\prime}$; broken {R, M, T}. When {T} is additionally broken, then ${\boldsymbol{\mathscr{D}}}$, ${\boldsymbol{\mathscr{C}}}$, ${\boldsymbol{\mathscr{P}}}$, and ${\boldsymbol{\mathscr{a}}}$ become ${\boldsymbol{\mathscr{D}}}^{\prime},\, {\boldsymbol{\mathscr{C}}}^{\prime},\, {\boldsymbol{\mathscr{P}}}^{\prime},$ ${\boldsymbol{\mathscr{a}}}^{\prime}$, respectively. Note that all left-hand-side 1D objects (${\boldsymbol{\mathscr{D}}},\, {\boldsymbol{\mathscr{C}}},\, {\boldsymbol{\mathscr{D}}}^{\prime},\, {\boldsymbol{\mathscr{C}}}^{\prime}$) have not-broken {R}, so they are director-like, and all right-hand-side 1D objects (${\boldsymbol{\mathscr{P}}},\, {\boldsymbol{\mathscr{R}}},\, {\boldsymbol{\mathscr{P}}}^{\prime},\, {\boldsymbol{\mathscr{R}}}^{\prime}$) have broken {R}, so they are vector-like. A large number of quasi-1D schematic examples are also shown: blue arrows are spins or magnetization, red arrows are polarizations or electric fields, wiggly arrows are velocity vectors or linear momenta, “+l” represents angular momentum or circular polarization, light-blue symbols depict the reference 1D direction, green dots are inversion centers, dashed black circles are anions, and golden springs represent mono-axial chiral objects. The reference 1D direction is the horizontal direction on the page plane, except when there is an explicit light-blue symbol depicting the 1D direction.

Results and discussion

Eight types of 1D objects

We have attempted to identify various exemplary 1D objects that show SOS with each of the eight Hlinka’s classifications⁴, which are listed in Fig. 1 and described below:

${\boldsymbol{\mathscr{D}}}$ (no broken symmetry): director. Simple antiferromagnetic order in a chain, up-up-down-down antiferromagnetic order in a chain, and up-up-down-down antiferromagnetic order in a chain with two kinds of bonding. For example, the magnetic point group mmm1′ (#8.2.25) has I, R, R, M, M, T, so fit the criteria for ${\boldsymbol{\mathscr{D}}}$.

${\boldsymbol{\mathscr{C}}}$ (broken {I, M, M}): chirality. Crystallographic chirality, helical spins, a magnetic toroidal moment with the out-of-plane canted moment, a magnetic quadrupole moment with alternating out-of-plane canted moments, linear momentum (velocity) with spin or orbital angular momentum along the linear momentum direction, circularly-polarized light, and vortex beam having orbital angular momentum along the vortex beam direction. For example, the point groups 222, 32, 422, 622, and 23 fit the criteria of broken {I, M, M}.

${\boldsymbol{\mathscr{P}}}$ (broken {R, I, M}): polarization (P). Strain gradient, thermal gradient, and cycloidal spins. For example, the point groups 2mm, 3m, 4mm, and 6mm fit the criteria of broken {R, I, M}.

${\boldsymbol{\mathscr{a}}}$ (broken {R, M}): axial vector of ferro-rotation. Crystallographic rotational distortions, and electric toroidal moment. For example, the point groups $\overline 1 ,\overline 3 ,\overline 4 ,\overline 6$, 2/m, 4/m, and 6/m fit the criteria of broken {R, M}.

${\boldsymbol{\mathscr{D}}}^{\prime}$ (broken {T}): a director with broken {T}. Up-up-down-down antiferromagnetic order in a chain with alternating two kinds of chiral bonding environments. For example, the magnetic point group mmm (#8.1.24) has I, R, R, M, M, so fit the criteria for ${\boldsymbol{\mathscr{D}}}^{\prime}$.

${\boldsymbol{\mathscr{C}}}^{\prime}$ (broken {I, M, M, T}): chirality with broken {T}. Simple antiferromagnetic order in a chain with two kinds of bonding, simple antiferromagnetic order in a chain with alternating two kinds of chiral bonding environments, which corresponds to the magnetic state of Cr₂O₃, magnetic monopole, an in-plane antiferromagnetic order on the honeycomb lattice, and an in-plane antiferromagnetic order with in-plane canting on the honeycomb lattice. For example, the magnetic point groups ${\overline 3}^{\prime}$ m′ (#20.4.74) and 6m′m′ (#25.4.94) fit the criteria of broken {I, M, M, T}.

${\boldsymbol{\mathscr{P}}}^{\prime}$ (broken {R, I, M, T}): velocity (k, linear momentum, wave vector). The act of applying electric field inducing electric current, magnetic toroidal moments, an in-plane antiferromagnetic order on a honeycomb lattice, Ising antiferromagnetic order on a honeycomb lattice, and antiferromagnetic order in a chain with alternating two kinds of chiral bonding environments, corresponding to the spin-flopped state of Cr₂O₃. Note that all specimen constituents with the ${\boldsymbol{\mathscr{P}}}^{\prime}$ character can exhibit non-reciprocal directional dichroism. For example, the magnetic point group 6mm1′ (#25.2.92) fits the criteria of broken {R, I, M, T}.

${\boldsymbol{\mathscr{a}}}^{\prime}$ (broken {R, M, T}): axial-vector with broken {T}. Magnetization (M), and two kinds of magnetic order in kagome lattice having SOS with M. For example, the magnetic point groups $\overline 3$m′ (#20.5.75) fits the criteria of broken {R, M, T}. The magnetic point groups 2’/m’ (5.5.16) and ${\overline {1}}$(#2.1.3), which correspond to the magnetic states of α-Fe₂O₃ above and below the Morin transition, respectively, have broken {R, R, M, M, T}, so does have SOS with ${\boldsymbol{\mathscr{a}}}^{\prime}$.

As exemplary cases, we, first, discuss how our SOS approach can be helpful to understand the physics of Cr₂O₃ with linear magnetoelectricity and α-Fe₂O₃ with a canted magnetic moment and also to predict a new phenomenon in α-Fe₂O₃. In both Cr₂O₃ and α-Fe₂O₃, the 3D lattice consists of a simple hexagonal stacking of 1D c-direction chains of magnetic ions with alternating left-right chiral bonding environments, as shown in Fig. 2a. Magnetic orders in Cr₂O₃ and α-Fe₂O₃ above the Morin transition are schematically shown in Fig. 2b, f, respectively, so they correspond to ${\boldsymbol{\mathscr{C}}}^{\prime}$ and ${\boldsymbol{\mathscr{a}}}^{\prime}$, respectively. In the case of Cr₂O₃, the magnetic state in Fig. 2b has broken {I, M, M, T}, and we can construct an SOS relationship by adding further broken symmetries such as broken {R, I, M} of P or electric field. As shown in Fig. 2c, d, the magnetic state of Cr₂O₃ in the presence of an electric field does have SOS with M, so it shows a diagonal linear magnetoelectric effect⁵. Applying a large magnetic field along the c axis induces a spin-flopped state, shown in Fig. 2e, and this state exhibits an off-diagonal linear magnetoelectric effect, as the SOS in Fig. 2e indicates. The canted magnetic state of α-Fe₂O₃ above the Morin transition is consistent with the SOS in Fig. 2f. The magnetic state in Fig. 2g has no SOS with any M, and is somewhat similar with the magnetic state of α-Fe₂O₃ below the Morin transition. However, the magnetic state of α-Fe₂O₃ below the Morin transition has lower symmetries $(\overline {1})$, and turns out to have SOS with M in any arbitrary direction. Note that the schematic in Fig. 2b has broken {M, M⊗R, T}, so is supposed to exhibit a magnetooptical Kerr effect (MOKE), and indeed, does show non-zero MOKE in Cr₂O₃^2,6. It is very interesting to notice that the magnetic state of α-Fe₂O₃ below the Morin transition in the presence of an electric field does show SOS with k, which means that it can exhibit a non-reciprocal effect such as an optical-diode effect, which can be experimentally confirmed in the future.

Fig. 2: Various magnetic states of Cr₂O₃ or α-Fe₂O₃, and their SOS relationships.

a Crystallographic structure of a c-direction chain of Cr₂O₃ or α-Fe₂O₃, and left-chiral and right-chiral arrangements of three oxygen tringles are shown in the left-hand-side and right-hand-side projections along the c axis, respectively. b The magnetic state of Cr₂O₃ with broken {M, M⊗R, T}, so can exhibit MOKE. c, d The magnetic state of Cr₂O₃ in E shows SOS with M. e The spin-flopped state of Cr₂O₃ in E shows SOS with M. f The magnetic state of α-Fe₂O₃ above the Morin transition has SOS with M. g This magnetic state has no SOS with any M, and is somewhat similar with the magnetic state of α-Fe₂O₃ below the Morin transition. However, the magnetic state of α-Fe₂O₃ below the Morin transition has lower symmetries $(\overline {1})$, and turns out to have SOS with M in any arbitrary direction. h, i The magnetic state of α-Fe₂O₃ below the Morin transition in E has SOS with k.

We emphasize that ${\boldsymbol{\mathscr{D}}},\, {\boldsymbol{\mathscr{C}}},\, {\boldsymbol{\mathscr{P}}},$ ${\boldsymbol{\mathscr{a}}},$ ${\boldsymbol{\mathscr{D}}}^{\prime},\, {\boldsymbol{\mathscr{C}}}^{\prime},\, {\boldsymbol{\mathscr{P}}}^{\prime}$, and ${\boldsymbol{\mathscr{a}}}^{\prime}$ are well-defined and all distinct, and when a specimen constituent has SOS with one of (${\boldsymbol{\mathscr{D}}},\, {\boldsymbol{\mathscr{C}}},\, {\boldsymbol{\mathscr{P}}},$ ${\boldsymbol{\mathscr{a}}},$ ${\boldsymbol{\mathscr{D}}}^{\prime},\, {\boldsymbol{\mathscr{C}}}^{\prime},\, {\boldsymbol{\mathscr{P}}}^{\prime},$ ${\boldsymbol{\mathscr{a}}}^{\prime}$), the specimen constituent can have more (but not less) broken symmetries than the one. We also note that, for example, broken {R, M, T} for M (or ${\boldsymbol{\mathscr{a}}}^{\prime}$) lists all “independently broken” symmetries, so, I is not broken and consequently I⊗T is broken for M (or ${\boldsymbol{\mathscr{a}}}^{\prime}$). Thus, I is not broken in M (or ${\boldsymbol{\mathscr{a}}}^{\prime}$), but some real 3D ferromagnets, having SOS with M (or ${\boldsymbol{\mathscr{a}}}^{\prime}$), can have broken I. However, no ferromagnets can have higher symmetries than M (or ${\boldsymbol{\mathscr{a}}}^{\prime}$). Thus, all ferromagnets do have also broken I⊗T since I⊗T is broken in M (or ${\boldsymbol{\mathscr{a}}}^{\prime}$). In other words, real 3D ferromagnets can have all broken I, T, and I⊗T. Thus, the necessary and sufficient condition for ferromagnetism or a non-zero net magnetic moment in real 3D materials is having SOS with M (or ${\boldsymbol{\mathscr{a}}}^{\prime}$) having broken {R, M, T}.

Permutable SOS of ${\boldsymbol{\mathscr{P}}}\, \times \, {\boldsymbol{\mathscr{P}}}^{\prime} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime}$

The usefulness of the SOS approach is that it can be commonly applied to various physical quantities that share the same set of broken symmetries. ${\boldsymbol{\mathscr{P}}}$ can be polarization (P) or an electric field (E), but it can be also a temperature gradient, strain gradient, or surface effective electric field, ${\boldsymbol{\mathscr{P}}}^{\prime}$ can be velocity/wave vector (k) of electric current, spin-wave or thermal current, or toroidal moment, and ${\boldsymbol{\mathscr{a}}}^{\prime}$ is magnetization (M) or magnetic field (H). Moreover, the SOS relationships established among them can sometimes be permutable. Figure 3a–c shows pictorially the permutable SOS relationships of ${\boldsymbol{\mathscr{P}}}\, \times$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\approx {\boldsymbol{\mathscr{P}}}^{\prime},$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\times {\boldsymbol{\mathscr{P}}}^{\prime} \approx {\boldsymbol{\mathscr{P}}},\, {\boldsymbol{\mathscr{P}}}^{\prime} \times {\boldsymbol{\mathscr{P}}} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime}$, respectively. Note that all of ${\boldsymbol{\mathscr{P}}}$, ${\boldsymbol{\mathscr{P}}}^{\prime}$, and ${\boldsymbol{\mathscr{a}}}^{\prime}$ are vector-like, i.e., not director-like.

Fig. 3: Three permutable SOS among ${\boldsymbol{\mathscr{a}}}^{\prime},\, {\boldsymbol{\mathscr{P}}}$, and ${\boldsymbol{\mathscr{P}}}^{\prime}$ and SOS relationships with ${\boldsymbol{\mathscr{a}}}$.

Magnetization (M or magnetic field H), polarization (P or electric field E), and velocity (k) are representative for ${\boldsymbol{\mathscr{a}}}^{\prime},\, {\boldsymbol{\mathscr{P}}}$, and ${\boldsymbol{\mathscr{P}}}^{\prime}$, respectively. a P × M has broken {R, I, M, T} along the horizontal direction in the page plane, so has SOS with k. b M × k has broken {R, I, M} along the horizontal direction, so has SOS with P. c k × P has broken {R, M, T} along the horizontal direction, so has SOS with M. d E × ${\boldsymbol{\mathscr{a}}}$ has broken {R, I, M} along the horizontal direction, so has SOS with P, H × ${\boldsymbol{\mathscr{a}}}$ has broken {R, M, T} along the horizontal direction, so has SOS with M, and k × ${\boldsymbol{\mathscr{a}}}$ has broken {R, I, M, T} along the horizontal direction, so has SOS with k.

It turns out that the motion of quasiparticles such as electrons, phonons, magnons, and photons in a specimen or the motion of the specimen itself can be non-reciprocal if the specimen constituent has SOS with k of the motion. If a symmetry operation links +k and −k, and a specimen constituent where quasiparticles are moving with ±k is invariant under the symmetry operation, then the experiment becomes reciprocal, i.e., there is no difference between the experimental results with +k and those with −k. On the other hand, when a specimen constituent has SOS with k, then there is no symmetry operation that can link these two experiments: a specimen constituent with +k and the identical specimen with −k. Thus, the experiments can be non-reciprocal. Note that the magnitude of non-reciprocal effects cannot be estimated from symmetry considerations alone, and this estimation requires an understanding of the microscopic mechanism of the non-reciprocal effects. Thus, Fig. 3a means that if H is applied to any polar magnets, then the electron, light, phonons, or spin-wave propagation can be non-reciprocal, i.e., exhibit directional dichroism. Indeed, for example, diode-like light propagation has been observed in polar (Fe, Zn)₂Mo₃O₈ in H⁷, and electron transport in polar BiTeBr⁸ in H turns out to be non-reciprocal in experimental configurations consistent with Fig. 3a. We anticipate that applying in-plane H to polar Fe(Mn, Ni, Zn)₂Mo₃O₈ or polar (and chiral) Ni₃TeO₆⁹ will induce a non-reciprocal spin-wave along the in-plane direction perpendicular to H.

Figure 3b represents all kinds of (anomalous) Hall-type effects (Hall, Ettingshausen, Nernst, and thermal Hall). Here, (k and P) represents (electric current and induced voltage), (electric current and induced thermal gradient), (thermal gradient and induced voltage), and (thermal gradient and induced thermal gradient) for the Hall, Ettingshausen, Nernst, and thermal Hall effects, respectively. Figure 3c can also represent numerous physical phenomena, including the off-diagonal linear magnetoelectric effect in Cr₂O₃ in the spin-flopped state (Fig. 2e), the spin Hall effect, the spin Nernst (or thermal spin Hall) effect, current-induced magnetization in polar conductors, and also non-linear Hall effects in polar conductors¹⁰. Note that ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\times \, {\boldsymbol{\mathscr{P}}}^{\prime} \approx {\boldsymbol{\mathscr{P}}}$ and ${\boldsymbol{\mathscr{P}}}^{\prime} \, \times \, {\boldsymbol{\mathscr{P}}} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ indicate that all magnetic states having SOS with ${\boldsymbol{\mathscr{P}}}^{\prime}$ should exhibit off-diagonal linear magnetoelectric effects. When P represents the surface effective electric field, electric current and thermal current for k can induce spin current flow along the direction perpendicular to P and the current direction—the resulting surface magnetization is represented by M. Here, the electric current and the thermal current correspond to the spin Hall effect and the spin Nernst (or thermal spin Hall) effect, respectively. Figure 3c also represents that electric current, thermal current, or light propagation along a direction perpendicular to P in polar materials can induce M along the direction perpendicular to both the P and the current/light propagation directions. Even though M in polar materials induced by thermal current/light has not been reported, M in polar conductors induced by electric current has been reported, interestingly in an exotic material of strained monolayer MoS₂^11,12. It will be interesting to observe this current-induced M in bulk non-magnetic polar conductors such as Ca₃Ru₂O₇, GeTe, TaAs, and BiTeI(Br, Cl)^13,14,15,16. In addition, it will be fundamentally important to observe M in polar materials induced by thermal current or light—in this case, the polar materials do not have to be electric conductors, in principle.

The monolayer of 2H-MoS₂, shown in Fig. 4a, is non-centrosymmetric, but non-polar due to the presence of C₃ symmetry. However, uniaxial uniform strain along a particular in-plane direction breaks the C₃ symmetry and induces P in the direction perpendicular to the strain. When an electric current is applied to an in-plane direction perpendicular to the strain-induced P, then M develops along the out-of-plane direction, which is depicted in Fig. 4b, c. Tensile and compressive strains result in opposite Ms. A similar situation, but without external strain, should also work for monolayer T_d-WTe₂ or T_d-MoTe₂. Monolayer T_d-WTe₂ or T_d-MoTe₂ with W/Mo zigzags does have in-plane polarization perpendicular to the zigzag direction. When an electric current is applied along the zigzag direction, M along the out-of-plane direction should be induced, which requires future experimental confirmation. In fact, this M induced by electric current in polar conductors is directly related to the presence of the non-linear Hall effect that we will discuss next.

Fig. 4: Current-induced M, circular dichroism Hall effect (CDHE), and non-linear Hall effect (NLHE).

a–c Monolayer of 2H-MoS₂: (a); no strain, (b); uni-directional uniform tensile strain along the vertical direction on the page plane, and (c); uni-directional uniform compressive strain along the vertical direction on the page plane. d, e show monolayer 1T-Mo(W)Te₂ and T_d-Mo(W)Te₂, respectively. Closed black circles, dark-blue arrows, open black circles, wiggly arrows, red arrows, and blue symbols represent cations, cation distortions, anions, uniform electric currents, polarizations, and induced magnetizations, respectively. Thus, (b), (c), and (e) represent the current-induced magnetization in polar conductors. This current-induced magnetization is directly related to the presence of non-linear Hall effects in polar conductors without any external magnetic field. f depicts the SOS relationship for CDHE with the electric current flow with k, circular-light illumination with −k and +l, and P representing the induced Hall voltage. g–j Four possible configurations of Hall-type voltages induced by electric currents in external electric fields.

First, we attempt to figure out the requirement for quadratic-type non-linear Hall effect (NLHE) without any applied magnetic field. We consider four Fig. 4g–j situations of Hall-type voltages with an applied external electric field (+ −E_ext). To discuss the 3D arrangements of NLHE measurements, we will use these notations: R_x = twofold rotation operation around the x-axis, M_x = mirror operation with the mirror perpendicular to the x-axis, etc. Any of {R_y, M_x, M_z, T} links between Fig. 4g, h (or, (g) or (h) itself). NLHE should not depend on the sign of the external E, so NLHE may require not-broken {R_y, M_x, M_z, T}. However, breaking any of {R_y, M_x, M_z, T} does not make NLHE vanish. Now, any cross-link between Fig. 4g/h, i/j can happen with {R_x, R_z, I, M_y}, so not-broken any of {R_x, R_z, I, M_y} will lead to NLHE to vanish. Therefore, broken {R_x, R_z, I, M_y} is required to have non-zero NLHE. {R_x, R_z, I, M_y} becomes {R, I, M} with the respect to the vertical reference direction on the page plane (i.e., the y-axis). Thus, broken {R, I, M}, more precisely speaking broken {R_x, R_z, I, M_y}, is the necessary and sufficient condition for non-zero NLHE. P has broken {R, I, M} and also not-broken {R_y, M_x, M_z, T}, but in principle, any specimen constituents having SOS with P can exhibit non-zero NLHE. In other words, the specimen constituents with non-zero NLHE can have lower symmetry than P (i.e., can have broken some of {R_y, M_x, M_z, T}). Note that in principle, broken {R_x, R_z, I, M_y} can be achieved in any of non-centrosymmetric materials when the x, y, and z axes are properly chosen, even though the magnitudes of NLHE maybe not significant when the x, y, and z axes are not along with the principal crystallographic directions.

Now, there exists a straightforward but elegant relationship between current-induced magnetization and NLHE in polar conductors. When an electric current, J, is applied to a polar conductor along a direction perpendicular to P, M is induced along a direction perpendicular to both J and P. This, induced M acts like a magnetic field for the standard Hall effect, and Hall voltage along the P direction goes like J × M ∝ J², which explains quadratic-type non-linear Hall effect in polar conductors. Therefore, strained monolayer MoS₂ should exhibit NLHE along the strain-induced P direction. In fact, the observation of NLHE in ultrathin WTe₂ may be consistent with the above discussion¹⁷. Note that bulk non-magnetic polar conductors such as Ca₃Ru₂O₇, GeTe, TaAs, and BiTeI(Br, Cl) should exhibit NLHE, in addition to current-induced M.

We also note that the so-called circular dichroism Hall effect can be understood on a similar footing¹⁸. Illumination of circularly-polarized light on a chiral material can induce an electric current, which is called a circular photogalvanic effect (CPGE)^19,20,21. In the case of CPGE, one can consider if or not the entire experimental setup with induced current changes in a systematic manner under all symmetry operations—the so-called symmetry operational systematics (SOSs). It turns out that in terms of SOSs, a similar phenomenon can occur in a material with a net magnetic moment, rather than chirality¹. Now, with the consideration of SOSs, one can also show that illumination of circularly-polarized light on any materials can induce M. This circularly-polarized light-induced M can act as a magnetic field, so when electric current flows along a direction perpendicular to the induced M, then a Hall voltage can develop along the direction perpendicular to both M and current without any applied magnetic field, which is called a circular dichroism Hall effect (CDHE). Therefore, in principle, this CDHE can occur in any materials where electric current flow is possible. This CDHE can be also understood in terms of the SOS relationship in Fig. 4f. Emphasize that the specimen showing with a blue rectangle appears to have no broken symmetries, but the SOS relationship still holds even if the specimen has any broken symmetries by the definition of an SOS relationship. This again guarantees that CDHE can occur in any materials where electric current flow is possible. In addition, the electric current flow can be replaced by the thermal current, and also P can stand for a thermal gradient, rather than a Hall voltage. Therefore, there can exist Ettingshausen, Nernst, or thermal Hall effect versions of CDHE in any materials with circularly-polarized light (or vortex beam with orbital angular momentum) illumination without any applied magnetic field.

We would like to discuss three more cross-product-type SOS relationships: ${\boldsymbol{\mathscr{P}}} \, \times$ ${\boldsymbol{\mathscr{a}}}$ $\approx {\boldsymbol{\mathscr{P}}},$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\times$ ${\boldsymbol{\mathscr{a}}}$ $\approx$ ${\boldsymbol{\mathscr{a}}}^{\prime}$, and ${\boldsymbol{\mathscr{P}}}^{\prime} \, \times$ ${\boldsymbol{\mathscr{a}}}$ $\approx {\boldsymbol{\mathscr{P}}}^{\prime}$, which are illustrated in Fig. 3d. Note that all of ${\boldsymbol{\mathscr{P}}},$ ${\boldsymbol{\mathscr{a}}},$ ${\boldsymbol{\mathscr{P}}}^{\prime}$, and ${\boldsymbol{\mathscr{a}}}^{\prime}$ are vector-like (thus, not director-like). The meaning of these SOS relationships is: when an electric field or a magnetic field is applied to a ferro-rotational system, the induced polarization or magnetization can have a component along the direction perpendicular to the applied E/H and also to the ${\boldsymbol{\mathscr{a}}}$ direction. In other words, in ferro-rotational systems in the presence of an external electric field or magnetic field, the induced polarization or magnetization can be tilted toward the direction perpendicular to the applied E/H and also to the ${\boldsymbol{\mathscr{a}}}$ direction. The tiled induced polarization can be a tilted current in ferro-rotational conductors, so a Hall-type voltage can develop without any external magnetic field. As far as we are aware of, any observations relevant to these SOS relationships have not theoretically and experimentally reported yet.

Permutable SOS of ${\boldsymbol{\mathscr{C}}} \cdot {\boldsymbol{\mathscr{P}}}^{\prime} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime},$ ${\boldsymbol{\mathscr{a}}}$ $\cdot$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\approx {\boldsymbol{\mathscr{D}}}^{\prime}$, and ${\boldsymbol{\mathscr{P}}} \cdot {\boldsymbol{\mathscr{D}}}^{\prime} \approx {\boldsymbol{\mathscr{P}}}^{\prime}$

We have also the dot product-type, rather than cross product-type, SOS relationships of ${\boldsymbol{\mathscr{C}}} \cdot {\boldsymbol{\mathscr{P}}}^{\prime} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime},$ ${\boldsymbol{\mathscr{a}}}$ $\cdot$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\approx {\boldsymbol{\mathscr{D}}}^{\prime}$, and ${\boldsymbol{\mathscr{P}}} \cdot {\boldsymbol{\mathscr{D}}}^{\prime} \approx {\boldsymbol{\mathscr{P}}}^{\prime}$, as well as their permutable SOS relationships, summarized below: The broken symmetry operations that do not cancel on the left-hand side are colored in green as the resultant broken symmetries on the right-hand side, while canceled ones are colored in dark gray. Note that a dot product between two 1D objects means the coexistence of two 1D objects, and when a symmetry is broken in both 1D objects that are coupled to each other and act as a new 1D object, the symmetry can be not broken in the 3^rd 1D object. For this situation, we have the following SOS relationships.

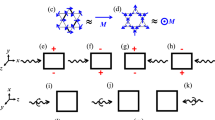
Note that ${\boldsymbol{\mathscr{C}}},\, {\boldsymbol{\mathscr{C}}}^{\prime},\, {\boldsymbol{\mathscr{D}}}$, and ${\boldsymbol{\mathscr{D}}}^{\prime}$ are director-like (i.e., not-broken {R}), so the resulting SOS orientation is fixed by vector-like objects of ${\boldsymbol{\mathscr{P}}},$ ${\boldsymbol{\mathscr{a}}},$ ${\boldsymbol{\mathscr{P}}}^{\prime}$, or ${\boldsymbol{\mathscr{a}}}^{\prime}$. Thus, the directions of ${\boldsymbol{\mathscr{C}}},\, {\boldsymbol{\mathscr{D}}}^{\prime}$, and ${\boldsymbol{\mathscr{C}}}^{\prime}$ in Fig. 5 can be in the vertical, horizontal, or out-of-plane direction. (1)–(9) list all SOS relationships permutable from ${\boldsymbol{\mathscr{C}}} \cdot {\boldsymbol{\mathscr{P}}}^{\prime} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ : each SOS relationship has two [′]s. Similar sets of permutable SOS relationships are possible from (10) to (12). First, Fig. 2c/d, reproduced in Fig. 5a, and Fig. 2h/i correspond to (2) and (12), respectively. When E and M in Fig. 2c/d are replaced by H and P, respectively, it corresponds to (5). This demonstrates a permutable SOS relationship as well as the permutable (and duality) nature of linear magnetoelectric effects. Note also that (2) and (6) mean that all diagonal linear magnetoelectrics belongs to ${\boldsymbol{\mathscr{C}}}^{\prime}$ and any specimen constituents having SOS with ${\boldsymbol{\mathscr{C}}}^{\prime}$ exhibit diagonal linear magnetoelectric effects. Table 1 lists the complete set of dot product-type SOS relationships among eight kinds of 1D objects (vector- or director-like quantities).

Fig. 5: Various SOS relationships.

The Yin-yang symbol represents ferro-rotation. a–g correspond to ${\boldsymbol{\mathscr{C}}}^{\prime} \cdot {\boldsymbol{\mathscr{P}}} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime},$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\cdot \, {\boldsymbol{\mathscr{C}}} \approx {\boldsymbol{\mathscr{P}}}^{\prime},\, {\boldsymbol{\mathscr{C}}} \cdot {\boldsymbol{\mathscr{P}}}^{\prime} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime},$ ${\boldsymbol{\mathscr{P}}}^{\prime} \cdot$ ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\approx {\boldsymbol{\mathscr{C}}},$ ${\boldsymbol{\mathscr{C}}} \cdot {\boldsymbol{\mathscr{P}}} \approx$ ${\boldsymbol{\mathscr{a}}}^{\prime},$ ${\boldsymbol{\mathscr{P}}} \cdot$ ${\boldsymbol{\mathscr{a}}}$ $\approx {\boldsymbol{\mathscr{C}}}$, and ${\boldsymbol{\mathscr{a}}}^{\prime}$ $\cdot \, {\boldsymbol{\mathscr{C}}} \approx {\boldsymbol{\mathscr{P}}} \cdot {\boldsymbol{\mathscr{D}}}^{\prime} \approx {\boldsymbol{\mathscr{P}}}^{\prime}$, respectively.

Table 1 Dot product-type SOS relationships among eight kinds of 1D objects (vector- or director-like quantities).

Permutable SOS relationships of (2), (5), and (7) can be also well exemplified in hexagonal rare-earth ferrites²². The A₂ phase of the system carries P (${\boldsymbol{\mathscr{P}}}$) along the c axis and in-plane magnetic monopole (${\boldsymbol{\mathscr{C}}}^{\prime}$), and a net magnetic moment M (${\boldsymbol{\mathscr{a}}}^{\prime}$) along the c axis is, indeed, observed experimentally, which is neatly consistent with (2). Through a spin reorientation transition, the magnetic state transforms into the A₁ phase with magnetic toroidal moments (${\boldsymbol{\mathscr{P}}}^{\prime}$), where the net magnetic moment M (${\boldsymbol{\mathscr{a}}}^{\prime}$) is no longer allowed according to ${\boldsymbol{\mathscr{P}}} \cdot {\boldsymbol{\mathscr{P}}}^{\prime} \approx {\boldsymbol{\mathscr{D}}}^{\prime}$. This is another premium example of how these permutable SOS relationships can be used to explain and predict physical properties in real materials.

Figure 5b corresponds to (6), which explains longitudinal and also transverse magnetochiral effects, i.e., non-reciprocal electronic transport or optical effects in chiral materials in the presence of external magnetic fields²³. Note that a twisted graphene bilayer is chiral, so exhibits a natural optical activity²⁴, and should exhibit non-reciprocal optical and also transport effects in the presence of magnetic fields, which need to be experimentally verified. Their inverse effects in Fig. 5c, corresponding to (1), include magnetization induced by electric current in chiral materials and spin-polarized tunneling in chiral materials. The magnetization induced by electric current in chiral Te single crystals has been reported in a Faraday-type optical experiment as well as a direct magnetization pulse measurement^25,26. The chirality-dependent spin-polarization of tunneling current was recently observed in chiral Co_1/3NbS₂²⁷ (see below). The existence of electric current in a magnetic field along the electric current direction corresponds to (9), so it corresponds to a chiral object (see Fig. 5d). In fact, this SOS relationship is closely related to the so-called chiral anomaly in topological Weyl semimetals, which are often non-chiral crystallographically^28,29,30,31. Since the toroidal moment, just like k, also belongs to ${\boldsymbol{\mathscr{P}}}^\prime$, the SOS in Fig. 5e should also work.

Chiral materials can exhibit natural optical activity, i.e., the rotation of light polarization of transmitted linearly-polarized light. Thus, Fig. 5f SOS relationship, corresponding to (10), explains the so-called linear-gyration, i.e., the linear change of the light polarization rotation of transmitted linearly-polarized light with the varying electric field. In fact, this linear-gyration can be utilized to visualize ferro-rotational domains, since opposite ferro-rotational domains show the opposite linear-gyration effects¹. This idea was, indeed, confirmed in the visualization of ferro-rotational domains in ilmenite NiTiO₃, as shown in Fig. 6b³². There exists a large number of ferro-rotational compounds with point group symmetry of $\overline 1 ,2/m,\overline 3 ,\overline 4 ,4/m,\overline 6$ or 6/m³³. Examples include Cu₃Nb₂O₈ (P$\overline 1$)³³, RbFe(MoO₄)₂ (P$\overline 3$ below 190 K)³⁴, CaMn₇O₁₂ (R$\overline 3$ below 440 K)³⁵, NbO₂ (I4₁/a below 1081 K)³⁶, and Pb₂CoTeO₆ (R$\overline 3$ below 370 K)³⁷. Ferro-rotational domain visualization of these compounds needs to be further investigated with the linear-gyration technique.

Fig. 6: Visualization of domains associated with various broken symmetries.

a A Z₆ vortex of Co_1/3NbS₂ with chiral domains. b Chirality-dependent SP-STM unveils a Z₆ vortex²⁷. (scale bar = 20 nm). c The atomic structure of ferro-rotational domains of NiTiO₃³². d Ferro-rotational domains in NiTiO₃ visualized with an electro-gyration technique. (scale bar = 100 μm). e The atomic structure of ferro-rotational domains of RbFe(MoO₄)₂. f Ferro-rotational domains observed in TEM on RbFe(MoO₄)₂³⁸ (scale bar = 500 nm).

Figure 6a exhibits the atomic model of a topological vortex surrounded by six structural chiral domain boundaries in Co_1/3NbS₂. Since Co intercalants occupy one of three possible Nb-atop sites, A, B, and C, there exist six possible combinations considering the two layers within a unit cell, exhibiting A/B-type stacking. Solid and dashed lines refer to structural chiral domain boundaries in the first and the second layer, respectively. As a result of intercalation site change, the chiral distortion of the S layer reverses as depicted by red and blue triangular arrows and gives the alternating structural chirality across the vortex domain boundaries. In reference to the SOS relationship shown in Fig. 5c, flowing electric current across the chiral structure induces a magnetization along the current direction, which should work even for local probes such as scanning tunneling microscopy (STM). Figure 6b shows the spin-polarized STM (SP-STM) measurement around a topological vortex that clearly reveals the alternating domain contrast locked to the chirality of each domain²⁷. It is noteworthy that the induced domain contrast does not require long-range ordered magnetic moments, in contrast to the conventional SP-STM. Instead, the specimen constituent comprised of the chiral structure and the tunneling current gives the same set of broken symmetries as magnetization, as shown in Fig. 5c.

We would like to note finally that ferro-rotation is rather common in numerous materials^{33,34,35,36,37}, but does not break inversion symmetry, so difficult to be coupled with measuring probes and thus has been studied only to a limited degree. The traditional way to study ferro-rotational domains is atomic-resolved transmission electron microscopy (TEM) such as high-resolution TEM or high-angle annular dark-field (HAADF)-STEM to observe the ferro-rotational distortions or ferro-rotational domains³². Figure 6e depicts a pair of ferro-rotational domains, corresponding to a clockwise and counterclockwise rotation of the FeO₆ octahedra in RbFe(MoO₄)₂. Utilizing the cryogenic dark-field TEM technique (Fig. 6f), the contrast difference between the two ferro-rotational domains shows up as the brighter G_a spot for the left domain and the darker G_b spot for the right domain are collected. Note that the Bragg spot G_a is converted into G_b in the reciprocal space by the twofold rotation as two ferro-rotation domains do in real space³⁸. The SOS relations of ferro-rotation such as Fig. 5f, g can be good guidance for the further exploration of ferro-rotations in the future.

In summary, the recent exotic experimental results such as electric current-induced magnetization in strained monolayer MoS₂, NLHE in monolayer WTe₂, spin-polarized tunneling in chiral Co_1/3NbS₂ in a paramagnetic state, and non-reciprocal electronic transport in polar BiTeBr can be understood in terms of permutable SOS relationships of 1D objects. We have presented all possible permutable SOS relationships among eight kinds of 1D objects. Based on the permutable SOS relationship, we have proposed a large number of new phenomena, which can be experimentally verified in the future. New predictions include (but are not limited to): (1) a twisted graphene bilayer in the presence of magnetic fields should exhibit non-reciprocal transport and optical effects ^{Note 1 39}, (2) NLHE in strained monolayer MoS₂, (3) electric current-induced magnetization in monolayer Mo(W)Te₂, (4) electric current-induced magnetization, NLHE, and non-reciprocal electronic transport in bulk polar conductors such as Ca₃Ru₂O₇, GeTe, TaAs, and BiTeI(Br,Cl), (5) light- or thermal current-induced magnetization in numerous polar materials, (6) electric/thermal current-, or light-induced magnetization of polar materials at polar domain walls, (7) CDHE in any materials with enough electric conduction, (8) Ettingshausen, Nernst, or thermal Hall effect versions of CDHE in any materials with circularly-polarized light (or vortex beam with orbital angular momentum) illumination without any applied magnetic field, (9) non-reciprocal spin wave propagation in polar materials such as Fe(Mn,Ni,Zn)₂Mo₃O₈ or Ni₃TeO₆ in magnetic fields, (10) non-reciprocal directional dichroism in α-Fe₂O₃ below the Morin transition in the presence of an electric field, (11) visualization of ferro-rotational domains of ferro-rotational compounds such as RbFe(MoO₄)₂, CaMn₇O₁₂, Cu₃Nb₂O₈, NbO₂, and Pb₂CoTeO₆ using a linear-gyration technique, (12) non-reciprocal directional dichroism of electric current, spin wave or light in ferro-rotational systems in the presence of both electric and magnetic fields, and (13) the tiled induced polarization (current) and magnetization in ferro-rotational systems in the presence of an external electric field and magnetic field, respectively. We also find this important systematics: all magnetic states having SOS with ${\boldsymbol{\mathscr{C}}}^{\prime}$ exhibit diagonal linear magnetoelectric effects, and all magnetic states having SOS with ${\boldsymbol{\mathscr{P}}}^{\prime}$ exhibit off-diagonal linear magnetoelectric effects. It will be exuberating to confirm these predictions in bulk quantum materials as well as 2D materials in the coming years. The following poem summaries our findings in an esthetic manner:

Symmetry defines evident beauty.

Once broken, it brings observables.

Unveiling duality and permutability.

These tricks that Nature plays become the crystal ball to see its hidden beauty.

In Nature, nothing is perfect, yet everything is perfect. ^{Note 2}

Note 1: After submission of our manuscript, the following paper³⁹, directly relevant to this prediction, has published.

Note 2: Walker A. In nature, nothing is perfect and everything is perfect. Trees can be contorted, bent in weird ways, and they’re still beautiful.

Methods

SOS analysis

The relationships between quasi-1D specimen constituents (lattice distortions or spin arrangements in external magnetic field, electric fields or stress, and also their time evolution) and measuring probes/quantities (observables such as transmitting electrons, phonons, magnons, photons in various polarization states, including electrons or photons with spin or orbital angular momentum, bulk magnetization or polarization, and also experimental setups to measure, e.g., Hall-type effects) are examined in terms of their characteristics under various symmetry operations of rotation, space inversion, mirror reflection, and time reversal. When quasi-1D specimen constituents have identical or more (but not less) broken symmetries, compared with measuring probes/quantities, except translation symmetry and rotation symmetry around the 1D direction, they are said to exhibit SOS, and the corresponding phenomena can take place. In terms of SOS, we have considered the specimen constituents for light- or current-induced magnetization, NLHE, the spin polarization of electric current in non-magnetic or paramagnetic states, linear magneto-electric effects, and natural optical activity or non-reciprocal effects in the presence of an electric field. In addition, we have also discussed what new phenomena can be observed in ferro-rotational systems from SOS considerations.