Influence of morphology on the effective hygro-elastic properties of softwood (spruce) and hardwood (balsa)

Abstract

Wood materials are characterized by complex, hierarchical material structures spanning across various length scales. The present work aims at establishing a relation between the hygro-elastic properties at the mesoscopic cellular level and the effective material response at the macroscopic level, both for softwood (spruce) and hardwood (balsa). The particular aim is to explore the influence on the effective hygro-elastic properties under variations in the meso-scale morphology. The multi-scale framework applied for this purpose uses the method of asymptotic homogenization, which allows to accurately and efficiently obtain the effective response of heterogeneous materials characterized by complex meso-structural geometries. The meso-structural model considered for softwood is based on a periodic, two-dimensional statistically representative volume element that is generated by a spatial repetition of tracheid cells. The tracheid cells are modeled as hexagonal elements characterized by a certain geometrical irregularity. The hardwood meso-structure consists of a region composed of hexagonal cellular fibers with large vessels embedded, which is connected to a ray region that is constructed of ray cells. The hardwood fibers are modeled as hexagonal cellular elements, similar to softwood tracheids. The rays are represented by quadrilateral cells oriented along the radial direction, whereby different arrangements are considered, i.e., the ray cells are either regularly stacked or organized as a staggered configuration. The interface between the fiber and ray regions may also be characterized by a regular or a staggered arrangement. The meso-structural models for softwood and hardwood are discretized by means of plane-strain, finite element models, which describe the hygro-elastic response of the wood material in the radial–tangential plane. For softwood, the sensitivity of the effective elastic and hygro-expansive properties is explored as a function of the geometrical irregularity of the tracheids. For hardwood, the effective properties are studied under a variation of the ray cell arrangement, the type of interface between ray and fiber regions, and the vessel volume fraction. The modeling results agree well with results obtained from other numerical homogenization studies and show to be in reasonable agreement with experimental data taken from the literature.

1 Introduction

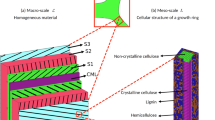
Wood is a versatile material that has been used throughout the centuries for a wide range of applications, varying from construction and infrastructure [1] to decoration and art [2]. The hierarchical material structure of wood involves different length scales, which range from the nano-scale to the macro-scale [3, 4]. At the nano-scale, cellulose molecules can be identified as shown in Fig. 1a. These molecules are bundled together into cellulose micro-fibrils, as shown in Fig. 1b, which are aligned and connected to form fibril aggregates named macro-fibrils. The macro-fibrils are embedded in a matrix that mainly consists of hemicellulose and lignin, as shown in Fig. 1c, thereby forming characteristic layers that compose the cell walls. As illustrated in Fig. 1d, cell walls consist of a primary wall and a secondary wall, whereby the secondary wall is constructed from three layers, commonly referred to as the S1, S2, and S3 layers. The S2 layer is the thickest of these three layers and provides the largest contribution to the mechanical properties of wood. The primary wall is connected to the middle lamella, which bonds together different adjacent wood cells. Wood cells are long and slender hollow tubes, which are oriented mainly along the axial direction of the stem of a tree. Depending on the wood type, their location, and their physiological role in the tree, the cells have different sizes and shapes. As shown in Fig. 1e, at the meso-scale softwood is mainly constructed by one cell type named axial (vertical) tracheids, which are oriented mostly or exclusively in the axial, or longitudinal, direction. Conversely, the meso-structure of hardwood is more complex and contains different types of cells. In the axial direction, fibers and axial parenchyma—which look similar to fibers—can be distinguished; these cells are disrupted by vessels, which are tubular structures with a relatively large diameter, as shown in Fig. 1f. Hardwood tissue further consists of ray parenchyma, or rays, which are cellular structures oriented in the radial material direction. At the macro-scale, the cellular elements along the radial material direction lead to a periodic pattern of concentric rings, called annual growth rings, as shown in Fig. 1g and h for softwood and hardwood, respectively. Each growth ring consists of earlywood (light color) and latewood (dark color), whereby latewood is characterized by a larger cell wall thickness and smaller cell cavities (i.e., lumen) than earlywood.

Fig. 1

Multi-scale structure of wood, indicating the different length scales involved. a Molecular structure of cellulose; b cellulose micro-fibrils, composed by both crystalline and non-crystalline regions, arranged into a macro-fibril; c a macro-fibril embedded into a hemicellulose and lignin matrix, forming a primary cell wall; d wood cell wall, consisting of a primary wall and a secondary wall composed of three layers (S1, S2, and S3). The cellulose micro-fibrils have different orientations in each layer. Adjacent cells are connected to each other by the middle lamella (not illustrated in the figure). Images a–d reproduced from [5]; e softwood cellular structure (spruce). Image reproduced from [6]; f hardwood cellular structure (balsa). Image reproduced from [3]; g cross section of a softwood log (red pine); and h cross section of a hardwood log (red oak). Images g–h adapted from [7]

The hygroscopic nature of wood makes the material relatively sensitive to variations in ambient humidity. The response of wood to humidity changes is determined by complex interactions between hygro-expansive phenomena at different length scales and results in dimensional changes and instabilities [8] that may promote fracture or distortion of the material [9]. For example, recent studies performed on museum objects have shown the presence of moisture-induced cracks and dimensional changes on decorated oak panels in panel paintings and historical cabinets [10, 11]. A detailed modeling of the mechanical, hygro-expansive behavior of wood in such applications requires the incorporation of the characteristics and diversity of the underlying material structure and thus should be based on a multi-scale approach. In the literature, most multi-scale models for wood focus on the mechanical behavior of softwood, thereby considering two-dimensional [4, 12,13,14,15,16] and three-dimensional [17, 18] representations of the hierarchical material structure. The length scales included in these models may range from the scale at which micro-fibrils can be identified to that of the annual growth rings, whereby the effective material properties are calculated by means of analytical and/or computational homogenization techniques, see [19] for a comprehensive overview. For example, the hygroscopic response of softwood has been determined at the macro-scale by applying computational homogenization of a hygro-expansive, periodic cellular structure, which includes microstructural information such as the geometry of wood cells, the local material density, and the microfibril angle [20,21,22]. In addition, several studies consider the uncertainty in the macroscopic response caused by variations and irregularities in the underlying cell structure [12, 23] or material properties [24]. Due to its relatively complex morphology, to date the multi-scale modeling of hardwood has only received limited attention. In [4], a two-dimensional multi-scale model based on the mean field theory is presented for the determination of the elasticity parameters of hardwood, which includes the low-scale stiffness properties of hemicellulose, amorphous cellulose, crystalline cellulose, lignin and water, and the meso-scale stiffness contribution of vessels. Furthermore, the effect of ray cells on the physical properties of hard wood has been investigated by means of several multi-scale approaches, see [25,26,27,28].

The present work aims at predicting the elastic and hygro-expansive properties of both softwood and hardwood in the radial–tangential (RT) material plane via a numerical multi-scale approach, thereby particularly focusing on the effects caused by morphological variations in the mesoscopic cellular structure. The multi-scale framework applied is based on the asymptotic homogenization method [29, 30] and follows the modeling strategy presented in [31,32,33]. Asymptotic homogenization applies to heterogeneous materials characterized by an underlying fine-scale periodic structure. This multi-scale method enables to represent the heterogeneous medium as an equivalent homogeneous domain, by calculating the effective material response from the fine-scale field variables describing the physics problem at hand. For the determination of the elastic and hygro-expansive properties of wood, the homogenization procedure starts from the assumption that the displacement field satisfying the local equilibrium conditions can be written in terms of an asymptotic expansion. This asymptotic expansion is subsequently combined with the equilibrium and constitutive equations for an arbitrary material point within the fine-scale domain. The effective mechanical and hygro-expansive properties are obtained numerically by computing with the finite element method the hygro-elastic response of a periodic unit cell representative of the fine-scale domain.

The current numerical study investigates for softwood and hardwood the relation between the characteristics at the mesoscopic scale, represented by the cellular structures displayed in Fig. 1e and f and the macroscopic scale depicted in Fig. 1g and h, respectively. The softwood unit cell is reflected by two-dimensional honeycomb-like structures composed of hexagonal elements representative of axial tracheid cells. Inspired by earlier works that explore the effect of geometrical irregularities on the mechanical response of cellular solids [34,35,36,37], a generic geometrical disorder is introduced in the regular softwood structure by shifting the positions of the vertical cell walls of the honeycombs randomly along the positive and negatives axes of the radial material direction. The hardwood unit cell includes fibers, vessels, and rays, whereby the fibers are described by axial hexagonal elements (similar to the softwood tracheids), and the rays are modeled as quadrilateral cells oriented along the radial material direction of the hardwood. Following the study presented in [28], different geometrical arrangements of ray cells are analyzed, whereby the ray regions consist either of cells regularly stacked on top of each other, or of cells stacked in a staggered fashion, with the staggering of rays quantified by a specific eccentricity parameter. Finally, two types of interfaces are considered between the fiber and ray regions, which are representative of regular and staggered connections. In all simulations, at the mesoscopic scale an orthotropic hygro-elastic constitutive behavior is assumed for the cell wall material. The extension of the present model toward a multi-scale model accounting for the nonlinear constitutive response of wood cell walls, which includes the effects of plasticity and fracture, can be performed along the lines of [38] and is a topic for future work.

After the construction of the mesoscopic models, the macroscopic effective mechanical and hygro-expansive properties of wood are computed. For this purpose, the size of the mesoscopic unit cell is chosen to be sufficiently large in order to be statistically representative of the effective material properties of wood [39,40,41]. Accordingly, the macro-scale properties computed for softwood and hardwood reveal the influence of specific geometrical meso-structural features, such as the irregularity of tracheids in softwood, the type of ray cell configurations in hardwood, the type of interface between ray and cell regions, and the vessel volume fraction of hardwood. A comparison of the computed material properties with experimental data taken from the literature illustrates the predictive capability of the present multi-scale approach.

The paper is organized as follows. Section 2 discusses the procedure of constructing mesoscopic unit cell models for softwood and hardwood. The asymptotic homogenization framework is reviewed in Sect. 3. The determination of the representative unit cell size and the influence of the irregularity of tracheid cells on the effective mechanical and hygro-expansive properties of softwood is investigated in Sect. 4. Subsequently, Sect. 5 illustrates the influence on the effective hygro-elastic properties of hardwood by the ray cell arrangement, the type of interface between fiber and ray regions, and the vessel volume fraction. Finally, in Sect. 6 the main conclusions of the study are summarized.

In the formulation of the model equations, the following notation for tensors and tensor products is employed: $a, \mathbf {a}, \mathbf {A}$, and $^n\mathbf {A}$ denote, respectively, a scalar, a vector, a second-order tensor, and an nth-order tensor. By making use of Einstein’s summation convention, vector and tensor operations are defined as follows: A dyadic product is represented by $\mathbf {a} \otimes \mathbf {b} = a_i b_j ~\mathbf {e}_i \otimes \mathbf {e}_j$, and inner products are provided by $\mathbf {A}\cdot \mathbf {b} = A_{ij}b_j ~\mathbf {e}_i$, $\mathbf {A}\cdot \mathbf {B} = A_{ij}B_{jk}\mathbf {e}_i \otimes \mathbf {e}_k$ and $\mathbf {A}:\mathbf {B} = A_{ij}B_{jk}$, with $\mathbf {e}_i$, (where $i = x, y, z$) the unit vectors of a Cartesian basis.

2 Meso-scale models

2.1 Softwood meso-structure

At the meso-scale level, softwood is defined by a cellular structure of which the predominant elements are tracheid cells [9], as shown in Fig. 1e. Tracheids are slender cells, with the cell length typically being more than 100 times larger than the cell width. Across a transverse section, tracheids appear as an irregular cell structure, which, in addition to hexagonal elements, also may contain collapsed square and/or rectangular elements. Within a growth ring, the cell structure is characterized by relatively thin walls in earlywood and by thicker walls in latewood. In addition, ray parenchyma cells are present, which appear as rectangular prisms that are oriented along the radial material direction of the softwood. The presence of rays may increase the effective elastic stiffness [42] and reduce the effective hygro-expansion [8] in the radial material direction. Nevertheless, since the volume fraction of rays in softwood commonly is small, they are neglected in the present modeling approach. This is also the case for other types of cells of which the volume fraction is small, such as axial parenchyma cells and resin canal complexes.

The mesoscopic model of softwood is based on a unit cell with a honeycomb-like configuration representative of the tracheid cell structure. The reference geometry is chosen as an ideally regular honeycomb structure consisting of a periodic repetition of hexagonal elements, as illustrated in Fig. 2a. The x- and y-axes of the Cartesian coordinate system used in this figure are aligned with the radial (R) and the tangential (T) material directions of the softwood, respectively.

The lengths of the inclined and vertical cell walls of the reference honeycomb geometry are designated by $\ell$ and h, respectively. The cell wall angle $\theta$ defines the slope of an inclined cell wall, in accordance with $\theta = \mathrm {arctan} (\ell _y/\ell _x)$, where $\ell _x$ and $\ell _y$ are the horizontal and vertical projections of the inclined cell wall, respectively. The cell walls have a thickness t, which in the simulations is adjusted to achieve the desired porosity $\phi$ of the honeycomb meso-structure. For an ideally regular honeycomb meso-structure, the effective macroscopic response of softwood can be derived from the response of a single hexagonal element. However, when introducing irregularities in the honeycomb meso-structure, a larger unit cell must be used. This unit cell is constructed by including a sequence of compatible, irregular hexagonal elements along the radial and tangential material directions, such that a rectangular $L \times H$ unit cell is obtained, with $L = 2 n \ell _x$ and $H = n(h + \ell _y)$, as shown in Fig. 2b. Note that the integer n indicates the number of repetitions of the hexagonal element along the radial direction, which should be chosen sufficiently large for the unit cell to be statistically representative of the underlying, irregular meso-structure.

A geometrical irregularity is introduced in the reference geometry by shifting the positions of the vertical walls of the hexagonal cells across a specific horizontal distance $\delta _\mathrm{fib}$ in either the positive or negative x-direction. In order to avoid overlap with adjacent vertical cell walls, the horizontal shift has a maximum value of $l_x/2$, in accordance with its dimensionless form

$$\begin{aligned} k_\mathrm{ir} = \frac{2 \delta _\mathrm{fib}}{l_x} \qquad \text{ with } \qquad 0 \le k_\mathrm{ir} \le 1. \end{aligned}$$

(1)

The positive or negative direction of the horizontal shift $k_\mathrm{ir}$ of an individual vertical cell wall is obtained through a multiplication by an integer value that is randomly chosen as either − 1 or 1. An example of the irregular mesoscopic structure obtained with this procedure is illustrated in Fig. 2c, which is considered to be representative of the cellular morphologies commonly observed in the softwood spruce, as shown in Fig. 1e. The irregular honeycomb cell structure depicted in Fig. 2c is composed by choosing $n =8$ hexagonal elements along the radial material direction and an irregularity factor of $k_\mathrm{ir} = 0.75$.

Fig. 2

Softwood meso-scale configuration. a Reference geometry represented by a regular hexagonal honeycomb configuration; b comparison of regular (black lines) and irregular (purple lines) meso-scale unit cells; c irregular meso-scale unit cell. The unit cell is here constructed by first repeating a set of $n=8$ regular hexagonal configurations, followed by shifting the positions of the vertical walls of the hexagonal cells randomly along the positive and negatives axes of the radial material direction using an irregularity factor $k_\mathrm{ir} =0.75$, see Eq. (1)

2.2 Hardwood meso-structure

The meso-structure of hardwood is more complex than that of softwood and consists of an arrangement of three different types of cells, i.e., fibers, rays, and axial parenchyma, which are disrupted by vessels [9]. Fibers are long cellular elements that are oriented in the axial direction of the stem of a tree, and serve to provide mechanical resistance. Conversely, rays are prismatic cells that are oriented along the radial direction of the growth rings. In hardwood, the volume fraction of ray cells is considerable, such that their presence has a significant influence on the effective macro-scale material properties [3, 10]. Furthermore, axial parenchyma cells are characterized by a size and shape similar to ray parenchyma cells. They are, however, oriented vertically and piled on top of each other, forming a parenchyma strand. Finally, vessels have the function of conducting water in hardwood; they appear as tubular structures with a diameter that is larger than that of fibers and parenchyma cells. In the axial direction, vessels are much shorter than fibers, and in the transition from earlywood to latewood, they can be organized in different patterns.

The proposed meso-structural model for hardwood includes the three main elements, which are the fibers, rays, and vessels. In the model description, the axial parenchyma cells are considered as fibers, with a similar hexagonal cell structure. The fiber region is constructed by following the same procedure as employed for the softwood tracheids, see Sect. 2.1. The reference element representing a hardwood fiber consists of a hexagonal honeycomb, which is characterized by the cell wall lengths $\ell$ and h, cell wall thickness t, and cell wall angle $\theta$, as defined in Sect. 2.1 and illustrated in Fig. 2a. With this reference element, the fiber region is constructed by copying the hexagons multiple times along the radial and tangential material directions, respectively, as shown in Fig. 3a.

In the fiber region, one (or more) vessel(s) can be introduced. The procedure of generating a vessel follows an approach based on the level set method [43, 44]. Accordingly, consider a fiber region $Q_\mathrm{f}$ consisting of a sequence of (regular or irregular) hexagonal elements, as described above. A vessel is idealized as an elliptical void with major and minor ellipse axes D and d, respectively. The vessel domain is referred to as V and its boundary as $\partial V$. The boundary of the vessel $\partial V$ can be expressed as the zero level set of a function $\phi (\mathbf {x})$, i.e.,

$$\begin{aligned} \partial V = \left\{ \mathbf {x} \in Q_\mathrm{f} : \phi (\mathbf {x}) = 0\right\} ~. \end{aligned}$$

(2)

In particular, the function $\phi (\mathbf {x})$ is selected as the signed distance function, whereby honeycomb corner nodes located inside the vessel, $\mathbf {x} \in V$, are characterized by a negative function value, $\phi (\mathbf {x}) < 0$, and honeycomb corner nodes located outside the vessel, $\mathbf {x} \in Q_\mathrm{f}/V$, are characterized by a positive function value, $\phi (\mathbf {x}) > 0$. Accordingly, for a vessel with specific dimensions D and d the corresponding level set function is defined and, for each hexagonal element in the fiber domain $Q_\mathrm{f}$, it is checked whether the corner nodes lie inside or outside the vessel domain. Subsequently, the nodes located inside the vessel domain are discarded, and the intersection points between the zero level set and the existing cell walls are connected by straight lines that form the vessel boundary. Figure 3b illustrates an example of a vessel generated within the hexagonal honeycomb domain. The green ellipse represents the ideal boundary of the vessel with $\phi (\mathbf {x}) = 0$, and the red dots indicate the nodes inside the vessel domain $\phi (\mathbf {x}) < 0$, which are eliminated from the model. The final vessel boundary obtained with this procedure virtually coincides with the green ellipse in Fig. 3b.

Fig. 3

Hardwood meso-scale configuration. a Meso-scale unit cell, including fibers and a vessel (in the fiber region) and rays (in the ray region); b example of a vessel generated within the fiber region of the hardwood meso-structure; c regular ray configuration (ray eccentricity $e = 0$, with e given by Eq. (3)); d staggered ray configuration (ray eccentricity $0< e < 1$); e ideally staggered ray configuration (ray eccentricity $e = 1$); f regular interface between the ray and fiber regions; g staggered interface between the fiber and ray regions

As further illustrated in Fig. 3a, the fiber region is connected to ray parenchyma, which are idealized as quadrilateral cells with relatively thin cell walls. In fact, a ray cell can be seen as the limit configuration of a honeycomb cell with a cell wall angle equal to zero, $\theta =0$. The geometrical features of a quadrilateral ray cell are described by the cell wall lengths $\ell _\mathrm{ray}$ and $h_\mathrm{ray}$ in the radial and tangential directions, respectively, and by the cell wall thickness $t_\mathrm{ray}$. For simplicity, it is assumed that in the radial direction the cell wall length $\ell _\mathrm{ray}$ of a ray relates to that of the honeycomb element as $\ell _\mathrm{ray} = 2\ell _x$. The ray cell region is generated by repeating the quadrilateral cell in the radial and tangential material directions. In accordance with ray cell morphologies observed in real hardwood meso-structures, as shown in Fig. 1f, the rays cells are generated by either stacking layers of cells ideally on the top each other, as shown in Fig. 3c, or by stacking layers of cells through applying a specific horizontal shift $\delta _\mathrm{ray}$ (in the positive x-direction) across each layer, leading to a so-called staggered configuration, as shown in Fig. 3d. This horizontal shift is quantified by means of a ray eccentricity parameter e as

$$\begin{aligned} e = \frac{2\delta _\mathrm{ray}}{\ell _\mathrm{ray}} \qquad \text{ with } \qquad 0 \le e \le 1 \, . \end{aligned}$$

(3)

If $\delta _\mathrm{ray} =0$, then $e = 0$, by which the regular ray configuration in Fig. 3c is retrieved. In contrast, if $\delta _\mathrm{ray}$ is equal to the cell wall length of the honeycomb structure in the radial direction, $\delta _\mathrm{ray} = \ell _x$, the eccentricity parameter becomes $e = 1$, and an ideally staggered configuration is obtained, as shown in Fig. 3e. These two configurations have also been studied in [28].

The interface between the fiber region and the ray region is characterized by a specific geometry that may influence the effective material response of hardwood. The vertical cell walls of the fibers can be either aligned with those of the rays, which results in a regular interface, as shown in Fig. 3f, or they can be shifted, leading to a staggered interface, as shown in Fig. 3g.

Based on the features described above, the rectangular, periodic unit cell for hardwood has a size $L \times H$, where $L = 2 n_{x} \ell _x = n_{x} \ell _\mathrm{ray}$ and $H = (n_{y}+1)h + n_y \ell _y + n_{y,ray} h_\mathrm{ray}$, where $n_x$ and $n_y$ are integer values denoting the repetitions of the fiber structure along the radial and tangential material directions, respectively, and $n_{y,ray}$ is the number of ray cells in the tangential material direction. An example of a meso-structural model for hardwood is depicted in Fig. 3a, showing a regular fiber region (with $n_x=36$ and $n_y=12$) containing a single vessel, which is connected to a regular ray region (with $n_{y,ray}=6$) via a regular interface. Note that this meso-structure shows similarities with the meso-structure typically observed for the hardwood balsa, as illustrated in Fig. 1f.

2.3 Hygro-elastic properties of cell walls

Wood cell walls consist of individual cell wall layers, which are composed of cellulose micro-fibrils embedded within a lignin and hemicellulose matrix. The cell wall layers are considered to be orthotropic and homogeneous, in correspondence with other modeling studies on wood [23, 28]. Since the size of the cell walls in the out-of-plane, longitudinal direction is much larger than in the in-plane length and thickness directions, for the determination of the in-plane hygro-elastic response of the wood meso-structure it is reasonable to assume plane-strain conditions in the longitudinal direction of the cell wall. Accordingly, the in-plane hygro-elastic constitutive properties in a plane-strain material point of the cell wall are defined by the orthotropic fourth-order compliance tensor $^4\mathbf {S}^{cw}$ and the second-order hygro-expansion tensor $\varvec{\beta }^{cw}$ as

$$\begin{aligned} \begin{array}{lcl} {}^4\mathbf {S}^{cw} &{} = &{}\left( \dfrac{1}{E_{1}}-E_{3}\dfrac{\nu _{13}^{2}}{E_{1}^{2}}\right) \mathbf {e}_1\otimes \mathbf {e}_1\otimes \mathbf {e}_1\otimes \mathbf {e}_1 - \left( \dfrac{\nu _{12}}{E_{1}} + E_{3}\dfrac{\nu _{13}\nu _{23}}{E_{1}E_{2}}\right) \mathbf {e}_1\otimes \mathbf {e}_1\otimes \mathbf {e}_2\otimes \mathbf {e}_2\\ &{} - &{} \left( \dfrac{\nu _{12}}{E_{1}} + E_{3}\dfrac{\nu _{13}\nu _{23}}{E_{1}E_{2}}\right) \mathbf {e}_2\otimes \mathbf {e}_2\otimes \mathbf {e}_1\otimes \mathbf {e}_1+ \left( \dfrac{1}{E_{2}}-E_{3}\dfrac{\nu _{23}^{2}}{E_{2}^{2}}\right) \mathbf {e}_2\otimes \mathbf {e}_2\otimes \mathbf {e}_2\otimes \mathbf {e}_2 \\ &{}+ &{} \dfrac{1}{G_{12}}\mathbf {e}_1\otimes \mathbf {e}_2\otimes \mathbf {e}_1\otimes \mathbf {e}_2 ~, \vspace{2mm}\\ \varvec{\beta }^{cw} &{}= &{} \beta _1 \mathbf {e}_1\otimes \mathbf {e}_1 + \beta _2\mathbf {e}_2\otimes \mathbf {e}_2 ~, \end{array} \end{aligned}$$

(4)

whereby the compliance tensor $^4\mathbf {S}^{cw}$ relates to the stiffness tensor $^4\mathbf {C}^{cw}$ via the common relation $^4\mathbf {S}^{cw} = \left( ^4\mathbf {C}^{cw}\right) ^{-1}$. The elastic moduli, Poisson’s ratios, and hygro-expansion coefficients appearing in equations (4) refer to a local Cartesian coordinate system defined along the principal material directions $j= 1,2,3$ of the cell wall, which are aligned parallel to the cell wall, perpendicular to the cell wall, and in the longitudinal direction of the cell wall, respectively. Note further that Eq. (4) is constructed by using the symmetry condition $\nu _{kl}E_k^{-1}=\nu _{lk}E_l^{-1}$, with $k,l \in \{1,2,3\}$. The local constitutive tensors given by relations (4) are transformed to the global Cartesian coordinate system $\mathbf {x} = (x,y)$, with the x- and y-axes oriented along the radial and the tangential material directions of wood, respectively. This is done by applying the usual operations for a coordinate transformation, which results in the stiffness tensor $^4\mathbf {C}(\mathbf {x})$ and the hygro-expansion tensor $\varvec{\beta }(\mathbf {x})$ that characterize the local response of wood in each material point $\mathbf {x}$ of its meso-structure. The elastic properties of wood correspond to specific, representative values of the moisture content, which here are equal to 12$\%$ and 6$\%$ for the softwood spruce and hardwood balsa, respectively. The analysis of the effect of the variation of the moisture content on the hygro-elastic stiffness properties of wood is a topic for future work, see also [28, 45].

3 Multi-scale modeling approach

Consider a two-dimensional macroscopic domain $\varOmega$ constructed of a periodic repetition of a heterogeneous meso-structural unit-cell Q, as illustrated in Fig. 4. The macroscopic and mesoscopic domains are associated with the characteristic lengths $\mathcal {L}$ and $L=\eta \mathcal {L}$, respectively. In the hypothesis of a strong separation between the two length scales, i.e., $\eta \ll 1$, the mechanical field variables governing the hygro-elastic problem (displacement, strain, stress) can be assumed to vary smoothly at the macro-scale, while being periodic at the meso-scale. Consequently, the mechanical quantities may be considered as explicit functions of two variables, namely a slow macroscopic variable $\mathbf {X}=(X,Y)$ and a fast mesoscopic variable $\mathbf {x}= (x,y)$, which are related as $\mathbf {x} = \mathbf {X}/\eta$. In addition, the moisture content varies smoothly at the macro-scale but is assumed to be uniform at the meso-scale, so that it only depends on the macroscopic variable $\mathbf {X}$. The asymptotic homogenization framework used for computing the effective, macroscopic properties from the hygro-elastic response of the meso-scale cellular wood structure is summarized below and follows the formulation presented in [31,32,33].

Fig. 4

Macroscopic domain and underlying periodic meso-structure

Under the application of a macroscopic mechanical load and/or moisture content variation, the governing equilibrium equation for a local material point—under the absence of body forces—reads

$$\begin{aligned} \varvec{\nabla }\cdot \varvec{\sigma }=\varvec{0}~\ , \end{aligned}$$

(5)

with $\varvec{\nabla }\cdot$ the divergence operator and $\varvec{\sigma }$ the Cauchy stress tensor that satisfies the hygro-elastic constitutive relation

$$\begin{aligned} \varvec{\sigma (X)}={}^4\mathbf {C}(\mathbf {x}): (\varvec{\nabla }\mathbf {u}(\mathbf {X})-\varvec{\beta }(\mathbf {x})~\Delta \chi (\mathbf {X})). \end{aligned}$$

(6)

Here, $\mathbf {u}(\mathbf {X})$ and $\chi (\mathbf {X})$ denote the displacement field and moisture content field, respectively, and $\varvec{\nabla }$ indicates the gradient operator. The response at the macro-scale depends on the material characteristics at the underlying meso-scale and therefore is described by local constitutive tensors that are periodic functions of the fast mesoscopic variable $\mathbf {x}$. As illustrated by Eq. (6), the relevant constitutive tensors are the fourth-order elasticity tensor $^4\mathbf {C}(\mathbf {x})$ and the second-order hygro-expansion tensor $\varvec{\beta }(\mathbf {x})$. In addition, $\varvec{\beta }(\mathbf {x})\Delta \chi (\mathbf {X})$ represents the hygro-expansive strain, as induced by a change in moisture content $\Delta \chi = \chi -\chi _\mathrm{r}$, with $\chi _\mathrm{r}$ a reference moisture content value. Substituting Eq. (6) into Eq. (5) results in a set of differential equations that are functions of the displacement field at the mesoscopic level. However, the solution of these equations over the full macroscopic domain $\Omega$ is computationally expensive; moreover, the computed values of the local meso-structural displacement field and moisture content field are often too detailed to be of practical use. Instead, the method of asymptotic homogenization assumes that the heterogeneous domain with rapidly oscillating material properties $^4\mathbf {C}(\mathbf {x})$ and $\varvec{\beta }(\mathbf {x})$ can be replaced by an equivalent homogeneous domain with effective material properties, which are calculated by an averaging procedure [30, 31, 33]. Accordingly, the displacement field $\mathbf {u}(\mathbf {X})$ is expressed by means of an asymptotic expansion in terms of $\eta$, i.e.,

$$\begin{aligned} \mathbf {u(X)}=\mathbf {u}_{0}(\mathbf {X})+\eta \mathbf {u}_{1}(\mathbf {X},\mathbf {X}/\eta )+\eta ^{2} \mathbf {u}_{2}(\mathbf {X},\mathbf {X}/\eta )+\cdots , \end{aligned}$$

(7)

while the moisture content field, which is uniform at the meso-scale, is defined as

$$\begin{aligned} \chi (\mathbf {X}) = \chi _{0}(\mathbf {X}). \end{aligned}$$

(8)

The averaging procedure departs from substituting Eqs. (7) and (8) into Eq. (6), followed by inserting the result into relation (5). This leads to the definition of two sets of mathematical problems. The first mathematical problem allows to calculate the influence functions $^3\mathbf {N}_{1}(\mathbf {x})$ and $\mathbf {b}_1(\mathbf {x})$ as the periodic solutions of the following two boundary-value problems, termed unit cell problems [31]

$$\begin{aligned}&\varvec{\nabla }_x\cdot ({}^{4}\mathbf {C}(\mathbf {x}):(\varvec{\nabla }_x{}^{3}\mathbf {N}_{1}(\mathbf {x})+{}^{4}\mathbf {I}^{S}))={}^{3}\varvec{0} ~, \end{aligned}$$

(9)

$$\begin{aligned}&\varvec{\nabla }_x\cdot ({}^{4}\mathbf {C}(\mathbf {x}):(\varvec{\nabla }_x \mathbf {b}_{1}(\mathbf {x})-\varvec{\beta }(\mathbf {x})))=\varvec{0} ~, \end{aligned}$$

(10)

where ${}^{4}\mathbf {I}^{S}$ is the fourth-order symmetric identity tensor, defined as $I^S_{ijkl} = (\delta _{il}\delta _{jk} + \delta _{ik}\delta _{jl} )/2$, with $\delta _{ij}$ the Kronecker delta symbol and $\varvec{\nabla }_x$ is the gradient operator referring to the fast meso-scale variable $\mathbf {x}$. The influence functions ${}^{3}\mathbf {N}_{1}$ and $\mathbf {b}_{1}$ represent the periodic, meso-scale fluctuations of the displacement field within the meso-scale structure, due to a variation of the macro-scale strain field $\varvec{\nabla } \mathbf {u}_{0}$ and moisture content field $\chi _0$, respectively.

The unit cell problems are completed by imposing periodic boundary conditions in terms of the (unknown) fields ${}^{3}\mathbf {N}_{1} (\mathbf {x})$ and $\mathbf {b}_{1}(\mathbf {x})$, which require the values assumed by each influence function at corresponding points on opposite boundaries (left and right; top and bottom) to be equal. Finally, for warranting uniqueness of the solution, the average of the influence functions across the meso-structural domain Q is required to vanish, i.e.,

$$\begin{aligned}&\dfrac{1}{|Q|}\int _{Q} {}^{3}\mathbf {N}_{1}(\mathbf {x})\mathrm {d}Q={}^{3}\varvec{0} ~, \end{aligned}$$

(11)

$$\begin{aligned}&\dfrac{1}{|Q|}\int _{Q} \mathbf {b}_{1}(\mathbf {x})\mathrm {d}Q=\varvec{0} ~. \end{aligned}$$

(12)

The second mathematical problem describes the average response of the meso-structural domain via the effective properties representative of an equivalent homogeneous domain at the macro-scale. Correspondingly, the effective elastic stiffness ${}^{4}\bar{\mathbf {C}}$ and hygro-expansion tensor $\bar{\varvec{\beta }}$ are calculated as [31]

$$\begin{aligned}&{}^{4}\bar{\mathbf {C}}=\dfrac{1}{|Q|}\int _{Q}{}^4 \mathbf {C}(\mathbf {x}):(\varvec{\nabla }_x{}^{3} \mathbf {N}_{1}(\mathbf {x})+{}^{4}\mathbf {I}^{S})\mathrm {d}Q ~, \end{aligned}$$

(13)

$$\begin{aligned}&\bar{\varvec{\beta }}=\dfrac{1}{|Q|}{}^{4}\bar{\mathbf {C}}^{-1} :\int _{Q}{}^4\mathbf {C}(\mathbf {x}):(\varvec{\beta }(\mathbf {x})-\varvec{\nabla }_x \mathbf {b}_{1}(\mathbf {x}))\mathrm {d}Q ~. \end{aligned}$$

(14)

To compute the effective hygro-elastic constants ${}^{4}\bar{\mathbf {C}}$ and $\bar{\varvec{\beta }}$, the unit cell problems (9) and (10) are first solved numerically for a given meso-structural geometry, followed by substituting the solutions for $^{3}\mathbf {N}_{1}(\mathbf {x})$ and $\mathbf {b}_{1}(\mathbf {x})$ into Eqs. (13) and (14). The meso-structural geometry is discretized by using a finite element method model consisting of four-node, plane-strain quadrilateral elements. Depending on the size of the meso-structural domain, the number of elements employed in the numerical simulations ranges between 8$\times 10^5$ and 15$\times 10^5$. A mesh convergence study was performed to guarantee that the adopted mesh size is sufficiently small to provide homogenized hygro-elastic properties that are independent of the mesh size. For more details on the derivation of the effective properties, the solution of the cell problems, and the numerical implementation of the asymptotic homogenization method, the reader is referred to [30,31,32,33].

4 Effective hygro-elastic properties of softwood

4.1 Geometrical features and material parameters

The ranges selected for the meso-scale geometrical and material parameters that serve as input for the computation of the effective macro-scale properties of softwood are based on several sources in the literature [13, 20, 23, 46, 47], and are representative of spruce, as shown in Fig. 1e. Three different wood densities are selected, $\rho = [296, 470, 620]$ kg/m$^3$, with the lowest and highest values reflecting earlywood and latewood spruce, respectively, and the intermediate value characteristic of the transition regime from earlywood to latewood spruce. Adopting a cell wall density of $\rho _\mathrm{cw} = 1470$ kg/m$^3$[46], the selected wood densities relate to the set of porosities $\phi = 1-\rho /\rho _\mathrm{cw} = [0.80, 0.68, 0.58]$, respectively. The meso-scale configurations corresponding to these porosities are characterized by the same value of the cell wall lengths, $\ell = 10.0~\mu$m, $h = 13.9~\mu$m, and cell wall angle $\theta = 15^\circ$[23]. From the set of porosities, the corresponding cell wall thicknesses are calculated as $t = [2.0, 3.3, 4.5]~\mu$m, which are indeed representative of cell wall thicknesses observed in the range of earlywood to latewood spruce [47]. As visualized in Fig. 2, the influence of disorder of the meso-structural morphology on the macro-scale hygro-elastic properties is investigated by varying the irregularity factor as $k_\mathrm{ir} = [0, 0.25, 0.5, 0.75, 1]$. The values of the densities and geometrical parameters are summarized in Table 1.

Table 1 Material density and geometrical properties selected for the regular hexagonal honeycomb configuration representing the meso-structure of softwood

The cell walls of spruce are characterized by orthotropic hygro-elastic properties, in accordance with relation (4). The elasticity parameters adopted in Eq. (4) are taken from [13]. In specific, the elastic moduli parallel to the cell wall, perpendicular to the cell wall, and in the longitudinal direction of the cell wall, are $E_1 = 7.02$ GPa, $E_2 = 4.36$ GPa, and $E_3 = 33.20$ GPa, respectively, the in-plane shear modulus is $G_{12} = 1.18$ GPa, and the Poisson’s ratios are $\nu _{12} = 0.649$, $\nu _{13} = 0.112$, and $\nu _{23} = 0.023$. Further, as indicated by the experiments reported in [23], the swelling coefficients of spruce at the mesoscopic level show a large scatter in value and also may vary substantially with the cell wall thickness. For simplicity, in the present study the hygro-expansion coefficients in the direction parallel and perpendicular to the cell wall are assumed to be constant and equal to $\beta _1 = 0.06$ and $\beta _2 = 0.60$, respectively; these values account for the experimental observation that the swelling parallel to the cell wall may be about an order of magnitude lower than in the thickness direction of the cell wall [23]. The hygro-elastic properties are summarized in Table 2.

Table 2 Elastic and hygro-expansive properties of the cell walls characterizing the meso-scale structure of spruce, taken from [13] and [23], respectively

4.2 Determination of the representative unit cell size

In order to obtain statistically representative information from the meso-structural analyses, the appropriate size of the mesoscopic unit cell needs to be determined first. The appropriate size of the unit cell is established from the convergence behavior of the effective elastic and hygro-expansive properties under increasing cell size, whereby the properties are calculated as a statistical average over 20 meso-structural realizations. This statistical volume element method typically leads to a considerably smaller unit cell size compared to when the effective properties are obtained from a single, representative volume element [40, 41]. Analogous to the meso-scale hygro-elastic properties given by Eq. (4), the effective plane-strain hygro-elastic properties at the macro-scale satisfy the relations

$$\begin{aligned} \begin{array}{ll} {}^4\bar{\mathbf {S}} &{} = \left( \dfrac{1}{\bar{E}_{x}}-\bar{E}_{z}\dfrac{\bar{\nu }_{xz}^{2}}{\bar{E}_{x}^{2}}\right) \mathbf {e}_x\otimes \mathbf {e}_x\otimes \mathbf {e}_x\otimes \mathbf {e}_x+ \left( \dfrac{\bar{\nu }_{xy}}{\bar{E}_{x}}-\bar{E}_{z}\dfrac{\bar{\nu }_{xz}\bar{\nu }_{yz}}{\bar{E}_{x}\bar{E}_{y}}\right) \mathbf {e}_x\otimes \mathbf {e}_x\otimes \mathbf {e}_y\otimes \mathbf {e}_y\\ &{} \quad + \left( \dfrac{\bar{\nu }_{xy}}{\bar{E}_{x}}-\bar{E}_{z}\dfrac{\bar{\nu }_{xz}\bar{\nu }_{yz}}{\bar{E}_{x}\bar{E}_{y}}\right) \mathbf {e}_y\otimes \mathbf {e}_y\otimes \mathbf {e}_x\otimes \mathbf {e}_x+ \left( \dfrac{1}{\bar{E}_{y}}-\bar{E}_{z}\dfrac{\bar{\nu }_{yz}^{2}}{\bar{E}_{y}^{2}}\right) \mathbf {e}_y\otimes \mathbf {e}_y\otimes \mathbf {e}_y\otimes \mathbf {e}_y \\ &{}\quad + \dfrac{1}{G_{xy}}\mathbf {e}_x\otimes \mathbf {e}_y\otimes \mathbf {e}_x\otimes \mathbf {e}_y ~, \end{array} \end{aligned}$$

(15)

with the x- and y- and z-directions reflecting the radial (R), tangential (T) and longitudinal (L) material directions of wood. Equation (15) shows that the in-plane stiffness properties $\bar{S}_{xxxx},\bar{S}_{yyyy},\bar{S}_{xxyy}$, and $\bar{S}_{yyxx}$ are dependent on the out-of-plane elastic modulus $\bar{E}_z$ and Poisson’s ratios $\bar{\nu }_{xz}$ and $\bar{\nu }_{yz}$. For spruce softwood, however, the values experimentally measured for $\bar{\nu }_{xz}$ and $\bar{\nu }_{yz}$ are typically very small and lie between 0.014 and 0.035 [6, 20, 48, 49]. Using the Poisson’s ratios for spruce provided in [20], together with the reported values of the stiffness moduli, shows that the magnitude of the second term of the compliance components $\bar{S}_{xxxx}$, $\bar{S}_{xxyy}$, and $\bar{S}_{yyyy}$ is less than 2.5% of that of the first term. For balsa hardwood, the experimental values for $\bar{\nu }_{xz}$ and $\bar{\nu }_{yz}$ are scarce; in [50], these parameters were measured as 0.014 and 0.011, respectively, which, in combination with the reported stiffness moduli, makes that the magnitude of the second term of the compliance components $\bar{S}_{xxxx}$, $\bar{S}_{xxyy}$, and $\bar{S}_{yyyy}$ is less than 2.1% of that of the first term. Consequently, in the forthcoming analyses on softwood and hardwood, the stiffness moduli in the radial and tangential material directions can be approximated with sufficient accuracy as $\bar{E}_\mathrm{R} = \bar{E}_{x} \approx \bar{S}_{xxxx}^{-1}$ and $\bar{E}_\mathrm{T} = \bar{E}_{y} \approx \bar{S}_{yyyy}^{-1}$, respectively, and the in-plane Poisson’s ratio may be subsequently determined as $\bar{\nu }_{xy} \approx \bar{E}_{x} \bar{S}_{xxyy}$.

The apparent stiffness moduli $\bar{E}_\mathrm{R}$ and $\bar{E}_\mathrm{T}$ following from the asymptotic homogenization procedure of spruce softwood are plotted in Fig. 5a and b, respectively, as a function of the dimensionless cell size $n = L/(2\ell _x)$, with the parameter n representing the number of hexagonal elements along the radial material direction, as shown in Fig. 2. Further, Fig. 6a and b illustrate the convergence behavior of the effective hygro-expansion coefficients $\bar{\beta }_\mathrm{R} = \bar{\beta }_{x}$ and $\bar{\beta }_\mathrm{T} = \bar{\beta }_{y}$ in the radial and tangential material directions, respectively. The results are computed for the maximum value of the irregularity factor, $k_\mathrm{ir} =1$, see Eq. (1), which provides the largest, and thus most critical size of the statistical volume element. The confidence bars used for plotting the results represent the scatter in values following from the 20 individual meso-structural simulations. Further, the average values are depicted by the red dotted lines for a density $\rho = 292$ kg/m$^3$, by the blue dashed lines for $\rho = 470$ kg/m$^3$ and by the black solid lines for $\rho = 620$ kg/m$^3$. Figure 5 shows that the elastic modulus $\bar{E}_\mathrm{R}$ in the radial direction is more than two times larger than the elastic modulus $\bar{E}_\mathrm{T}$ in the tangential direction, and that both stiffnesses increase with increasing density. The effective hygro-expansion coefficients illustrated in Fig. 6 also increase with density, with the value in the transverse direction being about 1.5 times larger than in the radial direction. It can be clearly observed that all curves asymptote to a limit value under an increasing (normalized) cell size $L/(2\ell _x)$. Further, the scatter in values decreases with increasing $L/(2\ell _x)$, which may be ascribed to the fact that a larger unit cell contains more statistical information. An effective property is assumed to be converged if the relative difference with the corresponding asymptotic limit is less than 2%. For both the effective elastic moduli and the hygro-expansion coefficients, this requirement is met for a relatively small cell size of $L/(2\ell _x) \ge 20$. Based on this result, in the forthcoming analyses on softwood the length of the statistically representative mesoscopic unit cell depicted in Fig. 2 is set as $L = 40\ell _x$, which leads to a corresponding height of $H=20(h+l_y)$.

Fig. 5

Convergence behavior of the effective, macro-scale stiffness properties under a varying size of the meso-scale unit cell for softwood. a Effective elastic modulus $\bar{E}_{R}$ in the radial direction, and b effective elastic modulus $\bar{E}_{T}$ in the tangential direction, as a function of dimensionless cell size $L/(2\ell _x)$ of a disordered meso-structural geometry with irregularity factor $k_\mathrm{ir} =1$. The effective properties are computed by averaging the responses of 20 meso-structural realizations; the confidence bars represent the range of values calculated from the individual meso-structural realizations

Fig. 6

Convergence behavior of the effective, macro-scale hygro-expansion properties under a varying size of the meso-scale unit cell for softwood. a Effective hygro-expansion coefficient $\bar{\beta }_{R}$ in the radial direction, and b effective hygro-expansion coefficient $\bar{\beta }_{T}$ in the tangential direction, as a function of dimensionless cell size $L/(2\ell _x)$ of a disordered meso-structural geometry with irregularity factor $k_\mathrm{ir} =1$. The effective properties are computed by averaging the responses of 20 meso-structural realizations; the confidence bars represent the range of values calculated from the individual meso-structural realizations

4.3 Influence of morphological irregularities on effective properties

The influence of morphological irregularities on the effective hygro-elastic properties of softwood is next investigated. Figure 7a–d shows the effective elastic modulus $\bar{E}_\mathrm{R}$ in the radial direction, the effective elastic modulus $\bar{E}_\mathrm{T}$ in the tangential direction, the in-plane Poisson’s ratio $\bar{\nu }_\mathrm{RT}$, and the in-plane shear modulus $\bar{G}_\mathrm{RT}$, respectively, all as a function of the irregularity factor $k_\mathrm{ir}$ given by Eq. (1). The modeling results refer to 20 meso-structural realizations. The elastic moduli $\bar{E}_\mathrm{R}$ and $\bar{E}_\mathrm{T}$ computed for spruce wood with a regular honeycomb structure, $k_\mathrm{ir} = 0$, turn out to be in good agreement with the results following from the multi-scale analysis presented in [23], as computed by a different computational homogenization method; in specific, for the common density value of $\rho =470$ kg/m$^3$ the stiffness values show a relative difference of less than 5%. In addition, the scatter in the results is generally larger for a greater meso-structural disorder, as reflected by an increasing value of the irregularity factor $k_\mathrm{ir}$. The elastic moduli $\bar{E}_\mathrm{R}$ and $\bar{E}_\mathrm{T}$ are approximately constant over a large range of values of the irregularity factor $k_\mathrm{ir}$ and only show a slight increase when the irregularity factor reaches unity. In contrast, the Poisson’s ratio $\bar{\nu }_\mathrm{RT}$ substantially decreases when the meso-structural disorder becomes larger. Further, the shear modulus $\bar{G}_\mathrm{RT}$ only decreases significantly with increasing $k_\mathrm{ir}$ for the highest and intermediate density values; for the lowest density value, it remains approximately constant. Note further that the values calculated for the Poisson’s ratio $\bar{\nu }_\mathrm{RT}$ appear to be relatively large, especially for low-density wood. It has been verified, however, that the corresponding effective stiffness tensor unconditionally has positive eigenvalues and thus is positive definite, by which elastic stability is guaranteed.

Fig. 7

Effective macro-scale stiffness properties for softwood (spruce) with different densities as a function of the meso-scale irregularity factor $k_\mathrm{ir}$ given by Eq.  (1). a Effective stiffness modulus $\bar{E}_\mathrm{R}$ in the radial direction; b effective stiffness modulus $\bar{E}_\mathrm{T}$ in the tangential direction; c effective in-plane Poisson’s ratio $\bar{\nu }_\mathrm{RT}$; d effective in-plane shear modulus $\bar{G}_\mathrm{RT}$. The effective properties are computed by averaging the responses of 20 meso-structural realizations; the confidence bars represent the range of values calculated from the individual meso-structural realizations

The influence of morphological irregularities on the effective hygro-expansion coefficients $\bar{\beta }_\mathrm{R}$ and $\bar{\beta }_\mathrm{T}$ is illustrated in Fig. 8a and b, respectively. Again, the values computed for spruce wood with a regular honeycomb structure, $k_\mathrm{ir} = 0$, are in good agreement with the values presented in [23]. Further, the radial hygro-expansion coefficient $\bar{\beta }_\mathrm{R}$ increases with increasing irregularity factor, as shown in Fig. 8a, while the tangential hygro-expansion coefficient decreases, as shown in Fig. 8b.

The effective stiffness properties corresponding to spruce wood with a meso-structural density $\rho = 470$ kg/m$^3$ are finally compared with experimental data obtained from the literature. In the numerical model, the intermediate density value of $\rho = 470$ kg/m$^3$ is representative of a spruce meso-structure in the transition regime between earlywood and latewood and thus may be assumed to reflect the average macro-scale behavior of spruce that includes contributions of both earlywood and latewood. The experimental data presented in Table 3 have been taken from various references [6, 51,52,53,54] and relate to spruce with a similar density as used in the numerical simulations. Table 3 shows for each macro-scale stiffness parameter the average values computed from meso-structures ranging from ideally regular ($k_\mathrm{ir}=0$) to maximally irregular ($k_\mathrm{ir}=1$). Despite the large variations in the experimental data, the ranges predicted for the radial elastic modulus $\bar{E}_\mathrm{R}$, the Poisson’s ratio $\bar{\nu }_\mathrm{TR}$, and the shear modulus $\bar{G}_\mathrm{RT}$ are in reasonable agreement with the corresponding experimental values. Conversely, the predictions for the transverse elastic modulus $\bar{E}_\mathrm{T}$ and the Poisson’s ratio $\bar{\nu }_\mathrm{RT}$ seem to, respectively, underestimate and overestimate the experimental values. On overall, the experimental data reported in [54] show to give the best match with the modeling results.

Comparable differences with experimental results have been reported in other multi-scale modeling studies of wood [23, 28] and are likely to be governed by differences in the values of the cell wall stiffness moduli adopted in the model and those of the experimental specimens. An additional reason for this discrepancy may be that the model is a simplification of the real meso-scale structure of softwood, whereby local meso-scale features, such as the presence of rays, structural differences in earlywood and latewood, and bordered pits, are ignored. It should be further mentioned that the spread in the experimental stiffness values listed in Table 3 is typical of wood and may originate from various aspects referring to the heterogeneous, biological character of the material, such as variations in cell size, the fact that cell walls are not ideally orthotropic, variations in moisture content, the possible use of a number of test samples that is too low for reaching statistical significance, and the possible application of tangential specimens for which the growth rings are not arranged ideally parallel to the load direction over the complete specimen length [6, 28].

Table 3 Elastic properties of spruce with a density $\rho \approx 470$ kg/m$^3$, as obtained by the numerical model and experiments

Fig. 8

Effective macro-scale hygro-expansion properties for softwood (spruce) with different densities as a function of the meso-scale irregularity factor $k_\mathrm{ir}$ given by Eq. (1). (a) Effective hygro-expansion coefficient $\bar{\beta }_\mathrm{R}$ in the radial direction; (b) effective hygro-expansion coefficient $\bar{\beta }_\mathrm{T}$ in the tangential direction. The effective properties are computed by averaging the responses of 20 meso-structural realizations; the confidence bars represent the range of values calculated from the individual meso-structural realizations

5 Effective hygro-elastic properties of hardwood

5.1 Geometrical features and material parameters

The volume fractions of the fiber, vessel and ray regions, and the material parameters adopted for the modeling of hardwood refer to balsa and are based on the data reported in [3, 28]. Several meso-structural configurations are considered, which are representative of densities ranging from low-density to high-density balsa, with the specific values selected as $\rho = [79, 135, 161, 205, 288, 369 ]$ kg/m$^3$. Using a cell wall density $\rho _\mathrm{cw} = 1469\,$kg/m$^3$ [3], the corresponding porosities are $\phi = 1 - \rho /\rho _\mathrm{cw} = [0.95, 0.91, 0.89, 0.86,0.80, 0.75]$, respectively. The total volume fractions of the fiber region and ray region are equal to 0.80 and 0.20, respectively, see also [28]. In the fiber region, the fiber cross sections in balsa are approximated by an ideally hexagonal shape, as shown in Fig. 3, in correspondence with a regular honeycomb structure with $k_\mathrm{ir}=0$. It is noted that this assumption was also taken in [28]. The cell wall angle is set to $\theta = 30^\circ$, and the cell wall thickness is taken $t = 0.9~\mu$m. The vertical and inclined cell walls are assumed to have the same length, with their specific value being varied such that the wood densities selected above are matched, i.e., $\ell =h = [20,10,8,6,4,3]~\mu$m. As indicated in Fig. 3, the meso-scale unit cell is further characterized by the presence of an elliptical vessel. The measurements presented in [3] indicated that a realistic range of the vessel volume fraction in balsa is $v_\mathrm{ves}=[0.028, 0.088]$; hence, the upper and lower values of this range are considered in the variation study on the vessel volume fraction (Sect. 5.3). For the variation studies regarding the ray eccentricity (Sect. 4.1) and the fiber–ray interface (Sect. 5.2), a constant, intermediate value of the vessel volume fraction is chosen, $v_\mathrm{ves}=0.066$, whereby the vessel aspect ratio equals $D/d \approx 1.28$, see also [28]. Correspondingly, for the six wood densities selected above, the major and minor axes of the vessel become $D = [178.2, 89.1, 71.3, 53.5, 35.6, 26.7 ]~\mu$m and $d = [139.4, 69.7, 55.8, 41.8, 27.9, 20.9 ]~\mu$m, respectively. With the above vessel volume fraction, the volume fraction of the honeycomb cell structure in the fiber region then becomes 0.80–0.066 = 0.734. The ray region is characterized by rectangular rays. As mentioned in Sect. 2.2, it is assumed that the cell wall length of the rays in the radial direction corresponds to length of the honeycomb elements as, $\ell _\mathrm{ray} = 2\ell _x$, whereby $\ell$ is varied as indicated above. Correspondingly, the cell wall lengths of the rays are $\ell _\mathrm{ray}= [34.6, 17.3, 13.9, 10.4, 6.9, 5.2 ]~\mu$m. The height and thickness of the rays are scaled such that the selected wood densities and the ray volume fraction of 0.2 are matched, leading to $h_\mathrm{ray}= [17.3, 8.7, 6.9, 5.2, 3.5, 2.6]~\mu$m and $t_\mathrm{ray}= [0.87, 0.43, 0.35, 0.26, 0.17, 0.13]~\mu$m, respectively. The geometrical properties of the honeycomb cell walls, the vessel, and the rays are summarized in Table 4. The length and height of the hardwood unit cell depicted in Fig. 3, respectively, are defined as $L = 2 n_{x} \ell _x = n_{x} \ell _\mathrm{ray}$ with $n_x=74$, and $H = (n_{y}+1) h + n_y \ell _y + n_{y,\mathrm{ray}} h_\mathrm{ray}$ with $n_y=12$ and $n_{y,\mathrm{ray}}=5$. Note that the periodic unit cell for the hardwood balsa has a somewhat larger size than that applied for the analyses on the softwood spruce, due to the presence of various meso-structural objects, i.e., fibers, vessels, and rays.

Table 4 Geometrical properties of the honeycomb cell walls, the vessel, and the rays constructing the meso-scale structure of hardwood balsa

The cell wall properties of balsa have been taken from [28]. Accordingly, the elastic moduli in the directions parallel to the cell wall, perpendicular to the cell wall, and in the longitudinal direction of the cell wall are equal to $E_1 = 15.8$ GPa, $E_2 = 7.1$ GPa, and $E_3 = 45.4$ GPa, respectively. The in-plane shear modulus is $G_{12} = 2.6$ GPa, and the Poisson’s ratios are $\nu _{12} = 0.29$, $\nu _{13} = 0.07$ and $\nu _{23} = 0.04$. Experimental values of the hygro-expansion coefficients of hardwood cell walls are not available in the literature; hence, as a working assumption, these parameters are set equal to those of the softwood spruce, as given in Table 2. The hygro-elastic material properties at the cell wall level of balsa are summarized in Table 5.

Table 5 Elastic and hygro-expansive properties of the cell walls characterizing the meso-scale structure of balsa

In the following subsections, the influence of various meso-structural features on the predicted effective hygro-elastic properties of hardwood is investigated, whereby these effective macroscopic properties have been computed according to relation (15). The response of meso-structures that possess rays with different degrees of eccentricity is analyzed in Sect. 5.2. In Sect. 5.3, the effect of the interface between the ray and the fiber regions on the effective hardwood properties is studied, finally followed by considering the effect of the vessel volume fraction in Sect. 5.4.

5.2 Influence of ray cell eccentricity on effective properties

Figures 9 and 10, respectively, illustrate the effective elastic and hygro-expansive properties of balsa as a function of the density $\rho$, for ray cell arrangements characterized by different degrees of eccentricity, $e = [0,0.25, 0.5, 0.75, 1]$, with the eccentricity parameter e given by Eq. (3). The effective elastic properties calculated with the asymptotic homogenization method are depicted together with experimental data taken from the literature [50, 55, 56]. In the simulations, the interface between the ray and fiber regions is assumed to be regular, as depicted in Fig. 3f. Further, the hexagonal honeycomb structure modeling the fibers is assumed to be regular, with $k_\mathrm{ir} = 0$, as shown in Fig. 3a. Figure 9 illustrates that the elastic moduli $\bar{E}_\mathrm{R}$ and $\bar{E}_\mathrm{T}$ and the in-plane shear modulus $\bar{G}_\mathrm{RT}$ increase with increasing density. Conversely, the in-plane Poisson’s ratio $\bar{\nu }_\mathrm{RT}$ drops when the density increases. Figure 9a clearly indicates that the eccentricity of the ray cells has a negligible influence on the predicted effective elastic modulus $\bar{E}_\mathrm{R}$ along the radial direction. This is caused by the fact that the load transfer by the ray cells along the radial direction is not affected by their eccentricity, as shown in Fig. 3. The experimental values for the radial stiffness $\bar{E}_\mathrm{R}$ of balsa are characterized by some scatter, but nevertheless fall relatively close to the model prediction, and, on average, show a comparable increase with growing density. The spread in the experimental stiffness values can be ascribed to the heterogeneous, biological character of wood, as explained in more detail in Sect. 4.3.

Figure 9b illustrates that the effective stiffness $\bar{E}_\mathrm{T}$ in the transverse direction is highly sensitive to the ray cell arrangement. In specific, the transverse modulus $\bar{E}_\mathrm{T}$ experiences a considerable drop under increasing ray eccentricity, which mainly takes place in the range $0<e\le 0.5$; for $e >0.5$ the transverse stiffness modulus turns out to be almost insensitive to ray eccentricity, and approaches the limit curve corresponding to an ideally staggered configuration with $e=1$. The experimental data for $\bar{E}_\mathrm{T}$ fall in between the numerical results obtained for a regular ray configuration, $e = 0$, and an ideally staggered ray configuration, $e = 1$. In particular, for a relatively low hardwood density $\rho < 150$ kg/m$^3$ the experimental data are close to the modeling result for a meso-scale hardwood structure with $e = 0.5$, while for a higher hardwood density $\rho \ge 150$ kg/m$^3$ they closely match the modeling results for $e = 0.25$. Figure 9c illustrates that the in-plane Poisson’s ratio $\bar{\nu }_\mathrm{RT}$ decreases with increasing density and increases only slightly with increasing ray eccentricity, with the experimental value being overestimated by 18%. Finally, the in-plane shear modulus $\bar{G}_\mathrm{RT}$ depicted in Fig. 9d shows to be strongly dependent on the ray eccentricity, especially at a higher wood density, where the stiffness value related to an ideally staggered configuration is almost two times the value found for a regular configuration.

It can be further confirmed that the curves in Fig. 9 for the configurations with regular ray cells ($e=0$) and ideally staggered ray cells ($e=1$) are similar to the numerical modeling results presented in Figures 5, 6 and 7 of [28], as computed with a different numerical homogenization approach.

Fig. 9

Effective macro-scale stiffness properties for hardwood (balsa) with different ray eccentricities e, as a function of the density $\rho$. a Effective stiffness modulus $\bar{E}_{R}$ in the radial direction; b effective stiffness modulus $\bar{E}_{T}$ in the tangential direction; c effective in-plane Poisson’s ratio $\bar{\nu }_\mathrm{RT}$; d effective in-plane shear modulus $\bar{G}_\mathrm{RT}$. The experimental data for the effective stiffness moduli have been taken from [50, 55, 56].

Figure 10 illustrates that the effective hygro-expansion coefficients $\bar{\beta }_\mathrm{R}$ and $\bar{\beta }_\mathrm{T}$ increase as a function of the wood density $\rho$. Note further that the effective hygro-expansion coefficient in the radial direction $\bar{\beta }_{R}$ is essentially unaffected by the eccentricity of ray cells, irrespective of the wood density, as shown in Fig. 10a. In contrast, the transverse hygro-expansion coefficient $\bar{\beta }_{T}$ shown in Fig. 10b increases with increasing ray eccentricity. Despite that the hygroscopic coefficients of softwood spruce and hardwood balsa at the cell wall level are assumed to be the same, the macro-scale hygroscopic coefficients $\bar{\beta }_\mathrm{R}$ and $\bar{\beta }_\mathrm{T}$ obtained for a specific density turn out to be different—compare Figs. 10 and 8, which obviously results from the geometrical differences and the different stiffness properties at the cell wall level.

Fig. 10

Effective macro-scale hygro-expansive properties for hardwood (balsa) with different ray eccentricities e, as a function of the density $\rho$. a Effective hygro-expansion coefficient $\bar{\beta }_{R}$ in the radial direction; b effective hygro-expansion coefficient $\bar{\beta }_{T}$ in the tangential direction

5.3 Influence of interface between fiber and ray regions on effective properties

The influence of the type of interface between the fiber region and ray region on the effective hygro-elastic properties of hardwood is sketched in Fig. 9. The effective properties are computed based on three meso-structural configurations, characterized by (i) a regular interface between the fiber and the ray region and regular ray cells, as shown in Fig. 3c and f, (ii) a regular interface between the fiber and the ray region and an ideally staggered ray arrangement, as shown in Fig. 3f and 3e, and (iii) a staggered interface between the fiber and the ray region and a regular ray cell arrangement, as shown in Fig. 3c and g. These three configurations are abbreviated as RI + RR (solid black line), RI + SR (dashed blue line), and SI + RR (dotted red line), respectively. Note that cases (i) and (ii) coincide with the configurations considered in Sect. 5.2 that correspond to a ray cell eccentricity of $e = 0$ and $e = 1$. The numerical simulations indicate that the effective properties along the radial direction are almost not affected by the type of interface configuration. The corresponding plots thus closely relate to the curves depicted in Fig. 9a for the radial elastic modulus $\bar{E}_\mathrm{R}$ and in Fig. 10a for the radial hygro-expansion coefficient $\bar{\beta }_\mathrm{R}$, and therefore are not shown here. In contrast, the effective properties along the transverse direction are much more sensitive to the interface configuration; this is illustrated in Fig. 11a and b, which, respectively, depict the transverse elastic modulus $\bar{E}_\mathrm{T}$ and the transverse hygro-expansion coefficient $\bar{\beta }_\mathrm{T}$ as a function of the density for the three selected interface geometries. When comparing cases (i) and (iii) that are both characterized by a regular ray cell arrangement, it can be observed that the presence of a staggered interface (SI + RR) results in a much lower transverse stiffness modulus compared to a regular interface (RI + RR). In addition, the configuration related to case (ii), whereby the interface is staggered and the rays are regular (SI + RR), clearly results in the lowest transverse elastic modulus. The experimental data, which have been taken from [50, 55], are in good agreement with the response of a meso-structure characterized by a staggered interface and a regular ray structure and show a comparable growth when the density increases. When comparing Fig. 11a and b with Fig. 9a and 10b, respectively, it can be concluded that the presence of a staggered interface has a similar effect on the macro-scale effective properties as a ray cell configuration with a regular interface and a ray eccentricity in the range $0.25\le e \le 0.5$. Finally, the in-plane shear modulus $\bar{G}_\mathrm{RT}$ for case (iii) with a staggered interface and a regular ray structure reveals a trend that virtually coincides with that for case i) with a regular interface and a regular ray structure, as depicted in Fig. 9d for $e=0$, respectively. In addition, the trend for the in-plane Poisson’s ratio $\bar{\nu }_\mathrm{RT}$ of case (iii) is very close to that of case (ii) with a regular interface and an ideally staggered ray configuration, shown in Fig. 9d for $e=1$.

Fig. 11

Effective macro-scale hygro-expansive properties for hardwood (balsa) with different interfaces between the fiber and ray regions, as a function of the density $\rho$. a Effective stiffness modulus $\bar{E}_\mathrm{T}$ in the tangential direction; b effective hygro-expansion coefficient $\bar{\beta }_\mathrm{T}$ in the tangential direction. RI + RR refers to a regular interface between the fiber and the ray region and regular ray cells, as shown in Fig. 3f and c, RI + SR refers to a regular interface between the fiber region and the ray region and an ideally staggered ray arrangement, as shown in Fig. 3f and e, and SI + RR refers to a staggered interface between the fiber and the ray region and a regular ray cell arrangement, as shown in Fig. 3g and c. The experimental data for $\bar{E}_\mathrm{T}$ have been taken from [50, 55]

5.4 Influence of vessel volume fraction on effective properties

The experimental measurements of balsa wood discussed in [3] reveal that the vessel volume fraction typically varies in the range $v_\mathrm{ves} =[0.028, 0.088]$. For this interval, the asymptotic homogenization simulations have shown that an increasing vessel volume fraction only results in a minor decrease of both the elastic and hygro-expansive properties. In specific, the maximum difference appears for the elastic modulus $\bar{E}_\mathrm{T}$ of high density balsa wood with $\rho =369$ kg/m$^3$, whereby the value for the meso-structure with the largest vessel volume fraction of $v_\mathrm{ves}=0.088$ is only $5.6\%$ lower compared to the value for a hardwood meso-structure without a vessel. It is noted that in the multi-scale analyses presented in [28] the presence of a vessel led to a more significant decrease of the effective elastic properties. However, this is due to the fact that in [28] the modeling approach is different: The effective properties of a unit cell consisting of only fibers were calculated first and were subsequently used as input for the analysis of a separate unit cell, consisting of a homogenized, continuous fiber matrix in which a hollow ellipse—representing a vessel—was embedded. Since the homogenized continuum model smears out the local load transfer around a vessel over a larger area, a change in vessel volume increases the influence on the effective properties calculated for the overall meso-scale unit cell. This can be easily understood by considering the limit case of a hypothetical, idealized meso-structure, in which the load transfer occurs via a single, local force trajectory; for this meso-structure, the effective properties will remain unaffected by the presence of a vessel (assuming the vessel does not traverse the force trajectory), unless the local load transfer is distributed over a finite area by means of a homogenization procedure.

6 Conclusions

A multi-scale approach is presented for the prediction of the effective elastic and hygro-expansive properties of the softwood spruce and hardwood balsa. The particular focus hereby aims at examining the sensitivity of the effective macroscopic properties to morphological variations in the underlying, mesoscopic cellular structure. The multi-scale framework adopted for this purpose is based on the asymptotic homogenization method. Detailed two-dimensional meso-structural unit cells are generated for both softwood and hardwood. The softwood cell is constructed by a repetition of irregular hexagonal cells representative of the tracheids. The hardwood meso-structure consists of a fiber region containing hexagonal cellular fibers with a large vessel embedded, which is connected to a ray region that includes ray cells. Rays are modeled as quadrilateral cells, characterized either by a regular or a staggered configuration. In addition, the interfacial connection between the fiber and ray regions can also be regular or staggered.

The numerical analyses illustrate that the homogenization procedure allows to realistically estimate the effective hygro-elastic properties of softwood and hardwood. Moreover, the geometrical irregularity of softwood cells appears to have a limited effect on the elastic moduli and in-plane shear modulus, while it has a substantial effect on the in-plane Poisson’s ratio and hygro-expansion coefficients. The simulations reveal that the type of arrangement of the ray cells (staggered or regular) has a significant influence on the in-plane shear modulus and the hygro-elastic properties along the tangential material direction. The type of interface between the fiber and ray regions also shows to have a considerable impact on these parameters; in specific, the in-plane shear modulus experiences a strong drop in value in the transition from a regular to a staggered interface, while the hygro-expansion coefficient in the transverse direction significantly increases under these circumstances. The effect of the vessel volume fraction on the effective hygro-elastic properties is minor.

The multi-scale simulation results strongly depend on the geometrical and material properties used as input at the cell wall level. More systematic research is needed to improve the correspondence between modeling and experimental results, for example, by simultaneously characterizing the properties at the mesoscopic and macroscopic scales for various types of wood. Through the application of scanning electron microscopy techniques, the unit cell configurations used in this study may be further refined toward more realistic meso-scale representations of softwood and hardwood.