Fish scales: Primitive basis for modern metamaterials

Fishes are primitive animals, appearing early during the Cambrian explosion of life forms about 500 million years ago [1–3]. Although the first fishes likely did not possess scales [3], they appeared soon [1] and eventually made their way forward to reptiles such as snakes and alligators, and mammals [4,5]. Natural scales are lightweight, stiff, and multifunctional [6,7]. Protection, locomotion, thermal regulation, and camouflaging have been attributed to scales [2,8,9]. From a physical standpoint, their lightweight structure, stiffness tunability, and damage tolerance are of great interest for designing bio-inspired advanced materials. Scales endow unusual properties to the underlying substrate by two pathways —via unusual parent (scale) material properties, and the complexity of organization and mutual engagement.

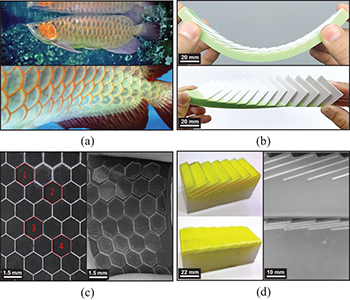
Properties of the parent scale material have been intensely scrutinized over the last decades. Scanning Electron Microscopy and X-Ray diffraction studies of naturally occurring scales show that they are essentially complex composites with intricate microstructures [10–13], to provide high strength and toughness against indentation through enhanced energy dissipation before failure [14] and excellent balance between strength and flexibility [11]. These mechanical properties are strongly dependent on hygroscopic states and loading rates [15,16]. In contrast to scale material behavior, scales' organization and engagement can also produce emergent multifunctionality. Overlapping or discrete arrangements of scales guarantee flexible locomotion and protection, fig. 1(a), by enhancing drag reduction and regulating body undulations [2,25]. On land, scales in snakes help in locomotion by manipulating friction [26]. Scales aid in protection against penetration by dispersing localized forces such as bites across greater areas via scale contact for damage mitigation [27–29]. Different overlap patterns, e.g., stacked, linear overlapped, and staggered overlap, influence these behaviors [24,30].

Zoom In Zoom Out Reset image size

Such enhanced survivability have made scales, and their geometric forms, universally prevalent in the animal kingdom. Yet the scales themselves and their organization are diverse, responding to the predators, environment, and the biology of the organism itself. Even within the organisms, they can vary in material, shape, size, arrangement and color depending on the functionality [11,13,31,32]. Thus, interest in scales architecture arose early in history.

Among these applications was the direct mimicry of the scaled integuments for producing lamellar and scaled armors in the mediaeval and ancient times [12,33]. In spite of this early interest, little was known about the fundamental mechanics behind superior performance, which resulted in similar designs reappearing over years. Only recently has greater scrutiny ensued, buoyed by rapid advances in 3D printing and the need for novel soft structural materials for tailored protection [11–13,34,35], and in wearables and robotics [36,37]. Here, the focus has been on creating novel mechanical behavior from the sliding and interlocking of scales, which leads to unusual combinations of force-displacement nonlinearity, anisotropy, penetration and structural damping [19–22,38–44]. Such unusual behavior originate from scales geometrical arrangements, rather than directly from the parent materials. This distinctly geometric or topological characteristic puts these biomimetic structures in the class of a fast developing frontier of synthetic materials called metamaterials.

Mechanical metamaterials typically consist of periodic assemblies of multiple elements or composites, which exhibit incredible property combinations distinct from their parent materials [45,46]. These include negative Poisson's ratio [47–49], tailorable elasticity [19–21], shape morphing [46,50,51], unprecedented damage and fracture tolerances [34,52], acoustic and photonic band gaps [53,54], tailored anisotropy and abnormal penetration resistance [23,24,28,55]. The origins of these phenomena are tied to the idea of emergence. Emergence is a phenomena where the overall properties of a system at the macroscopic scale are different from the microscopic scale due to the collective interactions of elements constituting the system [56]. Although synthetically conceived, some of the best examples of using geometry and topology to enhance properties are found in the natural world. Devoid of advanced parent materials that humans have mastered, other organisms are forced to improve mechanical properties using topological routes in response to evolutionary pressures over millions of years [13,57]. Thus, it is common to see complex patterns in natural structures such as honeycombs [54,58], fish scales [19–22,38–44], and nacre structure [59,60].

This makes bioinspiration a natural path to develop metamaterials. For instance, bioinspired honeycombs can provide unusual hardening and auxetic behavior controlled by the structure's geometry [54,58]. Hierarchical structure and instability induced by compression can further tune their band gaps [54]. Similarly the structure of nacre has been utilized to provide strain hardening, high toughness and impact resistance [59,60]. Biomimetic scales are in the same vein where emergence occurs due to the intricate mutual scales sliding kinematics. Such substrates exhibit complex strain stiffening, interlocking stages, anisotropy, and strange dissipation behavior, even in the deformation range where the scales and the substrates individually do not exhibit them, as characteristics of emergent behavior.

Scales have been adopted to make primarily two types of biomimetic structures. The first type is an exoskeletal architecture, which includes both the overlapping architecture, where a soft substrate is covered with partially embedded overlapping scales, fig. 1(b) [19–21,43], as well as the non-overlapping or segmented architecture, fig. 1(c) [23]. One fabrication strategy is to glue 3D printed stiff plates [19–21,43], or steel sheets [43], into prefabricated grooves of a Vinylpolysiloxane (VPS) elastomer [19–21,43], or 3D printed flexible material [43]. Other strategies comprise multi-material 3D printing [61], laser engraving of alumina strip for scales and stretch-and-release fabrication method [62], and sewing cellulose acetate butyrate (CAB) scales on a polypropylene mesh using cotton thread [63].

Other strategies include sequential molding and casting [64–67]. Similar strategies and along with laser engraving can be used for fabricating segmented samples architecture [23]. Topologically interlocked materials (TIMs) [68] is also another approach which uses either building blocks of various shapes or craving the interfaces of interlocking elements from the bulk of glass panel using focused laser beam [69–71]. In the second type of architecture, scales are fully embedded inside the matrix to form composite imbricated stiff inclusions into a thick soft substrate, fig. 1(d) [24]. This architecture can be manufactured using a multi-material 3D printer [72], or embedding 3D printed Acrylonitrile butadiene styrene (ABS) plates into a rubber substrate [24]. In spite of these differences in architecture, these metamaterials share many typical behaviors.

Bending and twisting are the most important deformation modes for slender structures. In a plain beam, the moment-curvature and torque-twist characteristics remain linear for small deflections, reflecting the linear elastic behavior of the parent materials. This behavior changes when scales are integrated into the structure. Here samples are partially embedded with scales on one side of substrate to highlight the differential properties, with and without scales engagement, fig. 1(b). As the substrate deforms, scales begin engaging and their mutual sliding gives rise to geometrically dictated nonlinearity.

The nature and origin of the nonlinearity can be best introduced in bending [19,38]. The substrate bent shape can be envisaged as circular arc of a beam, fig. 2(a). Assuming periodic scale engagement, a representative volume element (RVE) can be isolated, fig. 2(a). One can assume rigid scales if they are sufficiently stiff. The RVE geometry, fig. 2(a), reveals two kinematic variables —the local angular deflection of the scales θ, and the substrate angular change ψ (related to curvature κ). These variables can be interrelated by imposing periodicity [19,41]:

$$\begin{equation} \eta \psi \cos \psi/2 - \sin (\theta + \psi/2) = 0. \end{equation} \tag{ 1 }$$

Zoom In Zoom Out Reset image size

Here, $\psi = \kappa d$ and $\eta = l/d$, where d, l are the scales' spacing and exposed length respectively [19,41]. This relationship can be plotted for varied η generating a kinematic mechanisms map, fig. 2(b). This map indicates that the system performance spans three kinematic regimes of operations including linear (before the scale engagement), nonlinear stiffening, and finally a kinematically locked configuration. Note that this locked configuration is independent of friction and of purely kinematic origin. Realistically speaking, near this locked state, the internal forces would rise substantially, leading to a transition from substrate deformation to scale deformation, which is significantly stiffer. The moment-curvature response for this system can be derived by a micro-macro energy balance (Hill-Mandel condition) [73]. Thus, the total applied work on the beam can be written as $W=L_B \int_{0}^\kappa M \textrm{d}\kappa$, where L_B is the substrate length, M is the applied moment, and κ is the substrate curvature. This work is absorbed by the beam and scales leading to $W = \frac{1}{2} E_B I L_B \kappa^2 + \mathcal{E}_{\textit{scales}}$, where E_B and I are the Young's modulus and the second moment of area of the beam, respectively. Also, $\mathcal{E}_{\textit{scales}}$ is the energy from scales rotation on the substrate. Assuming a torsional spring to capture this rotational stiffness, $\mathcal{E}_{\textit{scales}} = \frac{1}{2} N K_B (\theta - \theta_0)^2$, where $N = L_B/d$, $\theta_0$, and $K_B = 1.75 E_B D^2 (L/D)^{0.66}$ are the number of scales, initial scale's inclination, and scales torsional stiffness of the scale-substrate joint, respectively. Here, D and L are the scale's thickness and scale's embedded length [19]. Plugging in $\theta = \theta(\psi)$ from eq. (1), we get the bending moment response from work–energy balance as follows:

$$\begin{equation} M(\kappa) = E_B I \kappa + K_B (\theta - \theta_0) \frac{\partial \theta}{\partial \psi} H (\kappa - \kappa_e). \end{equation} \tag{ 2 }$$

Here $\kappa_e$ and $H (\kappa - \kappa_e)$ are the engagement curvature and Heaviside step function to track engagement, respectively. This relationship shows that after scales engagement, the moment response of the structure displays nonlinear stiffening, as seen in fig. 3(b) for the frictionless case denoted by $\mu = 0$. In the above relationships, key simplifications arise in estimating the rotational stiffness of the scale-substrate joint, substrate material nonlinearity, scale rigidity assumption, scale distribution uniformity, and reference and post-engagement periodicity. This can raise concerns about the universality of results.

Zoom In Zoom Out Reset image size

However, extensive follow-up studies relaxing these restrictive simplifications have confirmed the surprisingly robust nature of the overall nonlinear strain stiffening and locking behavior [20,42,43]. More interestingly, the bending of 2D plate-like substrates also exhibits these behaviors [38–40]. For these studies, similar energy balance procedures were used to obtain the moment-curvature relationships, which revealed that scale-covered structures also exhibit strain stiffening and distinct anisotropic response along the two generators of the surface [38–40].

There is no straightforward way to generalize bending to twisting, due to the out of plane deformations. In fact, early studies on the bending and the torsional response of the 2D scaled system seemed to indicate no significant nonlinear stiffening [39]. However, the role of scale inclination turned out to be of critical importance. These studies assumed straight scales, similar to the bending case, fig. 1(b) (top). The lack of torsional strain-stiffening was due to the scales being parallel to the torsion axis [21], which requires excessive torsion for scales engagement. Thus, torsional strain-stiffening may emerge if scales are suitably oblique, fig. 1(b) (bottom). This was confirmed in recent works focusing on oblique scales under twisting [21,44]. Here, two angles α and θ capture the oblique orientation, fig. 2(c). Quantifying the kinematics of out of plane deformation requires new non-dimensional geometric parameters, including the overlap ratio $\eta = l/d$, dimensionless scale width $\beta = b/d$, and dimensionless substrate thickness $\lambda = h/2d$. Using periodicity assumption on twisting, a complex kinematic expression emerges, as follows:

$$\begin{eqnarray} & \hspace{-7pt} (\cos \varphi - 1 ) {( \beta \sin 2\alpha \sin \theta + \eta {{\cos }^2}\alpha \sin 2\theta + 2\lambda \cos 2\alpha \cos \theta)} \nonumber\\ & \hspace{-7pt}+ 2\sin \alpha \sin \varphi ( {\eta + \lambda \sin \theta } ) - 2\cos \alpha \cos \varphi \sin \theta \nonumber\\ & \hspace{-7pt}+ 2\cos \alpha \sin \varphi \cos \theta ( {\beta - \sin \alpha } ) = 0. \end{eqnarray} \tag{ 3 }$$

This equation can again be used to generate a kinematic mechanisms map, fig. 2(d), where the oblique angle α is fixed at 45°. Once again three distinct regimes emerge —linear, nonlinear, and kinematic locking, fig. 2(d). Using energy balance like bending case, a nonlinear torque-twist relationship can be derived. Although the relationship is now considerably more complicated than the bending case, it can be written in a simplified form, as follows [21]:

$$\begin{equation} T (\Phi) = C_f C_w G_B I \Phi + K_\theta (\theta - \theta_0) \frac{\partial \theta}{\partial \varphi} H (\Phi - \Phi_e).\quad \end{equation} \tag{ 4 }$$

Here, T is the toque, Φ is the twist rate $(\Phi=\varphi/d)$, $\Phi_e$ is the engagement twist, G_B is beam shear modulus, and C_w is the warping coefficient for the non-circular cross section. The factor C_f is required which accounts for the additional appreciable stiffness gain that arise due to embedded parts of the scales. $K_\theta = 3.62 E_B D^2 (L/D)^{1.55}$ is the appropriate torsional stiffness for a scale with unit width [21]. The strain-stiffening in the torque-twist relationship is shown in fig. 3(d) for the frictionless case denoted by $\mu = 0$.

In addition to overlapping exoskeletal architecture, investigations on the fully embedded designs also indicate distinct strain-stiffening behavior in bending [24,72,74]. However, material compression between fully embedded scales is the governing mechanism. Inclusions provide nonlinear stiffening, dependent on the volume fraction of stiff scales right from the beginning of the loading [24,72,74].

For exoskeletal architecture, friction between the sliding scales is of critical significance. The locking curvature is a kinematic idealization. In reality, normal forces start rising sharply as this configuration is approached. For rough surfaces, if Coulomb friction force is assumed between scales, it would also see a sharp rise leading to very high increase in the tangential forces. This can prevent further sliding, advancing locking curvatures. This hypothesis has been confirmed and quantified in detail for both bending and twisting deformations [41,44].

For simplicity, bending is again used to exemplify the analysis. In this case, using the same RVE concept introduced earlier, a force balance can be carried out with friction force $f_{\mathrm{fr}} = \mu N$, where N is the normal force and $\mu > 0$ is the coefficient of friction, fig. 2(a). This leads to frictional force dependence on curvature, shown in fig. 3(a). Here friction force is normalized by $K_B/l$, and subscript e indicates engagement values. Clearly, the frictional force is singular in nature, indicating a point of 'frictional lock', beyond which the scales cannot move. This lock is found to occur earlier than the frictionless kinematic lock. Juxtaposing this on the kinematic mechanism maps, we get a progressively advancing locking envelope with increasing μ, as shown in fig. 2(b) with dotted lines.

This behavior is also universal, with singularity in frictional force in twisting, fig. 3(c), where normalized by $K_\theta/l$. This leads to similarly advancing locking, seen in the dotted lines in fig. 2(d). Although the architecture-dissipation relationships are considerably more complicated than the frictionless case, friction can be included using extended energy balance for bending [41,44]:

$$\begin{equation} M(\kappa) = E_B I \kappa + \left( K_B (\theta - \theta_0) \frac{\partial \theta}{\partial \psi} + f_{\mathrm{fr}} \frac{\mathrm{d}r}{\mathrm{d}\psi} \right) H (\kappa - \kappa_e). \end{equation} \tag{ 5 }$$

Here, $\kappa_e$ is the engagement curvature value, and $\mathrm{d}r$ is the relative differential displacement in the direction of sliding, shown in fig. 2(a) for the bending case. Analogous relationship exists for the torque-twist relationship [44]. For both the bending and the twisting case, increasing the coefficient of friction leads to an increase in nonlinear strain-stiffening in a scaled system, fig. 3(b) and (d). This increase in strain-stiffening is tailorable with respect to the geometric parameters of the system [41,44]. Thus, friction can enhance resistive forces due to additional internal forces but also restricts the range of motion by advancing lock. Therefore, increasing μ may not necessarily increase the total dissipative work in a deformation cycle. This is shown in fig. 4(a), as the relative energy dissipation (RED) for the bending case, which is the ratio of frictional or dissipative work calculated as ${w_\mathrm{fr}=\frac{1}{d}} \int_{\kappa_e}^{\kappa_\mathrm{lock}} \hspace{-3pt} f_\mathrm{fr} \mathrm{d}r$, to the total work calculated as $w_\mathrm{sys}=w_\mathrm{fr}+\frac{1}{2}EI{\kappa_\mathrm{lock}}^2+\frac{1}{2}\frac{K_B}{d}(\theta_\mathrm{lock}-\theta_0)^2$ for different values of μ, and η [41]. Here, the substrate is considered as linear elastic material and the scales are rigid. Also, additional dissipation could come from material sources such as plasticity, viscoelasticity, Mullins effects in rubber, etc. [75]. Here for the bending case as shown in fig. 4(a), dissipation is maximized only at intermediate μ in bending.

Zoom In Zoom Out Reset image size

Interestingly, unlike elasticity, this dual nature of friction is not always universal. For twisting, another behavior has been observed, where RED monotonically increases with μ, without sensitivity to η [44].

In addition, the role of friction is not completely understood in the dynamic regimes. Oscillatory motion is important for locomotion, swimming, and structural vibrations. For the case of bending, assuming a dynamic excitation and neglecting any material viscoelasticity, but including only Coulomb friction, a time dependent load-displacement relationship can be derived by using the extended Hamilton's principle. Typically, Coulomb friction leads to the linear damping behavior of free vibration [76]. However, in biomimetic scale metamaterials, the moving lines of contact during motion give rise to an exponential decay of free vibration, similar to a viscous dashpot [22], fig. 4(b). We call this counterintuitive phenomenon viscous emergence, which arises purely due to metamaterial effect and not from any rate-dependent material or drag assumptions. This dynamic behavior is still not identical to a typical viscous dashpot. Traditional viscous damped oscillations decay till motion eventually stops. In contrast, in the biomimetic system, the decay will not lead to a complete stop, but only to the point where deflection is small enough to disengage the scales [22]. At this point, the system returns to a frictionless conservative system. Thus, in spite of only dry friction, the structure is capable of showing both viscous emergence as well as conservative response. The extent of these behaviors are determined by both the geometry and interfacial properties of the system.

Geometrical effects made possible by segmentation, overlap, and scales interaction can enhance mechanical properties beyond what is possible for monolithic materials at small or large strains. Here, failure mechanisms and elastic response are of interest. The penetration resistance of natural scales systems confirm the contributions of both the microstructure of the scales themselves as well as their organization [14,28]. Metamaterials inspired by these designs are investigated by applying indentation loading to scales attached to a soft elastic substrate [27–29,61,62,72] or by performing ballistic impact simulations or experiments [77–79]. In general, the puncture resistance of segmented systems, fig. 1(c), is significantly greater than a continuous glass plate attached to a soft substrate [23].

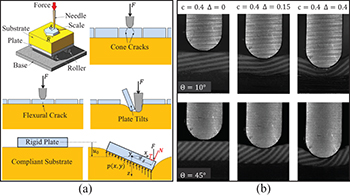
Additionally, these segmented scaled systems are capable of sustaining damage in different sections and maintaining functionality, unlike a monolithic glass plate that could completely shatter [29]. Several failure modes have been identified, including substrate material shearing [24], scale bending [24], scale puncture [28,32], and scale fracture [23]. However, in segmented systems, the most notable is the tilting failure mode [23,29,30], fig. 5(a). This failure mode occurs when scales rotate excessively during contact, allowing the indenter to slip through the gaps and penetrate the underlying substrate material. This mode is consistent regardless of the strength of the scale materials, and depends on the scale stability [23,29,30,57] as the scales resist rotation. It has been found that the tilting mechanism is more prevalent with decreasing scale size [23,29] and substrate stiffness [29], fig. 5(a).

Zoom In Zoom Out Reset image size

The engagement of scales dramatically increases the scale stability, with the contacting surfaces providing support [30,57] as well as friction between scale and indenter [62]. However, the friction between scales does not seem to provide additional benefits to the system [28]. This highlights the synergistic importance of material and geometry in determining the behavior of these systems including scale overlap, scale angle and volume fraction [55,62,63]. Some overlapping architectures can disperse the loads over much larger areas [28,63], even after a partial puncture, reducing damage to the underlying substrate [28]. The anisotropy of the contact area depends on the indenter radius, relative to the scale length [55]. The energy dissipation of a partially embedded system has shown a significant increase via the addition of surface grit and elastic cover, which delays the scales disengagement, maintains contact with the indenter tip and pulls on the surrounding scales through the indentation [66]. In a partially embedded systems, the effective contact area increases beyond the radius of the indenter [55], and increasing the load continues to increase the redistribution of strain through a greater portion of the sample until scale failure [38,55].

It has also been found that contact stiffness increases with scale density and decreasing interface rotational stiffness [38,55]. For fully embedded scales, fig. 1(b), flexible scales deform around a blunt indenter, increasing the stiffness and acting locally as a composite material [24]. The scale overlap and initial scale angle of a fully embedded system have been varied to determine the governing variables in the failure modes of the system [24]. The flexibility and protective properties of embedded systems have also been found to be tunable by altering the geometric properties and distribution of the scales [24,55,72]. For instance, low initial scale angle and high volume fraction display greatly reduced flexibility [72], fig. 5(b).

In spite of intense scrutiny for their mechanical behavior, even now relatively little is known about the mechanics and dynamics of more general 2D systems such as plate- and shell-type metamaterials, heterogeneous scales distribution or the synergetic behavior under combined loads. Such complexities can give rise to new and potentially unanticipated emergent behaviors. For these developments, several existing challenges need addressing. These metamaterials often test the limits of commercial FE software due to the large number of contact pairs and significant contact nonlinearity. Thus, major advances in computer models and multiscale modeling are necessary. The scale separation in this case is between scales length and structure length scale (e.g., m to cm). The time scales of structure and scales although assumed similar so far can also differ in the case of high frequency or sharp local transients. Thus, the models can be applied in the mesoscale length scale for few neighboring RVEs and in macroscale for the whole structure. In addition to current paradigms, potentially novel behaviors can be accessed by using phase change materials in biomimetic scales, which can provide unprecedented on-demand functional programmability. Currently, very little is known of the time dependent behavior of such dynamically changing scales systems. For these structures, fabrication techniques need to advance considerably. Lastly, natural scales are inherently multifunctional. Multiphysics interactions such as coupling between fluids, heat and the nonlinear structural response are still unexplored. Preliminary work on exploiting optical properties [51] shows dramatic color changes through angular manipulations of scales. Studies on thermal or electromagnetic behavior have not been undertaken yet, representing a key future frontier.

This work was supported by the United States National Science Foundation's Civil, Mechanical, and Manufacturing Innovation, CAREER Award No. 1943886.