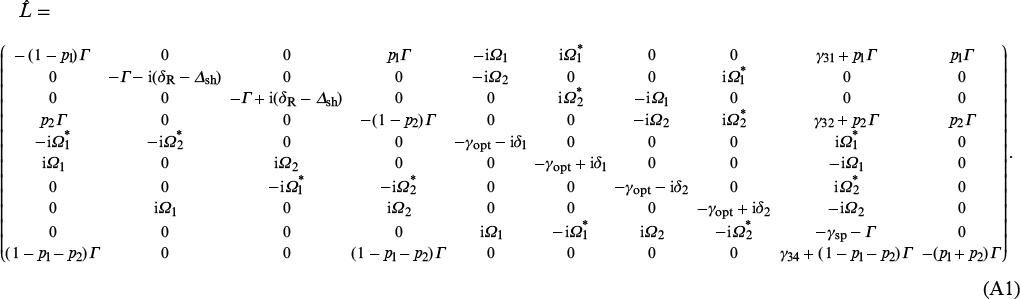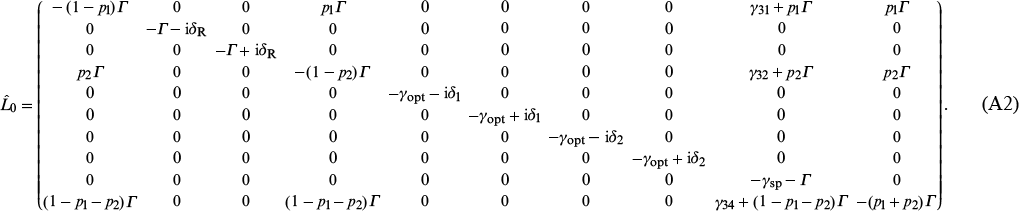Generalised Ramsey methods for suppressing light shifts in atomic clocks based on the coherent population trapping effect

Atomic clocks are important and demanded quantum devices that provide high-precision measurements of frequency and time [1 – 3]. They have a wide range of applications in such areas as navigation (GPS, GLONASS, GALILEO), communication and information transmission systems, geodesy, verification of fundamental physical theories, etc. [4 – 7]. A separate class of atomic clocks is the clocks based on coherent population trapping (CPT) [8 – 12], the essence of which is as follows. When interacting with a coherent bichromatic field, atoms pass into the so-called dark (nonabsorbing light) state. The latter is formed when the difference in the optical frequencies of the field varies near the hyperfine splitting of the ground state, which leads to the appearance of a narrow dip (peak) in the absorption (transmission) signal. The use of optical cells with a buffer gas or an antirelaxation coating can significantly reduce the width of the CPT resonance, which is usually 0.1 – 1 kHz. The main advantages of CPT clocks are compactness and low power consumption due to the use of an all-optical scheme for exciting a radio-frequency transition without using a microwave cavity [13 – 15].

The main goal of research devoted to atomic clocks is to increase the frequency stability, which characterises random changes in the reference frequency over time. In many cases, the key factor limiting the stability and accuracy of atomic clocks is the light shift of the clock transition frequency due to the dynamic Stark effect; in this case, fluctuations in the radiation power lead to instability of the oscillator frequency. This problem, in particular, can be solved using Ramsey spectroscopy [16], including its various modifications and generalisations. For example, to suppress light shifts in one of the modified Ramsey schemes described in [17], it was proposed to use pulses of different duration, with the second pulse being composite (i.e. its part has a phase shifted by π). This 'hyper-Ramsey' scheme was successfully implemented in optical clocks and demonstrated suppression of the light shift by several orders of magnitude [18, 19]. Further versions of the hyper-Ramsey approach development relied on other methods for generating the error signal [20 – 24].

Relatively recently, new methods for suppressing light shifts have been developed, such as autobalanced Ramsey spectroscopy (ABRS) [25] and its generalisation (GABRS) [26], as well as combined error signal in Ramsey spectroscopy (CESRS) [27]. These spectroscopic schemes 'do not suffer' from relaxation effects in an atomic medium, time-dependent pulse fluctuations, and other imperfections in the procedure for interrogating atoms. They are based on the excitation of atoms by two Ramsey sequences with different times of free evolution (dark times). The GABRS method uses two feedback loops, one of which is used to adjust the frequency of the clock signal, and the other is employed to control some concomitant, well-controlled parameter associated with Ramsey pulses. Simultaneous stabilisation of the atomic clock frequency and the concomitant parameter provides suppression of the light shift. Sanner et al. [25] proposed and implemented a frequency stabilisation scheme, in which an additional phase shift of the field during the action of the second Ramsey pulse is used as an concomitant parameter. Yudin et al. [26] showed theoretically that there are other scenarios when choosing the concomitant parameter. In contrast to GABRS, CESRS [27] uses only one feedback loop and the error signal for frequency stabilisation is formed by subtracting (with the corresponding calibration coefficient) two error signals for each Ramsey sequence. The use of ABRS made it possible to achieve stability at a level of 10⁻¹⁵ in CPT clocks with a caesium vapour cell [28, 29]. GABRS and CESRS were experimentally implemented in [30, 31] for laser-cooled rubidium atoms, in which the light shift was suppressed by more than an order of magnitude.

It should be noted that the theoretical analysis for optical clocks was carried out within the framework of a two-level atomic system [26, 27], and for CPT clocks, within the framework of a closed three-level Λ-system [32]. However, in the conventional scheme of pumping an atomic medium with a unidirectional circularly polarised light σ⁺- or σ⁻-field, in the case of the D₁ line of alkali metal atoms, there is a so-called trap state ('pocket'), that is, a sublevel of the ground state with a maximum or minimum projection of the total angular momentum of an atom. The presence of this state leads to a deterioration in the CPT resonance parameters (a decrease in the amplitude and contrast), since the atoms that accumulate in the 'pocket' as a result of optical excitation and relaxation of the excited state are no longer excited from there and do not participate in the formation of the dark state. Therefore, it was important to generalise the study performed in [32] to the case of an open Λ-system with allowance for a trap state.

In the present work, we have obtained analytical results that rigorously prove the applicability of GABRS and CESRS in CPT clocks within the framework of an open Λ-system with a trap state and are accompanied by various numerical calculations. For GABRS, in particular, a variant is considered when the concomitant parameter is an additional frequency jump during the action of both Ramsey pulses (pumping and detecting).

As a theoretical model of an atomic medium, we consider an open Λ-system (Fig. 1) taking into account the presence of a trap state (state |4〉) interacting with Ramsey pulses of a bichromatic field (Fig. 2)

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The CPT resonance is excited under the condition that the frequency difference ω₁ – ω₂ varies near the hyperfine splitting frequency ω_hfs of the transition between the sublevels |1〉 and |2〉 (clock transition) of the main state. We will describe the temporal dynamics of the atomic system using the formalism of the atomic density matrix in the basis of states {| j 〉} (see Fig. 1):

In the rotating wave approximation, the equations for the density matrix have the form:

Here Ω₁ = d₃₁ E₁e^−iφ₁ /ℏ and Ω₂ = d₃₂ E₂e^−iφ₂ /ℏ are the Rabi frequencies for the transitions |1〉 → |3〉 and |2〉→ |3〉, respectively (d₃₁ and d₃₂ are the matrix elements of the electric dipole moment operator); δ₁ = ω₁ – ω₃₁ and δ₂ = ω₂ – ω₃₂ are one-photon detunings of laser fields; δ_R = ω₁ – ω₂ – ω_hfs is the two-photon (Raman) detuning; Δ_sh is the light (Stark) shift of the clock transition frequency during the action of Ramsey pulses; γ_opt is the decay rate of optical coherences (due to spontaneous decay processes, collisions with a buffer gas, etc.); γ₃₁, γ₃₂ and γ₃₄ are the rates of spontaneous decay of the population from state |3〉 to states |1〉, |2〉 and |4〉, respectively; γ_sp is the rate of spontaneous decay of the excited state |3〉 (in the case of a closed atomic system, γ_sp = γ₃₁ + γ₃₂ + γ₃₄); the constant Γ determines the rate of relaxation of atoms (for example, due to transit effects) to an isotropic distribution over the sublevels of the ground state (in the absence of a light field); and p₁ and p₂ are the relaxation coefficients to this isotropic distribution.

We represent the system of linear equations (3) in the vector form

where the column vector ρ (t) is formed from the elements of the density matrix as follows:

and the matrix (Liouvillian) [see expression (A1) in the Appendix] is determined by the coefficients of equations (3).

As a spectroscopic signal, we investigate the absorption during the detecting pulse (for t > t₂, see Fig. 2), which in the approximation of an optically thin medium is proportional to

The signal accumulated during the detecting time τ_d is calculated by integrating expression (6) over time:

Using the standard definition of a scalar product

expression (6) can be expressed as

where the vector Ω is defined as

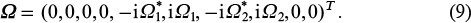
The vector ρ_in corresponds to the initial atomic state. The operators and determine the evolution of atoms interacting with the pump pulse (t₀ < t < t₁) and the detecting pulse (t > t₂), respectively. The operator [see (A3)] describes the free evolution of atoms (t₁ < t < t₂ = t₁ + T):

where the Liouvillian 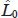(A2) is formed from Eqns (3) – (5) in the absence of a light field (i.e., when Ω₁ = Ω₂ = 0 and Δ_sh = 0).

In experiments, the dark time T, as a rule, significantly (by 2 – 4 orders of magnitude) exceeds the decay times of the population of the excited state and decay of optical coherences, which corresponds to the condition . Therefore, in the diagonal elements of the matrix 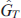, we can assume that e^{−γ_sp T} ≈ 0 and e^{−γ_opt T} ≈ 0. In this case, the operator 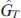has the form

Let us consider a stabilisation scheme in which jumps (i.e., a step-like change) in the relative phase of the bichromatic field (φ₁ – φ₂) are used to generate the error signal S_err(δ_R) before the second Ramsey pulse. Using formulae (7) and (8), we write the expression for the spectroscopic signal taking into account the phase jump:

where the phase jump operator for the bichromatic field has the form

The error signal is formed as the difference between signals (12) for two different phase jumps:

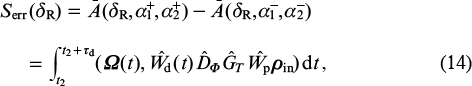
where the superscript '+' denotes the phase change for the first jump, and the subscript '–' corresponds to the second phase jump. The 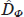operator in (14) is defined as

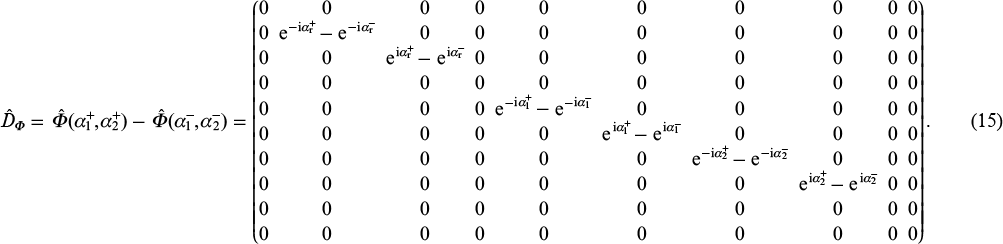
Here we have introduced the notation for the relative phase of the bichromatic field:

In accordance with (11) and (15), we obtain the following expression for the matrix product :

where the matrix has the form

Then, taking (17) into account, the error signal (14) is calculated by the formula

Thus, as follows from (18), the error signal is sensitive only to a change in the relative phase α_r = α₁ – α₂, but does not depend on the phases α_1,2 separately. We also note that the maximum amplitude of the error signal (19) is achieved for phase jumps and.

In an atomic clock, the frequency is stabilised at zero of the error signal for the central Ramsey resonance. Therefore, one of the key parameters affecting the metrological characteristics is the frequency , which corresponds to the solution of the equation

relative to δ_R.

The stabilisation scheme for GABRS contains two feedback loops acting in parallel on alternating Ramsey sequences with different free evolution times T₁ and T₂. The first loop controls the oscillator frequency (i.e., the Raman detuning δ_R), and the second loop controls some concomitant parameter ξ associated with the first and/or second Ramsey pulse. The GABRS algorithm is organised as a series of the following cycles. For a Ramsey sequence with a free evolution time T₁, the concomitant parameter is fixed (ξ = ξ_fix), and the frequency is stabilised at zero of the first error signal . Then measurements are carried out for a sequence of Ramsey pulses with a different dark time (T₂), when the previously obtained frequency is fixed (δ_R = δ_fix) and the concomitant parameter stabilises at zero of the second error signal . When these iterations are repeated, both parameters ( and ) eventually stabilise, which corresponds to solving the system of equations

for the variables δ_R and ξ.

Let us show that system (21) always has a solution δ_R = 0. Substituting expression (19) for the error signal into (21), we obtain

It follows from (18) that, in at δ_R = 0, we have an equality for the matrices and :

In this case, the system of two equations (22) is reduced to one equation with an unknown parameter ξ:

which always has a solution.

Thus, it has been analytically shown that the choice of the appropriate value of the concomitant parameter makes it possible to completely suppress the light shift of the clock frequency () stabilised by the CPT resonance. This result does not depend on the parameters of Ramsey pulses (amplitude, shape, phase), relaxation constants, errors in the formation of phase jumps, etc. The resistance of the method to various technical errors demonstrates its high reliability.

As a particular case of GABRS for CPT resonances, we consider an autobalanced scheme, in which the concomitant stabilised parameter is an additional 'jump' in the frequency difference ω₁ – ω₂ during the action of both Ramsey pulses, i.e., ξ = Δ_c. The frequency jump () that completely suppresses the light shift () can be found from equation (24).

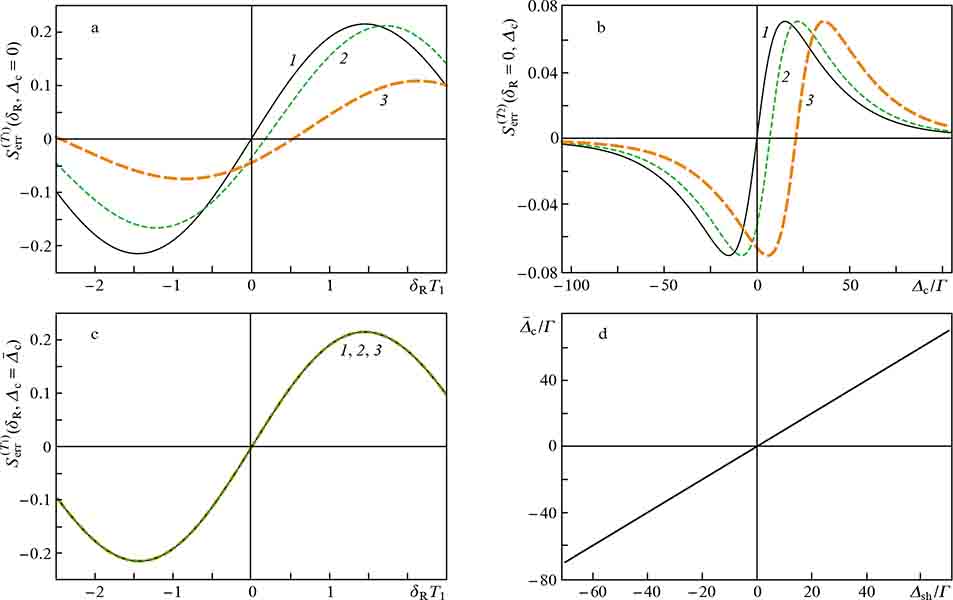
Figure 3a shows the behaviour of the error signal for the conventional Ramsey scheme for different values of the light shift Δ_sh. Graphs of error signals for stabilisation of the concomitant parameter Δ_c are presented in Fig. 3b. Figure 3c demonstrates the error signals for frequency stabilisation when 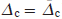. It can be seen that the light shift in this case is completely suppressed, and the error signals completely coincide and have an antisymmetric shape. Finally, from Fig. 3d it follows that the frequency jump linearly depends on the light shift: .

Zoom In Zoom Out Reset image size

This approach is based on the excitation and interrogation of atoms using two sequences of Ramsey pulses with different free evolution times T₁ and T₂. However, unlike GABRS, only one feedback loop is used here, and the error signal for frequency stabilisation is formed as a linear superposition of two ordinary error signals obtained separately for each Ramsey sequence:

where β_cal is some calibration coefficient. The stabilised frequency of the oscillator corresponds to the condition when the combined error signal is equal to zero: . Substituting (19) into expression (25), we obtain

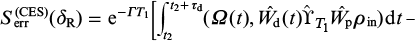
When choosing a calibration coefficient such that

the expression for the combined error signal (26) can be written as

Taking into account equality (23) for the matrices 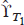and with δ_R = 0, expression (28) makes it possible to obtain

Thus, the performed analysis proves the absence of a light shift for the oscillator frequency stabilised at zero of the combined error signal (25) with the calibration coefficient (27).

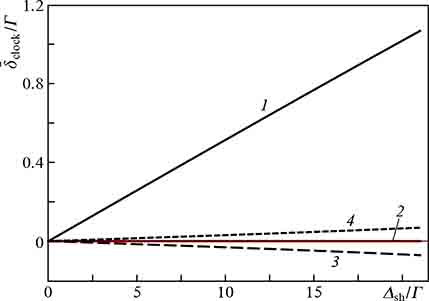
Figure 4 shows the error signals for the traditional Ramsey scheme at two different free evolution times (T₁/_{T 2} = 10) and the combined error signal as function of the Raman detuning δ_R. It can be seen that with an accurate calibration coefficient β_cal (27), the light shift for CESRS is completely suppressed. However, in real conditions, β_cal may differ from the ideal value, which leads to the appearance of a residual shift for CESRS. Nevertheless, as calculations show (Fig. 5), even at a ±5 % deviation of β_cal from the ideal value, suppression of the light shift is about 17 times greater in CESRS as compared to conventional Ramsey spectroscopy (with the free evolution time T₁).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

We have rigorously proven the applicability of generalised autobalanced Ramsey spectroscopy and the combined error signal in Ramsey spectroscopy of CPT resonances in an open Λ-system with a trap state, which simulates the case of the D₁ line of alkali metal atoms in a bichromatic circularly polarised field. The obtained analytical results are supported by numerical calculations demonstrating the high efficiency of suppression of the light shift and its fluctuations. With regard to GABRS, a variant is considered when an additional frequency jump in the value of the Raman detuning is an concomitant parameter for suppressing the light shift. Implementation of GABRS and CESRS will significantly improve long-term stability (to a level below 10⁻¹⁴) and the accuracy of CPT clocks. These methods can find application in atomic CPT magnetometers and interferometers. The advantage of these spectroscopic schemes is also their high immunity to various distortions of the pulse shape, relaxation processes, errors in the formation of phase jumps, etc.

This work was supported by the RF President's Grants Council (Grant No. MK-161.2020.2), the Russian Foundation for Basic Research (Grant Nos 19-32-90181, 20-02-00505, 20-52-18004, and 19-29-11014), the Ministry of Science and Higher Education of the Russian Federation (Grant No. FSUS-2020-0036), and the BASIS Foundation for the Advancement of Theoretical Physics and Mathematics (Project No. 19-1-1-67-2).

The Liouvillian defined by Eqns (3) – (5) has the form

In the absence of a light field (Ω₁ = Ω₂ = 0 and Δ_sh = 0), the Liouvillian is expressed as

The operator , which describes the free evolution of atoms, is defined as

where