Strategic diffusion in networks through contagion

Abstract

This paper studies the diffusion of products and behaviour with coordination effects through social networks when agents are myopic best responders. We develop a new network measure, the contagion threshold, that determines when a p-dominant action—an action that is a best response when adopted by at least proportion p of an agent’s opponents—spreads to the whole population starting from a group of players whose size is smaller than half and independent of the population size. We show that a p-dominant action spreads to the whole network whenever the contagion threshold of that network is greater or equal to p. We then show that in settings where agents regularly or occasionally experiment and choose non-optimal actions, there exists a threshold level of experimentation below which a p-dominant action is chosen with the highest probability in the long run. This result implies that targeted contagion, a network-wide diffusion of actions initiated by targeting agents, is justified even in settings where agents’ decisions are noisy.

Appendices

Appendix A: Expected waiting time

This section focuses on Model 2 to examine how the process of contagion affects the expected waiting time from any state to the state with the highest long-run probability. The problem of slow diffusion does not arise in situations where the level of experimentation is sufficiently high. Kreindler and Young (2013) and Kreindler and Young (2014) show that when β is sufficiently small, convergence is fast. Here, we examine the case where β is very large (i.e. $\beta \rightarrow \infty$).

We show that when β is large, the expected waiting time to the monomorphic convention corresponding to the contagious strategy is independent of the population size. The direct implication of this result is that even in large networks and with low levels of experimentation, the diffusion process converges fast to the long-run equilibrium. The expected waiting time is formally defined as follows.

Definition 8

Let W ⊂X be a subset of the configuration space and $\bar {W}$ its complement. Define $T(W)=\inf \{t\geq 0 |\mathbf {x}_{t}\in W\}$ to be the first time W is reached. The expected waiting time from some configuration $\mathbf {x}\in \bar {W}$ to W is then defined as $\mathbb {E}\left [T(W) |\mathbf {x}_{0}=\mathbf {x}\right ]$.

Let a^∗ be a p-dominant strategy of (A, U), and assume that p ≤ η(G) so that a^∗ is contagious on G. We aim to show that (A, U, N, G, P_ε) converges to a^∗ fast (i.e. the expected waiting time to a^∗ is independently of the population size). To do so, we show that if a^∗ is contagious on G, then there exists a function F(β) that is independent of n so that $\mathbb {E}\left [T(\mathbf {a}^{*}) |\mathbf {x}_{0}=\mathbf {x}\right ]\leq F(\beta )$ for all initial configurations $\mathbf {x}_{0}\neq \mathbf {a}^{*}$.

Proposition 2

Let a^∗ be a p-dominant strategy of (A, U) and assume that a^∗ is contagious on a strongly connected network G so that a^∗ is the long-run equilibrium of the diffusion process (A, U, N, G, P_β). Then there exists some $b^{*}\in (0,b^{*}_{2})$ such that

$$ \lim_{\beta\rightarrow\infty}\frac{\ln\mathbb{E}[T(\mathbf{a}^{*})]}{\beta} = b^{*} $$

(5)

Proof

See Appendix A□

Proposition 2 shows that the expected waiting time to the equilibrium configuration of the evolutionary process with mutations from any other configuration takes the form

$$ \mathbb{E}[T(\mathbf{a}^{*})] \leq \exp\left[\beta b^{*} + g(\beta)\right]=F(\beta) $$

(6)

where g(β) is a decreasing function of noise parameter β. As the level of experimentation tends to zero (i.e. $\beta \rightarrow \infty$), $g(\beta )\rightarrow 0$ and the expected waiting time increases at an exponential rate of b^∗, which is independent of the population size.

Compared to existing results on convergence rates of evolutionary processes such as Ellison (1993), Young (2011), Kreindler and Young (2013) and Kreindler and Young (2014), the result in Proposition 2 is driven more by contagion and less by noise. Kreindler and Young (2014) also find that learning is fast in networks, but they consider a 2 × 2 coordination game with random sampling and with deterministic dynamics. Moreover, they define fast learning as the case in which noise is large to the extent that only one unique equilibrium exists. On a contrary, Proposition 2 shows that contagion makes learning fast in stochastic evolutionary game dynamics for m × m coordination games.

Appendix B: Proof of Theorem 1

The proof of Theorem 1 follows in two steps. The first step, which is already discussed in detail in Section 3, demonstrates that if a^∗∈ A is a p-dominant strategy of (A, U) and p ≤ η(G), then a^∗ spreads contagiously on G, and that the size of the set of initial adopters is bounded from above by $b^{*}_{2}$. The second step demonstrates that if a^∗∈ A is a p-dominant strategy and p ≤ η(G), then the number of mutations needed to leave convention a^∗ is greater than $n^{\frac {3}{5}}$.

Strategy a ^∗ spreads contagiously on G

Given the diffusion process (A, U, N, G, P) on a strongly connected network G, and a p-dominant strategy a^∗∈ A, let p ≤ η(G). Let also A₁ = A∖a^∗. Since a^∗ is p-dominant, it is a best response when played by at least proportion p of a player’s neighbours and the rest play strategies in A₁. This implies that if all players in a given subgroup Z ⊂ N play a^∗, then a^∗ is a unique best response to any i ∈ N for whom α_i(Z) ≥ p.

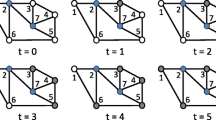
Let the evolutionary process start from any state a ∈ L∖a^∗, where a can consist of only strategies in A₁ or both a^∗ and strategies in A₁. Pick any i ∈ N and the respective $B_{i_{2}}$, and at period t = 1, let all players in $B_{i_{2}}$ mutate to play a^∗. The evolutionary process will evolve through best response from t = 1 onward as follows, where we write $\bar {B}_{i_{r}}=N\backslash B_{i_{r}}$ for the complement of $B_{i_{r}}$, $i\rightarrow A_{l}$ to mean that i plays a strategy in A_l, $Z\rightarrow A_{l}$ to mean that each j ∈ Z plays a strategy in A_l:

Table 1

We see from the above iterative process that after t = d_i − 1 iterations, the evolutionary process converges to convention a^∗. Thus, starting from any a ∈ L∖a^∗, there exists a best response sequence $\left \{\mathbf {x}_{t} \right \}_{t=0}^{d_{i}-1}$ with x₀ = a and ${x_{1}^{j}}=a^{*}$ for all $j\in N(\mathbf {a}\rightarrow \mathbf {a}^{*})=B_{i_{2}}$, for any i ∈ N, satisfying $x_{d_{i}-1}^{l}=a^{*}$ for all l ∈ N. Since this holds for $B_{i_{2}}$ of any i ∈ N, it follows that the size of the smallest set of initial adopters is $b^{*}_{2}= \operatorname *{arg min}_{i\in N}b_{i_{2}}$.

Since $b^{*}_{2}$ is independent of the population size, n, we conclude that when p ≤ η(G), strategy a^∗ spreads contagiously on G with $n(\mathbf {a}\rightarrow \mathbf {a}^{*})\leq b^{*}_{2}$ for all a ∈ L∖a^∗. Note that the upper bound for $n(\mathbf {a}\rightarrow \mathbf {a}^{*})$ follows because although $b^{*}_{2}$ mutations to a^∗ guarantee that a^∗ spreads contagiously, it is possible, in most networks, to find a smaller set than $b^{*}_{2}$ that sufficiently triggers the contagious spread of a^∗.

Uninvadability of a ^∗

Recall that convention a^∗ is uninvadable if $r(\mathbf {a}^{*})>n(\mathbf {a}\rightarrow \mathbf {a}^{*})$ for all a ∈ L∖a^∗, and that r(a^∗), which is the number of mutations required to leave the basin of attraction of convention a^∗, is a function of n. We first show that if a^∗ spreads contagiously on a strongly connected network G, then $r(\mathbf {a}^{*})\geq n^{\frac {3}{5}}$.

Let R(a^∗) ⊂ N be the smallest set of players that should mutate to strategies in A₁ for the evolutionary process to leave the basin of attraction of a^∗, where r(a^∗) is the cardinality of R(a^∗). We see from the preceding analysis that if there exists a player i in G for whom all players in $B_{i_{2}}$ play a^∗, then a^∗ spreads contagiously, and hence, the evolutionary process converges to a^∗ regardless of the strategy configuration of other players not in $B_{i_{2}}$. Thus, to leave a^∗, no such player must exist, and that each player must be at most two steps away from R(a^∗); that is, for each i, a sufficiently large proportion of players in $B_{i_{2}}$ are in R(a^∗). Since a^∗ is p-dominant, where $p\leq \frac {1}{2}$, strategies in A₁ are best responses only when more than proportion $(1-p)>\frac {1}{2}$ of neighbours play strategies in A₁. For strategies in A₁ to become best responses to players within $B_{i_{2}}$, more than $\frac {1}{2}$ of the interactions of players in $B_{i_{2}}$ must be in R(a^∗); and R(a^∗) must be chosen to satisfy this condition for each i ∈ N.

The identification of the smallest R(a^∗) is then equivalent to the problem of identifying the smallest 2-monopolies in graph theory, defined as follows. A player i in network G is said to be 2-controlled by the set Z ⊂ N of players if at least half of the players in $B_{i_{2}}$ are in Z. The set Z is called a 2-monopoly if it 2-controls every player in the network. Bermond et al (1996, Proposition 4) show that the minimum size of a 2-monopoly on any undirected and strongly connected network of size n is $n^{\frac {3}{5}}$ (see Peleg (2002) for a review of the literature on monopolies and local majorities in networks), and hence, $r(\mathbf {a}^{*})>n^{\frac {3}{5}}$. Note that the inequality follows because we require R(a^∗) to contain more than half of interactions of $B_{i_{2}}$ for all i ∈ N while the definition of a 2-monopoly requires R(a^∗) to contain at least half of the interactions of $B_{i_{2}}$.

Since $r(\mathbf {a}^{*})>n^{\frac {3}{5}}$ is an increasing function of n, it follows that convention a^∗ is uninvadable whenever $n^{\frac {3}{5}}\geq n(\mathbf {a}\rightarrow \mathbf {a}_{l})$ for all a ∈ L∖a^∗. And since $n(\mathbf {a}\rightarrow \mathbf {a}_{l})\leq b^{*}_{2}$ for all a ∈ L∖a^∗, convention a^∗ is uninvadable, and hence, also contagious, whenever $b^{*}_{2}\leq n^{\frac {3}{5}}$.

Appendix C: Proof of Proposition 1

To prove Proposition 1, we first characterize the structure of stationary distributions, and in particular, the ratio, $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {y})}$, of stationary distributions of any pair of configurations x, y ∈ X. We use the following results from Freidlin and Wentzell (1984).

Lemma 1

(Lemma 3.1 ; Freidlin and Wentzell 1984). Given a diffusion process P_β, the stationary distribution π_β(x) of some configuration x ∈ X is given by

$$ \pi_{\beta}(\mathbf{x})=\left( \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}P_{\beta}(g)\right)\left( \underset{\mathbf{y}\in \mathbf{X}}{\sum}\underset{g\in {{\varGamma}}(\{\mathbf{y}\})}{\sum}P_{\beta}(g)\right)^{-1} $$

(7)

where the total probability P_β(g) associated with each graph g is $\displaystyle P_{\beta }(g)=\underset {(\mathbf {z},\mathbf {y})\in g}{\prod }P_{\beta }(\mathbf {z},\mathbf {y})$ and Γ(x) graphs are defined in Definition 7.

To fully characterise the structure of π_β, we first characterise the structure of transition probabilities P_β(x, y) between pairs of states x, y ∈ X. Recall that c(x, y) is the number of mutations involved in the direct transition from x to y. That is, the number of players who choose different strategies in state y than those chosen in state x, and that their choices are a result of mutations. Employing Assumption 1, the transition probability P_ε(x, y) can directly be expressed in terms of c(x, y) as

$$ P_{\beta}(\mathbf{x},\mathbf{y}) = \left( \frac{e^{-\beta}}{m}\right)^{c(\mathbf{x}, \mathbf{y})}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n-c(\mathbf{x}, \mathbf{y})} $$

(8)

The right hand side of Eq. 8 follows because, first, if yⁱ (i.e. the strategy i plays in configuration y) is not a best response to x so that BR_i(yⁱ; x) = 0, then from Eq. 3, the probability that i plays yⁱ is $\frac {e^{-\beta }}{m}$. Consequently, the probability that c(x, y) players simultaneously play strategies that are not best responses to x in configuration y is $\left (\frac {e^{-\beta }}{m}\right )^{c(\mathbf {x}, \mathbf {y})}$.

Second, if yⁱ is instead a best response to x, so that, from Assumption 1, BR_i(yⁱ; x) = 1, then i plays yⁱ with probability

$$\frac{e^{-\beta}}{m} + (1-e^{-\beta}) = \frac{m+(1-m)e^{-\beta}}{m} $$

Thus, the probability that the remaining n − c(x, y) players simultaneously play strategies that are best responses to x is $\left (\frac {m+(1-m)e^{-\beta }}{m}\right )^{n-c(\mathbf {x}, \mathbf {y})}$.

Next, we characterise the probabilities of Γ(x) graphs. From the definition of Γ(x) graphs, every g ∈ Γ(x) spans the entire state space except x, which is the root of the graph. Each y ∈ X∖x has only one arrow emanating from it. Thus, each g ∈ Γ(x) contains a total of mⁿ − 1 directed edges, where mⁿ is the cardinality of X. Similarly, if we let d(L_j) be the cardinality of D(L_j) (the basin of attraction of L_j), then there are d(L_j) directed edges that originate from states in D(L_j).

Now, let g(D(L)) be a subgraph of g consisting of all d(L_j) directed edges that originate from states in D(L_j). Since D(L_j) for all L_j ⊂L are non-overlapping sets, we can rewrite P_β(g) as

$$ P_{\beta}(g)=\underset{L_{j}\in \mathbf{L}}{\prod}\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j}))}{\prod}P_{\beta}(\mathbf{y},\mathbf{z}) $$

(9)

We can further subdivide the set of edges of g(D(L_j)) into those that involve at least one mutation, denoted by g(D(L_j); β), and those whose dynamics are governed solely by best response, denoted by $\overline {g(D(L_{j});\beta )}$. That is, for each x ∈ D(L_j) and some y≠x, a directed edge (x, y) ∈ g(D(L_j); β) if c(x, y) > 0, and $(\mathbf {x},\mathbf {y})\in \overline {g(D(L_{j});\beta )}$ if c(x, y) = 0. Using these definitions and notation, P_β(g) can be rewritten as

$$ \begin{array}{@{}rcl@{}} P_{\beta}(g) &=&\underset{L_{j}\in \mathbf{L}}{\prod}\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j}))}{\prod} P_{\beta}(\mathbf{y},\mathbf{z})\\ &=&\underset{L_{j}\in \mathbf{L}}{\prod}\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j}))}{\prod} \left( \frac{e^{-\beta}}{m}\right)^{c(\mathbf{y}, \mathbf{z})}{\prod}_{i=1}^{n-c(\mathbf{y}, \mathbf{z})}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)\\ &=& \underset{L_{j}\in \mathbf{L}}{\prod}\left[\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}{\prod} \left( \frac{e^{-\beta}}{m}\right)^{c(\mathbf{y}, \mathbf{z})}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n-c(\mathbf{y}, \mathbf{z})} \right.\\ &&\left.\times\underset{(\mathbf{y},\mathbf{z})\in \overline{g(D(L_{j});\beta)}}{\prod} \left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n}\right] \end{array} $$

(10)

Let n(g; L_j; β) be the cardinality of subgraph g(D(L_j); β) (i.e. the number of directed edges in subgraph g(D(L_j); β)) so that the cardinality of $\overline {g(D(L_{j});\beta )}$ is d(L_j) − n(g; L_j; β). Then Eq. 10 can be rewritten as

$$ \begin{array}{@{}rcl@{}} P_{\beta}(g) &=&\! \underset{L_{j}\in \mathbf{L}}{\prod}\left[\left( \!\frac{e^{-\beta}}{m}\!\right)^{{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}c(\mathbf{y}, \mathbf{z})}\left( \!\frac{m + (1 - m)e^{-\beta}}{m}\!\right)^{{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}(n-c(\mathbf{y}, \mathbf{z}))}\right.\!\! \\ &&\times\left.\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n[d(L_{j})-n(g;L_{j};\beta)]}\right]\\ &=&\underset{L_{j}\in \mathbf{L}}{\prod}\left( \frac{e^{-\beta}}{m}\right)^{{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}c(\mathbf{y}, \mathbf{z})}\\&&\times\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{n[d(L_{j})-n(g;L_{j};\beta)]+{\sum}_{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}(n-c(\mathbf{y}, \mathbf{z}))} \end{array} $$

(11)

The summation $c(L_{j};g)={\sum }_{(\mathbf {y},\mathbf {z})\in g(D(L_{j});\beta )}c(\mathbf {y}, \mathbf {z})$ on the exponent of the expressions of P_β(g) in Eq. 11 is the total cost of leaving the basin of attraction of each L_j under graph g ∈ Γ(x). Using this definition, we can simplify $n[d(L_{j})-n(g;L_{j};\beta )]+{\sum }_{(\mathbf {y},\mathbf {z})\in g(D(L_{j});\beta )}(n-c(\mathbf {y}, \mathbf {z}))$ as follows:

$$ \begin{array}{@{}rcl@{}} n[d(L_{j})-n(g;L_{j};\beta)]+\underset{(\mathbf{y},\mathbf{z})\in g(D(L_{j});\beta)}{\sum}(n-c(\mathbf{y}, \mathbf{z})) &=& n[d(L_{j})-n(g;L_{j};\beta)]\\&&+n(g;L_{j};\beta)n - c(L_{j};g)\\ &=&nd(L_{j})-c(L_{j};g) \end{array} $$

Eq. 11 then simplifies to

$$ \begin{array}{@{}rcl@{}} P_{\beta}(g) &=& \underset{L_{j}\in \mathbf{L}}{\prod}\left( \frac{e^{-\beta}}{m}\right)^{c(L_{j};g)}\left( \frac{m+(1-m)e^{-\beta}}{m}\right)^{nd(L_{j})-c(L_{j};g)}\\ &=& \exp\left[-\underset{L_{j}\in \mathbf{L}}{\sum}\left( c(L_{j};g)\beta_{m} + (nd(L_{j})-c(L_{j};g))\beta_{m}^{\prime} \right)\right]\\ & =& \exp\left[-\underset{L_{j}\in \mathbf{L}}{\sum}\left( c(L_{j};g)(\beta_{m}-\beta_{m}^{\prime}) + nd(L_{j})\beta_{m}^{\prime} \right)\right] \end{array} $$

(12)

where $\beta _{m} =\beta -\ln m^{-1}$ and $\beta _{m}^{\prime }= -\ln \left [\frac {m+(1-m)e^{-\beta }}{m}\right ]$.

Recall the definition of the long-run equilibrium of (A, U, N, G, P_ε) as configurations that maximize the stationary distribution. So, to compute the long-run equilibrium, we take ratios of probabilities and identify configurations for which the ratio is less than one. Specifically, configuration a^∗ is a long-run equilibrium if $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {a}^{*})}\leq 1$ for all x≠a^∗. From π_β(x) in Eq. 7, the expression for the ratio of stationary distribution, $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}$ of any pair of configurations x, w ∈ X is given by

$$ \frac{\pi_{\beta}(\mathbf{x})}{\pi_{\beta}(\mathbf{w})}=\frac{{\sum}_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)}{{\sum}_{g\in {{\varGamma}}(\{\mathbf{w}\})}P_{\beta}(g)} $$

(13)

where the quantity $\left ({\sum }_{\mathbf {y}\in \mathbf {X}}{\sum }_{g\in {{\varGamma }}(\{\mathbf {y}\})}P_{\beta }(g)\right )^{-1}$ cancels out since it is identical for all configurations.

Let γ(x) = #Γ(x) be the cardinality of Γ(x). Since for any x ∈ X every g ∈ Γ(x) spans the entire state space except for one configuration (i.e. the number of edges in any g ∈ Γ(x) is equal to mⁿ − 1), the cardinality of Γ(x) is the same for any pair of configurations x, y ∈ X; that is, γ(x) = γ(y) = γ. Using this notation, the following bounds hold:

$$\underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}P_{\beta}(g)\leq \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}\max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)=\gamma \max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)$$

$$\underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\sum}P_{\beta}(g) \geq \max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)$$

Thus, the ratio $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}$ is bounded from below and above by

$$ \frac{\max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)}{\gamma \max_{g\in {{\varGamma}}(\{\mathbf{w}\})}P_{\beta}(g)} \leq \frac{\pi_{\beta}(\mathbf{x})}{\pi_{\beta}(\mathbf{w})}\leq \frac{\gamma \max_{g\in {{\varGamma}}(\{\mathbf{x}\})}P_{\beta}(g)}{\max_{g\in {{\varGamma}}(\{\mathbf{w}\})}P_{\beta}(g)} $$

(14)

Substituting for P_β(g) from Eq. 12 into the ratios of stationary distributions in Eq. 14 yields the following expression.

$$ \begin{array}{@{}rcl@{}} \frac{\max_{g\in {{{\varGamma}}}(\{\mathbf{x}\})}P_{\beta}(g)}{\max_{g\in {{{\varGamma}}}(\{\mathbf{w}\})}P_{\beta}(g)} &=& \frac{\max_{g\in {{{\varGamma}}}(\{\mathbf{x}\})}\exp\left[-{\sum}_{L_j\in \mathbf{L}}\left( c(L_j;g)(\beta_m-\beta_m^{\prime}) + nd(L_j)\beta_m^{\prime} \right)\right]}{\max_{g\in {{{\varGamma}}}(\{\mathbf{w}\})}\exp\left[-{\sum}_{L_j\in \mathbf{L}}\left( c(L_j;g)(\beta_m-\beta_m^{\prime}) + nd(L_j)\beta_m^{\prime} \right)\right]}\\ &=&\exp\left[\min_{g\in {{{\varGamma}}}(\{\mathbf{w}\})}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)(\beta_m-\beta_m^{\prime}) - \underset{g\in {{{\varGamma}}}(\{\mathbf{x}\})}{\min}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)(\beta_m-\beta_m^{\prime})\right]\\ &=&\exp\left[-(\beta_m-\beta_m^{\prime}) \left( \underset{g\in {{{\varGamma}}}(\{\mathbf{x}\})}{\min}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)- \underset{g\in {{{\varGamma}}}(\{\mathbf{w}\})}{\min}\underset{L_j\in \mathbf{L}}{\sum}c(L_j;g)\right)\right] \end{array} $$

(15)

whereby, due to the negative in the exponents, the expressions for P_β(g) are maximized when the costs of exiting the basins of attractions of absorbing sets are minimized. Substituting Eq. 15 into Eq. 14 yields the following lower and upper bounds for $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}$

$$ \frac{\pi_{\beta}(\mathbf{x})}{\pi_{\beta}(\mathbf{w})}= \exp\left[-(\beta_{m}-\beta_{m}^{\prime}) \left( \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)- \underset{g\in {{\varGamma}}(\{\mathbf{w}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)\right)\pm \ln\gamma \right] $$

(16)

Now, notice that for all β ≥ 0, $(\beta _{m}-\beta _{m}^{\prime })\geq 0$: that is,

$$ \begin{array}{@{}rcl@{}} (\beta_{m}-\beta_{m}^{\prime})&=& \beta-\ln m^{-1} + \ln \left[\frac{m+(1-m)e^{-\beta}}{m}\right]\\&=& \beta-\ln m^{-1} + \ln \left[m+(1-m)e^{-\beta}\right]+\ln m^{-1}\\ &=& \beta + \ln \left[m+(1-m)e^{-\beta}\right] \end{array} $$

(17)

Since m + (1 − m)e^−β ≥ 1 for all β ≥ 0, it follows from the right hand side of Eq. 17 that $(\beta _{m}-\beta _{m}^{\prime })\geq 0$ for all β ≥ 0. Let Φ(x, w) denote the difference between costs of graphs (i.e. the expression in the exponent of Eq. 16). That is,

$${{{\varPhi}}}(\mathbf{x},\mathbf{w})= \underset{g\in {{\varGamma}}(\{\mathbf{x}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)- \underset{g\in {{\varGamma}}(\{\mathbf{w}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g)$$

It then follows from Eq. 16 that $\frac {\pi _{\beta }(\mathbf {x})}{\pi _{\beta }(\mathbf {w})}\leq 1$ if Φ(x, w) ≥ 0 and that

$$ \begin{array}{@{}rcl@{}} -(\beta_{m}-\beta_{m}^{\prime}) {{{\varPhi}}}(\mathbf{x},\mathbf{w})+ \ln\gamma \leq0 \end{array} $$

(18)

Substituting for the values of β_m and $\beta _{m}^{\prime }$ in Eq. 18 yields

$$ \beta \geq \frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{x},\mathbf{w})}-\ln \left[m+(1-m)e^{-\beta}\right] $$

(19)

Let β^∗ be the solution to

$$ \beta = \frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{x},\mathbf{w})}-\ln \left[m+(1-m)e^{-\beta}\right] $$

(20)

By comparison β^∗ is smaller than $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}$. To see why, notice that the function $\ln \left [m+(1-m)e^{-\beta }\right ]$ increases from 0 to the upper bound $\ln m$ as $\beta \rightarrow \infty$, which implies that $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}-\ln \left [m+(1-m)e^{-\beta }\right ]$ decreases from $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}$ to $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}-\ln m$. This implies that the equilibrium value of β in Eq. 20, that is, the value of β at which the 45-degree line depicting β = β meets $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}-\ln \left [m+(1-m)e^{-\beta }\right ]$, is less than $\frac {\ln \gamma }{{{{\varPhi }}}(\mathbf {x},\mathbf {w})}$, and hence,

$$ \beta^{*} \leq \frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{x},\mathbf{w})} $$

(21)

It then follows that configuration a^∗ is the long-run equilibrium for all β ≥ β^∗ if it hase the least cost a^∗-tree, that is, Φ(x, a^∗) ≥ 0 for all x≠a^∗.

We now show that if a p-dominant strategy, a^∗, is contagious in a given network, then convention a^∗ has the minimum cost Γ(a^∗) graph. Note that configurations with the minimum cost graph belong to some absorbing state, and hence, it suffices to focus on examining the costs of graphs for configurations within L. Let ϕ(a, g) denote the total cost of some g ∈ Γ(a) for any a ∈ L; that is,

$$ \phi(\mathbf{a};g)= \underset{g\in {{\varGamma}}(\{\mathbf{a}\})}{\min}\underset{L_{j}\in \mathbf{L}}{\sum}c(L_{j};g) $$

(22)

We can see from Eq. 22 that ϕ(a; g) is identical to the cost derived from a reduced form of Γ(a), denoted by ${{\varGamma }}^{\prime }(\mathbf {a})$, on a state space L ×L (i.e. where vertices are absorbing sets). For any $g\in {{\varGamma }}^{\prime }(\mathbf {a})$ the cost of an arrow originating from some L_j ∈ L is c(L_j; g).

We deduce from the proof of Theorem 1 in Appendix B that for convention a^∗, the minimum cost graph in ${{\varGamma }}^{\prime }(\mathbf {a}^{*})$ involves direct transitions from every $\mathbf {a}\in L_{j}\subset \mathbf {L}\backslash \mathbf {a}^{*}$ to a^∗, and each has a cost bounded from above by $c(\mathbf {a};g)\leq b^{*}_{2}$. Note that if $c(\mathbf {a};g)\leq b^{*}_{2}$ for all a ∈ L_j, then $c(L_{j};g)\leq b^{*}_{2}$. Thus, if we let ζ^∗(L) be the number of independent absorbing sets in L (i.e. all L_j ⊂L) with a^∗ excluded, then

$$ \phi(\mathbf{a}^{*})= \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a}^{*})}{\min}\phi(\mathbf{a}^{*};g) \leq b^{*}_{2}\zeta^{*}(\mathbf{L}) $$

(23)

Now, consider any other a ∈ L ⊂L∖a^∗. The minimum cost graph in ${{\varGamma }}^{\prime }(\mathbf {a})$ will consist of an arrow $\mathbf {a}^{*}\rightarrow \mathbf {a}^{\prime }$ starting from a^∗ to some $\mathbf {a}^{\prime }\neq \mathbf {a}^{*}$. The minimum cost $g\in {{\varGamma }}^{\prime }(\mathbf {a})$ can thus be constructed from the minimum cost graph in ${{\varGamma }}^{\prime }(\mathbf {a}^{*})$ by deleting $\mathbf {a}\rightarrow \mathbf {a}^{*}$ and replacing it with $\mathbf {a}^{*}\rightarrow \mathbf {a}^{\prime }$, so that

$$ \phi(\mathbf{a})= \phi(\mathbf{a}^{*}) - \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a}^{*})}{\min}c(\mathbf{a};g)+\min_{g\in {{\varGamma}}^{\prime}(\mathbf{a})}c(\mathbf{a}^{*};g) $$

(24)

And hence,

$$ \phi(\mathbf{a})-\phi(\mathbf{a}^{*}) = \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a})}{\min}c(\mathbf{a}^{*};g)- \underset{g\in {{\varGamma}}^{\prime}(\mathbf{a}^{*})}{\min}c(\mathbf{a};g) > \left( n^{\frac{3}{5}}-b^{*}_{2}\right) $$

(25)

where the second inequality is because the minimum cost of leaving a^∗ is greater than $n^{\frac {3}{5}}$ mutations (see Appendix B) and that $c(\mathbf {a};g)\leq b^{*}_{2}$ for all $\mathbf {a}\in L_{j}\subset \mathbf {L}\backslash \mathbf {a}^{*}$.

Since $n^{\frac {3}{5}}\geq b^{*}_{2}$ is a condition for strategy a^∗ to be contagious, it follows that ϕ(a) − ϕ(a^∗) > 0 for all a ∈ L∖a^∗, and hence, a^∗ has the minimum cost a^∗-tree. The inequality, $\phi (\mathbf {a})-\phi (\mathbf {a}^{*})>n^{\frac {3}{5}}-b^{*}_{2}$, also implies that ${{{\varPhi }}}(\mathbf {a},\mathbf {a}^{*})> n^{\frac {3}{5}}-b^{*}_{2}$ for all a ∈ L∖a^∗. Thus,

$$\frac{\ln \gamma}{{{{\varPhi}}}(\mathbf{a},\mathbf{a}^{*})}< \frac{\ln \gamma}{n^{\frac{3}{5}}-b^{*}_{2}} \quad \text{for all $\mathbf{a}\in\mathbf{L}\backslash\mathbf{a}^{*}$}$$

It then follows that there exists some $\beta ^{*}\in \left (0, \ln \gamma /(n^{\frac {3}{5}}-b^{*}_{2})\right ]$ such that for all β ≥ β^∗, convention a^∗ has the least cost tree, and hence, the long-run equilibrium.

Appendix D: Proof of Proposition 2

The following definitions are used in the next steps of the proof. Given transition probabilities P_β(x, y) in Eq. 8, the cost function c(x, y) can be rewritten as follows

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{-\ln P_{\beta}(\mathbf{x},\mathbf{y})}{\beta} = c(\mathbf{x},\mathbf{y}) $$

(26)

The following definition is for Γ_{x, y}(W) graphs, which are a special form of Γ(W) graphs defined in Definition 7.

Definition 9

For any $\mathbf {x}\in \bar {W}$ and y ∈ W where x≠y, Γ_{x, y}(W) is a set of all Γ(W)-graphs which link x to y. For any two configurations $\mathbf {x}, \mathbf {y}\in \bar {W}$, Γ_{x, y}(W ∪{y}) is the set of Γ(W)-graphs in which x is joined to some point y possibly itself and not to W, and that all other points of $\bar {W}$ are joined to either the same point or to W.

Consider a configuration space X = {a, b, c, d, e, f, g, h} with examples of g-trees depicted in Fig. 4. Let W = {d, e, f, g, h}, with examples of Γ(W) graphs depicted in Fig. 5. Then examples of ${{\varGamma }}_{\mathbf {a},\mathbf {c}}\left (W\cup \{\mathbf {c}\}\right )$ graphs based on Γ(W) graphs in Fig. 5 are: $\{\mathbf {a}\rightarrow \mathbf {c}, \mathbf {b}\rightarrow W \}$ for the graph on the left, $\{\mathbf {c}\rightarrow W, \mathbf {b}\rightarrow W \}$ for the middle graph, and $\{\mathbf {a}\rightarrow \mathbf {b}, \mathbf {c}\rightarrow W \}$ for the graph on the right.

Fig. 5

Examples of Γ(W) graphs, where $\bar {W}=\{\mathbf {a}, \mathbf {b}, \mathbf {c}\}$

Recall the definition of ϕ(W; g) for some W ⊂X and g ∈ Γ(W) from Appendix C as $\phi (W;g)={\sum }_{(\mathbf {x},\mathbf {y})\in g}c(\mathbf {x},\mathbf {y})$. The following result is derived in Catoni (1999, Proposition 4.2).

Lemma 2

For any W ⊂X, W ≠ ∅ and $\bar {W}=\mathbf {X}\backslash W$, for any $\mathbf {x},\mathbf {y}\in \bar {W}$

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{\ln\mathbb{E}[T(W)| \mathbf{x}_{0}=\mathbf{x}]}{\beta} = \underset{g\in {{\varGamma}}(W)}{\min}\phi(W;g)-\underset{\mathbf{y}\in \bar{W}}{\min}\underset{g\in {{\varGamma}}_{\mathbf{x}, \mathbf{y}}(W\cup\{\mathbf{y}\})}{\min}\phi(W;g) $$

(27)

We are interested in the expected waiting time for convention a^∗ associated with the contagious strategy a^∗. Thus, we can substitute W = {a^∗} into Eq. 27. That is,

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{\ln\mathbb{E}[T(\mathbf{a}^{*})| \mathbf{x}_{0}=\mathbf{x}]}{\beta} = \underset{g\in {{\varGamma}}(\mathbf{a}^{*})}{\min}\phi(\mathbf{a}^{*};g)-\underset{\mathbf{y}\in \mathbf{L}\backslash\mathbf{a}^{*}}{\min}\underset{g\in {{\varGamma}}_{\mathbf{x}, \mathbf{y}}(\mathbf{a}^{*}\cup\{\mathbf{y}\})}{\min}\phi(\mathbf{a}^{*};g) $$

(28)

Recall from the analysis in Appendices B and C for the minimum cost graph g ∈ Γ(a^∗), the costs are bounded from above as $c(\mathbf {a};g)\leq b^{*}_{2}$ for all a ∈ L∖a^∗, and from Eq. 23, $\phi (\mathbf {a}^{*})=\min \limits _{g\in {{\varGamma }}(\mathbf {a}^{*})}\phi (\mathbf {a}^{*};g) \leq b^{*}_{2}\zeta ^{*}(\mathbf {L})$. Focusing on reduced form graphs, ${{\varGamma }}^{\prime }(\mathbf {a}^{*})$, it follows from the definition of ${{\varGamma }}^{\prime }_{\mathbf {a}, \mathbf {a}^{\prime }}(\mathbf {a}^{*}\cup \{\mathbf {a}^{\prime }\})$ graphs that $\min \limits _{\mathbf {a}^{\prime }\in \mathbf {L}\backslash \mathbf {a}^{*}}\min \limits _{g\in {{\varGamma }}^{\prime }_{\mathbf {a}, \mathbf {a}^{\prime }}(\mathbf {a}^{*}\cup \{\mathbf {a}^{\prime }\})}\phi (\mathbf {a}^{*};g)\leq b^{*}_{2}(\zeta ^{*}(\mathbf {L})-1)$. Thus, there exists some $b^{*}\in (0,b^{*}_{2})$ such that

$$ \underset{\beta\rightarrow\infty}{\lim}\frac{\ln\mathbb{E}[T(\mathbf{a}^{*})| \mathbf{x}_{0}=\mathbf{a}]}{\beta} = \underset{g\in {{\varGamma}}(\mathbf{a}^{*})}{\min}\phi(\mathbf{a}^{*};g) - \min_{\mathbf{a}^{\prime}\in \mathbf{L}\backslash\mathbf{a}^{*}}\underset{g\in {{\varGamma}}^{\prime}_{\mathbf{a}, \mathbf{a}^{\prime}}(\mathbf{a}^{*}\cup\{\mathbf{a}^{\prime}\})}{\min}\phi(\mathbf{a}^{*};g) =b^{*} $$

(29)