Radiative Surface Waves in Layered Plasma–Dielectric Structures and Prospects of Their Application in Plasma Microwave Electronics

Abstract

Surface waves in layered systems consisting of material media with different frequency dispersions are considered: dielectric–plasma–vacuum, vacuum–plasma–plasma, and dielectric–vacuum–plasma. It is shown that in such systems, one of the surface waves can be radiative into a medium that does not form an interface for the surface wave under consideration, in view of which the wave becomes decaying. In the dielectric–vacuum–plasma system, there is only one surface wave localized at the vacuum–plasma interface, which is radiative into the dielectric in a certain region of wavenumbers with a not too small thickness of the vacuum layer. For all cases, the possibilities of exciting surface waves of a layered structure by an electron beam are analyzed. It is indicated which surface waves will be excited most efficiently. The prospects of using such waves in plasma microwave electronics in the development of sub-terahertz and possibly terahertz frequency ranges are shown.

1. Surface waves are waves propagating along the interface between two media and decreasing in amplitude (usually exponentially) in both sides of the interface [1]. One of the media on the boundary of which surface waves are possible, is plasma. Surface waves have been studied in detail at the plasma–vacuum and plasma–dielectric boundaries, as well as at the boundaries of plasmas of different densities (see, e.g., review [2]). Surface plasma waves of various types are of great interest for applications in plasma microwave electronics [3]. Operating plasma microwave amplifiers and generators of electromagnetic radiation are based on the excitation of surface waves at the boundaries of the plasma layer by an electron beam [4, 5]. In this work, we consider more complex and, as we believe, promising systems of plasma microwave electronics, in which, in addition to the plasma layer, there is also a dielectric layer.¹ Similar systems have been studied in plasmonics and crystal optics [7]; however, in these fields of physics, the main attention was paid to the methods of excitation of surface plasma waves by an external bulk electromagnetic wave [7–10]. In plasma microwave electronics, a wave is excited by a synchronously moving electron beam; therefore, complex frequency spectra and field structures of surface plasma waves are of primary interest. The main material of this work is presented in this aspect. The main attention is paid to the so-called radiative surface waves, the energy of which is radiative through one of the boundaries of the layered plasma–dielectric system.²

2. We start with general relationships and definitions. We consider electromagnetic waves in a plane dielectric layer adjacent to two different dielectric media. Dielectrics are assumed to be isotropic; spatial dispersion is not taken into account. According to the above, the spatial distribution of the dielectric constant is given in the form

$$\varepsilon (\omega ,x) = \left\{ {\begin{array}{*{20}{l}} {{{\varepsilon }_{1}}(\omega ),\quad x < 0,} \\ {{{\varepsilon }_{0}}(\omega ),\quad 0 < x < {{L}_{0}},} \\ {{{\varepsilon }_{2}}(\omega ),\quad x > {{L}_{0}}.} \end{array}} \right.$$

(1)

Here, ${{L}_{0}}$ is the dielectric layer thickness, and ${{\varepsilon }_{{1,2}}}(\omega )$ and ${{\varepsilon }_{0}}(\omega )$ are some frequency functions. We study mainly (by default) the cases of nondissipative media when function (1) is real. Obviously, the electrodynamic structure (1) can be considered as a one-dimensional Fabry–Perot resonator (the layer $0 < x < {{L}_{0}}$) with devices for removing electromagnetic radiation from the resonator (regions $x < 0$ and $x > {{L}_{0}}$). In this case, x is the coordinate “along” the resonator.

Since the direction of the coordinate $y$ and $z$ axes does not matter in a system with the dielectric constant (1), we consider the vectors of the electromagnetic field to be independent of the coordinate $y$ and assume

$$\{ {\mathbf{E}}(t,{\mathbf{r}}),{\mathbf{B}}(t,{\mathbf{r}})\} = \{ {\mathbf{E}}(x),{\mathbf{B}}(x)\} \exp ( - i\omega t + i{{k}_{z}}z).$$

(2)

The exponential factor in Eq. (2) describes a wave traveling along the z axis, and therefore the electrodynamic structure (1) can be considered as a plane waveguide. In this case, z is the coordinate along the waveguide. The x-dependent amplitudes in (2), on the one hand, describe the transverse structure of the field in the waveguide, and on the other hand, they determine the field distribution along the resonator.

Natural oscillations in a plane Fabry–Perot resonator are formed by two natural bulk waves propagating in opposite directions. As a result, a bulk wave close to a standing wave is established in the resonator so that a certain number of half-waves fits along the length of the resonator. The spectrum of the natural frequencies of the resonator is a countable set of complex values. The fact that frequencies are complex in the absence of dissipation is due to the removal of radiation from the resonator through its boundaries. If the planes $x = 0,{{L}_{0}}$ are mirrors, the radiation from the resonator is absent, in this case, the functions ${\mathbf{E}}(x)$ and ${\mathbf{B}}(x)$ tend to zero at $x \to \pm \infty$, and the natural frequencies are real in the absence of dissipation. The cases are possible when the resonator has no own propagating bulk waves and there is no radiation into the surrounding space,³ but two surface waves are formed at the boundaries of the layer, and the frequency spectrum consists of only two real values. It occurs that intermediate cases are also possible when one of the surface waves of the dielectric layer is radiative from it. Such a surface wave is called an radiative surface wave. The frequency spectrum of a dielectric layer with an radiative surface wave usually contains two values, one of which is complex in the absence of dissipation, and the other is real, but there are cases when there is only one eigenvalue. The radiative surface waves have frequencies that lie outside the frequency range characteristic of conventional surface waves. An important feature of the radiative surface waves is that the damping decrement of these waves is exponentially small when the thickness of the dielectric layer is sufficiently large.

We restrict ourselves to the consideration of only electromagnetic waves with the nonzero electromagnetic field components ${{E}_{z}},\;{{E}_{x}},\;{{B}_{y}}$ (Е-type waves). The case of waves with the components ${{B}_{z}},\;{{B}_{x}},\;{{E}_{y}}$ (В‑type waves) is not of interest, since no B-type surface waves exist. It is not difficult to obtain the following equation for ${{E}_{z}}$ from Maxwell equations for E-type waves:

$$\frac{d}{{dx}}\left( {\frac{{\varepsilon (x)}}{{k_{x}^{2}(x)}}\frac{{d{{E}_{z}}}}{{dx}}} \right) + \varepsilon (x){{E}_{z}} = 0,$$

(3)

and relations for the calculation of the electromagnetic field components ${{E}_{x}}$ and ${{B}_{y}}$

$${{E}_{x}} = i\frac{{{{k}_{z}}}}{{k_{x}^{2}(x)}}\frac{{d{{E}_{z}}}}{{dx}},\quad {{B}_{y}} = i\frac{\omega }{{ck_{x}^{2}(x)}}\varepsilon (x)\frac{{d{{E}_{z}}}}{{dx}},$$

(4)

where

$$k_{x}^{2}(x) = \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}\varepsilon (x) - k_{z}^{2}.$$

(5)

Equation (3) is supplemented by the conditions of continuity of the tangential components of the electric field strength ${{E}_{z}}$ and magnetic field induction ${{B}_{y}}$ (or the continuity of the normal component of the electric field induction ${{D}_{x}} = \varepsilon (x)\,{{E}_{x}}$) at the interfaces, i.e., at the points where function (1) has discontinuities. These boundary conditions have the form

$${{\left\{ {{{E}_{z}}} \right\}}_{{x = 0,{{L}_{0}}}}} = 0,\quad {{\left\{ {\frac{{\varepsilon (x)}}{{k_{x}^{2}(x)}}\frac{{d{{E}_{z}}}}{{dx}}} \right\}}_{{x = 0,{{L}_{0}}}}} = 0,$$

(6)

where ${{\{ f(x)\} }_{{x = a}}} = f(a + 0) - f(a - 0)$.

3. We recall the necessary information from the theory of surface electromagnetic waves at the dielectric–plasma interface. Let the region $x < 0$ be filled by a non-dispersive dielectric with a dielectric constant ${{\varepsilon }_{1}} > 1$, and there is a cold collisionless electron plasma with a dielectric constant in the region $x > 0$ determined by the formula [12]

$${{\varepsilon }_{0}} = 1 - \frac{{\omega _{{p0}}^{2}}}{{{{\omega }^{2}}}},$$

(7)

where ${{\omega }_{{p0}}}$ is the electron Langmuir frequency. The solution of Eq. (3) decreasing at infinity (see below) can be written in the form

$${{E}_{z}}(x) = \left\{ {\begin{array}{*{20}{l}} {A\exp ({{\chi }_{1}}x),\quad x < 0,} \\ {B\exp ( - {{\chi }_{0}}x),\quad x > 0,} \end{array}} \right.$$

(8)

where $\chi _{{1,0}}^{2} = - k_{{x1,0}}^{2} = k_{z}^{2} - {{\varepsilon }_{{1,0}}}{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}$. Substituting solution (8) into boundary conditions (6) and excluding constants A and B, we obtain the following dispersion relation:

$$\begin{gathered} {{\varepsilon }_{1}}{{\chi }_{0}} + {{\varepsilon }_{0}}{{\chi }_{1}} = 0 \to {{\varepsilon }_{1}}\sqrt {\omega _{{p0}}^{2} + k_{z}^{2}{{c}^{2}} - {{\omega }^{2}}} \\ \, + \left( {1 - \frac{{\omega _{{p0}}^{2}}}{{{{\omega }^{2}}}}} \right)\sqrt {k_{z}^{2}{{c}^{2}} - {{\varepsilon }_{1}}{{\omega }^{2}}} = 0. \\ \end{gathered} $$

(9)

The solution of Eq. (9) of interest to us belongs to the frequency domain

$${{\omega }^{2}} < k_{z}^{2}{{c}^{2}}{\text{/}}{{\varepsilon }_{1}},\quad {{\omega }^{2}} < \omega _{{p0}}^{2},$$

(10)

and which is the region of existence of the surface wave. The solution to Eq. (9) satisfying conditions (10) is the following:

$$\begin{gathered} {{\omega }^{2}} = \frac{1}{2}\omega _{{p0}}^{2} + \frac{{{{\varepsilon }_{1}} + 1}}{{2{{\varepsilon }_{1}}}}k_{z}^{2}{{c}^{2}} \\ \, - \sqrt {\frac{1}{4}\omega _{{p0}}^{4} + {{{\left( {\frac{{{{\varepsilon }_{1}} + 1}}{{2{{\varepsilon }_{1}}}}} \right)}}^{2}}k_{z}^{4}{{c}^{4}} + \frac{{{{\varepsilon }_{1}} - 1}}{{2{{\varepsilon }_{1}}}}\omega _{{p0}}^{2}k_{z}^{2}{{c}^{2}}} . \\ \end{gathered} $$

(11)

In the long-wave and short-wave approximations, solution (11) can be presented in the form

$$\omega = \left\{ {\begin{array}{*{20}{l}} {{{k}_{z}}\frac{c}{{\sqrt {{{\varepsilon }_{1}}} }}\left( {1 - \frac{{k_{z}^{2}{{c}^{2}}}}{{2\omega _{{p0}}^{2}}}} \right),\quad {{k}_{z}}c \ll {{\omega }_{{p0}}},} \\ {\frac{{{{\omega }_{{p0}}}}}{{\sqrt {{{\varepsilon }_{1}} + 1} }}\left( {1 - \frac{{\omega _{{p0}}^{2}}}{{8k_{z}^{2}{{c}^{2}}}}\frac{{4\varepsilon _{1}^{2}}}{{{{{({{\varepsilon }_{1}} + 1)}}^{2}}}}} \right),\quad {{k}_{z}}c \gg {{\omega }_{{p0}}}.} \end{array}} \right.$$

(12)

The structure of the wave field (11)—the eigenfunction—is determined by formula (8), in which $B = A$. Using inequalities (10) or formula (11), it is easy to verify that the eigenfunction exponentially tends to zero at infinity. Thus, wave (11) is indeed a surface wave.

4. Another surface wave of interest for what follows is present at the interface between plasmas of different densities. Let the dielectric constants of the plasma at $x < {{L}_{0}}$ and $x > {{L}_{0}}$ be determined, respectively, by formulas

$${{\varepsilon }_{0}} = 1 - \frac{{\omega _{{p0}}^{2}}}{{{{\omega }^{2}}}},\quad {{\varepsilon }_{2}} = 1 - \frac{{\omega _{{p2}}^{2}}}{{{{\omega }^{2}}}}.$$

(13)

We denote $\chi _{2}^{2} = - k_{{x2}}^{2} = k_{z}^{2} - {{\varepsilon }_{2}}{{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}$ and write the solution to Eq. (3) in the form

$${{E}_{z}}(x) = \left\{ {\begin{array}{*{20}{l}} {A\exp ({{\chi }_{0}}x),\quad x < {{L}_{0}},} \\ {B\exp ( - {{\chi }_{2}}x),\quad x > {{L}_{0}}.} \end{array}} \right.$$

(14)

It is easy to see that for the solution to decrease at infinity, i.e., for the existence of a surface wave, it is necessary to satisfy the inequality

$${{\omega }^{2}} < k_{z}^{2}{{c}^{2}} + \omega _{{p\min }}^{2},$$

(15)

where ${{\omega }_{{p\min }}}$ is the lowest of the plasma frequencies. Let for definiteness ${{\omega }_{{p\min }}} = {{\omega }_{{p0}}} < {{\omega }_{{p2}}}$.

Substituting solution (14) into boundary conditions (6), we obtain the dispersion relation of surface waves at the boundary of plasmas of different densities in the usual way

$$\begin{gathered} {{\varepsilon }_{0}}{{\chi }_{2}} + {{\varepsilon }_{2}}{{\chi }_{0}} = 0 \to \left( {1 - \frac{{\omega _{{p0}}^{2}}}{{{{\omega }^{2}}}}} \right)\sqrt {\omega _{{p2}}^{2} + k_{z}^{2}{{c}^{2}} - {{\omega }^{2}}} \\ \, + \left( {1 - \frac{{\omega _{{p2}}^{2}}}{{{{\omega }^{2}}}}} \right)\sqrt {\omega _{{p0}}^{2} + k_{z}^{2}{{c}^{2}} - {{\omega }^{2}}} = 0. \\ \end{gathered} $$

(16)

Only the following solution of Eq. (16) satisfies the inequality (15):

$$\begin{gathered} {{\omega }^{2}} = \frac{1}{2}(\omega _{{p2}}^{2} + \omega _{{p0}}^{2}) + k_{z}^{2}{{c}^{2}} \\ \, - \sqrt {\frac{1}{4}{{{(\omega _{{p2}}^{2} - \omega _{{p0}}^{2})}}^{2}} + k_{z}^{4}{{c}^{4}}} , \\ \end{gathered} $$

(17)

and in the long-wave and short-wave approximations, the solution is determined by the formulas

$${{\omega }^{2}} = \left\{ {\begin{array}{*{20}{l}} \begin{gathered} \omega _{{p0}}^{2} + k_{z}^{2}{{c}^{2}}\left( {1 - \frac{{k_{z}^{2}{{c}^{2}}}}{{\omega _{{p2}}^{2} - \omega _{{p0}}^{2}}}} \right), \hfill \\ k_{z}^{2}{{c}^{2}} \ll \omega _{{p2}}^{2} - \omega _{{p0}}^{2}, \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{(\omega _{{p2}}^{2} + \omega _{{p0}}^{2})}}{2}\left( {1 - \frac{1}{4}\frac{{{{{(\omega _{{p2}}^{2} - \omega _{{p0}}^{2})}}^{2}}}}{{k_{z}^{2}{{c}^{2}}(\omega _{{p2}}^{2} + \omega _{{p0}}^{2})}}} \right), \hfill \\ k_{z}^{2}{{c}^{2}} \gg \omega _{{p2}}^{2} - \omega _{{p0}}^{2}. \hfill \\ \end{gathered} \end{array}} \right.$$

(18)

A distinctive feature of wave (17) is that at ${{k}_{z}} \to 0$ its frequency does not tend to zero but goes to the minimum of the plasma frequencies.

5. Now we proceed to the consideration of the electrodynamic system (1). The general solution of Eq. (3) in the regions $x < 0$, $0 < x < {{L}_{0}}$ and $x > {{L}_{0}}$ is expressed in terms of exponents $\exp [ \pm i{{k}_{{xn}}}(\omega )x]$ or $\exp [ \pm {{\chi }_{n}}(\omega )x]$, where $n = 1,0,2$. The quantities ${{k}_{{xn}}}(\omega )$ and ${{\chi }_{n}}(\omega )$ (they were defined above, see Eq. (5) and immediately after formulas (8) and (13)) are square roots of analytic functions of variables ω and ${{k}_{z}}$. Therefore, a question arises about the correct choice of the square root value. We follow the rule that a value with a non-negative real part is taken when calculating the square root (we used this rule earlier when writing solutions (8) and (14)).

In the region of the dielectric layer, the solution to Eq. (3) is written in the form

$$\begin{gathered} {{E}_{z}}(x) = B\exp [i{{k}_{{x0}}}(\omega )x] + C\exp [ - i{{k}_{{x0}}}(\omega )x], \\ 0 < x < {{L}_{0}}, \\ \end{gathered} $$

(19)

where B and C are constants. Since Eq. (19) contains the values of both branches of the function $\sqrt {k_{{x0}}^{2}(\omega )}$, no problem of choosing a square root arises. If $\operatorname{Re} k_{{x0}}^{2} > 0$, Eq. (19) gives a superposition of two opposite waves propagating along the x-axis. Otherwise, the waves do not propagate, and it is advisable to make the replacement $i{{k}_{{x0}}} \to {{\chi }_{0}}$ in Eq. (19).

Now we consider solutions to Eq. (3) in the regions $x < 0$ and $x > {{L}_{0}}$. When solving the tasks of this work, it is impossible to write the solution to Eq. (3) in the form (see Eqs. (8) and (14))

$${{E}_{z}}(x) = \left\{ {\begin{array}{*{20}{l}} {A\exp ({{\chi }_{1}}x),\quad x < 0,} \\ {D\exp ( - {{\chi }_{2}}x),\quad x > {{L}_{0}}.} \end{array}} \right.$$

(20)

In fact, in accordance with the accepted rule for determining the root, function (20) exponentially tends to zero at ${\text{|}}x{\text{|}} \to \infty$, and therefore describes only surface waves (or waves the amplitude of which is constant). The solution should be written to describe both conventional and radiative surface waves. In accordance with the principle of causality, the radiative wave in the direction of its propagation behaves differently depending on the sign of the imaginary part of the frequency [13, 14]. The wave decays exponentially in the direction of its propagation at $\operatorname{Im} \omega > 0$, and the wave increases exponentially in the direction of its propagation at $\operatorname{Im} \omega < 0$ in a nondissipative medium, which is due to the delay in the transfer of disturbances. We are interested in the second case $\operatorname{Im} \omega < 0$, since, due to radiation from the dielectric layer, the natural vibrations of the layer decay, and therefore the imaginary part of the frequency becomes negative. The solution with the above-mentioned behavior at infinity has the form

$$x < 0{\kern 1pt} :\quad {{E}_{z}}(x) = A\exp [{{\xi }_{1}}(\omega )x],$$

$$\begin{gathered} \,{{\xi }_{1}}(\omega ) = \left\{ {\begin{array}{*{20}{l}} { - {{\chi }_{1}}(\omega )\;\,{\text{or}}\;\, - {\kern 1pt} i{{k}_{{x1}}}(\omega ),\;\;\;\operatorname{Re} (\sqrt {{{\varepsilon }_{1}}} {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}) > {{k}_{z}},} \\ {{{\chi }_{1}}(\omega ),\quad \operatorname{Re} (\sqrt {{{\varepsilon }_{1}}} {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}) < {{k}_{z}},} \end{array}} \right. \\ x > {{L}_{0}}{\kern 1pt} :\quad {{E}_{z}}(x) = D\exp [ - {{\xi }_{2}}(\omega )x], \\ \end{gathered} $$

(21)

$${{\xi }_{2}}(\omega ) = \left\{ {\begin{array}{*{20}{l}} { - {{\chi }_{2}}(\omega )\;\,{\text{or}}\;\; - i{{k}_{{x2}}}(\omega ),\;\;\operatorname{Re} (\sqrt {{{\varepsilon }_{2}}} {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}) > {{k}_{z}},} \\ {{{\chi }_{2}}(\omega ),\;\;\operatorname{Re} (\sqrt {{{\varepsilon }_{2}}} {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c}) < {{k}_{z}}.} \end{array}} \right.$$

If the wave is not radiative in any direction, then function (21) decays exponentially in this direction. If radiation occurs in any direction, then function (21) increases in this direction (at $\operatorname{Im} \omega < 0$) and oscillates.

Substituting solutions Eqs. (19) and (21) into boundary conditions Eq. (6) and excluding constants A, B, C, and D, we obtain the following dispersion relation to determine the complex eigenfrequencies of an electrodynamic system (1):

$$\begin{gathered} (1 - {{p}_{1}})(1 - {{p}_{2}}) - (1 + {{p}_{1}})(1 + {{p}_{2}})\exp (2{{\xi }_{0}}{{L}_{0}}) = 0, \\ {{p}_{{1,2}}} = ({{\varepsilon }_{0}}{{\xi }_{{1,2}}}){\text{/}}({{\varepsilon }_{{1,2}}}{{\xi }_{0}}),\quad {{\xi }_{0}} = {{\chi }_{0}} = ik_{{x0}}^{{}}. \\ \end{gathered} $$

(22)

When deriving Eq. (22), we also obtain the formulas

$$\begin{gathered} B = A\frac{{{{p}_{1}} + 1}}{{2{{p}_{1}}}},\quad C = A\frac{{{{p}_{1}} - 1}}{{2{{p}_{1}}}}, \\ D = \exp ({{\xi }_{2}}{{L}_{0}})[B\exp ({{\xi }_{0}}{{L}_{0}}) + C\exp ( - {{\xi }_{0}}{{L}_{0}})], \\ \end{gathered} $$

(23)

which, together with formulas (19) and (21), determine the longitudinal field distribution in the resonator or the transverse structure of the field in the waveguide.

6. Now we turn to the solution of the dispersion relation (22) for the case when the layer contains the plasma with the dielectric constant Eq. (7), and ${{\varepsilon }_{{1,2}}}$ are real constants. Equation (22) determines the frequencies of two waves – by the number of layer boundaries, these are conventional surface waves, at ${{\varepsilon }_{2}} = {{\varepsilon }_{1}}$ in the frequency region of ${{\omega }^{2}} < \omega _{{p0}}^{2}$. They are called even and odd waves because the field component ${{E}_{z}}(x)$ in these waves is even and odd functions with respect to the middle of the plasma layer [3]. The dispersion relations of these waves at ${{\varepsilon }_{2}} = {{\varepsilon }_{1}}$ follow from Eq. (22) and can be written in the form

$$\frac{{{{\varepsilon }_{1}}{{\xi }_{0}} - {{\varepsilon }_{0}}{{\xi }_{1}}}}{{{{\varepsilon }_{1}}{{\xi }_{0}} + {{\varepsilon }_{0}}{{\xi }_{1}}}} = \pm \exp ({{\xi }_{0}}{{L}_{0}}).$$

(24)

In the limit ${{k}_{z}} \to \infty$ the solutions to Eqs. (24) come to the value ${{\omega }_{{p0}}}{\text{/}}\sqrt {{{\varepsilon }_{1}} + 1}$ (see the second formula (12)), and in the long-wave limit ${{k}_{z}}c \ll {{\omega }_{{p0}}}$ from Eqs. (24) we have

$${{\omega }^{2}} = \frac{{k_{z}^{2}{{c}^{2}}}}{{{{\varepsilon }_{1}}}}\left[ {1 - \frac{{k_{z}^{2}{{c}^{2}}}}{{\omega _{{p0}}^{2}}}{{{[{\text{tanh}}({{\omega }_{{p0}}}{{L}_{0}}{\text{/}}2c)]}}^{{ \pm 2}}}} \right].$$

(25)

In the case of an odd wave, the upper sign should be taken in Eqs. (24) and (25), and the lower sign in the case of an even wave.

At ${{\varepsilon }_{1}} \ne {{\varepsilon }_{2}}$ (let for definiteness ${{\varepsilon }_{1}} > {{\varepsilon }_{2}}$) the wave structure in the frequency range of ${{\omega }^{2}} < \omega _{{p0}}^{2}$ becomes much more complicated.⁴ There are still two waves, but the parity and oddness properties cease to exist. An idea of these waves can be obtained from the following considerations. The quantity $k_{{x0}}^{2} = - k_{z}^{2} -$ $(\omega _{{p0}}^{2} - {{\omega }^{2}}){\text{/}}{{c}^{2}} < - k_{z}^{2}$, therefore when the inequality ${{k}_{z}}{{L}_{0}} \gg 1$ is fulfilled, the dispersion relation (22) is split into two equations

$$\begin{gathered} ({{\varepsilon }_{1}}{{k}_{{x0}}} + {{\varepsilon }_{0}}{{k}_{{x1}}}) = 0, \\ ({{\varepsilon }_{0}}{{k}_{{x2}}} + {{\varepsilon }_{2}}{{k}_{{x0}}}) = 0, \\ \end{gathered} $$

(26)

which, up to the notation, coincide with Eq. (9). Thus, Eqs. (26) determine the dielectric–plasma surface waves at the boundaries $x = 0$ and $x = {{L}_{0}}$, i.e., waves localized at different plasma boundaries. The dispersion of these waves also differs significantly, since there are limiting relations

$$\begin{gathered} {{k}_{z}} \to \infty {\kern 1pt} : \\ \,\omega \to {{\omega }_{{p0}}}\left\{ {\begin{array}{*{20}{c}} {1{\text{/}}\sqrt {{{\varepsilon }_{1}} + 1} ,\;\;\,{\text{boundary wave}}\;\;x = 0,} \\ {1{\text{/}}\sqrt {{{\varepsilon }_{2}} + 1} ,\;\;\,{\text{boundary wave}}\;\;x = {{L}_{0}},} \end{array}} \right. \\ {{k}_{z}} \to 0{\kern 1pt} : \\ \,\omega \to {{k}_{z}}c\left\{ {\begin{array}{*{20}{c}} {1{\text{/}}\sqrt {{{\varepsilon }_{1}}} ,\;\;\,{\text{boundary wave}}\;\;x = 0,} \\ {1{\text{/}}\sqrt {{{\varepsilon }_{2}}} ,\;\;\,{\text{boundary wave}}\;\;x = {{L}_{0}}.} \end{array}} \right. \\ \end{gathered} $$

(27)

Formulas (27) at ${{k}_{z}} \to 0$ follow from Eqs. (26). It is seen from Eqs. (27) that when ${{k}_{z}}$ varies from infinity to zero, the frequency of the boundary wave $x = {{L}_{0}}$ gets inevitably in the region

$${{k}_{z}}c{\text{/}}\sqrt {{{\varepsilon }_{1}}} < \omega < {{k}_{z}}c{\text{/}}\sqrt {{{\varepsilon }_{2}}} ,$$

(28)

i.e., the wave becomes radiative (at ${{\varepsilon }_{1}} > {{\varepsilon }_{2}}$). Such a wave is radiative to the region with a higher dielectric constant, i.e., to the region $x < 0$.

Figure 1 shows dispersion curves $\omega ({{k}_{z}})$ of the surface waves in the considered plasma–dielectric system with the following parameters: ${{\varepsilon }_{1}} = 3$, ${{\varepsilon }_{2}} = 1$, ${{\omega }_{{p0}}}{{L}_{0}}{\text{/}}c = 3$. The dashed line—$\omega = {{k}_{z}}c{\text{/}}\sqrt {{{\varepsilon }_{1}}}$, and dash-dotted line—$\omega = {{k}_{z}}c{\text{/}}\sqrt {{{\varepsilon }_{2}}}$. The complex dispersion curve of the radiative wave of interest is shown by curves 1. The surface wave is the radiative one at ω and ${{k}_{z}}$ belonging to the region of the real part of the dispersion curve 1 enclosed between the dashed and dash-dotted lines. The frequency has a negative imaginary part in the corresponding range of wavenumbers. Curve 2 shows the real dispersion curve of a conventional (non-radiative) surface wave.

Fig. 1.

Dispersion curves of surface waves of a plasma layer adjacent to different dielectrics: (1) radiative wave and (2) non-radiative wave.

Figure 2 shows the field component ${{E}_{z}}$ of the radiative surface wave as a function of the coordinate x calculated in the point of the dispersion curve 1 with coordinates ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 0.5$ and $\omega {\text{/}}{{\omega }_{{p0}}} = 0.437{-} 0.00032{\kern 1pt} i$. The points $x{{\omega }_{{p0}}}{\text{/}}c = 0$ and $x{{\omega }_{{p0}}}{\text{/}}c = 3$ correspond to the boundaries of the plasma layer. It can be seen that the wave field decays in the region of the medium ${{\varepsilon }_{2}}$ ($x{{\omega }_{{p0}}}{\text{/}}c > 3$) as it should be in the case of the surface wave. The field structure corresponds to the surface wave also in the region of the plasma layer ($0 < x{{\omega }_{{p0}}}{\text{/}}c < 3$). However the spatial oscillations of the field amplitude are observed in the region of the medium ${{\varepsilon }_{1}}$ ($x{{\omega }_{{p0}}}{\text{/}}c < 0$) that indicates the radiation of the wave in this region.

Fig. 2.

Field distribution of the radiative wave of the plasma layer adjacent to different dielectrics: R—real part; I—imaginary part.

For comparison, Fig. 3 shows absolute values of the field component ${{E}_{z}}$ for the radiative surface wave (dispersion curve 1 in Fig. 1, point ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 0.5$, $\omega {\text{/}}{{\omega }_{{p0}}} = 0.437{-}0.00032{\kern 1pt} i$) and for the same wave with ω and ${{k}_{z}}$ outside the emission region (28) (dispersion curve 1 in Fig. 1, point ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 1.2$, $\omega {\text{/}}{{\omega }_{{p0}}} = 0.645$), and also the conventional surface wave (dispersion curve 2 in Fig. 1, point ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 0.5$, $\omega {\text{/}}{{\omega }_{{p0}}} =$ 0.2562). One can see an essential difference in the behavior of the field at $x \to - \infty$. In addition, the maximum of the field amplitude for the radiative and conventional surface waves is achieved at different boundaries of the plasma layer. The asymmetry of the fields with respect to the midpoint of the layer $x{{\omega }_{{p0}}}{\text{/}}c = 1.5$ due to the difference in dielectric constants of the left-hand and right-hand media: at ${{\varepsilon }_{1}} = {{\varepsilon }_{2}}$ the field distributions become odd and even with respect to the midpoint of the plasma layer, but there is no radiative surface wave in this case.⁵

Fig. 3.

Absolute values of the field component ${{E}_{z}}$ of waves of the plasma layer adjacent to different dielectrics: (1) radiative surface wave; (2) radiative wave outside the radiation region (28); (3) conventional surface wave.

According to Fig. 1, both waves of the plasma layer are slow, i.e., have a phase velocity less than the speed of light and can be resonantly excited by an electron beam (the excitation mechanism is the forced Cherenkov effect [3]). Of greatest interest is the case when the electron beam propagates over the vacuum region. According to Fig. 3, the beam most effectively excites the radiative surface wave pressed against the plasma-vacuum interface. Depending on the phase velocity of the electromagnetic wave in the dielectric and the velocity of the electron beam, a surface wave can be excited with or without emission into the dielectric.

The field amplitude of the radiative surface wave increases exponentially in the direction in which the wave is radiative. In our case, the field amplitude increases to the left. Figures 2 and 3 demonstrate no increase (see Fig. 6 below), since it becomes noticeable at significantly large distances due to the smallness of the imaginary part of the frequency. A natural question arises about the possibility of exciting a wave with a similar spatial distribution of the field amplitude. In principle, this is possible using an external source (with the corresponding resonant ω and ${{k}_{z}}$) acting in the plasma layer for an infinitely long period of time. If the source functions for a period of time ${{t}_{0}}$, the field distribution shown in Figs. 2 and 3 is established only in the region not exceeding $- c{{t}_{0}} < x < c{{t}_{0}}$, outside of which the amplitude is zero. If an ideal absorber of the electromagnetic energy is placed in the region $x \leqslant {{x}_{0}} < 0$, then the problem of increasing the amplitude of the radiative wave at infinity minus does not arise at all. The surface wave at the plasma–vacuum interface is radiative into the half-space $x < 0$ at the angle α to the z axis determined by the relation ${{\tan \alpha = {{k}_{{x1}}}} \mathord{\left/ {\vphantom {{\tan \alpha = {{k}_{{x1}}}} {{{k}_{z}}}}} \right. \kern-0em} {{{k}_{z}}}} = \sqrt {{{\varepsilon }_{1}}{{{(\operatorname{Re} \omega )}}^{2}}{\text{/}}k_{z}^{2}{{c}^{2}} - 1}$. When ${{k}_{z}}$ increases from zero to the value at which the emission of the surface wave disappears, the angle α decreases from ${\text{arctan}}\sqrt {{{\varepsilon }_{1}} - 1}$ to zero.

Now we obtain analytical formulas for the frequencies of long-wave radiative surface waves. The numerical calculations showed (Fig. 1) that in the case of a dielectric–plasma–vacuum system and in the long-wavelength limit, the real part of the dispersion curve 1 visually merges with the light line $\omega = {{k}_{z}}c$ (dash-dotted straight line), therefore ${{\xi }_{2}}(\omega ) = {{\chi }_{2}}(\omega ) \approx 0$ (see formulas (21)). To use this circumstance, we transform Eq. (22) to the form

$${{\chi }_{2}}(\omega ) = \Phi [{{k}_{z}},{{\xi }_{1}}(\omega ),{{\xi }_{0}}(\omega )]$$

(29)

and substitute into the right-hand part $\omega = {{k}_{z}}c$ that is justified only when the right-hand part of relation (29) is small. As a result of the indicated transformations for the square of the complex frequency, we obtain the following expression:

$${{\omega }^{2}} = k_{z}^{2}{{c}^{2}}\left( {1 - \frac{{k_{z}^{2}{{c}^{2}}}}{{\omega _{{p0}}^{2}}}{{{\left( {\frac{{i({{\varepsilon }_{1}} - 1) + {{\varepsilon }_{1}}\sqrt {({{\varepsilon }_{1}} - 1)k_{z}^{2}{{c}^{2}}{\text{/}}\omega _{{p0}}^{2}} \tanh ({{\omega }_{{p0}}}{{L}_{0}}{\text{/}}c)}}{{i({{\varepsilon }_{1}} - 1) + {{\varepsilon }_{1}}\sqrt {({{\varepsilon }_{1}} - 1)k_{z}^{2}{{c}^{2}}{\text{/}}\omega _{{p0}}^{2}} {\text{coth}}({{\omega }_{{p0}}}{{L}_{0}}{\text{/}}c)}}} \right)}}^{2}}} \right).$$

(30)

When the inequality $k_{z}^{2}{{c}^{2}} \ll \omega _{{p0}}^{2}$ is fulfilled, the second term in the parenthesis in expression (30) is small that is the condition for the applicability of this expression, which is transformed in this case to the form

$$\begin{gathered} \omega = {{k}_{z}}c \\ \, \times \left( {1 - \frac{{k_{z}^{2}{{c}^{2}}}}{{2\omega _{{p0}}^{2}}}\left( {1 + i\frac{{2{{\varepsilon }_{1}}}}{{\sqrt {{{\varepsilon }_{1}} - 1} }}\frac{{{{k}_{z}}c}}{{{{\omega }_{{p0}}}}}{{{\left[ {{\text{sinh}}\left( {\frac{{2{{\omega }_{{p0}}}{{L}_{0}}}}{c}} \right)} \right]}}^{{ - 1}}}} \right)} \right). \\ \end{gathered} $$

(31)

Formulas (30) and (31) in the long-wavelength limit are in good agreement with the results of numerical calculations. The imaginary part of the frequency Eq. (31) is exponentially small at ${{\omega }_{{p0}}}{{L}_{0}}{\text{/}}c > 1$ due to the presence of a hyperbolic sine in Eq. (31).

7. Now we take into account the effect of dissipation. To this end, instead of Eq. (7), we use the following expression for the dielectric constant of the plasma [12]:

$${{\varepsilon }_{0}} = 1 - \frac{{\omega _{{p0}}^{2}}}{{\omega (\omega + i\nu )}},$$

(32)

where ν is the collision frequency. The damping decrements $\operatorname{Im} \omega$ of the radiative surface wave for different frequencies of collisions of plasma particles $\nu$ are shown in Fig. 4.⁶ At $\nu {\text{/}}{{\omega }_{{p0}}} = 0.00001$ (curve 1) the decay is almost entirely due to wave radiation, since the collisional dissipation is still too small to manifest itself. Already at $\nu {\text{/}}{{\omega }_{{p0}}} = 0.0001$ (curve 2) the impact of collisions becomes noticeable. In particular, curve $\operatorname{Im} \omega \left( {{{k}_{z}}} \right)$ acquires a characteristic kink—the wave decay is due only to collisions to the right of the kink point, and the decay is due to both collisions and emission to the left of the kink point. The role of collisions increases at the further increase in $\nu$, and the contribution to the damping decrement from emission is very small at $\nu {\text{/}}{{\omega }_{{p0}}} > 0.0025$. Note that the smaller the ${{\omega }_{{p0}}}{{L}_{0}}{\text{/}}c$ value, the smaller the contribution of collisions to the damping decrement.

Fig. 4.

Damping decrement of the radiative surface wave of   the collisional plasma layer for different collision freq-uencies: $\nu {\text{/}}{{\omega }_{{p0}}} =$ (1) 0.00001, (2) 0.0001, (3) 0.001, and (4) 0.0025.

8. Now we proceed to the consideration of another layered system, in which the dielectric constant of the first medium is ${{\varepsilon }_{1}} = {\text{const}}$, and dielectric constants of the layer $x \in [0,{{L}_{0}}]$ and the second medium are determined by formulas (13). The solution of the field equations in this case is still given by formulas (19), (21), and (23), and the dispersion relation coincides with Eq. (22). Figure 5, which is a complete analog of Fig. 1, shows the results of solving the dispersion relation for the system with the following parameters: ${{\omega }_{{p0}}}{{L}_{0}}{\text{/}}c = 3$, ${{\omega }_{{p2}}}{\text{/}}{{\omega }_{{p0}}} = 2$, ${{\varepsilon }_{1}} = 1$. The structure of the field of the radiative wave calculated at the point of the dispersion curve 1 with coordinates ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 0.5$ and ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{{p0}}}}}} \right. \kern-0em} {{{\omega }_{{p0}}}}} = 1.097{-}0.018{\kern 1pt} i$ is shown in Fig. 6. The increase in the wave amplitude in the emission region of $x < 0$ is clearly visible.

Fig. 5.

Dispersion curves of the surface waves of a plasma layer adjacent to a plasma of another density and vacuum: (1) radiative wave and (2) non-radiative wave.

Fig. 6.

Field distribution of the radiative wave of the plasma layer adjacent to the plasma of another density and vacuum: $R$—real part and I—imaginary part.

For comparison, Fig. 7, which is an analog of Fig. 3, shows absolute values of the field component ${{E}_{z}}$ for the radiative surface wave (dispersion curve 1 in Fig. 5, point ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 0.5$, $\omega {\text{/}}{{\omega }_{{p0}}} = 1.097{-}0.018{\kern 1pt} i$) and for the same wave with ω and ${{k}_{z}}$ outside the emission region (dispersion curve 1 in Fig. 1, point ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 1.6$, $\omega {\text{/}}{{\omega }_{{p0}}} = 1.447$), and also a conventional surface wave (dispersion curve 2 in Fig. 5, point ${{k}_{z}}c{\text{/}}{{\omega }_{{p0}}} = 0.5$, $\omega {\text{/}}{{\omega }_{{p0}}} = 0.437$).

Fig. 7.

Absolute values of the field component ${{E}_{z}}$ of waves of the plasma layer adjacent to the plasma with different density and to vacuum: (1) radiative surface wave, (2) radiative wave outside the radiation region (28), and (3) normal surface wave.

According to Fig. 5, the surface wave of the vacuum–plasma boundary is slow (has a phase velocity less than the speed of light in vacuum) always and can be resonantly excited by an electron beam. A surface wave at the boundary of plasmas of different densities can be resonantly excited by an electron beam only in the nonradiative region. Moreover, as can be seen from Fig. 7, the excitation of this wave by a beam moving in the vacuum region is ineffective because of the vanishingly small field value. A surface wave at the boundary of plasmas of different densities is radiative into vacuum at an angle ${{\tan \alpha = {{k}_{{x1}}}} \mathord{\left/ {\vphantom {{\tan \alpha = {{k}_{{x1}}}} {{{k}_{z}}}}} \right. \kern-0em} {{{k}_{z}}}} =$ $\sqrt {{{{(\operatorname{Re} \omega )}}^{2}}{\text{/}}k_{z}^{2}{{c}^{2}} - 1}$, which varies from $\pi {\text{/}}2$ at small ${{k}_{z}}$ values to zero in the short-wave limit.

9. The last system to be considered here consists of a dielectric with a constant dielectric constant ${{\varepsilon }_{1}} > 1$, vacuum layer ${{\varepsilon }_{0}} = 1$ and plasma half-space ${{\varepsilon }_{2}} = 1 - \omega _{{p2}}^{2}{\text{/}}{{\omega }^{2}}$. This system called the Otto scheme [16] is considered in plasmonics as one of the devices for resonant excitation of a surface wave at the incidence of a plane wave on the plasma boundary. We note that the previously considered two dielectric–plasma–dielectric and dielectric–plasma–plasma systems are of interest in the study of a sliding gas discharge [17, 18] on the surface of a dielectric and a conductor. In the case of a dielectric–vacuum–plasma system, formulas (19) and (21) are still valid, and dispersion relation is preserved Eq. (22). However, the dielectric–vacuum–plasma system has an important feature. There is no surface wave at the dielectric–vacuum interface (the first equation in Eqs. (26) has no solutions). Therefore, there is only one surface wave in the dielectric–vacuum–plasma system, which is a radiative surface wave in a certain ${{k}_{z}}$ range.

First, we consider the results of an approximate analytical solution in the long-wavelength region of wavenumbers. Presenting the solution in the form

$${{\omega }^{2}} = \frac{{k_{z}^{2}{{c}^{2}}}}{{{{\varepsilon }_{1}}}}\left( {1 + \delta } \right),$$

(33)

where $\left| \delta \right| \ll 1$, we substitute it into the dispersion relation Eq. (22). Leaving the smallest orders of smallness in the expansion (22) in δ and ${{k}_{z}}$, we obtain the relation

$$ \pm \sqrt { - \delta } = {{k}_{z}}\left( {c{\text{/}}{{\omega }_{{p2}}} - {{L}_{0}}\left( {{{\varepsilon }_{1}} - 1} \right)} \right).$$

(34)

The sign “+” in Eq. (34) is taken if the wave is not radiative, i.e., $\operatorname{Re} \delta < 0$, and the sign “–” in the opposite situation. In the case of a sufficiently thin vacuum layer with

$${{L}_{0}} < \frac{c}{{{{\omega }_{{p2}}}\left( {{{\varepsilon }_{1}} - 1} \right)}}$$

(35)

the right-hand part in Eq. (34) is positive. In this case the quantity δ is real and negative, i.e., the wave is not radiative into the dielectric region. In the case when the inverse inequality (35) is fulfilled, the right-hand part of Eq. (34) is negative and the equation has no solutions.

Figure 8 shows complex dispersion curves of a single surface wave of the dielectric–vacuum–plasma system calculated for the following parameters: ${{\varepsilon }_{1}} = 3$, ${{\varepsilon }_{0}} = 1$, ${{\omega }_{{p2}}}{{L}_{0}}{\text{/}}c = 0.3$ (curve 1, thin vacuum layer under conditions Eq. (35)) and ${{\omega }_{{p2}}}{{L}_{0}}{\text{/}}c = 3$ (curves 2, thick vacuum layer under conditions opposite to Eq. (35)), dashed line—$\omega = {{k}_{z}}c{\text{/}}\sqrt {{{\varepsilon }_{1}}}$. In the case of a thin vacuum layer, the dispersion curve has no region corresponding to emission into the dielectric, and the surface wave does not decay in a nondissipative system,. If the vacuum layer is thick enough, then there is a region in which the surface wave is radiative into the dielectric and becomes decaying. At the same time, the solution of the dispersion relation is found neither by an approximate analytical method nor numerically in the long-wavelength region that agrees with the results of the analysis of equation (34).

Fig. 8.

Dispersion curves of the surface wave of the dielectric–vacuum–plasma system: (1) vacuum layer of small thickness (${{\omega }_{{p2}}}{{L}_{0}}{\text{/}}c = 0.3$) and (2) thick vacuum layer (${{\omega }_{{p2}}}{{L}_{0}}{\text{/}}c = 3$).

From our point of view, the surface wave in the Otto scheme is most promising for usage in plasma microwave electronics that is discussed below.

10. For the sake of completeness, we consider also the high-frequency radiative waves of a system with a dielectric constant Eq. (1). Obviously, these are conventional bulk waves radiative from the system through one or both layer boundaries. The real part of the frequency of these waves $\omega {\kern 1pt} '$ is determined from the relation $k_{{x0}}^{2} = q_{n}^{2}{{\pi }^{2}}{\text{/}}L_{0}^{2}$, where ${{q}_{n}}\sim n = 1,2, \ldots$. This relation means that a quasi-stationary electromagnetic wave is established in the layer $0 < x < {{L}_{0}}$, i.e., the superposition of counter-propagating waves with different amplitudes. The estimate $\omega {\kern 1pt} '{\kern 1pt} '\sim - {{V}_{{\text{g}}}}{\text{/}}{{L}_{0}}$, where ${{V}_{{\text{g}}}} = \left( {d{{k}_{{x0}}}{\text{/}}d\omega } \right)_{{\omega = \omega {\kern 1pt} '}}^{{ - 1}}$ is the group velocity, can be used for the imaginary part of the frequency. When the layer thickness ${{L}_{0}}$ decreases, the damping decrement ${\text{|}}\omega {\kern 1pt} '{\kern 1pt} '{\text{|}}$ increases and the last estimate becomes inappropriate.

As an example, we consider the radiative waves in the vacuum–plasma–plasma system. The previous two estimates for the frequency give

$$\begin{gathered} \omega {\kern 1pt} ' = \sqrt {\omega _{{p0}}^{2} + q_{n}^{2}{{\pi }^{2}}{{c}^{2}}{\text{/}}L_{0}^{2} + k_{z}^{2}{{c}^{2}}} , \\ \omega {\kern 1pt} '{\kern 1pt} '{\text{/}}\omega {\kern 1pt} '\sim - {{q}_{n}}\pi {{\left( {c{\text{/}}{{L}_{0}}\omega {\kern 1pt} '} \right)}^{2}}. \\ \end{gathered} $$

(36)

Figure 9 shows complex dispersion curves of high-frequency radiative waves obtained by numerically solving dispersion relation (22) for a system with the same parameters as in the case of Fig. 5 but ${{\omega }_{{p1}}}{{L}_{0}}{\text{/}}c = 10$. The increase in the layer thickness in comparison with the previous calculations is due to the tendency to the decrease in the damping decrement of the waves. Four modes $n = 1,\;2,\;3$, and 4 are considered. The larger the number n, the higher the frequency and the larger the damping decrement.

Fig. 9.

Complex dispersion curves of radiative bulk waves in the vacuum–plasma–plasma system.

Figure 10 shows spatial field distributions of the first and third radiative bulk modes. The volumetric and quasi-stationary character of the field distribution inside the layer is clearly visible. The waves are radiative into the $x < 0$ region.

Fig. 10.

Absolute values of the field component ${{E}_{z}}$ of the radiative bulk waves in the vacuum–plasma–plasma system, spatial modes with $n = 1$ and $n = 3$.

11. In conclusion, we consider the above-mentioned possibility of using layered plasma–dielectric systems in the development of new promising electrodynamic systems for plasma microwave electronics. We recall that segments of plasma waveguides with an emitter at one of the ends are used as electrodynamic systems in plasma microwave electronics [3–5]. Plasma emitters (amplifiers and generators) successfully implemented to date use the magnetized plasma of the tubular geometry. Such emitters work in the microwave range, i.e., at frequencies ω on the order of 10¹⁰ rad/s. A distinctive feature of plasma emitters is that their operating frequency is comparable to the electron Langmuir frequency of the plasma filling, i.e., ${{\omega }_{p}}\sim \alpha \times {{10}^{{10}}}$ rad/s, where $\alpha$ is several units.

Currently, the possibility of designing plasma emitters of a significantly higher frequency range—sub-terahertz and even terahertz ranges, i.e., $\omega \sim {{10}^{{11}}}$ rad/s and higher is under discussion. In fact, we are talking about a new direction—plasma terahertz electronics. An increase in the operating frequency inevitably entails the use of a denser plasma, which leads to significant difficulties. Indeed, it is difficult to magnetize a dense plasma, since it requires the creation of a very strong external magnetic field in a sufficiently large volume of the plasma waveguide. Therefore, one has to proceed from the assumption that the plasma will be non-magnetized. But in a non-magnetized plasma, only surface waves are suitable for the Cherenkov excitation by an electron beam⁷ what causes the main difficulties. First, the field of surface waves decays with distance from the plasma boundary the stronger, the higher the frequency. The fact that the field decreases deep into the plasma is even good but its decrease outside the plasma region leads to a sharp decrease in the efficiency of the interaction of the beam with the wave, which is extremely bad.⁸ Second, the wave, the field of which is pressed against the plasma boundary, cannot be efficiently radiative through the end of the waveguide. To overcome these difficulties, waveguides with a layered plasma–dielectric filling can be used.

We consider a circular waveguide of the radius $R$ with the following layered filling:

$$\varepsilon (r) = \left\{ {\begin{array}{*{20}{l}} {{{\varepsilon }_{p}} = 1 - {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}},\quad 0 < r < {{r}_{1}},} \\ {1,\quad {{r}_{1}} < r < {{r}_{2}},} \\ {{{\varepsilon }_{0}} > 1,\quad {{r}_{2}} < r < R.} \end{array}} \right.$$

(37)

Such a system differs little from the dielectric–vacuum–plasma system we considered above (the Otto scheme). In fact, the differences between flat and cylindrical geometries are insignificant in the short-wave range of interest to us ($c{\text{/}}\omega \ll {{r}_{1}}$). Moreover, the penetration depth of the field into the plasma is small at $\omega < {{\omega }_{p}}$; therefore, the singular point $r = 0$ has no effect at all. The waves of the system (37) are not radiative perpendicular to the z axis at the final R value, therefore the wave of this system of interest to us is not an radiative surface wave: it is such a wave only in the limit $R \to \infty$. However, this is not entirely true: in high-current plasma electronics, to reduce the figure of merit of an electrodynamic system, the boundary $r = R$ are coated with a layer of absorber resulting in a non-zero power flux through the lateral surface [19].

The field in the system (37) is determined by formulas (this is the solution to Eq. (3) in cylindrical coordinates)

$$E(r) = \left\{ {\begin{array}{*{20}{l}} {A{{I}_{0}}({{\chi }_{p}}r),\quad r < {{r}_{1}},} \\ {B{{I}_{0}}(\chi r) + C{{K}_{0}}(\chi r),\quad {{r}_{1}} < r < {{r}_{2}},} \\ {D{{F}_{0}}({{\chi }_{0}}r),\quad {{r}_{2}} < r < R,} \end{array}} \right.$$

(38)

where

$$\begin{gathered} {{F}_{0}}({{\chi }_{0}}r) = {{K}_{0}}({{\chi }_{0}}r){{I}_{0}}({{\chi }_{0}}R) - {{I}_{0}}({{\chi }_{0}}r){{K}_{0}}({{\chi }_{0}}R), \\ \chi _{p}^{2} = k_{z}^{2} - \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{p}},\quad {{\chi }^{2}} = k_{z}^{2} - \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}, \\ \chi _{0}^{2} = k_{z}^{2} - \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{0}}, \\ \end{gathered} $$

(39)

and ${{I}_{0}}(x)$ and ${{K}_{0}}(x)$ are Infeld and MacDonald functions. To obtain the dispersion relation and formulas for constant coefficients in expression (38), one should use the boundary conditions that differ from conditions (6) only by replacing x by r. Substituting (38) into the boundary conditions, we have the following system of equations:

$$A{{I}_{0}}({{\chi }_{p}}{{r}_{1}}) = B{{I}_{0}}(\chi {{r}_{1}}) + C{{K}_{0}}(\chi {{r}_{1}}),$$

$$\begin{gathered} A\frac{{{{\varepsilon }_{p}}}}{{{{\chi }_{p}}}}{{I}_{1}}({{\chi }_{p}}{{r}_{1}}) = \frac{1}{\chi }[B{{I}_{1}}(\chi {{r}_{1}}) - C{{K}_{1}}(\chi {{r}_{1}})], \\ B{{I}_{0}}(\chi {{r}_{2}}) + C{{K}_{0}}(\chi {{r}_{2}}) = D{{F}_{0}}({{\chi }_{0}}{{r}_{2}}), \\ \end{gathered} $$

(40)

$$\frac{1}{\chi }[B{{I}_{1}}(\chi {{r}_{2}}) - C{{K}_{1}}(\chi {{r}_{2}})] = \frac{{{{\varepsilon }_{0}}}}{{{{\chi }_{0}}}}D{{F}_{1}}({{\chi }_{0}}{{r}_{2}}),$$

where

$${{F}_{1}}({{\chi }_{0}}r) = - {{K}_{1}}({{\chi }_{0}}r){{I}_{0}}({{\chi }_{0}}R) - {{I}_{1}}({{\chi }_{0}}r){{K}_{0}}({{\chi }_{0}}R).$$

(41)

The desired dispersion relation is obtained by setting the system determinant (40) to zero. Assuming $A = 1$, we determine the coefficients B, C, and D from the first three equations of the system. We do not present all these expressions here because of their cumbersomeness. Here are only the results of preliminary calculations. Without intruding directly into the terahertz region, we consider for now only the possibility of increasing the plasma frequency and radiation frequency by an order of magnitude in comparison with the currently operating plasma emitters. We put ${{\omega }_{p}} = {{10}^{{12}}}$ rad/s, $R = 2$ cm, ${{r}_{1}} = 1.3$ cm, ${{r}_{2}} = 1.5$, and ${{\varepsilon }_{0}} = 2$. Figure 11 shows dispersion curves $\omega ({{k}_{z}})$ of the cylindrical plasma–dielectric waveguide with filling (37). The dash-dotted line shows a straight line $\omega = {{k}_{z}}c$, and the dashed line (merging with the lower dispersion curve) is the straight line $\omega = {{k}_{z}}c{\text{/}}\sqrt {{{\varepsilon }_{0}}}$.

Fig. 11.

Electromagnetic waves of a plasma–dielectric waveguide.

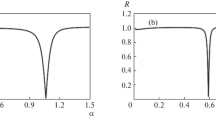
Structures of the component of the electric field strength ${{E}_{z}}(r)$ of the first two (by ascending frequency $\omega = 36.6 \times {{10}^{{10}}}$ rad/s (curve 1) and $\omega =$ 40.4 × 10¹⁰ rad/s (curve 2) at ${{k}_{z}} = 17$ cm^–1) radial waveguide modes are given in Fig. 12.

Fig. 12.

Electromagnetic wave field structures of a plasma–dielectric waveguide.

We note that there are slowed down electromagnetic waves in a waveguide with a dielectric inset also without plasma, which is easy to verify by calculations using system Eq. (40) and formula (38) at ${{\omega }_{p}} = 0$. The question may arise: why do we need plasma at all? Its role is twofold. First, the plasma neutralizes the static charge of the beam [20], which makes it possible to use high-current electron beams in terahertz plasma electronics. Secondly, it can be seen from Fig. 12 that the plasma almost completely screens the electromagnetic field in the $r < {{r}_{1}}$ region. The field is high enough in the vacuum region, and the electron beam should be transmitted there. The highest field is localized in the ${{r}_{2}} < r < R$ region, which is extremely beneficial for efficient radiation of energy from the plasma–dielectric waveguide. For example, it is possible to take a coaxial waveguide with radii ${{r}_{2}}$ and $R$. If the field would be significant in the $r < {{r}_{1}}$ region, it would be much more difficult to match the waveguide with the emitter.

12. In this work, surface waves in layered structures consisting of three regions with different types of frequency dispersion are considered, namely, the dielectric–plasma–vacuum, vacuum–plasma–plasma, and dielectric–vacuum–plasma structures. In the first two structures, each of the interfaces has its own surface wave, which decays with distance from this interface in both directions. The presence of the second boundary leads to the modification of the surface wave. In some cases, this surface wave ceases to be a surface wave in the third medium (which does not form an interface for the surface wave under consideration). That is, it spreads inward, taking energy with it, and thus decays. In the case of the wave decay in time, the boundary condition at infinity in this third medium (radiation condition) is formulated in the form of a propagating wave going to infinity or, which is the same, increasing at infinity. The latter is determined by the delay of disturbances during propagation, i.e., farther outgoing disturbances were radiative earlier, when the amplitude of the decaying wave was higher. In this case, in another half-infinite medium (which forms the interface for the considered surface wave), the radiation condition for a weakly decaying surface wave remains traditional—the perturbation decays at infinity. One of two surface waves (one for each interface) is radiative (in a certain region of wavenumbers) into one of the media and decays even in a nondissipative system. The other remains close to the traditional surface wave at the interface between two semi-infinite media. Taking into account dissipation leads to the additional decay of the surface wave.

The dielectric–vacuum–plasma structure has a feature associated with the absence of a surface wave at the dielectric–vacuum interface. The dispersion dependence of the surface wave at the vacuum–plasma interface differs depending on the thickness of the vacuum layer. For a sufficiently thin vacuum layer, the dispersion curve is similar to the dispersion curve of the surface wave of the dielectric–plasma interface. Starting from a certain thickness of the vacuum layer, the surface wave of the vacuum–plasma interface has a region of wavenumbers when it is radiative into the dielectric and becomes decaying. In this case, the dispersion relation has no solution at all in the form of a surface wave in the long-wavelength region.

The possibilities of exciting surface waves of a layered structure by an electron beam are analyzed for all cases. It is indicated what surface waves are excited most efficiently. The prospects of using surface waves of plasma–dielectric waveguides in plasma microwave electronics in the development of sub-terahertz and terahertz frequency ranges are shown. A separate work will be devoted to a detailed study of the application of radiative surface waves in plasma microwave electronics and their excitation by rectilinear electron beams, in which, in particular, the growth rates of the development of Cherenkov beam instabilities in layered plasma–dielectric structures will be determined.