Abstract
We prove a \(\varGamma \)-convergence result for a class of Ginzburg–Landau type functionals with \({\mathscr {N}}\)-well potentials, where \({\mathscr {N}}\) is a closed and \((k-2)\)-connected submanifold of \({\mathbb {R}}^m\), in arbitrary dimension. This class includes, for instance, the Landau-de Gennes free energy for nematic liquid crystals. The energy density of minimisers, subject to Dirichlet boundary conditions, converges to a generalised surface (more precisely, a flat chain with coefficients in \(\pi _{k-1}({\mathscr {N}})\)) which solves the Plateau problem in codimension k. The analysis relies crucially on the set of topological singularities, that is, the operator \({\mathbf {S}}\) we introduced in the companion paper [17].
Similar content being viewed by others
1 Introduction
Let \(n\geqq 0\), \(k\geqq 2\), \(m\geqq 2\) be integers, and let \(\varOmega \subseteq {\mathbb {R}}^{n+k}\) be a bounded, smooth domain. Let \(\varepsilon >0\) be a small parameter. For \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\), we define the functional
Here, \(f:{\mathbb {R}}^m\rightarrow {\mathbb {R}}\) is a non-negative, continuous potential, whose zero-set \({\mathscr {N}}:= f^{-1}(0)\) is assumed to be a smooth, compact, \((k-2)\)-connected manifold without boundary. The aim of this paper is to understand the asymptotic behaviour of the functionals \(E_\varepsilon \) in the limit as \(\varepsilon \rightarrow 0\), by a \(\varGamma \)-convergence approach. Our analysis builds upon the results obtained in a companion paper, [17].
Functionals of the form (1.1), which describe a kind of penalised k-harmonic map problem (see e.g. [19, 40]), arise naturally in different contexts. A well-known example is the Ginzburg–Landau functional, which corresponds to the case \(k=m=2\) and \(f(u) := (\left| u \right| ^2-1)^2\), so that the zero-set of f is the unit circle, \({\mathscr {N}}= {\mathbb {S}}^{1}\subseteq {\mathbb {R}}^2\). The Ginzburg–Landau functional was originally introduced as a (simplified) model for superconductivity, but has attracted considerable attention in the mathematical community since the pioneering work by Bethuel, Brézis and Hélein [8]. Another example, arising from materials science, is the Landau-de Gennes model for nematic liquid crystals (in the so-called one-constant approximation, see e.g. [23]). In this case, \(k=2\) and the zero-set of f is a real projective plane \({\mathscr {N}}= {\mathbb {R}}\mathrm {P}^2\), whose elements can be interpreted as the preferred configurations for the material. Functionals of the form (1.1) have also applications to mesh generation in numerical analysis, via the so-called cross-field algorithms (see e.g. [18]).
Minimisers of (1.1) subject to a boundary condition
may not satisfy uniform energy bounds, due to topological obstructions carried by the boundary datum v. When this phenomenon occurs, the energy of minimisers is of order \(\left| \log \varepsilon \right| \) (see e.g. [8, 11, 49] in case \(k=2\), \({\mathscr {N}}={\mathbb {S}}^1\)). A similar phenomenon arises for tangent vector fields on a closed manifold, due to the Poincaré-Hopf theorem (see e.g. [34]). The analysis of the Ginzburg–Landau case shows that the energy of minimisers (and other critical points) concentrates, to leading order, on a n-dimensional surface; see e.g. [8, 9, 41, 51]. From a variational viewpoint, the Ginzburg–Landau functional itself can be considered an approximation of an n-dimensional “weighted area” functional, in a sense that can be made precise by \(\varGamma \)-convergence [2, 3, 39, 51]. Therefore, the Ginzburg–Landau functional and its variants have been proposed as tools to construct “weak minimal surfaces” or, more precisely, stationary varifolds of codimension greater than one [4, 9, 42, 48, 52]. Energy concentration results have also been established for Landau-de Gennes minimisers [5, 15, 16, 22, 28, 35, 36, 43, 46]. To our best knowledge, minimisers of functionals associated with more general manifolds \({\mathscr {N}}\), in the logarithmic energy regime, have been studied only in case \(n=0\), \(k=2\) so far [15, 44, 45].
In this paper, we show that the re-scaled functionals \(\left| \log \varepsilon \right| ^{-1} E_\varepsilon \) do converge to an n-dimensional weighted area functional, thus extending the results in [2, 39] to more general potentials f. The key tool is the topological singular set of vector-valued maps, that is, the operator \({\mathbf {S}}\) we introduced in [17], which identifies the appropriate topology of the \(\varGamma \)-convergence. The operator \({\mathbf {S}}\) effectively serves as a replacement, or rather a generalisation, of the distributional Jacobian, which is commonly used when the distinguished manifold is a sphere, \({\mathscr {N}}={\mathbb {S}}^{k-1}\). In order to overcome the algebraic issues that make the distributional Jacobian incompatible with the topology of other manifolds \({\mathscr {N}}\), we work in the setting of flat chains with coefficients in \(\pi _{k-1}({\mathscr {N}})\) [26]. In the context of manifold-constrained problems, the use of flat chains with coefficients in an Abelian group was proposed by Pakzad and Rivière [47] and traces its roots back in the earlier literature on the subject: the very notion of “minimal connection”, introduced by Brezis et al. [13], can be interpreted as the flat norm of the distributional Jacobian.
We state our main \(\varGamma \)-convergence result, Theorem C, in Section 2, after introducing some background and notation. Here, we present an application (Theorem A below) to the asymptotic analysis of minimisers of (1.1) in the limit as \(\varepsilon \rightarrow 0\). We make the following assumptions on the potential f:
-
\(({{\hbox {H}}}_1)\) \(f\in C^1({\mathbb {R}}^m)\) and \(f\geqq 0\).
-
\(({{\hbox {H}}}_2)\) The set \({\mathscr {N}}:= f^{-1}(0)\ne \emptyset \) is a smooth, compact manifold without boundary. Moreover, \({\mathscr {N}}\) is \((k-2)\)-connected, that is \(\pi _0({\mathscr {N}}) = \pi _{1}({\mathscr {N}}) = \ldots = \pi _{k-2}({\mathscr {N}}) = 0\), and \(\pi _{k-1}({\mathscr {N}})\ne 0\). In case \(k=2\), we also assume that \(\pi _1({\mathscr {N}})\) is Abelian.
-
\(({{\hbox {H}}}_3)\) There exists a positive constant \(\lambda _0\) such that \(f(y) \geqq \lambda _0{{\,\mathrm{dist}\,}}^2(y, \, {\mathscr {N}})\) for any \(y\in {\mathbb {R}}^m\).
The assumption \(({\hbox {H}}_2)\) is consistent with the setting of [17] and is satisfied, for instance, when \(k=2\) and \({\mathscr {N}}={\mathbb {S}}^1\) (the Ginzburg–Landau case) or \(k=2\) and \({\mathscr {N}}={\mathbb {R}}\mathrm {P}^2\) (the Landau-de Gennes case). The assumption \(({\hbox {H}}_3)\) is both a non-degeneracy condition around the minimising set \({\mathscr {N}}\) and a growth condition.
Remark 1
We do not expect the assumption \(({\hbox {H}}_3)\) to be sharp. In fact, \(({\hbox {H}}_3)\) may probably be relaxed so as to include potentials that behave as \({{\,\mathrm{dist}\,}}^s(\cdot , \, {\mathscr {N}})\), for some \(s>2\), in a neighbourhood of \({\mathscr {N}}\).
We consider minimisers \(u_{\varepsilon ,\min }\) of (1.1), subject to the boundary condition \(u = v\) on \(\partial \varOmega \). On the boundary datum v, we assume
-
\(({\hbox {H}}_4)\) \(v\in W^{1-1/k,k}(\partial \varOmega ,\,{\mathscr {N}})\) — that is, \(v\in W^{1-1/k,k}(\partial \varOmega ,\, {\mathbb {R}}^m)\) and \(v(x)\in {\mathscr {N}}\) for \({\mathscr {H}}^{n+k-1}\)-a.e. \(x\in \partial \varOmega \).
Under the assumptions \(({\hbox {H}}_1)\)–\(({\hbox {H}}_4)\), the rescaled energy densities

have uniformly bounded mass (see e.g. Remark 9 below; here,
 denotes the Lebesgue measure restricted to \(\varOmega \)). Up to extraction of a subsequence, we may assume that \(\mu _{\varepsilon ,\min }\) converges \({\hbox {weakly}}^*\) (as measures in \({\mathbb {R}}^{n+k}\)) to a non-negative measure \(\mu _{\min }\), as \(\varepsilon \rightarrow 0\). We provide a variational characterisation of \(\mu _{\min }\) in terms of flat chains with coefficients in \((\pi _{k-1}({\mathscr {N}}), \, |\cdot |_*)\), where \(|\cdot |_*\) is a suitable norm, defined in Section 2 below. (For instance, in case \(k=2\) and \({\mathscr {N}}={\mathbb {S}}^1\), \(\left| d \right| _* = \pi \left| d \right| \) for any \(d\in \pi _1({\mathbb {S}}^1)\simeq {\mathbb {Z}}\).) We denote the mass of such a flat chain S by \({\mathbb {M}}(S)\), and the restriction of S to a set E by
denotes the Lebesgue measure restricted to \(\varOmega \)). Up to extraction of a subsequence, we may assume that \(\mu _{\varepsilon ,\min }\) converges \({\hbox {weakly}}^*\) (as measures in \({\mathbb {R}}^{n+k}\)) to a non-negative measure \(\mu _{\min }\), as \(\varepsilon \rightarrow 0\). We provide a variational characterisation of \(\mu _{\min }\) in terms of flat chains with coefficients in \((\pi _{k-1}({\mathscr {N}}), \, |\cdot |_*)\), where \(|\cdot |_*\) is a suitable norm, defined in Section 2 below. (For instance, in case \(k=2\) and \({\mathscr {N}}={\mathbb {S}}^1\), \(\left| d \right| _* = \pi \left| d \right| \) for any \(d\in \pi _1({\mathbb {S}}^1)\simeq {\mathbb {Z}}\).) We denote the mass of such a flat chain S by \({\mathbb {M}}(S)\), and the restriction of S to a set E by  . We have
. We have
Theorem A
Under the assumptions \(({\hbox {H}}_1)\)–\(({\hbox {H}}_4)\), there exists a finite-mass n-chain \(S_{\min }\), with coefficients in \((\pi _{k-1}({\mathscr {N}}),\,|\cdot |_*)\) and support in \({\overline{\varOmega }}\), such that  for any Borel set \(E\subseteq {\mathbb {R}}^{n+k}\). Moreover, \(S_{\min }\) minimises the mass in its homology class—that is, for any \((n+1)\)-chain R with coefficients in \((\pi _{k-1}({\mathscr {N}}),\,|\cdot |_*)\) and support in \({\overline{\varOmega }}\), we have
for any Borel set \(E\subseteq {\mathbb {R}}^{n+k}\). Moreover, \(S_{\min }\) minimises the mass in its homology class—that is, for any \((n+1)\)-chain R with coefficients in \((\pi _{k-1}({\mathscr {N}}),\,|\cdot |_*)\) and support in \({\overline{\varOmega }}\), we have
In other words, in the limit as \(\varepsilon \rightarrow 0\) the energy of minimisers concentrates, to leading order, on the support of a flat chain \(S_{\min }\) that solves a homological Plateau problem. The homology class of \(S_{\min }\) is uniquely determined by the domain \(\varOmega \) and the boundary datum v (that is, \(S_{\min }\) belongs to the class \({\mathscr {C}}(\varOmega , \, v)\) defined by (2.6) below). We stress that Theorem A does not require any topological assumption, such as simply connectedness, on the domain \(\varOmega \). However, the homology class of \(S_{\min }\) does depend on the topology of the domain and it can be described more easily if \(\varOmega \) has a simple topology (see the examples in Section 2 below). On the other hand, the topological assumption \(({\hbox {H}}_2)\) on the manifold \({\mathscr {N}}\) is essential. An analogue of Theorem A in case \(k=2\) and the fundamental group of \({\mathscr {N}}\) is non-Abelian would already be of interest in terms of the applications; manifolds with non-Abelian fundamental group arise quite naturally, for instance, in materials science (e.g., as a model for biaxial liquid crystals). Unfortunately, the very statement of Theorem A does not make sense in the non-Abelian setting, because homology requires the coefficient group to be Abelian. Convergence results in case \(n=0\), \(k=2\) (see e.g. [15, 44]) suggest that the energy concentration set may inherit some minimality properties, even if \(\pi _1({\mathscr {N}})\) is non-Abelian. However, a general convergence result in the non-Abelian setting, along the lines of Theorem A, would presumably require some ‘ad-hoc’ tools from Geometric Measure Theory.
Remark 2
Theorem A characterises the asymptotic behaviour of the energy of minimisers, to leading order:
In some cases, the next-to-leading order term can be characterised, too. For instance, when \(n=0\), \(k=2\), the energy concentrates on a finite number of points and the next-to-leading order term in the energy expansion is a ‘renormalised energy’ which describes the interaction among the singular points. The renormalised energy was introduced, in the Ginzburg–Landau setting, by Bethuel et al. [8] and it was extended very recently by Monteil et al. [44, 45] to more general functionals. This raises the question as to whether a renormalised energy may be derived in case \(n = 0\), \(k > 2\). A higher-order energy expansion for the three-dimensional Ginzburg–Landau functional (\(n = 1\), \(k=2\), \({\mathscr {N}}={\mathbb {S}}^1\)) was obtained by Contreras and Jerrard [21], in a setting where the energy concentrates on a cluster of ‘nearly parallel’ vortex filaments.
We deduce Theorem A from our \(\varGamma \)-convergence result, Theorem C in Section 2. The proof of the \(\varGamma \)-lower bound is based on the same strategy as in [2]. However, the construction of a recovery sequence is rather different from [2]. The main building block, Proposition 4 in Section 3.2, is inspired by the “dipole construction” [6, 7, 13]. Here, dipoles are suitably inserted into a non-constant and, in fact, singular background.
As an auxiliary result, we prove the following lower energy bound, which may be of independent interest.
Proposition B
Suppose that \(({\hbox {H}}_1)\)–\(({\hbox {H}}_4)\) hold. Let \(\varOmega \subseteq {\mathbb {R}}^k\) be a bounded, Lipschitz domain that is homeomorphic to a ball. Then, for any \(u\in W^{1,k}(\varOmega ,\,{\mathbb {R}}^m)\) such that \(u=v\) on \(\partial \varOmega \), it holds that
where \(\sigma \in \pi _{k-1}({\mathscr {N}})\) is the homotopy class of v and C is a positive constant that depends only on \(\varOmega \), v.
If \(\varOmega \subseteq {\mathbb {R}}^k\) is homeomorphic to a ball and \(v\in W^{1-1/k,k}(\partial \varOmega , \, {\mathscr {N}})\), the homotopy class of v can be defined as in [14]. In the Ginzburg–Landau case, this inequality was proved by Sandier [50] (with \(k=2\)) and Jerrard [38]; for the Landau-de Gennes functional, see e.g. [5, 16]. The proof of Proposition B in contained in Appendix C (in fact, a slightly stronger statement is given there).
Remark 3
In case \(\sigma =0\), Proposition B does not provide any information. However, there could be critical points of the functional \(E_\varepsilon \) whose energy diverges logaritmically even if the boundary datum is homotopically trivial. In other words, energy concentration may happen not only because of global topological contraints, but also for other reasons, such as symmetry. See, for instance, Ignat et al. [37] for an analysis of two-dimensional Landau-de Gennes solutions (\(n = 0\), \(k=2\), \({\mathscr {N}}={\mathbb {R}}\mathrm {P}^2\)).
The paper is organised as follows: in Section 2 we recall some notation from [17] and we state the main \(\varGamma \)-convergence result, Theorem C. We prove the \(\varGamma \)-upper bound first, in Section 3, and give the proof of the \(\varGamma \)-lower bound in Section 4. Theorem A is deduced from Theorem C in Section 5. A series of appendices, with proofs of technical results, completes the paper.
2 Setting of the Problem and Statement of the \(\varGamma \)-convergence Result
Throughout the paper, we will write \(A\lesssim B\) as a shorthand for \(A\leqq C B\), where C is a positive constant that only depends on n, k, f, \({\mathscr {N}}\), and \(\varOmega \). If \(F\subseteq {\mathbb {R}}^{n+k}\) is a rectifiable set of dimension d and \(u\in W^{1,k}_{\mathrm {loc}}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\) we will write
Additional notation will be set later on. Throughout the paper, we assume that \(({\hbox {H}}_1)\)–\(({\hbox {H}}_4)\) are satisfied.
2.1 Choice of the Norm on \(\pi _{k-1}({\mathscr {N}})\)
Under the assumption \(({\hbox {H}}_2)\), the group \(\pi _{k-1}({\mathscr {N}})\) is Abelian (and we use additive notation for the group operation). We recall that a function \(|\cdot |:\pi _{k-1}({\mathscr {N}})\rightarrow [0, \, +\infty )\) is called a norm if it satisfies the following properties:
-
(i)
\(|\sigma | = 0\) if and only if \(\sigma =0\)
-
(ii)
\(|-\sigma | = |\sigma |\) for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\)
-
(iii)
\(|\sigma _1 + \sigma _2|\leqq |\sigma _1|+|\sigma _2|\) for any \(\sigma _1\), \(\sigma _2\in \pi _{k-1}({\mathscr {N}})\).
As in [17], we assume that the norm satisfies
that is, \(|\cdot |\) induces the discrete topology on \(\pi _{k-1}({\mathscr {N}})\).
Remark 4
We do not require that \(|n\sigma | = n|\sigma |\) for any \(n\in {\mathbb {N}}\), \(\sigma \in \pi _{k-1}({\mathscr {N}})\); this is consistent with the theory of flat chains as developed in [26, 55].
While the results of [17] hold for any norm on \(\pi _{k-1}({\mathscr {N}})\) that satifies (2.1), Theorem A only holds for a specific choice of the norm. Let us define such a norm, following the approach in [20, Chapter 6]. A natural attempt, motivated by the analogy with the functional (1.1), is to define
for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\). Here \(\nabla _{\top }\) denotes the tangential gradient on \({\mathbb {S}}^{k-1}\), that is, the restriction of the Euclidean gradient \(\nabla \) to the tangent plane to the sphere. Due to the compact embedding \(W^{1,k}({\mathbb {S}}^{k-1}, {\mathscr {N}})\hookrightarrow C({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\), the set \(W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap \sigma \) is sequentially \(W^{1,k}\)-weakly closed and hence, the infimum in (2.2) is achieved. However, the function \(E_{\min }\) fails to be a norm, in general, because it may not satisfy the triangle inequality (iii). To overcome this issue, for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\) we define
Proposition 1
The function \(|\cdot |_*\) is a norm on \(\pi _{k-1}({\mathscr {N}})\) that satisfies (2.1) and \(\left| \sigma \right| _*\leqq E_{\min }(\sigma )\) for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\). The infimum in (2.3) is achieved, for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\). Moreover, the set
is finite, and for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\) there exists a decomposition \(\sigma = \sum _{i=1}^q\sigma _i\) such that \(|\sigma |_* = \sum _{i=1}^q|\sigma _i|_*\) and \(\sigma _i\in {\mathfrak {S}}\) for any i.
The proof of this result will be given in Appendix A. In case \({\mathscr {N}}={\mathbb {S}}^{k-1}\), the group \(\pi _{k-1}({\mathbb {S}}^{k-1})\) is isomorphic to \({\mathbb {Z}}\), \({\mathfrak {S}}= \{-1, \, 0, \, 1\}\), and for any \(d\in {\mathbb {Z}}\) we have
where \({\mathscr {L}}^k(B^k_1)\) is the Lebesgue measure of the unit ball in \({\mathbb {R}}^k\) and \(\left| d \right| \) is the standard absolute value of d (see Example A.1).
Remark 5
When \(k=2\), the infimum in (2.2) is achieved by a minimising geodesic in the homotopy class \(\sigma \), parametrised by multiples of arc-length. As a consequence, \(E_{\min }(\sigma )\) is — up to a multiplicative constant — the length squared of a minimising geodesic in the class \(\sigma \), and \(E_{\min }^{1/2}\) is a norm on \(\pi _1({\mathscr {N}})\). However, \(E_{\min }^{1/2}\) may not coincide with \(|\cdot |_*\), not even up to a multiplicative constant. For instance, when \({\mathscr {N}}\) is the flat torus, \({\mathscr {N}}= {\mathbb {R}}^2/(2\pi {\mathbb {Z}})^2 = {\mathbb {S}}^1\times {\mathbb {S}}^1\), we have \(\pi _1({\mathscr {N}}) \simeq {\mathbb {Z}}\times {\mathbb {Z}}\),
for any \((d_1, \, d_2)\in {\mathbb {Z}}\times {\mathbb {Z}}\). We did not investigate whether, for arbitrary \(k> 2\) and \({\mathscr {N}}\), \(E_{\min }^{1/k}\) is a norm on \(\pi _{k-1}({\mathscr {N}})\).
2.2 Notation for Flat Chains
We follow the notation adopted in [17, Section 2]. In particular, we denote by \({\mathbb {F}}_q({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\) the space of flat q-dimensional chains in \({\mathbb {R}}^{n+k}\) with coefficients in the normed group \((\pi _{k-1}({\mathscr {N}}), \, |\cdot |_*)\). We denote the flat norm by \({\mathbb {F}}\), and the mass by \({\mathbb {M}}\). The support of a flat chain S is denoted by \({{\,\mathrm{spt}\,}}S\). The restriction of S to a Borel set \(E\subseteq {\mathbb {R}}^{n+k}\) is denoted  . Given \(f\in C^1({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^{n+k})\), we write \(f_{*}S\) for the push-forward of S through f. (The reader is referred e.g. to [26, 55] for the definitions of these objects.)
. Given \(f\in C^1({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^{n+k})\), we write \(f_{*}S\) for the push-forward of S through f. (The reader is referred e.g. to [26, 55] for the definitions of these objects.)
Given a domain \(\varOmega \subseteq {\mathbb {R}}^{n+k}\), we define \({\mathbb {F}}_q({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) as the set of flat chains such that \({{\,\mathrm{spt}\,}}S\subseteq {\overline{\varOmega }}\). We also define \({\mathbb {M}}_q({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) as the set of flat chains \(S\in {\mathbb {F}}_q({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) such that \({\mathbb {M}}(S)<+\infty \). We will say that two chains \(S_1\), \(S_2\in {\mathbb {M}}_q({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) are cobordant in \({\overline{\varOmega }}\) if and only if there exists a finite-mass chain \(R\in {\mathbb {M}}_{q+1}({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) such that
In this case, we write \(S_1\sim _{{\overline{\varOmega }}} S_2\). The cobordism in \({\overline{\varOmega }}\) defines an equivalence relation on the space of finite-mass chains, \({\mathbb {M}}_q({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\). Moreover, due to the isoperimetric inequality (see e.g. [25, 7.6]), cobordism classes are closed with respect to the \({\mathbb {F}}\)-norm.
The group of flat q-chains relative to a domain \(\varOmega \subseteq {\mathbb {R}}^{n+k}\) is defined as the quotient
To avoid notation, the equivalence class of a chain \(S\in {\mathbb {F}}_q({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\) will still be denoted by S. The quotient norm may equivalently be rewritten as

(see [17, Section 2.1]).
For any \(S\in {\mathbb {F}}_n(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\) and \(R\in {\mathbb {F}}_k({\mathbb {R}}^{n+k}; \, {\mathbb {Z}})\) such that \({\mathbb {M}}(R) + {\mathbb {M}}(\partial R)<+\infty \), \({{\,\mathrm{spt}\,}}R \subseteq \varOmega \), and \({{\,\mathrm{spt}\,}}(\partial S)\cap {{\,\mathrm{spt}\,}}R = {{\,\mathrm{spt}\,}}S\cap {{\,\mathrm{spt}\,}}(\partial R) = \emptyset \), we denote the intersection index of S and R (as defined in [17, Section 2.1]) by \({\mathbb {I}}(S, \, R)\in \pi _{k-1}({\mathscr {N}})\). For instance, if S is carried by a n-polyhedron with constant multiplicity \(\sigma \in \pi _{k-1}({\mathscr {N}})\), R is carried by a k-polyhedron with unit multiplicity and (the supports of) S, R intersect transversally, then \({\mathbb {I}}(S, \, R) = \pm \sigma \), where the sign depends on the relative orientation of S and R. The intersection index \({\mathbb {I}}\) is a bilinear pairing and satisfies suitable continuity properties (see e.g. [17, Lemma 8]).
2.3 The Topological Singular Set
In [17], we constructed the topological singular set, \({\mathbf {S}}_y(u)\), for \(u\in (L^\infty \cap W^{1,k-1})(\varOmega , \, {\mathbb {R}}^m)\) and \(y\in {\mathbb {R}}^m\). Here, we introduce a variant of that construction and define \({\mathbf {S}}_y(u)\) in case \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\), without assuming that \(u\in L^\infty (\varOmega , \, {\mathbb {R}}^m)\). In both cases, the operator \({\mathbf {S}}_y(u)\) generalises the Jacobian determinant of u — and indeed, the Jacobian of \(u:{\mathbb {R}}^k\rightarrow {\mathbb {R}}^k\) is well-defined in a distributional sense if \(u\in (L^\infty \cap W^{1,k-1})({\mathbb {R}}^k, \, {\mathbb {R}}^k)\), and in a pointwise sense if \(u\in W^{1,k}({\mathbb {R}}^k, \, {\mathbb {R}}^k)\). The starting point of the construction is the following topological property:
Proposition 2
([30]). Under the assumption \(({\hbox {H}}_2)\), there exist a compact, polyhedral complex \({\mathscr {X}}\subseteq {\mathbb {R}}^m\) of dimension \(m-k\) and a smooth map \(\varrho :{\mathbb {R}}^m{\setminus }{\mathscr {X}}\rightarrow {\mathscr {N}}\) such that \(\varrho (z) = z\) for any \(z\in {\mathscr {N}}\), and
for any \(z\in {\mathbb {R}}^m{\setminus }{\mathscr {X}}\) and some constant \(C=C({\mathscr {N}}, \, m, \, {\mathscr {X}})>0\).
This result, or variants thereof, was proved in [30, Lemma 6.1], [12, Proposition 2.1], [33, Lemma 4.5]. While in our previous paper [17] we required \({\mathscr {X}}\) to be a smooth complex, in this paper we require \({\mathscr {X}}\) to be polyhedral, because this will simplify some technical points in the proofs.
Let us fix once and for all a polyhedral complex \({\mathscr {X}}\) and a map \(\varrho \), as in Proposition 2. Let \(\delta ^*\in (0, \, {{\,\mathrm{dist}\,}}({\mathscr {N}}, \, {\mathscr {X}}))\) be fixed, and let \(B^* := B^m(0, \, \delta ^*)\subseteq {\mathbb {R}}^m\). Let*
be the set of Lebesgue-measurable maps \(S:B^*\rightarrow {\mathbb {F}}_{n}(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\), respectively \(S:B^*\rightarrow {\mathbb {F}}_{n}({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) (we use the notation \(y\in B^*\mapsto S_y\) in both cases), such that
The sets Y, \({\overline{Y}}\) are complete normed moduli, with the norms \(\Vert \cdot \Vert _{Y}\), \(\Vert \cdot \Vert _{{\overline{Y}}}\) respectively. The space \({\mathbb {F}}_{n}(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\), respectively \({\mathbb {F}}_{n}({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\), embeds canonically into Y, respectively \({\overline{Y}}\). If need be, we will identify a chain \(S\in {\mathbb {F}}_{n}({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) with an element of \({\overline{Y}}\), i.e. the constant map \(y\mapsto S\).
By [17, Theorem 3.1], there exists a unique operator
that is continuous (if \(u_j\rightarrow u\) strongly in \(W^{1,k-1}(\varOmega )\) and \(\sup _j\Vert u_j\Vert _{L^\infty (\varOmega )}<+\infty \), then \({\mathbf {S}}(u_j)\rightarrow {\mathbf {S}}(u)\) in Y) and satisfies
-
\(({\hbox {P}}_0)\) for any smooth u, a.e. \(y\in B^*\) and any \(R\in {\mathbb {F}}_{k}({\mathbb {R}}^{n+k}; \, {\mathbb {Z}})\) such that \({\mathbb {M}}(R)+{\mathbb {M}}(\partial R)<+\infty \), \({{\,\mathrm{spt}\,}}(R)\subseteq \varOmega \), \({{\,\mathrm{spt}\,}}(\partial R)\subseteq \varOmega {\setminus }{{\,\mathrm{spt}\,}}{\mathbf {S}}_y(u)\), there holds
$$\begin{aligned} {\mathbb {I}}\left( {\mathbf {S}}_y(u), \, R\right) = \text {homotopy class of } \varrho \circ \left( u - y\right) \text { on } \partial R. \end{aligned}$$
We recall that \({\mathbb {I}}\) denotes the intersection index, defined as in [17, Section 2.1].
Proposition 3
There exists a (unique) continuous operator
that satisfies \(({\hbox {P}}_0)\) and the following properties:
-
\(({\hbox {P}}_1)\) For any \(u\in (L^\infty \cap W^{1,k})(\varOmega , \, {\mathbb {R}}^m)\) and a.e \(y\in B^*\), \({\overline{{\mathbf {S}}}}_y(u) = {\mathbf {S}}_y(u)\) — more precisely, the chain \({\overline{{\mathbf {S}}}}_y(u)\) belongs to the equivalence class \({\mathbf {S}}_y(u)\in {\mathbb {F}}_{n}(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\).
-
\(({\hbox {P}}_2)\) For any \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) and any Borel subset \(E\subseteq {\overline{\varOmega }}\), there holds

-
\(({\hbox {P}}_3)\) If \(u_0\), \(u_1\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) are such that \(u_{0|\partial \varOmega } = u_{1|\partial \varOmega }\in W^{1-1/k, k}(\partial \varOmega , \, {\mathscr {N}})\) (in the sense of traces), then \({\overline{{\mathbf {S}}}}_{y_0}(u_0) \sim _{{\overline{\varOmega }}} {\overline{{\mathbf {S}}}}_{y_1}(u_1)\) for a.e. \(y_0\), \(y_1\in B^*\).
The proof of Proposition 3 will be given in Apprendix B. Taking account of \(({\hbox {P}}_1)\), we abuse of notation and write \({\mathbf {S}}\) instead of \({\overline{{\mathbf {S}}}}\) from now on. As a consequence of \(({\hbox {P}}_3)\), for any boundary datum \(v\in W^{1-1/k, k}(\partial \varOmega , \, {\mathscr {N}})\) there exists a unique cobordism class \({\mathscr {C}}(\varOmega , \, v)\subseteq {\mathbb {M}}_n({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) such that
for any \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) with trace v on \(\partial \varOmega \) and for a.e. \(y\in B^*\).
2.4 The \(\varGamma \)-convergence Result
The main result of this paper is a generalisation of [2, Theorem 5.5]. We let \(W^{1,k}_v(\varOmega , \, {\mathbb {R}}^m)\) denote the set of maps \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) such that \(u = v\) on \(\partial \varOmega \) (in the sense of traces).
Theorem C
Suppose that the assumptions \(({\hbox {H}}_1)\)–\(({\hbox {H}}_4)\) are satisfied. Then, the following properties hold:
-
(i)
Compactness and lower bound. Let \((u_\varepsilon )_{\varepsilon > 0}\) be a sequence in \(W^{1,k}_v(\varOmega , \, {\mathbb {R}}^m)\) that satisfies \(\sup _{\varepsilon >0}\left| \log \varepsilon \right| ^{-1} E_\varepsilon (u_\varepsilon ) < +\infty \). Then, there exists a (non relabelled) countable subsequence and a finite-mass chain \(S\in {\mathscr {C}}(\varOmega , \, v)\) such that \({\mathbf {S}}(u_\varepsilon )\rightarrow S\) in \({\overline{Y}}\) and, for any open subset \(A\subseteq {\mathbb {R}}^{n+k}\),

-
(ii)
Upper bound. For any finite-mass chain \(S\in {\mathscr {C}}(\varOmega , \, v)\), there exists a sequence \((u_\varepsilon )\) in \(W^{1,k}_v(\varOmega , \, {\mathbb {R}}^m)\) such that \({\mathbf {S}}(u_\varepsilon )\rightarrow S\) in \({\overline{Y}}\) and
$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \frac{E_\varepsilon (u_\varepsilon )}{\left| \log \varepsilon \right| } \leqq {\mathbb {M}}(S). \end{aligned}$$
Theorem A follows almost immediately from Theorem C, combined with general properties of the \(\varGamma \)-convergence and standard facts in measure theory. There is a variant of Theorem C for the problem with no boundary conditions, which is analogous to [2, Theorem 1.1]. We will say that a chain S is a finite-mass, n-dimensional relative boundary if it has form  , where \(R\in {\mathbb {M}}_{n+1}({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\) is such that \({\mathbb {M}}(\partial R)<+\infty \).
, where \(R\in {\mathbb {M}}_{n+1}({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\) is such that \({\mathbb {M}}(\partial R)<+\infty \).
Proposition D
Suppose that the assumptions \(({\hbox {H}}_1)\)–\(({\hbox {H}}_3)\) are satisfied. Then, the following properties hold:
-
(i)
Compactness and lower bound. Let \((u_\varepsilon )_{\varepsilon > 0}\) be a sequence in \(W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) that satisfies \(\sup _{\varepsilon >0}\left| \log \varepsilon \right| ^{-1} E_\varepsilon (u_\varepsilon ) < +\infty \). Then, there exists a (non relabelled) countable subsequence and a finite-mass, n-dimensional relative boundary S such that \({\mathbf {S}}(u_\varepsilon )\rightarrow S\) in Y and, for any open subset \(A\subseteq \varOmega \),
-
(ii)
Upper bound. For any finite-mass, n-dimensional relative boundary S, there exists a sequence \((u_\varepsilon )\) in \(W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) such that \({\mathbf {S}}(u_\varepsilon )\rightarrow S\) in Y and
$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \frac{E_\varepsilon \left( u_\varepsilon \right) }{\left| \log \varepsilon \right| } \leqq {\mathbb {M}}(S). \end{aligned}$$
Proposition D is not quite informative as it stands, because minimisers of the functional (1.1) under no boundary conditions are constant. However, since \(\varGamma \)-convergence is stable with respect to continuous perturbations, Proposition D can be extended to non-trivial minimisation problems with lower-order terms or under integral constraints, as long as these are compatible with the topology of \(\varGamma \)-convergence.
2.5 A Few Examples
We illustrate our results by means of a few simple examples. If \(A\subseteq {\mathbb {R}}^{n+k}\) is an n-dimensional polyhedral (or smooth) set, with a given orientation, the unit-multiplicity chain carried by A will be denoted \(\llbracket A\rrbracket \in {\mathbb {M}}_{n}({\mathbb {R}}^{n+k}; \, {\mathbb {Z}})\).
Example 2.1
First, we suppose the domain is the unit ball in the critical dimension, i.e. \(n=0\) and \(\varOmega = B^k\), and consider the target \({\mathscr {N}}={\mathbb {S}}^{k-1}\subseteq {\mathbb {R}}^k\). We need to identify the class \({\mathscr {C}}(\varOmega , \, v)\) defined by (2.6). For simplicity, suppose that the boundary datum \(v:\partial B^k\rightarrow {\mathbb {S}}^{k-1}\) is smooth, of degree d. (General data \(v\in W^{1-1/k,k}(\partial B^k, \, {\mathbb {S}}^{k-1})\) could also be considered, by appealing to Brezis and Nirenberg’s theory of the degree in VMO, [14]). Let \(u:B^k\rightarrow {\mathbb {R}}^k\) be any smooth extension of v. Let \(y\in {\mathbb {R}}^k\) be a regular value for u (i.e., \(\det \nabla u(x) \ne 0\) for any \(x\in u^{-1}(y)\)) such that \(\left| y \right| <1\). Then, the inverse image \(u^{-1}(y)\) consists of a finite number points. Let \(r>0\) be a sufficiently small radius. By definition of \({\mathbf {S}}\), we have
where d(x) is the degree of the map \((u - y)/|u - y|:\partial B_r(x)\rightarrow {\mathbb {S}}^{k-1}\). The class \({\mathscr {C}}(\varOmega , \, v)\) consists of all and only the chains that differ from \({\mathbf {S}}_y(u)\) by a boundary. It is not difficult to characterise \({\mathscr {C}}(\varOmega , \, v)\) using the following topological property, which holds true for any (normed, Abelian) coefficient group \({\mathbf {G}}\) and any connected, open set \(D\subseteq {\mathbb {R}}^d\).
Fact
Let T be a 0-chain of the form \(T = \sum _{i=1}^q\sigma _j\llbracket z_i\rrbracket \), for \(z_j\in {\bar{D}}\), \(\sigma _j\in {\mathbf {G}}\). Then, there exists \(R\in {\mathbb {M}}_1({\bar{D}}; \, {\mathbf {G}})\) such that \(\partial R = T\) if and only if \(\sum _{j=1}^q \sigma _j = 0\).
For a proof of this fact, see e.g. [31, Proposition 2.7]. Now, Brouwer’s theory of the degree (or Property \(({\hbox {P}}_0)\) above) implies that
therefore
In agreement with the Ginzburg–Landau theory, mass-minimising chains in \({\mathscr {C}}(\varOmega , \, v)\) consist of exactly |d| points, with multiplicities equal to 1 or \(-1\) according to the sign of d. This argument extends to more general manifolds \({\mathscr {N}}\), with no essential change; we obtain
where \(\sigma \in \pi _{k-1}({\mathscr {N}})\) is the homotopy class of the boundary datum \(v:\partial B^k\rightarrow {\mathscr {N}}\). Mass-minimising chains in \({\mathscr {C}}(\varOmega , \, v)\) have the form \(\sum _{j = 1}^q \sigma _j\llbracket z_j\rrbracket \), where the multiplicities \(\sigma _j\) belong to the set \({\mathfrak {S}}\) defined in (2.4) and satisfy \(\sum _{j = 1}^q E_{\min }(\sigma _j) = \left| \sigma \right| _*\).
Example 2.2
Next, we discuss the case \(n=1\), \(\varOmega = B^{k+1}\). Suppose that the boundary datum \(v:\partial B^{k+1}\rightarrow {\mathscr {N}}\) is smooth, except for finitely many isolated singularities at the points \(x_1\), ..., \(x_p\). Let \(D_1\), ..., \(D_p\) be pairwise-disjoint closed geodesic disks in \(\partial B^{k+1}\), centred at the points \(x_1\), ..., \(x_p\). Each \(D_i\) is given the orientation induced by the outward-pointing unit normal to \(B^{k+1}\). Using orientation-preserving coordinate charts, we may identify \(v_{|\partial D_i}:\partial D_i\rightarrow {\mathscr {N}}\) with a map \({\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\); the homotopy class of the latter is an element of \(\pi _{k-1}({\mathscr {N}})\), which we denote \(\sigma _i\). The coefficents \(\sigma _i\) must satisfy the topological constraint
Indeed, let \(D^+\subseteq \partial B^{k+1}\) be a small geodesic disk that does not contain any singular point \(x_i\), and let \(D^- := \partial B^{k+1}{\setminus } D^+\). Topologically, \(D^-\) is a disk which contains all the singular points of v; therefore, the homotopy class of v restricted to \(\partial D^-\) is the sum of all the \(\sigma _i\)’s above. However, the homotopy class of v on \(\partial D^+\) must be trivial, because v is smooth in \(D^+\). Thus, (2.7) follows.
We consider the chain
Thanks to (2.7), \({\mathbf {S}}^{\mathrm {bd}}(v)\) is the boundary of some 1-chain supported in \({\bar{B}}^{k+1}\). More precisely, let \(u\in W^{1,k}(B^{k+1}, \, {\mathbb {R}}^m)\) be any extension of v. The results of [17] (see, in particular, Proposition 1, Proposition 3 and Lemma 18) imply that
for a.e. \(y\in {\mathbb {R}}^m\) of norm small enough. Chains in the same homology class have the same boundary; therefore, for any chain \(T\in {\mathscr {C}}(\varOmega , \, v)\), there holds \(\partial T = {\mathbf {S}}^{\mathrm {bd}}(v)\). Conversely, two chains in \({\bar{B}}^{k+1}\) that have the same boundary belong to same homology class (relative to \({\bar{B}}^{k+1}\)), because the domain \({\bar{B}}^{k+1}\) is contractible. As a consequence, we have
In particular, mass-minimising chains in \({\mathscr {C}}(\varOmega , \, v)\) will be carried by a finite union of segments, connecting the singularities of the boundary datum according to their multiplicities. In case \({\mathscr {N}}={\mathbb {S}}^{k-1}\), such union of segments realises a ‘minimising connection’, in the sense of Brezis et al. [13]. For \(k=2\) and \({\mathscr {N}}={\mathbb {R}}\mathrm {P}^2\), the condition (2.7) implies that v has an even number of non-orientable singularities; mass-minimising chains connect the non-orientable singularities in pairs.
The characterisation (2.8) extends to general data \(v\in W^{1-1/k,k}(\partial B^{k+1}, \, {\mathscr {N}})\), provided that we define \({\mathbf {S}}^{\mathrm {bd}}(v)\) in a suitable way (see [17, Section 3]). It also extend to more general domains \(\varOmega \subseteq {\mathbb {R}}^{n+k}\), so long as the n-th homology group \(H_n(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\) is trivial.
Example 2.3
If the domain has a non-trivial topology, then \({\mathscr {C}}(\varOmega , \, v)\) may contain non-trivial chains even if the boundary datum is smooth. For instance, take \(n=1\), \(k=2\), \({\mathscr {N}}={\mathbb {S}}^1\). Let \(\varOmega \subseteq {\mathbb {R}}^3\) be a solid torus of revolution, defined as the image of the map \(\varPsi :B^2\times {\mathbb {R}}\rightarrow {\mathbb {R}}^3\),
We consider the smooth map \(u:\varOmega \rightarrow {\mathbb {R}}^2\) given by \(u(\varPsi (x, \, \theta )) := x\) for \((x, \, \theta )\in B^2\times {\mathbb {R}}\). The trace of u at the boudary, v, takes its values in \({\mathbb {S}}^1\) and its restriction on each meridian curve of the torus \(\partial \varOmega \) has degree 1. Therefore, \({\mathscr {C}}(\varOmega , \, v)\) is the homology class of \(\llbracket u^{-1}(0) \rrbracket \in {\mathbb {M}}_1({\overline{\varOmega }}; \, {\mathbb {Z}})\), where \(u^{-1}(0)\) is the zero-set of u (i.e. the circle \(\varPsi (\{(0, \, 0)\}\times {\mathbb {R}})\)) with the orientation induced by \(\varPsi \). The elements of \({\mathscr {C}}(\varOmega , \, v)\) can be characterised by means of the intersection index \({\mathbb {I}}\). More precisely, let D be the closure of \(\varPsi (B^2\times \{0\})\). D is a 2-disk in the plane orthogonal to \((0, \, 1, \, 0)\); we give D the orientation induced by \((0, \, 1, \, 0)\). By the Poincaré-Lefschetz duality (see e.g. [27, Theorem 3, p. 631]), for any \(T\in {\mathbb {M}}_{1}({\overline{\varOmega }}; \, {\mathbb {Z}})\) we have
By a slicing argument, we deduce that the (unique) mass-minimising chain \(S_{\min }\) in \({\mathscr {C}}(\varOmega , \, v)\) is carried by an equator of \(\partial \varOmega \):
with the orientation induced by \(\varPsi \). (See, e.g., [16, Section 5.4] for a similar example, in case \({\mathscr {N}}={\mathbb {R}}\mathrm {P}^2\).)
3 Upper Bounds
3.1 Notations and Sketch of the Construction
We say that a map \(u:\varOmega \rightarrow {\mathbb {R}}^m\) is locally piecewise affine if u is continuous in \(\varOmega \) and, for any polyhedral set \(K\subset \!\subset \varOmega \), the restriction \(u_{|K}\) is piecewise affine. A set \(P\subseteq \varOmega \) is called locally n-polyhedral if, for any compact set \(K\subseteq \varOmega \), there exists a finite union Q of convex, compact, n-dimensional polyhedra such that \(P\cap K = Q\cap K\). In a similar way, we say that a finite-mass chain \(S\in {\mathbb {M}}_n({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) is locally polyhedral if, for any compact set \(K\subseteq \varOmega \), there exists a polyhedral chain T such that  . If M is a polyhedral complex and \(j\geqq 0\) is an integer, we denote by \(M_j\) the j-skeleton of M, i.e. the union of all its faces of dimension less than or equal to j. We set \(M_{-1} := \emptyset \).
. If M is a polyhedral complex and \(j\geqq 0\) is an integer, we denote by \(M_j\) the j-skeleton of M, i.e. the union of all its faces of dimension less than or equal to j. We set \(M_{-1} := \emptyset \).
Maps with nice and \(\eta \)-minimal singularities. To construct a recovery sequence, we will work with \({\mathscr {N}}\)-valued maps with well-behaved singularities, in a sense that is made precise by the definition below. Let M, S be polyhedral sets in \({\mathbb {R}}^{n+k}\) of dimension n, \(n-1\) respectively, and let \(u:\varOmega \subseteq {\mathbb {R}}^{n+k}\rightarrow {\mathbb {R}}^m\).
Definition 3.1
([1, 2]) We say that u has a nice singularity at M if u is locally Lipschitz on \({\overline{\varOmega }}{\setminus } M\) and there exists a constant C such that
We say that u has a nice singularity at (M, S) if u is locally Lipschitz on \({\overline{\varOmega }}{\setminus }(M\cup S)\) and, for any \(p>1\), there is a constant \(C_p\) such that
We say that u has a locally nice singularity at M (respectively, at \((M, \, S)\)) if, for any open subset \(W\subset \!\subset \varOmega \), the restriction \(u_{|W}\) has a nice singularity at M (respectively, at \((M, \, S)\)).
Remark 6
If u has a nice singularity at \((M, \, S)\) then \(u\in W^{1,k-1}(\varOmega , {\mathbb {R}}^m)\), since both M and S have codimension strictly larger than \(k-1\) (see e.g. [2, Lemma 8.3] for more details). In particular, if \(u:\varOmega \rightarrow {\mathscr {N}}\) has a nice singularity at \((M, \, S)\), then \({\mathbf {S}}_y(u)\in {\mathbb {F}}_{n}(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\) is well-defined for a.e. \(y\in B^*\). Actually, \({\mathbf {S}}_{y_1}(u) = {\mathbf {S}}_{y_2}(u)\) for a.e. \(y_1\), \(y_2\in B^*\) [17, Proposition 3], and we will write \({\mathbf {S}}(u) := {\mathbf {S}}_{y_1}(u) = {\mathbf {S}}_{y_2}(u)\). The chain \({\mathbf {S}}(u)\) is supported on M, and its multiplicities coincide with the homotopy class of u around each n-face of M (see [17, Lemma 18]).
Throughout Section 3, we will work with maps with nice (or locally nice) singularities. However, in order to obtain sharp energy estimates, we will need to impose a further restriction on the behaviour of our maps near the singularities. Let \(u:\varOmega \rightarrow {\mathscr {N}}\) be a map with nice singularity at \((M, \, S)\), where M, S are polyhedral sets of dimension n, \(n-1\) respectively. We triangulate M, i.e. we write M as a finite union of closed simplices such that, if \(K^\prime \), K are simplices with \(K\ne K^\prime \), \(K\cap K^\prime \ne \emptyset \), then \(K\cap K^\prime \) is a boundary face of both K and \(K^\prime \). Let \(K\subseteq M\) be a n-dimensional simplex of the triangulation, and let \(K^\perp \) be the k-plane orthogonal to K through the origin. Given positive parameters \(\delta \), \(\gamma \), we define the set
(see Figure 1). We will identify each \(x\in U(K, \, \delta , \, \gamma )\) with a pair \(x = (x^\prime , \, x^{\prime \prime })\), where \(x^\prime \), \(x^{\prime \prime }\) are as in (3.1). By choosing \(\delta \), \(\gamma \) small enough (uniformly in K), we can make sure that the sets \(U(K, \, \delta , \, \gamma )\) have pairwise disjoint interiors.
Definition 3.2
Let \(u:\varOmega \rightarrow {\mathscr {N}}\) be a map with nice singularity at \((M, \, S)\), and let \(\eta >0\). We say that u is \(\eta \)-minimal if there exist positive numbers \(\delta \), \(\gamma \), a triangulation of M and, for any n-simplex K of the triangulation, a Lipschitz map \(\phi _K:{\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) that satisfy the following properties.
-
(i)
If \(K\subseteq M\), \(K^\prime \subseteq M\) are n-simplices with \(K\ne K^\prime \), then \(U(K, \, \delta , \, \gamma )\) and \(U(K^\prime , \, \delta , \, \gamma )\) have disjoint interiors.
-
(ii)
For any n-dimensional simplex \(K\subseteq M\) and a.e. \(x = (x^\prime , \, x^{\prime \prime })\in U(K, \, \delta , \, \gamma )\), we have \(u(x) = \phi _K(x^{\prime \prime }/|x^{\prime \prime }|)\).
-
(iii)
For any n-dimensional simplex \(K\subseteq M\) and any map \(\zeta \in W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\) that is homotopic to \(\phi _K\), we have
$$\begin{aligned} \int _{{\mathbb {S}}^{k-1}} \left| \nabla _{\top }\phi _K \right| ^k \mathrm {d}{\mathscr {H}}^{k-1} \leqq \int _{{\mathbb {S}}^{k-1}} \left| \nabla _{\top }\zeta \right| ^k \mathrm {d}{\mathscr {H}}^{k-1} + \eta . \end{aligned}$$
The operator \(\nabla _{\top }\) is the tangential gradient on \({\mathbb {S}}^{k-1}\), i.e. the restriction of the Euclidean gradient \(\nabla \) to the tangent plane to the sphere.
Remark 7
Thanks to the Sobolev embedding \(W^{1,k}({\mathbb {S}}^{k-1}, \,{\mathscr {N}}) \hookrightarrow C({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\), smooth maps are dense in \(W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\). Therefore, for any \(\eta >0\) and any homotopy class \(\sigma \in \pi _{k-1}({\mathscr {N}})\), there exists a smooth map \(\phi :{\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) in the homotopy class \(\sigma \) that satisfies
for any \(\zeta \in W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap \sigma \).
Remark 8
It is possible to find \(C^1\)-maps that satisfy a stronger version of (3.2), with \(\eta =0\). Indeed, the compact Sobolev emebedding \(W^{1,k}({\mathbb {S}}^{k-1}, \,{\mathscr {N}}) \hookrightarrow C({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\) implies that homotopy classes of maps \({\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) are sequentially closed with respect to the weak \(W^{1,k}\)-convergence. Then, for each homotopy class \(\sigma \in \pi _{k-1}({\mathscr {N}})\), there exists a map \(\phi _\sigma \) the minimises the \(L^{k}\)-norm of the gradient in \(\sigma \). The map \(\phi _\sigma \) solves the k-harmonic map equation and, by Sobolev embedding, is continuous. Then, regularity results for k-harmonic maps (e.g. [24, Proposition 5.4]) imply that \(\phi _\sigma \in C^{1,\alpha }({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\). However, the weaker condition (3.2) is enough for our purposes.
Construction of a recovery sequence: a sketch. In most of this section, we focus on the proof of Theorem C.(ii), i.e. we study the problem in the presence of boundary conditions; only at the end of section, we present the proof of Proposition D.(ii). As in [2], in order to define a recovery sequence, we first construct a map \(w:\varOmega \rightarrow {\mathscr {N}}\) with (locally) nice singularity and prescribed singular set \({\mathbf {S}}(w) = S\). However, w must also satisfy the boundary condition, \(w = v\) on \(\partial \varOmega \), where \(v\in W^{1-1/k,k}(\partial \varOmega , \, {\mathscr {N}})\) is a datum. This boundary condition makes the construction of w substantially harder. For such a w to exists, we need a topological assumption on S, namely, that S belongs to the homology class (2.6) determined by \(\varOmega \) and v. Our approach is rather different from that of [2, Theorem 5.3]. In [2], the authors first construct w inside \(\varOmega \), then interpolate near \(\partial \varOmega \), using the symmetries of the target \({\mathbb {S}}^{k-1}\), so as to match the boundary datum. On the contrary, we start from a map that satifies the boundary conditions and we modify it inside \(\varOmega \) so to obtain \({\mathbf {S}}(w) = S\). Before giving the details, we sketch the main steps of our construction.
First, we consider a locally piecewise affine extension \(u_*\in (L^\infty \cap W^{1,k})(\varOmega , \, {\mathbb {R}}^m)\) of v. Since we have assumed that \({\mathscr {X}}\) is polyhedral, the singular set \({\mathbf {S}}_y(u_*)\) will be locally polyhedral, for a.e. y. By projecting \(u_*\) onto \({\mathscr {N}}\) (using Hardt et al. [29], see Section 3.3), we define a map \(w_*:\varOmega \rightarrow {\mathscr {N}}\) such that \(w_* = v\) on \(\partial \varOmega \), \({\mathbf {S}}(w_*) = {\mathbf {S}}_y(u_*)\) (for a well-chosen y) is locally polyhedral, and \(w_*\) has a locally nice singularity at \({{\,\mathrm{spt}\,}}{\mathbf {S}}(w_*)\). We cannot make sure that the singularity is nice up to the boundary of \(\varOmega \), because the boundary datum is not regular enough.
Let S be a finite-mass n-chain in the homology class \({\mathscr {C}}(\varOmega , \, v)\) defined by (2.6). Thanks to \(({\hbox {P}}_3)\), we know that \({\mathbf {S}}(w_*)= {\mathbf {S}}_y(u_*)\in {\mathscr {C}}(\varOmega , \, v)\) and hence, \({\mathbf {S}}(w_*)\) and S differ by a boundary. By approximation (see Section 3.4.2), we reduce to the case
where R is a polyhedral \((n+1)\)-chain with compact support in \(\varOmega \). Actually, we can make a further assumption on S. Let \(W_{{\mathfrak {S}}}\subset \!\subset \varOmega \) be an open set, with polyhedral boundary, whose closure contains the support of R (see Figure 2). Up to a density argument (Proposition 6), we can assume that  takes its multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4). Roughly speaking, we replace each polyhedron K of
takes its multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4). Roughly speaking, we replace each polyhedron K of  with a finite number of polyhedra, very close to each other, whose multiplicities add up to the multiplicity of K. This is possible, because \({\mathfrak {S}}\) generates \(\pi _{k-1}({\mathscr {N}})\) by Proposition 1. The assumption on the multiplicity of
with a finite number of polyhedra, very close to each other, whose multiplicities add up to the multiplicity of K. This is possible, because \({\mathfrak {S}}\) generates \(\pi _{k-1}({\mathscr {N}})\) by Proposition 1. The assumption on the multiplicity of  turns out to be essential to obtain sharp energy bounds for our recovery sequence.
turns out to be essential to obtain sharp energy bounds for our recovery sequence.
Let W be another open set, with polyhedral boundary, such that \(W_{{\mathfrak {S}}}\subset \!\subset W\subset \!\subset \varOmega \) (see Figure 2). In particular, W contains the support of R. We aim to modify \(w_*\) inside W, so to obtain a new map \(w:\varOmega \rightarrow {\mathscr {N}}\) with locally nice singularities and \({\mathbf {S}}(w) = {\mathbf {S}}(w_*) + \partial R = S\). In other words, we need to “move” the singularities of \(w_*\) along the boundary of R. This is the key step in the construction. We achieve this goal by a suitable generalisation of the so-called “insertion of dipoles”, Proposition 4 in Section 3.2. For any \((n+1)\)-polyhedron T of R, we modify \(w_*\) in a neighbourhood of T by inserting an \({\mathscr {N}}\)-valued map that depends only on the \(k-1\) coordinates in the orthogonal directions to T. To define w near \(\partial T\), we use radial projections repeatedly, first onto the n-skeleton of T, then onto its \((n-1)\)-skeleton, and so on. Eventually, we obtain a map \(w:\varOmega \rightarrow {\mathscr {N}}\) that agrees with \(w_*\) out of a neighbourhood of \({{\,\mathrm{spt}\,}}R\) (in particular, it matches the boundary datum), has locally nice singularities at S and satisfies \({\mathbf {S}}(w) = S\). By local surgery ([2, Lemma 9.3], stated below as Lemma 6), we can also make sure that \(w_{|W}\) is \(\eta \)-minimal.
The map w does not belong to the energy space \(W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\), unless \(S=0\), because it has a singularity of codimension k. Therefore, we must regularise w to construct a recovery sequence. For \(x\in W\), we define
Since w is \(\eta \)-minimal in W, a fairly explicit computation allows us to estimate the energy of \(u_\varepsilon \) on W, in terms of the area of \({{\,\mathrm{spt}\,}}S\) and the maps \(\phi _K\) given by Definition 3.2. Moreover, for any simplex K of  , the multiplicity \(\sigma _K\) of S at K belongs to \({\mathfrak {S}}\) and hence,
, the multiplicity \(\sigma _K\) of S at K belongs to \({\mathfrak {S}}\) and hence,
because of Definition 3.2 and (2.4). Thanks to this inequality, we can indeed estimate \(E_\varepsilon (u_\varepsilon , \, W)\) in terms of the mass of S, up to remainder terms that can be made arbitrarily small. However, this approach is not viable near the boundary of \(\varOmega \), because the regularity of w degenerates near \(\partial \varOmega \). Instead, we define \(u_\varepsilon \) on \(\varOmega {\setminus } W\) by adapting [49, Proposition 2.1], see Section 3.3. The two pieces—inside and outside W—are glued together by linear interpolation.
3.2 Insertion of Dipoles Along a Simplex
Our next result, Proposition 4, is the main building block in the construction of the recovery sequence.
Proposition 4
Let \(D\subseteq {\mathbb {R}}^{n+k}\) be a bounded domain. Let \(\varSigma \subseteq D\) be a polyhedral set of dimension n, and \(u\in W^{1,k-1}(D, \, {\mathscr {N}})\) a map with nice singularity at \(\varSigma \). Let \(T\subset \!\subset D\) be an oriented simplex of dimension \(n+1\) and \(\sigma \in \pi _{k-1}({\mathscr {N}})\). Then, there exists a map \(\tilde{u}\in W^{1, k-1}(D, \, {\mathscr {N}})\), with nice singularity at a polyhedral set of dimension n, such that \(\tilde{u} = u\) in a neighbourhood of \(\partial D\) and \({\mathbf {S}}(\tilde{u}) = {\mathbf {S}}(u) + \sigma \partial \llbracket T \rrbracket \).
Perhaps it is worth commenting on the assumptions of Proposition 4. In terms of regularity of \({\mathscr {N}}\), we do not need to work with smooth manifolds: a compact, connected Lipschitz neighbourhood retract would do. The assumption that \({\mathscr {N}}\) is \((k-2)\)-connected could also be relaxed. \((k-2)\)-connectedness is used in [17, 47] to construct \({\mathbf {S}}(u)\) for arbitrary \(u\in W^{1,k-1}(\varOmega , \, {\mathscr {N}})\); however, if u has nice singularities and \(\pi _{k-1}({\mathscr {N}})\) is Abelian, then \({\mathbf {S}}(u)\) can be defined in a straightforward way. On the other hand, we must assume that \({\mathscr {N}}\) is \((k-1)\)-free (that is, the fundamental group of \({\mathscr {N}}\) acts trivially on \(\pi _{k-1}({\mathscr {N}})\)). Should \({\mathscr {N}}\) not be \((k-1)\)-free, we could not identify free homotopy classes of maps \({\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) with elements of \(\pi _{k-1}({\mathscr {N}})\). In this case, the product of free homotopy classes \({\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) is multi-valued and hence, the equality \({\mathbf {S}}(\tilde{u}) = {\mathbf {S}}(u) + \sigma \partial \llbracket T\rrbracket \) may fail.
Idea of the proof of Proposition 4: an example with \(k=2\), \(n=0\) and \({\mathscr {N}}={\mathbb {S}}^1\). The initial map u is plotted in (a); the values of u are represented by the colour code. We aim to insert singularities of degrees 1, \(-1\) at the points \(x_+\), \(x_-\). First, we reparametrise u, creating a ‘slit’ along the segment of endpoints \(x_+\) and \(x_-\) (b). Then, we fill the slit by inserting a map that winds around the circle exactly once, as we move in the direction orthogonal to the segment of endpoints \(x_+\), \(x_-\) (c). Finally, we define \(\tilde{u}\) in the disks \(V_+\), \(V_-\) in such a way that \(\tilde{u}\) is homogeneous inside each disk (d). The new map \(\tilde{u}\) behaves as required. For instance, there are exactly three yellow points on \(\partial V_+\); as we move anticlockwise around \(\partial V_+\), two of them carry the orientation ‘from red to blue’ and the other one carries the opposite orientation ‘from blue to red’. If we orient the target \({\mathbb {S}}^1\) ‘from red to yellow to blue’, then the degree of \(\tilde{u}\) on \(\partial V_+\) is 1
The proof of Proposition 4 (see Figure 3) is based on a construction known as “insertion of dipoles”. Several variants of this construction are available in the literature (see e.g. [6, 7, 13, 27, 47]), but all of them rely of the following fact: a map \(B^{k-1}\rightarrow {\mathscr {N}}\) that takes a constant value on \(\partial B^{k-1}\) may be identified with a map \({\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\), by collapsing the boundary of the disk to a point. As a consequence, if a continuous map \(\phi :B^{k-1}\rightarrow {\mathscr {N}}\) is constant on \(\partial B^{k-1}\), then we may define the homotopy class of \(\phi \) as an element of \(\pi _{k-1}({\mathscr {N}})\). (In principle, we should distinguish between free or based homotopy, according to whether the boundary value of \(\phi \) is allowed to vary during the homotopy or not; however, the assumption \(({\hbox {H}}_2)\) guarantees that these two notions are equivalent.)
Lemma 1
Let K be a convex polyhedron, let \(h:K\rightarrow {\mathscr {N}}\) be a Lipschitz map, and let \(\sigma \in \pi _{k-1}({\mathscr {N}})\). Then, there exists a Lipschitz map \(u:K\times B^{k-1}\rightarrow {\mathscr {N}}\) such that
and, for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\), the homotopy class of \(u(x^\prime , \, \cdot )\) is \(\sigma \).
The proof of Lemma 1 is completely standard, but we provide it for the sake of convenience.
Proof of Lemma 1
We choose a point \(x^\prime _0\in K\) and consider the map \(\psi :[0, \, 1]\times K\rightarrow K\) as \(\psi (t, \, x^\prime ) := t x^\prime + (1 - t)x^\prime _0\). We define \(u:K\times (B^{k-1}{\setminus } B^{k-1}_{1/2})\rightarrow {\mathscr {N}}\) as
The map u is Lipschitz and satisfies (3.3); moreover, for \(\left| x^{\prime \prime } \right| = 1/2\) we have \(u(x^\prime , \, x^{\prime \prime }) = h(x^\prime _0)\). Now, we take a smooth map \(\phi :B^{k-1}\rightarrow {\mathscr {N}}\) that is constant on \(\partial B^{k-1}\) — say, \(\phi = z_0\in {\mathscr {N}}\) on \(\partial B^{k-1}\) — and has homotopy class \(\sigma \). Let \(\zeta :[0, \, 1]\rightarrow {\mathscr {N}}\) be a Lipschitz curve with \(\zeta (0) = z_0\), \(\zeta (1) = h(x^\prime _0)\). We define \(u:K\times B^{k-1}_{1/2}\rightarrow {\mathscr {N}}\) as
For any \(x^\prime \in K\), the map \(u(x^\prime , \, \cdot )\) is (freely) homotopic to \(\sigma \), via a reparametrisation and a change of base-point. Therefore, the homotopy class of \(u(x^\prime , \, \cdot )\) is \(\sigma \). \(\quad \square \)
Proof of Proposition 4
We triangulate \(\varSigma \cup T\), that is, we write \(\varSigma \cup T\) as a finite union of closed simplices in such a way that, for any simplices K, \(K^\prime \) with \(K\ne K^\prime \), \(K\cap K^\prime \) is either empty or a boundary face of both K and \(K^\prime \). We denote by \(T_n\) the n-skeleton of this triangulation (i.e., the union of all simplices of dimension n or less). We will construct a sequence of maps \(u^{n+1}\), \(u^n\), ..., \(u^1\), \(u^0\) by modifying the given map u first along the simplices of dimension \(n+1\) that are contained in T, then along those of dimension n, and so on. In order to do so, we first need to construct a suitable covering of T.
Step 1
(Construction of a covering of T) Let \(K\subseteq T\) be a simplex of dimension \(j>0\). Let \(K^\perp \) be the orthogonal \((n+k-j)\)-plane to K through the origin. We fix positive numbers \(\delta _K\), \(\gamma _K\) and define
(see Figure 4). If K is a 0-dimensional simplex, i.e. a point, we define \(V_K := B^{n+k}(K, \, \delta _K)\) and \(\varGamma _K:= \partial V_K\). By choosing \(\delta _K\), \(\gamma _K\) in a suitable way, we can make sure that the following properties are satisfied:
-
(a)
\(V_K\subset \!\subset D\) for any simplex \(K\subseteq T\).
-
(b)
For any j-dimensional simplex \(K\subseteq T\), we have
$$\begin{aligned} \partial V_K{\setminus }\varGamma _K \subseteq \bigcup _{K^\prime \subseteq T:\dim K^\prime < j} V_{K^\prime } \end{aligned}$$(in case \(j=0\), both sides of the inclusion are empty).
-
(c)
For any simplices \(K\subseteq T\), \(K^\prime \subseteq T\) with \(K\ne K^\prime \), \(\dim K = \dim K^\prime \), we have \(\overline{V_K} \cap \overline{V_{K^\prime }} = \emptyset \).
-
(d)
For any simplices \(K\subseteq T\), \(K^\prime \subseteq \varSigma \cup T\) with \(K\not \subseteq K^\prime \), we have \(\overline{V_K}\cap K^\prime = \emptyset \).
-
(e)
No simplex \(K\subseteq T\) is entirely contained in \(\cup \{\overline{V_{K^\prime }}:\dim K^\prime < \dim K\}\).
Property (b) implies that the \(V_K\)’s do cover T. To construct a covering that satisfies (a)–(e), we first cover the 0-skeleton of T by pairwise disjoint balls that are compactly contained in D. Then, we cover each 1-dimensional simplex in T by a “thin cylinder”, whose bases are contained in the balls we have chosen before. Next, we cover each 2-dimensional simplex by a “thin shell”, and so on, as illustrated in Figure 5. At each step, we can make sure that the properties (a)–(e) are satisfied, because the simplices have pairwise disjoint interiors and only intersect along their boundaries. As a consequence of (d), for any simplex \(K\subseteq T\) it holds that
For any integer \(j\in \{0, \, 1, \, \ldots , \, n+1\}\), we define
and \(V^{<0} := \emptyset \).
Step 2
(Construction of \(u^{n+1}\)) Let \(K\subseteq T\) be a \((n+1)\)-simplex of the triangulation, with the orientation induced by T. We identify \(V_K\) with \(\tilde{K}\times B^{k-1}(0, \, \delta _K)\), where \(\tilde{K}\) is given by (3.4). We construct a Lipschitz map \(u^{n+1}_K:V_K\rightarrow {\mathscr {N}}\) as follows. First, we let
Thus, \(u^{n+1}_K = u\) on \(\varGamma _K\), while \(u^{n+1}_K(x^\prime , \, x^{\prime \prime }) = u(x^\prime , \, 0)\) for \(|x^{\prime \prime }| = \delta _K/2\). Since the trace of \(u^{n+1}_K\) on \(\tilde{K}\times \partial B^{k-1}(0, \, \delta _K/2)\) only depends on the variable \(x^\prime \), we may apply Lemma 1 and define \(u^{n+1}_K\) in \(\tilde{K}\times B^{k-1}(0, \, \delta _K/2)\) in such a way that, for any \(x^\prime \in \tilde{K}\),
The sign \((-1)^{n+1}\) will be useful to compensate for orientation effects, later on in the proof.
We define a map
as follows: \(u^{n+1}(x):= u^{n+1}_K(x)\) if \(x\in V_K\) for some \((n+1)\)-simplex K, and \(u^{n+1}(x) := u(x)\) otherwise. This definition is consistent. Indeed, the sets \(\overline{V_K}\) are pairwise disjoint, due to (c). Moreover, if a point x belongs both to \(\overline{V_K}\) and to \(D{\setminus } V^{< n+1}\), then \(x\in \varGamma _V\) because of (b), so \(u^{n+1}_K(x) = u(x)\) by (i). Therefore, the map \(u^{n+1}\) is well-defined and locally Lipschitz out of \(\varSigma \), with nice singularity at \(\varSigma \).
Step 3
(Construction of \(u^{n}\)) Let \(K\subseteq T\) be a n-simplex. We identify \(V_K\) with \(\tilde{K}\times B^k(0, \, \delta _K)\). The map \(u^{n+1}\) is Lipschitz continuous on \(\varGamma _K\), due to (3.7). Let \(\sigma _K\in \pi _{k-1}({\mathscr {N}})\) be the homotopy class of \(u^{n+1}\) on an arbitrary slice of \(\varGamma _K\), of the form \(\{x^\prime \}\times \partial B^k(0, \, \delta _K)\). If \(\sigma _K = 0\) then, by adapting the arguments of Lemma 1, we can construct a Lipschitz continuous map \(u^n_K:V_K\rightarrow {\mathscr {N}}\) such that \(u^n_K = u^{n+1}\) on \(\varGamma _K\). If \(\sigma _K\ne 0\), we define \(u^n_K:V_K\rightarrow {\mathscr {N}}\) as
In both cases, by a straightforward computation, we obtain
where the proportionality constant at the right-hand side depends on \(\delta _K\) and \(u^{n+1}\). We define
as follows: \(u^{n}(x):= u^{n}_K(x)\) if \(x\in V_K\) for some n-simplex K, and \(u^{n}(x) := u^{n+1}(x)\) otherwise. Thanks to (b), (c) and (3.10), we can argue as in Step 2 and check that \(u^{n}\) is locally Lipschitz out of \(\varSigma \cup T_n\), with nice singularity at \(\varSigma \cup T_n\).
Step 4
(Construction of \(u^j\) for \(j < n\)) We proceed by induction. Let \(j\in \{0, \, 1, \, \ldots , n-1\}\). Suppose we have constructed a map
that is locally Lipschitz out of \(\varSigma \cup T_n\) and has a nice singularity at \(\varSigma \cup T_n\). Let \(K\subseteq T\) be a j-simplex. By identifying \(V_K\) with \(\tilde{K}\times B^{n+k-j}(0, \, \delta _K)\), we define \(u^j_K:V_K\rightarrow {\mathscr {N}}\),
The map \(u^j_K\) is locally Lipschitz out of the set
By Property (d), the only simplices of \(\varSigma \cup T_n\) that intersect \({\overline{V}}_K\) are those that contain K. Therefore, if \(H_1\), \(H_2\), ..., \(H_p\) denote the n-dimensional (closed) simplices of \(\varSigma \cup T_n\) that contain K, then
Moreover, Property (d) and the convexity of \(H_i\) imply that
where \(\tilde{H}_i\subseteq {\mathbb {R}}^{n+k-j}\) is a cone (i.e., \(\lambda x\in \tilde{H}_i\) for any \(x\in \tilde{H}_i\) and any \(\lambda \geqq 0\)). As a consequence,
that is, \(u^j_K\) is locally Lipschitz out of \(\varSigma \cup T_n\). We claim that
where the proportionality constant at the right-hand side may depend on \(\delta _K\). Given \(x = (x^\prime , \, x^{\prime \prime })\in V_K\), let \(y(x) := (x^\prime , \, \delta _K x^{\prime \prime }/\left| x^{\prime \prime } \right| )\). By the induction hypothesis, \(u^{j+1}\) has a nice singularity at \(\varSigma \cup T_n\). Therefore, an explicit computation gives
for a.e. \(x\in V_K\). By (3.11) and (3.12), the set \(\varSigma \cup T_n\) agrees with \(\tilde{K}\times \cup _i\tilde{H}_i\) in \(\overline{V_K}\), and \(\cup _i\tilde{H}_i\) is a cone. Then, by a geometric argument (see Figure 6), we have
By combining (3.14) and (3.15), (3.13) follows. Finally, we define
as follows: \(u^{j}(x):= u^{j}_K(x)\) if \(x\in V_K\) for some j-simplex \(K\subseteq T\), and \(u^{j}(x) := u^{j+1}(x)\) otherwise. Thanks to (b), (c) and (3.13), the map \(u^{j}\) is well-defined, locally Lipschitz out of \(\varSigma \cup T_n\) and has a nice singularity at \(\varSigma \cup T_n\).
Proof of (3.15). The picture represents a slice of \(V_K\), of the form \(\{x^\prime \}\times B^{n+k-j}(0, \, \delta _K)\)
Step 5
(Conclusion) By induction, we have constructed a sequence of maps \(u^{n+1}\), \(u^{n}\), ..., \(u^1\), \(u^0\). Let \(\tilde{u}:= u^0:D\rightarrow {\mathscr {N}}\). By construction, the map \(\tilde{u}\) has a nice singularity at \(\varSigma \cup T_n\) and agrees with u out of \(V^{< n+1}\cup V^{=n+1}\). In particular, \(\tilde{u} = u\) in a neighbourhood of \(\partial D\), because of (a).
It only remains to compute \({\mathbf {S}}(\tilde{u})\). Let K be an n-simplex of T. By Property (e), K is not entirely contained in \(\overline{V^{<n}}\); we take a point \(x\in K{\setminus }\overline{V^{<n}}\). Let \(K^\perp \) be the orthogonal k-plane to K at x, and let \(F := \overline{V_K}\cap K^\perp \). By Property (d), the only \((n+1)\)-simplices that intersect F are those that contain K; we call them \(H_1\), ..., \(H_p\). We consider the restriction of \(\tilde{u}\) to the \((k-1)\)-sphere \(\partial F\). By construction (see (3.8) and (3.9) in Step 2), \(\tilde{u}_{|\partial F}\) consists (up to homotopy) of a reparametrisation of \(u_{|\partial F}\), with the insertion of ‘bubbles’ around the points \(\partial F \cap H_i\). Each bubble carries the homotopy class \(\sigma \) or \(-\sigma \), depending on the orientation of \(H_i\) (which, we recall, is the one induced by T). The net topological contribution of all the bubbles may vanish or not, depending on whether the point x belongs to the boundary of T or not. As a result, we have
The sign of the second term in the right-hand side depends on the choice of the sign we made in Equation (3.9) (see, for instance, Property (iv) in Lemma 8 of [17]). Then, by Remark 6, \({\mathbf {S}}(\tilde{u}) = {\mathbf {S}}(u) + \sigma \partial \llbracket T\rrbracket \).\(\quad \square \)
3.3 Projection of a \(W^{1,k}\)-map onto \({\mathscr {N}}\)
Before we pass to the construction of a recovery sequence, we gather some useful results, based on earlier work by Hardt et al. [29, Lemma 2.3], [30], and Rivière [49, Proposition 2.1]; see also [2, Proposition 6.4] for similar statements in case \({\mathscr {N}}={\mathbb {S}}^{k-1}\).
For any \(y\in {\mathbb {R}}^m\), we consider the map \({\tilde{\varrho }}_y :z\mapsto \varrho (z - y)\) which is well defined for \(z\in {\mathbb {R}}^m{\setminus }({\mathscr {X}}+y)\). This is not a retraction onto \({\mathscr {N}}\), in general, because it does not restrict to the identity on \({\mathscr {N}}\). However, for sufficiently small \(\left| y \right| \) — say, \(y\in B^m_{\sigma }\) with \(\sigma >0\) small enough — the restriction \({\tilde{\varrho }}_{y|{\mathscr {N}}}\) is a small perturbation of the identity and, in particular, it is a diffeomorphism. For \(y\in B^m_\sigma \) and \(z\in {\mathbb {R}}^m{\setminus }({\mathscr {X}}+y)\), let us define
This map is indeed a smooth retraction of \({\mathbb {R}}^m{\setminus }({\mathscr {X}}+y)\) onto \({\mathscr {N}}\). We also define a function \(\psi :{\mathbb {R}}^m\rightarrow {\mathbb {R}}\) by
The function \(\psi \) is Lipschitz and \(\psi =1\) on \({\mathscr {N}}\). By Proposition 2 and (3.17), we have
for any \(y\in B^m_\sigma \) and \(z\in {\mathbb {R}}^m{\setminus }({\mathscr {X}}+y)\). The proportionality constants here depend on \(\sigma \), but \(\sigma = \sigma ({\mathscr {N}}, \, {\mathscr {X}}, \, \varrho )\) is fixed once and for all. Finally, let \(\xi _\varepsilon (t) := \min (t/\varepsilon , \, 1)\) for \(t\geqq 0\).
Lemma 2
Let \(\varLambda \) be a positive number, and let \(u\in (L^\infty \cap W^{1,k})(\varOmega , \, {\mathbb {R}}^m)\) be such that \(\Vert u\Vert _{L^\infty (\varOmega )}\leqq \varLambda \). For \(y\in B^m_\sigma \), \(\varepsilon >0\) and \(x\in \varOmega \), define
Then, the following properties hold:
-
(i)
For a.e. \(y\in B^m_\sigma \), \(w_y\in W^{1, k-1}(\varOmega , \, {\mathscr {N}})\) and \({\mathbf {S}}(w_y) = {\mathbf {S}}_y(u)\).
-
(i)
For a.e. \(y\in B^m_\sigma \) and sufficiently small \(\varepsilon \), \(w_{\varepsilon , y}\in (L^\infty \cap W^{1,k})(\varOmega , \, {\mathbb {R}}^m)\) and \(\Vert w_{\varepsilon ,y}\Vert _{L^\infty (\varOmega )}\leqq \max \{\left| z \right| :z\in {\mathscr {N}}\}\).
-
(iii)
For any open set \(D\subseteq \varOmega \), it holds that
$$\begin{aligned} \begin{aligned}&\int _{B^m_\sigma } \left( E_\varepsilon (w_{\varepsilon ,y}, \, D) + \varepsilon ^{-k} {\mathscr {L}}^{n+k}\{x\in D:w_{\varepsilon ,y}(x)\ne w_y(x)\}\right) \mathrm {d}y \\&\quad \leqq C_\varLambda \left( \left| \log \varepsilon \right| \left\| \nabla u \right\| ^k_{L^k(D)} + {\mathscr {L}}^{n+k}(D) \right) \!, \end{aligned} \end{aligned}$$where \(C_\varLambda \) is a positive constant that only depends on \({\mathscr {N}}\), k, \({\mathscr {X}}\) and \(\varLambda \).
-
(iv)
For a.e. \(y\in B^m_\sigma \) there exists a (non-relabelled) subsequence \(\varepsilon \rightarrow 0\) such that \(w_{\varepsilon ,y}\rightarrow w_y\) strongly in \(W^{1, k-1}(\varOmega , \, {\mathbb {R}}^m)\).
Remark 9
Statement (iii) of Lemma 2 implies, via an averaging argument, that
for any \(v\in W^{1-1/k,k}(\partial \varOmega , \, {\mathscr {N}})\) and any \(\varepsilon >0\).
Proof of Lemma 2
Throughout the proof, we denote by \(C_\varLambda \) a generic positive constant that only depends on \({\mathscr {N}}\), k, \({\mathscr {X}}\) and \(\varLambda \) (and may change from one occurence to the other).
Step 1
(Proof of (i)) For a.e. y, we have \(\varrho \circ (u - y)\in W^{1,k-1}(\varOmega , \, {\mathscr {N}})\) (see e.g. [17, Lemma 14] for a proof of this claim). Moreover, by Canevari and Orlandi [17, Lemma 17] we know that
Now, \(w_y\) is obtained from \(\varrho \circ (u-y)\) by composition with a map, \(({\tilde{\varrho }}_{y|{\mathscr {N}}})^{-1}\), which is homotopic to the identity on \({\mathscr {N}}\). Therefore, from the identity above we obtain
This can be first checked when u is smooth, using [17, Lemma 18], and remains true for a general u by a density argument, using the continuity of \({\mathbf {S}}\) and e.g. [17, Lemma 14].
Step 2
(Proof of (ii), (iii)) It is immediate to see that \(\Vert w_{\varepsilon ,y}\Vert _{L^\infty (\varOmega )}\leqq \max \{\left| z \right| :z\in {\mathscr {N}}\}\). By (i), \(w_{\varepsilon , y}\in (L^\infty \cap W^{1,k-1})(\varOmega , \, {\mathbb {R}}^m)\) for a.e. y, and by the chain rule, we have the pointwise bound
for a.e. \(x\in \varOmega \). Thanks to (3.18), we deduce that
(where, as usual, \(\mathbb {1}_A\) denotes the characteristic function of a set A). On the other hand, the \(L^\infty \)-norm of \(w_{\varepsilon ,y}\) is uniformly bounded in terms of \({\mathscr {N}}\) only, and hence it holds that
Together, (3.20) and (3.21) imply that
We integrate the previous inequality for \(y\in B^m_\sigma \), apply Fubini theorem and make the change of variable \(z = u(x) - y\):
Since \({\mathscr {X}}\) is a finite union of simplices of codimension k or higher, for \(\varepsilon \) sufficiently small it holds that
(see e.g. [2, Lemma 8.3]). As a consequence, we obtain (iii).
Step 3
(Proof of (iv)) For a.e. \(y\in B^m_\sigma \), the set \(\{\psi (u - y) = 0\} = (u - y)^{-1}({\mathscr {X}})\) has Lebesgue measure equal to zero (see e.g. [17, proof of Lemma 14]). Then, since \(\xi _\varepsilon \rightarrow 1\) pointwise on \((0, \, +\infty )\) as \(\varepsilon \rightarrow 0\), we have \(w_{\varepsilon ,y}\rightarrow w_y\) a.e. as \(\varepsilon \rightarrow 0\), for a.e. y. Using the chain rule, (3.18) and (3.20), we obtain that
for a.e. \(x\in \varOmega \). We raise both sides of this inequality to the \((k-1)\)-th power, integrate over \((x, \, y)\in \varOmega \times B^m_\sigma \), apply Fubini theorem and make the change of variable \(z = u(x) - y\):
We apply [2, Lemma 8.3] to estimate the integral with respect to z: since \({\mathscr {X}}\) has codimension k, we obtain
so
By Fatou lemma, we deduce
so (iv) follows.\(\quad \square \)
3.4 Construction of a Recovery Sequence
3.4.1 Construction of an \({\mathscr {N}}\)-valued Map with Nice Singularity at a Locally Polyhedral Set
In this section, we give the construction of a recovery sequence. We first construct a map \(\varOmega \rightarrow {\mathscr {N}}\) that matches the Dirichlet boundary datum and has nice singularities along a locally polyhedral set.
Lemma 3
Any boundary datum \(v\in W^{1-1/k, k}(\partial \varOmega , \, {\mathscr {N}})\) can be extended to a map \(u^*\in (L^\infty \cap W^{1,k}_v)(\varOmega , \, {\mathbb {R}}^m)\) that satisfies the following properties, for a.e. \(y\in {\mathbb {R}}^m\):
-
(a)
\({\mathbb {M}}({\mathbf {S}}_y(u_*))<+\infty \) and
 ;
; -
(b)
the chain \({\mathbf {S}}_{y}(u_*)\) is locally polyhedral;
-
(c)
the chain \({\mathbf {S}}_{y}(u_*)\) takes its multiplicities in a finite subset of \(\pi _{k-1}({\mathscr {N}})\), which depends only on \({\mathscr {N}}\), \(\varrho \), \({\mathscr {X}}\);
-
(d)
there exists a locally \((n-1)\)-polyhedral set \(P_y\) such that \(\varrho \circ (u_*-y)\) has a locally nice singularity at \({{\,\mathrm{spt}\,}}{\mathbf {S}}_{y}(u_*)\cup P_{y}\).
The proof of Lemma 3 relies on the following fact.
Lemma 4
Any boundary datum \(v\in W^{1-1/k, k}(\partial \varOmega , \, {\mathbb {R}}^m)\) has a locally piecewise affine extension \(u_*\in (L^\infty \cap W^{1,k}_v)(\varOmega , \, {\mathbb {R}}^m)\).
We give a proof of Lemma 4, for the convenience of the reader only.
Proof of Lemma 4
Arguing component-wise, we reduce to the case \(m=1\). Let \(u\in W^{1,k}_v(\varOmega )\) be an extension of v. By a truncation argument, we can make sure that \(v\in L^\infty (\varOmega )\). Let \(\varGamma _1 := \{x\in \varOmega :{{\,\mathrm{dist}\,}}(x, \, \partial \varOmega ) > 1/2\}\) and, for any integer \(j\geqq 2\), let \(\varGamma _j := \{x\in \varOmega :(j+1)^{-1}< {{\,\mathrm{dist}\,}}(x, \, \partial \varOmega ) < (j - 1)^{-1}\}\). Using a partition of unity, we construct a sequence of smooth functions \(\varphi _j \in C^\infty _{\mathrm {c}}(\varGamma _j)\) such that \(\sum _{j\geqq 1}\varphi _j = 1\). Thanks to e.g. [53, Theorem 1], for any j there exists a triangulation \({\mathcal {T}}_j\) of \({\mathbb {R}}^{n+k}\) such that the piecewise affine interpolant \(u_j\) of \(\varphi _j u\) along \({\mathcal {T}}_j\) is well-defined (that is, all the vertices of \({\mathcal {T}}_j\) are Lebesgue points of \(\varphi _j u\)) and there holds
Moreover, the proof of [53, Theorem 1] shows that for any \(r>0\), we can choose \({\mathcal {T}}_j\) such that all the simplices of \({\mathcal {T}}_j\) have diameter \(\leqq r\). In particular, we can make sure that \(u_j\) is still supported in \(\varGamma _j\). Now, we define \(u_* := \sum _{j\geqq 1} u_j\). Since the support of \(u_j\) intersects the support of \(u_i\) only for finitely many i, the function \(u_*\) is locally piecewise affine. Moreover, \(u_*\in L^\infty (\varOmega )\) because, by construction, \(\left\| u_j \right\| _{L^\infty (\varOmega )}\leqq \left\| u \right\| _{L^\infty (\varOmega )}\) for any j, and \(u\in W^{1, k}(\varOmega )\) due to (3.22). Finally, for any \(N\geqq 1\) the function \(\sum _{j=1}^N (u_j - \varphi _j u)\) is compactly supported in \(\varOmega \), and hence \(\sum _{j=1}^N (u_j - \varphi _j u)\in W^{1, k}_0(\varOmega )\). Passing to the limit as \(N\rightarrow +\infty \), we conclude that \(u_* - u \in W^{1,k}_0(\varOmega )\), and the lemma follows. \(\quad \square \)
Proof of Lemma 3
Let \(u_*\) be the locally piecewise extension of v given by Lemma 4. Statement (a) follows from \(({\hbox {P}}_2)\) in Proposition 3, because \(u_*\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\). Let \(K\subseteq \varOmega \) be a (closed) \((n+k)\)-simplex such that \(u_{*|K}\) is affine. Since we have assumed that \({\mathscr {X}}\) is polyhedral, for any \(y\in {\mathbb {R}}^m\) the inverse image \((u_* - y)^{-1}({\mathscr {X}})\cap K\) is polyhedral too. Take \(y\in {\mathbb {R}}^m\) such that \((u_* - y)_{|K}\) is transverse to each cell of \({\mathscr {X}}\). By [17, Corollary 1], we have  and by definition (see [17, Section 3.2] and Section B below), the latter is a polyhedral chain supported on \((u_* - y)^{-1}({\mathscr {X}})\cap K\). Thus, \({\mathbf {S}}_y(u_*)\) is locally polyhedral. Moreover, \({\mathbf {S}}_y(u_*)\) take its multiplicities in the set
and by definition (see [17, Section 3.2] and Section B below), the latter is a polyhedral chain supported on \((u_* - y)^{-1}({\mathscr {X}})\cap K\). Thus, \({\mathbf {S}}_y(u_*)\) is locally polyhedral. Moreover, \({\mathbf {S}}_y(u_*)\) take its multiplicities in the set
which is a finite subset of \(\pi _{k-1}({\mathscr {N}})\), because \({\mathscr {X}}\) is a finite union of polyhedra. Finally, let us prove Statement (d). Take an open set \(W\subset \!\subset \varOmega \), and take \(y\in {\mathbb {R}}^m\) such that \(u_{*|W}\) is transverse to each cell of \({\mathscr {X}}\). Let K be a \((n+k)\)-simplex such that \(K\cap W\ne \emptyset \) and \(u_{*|K}\) is affine. By transversality, we see that
where \(C_K > 0\) is a constant that depends on the (constant) gradient of \(u_*\) on K and on y. Since W is covered by finitely many simplices, we have
where \(C_{ W, y}:=\min _{K:K\cap W\ne \emptyset } C_{K,y}>0\). Then, by applying the chain rule and Proposition 2, we conclude that \(\varrho \circ (u_* - y)_{|W}\) has a nice singularity at \(({{\,\mathrm{spt}\,}}{\mathbf {S}}_y(u_*)\cup P_y)\cap W\), where \(P_y := (u_* - y)^{-1}({\mathscr {X}}_{m-k-1})\). \(\quad \square \)
3.4.2 Reduction of the Problem
Throughout the rest of Section 3, we fix the boundary datum \(v\in W^{1-1/k, k}(\partial \varOmega , \, {\mathscr {N}})\) and let \(u_*\) be the map given by Lemma 3. We also fix \(y^*\in {\mathbb {R}}^m\), with \(\left| y^* \right| \) sufficiently small, in such a way that Statements (a)–(d) in Lemma 3 are satisfied. Let \(w_* := \varrho _{y_*}\circ u_*\), where \(\varrho _{y_*}\) is defined by (3.16). By Lemma 3, the map \(w_*\) has a locally nice singularity at \({{\,\mathrm{spt}\,}}{\mathbf {S}}_{y_*}(u_*)\cup P_{y_*}\), where \(P_{y_*}\) is a locally polyhedral set of dimension \(n-1\). By Lemma 2, we can choose \(y_*\) so to have \(w_*\in W^{1, k-1}(\varOmega , \, {\mathscr {N}})\) and \({\mathbf {S}}(w_*) = {\mathbf {S}}_{y_*}(u_*)\) as well.
Remark 10
For a generic map \(w\in W^{1, k-1}(\varOmega , \, {\mathbb {R}}^m)\), \({\mathbf {S}}(w)\) is only well-defined as a relative flat chain, \({\mathbf {S}}(w)\in {\mathbb {F}}_n(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\) (see [17, Section 3]). However, \({\mathbf {S}}_{y_*}(u_*)\) is well-defined as an element of \({\mathbb {F}}_n({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\), because \(u_*\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) (see Proposition 3). With a slight abuse of notation, we will regard \({\mathbf {S}}(w_*)\) as an element of \({\mathbb {F}}_n({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\), too.
Let S be a finite-mass n-chain, supported in \({\overline{\varOmega }}\), that is cobordant to \({\mathbf {S}}(w_*)\). By definition of \({\mathscr {C}}(\varOmega , \, v)\), Equation (2.6), S and \({\mathbf {S}}(w_*)\) differ by a boundary. By an approximation argument, we will reduce to the case S has a special form.
Proposition 5
Let \(S\in {\mathscr {C}}(\varOmega , \, v)\) be a finite mass chain. Then, there exists a sequence of polyhedral \((n+1)\)-chains \(R_j\), with compact support in \(\varOmega \), such that \({\mathbf {S}}(w_*) + \partial R_j \rightarrow S\) (with respect to the \({\mathbb {F}}\)-norm) and \({\mathbb {M}}({\mathbf {S}}(w_*) + \partial R_j)\rightarrow {\mathbb {M}}(S)\) as \(j\rightarrow +\infty \).
The proof of Proposition 5 is left to Appendix D.1. Thanks to Proposition 5, and a diagonal argument, we can assume with no loss of generality that S has the form
where R is a polyhedral \((n+1)\)-chain, compactly supported in \(\varOmega \). There is one further assumption we can make. Let \(W_{{\mathfrak {S}}}\subset \!\subset \varOmega \) be an open set, with polyhedral boundary, such that \(\partial W_{{\mathfrak {S}}}\) is transverse to \({{\,\mathrm{spt}\,}}S\) (more precisely, there exist triangulations of \(\partial W_{{\mathfrak {S}}}\) and \({{\,\mathrm{spt}\,}}S\) such that any simplex of the triangulation of \(\partial W_{{\mathfrak {S}}}\) is transverse to any simplex of the triangulation of \({{\,\mathrm{spt}\,}}S\)) and

The condition  is satisfied because, by transversality, \({{\,\mathrm{spt}\,}}S\cap \partial W_{{\mathfrak {S}}}\) has dimension \((n-1)\) or less and hence, it cannot support a non-trivial polyhedral n-chain.
is satisfied because, by transversality, \({{\,\mathrm{spt}\,}}S\cap \partial W_{{\mathfrak {S}}}\) has dimension \((n-1)\) or less and hence, it cannot support a non-trivial polyhedral n-chain.
Proposition 6
There exists a sequence of polyhedral \((n+1)\)-chains \(R_j\), supported in \(\overline{W_{{\mathfrak {S}}}}\), such that the following hold:
-
(i)
\(S+\partial R_j \rightarrow S\), with respect to the \({\mathbb {F}}\)-norm, as \(j\rightarrow +\infty \);
-
(ii)
\({\mathbb {M}}(S+\partial R_j)\rightarrow {\mathbb {M}}(S)\) as \(j\rightarrow +\infty \);
-
(iii)
for any j,
 ;
; -
(iv)
for any j, the chain
 takes multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4).
takes multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4).
The proof of Proposition 6 will be given in Appendix D.1. Thanks to Proposition 6, it is not restrictive to assume that

in addition to (3.23), (3.24). Indeed, if (3.24) does not hold, we replace S with with a chain of the form \(S + \partial R_j\) as given by Proposition 6, we replace R with \(R+R_j\), then we use a diagonal argument to pass to the limit as \(j\rightarrow +\infty \).
3.4.3 Construction of an \({\mathscr {N}}\)-valued Map with Prescribed Singular Set
Our next task is to construct a map \(w:\varOmega \rightarrow {\mathscr {N}}\), with locally nice singularities, in such a way that \({\mathbf {S}}(w) = S\). To do so, we fix an open set \(W\subset \!\subset \varOmega \) such that \(W_{{\mathfrak {S}}}\subset \!\subset W\) and \(\partial W\) is transverse to \({{\,\mathrm{spt}\,}}S\) (i.e., there exist triangulations of \(\partial W_{{\mathfrak {S}}}\) and \({{\,\mathrm{spt}\,}}S\) such that any simplex of the triangulation of \(\partial W_{{\mathfrak {S}}}\) is transverse to any simplex of the triangulation of \({{\,\mathrm{spt}\,}}S\)). We also fix a small parameter \(\eta >0\).
Lemma 5
For any W as above and any \(\eta >0\), there exists a map \(w\in W^{1,k-1}(\varOmega , \, {\mathscr {N}})\) that satisfies the following properties:
-
(i)
\(w = w_*\) a.e. in \(\varOmega {\setminus } W\);
-
(ii)
w has a locally nice singularity at \(({{\,\mathrm{spt}\,}}S, \, Q_*)\), where \(Q_*\supseteq ({{\,\mathrm{spt}\,}}S)_{n-1}\) is a locally \((n-1)\)-polyhedral set;
-
(iii)
\({\mathbf {S}}(w) = S\);
-
(iv)
\(w_{|W}\) is \(\eta \)-minimal.
Lemma 5 follows from Proposition 4, combined with the following lemma from [2]:
Lemma 6
(Lemma 9.3, [2]) Let \(K\subseteq {\mathbb {R}}^{n+k}\) be a n-simplex, and let \(\delta \), \(\gamma \) be positive parameters.
Let \(u:U(K, \, \delta , \, \gamma )\rightarrow {\mathscr {N}}\) be a map with nice singularity at K, and let \(\sigma \in \pi _{k-1}({\mathscr {N}})\) the homotopy class of u around K. Let \(\phi :{\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) be a Lipschitz map in the homotopy class \(\sigma \). Then, there exists a map \(\tilde{u}:U(K, \, \delta , \, \gamma )\rightarrow {\mathscr {N}}\) that satisfies the following properties:
-
(i)
\(\tilde{u} = u\) on \(\partial U(K, \, \delta , \, \gamma )\);
-
(ii)
\(\tilde{u}\) has a nice singularity at \((K, \, \partial K)\);
-
(iii)
\({\mathbf {S}}(\tilde{u}) = {\mathbf {S}}(u)\);
-
(iv)
\(\tilde{u}(x) = \phi (x^{\prime \prime }/|x^{\prime \prime }|)\) for any \(x = (x^\prime , \, x^{\prime \prime })\in U(K, \, \delta /4, \, \gamma /4)\).
In [2], this result is proved in the particular case \({\mathscr {N}}={\mathbb {S}}^{k-1}\). However, the same proof applies to a general target \({\mathscr {N}}\): the map \(\tilde{u}\) is constructed by a suitable reparametrisation of the domain \(U(K, \, \delta , \, \gamma )\), and the arguments do not rely on properties of the target \({\mathscr {N}}\) other than (Lipschitz) path-connectedness. Property (iii) follows from Remark 6 and (ii), (iv).
Proof of Lemma 5
By (3.24), we have \({{\,\mathrm{spt}\,}}R \subseteq {\overline{W}}_{{\mathfrak {S}}}\subseteq W\). By triangulating, we can write R in the form
where the coefficients \(\sigma _i\) belong to \(\pi _{k-1}({\mathscr {N}})\) and each \(T_i\subset \!\subset W\) is a convex \((n+1)\)-simplex. We apply Proposition 4, so to modify \(w_*\) in a neighbourhood of \(T_1\). We obtain a new map \(w_1\in W^{1,k}(\varOmega , \, {\mathscr {N}})\) that has a locally nice singularity at \({{\,\mathrm{spt}\,}}{\mathbf {S}}(w_*)\cup (T_1)_n\cup P_{y_*}\) (with \((T_1)_n\) is the n-skeleton of a suitable triangulation of T), satisfies \(w_1 = w_*\) on \(\varOmega {\setminus } W\) and \({\mathbf {S}}(w_1) = {\mathbf {S}}(w_*) + \sigma _1\,\partial \llbracket T_1\rrbracket \). Now, we use Proposition 4 to modify \(w_1\) in a neighbourhood of \(T_2\), and so on. By applying iteratively Proposition 4, we construct a sequence of maps \(w_1\), \(w_2\), ..., \(w_q\). The map \(w_q\) has a locally nice singularity at \({{\,\mathrm{spt}\,}}{\mathbf {S}}(w_*) \cup ({{\,\mathrm{spt}\,}}R)_n \cup P_{y_*}\), satisfies \(w_q= w_*\) on \(\varOmega {\setminus } W\) and \({\mathbf {S}}(w_q) = {\mathbf {S}}(w_*) + \partial R = S\).
To complete the proof, it only remains to modify \(w_q\) so as to satisfy (iv). Since \(W\subset \!\subset \varOmega \) has polyhedral boundary, the restriction  is a polyhedral chain. Let K be a n-face of \({{\,\mathrm{spt}\,}}{\mathbf {S}}(w_*) \cup ({{\,\mathrm{spt}\,}}R)_n\). The interior of K is contained in W and hence, for sufficiently small parameters \(\delta >0\), \(\gamma >0\), the interior of \(U(K, \, \delta , \, \gamma )\) is contained in W. Let \(\sigma _K\in \pi _{k-1}({\mathscr {N}})\) be the homotopy class of \(w_q\) around K. By Remark 7, there exists a smooth map \(\phi _K:{\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) that satisfies
is a polyhedral chain. Let K be a n-face of \({{\,\mathrm{spt}\,}}{\mathbf {S}}(w_*) \cup ({{\,\mathrm{spt}\,}}R)_n\). The interior of K is contained in W and hence, for sufficiently small parameters \(\delta >0\), \(\gamma >0\), the interior of \(U(K, \, \delta , \, \gamma )\) is contained in W. Let \(\sigma _K\in \pi _{k-1}({\mathscr {N}})\) be the homotopy class of \(w_q\) around K. By Remark 7, there exists a smooth map \(\phi _K:{\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) that satisfies
for any \(\psi \in W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap \sigma _K\). If \(\sigma _K = 0\), we choose \(\phi _K\) to be constant. We apply Lemma 6 to \(u = w_q\) and \(\phi = \phi _K\). By doing so for each K, we obtain a map \(w:\varOmega \rightarrow {\mathscr {N}}\) that agrees with \(w_*\) on \(\varOmega {\setminus }{\overline{W}}\) and is \(\eta \)-minimal on W. By Remark 6, \({\mathbf {S}}(w) = {\mathbf {S}}(w_q) = S\). Moreover, since \(\phi _K\) is constant if \(\sigma _K = 0\), w has a locally nice singularity at \(({{\,\mathrm{spt}\,}}S, \, Q_*)\) where \(Q_* := ({{\,\mathrm{spt}\,}}{\mathbf {S}}(w_*))_{n-1}\cup ({{\,\mathrm{spt}\,}}R)_{n-1}\cup P_{y_*}\). Therefore, w has all the desired properties. \(\quad \square \)
3.4.4 \(\varepsilon \)-regularisation
The map \(w:\varOmega \rightarrow {\mathscr {N}}\) given by Lemma 5 has a singularity of codimension k at \({{\,\mathrm{spt}\,}}S\), so \(w\notin W^{1,k}(\varOmega , \, {\mathscr {N}})\) unless \(S = 0\). Therefore, in order to define a recovery sequence, we need to regularise w around \({{\,\mathrm{spt}\,}}S\). We do so by defining the maps
Lemma 7
For sufficiently small \(\varepsilon \), the map \(w_\varepsilon \) defined by (ii) belongs to \((L^\infty \cap W^{1,k}_{\mathrm {loc}})(\varOmega , \, {\mathbb {R}}^m)\). Moreover, the following properties holds:
-
(i)
\(w_\varepsilon \rightarrow w\) strongly in \(W^{1,k-1}_{\mathrm {loc}}(\varOmega )\) as \(\varepsilon \rightarrow 0\).
-
(ii)
For any open set \(D\subset \!\subset \varOmega \) with polyhedral boundary, it holds that

where the constant \(C_{w, D}\) depends on the map w and on \({{\,\mathrm{dist}\,}}(D, \, \partial \varOmega )\).
-
(iii)
We have
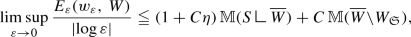
where C is a constant that depends only on \({\mathscr {N}}\), \({\mathscr {X}}\), \(\varrho \) and k.
Proof
Let \(Z_\varepsilon := \{x\in {\mathbb {R}}^{n+k}:{{\,\mathrm{dist}\,}}(x, \, {{\,\mathrm{spt}\,}}S)< \varepsilon \}\), and let \(\zeta _\varepsilon \) be the characteristic function of \(Z_\varepsilon \) (i.e. \(\zeta _\varepsilon := 1\) on \(Z_\varepsilon \), \(\zeta _\varepsilon := 0\) elsewhere).
Step 1
(Proof of (i)) Let \(D\subset \!\subset \varOmega \) be an open set. We choose a number p, with \(1< p < (k+1)/(k-1)\). Since w has a locally nice singularity at \(({{\,\mathrm{spt}\,}}S, \, Q_*)\), at a.e. point of D we have
where \(C_{w,D}\) is a constant that depends on w, \({{\,\mathrm{dist}\,}}(D, \, \partial \varOmega )\) and p, but not on \(\varepsilon \). Therefore,
By our choice of p, we have \(p-kp > -(k+1)\). Since \(Q_*\) has codimension \(k+1\), [2, Lemma 8.3] implies that the function \({{\,\mathrm{dist}\,}}^{p-kp}(\cdot , \, Q_*)\) is integrable and that
As a consequence, we have
as \(\varepsilon \rightarrow 0\), and (i) follows.
Step 2
(Proof of (ii)) Let \(D\subset \!\subset \varOmega \) and \(1< p < 1 + 1/k\). From (3.27), we deduce
The second and third term at the right-hand side are uniformly bounded with respect to \(\varepsilon \rightarrow 0\), due to [2, Lemma 8.3] and (3.28). Since \({{\,\mathrm{spt}\,}}S \cap D\) is contained in a finite union of polyhedra of codimension k or higher and D has polyhedral boundary, a computation based on Fubini theorem gives
On the other hand,  because the coefficient group \((\pi _{k-1}({\mathscr {N}}), \, |\cdot |_*)\) is discrete (Proposition 1). Thus, (ii) follows (and in particular, \(w_\varepsilon \in W^{1,k}_{\mathrm {loc}}(\varOmega , \, {\mathbb {R}}^m)\)).
because the coefficient group \((\pi _{k-1}({\mathscr {N}}), \, |\cdot |_*)\) is discrete (Proposition 1). Thus, (ii) follows (and in particular, \(w_\varepsilon \in W^{1,k}_{\mathrm {loc}}(\varOmega , \, {\mathbb {R}}^m)\)).
Step 3
(Proof of (iii)) The inequality (3.28) implies
so we only need to estimate the gradient terms. By Lemma 5, \(w_{|W}\) is \(\eta \)-minimal, with nice singularity at \((({{\,\mathrm{spt}\,}}S)\cap W, \, Q_*\cap W)\). Therefore, there exist positive numbers \(\delta \), \(\gamma \), a triangulation of \(({{\,\mathrm{spt}\,}}S)\cap W\) and, for any n-simplex K of the triangulation, a Lipschitz map \(\phi _K:{\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\) that satisfy the conditions (i)–(iii) in Definition 3.2. By taking smaller \(\delta \), \(\gamma \) if necessary, we can also assume that the interior of \(U(K, \, \delta , \, \gamma )\) is contained in W, for any n-simplex K of the triangulation. Let \(F:= W{\setminus } \cup _K U(K, \, \delta , \, \gamma )\), where the union is taken over all n-simplices K of the triangulation. We estimate separately the energy on F and on each \(U(K, \, \delta , \, \gamma )\).
Let us estimate the energy on F first. Since \(Q_*\supseteq ({{\,\mathrm{spt}\,}}S)_{n-1}\), the definition (3.1) of \(U(K, \, \delta , \, \gamma )\) implies that
(The proportionality constant at the right-hand side depends on \(\delta \), \(\gamma \).) Let us choose a number p with \(1< p < 1 + 1/k\). Since w has a locally nice singularity at \(({{\,\mathrm{spt}\,}}S\), \(Q_*)\), we obtain
for a.e. \(x\in F\) and some constant \(C_{w,W}\) that depends on w, W, p, \(\delta \) and \(\gamma \). This implies
The right-hand side is uniformly bounded with respect to \(\varepsilon \), due to [2, Lemma 8.3] and (3.28), so
Next, we estimate the energy on \(U(K, \, \delta , \, \gamma )\), with K an n-dimensional simplex in the triangulation of \(({{\,\mathrm{spt}\,}}S)\cap W\). We write \(U := U(K, \, \delta , \, \gamma )\) for brevity, and let \(x = (x^\prime , \, x^{\prime \prime })\) denote the variable in U, as in (3.1). Using Condition (ii) in Definition (3.2), we can compute explicitly the gradient of \(w_\varepsilon \), and we obtain
for a.e. \(x\in U\), where \(\nabla _{\top }\) denotes the tangential gradient on \({\mathbb {S}}^{k-1}\). (In the second inequality, we use that \(\phi _K\) is Lipschitz.) We raise to the power k both sides of this inequality, integrate over U, apply Fubini theorem and pass to polar coordinates for the integral with respect to \(x^{\prime \prime }\):
Using Condition (iii) in Definition 3.2, we deduce
where \(\sigma _K\in \pi _{k-1}({\mathscr {N}})\) is the homotopy class of \(\phi _K\) and \(E_{\min }(\sigma _K)\) is defined by (2.2). We need to distinguish two cases, depending on whether the interior of K is contained \(W_{{\mathfrak {S}}}\) or not. If the interior of K is contained in \(W_{{\mathfrak {S}}}\), then \(\sigma _K\in {\mathfrak {S}}\) because of (3.25), and (3.32) becomes

for some constant C that depends only on \({\mathscr {N}}\). (Here again, we have used that  , due to Proposition (1).) Suppose now that the interior of K is not contained in \(W_{{\mathfrak {S}}}\). The intersection between the interior of K and \(\partial W_{{\mathfrak {S}}}\) has dimension \(n-1\) at most, because we have taken \(\partial W_{{\mathfrak {S}}}\) to be transverse to \({{\,\mathrm{spt}\,}}S\). Therefore, up to refining the triangulation, we may assume that the interior of K is contained in \(W{\setminus }{\overline{W}}_{{\mathfrak {S}}}\). Then, thanks to (3.23) and (3.24), S agrees with \({\mathbf {S}}(w_*)\) in the interior of K. The chain \({\mathbf {S}}(w_*)\) takes its multiplicity in a finite set that depends only on \({\mathscr {N}}\), \({\mathscr {X}}\), \(\varrho \) (by Lemma 3) and hence, \(E_{\min }(\sigma _K)\leqq C\). Thus, (3.32) becomes
, due to Proposition (1).) Suppose now that the interior of K is not contained in \(W_{{\mathfrak {S}}}\). The intersection between the interior of K and \(\partial W_{{\mathfrak {S}}}\) has dimension \(n-1\) at most, because we have taken \(\partial W_{{\mathfrak {S}}}\) to be transverse to \({{\,\mathrm{spt}\,}}S\). Therefore, up to refining the triangulation, we may assume that the interior of K is contained in \(W{\setminus }{\overline{W}}_{{\mathfrak {S}}}\). Then, thanks to (3.23) and (3.24), S agrees with \({\mathbf {S}}(w_*)\) in the interior of K. The chain \({\mathbf {S}}(w_*)\) takes its multiplicity in a finite set that depends only on \({\mathscr {N}}\), \({\mathscr {X}}\), \(\varrho \) (by Lemma 3) and hence, \(E_{\min }(\sigma _K)\leqq C\). Thus, (3.32) becomes

Combining (3.29), (3.31), (3.33) and (3.34), the inequality (iii) follows.\(\quad \square \)
3.4.5 Proof of Theorem C.(ii) and Proposition D.(ii)
Proof of Theorem C.(ii)
Let \(S\in {\mathscr {C}}(\varOmega , \, v)\) be a finite-mass chain, and let \(\eta >0\) be a small number. Given a countable sequence \(\varepsilon \rightarrow 0\), we aim to construct \(u_\varepsilon \in (L^\infty \cap W^{1,k}_v)(\varOmega , \, {\mathbb {R}}^m)\), where \(\varepsilon \) ranges in a non-relabelled subsequence, in such a way that
where C is a constant that does not depend on \(\eta \). If we do so, the theorem will follow, by a diagonal argument. As we have seen, thanks to Proposition 5, Proposition 6 and a diagonal argument, it is not restrictive to assume that S satisfies (3.23), (3.24), (3.25). Moreover, we have

by Lemma 3 and hence, by taking a larger \(W_{{\mathfrak {S}}}\) if necessary, we can assume without loss of generality that

Step 1
(Definition of \(u_\varepsilon \)) To define the recovery sequence near the boundary of \(\varOmega \), we apply Lemma 2 to \(u_*\) and \(y_*\), and consider the map
(with \(\xi _\varepsilon \), \(\psi \) as in Lemma 2). Thanks to Lemma 2 and an averaging argument, by possibly modifying the value of \(y_*\) we have
Our recovery sequence will coincide with \(w_\varepsilon \) given by (ii) in W, where \(W_{{\mathfrak {S}}}\subset \!\subset W\subset \!\subset \varOmega \) is the open set introduced in Section 3.4.3. We need to interpolate between \(w_\varepsilon \) and \(w_{\varepsilon ,y_*}\) near W. To this end, we take a small parameter \(\theta >0\), and we let \(D_\theta := \{x\in \varOmega {\setminus }{\overline{W}} :{{\,\mathrm{dist}\,}}(x, \, W)< \theta \}\). For \(x\in D_\theta \), let \(t_\theta (x):= \theta ^{-1}{{\,\mathrm{dist}\,}}(x, \, W)\). We define
We have \(u_\varepsilon \in (L^\infty \cap W^{1,k}_v)(\varOmega , \, {\mathbb {R}}^m)\) and \(\sup _{\varepsilon }\Vert u_\varepsilon \Vert _{L^\infty (\varOmega )}<+\infty \).
Step 2
(Bounds on \(E_\varepsilon (u_\varepsilon )\)) The energy of \(u_\varepsilon \) on \(\varOmega {\setminus }({\overline{W}}\cup D_\theta )\) is bounded from above by (3.39). The energy of \(u_\varepsilon \) is bounded from above by Lemma 7:

It remains to estimate the energy of \(u_\varepsilon \) on \(D_\theta \). We first note that \(\left| \nabla t_\theta \right| = \theta ^{-1}\) and hence,
By Lemma 5, \(w = w_*\) a.e. in \(\varOmega {\setminus } W\) and in particular, \(w = w_*\) a.e. in \(D_\theta \). Therefore, for a.e. \(x\in D_\theta \) such that \(w_\varepsilon (x) = w(x)\) and \(w_{\varepsilon , y_*}(x) = w_*(x)\), we have \(u_\varepsilon (x) = w_*(x)\in {\mathscr {N}}\). Since the maps \(u_\varepsilon \) are uniformly bounded, we deduce that
From (3.41) and (3.42), we obtain
The set \(\{w_\varepsilon \ne w\}\) is the \(\varepsilon \)-neighbourhood of \({{\,\mathrm{spt}\,}}S\), which is a locally polyhedral set of codimension k, so
(see Lemma [2, Lemma 8.3] and (3.28)). Moreover, \({\mathscr {L}}^{n+k}(D_\theta )\lesssim \theta \). Then,
We choose \(\theta = \theta (\varepsilon )\) in such a way that \(\theta (\varepsilon )\rightarrow 0\) and \(\theta (\varepsilon )^{1-k}|\!\log \varepsilon |^{-1}\rightarrow 0\) as \(\varepsilon \rightarrow 0\); for instance, we take \(\theta (\varepsilon ):= |\!\log \varepsilon |^{-1/(2k - 2)}\). With this choice of \(\theta \), from (3.44), Lemma 7 and (3.39) we deduce

where \(C_{w,W}\) is a constant that depends on w and \({{\,\mathrm{dist}\,}}(W, \, \partial \varOmega )\), but not on \(\varepsilon \). By taking the limit as \(\varepsilon \rightarrow 0\), and recalling that \(\partial W\) is transverse to \({{\,\mathrm{spt}\,}}S\), we conclude that

Combining (3.39), (3.40) and (3.45), the inequality (3.36) follows.
Step 3
(\(u_\varepsilon \rightarrow w\) in \(W^{1,k-1}(\varOmega )\)) To complete the proof, it only remains to check (3.35). As an intermediate step, we prove that \(u_\varepsilon \rightarrow w\) strongly in \(W^{1,k-1}(\varOmega )\). Up to extraction of a subsequence, we have \(w_\varepsilon \rightarrow w\) in \(W^{1,k-1}(W)\) and \(w_{\varepsilon , y_*}\rightarrow w_* = w\) in \(W^{1,k-1}(\varOmega {\setminus } W)\) by Lemma 7 and Lemma 2, respectively. Thus, we only need to check that
From (3.41), using that \(w = w_*\) a.e. on \(D_{\theta (\varepsilon )}\), we deduce
The sequences \(w_\varepsilon \) and \(w_{\varepsilon , y_*}\) are strongly compact in \(W^{1,k-1}_{\mathrm {loc}}(\varOmega )\), \(W^{1,k-1}(\varOmega )\) respectively. Since \({\mathscr {L}}^{n+k}(D_{\theta (\varepsilon )})\rightarrow 0\), we have
Then, keeping in mind that \(w_{\varepsilon , y_*}\), \(w_\varepsilon \) are uniformly bounded, and using (3.39), (3.43), we obtain
Now (3.46) follows, because we have chosen \(\theta (\varepsilon )\) in such a way that \(\theta (\varepsilon )^{1-k}|\log \varepsilon |^{-1}\rightarrow 0\).
Step 4
(Proof of (3.35)) Let us take a larger, bounded domain \(\varOmega ^\prime \supset \!\supset \varOmega \) and a map \(V\in (L^\infty \cap W^{1,k}) (\varOmega ^\prime {\setminus }{\overline{\varOmega }}, \, {\mathbb {R}}^m)\) with trace v on \(\partial \varOmega \). We define
Since the traces of \(u_\varepsilon \), w agree with that of V on \(\partial \varOmega \), we have \(\tilde{u}_\varepsilon \in (L^\infty \cap W^{1,k})(\varOmega ^\prime , \, {\mathbb {R}}^m)\), \(\tilde{w}\in (L^\infty \cap W^{1,k-1})(\varOmega ^\prime , \, {\mathbb {R}}^m)\), \(\sup _\varepsilon \Vert \tilde{u}_{\varepsilon }\Vert _{L^\infty (\varOmega ^\prime )}<+\infty \) and \(\tilde{u}_{\varepsilon }\rightarrow \tilde{w}\) strongly in \(W^{1,k-1}(\varOmega ^\prime )\). By continuity of \({\mathbf {S}}\) [17, Theorem 3.1], this implies
Since \(\tilde{u}_\varepsilon =\tilde{w}\) a.e. on \(\varOmega ^\prime {\setminus }{\overline{\varOmega }}\) and the operator \({\mathbf {S}}\) is local [17, Corollary 1], we have  for a.e. y, and hence \({\mathbf {S}}_{y}(\tilde{u}_\varepsilon ) - {\mathbf {S}}_{y}(\tilde{w})\) is supported in \({\overline{\varOmega }}\) for a.e. y. For chains supported in a compact subset of \(\varOmega ^\prime \), the relative flat norm \({\mathbb {F}}_{\varOmega ^\prime }\) is equivalent to \({\mathbb {F}}\) (see e.g. [17, Remark 2.2]). Therefore, we have
for a.e. y, and hence \({\mathbf {S}}_{y}(\tilde{u}_\varepsilon ) - {\mathbf {S}}_{y}(\tilde{w})\) is supported in \({\overline{\varOmega }}\) for a.e. y. For chains supported in a compact subset of \(\varOmega ^\prime \), the relative flat norm \({\mathbb {F}}_{\varOmega ^\prime }\) is equivalent to \({\mathbb {F}}\) (see e.g. [17, Remark 2.2]). Therefore, we have
By [17, Eq. (3.25)] we have  and
and  for a.e. y, so
for a.e. y, so

Since \(\tilde{u}_\varepsilon =u_\varepsilon \) and \(\tilde{w} = w\) a.e. on \(\varOmega \), [17, Corollary 1] implies

and finally, recalling (3.37), we obtain
From (3.47) and (3.48) we deduce (3.35), and the proof is complete.\(\quad \square \)
The proof of Proposition D.(ii) follows along the same lines, and in fact, is even simpler.
Proof of Proposition D
Let S be an n-dimensional relative boundary of finite mass — that is, S has the form  , where R is an \((n+1)\)-chain of finite mass such that \({\mathbb {M}}(\partial R)<+\infty \). By a density argument, we can assume without loss of generality that R is polyhedral. By Proposition 6, we can also assume that \(\partial R\) takes its multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4). Finally, by translating the support of R and applying Thom’s transversality theorem, we can assume that
, where R is an \((n+1)\)-chain of finite mass such that \({\mathbb {M}}(\partial R)<+\infty \). By a density argument, we can assume without loss of generality that R is polyhedral. By Proposition 6, we can also assume that \(\partial R\) takes its multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4). Finally, by translating the support of R and applying Thom’s transversality theorem, we can assume that

Let \(w_*\in {\mathscr {N}}\) be a constant, and let \(\eta >0\) be a small parameter. We repeat the same arguments of Lemma 5 and modify the constant map \(w_*\) in a neighbourhood of \({{\,\mathrm{spt}\,}}R\). We obtain a new map \(w:{\mathbb {R}}^{n+k}\rightarrow {\mathscr {N}}\) that
-
(i)
has a nice singularity at \(({{\,\mathrm{spt}\,}}(\partial R), \, ({{\,\mathrm{spt}\,}}(\partial R))_{n-1})\);
-
(ii)
satisfies \({\mathbf {S}}(w) = {\mathbf {S}}(w_*) + \partial R = \partial R\);
-
(iii)
is \(\eta \)-minimal.
Let
By the same computations as in Lemma 7, we obtain that \(w_\varepsilon \rightarrow w\) strongly in \(W^{1,k-1}({\mathbb {R}}^{n+k})\) and that

where \(\varOmega ^\prime \supset \!\supset \varOmega \) is any open set, with polyhedral boundary, such that \(\partial \varOmega \) is transverse to \({{\,\mathrm{spt}\,}}(\partial R)\). (The latter condition is generic, by Thom’s transversality theorem.) The continuity of \({\mathbf {S}}\) [17, Theorem 3.1], together with the fact that the operator \({\mathbf {S}}\) is local [17, Corollary 1], implies  in Y. We let \(\varOmega ^\prime \searrow \varOmega \) in (3.50), and we deduce
in Y. We let \(\varOmega ^\prime \searrow \varOmega \) in (3.50), and we deduce

Since \(\eta \) may be taken arbitrarily small, Proposition D.(ii) follows, by a diagonal argument. \(\quad \square \)
4 Compactness and Lower Bounds
4.1 A Local Compactness Result
The aim of this section is to prove Statement (i) of Theorem C. As an intermediate step, we will prove the following result, which is a local version of Theorem C.(i). We recall that we have fixed a number \(\delta ^*\in (0, \, {{\,\mathrm{dist}\,}}({\mathscr {N}}, \, {\mathscr {X}}))\) and that \(B^* := B^m(0, \, \delta ^*)\subseteq {\mathbb {R}}^m\).
Proposition 7
Let \(U\subset \!\subset U^\prime \) be bounded domains in \({\mathbb {R}}^{n+k}\). Let \((u_\varepsilon )_\varepsilon \) be a countable sequence of maps in \(W^{1,k}(U^\prime , \, {\mathbb {R}}^m)\) such that
Then, there exist a (non-relabelled) subsequence and a finite-mass chain \(S\in {\mathbb {M}}_n({\overline{U}}^\prime ; \, \pi _{k-1}({\mathscr {N}}))\) such that

(\({\mathbb {F}}_U\) is the relative flat norm, see (2.5)).
Throughout this section, we fix bounded domains \(U\subset \!\subset U^\prime \subseteq {\mathbb {R}}^{n+k}\) and a countable sequence \((u_\varepsilon )\) in \(W^{1,k}(U^\prime , \, {\mathbb {R}}^m)\) that satisfies (4.1). By an approximation argument, using the continuity of \({\mathbf {S}}\) (Proposition 3 and [17, Theorem 3.1]), we can assume without loss of generality that the maps \(u_\varepsilon \) are smooth and bounded. For any \(\varepsilon >0\) and \(y\in B^*\), we define the measure

Thanks to \(({\hbox {P}}_2)\) (Proposition 3), \(\mu _{\varepsilon ,y}\) is a bounded Radon measure for a.e. y.
4.1.1 Choice of a Grid
As in [2], we define a grid \({\mathscr {G}}\) of size \(h > 0\) as a collection of closed cubes of the form
for some \(a\in {\mathbb {R}}^{n+k}\). For \(j\in {\mathbb {N}}\), \(0 \leqq j\leqq n+k\), we denote by \({\mathscr {G}}_j\) the collection of the (closed) j-cells of \({\mathscr {G}}\), and we define the j-skeleton of \({\mathscr {G}}\), \(R_j := \cup _{K\in {\mathscr {G}}_j} K\). We let \(\tilde{R}_{k}\) be the union of all the cells \(K\in {\mathscr {G}}_k\) that are parallel to the k-plane spanned by \(\{{\mathbf {e}}_{n+1}, \, \ldots , \, {\mathbf {e}}_{n+k}\}\). Given an open set \(V\subseteq U^\prime \), we denote by \(R_k(V)\) the union of the k-cells \(K\in {\mathscr {G}}\) such that \(K\cap V \ne \emptyset \) (so \(R_k(V)\supseteq R_k\cap V\)). Given \({\mathscr {G}}= {\mathscr {G}}(a, \, h)\), the grid
will be called the dual grid of \({\mathscr {G}}\). We will denote by \({\mathscr {G}}^\prime _k\) the collections of k-cells of \({\mathscr {G}}^\prime \) and by \(R^\prime _k\) its k-skeleton. For each \(K\in {\mathscr {G}}_k\) there exists a unique \(K^\prime \in {\mathscr {G}}^\prime _{n}\), called the dual cell of K, such that \(K\cap K^\prime \ne \emptyset \).
We are now going to construct a sequence of grids \({\mathscr {G}}^\varepsilon \) with suitable properties. The construction is analogous to [2, Lemma 3.11]. Let us take a function \(h:(0, 1)\rightarrow {\mathbb {R}}^+\) such that
For instance, we may take \(h(\varepsilon ) := \left| \log \varepsilon \right| ^{-2}\).
Lemma 8
For any fixed parameter \(\delta > 0\) and any \(\varepsilon < 1\) there exists a grid \({\mathscr {G}}^\varepsilon \) of size \(h(\varepsilon )\) that satisfies the following properties:
Here \(\mu _{\varepsilon ,y}\) is the measure defined by (4.4).
Proof
We take a grid \({\mathscr {G}}^\varepsilon := {\mathscr {G}}(a, \, h(\varepsilon ))\) of the form (4.5). We claim that it is possible to choose \(a\in (0, \, h(\varepsilon ))^{n+k}\) in such a way that (4.7)–(4.10) are satisfied. For (4.7)–(4.9), we can repeat verbatim the arguments in [2]. As for (4.10), let us call \(R^\varepsilon _{k-1}(a)\) the \((k-1)\)-skeleton of the grid \({\mathscr {G}}(a, \, h(\varepsilon ))\). Thanks to \(({\hbox {P}}_2)\) in Section 2, \(\mu _{\varepsilon ,y}\) is a finite, non-negative Radon measure for a.e. \(y\in B^*\). By applying [25, Lemma 5.2], together with a scaling argument, we obtain

for a.e \(y\in B^*\). By integrating the previous inequality with respect to y and applying \(({\hbox {P}}_2)\), we obtain
Now the lemma follows by an averaging argument, see e.g. [2, Lemma 8.4]. \(\quad \square \)
Throughout the rest of this section, we suppose that (4.6) is satisfied, we fix \(\delta \in (0, \, 1)\) and we consider the sequence of grids \({\mathscr {G}}^\varepsilon \) given by Lemma 8. Without loss of generality, we will also assume that
(\(R^\varepsilon _{n+k}({\overline{U}})\) is the union of the closed cubes \(K\in {\mathscr {G}}^\varepsilon \) such that \(K\cap {\overline{U}}\ne \emptyset \)).
Lemma 9
For any \(\alpha \in (0, \, k/(k^2-k+2))\), there holds
where \(C(\delta , \, \alpha )\) is a positive constant that only depends on \({\mathscr {N}}\), k, f, n, \(\delta \) and \(\alpha \).
Proof
We repeat the arguments of [2, Lemma 3.4]. Let \(d_\varepsilon := {{\,\mathrm{dist}\,}}(u_\varepsilon , \, {\mathscr {N}})\), let \(\lambda \in (0, \, 1/k)\) be a parameter, and let \(G:{\mathbb {R}}^+\rightarrow {\mathbb {R}}^+\) be defined by \(G(t) := t^{2\lambda /(k - k\lambda ) + 1}\). Thanks to \(({\hbox {H}}_3)\), we have \(d_\varepsilon ^2\lesssim f(u_\varepsilon )\). Therefore, by (4.9) and (4.11), we obtain
The Young inequality and the chain rule imply that
Since we have assumed that \(\lambda < 1/k\), we have \(k - k\lambda > k-1\) and hence, for any \((k-1)\)-cell \(K\subseteq R^\varepsilon _{k-1}(U)\), we can bound the oscillation of \(G\circ d_\varepsilon \) on K by Sobolev embedding:
The inverse \(G^{-1}\) of G is well-defined and Hölder continuous of exponent \((k-k\lambda )/(2\lambda + k - k\lambda )\), so
On the other hand, we can bound the integral average of \(d_\varepsilon \) on K thanks to (4.12):
Combining (4.14) with (4.15), and letting \(\lambda \nearrow 1/k\), the lemma follows. \(\quad \square \)
4.1.2 A Polyhedral Approximation of \({\mathbf {S}}_y(u_\varepsilon )\)
Let \(y\in B^*\) be fixed in such a way that \({\mathbf {S}}_{y}(u_\varepsilon )\) has finite mass for any \(\varepsilon \). (Thanks to \(({\hbox {P}}_2)\), the set of y such that this property is not satisfied is negligible, because the sequence \((u_\varepsilon )\) is assumed to be countable.) We are going to construct a polyhedral approximation of \({\mathbf {S}}_{y}(u_\varepsilon )\), supported on the dual n-skeleton \((R^\varepsilon )^\prime _n\) of the grid.
Thanks to Lemma 9, there exists \(\varepsilon _0>0\) (depending on \(\delta _*\), but not on y) such that
for any \(x\in R^\varepsilon _{k-1}(U)\) and any \(\varepsilon \in (0, \, \varepsilon _0]\). As a consequence, the projection \(\varrho (u_\varepsilon - y)\) is well-defined and smooth on \(R^\varepsilon _{k-1}(U)\) for \(\varepsilon \in (0, \, \varepsilon _0]\). For any \(K\in {\mathscr {G}}^\varepsilon _{k}\), let \(\gamma ^\varepsilon (K)\in \pi _{k-1}({\mathscr {N}})\) be the homotopy class of \(\varrho (u_\varepsilon - y)\) on \(\partial K\). The quantity \(\gamma ^\varepsilon (K)\) does not depend on the choice of \(y\in B^*\), because \(\varrho (u_\varepsilon - y)_{|\partial K}\) and \(\varrho (u_\varepsilon )_{|\partial K}\) are homotopic to each other, due to (4.16); a homotopy is defined by \((x, \, t)\in \partial K\times [0, \,1]\mapsto \varrho (u_\varepsilon (x) - ty)\). We define the polyhedral chain
where \(K^\prime \in ({\mathscr {G}}^\varepsilon )^\prime _n\) is the dual cell to K. The chain \(T^\varepsilon \) depends on the choice of the grid, but not on y.
Lemma 10
For any \(\varepsilon \in (0, \, \varepsilon _0]\) and any \(y\in B^*\) such that \({\mathbf {S}}_{y}(u_\varepsilon )\) has finite mass, there holds

Moreover,  .
.
Proof
Essentially, this lemma is a particular instance of the Deformation Theorem for flat chains [26, Theorem 7.3] (see also [2, Lemma 3.8] for a statement which is specifically tailored for application to Ginzburg–Landau functionals). Nevertheless, we provide details for the convenience of the reader.
Let \(\varepsilon \in (0, \, \varepsilon _0]\) be fixed. By [2, Lemma 3.8.(i)] there exists a locally Lipschitz retraction \(\zeta ^\varepsilon :{\mathbb {R}}^{n+k}{\setminus } R^\varepsilon _{k-1}\rightarrow (R^\varepsilon )^\prime _{n}\), which maps each cube of \({\mathscr {G}}^\varepsilon \) into itself and satisfies
By (4.16), we have \(u_\varepsilon (x) - y\notin {\mathscr {X}}\) for any \(x\in R^\varepsilon _{k-1}(U)\). By construction (see [17, Section 3]), this implies \({{\,\mathrm{spt}\,}}({\mathbf {S}}_{y}(u_\varepsilon ))\cap R^\varepsilon _{k-1}(U) = \emptyset \), so the push-forward  is well-defined. Let \(\tau ^\varepsilon :[0, \, 1]\times ({\mathbb {R}}^{n+k}{\setminus } R^\varepsilon _{k-1})\rightarrow {\mathbb {R}}^{n+k}\) be given by
is well-defined. Let \(\tau ^\varepsilon :[0, \, 1]\times ({\mathbb {R}}^{n+k}{\setminus } R^\varepsilon _{k-1})\rightarrow {\mathbb {R}}^{n+k}\) be given by
and let I be the 1-chain, with integer multiplicity, carried by the interval \([0, \, 1]\) with positive orientation. We remark that

Indeed, since \(\zeta ^\varepsilon \) maps each cell K of \({\mathscr {G}}^\varepsilon \) into itself, we have \((\tau ^\varepsilon )^{-1}(U)\subseteq [0, \, 1]\times R^\varepsilon _{n+k}({\overline{U}}) \subset \!\subset [0, \, 1]\times U^\prime \) by (4.11). This implies

because  [17, Theorem 3.1]. This proves (4.20). As a consequence, by applying the homotopy formula (see e.g. [26, Eq. (6.3) p. 172]), we deduce that
[17, Theorem 3.1]. This proves (4.20). As a consequence, by applying the homotopy formula (see e.g. [26, Eq. (6.3) p. 172]), we deduce that

From [26, Eq. (6.5) p. 172]
and (4.19), we obtain
Then, by the properties of the relative flat norm (see e.g. [17, Lemma 2]) and (4.21), we deduce
To conclude the proof of (4.18), it suffices to show that \(\zeta ^\varepsilon _{*}({\mathbf {S}}_{y}(u_\varepsilon ))\) agrees with \(T^\varepsilon \) inside U. By [26, Lemma 7.2],  is a n-polyhedral chain of the grid \(({\mathscr {G}}^\varepsilon )^\prime \); in particular, its multiplicity is constant on every n-cell of \(({\mathscr {G}}^\varepsilon )^\prime \). We want to compute such multiplicities. Let us take \(K\in {\mathscr {G}}^\varepsilon _k\) and its dual cell \(K^\prime \in ({\mathscr {G}}^\varepsilon )^\prime _n\), and let x be the unique element of \(K\cap K^\prime \). By construction of \(\zeta ^\varepsilon \) (see [2, Lemma 3.8 and Figure 3.2]), we have \((\zeta ^\varepsilon )^{-1}(x) = K{\setminus }\partial K\). By Thom’s parametric transversality theorem, we can assume with no loss of generality that K intersects transversally the support of \({\mathbf {S}}_{y}(u_\varepsilon )\). Then, by definition of push-forward, we have
is a n-polyhedral chain of the grid \(({\mathscr {G}}^\varepsilon )^\prime \); in particular, its multiplicity is constant on every n-cell of \(({\mathscr {G}}^\varepsilon )^\prime \). We want to compute such multiplicities. Let us take \(K\in {\mathscr {G}}^\varepsilon _k\) and its dual cell \(K^\prime \in ({\mathscr {G}}^\varepsilon )^\prime _n\), and let x be the unique element of \(K\cap K^\prime \). By construction of \(\zeta ^\varepsilon \) (see [2, Lemma 3.8 and Figure 3.2]), we have \((\zeta ^\varepsilon )^{-1}(x) = K{\setminus }\partial K\). By Thom’s parametric transversality theorem, we can assume with no loss of generality that K intersects transversally the support of \({\mathbf {S}}_{y}(u_\varepsilon )\). Then, by definition of push-forward, we have
and hence

Now, (4.18) follows from (4.22) and (4.23). Moreover, (4.23) implies

because \({\mathbf {S}}_{y}(u_\varepsilon )\) has no boundary inside \(U^\prime \) [17, Theorem 3.1, \(({\hbox {S}}_{3})\)]. \(\quad \square \)
To bound the mass of \(T^\varepsilon \), we will use the following result.
Lemma 11
There exist positive numbers \(\delta _1=\delta _1({\mathscr {N}}, \, f)\), \(C_0 = C_0({\mathscr {N}}, \, f)\) and, for \(r>0\), \(\varepsilon _r=\varepsilon _r(r, \, {\mathscr {N}}, \, f)\), \(C_r = C_r(r, \, {\mathscr {N}}, \, f)\) such that the following statement holds. Let \(Q^k_h := [-h/2, \, h/2]^k\) be a cube of edge length \(h>0\). Suppose that \(u\in W^{1,k}(Q^k_h, \, {\mathbb {R}}^m)\) satisfies
Let \(\gamma \in \pi _{k-1}({\mathscr {N}})\) be the homotopy class of u on \(\partial Q^k_h\). Let \(0< \varepsilon < h^{k/2}/2\) be such that
Then,
The proof of Lemma 11 will be given in Appendix C.
Lemma 12
For any r, \(\delta \) and for sufficiently small \(\varepsilon \), there holds

where \(c_{r,\delta }(\varepsilon )>0\) is such that \(c_{r,\delta }(\varepsilon )\rightarrow 0\) as \(\varepsilon \rightarrow 0\). Moreover, if L is the k-plane spanned by \(\{{\mathbf {e}}_{n+1}, \, \ldots , \, {\mathbf {e}}_{n+k}\}\), then there holds

Proof
We first remark that

Let \(K\in {\mathscr {G}}^\varepsilon _k\) be a k-cell such that \(K\cap U\ne \emptyset \). We claim that
Indeed, thanks to \(({\hbox {P}}_0)\) and the definition of \({\mathbb {I}}\) (see e.g. [17, Section 2.1]), we have
for any \(y\in B^*\). By averaging both sides with respect to \(y\in B^*\), and by applying \(({\hbox {P}}_2)\) from Proposition 3, we obtain
We can bound the right-hand side from above with the help of (4.8), so the claim (4.27) follows.
From (4.1), (4.6) and (4.27), we deduce
and this fact, together with (4.16), shows that the assumptions of Lemma 11 are satisfied for \(\varepsilon \) small enough. By applying Lemma 11, (4.6) and (4.27), we obtain the following bound:
We multiply both sides by \(h(\varepsilon )^n\left| \log \varepsilon \right| ^{-1}\) and sum over K. Thanks to (4.26), we obtain

The right-hand side can now be bounded from above with the help of Lemma 8, so (4.24) follows. The proof of (4.25) is analougous; in this case, we sum over the cells K that are parallel to the k-plane spanned by \(\{{\mathbf {e}}_{n+1}, \, \ldots , \, {\mathbf {e}}_{n+k}\}\) and use (4.7). \(\quad \square \)
4.1.3 Proof of Proposition 7
By combining the results in the previous section, we prove the following lemma, which is analougous to [2, Proposition 3.1]. For any n-plane \(L\subseteq {\mathbb {R}}^{n+k}\), we denote by \(\pi _{L}:{\mathbb {R}}^{n+k}\rightarrow L\) the orthogonal projection onto L.
Lemma 13
Let \(U\subset \!\subset U^\prime \) be bounded domains in \({\mathbb {R}}^{n+k}\). Let \((u_\varepsilon )_\varepsilon \) be a countable sequence of smooth, bounded maps that satisfy (4.1). Let \(L\subseteq {\mathbb {R}}^{n+k}\) be a n-plane. Then, there exist a (non-relabelled) subsequence and a finite-mass chain \(S\in {\mathbb {M}}_n({\overline{U}}^\prime ; \, \pi _{k-1}({\mathscr {N}}))\) such that

Proof
Up to rotations we can assume without loss of generality that L is the k-plane spanned by \(\{{\mathbf {e}}_{n+1}, \, \ldots , \, {\mathbf {e}}_{n+k}\}\). By Lemma 10 and Lemma 12, we know that  and
and  is uniformly bounded with respect to \(\varepsilon \). Then, by applying compactness results for the flat norm (see e.g. [17, Lemmas 5 and 6] for a statement in terms of the relative flat norm), we find a (non-relabelled) subsequence and a finite-mass chain \(S\in {\mathbb {M}}_n({\overline{U}}; \, \pi _{k-1}({\mathscr {N}}))\) such that
is uniformly bounded with respect to \(\varepsilon \). Then, by applying compactness results for the flat norm (see e.g. [17, Lemmas 5 and 6] for a statement in terms of the relative flat norm), we find a (non-relabelled) subsequence and a finite-mass chain \(S\in {\mathbb {M}}_n({\overline{U}}; \, \pi _{k-1}({\mathscr {N}}))\) such that

The triangle inequality and Lemma 10 imply
and the right-hand side tends to zero as \(\varepsilon \rightarrow 0\), due to (4.1) and (4.30). Thus, (4.28) follows. By passing to the limit in (4.31) first as \(r\rightarrow 0\), then as \(\delta \rightarrow 0\), we obtain (4.29). \(\quad \square \)
Now, Proposition 7 can be deduced from Lemma 13 by a localisation argument, with the help of the following lemma.
Lemma 14
Let \(S\in {\mathbb {M}}_n({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\) be a chain of finite mass. Then, there holds

where the supremum is taken over all sequences of pairwise disjoint open sets \(U_i\) and n-planes \(L_i\subseteq {\mathbb {R}}^{n+k}\).
The proof will be given in Appendix D.2. Once Lemma 14 is proved, Proposition 7 follows by repeating verbatim the arguments of [2, Theorem 1.1.(i)], so we skip the proof of Proposition 7.
4.2 Compactness and Lower Bounds for the Boundary Value Problem
The aim of this section is to complete the proof of Theorem C.(i). We will deduce Theorem C.(i) from its local counterpart, i.e. Proposition 7, with the help of the extension result, Lemma 2.
Proof of Theorem C.(i)
Let \((u_\varepsilon )_\varepsilon \subseteq W^{1,k}_v(\varOmega , \, {\mathbb {R}}^m)\) be such that \(\sup _\varepsilon {\left| \log \varepsilon \right| ^{-1}}{E_\varepsilon (u_\varepsilon )} <+\infty \). Let \(\tilde{u}\in (L^\infty \cap W^{1,k})({\mathbb {R}}^{n+k}, \,{\mathbb {R}}^m)\) be such that \(\tilde{u} = v\) on \(\partial \varOmega \). Let \(\varOmega ^\prime \), \(\varOmega ^{\prime \prime }\) be bounded domains in \({\mathbb {R}}^{n+k}\), such that \(\varOmega \subset \!\subset \varOmega ^\prime \subset \!\subset \varOmega ^{\prime \prime }\). By applying Lemma 2, we find \(y\in B^*\), a subsequence \(\varepsilon \rightarrow 0\) and maps \(w_{\varepsilon ,y}\in (L^\infty \cap W^{1,k}) (\varOmega ^{\prime \prime }{\setminus }{\overline{\varOmega }}, \, {\mathbb {R}}^m)\) that agree with v on \(\partial \varOmega \) and satisfy
Lemma 2 also implies that the sequence \((w_{\varepsilon , y})\) converges \(W^{1,k-1}(\varOmega ^{\prime \prime }{\setminus }{\overline{\varOmega }})\)-strongly to a limit \(w_y\), and that \({\mathbf {S}}(w_y) = {\mathbf {S}}_y(\tilde{u})\). Then, the continuity of \({\mathbf {S}}\) [17, Theorem 3.1] implies
We define the map \(\tilde{u}_\varepsilon \in (L^\infty \cap W^{1,k}) (\varOmega ^{\prime \prime }, \, {\mathbb {R}}^m)\) by setting \(\tilde{u}_\varepsilon := u_\varepsilon \) on \(\varOmega \) and \(\tilde{u}_\varepsilon := w_{\varepsilon ,y}\) on \(\varOmega ^{\prime \prime }{\setminus }{\overline{\varOmega }}\). Since the operator \({\mathbf {S}}\) is local [17, Corollary 1], we have

for a.e. \(y^\prime \in B^*\). Therefore, from (4.33) and [17, Lemma 3] we obtain
We are now in the position to apply our local result, Proposition 7, to the sequence \(\tilde{u}_\varepsilon \) and the open sets \(\varOmega ^\prime \subset \!\subset \varOmega ^{\prime \prime }\). As a result, we obtain a finite-mass chain \(\tilde{S}\) such that, up to subsequences,
By [17, Lemma 3],
This condition, combined with (4.34), implies that  and hence, the chain
and hence, the chain

is supported in \({\overline{\varOmega }}\). At the same time, we have  for a.e. \(y^\prime \in B^*\). For chains supported in a compact subset of \(\varOmega ^\prime \), the relative flat norm \({\mathbb {F}}_{\varOmega ^\prime }\) is equivalent to \({\mathbb {F}}\) (see e.g. [17, Remark 2.2]) and hence, (4.35) implies
for a.e. \(y^\prime \in B^*\). For chains supported in a compact subset of \(\varOmega ^\prime \), the relative flat norm \({\mathbb {F}}_{\varOmega ^\prime }\) is equivalent to \({\mathbb {F}}\) (see e.g. [17, Remark 2.2]) and hence, (4.35) implies
By \(({\hbox {P}}_3)\), \({\mathbf {S}}_{y^\prime }(u_\varepsilon )\in {\mathscr {C}}(\varOmega , \, v)\) for any \(\varepsilon \) and a.e. \(y^\prime \in B^*\). The set \({\mathscr {C}}(\varOmega , \, v)\) is closed with respect to the \({\mathbb {F}}\)-norm (this follows from the isoperimetric inequality, see e.g. [26, Statement (7.6)]). Therefore, \(S\in {\mathscr {C}}(\varOmega , \, v)\).
It only remain to prove the upper bound on the mass of S. Let \(A\subseteq {\mathbb {R}}^{n+k}\) be an open set. We extract a (non-relabelled) subsequence, in such a way that \(\liminf _{\varepsilon \rightarrow 0}\left| \log \varepsilon \right| ^{-1} E_\varepsilon (u_\varepsilon , A\cap \varOmega )\) is achieved as a limit. For any integer \(j\geqq 1\), let \(A_j :=\{x\in A:{{\,\mathrm{dist}\,}}(x, \, \partial A)\geqq 1/j\}\). By applying Proposition 7 and a diagonal argument, we find a subsequence such that

By construction, S is supported in \({\overline{\varOmega }}\), so  . Then, by applying Lemma 2, we obtain
. Then, by applying Lemma 2, we obtain

for some constant C that does not depend on \(\varepsilon \), j, \(\varOmega ^{\prime \prime }\). Letting \(j\rightarrow +\infty \), \(\varOmega ^{\prime \prime }\searrow \varOmega \), we conclude that

and the proof is complete. \(\quad \square \)
Statement (i) in Proposition D also follows by Proposition 7, in a similar way.
5 Proof of Theorem A
Let \(u_{\varepsilon ,\min }\) be a minimiser of the functional \(E_\varepsilon \) subject to the boundary condition \(u = v\) on \(\partial \varOmega \), and let

We have \(\sup _\varepsilon \mu _{\varepsilon ,\min }({\mathbb {R}}^{n+k}) < +\infty \) by Remark 9 and hence, up to a subsequence, \(\mu _{\varepsilon ,\min }\) converges \({\hbox {weakly}}^*\) to a limit \(\mu _{\min }\), in the sense of measures on \({\mathbb {R}}^{n+k}\). By applying Theorem C.(i), we find a chain \(S_{\min }\in {\mathscr {C}}(\varOmega , \, v)\) such that

Theorem C.(ii) implies that \(S_{\min }\) is mass-minimising in \({\mathscr {C}}(\varOmega , \, v)\). Moreover, by the properties of \({\hbox {weak}}^*\) convergence, from (5.1) we obtain

Let \(E\subseteq {\mathbb {R}}^{n+k}\) be a Borel set, let \(U\subseteq {\mathbb {R}}^{n+k}\) be an open set and let \(K\subseteq {\mathbb {R}}^{n+k}\) be a compact set such that \(K\subseteq E \subseteq U\). For any \(t\in (0, \, {{\,\mathrm{dist}\,}}(K, \, \partial U))\), let \(U_t := \{x\in U:{{\,\mathrm{dist}\,}}(x, \, \partial U)> t\} \supseteq K\). Since \(\mu _{\min }\) is a finite measure, we have \(\mu _{\min }(\partial U_{t}) = 0\) for all but countably many \(t\in (0, \, {{\,\mathrm{dist}\,}}(K, \, \partial U))\). Therefore, there holds

Letting \(U\searrow K\), \(K\nearrow E\), we conclude that  . (The measure
. (The measure  is Radon, because by construction, it is the \({\hbox {weak}}^*\) limit of a sequence of Radon measures, associated with polyhedral approximations of \(S_{\min }\); see [26, Section 4].) As a consequence,
is Radon, because by construction, it is the \({\hbox {weak}}^*\) limit of a sequence of Radon measures, associated with polyhedral approximations of \(S_{\min }\); see [26, Section 4].) As a consequence,  is a non-negative measure. However, Theorem C.(ii) implies that \(\mu _{\min }({\mathbb {R}}^{n+k}) = \lim _{\varepsilon \rightarrow 0} \mu _{\varepsilon ,\min }({\mathbb {R}}^{n+k})\leqq {\mathbb {M}}(S_{\min })\), so
is a non-negative measure. However, Theorem C.(ii) implies that \(\mu _{\min }({\mathbb {R}}^{n+k}) = \lim _{\varepsilon \rightarrow 0} \mu _{\varepsilon ,\min }({\mathbb {R}}^{n+k})\leqq {\mathbb {M}}(S_{\min })\), so  .
.
References
Alberti, G., Baldo, S., Orlandi, G.: Functions with prescribed singularities. J. Eur. Math. Soc. (JEMS) 5(3), 275–311, 2003. https://doi.org/10.1007/s10097-003-0053-5
Alberti, G., Baldo, S., Orlandi, G.: Variational convergence for functionals of Ginzburg-Landau type. Indiana Univ. Math. J. 54(5), 1411–1472, 2005. https://doi.org/10.1512/iumj.2005.54.2601
Alicandro, R., Ponsiglione, M.: Ginzburg–Landau functionals and renormalized energy: a revised \(\Gamma \)-convergence approach. J. Funct. Anal. 266(8), 4890–4907, 2014. https://doi.org/10.1016/j.jfa.2014.01.024
Ambrosio, L., Soner, H.M.: Level set approach to mean curvature flow in arbitrary codimension. J. Differ. Geom. 43(4), 693–737, 1996
Bauman, P., Park, J., Phillips, D.: Analysis of nematic liquid crystals with disclination lines. Arch. Ration. Mech. Anal. 205(3), 795–826, 2012. https://doi.org/10.1007/s00205-012-0530-7
Bethuel, F.: A characterization of maps in \({H}^1({B}^3, {S}^2)\) which can be approximated by smooth maps. Ann l’Inst Henri Poincare Non Linear Anal 7(4), 269–286, 1990. https://doi.org/10.1016/S0294-1449(16)30292-X
Bethuel, F., Brezis, H., Coron, J.M.: Relaxed Energies for Harmonic Maps, pp. 37–52. Birkhäuser Boston, Boston, MA (1990). https://doi.org/10.1007/978-1-4757-1080-9_3
Bethuel, F., Brezis, H., Hélein, F.: Ginzburg–Landau Vortices. Progress in Nonlinear Differential Equations and their Applications, 13. Birkhäuser Boston Inc., Boston, MA (1994). https://doi.org/10.1007/978-1-4612-0287-5
Bethuel, F., Brezis, H., Orlandi, G.: Asymptotics for the Ginzburg–Landau equation in arbitrary dimensions. J. Funct. Anal. 186(2), 432–520, 2001. https://doi.org/10.1006/jfan.2001.3791
Bethuel, F., Demengel, F.: Extensions for Sobolev mappings between manifolds. Cal. Var. Partial Differ. Equ. 3(4), 475–491, 1995. https://doi.org/10.1007/BF01187897
Bourgain, J., Brezis, H., Mironescu, P.: On the structure of the Sobolev space \({H}^{1/2}\) with values into the circle. C. R. l’Acad. Sci. Ser. I Math. 331(2), 119–124, 2000. https://doi.org/10.1016/S0764-4442(00)00513-9
Bousquet, P., Ponce, A.C., Van Schaftingen, J.: Density of smooth maps for fractional Sobolev spaces \({W}^{s, p}\) into \(\ell \) simply connected manifolds when \(s\ge 1\). Conflu. Math. 5(2), 3–24, 2013. https://doi.org/10.5802/cml.5
Brezis, H., Coron, J.M., Lieb, E.H.: Harmonic maps with defects. Commun. Math. Phys. 107(4), 649–705, 1986
Brezis, H., Nirenberg, L.: Degree theory and BMO. I. Compact manifolds without boundaries. Sel. Math. (N.S.) 1(2), 197–263, 1995. https://doi.org/10.1007/BF01671566
Canevari, G.: Biaxiality in the asymptotic analysis of a 2D Landau-de Gennes model for liquid crystals. ESAIM Control Optim. Calc. Var. 21(1), 101–137, 2015. https://doi.org/10.1051/cocv/2014025
Canevari, G.: Line defects in the small elastic constant limit of a three-dimensional Landau-de Gennes model. Arch. Ration. Mech. Anal. 223(2), 591–676, 2017. https://doi.org/10.1007/s00205-016-1040-9
Canevari, G., Orlandi, G.: Topological singular set of vector-valued maps, I: applications to manifold-constrained Sobolev and BV spaces. Calc. Var. Partial Differ. Equ. 58(2), 72, 2019. https://doi.org/10.1007/s00526-019-1501-8
Chemin, A., Henrotte, F., Remacle, J.F., van Schaftingen, J.: Representing Three-Dimensional Cross Fields Using Fourth Order Tensors, pp. 89–108. Springer, Cham 2019. https://doi.org/10.1007/978-3-030-13992-6_6
Chen, Y.M., Struwe, M.: Existence and partial regularity results for the heat flow for harmonic maps. Math. Z. 201(1), 83–103, 1989. https://doi.org/10.1007/BF01161997
Chiron, D.: étude mathématique de modèles issus de la physique de la matière condensée. Ph.D. Thesis, Université Pierre et Marie Curie–Paris 6 (2004)
Contreras, A., Jerrard, R.L.: Nearly parallel vortex filaments in the 3D Ginzburg–Landau equations. Geom. Funct. Anal. 27(5), 1161–1230, 2017. https://doi.org/10.1007/s00039-017-0425-8
Contreras, A., Lamy, X.: Singular perturbation of manifold-valued maps with anisotropic energy (2018). Preprint arXiv: 1809.05170
De Gennes, P.G., Prost, J.: The Physics of Liquid Crystals. International Series of Monographs on Physics. Clarendon Press, Oxford 1993
Diening, L., Stroffolini, B., Verde, A.: The \(\phi \)-harmonic approximation and the regularity of \(\phi \)-harmonic maps. J. Differ. Equ. 253(7), 1943–1958, 2012. https://doi.org/10.1016/j.jde.2012.06.010
Federer, H., Fleming, W.H.: Normal and integral currents. Ann. Math. 2(72), 458–520, 1960
Fleming, W.H.: Flat chains over a finite coefficient group. Trans. Am. Math. Soc. 121, 160–186, 1966
Giaquinta, M., Modica, G., Souček, J.: Cartesian currents in the calculus of variations., Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 37–38. Springer, Berlin (1998). https://doi.org/10.1007/978-3-662-06218-0. Cartesian currents
Golovaty, D., Montero, J.A.: On minimizers of a Landau-de Gennes energy functional on planar domains. Arch. Ration. Mech. Anal. 213(2), 447–490, 2014
Hardt, R., Kinderlehrer, D., Lin, F.H.: Existence and partial regularity of static liquid crystal configurations. Commun. Math. Phys. 105(4), 547–570, 1986
Hardt, R., Lin, F.H.: Mappings minimizing the \(L^p\) norm of the gradient. Commun. Pure Appl. Math. 40(5), 555–588, 1987. https://doi.org/10.1002/cpa.3160400503
Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge 2002
Hirsch, M.W.: Differential Topology. Springer, New York 1976. Graduate Texts in Mathematics, No. 33
Hopper, C.P.: Partial regularity for holonomic minimisers of quasiconvex functionals. Arch. Rational Mech. Anal. 222(1), 91–141, 2016. https://doi.org/10.1007/s00205-016-0997-8
Ignat, R., Jerrard, R.: Renormalized energy between vortices in some Ginzburg–Landau models on 2-dimensional Riemannian manifolds. Arch. Rational Mech. Anal. 239(1), 1–90, 2021. https://doi.org/10.1007/s00205-020-01598-0
Ignat, R., Nguyen, L., Slastikov, V., Zarnescu, A.: Stability of the melting hedgehog in the Landau–de Gennes theory of nematic liquid crystals. Arch. Ration. Mech. Anal. 215(2), 633–673, 2015. https://doi.org/10.1007/s00205-014-0791-4
Ignat, R., Nguyen, L., Slastikov, V., Zarnescu, A.: Stability of point defects of degree \(\pm \frac{1}{2}\) in a two-dimensional nematic liquid crystal model. Calc. Var. Partial Differ. Equ. 55(5), 33, 2016. https://doi.org/10.1007/s00526-016-1051-2
Ignat, R., Nguyen, L., Slastikov, V., Zarnescu, A.: Symmetry and multiplicity of solutions in a two-dimensional Landau-de Gennes model for liquid crystals. Arch. Ration. Mech. Anal. 237(3), 1421–1473, 2020. https://doi.org/10.1007/s00205-020-01539-x
Jerrard, R.L.: Lower bounds for generalized Ginzburg–Landau functionals. SIAM J. Math. Anal. 30(4), 721–746, 1999. https://doi.org/10.1137/S0036141097300581
Jerrard, R.L., Soner, H.M.: The Jacobian and the Ginzburg–Landau energy. Cal. Var. Partial Differ. Equ. 14(2), 151–191, 2002. https://doi.org/10.1007/s005260100093
Lin, F., Wang, C.: Harmonic and quasi-harmonic spheres. Commun. Anal. Geom. 7(2), 397–429, 1999. https://doi.org/10.4310/CAG.1999.v7.n2.a9
Lin, F.H., Rivière, T.: Complex Ginzburg-Landau equations in high dimensions and codimension two area minimizing currents. J. Eur. Math. Soc. (JEMS) 1(3), 237–311, 1999. https://doi.org/10.1007/s100970050008
Lin, F.H., Rivière, T.: A quantization property for static Ginzburg–Landau vortices. Commun. Pure Appl. Math. 54(2), 206–228, 2001
Majumdar, A., Zarnescu, A.: Landau–De Gennes theory of nematic liquid crystals: the Oseen-Frank limit and beyond. Arch. Ration. Mech. Anal. 196(1), 227–280, 2010. https://doi.org/10.1007/s00205-009-0249-2
Monteil, A., Rodiac, R., Van Schaftingen, J.: Ginzburg–Landau relaxation for harmonic maps on planar domains into a general compact vacuum manifold. Preprint arXiv:2008.13512
Monteil, A., Rodiac, R., Van Schaftingen, J.: Renormalised energies and renormalisable singular harmonic maps into a compact manifold on planar domains. Math. Ann. https://doi.org/10.1007/s00208-021-02204-8
Nguyen, L., Zarnescu, A.: Refined approximation for minimizers of a Landau–de Gennes energy functional. Cal. Var. Partial Differ. Equ. 47(1–2), 383–432, 2013. https://doi.org/10.1007/s00526-012-0522-3
Pakzad, M.R., Rivière, T.: Weak density of smooth maps for the Dirichlet energy between manifolds. Geom. Funct. Anal. 13(1), 223–257, 2003. https://doi.org/10.1007/s000390300006
Pigati, A., Stern, D.: Minimal submanifolds from the abelian Higgs model. Preprint arXiv:1905.13726 (2019).
Rivière, T.: Dense subsets of \(H^{1/2}(S^2, S^1)\). Ann. Global Anal. Geom. 18(5), 517–528, 2000. https://doi.org/10.1023/A:1006655723537
Sandier, E.: Lower bounds for the energy of unit vector fields and applications. J. Funct. Anal. 152(2), 379–403, 1998. https://doi.org/10.1006/jfan.1997.3170. See Erratum, ibidem 171(1), pp. 233, 2000
Sandier, É., Serfaty, S.: Vortices in the Magnetic Ginzburg–Landau Model. Progress in Nonlinear Differential Equations and their Applications, vol. 70. Birkhäuser Boston, Inc., Boston 2007
Stern, D.: Existence and limiting behavior of min-max solutions of the Ginzburg–Landau equations on compact manifolds. To appear in J. Diff. Geom.
Van Schaftingen, J.: Approximation in Sobolev spaces by piecewise affine interpolation. J. Math. Anal. Appl. 420(1), 40–47, 2014. https://doi.org/10.1016/j.jmaa.2014.05.036
White, B.: The deformation theorem for flat chains. Acta Math. 183(2), 255–271, 1999. https://doi.org/10.1007/BF02392829
White, B.: Rectifiability of flat chains. Ann. Math. (2) 150(1), 165–184, 1999. https://doi.org/10.2307/121100
Acknowledgements
The authors are grateful to the referees for their careful reading of the manuscript and their insightful comments. The authors were partially supported by GNAMPA-INdAM.
Funding
Open access funding provided by Università degli Studi di Verona within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by A. Braides
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
The Norm on \(\pi _{k-1}({\mathscr {N}})\): Proof of Proposition 1
The aim of this section is to prove Proposition 1. In Section 2, we have defined
for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\), with \(\nabla _{\top }\) the tangential gradient on \({\mathbb {S}}^{k-1}\) (i.e. the restriction of \(\nabla \) to the tangent plane to \({\mathbb {S}}^{k-1}\)). The compact Sobolev embedding \(W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\hookrightarrow C({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\) implies that \(W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap \sigma \) is sequentially \(W^{1,k}\)-weakly closed, so the infimum at the right-hand side is achieved. We must have
for otherwise there would exist a sequence of non-null-homotopic maps \(v_j\in W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\) that converge \(W^{1,k}\)-strongly, and hence uniformly, to a constant. Moreover, there holds
Indeed, for any \(v\in W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap \sigma \) and any \(x\in {\mathbb {S}}^{k-1}\), define \({\bar{v}}(x) := v(-x_1, \, x_2, \, \ldots , \, x_k)\). The map that sends \(v\mapsto {\bar{v}}\) is a bijection \(W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap \sigma \rightarrow W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap (-\sigma )\) that preserves the \(L^k\)-norm of the gradient, and hence (A.3) follows.
Our candidate norm \(|\cdot |_*\) on \(\pi _{k-1}({\mathscr {N}})\), which was also introduced in Section 2, is defined for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\) by
Proposition 8
The function \(|\cdot |_*\) is a norm on \(\pi _{k-1}({\mathscr {N}})\) that satisfies
and
The infimum in Equation (A.4) is achieved, for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\). Moreover, the set
is finite, and for any \(\sigma \in \pi _{k-1}({\mathscr {N}})\) there exists a decomposition \(\sigma = \sum _{i=1}^q\sigma _i\) such that \(\left| \sigma \right| _* = \sum _{i=1}^q\left| \sigma _i \right| _*\) and \(\sigma _i\in {\mathfrak {S}}\) for any i.
Proof
The function \(|\cdot |_*\) is certainly non-negative, and its definition (A.4) immediately implies the triangle inequality, \(|\sigma _1+\sigma _2|_*\leqq |\sigma _1|_* + |\sigma _2|_*\). The property \(|\sigma |_* = |-\sigma |_*\) follows by (A.3), while (A.2) yields (A.5) (in particular, \(|\sigma |_* = 0\) only if \(\sigma =0\)). The property (A.6) is immediate from the definition of \(|\cdot |_*\).
We check now that the set \({\mathfrak {S}}\) is finite. Under the assumption \(({\hbox {H}}_2)\), Hurewicz theorem (see e.g. [31, Theorem 4.37 p. 371]) implies that \(\pi _{k-1}({\mathscr {N}})\) is isomorphic to the homology group \(H_{k-1}({\mathscr {N}})\). The latter is Abelian and finitely generated, because the manifold \({\mathscr {N}}\) is compact and hence, homotopically equivalent to a finite cell complex. Therefore, we have
where \(p\geqq 0\) is an integer and T is a finite group. Let \((g_i)_{i=1}^p\) be a basis for the torsion-free part of \(H_{k-1}({\mathscr {N}})\) (i.e., the quotient \(H_{k-1}({\mathscr {N}})/T\simeq {\mathbb {Z}}^p\)). By de Rham theorem, there exist closed, smooth \((k-1)\)-forms \(\omega _1, \, \ldots , \, \omega _p\) that satisfy
where \(c_i\) is a smooth \((k-1)\)-cycle in the homology class \(g_i\). Let \(\sigma \in \pi _{k-1}({\mathscr {N}})\). By abusing of notation, and identifying \(g_i\) with its image under the Hurewicz isomorphism, we can write uniquely
where \(d_i \in {\mathbb {Z}}\) and \(\sigma _T\in T\). Then, for any \(v\in W^{1,k}({\mathbb {S}}^{k-1}, \, {\mathscr {N}})\cap \sigma \), we have
where \(C_{k, \, {\mathscr {N}}}>0\) is a constant depending only on k and the \(\omega _i\)’s. This implies
for a different constant \(C_{k, {\mathscr {N}}}^\prime \). On the other hand, the definition of \(|\cdot |_*\) immediately gives the upper bound
If \(\sigma \in {\mathfrak {S}}\) then, by comparing (A.8) and (A.9), we obtain \(\sum _i |d_i|\leqq M\) for some constant \(M>0\) depending only on k, \({\mathscr {N}}\). Therefore, \({\mathfrak {S}}\) is a finite set.
For any \(\sigma \in \pi _{k-1}({\mathscr {N}})\) there exists a finite decomposition \(\sigma = \sum _{i=1}^q\sigma _i\) which achieves the infimum in the right-hand side of (A.4). Indeed, it suffices to minimise among the decompositions with \(q \leqq (\inf _{g\in \pi _{k-1}({\mathscr {N}}){\setminus }\{0\}} E_{\min }(g))^{-1} E_{\min }(\sigma )\) and \(E_{\min }(\sigma _i) \leqq E_{\min }(\sigma )\) for any i, and there are only finitely many such decompositions because of (A.2), (A.8). Let \(\sigma = \sum _{i=1}^q\sigma _i\) be a decomposition that achieves the minimum in (A.4). Then, the triangle inequality implies
and, since \(\left| \sigma _i \right| _*\leqq E_{\min }(\sigma _i)\) for any i, we must have \(\left| \sigma _i \right| _* = E_{\min }(\sigma _i)\), i.e. \(\sigma _i\in {\mathfrak {S}}\), for any i. \(\quad \square \)
Example A.1
Let \(k=2\), \({\mathscr {N}}= {\mathbb {S}}^{1}\). Then, \(\pi _{k-1}({\mathscr {N}})\simeq {\mathbb {Z}}\) and \(E_{\min }(d) = \pi d^2\) for any \(d\in {\mathbb {Z}}\), since the infimum in (A.1) is achieved by a curve that parametrises the unit circle |d| times, with constant speed and orientation depending on the sign of d. Therefore, \({\mathfrak {S}}= \{-1, \, 0, \, 1\}\) and \(\left| d \right| _* = \pi \left| d \right| \) for any \(d\in {\mathbb {Z}}\).
More generally, when \({\mathscr {N}}={\mathbb {S}}^{k-1}\) the constant that appears in the lower bound (A.8) can be computed explicitely, and we have
where \(\beta _k := (k-1)^{k/2}{\mathscr {L}}^k(B^k_1)\). On the other hand, by using the identity as a comparison map for (A.1), we see that \(E_{\min }(1) \leqq (k-1)^{k/2}\mathrm {vol}({\mathbb {S}}^{k-1})/k = \beta _k\), hence \(E_{\min }(1) = E_{\min }(-1) = \beta _k\). It follows that
Therefore, also in case \({\mathscr {N}}={\mathbb {S}}^{k-1}\) we have \({\mathfrak {S}}= \{-1, \, 0, \, 1\}\). By Proposition 1, we conclude that \(\left| d \right| _* = \beta _k\left| d \right| \) for any \(d\in \pi _{k-1}({\mathbb {S}}^{k-1})\simeq {\mathbb {Z}}\).
The Operator \({\overline{{\mathbf {S}}}}\): Proof of Proposition 3
The aim of this section is to prove Proposition 3, which we recall here for the convenience of the reader. We recall that \(\delta ^*\in (0, \, {{\,\mathrm{dist}\,}}({\mathscr {N}}, \, {\mathscr {X}}))\) is a fixed constant, \(B^* := B^m(0, \, \delta ^*)\subseteq {\mathbb {R}}^m\), and \({\overline{Y}} := L^1(B^*, \, {\mathbb {F}}_{n}({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}})))\) is equipped with the norm
Proposition 9
There exists a continuous operator \({\overline{{\mathbf {S}}}}:W^{1,k}(\varOmega , \, {\mathbb {R}}^*)\rightarrow {\overline{Y}}\) that satisfies the following properties:
-
\(({{\hbox {P}}_0})\) for any smooth u, a.e. \(y\in B^*\) and any \(R\in {\mathbb {F}}_{k}({\mathbb {R}}^{n+k}; \, {\mathbb {Z}})\) such that \({\mathbb {M}}(R)+{\mathbb {M}}(\partial R)<+\infty \), \({{\,\mathrm{spt}\,}}(R)\subseteq \varOmega \), \({{\,\mathrm{spt}\,}}(\partial R) \subseteq \varOmega {\setminus }{{\,\mathrm{spt}\,}}{\mathbf {S}}_y(u)\), there holds
$$\begin{aligned} {\mathbb {I}}\left( {\mathbf {S}}_y(u), \, R\right) = \text {homotopy class of } \varrho \circ (u - y) \text { on } \partial R. \end{aligned}$$ -
\(({{\hbox {P}}_1})\) For any \(u\in (L^\infty \cap W^{1,k})(\varOmega , \, {\mathbb {R}}^m)\) and a.e \(y\in B^*\), \({\overline{{\mathbf {S}}}}_y(u) = {\mathbf {S}}_y(u)\) (more precisely, the chain \({\overline{{\mathbf {S}}}}_y(u)\) belongs to the equivalence class \({\mathbf {S}}_y(u)\in {\mathbb {F}}_{n}(\varOmega ; \, \pi _{k-1}({\mathscr {N}}))\)).
-
\(({{\hbox {P}}_2})\) For any \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) and any Borel subset \(E\subseteq {\overline{\varOmega }}\), there holds

-
\(({{\hbox {P}}_3})\) Let \(u_0\), \(u_1\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) be such that \(u_{0|\partial \varOmega } = u_{1|\partial \varOmega }\in W^{1-1/k, k}(\partial \varOmega , \, {\mathscr {N}})\) (in the sense of traces). Then, for a.e. \(y_0\), \(y_1\in B^*\) there exists \(R\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\) such that \({\overline{{\mathbf {S}}}}_{y_1}(u_1) - {\overline{{\mathbf {S}}}}_{y_0}(u_0) = \partial R\).
In the proof, we will use the following
Lemma 15
Let \(\rho >0\), and let \(\varGamma _\rho := \{x\in {\mathbb {R}}^{n+k}{\setminus }{\overline{\varOmega }}:{{\,\mathrm{dist}\,}}(x, \, \varOmega )<\rho \}\). Then, for any finite-mass chain \(T\in {\mathbb {M}}_n({\mathbb {R}}^{n+k}; \, \pi _{k-1}({\mathscr {N}}))\), there holds

Proof
For any \(t>0\), let \(\varOmega _t := \{x\in {\mathbb {R}}^{n+k}:{{\,\mathrm{dist}\,}}(x, \, \varOmega )<t\}\). There holds

(see e.g. [17, Lemma 4, Eq. (2.8)]). By an averaging argument, we can find \(t\in (0, \, \rho )\) such that

Now, there holds  and hence,
and hence,

so the lemma follows. \(\quad \square \)
Proof of Proposition 9
For the sake of clarity, we split the proof into steps.
Step 1
(Construction of \({\overline{{\mathbf {S}}}}\)) First, we consider a smooth map \(u\in C^\infty _{\mathrm {c}}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\) and the topological singular operator, \({\mathbf {S}}_y(u)\), as defined in [17, Section 3.2, Eq. (3.4)]. By definition, we can write
Here, the sum is taken over all \((m-k)\)-dimensional polyhedra K in \({\mathscr {X}}\). The coefficient \(\gamma (K)\in \pi _{k-1}({\mathscr {N}})\) is the homotopy class of \(\varrho \) restricted to a small \((k-1)\)-sphere \(\varSigma \) around K, \(\varrho _{|\varSigma }:\varSigma \simeq {\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\). For a.e. \(y\in B^*\), the set \((u-y)^{-1}(K)\) is a smooth, compact n-dimensional manifold (as a consequence of Thom’s transversality theorem, see e.g. [32, Theorem 2.7 p. 79]) and \(\llbracket (u-y)^{-1}(K)\rrbracket \) denotes the smooth chain carried by \((u-y)^{-1}(K)\), with unit multiplicity and a suitable orientation (see [17, Section 3.2] for more details).
We claim that, for any u, \(u_0\), \(u_1\in C^\infty _{\mathrm {c}}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\) and any open set \(U\subseteq {\mathbb {R}}^{n+k}\), there holds

These inequalities differ from the corresponding ones in [17, Theorem 3.1] because the multiplicative constants in front of the right-hand sides do not depend on the \(L^\infty \)-norm of u, \(u_0\), \(u_1\). We postpone the proof of (B.3)–(B.4). As a consequence of (B.4), by a density argument we can extend \({\mathbf {S}}\) to a continuous operator \(W^{1,k}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\rightarrow L^1(B^*, \, {\mathbb {F}}({\mathbb {R}}^{n+k}, \, \pi _{k-1}({\mathscr {N}})))\), still denoted \({\mathbf {S}}\) for simplicity. The property (B.3) is preserved for any \(u\in W^{1,k}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\), by the lower semi-continuity of \({\mathbb {M}}\) (see e.g. [17, Lemma 3 and Lemma 5]).
Since the domain \(\varOmega \subseteq {\mathbb {R}}^{n+k}\) is bounded and smooth, by reflection about \(\partial \varOmega \) and multiplication with a cut-off function we can define a linear extension operator \(T:W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\rightarrow W^{1,k}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\), such that
For any \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) and a.e. \(y\in B^*\), the chain \({\mathbf {S}}_y(Tu)\) has finite mass, due to (B.3). Therefore, the restriction

is well-defined and belongs to \({\mathbb {M}}_n({\overline{\varOmega }}; \, \pi _{k-1}({\mathscr {N}}))\).
Step 2
(\({\overline{{\mathbf {S}}}}\) is continuous) Let \((u_j)_{j\in {\mathbb {N}}}\) be a sequence in \(W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) such that \(u\rightarrow u\) in \(W^{1,k}(\varOmega )\). From (B.4) and (B.5), we deduce
Let \(\rho >0\) and \(\varGamma _\rho := \{x\in {\mathbb {R}}^{n+k} {\setminus }{\overline{\varOmega }}:{{\,\mathrm{dist}\,}}(x, \, \varOmega )<\rho \}\). By applying Lemma 15 and (B.3), (B.6), we obtain

By taking the limit in the inequality above first as \(j\rightarrow +\infty \), then as \(\rho \rightarrow 0\), we conclude that \({\overline{{\mathbf {S}}}}(u_j)\rightarrow {\overline{{\mathbf {S}}}}(u)\) in \({\overline{Y}}\).
Step 3
(Proof of \(({\hbox {P}}_1)\)) By construction, \({\overline{{\mathbf {S}}}}_y(u) = {\mathbf {S}}_y(u)\) for any \(u\in C^\infty _{\mathrm {c}}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\) and a.e. \(y\in B^*\). By continuity of both \({\overline{{\mathbf {S}}}}\) and \({\mathbf {S}}\) [17, Theorem 3.1], we deduce that \({\overline{{\mathbf {S}}}} = {\mathbf {S}}\) on \((L^\infty \cap W^{1,k})(\varOmega , \, {\mathbb {R}}^m)\).
Step 4
(Proof of \(({\hbox {P}}_2)\)) Let \(E\subseteq {\overline{\varOmega }}\) be a Borel set and \(U\supseteq E\) be open. By (B.3), we have

and \(({\hbox {P}}_2)\) follows by letting \(U\searrow E\).
Step 5
(Proof of \(({\hbox {P}}_3)\)) Take \(u_0\), \(u_1\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\). For \(i\in \{0, \, 1\}\) and \(M >0\), we define
Since \(u_{i,M}\rightarrow u_i\) strongly in \(W^{1,k}(\varOmega )\) as \(M\rightarrow 0\), the continuity of \({\overline{{\mathbf {S}}}}\) gives, upon extraction of a (non-relabelled) subsequence,
Let \({\mathbb {B}} := \{\partial R:R\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, {\mathbb {R}}^{n+k})\}\). By [17, Proposition 2], we have \({\overline{{\mathbf {S}}}}_{y_0}(u_{1,M}) - {\overline{{\mathbf {S}}}}_{y_1}(u_{0, M})\in {\mathbb {B}}\) for any \(M>0\) and a.e. \(y_0\), \(y_1\in B^*\). On the other hand, the set \({\mathbb {B}}\) is closed with respect to the \({\mathbb {F}}\)-norm, as a consequence of the isoperimetric inequality (see e.g. [25, 7.6]). Therefore, \(({\hbox {P}}_3)\) follows by (B.7).
Step 6
(Proof of (B.3)) Let \(u\in C^\infty _{\mathrm {c}}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\) and let \(E\subseteq {\mathbb {R}}^{n+k}\) be a Borel set. Since \({\mathscr {X}}\) contains finitely many \((m-k)\)-cells K, there exists a constant C such that \(\left| \gamma (K) \right| _*\leqq C\) for any K. Then, using the definition (B.2) of \({\mathbf {S}}_y(u)\), we deduce

where the sum is taken over all the \((m-k)\)-dimensional polyhedra K in \({\mathscr {X}}\). We fix K and assume, without loss of generality, that \(K\subseteq \left\{ y\in {\mathbb {R}}^m:y_1=\ldots = y_k=0 \right\} \simeq {\mathbb {R}}^{m-k}\). Let \(\zeta ^\perp \) be the orthogonal projection \({\mathbb {R}}^m\rightarrow \left\{ y\in {\mathbb {R}}^m:y_{m-k+1}=\ldots = y_m=0 \right\} \simeq {\mathbb {R}}^{k}\). Then,
If we integrate this inequality over \(y\in B^*\), and use the variable \(y = (z, \, z^\perp )\in {\mathbb {R}}^{m-k}\times {\mathbb {R}}^m\), we obtain
The right-hand side can be estimated by applying the coarea formula:
Combining (B.8) and (B.9), (\({\hbox {P}}_2\)) follows.
Step 7
(Proof of (B.4)) Let \(u_0\), \(u_1\in C^\infty _{\mathrm {c}}({\mathbb {R}}^{n+k}, \, {\mathbb {R}}^m)\), and let \(u:[0, \, 1]\times {\mathbb {R}}^{n+k}\rightarrow {\mathbb {R}}^m\) be defined by \(u(t, \, x) := (1-t)u_0(x) + tu_1(x)\). Let \(\pi :[0, \, 1]\times {\mathbb {R}}^{n+k}\rightarrow {\mathbb {R}}^{n+k}\) be the canonical projection, \(\pi (t, \, x) := x\). By [17, Proposition 4], we have
Therefore, using (B.2), we obtain
where the sum is taken over all the \((m-k)\)-polyhedra K in \({\mathscr {X}}\). Fix such a K. As above, we assume that that \(K\subseteq \left\{ y\in {\mathbb {R}}^m:y_1=\ldots = y_k=0 \right\} \). Let \(\zeta \), \(\zeta ^\perp \) be the orthogonal projections of \({\mathbb {R}}^m\) onto \(\{y\in {\mathbb {R}}^m:y_1=\ldots = y_{m-k}=0\}\simeq {\mathbb {R}}^{m-k}\), \(\{y\in {\mathbb {R}}^m:y_{m-k+1}=\ldots = y_m=0\}\simeq {\mathbb {R}}^{k}\), respectively. We wite \(z := \zeta (y)\), \(z^\perp := \zeta ^\perp (y)\) and identify \(y = (z, \, z^\perp )\). Then, for a suitable choice of orientation of K, we obtain

where \(\llbracket (\zeta ^\perp \circ u)^{-1}(z^\perp ) \rrbracket \) is the chain carried by the set \((\zeta ^\perp \circ u)^{-1}(z^\perp )\), with unit multiplicity, oriented by the Jacobian of \(\zeta ^\perp \circ u\) (see e.g. [17, p. 72]). Let us define \(v := \zeta ^\perp \circ u\), \(K_z := (\zeta \circ u - z)^{-1}(K)\). By integrating (B.11) with respect to \(y\in B^*\), we obtain

We may write \(v(t, \, x) = (1-t)v_0(x) + tv_1(x)\), where \(v_0 := \zeta ^\perp \circ u_0\), \(v_1 := \zeta ^\perp \circ u_1\). By applying [17, Lemma 15], we deduce
Combining (B.10) and (B.12), using that the function \(\zeta \) is 1-Lipschitz, and applying the Hölder inequality, (B.4) follows.\(\quad \square \)
Energy Lower Bounds When \(n=0\)
The aim of this section is to prove energy lower bounds in the critical dimension, i.e. when \(n=0\). In the contest of the Ginzburg–Landau theory, i.e. when \({\mathscr {N}}={\mathbb {S}}^{k-1}\), energy bounds of this type were proved by Jerrard [38] and, in case \(k=2\), by Sandier [50].
Let \(\delta _0>0\), \(r>0\) be small numbers. Suppose that a map \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) satisfies
Then, we can define the homotopy class of u (or, more precisely, of \(\varrho \circ u\)) on \(\partial \varOmega \) as an element of \(\pi _{k-1}({\mathscr {N}})\). This is immediate in case u is continuous on \(\partial \varOmega \) and \({\overline{\varOmega }}\) is homeomorphic to a disk. If \(\varOmega \) has not the topology of a disk, this is still possible due to the Hurewicz isomorphism \(\pi _{k-1}({\mathscr {N}})\simeq H_{k-1}({\mathscr {N}})\), which holds true thanks to \(({\hbox {H}}_2)\) (see e.g. [31, Theorem 4.37 p. 371] and (C.10) below). If u is not continuous we can define its homotopy class by approximating \(\varrho \circ u\) with smooth functions \(\varOmega \rightarrow {\mathscr {N}}\), as in [14] (see also (C.10) below for more details).
Proposition 10
Let \(\varOmega \subseteq {\mathbb {R}}^k\) be a bounded, Lipschitz domain and let \(r>0\). There exist a number \(\delta _0>0\), depending only on \({\mathscr {N}}\), and positive constants \(\varepsilon _0\), M, depending only on \(\varOmega \), r, \({\mathscr {N}}\), k and f, such that the following statement holds. Suppose that \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) satisfies (C.1), and let \(\sigma \in \pi _{k-1}({\mathscr {N}})\) be the homotopy class of u on \(\partial \varOmega \). Let \(\varepsilon \in (0, \, 1/2)\) be such that \(\varepsilon \left| \log \varepsilon \right| |\sigma |_*\leqq \varepsilon _0\). Then,
The aim of this section is to prove Proposition 10. Once Proposition 10 is proved, Proposition B follows by an extension argument in a neighbourhood of \(\partial \varOmega \) (see e.g. [10, Theorem 2]). Lemma 11 also follows from Proposition 10, by exactly the same arguments as in [2, Lemma 3.10].
1.1 Reduction to the Cone-Valued Case
For the purposes of this section, it will be convenient to consider the nearest-point projection onto \({\mathscr {N}}\). If \(z\in {\mathbb {R}}^m\) is sufficiently close to \({\mathscr {N}}\), there exists a unique \(\pi (z)\in {\mathscr {N}}\) such that \(\left| z-\pi (z) \right| \leqq \left| z - w \right| \) for any \(w\in {\mathscr {N}}\). Moreover, the map \(z\mapsto \pi (z)\) is a smooth in a neighbourhood of \({\mathscr {N}}\). Throughout the rest of the section, we fix a small parameter \(\theta _0\) and assume that \(\pi \) is well-defined and smooth in a \(\theta _0\)-neighbourhood of \({\mathscr {N}}\).
Lemma 16
If \(u:\varOmega \rightarrow {\mathbb {R}}^m\) is a smooth map that satisfies \({{\,\mathrm{dist}\,}}(u(x), \, {\mathscr {N}})<\theta _0\) for any \(x\in \varOmega \) and if \(d := {{\,\mathrm{dist}\,}}(u, \, {\mathscr {N}})\), then there holds
where \(C_1\), \(C_2\) are positive constants that only depend on \({\mathscr {N}}\).
Proof
Let \(x_0\in \varOmega \) be arbitrarily fixed. Let \(\nu _1, \, \ldots , \, \nu _p\) be a smooth orthonormal frame for the normal space to \({\mathscr {N}}\), locally defined in a neighbourhood of \((\pi \circ u)(x_0)\). Then, for each x in a neighbourhood of \(x_0\) there exist numbers \(\alpha _1(x), \, \ldots , \, \alpha _p(x)\) such that
The functions \(\alpha _i\) are as regular as u. By differentiating this equation, raising both sides to the square, using the fact that \(\partial _j(\pi \circ u)\) is tangent to \(\mathscr {N}\) and \(\nu \cdot \partial _j\nu = 0\), we obtain
Since \({\mathscr {N}}\) is smooth and compact, we have \(|\nabla \nu _i|\leqq C\) for some constant C that only depends on \({\mathscr {N}}\) and not on u. Therefore, setting \(d := {{\,\mathrm{dist}\,}}(u, \, {\mathscr {N}}) = (\sum _i\alpha _i^2)^{1/2}\), we obtain
On the other hand, by differentiating the identity \(d = (\sum _i\alpha _i^2)^{1/2}\), we see that
By combining (C.2) and (C.3), the lemma follows. \(\quad \square \)
Lemma 17
Suppose that \(f:{\mathbb {R}}^m\rightarrow {\mathbb {R}}\) satisfies the assumptions \(({\hbox {H}}_1)\)–\(({\hbox {H}}_3)\). Then, there exist positive constants \(\alpha \), \(\beta \) and a smooth function \(\phi :{\mathbb {R}}^m\rightarrow [0, \, 1]\) such that the following holds:
-
(i)
\(\phi (y) = 1\) for any \(y\in {\mathscr {N}}\);
-
(ii)
\(\phi (y) = 0\) if \({{\,\mathrm{dist}\,}}(y, \, {\mathscr {N}})\geqq \theta _0\), and in particular \(\pi (y)\) is well-defined for any \(y\in {\mathbb {R}}^m\) such that \(\phi (y) >0\);
-
(iii)
for any \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\), there holds
$$\begin{aligned} \frac{1}{k}\left| \nabla u \right| ^k + \frac{1}{\varepsilon ^k} f(u) \geqq \alpha \left| \nabla (\phi \circ u) \right| ^k + \frac{1}{k}(\phi \circ u)^k\left| \nabla (\pi \circ u) \right| ^k + \frac{\beta }{\varepsilon ^k} (1 - \phi \circ u)^2 \end{aligned}$$pointwise a.e. on \(\varOmega \).
Proof
Let \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) be given. By a density argument, we can assume without loss of generality that u is smooth. Let \(d:={{\,\mathrm{dist}\,}}(u, \, {\mathscr {N}})\), and let \(x_0\in \varOmega \) be such that \(d(x_0)<\theta _0\). By applying Lemma 16, and using the convexity of the function \(t\mapsto t^{k/2}\), we see that the inequality
holds pointwise in a neighbourhood of \(x_0\) (though we may need to re-define the constants \(C_1\), \(C_2\).) Let \(\xi \in C^\infty _{\mathrm {c}}[0, \, +\infty )\) be a non-increasing function, such that \(\xi = 1\) in a neighbourhood of 0 and \(\xi (\min \{\theta _0/2, 1/(2C_2)\}) = 0\). We set
for any \(y\in {\mathbb {R}}^m\). This defines a smooth function \(\phi :{\mathbb {R}}^m\rightarrow [0, \, 1]\) which satisfies (i) and (ii). Since \((\phi \circ u)^k\leqq 1 - C_2 d\) and \(|\nabla (\phi \circ u)| \lesssim |\nabla d|\), from (C.4) we deduce that
pointwise in the open set \(\{d<\theta _0\}\). Here \(\alpha \) is a positive constant that only depends on \({\mathscr {N}}\), k and \(\xi \). Because the function \(\phi \circ u\) is identically equal to zero on the open set \(\{d>\theta _0/2\}\), the inequality (C.5) actually holds in the whole of \(\varOmega \).
We consider now the potential term f(u). Due to the assumption \(({\hbox {H}}_3)\), \(f(u) > rsim d^2\) and hence, there exists a positive number \(\beta >0\) such that
By combining (C.5) and (C.6), and using the elementary inequality \(1 - x^k \geqq 1 - x\) for \(0 \leqq x \leqq 1\), the lemma follows. \(\quad \square \)
1.2 Proof of Proposition 10
Throughout this section, we fix a bounded, smooth map \(u:\varOmega \rightarrow {\mathbb {R}}^m\) and we let \(s:= \phi \circ u\), \(v:=\pi \circ u\), where \(\phi \) is the function given by Lemma 17 and \(\pi \) is the nearest-point projection onto \({\mathscr {N}}\). Thanks to Lemma 17, in order to provide lower bounds for \(E_\varepsilon (u)\) it suffices to bound from below the functional
To this end, we adapt Jerrard’s approach in [38]. We explain here the main steps of the construction and point out the differences, referring the reader to [38] for more details.
Let us fix a small number \(\eta _0\), such that
Let \(V\subseteq \varOmega \) be an open set such that \(s>0\) on \(\partial V\). By Lemma 17, we have \({{\,\mathrm{dist}\,}}(u(x), \, {\mathscr {N}}) < \theta _0\) for any \(x\in \partial V\). Therefore, by (C.8), we have \({{\,\mathrm{spt}\,}}({\mathbf {S}}_y(u))\cap \partial V = \emptyset \) for a.e. \(y\in {\mathbb {R}}^m\) such that \(|y|\leqq \eta _0\). In fact, \({\mathbf {S}}_y(u)\) is a 0-chain of finite mass, and hence we can write

where \(\sigma _i\in \pi _{k-1}({\mathscr {N}})\) and \(x_i\in V\). The quantity \({\mathbb {I}}({\mathbf {S}}_y(u), \llbracket V\rrbracket ) := \sum _{i=1}^q \sigma _i\in \pi _{k-1}({\mathscr {N}})\) plays the rôle of the topological degree and indeed, it coincides with the homotopy class of \(\pi \circ u\) on \(\partial V\) because of Proposition 9.\(({{\hbox {P}}_0})\) and (C.8) (see [17, Section 2.4 and Theorem 3.1] for the details on the case u is not smooth). In particular, \({\mathbb {I}}({\mathbf {S}}_y(u), \llbracket V\rrbracket )\) is independent of the choice of y.
As in [38], we define an “approximate homotopy class”, which allows us to disregard sets where s is small but u does not carry topological obstruction. We let \(S := \{x\in \varOmega :s(x)\leqq 1/2\}\). The components \(\tilde{S}\) of S are closed sets and it is possible to define \({\mathbb {I}}({\mathbf {S}}_y(u), \, \llbracket \tilde{S}\rrbracket )\) as above. We define the “essential part” of S:
For \(V\subseteq \varOmega \), we define the “approximate homotopy class” of u on \(\partial V\) as
where the sum is taken over all the components \(\tilde{S}\) of \(S_E\) such that \(\tilde{S}\subset \!\subset V\). If \(V\subseteq \varOmega \) is an open disk and \(s>1/2\) on \(\partial V\), then \({{\,\mathrm{hc}\,}}(u, \, \partial V)\) is the homotopy class of \(v:\partial V\simeq {\mathbb {S}}^{k-1}\rightarrow {\mathscr {N}}\).
For any \(\rho >0\), we define
and
where \(C_0>0\), \(C_1>0\) and \(N>1\) are parameters that we will need to choose, depending on k, \(\alpha \) and \(\beta \). It can be shown (see [38, Theorem 2.1, proof of (2.2)]) that
where \(C>0\) only depends on k, \(C_0\) and \(\nu := 1/(N-1)>0\). As a consequence, \(\lambda _\varepsilon (\rho )\geqq C_1/\varepsilon \) if \(\rho \geqq C_2\varepsilon \), for some constant \(C_2>0\) depending on k, \(C_0\), \(C_1\) and N. Therefore, after integration we obtain that
for any \(\rho \geqq 0\), where the constant C only depends on k, \(\alpha \), \(\beta \). We have the following analogue of [38, Proposition 3.2].
Lemma 18
Let \(\varepsilon \leqq \rho _1\leqq \rho _2\) and let \(u\in W^{1,k}(B^k_{\rho _2}{\setminus } B^k_{\rho _1}, \, {\mathbb {R}}^m)\) be smooth. Suppose that \({{\,\mathrm{hc}\,}}(u, \, \partial B^k_\rho ) = \sigma \) for any \(\rho \in (\rho _1, \, \rho _2)\). Then, there holds
Proof
First of all, given \(\rho >0\) and a map \(v\in W^{1,k}(\partial B^k_\rho , \, {\mathscr {N}})\) in the homotopy class \(\sigma \in \pi _{k-1}({\mathscr {N}})\), there holds
where \(E_{\min }(\sigma )\) is defined by (A.1). This inequality follows immediately from the definition of \(E_{\min }(\sigma )\), combined with a scaling argument.
Now, for any \(\rho \geqq \varepsilon >0\) and any smooth \(u:\partial B^k_\rho \rightarrow {\mathbb {R}}^m\) such that \(\mu := \min _{\partial B^k_\rho } \phi \circ u > 1/2\), it holds that
Here \(G_\varepsilon \) is defined by (C.7), \(s:=\phi \circ u\), \(v:=\pi \circ u\), and \(\sigma \) denotes the homotopy class of v on \(\partial B^k_\rho \). The constants \(C_0\), N are suitably chosen at this stage. The proof of this claim follow by repeating, almost word by word, the arguments in [38, Theorem 2.1]; the only difference is that we need to apply (C.12) instead of [38, Lemma 2.4]. Due to (A.6), we obtain
On the other hand, in case \(0\leqq \mu \leqq 1/2\), [38, Lemma 2.3] implies that
for some \(C_1>0\) that depends on k, \(C_0\) and N. Therefore, by integrating the inequalities (C.13)–(C.14) with respect to \(\rho \), we deduce that
and, thanks to Lemma 17, the lemma follows. \(\quad \square \)
We also have an analogue of [38, Proposition 3.3].
Lemma 19
Suppose that \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) is smooth and that \(S_E\subset \!\subset \varOmega \). Then, there exists a finite collection of closed, pairwise disjoint balls \((B_i)_{i=1}^p\), of radii \(\rho _i\geqq \varepsilon \), such that \(S_E\subseteq \cup _{i=1}^p B_i\), \(B_i\cap S_E\ne \emptyset \) for any i, and
Proof
We claim that, if \(\tilde{S}\) is a connected component of \(S_E\) such that \(\tilde{S}\subset \!\subset \varOmega \), then
This inequality parallels [38, Lemma 3.2]; once (C.15) is established, the rest of the proof follows exactly as in [38]. The definition (C.10) of \({{\,\mathrm{hc}\,}}\) and (C.9) imply that

for a.e. \(y\in {\mathbb {R}}^m\) such that \(|y|\leqq \eta _0\). On the other hand, (\({\hbox {P}}_2\)) gives that

so there exists (a set of positive measure of) y such that \(|y|\leqq \eta _0\) and  . Then, (C.15) follows from (C.16). \(\quad \square \)
. Then, (C.15) follows from (C.16). \(\quad \square \)
Lemma 19 and the definition of \(\varLambda _\varepsilon \) imply that
The last step in the proof of Proposition 10 is the so-called “ball construction” [38, Proposition 4.1]. If u satisfies (C.1) for some \(r>0\) then, by choosing \(\delta _0 = \delta _0({\mathscr {N}}) < \theta _0\) sufficiently small, we obtain as a consequence
Moreover, we can assume without loss of generality that u satisfies
for some \(\varepsilon \)-independent constant C, for otherwise Proposition 10 holds trivially.
Lemma 20
There exists a constant \(\varepsilon _0>0\) such that the following statement holds. Let \(u\in W^{1,k}(\varOmega , \, {\mathbb {R}}^m)\) be a smooth function that satisfies (C.18) for some \(r>0\) and (C.19). For any \(\tau > 0\) and any \(\varepsilon \in (0, \, 1/2)\) such that
there exists a finite collection of closed ball \((\tilde{B}_i)_{i=1}^q\), of radii \(r_i\), that satisfy the following properties:
-
(i)
the interiors of the balls are pairwise disjoint;
-
(ii)
\(S_E\subset \!\subset \cup _{i=1}^q \tilde{B}_i\) and \(\tilde{B}_i\cap S_E\ne \emptyset \) for any i;
-
(iii)
letting \(s:= \min _{i} r_i/|{{\,\mathrm{hc}\,}}(u, \, \partial \tilde{B}_i)|_*\), we have
$$\begin{aligned} E_\varepsilon (u, \, \tilde{B}_i\cap \varOmega ) \geqq \frac{r_i}{s} \varLambda _\varepsilon (s); \end{aligned}$$ -
(iv)
\(\tau /2 \leqq s \leqq \tau \);
-
(v)
\(\left| {{\,\mathrm{hc}\,}}(u, \, \partial \varOmega ) \right| _* = \sum _{i=1}^q |{{\,\mathrm{hc}\,}}(u, \, \partial \tilde{B}_i)|_*\).
Lemma 20 follows by repeating the arguments of [38, Proposition 4.1] (see also [2, Remark at p. 22]), and using Lemmas 18, 19 and (C.17).
Proof of Proposition 10
We assume that u is smooth, satisfies (C.18) (as a consequence of our assumption (C.1)) and (C.19). We apply Lemma 20 and use the fact that, by definition of s, \(|{{\,\mathrm{hc}\,}}(u, \, \partial \tilde{B}_i)|_*\leqq r_i/s\) for any i:
The constant C here only depends on k, \(\alpha \), \(\beta \). Now, we choose \(\tau := r/(8|{{\,\mathrm{hc}\,}}(u, \, \partial \varOmega )|_*)\) (which is admissible in view of (C.20)). Taking (A.5) into account, we obtain the desired estimate in case u is smooth. Now the proposition follows by a density argument. \(\quad \square \)
Technical Results about Flat Chains
Throughout this appendix, we consider chains with coefficients in a normed Abelian group \(({\mathbf {G}}, \, |\cdot |)\) such that
This assumption is satisfied by \((\pi _{k-1}({\mathscr {N}}), \, |\cdot |_*)\), due to Proposition 1.
1.1 Approximation Results for Flat Chains
We give the proof of the approximation results, Proposition 5 and 6 , we have used in Section 3.4.2. For convenience, we recall the statements here. Let \({\mathfrak {S}}\subseteq {\mathbf {G}}\) be a set of generators for \({\mathbf {G}}\). We assume that, for any \(g\in {\mathbf {G}}\), there exist \(g_1, \, \ldots , \, g_p\in {\mathfrak {S}}\) such that
The set defined by (A.7) satisfies this assumption, by Proposition 1.
Proposition 11
Let \(S\in {\mathbb {M}}_{n}({\mathbb {R}}^{n+k}; \, {\mathbf {G}})\) be a polyhedral chain. Let \(W_{{\mathfrak {S}}}\subseteq {\mathbb {R}}^{n+k}\) be an open set, with polyhedral boundary, such that \(\partial W_{{\mathfrak {S}}}\) is transverse to \({{\,\mathrm{spt}\,}}S\) (i.e., there exist triangulations of \(\partial W_{{\mathfrak {S}}}\) and \({{\,\mathrm{spt}\,}}S\) such that any simplex of the triangulation of \(\partial W_{{\mathfrak {S}}}\) is transverse to any simplex of the triangulation of \({{\,\mathrm{spt}\,}}S\)). Then, there exists a sequence of polyhedral \((n+1)\)-chains \(R_j\), supported in \(\overline{W_{{\mathfrak {S}}}}\), such that the following hold:
-
(i)
\(S+\partial R_j \rightarrow S\), with respect to the \({\mathbb {F}}\)-norm, as \(j\rightarrow +\infty \);
-
(ii)
\({\mathbb {M}}(S+\partial R_j)\rightarrow {\mathbb {M}}(S)\) as \(j\rightarrow +\infty \);
-
(iii)
for any j,
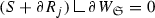 ;
; -
(iv)
for any j, the chain
 takes multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4).
takes multiplicities in the set \({\mathfrak {S}}\subseteq \pi _{k-1}({\mathscr {N}})\) defined by (2.4).
Proposition 11 implies Proposition 6.
Proof
Since \(\partial W_{{\mathfrak {S}}}\) is transverse to \({{\,\mathrm{spt}\,}}S\), the intersection \({{\,\mathrm{spt}\,}}S \cap \partial W_{{\mathfrak {S}}}\) has dimension \(n-1\) at most and hence,  . By triangulating S, we can write
. By triangulating S, we can write  as a finite sum
as a finite sum

where \(\sigma _K\in \pi _{k-1}({\mathscr {N}})\) and the K’s are closed n-simplices, whose interiors are contained in \(W_{{\mathfrak {S}}}\) and pairwise disjoint. We fix positive parameters \(\delta \), \(\gamma \) and, for any n-simplex K of  , we consider the set \(U(K, \, \delta , \, \gamma )\) defined by (3.1). We choose \(\delta \), \(\gamma \) small enough, so that the interiors of the \(U(K, \, \delta , \, \gamma )\)’s are pairwise disjoint and contained in \(W_{{\mathfrak {S}}}\). By assumption (D.2), we can write \(\sigma _K = \sum _{i=1}^p \sigma _{K,i}\) where \(\sigma _{K,i}\in {\mathfrak {S}}\) and
, we consider the set \(U(K, \, \delta , \, \gamma )\) defined by (3.1). We choose \(\delta \), \(\gamma \) small enough, so that the interiors of the \(U(K, \, \delta , \, \gamma )\)’s are pairwise disjoint and contained in \(W_{{\mathfrak {S}}}\). By assumption (D.2), we can write \(\sigma _K = \sum _{i=1}^p \sigma _{K,i}\) where \(\sigma _{K,i}\in {\mathfrak {S}}\) and
Take distinct vectors \(y^{K,1}, \, \ldots , \, y^{K,p}\in {\mathbb {R}}^{n+k}\) that are orthogonal to K and satisfy \(|y^{K,1}| = \ldots = |y^{K,p}| = 1\). For each \(i\in \{1, \, \ldots , \, p\}\), we define \(h^{K,i}:[0, \, 1]\times K\rightarrow {\mathbb {R}}^{n+k}\) by
For any integer \(j\geqq 1\), we define
(see Figure 7).
The chain \(R_j\) is polyhedral, because the \(h^{K,i}\)’s are piecewise affine, and supported in \(\overline{W_{{\mathfrak {S}}}}\). The support of \(R_j\) may intersect \(\partial W_{{\mathfrak {S}}}\) only along its \((n-1)\)-skeleton, so  . We compute the mass of \(R_j\). Since the maps \(h^{K,i}\) are Lipschitz, and their Lipschitz constant only depends on \(\gamma \), which is fixed, the area formula implies
. We compute the mass of \(R_j\). Since the maps \(h^{K,i}\) are Lipschitz, and their Lipschitz constant only depends on \(\gamma \), which is fixed, the area formula implies

Thus, (i) follows. Now, we compute the boundary of \(R_j\). For each simplex K and each i, we have \(h^{K,i}(t, \, x^\prime ) = x^\prime \) if \(x^\prime \in \partial K\) and \(h^{K,i}(0, \, x^\prime ) = x^\prime \) for any \(x^\prime \in K\). As a consequence,
By multiplying this identity by \(\sigma _{K,i}\), and taking the sum over i, K, we obtain

In particular,  takes multiplicities in \({\mathfrak {S}}\). Finally, by applying the area formula to (D.4), we deduce
takes multiplicities in \({\mathfrak {S}}\). Finally, by applying the area formula to (D.4), we deduce

and (ii) follows. \(\quad \square \)
Let \(\varOmega \subseteq {\mathbb {R}}^{n+k}\) be a domain and let \(S\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\). Recall that S is called locally polyhedral if, for any compact set \(K\subseteq \varOmega \), there exists a polyhedral chain T such that  . We write \(S_0\sim _{{\overline{\varOmega }}} S_1\) if there exists \(R\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, {\mathbf {G}})\) such that \(S_1 = S_0 + \partial R\).
. We write \(S_0\sim _{{\overline{\varOmega }}} S_1\) if there exists \(R\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, {\mathbf {G}})\) such that \(S_1 = S_0 + \partial R\).
Proposition 12
Let \(\varOmega \subseteq {\mathbb {R}}^{n+k}\) be a bounded, Lipschitz domain. Let \(S_0\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) be a locally polyhedral chain such that  . Let \(S\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) be such that \(S \sim _{{\overline{\varOmega }}} S_0\). Then, there exists a sequence of polyhedral \((n+1)\)-chains \(R_j\), with compact support in \(\varOmega \), such that \(S_0 + \partial R_j\rightarrow S\) (with respect to the \({\mathbb {F}}\)-norm) and \({\mathbb {M}}(S_0 + \partial R_j)\rightarrow {\mathbb {M}}(S)\) as \(j\rightarrow +\infty \).
. Let \(S\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) be such that \(S \sim _{{\overline{\varOmega }}} S_0\). Then, there exists a sequence of polyhedral \((n+1)\)-chains \(R_j\), with compact support in \(\varOmega \), such that \(S_0 + \partial R_j\rightarrow S\) (with respect to the \({\mathbb {F}}\)-norm) and \({\mathbb {M}}(S_0 + \partial R_j)\rightarrow {\mathbb {M}}(S)\) as \(j\rightarrow +\infty \).
Proposition 5 follows from Proposition 12, with the help of \(({\hbox {P}}_3)\) and Lemma 3. We split the proof of Proposition 12 into several lemmas. The first one is a straightforward consequence of the deformation theorem for flat chains; we provide a proof for completeness.
Lemma 21
Let \(q\in \{0, \, \ldots , \, n+k-1\}\), \(T\in {\mathbb {M}}_q({\mathbb {R}}^{n+k}; \, {\mathbf {G}})\) anq \(\eta > 0\) be given. Suppose that T is compactly supported and \(\partial T\) is polyhedral. Then, there exist a polyhedral q-chain P and a finite-mass chain \(C\in {\mathbb {M}}_{q+1}({\mathbb {R}}^{n+k}; \, {\mathbf {G}})\), supported in the \(\eta \)-neighbourhood of \({{\,\mathrm{spt}\,}}T\), that satisfy
Proof
We apply the deformation theorem (see e.g. [26, Theorem 7.3] or [54, Theorem 1.1]) to T. We find a polyhedral q-chain A, a finite-mass q-chain B and a finite-mass \((q+1)\)-chain C that satisfy the following properties:
-
(a)
\(T = A + B + \partial C\);
-
(b)
\({\mathbb {M}}(A)\lesssim {\mathbb {M}}(T) + \eta \,{\mathbb {M}}(\partial T)\), \({\mathbb {M}}(B)\lesssim \eta \,{\mathbb {M}}(\partial T)\) and \({\mathbb {M}}(C)\lesssim \eta \,{\mathbb {M}}(T)\);
-
(c)
A, B, C are supported in the \(\eta \)-neighbourhood of \({{\,\mathrm{spt}\,}}T\).
Since we have assumed that \(\partial T\) is polyhedral, we can take B to be polyhedral, too (see e.g. [54, Theorem 1.1.(7)]). Then, the chains \(P:=A+B\) and C have all the required properties. \(\quad \square \)
Lemma 22
Let \(\varOmega \subseteq {\mathbb {R}}^{n+k}\) be a bounded, Lipschitz domain. Let \(S_0\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) be such that  . Let \(R\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, {\mathbf {G}})\) be such that \({\mathbb {M}}(\partial R)<+\infty \). Then, there exists a sequence of chains \(R_j\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, {\mathbf {G}})\), compactly supported in \(\varOmega \), such that \(\partial R_j\rightarrow \partial R\) (with respect to the \({\mathbb {F}}\)-norm) and \({\mathbb {M}}(S_0 + \partial R_j)\rightarrow {\mathbb {M}}(S_0 + \partial R)\) as \(j\rightarrow +\infty \).
. Let \(R\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, {\mathbf {G}})\) be such that \({\mathbb {M}}(\partial R)<+\infty \). Then, there exists a sequence of chains \(R_j\in {\mathbb {M}}_{n+1}({\overline{\varOmega }}; \, {\mathbf {G}})\), compactly supported in \(\varOmega \), such that \(\partial R_j\rightarrow \partial R\) (with respect to the \({\mathbb {F}}\)-norm) and \({\mathbb {M}}(S_0 + \partial R_j)\rightarrow {\mathbb {M}}(S_0 + \partial R)\) as \(j\rightarrow +\infty \).
The proof of Lemma 22 is identical to that of [2, Proposition 8.6]. In [2], the authors work in the setting of currents; however, the arguments used in the proof of Proposition 8.6 carry over to the setting of flat chains, thanks to the results in [26, Sections 5 and 6].
Lemma 23
Let \(\varOmega \subseteq {\mathbb {R}}^{n+k}\) be a bounded, Lipschitz domain. Let \(S_0\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) be a locally polyhedral chain such that  , and let \(S\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) be such that \(S \sim _{{\overline{\varOmega }}} S_0\). Then, there exists a sequence of locally polyhedral chains \(S_j\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) with the following properties:
, and let \(S\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) be such that \(S \sim _{{\overline{\varOmega }}} S_0\). Then, there exists a sequence of locally polyhedral chains \(S_j\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) with the following properties:
-
(i)
\({\mathbb {F}}(S_j-S)\rightarrow 0\) as \(j\rightarrow +\infty \);
-
(ii)
\({\mathbb {M}}(S_j)\rightarrow {\mathbb {M}}(S)\) as \(j\rightarrow +\infty \);
-
(iii)
for any j, we can write \(S_j = S_0 + \partial R_j\) for some finite-mass \((n+1)\)-chain \(R_j\) with compact support in \(\varOmega \).
Proof
By assumption, there exists \(R\in {\mathbb {M}}_n({\overline{\varOmega }}; \, {\mathbf {G}})\) such that \(S = S_0 + \partial R\). Thanks to Lemma 22 and a diagonal argument, we can assume without loss of generality that R is compactly supported in \(\varOmega \). For any positive t, let \(\varOmega _t := \{x\in \varOmega :{{\,\mathrm{dist}\,}}(x, \, \partial \varOmega )>t\}\). We take a positive number \(t_0\) such that \({{\,\mathrm{spt}\,}}R\subseteq \varOmega _{2t_0}\), and an open set U, with polyhedral boundary, such that \(\varOmega _{2t_0}\subset \!\subset U \subset \!\subset \varOmega _{t_0}\). Because S and \(S_0\) differ by a boundary, we have

However, S and \(S_0\) agree out of U, so  . In particular, since \(S_0\) is locally polyhedral in \(\varOmega \) and U is polyhedral,
. In particular, since \(S_0\) is locally polyhedral in \(\varOmega \) and U is polyhedral,  is a polyhedral chain. Thanks to, e.g., [26, Theorem 5.6 and 7.7], there exists a sequence of polyhedral n-chains \(T_j\) that \({\mathbb {F}}\)-converges to
is a polyhedral chain. Thanks to, e.g., [26, Theorem 5.6 and 7.7], there exists a sequence of polyhedral n-chains \(T_j\) that \({\mathbb {F}}\)-converges to  , satisfies \({{\,\mathrm{spt}\,}}T_j \subseteq \varOmega _{t_0}\) for any j and
, satisfies \({{\,\mathrm{spt}\,}}T_j \subseteq \varOmega _{t_0}\) for any j and

By definition of the \({\mathbb {F}}\)-norm, there exist sequences \(P_j\in {\mathbb {M}}_{n+1}({\mathbb {R}}^{n+k}; \, {\mathbf {G}})\) and \(Q_j\in {\mathbb {M}}_{n}({\mathbb {R}}^{n+k}; \, {\mathbf {G}})\) such that

We do not know a priori whether the chains \(P_j\), \(Q_j\) are supported in \(\varOmega \), so we perform a truncation argument. Define

for \(t\in (0, \, t_0)\) and \(j\in {\mathbb {N}}\). By applying Fatou’s lemma and [26, Theorem 5.7], we obtain that
Therefore, for a.e. \(t\in (0, \, t_0)\) there exists a (non-relabelled) subsequence \(j\rightarrow +\infty \) such that \({\mathbb {M}}(P_{j,t})\rightarrow 0\). By taking the restriction of (D.6) to \(\varOmega _t\), we obtain

By construction, \(P^\prime _j\) and \(Q^\prime _j\) are supported in \(\overline{\varOmega _t}\subseteq \varOmega \), and there holds
Moreover, by taking the boundary of both sides of (D.8), we deduce that

By applying Lemma 21 to \(Q_j^\prime \), we find a decomposition
where
-
(a)
\(Q_j^{\prime \prime }\) is a polyhedral n-chain such that \({\mathbb {M}}(Q_j^{\prime \prime })\lesssim {\mathbb {M}}(Q_j^\prime )\);
-
(b)
\(C_j\) is a \((n+1)\)-chain of finite mass and \({\mathbb {M}}(C_j)\lesssim j^{-1}{\mathbb {M}}(Q_j^\prime )\);
-
(c)
\(Q_j^{\prime \prime }\) and \(C_j\) are supported in \(\overline{\varOmega _{t_0-1/j}}\).
From (a), (b) and (D.9), we deduce that
Now, we define

By construction, \(S_j\) is locally polyhedral. We have

and hence, \({\mathbb {F}}(S_j-S)\rightarrow 0\) due to (D.9) and (D.11). By the lower semi-continuity of the mass, we deduce that \({\mathbb {M}}(S)\leqq \liminf _{j\rightarrow +\infty }{\mathbb {M}}(S_j)\). On the other hand, if we apply the triangle inequality to (D.12) and use the identity  , we obtain
, we obtain

The right hand side converges to zero as \(j\rightarrow +\infty \), due to (D.5) and (D.11). Thus, we deduce that \(\limsup _{j\rightarrow +\infty }{\mathbb {M}}(S_j)\leqq {\mathbb {M}}(S)\), and hence \({\mathbb {M}}(S_j)\rightarrow {\mathbb {M}}(S)\) as \(j\rightarrow +\infty \). Finally, we define \(R_j := R - P^\prime _j - C_j\). Then, (D.13) gives \(S_j - S_0 = \partial R_j\) and the lemma follows. \(\quad \square \)
Proof of Proposition 12
Let \(S_0\), S be given, as in the statement. By applying Lemma 23, we find a sequence of locally polyhedral chains \(S_j\in {\mathbb {M}}_{n}({\overline{\varOmega }}; \, {\mathbf {G}})\) and a sequence of finite-mass \((n+1)\)-chains \(\tilde{R}_j\), compactly supported in \(\varOmega \), such that \(S_j\rightarrow S\) in the \({\mathbb {F}}\)-norm, \({\mathbb {M}}(S_j)\rightarrow {\mathbb {M}}(S)\) and \(S_j = S_0 + \partial \tilde{R}_j\) for any j. Since \(S_0\), \(S_j\) are locally polyhedral in \(\varOmega \), \(\partial \tilde{R}_j\) is polyhedral. We apply Lemma 21 to each \(\tilde{R}_j\). We find polyhedral \((n+1)\)-chains \(R_j\), compactly supported in \(\varOmega \), and \((n+2)\)-chains \(C_j\) of finite mass, such that
Then, \(S_j = S_0 + \partial (R_j + \partial C_j) = S_0 + \partial R_j\), and the proposition follows. \(\quad \square \)
1.2 A Characterisation of the Mass of a Rectifiable Chain
For any linear subspace \(L\subseteq {\mathbb {R}}^{n+k}\), we let \(\pi _L:{\mathbb {R}}^{n+k}\rightarrow L\) be the orthogonal projection onto L. A n-chain of class \(C^1\) is a chain S that can be written in the form \(S = f_{*}P\), with f a map of class \(C^1\) and P a polyhedral chain. The set of rectifiable n-chains is defined as the closure of n-chains of class \(C^1\) with respect to the \({\mathbb {M}}\)-norm.
Lemma 24
Let \(S\in {\mathbb {M}}_n({\mathbb {R}}^{n+k}; \, {\mathbf {G}})\) be a rectifiable n-chain. Then,

where the supremum is taken over all sequences of pairwise disjoint open sets \(U_i\) and n-planes \(L_i\subseteq {\mathbb {R}}^{n+k}\).
If the coefficient group satisfies (D.1), as is the case for \({\mathbf {G}}= \pi _{k-1}({\mathscr {N}})\), then any chain of finite mass is rectifiable, by White’s Rectifiability Theorem [55, Theorem 7.1]. Therefore, Lemma 24 implies Lemma 14.
Proof
Let \((U_i)_{i\in {\mathbb {N}}}\) be a sequence of pairwise disjoint open sets, and let \((L_i)_{i\in {\mathbb {N}}}\) be a sequence of n-planes in \({\mathbb {R}}^{n+k}\). For any i, the projection \(\pi _{L_i}\) is a 1-Lipschitz map and hence  (see e.g. [26, Eq. (5.1)]). Since the \(U_i\)’s are assumed to be pairwise disjoint, we obtain
(see e.g. [26, Eq. (5.1)]). Since the \(U_i\)’s are assumed to be pairwise disjoint, we obtain

This proves one of the inequalities. To prove the opposite inequality, we first suppose that S is a \(C^1\)-polyhedron, then a \(C^1\)-chain, and finally we extend the result to an arbitrary rectifiable chain. We denote by \(\mathrm {int}\, A\) the interior of a set \(A\subseteq {\mathbb {R}}^{n+k}\), and by \(\mathrm {diam}\, A\) its diameter.
Step 1
(S is a \(C^1\)-polyhedron) We suppose that \(S=f_*(\sigma \llbracket K\rrbracket )\), where \(\sigma \in {\mathbf {G}}\), K is a convex, compact n-polyhedra, and \(f:{\mathbb {R}}^{n+k}\rightarrow {\mathbb {R}}^{n+k}\) is a \(C^1\)-diffeomorphism. Let \(\eta > 0\) be arbitrarily fixed. Since f is \(C^1\) and K is compact, there exists \(\rho >0\) such that
where \(\Vert \cdot \Vert \) denotes the operator norm on the space of real \((n+k)\times (n+k)\)-matrices. Let \((T_i)_{i=1}^q\) be a collection of n-simplices that triangulate K, such that
Let \(V_i := \mathrm {int}\, U(T_i, \, \rho /2, \, \rho /2)\) where \(U(T_i, \, \rho /2, \, \rho /2)\) is defined as in (3.1), and \(U_i:=f(V_i)\). The \(U_i\)’s are pairwise disjoint open sets, because f is a diffeomorpism. Let L be the n-plane passing through the origin that is parallel to K. For any i, we choose a point \(x_i\in \mathrm {int}\, T_i\) and we define \(L_i := \nabla f(x_i)(L)\). The \(L_i\)’s are indeed n-planes, because \(\nabla f(x_i)\) is an invertible linear map. For any \(x\in K\cap T_i\) and any \(y\in L\), we have
Therefore, by applying the area formula we obtain

for some constant C depending only on n, k. This implies

where \(\eta \) is arbitrarily small. To complete the proof in this case, it only remains to notice that  , because \({\mathscr {H}}^n(K{\setminus }\cup _i V_i) = 0\) and \({\mathscr {H}}^n(S{\setminus }\cup _i U_i)=0\) by the area formula.
, because \({\mathscr {H}}^n(K{\setminus }\cup _i V_i) = 0\) and \({\mathscr {H}}^n(S{\setminus }\cup _i U_i)=0\) by the area formula.
Step 2
(S is a \(C^1\)-chain) We suppose that \(S=f_*P\), where P is a polyhedral n-chain and \(f:{\mathbb {R}}^{n+k}\rightarrow {\mathbb {R}}^{n+k}\) is a \(C^1\)-diffeomorphism. This case follows easily from the previous one, by additivity. Indeed, let us write \(S = \sum _{j=1}^p \sigma _j\llbracket K_j\rrbracket \) with \(\sigma _j\in {\mathbf {G}}\), \(K_j\) a convex, compact n-polyhedra. Given positive parameters \(\delta \), \(\gamma \), let \(W^j := f(\mathrm {int}\,U(K_j, \, \delta , \, \gamma ))\). For \(\delta \), \(\gamma \) small enough, the \(W^j\) have pairwise disjoint interiors. Let \(\eta >0\) be fixed. By applying Step 1, for any j we find a sequence \((V_i^j)_{i\in {\mathbb {N}}}\) of pairwise disjoint open sets and a sequence \((L_i^j)_{i\in {\mathbb {N}}}\) of n-planes such that

We define \(U_i^j := V_i^j\cap W^j\). The \(U_i^j\)’s are pairwise disjoint open sets. We have \({\mathscr {H}}^n(K_j{\setminus }\mathrm {int}\, U(K_j, \, \delta , \, \gamma )) = 0\) and hence, by the area formula,  . Therefore, we obtain
. Therefore, we obtain

and the lemma is proved also in this case, because \(\eta \) may be taken arbitrarily small.
Step 3
(S is a rectifiable chain) Since S is rectifiable, for any \(\eta >0\) there exist a polyhedral n-chain P and a \(C^1\)-diffeomorphism \(f:{\mathbb {R}}^{n+k}\rightarrow {\mathbb {R}}^{n+k}\) such that
(see e.g. [55, 1.2 at p. 169] and the references therein). By Step 2, there exists a sequence \((U_i, \, L_i)_{i\in {\mathbb {N}}}\) such that

Let us set \(Q := S - f_*P\). Then, using the linearity of \(\pi _{L_i,*}\),  , and the triangle inequality for \({\mathbb {M}}\), we obtain
, and the triangle inequality for \({\mathbb {M}}\), we obtain

so the lemma follows.\(\quad \square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Canevari, G., Orlandi, G. Topological Singular Set of Vector-Valued Maps, II: \(\varGamma \)-convergence for Ginzburg–Landau type functionals. Arch Rational Mech Anal 241, 1065–1135 (2021). https://doi.org/10.1007/s00205-021-01671-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-021-01671-2



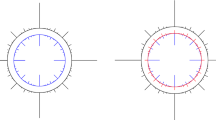


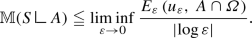






 ;
; ;
; takes multiplicities in the set
takes multiplicities in the set 
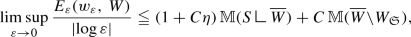

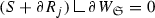 ;
; takes multiplicities in the set
takes multiplicities in the set 