1 Introduction

The outbreak of SARS-CoV-2 disease has been one of the worst pandemics the world is experiencing in the present century. The disease had started in Wuhan, China, in December 2019 and has currently infected almost all the countries across the globe. WHO declared this new coronavirus disease (also known as COVID-19) as a pandemic on 11 March 2020 [34, 36]. As COVID-19 is a pandemic, which is still evolving, mathematical models help us analyse the evolution of the disease and also helps us predict the future scenario of the disease transmission, based on which governments may take necessary actions to suppress future transmissions. Many mathematical models are being formulated to study the spread of COVID-19 in different countries and to predict the evolution of the outbreak [2, 9, 11, 12, 16, 18, 21, 25, 34, 37, 44]. As of mid-March 2021, total global cases of the pandemic have reached more than 120 million [14].

In India, the first COVID-19 case was confirmed on the 30 January 2020 [8]. In the early phase of the epidemic in India, certain events during March 2020 in the states of Delhi and Punjab have appeared to become the ‘super-spreaders’ of COVID-19 and Delhi became the hotspot in India [15, 32] along with the city of Mumbai. One unique cause which fuelled the spreading of the disease in certain states such as Bihar, Assam, West Bengal, and Odisha was the movement of migrant workers during May 2020 [28, 39].

Table 1 Comparison of population of some of the Indian states [7]
Full size table

The Indian scenario as far as the pandemic is concerned is quite intriguing. Some of the major facts which justify an India-specific modelling are the huge population size and its density, the status of the economy, extreme diversity in the working population and economic status of the people, diversity in culture, language, and the way of living. The socio-economic perspective of the response to the pandemic and its related measures assume immense importance when one realises the fact that the social behaviour of the population can vary widely from state to state as the lifestyle and culture, which govern the social behaviour, are very different as one travels across the length and breadth of the country. The same can be said for the economy. The gross domestic product (GDP) stands at a staggering 450 billion USD for the state of Maharashtra to a minimal 1.2 billion USD for the union territory of Andaman and Nicobar Islands [1, 26]. More than 19,500 languages and dialects are spoken in India as mother tongues of which about 120 languages are spoken by more than 10,000 people in India [6]. It is also important to note that the lifestyle of the people of one state is greatly influenced by its culture, which is identified with the language spoken. The food habits of the people also vary widely from state to state. For example, meat and poultry products are quite common in the eastern part of the country, while vegetarianism is very popular in some northern states like Haryana, Rajasthan, etc. According to government surveys [35], about 30% of the Indian population are vegetarian. As this socio-economic behaviour is closely related to the progress of the pandemic, the response of the state population to the pandemic is worth studying. The population of many Indian states is even comparable to some countries. Table 1 shows how the populations of certain Indian states can be compared with some countries of the world [7].

In this work, we have constructed a compartmental non-autonomous disease model based on the well-known susceptible-exposed-infectives-removed (SEIR) model [17, 22]. We have applied this model to eleven Indian states, which have the highest number of infectives of COVID-19, except for the states of Andhra Pradesh and Telangana, which were newly created states and do not have the updated census data. At this point, we must caution the reader that this is a pandemic that is still evolving and even during the course of writing this paper, the pandemic has evolved beyond the time that was originally intended as a prediction limit for this work. While, at the time of initiating this work, the surge of the infections in India was yet to attain its peak, at present, we are witnessing the second wave of the pandemic, which started from about March 2021. However, we have found that the model described here is able to predict the first phase of the pandemic, almost in entirety, well beyond its intended prediction limit—about 180 days beyond the analysed data. We note that, very early into the pandemic, India has witnessed a prolonged national-level lockdown followed by a huge migration, primarily affecting the people with low income and employed in the informal sector. Besides, there were certain large-scale localised events at the time when the lockdown was being imposed [15, 32]. Both these factors are believed to have affected the way the pandemic has progressed in India. Our analysis of the federal states, which is based on this model, suggests certain uniform and unique behaviour the way the pandemic has advanced. We have limited our analysis of the data to the end of August 2020—to the 170th day into the pandemic from the day of first detected infection, and all the predictions beyond the 170th day are based on the analysis of data only up to this date. We have limited the analysis of data up to this date, as most of the establishments and business have started to open, including some educational institutions, from September onwards. Besides, from September onwards, the winter festival season begins in India during which the infections are expected to rise considerably. In what follows, we first describe and develop our model in Sect. 2. Next, we present an equilibria analysis for our model and calculated the basic reproduction number \(R_{0}\) in Sect. 3. Then, we analyse the progress of the pandemic for eleven Indian states in Sect. 4. In Sect. 5, we provide an overall scenario for the whole country and provide our projections of the pandemic. In Sect. 6, we compare the results obtained from our model with the logistic models. Finally, we summarise and conclude with the novel ideas used and the main results obtained in this work in Sect. 7. We would also like to point to the fact that all the figures up to Sect. 5 are based on the data that were available till about mid-October 2020 (212th day into the pandemic). In Sect. 6, however, we have used the latest data, available till March 2021.

2 The model

2.1 The limitations on data

It is worth noting that though the gross official COVID-19 data are maintained by the Ministry of Health and Family Welfare (MoHFW) in India [24], it is difficult to obtain the fine-scale reliable data. For example, while we know the daily statistics of the newly infected and recovered people as well as the daily deaths, the reliable data about patients in non-critical and critical stage (patients requiring ventilators), hospital discharge statistics with reference to different age groups, statistics about patients whether they are home-quarantined or officially quarantined (the so-called COVID Centres), etc., are not easily available. Based on these observations, we have modelled the pandemic on the basis of data what is available in the public domain. For modelling the state data, we have use crowdsourced data, which is maintained by https://www.covid19india.org [8]. It should be noted that this dataset closely matches the official data provided by the MoHFW and the data maintained by John Hopkins’ COVID database [14].

2.2 The facts and assumptions

It is understood that a considerable part of the infectious population is asymptomatic. It is important to note that our asymptomatic population is not what is reported after detection of the disease in an asymptomatic person. When an asymptomatic person is listed as an infected person, it adds to the total number of infectives, irrespective of whether the disease is asymptomatic or symptomatic. However, there is a large population of people, which are potential infectives but never detected. This population is always hidden as an asymptomatic person does not show any kinds of signs of the disease but equally infectious just like a person who is known to have the disease. At present, there is no known method to isolate this population except large-scale systematic testing of the general population.

We also know that the disease has an incubation period after a person being exposed to the virus. However, the incubation period is only known for the population who is known to have been exposed. The incubation stage for the asymptomatic population simply does not exist. We further assume that the number of deaths due to causes other than COVID-19 is negligible during the pandemic period. We also assume that once a person is known to have been exposed to the virus, the person is being quarantined or being closely monitored, thereby preventing such a person to become an asymptomatic carrier.

As almost all nations have resorted to a lockdown or other restrictive measures once they have detected that there is a section of the population known to have contracted the disease, the infection rate definitely decreases over time. Besides, during the initial phase of the spread of the disease, it is expected that the infection rate through the asymptomatic population remains negligible only to become significant as the disease spreads over time. The other significant deviation from the classic models is the inclusion of time dependence of the rate at which the exposed population starts contracting the disease. We assume that at the start of the pandemic, the incubation period is negligible as most of the population starts in the infected compartment. Based on these observations, we can now write down the following non-autonomous disease model which is sourced from the basic susceptible-exposed-infectives-removed (SEIR) model [17, 22],

$$\begin{aligned} \frac{{\mathrm {d}}S}{{\mathrm {d}}t}= & {} \lambda -(\beta _{t}+\rho _{t})\frac{IS}{N}-\delta S, \end{aligned}$$
(1)
$$\begin{aligned} \frac{{\mathrm {d}}E}{{\mathrm {d}}t}= & {} \beta _{t}\frac{IS}{N}-(\nu _{t}+\delta )E, \end{aligned}$$
(2)
$$\begin{aligned} \frac{{\mathrm {d}}I}{{\mathrm {d}}t}= & {} \nu _{t}E-(\gamma +\delta )I+\rho _{t}\frac{IS}{N}, \end{aligned}$$
(3)
$$\begin{aligned} \frac{{\mathrm {d}}R}{{\mathrm {d}}t}= & {} \gamma I-\delta R, \end{aligned}$$
(4)

where N is the total population. The variables S, E, I, R denote the instantaneous size of the population related to the model. The total number of the population susceptible to the disease at any instant of time is denoted by S, while the number of population which is being exposed is denoted by E. The variable I denotes the size of the population at a given instant, which has been infected (fallen sick). The variable R denotes the combined size of the population which has either recovered from the disease or has succumbed to the disease, i.e. the removed population. Naturally

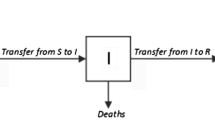
$$\begin{aligned} S(t)+E(t)+I(t)+R(t)=N=\mathrm{const.} \end{aligned}$$
(5)

In the above equations, \(\beta _{t}\) is the rate of exposure of the population to the virus, \(\rho _{t}\) is the rate of infection through the asymptomatic population, \(\nu _{t}\) is the rate at which the exposed population contracts the disease, i.e. the incubation period, \(\gamma \) is the rate at which the population is removed from the infected population, and \(\delta \) is the average death rate of the population (not due to the disease). The parameter \(\lambda \) represents the import to the susceptible population from outside. The subscript ‘t’ in the rates indicates that the corresponding rates depend on time. All rates are expressed in terms of persons per day. The removed group includes the population, which gets removed from the infected group either by recovery or by death. Note that at the limit \(\nu _{t}\rightarrow \infty ,\rho _{t}\rightarrow 0,\beta _{t}=\mathrm{const.}\), the model reduces to the classic SIR model. The schematic compartmental diagram for the model is shown in Fig. 1.

The disease-free equilibrium (DFE) state of the system is given by \(I(t)=E(t)=R(t)=0\) and \(\lambda =\delta S\), which is used to find the basic reproduction number \(R_{0}\).

Fig. 1
figure 1

The compartmental diagram for the model

Full size image

2.3 Modelling the rates

The base-level average values of the rates for India are tabulated in Table 2. As we have argued that at the start of the pandemic, the incubation period is almost zero as the most number of population start at the infected compartment. In time, however, the incubation period will be applied to all the exposed population, who are being monitored. In the same way, in the beginning, the infection through the asymptomatic population would be very small unless there is a large scale of migration of people. This always happens, but not at the beginning. Again, if we consider the effect of the nationwide lockdown, which most countries have resorted to, we can safely assume that the disease transmission rate constantly decreases, eventually becoming zero as people become accustomed to social distancing norms.

Table 2 Base-level average rates and total population
Full size table

Based on these observations, we propose the following ansätze,

$$\begin{aligned} \beta _{t}= & {} \alpha _{t}e^{-\zeta _{t}t}, \end{aligned}$$
(6)
$$\begin{aligned} \rho _{t}= & {} \eta _{t}\mathrm{erf}(\rho _{0}t), \end{aligned}$$
(7)
$$\begin{aligned} \nu _{t}= & {} \nu _{0}e^{-\varphi t}+\nu _{f}. \end{aligned}$$
(8)

In the first expression, \(\alpha _{t}=\alpha _{0}{\hat{\alpha }}(t)\) is a piecewise function, starting at the basic equivalent value for the classic SIR model at \(t=0\) and \(\zeta _{t}=\zeta _{0}{\hat{\zeta }}(t)\) is a piecewise function which basically represents at what rate the transmission rate is decreasing. The piecewise property is necessary as at different times, we see different reasons which change the behaviour of the pandemic. A sudden influx of migrants or a sudden uncontrolled congregation can be modelled with the piecewise behaviour as and when needed. In the second expression, we assume that the asymptomatic transmission rate starts from a very low value \(\rho _{0}\sim 0\), gradually approaching a constant rate \(\eta _{t}\), which is again a piecewise function and can be adjusted to suit sudden unexpected behaviour of the pandemic. In the third expression, we assume that the incubation period approaches a final value of \(\nu _{f}\simeq 1/14\,\mathrm{days}^{-1}\) [19] as the pandemic progresses. The quantity \(\nu _{0}\) represents the inverse of the initial incubation period at which the pandemic starts, which is a very large number, quickly decreasing determined by the rate \(\varphi \).

3 The equilibria

The equilibria of the system, Eqs. (1–4), are given by

$$\begin{aligned}&(S,E,I,R)\nonumber \\&\quad =\left\{ \begin{array}{l} \left( {\displaystyle \frac{\lambda }{\delta }},0,0,0\right) \\ \\ \left( {\displaystyle \frac{\lambda }{R_{0}\delta },{\displaystyle \frac{\beta _{t}\lambda (R_{0}-1)}{R_{0}(\delta +\nu _{t})(\beta _{t}+\rho _{t})},\frac{\lambda (R_{0}-1)}{(\beta _{t}+\rho _{t})},\frac{\gamma \lambda (R_{0}-1)}{\delta (\beta _{t}+\rho _{t})}}}\right) \end{array}\right. ,\nonumber \\ \end{aligned}$$
(9)

where \(R_{0}\) is the basic reproduction number (see the next section), which is given by

$$\begin{aligned} R_{0}=\frac{\beta _{t}\nu _{t}+\rho _{t}(\nu _{t}+\delta )}{(\gamma +\delta )(\delta +\nu _{t})}, \end{aligned}$$
(10)

which we derive in the next section. Besides, we have also used the constraint given by (5). The first equilibrium point is the disease-free equilibrium (DFE) and the other one is the endemic equilibrium (EE) and it is amply clear that the system can reach EE only when \(R_{0}>1\).

3.1 The basic reproduction number \(R_{0}\)

As we know that the basic reproduction number \(R_{0}\) is defined as the average number of secondary cases that would be generated by a primary case in a totally susceptible population [23]. It provides an overall measure of transmission of an infectious disease within a given population, which is dependent on the transmission coefficient of the disease as well as on the average duration of infectiousness [23]. For \(R_{0}>1\), the disease-free equilibrium (DFE) of an infectious disease is unstable, while for \(R_{0}<1\), the DFE is asymptotically stable [41].

In order to compute \(R_{0}\), we consider our two infected compartments E and I of the model, and we re-structure our model in terms of the rate of appearance of new infections \(\mathcal{F}_{i}(x)\) and the rate of transfer of individuals \(\mathcal{V}_{i}(x)\) [41],

$$\begin{aligned} {\dot{x}}_{i}=\mathcal{F}_{i}(x)-\mathcal{V}_{i}(x),\quad i=1,\ldots ,n \end{aligned}$$
(11)

with \(n=4\) and \(\varvec{x}=(E,I,S,R)'\). We note that the rate of transfer can further be divided into two transfer rates \(\mathcal{V}_{i}=\mathcal{V}_{i}^{-}-\mathcal{V}_{i}^{+}\), with \(\mathcal{V}_{i}^{\pm }\) denoting transfer into the ith compartment and out of it. The components are thus

$$\begin{aligned} \mathcal{F}= & {} \left( \beta _{t}\frac{IS}{N},\rho _{t}\frac{IS}{N},0,0\right) ', \end{aligned}$$
(12)
$$\begin{aligned} \mathcal{V}= & {} \left( (\nu _{t}+\delta )E,-\nu _{t}E+(\gamma +\delta )I,\right. \nonumber \\&\left. -\lambda +(\beta _{t}+\rho _{t})\frac{IS}{N}+\delta S,-\gamma I+\delta R\right) '. \end{aligned}$$
(13)

The basic reproduction number \(R_{0}\) is thus the leading eigenvalues of the matrix \(FV^{-1}\), where

$$\begin{aligned} F=\left( \frac{\partial \mathcal{F}_{i}}{\partial x_{j}}\right) _{x_{\mathrm{DFE}}},\quad V=\left( \frac{\partial \mathcal{V}_{i}}{\partial x_{j}}\right) _{x_{\mathrm{DFE}}},\quad i,j=1,2\nonumber \\ \end{aligned}$$
(14)

evaluated at the DFE state. For our model, we have

$$\begin{aligned} F=\left( \begin{array}{cc} 0 &{} \beta _{t}\\ 0 &{} \rho _{t} \end{array}\right) ,\quad V=\left( \begin{array}{cc} \nu _{t}+\delta &{} 0\\ -\nu _{t} &{} \gamma +\delta \end{array}\right) , \end{aligned}$$
(15)

where we have used the DFE state as \(S/N=1\). The basic reproduction number can now be found as

$$\begin{aligned} R_{0}=\frac{\beta _{t}\nu _{t}+\rho _{t}(\nu _{t}+\delta )}{(\gamma +\delta )(\delta +\nu _{t})}. \end{aligned}$$
(16)
Fig. 2
figure 2

The endemic equilibrium values of the variables. The top panel is for \(\rho _{t}=10\%\) of \(\beta _{t}\), while the middle panel is when \(\rho _{t}=10^{-4}\,\mathrm{day^{-1}}\). The bottom panel is for \(\beta _{t}=10^{-4}\,\mathrm{day^{-1}}\). The dotted line in each panel represents the limiting value when the variable at abscissa becomes \(\gg 1\)

Full size image

3.2 Endemic equilibrium

As shown at the beginning of the section, the EE of the system is given by the second solution of Eq. (9), which is expressed in terms of the basic reproduction number \(R_{0}\), which can be reached only when \(R_{0}>1\). It is interesting to see this EE limit of the variables which are the values when the epidemic is completely out of control, which is, however, not expected to reach. The EE values of the variables in terms of the basic rates are given by,

$$\begin{aligned} E_{\mathrm{EE}}= & {} \frac{\beta _{t}\lambda }{(\beta _{t}+\rho _{t})}\left[ \frac{1}{(\delta +\nu _{t})}-\frac{(\gamma +\delta )}{\beta _{t}\nu _{t}+\rho _{t}(\delta +\nu _{t})}\right] ,\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned} I_{\mathrm{EE}}= & {} \frac{\lambda }{(\beta _{t}+\rho _{t})}\left[ \frac{\rho _{t}}{(\gamma +\delta )}+\frac{\beta _{t}\nu _{t}}{(\delta +\nu _{t})(\gamma +\delta )}-1\right] ,\nonumber \\ \end{aligned}$$
(18)
$$\begin{aligned} R_{\mathrm{EE}}= & {} \frac{\gamma }{\delta }I_{\mathrm{EE}}. \end{aligned}$$
(19)

From the above expressions, it can be shown that a sufficient condition for the system to reach an endemic equilibrium (EE) is \(\rho _{t}>\gamma +\delta \) or when the asymptomatic transmission rate overtakes the combined value of removal and death rates.

As mentioned at the beginning, it is logical to assume that the asymptomatic transmission rate \(\rho _{t}\) is proportional to the usual transmission rate \(\beta _{t}\) of disease, though a completely independent asymptomatic transmission rate is not impossible to have. Various endemic equilibrium values of the variables in the two limiting cases—when \(\beta _{t}\gg 1\) (independent of \(\rho _{t})\) and \(\rho _{t}\gg 1\), are shown in Table 3. In the limit of a very high asymptomatic transmission rate, we have no exposed population left in the system as people become infected (asymptomatically) without being considered as exposed. The incubation rate \(\nu _{t}\), mean infection rate \(\gamma \), and the total number of population (for India) are as per Table 2.

Table 3 The endemic equilibrium (EE) values of the variables in two limits. The numbers are shown in millions
Full size table
Fig. 3
figure 3

The endemic equilibrium regions \((R_{0}>1)\) in the \((\rho _{t},\beta _{t})\) space. The left panel is when both \(\rho _{t}\) and \(\beta _{t}\) are independent of each other, and the right panel is when \(\rho _{t}=\xi \beta _{t}\), where \(\xi _{t}\) is a proportionality factor

Full size image

In Fig. 2, we have shown the values of the exposed population, infectives, and removed population approaching the EE state when \(R_{0}>1\). The top panel shows the variable when the asymptomatic transmission rate \(\rho _{t}\) stays at \(10\%\) of the transmission rate \(\beta _{t}\), i.e. at all times \(\rho _{t}=0.1\beta _{t}\). In the middle panel, we show the variables when \(\rho _{t}\) is kept independent of \(\beta _{t}\) and has a value of \(10^{-4}\,\mathrm{day}^{-1}\). The bottom panel shows the variables when \(\beta _{t}\) is kept independent of \(\rho _{t}\) and has a value of \(10^{-4}\,\mathrm{day}^{-1}\). The dotted lines in the figure are the limiting values of each variable as given in Table 3. In Fig. 3, we show the regions of EE in the \((\rho _{t},\beta _{t})\) space, which is the darkened region with \(R_{0}>1\). While the left panel in the figure is for independent \(\rho _{t}\) and \(\beta _{t}\), the right panel is when \(\rho _{t}=\xi \beta _{t}\), where \(\xi \) is a proportionality factor. As we can see from the figure that for a country like India, for the disease to reach an endemic state, the asymptomatic transmission rate \(\rho _{t}\simeq 0.54\beta _{t}\) (the red coloured straight lines in the panels of Fig. 3) or the asymptomatic transmission rate should be as high as about \(54\%\) of the normal transmission rate.

Table 4 Convergence region for optimisation
Full size table

4 Case examples

In this section, we try to map the pandemic in the federal states of India with our model. The Indian context possesses a unique model to study this pandemic in terms of heterogeneous groups of populations. As all the federal states of India are based on their respective cultures and languages, the states make somewhat homogeneous groups of people over which these compartmental models are applicable. So, it is more appropriate to apply a model to individual states to get the overall picture for the whole country.

We assume that the asymptomatic infection rate starts from zero at the beginning of the pandemic and saturates at \(\eta _{t}\), which is expressed as a fraction of the current disease transmission rate \(\beta _{t}\). In the same way, the incubation period starts at a very large value \(\gg 1\) at the beginning and saturates to about \(1/14\,\mathrm{days^{-1}}\) as the case of new infections peaks up.

4.1 Optimisation

The mathematical formulation to model the pandemic is set up as a nonlinear global optimisation problem, where we try to solve the model equations numerically so that the deviation of the solution from the actual data is minimised globally with respect to the parameters \(\alpha _{t},\zeta _{t},\rho _{0},\varphi \). The parameter \(\nu _{0}\) is fixed at \(10^{4}\), although any large positive number will do. The quantity which is minimised is given by

$$\begin{aligned} \mathcal{R}=\sum _{t=1,2,\ldots }^{N}\sum _{j=1,2,\ldots }^{n}\left| x_{j}^{t}-{\tilde{x}}_{j}^{t}\right| ^{2} \end{aligned}$$
(20)

which is the residue (or global error) in fitting the data. This residue is the absolute squared difference between the numerically found values of the variables \(\varvec{x}=(E,I,S,R)'\) and their corresponding actual values \(\tilde{\varvec{x}}\) (from the data). The residue is accumulated over N sampling points on the data train denoting different time stamps over n number of solutions of the dynamical equations, which in this case is 4. The constrained global minimisation is carried out through the derivative-free Nelder–Mead algorithm [27], though any other method such as trust-region-reflective can also be used. The minimisation returns the best-fit parameters for the model.

It should, however, be noted that an unconstrained minimisation is not possible due to the complexity of the fitting functions which have piecewise time-dependent functions as there may be several local minima and the minimisation may converge to any one of them. Therefore, the strategy has been to judiciously constrain the variables based on the possible parameter ranges of the time-independent versions of the functions. In Table 4, we give the region of convergence with the constraints on \(\alpha _{0},\zeta _{0},\varphi ,\) and \(\rho _{0}\) [see Eqs. (6–8)] for the asymptomatic transmission rate \(\xi =10\%\) for two states, where \({\hat{\alpha }}(t)\in [0.51,1.05]\) and \({\hat{\zeta }}(t)\equiv 1\). In Fig. 4, we show the convergence patterns of the variables for these two states.

Fig. 4
figure 4

The convergence of the constrained global minimisation for two states—Maharashtra (MH) and Gujarat (GJ) for the asymptomatic rate of \(10\%\)

Full size image
Fig. 5
figure 5

a Total infectives I, daily new infectives \(I_{\mathrm{new}}\), and \(R_{0}\). Every row represents one state with three panels of which the first panel shows the total infectives I as calculated from our numerical compartmental model (shown as dark black solid curve), which is superimposed with the actual data (shown as open red circles). The second panel shows the daily new infections as predicted by our model (shown as dark black curve), superimposed over the actual data (shown as yellow solid line). The third panel shows the corresponding \(R_{0}\), where the dotted line indicates the level \(R_{0}=1\). b Total infectives I, daily new infectives \(I_{\mathrm{new}}\), and \(R_{0}\) [See the explanatory texts in the caption of (a)] c Total infectives I, daily new infectives \(I_{\mathrm{new}}\), and \(R_{0}\). [See the explanatory texts in the caption of (a)]

Full size image
Table 5 Socio-economic parameters of 11 federal states of India
Full size table

4.2 Modelling at state level

We have tabulated the key parameters for each of these states in Table 5. In the table, the population P is indicated in millions as per the latest data [40], the gross domestic product (GDP) [1] for the year 2020–21 (\(P_{\mathrm{GDP}}\)) is shown in equivalent billion USD, \(P_{\mathrm{Econ}}\) is the percentage of the population which has an average annual income less than about 380 USD [10, 38], \(P_{\mathrm{Urban}}\) is the percentage of the population living in urban areas, \(P_{\mathrm{Child}}\) is the percentage of the children population (up to the age of 14 years), and \(P_{\mathrm{Youth}}\) is the percentage of the youth population (from the age of 15 years to 59 years) [29, 31]. In Fig. 5, we have plotted the total cumulative number of infectives I, daily new infectives \(I_{\mathrm{new}}\), and the basic reproduction number \(R_{0}\) for each of the eleven federal states of India. In each of these figures, every row represents one state containing three panels of which the first panel shows the total infectives I as calculated from our numerical compartmental model (shown as dark black solid curve), which is superimposed with the actual data (shown as open red circles). The second panel shows the daily new infections as predicted by our model (shown as dark black curve), superimposed over the actual data (shown as a yellow solid line). The third panel shows the corresponding \(R_{0}\) for the particular state where the dotted line indicates the level \(R_{0}=1\). The name of the state is abbreviated as per Table 5 and is indicated in each row in the first panel. The x-axis of each panel is the number of days elapsed since 14 March 2020. Note that this axis is different for each of these eleven states. In all these cases, we have assumed that the transmission rate \(\rho _{t}\) for the asymptomatic population saturates at \(10\%\) of the transmission rate, i.e. \(\rho _{t}=0.1\beta _{t}\).

We note that the first COVID-19 case was reported in India on 30 January 2020. However, after that the occurrence of cases has either been sporadic or confined in certain localised households only. The major continuous detection of cases started in mid-March 2020, and in all our analyses, we have taken the zeroth day as 14 March 2020.

4.3 Transmission analysis: criticality

In the case of an infectious disease like COVID-19, as the disease progresses, the number of people getting infected increases rapidly, a measure of which can be defined through the basic reproduction number \(R_{0}\). In this section, we aim to find the day at which there is a sudden shift in the pattern of increase in the number of reported cases in various states of India. This sudden shift is present in almost every states, though we have here analysed only 11 states which mostly contributed to the pandemic. We call this day the critical day or the day of community transmission with an assumption that at around this day first major fluctuation takes place. We can also define this day as the day at which there is a shift from small-scale fluctuations of reported cases to large-scale fluctuations.

Fig. 6
figure 6

a Transmission analysis of 11 worst-affected states. The left-hand panels show the daily reported new cases \(I_{\mathrm{new}}\) vs. the total cumulative cases, i.e. total infectives I, plotted as per real data (shown as the blue curve) and 5–30 day mean \(I_{\mathrm{av}}\) (shown as the red curve). The right-hand panels show the absolute deviation of the real data from its mean \(\varDelta I_{\mathrm{new}}\) [see Eq. (21)], which show a uniform behavioural pattern of the transmission. The fluctuation pattern of reported cases from its mean suddenly changes its behaviour from a uniform small-scale fluctuation to a large-scale fluctuation (denoted by a vertical dashed line). The number \(d_{C}\) denotes the position of this transition of behaviour in the number of days elapsed since the beginning of the data set, i.e. 14 March 2020. b Transmission analysis of 11 states [See the explanatory texts in the caption of (a)] c Transmission analysis of 11 states. [See the explanatory texts in the caption of (a)]

Full size image

Figure 6 shows the transmission analysis of the disease in most 11 worst-affected states. The left-hand panels show the daily reported new cases \(I_{\mathrm{new}}\) vs. the total cumulative cases, i.e. total infectives I, plotted as per real data (shown as the blue curve) and \(5-30\) day mean \(I_{\mathrm{av}}\) (shown as the red curve). The right-hand panels show the absolute deviation of the real data from its mean \(\varDelta I_{\mathrm{new}}\),

$$\begin{aligned} \varDelta I_{\mathrm{new}}=|I_{\mathrm{new}}-I_{\mathrm{av}}|, \end{aligned}$$
(21)

which show a uniform behavioural pattern of the transmission. It is interesting to note that the fluctuation pattern of reported cases from its mean suddenly changes its behaviour from a uniform small-scale fluctuation to a large-scale fluctuation (denoted by a vertical dashed line). The number \(d_{C}\) denotes the position of this transition of behaviour in number of days elapsed since the beginning of the data set, i.e. 14 March 2020. We have denoted this day as a critical day \(d_{C}\) which denotes the first major change of transmission rate in the respective states. We may very well call it as the day when the community transmission (or large-scale transmission) starts. It is worth noting that following continuous reporting of positive COVID-19 cases, which started on 14 March 2020, national-level lockdown in the country was imposed in four phases [4]

  1. 1.

    1st phase—from 25 March to 14 April 2020 (up to 31st day)

  2. 2.

    2nd phase—from 15 April to 3 May 2020 (up to 50th day)

  3. 3.

    3rd phase—from 4 May to 17 May 2020 (up to 64th day)

  4. 4.

    4th phase—from 17 May to 31 May 2020 (up to 78th day)

As we see that on average, the criticality started in and around the end of the 4th level of lockdown, i.e. near about 80th day (the average being 78.8 days). While in five states, the criticality started around the 100th day, in six other states it started within the 44th and the 79th day. From these observations, we can see that these plots correctly capture the transmission characteristics of the pandemic in these major states.

4.4 Scatter plots: the socio-economic pattern

As mentioned before, in our present analysis, we have taken 11 most affected states of India. From a population point of view, most of the Indian states have comparable populations with other individual countries. Within India, most of the states differ in terms of culture, economy, and demography. In this section, we aim to draw some relations in respect of spreading of the SARS-CoV-2 disease and different socio-economic parameters.

We show the scatter plots of the disease transmission parameters—\(\beta _{C,N}\) and \(d_{C}\) versus the socio-economic parameters as described in Table 5. \(\beta _{C,N}\) are the disease transmission rates at the criticality, i.e. on the critical day \(d_{C}\) and at the end of the data interval (Nth day), which is 31 August 2020, respectively. In all the following analyses, we have taken three limiting values for the asymptomatic transmission rate \(\rho _{t}\)—\(10\%,20\%,\) and \(30\%\) of the transmission rate \(\beta _{t}\).

Fig. 7
figure 7

\(\beta _{C}\) vs. \(P_{\mathrm{Youth}}\) and \(P_{\mathrm{Child}}\) : The youth population seems to drive the first major transmission. Each column is, respectively, for 10, 20, and \(30\%\) asymptomatic transmission rate. These plots show a power-law dependence of \(\beta _{C}\) on the youth and child population. While \(\beta _{C}\) seems to increase with the youth population, it decreases with the child population

Full size image

For fitting the data, we have used the nonlinear Levenberg–Marquardt method [30] with all data points weighted equally, i.e. with a weight one. The goodness of fitting is denoted by the so-called quality factor Q, which can be defined in terms of normalised incomplete gamma function \(\varGamma (N_{\mathrm{DOF}}/2,\chi ^{2}/2)\) [43]

$$\begin{aligned} Q=\frac{1}{\varGamma (N_{\mathrm{DOF}}/2)}\int _{\chi ^{2}/2}^{\infty }x^{N_{\mathrm{DOF}}/2-1}e^{-x}\,{\mathrm {d}}x\le 1, \end{aligned}$$
(22)

where \(N_{\mathrm{DOF}}\) is the ‘number of degrees of freedom’, which is defined as \(N_{\mathrm{DOF}}=N_{p}-M\), where \(N_{p}\) is the number of independent data points and M is the independent parameters of the fitting. The Chi-square is defined as

$$\begin{aligned} \chi ^{2}=\sum _{i=1}^{N_{p}}\left[ \frac{y_{i}-f(x_{i})}{\sigma _{i}}\right] ,^{2} \end{aligned}$$
(23)

with the nonlinear fitting model \(y=f(x)\). The value of Q is indicated in each of the scatter plots.

Fig. 8
figure 8

\(\beta _{C}\) vs. \(P_{\mathrm{Urban}}\) (Delhi omitted) : The urban population also seems to drive the first major transmission. The more is the urban population, the more quickly the day of first major transmission \(d_{C}\) is reached

Full size image
Fig. 9
figure 9

\(\beta _{C}\) vs. \(P_{\mathrm{GDP}}\) : The more affluent is the population, the more is the transmission rate at the first major transmission. So, it is the purchasing power of the population that has driven the transmission

Full size image
Fig. 10
figure 10

\(\beta _{C}\), \(\beta _{N}\) vs. \(P_{\mathrm{Econ}}\) : \(P_{\mathrm{Econ}}\) is the % of the population below a certain income denoted as the Economy group. The lower is the value of \(P_{\mathrm{Econ}}\), the richer is the population

Full size image
Fig. 11
figure 11

\(d_{C}\) vs. \(P_{\mathrm{Econ}},P_{\mathrm{Urban}}\) : The richer is the population (lower \(P_{\mathrm{Econ}}\), in the first panel), and the more is the urban population (higher \(P_{\mathrm{Urban}}\), in the second panel), the quicker it takes to reach the criticality (lower \(d_{C}\))

Full size image

4.4.1 Disease transmission and population age

In Fig. 7, we show the critical transmission rate \(\beta _{C}\) versus the youth and child populations in the selected states. Each row of the figure contains three columns of scatter plots which are, respectively, for 10, 20, and \(30\%\) asymptomatic transmission rate (see the beginning of this section). The scatter plots show a power-law dependence of \(\beta _{C}\) on the youth and child population. While \(\beta _{C}\) seems to increase with the youth population, it decreases with the child population. This is quite understandable as the child population is effectively confined during the lockdown period and thereafter owing to the closure of educational institutions, the youth population—primarily the working population begins to go out thus contributing to the growth of the disease. So, we can conclude that during the extended lockdown phase, the youth population seems to drive the pandemic.

4.4.2 Disease transmission and urban population

In Fig. 8, we show how does the critical transmission rate \(\beta _{C}\) depend on the urban population. The scatter plots clearly show that the urban population is one of the major parameters which drives the pandemic. The asymptomatic transmission rate is modelled at 10, 20, and \(30\%\) of the primary transmission rate as before.

4.4.3 The critical day, disease transmission, and economy

In Fig. 9, we have shown the dependence of \(\beta _{C}\) on the GDP of the respective state. The scatter plots suggest that the more affluent is the population (having more purchasing power), the more is the transmission rate at the first major transmission. So, it is the purchasing power of the population that has also driven the transmission.

Fig. 12
figure 12

I and \(I_{\mathrm{New}}\) for India as analysed by the model based on the experiment period of 170 days (from 14 March to 31 August 2020) and the projection till 351 days (28 February 2021). The red coloured dotted parts in the panels show the projection. The number inscribed in each row is the value of \(\xi \)

Full size image

Figure 10 contains two rows of which the first row shows the dependence of \(\beta _{C}\) on the economy population \(P_{\mathrm{Econ}}\) and the second row shows the dependence of the end transmission rate \(\beta _{N}\) (as on 31 August 2020) on \(P_{\mathrm{Econ}}\). So, the less is the \(P_{\mathrm{Econ}}\) for a state, the more is the people in the state with more purchasing power and the richer is the population. This figure presents an interesting study. We see that during the national-level lockdown, which lasted for about 68 days, the transmission of the disease was mainly driven by the affluent people which points to the fact that the population with less purchasing power stayed confined. The lower is the purchasing power of the population (i.e. poorer people), lower is the transmission rate at the first major transmission and the longer it requires to have the first major transmission (see Fig. 11). It is interesting to note that this behaviour is in contrast with the behaviour at the later phase of the pandemic. As the pandemic progresses, the transmission rate becomes proportional to the \(P_{\mathrm{Econ}}\), indicating the pandemic fatigue of the low-income group.

As shown in Fig. 11, the richer is the population and the more is the urban population, the quicker it takes to reach the criticality (lower \(d_{C}\)), which corroborates our earlier observations about the affluent and urban people driving the early phase of the pandemic.

5 The overall scenario for the whole country

We now apply our model to the entire country. In what follows, we present the results with the data available from 14 March to 31 August 2020, for a duration of 170 days in Fig. 12. Each row in Fig. 12 has three panels. The first two panels show the results for the cumulative infectives I and daily new infectives \(I_{\mathrm{New}}\) for the duration of 170 days. The model uses these 170 days of data to model the pandemic. The real data for this period are shown by the thick orange solid line, whereas the data beyond 170 days up to 212 days (for a period of 42 days) are represented by a dotted red line. The numerically calculated curve is shown by the black solid curve. So, the dotted portion of the data shows the projection of the pandemic by the model based on its analysis during the past 170 days. The third panel in each row shows the reproduction number \(R_{0}\). In each row, we have indicated the actual date for the entire period and the thin vertical line marks the 170th day, i.e. 31 August 2020 till when the data were used for the model to predict the rest of the figure.

There are five rows in Fig. 12, and each row is for the limiting asymptomatic rate \(\rho _{t}=\xi \beta _{t}\), \(\xi =5,7.5,10,12.5,\) and \(15\%\). The mean square error \(\epsilon _{\mathrm{MSE}}\), defined as

$$\begin{aligned} \epsilon _{\mathrm{MSE}}=\frac{1}{n}\sum _{i=1}^{n}\left( Y_{i}-{\hat{Y}}_{i}\right) ^{2}, \end{aligned}$$
(24)

expressed per million of the population for each value of \(\xi \) tabulated in Table 6. In the above expression, \(Y_{i}\) is the actual data and \({\hat{Y}}_{i}\) is the corresponding estimated value predicted by the model. One can see that the \(\epsilon _{\mathrm{MSE}}\) is minimum for \(\xi =7.5\%\). As per the available data till 31 August 2020, the optimum asymptomatic transmission rate of the disease for India was \(<10\%\). However, as we shall see in the next section, where we use the latest data till March 2021, the suggested asymptomatic transmission rate is \(\sim 15\%\).

As can be seen from these figures, the model is able to correctly predict the peak of the pandemic, which occurred around the 180th day (10 September 2020) with daily new infections of about \(\sim 10,000\) per day by the end of February 2021. We shall see in the next section that these figures are indeed correct and compare quite well with the logistic curves (see in the next section).

6 Comparison with logistic modelling

In contrast to a generalised compartmental dynamic model of the pandemic of an infectious disease such as the one considered in this paper, it is also quite interesting to model a pandemic with a single logistic function, which can be used to compare the development of the dynamic of the disease in different countries, regions, and areas [4, 33, 44]. Though a long-term prediction of an epidemic based on a logistic function is not useful, it is useful to gain insights into the pandemic as a single function can be used to model the pandemic in diverse circumstances. In this section, we use two logistic functions to model the pandemic based on available data for India (as a country) and compare the results to those obtained with our compartmental model. It is to be noted, however, that in contrast to the compartmental models, the logistic modelling gets better and better as more and more data become available, which makes them less useful for making predictions.

6.1 Generalised logistic model (GLM)

Following Richard’s work on generalised logistic function [3, 20, 33], a single dynamical system for the infectives I of a pandemic can be written as

$$\begin{aligned} \frac{{\mathrm {d}}I}{{\mathrm {d}}t}=\rho I\left[ 1-\left( \frac{I}{K}\right) ^{\mu }\right] , \end{aligned}$$
(25)

where K is the carrying capacity of the disease (the maximum number of infectives allowed by the model). This equation can be compared to the corresponding equation, Eq. (3), of the compartmental model. It is to be noted, however, that unlike in the compartmental model, K in the above equation is not the total population. The above equation can be directly integrated to obtain the logistic function in I as

$$\begin{aligned} I(t)=K\left[ 1+e^{-\rho \mu (t-t_{m})}\right] ^{-1/\mu }, \end{aligned}$$
(26)

where \(t_{m}\) is the time when a maximum number of infections occur. We call this model as generalised logistic model (GLM). The quantity \(\omega =\rho \mu \) is the intrinsic growth rate during the exponential phase of the epidemic. The basic reproduction number \(R_{0}\) during the exponential growth phase of the pandemic is given by \(R_{0}=e^{\omega T}\), where T is the mean incubation period, which is \(\sim \nu _{t}^{-1}\) in the case of compartmental model.

Table 6 Mean squared error \(\epsilon _{\mathrm{MSE}}\) (expressed per million) for the projected data for various values of \(\xi \), \(\rho _{t}=\xi \beta _{t}\)
Full size table
Fig. 13
figure 13

Comparison of the infectives I as predicted from the compartmental model (CM, dashed) with actual data (blue and yellow circles) and the two logistic models. The number in brackets shows the value of \(\xi \). The dotted vertical line marks the 170th day. The last panel shows the daily new infections \(I_{\mathrm{new}}\) as obtained from each model plotted with the real data till March 2021

Full size image
Table 7 Nonlinear regression parameters of the generalised logistic model (GLM)
Full size table
Fig. 14
figure 14

The nonlinear regression curves for the GLM, as more data become available beginning from August 2020 till March 2021. Note how more data points are required to arrive at the present scenario of the pandemic in contrast to the CM, for which the prediction was based on data only up to August 2020

Full size image

6.2 Error function-based logistic model (ELM)

It is also suggestive that the daily new infections \(I_{\mathrm{new}}\) follow a Gaussian curve [13] and can be modelled with a generalised Gaussian function

$$\begin{aligned} I_{\mathrm{new}}=\kappa e^{-\psi (t-t_{m})^{2}},\quad \psi >0, \end{aligned}$$
(27)

which can be used to obtain the logistic function for I as

$$\begin{aligned} I(t)= & {} \kappa _{0}+\int ^{t}I_{\mathrm{new}}(t)\,{\mathrm {d}}t\nonumber \\= & {} \kappa _{0}+\frac{1}{2}\kappa \sqrt{\frac{\pi }{\psi }}\mathrm{erf}\left[ \sqrt{\psi }(t-t_{m})\right] . \end{aligned}$$
(28)

6.3 Comparison

A fitting through nonlinear regression of the above models with the real data is shown in Fig. 13. The regression is carried out with the help of Mathematica through the Levenberg–Marquardt algorithm [30]. The daily new cases \(I_{\mathrm{new}}\) can be found from this model simply by calculating \(I'(t)\), which is also shown in Fig. 13.

In the figure, the comparison of the cumulative infectives I as predicted from our compartmental model (CM, dashed) with actual data are shown along with the curves as obtained from nonlinear regression with the two logistic models. The number in the bracket in the curve (CM, dashed) indicates the limiting asymptomatic rate constant \(\xi \), as mentioned before. The last panel shows the daily new infections \(I_{\mathrm{new}}\) as obtained from each model plotted with the real data till 14 March 2021. In each panel of Fig. 13, the dotted vertical line indicates the 170th day, which marks the end of real data used for constructing the compartmental model and the rest of the dashed curve is the prediction based on the data used till 170th day. In contrast to this, the curves from the logistic models (GLM and ELM) use all available data. As can be seen from these panels, our prediction based on data till 170th day with \(\xi =15\%\) almost mimics the real data (the first panel in the third row) and the logistic curves up to about a year (more than six months in advance), which amply proves the efficacy of the model presented here and also establishes its robustness . This can also be seen from the \(I_{\mathrm{new}}\) curve shown in the second panel of the third row of Fig. 13, where we have shown the \(I_{\mathrm{new}}\) calculated with our model with \(\xi =15\%\) based on real data only up to 170th day, predicted till 365th day. It also correctly predicts the day with the newest infection as well as the cumulative number of infections.

It should, however, be noted that India is now seeing the second wave of the infection, which has started from March 2021. The modelling of the second wave will be considerably difficult as by this time the social behaviour of the population is practically largely uncontrolled with a considerable fraction of the population not sticking to the mandatory COVID protocols.

The convergence of nonlinear regression parameters of the GLM model as more and more data become available beyond the 170th day (August 2020) is shown in Table 7 and Fig. 14. (the solid lines). In Table 7, the last two columns are, respectively, the growth rate \(\omega \) of the pandemic and the corresponding basic reproduction number \(R_{0}\) as calculated with the GLM during the exponential growth phase of the pandemic which is during the period ranging from about the 100th day till about the 170th day (see Fig. 12). The basic reproduction number \(R_{0}\) as given by our compartmental model is about \(R_{0}^{\mathrm{CM}}\sim 1.2-1.8\) (see Fig. 12), which is within the range of the GLM.

7 Summary and conclusions

To summarise, taking into consideration of asymptomatic carriers for the COVID-19 pandemic, an SEIR model for India is proposed with time-varying transmission rates and incubation period, as it is believed that the asymptomatic population seems to play an important role in the propagation of the SARS-CoV-2 disease. With the assumption that the asymptomatic transmission rate \((\rho _{t})\) can be written as a fraction of the symptomatic transmission rate \((\beta _{t})\), the disadvantage of the non-availability of asymptomatic infective data can be incorporated in our model without taking an extra compartment for the asymptomatic population. We have also incorporated a time-varying incubation period for the virus in our model.

Numerical results obtained from the model are first fitted for 11 Indian states, which are the major contributors to the pandemic and also fitted for the entire country. The mathematical modelling is based on data for India up to 31 August 2020, which has been used to model the behaviour of the pandemic for a total of 351 days (14 March 2020–28 February 2021). We observed that our predicted results agree well with the data up to 42 days, beyond the end of the data used in the modelling—that was available at the time of undertaking this work. The mean squared error between the predicted data and the actual data is minimum for the asymptomatic transmission rate of \(7.5\%\). However, as of writing the final version of this work, more data became available and it seems that the first phase of the pandemic has passed with its peak by the second week of September 2020 (180 days into the pandemic), as predicted by our model, and has subsided with a daily infection of \(\sim 10,000\) cases per day by February 2021, which is also within the range predicted by the model. As such, what we have seen that the prediction of our model based on data up to the 170th day into the pandemic agree quite well with the real data till February 2021, about the 351th day into the pandemic. However, by March 2021, the second surge of infections has started and now we are witnessing the second phase of the pandemic. Apparently, at present there are no enough data to analyse the second phase and would possibly require different sets of conditions as the second phase is believed to be different from its first phase in terms of behaviour and is beyond the scope of the present work. In the last section, we have also analysed the latest data with the help of two logistic models, and the logistic curves agree very well with the prediction of our model with an asymptomatic transmission rate of \(15\%\).

We also proposed a way to pinpoint the time when the first major transmission occurs (we called it a critical day) for a particular state, and the transmission rate at that day is calculated and compared with various socio-economic parameters for the respective states. Variation of the transmission rates at the critical day with youth and children population was studied, and it is found that states with higher youth population have larger transmission rates on the critical day. If a state has a higher child population, the critical transmission rate has been found to be lower for that state. We also find that the higher is the urban population of a state, the higher is the critical transmission rate and the earlier is the day on which a major transmission occurs. States with higher GDP (more purchasing power) experience a higher rate of transmission at the critical day. These are some interesting results of this work that reflect the correlation between the behaviour of the pandemic with the socio-economic and demographic structure of Indian states.

We also note that as per the results of our analysis, at the start of the national-level lockdown, the pandemic was driven primarily by the people with higher income, while as the pandemic progresses, it has been gradually found to be driven by the people with relatively lower income, demonstrating the so-called pandemic fatigue. On the basis of the available data till the 170th day for India, we have found an asymptomatic transmission rate of \(\sim 7.5\%\) to be an optimum rate for the best-fit parameters. However, a projection predicted by our model with an asymptomatic transmission rate of \(15\%\) closely agrees with the latest data that are available till writing of this paper, which is also suggested by the logistic fittings. As is shown in Fig. 12, the value of \(R_{0}\) should have fallen to \(\sim 0.5\) by the end of April 2021, when the disease could have been taken as contained, if not for the second surge of infections, which India is presently witnessing. Our equilibria analysis shows that in India, an endemic equilibrium can reach when the infectives can reach about 415 million, which is very far from the cumulative total of about 11.4 million cases (as of mid-March 2021). Thus, we can probably safely assume that India will not ever reach an EE state, now that the vaccination program has already started.

To conclude, we have proposed a compartmental model for modelling the COVID-19 pandemic in India, which shows excellent agreement with the real data well beyond the intended prediction period. We have also shown how the pandemic can be related to the socio-economic status and demography of a particular region of India. The results of this model can be used for early dynamic preventive measures for similar situations in developing countries.