Sub-diffusive behavior in the Standard Map

Abstract

In this work, we investigate the presence of sub-diffusive behavior in the Chirikov–Taylor Standard Map. We show that trajectories started from special initial conditions, close to unstable periodic orbits, exhibit sub-diffusion due to stickiness, and can be modeled as a continuous-time random walk. Additionally, we choose a variant of the Ulam method to numerically approximate the Perron–Frobenius operator for the map, allowing us to calculate the exponent of anomalous diffusion by solving an eigenvalue problem and comparing its time dependence to the solution of the fractional diffusion equation. The results here corroborate other findings in the literature of anomalous transport in Hamiltonian maps and can be suitable to describe transport properties of other dynamical systems.

Appendix: Stochastic representation and RW/CTRW simulations

This Appendix is devoted to verify and support our analysis made for the selected setup of the Standard Map, based on the connection between the eigenvalue of the Perron–Frobenius transfer operator and the Mittag–Leffler function.

We address here how to simulate a random walk (RW) and a continuous time random walk (CTRW) using the Itô stochastic representation [39].

A classical CTRW is a process subordinated to a simple RW, in which steps (jumps) follow at random instants of time. The waiting time $t_i$ for the next step follows the probability distribution with the known probability density $\psi (t_i)$. The number of steps performed up to time t, $\nu (t)$, is the operational time, or the subordinator of the corresponding subordination scheme. The clock time t of the $\nu$th step is then the following sum:

$$\begin{aligned} t(\nu ) = \sum _{i=1}^\nu t_i~, \end{aligned}$$

(18)

which, for fat-tailed $\psi (t_i)\sim t^{-1-\alpha }$ with $0< \alpha < 1$, tends in distribution to a one-sided Levy law. The value of $\nu$ as a function of t is then $\nu (t) = \mathrm {inf}\{ \nu , t(\nu )>t \}$ [41]. This gives us the prescription for stochastic simulations of the CTRW.

For long times, the variable $\nu$ can be taken continuous; the corresponding continuous limit for the probability density function $\rho (x,t)$ is then given by the fractional diffusion equation showed in Eq. (8).

In the displacement, X(t) then follows from a couple of stochastic differential equations [40]

$$\begin{aligned} dX(\nu )= & {} \sqrt{2D}dB(nu), \end{aligned}$$

(19)

$$\begin{aligned} dt(\nu )= & {} \tau d L_\alpha (\nu ) \end{aligned}$$

(20)

with $B(\nu )$ being a standard Brownian motoin, $L_\alpha (\nu )$ a one-sided Lévy flight, and D and $\tau$ the appropriate constants. From this representation, Eq. (8) follows as well.

Fig. 6

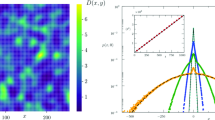
Examples of trajectories for an RW process ($\alpha =1)$ in black. Also, for two distinct CRTW processes considering a relatively not so long trap-time ($\alpha =0.6$) in red, and a long trap-time ($\alpha =0.3$) in green. The time-axis was chosen to be linear to properly illustrate the different trap-times

With that, we followed the numerical method proposed by Magdziarz and Weron in [33, 39] to simulate the dynamics of a RW process, setting $\alpha =1$ and CTRW processes, setting $\alpha =0.6$ (relatively not so long trap-time) and $\alpha =0.3$ (relatively long trap-time). In Fig. 6, we show examples of simulated trajectories of these three different dynamic scenarios.

The discussed Ulam method, shown in Sect. 5, used for approximate the Perron–Frobenius-like operator to approach the anomalous diffusion exponent $\alpha _1$ for the selected setup of the Standard Map, can also be applied to an ensemble of particles whose movement is governed by RW. However, it is not an appropriate method to analyze cases where $\alpha \ne 1$. In that case of anomalous diffusion, it is necessary to apply a kernel density estimator to have a good approach to the probability density from a histogram [39]. To avoid the expensive use of a kernel density estimator, we choose to use a different method called the extended dynamic mode decomposition (EDMD) [42, 43].

The EDMD in [43] is method to approximate the Perron–Frobenius operator, using the fact this operator and the Koopman operator² are adjoint to each other. The EDMD method focuses on a dictionary of observables $D=\left[ \phi _1(x),\phi _2(x),\ldots ,\phi _k(x)\right]$, functions of state space, and how they change along the trajectory. With this information, and the definition of the Koopman operator is possible to approximate the eigenfunctions and eigenvalues both of the Koopman operator as of the Perron–Frobenius operator. Much of the method relies in an educated guess for the dictionary of observables, that must be rich enough to approximate the Koopman operator eigenfunctions, see [42, 43] for further details.

We consider the region $0\le x\le 2\pi$ with periodic boundary conditions and choose the observables

$$\begin{aligned} \small { \text {{D}}= \left[ 1,\cos \left( x\right) ,\sin \left( x\right) ,\cos \left( 2x\right) ,\sin \left( 2x\right) ,\ldots ,\cos \left( 5x\right) ,\sin \left( 5x\right) \right] }~,\nonumber \\ \end{aligned}$$

(21)

as the dictionary for the EDMD method.

The behavior of the eigenvalue $\lambda _{1}$ as function of the skipped iterations $n^{\prime }$ is shown in Fig. 7 for the same simulations depicted in Fig. 6. Considering its relation to the solution of the FDE, as explained in Sect. 4, we selected the Mittag-Leffler function, given by

$$\begin{aligned} E_{\alpha }\left( z\right)= & {} \sum _{k=0}^{\infty }\frac{z^{k}}{\Gamma \left( 1+\alpha k\right) }~, \end{aligned}$$

(22)

to fit these three different dynamic scenarios for three different values of $\alpha$.

Fig. 7

Behavior of the eigenvalue $\lambda _{1}$ as function of the log of the number of iterations $n^{\prime }$ to calculate the correspondingly matrices, considering the dynamics of a RW and the two CTRW examples. The points mark the simulated dynamics in each case and the dashed line is the fitting provided by a numerical representation of the Mittag–Leffler function

The Mittag–Leffler is the suitable function because of the assumed behavior

$$\begin{aligned} \lambda _l\left( n\right)= & {} E_{\alpha _l}\left( -d_l n^{\alpha _l}\right) ~, \end{aligned}$$

(23)

where it was defined $\alpha _l$ and $d_l$ as, respectively, the anomalous diffusion exponent and coefficient related to the $l^{th}$eigenpair of the Perron–Frobenius-like operator.

It is important to mind that in these particular cases, the anomalous diffusion exponent $\alpha _l$ related to the $l^{th}$eigenpair is the same as $\alpha _1$. Then, the anomalous diffusion exponent $\alpha$, that characterize the anomalous dynamics, is $\alpha \approx \alpha _1=\alpha _l$.

Finally, one can observe that the values of the fitted functions are close to the actual values set for its simulations. Specially, for the CTRW model, the given values of $\alpha _1=0.637\pm 0.009$ and $\alpha _1=0.329\pm 0.004$ imply a dependence slower than exponential, as expected from the theory.