Enhancing the accuracy and precision of forecasting the productivity of a factory: a fuzzified feedforward neural network approach

Abstract

Most existing methods for forecasting the productivity of a factory cannot estimate the range of productivity reliably, especially when future conditions are distinct from those in the past. To address this issue, a fuzzified feedforward neural network (FFNN) approach is proposed in this study. The FFNN approach improves the forecasting precision after generating accurate fuzzy productivity forecasts. In addition, the acceptable range of a fuzzy productivity forecast is specified, based on which the sum of the memberships of actual values is maximized. In this way, the range of productivity can be precisely estimated. After applying the FFNN approach to a real case, the experimental results revealed the superiority of the FFNN approach by improving the forecasting precision, in terms of the hit rate, by 25%. Such an improvement also contributed to a better forecasting accuracy. The superiority of the FFNN approach is in the context that the accuracy of forecasting productivity is optimized only after the range of productivity has been precisely estimated. In contrast, most state-of-the-art methods focus on optimizing the forecasting accuracy, but may be ineffective without information about the range of productivity when future conditions are distinct from the past.

Introduction

The productivity of a factory can be evaluated by dividing the output by the input [34]. A high productivity is critical to maintaining a competitive edge in the industry, which contributes to the sustainability of a factory [13, 29]. For this reason, the productivity of a factory needs to be evaluated and enhanced. In addition, it is also necessary to forecast the future productivity of a factory and take actions, such as moving the factory to another region with a lower wage level [4], or switching to a less expensive supplier [30], to elevate productivity.

Forecasting the future productivity of a factory is a challenging task, because productivity is subject to much uncertainty caused by unstable product yield [24, 28], changing workforce [32], etc. Therefore, this study aims to enhance the accuracy and precision of forecasting the productivity of a factory.

Some of the relevant references are reviewed as follows. Mirahadi and Zayed [26] forecasted the productivity of a construction site using a fuzzy inference system (FIS). The antecedents of fuzzy inference rules in the FIS were factors affecting productivity which membership functions were optimized by applying a genetic algorithm (GA). Baumers et al. [6] compared the productivity levels of two manufacturing systems based on three-dimensional (3D) printing—an electron beam melting (EBM) 3D printing system and a direct metal laser sintering (DMLS) 3D printing system. They concluded that the two manufacturing systems based on 3D printing were not productive enough for mass production purposes. To increase the possibility for a fuzzy productivity forecast to contain actual value, Chen and Wang [13] proposed a fuzzy collaborative forecasting (FCF) method, in which the improvement in productivity was modeled as a fuzzy learning process that was applied to forecast the future productivity. Akano and Asaolu [2] constructed an adaptive neuro-fuzzy inference system (ANFIS) to forecast the productivity of a manufacturing system. The ANFIS enumerated all possible fuzzy inference rules and kept only effective rules after training. Mankins [25] distinguished the concepts of productivity and efficiency. In addition, Mankins highlighted the importance of human resource management to productivity enhancement. Lee and Kim [23] applied building information modeling-based four-dimensional (4D) simulation to improve the productivity of a construction project. Recently, predictive maintenance has been recognized as an important strategy to reduce unscheduled downtime and improve productivity. Following this view, Chiu et al. [17] developed a factory-wide intelligent predictive maintenance system based on Industry 4.0. Chen [9] modeled the improvement in productivity as a fuzzy learning process, and constructed an artificial neural network (ANN) to derive the values of parameters in the fuzzy productivity learning model. Zahraee et al. [36] combined factory simulation, response surface methodology (RSM), and design of experiments (DOE) to analyze and improve the productivity of a factory. Instead of forecasting the future productivity, Grabner et al. [19] estimated the impacts of improvement actions, such as lean production, on productivity. Repina et al. [31] applied several statistical analysis techniques, including time series analysis, index method, and factor analysis, to forecast the productivity of a machine-building company. Chen et al. [12] proposed a fuzzy polynomial fitting and mathematical programming approach. Chen et al. [14] considered the uncertainty of productivity with a type-II fuzzy number, and proposed a type-II fuzzy collaborative forecasting approach for productivity forecasting. In the view of Chen and Lin [11], acquiring diversified three-dimensional (3D) printers can increase the productivity of a manufacturer.

Existing methods in this field have the following problems:

• 1. A productivity forecast is seldom equal to actual value. For this reason, estimating the range of productivity is also important, which, however, has rarely been addressed in the past.

• 2. A conventional statistical analysis method estimates the range of productivity by constructing a confidence interval [34]. Existing FIS or ANFIS methods generate a fuzzy productivity forecast which range is representative of the range of productivity [2, 29]. However, these methods cannot guarantee that all actual values are included in the corresponding confidence intervals or fuzzy productivity forecasts [8].

To solve the aforementioned problems, a fuzzified feedforward neural network (FFNN) approach is proposed in this study. The novelty of the proposed methodology resides in the following. Existing FCF methods minimizes the sum of the ranges of fuzzy productivity forecasts, while the FFNN approach maximizes the sum of the memberships of actual values in fuzzy productivity forecasts. In this way, the possibility of including actual values in fuzzy productivity forecasts, in terms of the hit rate for test data, can be enhanced. The contribution of this study includes:

• a new FFNN method for forecasting the productivity of a factory,

• a new algorithm (i.e., the NLP model) for training the FFNN, and

• a new method for defuzzifying a fuzzy productivity forecast.

The remainder of this paper is organized as follows. The proposed FFNN approach is detailed in “The FFNN Approach”. To illustrate the applicability of the FFNN approach, and to evaluate its advantages and/or disadvantages over some existing methods, a real case has been investigated, which is described in “Application to a real case”. Finally, the conclusions of this study are made in “Conclusions”. Some directions for future research are also provided.

The FFNN approach

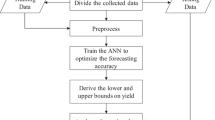
In the proposed FFNN approach, an FFNN [1, 3, 27] is constructed to forecast the productivity of a factory. The training of the FFNN is divided into three steps. First, the FFNN is treated as a crisp one, and then, a feedforward neural network (FNN) is constructed and trained to derive the core of each fuzzy parameter in the FFNN, thereby optimizing the forecasting accuracy for the training data. Subsequently, a nonlinear programming (NLP) model is optimized to determine the upper bound on each fuzzy parameter, thereby optimizing the forecasting precision. After that, another NLP problem is solved to determine the lower bound on each fuzzy parameter. Table 1 summarizes the differences between the FFNN approach and some existing methods.

Table 1 Differences between the FFNN approach and some existing methods

The FFNN approach comprises the following steps:

Step 1. Construct an FFNN to forecast the productivity of the target factory.

Step 2. Train the FFNN as a crisp one to derive the core of each fuzzy parameter in the FFNN.

Step 3. Optimize an NLP model to determine the upper bound on each fuzzy parameter.

Step 4. Optimize another NLP problem to determine the lower bound on each fuzzy parameter.

Step 5. Apply the trained FFNN to test data.

Step 6. Evaluate the forecasting performance using the FFNN approach.

Construction of an FFNN

First, an FFNN is constructed to forecast the productivity of a factory by fitting the relationship between productivity and relevant factors. Letting the productivity of the target factory at period j be indicated with $y_{j}$. The configuration of the FFNN is established as follows:

• Inputs: the values of relevant factors at the jth period, indicated with $\{ x_{ji} |i = 1\sim m\}$.

• Single hidden layer: generally, one or two hidden layers are beneficial for the convergence property of the FFNN.

• Number of neurons in the hidden layer: 2m.

• Output: the normalized value of the fuzzy productivity forecast, i.e., $N(\tilde{y}_{j} )$ [15]:

  $$ N(\tilde{y}_{j} ) = 0.9 \cdot \frac{{\tilde{y}_{j} - \mathop {\min }\limits_{l} \tilde{y}_{l} }}{{\mathop {\max }\limits_{l} \tilde{y}_{l} - \mathop {\min }\limits_{l} \tilde{y}_{l} }} + 0.1. $$

  (1)

To convert it back to the un-normalized value

$$ \tilde{y}_{j} = \frac{{(N(\tilde{y}_{j} ) - 0.1)(\mathop {\max }\limits_{l} \tilde{y}_{l} - \mathop {\min }\limits_{l} \tilde{y}_{l} )}}{0.9} + \mathop {\min }\limits_{l} \tilde{y}_{l} . $$

(2)

• Learning rate (η): 0.01 ~ 1.0.

• Initial conditions: the initial values of network parameters are randomized.

• Batch learning.

The parameters in the FFNN are defined as follows:

• ◆ $x_{ji}$: the ith input at period j.

• ◆ $\tilde{w}_{ik}^{h}$: the connection weight between the ith input node and the kth hidden-layer node.

• ◆ $\tilde{I}_{jk}^{h}$: the input to the kth hidden-layer node.

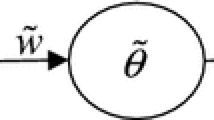
• ◆ $\tilde{\theta }_{k}^{h}$: the threshold on the kth hidden-layer node.

• ◆ $\tilde{h}_{jk}$: the output from the kth hidden-layer node.

• ◆ $\tilde{w}_{k}^{o}$: the connection weight between the kth hidden-layer node and the output node.

• ◆ $\tilde{I}_{j}^{o}$: the input to the output node.

• ◆ $\tilde{\theta }^{o}$: the threshold on the output node.

• ◆ $\tilde{o}_{j}$: the network output; $\tilde{o}_{j} = N(\tilde{y}_{j} )$.

Without loss of generality, all fuzzy parameters are given in or approximated with triangular fuzzy numbers (TFNs).

Inputs to the FFNN are propagated from the input layer to the hidden layer as

$$ \tilde{I}_{jk}^{h} = \sum\limits_{i = 1}^{m} {\tilde{w}_{ik}^{h} x_{ji} } . $$

(3)

After receiving this, the output from the hidden-layer node is generated as

$$ \tilde{h}_{jk} = \frac{1}{{1 + {\text{e}}^{{ - (\tilde{I}_{jk}^{h} {(} - {)}\tilde{\theta }_{k}^{h} )}} }}. $$

(4)

where (–) indicates fuzzy subtraction. Outputs from the hidden layer are transmitted to the output layer in the same manner

$$ \tilde{I}_{j}^{o} = \sum\limits_{k = 1}^{m} {\tilde{w}_{k}^{o} {(} \times {)}\tilde{h}_{jk} } , $$

(5)

where (×) denotes fuzzy multiplication. Finally, the output from the FFNN is generated as

$$ \tilde{o}_{j} = \frac{1}{{1 + {\text{e}}^{{ - (\tilde{I}_{j}^{o} {(} - {)}\tilde{\theta }^{o} )}} }}, $$

(6)

which is the normalized fuzzy productivity forecast. The problem is, therefore, how to determine the values of fuzzy parameters (including $\tilde{w}_{ik}^{h}$, $\tilde{\theta }_{k}^{h}$, $\tilde{w}_{k}^{o}$, and $\tilde{\theta }^{o}$) to ensure that each fuzzy productivity forecast is close to actual value, which relies on an effective training of the FFNN.

Training of the FFNN

The training process of the FFNN comprises three parts:

• 1. Applying an existing algorithm to derive the core of each fuzzy network parameter.

• 2. Optimizing NLP Model I to establish the upper bound on each fuzzy network parameter.

• 3. Optimizing NLP Model II to establish the lower bound on each fuzzy network parameter.

Deriving the core of each fuzzy parameter

First, to derive the core of each fuzzy parameter, the FFNN is treated as a crisp one and trained using an existing algorithm such as the gradient descent (GD) algorithm, the Levenberg–Marquardt (LM) algorithm, the Fletcher–Powell conjugate gradient (CGF) algorithm, and others. A comparison of these algorithms refers to Eraslan [17]. After training, the optimized cores of fuzzy parameters are indicated with $w_{ik2}^{h*}$, $\theta_{k2}^{h*}$, $w_{k2}^{o*}$, and $\theta_{2}^{o*}$, respectively. In addition, examples with actual values greater than the cores of fuzzy productivity forecasts are placed in a set ${{\varvec{\Lambda}}}_{{\mathbf{R}}}$, while examples with actual values smaller than cores are placed in another set ${{\varvec{\Lambda}}}_{{\mathbf{L}}}$.

Establishing the upper bound on each fuzzy parameter

Subsequently, the following NLP problem is solved to determine the upper bound on each fuzzy parameter: (NLP MODEL I)

$$ {\text{Max}}\;Z_{1} = \sum\limits_{{j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} }} {s_{j} } , $$

(7)

subject to:

$$ s_{j} = \frac{{N(y_{j} ) - o_{j3} }}{{o_{j2}^{*} - o_{j3} }};\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} , $$

(8)

$$ o_{j3} \ge o_{j2}^{*} ;\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} , $$

(9)

$$ o_{j3} \ge N(y_{j} );\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} , $$

(10)

$$ \sum\limits_{{j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} }} {(o_{j3} - o_{j2}^{*} )} \le d_{{\text{R}}} , $$

(11)

$$ o_{j3} = \frac{1}{{1 + {\text{e}}^{{ - (I_{j3}^{o} - \theta_{1}^{o} )}} }};\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} , $$

(12)

$$ I_{j3}^{o} = \sum\limits_{k = 1}^{m} {w_{k3}^{o} h_{jk3} } ;\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} , $$

(13)

$$ h_{jk3} = \frac{1}{{1 + {\text{e}}^{{ - (I_{jk3}^{h} - \theta_{k1}^{h} )}} }};\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} ;\quad k = 1 \sim K, $$

(14)

$$ I_{jk3}^{h} = \sum\limits_{i = 1}^{m} {w_{ik3}^{h} x_{ji} } ;\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{R}}} ;\quad k = 1 \sim K, $$

(15)

$$ \theta_{1}^{o} \le \theta_{2}^{o*} , $$

(16)

$$ w_{k3}^{o} \ge w_{k2}^{o*} ;\quad k = 1 \sim K, $$

(17)

$$ \theta_{k1}^{h} \le \theta_{k2}^{h*} ;\quad k = 1 \sim K, $$

(18)

$$ w_{ik3}^{h} \ge w_{ik2}^{h*} ;\quad i = 1 \sim m;\quad k = 1 \sim K, $$

(19)

$$ \theta_{k1}^{h} ,\theta_{1}^{o} \ge 0;\quad k = 1 \sim K. $$

(20)

The objective function (7) maximizes the sum of the memberships of actual values of fuzzy productivity forecasts on the right side, which are derived according to Eq. (8). In contrast, Chen and Lin’s goal programming (GP) method [10, 22] minimizes the sum of the ranges of fuzzy productivity forecasts. The upper bound of a fuzzy productivity forecast should be greater than the core and the normalized actual value, as required by Constraints (9) and (10). Constraint (11) limits the sum of the half ranges of fuzzy productivity forecasts on the right-hand side to be less than a prespecified threshold $d_{{\text{R}}}$. Equations (12)–(15) derive the upper (or lower) bounds on fuzzy parameters. Constraints (16)–(20) request each upper (or lower) bound to be greater than (or lower than) the core.

Establishing the lower bound on each fuzzy parameter

In a similar way, another NLP problem is solved to derive the lower bound on each fuzzy parameter: (NLP Model II)

$$ {\text{Max}}\;Z_{2} = \sum\limits_{{j \in \Lambda_{{\text{L}}} }} {s_{j} } , $$

(21)

subject to:

$$ s_{j} = \frac{{N(y_{j} ) - o_{j1} }}{{o_{j2}^{*} - o_{j1} }};\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} , $$

(22)

$$ o_{j1} \le o_{j2}^{*} ;\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} , $$

(23)

$$ o_{j1} \le N(y_{j} );\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} , $$

(24)

$$ \sum\limits_{{j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} }} {(o_{j2}^{*} - o_{j1} )} \le d_{{\text{L}}} , $$

(25)

$$ o_{j1} = \frac{1}{{1 + {\text{e}}^{{ - (I_{j1}^{o} - \theta_{3}^{o} )}} }};\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} , $$

(26)

$$ I_{j1}^{o} = \sum\limits_{k = 1}^{m} {w_{k1}^{o} h_{jk1} } ;\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} , $$

(27)

$$ h_{jk1} = \frac{1}{{1 + {\text{e}}^{{ - (I_{jk1}^{h} - \theta_{k3}^{h} )}} }};\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} ;\quad k = 1 \sim K, $$

(28)

$$ I_{jk1}^{h} = \sum\limits_{i = 1}^{m} {w_{ik1}^{h} x_{ji} } ;\quad j \in {{\varvec{\Lambda}}}_{{\mathbf{L}}} ;\quad k = 1 \sim K, $$

(29)

$$ \theta_{3}^{o} \ge \theta_{2}^{o*} , $$

(30)

$$ w_{k1}^{o} \le w_{k2}^{o*} ;\quad k = 1 \sim K, $$

(31)

$$ \theta_{k3}^{h} \ge \theta_{k2}^{h*} ;\quad k = 1 \sim K, $$

(32)

$$ w_{ik1}^{h} \le w_{ik2}^{h*} ;\quad i = 1 \sim m;\quad k = 1 \sim K, $$

(33)

$$ \theta_{k1}^{h} ,\theta_{1}^{o} \ge 0;\quad k = 1 \sim K. $$

(34)

The lower bound of a fuzzy productivity forecast should be lower than the core and the normalized actual value, as required by Constraints (23) and (24).

Application to a real case

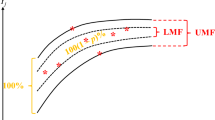
The FFNN approach has been applied to forecast the productivity of a factory in Nigeria to evaluate its effectiveness. The case contained the productivity data of the factory during twenty periods, as shown in Fig. 1. This case had been investigated by Akano and Asaolu [2]. The productivity data were decomposed into two parts: data of the first 12 periods for building models, and the remaining data for evaluating the forecasting performance. The relationship between productivity and four factors (including preventive maintenance time, off-duty time, machine downtime, and power failure time, as shown in Fig. 2) was to be fitted with an FFNN, so as to forecast the productivity at a future period by considering uncertainty.

Fig. 1

The productivity data

Fig. 2

The data of relevant factors

At first, the FFNN was treated as a crisp one with the following architecture and trained to derive the cores of fuzzy parameters in it:

• 1. Four inputs corresponding to the values of the four factors at a period;

• 2. A single hidden layer with eight nodes;

• 3. Initial values of network parameters: randomly generated;

• 4. Training algorithm: the LM algorithm;

• 5. Learning rate (η): 0.25;

• 6. Stopping criteria: the network training stopped if the sum of squared error (SSE) fell below 0.001, or 1000 epochs have been run.

The network was constructed and trained on a PC with i7-7700 CPU 3.6 GHz and 8 GB RAM using the neural network toolbox of MATLAB 2017 [5]. The execution time was less than 3 s. Table 2 shows the optimal solution. Preventive maintenance time had the greatest impact on productivity, while power failure time had the most uncertain impact on productivity. Based on Table 2, the core of each fuzzy productivity forecast, i.e., $y_{j2}^{*}$, was derived, as shown in Fig. 3. As expected, the training data were very precisely fitted; however, there were considerable deviations in forecasting productivity for test data, which might be owing to overfitting. To address this issue, estimating the range of productivity was necessary.

Table 2 The optimal solution

Fig. 3

The cores of fuzzy productivity forecasts

To establish the lower and upper bounds on productivity, the two NLP problems were formulated and solved using Lingo [19] on the same PC. The execution time was about 20 s. The thresholds on the sums of half ranges, $d_{{\text{R}}}$ and $d_{{\text{L}}}$, were specified as 2.3 and 0.85, respectively. As a result, the range of a fuzzy productivity forecast should be narrower than 2.3/7 + 0.85/5 = 0.5 on average. The optimal solutions to the NLP problems are presented in Tables 3 and 4, respectively, for reproducibility. Obviously, the lower bound of each fuzzy parameter was less than the core, and the core was less than the upper bound. In addition, the lower bound, core, and upper bound of each fuzzy parameter had the same sign, thereby ensuring a consistent impact of the corresponding factor on productivity. The established lower and upper bounds on productivity are illustrated in Fig. 4. The forecasting precision, measured in terms of hit rate, using the proposed methodology was 38% for test data.

Table 3 The optimal solution to problem NLP I

Table 4 The optimal solution to problem NLP II

Fig. 4

The lower and upper bounds on productivity

For making a comparison, four existing methods were also applied to the collected data. The first compared existing method was the fixed allowance method which constructed a confidence interval of productivity. For a fair comparison, a fixed allowance of 0.5/2 = 0.25 was added to and subtracted from the core of each fuzzy productivity forecast. The forecasting results are shown in Fig. 5. In this way, fuzzy productivity forecasts were symmetric. In addition, the ranges of fuzzy productivity forecasts were equally wide. The hit rate achieved using the fixed allowance method was only 13%.

Fig. 5

The forecasting results using the fixed allowance method

The second compared method was the fixed parametric adjustment method, in which the modifications made to all network parameters were equal. To meet the requirement for each half range to be narrower than 0.25 on average, each network parameter was reduced by 12.83% to determine the lower bound and increased by 15.68% to determine up the upper bound, respectively. The forecasting results are shown in Fig. 6. However, due to the nonlinear transformation function adopted in the FFNN, fuzzy productivity forecasts were not symmetric. In addition, fuzzy productivity forecasts were not equally wide. The hit rate achieved using the fixed parametric adjustment method for test data was 13%.

Fig. 6

The forecasting results using the fixed parametric adjustment method

The third method compared in the experiment was the hybrid statistical analysis and ANN method [7] in which only the threshold on the output node was modified to determine the lower and upper bounds on productivity. The optimization results were:

$\theta_{1}^{o*} = 0.990;\quad \theta_{3}^{o*} = 2.091.$

In this way, the average range of fuzzy productivity forecasts was also 0.5. The forecasting results are illustrated in Fig. 7. Fuzzy productivity forecasts generated in this way were asymmetric and unequally wide. In test data, only a single actual value was included in the fuzzy productivity forecast, giving a hit rate of 13%.

Fig. 7

The forecasting results using the hybrid statistical analysis and ANN method [7]

The fourth compared existing method was the GP method [10], in which two series of GP problems were solved to determine the lower and upper bounds on productivity, respectively. When the minimal satisfaction level was greater than 0.95, the average range of fuzzy productivity forecasts was minimized as 0.50, making the results comparable to those obtained using the proposed methodology. Fuzzy productivity forecasts made using Chen and Lin’s GP method are shown in Fig. 8. When the core of a fuzzy productivity forecast was closer to actual value, the fuzzy productivity forecast became narrower. As a result, the widths of fuzzy productivity forecasts varied considerably. The hit rate achieved using Chen and Lin’s GP method for test data was only 13%.

Fig. 8

The fuzzy productivity forecasts made using Chen and Lin’s GP method

According to the experimental result, the following discussion was made:

• 1. The FFNN approach surpassed the compared existing methods in elevating the hit rate by 25% for test data.

• 2. For the training data, a lower bound on productivity was never greater than the core, and the upper bound was never smaller than the core. However, such a property might not hold for test data, since the lower bound of a positive parameter might be negative, which changed the sequence of the two bounds.

• 3. To evaluate the forecasting accuracy of each method, fuzzy productivity forecasts were defuzzified using the center-of-gravity method. The deviations between fuzzy productivity forecasts and actual values were then measured in terms of mean absolute error (MAE), mean absolute percentage error (MAPE), and root-mean-squared error (RMSE). The results are summarized in Table 5. The FFNN approach achieved the best forecasting accuracy in terms of MAE, MAPE, or RMSE. The most significant advantage of the FFNN approach over existing methods happened when MAE was minimized, which was up to 30% on average.

• 4. Nevertheless, there was much space for improving the forecasting accuracy, which was owing to the following reasons. First, some data used to calculate productivity may be missing, incorrect, or conflicting, thereby reducing the credibility of the data collected for training the FFNN. In addition, future conditions may be distinct from the past. To overcome these problems, a forecaster may adjust fuzzy productivity forecasts based on his/her subjective judgment [20, 33]. Chiu et al. [16] proposed several strategies to reflect the subjective judgment of a forecaster who adjusts fuzzy productivity forecasts by changing the defuzzification method. In this study, the moderately optimistic strategy was adopted, because the forecaster believed that the productivity of the factory gradually improved through learning, which assigned weights 0.76, 0.1, and 0.14 to the upper bound, core, and lower bound of a fuzzy productivity forecast. After defuzzification, the forecasting accuracy was re-evaluated as

  $$ {\text{MAE}} = 0.14 $$
  $$ {\text{MAPE}} = 11\% $$
  $$ {\text{RMSE}} = 0.03, $$

  which was much better than that achieved without considering the subjective judgment of the forecaster.

• 5. To evaluate whether the advantage of the proposed methodology over existing methods was significant, a paired t test has been conducted with the following hypotheses:

• 6. If the network had not been fuzzified using the proposed methodology, then the forecasting accuracy would be

  $$ {\text{MAE}} = 0.39 $$
  $$ {\text{MAPE}} = 28\% $$
  $$ {\text{RMSE}} = 0.17, $$

  which was much worse than that using the proposed methodology. Therefore, the treatments taken in the proposed methodology did strengthen the confidence of the network.

• 7. To further elaborate the effectiveness of the FFNN approach, it has been applied to another case that contained the productivity of a dynamic random access memory (DRAM) factory located in Taichung Science Park, Taiwan. This case has been discussed by Chen [8], and was representative, because the DRAM factory belonged to one of the largest DRAM producers in the world. The productivity of the DRAM factory was measured by dividing the monetary output by the monetary input during fourteen months. The productivity during a future period was forecasted based on those during the previous three periods. The forecasting results are shown in Fig. 9, with the following forecasting performance:

  $$ {\text{MAE}} = 0.048 $$
  $$ {\text{MAPE}} = 4.8\% $$
  $$ {\text{RMSE}} = 0.068 $$
  $$ {\text{Hit rate}} = 100\% $$
  $$ {\text{Average range}} = 0.280. $$

  Obviously, the FFNN approach achieved good forecasting accuracy and precision in this case.

• 8. By maximizing the hit rate, the FFNN can generate fuzzy productivity forecasts that are very likely to contain actual values. For a new example, if this property holds, there may be no need to learn this new example, which is beneficial to the scalability of the proposed methodology. In contrast, existing methods rarely estimate the range of productivity reliably to support this purpose.

• 9. In the proposed methodology, the training of the FFNN stopped when the convergence criteria were reached. The forecasting error was not really minimized, and the solution was only suboptimal. Similarly, in solving the two NLP problems, the successive linear programming (SLP) directions algorithm [18] stopped after a number of iterations have been repeated. Only the local optimality of the solutions was guaranteed [35].

Fig. 9

The forecasting results in another case

Table 5 The forecasting accuracy achieved by each method

H₀

The forecasting accuracy using the proposed methodology in terms of absolute error is the same as that using the existing method;

H₁

The forecasting accuracy using the proposed methodology in terms of absolute error is more effective than that using the existing method.

The results are shown in Table 6. The forecasting accuracy using the proposed methodology was significantly improved (α = 0.05) when compared with existing methods.

Table 6 Paired t test results

Conclusions

An FFNN approach is proposed in this study for enhancing the accuracy and precision of forecasting the productivity of a factory. In the FFNN approach, an FFNN is constructed to forecast the productivity of a factory. The FFNN is trained as a crisp one to derive the core of a fuzzy productivity forecast. Then, two NLP models are formulated and optimized to determine the range of the fuzzy productivity forecast. Unlike existing methods in this field that optimize the forecasting accuracy only or prioritize that optimization, the FFNN approach improves the forecasting precision after optimizing the forecasting accuracy. In this way, the range of productivity can be reliably estimated, which is especially helpful when future conditions are distinct from those in the past.

The FFNN approach has been applied to a real case. The experimental results revealed the following:

• 1. The FFNN approach considerably improved the accuracy and precision of forecasting the productivity of the target factory. In particular, the forecasting precision measured in terms of the hit rate for test data was elevated by 25%.

• 2. In this case, future conditions seemed to be quite different from those in the past, which made forecasting the future productivity a challenging task.

• 3. Moreover, the overfitting problem was clearly illustrated by this case.

• 4. Through specifying the acceptable range and maximizing the sum of memberships, the impact of the overfitting problem was significantly lessened, which accounted for the superiority of the FFNN approach.

The FFNN approach needs to be applied to more cases to further elaborate its effectiveness. In addition, the experimental results revealed that there was still considerable space for improving the forecasting accuracy, which relies on a better mechanism for aggregating the core, lower bound, and upper bound of a fuzzy productivity forecast to arrive at a crisp/representative value. These constitute some directions for future research.