1 INTRODUCTION

The current pandemic due to the SARS-CoV-2 virus spurred an unprecedented activity in modelling. Mathematical models are particularly interesting in the domain of epidemics since they allow experimentation which in real-life situations would have been unethical or well-nigh impracticable. Once one has set properly a model, having identified the important constituents, one can use it not only to interpret the available data, but also to make predictions about the future. In the domain of the COVID-19 epidemic a slew of publications have focused on non-pharmaceutical interventions, i.e., actions undertaken by the various governments aiming at mitigating the epidemic.

In this context, the team of the London School of Hygiene and Tropical Medicine published a study [1] which shows that the combination of isolation of symptomatic cases and tracing strategies is more efficient than mass testing or self-isolation alone. However, given the difficulties presented by a detailed contact tracing, an appealing alternative emerges in the form of a limiting number of participants in all gatherings, combined with a simple, “manual”, contact tracing of acquaintances. Firth and collaborators [2] examined strategies based on the tracing of the contacts of contacts, but they found that, were quarantine prescriptions to be issued based on such results, half of the total population would end up being quarantined. Since such a situation becomes easily untenable, they propose as an alternative just a simple tracing complemented by physical distancing recommendations. While the two aforementioned works were based on stochastic approaches, Ianni and Rossi [3] used a simple, time-dependent, variant of the standard SIR model in order to describe the situation prevailing during lockdown and social distancing. In this sense their model is quite similar to the one we proposed in [4], which focused on the possible strategies for a satisfactory exit from lockdown. Exit strategies have been the object of a workshop organised in the Newton Institute. Thompson and collaborators present a synthesis [5] of the key questions raised at this workshop, which go even beyond the main theme, addressing questions like “is the global eradication of SARS-CoV-2 a realistic possibility?” (the bad news being that the answer to this question is most probably negative). Weitz and collaborators [6] used a variant of the SEIR model in order to describe the evolution of the epidemic in the various states of the USA. Given that mandatory lockdowns were either not decreed or, in many cases, not followed, the authors introduced the notion of fatality-driven awareness in order to explain the observed evolution of the epidemic. An interesting conclusion concerning the confinement measures was the one reached by Brauner and collaborators [7]. They used a Bayesian hierarchical model in order to analyse the effectiveness of the non-pharmaceutical interventions adopted by the various governments. They found that the main effect in reducing the transmission was obtained by closing educational institutions, limiting the number of people in gatherings and closing what they called “face-to-face” businesses. The stay-at-home orders had only a small additional effect, and could have been disposed with. The question of future outbreaks of the epidemic was addressed by Faranda and Alberti, in a work [8] which focused on France and Italy. Their approach was a stochastic version of the SEIR model. They acknowledged the fact that uncertainties in the model parameters and the initial conditions can result in different outcomes of the epidemic, leading, or not, to a second wave of infections. In [4] we addressed the question of a possible existence of a second wave, our conclusion being that it depended crucially on the aforementioned strategies.

In this paper we shall revisit the question of a second epidemic wave. In particular, we shall ask whether this second wave is related to the lifting of the lockdown measures and why it was observed at roughly the same time all over Europe. This leads naturally to the second question, namely, why do the epidemic evolution patterns vary so much across the various countries of the globe. When one talks about observed patterns it is necessary to keep in mind that raw numbers do not always tell the whole story. Unfortunately, the way the data are presented to the public at large are far from conveying an accurate information. This is even more complicated by the fact that the cases detected by the performed tests may represent a serious undercounting of the existing infections. This was stressed in the publication by Russel and collaborators in [9] and was also our conclusion [4]. Pulano and collaborators [10] point out that the under-detection of cases (by a factor they estimate at around 10 for France) might compromise the epidemic control effort, allowing the virus to propagate silently. Curiously, the data which would have been much more telling is the rate of positivity of performed tests (assuming that the latter were sufficiently extended geographically and age-wise), but it is seldom the first number used in order to describe the extent of the epidemic. The tally of deaths, which is used in our work [11], can also be misleading as far as the evolution of the epidemic is concerned. It is by now clear that the mortality rate of hospitalised patients has been diminishing over time, essentially due to the efficiency of the treatment of severe cases. It is probably more accurate to refer to the number of hospitalisations, rather than to the number of deaths (but even this number, as we argue in the conclusion, may also present specious variations). To sum it up, we expect the number of cases, while still underestimating the number of infections, to have artificially gone up due to the increase of the number of tests, while the number of deaths has been diminishing, due to better curative regimes. Thus, the comparison to the situation prevailing, say, six months ago, is not totally reliable.

Keeping this in mind, we shall, in what follows, propose a possible explanation of the autumn resurgence of the epidemic all across Europe. While the climate-induced seasonality of the epidemic may play a role, we believe that the important factor is what we refer to as recruitment and which is meant to encapsulate effects of the spatial spreading of the epidemic. Using the notion of recruitment, we will present a possible explanation of the variety of the observed epidemic evolution patterns.

2 THE DATA

In this section, we present the experimental data that motivated this work: the first figure depicts the epidemic evolution profiles of several countries. The countries were selected for the variety of their profiles: France was chosen because its pattern can represent most European countries that display a profile with two peaks well-separated in time, one in spring 2020 and the second one in the autumn of 2020. Brazil has a profile which is very different from the European countries, with a very large peak. The epidemic profile of the United States displays three peaks that are not well-separated in time. Finally, the epidemic profile of Australia was chosen to represent the Southern Hemisphere countries.

Fig. 1
figure 1

Temporal evolution of the number of daily deaths per million for four countries: France (top, left), the United States (top, right), Brazil (bottom, left), Australia (bottom, right). The origin of time is January 1st, 2020, and the last time point is December 28th, 2020. The data were collected from the website: https://ourworldindata.org/coronavirus (update of December 28th, 2020).

Full size image

The second figure represents the temporal evolution of the relative number of patients in ICU in several French regions. In France, the most populated region is the Ile-de-France. During summer, the inhabitants of this region traditionally spend their holidays mostly in the south part of France (in the Provence-Alpes-Côte d’Azur region, in Occitanie or in Auvergne-Rhône-Alpes). In the left figure, a peak is clearly visible for the Ile-de-France region (dashed line) around July 2020, meaning that at that time the majority of the ICU patients were located in the Ile-de-France region. Interestingly, a peak in the touristic regions appears a few weeks later, at the beginning of autumn (left figure, Provence-Alpes-Côte d’Azur, full line; Occitanie, dashed-dotted line; Auvergne-Rhône-Alpes, dotted line). We can also observe that less touristic regions, such as the Grand-Est (right figure, full line) and Hauts-de-France (right figure, dashed line) regions, do not display any peak in autumn.

Fig. 2
figure 2

Temporal evolution of the relative number of patients in ICU for several French regions (the ratio of the number of ICU patients in the region to the total number of ICU patients in France), between March 18th 2020 and January 13th 2021: Ile-de-France (left figure, dashed line), Provence-Alpes-Côte d’Azur (left figure, full line), Occitanie (left figure, dashed-dotted line), Auvergne-Rhône-Alpes (left figure, dotted line). Grand-Est (right figure, full line), Hauts-de-France (right figure, dashed line). The data were collected from the website : https://geodes.santepubliquefrance.fr/ (update of January 16th, 2021).

Full size image

3 THE SIR MODEL

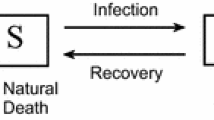
The model we are going to base our simulations on is the venerable SIR model. Proposed almost a century ago by Kermack and McKendrick [12], the deterministic SIR model studies the evolution of an epidemic within a given population, based on a simple interaction assumption. In its initial form the model consists in a population split into three groups: “healthy” individuals that are susceptible to infection (\(S\)), “infective” individuals who can transmit the disease (\(I\)), and the “removed” (\(R\)) who either died from the disease or, having recovered, are immune to it. The model can be expressed as a differential system:

$$\begin{gathered}\displaystyle\frac{dS}{dt}=-aSI,\\ \displaystyle\frac{dI}{dt}=aSI-\lambda I,\\ \displaystyle\frac{dR}{dt}=\lambda I,\end{gathered}$$
(3.1)

with \(a\) being the infection rate and \(\lambda\) the removal rate of the infected individuals. The main assumption here is that the number of infected individuals increases at a rate proportional to the number of both infected and healthy. The model equations (3.1) are such that the total population \(S+I+R\) is constant, and, by assuming that \(S\), \(I\) and \(R\) are fractions of the population, we shall normalise this constant to 1. The ratio \(a/\lambda\) defines what is called the basic reproduction number, i. e., the expected number of infections in the susceptible population resulting from a single infection, which is usually referred to as \(R_{0}\). The parameter \(\lambda\) fixes the time scale. In all our simulations we fix its value to 1 and consider (with reference to the COVID-19 epidemic) that the unit of time corresponds to 5 days.

Some basic assumptions go into the SIR model. In a sense they may be considered as weaknesses, but they are the price to pay for the utmost simplicity of the model. First we have the assumption of total mixing: all susceptible individuals can be in contact with all infective. The underlying assumption is that the contacts are random. While this may be true for small population samples, it certainly breaks down when the population is spread over a large spatial domain. Another assumption, not totally unrelated to the first, is that the populations are homogeneous. While this can be overcome by introducing various subgroups (just as we did in [4]), the basic SIR model is still built upon the homogeneity assumption.

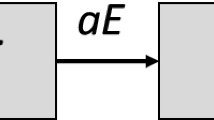
The most common extension of the SIR model is the one known under the moniker of SEIR. In the latter an intermediate population comes into play, that of the “exposed”. It corresponds to individuals who have been infected but which are not yet infective due to a finite incubation time of the infection:

$$\begin{gathered}\displaystyle\frac{dS}{dt}=-aSI,\\ \displaystyle\frac{dE}{dt}=aSI-\mu E,\\ \displaystyle\frac{dI}{dt}=\mu E-\lambda I,\\ \displaystyle\frac{dR}{dt}=\lambda I.\end{gathered}$$
(3.2)

However, adding one extra subgroup to the population means adding one more parameter, the estimation of which may, in general, not be straightforward. As Aleta and Merano have shown [13], using the SEIR model does not present a tangible advantage over the plain SIR one: the correlation between the results of the two is perfect, the main effect of the presence of the extra component being a delay in the growth of the epidemic compared to the SIR results. Roda and collaborators [14] go even further, arguing, based on the Akaike information criterion for model selection [15], that the SIR model performs better than the SEIR in representing the information contained in the confirmed-case data.

Other extensions of the SIR model can be, and have been, proposed. One possible direction has to do with the infection rate per susceptible individual, and the term \(aSI\). For instance, in [16] we proposed a modification of this term, but one which was admittedly based on dynamical system, rather than epidemiological, considerations. Another possible assumption of the SIR model is that the reproduction number \(R_{0}=a/\lambda\) is time-independent. Concerning the COVID-19, which is the epidemic we are focusing on in this paper, the constant character of \(R_{0}\) is an unwarranted assumption. Government-imposed measures, like total or partial lockdown, distancing strategies or even simple population awareness, have as a result a modification (in fact a decrease) of this parameter.

There exist by now indications that the COVID-19 epidemic may follow a climate-induced seasonal pattern. It is most interesting that Merow and Urban[17] predicted this based on laboratory studies of the effect of ultraviolet radiation on the virus. Their prediction (alas, confirmed since) was that the epidemic would decrease temporarily during summer, rebound by autumn, and peak in winter. Carleton and collaborators [18] also studied the effect of ultraviolet radiation and found that it has a statistically significant effect on the epidemic growth, while the effects of temperature and humidity were not statistically significant. On the other hand, the effect of humidity on the spreading of the virus has been the object of very detailed simulations by Tsubokura [19] who showed that it does play a major role in the persistence of aerosolised droplets. This result is in agreement with the findings of the Institut Pasteur group [20] who concluded that the drier winter conditions favour the spreading of the epidemic. Sajadi and collaborators [21] observed a correlation between the geographic latitude and the transmission of the virus consistent with the behaviour of a seasonal respiratory virus. A stronger argument in support of climate-induced seasonality is presented in the work of Watanabe [22] who presented a comparison of the evolution of the epidemic over the first few months of the year in the Northern and Southern Hemispheres. The differences between the two regions are striking and Watanabe takes extra care to eliminate other possible explanations of the observed behaviour, concluding that the statistical evidence in favour of a seasonality effect is sufficient.

Incorporating confinement and seasonality effects into SIR is straightforward. In [4], where we investigated the various strategies for a successful confinement exit, we had introduced two sub-populations of susceptible: one strictly confined and one which, due to employment imperatives, was unconfined. The two groups had, of course, different reproduction numbers. However, the coexistence of these two populations is not requisite in order to describe lockdown effects; it was introduced only in order to follow closely the situation prevailing in France. Seasonal effects can (and will) be mimicked by letting the reproduction number parameter vary with the seasons, going from a maximum in winter to a minimum in summer, following roughly the variation of daylight in temperate zones.

4 SETTING THE MODEL FOR SIMULATIONS

As explained in the previous section, in order to account for confinement and seasonality effects, the SIR model must incorporate an explicit time-dependence of the infection rate:

$$\begin{gathered}\displaystyle\frac{dS}{dt}=-a(t)SI,\\ \displaystyle\frac{dI}{dt}=a(t)SI-\lambda I,\\ \displaystyle\frac{dR}{dt}=\lambda I.\end{gathered}$$
(4.1)

A typical scenario of lockdown consists in \(a(t)\) having some value before and after confinement and a different (smaller) one, during the confinement period. Seasonality effects can be simulated by assuming that \(a(t)\) (and thus \(R_{0}(t)\)) varies periodically around some mean value with a period corresponding to one year. This can be represented by a simple sinusoidal expression \(R_{0}(t)=\alpha+\beta\cos(2\pi t/T)\) where \(T\) stands for the duration of a year. The phase of the cosine has been chosen here for the maximum of \(R_{0}(t)\) to occur at the beginning of the year, which we expect represents the situation in the Northern Hemisphere. A phase shift of \(T/2\) would be necessary in the case of the Southern Hemisphere.

The quantities \(S\), \(I\) and \(R\) appearing in the SIR equations are by definition positive, since they represent populations. As shown by Hethcote [23], their positivity over time is guaranteed provided one starts from positive initial conditions. In order to proceed to numerical simulations based on the SIR model, we need to construct a discrete version thereof. Our discretisation approach follows the ideas of Mickens [24]. His recommendations are that “nonlinear terms must be, in general, replaced by nonlocal discrete representations” and “a property that holds for the differential equation should also be present in the discrete model”. In [25] we introduced the handy prescription “if all quantities are positive, no minus sign should appear anywhere”. We start by introducing a forward difference of the time derivative, with time step \(\delta\), and, which is more important, a specific staggering

$$\begin{gathered}\displaystyle\frac{S_{n+1}-S_{n}}{\delta}=-aI_{n}S_{n+1},\\ \displaystyle\frac{I_{n+1}-I_{n}}{\delta}=aI_{n}S_{n+1}-\lambda I_{n+1},\\ \displaystyle\frac{R_{n+1}-R_{n}}{\delta}=\lambda I_{n+1}.\end{gathered}$$
(4.2)

Solving for the points at \((n+1)\), we obtain

$$\begin{gathered}\displaystyle S_{n+1}=\frac{S_{n}}{1+a\delta I_{n}},\\ \displaystyle I_{n+1}=\frac{I_{n}(1+a\delta S_{n+1})}{1+\lambda\delta},\\ \displaystyle R_{n+1}=R_{n}+\lambda\delta I_{n+1}.\end{gathered}$$
(4.3)

Given the structure of (4.3), it is clear that \(S_{n}+I_{n}+R_{n}\) is a constant and, just as in the differential case, since we shall work with fractions of the population, we normalise it to 1. The discrete system has the very same properties as the differential one. It is a very robust scheme which gives a realistic answer for any time step, even a large one. This is the scheme we shall use in order to integrate the differential SIR equations. All the simulations presented in this paper were carried out with an initial infective population of 10\({}^{-7}\), while the initial recovered population is zero. When considering the time-dependent extension (4.1) of SIR, the parameter \(a\) entering (4.2) or (4.3) must be understood as one dependent on the point in time, i. e., as \(a_{n}\).

One of the weaknesses of the SIR model is the absence of spatial dependence: it is as if the whole population were concentrated on a single point. But all epidemics (and thus the current one) do have a clear spatial dependence. Bringing some spatiality into the SIR model has been the object of studies, some predating the COVID-19 epidemic. Flahaut and collaborators [26] introduced a model of coupled SEIR equations in order to describe the spread of influenza over 9 major European cities. Saito et al. [27] used a similar model, based on SEIR, to describe the 2009, H1N1 influenza in Japan. A most interesting approach is that of Munshi [28] and collaborators who introduced an extended SIR-based cellular automaton in order to describe the spreading of COVID-19 in the state of New York.

However, making the SIR model explicitly space-dependent can lead to an unmanageable proliferation of parameters. A different way to address the difficulty is by resorting to recruitment. The basic assumption behind this notion is that the population is not fixed, but increases with time. The idea of recruitment in connection to SIR is already present in the works of Jacquez [29], Allen [30] and Franke [31], to name but a few. However, these works are mathematically oriented and do not bring new epidemiological insights. A more recent work by Zhao et al [32] sets out to study the effect of population recruitment on the HIV epidemic, but, again, the approach is more mathematical than epidemiological. A recent paper by Cooper and collaborators [33] investigates the spreading of COVID-19 in an SIR framework, one where the susceptible population is taken as a variable to be adjusted at various times in order to account for the infection spreading. Practically this is done by introducing surges in the susceptible population whenever the authors deem this necessary.

Our approach to recruitment is different from that of Cooper et al. Starting from the discrete system (4.3), we add to \(S_{n+1}\) obtained from the first equation a quantity \(\Delta_{n}\). And we normalise all three quantities by introducing

$$\begin{gathered}\displaystyle{\tilde{S}}_{n}=\frac{S_{n}+\Delta_{n}}{1+\Delta_{n}},\\ \displaystyle{\tilde{I}}_{n}=\frac{I_{n}}{1+\Delta_{n}},\\ \displaystyle{\tilde{R}}_{n}=\frac{R_{n}}{1+\Delta_{n}}.\end{gathered}$$
(4.4)

It is clear that, thanks to this normalisation we have already introduced, we have \({\tilde{S}}_{n}+{\tilde{I}}_{n}+{\tilde{R}}_{n}=S_{n}+I_{n}+R_{n}=1\).

There is no a priori guide for the proper choice of the function \(\Delta_{n}\). All we can say is that it must become 0 after some point in time. A simple choice of the recruitment function \(\Delta_{n}\), one that will be used in the next section, is a trapezoidal shape, like the one shown in Fig. 3.

Fig. 3
figure 3

An example of a possible profile for the recruitment function.

Full size image

The disadvantage of such a shape is that, were we to work with the differential system, it would have introduced discontinuities in the second derivative of the solutions, but given that we use the discrete form (4.3), this is immaterial. (The discontinuities could be easily made to disappear by using a continuous function for \(\Delta_{n}\), for instance, one expressed as a sum of Gaussians. We have indeed performed simulations using Gaussians, but the results obtained thus do not differ significantly from those from the trapezoidal form, and the latter is much easier to control). In the following, the values of the time points \(n_{i}\) and the corresponding values of the function \(\Delta_{n_{i}}\) will be given in each figure caption where the recruitment is used.

5 THE CASE OF FRANCE: SEASONALITY VS RECRUITMENT

France has undergone a strict lockdown from March to May 2020, followed by several restrictive measures, corresponding to a “soft” lockdown, which were not lifted till almost July. During the lockdown period only the persons doing essential work were allowed to circulate freely, while the remaining population was allowed short exits from home in order to cover absolute necessities. As a consequence, the reproduction number did decrease substantially during that period, only to grow again once the confinement measures were lifted. In [4] we addressed the question of the confinement exit strategy. To this end we introduced a variant of the SIR model comprising two populations, one which is confined, and has thus a decreased value for the reproduction number, and one which is unconfined for which the reproduction number stays unaltered. This was important in the setting of that work, where fine details could play a role in defining the optimal exit strategy. However, this is not essential for the analysis we shall present in this section and thus we shall simplify our assumptions by considering a single susceptible population subject to confinement and a reproduction number which globally diminishes during confinement (but still staying larger than 1).

Fig. 4
figure 4

Simulation of the evolution of the density of infective in France during the year 2020 (full line). Time is indicated in months and starts on January 1st, 2020. The confinement starts at \(t=2\) months (this corresponds to March) and is lifted at \(t=5.5\) months (mid-June). During confinement \(R_{0}=1.2\) and out of the confinement period \(R_{0}=2\). Here there is no recruitment, so \(\Delta=0\).

Full size image

The simplest confinement exit scenario, that of an abrupt exit without any non-pharmaceutical interventions, leads typically to a resurgence of the epidemic and the appearance of a second wave just after the restrictions are lifted. Such a situation is represented in Fig. 4.

Fig. 5
figure 5

Simulation of the evolution of the density of infective in France, during the year 2020 (full line). The parameters are the same as in Fig. 4, except that, during the confinement, \(R_{0}=1.4\). Here there is no recruitment, so \(\Delta=0\).

Full size image

However, this is not the only possibility. If the reproduction number is high enough during the confinement period, it may turn out that the pool of susceptible is drained during the confinement period and no resurgence appears, as can be seen in Fig. 5.

Fig. 6
figure 6

Simulation of the evolution of the density of infective in France during the year 2020 (full line). The parameters are the same as in Fig. 4, except that the confinement is lifted at \(t=7\) months (August). Here there is no recruitment, so \(\Delta=0\).

Full size image

In the case of France, none of these scenarios comes close to what was observed, namely, the appearance of a second wave in autumn with more than three months hiatus between the end of the lockdown and the epidemic resurgence. Having a late resurgence is always possible within the confinement model considered here. But it can only be obtained in the case where the lockdown period is extended over several months, as shown in Fig. 6. Although one can argue that social distancing measures during the summer months could have lowered the value of infectivity, this value would still have been higher than the one reached during confinement. And if one made the (unwarranted) assumption of a very low value so as to have a second peak appearing not before autumn, the height of the resulting peak would have been much lower than that of the first peak. Thus, no direct link between the second epidemic wave and the lifting of the confinement restrictions can be established.

How can one then explain the appearance of a second epidemic wave in France (and, as a matter of fact, in most European countries)? As announced in the previous section, two mechanisms come into play: climate-induced seasonality and recruitment. The first mechanism assumes that the reproduction number varies with seasons, diminishing during summer. We performed simulations of this effect, assuming a sinusoidal variation of the reproduction number with the remaining parameters having the same values as in Fig. 4. As can be seen in Fig. 7, this can lead indeed to the appearance of a second epidemic wave.

Fig. 7
figure 7

Simulation of the evolution of the density of infective in France during the year 2020 (full line), with the influence of seasonality. The confinement starts at \(t=2\) months (March) and is lifted at \(t=5.5\) months (mid-June). During confinement, \(R_{0}=1.2\). Out of the confinement period: \(R_{0}(t)=1.6+0.4\cos(2\pi t/T)\) with \(T=12\) months. The profile of the reproduction number \(R_{0}\) due to seasonality is shown as a dashed-dotted line. Here there is no recruitment, so \(\Delta=0\).

Full size image

However, two points should be stressed here. If the reproduction number during lockdown is such that no second wave may appear, as is the case of Fig. 5, then a seasonal effect cannot lead to the appearance of a second wave. This is only possible in the cases where a lift of confinement would lead to the immediate appearance of a second wave. In this case seasonality does produce a delayed second wave, but it turned out that in all our simulations this second wave did arrive rather late, not peaking before December (corresponding to the maximum of the reproduction number). The implementation of a new “moderate” confinement in France did curb the epidemic, leading to a peak in early November. Thus, it is not possible to conclude when the epidemic would have peaked without external interventions.

Another possible explanation of the second epidemic wave in France (and in the other European countries) can be attributed to the fact that, profiting from the fact that the epidemic had abated during summer, the populations did spend their summer vacations travelling, thus increasing the number of susceptible in areas that had be spared by the epidemic up to that point. In order to model this, we introduced a simple recruitment function concentrated over July, August and September. The results of the simulation are shown in Fig. 8.

Fig. 8
figure 8

Simulation of the evolution of the density of infective in France during the year 2020 (full line), with recruitment. The confinement starts at \(t=2\) months (March) and is lifted at \(t=5.5\) months (mid-June). During confinement, \(R_{0}=1.4\). Out of the confinement period: \(R_{0}=2\). Parameters of the recruitment: \(n_{1}=6.5\) months and \(\Delta_{n_{1}}=0\), \(n_{2}=7\) months and \(\Delta_{n_{2}}=2\cdot 10^{-3}\), \(n_{3}=8.5\) months and \(\Delta_{n_{3}}=2\cdot 10^{-3}\) and \(n_{4}=9\) months and \(\Delta_{n_{4}}=0\). The profile of the recruitment function is shown as a dashed line.

Full size image

The second wave arrives now earlier, with a peak around October. Thus, it is natural to wonder what would happen when the two effects of seasonality and recruitment are combined. We present the result of such a simulation in Fig. 9.

Fig. 9
figure 9

Simulation of the evolution of the density of infective in France during the year 2020, with recruitment and seasonality. The parameters are the same as in Figs. 7 and 8.

Full size image

The epidemic peak is now situated at the beginning of November and is higher than the peak of the first wave. While this is indeed what has been observed in many European countries, in the case of France the second peak was roughly comparable to the first. We believe that this is due to the measures taken by the government and will not seek to proceed to further modelling in this direction, all the more so since the second lockdown in France was plagued by ever changing directives and loose enforcement.

6 SELECTED COUNTRIES AND THE CASE OF THE SPANISH FLU

The epidemic profiles observed over the various countries of the world show a big variety. We think that a substantial part of the observed variations can be associated to recruitment mechanisms. In what follows we shall present examples that will reinforce this argument. But before proceeding further, we shall examine the epidemic profile of Australia. Given the latitude of the country, provided one abides by the hypothesis of a climate-induced seasonality, one would have expected the epidemic to manifest itself around July, as observed in the case of South Africa. However, in Australia the epidemic has already presented a first flare around April. How could this come to be? We argue that the first wave in Australia was due to an influx of infective persons. (At this point we should thank the reviewer who pointed out the role that might have been played by the Chinese New Year celebrations and the travels to mainland China and back of a non-negligible part of the population). Our model seems to support this argument. In fact, we have carried out our simulations after modifying the infective population, introducing an infective recruitment (along the same lines as the susceptible one) centred around February. The direct consequence of this is the appearance of a first epidemic wave centred around April, Fig. 10. And the effect one would have expected, were the virus to show a seasonal dependence, did manifest itself through a second peak centred around August, i. e., in the middle of austral winter.

Fig. 10
figure 10

Simulation of the evolution of the density of infective in Australia during the year 2020, with seasonality and recruitment. Parameters of seasonality: \(R_{0}(t)=1.6+0.4\cos(2\pi(t-6)/T)\) with \(T=12\) months. The profile of the reproduction number \(R_{0}\) due to seasonality is shown as a dashed-dotted line. Parameters of the recruitment of susceptible: \(n_{1}=5.8\) months and \(\Delta_{n_{1}}=0\), \(n_{2}=5.8\) months and \(\Delta_{n_{2}}=5\cdot 10^{-3}\), \(n_{3}=6.7\) months and \(\Delta_{n_{3}}=5\cdot 10^{-3}\) and \(n_{4}=6.7\) months and \(\Delta_{n_{4}}=0\). The profile of the recruitment function for susceptible is shown as a dashed line. Parameters of the recruitment of infective: \(n_{1}=1.2\) months and \(\Delta_{n_{1}}=0\), \(n_{2}=1.2\) months and \(\Delta_{n_{2}}=4\cdot 10^{-5}\), \(n_{3}=1.7\) months and \(\Delta_{n_{3}}=4\cdot 10^{-5}\) and \(n_{4}=1.7\) months and \(\Delta_{n_{4}}=0\). The profile of the recruitment function for infective is shown as a dotted line. The two rectangles representing the recruitment of susceptible and infective are not drawn to scale.

Full size image

Next, we turn to a mainly tropical country like Brazil, where we do not expect seasonal effects to have a particular importance. We think that the pattern observed with a broad plateau followed by a small abatement and resurgence (better appraised in the case of daily deaths) can be due to the gradual recruitment of susceptible individuals. We expect the recruitment mechanism to be particularly important in a country like Brazil with a vast area and big urban centres spread all over. In Fig. 11 we present the results of our simulation where the initial plateau is followed by a resurgence arriving towards the end of the year.

Fig. 11
figure 11

Simulation of the evolution of the density of infective in Brazil during the year 2020, with recruitment. Reproduction number: \(R_{0}=2\). Parameters of the recruitment: \(n_{1}=0\) months and \(\Delta_{n_{1}}=0\), \(n_{2}=1.7\) months and \(\Delta_{n_{2}}=5.10^{-3}\), \(n_{3}=4.3\) months and \(\Delta_{n_{3}}=5.5\cdot 10^{-3}\), \(n_{4}=8.3\) months and \(\Delta_{n_{4}}=1.5\cdot 10^{-3}\), \(n_{5}=10\) months and \(\Delta_{n_{5}}=3.5\cdot 10^{-3}\), \(n_{6}=13.3\) months and \(\Delta_{n_{6}}=0\). The profile of the recruitment function is shown as a dashed line.

Full size image

Finally, we address the question of the USA (Fig. 12). The country has been the object of chaotic policies, contradictory directives and randomly followed measures. It is thus not surprising that the epidemic pattern of the country should be rather unique.

Whether one looks at the number of infected individuals or at the number of deceased, there exist three distinct humps evenly spaced over the year. It would appear that in the case of the USA the seasonal effects are playing a minor role compared to important events like pre-election rallies, massive protests and public unrest. Again the determinant mechanism is the recruitment of susceptible individuals resulting from travels and/or meetings. We do not claim that this mechanism is sufficient to account for all the variety observed (and one should not forget the famous saying of Von Neumann [34] on fitting an elephant). Still it appears that in the case of epidemics the mechanism of recruitment is quite efficient.

Fig. 12
figure 12

Simulation of the evolution of the density of infective in the United States during the year 2020, with recruitment. Reproduction number: \(R_{0}=2\). Parameters of the recruitment: \(n_{1}=0\) months and \(\Delta_{n_{1}}=0\), \(n_{2}=5\) months and \(\Delta_{n_{2}}=5.5\cdot 10^{-3}\), \(n_{3}=8\) months and \(\Delta_{n_{3}}=3\cdot 10^{-3}\), \(n_{4}=9.7\) months and \(\Delta_{n_{4}}=5.5\cdot 10^{-3}\), \(n_{5}=13.3\) months and \(\Delta_{n_{5}}=0\). The profile of the recruitment function is shown as a dashed line.

Full size image

As another argument in favour of this, we present below a simulation aiming at reproducing the evolution of the 1918-19 influenza epidemic, commonly known as “Spanish flu”. The pandemic occurred between 1918 and 1919 affecting many industrialised nations across the globe. It remains to this date as a warning to the dire consequences of uncontrolled spreading of communicable diseases with unusual virulence.

Fig. 13
figure 13

Temporal evolution of the number of deceased due to the Spanish Flu in Great Britain at the beginning of the 20th century. The data were plotted based on [35].

Full size image

The first wave was limited to the USA and Europe during the spring of 1918 in the Northern Hemisphere. It was characterised by milder cases, with reported death rates not above the usual values for influenza. The second (Autumn 1918) and the third (Winter 1919) waves lead to more severe cases and thus more fatalities (Fig. 13). It is believed that these two waves were not due to mutations of the virus itself, but were rather brought about by external environmental causes and transmission patterns of the hosts. In order to simulate the evolution of the influenza epidemic, we used a reproduction number smaller than the one used in all those related to the COVID-19 epidemic. It turned out that it was possible, using the appropriate recruitment profile, to obtain the three characteristic peaks observed during the epidemic (Fig. 14).

Fig. 14
figure 14

Simulated evolution of the number of deceased due to the Spanish flu (full line), to be compared to Fig. 13. Reproduction number: \(R_{0}=1.6\). Parameters of the recruitment: \(n_{1}=0.3\) months and \(\Delta_{n_{1}}=0\), \(n_{2}=1.2\) months and \(\Delta_{n_{2}}=9\cdot 10^{-3}\), \(n_{3}=2.8\) months and \(\Delta_{n_{3}}=9\cdot 10^{-3}\), \(n_{4}=3.7\) months and \(\Delta_{n_{4}}=0\), \(n_{5}=8.7\) months and \(\Delta_{n_{5}}=10^{-3}\). The profile of the recruitment function is shown as a dashed line.

Full size image

There are roughly ten months separating the first from the third peak with the middle peak being the most death-dealing one. A look at the recruitment profile allows one to formulate a scenario for the epidemic spreading. After the onset of the epidemic (first wave), geographic spreading recruited more and more susceptible, giving rise to the second and most important wave. The third wave came about from the recruitment of the “leftovers”, a small number of persons who had escaped infection up to that point. Although we do not claim that this is exactly what happened, this scenario appears plausible.

7 CONCLUSION

In this paper we set out to reproduce (part of) the variety observed in the temporal evolution of the COVID-19 epidemic in the various countries. As we explained in the Introduction, the usual metrics, the daily number of infections and deaths, are not quite reliable. Instead we suggested that one should rather base oneself on data on positivity and/or hospitalisations. But even the latter metrics have to be handled with caution. In fact, positivity can be influenced by a number of persons who undergo a test as a mere precaution. As of purely anecdotical value one can mention the surge of tests performed in France in the days preceding Christmas, due to people who sought to be reassured before spending the festive days with older members of their family. Similar cautionary arguments do apply to the number of hospitalisations. The evolution of curative procedures related to the advancement of our understanding of the epidemic does influence the decision concerning hospital admission. Moreover, the stress on the infrastructures due to surges of the epidemic can also be a criterion for the admission or not of milder cases. Whatever criterion is adopted, one must bear in mind that the evolution of the virus can affect the temporal features of the epidemic. This is, for instance, what happens when a mutation leads to the appearance of a virus with enhanced infectivity. Despite all those cautionary arguments, there are features of the epidemic which are particularly robust, like the number of the waves and their temporal succession. And although the precise widths of the epidemic surges may be not so robust a feature, the fact that the waves are well separated or not does constitute one. Our work thus aimed at reproducing qualitatively such features for a selection of countries.

Our method was based on the venerable SIR model. We have argued in the Introduction that the model, although extremely simple, is able to capture the gist of the epidemic evolution. The two effects we have endowed our SIR model with were what we called seasonality and recruitment. The former refers to a climate-induced effect and was motivated by the observation of an epidemic summer respite in the European continent. The notion of recruitment is based on more involved arguments. As it stands, the SIR model lacks a spatial dependence. Its main assumption is that everybody is, from the outset, in contact with everybody else. This is clearly not true in real-life situations where it is observed that the epidemic does propagate in the territory of each country, often with long-range jumps facilitated by high-speed transportation. As a result, the susceptible population does increase over time. We introduced thus the notion of recruitment (the details of which were explained in the body of the article) and showed that it was a quite efficient way to reproduce the observed epidemic patterns.

In the case of France the observed relaxed attitude during the summer months kindled the, in any case inevitable due to seasonality, epidemic resurgence in autumn. For the remaining countries under COVID-19, as well as in the case of the Spanish flu, we were able to reproduce the observed patterns using quite “tame” recruitment patterns. It goes without saying that we are aware that, with quirky assumptions involving a slew of parameters, one can reproduce anything (and the Von Neumann dictum [34] has been our guide throughout all our research). Still, it is remarkable that the recruitment assumption coupled to a (very) simple model can lead to such variety of results.

Having established the importance of the spatial component, admittedly in an indirect way, it is natural to wonder whether it would be possible to extend the SIR model so as to take into account directly the spatiality of the epidemic. While this is beyond the scope of the present paper, we consider this an interesting challenge and we have the intention to rise to it in some future work of ours.