On transmissible load formulations in topology optimization

Abstract

Transmissible loads are external loads defined by their line of action, with actual points of load application chosen as part of the topology optimization process. Although for problems where the optimal structure is a funicular, transmissible loads can be viewed as surface loads, in other cases such loads are free to be applied to internal parts of the structure. There are two main transmissible load formulations described in the literature: a rigid bar (constrained displacement) formulation or, less commonly, a migrating load (equilibrium) formulation. Here, we employ a simple Mohr’s circle analysis to show that the rigid bar formulation will only produce correct structural forms in certain specific circumstances. Numerical examples are used to demonstrate (and explain) the incorrect topologies produced when the rigid bar formulation is applied in other situations. A new analytical solution is also presented for a uniformly loaded cantilever structure. Finally, we invoke duality principles to elucidate the source of the discrepancy between the two formulations, considering both discrete truss and continuum topology optimization formulations.

1 Introduction

In classical structural layout and topology optimization formulations the locations of external loads to be carried by the structure are specified in advance. While problems of this type are common in practice, there are also many situations where the applied loads depend on the topology or layout. For example, loads produced by snow, wind or surrounding fluid all depend on the configuration of the surface of the structure. Therefore, changes to the structural form will normally result in changes to the loads, which are consequently called design-dependent loads (see Hammer and Olhoff 2000). Optimization of such structures is intrinsically coupled to the appropriate recalculation of the configuration of external loads.

The specific relationships between the structural form and external loads may vary significantly depending on the particular loading situation. Gao and Zhang (2010) proposed the following classification of design-dependent loads:

• Transmissible loads, the main focus of the present study, are loads that are applied along a prescribed line of action, such that the specific point of application of a given load is not known a priori. Since each potential point of load application will normally correspond to a different optimal structure, the optimization now involves identifying which of a family of structures best meets the optimization objective (e.g. see Fig. 1).

• Body loads, which are distributed loads whose magnitudes are dependent on the location of material forming the optimized body or structure. These have for example been studied by Huang and Xie (2011), Kanno and Yamada (2017), and Fairclough et al. (2018). Most papers focus on body loads due to self-weight, but inertial, centrifugal and other types of loads may also be considered. For example, Gao et al. (2008) studied a heat conduction problem with a distributed, design-dependent, heat generation rate.

• Surface pressure loads, which have attracted significant attention from researchers. These include hydrostatic pressure loads, considered by workers such as Hammer and Olhoff (2000), Bourdin and Chambolle (2003), Allaire et al. (2004), Sigmund and Clausen (2007), Lee and Martins (2012), Xia et al. (2015), Picelli et al. (2019), Zhou et al. (2019) and many others. The pressures produced by the weight of snow or by wind loading usually require similar approaches (see, for example, Chen and Kikuchi 2001). Contact pressures produced by the weight of a rigid object placed onto a surface can also be considered.

• Other types of design-dependent loads, for example thermoelastic stress loads, as studied by Gao et al. (2008) and Gao and Zhang (2010), or non-stationary thermal loads, as considered by Zhuang and Xiong (2015) and Long et al. (2018).

Fig. 1

Example of the influence of vertical load position on the form of an optimal structure (after Wang and Rozvany 1983a). When a transmissible loads formulation is used the optimal point of application of the load is sought as part of the optimization process, with the h = l structure (highlighted) therefore identified as optimal in this case (where here P represents the magnitude of the load, l represents the half span, h represents the vertical elevation of the load, σ represents the limiting material stress)

Although the term transmissible loads was coined at the turn of the millennium by Fuchs and Moses (2000), the idea of loads with unspecified point of application was introduced in the context of layout optimization much earlier by Rozvany, Prager and co-workers (Rozvany and Prager 1979; Rozvany et al. 1982; Rozvany and Wang 1983). These studies described a special class of optimal structures satisfying two key requirements: (a) structural elements must be fully in tension or compression, and (b) the vertical positions of external loads must be determined as part of the optimization procedure (e.g. see Fig. 1). The resulting layouts, often referred to as Prager-structures, turned out to be necessarily funicular; thus, 3D Prager-structures in compression are archgrids and 3D Prager-structures in tension are cable networks. In common with most studies employing transmissible loads, these latter studies involved gravity loading, where the direction of the loading is fixed.

A convenient way of deriving Prager-structures involves postulating that the virtual strains vanish along the line of action of a transmissible load. This is equivalent to introducing a ‘virtual’ rigid bar along this line, which can transmit the load from an arbitrary point of application to the ‘real’ structure. Since this rigid bar can carry the load using zero cross-sectional area, it can be of arbitrary length without adding to the overall structural volume. A number of finite element-based topology optimization studies used this idea to motivate the introduction of constraints of zero virtual displacement along the lines of action of transmissible loads (e.g. Fuchs and Moses 2000; Yang et al. 2005; Chiandussi et al. 2009; Zhu et al. 2017).

The use of rigid bars along the line of action of external loads is entirely reasonable for funicular structures, where the bars transfer these loads to the structure, but do not interact with it. However, the validity of using rigid bars in more general cases is dubious. This is because of the potential for weightless rigid bars to exist within the structural domain, potentially interacting with the structure and inadvertently affecting the generated structural form. In fact, Tyas and Gilbert (2011) and Jiang et al. (2018) reported cases where solutions obtained using the rigid bar (constrained displacement) approach appeared physically unrealistic. However, neither of these publications explained why unrealistic solutions are obtained, nor linked it explicitly with limitations of the rigid bar approach.

An alternative ‘migrating loads’ approach to layout optimization with transmissible loads has been developed by Gilbert et al. (2005) and Darwich et al. (2010) as an extension of the classical plastic, linear programming (LP), based ground structure formulation (after Dorn et al. (1964)). In their formulation, additional LP variables were introduced to represent potential loads applied at each node present along the line of action of every given transmissible load. Additional LP constraints were also added to ensure that the total load applied to nodes lying along a given line of action coincides with the total applied load; the LP variables involved were also constrained to be non-negative.

The current article provides a critical appraisal of the two approaches, identifying and highlighting the practical consequences of differences between them. Michell-Hemp optimality criteria are used together with Mohr’s circle of strain analysis to show that only very special types of non-funicular optimal structures are compatible with the assumptions of the rigid bar approach, whereas the migrating load approach has a much greater range of applicability. Specifically, two numerical examples are used to show that introduction of weightless rigid members severely affects the optimal layout and is likely to result in physically unrealistic solutions. In the interests of rigour, solutions from both numerical examples are verified against exact analytical solutions (the analytical solution for the second numerical example is a new Michell structure, derived in Appendix 2). We also analyse the classical LP formulation for optimization of discrete truss structures using the migrating load approach and show explicitly the difference between it and the rigid bar approach. The resulting insight is then shown to also apply to the continuous topology optimization formulation of Fuchs and Moses (2000).

2 Comparison between rigid bar and migrating load approaches

2.1 Conceptual formulation

A simple layout optimization example problem containing only six nodes (Fig. 2a) can be used to illustrate key features of the rigid bar and migrating load approaches. In this example, the left boundary is fixed in both x and y directions. The transmissible load P can be applied to any node(s) on the right boundary. The optimal point of application of P is in this case the middle point. Key features of the two approaches are as follows:

• For the rigid bar approach, as shown in Fig. 2b, the load is transmitted to the optimal point through forces generated in virtual, cost-free, rigid bars. It is important to note that, due to the presence of these rigid bars, the vertical virtual displacements in the dual formulation (e.g. see Gilbert and Tyas 2003) must remain constant along the right boundary.

• For the migrating load approach the single external load P is replaced by three load variables, applied to the three nodes that lie along the line of action of P. These three load variables must satisfy the sign and sum constraints (i.e. P_1,2,3 ≥ 0 and $\sum \limits _{i=1}^{3} \text {P}_{i}=\text {P}$). In the layout presented in Fig. 2c the full load is transmitted to the middle node, so P₁ = P₃ = 0 and P₂ = P. In this case in the dual formulation there are no constraints on the virtual displacements along the line of action of P.

Fig. 2

Rigid bar and migrating load approaches for a layout optimization problem involving six nodes: a the design domain and the trajectory of the transmissible load P; b solution obtained using the rigid bar approach, where solid and dotted grey lines indicate rigid bars that carry non-zero and zero internal force, respectively; c a possible solution obtained via the migrating load approach, where P₁, P₂ and P₃ are the load variables that must satisfy the indicated sum and sign constraints

2.2 Mohr’s circle analysis

The optimal layout theory pioneered by Michell (1904) and generalized to its modern form by Hemp (1973) states that optimal structures can contain, or be fully contained within, regions of three types: (i) structurally ‘rich’ layouts in which mutually orthogonal members are strained to their respective limits in tension and compression, (ii) layouts where members are all fully in compression or tension, and can cross and have arbitrary orientations, and (iii) simpler layouts where members cannot cross, and once again are all fully in compression or tension. Rozvany (1997) described these as (i) T-type, (ii) S-type, and (iii) R-type regions respectively. It can be shown that Prager-structures are actually a particular case of Michell-Hemp trusses, and in fact, Rozvany and Wang (1983) effectively use a rigid bar approach to identify the layouts that are all of R-type. However, no rigorous assessment of the applicability of the rigid bar approach to richer T-type and S-type layouts appears to have been published in the literature.

As already noted, the rigid bar approach requires constant virtual displacements along the line of action of a transmissible load, which means that the virtual strain will be zero along the same line. For sake of simplicity we will assume henceforth, without loss of generality, that our problem is confined to 2 dimensions, and that the transmissible load acts in a direction normal to the x-axis, so that the y-virtual strain, ε_yy is zero.

From analysis of the corresponding Mohr’s circle of strain, with the added requirement that ε_yy = 0, we obtain:

$$ \begin{array}{@{}rcl@{}} \varepsilon_{xx} &=& \varepsilon_{1}+ \varepsilon_{2} , \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} \gamma_{xy} &=& 2\sqrt{-\varepsilon_{1}\varepsilon_{2}} , \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} \theta_{p} &=& \frac{1}{2}\tan^{-1}\left( \frac{\sqrt{-\varepsilon_{1}\varepsilon_{2}}}{\varepsilon_{1}+\varepsilon_{2}}\right) , \end{array} $$

(3)

where ε_1,2 are principal strains, ε_xx is the x-virtual strain, γ_xy is the engineering shear strain and 𝜃_p is the angle between the trajectory of the maximum principal strain and the x-axis.

For T-type layouts, ε₁ = 1/σ⁺, ε₂ = − 1/σ⁻, where σ⁺ and σ⁻ are the maximum allowable stresses in tension and compression respectively, we obtain:

$$ \begin{array}{@{}rcl@{}} \varepsilon_{xx}^{T} &= &\frac{\sigma^{-}-\sigma^{+}}{\sigma^{+}\sigma^{-}} , \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} \gamma^{T}_{xy} &=& 2/\sqrt{\sigma^{+}\sigma^{-}} , \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} {\theta_{p}^{T}} &=& \frac{1}{2}\tan^{-1}\left( \frac{\sqrt{\sigma^{+}\sigma^{-}}}{\sigma^{-}-\sigma^{+}} \right) . \end{array} $$

(6)

For the particular case of equal magnitudes of allowable tension and compression stress σ⁺ = σ⁻ = σ, these relationships simplify to:

$$ \begin{array}{@{}rcl@{}} \varepsilon_{xx}^{T} &=& 0, \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} \gamma_{xy}^{T} &=& 2/\sigma , \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} {\theta_{p}^{T}} &=& \pm\frac{\pi}{4} . \end{array} $$

(9)

The constraint on the geometry imposed by (9) (and, of course, more generally, by (6)) is particularly noteworthy since it shows that the rigid bar formulation is incompatible with T-type layouts apart from the special case where the trajectories of principal strain are aligned at the specific angle of 𝜃_p = ±π/4 relative to the line of action of the transmissible load (see Fig. 3a).

Fig. 3

Mohr’s circle analysis showing interaction between a rigid bar and three types of optimal regions: a interaction between a rigid bar and T-type region, b interaction between a rigid bar and R⁺-type region, c for an S⁺-region no intersection point exists between the rigid bar and the Mohr’s circle. It is assumed in these examples that the maximum allowable tension and compression stress are equal in magnitude, i.e. that σ⁺ = σ⁻; ε_1,2 are the principal strains, ε_xx and ε_yy the x- and y-virtual strains, γ_xy is the engineering shear strain, 𝜃_p the angle between the trajectory of the maximum principal strain and the x-axis) and line ε_yy = 0 represents the rigid bar

It is worth remarking that the migrating load approach imposes no such restrictions. In fact, the present authors and their co-workers used this formulation to model transmissible loads (Gilbert et al. 2005; Darwich et al. 2007; 2010), and the high resolution results from the second and third articles clearly show that this approach is perfectly capable of identifying curvilinear T-type layouts. Indeed, the structure considered in those articles (see Fig. 4b) was later demonstrated by Tyas et al. (2011) to be globally optimal, thus confirming the validity of the numerical results.

Fig. 4

Example 1 (migrating load approach): uniform load between pinned supports, where a specifies the design problem, b shows transmissible load trajectories and the discrete layout optimization result, and c shows the resulting optimal structure with the final positions of the loads, which matches the analytical solution obtained by Tyas et al. (2011). Red lines indicate members in tension and blue lines indicate members in compression

For R-type layouts, for sake of brevity, we consider R⁺-type (i.e. tensile) layouts with equal magnitudes of allowable tension and compression stress, where ε₁ = 1/σ⁺, − 1/σ⁻≤ ε₂ ≤ 0 and σ⁺ = σ⁻. In this case, the Mohr’s circle analysis in Fig. 3b shows that the rigid bar formulation is compatible with R⁺-type layouts when $\theta _{P}^{\text {R}^{+}} \in [-\pi /4,\pi /4]$. This analysis can easily be extended to other cases, e.g. R⁻-type (i.e. compressive) layouts and/or unequal maximum tension and compression stress.

Last but not least, it is readily established that the rigid bar approach is incompatible with S-type structures (see Fig. 3c). This is because the principal strains in such structures are of the same sign, and so no real values can be found for the shear strain or principal angle. (This is of course to be expected, since S-type structures intrinsically comprise bi-axial tension or compression fields and any opposing external loads at the boundaries of such a region would simply migrate to a position where they could equilibrate each other, thus rendering a structure unnecessary.) With this background, we now proceed to illustrate the situation by considering a number of numerical examples.

3 Numerical examples

The suitability of migrating load and rigid bar approaches can be succinctly demonstrated by considering two numerical examples. In these examples, we apply the migrating load approach to discrete layout optimization problems only and the rigid bar approach to both discrete layout optimization and continuum topology optimization problems. In applying the rigid bar approach to continuum topology optimization problems we sought to reproduce the results obtained by Fuchs and Moses (2000), to enable their results to be viewed in the light of the Mohr’s circle analysis set out in the previous section. The SIMP-based continuum topology optimization is performed here using the formulation presented by Sigmund (2001), while the displacement constraints set out by Fuchs and Moses (2000) are imposed using the method presented by Houlsby et al. (2000). A brief description of the formulation is provided in Appendix 1. The η₁ and η₂ parameters described by Fuchs and Moses (2000) are employed for the continuum topology optimization problems, which are respectively the SIMP penalization factor p and a tuning parameter designed to improve convergence. The SIMP iteration process stops when the largest change in element density is smaller than a pre-defined threshold (Sigmund 2001) and this remained the same in our implementation. For the discrete layout optimization problems, the post-possessing rationalization technique described by He and Gilbert (2015) is used to improve the visual clarity of the solutions shown in Figs. 4 and 6.

3.1 Example 1 — Uniform load between pinned supports

The first numerical example considered comprises a rectangular domain with fixed pin supports at the bottom left and right corners of the domain. A uniformly distributed transmissible load is applied across the full width of the domain, such that loads are free to migrate along vertical lines of action (Fig. 4a). In the context of optimization under the action of transmissible loads, this problem was first considered by Fuchs and Moses (2000), who identified a parabolic funicular form as the optimal solution.

In the case of the discrete layout optimization runs considered herein, a 100×100 grid was used unless stated otherwise. In the case of continuum topology optimization runs, a design domain comprising 50×50 elements was used, with a Poisson’s ratio of 0.3 (as used by Fuchs and Moses (2000)).

Figure 4b and c show the results obtained when using discrete layout optimization with the migrating loads approach. The optimal form obtained is very similar to the layout identified by Darwich et al. (2007) and Darwich et al. (2010), later demonstrated by Tyas et al. (2011) to be globally optimal for this problem. This layout includes both rich T-type regions around the haunches and a central funicular R-type region. (Note that the presence of T-type regions means that the solution is not the simple parabolic funicular form that had until recently been assumed to be optimal for this problem.)

Figure 5a shows the ‘optimal’ form obtained when using discrete layout optimization with the rigid bar approach; a 20×20 grid was in this case used for sake of visual clarity. A similar result was recently obtained for this problem by Jiang et al. (2018), who suggested that this indicated that the rigid bar approach is ‘flawed’. However, based on the analysis outlined in Section 2.2, it is clear that issues will only arise if rigid bars intrude on T-type or S-type regions, or have an incompatible interaction angle in R-type regions. Here, since the optimal structure includes T-type regions, the end result shown in Fig. 5a is indeed erroneous; this appears to comprise a central funicular R-type region with geometry defined by $\theta _{P}^{\text {R}^{-}} \in [-\pi /4,\pi /4]$, spanning between two T-type regions in which the structural members are aligned at ± π/4 to the line of action of the transmissible load, and artificially braced by the presence of the zero-cost vertical rigid bars. In other words, this is precisely the form that would be expected from the preceding Mohr’s circle analysis.

Fig. 5

Example 1 (rigid bar approach): uniform load between pinned supports, where a is the discrete layout optimization result, obtained when rigid vertical bars are made available to the optimizer; b is the preliminary (unfiltered) continuum topology optimization result — note its similarity to the structure in a — and c is the final (filtered) continuum topology optimization result. Red lines indicate members in tension and blue lines indicate members in compression. Solid and dotted grey lines indicate rigid weightless bars that carry non-zero or zero axial force, respectively

Solutions from the modified SIMP continuum topology optimization approach shown in Fig. 5b and c are visually very similar to the results obtained by Fuchs and Moses (2000) (see relevant outputs in Figs. 5 and 6 of their paper). The discussion of Fuchs and Moses (2000) suggested that in their initial solution the optimal form (assumed to be a parabola) was obscured by ‘noise’ which could be removed by the application of a filter parameter η₁. Figure 5c shows, as Fuchs and Moses (2000) found, that the filtering does indeed reveal a parabolic solution. Given the comparatively coarse resolution of the mesh used in this study, this solution is almost indistinguishable from the true optimal form, which was actually shown by Tyas et al. (2011) to differ from a simple parabola and, furthermore, be non-funicular. However, note that the span-to-height ratio of the parabola in Fig. 5c is somewhat larger than the span-to-height ratio of the true optimal pin-jointed structure, so this is not the same solution. A numerical representation of this form is shown in Fig. 4c. Note also that the use of a filter causes the compliance to rise markedly, from 3.3285 to 5.0433. Also, if the variable thickness problem is instead considered (where penalization factor p = 1 for all iterations), a compliance of 3.2918 is obtained, which is within 1.1% of the solution shown in Fig. 5b. This will be discussed further in Section 3.3.

3.2 Example 2 - Cantilever subject to uniform load

Figure 6a summarizes the set up for the next numerical problem considered. Instead of the pinned point supports of Example 1, here a fixed line support occupies one third of the vertical extent of the design domain, positioned symmetrically about the horizontal centre-line. Also, instead of a point load applied at the right edge of the design domain, here a uniformly distributed load is applied.

Fig. 6

Example 2 (migrating load approach): cantilever subject to uniform load, where a specifies the design problem, b shows transmissible load trajectories and the discrete layout optimization result, and c shows the resulting optimal structure and the final positions of the loads, which matches the analytical solution derived in Appendix 2. Red lines indicate members in tension and blue lines indicate members in compression

Figure 6b and c show the result for the migrating load formulation. Here, the optimal structural form is closely related to the optimal Michell cantilever problem first studied by Chan (1962); a more detailed overview of the literature relating to this problem is provided in Appendix 2. The standard analytical solution for the Michell cantilever assumes that a single point load is to be transmitted to the fixed line support located at the bisector to the support. It turns out that a very similar solution is also applicable to the problem of the uniformly distributed transmissible load, where individual Michell cantilevers are superimposed to carry increments of the distributed load. An analytical solution of this problem is presented in Appendix 2; the material volume for the numerical solution shown in Fig. 6c is within 0.12% of our analytical result.

The result of the layout optimization obtained using the rigid bar formulation is shown in Fig. 7a. It is clear that, without the presence of the rigid bars, which artificially strengthen the structure along each vertical line, this solution would be unstable. This highlights the fundamental problem of the rigid bar approach. The rigid bars that were introduced into the problem definition to facilitate transmission of the external load(s) onto the structure are now inadvertently and inadmissibly serving as load bearing members (see Fig. 7a).

Fig. 7

Example 2 (rigid bar approach): cantilever subject to uniform load, where a is the result of discrete layout optimization with rigid vertical bars made available to the optimizer, b is a preliminary (unfiltered) continuum topology optimization result — note that this is qualitative similar to the structure in a — and c is the final (filtered) continuum topology optimization result. Red lines indicate members in tension and blue lines indicate members in compression. Solid and dotted grey lines indicate rigid weightless bars that carry non-zero or zero axial force, respectively

Figure 7b shows an equivalent result obtained using the modified SIMP topology optimization approach. As with the previous example, the initial, unfiltered, continuum solution is qualitatively similar in form to the discrete solution in Fig. 7a. Application of the filter employed by Fuchs and Moses (2000) results in the form shown in Fig. 7c, which bears little resemblance to the optimal form shown in Fig. 6c. The use of the filter causes the compliance to rise even more markedly this time, from 23.5161 to 116.3119. Finally, note that if the variable thickness problem is instead considered (where penalization factor p = 1 for all iterations), a compliance of 23.4901 is obtained, which is within 0.11% of the solution shown in Fig. 7b.

3.3 Commentary

The examples presented in Sections 3.1 and 3.2 clearly follow from the Mohr’s circle analysis, and indicate that, when the optimal form comprises curvilinear T-type structural regions, the rigid bar approach will produce structurally illogical forms that are artificially strengthened by cost-free rigid bars. Comparison of the discrete and continuum rigid bar ‘optimal structures’ suggests that the unfiltered continuum solution does not, in fact, comprise the correct solution over-written by noise as suggested by Fuchs and Moses (2000). Instead, the unfiltered structure is the correct solution to a different problem, one that in most circumstances does not correctly reflect the intent of the user wishing to apply transmissible loads. Filtering the results of Example 1 does lead to a structure (Fig. 5c) that broadly resembles the true optimal form (Fig. 4c). This is likely to be due to the fact that the T-type regions in the optimal structure are limited in extent. However, in the case of Example 2, the filtered result (Fig. 7c) bears little resemblance to the true optimal form (Fig. 6c).

The iterative numerical technique used by Fuchs and Moses (2000) implements what Sigmund and Petersson (1998) refer to as a continuation method. A typical continuation method starts by solving an unpenalized and, typically, convex problem (i.e. the problem with penalization factor p = 1) and then performs successive gradient-based optimizations of (non-convex) problems while gradually increasing the value of the penalization factor. This is done in an attempt to ensure that the local solution of the penalized problem is situated not very far from the global solution of the unpenalized problem (Rozvany 2009). However, this approach is not guaranteed to provide satisfactory solutions (Stolpe and Svanberg 2001) and different continuation schemes may lead to completely different results (Li and Khandelwal 2015). Fuchs and Moses (2000) used a continuation method which starts with p = 0.5 instead of p = 1. Our numerical results suggest that their procedure ends up increasing the compliance of the structure in Example 1 by 52% (cf. Fig. 5b vs c) and the structure in Example 2 by 395% (cf. Fig. 7b vs c). Therefore, the solutions obtained are not in any sense ‘close’ to the solutions of the original problems with p = 0.5, nor to the solutions obtained with p = 1 (i.e. the variable thickness problem); instead, such ‘filtering’ actually drives the solutions to fundamentally different structural forms. This also suggests that ‘filtering’ should be used with caution since although qualitatively reasonable solutions can sometimes be obtained (e.g. Fig. 5c), this will not always be the case (e.g. Fig. 7c).

We emphasize that these issues only arise in the case of rigid bars interacting with a curvilinear T-type structure. In the case of funicular structures, typically residing within R-type regions, these issues do not arise since the structures comprise entirely of line or surface elements. This is because, in R-type regions, external loads are resisted through internal axial forces only, and equilibrium dictates that the structural members cannot be co-axial with the line of action of the transmissible loads.¹ The virtual rigid bars thus never form part of the real load carrying structure.

This can be demonstrated by re-visiting the problem set out in Section 3.1. Wang and Rozvany (1983b) showed that when σ⁻/σ⁺ ≥ 3, the optimal form is a funicular R-type structure. This was supported by numerical results presented by Darwich et al. (2010), which showed that as σ⁻/σ⁺ dropped below 3, T-type region Hencky nets emerged adjacent to the supports (see Fig. 4b and c for example). Thus, it should be expected that the rigid bar formulation will find the correct funicular structure for σ⁻/σ⁺ ≥ 3, with inadmissible, artificially strengthened ‘structures’ obtained for lower values. The results presented in Fig. 8 show this to be the case.

Fig. 8

Example 1 (rigid bar approach): uniform load between pinned supports, where a is the (correct) funicular solution when σ⁻/σ⁺ = 3.33, b the result when small parts of the true optimal structure become non-funicular σ⁻/σ⁺ = 2.00 and c the result when the true optimal structure is only funicular around midspan, σ⁻/σ⁺ = 1.00. Here σ⁻ and σ⁺ represent compressive and tensile limiting stresses, red lines indicate members in tension and blue lines indicate members in compression. Solid and dotted grey lines indicate rigid weightless bars that carry non-zero or zero axial force, respectively

It is worth noting that, while (as explained in Section 2.2) the rigid bar approach is not generally compatible with regions where ‘curvilinear’ T-type regions exist, there is one special T-type geometry that is compatible with the rigid bar formulation. For equal compressive and tensile stresses, (9) shows that the rigid bar formulation will be admissible when the true optimal form comprises a rectilinear net oriented at ± 45^∘ to the line of action of the applied load. In the cantilever example, such a region exists in the triangular area immediately adjacent to the vertical support line; the rigid bar approach does indeed find the correct layout in this region (see Fig. 7a).

4 Comparison of the mathematical formulations for the rigid bar and migrating load approaches

Having demonstrated the differences between the rigid bar and migrating load approaches via Mohr’s circle analyses, illustrated via the use of numerical examples, we now investigate differences in the mathematical formulations of the two approaches.

4.1 Use of duality theory to determine the difference between migrating load and rigid bar approaches

Consider a planar design domain comprising n nodes and m potential members, and let l_i denote member lengths, $q_{i}^{+}$ and $q_{i}^{-}$ tensile and compressive member forces, and $\sigma _{i}^{+}$ and $\sigma _{i}^{-}$ tensile and compressive allowable member stresses. For sake of simplicity, noting that both Example 1 and Example 2 are planar problems featuring strictly vertical downward, uniformly distributed, transmissible loads, we follow Darwich et al. (2010) and state a simplified equilibrium-based LP transmissible loads formulation (migrating load approach) in the form

$$ \underset{\mathbf{q},\tilde{\mathbf{f}}}{\min}\qquad\qquad\qquad V = \mathbf{c}^{T}\mathbf{q} , $$

(10a)

subject to:

$$ \begin{array}{@{}rcl@{}} \qquad\qquad\quad\quad \mathbf{B}_{x}\mathbf{q} &=& \mathbf{0} , \quad \mathbf{B}_{y}\mathbf{q} - \tilde{\mathbf{f}}_{y} = \mathbf{0} ; \end{array} $$

(10b)

$$ \begin{array}{@{}rcl@{}} \mathbf{H}\tilde{\mathbf{f}}_{y} &=& \hat{f}\mathbf{1}; \end{array} $$

(10c)

$$ \begin{array}{@{}rcl@{}} \mathbf{q} &\geq& \mathbf{0}; \end{array} $$

(10d)

$$ \begin{array}{@{}rcl@{}} \tilde{\mathbf{f}}_{y} &\geq& \mathbf{0} ; \end{array} $$

(10e)

where $\mathbf {c}^{\text {T}}=\left (l_{1}/\sigma _{1}^{+},-l_{1}/\sigma _{1}^{-},\dots ,l_{m}/\sigma _{m}^{+},-l_{m}/\sigma _{m}^{-} \right )$, $\mathbf {q}^{\text {T}}=\left (q_{1}^{+}, -q_{1}^{-},\dots ,q_{m}^{+},-q_{m}^{-} \right )$, and $\mathbf {B}=\left (\mathbf {B}_{x}^{\text {T}} \mathbf {B}_{y}^{\text {T}}\right )^{\text {T}}$ is a suitable (2n × 2m) equilibrium matrix containing direction cosines. The components of the vertical nodal loads vector $\tilde {\mathbf {f}}_{y}^{\text {T}}=\left (\tilde {f}_{1}^{y},\dots ,\tilde {f}_{n}^{y} \right )$, together with components of q, are LP variables (2m + n variables in total). The transmissibility of the uniformly distributed vertical load with magnitude $\hat {f}$, where $\hat {f}>0$, is achieved by applying it to p groups of nodal load components corresponding to p vertical columns of nodes in the nodal grid. This is achieved by including p additional constraints (10c) in the formulation, with elements of binary matrix H (of dimensions p × n) specifying which nodal loads are affected by which transmissible loads. The non-zero components of $\tilde {\mathbf {f}}_{y}$ must also satisfy inequality constraints (10e) to ensure that nodal loads always act in the same direction as the external load, thereby ensuring that loads are transmitted as intended.

Now, LP duality principles can be used to state the dual formulation of (10b) as follows:

$$ \underset{\mathbf{u},\mathbf{u}_{*}}{\max} \qquad\qquad\qquad W = \hat{f}\mathbf{1}^{\text{T}}\mathbf{u}_{*} , $$

(11a)

subject to:

$$ \begin{array}{@{}rcl@{}} \qquad\qquad\qquad\quad \mathbf{B}^{\text{T}}\mathbf{u} &\leq& \mathbf{c}; \end{array} $$

(11b)

$$ \begin{array}{@{}rcl@{}} \mathbf{u}_{y} &\geq& \mathbf{H}^{\text{T}}\mathbf{u}_{*}; \end{array} $$

(11c)

where $\mathbf {u^{T}}=\left (\mathbf {u}_{x}^{\text {T}} \mathbf {u}_{y}^{\text {T}}\right )=\left ({u_{1}^{x}},\dots ,{u_{n}^{x}},{u_{1}^{y}},\dots ,{u_{n}^{y}}\right )$ are the virtual displacements, u_∗ is the vector of p additional dual variables associated with constraints (10c) and W is the virtual work done by the transmissible loads. Constraint (11c) stipulates that vertical displacements in a column of nodes must be greater or equal to the component of u_∗ corresponding to this column. Thus, components of u_∗ are the minimum vertical displacements in each vertical column of nodes.

The inequality sign within the dual constraint (11c) is obtained when performing the dual transformation due to the presence of primal constraint (10e), that ensures the associated primal variables $\tilde {\mathbf {f}}_{y}$ are non-negative. Alternatively, if these constraints were omitted from the formulation, then primal variables $\tilde {\mathbf {f}}_{y}$ would become unrestricted and inequality constraint (11c) would become the following equality constraint

$$ \mathbf{u}_{y} = \mathbf{H}^{\text{T}}\mathbf{u}_{*} , $$

(12)

which has the effect of eliminating the vertical strain in every vertical column of nodes (by ensuring the vertical virtual displacements of each node in a column are identical). Equation (12) is therefore key to the mathematical basis of the rigid bar approach. If constraint (10e) is removed, the migrating load and rigid bar formulations become identical. Hence, the only difference between the two approaches lies in inequality (10e), which ensures that nodal loads are acting in the same direction as the external transmissible load.

Note that in the interests of clarity, only 2D vertical downward transmissible loads are treated by (10b). However, the migrating load approach presented, and the observations made in relation to inequality (10e), are more generally applicable (e.g. to 3D cases and/or cases involving transmissible loads in arbitrary directions).

4.2 Use of Lagrangian function to determine the difference between the migrating load and rigid bar approaches

The findings of Section 4.1 were obtained for a discrete layout optimization problem; however, they also apply to the continuous topology optimization problem. To demonstrate this, we consider the formulation used in Fuchs and Moses (2000)² and Yang et al. (2005). The compliance minimization problem with transmissible loads is stated therein as:

$$ \begin{array}{@{}rcl@{}} \underset{\rho}{\max} \underset{p_{im}}{\max} \underset{u}{\min} \left\{ \left( \mathbf{u}'\mathbf{K}\mathbf{u}-\mathbf{p}'\mathbf{u} \right) | \sum\limits_{j} \rho_{j}V_{j}=\rho_{0}V;\right. \\ \left.\sum\limits_{m\in\mathbf{M}_{i}} p_{im}=p_{i} , i\in\mathbf{I} \right\} , \end{array} $$

(13)

where K is the stiffness matrix, u the displacement vector, p the applied loads vector, ρ_j and V_j the density and the volume of element j, ρ₀ the parameter which controls the amount of material available for the design, V the total volume of the design domain, p_i the transmissible load i ∈I, and I the set of indices of all such loads. Each p_i further splits into a group of loads p_im acting on nodes located along the line of action of p_i, where m ∈M_i, and M_i is the set of indices of loads p_im constituting p_i.

Equation (13) leads to the following Lagrangian function:

$$ \begin{array}{@{}rcl@{}} L(\pmb{\rho},p_{im},\mathbf{u},\lambda,\mu_{i}) &=&\left( \mathbf{u}'\mathbf{K}\mathbf{u}-\mathbf{p}'\mathbf{u} \right) -\lambda\left( \rho_{j} V_{j}-\rho_{0} V \right) \\ &&-\sum\limits_{i\in \mathbf{I}}\mu_{i}\left( \sum\limits_{m\in\mathbf{M}_{i}} p_{im}-p_{i} \right) , \end{array} $$

(14)

The stationarity of the Lagrangian function (14) with respect to p_im necessitates that

$$ u_{im}-\mu_{i}=0 ,\quad m\in \mathbf{M}_{i} , $$

(15)

where u_im are the displacements produced by p_im. Equation (15) means that displacements of all nodes along the line of action of transmissible load take on the same value. Based on this observation, Fuchs and Moses (2000) suggested that ‘one could assume the existence of infinity stiff axial elements of zero mass along this line’.

The findings in Section 4.1 suggest that it is also important to control the sign of the nodal loads p_im, to ensure that p_imp_i ≥ 0. A variation on the formulation proposed by Fuchs and Moses (2000) that incorporates the appropriate constraints can be written in the form:

$$ \begin{array}{@{}rcl@{}} \underset{\rho}{\max} \underset{p_{im}}{\max} \underset{u}{\min} \left\{ \left( \mathbf{u}'\mathbf{K}\mathbf{u}-\mathbf{p}'\mathbf{u} \right) | \sum\limits_{j} \rho_{j}V_{j}=\rho_{0}V;\right. \\\left. p_{im}p_{i}\geq0 , m\in\mathbf{M}_{i}; \sum\limits_{m\in\mathbf{M}_{i}} p_{im}=p_{i} , i\in\mathbf{I} \right\} , \end{array} $$

(16)

with the corresponding Lagrangian function given by

$$ \begin{array}{@{}rcl@{}} L(\pmb{\rho},p_{im},\mathbf{u},\lambda,\mu_{i},\xi_{im}) &=&\left( \mathbf{u}'\mathbf{K}\mathbf{u}-\mathbf{p}'\mathbf{u} \right) -\lambda\left( \rho_{j} V_{j}-\rho_{0} V \right) \\ && -\sum\limits_{i\in \mathbf{I}}\mu_{i}\left( \sum\limits_{m\in\mathbf{M}_{i}} p_{im}-p_{i} \right)\\&& -\sum\limits_{i\in \mathbf{I},m\in\mathbf{M}_{i}} \xi_{im}(p_{im}p_{i}-\phi_{im}) , \end{array} $$

(17)

where ϕ_im are slack variables added to satisfy inequality constraints in (16). Equating the derivative of (17) with respect to p_im to zero gives:

$$ u_{im}-\mu_{i}-\xi_{im}p_{i}=0 ,\quad m\in\mathbf{M}_{i} . $$

(18)

Clearly, a slack variable, equal to ξ_imp_i, has now been added between μ_i and u_im, and displacements u_im along the line of action of transmissible load p_i are generally not all the same. Thus, (18) is, essentially, a component-wise equivalent of (11c), which indicates that optimization problem (16) now describes the migrating load, rather than the rigid bar, approach. This confirms the controlling influence of the constraint that ensures the partial load variables must all have the same sign, i.e. terms p_imp_i ≥ 0 in this case.

5 Conclusions

Two approaches to modelling load transmission through a design domain to the optimal point of application in a structure have been considered. It has been demonstrated that there is a fundamental difference between the rigid bar (constrained displacement) and equilibrium (migrating load) approaches. A simple Mohr’s circle of strain analysis has demonstrated the limitations of the rigid bar approach, and shown that it is only suitable for use when the actual optimal structure is either a funicular, or a rectilinear net oriented at a specific angle to the line of action of the applied loads.

Our numerical examples demonstrate that, in general, the rigid bar approach is prone to generating physically illogical forms, with the ‘optimal’ structure being artificially strengthened by the presence of zero-cost rigid bars that may unintentionally form part of the load carrying structure. The use of filtering methods, commonly used in continuum topology optimization, seems to exacerbate the issue. The rigid bar approach with filtering has been shown to converge to very different structural forms from the true optimal solutions, with differences in topology accompanied by large increases in compliance.

Conversely, the migrating load approach does not suffer from this limitation and produces numerical results that match known optimal forms. We have also shown that the mathematical formulations for the migrating load and rigid bar formulations differ only in one small but important respect; this is that the rigid bar formulation omits constraints ensuring that all nodal loads along the line of action of a transmissible load are of the same sign.

In summary, it is shown that the rigid bar approach generally fails to identify correct optimal structural forms and should therefore be used with extreme caution.

Appendices

Appendix 1. SIMP-based rigid bar transmissible load topology optimization formulation

The continuum topology optimization formulation used in this paper follows that presented by Sigmund (2001), and can be written as follows:

$$ \underset{\mathbf{\rho}}{\min}\qquad\qquad\quad C = \mathbf{U}^{T}\mathbf{K}\mathbf{U} = \sum\limits_{e=1}^{N} (\rho_{e})^{p}\mathbf{u}_{e}^{T} \mathbf{k}_{0}\mathbf{u}_{e} $$

(19a)

subject to:

$$ \begin{array}{@{}rcl@{}} \qquad\qquad\quad V(\mathbf{\rho})& = &fV_{0}; \end{array} $$

(19b)

$$ \begin{array}{@{}rcl@{}} \mathbf{K}\mathbf{U}& =& \mathbf{F}; \end{array} $$

(19c)

$$ \begin{array}{@{}rcl@{}} 0&<&\mathbf{\rho}_{\min}\leq\mathbf{\rho}\leq\mathbf{1}; \end{array} $$

(19d)

where C is the compliance of the structure, U and F are respectively global displacement and force vectors, K is the global stiffness matrix, and u_e and k₀ are respectively the element displacement vector and stiffness matrix. Also ρ is a vector containing density variables, $\rho _{\min \limits }$ is a vector of minimum relative densities (non-zero to avoid singularities), N is the number of elements used to discretize the design domain, p is the penalization power (typically p = 3) and V (ρ) and V₀ are respectively the volumes of the structure and the design domain. Finally, f is the prescribed volume fraction.

The sensitivity of the objective function can be written as:

$$ \frac{\partial C}{\partial \rho_{e}}=p\rho_{e}^{p-1}\mathbf{u}_{e}^{T} \mathbf{k}_{0}\mathbf{u}_{e} $$

(20)

This is used in the variable update scheme (for further details, see Sigmund 2001).

To apply transmissible loads via the rigid bar approach, displacement constraints are applied to limit displacements in the relevant direction (i.e. here in the y direction). Therefore, (19c) needs to be modified to:

$$ \begin{bmatrix} \mathbf{K}& \overline{\mathbf{K}}\\ \overline{\mathbf{K}} & \mathbf{0} \end{bmatrix} \begin{bmatrix} \mathbf{U}&\\\overline{\mathbf{U}} \end{bmatrix} = \begin{bmatrix} \mathbf{F}&\\\mathbf{0} \end{bmatrix} $$

(21)

where $\overline {\mathbf {K}}$ is a matrix containing information on the degrees of freedom to be constrained and $\overline {\mathbf {U}}$ is a supplementary displacement vector.

Since (21) only affects the finite element analysis, the variable update scheme remains unchanged. Further details of how the displacement constraints are applied can be found in Houlsby et al. (2000).

Appendix 2. A symmetric Michell cantilever that carries a uniformly distributed load along its centre axis

A symmetric cantilever for a point load applied on the bisector of a fixed line support is one of the most recognizable Michell structures. It was seemingly first described by Chan (1962), based on earlier work on an equivalent rigid placticity problem (Hill 1998, Chapter VI, Section 7). Extensions of the problem were considered by Chan (1967), Lewiński et al. (1994), Graczykowski and Lewiński (2006a), Graczykowski and Lewiński (2006b), Graczykowski and Lewiński (2007a), and Graczykowski and Lewiński (2007b). A basic solution comprises three kinds of T-type regions (see Fig. 9).

• I A triangular region near the support (shaded in Fig. 9) contains a grid of mutually orthogonal straight members. If the length of the support is denoted by h, the distance l from the support to the tip of the triangular region O is given by l = h/2. If the external point force was placed within the triangle, i.e. for L ≤ l, the optimal solution reduces simply to a strut and a tie aligned with the lines of principal strains to transfer the load to the support line.

• II Two sectorial regions of orthogonal straight lines and circular arcs are placed symmetrically along the outer sides of the triangle. The radius of the relevant circular arcs R is found as $R=h/\sqrt {2}$. The angle of each sector is denoted 𝜃; 𝜃 > 0 as long as L > l. If the cantilever is to remain in the right half-plane from the line support, we must assume that 𝜃 ≤ 3π/4.

• III The remaining fourth T-type region features a curvilinear Hencky net that can be built from two outer circular arcs intersecting at point O by using Riemann’s method for solving hyperbolic PDEs (see Chan 1962 for detailed derivations).

Fig. 9

Symmetric Michell cantilever for a point load on the bisector to a fixed line support

Angles 𝜃 are related to the cantilever length L via the following implicit formula

$$ \frac{L}{h}=\frac{1}{2}I_{0}(2\theta)+\sum\limits_{n=0}^{\infty}(-1)^{n}I_{2n+1}(2\theta) , $$

(22)

where I_k(x) is the modified Bessel function of the first kind (Hemp 1973, eqn. (4.120)). Length L is a monotonically increasing function of 𝜃, so for cantilevers contained in the right half-plane from the support, the maximum possible value of $L=L_{\max \limits }$ corresponds to the angle 𝜃 = 3π/4 and is given by $L_{\max \limits }\approx 23.0132h$. A more complex layout for a cantilever is needed for lengths $L>L_{\max \limits }$ (see Lewiński et al. 1994). Thus, for the sake of brevity, we will here always assume that our $L\le L_{\max \limits }$.

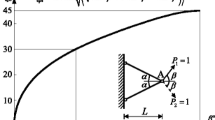
The volume of such symmetric cantilevers is given by

$$ V_{F}=\frac{Fh}{\sigma}\left( I_{0}(2\theta) + 2\theta I_{*}(2\theta) \right) , $$

(23)

where I_∗(2𝜃) = I₀(2𝜃) + I₁(2𝜃), F is the magnitude of the point load and σ is the maximum allowable stress (Hemp 1973, eqn. (4.123)). For example, for a cantilever with L = 3h, one uses (22) to find that 𝜃 ≈ 1.11156 and then (23) gives V_F ≈ 12.9649Fh/σ. This specific layout was considered by Gilbert et al. (2005), who employed large scale numerical layout optimization to obtain V_F ≈ 12.978Fh/σ, which is within 0.1% of the exact value.

Suppose now that, just like in Section 3.2, a uniformly distributed load with intensity w per unit length is applied to the entire centre axis from the support to the point L. The construction of an appropriate solution can be simplified greatly by noticing that the symmetric Michell cantilever is an example of a statically determined structure, in the sense that the stress field in this case is not coupled to the virtual displacement field (Hill 1998, p. 131). In particular, this implies that one can superimpose an infinite number of point load cantilevers for incremental components of the distributed load and determine the volume of the resulting structure directly.

Let us first consider the case when L ≤ l. The whole structure in this case is contained in the shaded triangular region I. If the total distributed force is denoted as F(L) = wL, we have for the infinitesimal force increment

$$ \frac{\partial F}{\partial L}=w . $$

(24)

This force increment is transferred to the support by a combination of a mutually orthogonal tie and strut, inclined at angles ∓ π/4 to the centre axis, respectively. The lengths of the tie and the strut would be $\sqrt {2}L$; hence, the corresponding volume increment can be written as

$$ \frac{\partial V_{1}}{\partial L} = \frac{2wL}{\sigma} ,\! \quad\text{so}\!\quad V_{1}(L) = \frac{wL^{2}}{\sigma} ,\! \quad\text{where}\quad L\!\le\! l . $$

(25)

The volume in the case when L > l would be a combination

$$ V(L)=V_{1}(l)+V_{2}(L) , $$

(26)

with V₁(l) = wh²/4σ. The term V₂(L) represents the combined contribution from all the symmetric point load cantilevers for the infinitesimal increments of distributed load for all L > l. To express V₂(L) analytically, we note that (22) implies that

$$ \frac{\partial L}{\partial\theta}=h I_{*}(2\theta) , $$

(27)

with the key facts underlying this identity summarized e.g. in Appendix A of Tyas et al. (2011). We also note that since every increment of the distributed load is supported by, effectively, a symmetric cantilever for a point load, we can use (23) to write

$$ \frac{\partial V_{2}}{\partial F}=\frac{h}{\sigma} \left( I_{0}(2\theta)+2\theta I_{*}(2\theta) \right) . $$

(28)

We can now combine (24), (27) and (28) to write

$$ \begin{array}{@{}rcl@{}} \frac{\partial V_{2}}{\partial\theta} &=& \frac{\partial L}{\partial\theta}\frac{\partial F}{\partial L}\frac{\partial V_{2}}{\partial F} \\ &=& \frac{wh^{2}}{\sigma} I_{*}(2\theta) (I_{0}(2\theta)+2\theta I_{*}(2\theta)) . \end{array} $$

(29)

Therefore, we have

$$ \begin{array}{@{}rcl@{}} V_{2}(\theta) &=& \frac{wh^{2}}{\sigma}{\int}_{0}^{\theta} I_{*}(2\xi) (I_{0}(2\xi)+2\xi I_{*}(2\xi))\mathrm{d}\xi \\ &=&\frac{wh^{2}}{\sigma} \left( P_{1}+P_{2}+P_{3} \right) , \end{array} $$

(30)

within which

$$ \begin{array}{@{}rcl@{}} P_{1} \!&=&\! {\int}_{0}^{\theta}{I_{0}^{2}}(2\xi)\mathrm{d}\xi +4{\int}_{0}^{\theta}\xi I_{0}(2\xi)I_{1}(2\xi)\mathrm{d}\xi \\&=&\theta {I_{0}^{2}}(2\theta), \end{array} $$

(31)

$$ \begin{array}{@{}rcl@{}} P_{2}\!& =&\! 2{\int}_{0}^{\theta}\xi {I_{0}^{2}}(2\xi)\mathrm{d}\xi +2{\int}_{0}^{\theta}\xi {I_{1}^{2}}(2\xi)\mathrm{d}\xi\\ &=&\theta I_{0}(2\theta)I_{1}(2\theta) \end{array} $$

(32)

$$ \begin{array}{@{}rcl@{}} \text{and}\quad P_{3}\!& =&\! {\int}_{0}^{\theta}I_{0}(2\xi)I_{1}(2\xi)\mathrm{d}\xi =\frac{1}{4}{I_{0}^{2}}(2\theta)-\frac{1}{4}. \end{array} $$

(33)

Identities (31)–(33) are easily established by using integration by parts as well as the standard recurrent relationships for Bessel functions (see, e.g., Gradshteyn and Ryzhik 2007).

Overall, we combine (25), (26), (30)–(33) and express the volume of uniformly loaded cantilever as

$$ V=\frac{wh^{2}}{4\sigma}\cdot\left\{ \begin{array}{ll} 4L^{2}/h^{2} , & L\le l , \\ {I_{0}^{2}}(2\theta)+4\theta I_{0}(2\theta)I_{*}(2\theta) , & L>l . \end{array} \right. $$

(34)

Figure 10 illustrates typical volumes obtained using (34). The volumes are presented in the normalized form V/(L/h), which ensures that the total distributed force remains constant for a varying non-dimensional cantilever length L/h.

Fig. 10

Normalized volume V/(L/h) of the symmetric Michell cantilever loaded along its centre axis as the function of its length L/h

The uniformly loaded cantilever in Fig. 6c has L = 3h and, therefore, the same angle 𝜃 as in the point load case, i.e. 𝜃 ≈ 1.11156. Formula (34) then suggests that the volume of cantilever in Fig. 6c must be equal to V = 15.5459wh²/σ. For the sake of comparison, the numerically obtained volume of cantilever presented in Fig. 6c, V_num = 15.564wh²/σ, exceeds the analytical answer by just 0.12%.