1 Introduction

Materials which show rate-dependent behaviour are relevant for a large variety of engineering applications, cf. for instance [1, 2]. In order to optimise the design and reduce experimental effort, the computational modelling and simulation of crack phenomena in rate-dependent materials owe to the dramatically increasing interests. In particular, an adequate prediction of combined fracture and viscous mechanisms that depend on the time scale of loading is highly complex.

1.1 The phase-field approach to brittle fracture

For the modelling of crack phenomena, the phase-field approach to fracture has become a well-established concept. This is mainly due to its capability to predict crack patterns which are not a priori known and to simulate crack growth without the need for remeshing. Originally, the method bases upon the variational formulation of quasi-static brittle fracture of Francfort and Marigo [3], who recasted the Griffith criterion [4] for crack propagation into an energy minimisation problem. Bourdin et al. [5, 6] introduced a regularisation of the underlying energy functional. The key idea of this approach is a diffuse crack representation, i.e. the crack surface is described by an auxiliary field variable which continuously varies from the intact to the fully broken material state. In general, this auxiliary variable is referred to as phase field. In other words, cracks are no longer seen as sharp discontinuities, but approximated over a finite length scale \({\ell _\text {c}}\). Furthermore, the loss of stiffness that comes along with failure is expressed by means of a degradation function depending on the phase-field. For small \({\ell _\text {c}}\), the regularised functional \(\Gamma \)-converges against the sharp formulation [7], i.e. the fundamental theory of Griffith is recovered. Based upon the diffuse crack representation, phase-field models of brittle fracture have been proposed which include several advancements and a variety of improvements, see [8,9,10] and [11], or [12, 13], inter alia. For a detailed review on different formulations for brittle fracture at small strains, the reader is referred to [14].

1.2 Phase-field models for inelastic materials

Rate-independent material behaviour. More recently, the phase-field approach is extended to materials which undergo an irreversible deformation before failure. In the literature, different modelling approaches to ductile fracture are introduced. For a detailed comparison of several formulations in the small strain context, see [15].

A first attempt to describe brittle fracture of elasto-plastic solids is made by Duda et al. [16]. Although the inelastic permanent deformations are considered, the coupling between plastic deformation and damage is not taken into account. However, the implementation of such a coupling is crucial if typical crack phenomena which are experimentally observed in ductile materials shall be reproduced, cf. for instance [17].

For this purpose, a non-energetic ductile fracture driving force based on the accumulated plastic strain is introduced by Miehe et al. [18, 19]. Ambati et al. [17, 20] considered an enhanced degradation function which, in addition to the phase-field variable, depends on plastic deformation. This coupling resulted in a distinct plastic contribution to the fracture driving force. Yin and Kaliske [21] recently adapted a concept which is well-established in the phase-field modelling of fatigue, cf. [22,23,24], to the description of ductile failure. Instead of defining a fracture driving force related to plastic deformation, the fracture toughness is assumed to decrease with increase of inelastic deformations. In all these contributions, plastic deformations play an essential role during the evolution of the phase-field variable. However, the phase-field variable does not explicitly influence the evolution of inelastic strain.

In several other models of ductile fracture, a total energy functional is considered in which both elastically stored energy and plastic work, or plastic energy, are assumed to be affected by fracture. In other words, degradation functions decrease the respective contributions to the energy functional. Consequently, the plastic energy which actually corresponds to the dissipation due to inelastic deformation and possibly includes hardening terms, naturally becomes part of the fracture driving force which is deduced from the functional. Alessi et al. [25, 26] introduced this approach in the context of gradient damage models. Related phase-field rate-independent fracture models are proposed in [27, 28]. Based on similar considerations, and furthermore, in order to capture the influence of failure on the evolution of inelastic deformation, a yield condition which depends on the phase-field is postulated by Borden et al. [29]. To the best of the authors’ knowledge, only models which can be attributed to this group of formulations establish a two-way coupling between plastic deformation and failure.

Rate-dependent material behaviour. In recent years, few efforts have been devoted to describe the rate-dependent material fracture behaviour using the phase-field fracture models.

A phase-field fracture model for viscoelastic solids is proposed by Schänzel [19]. Considering a viscoelastic material model and a phase-field driving force based on a generalised principal stress criterion, fracture response in rubber polymers is investigated. Furthermore, the viscosity assumed for the evolution of the phase-field which originally is solely numerically motivated, cf. [9, 10], is understood as a material parameter and identified from experimental data.

Similar to the models of fracture in rate-independent materials which are based on energetic considerations, more recently, some formulations adapted to a rate-dependent response of the bulk were proposed. Shen et al. [30] presented a phase-field model for viscoelastic solids in the small strain context. Therein, the evolution equation for the viscous internal variables is assumed a priori and an energy functional which incorporates a stored viscous free energy is postulated. This term corresponds to a portion of accumulated viscous dissipation and is degraded in the same manner as equilibrium and non-equilibrium part of the elastic strain energy density. From the free energy functional, the phase-field equation is deduced by means of a microforce balance. Loew et al. [31, 32] considered a finite linear viscoelastic material model [33] which does not allow to distinguish between the non-equilibrium part of actually stored strain energy and accumulated viscous dissipation. Accordingly, a viscous contribution to the free energy is defined as the sum of the two quantities and assumed, as well as the equilibrium part of elastic strain energy, to be degraded in case of fracture. A similar finite linear viscoelastic material model was investigated by Liu et al. [34]. Yin and Kaliske [35] combined the phase-field approach to fracture with a model of finite viscoelasticity [36]. Unlike [30] or [31, 32], in [35], the effectively stored strain energy is assumed to promote crack propagation, i.e. a dissipative contribution is not accounted to the crack driving force. Recently, a similar formulation is adopted by Brighenti et al. [37] based on statistical mechanics-based equations for the response of the bulk material.

While the aforementioned models address a rate-dependent response of the bulk material, Miehe et al. [18] and later Yin et al. [38] studied a strain rate-dependent resistance against fracture combined with a rate-independent model of deformation.

1.3 Intent of the present contribution

The aim of the present contribution is to present a unified, thermodynamically consistent phase-field model for fracture of viscoelastic solids. With the central purpose of describing a two-way coupling between damage and viscous effects, we introduce an energy functional which consists of the free energy that includes a contribution which is related to viscous dissipation, and the fracture contribution. From the proposed functional, the governing equations of the phase-field and viscous internal variables are derived in a thermodynamic consistent manner. Depending on the specific choice of the degradation functions and model parameters, respectively, the modelling approaches of [30,31,32] or [35, 37] can be retained as limiting cases of the present model. With this unified formulation at hand, we study the coupling between viscous effects and fracture.

This paper proceeds as follows. In Sect. 2, the proposed phase-field model of fracture in viscoelastic material and its thermodynamic consistency proof are illustrated. Furthermore, algorithmic aspects are addressed. In Sect. 3, the analysis of coupling between viscoelastic material response and fracture by means of numerical examples is presented. The paper concludes with a short summary and an outlook regarding the future work.

Within this paper, the summation convention applies for tensor quantities. In index notation, partial derivatives are denoted by \((\circ )_{,j} = {\, \partial \circ }/{\, \partial x_j}\).

2 Derivation of the unified phase-field model

In this section, the unified phase-field description of fracture in viscoelastic materials is presented. A general energetic formulation of fracture adapted to viscoelastic materials is presented first. Subsequently, the specific constitutive assumptions for the bulk are specified and thermodynamic consistency is proven. Finally, governing equations and algorithmic aspects are provided. Without loss of generality, for the present contribution, we limit ourselves to the small strain setting and neglect inertia effects.

2.1 The energetic approach to fracture

The hypothesis of Griffith [4] defines the starting point for the phase-field approach to fracture. Dissipation due to crack growth is referred to as surface energy which is assumed to increase proportionally to newly created crack surface. In a simplified setting, crack growth is assumed to take place if the strain energy stored in the material equals the amount of surface energy corresponding to the increase in fracture surface. Following [3], this fundamental theorem can be reformulated by means of an energy functional

$$\begin{aligned} \varPi = \int \limits _{ \varOmega \backslash \varGamma } \psi \; \mathrm {d} V + \int \limits _{ \varGamma } {\mathscr {G}}_\text {c} \; \mathrm {d} A \, =: \varPi ^\text {sd}+ \varPi ^\text {fr} \end{aligned}$$
(1)

wherein \(\psi \) and \({\mathscr {G}}_\text {c}\) denote the density of free energy stored in the material and the fracture toughness, respectively. The two constituents to the functional \(\varPi \) correspond to stored free energy \(\varPi ^\text {sd}\) and dissipation due to formation of crack surface or surface energy \(\varPi ^\text {fr}\) . The domain under consideration is denoted by \(\varOmega \subset {\mathbb {R}}^N\) and \(\varGamma \subset {\mathbb {R}}^{N-1}\) is the crack surface. For sake of brevity, terms arising from external loads are omitted.

In order to make this energetic approach to fracture accessible to numerical implementation, a regularisation of the functional \(\varPi \) is introduced [5]. For this purpose, a phase-field variable

$$\begin{aligned} d: {\mathbb {R}}^N \rightarrow [0,1] \end{aligned}$$
(2)

which continuously varies from the intact (\(d=0\)) to the fully broken (\(d=1\)) material state is defined. Using this variable, the crack surface is approximated by means of the functional

$$\begin{aligned} \varGamma _{\ell _\text {c}}=\int \limits _{ \varOmega } \gamma _{\ell _\text {c}} \; \mathrm {d} V \end{aligned}$$
(3)

with the crack surface densityFootnote 1

$$\begin{aligned} \gamma _{\ell _\text {c}}= \frac{1}{4 \, {\ell _\text {c}}} \left[ d^2 + 4 \, {\ell ^2_\text {c}}\, d_{,k} \, d_{,k}\right] \, , \end{aligned}$$
(4)

cf. [9], which incorporates the regularisation parameter \({\ell _\text {c}}\). This parameter defines the characteristic width of the crack approximated by the phase-field variable d. A part from its geometrical role, it also influences the critical stress and strain and can be seen as material parameter, cf. [40]. Figure 1 illustrates the concept of diffuse crack approximation in comparison to the sharp representation. With the diffuse approximation of crack surface at hand, dissipation due to crack evolution can be expressed as

Fig. 1
figure 1

Crack representation within a domain \(\varOmega \) with boundary \(\partial \, \varOmega \). The originally sharp crack \(\varGamma \) (a) is approximated by means of the phase-field variable d which describes a smooth transition between the intact (\(d=0\)) and fully broken (\(d=1\)) material state (b). The diffuse crack can be assigned a characteristic width \(2\, \ell _{\text {c}}\)

Full size image
$$\begin{aligned} \varPi ^\text {fr}_{\ell _\text {c}}= \int \limits _{ \varOmega } \gamma _{\ell _\text {c}}\, {\mathscr {G}}_\text {c} \; \mathrm {d} V := \int \limits _{ \varOmega } \varPhi \; \mathrm {d} V \, , \end{aligned}$$
(5)

wherein \(\varPhi \) is defined as density of fracture dissipation. In order to account for the decrease of free energy due to evolution of cracks, the degradation function

$$\begin{aligned} g: [0,1] \rightarrow [0,1], \quad \, d \mapsto g(d) \end{aligned}$$
(6)

is defined which has to fulfil the conditions

$$\begin{aligned} g(d=0)=1 \quad ,\quad g(d=1)=0 \quad ,\quad \frac{\, \partial g}{\, \partial d} \le 0 \quad ,\quad \left. \frac{\, \partial g}{\, \partial d}\right| _{d=1}=0 \quad . \end{aligned}$$
(7)

Based on the degraded free energy density

$$\begin{aligned} \varPsi = g(d) \, \psi \, , \end{aligned}$$
(8)

the regularised functional of free energy is given by

$$\begin{aligned} \varPi ^\text {sd}_{\ell _\text {c}}= \int \limits _{ \varOmega } \varPsi \; \mathrm {d} V \, , \end{aligned}$$
(9)

and the regularised total energy, or pseudo-energy, functional readsFootnote 2

$$\begin{aligned} \varPi _{\ell _\text {c}}= \varPi ^\text {sd}_{\ell _\text {c}}+ \varPi ^\text {fr}_{\ell _\text {c}}= \int \limits _{ \varOmega } \varPsi + \varPhi \; \mathrm {d} V \, . \end{aligned}$$
(10)

In case of linear elasticity, it can be discussed that \(\varPi _{\ell _\text {c}}\) \(\gamma \)-converges to \(\varPi \) for \({\ell _\text {c}}\rightarrow 0\), see e.g. [41]. For \(\gamma _{\ell _\text {c}}\) according to (4) and a specific choice of the degradation function g(d), an analytical proof of \(\gamma \)-convergence can be provided, cf. [7].

Generalisation for inelastic material response. In case of an non-elastic response of the bulk material, in the total energy functional \(\varPi _{\ell _\text {c}}\), an expression for the free energy density \(\varPsi \) can be considered which adequately accounts for coupled inelastic deformations. For the description of combined fracture and viscous mechanisms, the proposed free energy density functional

$$\begin{aligned} \varPsi = g_\text {st}(d)\, \psi ^\text {st}+ \beta _\text {vi}\, g_\text {vi}(d)\, \psi ^\text {vi}\; =: \varPsi ^\text {st}+ \varPsi ^\text {vi} \end{aligned}$$
(11)

consists of two essential constituents: Naturally, the first one is the effectively stored strain energy which, in case of damage, is decreased by means of the degradation function \(g_\text {st}(d)\). In addition, a free energy contribution related to accumulated viscous dissipation is assumed. The definition of \(\psi ^\text {st}\) and \(\psi ^\text {vi}\) can take any form suitable for describing viscoelastic deformations. The specific definition considered in this work is given in Sect. 2.2. In order to keep the formulation as general as possible, similar to [29] and [30], the parameter \(\beta _\text {vi}\in [0,1]\) is introduced as a weight of the contribution related to inelastic deformation. For the viscous term, the degradation function \(g_\text {vi}(d)\) is prescribed. In contrast to e.g. [30], coincidence of \(g_\text {st}(d)\) and \(g_\text {vi}(d)\) is not a priori supposed. Therefore, the present formulation enables to account for an influence of damage on energy storage and dissipative viscous mechanisms, and vice versa, which may be not completely identical.

The free energy density contribution \(\varPsi ^\text {vi}\) in (11), related to viscous dissipation, can be interpreted as follows. Firstly, mechanical energy can be released due to the relaxation mechanisms present in the viscoelastic material, where an amount of strain energy which has been set free can convert into heat, i.e. lead to an increase in temperature. As experimental evidence has shown that resistance against failure of many rate-dependent materials decreases with temperature, see e.g. [42, 43], viscous dissipation can be assumed to promote fracture. By means of proposed \(\varPsi ^\text {vi}\), the formulation enables to capture this effect, although the thermomechanical coupling is not explicitly modelled. Secondly, micro-mechanical mechanisms which lead to viscous dissipation can directly diminish the amount of strain energy that has to be stored in the material so that crack propagation can take place. Consider, for example, rubbery polymers under tensile loading. Viscous dissipation can be attributed to relaxation, i.e. reorientation and disentanglement of chain segments. These mechanisms go along with a redistribution of loading from entangled to crosslinked polymer chains, as discussed in [19]. As a result, in case of fracture, crosslinked chains are broken, essentially. The amount of strain energy necessary for crack propagation thus is lowered compared to the case where no viscous dissipation has taken place, cf. [42] for experimental results.

Choice of the degradation functions. In the literature, the quadratic degradation function

$$\begin{aligned} g(d) = (1-k) \, (1-d)^2 + k, \end{aligned}$$
(12)

in which a small residual k is included in order to enhance numerical stability, is adopted frequently, cf. for instance [5, 9, 27, 30]. Nevertheless, several alternatives were proposed. In order to obtain a more brittle response, quartic and cubic expressions were introduced by [44] and [45]. With the same objective, [46] suggested an exponential function and [35, 38] studied a sinusoidal expression. The functions of [45] and [46] as well as the expressions proposed by [47, 48] and [49] are parametric, i.e. they include additional parameters which can be fitted to the physical behaviour of the material under consideration. The present formulation for the free energy allows to apply this concept for both the actually energy storage and dissipative mechanisms by means of \(g_\text {st}(d)\) and \(g_\text {vi}(d)\), separately.

Within the scope of this contribution, we focus on the development of the phase-field formulation rather than modelling the response of a particular material. To that end, herein, the quadratic function defined in (12) is considered for \(g_\text {st}(d)\). In Sect. 3, regarding \(g_\text {vi}(d)\), we study two limiting cases. Firstly, \(g_\text {vi}(d)= g_\text {st}(d)\) is assumed, wherein an identical influence of damage on energy storage and dissipative mechanisms is supposed. Secondly, assuming that the nature of relaxation mechanisms remains unaffected even if damage compromises the stiffness of the material, \( g_\text {vi}= 1 = \text {const}.\) is set.Footnote 3

2.2 Constitutive modelling of the bulk response

Fig. 2
figure 2

Generalised Maxwell model

Full size image

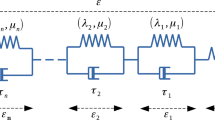
For the viscoelastic behaviour of the bulk material, a generalised Maxwell model, as depicted in Fig. 2, is adopted.

Kinematic assumptions. For the response of viscoelastic materials, often significant differences between volumetric and isochoric deformation are observed, cf. [50]. Accordingly, the strain tensor

(13)

is additively decomposed into the volumetric

(14)

and isochoric parts

(15)

Furthermore, for each non-equilibrium branch \({m} \in [1,n]\) of the generalised Maxwell element, the strain is split into a viscous portion and an elastic fraction. Descriptively, and can be interpreted as the strain of the dampers depicted in Fig. 2, while and correspond to the strain of the spring in the respective non-equilibrium branch.

Elastic strain energy density. The strain energy density \(\varPsi ^\text {st}\) which is stored in the material is additively decomposed as

(16)

where the equilibrium part is

(17)

and the non-equilibrium or over-stress contribution reads

(18)

with either contribution additively decomposed into a volumetric and isochoric fraction.Footnote 4 For both the equilibrium and non-equilibrium part, linear elasticity is assumed. Accordingly, the respective terms are given by

(19)
(20)

with \(K^\text {eq}, \, {}_mK^\text {ov}> 0\) and \(\mu ^\text {eq}, \, {}_m\mu ^\text {ov}> 0\) denoting the corresponding compression and shear moduli, respectively.Footnote 5 Note that in the above definitions, the summation convention does not apply for the index m.

Free energy contribution related to viscous dissipation. Similar to \(\varPsi ^\text {st}\), the dissipative contribution is decomposed into the volumetric and isochoric part

(21)

Assuming constant viscosities , we define

(22)

The viscous term \(\psi ^\text {vi}\) can be interpreted in analogous manner to the virtually undamaged strain energy density \(\psi ^\text {st}\): Descriptively, it can be understood as the viscous dissipation which would have been accumulated over time in the absence of damage.

2.3 Thermodynamic consistency

In order to prove that the proposed model is conform to the second law of thermodynamics, the density of dissipation power

(23)

is considered which corresponds to the difference between external stress power and rate of free energy. The Clausius–Duhem inequality

(24)

demands a locally non-negative dissipation power. Inserting the above definition of \(\varPsi \), Eq. (11), this constraint expands to

(25)

wherein \(\dot{{\mathscr {d}}}^\text {fr}\) and \({}^\text {vol}\dot{{\mathscr {d}}}^\text {vi}\), \({}^\text {iso}\dot{{\mathscr {d}}}^\text {vi}\) correspond the density of dissipation power due to crack evolution and viscous mechanisms, respectively. Standard arguments [52, 53] lead to the definition of stress

(26)

and the residual inequalities

(27)
(28)
(29)

As the elastic constants as well as \(\beta _\text {vi}\) are defined to be positive, and both \(\psi ^\text {st}\) and \(\psi ^\text {vi}\) are quadratic, together with (7)3,

$$\begin{aligned} - \left[ \frac{\partial \; g_\text {st}}{\partial \; d} \, \psi ^\text {st}+ \beta _\text {vi}\frac{\partial \; g_\text {vi}}{\partial \; d} \, \psi ^\text {vi}\right] \ge 0 \end{aligned}$$
(30)

holds, i.e. the thermodynamic conjugate to the phase-field variable is non-negative. Accordingly, constraint (27) reduces to

$$\begin{aligned} {\dot{{{d}}}} \ge 0 \, , \end{aligned}$$
(31)

i.e. irreversibility of damage. In Sect. 2.5, the fulfilment of this constraint will be addressed.

Evolution of viscous strain. With (28) and (29), the evolution equations for the viscous internal variables are obtained from

(32)
(33)

Note that, with ,

(34)

i.e. evolution of viscous strain is essentially related to the over-stress in the corresponding non-equilibrium branch. In the absence of damage, i.e. \(g_\text {st}(d=0) = g_\text {vi}(d=0)=1\), the equations resemble the classical linear-elastic assumption \(\eta \, {\dot{\alpha }} = \sigma ^\text {ov}\).

Inserting the above definitions, the residual inequalities (28) and (29) read

(35)
(36)

which is fulfilled for arbitrary due to (6)1 and if \(\beta _\text {vi}\in [0,1]\).

Remark on the definition of \(\varPsi ^\text {vi}\). With the above constitutive equations at hand, a short remark on coherency between the viscous contribution to free energy density \(\varPsi ^\text {vi}\) and the time integral of stress power \({{\mathscr {D}}}^\text {vi}\) in the damper elements of the non-equilibrium branches of the generalised Maxwell model is given, cf. Fig. 2. Classically, the damper elements are assumed to account for inelastic mechanisms and \({{\mathscr {D}}}^\text {vi}\) is referred to as density of accumulated viscous dissipation. Considering, exemplary, the volumetric response of a single non-equilibrium branch m on time t, the former reads

(37)

while the latter is given by

(38)

where denotes the volumetric over stress contribution. Note that for \(\varPsi ^\text {vi}(t)\), degradation upon time t is assumed, while the permanently degraded over stress enters accumulated viscous dissipation . Applying the mean value theorem, can be rewritten as

(39)

with \({\tilde{t}} \in [0,t]\). From (7) and (31), it follows

$$\begin{aligned} g_\text {vi}\left[ d(t)\right] \le g_\text {vi}\left[ d({\tilde{t}})\right] \end{aligned}$$
(40)

which leads, together with \(\beta _\text {vi}\in [0,1]\), to

(41)

Descriptively, \(\varPsi ^\text {vi}\) recovers a certain fraction of accumulated viscous dissipation. The fact that for \(\varPsi ^\text {vi}(t)\), in contrast to , degradation is prescribed not before current time t, does not lead to an overestimation of the respective fraction of .

2.4 Governing equations

The evolution of the phase-field variable is deduced from the total energy functional \(\varPi _{\ell _\text {c}}\) by means of the variational derivative

$$\begin{aligned} \frac{\delta \; \varPi _{\ell _\text{ c }}}{\delta \; d} = - {\eta _\text{ f }}\, {\dot{{{d}}}} \qquad \text{ with } \qquad \left. d_{,k} \, n_k\right| _{\partial \, \varOmega } \, , \end{aligned}$$
(42)

where \({\eta _\text {f}}\) is introduced as a kinetic fracture parameter for purely numerical purposes, i.e. for enhancing the stability of the solution scheme, cf. [27, 54]. The constant \({\eta _\text {f}}\) is chosen such small that its influence on the simulation results vanishes which is verified by means of a comparative study of different values.Footnote 6 Inserting the definition of \(\varPsi \) (11) into \(\varPi _{\ell _\text {c}}\), (42)\(_{1}\) takes the form

$$\begin{aligned} \frac{\partial \; g_\text{ st }}{\partial \; d} \, \psi ^\text{ st }+ \beta _\text{ vi }\, \frac{\partial \; g_\text{ vi }}{\partial \; d} \psi ^\text{ vi }+ {\mathscr {G}}_\text{ c }\left[ \frac{1}{2 \, {\ell _\text{ c }}} d - 2\, {\ell _\text{ c }}d_{,kk} \right] = - {\eta _\text{ f }}\, {\dot{{{d}}}} \end{aligned}$$
(43)

from which it becomes clear that, depending on the specific choice of \(\beta _\text {vi}\) and \(g_\text {vi}\), fracture is driven by stored strain energy and the free energy contribution related to a portion of accumulated viscous dissipation. Note that for \(g_\text {vi}(d)=g_\text {st}(d)\), the phase-field equation resembles the formulation of [30], while the assumptions on the fracture driving force of [31] and [35] are preserved for \(g_\text {vi}(d)=g_\text {st}(d)\) and \(\beta _\text {vi}=1\) or \(\beta _\text {vi}=0\), respectively. The governing differential equations of the proposed model are summarised in Table 1.

Table 1 Governing differential equations for the present model: Balance of linear momentum (a), phase-field equation (b) and evolution equations for the viscous internal variables (c), (d). Without loss of generality, volume forces are neglected in (a). In (c) and (d), the relaxation times View full size image and View full size image, respectively, are introduced
Full size table

2.5 Algorithmic aspects

Weak forms of the governing equations. For the derivation of the weak forms of balance of linear momentum and phase-field equation, the test functions and \(\delta \,c\in {\mathbb {W}}_c\) are defined with

(44)

Therein, \({\mathbb {H}}^1\) is the Sobolev space of functions possessing square integrable derivatives and \(\varOmega _{u_j}\) denotes the part of the boundary where the displacement \({\bar{u}}_j\) is prescribed, cf. [55]. Then, (a) and (b) from Table 1 are multiplied by and \(\delta \,c\), respectively. Integration by parts and making use of the divergence theorem yields

(45)
(46)

where \({\bar{t}}_j\) denotes the traction vector given on \(\partial \, \varOmega _{t_j}\) with \(\partial \, \varOmega _{t_j} \cup \partial \, \varOmega _{u_j} = \partial \, \varOmega \) and \(\partial \, \varOmega _{t_j} \cap \partial \, \varOmega _{u_j} = \varnothing \), and \(n_{k}\) is the outward-pointing unit normal vector on \(\partial \varOmega \). Time discrete forms of (46) and the evolution equations (c) and (d) from Table 1 are obtained by approximating the respective rates using an Euler backward scheme. For spatial discretization, Galerkin’s method is applied. Then, the discretized equations are implemented into a standard finite element framework.

Irreversibility of fracture. In order to guarantee irreversibility of fracture, we follow the approach of [10, 56] and apply Dirichlet boundary conditions to the phase-field on all nodes

$$\begin{aligned} x_{j}^\text {irrBC}\in \left\{ x_j \in \varOmega \; \left| \; \exists \, \tau \in [0,t] : d(x_j,\tau ) \ge d_\text {crit} \right. \right\} \end{aligned}$$
(47)

where the phase-field variable has reached a critical value \(d_\text {crit}\):

$$\begin{aligned} d(x_{j}^\text{ irrBC}) {\mathop {=}\limits ^{!}} 1 \; \forall \; x_{j}^\text{ irrBC }\, . \end{aligned}$$
(48)

Alternatively, in line with [9], one may introduce a history variable which comprises the maximum of virtually undamaged fracture driving force which has occurred and consider a phase-field equation which is altered accordingly. In contrast to the former approach for crack irreversibility, the latter enables to fulfil constraint (31) exactly, see [9]. However, it has the important disadvantage that it leads to an overestimation of crack surface, cf. [41]. Therefore, we adopt (48) and set \(d_\text {crit} = 0.97\) unless stated differently.

Staggered solution strategy. Due to its robustness, the staggered solution strategy widely spread in the context of phase-field modelling, cf. [9, 14], is adapted. For every increment, initially, the phase-field variable is frozen and the update of the displacement field is determined from the balance of linear momentum. Subsequently, the evolution of phase-field is evaluated assuming constant displacements. In order to avoid inaccuracy of the numerically determined solution due the decoupled approach, multiple staggered iterations are performed at each increment and a convergence criterion for the staggered scheme is established based on the maximum change of the nodal degrees of freedom. The time step is adaptively controlled by means of a heuristic method.

3 Numerical examples

In this section, numerical examples are presented in order to analyse the fundamental principles of the present model and to discuss the consequences of different modelling assumptions. Firstly, the local response of the material is studied with a focus on the coupling between viscous mechanisms and damage. Subsequently, crack propagation within a domain where stress localisation is triggered by a preexisting notch is considered. While the presented examples can serve for qualitative verification and a better understanding of the coupling between fracture and rate-dependent response of the bulk material, the comparison with experimental results goes beyond the scope of this publication.

For all the numerical simulations, a two-dimensional setting is considered. Plane-strain conditions are assumed. Unless stated differently, the kinetic fracture parameter \({\eta _\text {f}}\) is set to zero, i.e. no viscous regularisation of crack growth is considered.

3.1 Local response of the material under monotonic loading

Fig. 3
figure 3

Simulation setup for the investigation of the local material response

Full size image

In order to study the local material response, a homogeneous domain of unit size under tension is investigated. Displacement boundary conditions are applied as depicted in Fig. 3 which leads to spatially constant field variables within the domain under consideration. For different choices of \(g_\text {vi}\) and \(\beta _\text {vi}\), respectively, and different loading rates, the response of the material is compared.

In order to facilitate discussion, a generalised Maxwell model with only one non-equilibrium branch is considered. Identical relaxation times are assumed and \(K^\text {eq}= {}_1K^\text {ov}= {175}{\hbox {kN}/\hbox {mm}^2}\), , \({\mathscr {G}}_\text {c}={2.7}{\hbox {N}/\hbox {mm}}\), \({\ell _\text {c}}={0.5}{\hbox {mm}}\), \(k=10^{-5}\) are defined. Various strain rates \({\dot{\varepsilon }} \in [10^{-8},10] \, \text {s}^{-1}\) are investigated. In what follows, the scalars \(\sigma \), \(\varepsilon \) and \(\alpha \) denote the normal components of the respective tensor quantities in the direction of external load.

Influence of viscous dissipation on damage. With the goal to investigate the influence of the viscous contribution to the fracture driving force, we set \(g_\text {vi}= g_\text {st}\) and compare the two limiting cases \(\beta _\text {vi}\in \{0 \,; 1\}\). For a representative selection of strain rates \({\dot{\varepsilon }}\), the corresponding stress–strain curves are depicted in Fig. 4.

Fig. 4
figure 4

Influence of the viscous contribution to the fracture driving force on the rate-dependent local response of the material. Stress–strain curves for \(g_\text {vi}(d)= g_\text {st}(d)\) and \(\beta _\text {vi}=0\) (solid lines) or \(\beta _\text {vi}=1\) (dash-dotted). For \({\dot{\varepsilon }} = {1}\, \hbox {s}^{-1}\) and \({\dot{\varepsilon }} = {10^{-6}}\, \hbox {s}^{-1}\), \(\varPsi ^\text {vi}\) vanishes. Accordingly, the respective curves for \(\beta _\text {vi}=0\) and \(\beta _\text {vi}=1\) coincide

Full size image
Fig. 5
figure 5

Rate-dependency of the local material response. Accumulated viscous dissipation \({{\mathscr {D}}}^\text {vi}\) for \(g_\text {vi}(d)= g_\text {st}(d)\) and \(\beta _\text {vi}=0\). The curves for both \({\dot{\varepsilon }} = {1}\, \hbox {s}^{-1}\) and \({\dot{\varepsilon }}={10^{-6}}\hbox {s}^{-1}\) approximately coincide with the axis of abscissae. For \(g_\text {vi}(d)= g_\text {st}(d)\) and \(\beta _\text {vi}=1\) as well as for \(g_\text {vi}= 1\), qualitatively similar curves are obtained which are not depicted

Full size image
Fig. 6
figure 6

Rate dependency of the local material response. Free energy \(\Psi \) in case \(g_\text {vi}(d)= g_\text {st}(d)\) for \(\beta _\text {vi}=0\), i.e. \(\varPsi ^\text {vi}=0\), (a—solid lines) and \(\beta _\text {vi}=1\) (b—dash-dotted lines)

Full size image

Regardless of the choice of \(\beta _\text {vi}\), the overall rate-dependency of the material response coincides qualitatively. As in classical viscoelasticity, for very high strain rates, the stress–strain curves converge against the upper elastic limit corresponding to the instantaneous moduli

$$\begin{aligned} K^\text{ inst }= K^\text{ eq }+ \sum _m {}_mK^\text{ ov } \qquad \text{ and } \qquad \mu ^\text{ inst }= \mu ^\text{ eq }+ \sum _m {}_m\mu ^\text{ ov }\, , \end{aligned}$$

respectively. For low \({\dot{\varepsilon }}\), the material response likewise approaches the lower elastic limit where the contribution of the non-equilibrium branches to the resistance of the material vanishes, i.e.

$$\begin{aligned} K|_{{\dot{\varepsilon }} \rightarrow 0} = K^\text{ eq } \qquad \text{ and } \qquad \mu |_{{\dot{\varepsilon }} \rightarrow 0} = \mu ^\text{ eq }\, . \end{aligned}$$

It becomes clear from Fig. 5, almost no viscous dissipation takes places until failure for very large as well as for very low strain rates. Accordingly, for both \(\beta _\text {vi}=0\) and \(\beta _\text {vi}=1\), there is no notable viscous contribution \(\varPsi ^\text {vi}\) to the free energy. Independent of \(\beta _\text {vi}\), in the limiting cases, the respective stress–strain curves thus coincide.

For intermediate strain rates, the critical stress continuously increases with \({\dot{\varepsilon }}\), whereas the critical value of strain decreases. This phenomenon arises from the fact that the effective stiffness of the viscoelastic material under consideration is the higher, the larger the rate of strain. Accordingly, the amount of energy stored in the material at a certain level of deformation is more significant the higher \({\dot{\varepsilon }}\). In contrast, the maximum amount of free energy density which can be stored remains constant, cf. Fig. 6.

When there is a notable amount of viscous dissipation, i.e. at intermediate strain rates, the viscous contribution to the crack driving force leads to lower critical values of both stress and strain compared to the case where only elastically stored energy is assumed to promote fracture. For the material parameters under consideration, the influence of \(\beta _\text {vi}\) is not prominent. Regarding the critical stress, the relative difference between the respective values for \(\beta _\text {vi}=0\) and \(\beta _\text {vi}=1\) does not exceed 20 % for any \({\dot{\varepsilon }}\).

As the parameter \(\beta _\text {vi}\) does not explicitly enter the evolution equations of the viscous internal variables, the dependency of \(\alpha \) on \(\varepsilon \) is unaffected by the choice of \(\beta _\text {vi}\). Exemplary, an \(\alpha \)-\(\varepsilon \) curve is depicted in Fig. 8a for an intermediate strain rate and \(\beta _\text {vi}=0\).

Comparison of assumptions for the degradation function \(g_\text {vi}\). For the purpose of studying the influence of different assumptions for the degradation of the viscous contribution to the free energy, the two limiting cases \(g_\text {vi}= g_\text {st}\) with \(\beta _\text {vi}=0\) and \(g_\text {vi}= 1 = \text {const}.\) are compared. Figure 7 depicts the respective stress–strain curves. Regarding the overall rate-dependency of the material response, the above statements remain valid. For intermediate \({\dot{\varepsilon }}\), compared to \(g_\text {vi}= g_\text {st}\) with \(\beta _\text {vi}=0\), the choice of \(g_\text {vi}= 1\) leads to slightly higher values of critical stress. This effect can be understood by analysing the evolution of the viscous internal variable \(\alpha \). To this end, \(\alpha \)-\(\varepsilon \) and d-\(\varepsilon \) curves are depicted in Fig. 8 for either \(g_\text {vi}\) and a representative, intermediate \({\dot{\varepsilon }}\). For \(g_\text {vi}=g_\text {st}\), the phase-field eliminates from the evolution of viscous strain. Accordingly, the \(\alpha \)-\(\varepsilon \) curves resemble the shape which would have been obtained in classical linear viscoelasticity. The assumption \(g_\text {vi}=g_\text {st}\) thus can be seen as analogy to the hypothesis of strain equivalence which can be made within the framework of classical continuum damage models, cf. [57]. In contrast, for \(g_\text {vi}=1\), the increase in viscous strain \(\alpha \) slows down with growth of the crack phase-field variable. In what follows, this effect is discussed by means of the evolution equation for the viscous strain. Exemplary, the volumetric response is considered. For \(g_\text {vi}=1\), (c) in Table 1 takes the form

Fig. 7
figure 7

Local response of the material for different degradation functions \(g_\text {vi}\) decreasing the viscous contribution to the free energy. Stress–strain curves for \(g_\text {vi}(d)= g_\text {st}(d)\) and \(\beta _\text {vi}=0\) (solid lines) or \(g_\text {vi}= 1 = \text {const}.\) (dashed). For \({\dot{\varepsilon }} = {1}\, {\text {s}}^{-1}\) and \({\dot{\varepsilon }} = {10^{-6}} \hbox {s}^{-1}\), \(\varPsi ^\text {vi}\) vanishes. Accordingly, the respective curves for \(g_\text {vi}=g_\text {st}\) and \(g_\text {vi}= 1 = \text {const}.\) coincide

Full size image
(49)

It is evident that damage leads to an increase of the effective relaxation time which can be defined as . From a physical point of view, \(g_\text {vi}= 1\) corresponds to the assumption that the nature of the viscous mechanisms remains unaffected by fracture. For \(g_\text {vi}=1\), the activation energy of the underlying viscous relaxation processes is not supposed to decrease with damage whereas the stiffness of the material or the elastically stored energy degrade. Therefore, in this case, the characteristic time scale associated with the viscous or relaxation mechanisms is assumed to increase with damage.

In particular, when compared to the overall rate-dependency, the influence of the choice of \(g_\text {vi}\) on the response of the material has revealed to be rather small. Nevertheless, from a physical point of view, an a priori assumption of identical degradation functions \(g_\text {vi}=g_\text {st}\) may not always be straightforward. A thorough analysis which takes the specific behaviour of different materials into account can give further insight. This, however, goes beyond the scope of the present study.

Fig. 8
figure 8

Local response of the material for different degradation functions \(g_\text {vi}\) decreasing the viscous contribution to the free energy. Evolution of phase-field variable d (red) and viscous strain \(\alpha \) (solid blue) for \(g_\text {vi}(d)= g_\text {st}(d)\) and \(\beta _\text {vi}=0\) (a) or \(g_\text {vi}= 1 = \text {const}.\) (b). The blue dotted line marks the evolution of \(\varepsilon \)

Full size image

3.2 Local response of the material under temporally constant strain or stress

For viscoelastic materials, in addition to monotonically increasing loading, it is of considerable interest to study a temporally constant load as creep phenomena can occur or stress may reduce due to relaxation. Therefore, in the following, the evolution of the local response of the material when a certain level of stress or strain, respectively, is held constant is investigated. In order to account for the rate-dependency of the response, different strain or stress rates are considered during loading stage.

Fig. 9
figure 9

Boundary conditions applied for investigation of the local material response under constant external loading: Stress–time function applied for the investigation of creep (a) and strain–time function applied in order to study relaxation (b)

Full size image

Creep phenomena. In order to study creep phenomena, different stress rates \({\dot{\sigma }}\) are applied until a certain level of stress \(\sigma ^\text {ref}\) is reached which is then held constant, see Fig. 9a. Various values of maximum stress \(\sigma ^\text {ref} \in \left[ 0.2,0.3\right] {\text {kN}/{\hbox {mm}}^{2}}\) and stress rates \({\dot{\sigma }} \in \left[ 10^{-5}, 10\right] \; {\text {kN}/\text {mm}^{2}/\text {s}}\) have been investigated. As a representative example, the response for \(\sigma ^\text {ref} = {0.25}{\hbox {kN}/\hbox {mm}^{2}}\) is depicted in Fig. 10 for \(g_\text {vi}= g_\text {st}\), and \(\beta _\text {vi}\in \{0,1\}\). In order to enhance the stability of the solution scheme when it comes to creep failure, \({\eta _\text {f}}= {{10}^{-9}}{\hbox {kNs}/\hbox {mm}^{2}}\) is set.

Fig. 10
figure 10

Local response of the material under creep loading: Stress prescribed increases with different rates \({\dot{\sigma }}\) while \(t<0\) and is then held at constant value \(\sigma ^\text {ref}\), see Fig. 9a. Evolution of strain \(\varepsilon \) (a), fracture phase-field d (b) and free energy \(\varPsi \) (c) with creep time t for \(\sigma ^\text {ref} ={0.25}{\hbox {kN}/\hbox {mm}^2}\) and \(g_\text {vi}= g_\text {st}\) with \(\beta _\text {vi}=0\) (solid lines) or \(\beta _\text {vi}=1\) (dash-dotted)

Full size image

From Fig. 10, it becomes clear that for \(\sigma ^\text {ref} = {0.25}{\hbox {kN}/\hbox {mm}^{2}}\), in the absence of a viscous contribution to the fracture driving force, i.e. for \(\beta _\text {vi}=0\), the response does qualitatively coincide for all stress rates \({\dot{\sigma }}\). Regardless of the rate of stress during the loading stage (\(t<0\)), with creep time t, strain converges towards an identical, finite equilibrium level. Generally, the strain at the end of the loading stage, \(\varepsilon (t=0)\), increases with \({\dot{\sigma }}\). However, very low rates \({\dot{\sigma }} \lesssim {10}^{-3}{\hbox {kN}/\hbox {mm}^{2}/\hbox {s}}\) correspond to almost quasi-static application of load, i.e. the lower purely elastic limit case, while for \({\dot{\sigma }} \gtrsim {10^{-3}}{\hbox {kN}/\hbox {mm}^{2}/\hbox {s}}\), during the loading stage, the upper purely elastic limit is reached for which the increase in strain due to creep, \(\varepsilon (t\rightarrow \infty ) - \varepsilon (t=0)\), becomes maximal. Increase in strain due to creep goes along with a growth of strain energy density \(\varPsi ^\text {st}\) and the phase-field variable d rises accordingly. As, in case \(\beta _\text {vi}= 0\), the maximum amount of free energy \(\left. \varPsi \right| _{t\rightarrow \infty } = \left. \varPsi ^\text {st,eq}\right| _{t\rightarrow \infty }\) is not sufficient, it does not come to creep failure for any stress rate \({\dot{\sigma }}\) when \(\sigma ^\text {ref} = {0.25}{\hbox {kN}/\hbox {mm}^{2}}\). However, for larger \(\sigma ^\text {ref}\), creep failure can also be predicted in the absence of a viscous fracture driving force contribution which is not depicted here. Since, for \(\beta _\text {vi}=0\), the maximum value of fracture driving force only depends on \(\sigma ^\text {ref}\), failure then occurs for all rates \({\dot{\sigma }}\). In that case, the time which elapses until it comes to failure increases with \({\dot{\sigma }}\) as the critical amount of strain energy is reached the earlier the smaller \({\dot{\sigma }}\), cf. Fig. 10c.

In contrast to \(\beta _\text {vi}=0\), when a viscous contribution to the fracture driving force is assumed, e.g. \(\beta _\text {vi}=1\), both \(\sigma ^\text {ref}\) and \({\dot{\sigma }}\) influence if it comes to creep failure, as \(\varPsi ^\text {vi}\) decisively depends on \({\dot{\sigma }}\). In particular, for an identical maximum stress \(\sigma ^\text {ref}\) prescribed, it is possible to predict failure for higher \({\dot{\sigma }}\), only: The material response is identical for any \(\beta _\text {vi}\) in case of the lower elastic limit case, i.e. for \({\dot{\sigma }} \rightarrow 0\), and \(\beta _\text {vi}>0\) only leads to a slender increase in the equilibrium strain with respect to \(\beta _\text {vi}\) for small, finite \({\dot{\sigma }}\), since there is almost no viscous dissipation for small rates. In contrast, for higher \({\dot{\sigma }}\), there are more considerable values of \(\varPsi ^\text {vi}\). Accordingly, in the latter case, \(\varPsi ^\text {vi}\) can essentially trigger creep failure, e.g. for \({\dot{\sigma }} \ge {0.05}{\hbox {kN}/\hbox {mm}^{2}/\hbox {s}}\) in Fig. 10. As \(\varPsi ^\text {vi}\) is the greater the higher \({\dot{\sigma }}\), in contrast to \(\beta _\text {vi}=0\), for \(\beta _\text {vi}=1\), the time which elapses until failure is the smaller the higher \({\dot{\sigma }}\). If a critical value of free energy \(\varPsi \) is reached, it suddenly comes to failure. From Fig. 10c, it can be seen that the critical amount of \(\varPsi \) is identical for any \({\dot{\sigma }}\) and coincides with the value obtained for monotonically increasing load, cf. Fig. 6. It is obvious that there are smaller \(\sigma ^\text {ref}\) which are not depicted here, where failure can not be observed for any finite \({\dot{\sigma }}\) or assumption on the coupling since they do not go along with a sufficiently large amount of \(\varPsi \).

Fig. 11
figure 11

Local response of the material—stress relaxation. Strain prescribed increases with different rates \({\dot{\varepsilon }}\) while \(t<0\) and is then held at constant value \(\varepsilon ^\text {ref} = 0.002\), see Fig. 9b. Evolution of stress \(\sigma \) (a) and fracture phase-field d (b) with relaxation time t for \(g_\text {vi}= g_\text {st}\) with \(\beta _\text {vi}=0\) (solid lines) or \(\beta _\text {vi}=1\) (dash-dotted). For \({\dot{\varepsilon }} \in \{10^{-6}, 1 \} \; \text {s}^{-1}\), the solid and dash-dotted curves coincide

Full size image

Unlike the assumption on \(\beta _\text {vi}\), the choice of the degradation functions does only quantitatively influence the material behaviour which can be predicted. If, for example, in case of \(\beta _\text {vi}=0\), viscosity is not assumed to be degraded, i.e. \(g_\text {vi}=1\), this can lead to an increase of the time which elapses until it comes to creep failure with respect to \(g_\text {vi}=g_\text {st}\), since for \(g_\text {vi}=1\), the effective relaxation time grows with the phase-field variable, cf. Eq. (49).

Stress relaxation. With the goal to demonstrate the capability of the present model to adequately account for relaxation phenomena, different strain rates \({\dot{\varepsilon }}\) are applied until a certain level of strain \(\varepsilon ^\text {ref}\) is reached which is then held constant, see Fig. 9b. Various values of maximum strain \(\varepsilon ^\text {ref} \in \left[ 0.001, 0.004 \right] \) and rates \({\dot{\varepsilon }} \in \left[ 10^{-8}, 10\right] \; \text {s}^{-1}\) have been investigated. As a representative example, the response for \(\varepsilon ^\text {ref} = 0.002\) is depicted in Fig. 11 for \(g_\text {vi}= g_\text {st}\), and \(\beta _\text {vi}\in \{0,1\}\). In order to exactly fulfil constraint (31) within the scope of this analysis of the local response, the history variableFootnote 7

$$\begin{aligned} {\mathscr {H}}= \max _{\tau \in [0,t]} \left[ \psi ^\text {st}(\tau ) + \beta _\text {vi}\, \psi ^\text {vi}(\tau ) \right] \end{aligned}$$
(50)

is considered instead of irreversibility constraint (48).

Independent of the strain rate or the assumption on the fracture driving force, when strain is held constant, stress relaxes towards a certain equilibrium level while the fracture phase-field remains constant. Since the amount of damage which has been reached at \(t=0\), i.e. when relaxation begins, depends on both \({\dot{\varepsilon }}\) and \(\beta _\text {vi}\), the equilibrium stress \(\left. \sigma \right| _{t \rightarrow \infty }\) changes accordingly. As there is almost no viscous dissipation while \(\varepsilon \) increases for very high or very small \({\dot{\varepsilon }}\) and free energy \(\varPsi \) does not increase when stress relaxes, \(\left. \sigma \right| _{t \rightarrow \infty }\) becomes independent of \(\beta _\text {vi}\) for \({\dot{\varepsilon }} \rightarrow 0\) and \({\dot{\varepsilon }} \rightarrow \infty \). For \(g_\text {vi}=1\), qualitatively identical results are obtained. Compared to the reference \(g_\text {vi}=g_\text {st}\) for \(\beta _\text {vi}=0\), if \(g_\text {vi}=1\) is adopted, a slight increase in effective relaxation time with phase-field is stated, cf. Eq. (49).Footnote 8

3.3 Heterogeneous case: SENT benchmark

As a representative example for the response of non-homogeneous structure, we follow [8, 28, 31, 38], inter alia, and consider the single edge notched tension test (SENT), i.e. a notched specimen under tensile loading. For the geometry and the displacement boundary conditions which are prescribed, see Fig. 12a. In contrast to the previous section, we adopt the material parameters \(E^\text {eq}={0.327}{\; \hbox {N}/\hbox {mm}^{2}}\), \(\nu ^\text {eq} ={}^{}_{m}\nu ^\text {ov}=0.4\),

with \(K = E/(3 \, (1-2 \, \nu ))\) and \(\mu = E / (2\, (1+\nu ))\) from [58] and set \({\mathscr {G}}_\text{ c }=\text{10 }^{-3}{\text{ N }/\text{mm }}\), \({\ell _\text {c}}={0.04}{\hbox {mm}}\), \(k=10^{-4}\). For optimal computational efficiency, Isogeometric analysis combined with adaptive refinement is employed, see [59], guaranteeing a characteristic element size \(h<{\ell _\text {c}}/4\) in the vicinity of the crack. For \(\beta _\text {vi}\) and \(g_\text {vi}\), the same limiting cases are investigated as in the previous section.

Fig. 12
figure 12

SENT benchmark. Setup (a) and crack pattern (red—\(d=0\), blue—\(d=1\)) obtained as result of all the simulations (b)

Full size image

Monotonically increasing load. Similar to the local response, a monotonically increasing external displacement is investigated first. A large variety of displacement rates \({\dot{u}} \in [10^{-8}, 10] \; \hbox {mm}/\hbox {s}\) is considered.

Fig. 13
figure 13

SENT—monotonically increasing load. Force–displacement curves for \(g_\text {vi}(d)= g_\text {st}(d)\) and \(\beta _\text {vi}=0\) (solid lines) or \(\beta _\text {vi}=1\) (dash-dotted). Since the upper elastic limit is approached for very high \({\dot{u}}\), the blue solid and dash-dotted curves do almost coincide

Full size image

The same considerations observed in the previous example apply here as well. Independent of the choice of \(\beta _\text {vi}\) or \(g_\text {vi}\), qualitatively coinciding simulation results are obtained. In each case, straight crack growth from the tip of the notch towards the upper edge of the domain is predicted when a certain amount of load is reached, see Fig. 12b. The corresponding force–displacement curves are depicted in Figs. 13 and 14, respectively.

For high displacement rates \({\dot{u}} \), all the curves converge against the upper elastic limit. For very low \({\dot{u}} \), the response of the structure likewise approaches the lower limiting case where the non-equilibrium branches do not contribute to the resistance. However, crack propagation leads to finite strain rates even for \({\dot{u}} \rightarrow 0\). Therefore, in contrast to the stress–strain curves depicted in Figs. 4 and 7, a slight difference is stated between the \(F\text {-}\) curves for different \(\beta _\text {vi}\) and \(g_\text {vi}\), respectively, even if the rate of the external load approaches zero.

For intermediate displacement rates, the critical force level continuously grows with \({\dot{u}} \), whereas the displacement at failure decreases. As it has been outlined in the previous section, this effect is explained as follows. The effective stiffness of the viscoelastic material under consideration increases with the rate of strain. In contrast, the amount of fracture driving force necessary for crack growth remains constant.

The significant increase in displacement at failure with decreasing rate of external load can be interpreted as a kind of brittle-to-ductile transition: For the lower elastic limit case, the maximum displacement is more than twice as high as for the upper.

Similar to its influence on the local response of the material, for \(g_\text {vi}=g_\text {st}\), the viscous contribution to the crack driving force, i.e. the assumption of \(\beta _\text {vi}=1\), leads to a lower level of both critical force and displacement compared to \(\beta _\text {vi}=0\), see Fig. 13. In particular for intermediate \({\dot{u}}\), its influence is clearly noticeable. In contrast, the definition of \(g_\text {vi}=1\), compared with \(g_\text {vi}=g_\text {st}\) and \(\beta _\text {vi}=0\), leads to a slightly higher critical force level, see Fig. 14. However, for the specific material parameters under consideration, the differences between the response of the notched structure predicted for various modelling assumptions reveal to be not too pronounced.

Fig. 14
figure 14

SENT—monotonically increasing load. Force–displacement curves for \(g_\text {vi}(d)= g_\text {st}(d)\) and \(\beta _\text {vi}=0\) (solid lines) and for \(g_\text {vi}(d)=1\) (dashed). Since the upper elastic limit is approached for very high \({\dot{u}}\), the blue solid and dashed curves do almost coincide

Full size image

Creep. In order to study creep phenomena, different force rates \({\dot{F}}\) are applied in horizontal direction upon the right edge of domain until a certain level of froce \(F^\text {ref}\) is reached which is then held constant, cf. Fig. 9a. To enhance the stability of the solution scheme when it comes to creep failure, \({\eta _\text {f}}= {10^{-7}}{\hbox {kNs}/\hbox {mm}^{2}}\) is set. Various values of maximum force \(F^\text {ref} \in \left[ 0.2,0.3\right] {\text {kN}/{\hbox {mm}}^{2}}\) and rates \({\dot{F}} \in \left[ 10^{-10}, 10\right] \; {\hbox {kN}/\hbox {s}}\) have been investigated. As representative examples, the displacement responses of the specimen are depicted in Fig. 15 for \(F^\text {ref} \in \{0.0113, 0.012\} \, \text {kN}\) and the same three limiting cases which have been considered above.

Fig. 15
figure 15

SENT—creep. Force prescribed increases with different rates \({\dot{F}}\) while \(t<0\) and is then held at constant value \(F^\text {ref}\), cf. Fig. 9a. Displacement response for \(F^\text {ref} = 0.0113 \, \text {kN}\) (a, b) and \(F^\text {ref} = 0.012 \, \text {kN}\) (c, d) for the limiting cases \(g_\text {vi}= g_\text {st}\) with \(\beta _\text {vi}= 0\) (solid lines) or \(\beta _\text {vi}=1\) (dash-dotted) and \(g_\text {vi}=1\) (dashed). In (b), solid and dashed lines do almost coincide

Full size image

Depending on the maximum force \(F^\text {ref}\) prescribed, the simulation results can be divided into three groups. Firstly, for low \(F^\text {ref}\), there is an increase in displacement with creep time towards an identical equilibrium value for all \({\dot{F}}\) and assumptions on the coupling. This increase does not go along with crack propagation. In that case, almost no difference is stated between the results for \(g_\text {vi}= g_\text {st}\) with \(\beta _\text {vi}=0\) and \(g_\text {vi}=1\). Secondly, for intermediate \(F^\text {ref}\), this phenomenon is observed in absence of a dissipative fracture driving force contribution, only. In contrast, \(\beta _\text {vi}>0\) can trigger creep failure for sufficiently large \({\dot{F}}\), see Fig. 15a, b. Then, in terms of crack path, the result is similar to the case of strictly monotonically increasing external load. Thirdly, for high \(F^\text {ref}\), failure is observed for any assumption on the coupling between viscous mechanisms and fracture, see Fig. 15c, d. For small \({\dot{F}}\), in this case, failure can also occur while force is still increasing (\(t<0\)), whereas for higher \({\dot{F}}\), crack propagation does not start before a sufficiently large amount of creep time \(t>0\) has passed. Viscous fracture driving force then can lead to an earlier occurrence of failure. In contrast, the assumption of a non-degraded viscosity can effect a notably larger amount of time which has to elapse until it comes to crack propagation compared to \(g_\text {vi}=g_\text {st}\) for \(\beta _\text {vi}=0\).

The present numerical study demonstrates that in case of creep loads, varied assumptions on the coupling between viscous mechanisms and fracture can lead to significant differences between the predicted responses. From the comparison to experimental data, it remains to be verified which choice for the fracture driving or the degradation functions, respectively, may be most appropriate.

4 Conclusion and outlook

A unified phase-field model of fracture in viscoelastic materials is presented which enables a two-way coupling between viscous mechanisms and crack growth. For this purpose, a pseudo-energy functional is introduced which consists of the free energy and the dissipation due to crack evolution, and a contribution to the free energy that is related to viscous dissipation is defined. From the energy functional, the differential equations governing the response of the material are deduced in a thermodynamically consistent manner. The approaches of recently published models [30, 31, 35] are obtained as limiting cases.

By means of numerical examples, the consequences of different modelling assumptions on the local material response as well as on failure of a notched domain are discussed. Especially in case of strictly monotonically increasing external load, predictions are qualitatively similar and the overall rate dependency of failure is captured for all model variants, whereas quantitative differences arise, for instance regarding the critical load level. In contrast, in case of creep, the simulation result can decisively depend on the assumption made for the fracture driving force: A viscous contribution can essentially trigger failure which is not predicted for the same load level if only strain energy is assumed to drive fracture. Furthermore, in the latter case, occurrence of failure does only depend on the maximum value of force, whereas in the former, a possible influence of the rate during the application of load can also be taken into account.

Further work will focus on the comparison of model predictions and experimental data. In addition, an extension to the framework of finite viscoelasticity, cf. [36], is subject of current research. In that case, larger derivations away from the thermodynamic equilibrium path can be captured, possibly leading to a more pronounced influence of coupling between viscous dissipation and fracture.