Local density of states in a vortex at the surface of a topological insulator in a magnetic field

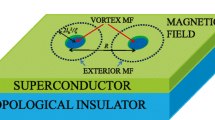
Abstract

Fermion bound states at the center of the core of a vortex in a two-dimensional superconductor are investigated by analytically solving the Bogoliubov–de Gennes equations in a magnetic field. The metallic surface states of a strong topological insulator become superconducting via proximity effect with an s-wave superconductor. Due to the magnetic field, the states undergo Landau quantization. A zero-energy Majorana state arises for the Landau level $n=0$ together with an equally spaced ($\Delta ^2_{\infty }/E_F$) sequence of fermion excitations. The spin-momentum locking due to the Rashba spin–orbit coupling is key to the formation of the Majorana state. Extending previous results in zero magnetic field, we present analytical expressions for the energy spectrum and the wave functions of the bound states in a finite magnetic field. The solutions consist of harmonic oscillator wave functions (associated Laguerre polynomials) times a function that falls off exponentially with distance $\rho$ from the core of the vortex as $\exp [-\int _0^{\rho } d\rho ' \Delta (\rho ')/v_F]$. An analytic expression for the local density of states (LDOS) for the bound states is obtained. It depends on two length scales, $1/k_F$ and the magnetic length, $l_H$, and the angular momentum index $\mu$. The particle-hole symmetry is broken in the LDOS as a consequence of the spin–orbit coupling and the chirality of the vortex. We also discuss the spin polarization of the bound states.

Appendices

Appendix A: Landau quantization

The energy levels of Hamiltonian (2) are quantized in the presence of a magnetic field. In the symmetric gauge, we have $\mathbf{A} =(H/2)(-y,x)$, so that the curl of $\mathbf{A}$ yields the magnetic field pointing in the positive z-direction. We define ${\tilde{p}}_x = p_x - (e/c)A_x = p_x + (eH/2c)y$ and ${\tilde{p}}_y = p_y - (e/c)A_y = p_x - (eH/2c)x$, so that the commutator of ${\tilde{p}}_x -i {\tilde{p}}_y$ and ${\tilde{p}}_x +i {\tilde{p}}_y$ yields

$$\begin{aligned} {[}{\tilde{p}}_x -i {\tilde{p}}_y, {\tilde{p}}_x +i {\tilde{p}}_y] = 2(|e|H/c)\hbar \ \ , \ \ \end{aligned}$$

(22)

where $e = -|e|$ and the magnetic length is given by $l_H = \sqrt{\hbar c/|e| H}$. The magnetic length diverges in zero-field and gradually decreases as the field grows. It is convenient to introduce lowering and rising operators

$$\begin{aligned} a = ({\tilde{p}}_x - i {\tilde{p}}_y) l_H /(\hbar \sqrt{2}) \ , \ \ a^{\dagger } = ({\tilde{p}}_x + i {\tilde{p}}_y) l_H /(\hbar \sqrt{2}) \ , \end{aligned}$$

(23)

which satisfy the commutation relation $[a,a^{\dagger }] = 1$, in analogy to an harmonic oscillator. The Hamiltonian (2) can now be written in the form

$$\begin{aligned} {\hat{h}}(\mathbf{r}) = i v_F \frac{\sqrt{2} \hbar }{l_H} \left[ \begin{array}{cc} 0 &{} a \\ - a^{\dagger } &{} 0 \end{array} \right] - E_F {\hat{I}} \ . \end{aligned}$$

(24)

To diagonalize the matrix, we square ${\hat{h}}(\mathbf{r}) + E_F {\hat{I}}$:

$$\begin{aligned} 2\Bigl (\frac{v_F \hbar }{l_H}\Bigr )^2 \left[ \begin{array}{cc} a^{\dagger }a + 1 &{} 0 \\ 0 &{} a^{\dagger }a \end{array} \right] \ . \end{aligned}$$

(25)

The energy eigenvalues of the Hamiltonian (2) are then $E_{\pm ,n} = \pm (\hbar v_F/ l_H) \sqrt{2n} - E_F$ for $n \ne 0$ and the corresponding eigenvectors are ($n \ne 0$)

$$\begin{aligned} \left[ \begin{array}{c} B_{\uparrow ,\pm ,n} \\ B_{\downarrow ,\pm ,n} \end{array} \right] = \frac{1}{\sqrt{2}} \left[ \begin{array}{c} |n-1 \rangle \\ \mp i |n \rangle \end{array} \right] \ . \end{aligned}$$

(26)

For $n=0$, the energy is $E_0 = - E_F$ and the eigenvector

$$\begin{aligned} \left[ \begin{array}{c} B_{\uparrow ,n=0} \\ B_{\downarrow ,n=0} \end{array} \right] = \left[ \begin{array}{c} 0 \\ |0 \rangle \end{array} \right] \ . \end{aligned}$$

(27)

Hence, the $n=0$ state is fully (down) spin-polarized.

The Landau levels are degenerate with respect to the center coordinates of the cyclotron orbit given by

$$\begin{aligned} X = x - (l_H^2/\hbar ) {\tilde{p}}_y \ , \ \ Y = y + (l_H^2/\hbar ) {\tilde{p}}_x \ . \end{aligned}$$

(28)

We define a second set of ladder operators

$$\begin{aligned} b = \frac{1}{\sqrt{2} l_H} (X + iY) \ , \ \ b^{\dagger } = \frac{1}{\sqrt{2} l_H} (X - iY) \ , \end{aligned}$$

(29)

which satisfy the usual boson commutation relations $[b,b^{\dagger }] = 1$. Within the same Landau level, the quantum states are specified by the number operator $b^{\dagger } b$, $b^{\dagger } b |n,m\rangle = m |n,m\rangle$, where $m \ge 0$.

The angular momentum operator $L_z = (\mathbf{r} \times \mathbf{p})_z$ expressed in terms of the boson operators is

$$\begin{aligned} L_z = \frac{l_H^2}{2\hbar } ({\tilde{p}}_x^2 + {\tilde{p}}_y^2) - \frac{\hbar }{2l_H^2} (X^2 + Y^2) = \hbar (a^{\dagger }a - b^{\dagger }b) \ . \end{aligned}$$

(30)

Consequently, the quantum state $|n,m\rangle$ has angular momentum $L_z = \hbar (n-m)$ with both, n and m being nonnegative. The particle branches of energy $E = E_{\pm ,n}$ arise for negative angular momentum, while the hole branches for positive $L_z$.

The above representation in terms of ladder operators is very similar to that of a Dirac Hamiltonian (parallel spin and momentum locking, see Suzuki et al., Ref. [13]) and to the Landau quantization in graphene [53].

Appendix B: Solution of the Bogoliubov–de Gennes equations

Using the method by Caroli, de Gennes and Matricon [25, 26], Eqs. (7–10) are solved (i) for small distances $x=\rho /l_H$, and (ii) for larger distances (but smaller than the coherence length over the magnetic length). These two solutions are then matched at an intermediate radius, $x_c$. If the matching condition is such that it is independent of the distance from the vortex core, the solution is valid for the entire region of the vortex. This condition as well determines the values of the energies of the bound states inside the vortex core. It is convenient to investigate the cases $\mu >0$ and $\mu <0$ separately.

1.1 B.1: Solution for $x < x_c$

It is convenient to convert the first-order differential equations, (7–10), into second-order ones. From Eq. (7), we can express $f^{\mu }_2(x)$ and insert it into Eq. (8). Similar substitutions can be performed for the remaining equations. Defining $N_+=[l_H(E_F+E)/v_F]^2/2$ and $N_-=[l_H(E_F-E)/v_F]^2/2$ (for particles and holes, respectively), we obtain

$$\begin{aligned}&\left[ \frac{{\partial }^2}{\partial x^2} + \frac{1}{x}\frac{\partial }{\partial x} - \frac{(\mu -1)^2}{x^2} - \frac{x^2}{4} - \mu + 2N_+\right] f^{\mu }_1\nonumber \\&\quad = {\tilde{\Delta }} (k_F l_H + {\tilde{E}}) f_4^{\mu } - {\tilde{\Delta }} \left( \frac{\partial }{\partial x} + \frac{\mu +1}{x} + \frac{x}{2} \right) f_3^{\mu } \ \ , \end{aligned}$$

(31)

$$\begin{aligned}&\left[ \frac{{\partial }^2}{\partial x^2} + \frac{1}{x}\frac{\partial }{\partial x} - \frac{\mu ^2}{x^2} - \frac{x^2}{4} - (\mu -1) + 2N_+\right] f^{\mu }_2 \nonumber \\&\quad = - {\tilde{\Delta }} (k_F l_H + {\tilde{E}}) f_3^{\mu } - {\tilde{\Delta }} \left( \frac{\partial }{\partial x} - \frac{\mu -2}{x} - \frac{x}{2} \right) f_4^{\mu } \ \ , \end{aligned}$$

(32)

$$\begin{aligned}&\left[ \frac{{\partial }^2}{\partial x^2} + \frac{1}{x}\frac{\partial }{\partial x} - \frac{(\mu +1)^2}{x^2} - \frac{x^2}{4} + \mu + 2N_-\right] f^{\mu }_3 \nonumber \\&\quad = {\tilde{\Delta }} (k_F l_H - {\tilde{E}}) f_2^{\mu } - {\tilde{\Delta }} \left( \frac{\partial }{\partial x} - \frac{\mu -1}{x} + \frac{x}{2} \right) f_1^{\mu } \ \ , \end{aligned}$$

(33)

$$\begin{aligned}&\left[ \frac{{\partial }^2}{\partial x^2} + \frac{1}{x}\frac{\partial }{\partial x} - \frac{\mu ^2}{x^2} - \frac{x^2}{4} + (\mu +1) + 2N_-\right] f^{\mu }_4 \nonumber \\&\quad = - {\tilde{\Delta }} (k_F l_H - {\tilde{E}}) f_1^{\mu } - {\tilde{\Delta }} \left( \frac{\partial }{\partial x} + \frac{\mu +2}{x} - \frac{x}{2} \right) f_2^{\mu } \ \ , \end{aligned}$$

(34)

where ${\tilde{\Delta }} = \Delta l_H /v_F$, ${\tilde{E}} = E l_H /v_F$ and $k_F = E_F/v_F$. In Eqs. (31)–(34), we used that $\Delta (x)$ is linear in x for $\rho$ smaller than the coherence length.

Since $\Delta (x)$ increases linearly from zero, we may neglect $\Delta (x)$ for $x < x_c$, i.e., set the rhs of Eqs. (31)–(34) equal to zero. For the lhs, we then expect a wave function of an harmonic oscillator and use the Ansatz: $f = \zeta ^\lambda e^{-\zeta /2} w(\zeta )$ for each of the four equations. For instance for the function $f_1^{\mu }$, we obtain $\lambda = |\mu - 1|/2$ and the differential equation for $w_1$ is

$$\begin{aligned}&\zeta \frac{d^2 w_1}{d \zeta ^2} + \Bigl (|\mu -1| + 1 -\zeta \Bigr ) \frac{d w_1}{d\zeta } \nonumber \\&\ \ \ - \Bigl (\frac{|\mu -1| +\mu +1}{2} -N_+\Bigr ) w_1 = 0 \ , \end{aligned}$$

(35)

which is the equation satisfied by the associated Laguerre polynomial $L^{|\mu -1|}_{N_+-\frac{|\mu -1| +\mu +1}{2}}(\zeta )$.

The solutions for $x < x_c$ are then

$$\begin{aligned}&f_1^{\mu }(\zeta ) = A_1^{\mu } \zeta ^{|\mu -1|/2} e^{-\zeta /2} L^{|\mu -1|}_{N_+-\frac{|\mu -1| +\mu +1}{2}}(\zeta ) \ \ , \nonumber \\&f_2^{\mu }(\zeta ) = A_2^{\mu } \zeta ^{|\mu |/2} e^{-\zeta /2} L^{|\mu |}_{N_+-\frac{|\mu | +\mu }{2}}(\zeta ) \ \ , \nonumber \\&f_3^{\mu }(\zeta ) = A_3^{\mu } \zeta ^{|\mu +1|/2} e^{-\zeta /2} L^{|\mu +1|}_{N_--\frac{|\mu +1| -\mu +1}{2}}(\zeta ) \ \ , \nonumber \\&f_4^{\mu }(\zeta ) = A_4^{\mu } \zeta ^{|\mu |/2} e^{-\zeta /2} L^{|\mu |}_{N_--\frac{|\mu | -\mu }{2}}(\zeta ) \ \ . \end{aligned}$$

(36)

The constants $A_j^{\mu }$ are not all independent. Substituting the solution (36) into the first-order differential equations, we have for $\mu >0$ $A_1^{\mu } = \sqrt{N_+} A_2^{\mu }$ and $A_4^{\mu } = - \sqrt{N_-} A_3^{\mu }$, while for $\mu <0$ $A_2 =-\sqrt{N_+} A_1$ and $A_3 = \sqrt{N_-} A_4$. The constants $A_1$ and $A_4$ are independent for $\Delta =0$, but become coupled when $\Delta \ne 0$.

1.2 B.2: Solution for $x > x_c$

$\Delta$ plays a relevant role for $x > x_c$. For $\mu >0$, we write the solution of Eqs. (31)–(34) as $f_j = \zeta ^{\mu /2}e^{-\zeta /2} w_j(\zeta )$

$$\begin{aligned}&\zeta \frac{d^2 w_1}{d \zeta ^2} + \Bigl (\mu + 1 -\zeta \Bigr )\frac{d w_1}{d \zeta } + \left( \frac{\mu - {\textstyle \frac{1}{2}}}{2 \zeta } -\mu -\frac{1}{2} + N_+ \right) w_1 \nonumber \\&\quad - \frac{k_F l_H + {\tilde{E}}}{2} {\tilde{\Delta }} w_4 + \frac{\tilde{\Delta }}{x} \Bigl [ \zeta \frac{d w_3}{d\zeta } + \bigl (\mu +{\textstyle \frac{1}{2}}\bigr )w_3 \Bigr ] =0 \ , \end{aligned}$$

(37)

$$\begin{aligned}&\zeta \frac{d^2 w_2}{d \zeta ^2} + \Bigl (\mu + 1 -\zeta \Bigr )\frac{d w_2}{d \zeta } + (-\mu + N_+ )w_2 + \frac{k_F l_H + {\tilde{E}}}{2} {\tilde{\Delta }} w_3 \nonumber \\&\quad + \frac{\tilde{\Delta }}{x} \Bigl [\zeta \frac{d w_4}{d\zeta } + \bigl (1 - \zeta \bigr )w_4 \Bigr ] =0 \ , \end{aligned}$$

(38)

$$\begin{aligned}&\zeta \frac{d^2 w_3}{d \zeta ^2} + \Bigl (\mu + 1 -\zeta \Bigr )\frac{d w_3}{d \zeta } + \left( -\frac{\mu + {\textstyle \frac{1}{2}}}{2 \zeta } -\frac{1}{2} + N_- \right) w_3 \nonumber \\&\quad - \frac{k_F l_H - {\tilde{E}}}{2} {\tilde{\Delta }} w_2 + \frac{\tilde{\Delta }}{x} \Bigl [ \zeta \frac{d w_1}{d\zeta } + {\textstyle \frac{1}{2}}w_1 \Bigr ] =0 \ , \end{aligned}$$

(39)

$$\begin{aligned}&\zeta \frac{d^2 w_4}{d \zeta ^2} + \Bigl (\mu + 1 -\zeta \Bigr )\frac{d w_4}{d \zeta } + N_- w_4 \nonumber \\&\quad + \frac{k_F l_H - {\tilde{E}}}{2} {\tilde{\Delta }} w_1 + \frac{\tilde{\Delta }}{x} \Bigl [\zeta \frac{d w_2}{d\zeta } + \bigl (\mu + 1 - \zeta \bigr )w_2 \Bigr ] =0 \ . \end{aligned}$$

(40)

The Ansatz for the $w_j$ functions is an associated Laguerre polynomial $L_N^{(\mu )}(\zeta )$ times an envelop function $g_j(\zeta )$. This is analogous to Caroli et al.’s [25] procedure for the non-relativistic case (see also Deng et al. [17] and Bardeen et al. [34]), who used a Hankel function times an envelop function. The differential equations (31)–(34) are real and so are the associated Laguerre function. Hence, $g_j(\zeta )$ are real functions. In Appendix C (Eq. (76)), we established that $L_N^{(\mu )}(\zeta )$ is asymptotically proportional to a cosine function and, hence, can be written as a sum of two exponential functions. Considering $L_N^{(\mu )}(\zeta ) = {\textstyle \frac{1}{2}} (L_N^{(\mu ),+}(\zeta ) + L_N^{(\mu ),-}(\zeta ))$, we write our Ansatz for $w_j(\zeta )$ as $L_N^{(\mu ),+}(\zeta )g_j(\zeta )$. The $L_N^{(\mu ),+}(\zeta )$ play the role of the Hankel functions in Refs. [17, 25, 34].

Next, we insert $w_j(\zeta )$ into Eqs. (37–40), use the recurrence relations for the associated Laguerre function and divide the equations by $\zeta L_N^{(\mu ),+}(\zeta )$. This way we arrive at the following four coupled second-order differential equations for the functions $g_j(\zeta )$:

$$\begin{aligned}&\frac{d^2}{d\zeta ^2} \left[ \begin{array}{c} g_1 \\ g_2 \\ g_3 \\ g_4 \end{array} \right] + \left( 2 \frac{d L_N^{(\mu ),+}/d\zeta }{L_N^{(\mu ),+}} + \frac{\mu +1}{\zeta } - 1\right) \frac{d}{d\zeta } \left[ \begin{array}{c} g_1 \\ g_2 \\ g_3 \\ g_4 \end{array} \right] \nonumber \\&\quad + \frac{1}{2 \zeta ^2} \left[ \begin{array}{c} (\mu - \textstyle \frac{1}{2}) g_1 \\ 0 \\ -(\mu + \textstyle \frac{1}{2}) g_3 \\ 0 \end{array} \right] + \frac{1}{\zeta } \left[ \begin{array}{c} (k_F l_H {\tilde{E}} + {\textstyle \frac{1}{2}} {\tilde{E}}^2) g_1 \\ (k_F l_H {\tilde{E}} + {\textstyle \frac{1}{2}} {\tilde{E}}^2) g_2 \\ (-k_F l_H {\tilde{E}} + {\textstyle \frac{1}{2}} {\tilde{E}}^2) g_3 \\ (-k_F l_H {\tilde{E}} + {\textstyle \frac{1}{2}} {\tilde{E}}^2) g_4 \end{array} \right] \nonumber \\&- \frac{1}{\zeta } \left[ \begin{array}{c} (\mu + {\textstyle \frac{1}{2}}) g_1 \\ \mu g_2 \\ {\textstyle \frac{1}{2}} g_3 \\ 0 \end{array} \right] + \frac{\tilde{\Delta }}{x} \frac{d}{d\zeta } \left[ \begin{array}{c} g_3 \\ g_4 \\ g_1 \\ g_2 \end{array} \right] + \frac{\tilde{\Delta }}{2\zeta } \left[ \begin{array}{c} -(k_Fl_H + {\tilde{E}})g_4 \\ (k_Fl_H + {\tilde{E}})g_3 \\ - (k_Fl_H - {\tilde{E}})g_2 \\ (k_Fl_H - {\tilde{E}})g_1 \end{array} \right] \nonumber \\&\quad + \frac{\tilde{\Delta }}{x} \frac{d L_N^{(\mu ),+}/d\zeta }{L_N^{(\mu ),+}} \left[ \begin{array}{c} g_3 \\ g_4 \\ g_1 \\ g_2 \end{array} \right] + \frac{\tilde{\Delta }}{x} \left[ \begin{array}{c} (\mu +{\textstyle \frac{1}{2}})/\zeta \ g_3 \\ (1/\zeta -1) g_4 \\ 1/(2\zeta ) \ g_1 \\ ({\textstyle \frac{\mu +1}{\zeta }} -1) g_2 \end{array} \right] = 0 . \end{aligned}$$

(41)

Using the asymptotic expansion of the associated Laguerre polynomials for large N (see Eq. (75)), we obtain

$$\begin{aligned} \frac{d L_N^{(\mu ),+}/d\zeta }{L_N^{(\mu ),+}} = \frac{1}{2} - \frac{\mu + {\textstyle \frac{1}{2}}}{2 \zeta } + i \sqrt{\frac{N}{\zeta }} . \end{aligned}$$

(42)

Note that the next order in the expansion in Eq. (42) does not add relevant terms for the present purpose.

Equation (41) is solved perturbatively. The dominant terms, which arise from the second, seventh and eighth terms of Eq. (41), yield the zeroth order ($g_j^{(0)}$), which satisfies

$$\begin{aligned} 2i\frac{d}{dx} \left[ \begin{array}{c} g_1^{(0)} \\ g_2^{(0)} \\ g_3^{(0)} \\ g_4^{(0)} \end{array} \right] + i {\tilde{\Delta }} \left[ \begin{array}{c} g_3^{(0)} \\ g_4^{(0)} \\ g_1^{(0)} \\ g_2^{(0)} \end{array} \right] + {\tilde{\Delta }} \left[ \begin{array}{c} -g_4^{(0)} \\ g_3^{(0)} \\ -g_2^{(0)} \\ g_1^{(0)} \end{array} \right] = 0 \ . \end{aligned}$$

(43)

The solution of Eq. (43) is

$$\begin{aligned}&g_1^{(0)}(x) = g_3^{(0)}(x) = C e^{-K(x)} \ \ , \nonumber \\&g^{(0)}_2(x) = g^{(0)}_4(x) = -i C e^{-K(x)} \ \ . \end{aligned}$$

(44)

where $K(x) = \int _0^x d x' {\tilde{\Delta }}(x')$ has been defined before, $C=e^{i \gamma }$ and $\gamma$ is to be determined. The remaining terms in Eq. (41) will be treated in first-order perturbation, $g_j^{(1)}$.

The equations for $g_j^{(1)}$ are

$$\begin{aligned}&2i\frac{d}{dx} \left[ \begin{array}{c} g_1^{(1)} \\ g_2^{(1)} \\ g_3^{(1)} \\ g_4^{(1)} \end{array} \right] + i{\tilde{\Delta }} \left[ \begin{array}{c} g_3^{(1)} \\ g_4^{(1)} \\ g_1^{(1)} \\ g_2^{(1)} \end{array} \right] + {\tilde{\Delta }} \left[ \begin{array}{c} -g_4^{(1)} \\ g_3^{(1)} \\ -g_2^{(1)} \\ g_1^{(1)} \end{array} \right] \nonumber \\&\quad = - \sqrt{\frac{\zeta }{N}}x \frac{d^2}{d\zeta ^2} \left[ \begin{array}{c} g_1^{(0)} \\ g_2^{(0)} \\ g_3^{(0)} \\ g_4^{(0)} \end{array} \right] - \frac{{\tilde{E}}^2 x}{2 \sqrt{N \zeta }}\left[ \begin{array}{c} g_1^{(0)} \\ g_2^{(0)} \\ g_3^{(0)} \\ g_4^{(0)} \end{array} \right] - 2 {\tilde{E}} \left[ \begin{array}{c} g_1^{(0)} \\ g_2^{(0)} \\ -g_3^{(0)}\\ - g_4^{(0)} \end{array} \right] \nonumber \\&- \frac{{\tilde{\Delta }}{\tilde{E}} x}{2\sqrt{N \zeta }} \left[ \begin{array}{c} -g_4^{(0)} \\ g_3^{(0)} \\ g_2^{(0)} \\ -g_1^{(0)} \end{array} \right] -\frac{1}{2 \sqrt{N \zeta }} \frac{d}{d\zeta } \left[ \begin{array}{c} g_1^{(0)} \\ g_2^{(0)} \\ g_3^{(0)} \\ g_4^{(0)} \end{array} \right] \nonumber \\&\quad - {\tilde{\Delta }} \sqrt{\frac{\zeta }{N}} \frac{d}{d \zeta } \left[ \begin{array}{c} g_3^{(0)} \\ g_4^{(0)} \\ g_1^{(0)} \\ g_2^{(0)} \end{array} \right] - \frac{\tilde{\Delta }}{2} \sqrt{\frac{\zeta }{N}} \left( 1 - \frac{\mu + {\textstyle \frac{1}{2}}}{\zeta } \right) \left[ \begin{array}{c} g_3^{(0)} \\ g_4^{(0)} \\ g_1^{(0)} \\ g_2^{(0)} \end{array} \right] \nonumber \\&-{\tilde{\Delta }} \sqrt{\frac{\zeta }{N}} \left[ \begin{array}{c} (\mu +{\textstyle \frac{1}{2}})/\zeta \ g_3^{(0)} \\ (1/\zeta -1) g_4^{(0)} \\ 1/(2\zeta ) \ g_1^{(0)} \\ ({\textstyle \frac{\mu +1}{\zeta }} -1)g_2^{(0)} \end{array} \right] -\frac{x}{2 \zeta ^2} \sqrt{\frac{\zeta }{N}} \left[ \begin{array}{c} (\mu -{\textstyle \frac{1}{2}}) g_1^{(0)} \\ 0 \\ -(\mu +{\textstyle \frac{1}{2}}) g_3^{(0)} \\ 0 \end{array} \right] \nonumber \\&\quad + \sqrt{\frac{2}{N}}\left[ \begin{array}{c} (\mu + {\textstyle \frac{1}{2}}) g_1^{(0)} \\ \mu g_2^{(0)} \\ {\textstyle \frac{1}{2}} g_3^{(0)} \\ 0 \end{array} \right] \ . \end{aligned}$$

(45)

Inserting our solutions for $g_j^{(0)}$ into Eq. (45), and with the Ansatz $g_1^{(1)} = C a_1 e^{-K}$, $g_2^{(1)} = -iCa_2 e^{-K}$, $g_3^{(1)} = Ca_3 e^{-K}$ and $g_4^{(1)} = -iCa_4 e^{-K}$, the differential equations for $a_j$ are

$$\begin{aligned}&2\frac{d}{dx} \left[ \begin{array}{c} a_1 \\ a_2 \\ a_3 \\ a_4 \end{array} \right] + {\tilde{\Delta }} \left[ \begin{array}{c} (a_3+a_4)-2a_1 \\ (a_3+a_4)-2a_2 \\ (a_1+a_2)-2a_3 \\ (a_1+a_2)-2a_4 \end{array} \right] \nonumber \\&\quad = i \frac{1}{\sqrt{2N}} \left[ \begin{array}{c} {\tilde{E}}^2 + 2\sqrt{2N}{\tilde{E}}+\frac{2\mu -1}{x^2} \\ {\tilde{E}}^2 + 2\sqrt{2N}{\tilde{E}} \\ {\tilde{E}}^2 - 2\sqrt{2N}{\tilde{E}}-\frac{2\mu +1}{x^2} \\ {\tilde{E}}^2 - 2\sqrt{2N}{\tilde{E}} \end{array} \right] + \frac{{\tilde{\Delta }}{\tilde{E}}}{\sqrt{2N}} \left[ \begin{array}{c} -1 \\ -1 \\ 1 \\ 1 \end{array} \right] \nonumber \\&-i \frac{1}{\sqrt{2N}} \left[ \begin{array}{c} \mu + {\textstyle \frac{1}{2}} \\ \mu - {\textstyle \frac{1}{2}} \\ -(\mu - {\textstyle \frac{1}{2}}) \\ -(\mu + {\textstyle \frac{1}{2}}) \end{array} \right] - i\frac{\mu + {\textstyle \frac{1}{2}}}{\sqrt{2N}}\left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array} \right] \nonumber \\&\quad + i\frac{\tilde{\Delta }}{x \sqrt{2N}} \left[ \begin{array}{c} \mu - {\textstyle \frac{1}{2}} \\ -(\mu - {\textstyle \frac{1}{2}}) \\ -(\mu + {\textstyle \frac{1}{2}}) \\ \mu + {\textstyle \frac{1}{2}} \end{array} \right] +i \frac{{\tilde{\Delta }} x}{2 \sqrt{2 N}} \left[ \begin{array}{c} 1 \\ -1 \\ 1 \\ -1 \end{array} \right] . \end{aligned}$$

(46)

Since all the terms are proportional to $C e^{-K(x)}$, this factor has been canceled out. It should also be pointed out that all the ${\tilde{\Delta }}^2$-terms cancel.

The above equations decouple by taking the following linear combinations:

$$\begin{aligned}&2 \frac{d}{dx} (a_1 - a_2) - 2{\tilde{\Delta }}(a_1 - a_2) \nonumber \\&\quad = i \frac{2\mu -1}{x^2\sqrt{2N}} -i \frac{1}{\sqrt{2N}} + i\frac{\tilde{\Delta }}{x\sqrt{2N}}(2\mu -1) +i \frac{{\tilde{\Delta }}x}{\sqrt{2N}} \ , \nonumber \\&2 \frac{d}{dx} (a_3 - a_4) - 2{\tilde{\Delta }}(a_3 - a_4) \nonumber \\&\quad = - i \frac{2\mu +1}{x^2\sqrt{2N}} -i \frac{1}{\sqrt{2N}} - i\frac{\tilde{\Delta }}{x\sqrt{2N}}(2\mu +1) +i \frac{{\tilde{\Delta }}x}{\sqrt{2N}}, \nonumber \\&\frac{d}{dx} (a_1+a_2+ a_3 + a_4)\nonumber \\&\quad = 2 i \frac{{\tilde{E}}^2}{\sqrt{2N}} - i \frac{1}{x^2\sqrt{2N}} -i \frac{2 \mu +1}{\sqrt{2N}}, \nonumber \\&\frac{d}{dx} (a_1+a_2- a_3 - a_4)- 2{\tilde{\Delta }}(a_1+a_2- a_3 - a_4) \nonumber \\&\quad = 4 i {\tilde{E}} + i \frac{2\mu }{x^2\sqrt{2N}} -2\frac{{\tilde{\Delta }}{\tilde{E}}}{\sqrt{2N}} - i \frac{2 \mu }{\sqrt{2N}} \ . \end{aligned}$$

(47)

The integration of the decoupled differential equations yields

$$\begin{aligned}&a_1 - a_2 = -i \frac{\mu -{\textstyle \frac{1}{2}}}{\sqrt{2N}} \int _x^{\infty } dx' \exp [K(x) - K(x')] \left[ \frac{1}{x'^2} + \frac{{\tilde{\Delta }}(x')}{x'} \right] \nonumber \\&\quad -i \frac{1}{2\sqrt{2N}} \int _0^x dx'\exp [K(x) - K(x')] [1 -x'{\tilde{\Delta }}(x')] \ , \end{aligned}$$

(48)

$$\begin{aligned}&a_3 - a_4 = i \frac{\mu +{\textstyle \frac{1}{2}}}{\sqrt{2N}} \int _x^{\infty } dx' \exp [K(x) - K(x')] \left[ \frac{1}{x'^2} + \frac{{\tilde{\Delta }}(x')}{x'} \right] \nonumber \\&\quad -i \frac{1}{2\sqrt{2N}} \int _0^x dx'\exp [K(x) - K(x')] [1 -x'{\tilde{\Delta }}(x')] \ , \end{aligned}$$

(49)

$$\begin{aligned}&a_1+a_2+a_3+a_4 = 2i \frac{{\tilde{E}}^2 x}{\sqrt{2N}} + \frac{i}{\sqrt{2N} x} - i \frac{2 \mu +1}{\sqrt{2N}} x \ , \end{aligned}$$

(50)

$$\begin{aligned}&a_1+a_2-a_3-a_4 = -i \int _x^{\infty } dx' \exp [2K(x) - 2K(x')]\nonumber \\&\times \left[ 4{\tilde{E}} + \frac{2\mu }{x'^2\sqrt{2N}} \right] \nonumber \\&\ \ \ \ \ \ \ - \frac{2}{\sqrt{2N}}\int _0^x dx' \exp [2K(x) - 2K(x')] [ {\tilde{E}}{\tilde{\Delta }}(x') +i\mu ] \ \ . \end{aligned}$$

(51)

The first term in Eq. (50) and the last term in Eq. (51) are of third order in the small parameters ${\tilde{\Delta }({\tilde{\rho }})}$, ${\tilde{E}}$ and x and can be neglected.

The integrals can be simplified by integrating by parts

$$\begin{aligned}&\int _x^{\infty } dx' \exp [K(x) - K(x')] \Bigl [ \frac{1}{x'^2} + \frac{{\tilde{\Delta }}(x')}{x'} \Bigr ] = \frac{1}{x} \ , \end{aligned}$$

(52)

$$\begin{aligned}&\int _x^{\infty } dx' \exp [2K(x) - 2K(x')] \left[ 2 {\tilde{E}} + \frac{\mu }{x^2 \sqrt{2N}} \right] \nonumber \\&\ \ \ \ \ \ \ \ = - 2{\tilde{E}}x + \frac{\mu }{x \sqrt{2N}} - i 2 G(x) \ , \end{aligned}$$

(53)

$$\begin{aligned}&G(x) = \int _x^{\infty } dx' e^{[2K(x) - 2K(x')]} \Bigl [4 {\tilde{\Delta }}(x') {\tilde{E}} x' - \frac{2\mu {\tilde{\Delta }}(x')}{x'\sqrt{2N}}\Bigr ] \ . \end{aligned}$$

(54)

For $\rho \le l_H$ the remaining integrals are approximately

$$\begin{aligned}&\int _0^x dx'\exp [K(x) - K(x')] [1 -x'{\tilde{\Delta }}(x')] = x \ , \end{aligned}$$

(55)

$$\begin{aligned}&\int _0^x dx'\exp [2K(x) - 2K(x')] = x \ . \end{aligned}$$

(56)

It is straightforward to solve Eqs. (48)–(51) for the $a_j$:

$$\begin{aligned}&a_1 = i\Bigl ({\tilde{E}}x - \frac{\mu -{\textstyle \frac{1}{2}}}{x \sqrt{2N}} - \frac{\mu +{\textstyle \frac{1}{2}}}{\sqrt{2N}}x - {\textstyle \frac{1}{2}} G(x) \Bigr ) \ , \end{aligned}$$

(57)

$$\begin{aligned}&a_2 = i\Bigl ({\tilde{E}}x - \frac{\mu }{\sqrt{2N}}x - {\textstyle \frac{1}{2}} G(x) \Bigr )\ , \end{aligned}$$

(58)

$$\begin{aligned}&a_3 = -i\Bigl ({\tilde{E}}x - \frac{\mu +{\textstyle \frac{1}{2}}}{x \sqrt{2N}} +\frac{1}{2\sqrt{2N}}x - {\textstyle \frac{1}{2}} G(x) \Bigr ) \ , \end{aligned}$$

(59)

$$\begin{aligned}&a_4 = -i \Bigl ({\tilde{E}}x - {\textstyle \frac{1}{2}} G(x)\Bigr ) \ . \end{aligned}$$

(60)

The common term G(x) in Eqs. (57)–(60) is zero and defines the bound state energy.

1.3 B.3: Matching of wave functions

The final step consists in matching the solution for small x and large x at an intermediate distance $x_c$ from the core of the vortex. The condition that this matching is independent of $x_c$ determines a unique wave function valid for all x and the energy of the bound state.

The solution for $x > x_c$ is now given by $f_j^{\mu } = \zeta ^{\mu /2} e^{-\zeta /2} L_N^{(\mu ),+}(\zeta ) g_j(x)$, which has to be matched at $x_c$ to $f^{\mu }_j(x)$ given by Eq. (36) for $x < x_c$ following a similar procedure as in Refs. [17] and [25]. The functions $g_j$ have been calculated consistently to first order of perturbation and can be written as an exponential, i.e., $g_j(x) \propto C \exp [-K(x) + a_j(x)]$, which remains correct to first order. The complex conjugated function is also a solution, involving $L_N^{(\mu ),-}(\zeta )$. The sum of both solutions is needed to complete the matching. For the wave functions, we employ the large-N asymptotic expansions for the associated Laguerre polynomials given by Eq. (76) in Appendix C.

We explicitly work out the matching for the function $f_1^{\mu }$; the other three functions follow similarly. For $x < x_c$, we have

$$\begin{aligned}&f_1^{\mu }(x_c) = \frac{A_1}{2\sqrt{\pi }} \zeta _c^{-{\textstyle \frac{1}{4}}} (N+\beta )^{{\textstyle \frac{\mu -1}{2}}-{\textstyle \frac{1}{4}}} \nonumber \\&\times \exp \left[ 2i\sqrt{\xi _c(N + \beta )} - i \frac{\pi (\mu -1)}{2} - i \frac{\pi }{4}\right] e^{i\delta _N^{(\mu -1)}} + c.c. \ , \end{aligned}$$

(61)

where $\beta = \sqrt{2N} {\tilde{E}} -\mu$ and $\delta _N^{(\mu -1)}$ is defined after Eq. (76), while for $x > x_c$, we obtain

$$\begin{aligned}&f_1^{\mu }(x_c) = \frac{C}{2\sqrt{\pi }} \zeta _c^{-{\textstyle \frac{1}{4}}} N^{{\textstyle \frac{\mu -1}{2}}-{\textstyle \frac{1}{4}}} \exp \left[ 2i\sqrt{\xi _cN} - i \frac{\pi \mu }{2} - i \frac{\pi }{4}\right] \nonumber \\&\times \exp \left[ i{\tilde{E}} x_c - i\frac{\mu -{\textstyle \frac{1}{2}}}{x_c \sqrt{2N}} - i\frac{\mu +{\textstyle \frac{1}{2}}}{\sqrt{2N}}x_c + i \delta _N^{(\mu )} \right] e^{-K(x_c)} + c.c. \ . \end{aligned}$$

(62)

Notice that C has a phase $\gamma$ and $A_1$ is real.

From comparing these two expressions, it follows that $\gamma = \pi /2$ and $A_1 = \sqrt{N} |C|$. As in Ref. [25] we neglect the factor $e^{-K(x_c)}$ in Eq. (62), and the factor

$$\begin{aligned} \exp \left[ \frac{{\tilde{E}} (\mu -1)}{\sqrt{2N}} - \frac{\mu (\mu -1)}{2N} -\frac{\sqrt{2N}{\tilde{E}} -\mu }{4N}\right] \approx 1 \end{aligned}$$

(63)

in Eq. (61) can be ignored. The two expressions, (61) and (62) are then equivalent and the matching is satisfied for a large interval of $x_c$. The above hinges on the vanishing of $G(x \rightarrow 0)$, which determines the energy of the bound state.

The solutions for $f_2^{\mu }$ are also satisfied for $\gamma = \pi /2$ and $A_1 = \sqrt{N} |C|$. Similarly, for $f_3^{\mu }$ and $f_4^{\mu }$ the small and large x wave functions are matched for $\gamma = \pi /2$ and $A_3 = -|C|/\sqrt{N}$.

1.4 B.4: The case $\mu < 0$

The procedure for $\mu < 0$ is very similar to the one for $\mu >0$. In fact, Eq. (36) is valid for small x for all $\mu \ne 0$. For large x the Ansatz for the functions $f_j$ is of the form $C_j \zeta ^{|\mu |/2} e^{-\zeta /2} L_N^{(|\mu |)}(\zeta ) g_j(\zeta )$ leading to four coupled second-order differential equations for the $g_j$, which is solved perturbatively as for $\mu >0$. The zero-order solution is again given by Eq. (44). The first order perturbation now contains $\mu$ (from the original differential equations) and $|\mu |$ (from the solution Ansatz). Following the same procedure as above, we have

$$\begin{aligned}&a_1 = i\Bigl ({\tilde{E}}x - \frac{\mu -{\textstyle \frac{1}{2}}}{x \sqrt{2N}} - \frac{1}{2\sqrt{2N}}x - {\textstyle \frac{1}{2}} G(x) \Bigr ) \ , \end{aligned}$$

(64)

$$\begin{aligned}&a_2 = i\Bigl ({\tilde{E}}x - {\textstyle \frac{1}{2}} G(x) \Bigr )\ , \end{aligned}$$

(65)

$$\begin{aligned}&a_3 = -i\Bigl ({\tilde{E}}x - \frac{\mu +{\textstyle \frac{1}{2}}}{x \sqrt{2N}} +\frac{|\mu |+{\textstyle \frac{1}{2}}}{\sqrt{2N}}x - {\textstyle \frac{1}{2}} G(x) \Bigr ) \ , \end{aligned}$$

(66)

$$\begin{aligned}&a_4 = -i \Bigl ({\tilde{E}}x +\frac{|\mu |}{\sqrt{2N}}x- {\textstyle \frac{1}{2}} G(x)\Bigr ) \ . \end{aligned}$$

(67)

As before, the common term $G(x \rightarrow 0)$ in Eqs. (64)–(67) is zero and defines the bound state energy. The matching of the functions for small and large x yields $A_1 = - |C| / \sqrt{N}$, $A_3 = |C| \sqrt{N}$ and $\gamma = \pi /2$.

1.4.1 B.5: Expressions for the local density of states

From Eq. (21), it follows for $\mu > 0$

$$\begin{aligned}&N_{\mu \uparrow }(\omega ,\rho ) = |C_{\mu }|^2 N \zeta ^{\mu -1} e^{-\zeta } \bigl [L^{(\mu -1)}_{N-\mu }(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega - E_{\mu }) \nonumber \\&\quad + |C_{\mu }|^2 \frac{1}{N} \zeta ^{\mu +1} e^{-\zeta } \bigl [L^{(\mu +1)}_{N-1}(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega + E_{\mu }) , \nonumber \\&N_{\mu \downarrow }(\omega ,\rho ) = |C_{\mu }|^2 \zeta ^{\mu } e^{-\zeta } \bigl [L^{(\mu )}_{N-\mu }(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega - E_{\mu }) \nonumber \\&\quad + |C_{\mu }|^2 \zeta ^{\mu } e^{-\zeta } \bigl [L^{(\mu )}_{N}(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega + E_{\mu }) \ , \end{aligned}$$

(68)

while for $\mu <0$

$$\begin{aligned}&N_{\mu \uparrow }(\omega ,\rho ) = |C_{\mu }|^2 \frac{1}{N} \zeta ^{|\mu -1|} e^{-\zeta } \bigl [L^{(|\mu -1|)}_{N-1}(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega - E_{\mu }) \nonumber \\&\quad + |C_{\mu }|^2 N \zeta ^{|\mu +1|} e^{-\zeta } \bigl [L^{(|\mu +1|)}_{N+\mu }(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega + E_{\mu }) , \nonumber \\&N_{\mu \downarrow }(\omega ,\rho ) = |C_{\mu }|^2 \zeta ^{|\mu |} e^{-\zeta } \bigl [L^{(|\mu |)}_{N}(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega - E_{\mu }) \nonumber \\&\quad + |C_{\mu }|^2 \zeta ^{|\mu |} e^{-\zeta } \bigl [L^{(|\mu |)}_{N+\mu }(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega + E_{\mu }) \ , \end{aligned}$$

(69)

and for the Majorana state $\mu = 0$

$$\begin{aligned}&N_{0 \uparrow }(\omega ,\rho ) = 4|C_0|^2 \zeta e^{-\zeta } \bigl [L^{(1)}_{N-1}(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega ) , \nonumber \\&N_{0 \downarrow }(\omega ,\rho ) = 4N|C_0|^2 e^{-\zeta } \bigl [L^{(0)}_{N}(\zeta )\bigr ]^2 e^{-2 K(x)} \delta (\omega ).\nonumber \\ \end{aligned}$$

(70)

Appendix C: Asymptotic expansion and recurrence relations for the associated Laguerre polynomials

The following recursion relations for the associated Laguerre polynomials have been used

$$\begin{aligned}&L_n^{(\alpha )}(\zeta ) = L_n^{(\alpha +1)}(\zeta ) - L_{n-1}^{(\alpha +1)}(\zeta ) \ , \end{aligned}$$

(71)

$$\begin{aligned}&n L_n^{(\alpha )}(\zeta ) = (n+\alpha ) L_{n-1}^{(\alpha )}(\zeta ) - \zeta L_{n-1}^{(\alpha +1)}(\zeta ) \ , \end{aligned}$$

(72)

$$\begin{aligned}&\frac{d}{d\xi }L_n^{(\alpha )}(\zeta ) = - L_{n-1}^{(\alpha +1)}(\zeta ) \ . \end{aligned}$$

(73)

The associated Laguerre polynomials can also be obtained recursively, defining the first two polynomials as $L_0^{(\alpha )}(\zeta )=1$ and $L_1^{(\alpha )}(\zeta ) = 1 + \alpha -\zeta$ and using the following recurrence relation for $n\ge 1$

$$\begin{aligned} L_{n+1}^{(\alpha )}(\zeta ) = \frac{(2n+1+\alpha -\zeta )L_n^{(\alpha )}(\zeta ) - (n+\alpha )L_{n-1}^{(\alpha )}(\zeta )}{n+1} \ . \end{aligned}$$

(74)

This equation only holds for integer n and can be used to compute the polynomials.

The asymptotic expansion of the associated Laguerre polynomial for large n is given by [54]

$$\begin{aligned}&L_n^{(\alpha )}(\zeta ) = \frac{n^{{\textstyle \frac{1}{2}}\alpha -{\textstyle \frac{3}{4}}}e^{{\textstyle \frac{1}{2}}\zeta }}{\sqrt{\pi }\zeta ^{{\textstyle \frac{1}{2}}\alpha +{\textstyle \frac{1}{4}}}}[ \cos (\omega _n^{(\alpha )}) + \sin (\omega _n^{(\alpha )}) \nonumber \\&\times \frac{(4\zeta ^2-12\alpha ^2-24\alpha \zeta -24\zeta +3)}{48\sqrt{n\zeta }} + {\mathcal {O}}(1/n)] \ , \nonumber \\ \end{aligned}$$

(75)

where $\omega _n^{(\alpha )} = 2 \sqrt{n\zeta } - ({\textstyle \frac{1}{2}}\alpha +{\textstyle \frac{1}{4}})\pi$. The above expression can be resumed into the argument of one circular function. Keeping only the next-to-leading terms in the argument of the circular function corresponds to

$$\begin{aligned} L_n^{(\alpha )}(\zeta ) = \frac{n^{{\textstyle \frac{1}{2}}\alpha -{\textstyle \frac{3}{4}}}e^{{\textstyle \frac{1}{2}}\zeta }}{\sqrt{\pi }\zeta ^{{\textstyle \frac{1}{2}}\alpha +{\textstyle \frac{1}{4}}}}\cos (\omega _n^{(\alpha )} + \delta _n^{(\alpha )}) \end{aligned}$$

(76)

with $\delta _n^{(\alpha )} = - \frac{(4\zeta ^2-12\alpha ^2-24\alpha \zeta -24\zeta +3)}{48\sqrt{n\zeta }}$. These equations are exact to this order.