Vortex Phantoms in the Stationary Kochin–Yudovich Flow Problem

Abstract

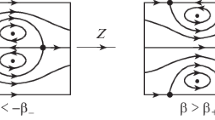
The dynamics of a continuous medium in a pipe is not exhausted by spontaneous unsteady turbulence vortices (first seen in flashes of light and generated at high Reynolds numbers), which permanently level the parabolic velocity profile in the pipe. The ambient space also includes steady swirls and curls, which are usually approximated by analytical dependences decomposable in power series. It turns out that, in the Kochin–Yudovich boundary value flow problem, the existence of an ideal incompressible steady flow that is arbitrarily smooth, but not analytic (and, hence, a phantom, i.e., it cannot be classically approximated by polynomials with any prescribed degree of accuracy or, in other words, cannot be computed exactly, but is established over time) is also reduced to vortices of this type. Specifically, the existence analysis is reduced to finding an infinitely smooth uncomputable mass rate of such vortices in the form of a stream function solving the two-dimensional Dirichlet problem for the negative Laplacian with a right-hand side specified as an infinitely smooth Sobolev cutoff function, which was introduced as early as the 1930s and later became known as a Friedrichs mollifier. This problem is briefly discussed below.