1 Introduction

In many industrial applications, fibre-reinforced composites are in high demand because of their advantageous properties compared to non-reinforced materials. Specifically speaking, a reinforcement by certain types of fibres can enhance the stiffness, durability and strength-to-weight ratio of materials to name only a few benefits, cf. [1, 2]. Due to the high popularity of fibre-reinforced composites, efficient simulation methods are required to predict the behaviour of these kinds of materials. A broad range of simulation approaches already exists in which the fibres are assumed to be perfectly flexible. This implies that they exhibit a stiffness only in the direction of the fibre, which can be modelled by a structural tensor approach as in, e.g., [3,4,5,6,7,8].

A more elaborated theory has been presented in [9] where additional higher-gradient energy contributions of the deformation map are considered to account for the fibre bending stiffness. As a consequence, a length scale is introduced in the generalised continuum model which is associated with positive size effects in the sense “smaller is stiffer”. This is characteristic for strain gradient theories and in contrast to stress gradient theories in which negative size effects in the sense “smaller is softer” are observed, cf. [10,11,12]. One specific approach to generalised continua is the couple-stress theory, as discussed in detail in [13, 14]. Together with the constitutive equations derived in [9], it incorporates higher-gradient contributions that are associated with the fibre curvature and fibre stretch gradient. Consequently, this modelling approach can account for particular deformation modes such as fibre stretching and bending which have been discussed in detail in [15, 16] with further consideration of fibre twisting. Besides taking one single family of fibres into account, these fibre-related gradient effects have been elaborated in [17] for woven fibre structures. In [18], fibre bundles have been examined with regard to fibre bending stiffness and twisting.

From the consideration of the respective higher-gradient terms in the balance equations of the couple-stress theory, a partial differential equation (PDE) of fourth order is obtained. In order to solve the resulting equation system in a finite element framework, different methods have been employed in past works. In [19,20,21] the equation system has been treated by a multi-field method in order to reduce the problem to two PDEs of second order which can be solved by means of a classic finite element approach with Lagrangian basis functions. In [22], an isogeometric finite element approach has been used to directly solve the fourth-order PDE, since the therein used Non-Uniform Rational B-Splines (NURBS) basis functions can fulfil the higher continuity requirements resulting from the weak form of the respective equation. Due to the omission of additional fields, the number of degrees of freedom can be significantly reduced in this way. In [22], the isogeometric approach has only been applied to small strain problems, whereas we will use the method in this contribution for more advanced modelling by assuming finite deformations. In doing so, the effect of the fibre bending stiffness can be examined together with an overall non-linear material behaviour and more practical applications can be covered by the proposed simulation method. Furthermore, the fibre stretch gradient will be incorporated which has so far been neglected in the small strain setting, cf. [9, 22].

The contribution is structured as follows: In Sect. 2, the modelling approach for fibre-reinforced composites with fibre bending stiffness from [9] is presented. After an introduction of all required kinematic quantities, the balance equations from the couple-stress theory, which will be solved in the simulation of fibre-reinforced composites, are summarised. In Sect. 3, a discretised and linearised form of the governing equation is derived for the solution by means of an isogeometric finite element method. Finally, Sect. 4 provides two numerical examples. At first, a cylindrical tube subject to a pure azimuthal shear deformation is examined. For a transversely isotropic material, an analysis of this boundary value problem has been conducted in [23]. Considering fibre bending stiffness in the analysis and assuming small deformations, the azimuthal shear problem has been elaborated in [24, 25] by employing different assumptions on the compressibility of the bulk material and on the extensibility of the fibres. In [26], the respective boundary value problem for the general case of finite deformations has been discussed. Within an isogeometric finite element framework, the small strain version of the problem has been analysed in [22] and a comparison to the semi-analytical solutions provided in [25] has been made. In analogy, the results of the simulation approach developed in this contribution are compared to the solutions presented in these works. For the second example, a notched plate is analysed in terms of a uni-axial tensile test. In this more complex example, the influence of the fibre bending stiffness and of the initial fibre direction will be examined.

Notation    For two tensor-valued quantities \({\varvec{T}}\) and \({\varvec{S}}\) of arbitrary order, different types of contractions are introduced. Using Einstein’s summation convention, the single, double, and triple contractions are represented by

$$\begin{aligned} {\varvec{T}}\cdot {\varvec{S}} =&\,[T_{ij\ldots kl}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l]\cdot [S_{mn\ldots op}\,{\varvec{e}}_m\otimes {\varvec{e}}_n\ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p] \nonumber \\ =&\, T_{ij\ldots kl}\,S_{ln\ldots op}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_n \ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p, \end{aligned}$$
(1)
$$\begin{aligned} {\varvec{T}}:{\varvec{S}} =&\,[T_{ij\ldots kl}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l]:[S_{mn\ldots op}\,{\varvec{e}}_m\otimes {\varvec{e}}_n\ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p] \nonumber \\ =&\, T_{ij\ldots kl}\,S_{kl\ldots op}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p, \end{aligned}$$
(2)
$$\begin{aligned} {\varvec{T}}:\!\cdot \,{\varvec{S}} =&\,[T_{ij\ldots klm}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l\otimes {\varvec{e}}_m]:\!\cdot \,[S_{nop\ldots qr}\,{\varvec{e}}_n\otimes {\varvec{e}}_o\otimes {\varvec{e}}_p\ldots \otimes {\varvec{e}}_q\otimes {\varvec{e}}_r] \nonumber \\ =&\, T_{ij\ldots klm}\,S_{klm\ldots qr}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_q\otimes {\varvec{e}}_r \end{aligned}$$
(3)

with \({\varvec{e}}_1,\dots \) representing an orthonormal basis system.

For the same tensors, the standard dyadic product as well as two special dyadic products are defined as

$$\begin{aligned} {\varvec{T}}\otimes {\varvec{S}} =\,&[T_{ij\ldots kl}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l]\otimes [S_{mn\ldots op}\,{\varvec{e}}_m\otimes {\varvec{e}}_n\ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p] \nonumber \\ =\,&T_{ij\ldots kl}\,S_{mn\ldots op}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l\otimes {\varvec{e}}_m\otimes {\varvec{e}}_n\ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p, \end{aligned}$$
(4)
$$\begin{aligned} {\varvec{T}}\,{\overline{\otimes }}\,{\varvec{S}} =\,&[T_{ij\ldots kl}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l]\,{\overline{\otimes }}\,[S_{mn\ldots op}\,{\varvec{e}}_m\otimes {\varvec{e}}_n\ldots {\varvec{e}}_o\otimes {\varvec{e}}_p] \nonumber \\ =\,&T_{ij\ldots km}\,S_{ln\ldots op}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l\otimes {\varvec{e}}_m\otimes {\varvec{e}}_n\ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p, \end{aligned}$$
(5)
$$\begin{aligned} {\varvec{T}}\,{\underline{\otimes }}\,{\varvec{S}} =\,&[T_{ij\ldots kl}\, {\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l] \,{\underline{\otimes }}\,[S_{mn\ldots op}\,{\varvec{e}}_m\otimes {\varvec{e}}_n\ldots {\varvec{e}}_o\otimes {\varvec{e}}_p] \nonumber \\ =\,&T_{ij\ldots kn}\,S_{lm\ldots op}\,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l\otimes {\varvec{e}}_m\otimes {\varvec{e}}_n\ldots \otimes {\varvec{e}}_o\otimes {\varvec{e}}_p. \end{aligned}$$
(6)

The transposition of a second-order tensor \({\varvec{T}}\) is denoted as

$$\begin{aligned} {\varvec{T}}^\mathrm {t} = T_{ji} \,{\varvec{e}}_i\otimes {\varvec{e}}_j. \end{aligned}$$
(7)

Similarly, two types of transpositions are employed for a fourth-order tensor \({\varvec{S}}\), namely

$$\begin{aligned} {\varvec{S}}^\mathrm {t} = S_{jikl} \,{\varvec{e}}_i\otimes {\varvec{e}}_j\otimes {\varvec{e}}_k\otimes {\varvec{e}}_l \quad \text {and} \quad {\varvec{S}}^\mathrm {T} = S_{klij} \,{\varvec{e}}_i\otimes {\varvec{e}}_j\otimes {\varvec{e}}_k\otimes {\varvec{e}}_l. \end{aligned}$$
(8)

For the differentiation of tensorial quantities, the gradient operator with respect to the (spatial) coordinates \({\varvec{x}}\), applied to a tensor \({\varvec{T}}\) of arbitrary order, is introduced as

$$\begin{aligned} \nabla _{\!\varvec{x}}{\varvec{T}} = \frac{\partial T_{ij\ldots kl}}{\partial x_m} \,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k\otimes {\varvec{e}}_l\otimes {\varvec{e}}_m. \end{aligned}$$
(9)

On this basis, the divergence operator is obtained by the double contraction of the gradient with the second-order identity tensor \({\varvec{I}}\) such that

$$\begin{aligned} \nabla _{\!\varvec{x}}\cdot {\varvec{T}} = \nabla _{\!\varvec{x}}{\varvec{T}} : {\varvec{I}} = \frac{\partial T_{ij\ldots kl}}{\partial x_l} \,{\varvec{e}}_i\otimes {\varvec{e}}_j\ldots \otimes {\varvec{e}}_k. \end{aligned}$$
(10)

The curl of a first-order tensor \({\varvec{a}}\) is defined as

$$\begin{aligned} \nabla _{\!\varvec{x}}\times {\varvec{a}} = -\nabla _{\!\varvec{x}}{\varvec{a}} : \varvec{\epsilon } = \epsilon _{ijk} \frac{\partial a_{k}}{\partial x_j} \,{\varvec{e}}_i \end{aligned}$$
(11)

with \(\varvec{\epsilon }\) denoting the third-order Levi-Civita tensor.

2 Fibre-reinforced composites possessing fibre bending stiffness

The enhanced approach for the modelling of fibre-reinforced composites, which takes not only the fibre direction but also a fibre bending stiffness into account by introducing an extended form of the stored energy function, has been presented in [9]. Along with new material parameters, additional kinematic quantities in terms of the fibre stretch gradient as well as the fibre curvature are considered, and a generalised continuum theory which includes higher-gradient contributions in the balance equations is assumed.

2.1 Finite strain kinematics

Fig. 1
figure 1

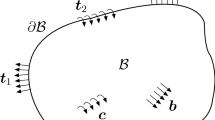
Domain \({\mathcal {B}}\) in the reference configuration (\({\mathcal {B}}_0\)) and current configuration (\({\mathcal {B}}_t\)) assuming a couple-stress theory. Employed vectors and tensors: placement function \(\varvec{\varphi }\), deformation gradient \({\varvec{F}}\), referential outward surface normal unit vector \({\varvec{N}}\), current outward surface normal unit vector \({\varvec{n}}\), referential fibre direction vector \({\varvec{a}}_0\), current fibre direction vector \({\varvec{a}}_t\), body force vector \({\varvec{b}}\), body couple vector \({\varvec{c}}\), vector of tractions \({\varvec{t}}_1\) acting on the surface \(\partial {\mathcal {B}}_t\), vector of couples \({\varvec{t}}_2\) acting on the surface \(\partial {\mathcal {B}}_t\), vector of displacements \(\overline{{\varvec{u}}}\) prescribed on the surface \(\partial {\mathcal {B}}_t\)

Full size image

For a body \({\mathcal {B}}\) undergoing finite deformations, two configurations may be considered, namely a reference configuration at time \(t_0\) as well as the current configuration which inherits the deformation of the body at time t. As shown in Fig. 1, the non-linear function \(\varvec{\varphi }: {\mathcal {B}}_0 \rightarrow {\mathcal {B}}_t\) describes the mapping of the position of a material point \({\varvec{X}}\) of the reference configuration to its position \({\varvec{x}}\) in the current configuration. The gradient of the mapping with respect to the reference position \({\varvec{X}}\) is the deformation gradient \({\varvec{F}}= \nabla _{\!\varvec{X}}\varvec{\varphi }\) with \(J=\det ({\varvec{F}})>0\). The deformation gradient describes a linear relation between line elements \({{\mathrm{d}}}{\varvec{x}}\) in the current configuration and \({{\mathrm{d}}}{\varvec{X}}\) in the reference configuration, while its cofactor and determinant relate infinitesimal area as well as infinitesimal volume elements in a similar manner, i.e.

$$\begin{aligned} {{\mathrm{d}}}{\varvec{x}} = {\varvec{F}}\cdot {{\mathrm{d}}}{\varvec{X}}, \quad {\varvec{n}}\,{{\mathrm{d}}}{} \textit{a} = \text {cof}({\varvec{F}})\cdot {\varvec{N}}\,{{\mathrm{d}}}{} \textit{A}, \quad {{\mathrm{d}}} v = J \,{{\mathrm{d}}} V . \end{aligned}$$
(12)

Vectors \({\varvec{N}}\) and \({\varvec{n}}\) denote the outward surface normal unit vectors in the reference and in the current configuration and the cofactor is defined as \(\text {cof}({\varvec{F}})=J\,{\varvec{F}}^{\mathrm{-t}}\). For the specific modelling approach examined in this contribution and presented in [9], the second gradient of the placement function is considered further, so that

$$\begin{aligned} \varvec{\varUpsilon } = \nabla _{\!\varvec{X}}{\varvec{F}}= \nabla _{\!\varvec{X}}\nabla _{\!\varvec{X}}\varvec{\varphi } \end{aligned}$$
(13)

is introduced.

Within the scope of modelling fibre-reinforced composites, a unit vector field \({\varvec{a}}_0\) is commonly incorporated into the model as an additional directional quantity. It describes the fibre direction in the reference configuration for a material which is reinforced by a single family of fibres. Under the assumption that the fibres are embedded in the matrix material and convected with the deformation, the fibre direction vector in the deformed configuration is obtained as

$$\begin{aligned} {\varvec{a}}_t = \lambda _a\,\overline{{\varvec{a}}}_t={\varvec{F}}\cdot {\varvec{a}}_0 \quad \text {with} \quad \Vert \overline{{\varvec{a}}}_t\Vert = 1. \end{aligned}$$
(14)

Since not only the direction but also the length of the fibres changes consequently to the deformation, the fibre stretch \(\lambda _a\) occurs in (14).

Assuming that the embedded fibres are not perfectly flexible but instead exhibit a certain bending stiffness, the gradient of the fibre direction vector is incorporated into the enhanced material model. With respect to the reference configuration, this gradient takes the form

$$\begin{aligned} \varvec{\varLambda }={\varvec{F}}^{\mathrm{t}}\cdot {\varvec{G}} \quad \text {with} \quad {\varvec{G}}=\nabla _{\!\varvec{X}}{\varvec{a}}_t={\varvec{a}}_0\cdot \nabla _{\!\varvec{X}}{\varvec{F}}^{\mathrm{t}} + {\varvec{F}}\cdot \nabla _{\!\varvec{X}}{\varvec{a}}_0, \end{aligned}$$
(15)

cf. [9]. As discussed in detail in [20], the stress and energy contributions related to this gradient term do, in general, not vanish in the initial state. In order to obtain an initially stress- and energy-free condition, the fibres are assumed to be straight in the reference configuration, i.e. \(\nabla _{\!\varvec{X}}{\varvec{a}}_0={\varvec{0}}\).

2.2 Local balance equations

For the consideration of higher gradients of the placement function, an enhanced continuum model is required. In the present contribution, the couple-stress theory presented in [14] is applied. The spatial versions of the local balance equations will be summarised in the following for the quasi-static case and under the assumption of vanishing body forces and body couples, accordingly \({\varvec{b}}={\varvec{0}}\) and \({\varvec{c}}={\varvec{0}}\), cf. [9, 20].

Considering a closed system, the local form of the balance of mass reads

$$\begin{aligned} {\dot{\rho }}+\rho \,\nabla _{\!\varvec{x}}\cdot \dot{\varvec{\varphi }} = 0 \end{aligned}$$
(16)

with spatial mass density \(\rho \) and with the material time derivative of \(\bullet \) denoted as \({\dot{\bullet }}\).

The local form of the balance of linear momentum follows as

$$\begin{aligned}&\rho \, \ddot{\varvec{\varphi }} = \nabla _{\!\varvec{x}}\cdot \varvec{\sigma }^\mathrm {t} \end{aligned}$$
(17a)
$$\begin{aligned}&\overset{\text{ quasi-static }}{\Rightarrow } \quad {\varvec{0}} = \nabla _{\!\varvec{x}}\cdot \varvec{\sigma }^\mathrm {t} \end{aligned}$$
(17b)

with an, in general, non-symmetric Cauchy-type stress tensor \(\varvec{\sigma }\).

From the local form of the balance of angular momentum, its skew-symmetric part can be directly obtained as a function of the divergence of the couple-stress tensor \({\varvec{m}}\), to be specific

$$\begin{aligned}&{\varvec{0}} = \nabla _{\!\varvec{x}}\cdot {\varvec{m}}^\mathrm {t} + \varvec{\epsilon } : \varvec{\sigma } \end{aligned}$$
(18a)
$$\begin{aligned}&\Rightarrow \quad \varvec{\sigma }^{\mathrm{skw}} = -\frac{1}{2} \left[ \nabla _{\!\varvec{x}}\cdot {\varvec{m}}^{\mathrm{t}}\right] \cdot \varvec{\epsilon }. \end{aligned}$$
(18b)

By using the balance equations (17a) and (18a), the local form of the balance of energy follows as

$$\begin{aligned} \rho \, {\dot{U}} = \varvec{\sigma }^{\mathrm{{sym}}}: \nabla _{\!\varvec{x}}\dot{\varvec{\varphi }} + \frac{1}{2}{\varvec{m}}^\mathrm {t} : \nabla _{\!\varvec{x}}\nabla _{\!\varvec{x}}\times \dot{\varvec{\varphi }}, \end{aligned}$$
(19)

where U denotes the (mass specific) internal energy.

For the isogeometric finite element analysis, the balance equations of linear and angular momentum are combined into one partial differential equation which is of fourth order since the couple-stress tensor, in general, may contain second-order derivatives of the placement function. Retaining the assumptions mentioned above, inserting (18b) into (17b) yields

$$\begin{aligned} {\varvec{0}} = \nabla _{\!\varvec{x}}\cdot \varvec{\sigma }^{\mathrm{{sym}}}+ \frac{1}{2} \nabla _{\!\varvec{x}}\times \left[ \nabla _{\!\varvec{x}}\cdot {\varvec{m}}^\mathrm {t}\right] . \end{aligned}$$
(20)

As discussed in detail in [14] and typical for the couple-stress theory, only the deviatoric part \(\overline{{\varvec{m}}} = {\varvec{m}}-\tfrac{1}{3}{\text {tr}}({\varvec{m}})\,{\varvec{I}}\) of the couple-stress tensor contributes to the energy balance (19) because \({\varvec{I}}:\nabla _{\!\varvec{x}}\nabla _{\!\varvec{x}}\times \dot{\varvec{\varphi }}=0\) holds. The same applies to the partial differential equation (20), where the spherical part of the couple-stress tensor similarly vanishes as a result of the curl and divergence operation. Consequently, the spherical part of the couple-stress tensor does not have any impact on the balance equations relevant for the proposed simulation approach and accordingly remains undetermined as this work proceeds.

2.3 Constitutive model

The constitutive model for fibre-reinforced composites including fibre bending stiffness has been derived in [9]. The basis for this model is an extended list of invariants for the stored energy density function. Specifically speaking, the energy is considered as an isotropic function of invariants \(I_i\) including three main arguments that have been introduced in Sect. 2.1, i.e.

$$\begin{aligned} W(I_i({\varvec{C}},\varvec{\varLambda },{\varvec{a}}_0)). \end{aligned}$$
(21)

This purely referential representation is based on the Cauchy–Green tensor \({\varvec{C}}={\varvec{F}}^{\mathrm{t}}\cdot {\varvec{F}}\), the referential fibre direction vector \({\varvec{a}}_0\) and the gradient \(\varvec{\varLambda }\) of the deformed fibre vector. In order to reduce the number of invariants, additional assumptions are made in [9] and adopted in this work. By employing only the directional projection \(\varvec{\kappa }_0=\varvec{\varLambda }\cdot {\varvec{a}}_0\), effects from fibre splay are neglected in addition to effects from fibre twist. Apart from that, the sense of the fibre orientation is not relevant from a physical point of view so that the fibre vector may appear in the stored energy only in even powers.

From the general form of the stored energy density function in (21), the stress and couple-stress tensor are derived in [9] by considering the particular dependencies of the invariants. Accordingly, the symmetric part of the stress tensor follows as

$$\begin{aligned} \varvec{\sigma }^{\mathrm{sym}} = J^{-1}\left[ 2{\varvec{F}}\cdot \frac{\partial W}{\partial {\varvec{C}}} \cdot {\varvec{F}}^{\mathrm{t}} + {\varvec{G}}\cdot \left[ \frac{\partial W}{\partial \varvec{\varLambda }}\right] ^{\mathrm{t}} \cdot {\varvec{F}}^{\mathrm{t}} + {\varvec{F}}\cdot \frac{\partial W}{\partial \varvec{\varLambda }} \cdot {\varvec{G}}^{\mathrm{t}}\right] \end{aligned}$$
(22)

and the deviatoric part of the couple-stress tensor takes the form

$$\begin{aligned} \overline{{\varvec{m}}}^{\mathrm{t}} = -\frac{2}{3}J^{-1}\varvec{\epsilon }:\left[ {\varvec{F}}\cdot \frac{\partial W}{\partial \varvec{\varLambda }} \cdot \left[ {\varvec{F}}^{\mathrm{t}} \,{\overline{\otimes }}\,{\varvec{a}}_t + {\varvec{F}}^{\mathrm{t}} \otimes {\varvec{a}}_t \right] \right] . \end{aligned}$$
(23)

The specific form of the energy function used for the determination of the partial derivatives in (22) and (23) in this work will be presented in Sect. 4.

3 Isogeometric finite element approach

For the solution of the fourth-order partial differential equation in the simulation of fibre-reinforced composites with fibre bending stiffness, the isogeometric finite element method is employed. Since NURBS basis functions, used within the isogeometric analysis, provide \(C^{p-1}\)-continuity everywhere, except for the locations of repeated knots or control points, global continuity higher than \(C^0\) can be realised. The NURBS basis functions are used in the discretised weak form of the balance equation which will be developed in the following section. For the application of the finite element method, a linearisation is performed afterwards so that the globally assembled system of equations can be solved by means of the Newton–Raphson method. Detailed information on the isogeometric analysis and on NURBS is provided in [27,28,29].

3.1 Discretised weak form

With regard to a finite element formulation of the governing equation (20), a weak form is derived. For this purpose, (17b) is multiplied by a test function \( \varvec{\eta }\) and integrated over the spatial domain \({\mathcal {B}}_t\), accordingly

$$\begin{aligned} 0 = \int _{{\mathcal {B}}_t} \varvec{\eta } \cdot \left[ \nabla _{\!\varvec{x}}\cdot \varvec{\sigma }^{\mathrm{t}}\right] \,{{\mathrm{d}}} v . \end{aligned}$$
(24)

The application of the divergence theorem and of integration by parts yields

$$\begin{aligned} 0 = \int _{{\mathcal {B}}_t} \nabla _{\!\varvec{x}}\varvec{\eta } : \varvec{\sigma }^{\mathrm{t}} \,{{\mathrm{d}}} v - \int _{\partial {\mathcal {B}}_t} \varvec{\eta } \cdot \varvec{\sigma }^{\mathrm{t}} \cdot {\varvec{n}} \,{{\mathrm{d}}} a . \end{aligned}$$
(25)

Considering an additive decomposition of the stress tensor in the form of

$$\begin{aligned} \varvec{\sigma } = \varvec{\sigma }^{\mathrm{{sym}}}+\varvec{\sigma }^{\mathrm{{skw}}}\end{aligned}$$
(26)

and making use of the definition of the skew-symmetric stress part from (18b) with \(\varvec{\sigma }^{\mathrm{{skw}}}=-\left[ \varvec{\sigma }^{\mathrm{{skw}}}\right] ^{\mathrm{t}}\), (25) can be rewritten as

$$\begin{aligned} 0 = \int _{{\mathcal {B}}_t} \nabla _{\!\varvec{x}}\varvec{\eta } : \varvec{\sigma }^{\mathrm{{sym}}}\,{{\mathrm{d}}} v - \int _{\partial {\mathcal {B}}_t} \varvec{\eta } \cdot {\varvec{t}}_1 \,{{\mathrm{d}}} a + \int _{{\mathcal {B}}_t} \nabla _{\!\varvec{x}}\varvec{\eta } : \left[ \tfrac{1}{2} \left[ \nabla _{\!\varvec{x}}\cdot {\varvec{m}}^{\mathrm{t}} \right] \cdot \varvec{\epsilon }\right] \,{{\mathrm{d}}} v . \end{aligned}$$
(27)

Therein, Cauchy’s theorem is employed so that the traction vector \({\varvec{t}}_1=\varvec{\sigma }^{\mathrm{t}}\cdot {\varvec{n}}\) is introduced.

For the last term in (27), integration by parts as well as the divergence theorem are applied a second time so that

$$\begin{aligned} 0 = \int _{{\mathcal {B}}_t} \nabla _{\!\varvec{x}}\varvec{\eta } : \varvec{\sigma }^{\mathrm{{sym}}}\,{{\mathrm{d}}} v - \int _{\partial {\mathcal {B}}_t} \varvec{\eta } \cdot {\varvec{t}}_1 \,{{\mathrm{d}}} a - \int _{{\mathcal {B}}_t} \tfrac{1}{2}\left[ \varvec{\epsilon } : \nabla _{\!\varvec{x}}\nabla _{\!\varvec{x}}\varvec{\eta }\right] : {\varvec{m}}^{\mathrm{t}} \,{{\mathrm{d}}} v + \int _{\partial {\mathcal {B}}_t} \tfrac{1}{2}\, \nabla _{\!\varvec{x}}\varvec{\eta } :\left[ {\varvec{t}}_2 \cdot \varvec{\epsilon } \right] \,{{\mathrm{d}}} a \end{aligned}$$
(28)

is obtained. Vector \({\varvec{t}}_2={\varvec{m}}^{\mathrm{t}}\cdot {\varvec{n}}\) represents the couples acting on the surface such as the previously introduced vector \({\varvec{t}}_1\) accounts for the surface tractions.

The terms which are related to the couple-stress tensor in (28) can be rewritten by using the definition of the curl operator, so that an alternative representation of the weak form reads

$$\begin{aligned} 0 = \int _{{\mathcal {B}}_t} \nabla _{\!\varvec{x}}\varvec{\eta } : \varvec{\sigma }^{\mathrm{{sym}}}\,{{\mathrm{d}}} v - \int _{\partial {\mathcal {B}}_t} \varvec{\eta } \cdot {\varvec{t}}_1 \,{{\mathrm{d}}} a + \int _{{\mathcal {B}}_t} \left[ \nabla _{\!\varvec{x}}\left[ \tfrac{1}{2}\,\nabla _{\!\varvec{x}}\times \varvec{\eta } \right] \right] : {\varvec{m}}^{\mathrm{t}} \,{{\mathrm{d}}} v - \int _{\partial {\mathcal {B}}_t} \left[ \tfrac{1}{2}\,\nabla _{\!\varvec{x}}\times \varvec{\eta } \right] \cdot {\varvec{t}}_2 \,{{\mathrm{d}}} a . \end{aligned}$$
(29)

This format allows an interpretation of the specific occurrences of the test function from the perspective of the principle of virtual power. The test function \(\varvec{\eta }\) itself may be regarded as a virtual velocity field which is related to the classic tensorial quantities in (29). In analogy, the term \(\tfrac{1}{2}\,\nabla _{\!\varvec{x}}\times \varvec{\eta }\), which corresponds to the higher-gradient terms in (29), may be interpreted as a virtual spin vector, cf. [20].

From the weak form (28) that has been derived for the deformed configuration, the respective formulation in the reference configuration is obtained by making use of the relations specified in (12). From the third term on the right-hand side in (28), which includes the second-order gradient of the test function, two separate terms follow from the pull-back operation. The weak form in the reference configuration accordingly reads

$$\begin{aligned} 0&= \int _{{\mathcal {B}}_0} \nabla _{\!\varvec{X}}\varvec{\eta } : \left[ \varvec{\sigma }^{\mathrm{sym}} \cdot \, \text {cof} ({\varvec{F}}) \right] \,{{\mathrm{d}}} V - \int _{\partial {\mathcal {B}}_0} \varvec{\eta } \cdot \varvec{\sigma }^{\mathrm{t}} \cdot \,\text {cof}({\varvec{F}}) \cdot {\varvec{N}}\,{{\mathrm{d}}} A \nonumber \\&\quad - \int _{{\mathcal {B}}_0} \tfrac{1}{2}\, \nabla _{\!\varvec{X}}\nabla _{\!\varvec{X}}\varvec{\eta } :\!\cdot \left[ \left[ \varvec{\epsilon } \cdot {\varvec{m}}^{\mathrm{t}} \right] : \left[ {\varvec{F}}^{\mathrm{-t}} \,{\overline{\otimes }}\,\text {cof} ({\varvec{F}}) \right] \right] \,{{\mathrm{d}}} V \nonumber \\&\quad - \int _{{\mathcal {B}}_0} \tfrac{1}{2}\, \nabla _{\!\varvec{X}}\varvec{\eta } : \left[ \left[ \varvec{\epsilon } \cdot {\varvec{m}}^{\mathrm{t}} \cdot \text {cof}({\varvec{F}}) \right] : \bigg [ \left[ \left[ -{\varvec{F}}^{\mathrm{-t}}\,{\underline{\otimes }}\,{\varvec{F}}^{-1}\right] : \varvec{\varUpsilon } \right] : \left[ {\varvec{I}} \,{\underline{\otimes }}\,{\varvec{I}} \right] \bigg ] \right] \,{{\mathrm{d}}} V \nonumber \\&\quad + \int _{\partial {\mathcal {B}}_0} \tfrac{1}{2} \,\nabla _{\!\varvec{X}}\varvec{\eta } : \left[ \left[ \varvec{\epsilon } \cdot {\varvec{m}}^{\mathrm{t}} \right] : \left[ \text {cof}({\varvec{F}}) \,{\overline{\otimes }}\,{\varvec{F}}^{\mathrm{-t}} \right] \right] \cdot {\varvec{N}}\,{{\mathrm{d}}} A . \end{aligned}$$
(30)

Following the isoparametric concept and employing a Bubnov–Galerkin interpolation scheme, domain \({\mathcal {B}}_0\), test function \(\varvec{\eta }\) and placement function \(\varvec{\varphi }\) are approximated by the same basis functions. Within the scope of this work, NURBS basis functions R are employed so that the discretised kinematic quantities are

$$\begin{aligned} \varvec{\eta }^h = \sum _{A=1}^{\mathrm{{n_{en}}}} \varvec{\eta }^{eA} R^A&, \quad \varvec{\varphi }^h = \sum _{A=1}^{\mathrm{{n_{en}}}} \varvec{\varphi }^{eA} R^A, \end{aligned}$$
(31)

with the number of active basis functions on one element e denoted as \(\mathrm {n_{en}}\). Inserting both relations into the referential weak form (30), a representation is obtained which includes derivatives of the basis functions up to second order. Accordingly, the internal force vector takes the discretised form

(32)

where \(\mathrm {n_{el}}\) denotes the total number of elements. The external force vector respectively is

(33)

Operator establishes an assembly of the local force contributions to the global degrees of freedom.

From the integrability condition of the weak form, it follows that global \(C^0\)-continuity is not sufficient for a proper approximation of the field variable and test function, since, e.g., products of second-order gradients occur in the second integral in (32). Within the examples presented in this work, an at least \(C^1\)-continuous NURBS-based interpolation is employed throughout the whole domain.

3.2 Linearisation

The solution of the equation system (30) within the isogeometric finite element framework is obtained by employing a Newton–Raphson scheme. The residuum is determined by the internal and external force vectors discussed in detail in Sect. 3.1, i.e.

$$\begin{aligned} {\varvec{r}}^{\mathrm{h}} = {\varvec{f}}_{\mathrm{int}}^{\mathrm{h}} - {\varvec{f}}_{\mathrm{ext}}^{\mathrm{h}}. \end{aligned}$$
(34)

In the kth iteration step, the linearised form of the residuum reads

$$\begin{aligned} {\varvec{r}}_{k+1}^{\mathrm{h}} = {\varvec{r}}_{k}^{\mathrm{h}} + \varDelta {\varvec{r}}^{\mathrm{h}}. \end{aligned}$$
(35)

Due to the particular dependencies of the residual function \({\varvec{r}}^{\mathrm{h}}=\widetilde{{\varvec{r}}}^{\mathrm{h}}({\varvec{F}}^{\mathrm{h}}(\widehat{\varvec{\varphi }}),\varvec{\varUpsilon }^{\mathrm{h}}(\widehat{\varvec{\varphi }}))\), two contributions are considered for the increment \(\varDelta {\varvec{r}}^{\mathrm{h}}\), to be specific

$$\begin{aligned} \varDelta {\varvec{r}}^{\mathrm{h}} = \frac{{{\mathrm{d}}} {\varvec{r}}^{\mathrm{h}}}{{{\mathrm{d}}} \widehat{\varvec{\varphi }}} \cdot \varDelta \widehat{\varvec{\varphi }} = \left[ \frac{\partial {\varvec{r}}^{\mathrm{h}}}{\partial {\varvec{F}}^{\mathrm{h}}} : \frac{\partial {\varvec{F}}^{\mathrm{h}}}{\partial \widehat{\varvec{\varphi }}} + \frac{\partial {\varvec{r}}^{\mathrm{h}}}{\partial \varvec{\varUpsilon }^{\mathrm{h}}} :\!\cdot \, \frac{\partial \varvec{\varUpsilon }^{\mathrm{h}}}{\partial \widehat{\varvec{\varphi }}} \right] \cdot \varDelta \widehat{\varvec{\varphi }} = {\varvec{K}}\cdot \varDelta \widehat{\varvec{\varphi }} \end{aligned}$$
(36)

with the global list of degrees of freedom \(\widehat{\varvec{\varphi }}\), the tangent stiffness matrix \({\varvec{K}}\) and with the partial derivatives

(37)

in the discretised form. Under the assumption of dead loads, only the sensitivities of the internal force contributions need to be considered. The global system of equations is finally obtained as

$$\begin{aligned} -\left[ {\varvec{r}}^{\mathrm{h}}\right] _k=\left[ {\varvec{K}}\right] _k \cdot \left[ \varDelta \widehat{\varvec{\varphi }}\right] _k. \end{aligned}$$
(38)

The general form of the tangent stiffness matrix \({\varvec{K}}\) is derived in Appendix A.

4 Representative numerical examples

Two numerical examples are presented in this section to demonstrate the behaviour of a material reinforced by fibres possessing bending stiffness. The first example is used for a comparison of the numerical results obtained by the proposed isogeometric approach against the semi-analytical solution provided in [25]. The second model contains a more complex geometry and is more closely related to practical applications. For both examples, a plane strain condition is employed and the constitutive equations are based on the same energy function.

4.1 Specific form of the energy function and stress tensors

In (21), the general form of the stored energy density function for the material model introduced in [9] has been provided. For the particular examples presented in this contribution, the energy takes an additive decomposition and, as in [20], specifically consists of three parts, namely

$$\begin{aligned} W = W^{\mathrm{iso}} + W^{\lambda _a} + W^{\varvec{\kappa }_0}. \end{aligned}$$
(39)

The isotropic part resembles the behaviour of the matrix material without taking into account the reinforcement by fibres. It takes the form

$$\begin{aligned} W^{\mathrm{iso}} = \lambda \, \frac{I_3-1}{4} - \left[ \frac{\lambda }{2} +\mu \right] \ln (\sqrt{I_3}) + \frac{\mu }{2} \left[ I_1-3\right] \quad \text {with} \quad I_1 = {\varvec{C}}:{\varvec{I}},\quad I_3 = \det ({\varvec{C}}). \end{aligned}$$
(40)

The Lamé-type constants are set to \(\lambda = 1.037\times 10^5\,\hbox {N}\, \hbox {mm}^{-2}\) and \(\mu = 4.4444\times 10^4\,\hbox {N}\, \hbox {mm}^{-2}\). The second part \(W^{\lambda _a}\) corresponds to the classic fibre stretch-related transversely isotropic contributions of the fibre-reinforced material. It has already been studied extensively, e.g. in [7, 30, 31], and is thus not in the focus of the present contribution. As this work proceeds, the part \(W^{\lambda _a}\) is accordingly assumed to be constant. The last contribution

$$\begin{aligned} W^{\varvec{\kappa }_0} = c\, I_6 \quad \text {with} \quad I_6 = \left[ \varvec{\varLambda } \cdot {\varvec{a}}_0\right] \cdot \left[ \varvec{\varLambda } \cdot {\varvec{a}}_0\right] =\varvec{\kappa }_0\cdot \varvec{\kappa }_0 \end{aligned}$$
(41)

incorporates the energy which is related to the higher-gradient terms that are specific for the material model proposed in [9]. From the particular form of the referential gradient of the fibre direction vector (15), it follows that invariant \(I_6\) in (41) includes the gradient of the fibre stretch as well as the fibre curvature, see the discussion in [19]. In accordance with the latter, parameter c is associated with a bending stiffness of the fibres. However, the contributions of the fibre stretch gradient are not to be neglected when finite deformations are considered. The sense of the fibre orientation does not have any impact on the energy contribution in (41) since invariant \(I_6\) is of even order in the fibre direction vector \({\varvec{a}}_0\). In the examples presented in this contribution, parameter c as well as the fibre direction will take different values in order to examine their influence on the simulation results.

Considering the stored energy density function specified in (39) and using the general derivations of the symmetric part of the stress tensor and the couple-stress tensor (22) and (23), their specific forms follow as

$$\begin{aligned} \varvec{\sigma }^{\mathrm{sym}}&= J^{-1}{\varvec{F}} \cdot \left[ \tfrac{\lambda }{2} \left[ I_3-1\right] {\varvec{C}}^{-1} + \mu \left[ {\varvec{I}}-{\varvec{C}}^{-1}\right] \right] \cdot {\varvec{F}}^{\mathrm{t}} \nonumber \\&\quad + 2\,c\,J^{-1} \left[ {\varvec{G}}\cdot \left[ {\varvec{a}}_0 \otimes \varvec{\varLambda }\cdot {\varvec{a}}_0\right] \cdot {\varvec{F}}^{\mathrm{t}} + {\varvec{F}}\cdot \left[ \varvec{\varLambda }\cdot {\varvec{a}}_0 \otimes {\varvec{a}}_0 \right] \cdot {\varvec{G}}^{\mathrm{t}}\right] \end{aligned}$$
(42)

and

$$\begin{aligned} \overline{{\varvec{m}}}^{\mathrm{t}} = -\frac{4}{3}\,c\,J^{-1}\varvec{\epsilon }:\left[ {\varvec{F}}\cdot \left[ \varvec{\varLambda }\cdot {\varvec{a}}_0 \otimes {\varvec{a}}_0\right] \cdot \left[ {\varvec{F}}^{\mathrm{t}} \,{\overline{\otimes }}\,{\varvec{a}}_t + {\varvec{F}}^{\mathrm{t}} \otimes {\varvec{a}}_t \right] \right] . \end{aligned}$$
(43)

Recapitulating the structure of the stored energy density function (39), the first term in the above given form of the stress tensor represents the isotropic part, whereas the second term and the contributions of the couple-stress tensor correspond to the part that incorporates the fibre properties. For a vanishing fibre bending stiffness, i.e. \(c=0\), the model reduces to a classic neo-Hookean material.

In the small strain version of the model that has been discussed in detail in [9, 22], the contributions from the fibre stretch gradient are neglected in the derivation of the stress and couple-stress tensor because they are of higher order. In contrast thereto, both contributions, namely the fibre curvature and the fibre stretch gradient, are included in the form of the stress tensors in (42) and (43).

In order to obtain the specific form of the tangent stiffness matrix for the considered energy function, the sensitivities of the stress and couple-stress tensor are derived and presented in Appendix A.

4.2 Cylindrical tube subject to a pure azimuthal shear deformation

The pure azimuthal shear deformation of a cylindrical tube with radially aligned fibres is considered in order to compare the numerical results with the semi-analytical solution provided in [25]. In [22], the same problem has been analysed by means of an isogeometric finite element method for a small strain setting. The model including finite deformations has been elaborated in [21] by employing a multi-field method.

For an accurate comparison of the results, dimensionless versions of the stress and couple-stress tensor are used, to be specific

$$\begin{aligned} \varvec{\sigma }^*&= \frac{r_i}{{\overline{u}}_\varphi \, \mu } \frac{\zeta ^2-1}{\zeta }\, \varvec{\sigma }, \quad {\varvec{m}}^* = \frac{1}{{\overline{u}}_\varphi \, \mu } \frac{\zeta ^2-1}{\zeta } \, {\varvec{m}} \quad \text {with} \quad \zeta = \frac{r_o}{r_i}. \end{aligned}$$
(44)

By using a cylindrical base system {\({\varvec{e}}_r,{\varvec{e}}_\varphi ,{\varvec{e}}_z\)}, \({\overline{u}}_\varphi \) represents the prescribed azimuthal displacement on the surface of a tube with inner radius \(r_i\) and outer radius \(r_o\), see Fig. 2. The particular values for these quantities will be determined in Sect. 4.2.1.

4.2.1 Isogeometric model

The isogeometric model for the cylindrical tube with radii \(r_i=1\,\hbox {mm}\) and \(r_o=2.5\,\hbox {mm}\) is adopted from [22]. A polynomial degree of \(p=4\) is chosen. The employment of linear constraints for the location as well as displacement of repeated control points leads to global \(C^1\)-continuity which is sufficient for the fulfilment of the integrability condition posed by (32). More details on the construction of the cylindrical tube model can be found in [22] and references cited therein.

In accordance with the calculations in [25], the tube is analysed under a pure azimuthal shear deformation which is prescribed on the outer radius by means of Dirichlet boundary conditions, whereas the inner radius is fixed. The azimuthal displacement is chosen in such a way that the outer surface undergoes a rotation of \(\pi /9\) around the tube’s middle axis. The outer radius of the tube is not changed by this deformation so that the applied boundary conditions yield the total volume of the tube to be conserved. Along with this observation, extensible fibres are assumed in order to obtain pure azimuthal shear in the finite deformation setting, cf. [26]. Surface tractions and surface couples are assumed to vanish at the outer cylinder radius, i.e. \({\varvec{t}}_1={\varvec{0}}\) and \({\varvec{t}}_2={\varvec{0}}\). The discretised model including the particular boundary conditions is shown in Fig. 2. The mesh contains \(\mathrm{{n_{el}}=832}\) elements and is based on \(\mathrm {n}_{\mathrm{cp}} = 1260\) control points.

Fig. 2
figure 2

Boundary conditions and mesh of the cylindrical tube with \(\mathrm {n}_{\mathrm{cp}} = 1260\) and \(\mathrm{{n_{el}}=832}\)

Full size image
Fig. 3
figure 3

Deformation plots of the cylindrical tube

Full size image
Fig. 4
figure 4

Distribution of the dimensionless stress and couple-stress contributions

Full size image

4.2.2 Numerical results

In the present example, the fibre bending stiffness is represented by the non-dimensional parameter

$$\begin{aligned} \lambda ^* = \frac{d_f}{2\,\mu \,r_i\, [r_o-r_i]} \quad \text {with} \quad d_f = \frac{8}{3}c, \end{aligned}$$
(45)

cf. [22, 25]. Within the simulations performed by means of the proposed isogeometric approach, different values have been employed for this parameter, namely \({\lambda ^*\in \{0.0,0.005,0.03,0.1\}}\). In all cases, the fibres are initially aligned in radial direction.

In Fig. 3, the deformation pattern of the tube is shown. In the case where \(\lambda ^*=0\), no fibres are present in the material. As the energy contributions belonging to the fibres become active by employing non-zero values for the parameter, a resistance against bending, which increases in accordance with higher values of \(\lambda ^*\), can be observed.

In Fig. 4a, the results for the dimensionless stress contributions \([\sigma _{r\varphi }]^*\) and \([\sigma _{\varphi r}]^*\) are presented as a function of the cylinder radius. Fig. 4b shows the respective results for the symmetric stress part \([\sigma _{r\varphi }^{\mathrm{{sym}}}]^*\) as well as for the only non-zero couple-stress contribution \([m_{rz}]^*\). The presented solutions for the finite strain setting are not only in accordance with the results from [21] produced by a multi-field method by using the same constitutive model, but also with those obtained by the linearised formulation documented in [22]. For a prescribed rotation up to \(\pi /9\), as employed in this contribution, both formulations show quantitatively coinciding results. Also the semi-analytical solution, which has been obtained in [25] from the application of a power series method, is in quantitative agreement with the results as shown in [22]. Whereas these observations hold for the prescribed rotation of \(\pi /9\) of the outer tube radius, a deviation from the small strain results in [22, 25] is observable when significantly larger deformations are considered. In Fig. 5a–d, simulation results corresponding to rotations of \(\pi /9,\pi /6\) and \(2\pi /9\) around the tube’s middle axis are presented for \(\lambda ^*=0.03\). With an increasingly large deformation, the difference between the linearised and the non-linear modelling approach becomes more pronounced in all stress and couple-stress contributions considered.

4.3 Tensile test of a notched plate

A more complex example is represented by the fibre-reinforced notched plate shown in Fig. 6. By employing an offset between the notches, a bending deformation mode is activated as a tensile test is performed. The influence of the fibre bending stiffness parameter c as well as of the initial fibre direction field will be elaborated in this example.

4.3.1 Isogeometric model

In Fig. 6, the mesh for the notched plate is shown and the dimensions of the model are presented. The width of the inner part of the plate is \(w=12\,\hbox {mm}\) and the total length is \(l=120\,\hbox {mm}\). Between the centre points of the circular notches with radii \(r=\tfrac{3}{8}\,w=4.5\,\hbox {mm}\), an offset of \(d=\tfrac{3}{2}\,w=18\,\hbox {mm}\) is employed.

The discretisation of the notched plate is obtained by \(\mathrm {n_{el}}=990\) elements. For the approximation of the placement field and the test function, NURBS basis functions with a polynomial degree of \(p=4\) are used in accordance with the previous example. The control polygon thus consists of \(\mathrm{{n}_{\mathrm{cp}} = 1410}\) control points. Within the whole domain, a global continuity of \(C^{p-1}\), accordingly \(C^3\), is ensured due to the characteristic properties of NURBS, cf. [27,28,29].

In analogy to a uni-axial tensile test, the plate is clamped at both ends, meaning that displacements in \({\varvec{e}}_2\)-direction of the left and right boundary nodes are prevented. In \({\varvec{e}}_1\)-direction, a uniform displacement is prescribed on both sides. The total elongation of the plate is set to 1/5 of its length so that \(\Vert \overline{{\varvec{u}}}\Vert =12\,\hbox {mm}\). Similar to the previous example, it is assumed that no surface tractions or surface couples are present, i.e. \({\varvec{t}}_1={\varvec{0}}\) and \({\varvec{t}}_2={\varvec{0}}\).

4.3.2 Numerical results

Within the isogeometric finite element analysis of the notched plate, two different values of the fibre bending stiffness parameter are employed and two initial fibre orientations are considered. Specifically speaking, a reinforcement with fibres that are aligned in \({\varvec{e}}_1\)-direction as well as diagonally aligned fibres are taken into account for fibre bending stiffness parameters \(c\in \{2\times 10^4\,\hbox {N},3\times 10^4\,\hbox {N}\}\). In the case of diagonally aligned fibres, the fibre direction vector exhibits an angle of \(\alpha =\pi /4\) to the \({\varvec{e}}_1\)-direction.

In Fig. 7, the deformed configuration of the notched plate is shown after the analysis under the above-mentioned boundary conditions without the presence of fibres. Due to the particular boundary conditions discussed in Sect. 4.3.1, the plate is stretched in \({\varvec{e}}_1\)-direction and the notches change their shape significantly. The middle part of the plate undergoes a bending deformation in consequence of the offset between the two notches.

Figure 8 provides a more detailed view on the deformed mesh and compares the deformation pattern for \(c=0\) and \(c=3\times 10^4\,\hbox {N}\) for fibres aligned with the \({\varvec{e}}_1\)-direction, i.e. \(\alpha =0\). The largest influence of the fibres on the overall deformation is obtained in the region of the notches. Due to the bending deformation, the fibre curvature part in the energy contribution (41) is activated. For the different fibre orientations, Fig. 9 presents the deformed mesh in more detail. It is shown that for fibres which are aligned with the \({\varvec{e}}_1\)-direction in the initial configuration, the deformation of the vertical element edges is rather similar to the case of a non-reinforced material. However, if a fibre angle of \(\alpha =\pi /4\) is employed in the initial state, a different deformation pattern is obtained in the region of the circular notches. In particular, the vertical element edges are bent into one preferred direction near the lower boundary, cf. Fig. 9b.

Fig. 5
figure 5

Distribution of the dimensionless stress and couple-stress contributions for different prescribed rotations

Full size image
Fig. 6
figure 6

Boundary conditions and mesh of the notched plate with \(\mathrm{{n}_{\mathrm{cp}} = 1410}\) and \(\mathrm {n_{el}}=990\)

Full size image
Fig. 7
figure 7

Deformed configuration of the notched plate without fibres

Full size image
Fig. 8
figure 8

Detailed view on the deformed configuration of the notched plate without fibres (solid lines) and with fibres initially aligned in \({\varvec{e}}_1\)-direction (dashed lines) with \(c=3\times 10^4\,\hbox {N}\)

Full size image
Fig. 9
figure 9

Detailed views on the deformed configurations of the notched plate

Full size image
Fig. 10
figure 10

Distribution of the couple-stress contribution \(m_{13}\) for the notched plate with fibres aligned in \({\varvec{e}}_1\)-direction (top) and with diagonally aligned fibres (bottom) with \(c=2\times 10^4\,\hbox {N}\)

Full size image
Fig. 11
figure 11

Distribution of the couple-stress contribution \(m_{13}\) for the notched plate with fibres aligned in \({\varvec{e}}_1\)-direction (top) and with diagonally aligned fibres (bottom) with \(c=3\times 10^4\,\hbox {N}\)

Full size image
Fig. 12
figure 12

Distribution of the couple-stress contribution \(m_{23}\) for the notched plate with fibres aligned in \({\varvec{e}}_1\)-direction (top) and with diagonally aligned fibres (bottom) with \(c=2\times 10^4\,\hbox {N}\)

Full size image
Fig. 13
figure 13

Distribution of the couple-stress contribution \(m_{23}\) for the notched plate with fibres aligned in \({\varvec{e}}_1\)-direction (top) and with diagonally aligned fibres (bottom) with \(c=3\times 10^4\,\hbox {N}\)

Full size image
Fig. 14
figure 14

Distribution of the stress contributions \(\sigma _{12}\), \(\sigma ^{\mathrm{sym}}_{12}\) and \(\sigma ^{\mathrm{skw}}_{12}\) for the notched plate with fibres aligned in \({\varvec{e}}_1\)-direction with \(c=3\times 10^4\,\hbox {N}\)

Full size image
Fig. 15
figure 15

Integrated reaction force in \({\varvec{e}}_1\)-direction in dependence of the prescribed displacement on the right boundary of the notched plate

Full size image

The distribution of the couple-stresses for the current example is presented in Figs. 10, 11, 12 and 13. Due to the two-dimensional setting, the only non-zero couple-stress contributions are \(m_{13}\) and \(m_{23}\). The highest values of these two quantities concentrate in the region of the notches. In addition, non-zero couple-stresses occur in the transition zones between the middle and end sections of the plate and at the boundary nodes on the left and on the right ends where the displacement in \({\varvec{e}}_2\)-direction is prevented.

Regarding the different fibre orientations employed in the simulation, a varying distribution of the couple-stresses can be observed. In the case of an initial fibre alignment in \({\varvec{e}}_1\)-direction, couple-stresses especially appear in the region of the notches throughout the whole width of the plate. The absolute values of the contribution \(m_{13}\) are significantly larger than those of \(m_{23}\). If, on the other hand, the fibres are initially aligned diagonally in the material, the stresses are more localised at the notches and decrease over the width of plate. Besides, \(m_{13}\) and \(m_{23}\) show similar distributions.

The distribution of the shear stress contribution \(\sigma _{12}\) is shown in Fig. 14 together with its symmetric and skew-symmetric parts exemplary for the case of fibres initially aligned in \({\varvec{e}}_1\)-direction. Similar to the couple-stresses, the stresses take their maximum values in the inhomogeneously deforming regions close to the notches. In the presented example the skew-symmetric stresses take values of the same order as their symmetric counterparts so that both contributions have a significant impact on the total stress values. This relation, however, depends on the prescribed fibre bending stiffness parameter. For rather small values, the symmetric part of the stress tensor becomes more prominent in comparison to the skew-symmetric part, whereas for an increasing fibre bending stiffness, the skew-symmetric stresses exceed the symmetric contributions. For a fibre bending stiffness parameter of \(c=3\times 10^4\,\hbox {N}\), as employed in the results in Fig. 14, the skew-symmetric part of the stress contribution \(\sigma _{12}\) is dominant.

Figure 15 presents the integrated reaction force in \({\varvec{e}}_1\)-direction over the prescribed displacement value for the different cases of initial fibre alignment and fibre bending stiffness. It can be observed that the curvature of the graphs, which show an overall non-linear behaviour, is slightly different depending on the initial fibre direction and fibre bending stiffness. Especially in the last simulation steps an alignment in \({\varvec{e}}_1\)-direction yields the highest reaction force. For higher values of the fibre bending stiffness parameter, the material response becomes stiffer and increasingly distinguishable from the case of a non-reinforced material.

Remark 1

In Sect. 4.1, the energy contribution belonging to a transversely isotropic material behaviour has been assumed to be constant in order to examine the influence of the higher-gradient contributions, respectively of the fibre bending stiffness, exclusively. If the influence of this energy part had additionally been taken into account instead, a more significant difference in the deformations and in the reaction force would have been expected when comparing the non-reinforced with the fibre-reinforced material.

5 Concluding remarks

In extension to the isogeometric finite element approach to fibre-reinforced composites possessing fibre bending stiffness developed in [22] subject to a small strain setting, an isogeometric approach to the general finite strain version of the problem has been presented in this contribution.

On the basis of the framework introduced in [9], a referential form of the fibre direction gradient has been included in the stored energy density function through an additional invariant. In particular, this gradient includes the fibre curvature as well as the gradient of the fibre stretch. For the incorporation of these higher-gradient contributions into the continuum model, the couple-stress theory has been employed and a partial differential equation of fourth order has been obtained.

Due to the continuity properties of NURBS basis functions, an isogeometric approach has been used to solve a discretised version of this equation within a finite element framework. To this end, a global continuity of at least \(C^1\) has been realised for both examples presented in this contribution.

The analysis of a cylindrical tube under pure azimuthal shear with radially aligned fibres has shown that the results obtained by the presented method are in accordance with the finite element results from [20, 22] as well as with the semi-analytical solution from [25] up to a certain amount of prescribed shear. For significantly large deformations, a deviation from the results obtained by the linearised formulation can, however, be observed. By the analysis of a plate with circular offset notches, a more detailed view on the impact of the fibre bending stiffness and initial fibre direction has been achieved. Especially in the region of the inhomogeneous deformation, the higher-gradient contributions to the stored energy density function significantly influence the deformation pattern as well as the stress and couple-stress distribution in the material. Depending on the value of the fibre bending stiffness parameter, the skew-symmetric and symmetric stress contributions can take similar values. Thus, both parts contribute significantly to the total stresses.

Overall, this contribution established a basis for the modelling of complex boundary value problems including fibre-reinforced composites with fibre bending stiffness in a general finite deformation setting. In future works, this basic approach shall be used for advanced constitutive modelling such as for materials with initially curved fibres and extended by employing additional deformation modes like fibre twist. Also complex three-dimensional structures shall be analysed with the proposed method.