Abstract
We study the Langevin dynamics of a U(1) lattice gauge theory on the two-dimensional torus, and prove that they converge for short time in a suitable gauge to a system of stochastic PDEs driven by space-time white noises. We fix gauge via a DeTurck trick. This also yields convergence of some gauge invariant observables on a short time interval. The proof relies on a discrete version of the theory of regularity structures.



Similar content being viewed by others
Notes
The specific value of the coupling constant \(\lambda \) is not important. We prefer to have this parameter in the model for convenience so that a “perturbation theory” will be more organized.
If we view \(D^A\) as an operator which gives a 1-form, then for a 1-form B, \((D^A)^* B = -\text{ div }B + i A\cdot B\).
Of course the initial condition will change under this transformation.
Let’s mention that [Rad92] used another way to tackle the lack of parabolicity in a deterministic case by studying the coupled system for the evolution of A and its curvature.
In discussion with I.Bailleul we learned a way of continuously regularizing the equation without breaking the gauge symmetry in the physics literature, that is, mollifying the noise by a function of the gauge covariant Laplacian, see [BHST87, Eq. (2.1)–(2.5)]; a natural choice of such function therein being the “heat kernel regulator” \(\exp (\varepsilon ^2\Delta _A )\) where \(\Delta _A\) is the gauge covariant Laplacian. It would be very interesting to study this rigorously, in particular show that this regularization yields the same limit.
We take this chance to make a few remarks on reflection positivity. Jaffe [Jaf15] pointed out the stochastic quantization equation starting from a generic initial condition would generally break reflection positivity for finite time. Therefore, it is unclear to us whether our approach to abelian gauge theory could restore reflection positivity in infinite time, since we haven’t obtained any global-in-time estimates. On the other hand, note that [GH18] used SPDE method to derive bounds which are strong enough to prove the tightness of the family of lattice \(\Phi ^4 \) measures which do have reflection positivity. It would be very interesting to see if the method of [GH18] could be applied to gauge theories.
Each square is simply an \(\varepsilon \times \varepsilon \) area surrounded by four edges. The notation \({\mathcal P}_\varepsilon \) here should not be confused with the operator \({\mathcal P}^\varepsilon \) introduced in (4.20).
The scaling parameter \(\lambda \) appearing in functions \(\varphi ^\lambda \) should be distinguished from the coupling constant in our system (1.5). Since this is always clear from the context, we choose to use the same letter (which is a slight abuse of notation).
Here the fact that the transformation (3.3) is identity at \(t=0\) is only a matter of convenience. One could also change the initial condition to a gauge equivalent one.
Alternatively one could introduce modeled distributions on both vertices and edges, and two reconstruction operators (one on \(\Lambda _\varepsilon \) and one on \({\mathcal E}_\varepsilon \)). This however would probably cause notational complication.
Be cautious that product rule \(\partial (fg)=\partial f g+f\partial g\) does not exactly hold on lattice.
We thank the anonymous referee who suggested us to make this remark.
This does not follow automatically from the discrete analogue of (4.6a) since these are only assumed to hold for test functions at scale \(\lambda \ge \varepsilon \).
Here \(\nabla \varphi \) is merely a notation for a d component field and does not mean a gradient of a function. We also remark that in this paper we will only need abstract polynomials of order one. For higher order polynomials it is a bit more subtle because the finite difference of \(x^k\) is not \(k x^{k-1}\) for \(k\ge 2\).
We expect (see (5.7) below) our solutions to have the form
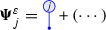 where “\((\cdots )\)” take values in the subspace spanned by \(\mathbf {1}\) and elements with strictly positive homogeneity; so the symbols
where “\((\cdots )\)” take values in the subspace spanned by \(\mathbf {1}\) and elements with strictly positive homogeneity; so the symbols 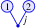 —which is not in the truncated regularity structure \(\hat{\mathscr {T}}\) as one may worry—will be cancelled by the “leading order” part of \(\varvec{\Psi }_1^\varepsilon \mathscr {D}_j \varvec{\Psi }_2^\varepsilon \) in (4.21). Same remark for the other abstract symbols of such kind in (4.21).
—which is not in the truncated regularity structure \(\hat{\mathscr {T}}\) as one may worry—will be cancelled by the “leading order” part of \(\varvec{\Psi }_1^\varepsilon \mathscr {D}_j \varvec{\Psi }_2^\varepsilon \) in (4.21). Same remark for the other abstract symbols of such kind in (4.21).We omit the dependence of \(b_j ,\varphi _j,\nabla b_j ,\nabla \varphi _j\) on \(\varepsilon \) in our notation.
The constant in front of the left hand side of [CST18, (4.9)] is \(\frac{1}{d}\) instead of 2 as here, because the heat kernel is defined as \((\partial _t - \frac{1}{2d}\Delta )^{-1} \) therein.
This is by a discrete version of Helmholtz decomposition or Hodge decomposition (see e.g. [War13, Chapter 6]) and its proof is exactly the same as its continuous version and thus is omitted.
References
Balaban, T.: (Higgs)\(_{2,3}\) quantum fields in a finite volume. I. A lower bound. Commun. Math. Phys. 85(4), 603–626 (1982)
Balaban, T.: (Higgs)\(_{2,\,3}\) quantum fields in a finite volume. II. An upper bound. Commun. Math. Phys. 86(4), 555–594 (1982)
Balaban, T.: (Higgs)\(_{2,3}\) quantum fields in a finite volume. III. Renormalization. Commun. Math. Phys. 88(3), 411–445 (1983)
Balaban, T.: Large field renormalization. II. Localization, exponentiation, and bounds for the \({ R}\) operation. Commun. Math. Phys. 122(3), 355–392 (1989)
Bailleul, I., Bernicot, F.: High order paracontrolled calculus. Forum Math. Sigma 7, e44, 94 (2019). https://doi.org/10.1017/fms.2019.44
Balaban, T., Brydges, D., Imbrie, J., Jaffe, A.: The mass gap for Higgs models on a unit lattice. Ann. Phys. 158(2), 281–319 (1984). https://doi.org/10.1016/0003-4916(84)90121-0
Bruned, Y., Chandra, A., Chevyrev, I., Hairer, M.: Renormalising SPDEs in regularity structures (2017). arXiv preprint arXiv:1711.10239
Brydges, D., Fröhlich, J., Seiler, E.: Diamagnetic and critical properties of Higgs lattice gauge theories. Nucl. Phys. B 152(3–4), 521–532 (1979). https://doi.org/10.1016/0550-3213(79)90095-6
Brydges, D., Fröhlich, J., Seiler, E.: On the construction of quantized gauge fields. I. General results. Ann. Phys. 121(1–2), 227–284 (1979). https://doi.org/10.1016/0003-4916(79)90098-8
Brydges, D.C., Fröhlich, J., Seiler, E.: Construction of quantised gauge fields. II. Convergence of the lattice approximation. Commun. Math. Phys. 71(2), 159–205 (1980)
Brydges, D.C., Fröhlich, J., Seiler, E.: On the construction of quantized gauge fields. III. The two-dimensional abelian Higgs model without cutoffs. Commun. Math. Phys. 79(3), 353–399 (1981)
Bern, Z., Halpern, M., Sadun, L., Taubes, C.: Continuum regularization of quantum field theory (ii).: Gauge theory. Nucl. Phys. B 284, 35–91 (1987)
Bruned, Y., Hairer, M., Zambotti, L.: Algebraic renormalisation of regularity structures. Invent. Math. 215(3), 1039–1156 (2019). https://doi.org/10.1007/s00222-018-0841-x
Balaban, T., Imbrie, J., Jaffe, A.: Renormalization of the Higgs model: minimizers, propagators and the stability of mean field theory. Commun. Math. Phys. 97(1–2), 299–329 (1985)
Balaban, T., Imbrie, J.Z., Jaffe, A.: Effective action and cluster properties of the abelian Higgs model. Commun. Math. Phys. 114(2), 257–315 (1988)
Chandra, A., Chevyrev, I., Hairer, M., Shen, H.: Langevin dynamic for the 2D Yang–Mills measure (2020). arXiv:2006.04987
Charalambous, N., Gross, L.: The Yang–Mills heat semigroup on three-manifolds with boundary. Commun. Math. Phys. 317(3), 727–785 (2013)
Charalambous, N., Gross, L.: Neumann domination for the Yang–Mills heat equation. J. Math. Phys. 56(7), 073505 (2015)
Chouk, K., Gairing, J., Perkowski, N.: An invariance principle for the two-dimensional parabolic Anderson model with small potential. Stoch. Partial Differ. Equ. Anal. Comput. 5(4), 520–558 (2017)
Chandra, A., Hairer, M.: An analytic BPHZ theorem for regularity structures (2016). arXiv preprint arXiv:1612.08138
Chandra, A., Hairer, M., Shen, H.: The dynamical sine-Gordon model in the full subcritical regime (2018). arXiv preprint arXiv:1808.02594
Cannizzaro, G., Matetski, K.: Space-time discrete KPZ equation. Commun. Math. Phys. 358(2), 521–588 (2018). https://doi.org/10.1007/s00220-018-3089-9
Chandra, A., Shen, H.: Moment bounds for SPDEs with non-Gaussian fields and application to the Wong–Zakai problem. Electron. J. Probab. 22, Paper No. 68, 32 (2017). https://doi.org/10.1214/17-EJP84
Corwin, I., Shen, H., Tsai, L.-C.: \({\rm ASEP}(q, j)\) converges to the KPZ equation. Ann. Inst. Henri Poincaré Probab. Stat. 54(2), 995–1012 (2018). https://doi.org/10.1214/17-AIHP829
DeTurck, D.M.: Deforming metrics in the direction of their Ricci tensors. J. Differ. Geom. 18(1), 157–162 (1983)
Damgaard, P.H., Hüffel, H.: Stochastic quantization. Phys. Rep. 152(5–6), 227–398 (1987)
Donaldson, S.K., Kronheimer, P.B.: The geometry of four-manifolds. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (1990). Oxford Science Publications
Da Prato, G., Debussche, A.: Two-dimensional Navier–Stokes equations driven by a space-time white noise. J. Funct. Anal. 196(1), 180–210 (2002). https://doi.org/10.1006/jfan.2002.3919
Da Prato, G., Debussche, A.: Strong solutions to the stochastic quantization equations. Ann. Probab. 31(4), 1900–1916 (2003)
Driver, B.K.: Convergence of the \({\rm U}(1)_4\) lattice gauge theory to its continuum limit. Commun. Math. Phys. 110(3), 479–501 (1987)
Driver, B.K.: YM\({}_2\): continuum expectations, lattice convergence, and lassos. Commun. Math. Phys. 123(4), 575–616 (1989)
Erhard, D., Hairer, M.: Discretisation of regularity structures. Ann. Inst. Henri Poincaré Probab. Stat. 55(4), 2209–2248 (2019). https://doi.org/10.1214/18-AIHP947
Feehan, P.: Global existence and convergence of solutions to gradient systems and applications to Yang–Mills gradient flow (2014). arXiv preprint arXiv:1409.1525
Gubinelli, M., Hofmanová, M.: A PDE construction of the Euclidean \(\phi ^4_3 \) quantum field theory (2018). arXiv preprint arXiv:1810.01700
Gubinelli, M., Imkeller, P., Perkowski, N.: Paracontrolled distributions and singular PDEs. Forum Math. Pi 3, e6, 75 (2015). https://doi.org/10.1017/fmp.2015.2
Gubinelli, M., Perkowski, N.: KPZ reloaded. Commun. Math. Phys. 349(1), 165–269 (2017). https://doi.org/10.1007/s00220-016-2788-3
Gross, L.: Convergence of \({\rm U}(1)_{3}\) lattice gauge theory to its continuum limit. Commun. Math. Phys. 92(2), 137–162 (1983)
Gross, L.: The Yang–Mills heat equation with finite action (2016). arXiv preprint arXiv:1606.04151
Hairer, M.: Solving the KPZ equation. Ann. Math. (2) 178(2), 559–664 (2013). https://doi.org/10.4007/annals.2013.178.2.4
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014). https://doi.org/10.1007/s00222-014-0505-4. arXiv:1303.5113
Hairer, M., Matetski, K.: Discretisations of rough stochastic PDEs. Ann. Probab. 46(3), 1651–1709 (2018). https://doi.org/10.1214/17-AOP1212
Hairer, M., Quastel, J.: A class of growth models rescaling to KPZ. Forum Math. Pi 6, e3, 112 (2018). https://doi.org/10.1017/fmp.2018.2
Hairer, M., Shen, H.: The dynamical sine-Gordon model. Commun. Math. Phys. 341(3), 933–989 (2016). https://doi.org/10.1007/s00220-015-2525-3
Hairer, M., Shen, H.: A central limit theorem for the KPZ equation. Ann. Probab. 45(6B), 4167–4221 (2017)
Hairer, M., Xu, W.: Large-scale behavior of three-dimensional continuous phase coexistence models. Commun. Pure Appl. Math. 71(4), 688–746 (2018). https://doi.org/10.1002/cpa.21738
Hairer, M., Xu, W.: Large scale limit of interface fluctuation models. Ann. Probab. 47(6), 3478–3550 (2019). https://doi.org/10.1214/18-aop1317
Iyer, G., Spirn, D.: A model for vortex nucleation in the Ginzburg–Landau equations. J. Nonlinear Sci. 27(6), 1933–1956 (2017)
Jaffe, A.: Stochastic quantization, reflection positivity, and quantum fields. J. Stat. Phys. 161(1), 1–15 (2015)
King, C.: The \({\rm U}(1)\) Higgs model. I. The continuum limit. Commun. Math. Phys. 102(4), 649–677 (1986)
King, C.: The \({\rm U}(1)\) Higgs model. II. The infinite volume limit. Commun. Math. Phys. 103(2), 323–349 (1986)
Kennedy, T., King, C.: Spontaneous symmetry breakdown in the abelian Higgs model. Commun. Math. Phys. 104(2), 327–347 (1986)
Kupiainen, A.: Renormalization group and stochastic PDEs. Ann. Henri Poincaré 17(3), 497–535 (2016)
Lévy, T.: Yang–Mills measure on compact surfaces. Mem. Am. Math. Soc. 166(790), xiv+122 (2003). https://doi.org/10.1090/memo/0790
Lawler, G.F., Limic, V.: Random Walk: A Modern Introduction. Cambridge Studies in Advanced Mathematics, vol. 123. Cambridge University Press, Cambridge (2010)
Lui, S.H.: Numerical Analysis of Partial Differential Equations. Pure and Applied Mathematics (Hoboken). Wiley, Hoboken (2011)
Martin, J., Perkowski, N.: Paracontrolled distributions on Bravais lattices and weak universality of the 2d parabolic Anderson model. Ann. Inst. Henri Poincaré Probab. Stat. 55(4), 2058–2110 (2019). https://doi.org/10.1214/18-AIHP942
Magnen, J., Rivasseau, V., Sénéor, R.: Construction of \({\rm YM}_4\) with an infrared cutoff. Commun. Math. Phys. 155(2), 325–383 (1993)
Mourrat, J.-C., Weber, H.: Convergence of the two-dimensional dynamic Ising–Kac model to \(\Phi ^4_2\). Commun. Pure Appl. Math. 70(4), 717–812 (2017). https://doi.org/10.1002/cpa.21655
Mourrat, J.-C., Weber, H.: The dynamic \(\Phi ^4_3\) model comes down from infinity. Commun. Math. Phys. 356(3), 673–753 (2017)
Moinat, A., Weber, H.: Local bounds for stochastic reaction diffusion equations (2018). arXiv preprint arXiv:1808.10401
Moinat, A., Weber, H.: Local bounds for stochastic reaction diffusion equations. Electron. J. Probab. 25, Paper No. 17, 26 (2020). https://doi.org/10.1214/19-ejp397
Parisi, G., Wu, Y.S.: Perturbation theory without gauge fixing. Sci. Sin. 24(4), 483–496 (1981)
Rade, J.: On the Yang–Mills heat equation in two and three dimensions. Journal für die reine und angewandte Mathematik 1992(431), 123–164 (1992)
Rothe, H.J.: Lattice Gauge Theories: An Introduction, vol. 82. World Scientific Publishing Co Inc, Singapore (2012)
Sadun, L.A.: Continuum regularized Yang–Mills theory. Technical Report, California University, Berkeley (1987)
Sengupta, A.: Quantum Yang–Mills theory on compact surfaces. In: Stochastic Analysis and Applications in Physics (Funchal, 1993), vol. 449 of NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., pp. 389–403. Kluwer Acad. Publ., Dordrecht (1994)
Shen, H., Xu, W.: Weak universality of dynamical \(\Phi ^4_3\): non-Gaussian noise. Stoch. Partial Differ. Equ. Anal. Comput. 6(2), 211–254 (2018). https://doi.org/10.1007/s40072-017-0107-4
Warner, F.W.: Foundations of Differentiable Manifolds and Lie Groups, vol. 94. Springer, Berlin (2013)
Wilson, K.G.: Confinement of quarks. Phys. Rev. D 10(8), 2445 (1974)
Zwanziger, D.: Covariant quantization of gauge fields without Gribov ambiguity. Nucl. Phys. B 192(1), 259–269 (1981)
Zhu, R., Zhu, X.: Three-dimensional Navier–Stokes equations driven by space-time white noise. J. Differ. Equ. 259(9), 4443–4508 (2015)
Zhu, R., Zhu, X.: Lattice approximation to the dynamical \(\Phi _3^4\) model. Ann. Probab. 46(1), 397–455 (2018). https://doi.org/10.1214/17-AOP1188
Acknowledgements
The author is very grateful to Ismael Bailleul, David Brydges and Martin Hairer for the helpful discussions on stochastic quantization and gauge theories, and would also like to thank Konstantin Matetski for helpful discussions on discrete regularity structures. The author is partially supported by NSF through DMS-1712684 / DMS-1909525 and DMS-1954091.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Hairer
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A Discussions and possible extensions
1.1 A.1 Review of blackbox theorems and possible extension to three dimensions
The model under consideration is also defined in three spatial dimensions, with fields \(A=(A_1,A_2,A_3)= \sum _{j=1}^3 A_j \text{ d }x_j\) and \(\Phi : \mathbf {T}^3 \rightarrow \mathbf{C}\):
Here, the curvature field \(F_A = dA \) with components \(F_{A,j}\) defined by
and \(D^A_j \Phi \) is defined the same way. The SPDE is a system for \((A_1,A_2,A_3,\Phi )\) driven by independent white noises \(\xi _1,\xi _2,\xi _3\) and a complex valued white noise \(\zeta \). The system is again not parabolic, for instance, the equation for \(A_1\) is of the form
where \(\big ( \cdots \big )\) denotes the nonlinearities. Using the same gauge tuning trick, one obtains a parabolic system, and the regularity of its solutions is expected to be \(\alpha \) for \( \alpha < -\tfrac{1}{2}\). Since it is more singular than the situation in two spatial dimensions, to obtain a local solution theory via lattice approximations, certain “general tools” should then be in place.
We thus take this chance to review the fast-growing literature in the theory of regularity structures—particularly focusing on the “blackbox” theorems, and discuss the possibility and challenge of applying them to the three dimensional convergence problem of (Abelian) lattice gauge theory.
The key idea of the theory is to lift the noise input of an SPDE to a space of models denoted by \(\mathscr {M}\). The seminal work [Hai14] constructed this space \(\mathscr {M}\), and proved continuity of the solution map from \(\mathscr {M}\) to the space of distributions. Discrete analogues of these results are then developed by [HM18] on which the present article crucially relies; soon later [EH19] developed a more general discrete framework. These results would constitute the analytical foundation if one were to study the 3D lattice gauge theory (A.1). In parallel, “universality results” in regularity structures are proved in a series of papers [HQ18, HX19, HX18, SX18]; one possible challenge for 3D Abelian lattice gauge theory would be to see whether the techniques developed in these papers—suitably implemented on lattice—are sufficient to control the “remainder terms”. In 2D, in some sense, the “remainder terms” (4.23) are in a situation that is similar as in the “intermediate disorder” regime in [HQ18].
The algebraic step was then developed in [BHZ19], which has a systematic description of a group action on the space \(\mathscr {M}\), which allows for the transformation from the canonical model to the renormalized model. This algebraic “blackbox” result is very general and applies to 2D (as in the starting part of Sect. 5.1) and 3D gauge theories as well.
A probabilistic step was then achieved by [CH16] which gives us—in an automatic way under very general conditions—convergence in probability of the renormalized models (in continuous regularizations) to a limit model. In 3D, there would be much more elements in the regularity structure, and explicit moment calculations as done in Sect. 5.2 would be a formidable task, thus it would require a discrete version of the BPHZ theorem in [CH16] to prove convergence of the discrete models. Although it seems to me that the arguments in [CH16] should be adapted to discrete settings given substantial effort, a complete formulation and proof for such a discrete theorem is not available yet at the moment.
Finally, another component of the “blackbox” which is also algebraic (or combinatoric), is established in [BCCH17] to identify the renormalized equations satisfied by the sequence of solutions given by the solution map for the renormalized models.
Regarding observables, the loop or string observables would be more difficult (if possible) to construct since one has to integrate a more singular gauge field along a curve.
Remark A.1
It would also be interesting to construct long time solutions as done by [MW17b, MW20, MW18] for the dynamical \(\Phi ^4\) equation. To obtain some bound uniform in time, it might be helpful to have some damping terms, for instance adding more gauge invariant terms \(\mu |\Phi ^2| - |\Phi |^4\) to (1.1). Let’s mention a very simple trick that the equation for B in for instance (6.6) can obtain a term \(-\lambda ^2 c^2 B\) by considering the equations for B and the shifted field \(\Psi \mapsto \Psi +c\). This would be reminiscent to the “Higgs mechanism” for the gauge field to acquire a mass by shifting the scalar field to a point in the bottom of a mexican-hat potential. These heuristics still seem to be far from achieving any rigorous results.
1.2 A.2 Non-Abelian case
As hinted in Remark 1.2, the gauge tuning method being exploited in the present paper is very likely to be generalized into the non-Abelian case (whereas a gauge fixing with a linear decomposition by (1.12) seems not generalizable). We would like to have some further discussion on this point (informally), and also make a comparison between gauge fixing in stochastic PDE formulation and that in functional integral formulation of quantum gauge theories.
In general gauge theories, with only gauge field A, one has \(F_A {\mathop {=}\limits ^{ \text{ def }}}dA + A\wedge A\), where A is a 1-form taking values in an Lie algebra—for instance \(\mathfrak u(N)\) for some \(N\ge 1\). In the Abelian case, \(N=1\), and \(A\wedge A=0\) which is studied in this paper. In the functional integral approach, one is interested in the formal measure \(e^{-\mathcal {H}(A)} {\mathcal D}A\) where \(\mathcal {H}(A)= \frac{1}{2} \int _{\mathbf {T}^d} \hbox {tr}(F\wedge *F) \) is invariant under the gauge transformation \(A\rightarrow g^*A {\mathop {=}\limits ^{ \text{ def }}}g^{-1}Ag+g^{-1}dg\) for \(g: \mathbf {T}^d\rightarrow U(N)\). Note that in Abelian case \(g=e^{i f}\) and this is precisely the first transformation in (1.2). To make the “measure” normalizable, a Fadeev–Popov trick based on the identity \( 1= \int \delta (g(x)) \,\text{ det }(\frac{\partial g}{\partial x})\, dx \) is often used. In Abelian lattice gauge theory, writing \(A_f = A+df\) so that \(d^* A_f = d^* A + \Delta f\), one then writes the formal partition function as
The Jacobian factor \(\text{ det }(\frac{\delta (d^* A_f-\omega )}{\delta f})=\text{ det }(\Delta )\) can be factorized out, and using gauge invariance one can also replace \(A_f\) by A and factor out the “infinite integral” \(\int {\mathcal D}f\). If \(\omega =0\) this simply amounts to imposing the divergence free condition as mentioned in Remark 1.2. (The only reason one usually introduces the field \(\omega \) in the Abelian case being considered here is that upon integrating it against a Gaussian weight one obtains a factor \(e^{-\frac{(d^* A)^2}{2}}\) that is slightly more convenient to analyze.)
The Fadeev–Popov trick gets much more complicated in non-Abelian case, because the determinant will generally depend on A and thus does not factor out. This determinant however can be expressed by an integral over anti-commuting variables, which are called ghost fields. One then studies the model for gauge field A coupled with ghost fields. Furthermore, fixing the gauge globally is not always possible in non-Abelian theories, due to topological obstructions, a phenomena usually referred to as Gribov ambiguity.
The ghost fields would not show up in the stochastic PDE approach with gauge fixed by DeTurck trick; this seems to be already observed by physicists [Zwa81, Sad87, BHST87]. In fact, for the corresponding stochastic quantization equation
with a Lie algebra valued d-component space-time white noise \(\xi \), where \(d_A\) is the gauge covariant derivative, one can check by straightforward computation that \(B{\mathop {=}\limits ^{ \text{ def }}}g^* A\) satisifes \(\frac{\partial B}{\partial t} = g^{-1}\frac{\partial A}{\partial t}g + d_{B}\left( g^{-1} \frac{\partial g}{\partial t}\right) \), so by solving g from the ODE \( g^{-1}\frac{\partial g}{\partial t} = -d_B^*B \) and invoking gauge invariance of \(d_{A}^*F_{A}\) one obtains a parabolic equation \(\frac{\partial B}{\partial t} = -d_{B}^*F_{B} - d_{B}d_B^*B + g^{-1}\xi g\) where \(g^{-1}\xi g {\mathop {=}\limits ^{law}} \xi \). This is well-know when \(\xi =0\), see [DK90, Section 6.3]; and in the presence of the noise \(\xi \), the aforementioned physics literature simply put a term \(- d_{A}d_A^*A\) into the Eq. (A.2) and call this a gauge-fixing term.
To obtain a local solution theory to (A.2) via lattice approximations, one again needs some general tools as discussed in the three dimensional Abelian case.
Appendix B Ward identity
We derive an important identity that will be useful for cancellation of renormalization in Sect. 5.2 as well as showing convergence of certain observables in Sect. 6.1.
A reader familiar with renormalization would imagine that the equations (3.11) or (3.15) would need a mass renormalization for \(B_j^\varepsilon \) (i.e. a term \(\tilde{C}^\varepsilon B^\varepsilon \) for some constant \(\tilde{C}^\varepsilon \)). However, a mass renormalization for \(B_j^\varepsilon \) would break gauge symmetry so many proofs such as Lemma 3.2 would break down. We will see that actually there will be several contributions to a mass renormalization for \(B_j^\varepsilon \) and these contributions cancel. This cancellation is due to gauge symmetry. One can prove such cancellation by some elementary tricks (see Remark 5.7), but here we derive a version of “Ward identity” which seems more systematic, and could be more useful when certain tricks are not available (i.e. in \(d=3\)). The idea is straightforward: renormalization constants arise from expansion of nonlinearities [see (B.4)] in \(\lambda \) and taking expectations, and we can make use of gauge invariance of such nonlinearities to obtain useful identities.
Fix \(\varepsilon >0\). Consider Eq. (3.11), but now on \(\Lambda _\varepsilon ^M\) which is the discrete torus of length size \(M\ge 1\) and lattice spacing \(\varepsilon \), and with initial condition \( B^\varepsilon (-T)=0\) and \(\Psi ^\varepsilon (-T)=0\) at time \(-T\) for \(T>0\). Let \({\mathcal E}^{M,j}_\varepsilon \) for \(j\in \{1,2\}\) denote the sets of horizontal and vertical edges of \(\Lambda _\varepsilon ^M\). With a slight abuse of notation we write \(P_M^\varepsilon \) for the transition probability of continuous time random walk either on the vertices \(\Lambda _\varepsilon ^M\), or the edges \({\mathcal E}^{M,j}_\varepsilon \) for some \(j\in \{1,2\}\); they are essentially the same kernel since \(\Lambda _\varepsilon ^M\) and \({\mathcal E}^{M,j}_\varepsilon \) only differ by a small translation, and it will be clear which case is under consideration in the context.
Fix a function \(f^\varepsilon \) on \(\Lambda _\varepsilon ^M\) which is independent of time. Let
where \((B^\varepsilon ,\Psi ^\varepsilon )\) is the solution to the above initial value problem. One then has \( B_f^\varepsilon (-T)=\nabla ^\varepsilon f^\varepsilon \) and \(\hat{\Psi }_f^\varepsilon (-T)=0\). By gauge invariance of the nonlinearity as shown in (3.8), one has
Here, for \(\Lambda \in \{\Lambda ^M_\varepsilon ,{\mathcal E}^{M,1}_\varepsilon ,{\mathcal E}^{M,2}_\varepsilon \}\), \(x\in \Lambda \), and any space-time function \(g^\varepsilon \in C(\mathbf{R},\mathbf{R}^\Lambda )\) we have introduced the convolution notation
By the covariance property (3.9) of the covariant Laplacian one also has
where \(\hat{\zeta }^\varepsilon (x) {\mathop {=}\limits ^{ \text{ def }}}e^{i\lambda f^\varepsilon (x)} \zeta ^\varepsilon (x)\). Let \(\Psi _f^\varepsilon \) solve
with initial condition \(\Psi _f^\varepsilon (-T)=0\). We have \((B_f^\varepsilon , \Psi _f^\varepsilon ) {\mathop {=}\limits ^{law}} (B_f^\varepsilon , \hat{\Psi }_f^\varepsilon )\). Define
(We drop the M dependence in the notation \(b_j^\varepsilon \) and \(\psi ^\varepsilon \) for simplicity.) Also, differentiating (B.1) with respect to \(\lambda \) and by similar computation as in proof of Lemma 3.5, one can check that
where \(\mathbf {e}\in \{\pm \mathbf {e}_1,\pm \mathbf {e}_2\}\), namely
Note that this quantity depends on \(f^\varepsilon \) via \(b^\varepsilon \) and \(\Delta f^\varepsilon \).
For any \(x\in \Lambda ^M_\varepsilon \) and \(t\ge -T\) consider the following observable
where \(e=\{x,x+\mathbf {e}_j\}\). Applying (B.2) (B.3) (dropping t for simplicity of notation)
where k sums over \(\{1,2\}\), \(\psi ^\varepsilon = \psi ^\varepsilon _1+ i \psi ^\varepsilon _2\). Here, we have expanded a factor in the third line as \(\psi ^\varepsilon (x+\mathbf {e}_j) =\psi ^\varepsilon (x) +\varepsilon \nabla ^\varepsilon _j \psi ^\varepsilon (x) \), and expanded a factor in the second line as \(P_M^\varepsilon *_{\varepsilon ,T} ( \cdots )(x+\mathbf {e}_j) = P_M^\varepsilon *_{\varepsilon ,T} ( \cdots )(x) + \varepsilon \nabla ^\varepsilon _j P_M^\varepsilon *_{\varepsilon ,T} ( \cdots )(x)\); the two terms of order \(\varepsilon ^{-1}\) cancel each other, therefore the factor \(\varepsilon ^{-1}\) does not show up in the last two lines of the above equation.
It is important to note that \(Z^\varepsilon _j (t,x)\) is gauge-invariant in law, in the sense that although \(( B_f^\varepsilon , \Psi _f^\varepsilon )\) depends on \(f^\varepsilon \), the law of the quantity \(Z^\varepsilon _j (t,x)\) is independent of \(f^\varepsilon \). Indeed, \(Z^\varepsilon _j (t,x)\) would be deterministically gauge invariant by the calculation (3.8) if \(\Psi _f^\varepsilon \) was replaced by \(\hat{\Psi }_f^\varepsilon \); on the other hand \((B_f^\varepsilon , \Psi _f^\varepsilon ) {\mathop {=}\limits ^{law}} (B_f^\varepsilon , \hat{\Psi }_f^\varepsilon )\). Therefore the expectation of \(\partial _\lambda Z^\varepsilon _j (t,x) |_{\lambda =0}\) is independent of \(f^\varepsilon \).
Replacing \(f^\varepsilon \) by \(\alpha f^\varepsilon \) in the above arguments, the expectation of \(\partial _\alpha \partial _\lambda Z^\varepsilon _j (t,x) |_{\lambda =0}\) must then be zero, namely,
where all the functions without time variables are evaluated at t, and the function \({\mathcal U}_j^\varepsilon (y)\), whose precise form will not actually matter much in the sequel, is given by
Summing over \(j\in \{1,2\}\) and integrating by parts, noting that \(f^\varepsilon \) is arbitrary, one obtains
where the vector field \({\mathcal V}^\varepsilon = ({\mathcal V}^\varepsilon _1,{\mathcal V}^\varepsilon _2)\) is defined as
for \(\ell \in \{1,2\}\), and the function \({\mathcal U}^\varepsilon {\mathop {=}\limits ^{ \text{ def }}}\sum _{j=1}^2{\mathcal U}^\varepsilon _j\); we suppressed their dependence on M, T for cleaner notation. Note that the left hand side of (B.5) is analytic in \(t>-T\) so once we have obtained (B.5) for small \(t-(-T)\) we have it for any \(t>-T\). We can now take \(T\rightarrow \infty \), because the quantities \({\mathcal U}^\varepsilon \), \({\mathcal V}^\varepsilon \) are nothing but combinations of heat kernels, and are analytic in T so once (B.5) holds for a small range of T it can be extend for all \(T>0\). (In particular this is just a property of heat kernels and we are not using any long-time existence of the SPDE.) Also since (B.5) holds for any \(M\ge 1\) we can send \(M\rightarrow \infty \). So (B.5) holds with \(P^\varepsilon \) in place of \(P^\varepsilon _M\) and the time integrals over entire \(\mathbf{R}\). We then have that there exists a function \({\mathcal W}^\varepsilon \) such thatFootnote 19
It is easy to see that \({\mathcal U}^\varepsilon \) and \({\mathcal V}^\varepsilon \) both decay to zero at infinity, so \({\mathcal W}^\varepsilon \) must go to a constant at infinity; we can well shift \({\mathcal W}^\varepsilon \) by constant so that \({\mathcal W}^\varepsilon \) also decays to zero at infinity. Summing the above identity over horizontal or vertical edges of \(\mathbf{Z}^2_\varepsilon \), one has
This is precisely what we use for cancellation of mass renormalization of the gauge field as well as the convergence of the composite field observable (see Lemma 6.6). (Alternatively this can be also done using Remark 5.7.)
Remark B.1
Identities of the type (B.5) are usually called Ward–Takahashi identities in QFT, see [BFS80, Eq. (A.3)] and [Bal83, Eq. (2.27)] similar identities in the context of Abelian gauge theory (i.e. Higgs model). Note that the “useless” term of the form \(\Delta ^\varepsilon {\mathcal U}^\varepsilon \) did not appear in these references; this is probably because their gauge fixing condition amounts to imposing the gauge field to be divergence free, and without the div term in (B.1) the term \(\Delta ^\varepsilon {\mathcal U}^\varepsilon \) would not appear. For a reader who is familiar with quantum electrodynamics (QED), (B.5) (without the term \(\Delta ^\varepsilon {\mathcal U}^\varepsilon \)) is reminiscent to the QED Ward identity \(\sum _j k_j {\mathcal M}^j (k)=0\) in Fourier space where \({\mathcal M}(k)\) is an amplitude for some QED process involving an external photon (i.e. gauge field) with momentum k.
Rights and permissions
About this article
Cite this article
Shen, H. Stochastic Quantization of an Abelian Gauge Theory. Commun. Math. Phys. 384, 1445–1512 (2021). https://doi.org/10.1007/s00220-021-04114-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04114-x




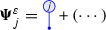 where “
where “ —which is not in the truncated regularity structure
—which is not in the truncated regularity structure