Queueing models for cognitive wireless networks with sensing time of secondary users

Abstract

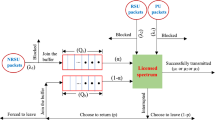
This paper considers queueing models for cognitive radio networks that account for the sensing time of secondary users (SUs). In cognitive radio networks, secondary users are allowed to opportunistically use idle channels originally allocated to primary users (PUs). To this end, SUs must sense the state of the channels before transmission. After sensing, if an idle channel is available, the SU can start transmission immediately; otherwise, the SU must carry out another channel sensing. In this paper, we study two retrial queueing models with an unlimited number of sensing SUs, where PUs have preemptive priority over SUs. The two models differ in whether or not an arriving PU can interrupt a SU transmission also in case there are still idle channels available. We show that both models have the same stability condition and that the model without interruptions in case of available idle channels has a slightly lower number of sensing SUs than the model with interruptions.

Appendix A: Stability condition

In this appendix, we obtain a sufficient condition for our multiserver models.

1.1 A.1 Markov chain

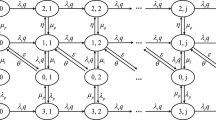
As in Sect. 4, we define $N(t), C_{1}(t)$ and $C_{2}(t)$ as the number of SUs in the orbit, the number of PUs on transmission and the number of SUs on transmission, respectively. Those three random variables can be used as state variables to describe the Markov chain of the cognitive radio system. However, we rearrange the state description for the simplicity of the stability analysis. To this end, we define $B(t) = C_{1}(t) + C_{2}(t)$ as the number of PUs or SUs on transmission. It can be shown that $\{ X(t) = (N(t), B(t), C_{1}(t)) \ | \ t \ge 0\}$ forms a continuous-time Markov chain on the state space ${\mathcal {S}}$ defined by

$$\begin{aligned} {\mathcal {S}} = \{(i,j,k);\, i \in {\mathbb {Z}}_{+}, j=0,1,\ldots ,c,\, k=0,1,\ldots ,j\, \}. \end{aligned}$$

Then it is easy to see that the Markov chain $\{X(t) \ | \ t \ge 0\}$ is a level-dependent quasi birth-and-death (QBD) process with infinitesimal generator ${\varvec{Q}}$ in the form

$$\begin{aligned} {\varvec{Q}}&= \begin{bmatrix} {\varvec{Q}}_{1}^{(0)} &{}\quad {\varvec{Q}}_{0}^{(0)} &{}\quad {\varvec{O}} &{}\quad \cdots \\ {\varvec{Q}}_{2}^{(1)} &{}\quad {\varvec{Q}}_{1}^{(1)} &{}\quad {\varvec{Q}}_{0}^{(1)} &{}\quad \ddots &{} \\ {\varvec{O}} &{}\quad {\varvec{Q}}_{2}^{(2)} &{}\quad {\varvec{Q}}_{1}^{(2)} &{}\quad \ddots &{} \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{} \\ \end{bmatrix}. \end{aligned}$$

The block matrices ${\varvec{Q}}_{0}^{(i)}$ and ${\varvec{Q}}_{1}^{(i)}$ for $i \in {\mathbb {Z}}_{+}$, and ${\varvec{Q}}_{2}^{(i)}$ for $i \in {\mathbb {Z}}_{+} \setminus \{0\}$ have block structure forms:

$$\begin{aligned} {\varvec{Q}}^{(i)}_{0} = \begin{bmatrix} \varvec{\varLambda }_{0,0} &{}\quad {\varvec{O}} &{}\quad \cdots &{}\quad \cdots &{}\quad {\varvec{O}} \\ {\varvec{O}} &{}\quad \varvec{\varLambda }_{1,1} &{}\quad \ddots &{}\quad &{} \quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad {\varvec{O}} \\ {\varvec{O}} &{}\quad \cdots &{}\quad \cdots &{}\quad {\varvec{O}} &{}\quad \varvec{\varLambda }_{c,c} \end{bmatrix}, \quad {\varvec{Q}}^{(i)}_{2} = i\sigma \begin{bmatrix} {\varvec{O}} &{}\quad {\varvec{E}}_{0,1} &{}\quad {\varvec{O}} &{}\quad \cdots &{}\quad {\varvec{O}} \\ {\varvec{O}} &{}\quad {\varvec{O}} &{}\quad {\varvec{E}}_{1,2} &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad {\varvec{O}} \\ \vdots &{} \quad &{}\quad \ddots &{}\quad {\varvec{O}} &{}\quad {\varvec{E}}_{c-1,c} \\ {\varvec{O}} &{}\quad \cdots &{} \quad \cdots &{}\quad {\varvec{O}} &{}\quad {\varvec{O}} \end{bmatrix}, \\ {\varvec{Q}}^{(i)}_{1} = \begin{bmatrix} \varvec{L}_{0,0} - i\sigma \varvec{I} &{}\quad \varvec{B}_{0,1} &{}\quad {\varvec{O}} &{}\quad \cdots &{}\quad {\varvec{O}} \\ \varvec{D}_{1,0} &{}\quad \varvec{L}_{1,1} - i\sigma \varvec{I} &{}\quad \varvec{B}_{1,2} &{}\quad \ddots &{}\quad \vdots \\ {\varvec{O}} &{}\quad \varvec{D}_{2,1} &{}\quad \ddots &{}\quad \ddots &{}\quad {\varvec{O}} \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \varvec{L}_{c-1,c-1} - i\sigma \varvec{I} &{}\quad \varvec{B}_{c-1,c} \\ {\varvec{O}} &{}\quad \cdots &{}\quad {\varvec{O}} &{}\quad \varvec{D}_{c,c-1} &{}\quad \varvec{L}_{c,c} \end{bmatrix}. \end{aligned}$$

The block matrices $\varvec{\varLambda }_{j,j}, \varvec{L}_{j,j}$ for $j=0,1,\ldots ,c$, and $\varvec{E}_{j-1,j}, \varvec{B}_{j-1,j}, \varvec{D}_{j,j-1}$ for $j=1,2,\ldots ,c$ are explicitly written as follows:

$$\begin{aligned}&\varvec{\varLambda }_{j,j} = \begin{bmatrix} \lambda _{2} &{}\quad \lambda _{0,j}^{*} &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad \lambda _{2} &{}\quad \lambda _{1,j-1}^{*} &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad 0 \\ \vdots &{}\quad &{}\quad \ddots &{}\quad \lambda _{2} &{}\quad \lambda _{j-1,1}^{*} \\ 0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 &{}\quad \lambda _{2} \end{bmatrix}, \quad \varvec{E}_{j-1,j} = \begin{bmatrix} 1 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad 0 &{}\quad \vdots \\ 0 &{}\quad \cdots &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{bmatrix}, \\&\varvec{B}_{j-1,j} = \begin{bmatrix} 0 &{}\quad \lambda _{0,j-1}^{**} &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad 0 &{}\quad \lambda _{1,j-2}^{**} &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 &{}\quad \lambda _{j-1,0}^{**} \end{bmatrix}, \quad \\&\varvec{D}_{j,j-1} = \begin{bmatrix} j\mu _{2} &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ \mu _{1} &{}\quad (j-1)\mu _{2} &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \ddots &{}\quad \ddots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad (j-1)\mu _{1} &{}\quad \mu _{2} \\ 0 &{}\quad \cdots &{}\quad 0 &{}\quad j\mu _{1} \end{bmatrix}, \\&\varvec{L}_{j,j} = - \text {diag} \{ q_{j,0}, q_{j,1}, \ldots , q_{j,j} \}, \end{aligned}$$

where $q_{j,k}\, (j = 0,1,\ldots ,c)$ are given by $q_{j,k} = \lambda _{1} + \lambda _{2} + j\mu _{1} + (c-j)\mu _{2}$ if $k=0,1,\ldots ,j-1$, and $q_{j,k} = \lambda _{2} + j\mu _{1} + (c-j)\mu _{2}$ if $k=j$. We specify $\lambda _{i,j}^{*}$ and $\lambda _{i,j}^{**}$ depending on the selection policy of an available channel on PU arrival. If an idle channel is assigned to an arriving PU, and the PU preempts one of the SUs on transmission only when no idle channels are available, then

$$\begin{aligned} \lambda _{i,j}^{*} = \lambda _{1}\delta _{i+j,c}, \quad \lambda _{i,j}^{**} = \lambda _{1}(1-\delta _{i+j,c}), \quad i=0,\ldots ,c-1, \, j = 0, \ldots , c-i, \end{aligned}$$

where $\delta _{i+j,c} = 1$ if $i+j = c$, and $\delta _{i+j,c} = 0$ if $i+j \ne c$. If a channel randomly selected among the idle channels or the ones occupied by SUs is assigned to an arriving PU, then

$$\begin{aligned} \lambda _{i,j}^{*} = \lambda _{1}\frac{j}{c-i}, \quad \lambda _{i,j}^{**} = \lambda _{1}\frac{c-i-j}{c-i}, \quad i=0,\ldots ,c-1, \, j = 0, \ldots , c-i. \end{aligned}$$

It should be noted that both policies yield us the same $\varvec{\varLambda }_{c,c}$ as

$$\begin{aligned} \varvec{\varLambda }_{c,c} = \begin{bmatrix} \lambda _{2} &{}\quad \lambda _{1} &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad \lambda _{2} &{}\quad \lambda _{1} &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad 0 \\ \vdots &{}\quad &{}\quad \ddots &{}\quad \lambda _{2} &{}\quad \lambda _{1} \\ 0 &{}\quad \cdots &{}\quad \cdots &{}\quad 0 &{}\quad \lambda _{2} \end{bmatrix}. \end{aligned}$$

A description of the block matrices is summarized in Table 2.

Table 2 Description of block matrices

1.2 A.2 Stability analysis

Let $\varvec{\varDelta }_{c}$ be a diagonal matrix defined by $\varvec{\varDelta }_{c} = -\varvec{L}_{c,c}$. We define square matrices

$$\begin{aligned} \varvec{A}_{0} = \varvec{\varDelta }_{c}^{-1}\varvec{\varLambda }_{c,c}, \quad \varvec{A}_{1} = \varvec{I} + \varvec{\varDelta }_{c}^{-1}\varvec{L}_{c,c}, \quad \varvec{A}_{2} = \varvec{\varDelta }_{c}^{-1}\varvec{D}_{c,c-1} \varvec{E}_{c-1,c}. \end{aligned}$$

$\varvec{A}_{0}, \varvec{A}_{1}$ and $\varvec{A}_{2}$ are non-negative matrices and $\varvec{A} = \varvec{A}_{0} + \varvec{A}_{1} + \varvec{A}_{2}$ is a stochastic matrix. Since $\varvec{A}$ is irreducible, the invariant probability vector $\varvec{\nu }$ of $\varvec{A}$ is uniquely determined by $\varvec{\nu }\varvec{A} = \varvec{\nu },\, \varvec{\nu } \varvec{e} = 1$.

Let $\varvec{A}(z)$ be the matrix defined by

$$\begin{aligned} \varvec{A}(z)&= \varvec{A}_{0} + \varvec{A}_{1} z + \varvec{A}_{2} z^{2}, \quad 0 \le z \le 1. \end{aligned}$$

Let $\chi (z)$ be the maximal eigenvalue of $\varvec{A}(z)$ with the right eigenvector $\varvec{v}(z)$. Since $\varvec{A}(z)$ is irreducible and non-negative, $\varvec{v}(z) > \varvec{0}$. If $\varvec{\nu } \varvec{A}_{0}\varvec{e} < \varvec{\nu }\varvec{A}_{2}\varvec{e}$ and $\chi (0) > 0$, then $\chi (z) = z$ has a solution for $z \in (0,1)$.We denote the solution by $\eta$. For $z \in (\eta , 1)$, we have $\chi (z) < z$ and hence $\varvec{A}(z) \varvec{v}(z) = \chi (z) \varvec{v}(z) < z \varvec{v}(z)$ (Neuts 1981). We then obtain the following lemma.

Lemma 1

If $\varvec{\nu } \varvec{A}_{0}\varvec{e} < \varvec{\nu }\varvec{A}_{2}\varvec{e}$ and $\chi (0) > 0$, we have $z \in (\eta , 1)$ and $\varvec{v}(z) > \varvec{0}$ such that

$$\begin{aligned} (\varvec{\varLambda }_{c,c} + z\varvec{L}_{c,c} + z^{2}\varvec{D}_{c,c-1}\varvec{E}_{c-1,c}) \varvec{v}(z) < \varvec{0}. \end{aligned}$$

Proof

The proof is immediately followed from $\varvec{A}(z) \varvec{v}(z) < z \varvec{v}(z)$. $\square$

If we define $\varvec{Q}_{p} = \varvec{\varLambda }_{c,c} + \varvec{L}_{c,c} + \varvec{D}_{c,c-1}\varvec{E}_{c-1,c}$, then $\varvec{Q}_{p}$ can be an infinitesimal generator given by

$$\begin{aligned} \varvec{Q}_{p}&= \begin{bmatrix} -\lambda _{1} &{}\quad \lambda _{1} &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ \mu _{1} &{}\quad -\lambda _{1}-\mu _{1} &{}\quad \lambda _{1} &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad (c-1)\mu &{}\quad -\lambda _{1}-(c-1)\mu _{1} &{}\quad \lambda _{1} \\ 0 &{}\quad \cdots &{}\quad 0 &{}\quad c\mu _{1} &{}\quad -c\mu _{1} \\ \end{bmatrix}. \end{aligned}$$

Since $\varvec{Q}_{p}$ is irreducible, the invariant probability vector $\varvec{\pi } = (\pi _{0}, \pi _{1}, \ldots , \pi _{c})$ satisfying $\varvec{\pi }\varvec{Q}_{p} = \varvec{0}, \varvec{\pi }\varvec{e} = 1$ is uniquely determined and is given by

$$\begin{aligned} \pi _{0} = \left[ 1+\frac{\lambda _{1}}{\mu _{1}}+\cdots +\frac{1}{c!}\left( \frac{\lambda _{1}}{\mu _{1}}\right) ^{c}\right] ^{-1}, \quad \pi _{j} = \frac{1}{j!}\left( \frac{\lambda _{1}}{\mu _{1}}\right) ^{j} \pi _{0} \quad (j = 1,2,\ldots ,c). \end{aligned}$$

It can be shown that $\varvec{\nu } \varvec{A}_{0}\varvec{e} < \varvec{\nu }\varvec{A}_{2}\varvec{e}$ is rewritten to be $\varvec{\pi }\varvec{\varLambda }_{c,c}\varvec{e} < \varvec{\pi }\varvec{D}_{c,c-1}\varvec{e}$. The next theorem gives us a sufficient condition of the ergodicity of $\{X(t) \ | \ t \ge 0\}$.

Theorem 1

If $\varvec{\pi }\varvec{\varLambda }_{c,c}\varvec{e} < \varvec{\pi }\varvec{D}_{c,c-1}\varvec{e}$, or equivalently,

$$\begin{aligned} \frac{\lambda _{2}}{\mu _{2}} < \sum _{i=0}^{c}(c-i)\pi _i, \end{aligned}$$

(22)

then $\{X(t) \ | \ t \ge 0\}$ is regular and ergodic.

Proof

According to Tweedie (1975) or Statement 8, p. 97 in Falin and Templeton (1997), a Markov process with infinitesimal generator $\varvec{Q} = [q_{s,p}]$ on state space ${\mathcal {S}}$ is regular and ergodic, if there exist a lower bounded function $\varphi (\cdot )$ on ${\mathcal {S}}$, some finite subset ${\mathcal {S}}_{0} \subset {\mathcal {S}}$ and some $\epsilon > 0$ such that

$$\begin{aligned} y(s)&= \sum _{p \in {\mathcal {S}}} q_{s, p} \varphi (p) \le -\epsilon \end{aligned}$$

for $s \notin {\mathcal {S}}_{0}$, and $y(s) < \infty$ for $s \in {\mathcal {S}}_{0}$.

We show that the Lyapunov function by Diamond and Alfa (1999) is still effective to our multiserver models of the cognitive network system. To construct the Lyapunov function, we define a column vector $\varvec{w}(z)$ of size $(c+1)(c+2)/2$ by

$$\begin{aligned} \varvec{w}(z)&= (\varvec{I} + z \varvec{K} + z^{2} \varvec{K}^{2} + \cdots + z^{c} \varvec{K}^{c}) \begin{bmatrix} \varvec{0} \\ \varvec{v}(z) \end{bmatrix}, \end{aligned}$$

where $\varvec{K}$ is determined by the relation $\varvec{Q}^{(i)}_{2} = i\sigma \varvec{K}\, (i \in {\mathbb {Z}}_{+} \setminus \{0\})$. For $z \in (\eta , 1)$, we also define a column vector $\varvec{\varphi }^{(k)}$ of size $(c+1)(c+2)/2$ by

$$\begin{aligned} \varvec{\varphi }^{(i)}&= z^{-i} (\varvec{w}(z) + b \varvec{e}) = z^{-i} \left( \begin{bmatrix} z^{c} \varvec{w}_{0}(z) \\ z^{c-1} \varvec{w}_{1}(z) \\ \vdots \\ z \varvec{w}_{c-1}(z) \\ \varvec{w}_{c}(z) \end{bmatrix} + b\varvec{e} \right) , \quad i \in {\mathbb {Z}}_{+}, \end{aligned}$$

where $b \in (0,1)$, $\varvec{w}_{c}(z) = \varvec{v}(z)$, and $\varvec{w}_{j}(z) = \varvec{E}_{j,j+1}\varvec{w}_{j+1}(z)$ for $j=0, 1, \ldots ,c-1$. It is clear that each element of $\varvec{\varphi }^{(i)}$ is lower bounded. We define a column vector $\varvec{\varphi }$ composed of $\varvec{\varphi }^{(i)}$’s by

$$\begin{aligned} \varvec{\varphi }&= [(\varvec{\varphi }^{(0)})^{{\mathsf {T}}}, (\varvec{\varphi }^{(1)})^{{\mathsf {T}}}, \ldots , (\varvec{\varphi }^{(i)})^{{\mathsf {T}}}, \ldots ]^{{\mathsf {T}}}. \end{aligned}$$

Let $\ell (i) = \{(i,j,k) \in {\mathcal {S}} \mid j = 0,1,\ldots ,c, k = 0,1,\ldots ,j\}$ and $\varvec{y}^{(i)}$ be a column vector of size $(c+1)(c+2)/2$ given by the elements of $\ell (i)$ of $\varvec{Q}\varvec{\varphi }$, i.e.,

$$\begin{aligned} \varvec{y}^{(i)}&= {\left\{ \begin{array}{ll} \varvec{Q}_{0}^{(0)}\varvec{\varphi }^{(1)} + \varvec{Q}_{1}^{(0)}\varvec{\varphi }^{(0)}, &{} i = 0, \\ \varvec{Q}_{0}^{(i)}\varvec{\varphi }^{(i+1)} + \varvec{Q}_{1}^{(i)}\varvec{\varphi }^{(i)} + \varvec{Q}_{2}^{(i)}\varvec{\varphi }^{(i-1)}, &{} i \in {\mathbb {Z}}_{+} \setminus \{0\}. \end{array}\right. } \end{aligned}$$

For $i \in {\mathbb {Z}}_{+}$, we have

$$\begin{aligned} \varvec{y}^{(i)}&= z^{-(i+1)} \left( \begin{bmatrix} z^{c} \varvec{f}_{0}(z) \\ z^{c-1} \varvec{f}_{1}(z) \\ \vdots \\ z \varvec{f}_{c-1}(z) \\ \varvec{f}_{c}(z) \end{bmatrix} + b(1-z) \begin{bmatrix} \varvec{\varLambda }_{0,0}\varvec{e} \\ \varvec{\varLambda }_{1,1}\varvec{e} \\ \vdots \\ \varvec{\varLambda }_{c-1,c-1}\varvec{e} \\ \varvec{\varLambda }_{c,c}\varvec{e} \end{bmatrix} -i\sigma bz(1-z) \begin{bmatrix} \varvec{e} \\ \varvec{e} \\ \vdots \\ \varvec{e} \\ \varvec{0} \end{bmatrix} \right) , \end{aligned}$$

where

$$\begin{aligned} \varvec{f}_{0}(z)&= \varvec{B}_{0,1} \varvec{w}_{1}(z) + (\varvec{\varLambda }_{0,0} + z\varvec{L}_{0,0}) \varvec{w}_{0}(z), \end{aligned}$$

and for $j=1,2,\ldots ,c-1$

$$\begin{aligned} \varvec{f}_{j}(z)&= \varvec{B}_{j,j+1} \varvec{w}_{j+1}(z) + (\varvec{\varLambda }_{j,j} + z\varvec{L}_{j,j}) \varvec{w}_{j}(z) + z^{2} \varvec{D}_{j,j-1} \varvec{w}_{j-1}(z), \end{aligned}$$

and

$$\begin{aligned} \varvec{f}_{c}(z)&= (\varvec{\varLambda }_{c,c} + z \varvec{L}_{c,c} + z^{2} \varvec{D}_{c,c-1} \varvec{E}_{c-1,c})\varvec{w}_{c}(z). \end{aligned}$$

By Lemma 1, we can choose $z \in (\eta , 1)$ such that $\varvec{f}_{c}(z) < \varvec{0}$ if $\varvec{\nu } \varvec{A}_{0}\varvec{e} < \varvec{\nu }\varvec{A}_{2}\varvec{e}$ which is equivalent to $\varvec{\pi }\varvec{\varLambda }_{c,c}\varvec{e} < \varvec{\pi }\varvec{D}_{c,c-1}\varvec{e}$. Therefore, there exists some $b \in (0,1)$ such that

$$\begin{aligned} \varvec{f}_{c}(z) + b(1-z)\varLambda _{c,c}\varvec{e}&< \varvec{0}. \end{aligned}$$

Clearly, we can choose an integer $i_{0}$ such that

$$\begin{aligned} z^{c-j} \varvec{f}_{j}(z) + b(1-z)\varLambda _{j,j}\varvec{e} - i\sigma bz(1-z) \varvec{e}&< \varvec{0} \end{aligned}$$

for all $i > i_{0}$ and $j=0,1,\ldots ,c-1$. Therefore, there exists some $\epsilon > 0$ such that

$$\begin{aligned} \varvec{Q}\varvec{\varphi }&\le -\epsilon \varvec{e}, \end{aligned}$$

except for some finite subset ${\mathcal {S}}_{0} \subset {\mathcal {S}}$, from which we conclude that $\{X(t) \ | \ t \ge 0 \}$ is ergodic if $\varvec{\pi }\varvec{\varLambda }_{c,c}\varvec{e} < \varvec{\pi }\varvec{D}_{c,c-1}\varvec{e}$. Note here that $\varvec{\pi }$ is the stationary distribution of the Erlang loss system M/M/c/c with arrival rate $\lambda _{1}$ and service rate $\mu _{1}$. It is easy to see that (22) follows from $\varvec{\pi }\varvec{\varLambda }_{c,c}\varvec{e} < \varvec{\pi }\varvec{D}_{c,c-1}\varvec{e}$.

$\square$