Intersections of Boerdijk–Coxeter Helices in Three-Dimensional Euclidian Space

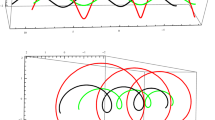
Abstract

Various intersections of Boerdijk–Coxeter (BC) helices consisting of regular tetrahedra and having the same chirality are considered in a three-dimensional Euclidean space. The angles between their axes are calculated. Next, these rigorous geometric models of intersections of BC helices are subjected to physically justified distortions (merging of closely spaced vertices and formation of additional bonds between vertices spaced by a distance of about a tetrahedron-edge length). It is shown that with introduction of these distortions there are seven different types of intersection of two BC helices passing through the same icosahedron. They correspond to seven types of intersection of helices 30/11 in a polytope {3, 3, 5}. For different discretized Hopf fibrations of the set of polytope {3, 3, 5} vertices, it is demonstrated that the local structure of a polytope {3, 3, 5} in the vicinity of a Hopf circle passing through the polytope vertices can be described as a certain set of intersecting helices 30/11.