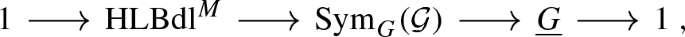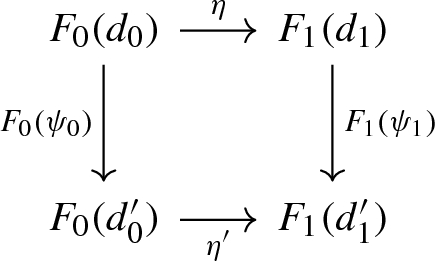Smooth 2-Group Extensions and Symmetries of Bundle Gerbes

Abstract

We study bundle gerbes on manifolds M that carry an action of a connected Lie group G. We show that these data give rise to a smooth 2-group extension of G by the smooth 2-group of hermitean line bundles on M. This 2-group extension classifies equivariant structures on the bundle gerbe, and its non-triviality poses an obstruction to the existence of equivariant structures. We present a new global approach to the parallel transport of a bundle gerbe with connection, and use it to give an alternative construction of this smooth 2-group extension in terms of a homotopy-coherent version of the associated bundle construction. We apply our results to give new descriptions of nonassociative magnetic translations in quantum mechanics and the Faddeev–Mickelsson–Shatashvili anomaly in quantum field theory. We also propose a definition of smooth string 2-group models within our geometric framework. Starting from a basic gerbe on a compact simply-connected Lie group G, we prove that the smooth 2-group extensions of G arising from our construction provide new models for the string group of G.

1 Introduction

This paper is motivated by the following problem from physics: In [BMS19] we showed how a bundle gerbe with connection on ${\mathbb {R}}^d$ gives rise to a 3-cocycle on the translation group ${\mathbb {R}}^d_{\mathtt {t}}$ of ${\mathbb {R}}^d$. Even though this 3-cocycle is trivial in group cohomology, it is very interesting from a physical as well as from a mathematical perspective: it gives a geometric explanation to the presence of nonassociativity in quantum mechanics with magnetic monopole backgrounds, and it implements the action of the parallel transport of a bundle gerbe on its 2-Hilbert space of sections. This appearence of nonassociativity in quantum mechanics goes back to [Jac85, GZ86], but as of yet the more natural extension to realistic scenarios involving periodically confined motion on configuration spaces such as tori ${{\mathbb {T}}}^d$ has not been worked out. The discussion of [Jac85] was a response to the observed violation of the Jacobi identity for the algebra of field operators in quantum gauge theories with chiral fermions [Jo85], which is a manifestation of the chiral anomaly. Interest in these models has been recently revived through their conjectural relevance to non-geometric flux compactifications of string theory, which is based on backgrounds that are tori or more generally torus bundles [Lüs10, MSS12, BL14, MSS14]. However, the original finding [BP11] of nonassociativity in Wess–Zumino–Witten models based on other compact Lie groups has so far received considerably less attention, and in particular has not been understood from a geometric perspective.

In the present paper we work out the geometric framework and origin behind these results in complete generality. Subsequently, we present several applications of our results in both physics and mathematics, along the lines discussed above. We consider an action $\varPhi :G \times M \longrightarrow M$ of a connected Lie group G on a manifold M, where M is endowed with a bundle gerbe ${\mathcal {G}}$. One can now ask whether ${\mathcal {G}}$ admits a G-equivariant structure. At the very least, such a structure should consist of a choice of 1-isomorphism ${\mathcal {G}}\longrightarrow \varPhi _g^*{\mathcal {G}}$ for every $g \in G$. Instead of considering possible choices for such 1-isomorphisms individually, we assign to g the groupoid of all such 1-isomorphisms. This yields an object which can be understood as a bundle ${\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow G$ of groupoids over G. Considering $g=e$, the identity element of G, we see that its typical fibre is the groupoid $\mathrm {HLBdl}(M)$ of hermitean line bundles on M.

The definition of ${\mathrm {Sym}}_G({\mathcal {G}})$ so far does not capture the smooth structure of the gerbe ${\mathcal {G}}$. We thus enhance the construction to take into account smooth families of elements of G. Then one can make sense of ${\mathrm {Sym}}_G({\mathcal {G}})$ as a category fibred in groupoids over a base category ${{\mathscr {C}}\mathrm{art}}$ that encodes smooth families of geometric objects. Categories fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$ assemble into a 2-category ${\mathscr {H}}$, and there exists a fully faithful inclusion of the category of smooth manifolds into ${\mathscr {H}}$. Motivated by [SP11] we define a smooth 2-group to be a group object in ${\mathscr {H}}$. One of the central examples for us is the smooth 2-group $\mathrm {HLBdl}^M$ of hermitean line bundles on M. We introduce a notion of smooth principal 2-bundle in ${\mathscr {H}}$ that lies between the definitions of higher principal bundles used in [SP11] and [NSS15] (see in particular Appendix A.2). We show that our principal 2-bundles are well behaved from a homotopical as well as from a geometric point of view (more precisely, they form effective epimorphisms while also admitting local sections). With the notion of smooth 2-group and principal 2-bundles, we can make precise what it means to be a (central) extension of smooth 2-groups in analogy to extensions of Lie groups. Then, our first main results can be summarised as

Theorem 1.1

Let G be a connected Lie group acting on a manifold M, and let ${\mathcal {G}}$ be a bundle gerbe on M. Then:

• (1) There is a (non-central) extension of smooth 2-groups

  

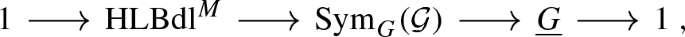
  where $\underline{G} \in {\mathscr {H}}$ denotes the category fibred in groupoids associated to G.

• (2) The smooth 2-group ${\mathrm {Sym}}_G({\mathcal {G}})$ acts on ${\mathcal {G}}$, and the action covers that of G on M.

• (3) The gerbe ${\mathcal {G}}$ admits a G-equivariant structure if and only if there exists a morphism $\underline{G} \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$ of smooth 2-groups which splits the extension (1.2).

An extension similar to (1.2) was considered in [FRS16], where symmetries of a gerbe with connection were investigated in relation with higher geometric prequantisation. Infinitesimal versions of the extension (1.2) were considered in [Col11, FRS16], where it was shown that these give rise to the standard H-twisted Courant algebroid on M, where H is the 3-form curvature of the connection on ${\mathcal {G}}$. These considerations have been expanded on and applied to higher versions of Kaluza-Klein reductions of string theory in [Alf20].

Our point here is that in many applications, such as nonassociativity in quantum mechanics and string theory, anomalies in quantum field theory, as well as interesting topological constructions, connections on ${\mathcal {G}}$ only play a secondary role: in this context, they can be seen as a tool to compute the extensions (1.2) and their associated cocycles. The key to this computability is an alternative presentation of ${\mathrm {Sym}}_G({\mathcal {G}})$ in terms of a categorified descent construction.

In order to work out this construction, we introduce a novel global approach to the parallel transport of a bundle gerbe. Parallel transport for gerbes has been constructed in [SW11, SW09, SW17], but for our purposes a global, rather than local, treatment is necessary. Our construction relies heavily on the transgression-regression machine for bundle gerbes [Wal16] together with the properties of the fusion product and the connection on the transgression line bundle that were studied in [Wal16, BW18]. Given a connection on ${\mathcal {G}}$, we construct its parallel transport as a quadruple ${\mathtt {pt}}^{\mathcal {G}}= ({\mathtt {pt}}^{\mathcal {G}}_1, {\mathtt {pt}}^{\mathcal {G}}_2, {\mathtt {pt}}^{\mathcal {G}}_\star , \varepsilon ^{\mathcal {G}})$, consisting of the following data: first, there is a 1-isomorphism ${\mathtt {pt}}_1^{\mathcal {G}}:{\mathrm {ev}}_0^*{\mathcal {G}}\longrightarrow {\mathrm {ev}}_1^*{\mathcal {G}}$ over the path space PM of M, where ${\mathrm {ev}}_t :PM \longrightarrow M$ is the evaluation of a path at $t \in [0,1]$. Second, there is a 2-isomorphism ${\mathtt {pt}}_2^{\mathcal {G}}:{\mathtt {pt}}_{1|\gamma _0}^{\mathcal {G}}\longrightarrow {\mathtt {pt}}_{1|\gamma _1}^{\mathcal {G}}$ for every smooth homotopy with fixed endpoints between paths $\gamma _0$ and $\gamma _1$, which depends smoothly on the paths and the homotopy. The 2-isomorphisms ${\mathtt {pt}}_\star ^{\mathcal {G}}$ and $\varepsilon ^{\mathcal {G}}$ implement the compatibility of the parallel transport with concatenation of paths and with constant paths, respectively. Furthermore, the collection ${\mathtt {pt}}^{\mathcal {G}}$ is required to be invariant under thin homotopies in a precise way. We show

Theorem 1.3

Every bundle gerbe with connection has a canonical parallel transport.

Using the parallel transport, we are able to write down a $\mathrm {HLBdl}^M$-valued Čech 1-cocycle on the covering of G by its space of based paths. These data are equivalently transition functions for an $\mathrm {HLBdl}^M$-principal 2-bundle ${\mathfrak {Des}}_{{\mathsf {L}}}\longrightarrow \underline{G}\,$. We construct ${\mathfrak {Des}}_{{\mathsf {L}}}$ explicitly by a homotopy-coherent version of the associated bundle construction. Then we prove

Theorem 1.4

The principal 2-bundle ${\mathfrak {Des}}_{{\mathsf {L}}}\longrightarrow \underline{G}$ is a smooth 2-group extension of $\underline{G}$ by $\mathrm {HLBdl}^M$. There is a weakly commutative diagram of smooth 2-groups

The morphism $\varPsi$ is an equivalence.

In the case $M = {\mathbb {R}}^d$, where $G = {\mathbb {R}}^d_{\mathtt {t}}$ is the translation group of ${\mathbb {R}}^d$, and where ${\mathcal {G}}= {\mathcal {I}}_B$ is a trivial gerbe on ${\mathbb {R}}^d$ with a connection $B \in \Omega ^2({\mathbb {R}}^d)$ corresponding to a magnetic field, we show that the extension ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {I}}) \longrightarrow \underline{{\mathbb {R}}}^d_{\,{\mathtt t}}$ reproduces the 3-cocycles we obtained in [BMS19]. We achieve this by choosing a certain global section of the path fibration of ${\mathbb {R}}^d_\mathtt{t}$ and implicitly pass through ${\mathfrak {Des}}_{{\mathsf {L}}}$ in the computation. We show that the parallel transport we defined implements nonassociative magnetic translations on the sections of the gerbe, whereas the 2-group extension ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {I}}) \longrightarrow \underline{{\mathbb {R}}}^d_{\,{\mathtt t}}$ allows us to understand the algebraic structure of nonassociative magnetic translations even without making any reference to sections. The latter is particularly useful in cases where there is no good notion of sections, such as when the Dixmier–Douady class of ${\mathcal {G}}$ is non-torsion. In particular, we study in detail the action of nonassociative magnetic translations on tori ${{\mathbb {T}}}^d$ and give an explicit description of ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {G}})$ for general choice of a gerbe ${\mathcal {G}}$ on ${{\mathbb {T}}}^d$.

As a further application, we show that if ${\varGamma }$ is a group of gauge transformations, the smooth 2-group extensions ${\mathrm {Sym}}_{\varGamma }({\mathcal {G}}) \longrightarrow \underline{{\varGamma }}$ control the Faddeev–Mickelsson–Shatashvili anomalies in quantum field theory [Fad84, FS85, Mic85]. The relation between gerbes and these anomalies has been investigated in [CM95, CM96], but only as algebraic objects, disregarding the smooth structures. The relevant bundle gerbe ${\mathcal {G}}$ lives on the space ${{\mathscr {A}}}$ of gauge fields and describes the obstruction to a Fock bundle descending to the orbit space ${{\mathscr {A}}}/{\varGamma }$. Here the extension ${\mathrm {Sym}}_{\varGamma }({\mathcal {G}}) \longrightarrow \underline{{\varGamma }}$ is split, so that ${\mathcal {G}}$ admits an equivariant structure. At the same time ${\mathcal {G}}$ is trivialisable as a bundle gerbe, but the anomaly is precisely the obstruction to choosing a ${\varGamma }$-equivariant trivialisation. This allows us to understand the anomaly in a conceptual way as a higher smooth 1-cocycle on ${\varGamma }$.

Finally, we consider the situation where $M = G$ is a compact simply-connected Lie group, acting on itself by left multiplication, and where ${\mathcal {G}}$ is a bundle gerbe on G whose Dixmier–Douady class generates $\mathrm {H}^3(G;{\mathbb {Z}}) \cong {\mathbb {Z}}$. We motivate and propose a new smooth string 2-group model for the string group of G. For this, we first show that with our definition of principal 2-bundle, principal ${{\mathsf {A}}}$-bundles on a manifold give rise to ${{\mathsf {A}}}$-valued Čech 1-cocycles, for any smooth 2-group ${{\mathsf {A}}}$. Then we call a smooth 2-group extension ${{\mathsf {A}}}\longrightarrow {{\mathsf {P}}}\longrightarrow \underline{G}$ a smooth 2-group model for the string group of G if ${{\mathsf {A}}}$ is equivalent to an Eilenberg-MacLane space $K({\mathbb {Z}};2)$ in a certain sense and the class in ${\check{\mathrm {H}}}{}^1(G;{{\mathsf {B}}}{{\text {U}}}(1)) \cong \mathrm {H}^3(G;{\mathbb {Z}})$ extracted from the 2-bundle ${{\mathsf {P}}}\longrightarrow \underline{G}$ is a generator. Using this definition of smooth string 2-group models, we show

Theorem 1.5

Let ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ be the smooth 2-group extensions of $\underline{G}$ by $\mathrm {HLBdl}^G$ constructed from ${\mathcal {G}}$ with respect to the left action of G on itself via left multiplication. Then both ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ are smooth 2-group models for the string group of G.

The remainder of this paper is organised as follows. In Sect. 2 we briefly recall some background material on diffeological spaces, bundle gerbes, and transgression. Section 3 provides a motivation of the later constructions on the level of principal bundles; many concepts become clear already at this level. In Sect. 4 we provide our definition and construction of the parallel transport associated to a bundle gerbe with connection. The construction of ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ takes place in Sect. 5. Here we first motivate and then introduce the necessary language of Grothendieck fibrations, smooth 2-groups, and principal 2-bundles, before defining and studying the extensions ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$. We conclude this section by relating these extensions to equivariant structures on ${\mathcal {G}}$. In the remaining three sections we apply our general results: in Sect. 6 we study nonassociative magnetic translations using our parallel transport, Sect. 7 contains the discussion of chiral anomalies and the Faddeev–Mickelsson–Shatashvili anomaly, and in Sect. 8 we show that ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ provide new models for the string group. We defer some technical results on categories fibred in groupoids and on principal 2-bundles to Appendix A.

2 Preliminaries on Diffeological Spaces and Gerbes

In this section we review some of the relevant background material related to diffeological spaces and bundle gerbes that will be used throughout this paper.

2.1 Diffeological spaces

Throughout this paper we will use diffeological spaces (see [IZ13] for an extensive introduction) to describe the smooth structure on infinite-dimensional spaces such as path and mapping spaces. The idea behind diffeological spaces is to describe the smooth structure on a space X by specifying the set of smooth maps from Cartesian spaces to X. A Cartesian space c is a smooth manifold diffeomorphic to ${\mathbb {R}}^n$ for some $n \in {\mathbb {N}}_0$. We denote by ${{\mathscr {C}}\mathrm{art}}$ the category with Cartesian spaces as objects and smooth maps as morphisms.

Definition 2.1

A diffeological space is a set X together with a collection of maps $c \longrightarrow X$ from Cartesian spaces into X, called plots, such that

• (1) the composition of a plot with a smooth map between Cartesian spaces is again a plot,

• (2) every map ${\mathbb {R}}^0\longrightarrow X$ is a plot, and

• (3) if $f:c \longrightarrow X$ is a map such that there exists an open cover $\{ c_i \}_{i\in I}$ of c by Cartesian spaces and $f_{|c_i}$ is a plot for all $i\in I$, then f is a plot.

A map $f:X \longrightarrow Y$ between diffeological spaces is smooth if it maps plots of X to plots of Y. We denote by ${\mathscr {D}}\mathrm{fg}$ the category of diffeological spaces and smooth maps. Isomorphisms in ${\mathscr {D}}\mathrm{fg}$ are diffeomorphisms.

Remark 2.2

Usually plots are defined to be maps from open subsets U of Cartesian spaces to X. Since every open subset U of a Cartesian space can be covered by Cartesian spaces, both definitions are equivalent. Diffeological spaces are exactly the concrete sheaves on the site of Cartesian spaces [BH11]. This implies that the category of diffeological spaces ${\mathscr {D}}\mathrm{fg}$ admits all limits and colimits, and is Cartesian closed. For more background on this perspective on diffeological spaces, see also [Bun20a]. $\square$

Important examples of diffeological spaces include the following.

Example 2.3

Every manifold M (possibly with boundaries or corners) defines a diffeological space by declaring a map $f:c\longrightarrow M$ to be a plot if and only if f is a smooth map of differentiable manifolds. This defines a fully faithful embedding of the category of smooth manifolds ${\mathscr {M}}\mathrm{fd}$ into the category of diffeological spaces ${\mathscr {D}}\mathrm{fg}$. $\square$

Example 2.4

Let X be a diffeological space and $Y\subset X$ a subset. We can equip Y with a diffeology by declaring a map $c\longrightarrow Y$ to be a plot if and only if the composition with the embedding $Y\longrightarrow X$ is a plot. This is called the subspace diffeology on Y. $\square$

Example 2.5

Let X and Y be diffeological spaces. The Cartesian product $X\times Y$ is a diffeological space by declaring a map $f:c \longrightarrow X\times Y$ to be a plot if and only if ${\text {pr}}_X \circ f$ and ${\text {pr}}_Y \circ f$ are plots, where ${\text {pr}}_X$ and ${\text {pr}}_Y$ are the respective projections of $X\times Y$ onto X and Y. This is called the product diffeology on $X\times Y$. $\square$

Example 2.6

Let X and Y be diffeological spaces. The set of smooth maps $Y^X$ from X to Y becomes a diffeological space by declaring a map $f:c \longrightarrow Y^X$ to be a plot if and only if the map

$$\begin{aligned} {f^{\dashv }}:c \times X&\longrightarrow Y \\ (u, x)&\longmapsto f(u)(x) \end{aligned}$$

is smooth. This is called the mapping space diffeology on $Y^X$. $\square$

A smooth map $f:M \longrightarrow M'$ between smooth manifolds is a surjective submersion if and only if it admits local sections through every point in M, i.e. for every point $y \in M$ there exists an open neighbourhood U of f(y) in $M'$ and a smooth map ${\widehat{s}} :U \longrightarrow M$ such that $f \circ {\widehat{s}} = 1_U$ is the identity map of U. Surjective submersions define a Grothendieck topology on the category of manifolds, and many (higher) geometric objects on manifolds can be constructed via sheafification with respect to this topology (see, for instance, [NS11]). On the category of diffeological spaces, a useful Grothendieck topology is induced by the subductions:

Definition 2.7

A smooth map $f:X \longrightarrow Y$ of diffeological spaces is a subduction if for all plots $\varphi :c \longrightarrow Y$ and $x\in c$ there exists an open neighbourhood $U_x \subset c$ of x and a plot ${\widehat{\varphi }}_x:U_x \longrightarrow X$ such that $\varphi _{|U_x}=f\circ {\widehat{\varphi }}_x$.

Example 2.8

Let M be a connected manifold. The space of paths in M with sitting instants PM is the subspace of $M^{[0,1]}$ of maps which are constant in an open neighbourhood of 0 and 1, equipped with the subspace diffeology. The evaluation maps ${\mathrm {ev}}_0 :PM \longrightarrow M$ and ${\mathrm {ev}}_1 :PM \longrightarrow M$ at 0 and 1, respectively, are subductions. $\square$

Another source for subductions are quotient maps. Let X be a diffeological space and $\sim$ an equivalence relation on X. Then the space $X/{\sim }$ becomes a diffeological space in a canonical way making the map $\pi :X\longrightarrow X/{\sim }$ into a subduction: a map $\varphi :c \longrightarrow X/{\sim }$ is a plot if and only if for all $x\in c$ there exists an open neighbourhood $U_x \subset c$ of x and a plot ${\widehat{\varphi }}_x:U_x \longrightarrow X$ such that $\varphi _{|U_x}=\pi \circ {\widehat{\varphi }}_x$. Clearly all subductions are of this type for appropriate equivalence relations. Diffeological quotients behave nicely with respect to quotients of manifolds when they exist.

Proposition 2.9

Let M be a manifold with a free and proper action of a Lie group G. Define an equivalence relation $\sim _G$ on M by $m_1\sim _G m_2$ if and only if there exists $g\in G$ such that $g\cdot m_1=m_2$. Then the manifold M/G and the diffeological space $M/{\sim }_G$ agree.

Proof

From [Lee13, Theorem 21.10] it follows that $\pi :M \longrightarrow M/G$ is a surjective submersion. Since every surjective submersion is a subduction, the statement follows. $\square$

Definition 2.10

Let X be a diffeological space and $k\ge 0$. A k-form $\omega$ on X consists of a family of differential forms $\omega _\varphi \in \Omega ^k(c)$ indexed by the plots $\varphi :c \longrightarrow X$ of X such that $\omega _{\varphi _1}= f^*\omega _{\varphi _2}$ for all commuting triangles

Definition 2.11

([Wal12b, Section 3]). Let G be a Lie group and X a diffeological space. A principal G-bundle on X consists of a subduction $\pi :P\longrightarrow X$ together with a fibre-preserving right action $P\times G \longrightarrow P$ such that the map

$$\begin{aligned} P\times G&\longrightarrow P \times _X P \nonumber \\ (p, g)&\longmapsto (p,p\cdot g) \end{aligned}$$

(2.12)

is a diffeomorphism. A connection on a principal G-bundle P is a 1-form $A\in \Omega ^1(P; {\mathfrak {g}})$ satisfying

$$\begin{aligned} \rho ^* A = {\mathrm {Ad}}^{-1}_{{\text {pr}}_G}({\text {pr}}_P^* A)+ {\text {pr}}_G^* \theta \end{aligned}$$

on $P\times G$, where $\rho :P\times G \longrightarrow P$ is the right G-action, $\theta$ is the left-invariant Maurer-Cartan 1-form on G, and ${\text {pr}}_P:P\times G \longrightarrow P$ and ${\text {pr}}_G :P\times G \longrightarrow G$ are the projections onto P and G, respectively.

2.2 Bundle gerbes and transgression

Bundle gerbes are higher categorical analogues of line bundles. They provide a geometric realisation for the third cohomology group with integer coefficients. Similarly to line bundles, bundle gerbes can be equipped with connections. We briefly recall the definition of the 2-groupoid of bundle gerbes and their transgression to loop space. For details we refer to [Wal07b, Wal16, Bun17, Mur96].

Let X be a diffeological space. We denote by $\mathrm {HLBdl}(X)$ (resp. $\mathrm {HLBdl}^\nabla (X)$) the category of hermitean line bundles (resp. with connection) on X. Before defining bundle gerbes we need to introduce some notation: for a subduction $\pi :Y \longrightarrow X$ of diffeological spaces we denote by

$$\begin{aligned} Y^{[n]}= \big \{ (y_0,y_1, \ldots , y_{n-1})\in Y^{\times n} \ \big | \ \pi (y_0)=\pi (y_1)=\dots =\pi (y_{n-1}) \big \}\subset Y^{\times n} \end{aligned}$$

the n-fold iterated fibre product $Y^{[n]}=Y\times _X\cdots \times _X Y$ over X equipped with the subspace diffeology. Then $Y^{[\bullet ]}$ is a simplicial diffeological space corresponding to the subduction groupoid $Y\times _X Y \rightrightarrows Y$, and for $k<n$ and $0\le i_1<\dots< i_k < n$ we define the smooth face maps

$$\begin{aligned} \pi _{i_1, \ldots , i_k} :Y^{[n]}&\longrightarrow Y^{[k]} \\ (y_0,y_1, \ldots , y_{n-1})&\longmapsto (y_{i_1}, \ldots , y_{i_k}) \ . \end{aligned}$$

Definition 2.13

([Wal16]). Let X be a diffeological space. A hermitean bundle gerbe on X consists of a subduction $\pi :Y\longrightarrow X$, a hermitean line bundle $L\longrightarrow Y^{[2]}$, and a unitary isomorphism $\mu :\pi _{1,2}^*L\otimes \pi _{0,1}^*L \longrightarrow \pi _{0,2}^*L$ of line bundles over $Y^{[3]}$, called the bundle gerbe multiplication, which is associative over $Y^{[4]}$, i.e. $\pi _{0,2,3}^*\mu \circ (\pi _{0,1,2}^*\mu \otimes 1) = \pi _{0,1,3}^*\mu \circ (1\otimes \pi _{1,2,3}^*\mu )$.

A connection on a hermitean bundle gerbe ${\mathcal {G}}=(\pi :Y\longrightarrow X, L, \mu )$ consists of a hermitean connection $\nabla ^L$ on L and a 2-form $B\in \Omega ^2(Y)$ such that

• (1) the isomorphism $\mu :\pi _{1,2}^*L\otimes \pi _{0,1}^*L \longrightarrow \pi _{0,2}^*L$ is parallel with respect to $\nabla ^L$, and

• (2) the curvature of $\nabla ^L$ is equal to $\mathrm {i}\,(\pi _1^*B-\pi _0^*B)$.

The 2-form B is called a curving. The second condition implies that the closed 3-form $\mathrm {d}B=\pi ^*H$ descends to a unique closed 3-form H on X with integer periods, which is called the curvature of the bundle gerbe connection $(\nabla ^L, B)$ .

Schematically, the data corresponding to a bundle gerbe can be visualised by the diagram

illustrating that hermitean bundle gerbes are equivalent to ${{\text {U}}}(1)$-central extensions of subduction groupoids.

Example 2.14

Let X be a diffeological space. The trivial hermitean bundle gerbe ${\mathcal {I}}$ on X consists of the identity subduction $1_X :X\longrightarrow X$ together with the trivial hermitean line bundle $I :=X\times {\mathbb {C}}$ over $X^{[2]}=X$ and bundle gerbe multiplication

$$\begin{aligned} X\times ({\mathbb {C}}\otimes {\mathbb {C}})&\longrightarrow X\times {\mathbb {C}}\\ \big (x, (z_1\otimes z_2)\big )&\longmapsto (x, z_1\, z_2) \ . \end{aligned}$$

For every 2-form $B \in \Omega ^2(X)$ we can define a connection on ${\mathcal {I}}$ by setting $\nabla ^{I}=\mathrm {d}$ and taking B as the curving. We denote the resulting hermitean bundle gerbe with connection by ${\mathcal {I}}_B$. The curvature of ${\mathcal {I}}_B$ is given by $H=\mathrm {d}B$. $\square$

Hermitean bundle gerbes (resp. with connection) on a diffeological space X are the objects of a symmetric monoidal bicategory which we denote by $\mathrm {BGrb}(X)$ (resp. $\mathrm {BGrb}^\nabla (X)$) [Wal07b].

Definition 2.15

Let ${\mathcal {G}}=(\pi :Y\longrightarrow X, L, \mu , \nabla ^L, B)$ and ${\mathcal {G}}'=(\pi ' :Y'\longrightarrow X, L', \mu ', \nabla ^{L'}, B')$ be hermitean bundle gerbes with connection on a diffeological space X. A 1-isomorphism ${\mathcal {G}}\longrightarrow {\mathcal {G}}'$ of hermitean bundle gerbes (with connection) consists of a subduction $\xi :Z\longrightarrow Y\times _X Y'$, a hermitean line bundle E (with hermitean connection $\nabla ^E$) on Z and (parallel) unitary isomorphisms

$$\begin{aligned} \alpha :\big (({\text {pr}}_Y \circ \, \xi )^{[2]}\big ) ^* L \otimes \xi _1^*E \longrightarrow \xi _0^*E \otimes \big (({\text {pr}}_{Y'} \circ \, \xi )^{[2]}\big ) ^* L' \end{aligned}$$

over $Z^{[2]}$ satisfying a natural set of compatibility conditions, see [Wal16] for details. We will denote such a 1-isomorphism by $(E,\xi )$ (resp. $(E,\xi ,\nabla ^E)$), or sometimes simply by E.

Remark 2.16

One can also define non-invertible 1-morphisms of bundle gerbes by using higher rank hermitean vector bundles E in Definition 2.15 [Wal07b]. In that case, a 1-morphism is weakly invertible if and only if the underlying hermitean vector bundle E is of rank 1 [Wal07a, Proposition 2.3.4]. However, with the exception of Sect. 6, we will only consider invertible 1-morphisms of bundle gerbes in the present paper. $\square$

Definition 2.17

Let $(\xi _a :Z_a \longrightarrow Y\times _X Y',E_a, \nabla ^{E_a}, \alpha _a)$ and $(\xi _b :Z_b \longrightarrow Y\times _X Y',E_b, \nabla ^{E_b}, \alpha _b)$ be 1-isomorphisms ${\mathcal {G}}\longrightarrow {\mathcal {G}}'$ of hermitean bundle gerbes with connection. A 2-isomorphism of bundle gerbes is an equivalence class of a subduction $\omega :W\longrightarrow Z_a \times _{Y\times _X Y'} Z_b$ and a parallel unitary isomorphism $({\text {pr}}_{Z_a} \circ \, \omega )^*E_a \longrightarrow ({\text {pr}}_{Z_b} \circ \, \omega )^*E_b$ satisfying a natural compatibility condition, see e.g. [Wal07b] for details and the equivalence relation.

Bundle gerbes on a diffeological space X are classified by their Dixmier–Douady class in $\mathrm {H}^3(X;{\mathbb {Z}})$, analogously to the Chern-Weil classification of line bundles by their Chern class in $\mathrm {H}^2(X;{\mathbb {Z}})$. For a bundle gerbe with connection, the Dixmier–Douady class maps to the de Rham cohomology class of the curvature under the homomorphism $\mathrm {H}^3(X;{\mathbb {Z}})\longrightarrow \mathrm {H}^3(X;{\mathbb {R}})$ induced by the inclusion of coefficient groups ${\mathbb {Z}}\hookrightarrow {\mathbb {R}}$.

Let ${\mathcal {G}}$ be a hermitean bundle gerbe defined over a subduction $\pi :Y \longrightarrow X$, with underlying hermitean line bundle $L \longrightarrow Y^{[2]}$. Let $\AA :{\mathcal {G}}\longrightarrow {\mathcal {G}}$ be an endomorphism of ${\mathcal {G}}$, with underlying hermitean vector bundle A over some subduction $\xi :Z \longrightarrow Y^{[2]}$. Consider the hermitean vector bundle $L^\vee \otimes A$ on Z, where we denote the dual line bundle by $L^\vee$. This comes with a canonical descent isomorphism defined by the diagram [Wal07b, Bun17]

In fact, this construction establishes an equivalence of categories ${\mathsf {R}}:\mathrm {BGrb}(X)({\mathcal {G}}, {\mathcal {G}}) \longrightarrow \mathrm {HLBdl}(X)$.

From a hermitean bundle gerbe with connection ${\mathcal {G}}$ on a diffeological space X we can construct the transgression line bundle ${\mathcal {T}}{\mathcal {G}}$ over the loop space LX of X. The fibre ${\mathcal {T}}{\mathcal {G}}_{\gamma }$ over a loop $\gamma :{\mathbb {S}}^1 \longrightarrow X$ consists of equivalence classes $[[{\mathcal {S}}],z]$ of a 2-isomorphism class of a trivialisation ${\mathcal {S}}:\gamma ^* {\mathcal {G}}\longrightarrow {\mathcal {I}}_0$ in $\mathrm {BGrb}^\nabla ({\mathbb {S}}^1)$ over the unit circle ${\mathbb {S}}^1$ and an element $z\in {\mathbb {C}}$. Two pairs $([{\mathcal {S}}],z)$ and $([{\mathcal {S}}'],z')$ are equivalent if and only if $z'={\text {hol}}({\mathbb {S}}^1,{\mathsf {R}}({\mathcal {S}}'\circ {\mathcal {S}}^{-1}))\, z$. For the construction of a diffeological structure on ${\mathcal {T}}{\mathcal {G}}:=\coprod _{\gamma \in LX}\, {\mathcal {T}}{\mathcal {G}}_{\gamma }$ we refer to [Wal16]. A connection on a line bundle over the loop space LX is superficial if the holonomy around every thin loop¹ is equal to 1 and thin homotopic loops² have the same holonomy. In the situation where $X = M$ is a manifold, a superficial connection on ${\mathcal {T}}{\mathcal {G}}$ has been constructed from the connection on ${\mathcal {G}}$ in [Wal16, Prop. 3.3.1]; note that in our later constructions, we will always work with bundle gerbes over manifolds. The bundle gerbe multiplication induces, for all triples of paths $(\gamma _1,\gamma _2, \gamma _3)$ with sitting instants and the same start and end points, a fusion product

$$\begin{aligned} \lambda :{\mathcal {T}}{\mathcal {G}}_{\overline{\gamma _2} \star \gamma _1} \otimes {\mathcal {T}}{\mathcal {G}}_{\overline{\gamma _3} \star \gamma _2} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{ \overline{\gamma _3} \star \gamma _1} \ , \end{aligned}$$

where $\star$ denotes the concatenation of paths and ${\overline{\gamma }}$ is the path $t\longmapsto \gamma (1-t)$. The fusion product depends smoothly on the paths, is parallel with respect to the superficial connection, and is associative. The connection and fusion product satisfy one further compatibility condition, related to the rotation of all loops involved by $180^\circ$ (see [Wal16, Definition 2.1.5]). A line bundle over LX admitting all the structures discussed above is a fusion line bundle with superficial connection.

For $X = M$ a manifold, transgression extends to a functor ${\mathcal {T}}$ from $\mathtt {h}\mathrm {BGrb}^\nabla (M)$, the 1-category obtained from $\mathrm {BGrb}^\nabla (M)$ by identifying isomorphic 1-morphisms, to the category of fusion line bundles with superficial connection over LM. The central result of [Wal16] is that ${\mathcal {T}}$ defines an equivalence of categories. An explicit inverse functor ${\mathcal {R}}$ is constructed in [Wal16] and is called regression.

3 Group Extensions from Principal Bundles

In this section we construct group extensions from group actions on manifolds with principal bundles. We generalise this extension to higher geometry in Sect. 5. We present two perspectives on this group extension. The first one is global. The second one is local and can be formulated in terms of the parallel transport of an auxiliary connection on a principal bundle.

3.1 Global description

Let H be a Lie group and $P \longrightarrow M$ a principal H-bundle on a manifold M; principal H-bundles on M and isomorphisms form a groupoid which we denote by ${\mathrm {Bun}}_H(M)$. We consider a Lie group action

$$\begin{aligned} \varPhi :G \times M&\longrightarrow M \\ (g,x)&\longmapsto \varPhi _g(x)=\varPhi (g,x) \end{aligned}$$

on the base manifold M, and ask whether and how this action lifts to P. An action of a Lie group G on M can equivalently be written as a smooth homomorphism of groups $\varPhi :G \longrightarrow \mathrm {Diff}(M)$, where $\mathrm {Diff}(M)$ is the diffeological group of diffeomorphisms $M \longrightarrow M$. In general, the action of G does not lift to P. Instead, we will construct a group extension

$$\begin{aligned} 1\longrightarrow {\mathrm {Gau}}(P) \longrightarrow {\mathrm {Sym}}_G(P)\longrightarrow G \longrightarrow 1 \end{aligned}$$

of G by the gauge group ${\mathrm {Gau}}(P)$ of P. The group ${\mathrm {Sym}}_G(P)$ acts on the total space P in a way compatible with the action of G on M. We show that it is the universal extension of G having this property.

Remark 3.1

The extension can be constructed as the pullback of the short exact sequence

$$\begin{aligned} 1 \longrightarrow {\mathrm {Gau}}(P) \longrightarrow \mathsf {Aut}_G(P) \longrightarrow \mathrm {Diff}_P(M) \longrightarrow 1 \end{aligned}$$

of diffeological groups along $\varPhi$, where $\mathsf {Aut}_G(P)$ is the group of G-equivariant diffeomorphisms of P and $\mathrm {Diff}_P(M)$ is the subgroup of diffeomorphisms of M which admit an equivariant lift to P. In the following we present a different construction which generalises directly to bundle gerbes.

We can pull back the bundle P along the source and target maps of the action groupoid

We define a bundle

$$\begin{aligned} {\mathrm {Sym}}_G(P) \overset{\pi }{\longrightarrow } G \qquad \text{ with } \quad {\mathrm {Sym}}_G(P)_{|g} :={\mathrm {Bun}}_{H}(M)(P, \varPhi _g^*P) \end{aligned}$$

(3.2)

for all $g\in G$, where ${\mathrm {Bun}}_{H}(M)(P, \varPhi _g^*P)$ is the collection of gauge transformations from P to $\varPhi _g^* P$. In order for ${\mathrm {Sym}}_G(P)$ to be a bundle over G, we must ensure that the fibres of ${\mathrm {Sym}}_G(P)$ are actually pairwise diffeomorphic. It might happen that a pullback bundle $\varPhi _g^*P$ is no longer isomorphic to P and hence the fibre over g is empty. As an example, consider the action of the group $G={\mathbb {Z}}$ on the 2-torus $M={{\mathbb {T}}}^2$ generated by an orientation-reversing diffeomorphism f, and let $P \longrightarrow {{\mathbb {T}}}^2$ be a ${{\text {U}}}(1)$-bundle with non-trivial Chern class. Then $[f^*P] = -[P]$, and thus ${\mathrm {Sym}}_{\mathbb {Z}}(P)_{|1}={\mathrm {Bun}}_{{{\text {U}}}(1)}(P, f^*P) = \varnothing$. Hence in (3.2) we have to ensure that the fibres of ${\mathrm {Sym}}_G(P)$ are actually all non-trivial.

We restrict our attention to connected Lie groups G; otherwise, if G is not connected, we consider only the connected component of the identity $e\in G$. We show that in this case the fibres are always non-trivial: we need to show that for any $g \in G$ the fibre of ${\mathrm {Sym}}_G(P) \longrightarrow G$ over g is non-empty. That is, we need to show that there exists an isomorphism $P \longrightarrow \varPhi _g^*P$ of H-bundles over M. Let $f_P :M \longrightarrow {{\mathsf {B}}}H$ be a map that classifies the bundle $P \longrightarrow M$. Then $\varPhi _g^*P$ is classified by the map $f_P \circ \varPhi _g :M \longrightarrow {{\mathsf {B}}}H$. Since G is connected, we can find a smooth path $\gamma :[0,1] \longrightarrow G$ with $\gamma (0) = e$ and $\gamma (1) = g$. Consider the smooth map

$$\begin{aligned} \varPhi _\gamma :[0,1] \times M&\longrightarrow M \\ (t,x)&\longmapsto \varPhi _{\gamma (t)}(x) \ . \end{aligned}$$

We can postcompose this map by $f_P$ to obtain a homotopy

$$\begin{aligned} f_P \circ \varPhi _\gamma :[0,1] \times M \longrightarrow {{\mathsf {B}}}H \end{aligned}$$

from $f_P$ to $f_P \circ \varPhi _g$. This shows that there exists a bundle isomorphism $P \longrightarrow \varPhi _g^*P$. We note for later use that this argument generalises to n-gerbes ${\mathcal {G}}$, as these are classified by maps $f_{\mathcal {G}}:M \longrightarrow {{\mathsf {B}}}^{n+1}{{\text {U}}}(1)$.

In order to equip the set ${\mathrm {Sym}}_G(P)$ with a diffeology, we note that ${\mathrm {Sym}}_G(P)$ can be identified with the subspace of the Cartesian product of the space of H-equivariant diffeomorphisms $P\longrightarrow P$ which cover the action of an arbitrary element $g\in G$ on M with G, and equip ${\mathrm {Sym}}_G(P)$ with the subspace diffeology. Concretely, for $c\in {{\mathscr {C}}\mathrm{art}}$, a map $f:c \longrightarrow {\mathrm {Sym}}_G(P)$ is a plot if and only if the composition $\pi \circ f :c\longrightarrow G$ is smooth and the induced map ${\text {pr}}_M^*P \longrightarrow \varPhi _{f}^*P$ is an isomorphism in ${\mathrm {Bun}}_H(c\times M)$, where ${\text {pr}}_M :c\times M \longrightarrow M$ is the projection onto M and $\varPhi _f=\varPhi \circ (f\times 1_M)$. The automorphism group or group of gauge transformations

$$\begin{aligned} {\mathrm {Gau}}(P) :={\mathrm {Bun}}_{H}(M)(P,P) \end{aligned}$$

acts simply and transitively on each fibre ${\mathrm {Sym}}_G(P)_{|g}$ from the right via precomposition. The set ${\mathrm {Gau}}(P)$ forms a diffeological group with respect to the composition of automorphisms and the smooth structure induced from the mapping space diffeology on $P^P$.

Proposition 3.3

$\pi :{\mathrm {Sym}}_G(P) \longrightarrow G$ is a principal ${\mathrm {Gau}}(P)$-bundle on G.

Proof

We verify that the map $\pi :{\mathrm {Sym}}_G(P) \longrightarrow G$ is a subduction. Let $f:c\longrightarrow G$ be a plot. We can pick an isomorphism $\varphi _f :{\text {pr}}_M^*P \longrightarrow \varPhi _f^*P$ (since c is contractible) and define the map

$$\begin{aligned} {\widehat{f}} :c&\longrightarrow {\mathrm {Sym}}_G(P) \\ x&\longmapsto \varphi _{f|\{x \} \times M} \ . \end{aligned}$$

The map ${\widehat{f}}$ is a smooth lift of the plot f, showing that ${\mathrm {Sym}}_G(P) \longrightarrow G$ is a subduction.

The map

$$\begin{aligned} {\mathrm {Sym}}_G(P)\times _G {\mathrm {Sym}}_G(P)&\longrightarrow {\mathrm {Sym}}_G(P)\times {\mathrm {Gau}}(P) \\ (\varphi :P \longrightarrow \varPhi _g^* P, \varphi ' :P \longrightarrow \varPhi _g^* P)&\longmapsto (\varphi , \varphi ^{-1} \circ \varphi ') \end{aligned}$$

provides a smooth inverse to the map ${\mathrm {Sym}}_G(P)\times {\mathrm {Gau}}(P) \longrightarrow {\mathrm {Sym}}_G(P) \times _G {\mathrm {Sym}}_G(P)$ from (2.12), and the result follows. $\square$

Proposition 3.4

${\mathrm {Sym}}_G(P)$ is a diffeological group. The principal bundle ${\mathrm {Sym}}_G(P) \longrightarrow G$ is part of an extension of diffeological groups

$$\begin{aligned} 1\longrightarrow {\mathrm {Gau}}(P)\longrightarrow {\mathrm {Sym}}_G(P)\longrightarrow G \longrightarrow 1 \ . \end{aligned}$$

Proof

To complete the proof we need to equip ${\mathrm {Sym}}_G(P)$ with a diffeological group structure such that the map ${\mathrm {Sym}}_G(P) \longrightarrow G$ becomes a morphism of diffeological groups. Consider isomorphisms $\psi :P \longrightarrow \varPhi _g^*P$ and $\phi :P \longrightarrow \varPhi _{g'}^*P$ for $g,g' \in G$. We set

$$\begin{aligned} \mu (\psi , \phi ) :=\varPhi _{g'}^*\psi \circ \phi \ :P \longrightarrow \varPhi _{g'}^*P \longrightarrow \varPhi _{g'}^*\varPhi _{g}^*P = \varPhi _{g\,g'}^*P \ . \end{aligned}$$

This is associative by the associativity of pullbacks, the multiplication in G, and composition of morphisms. The inverse of an element $\psi :P \longrightarrow \varPhi _g^* P$ with respect to $\mu$ is the isomorphism

$$\begin{aligned} P= \varPhi _{g^{-1}}^*\varPhi _{g}^*P \xrightarrow {\varPhi _{g^{-1}}^*\psi ^{-1}} \varPhi _{g^{-1}}^*P \ , \end{aligned}$$

and the result follows from the observation that these maps are smooth. $\square$

Proposition 3.5

The group ${\mathrm {Sym}}_G(P)$ acts smoothly on P, lifting the action of G on M. It is universal in the following sense: let ${\widehat{G}}$ be a Lie group, $\varphi :{\widehat{G}} \longrightarrow G$ a Lie group homomorphism and ${\widehat{\psi }} :{\widehat{G}} \times P \longrightarrow P$ an action of ${\widehat{G}}$ on P making the diagram

commute, where $\varpi :P \longrightarrow M$ is the bundle projection. Then there exists a unique smooth group homomorphism ${\widehat{G}}\longrightarrow {\mathrm {Sym}}_G(P)$ such that the diagram

commutes.

Proof

The action is via the evaluation

$$\begin{aligned} {\widehat{\varPhi }} :{\mathrm {Sym}}_G(P) \times P&\longrightarrow P \\ (\phi ,p)&\longmapsto \phi (p) = \phi _{|\varpi (p)}(p) \ . \end{aligned}$$

The unique smooth group homomorphism in the universality statement is

$$\begin{aligned} {\widehat{G}}&\longrightarrow {\mathrm {Sym}}_G(P) \\ {\widehat{g}}&\longmapsto \big ({\widehat{\psi }}_{{\widehat{g}}} :P \longrightarrow \varPhi _{\varphi ({\widehat{g}})}^*P\big ) \ , \end{aligned}$$

and the result follows. $\square$

The construction of the group ${\mathrm {Sym}}_G(P)$ is functorial in P, i.e. an isomorphism of bundles $\psi :P \longrightarrow P'$ induces an isomorphism of group extensions

$$\begin{aligned} {\widehat{\psi }}:{\mathrm {Sym}}_G(P)&\longrightarrow {\mathrm {Sym}}_G(P') \nonumber \\ ( f:P\longrightarrow g^* P)&\longmapsto \Big ( P' \xrightarrow {\psi ^{-1}} P\overset{f}{\longrightarrow } g^* P \xrightarrow {g^*\psi } g^*P' \Big ) \ . \end{aligned}$$

(3.6)

3.2 Equivariant bundles

Let G be a connected Lie group, M a manifold with G-action $\varPhi :G\times M \longrightarrow M$, and P a principal H-bundle over M. A G-equivariant structure on P consists of an isomorphism $\chi :{\text {pr}}_M^* P \longrightarrow \varPhi ^* P$ of principal bundles over $G\times M$ such that the diagram

commutes for all $g,g'\in G$ and $x\in M$. We denote by ${\mathcal {E}}(P)$ the set of equivariant structures on P. A splitting s of $\pi :{\mathrm {Sym}}_G(P)\longrightarrow G$ is a smooth group homomorphism $s:G \longrightarrow {\mathrm {Sym}}_G(P)$ such that $\pi \circ s = 1_G$. We denote the set of splittings of $\pi :{\mathrm {Sym}}_G(P)\longrightarrow G$ by ${\mathcal {S}}(G;{\mathrm {Sym}}_G(P))$.

Proposition 3.7

There is a natural bijection of sets $\Xi :{\mathcal {E}}(P)\longrightarrow {\mathcal {S}}(G;{\mathrm {Sym}}_G(P))$. In particular, the bundle P admits an equivariant structure if and only if the extension

$$\begin{aligned} 1 \longrightarrow {\mathrm {Gau}}(P) \longrightarrow {\mathrm {Sym}}_G(P)\longrightarrow G \longrightarrow 1 \end{aligned}$$

is trivial as an extension of diffeological groups.

Proof

Let $(P,\chi )$ be an equivariant bundle. We define $\Xi (P,\chi ) (g) :P \longrightarrow \varPhi _g^*P$ to be $\chi _{|\{g\}\times M}$. The inverse $\Xi ^{-1}:{\mathcal {S}}(G;{\mathrm {Sym}}_G(P))\longrightarrow {\mathcal {E}}(P)$ can be constructed by sending a splitting $s:G \longrightarrow {\mathrm {Sym}}_G(P)$ to the isomorphism $\Xi ^{-1}(s) :{\text {pr}}_M^* P \longrightarrow \varPhi ^* P$ which is given by $s(g)(x):P_x \longrightarrow P_{\varPhi _g(x)}$ at $(g,x)\in G\times M$. $\square$

Let $(P, \chi )$ and $(P', \chi ')$ be G-equivariant H-bundles on M. An isomorphism $\psi :P \longrightarrow P'$ is equivariant if the diagram

commutes for all $g\in G$. The equivariant structures on P and $P'$ can be described by smooth group homomorphisms $s_P :G \longrightarrow {\mathrm {Sym}}_G(P)$ and $s_{P'} :G \longrightarrow {\mathrm {Sym}}_G(P')$. Since the isomorphism ${\widehat{\psi }}$ defined in (3.6) intertwines the action of ${\mathrm {Sym}}_G(P)$ and ${\mathrm {Sym}}_G(P')$ on P and $P'$, respectively, it follows that $\psi$ is equivariant if and only if $s_{P'}= {\widehat{\psi }} \circ s_P$. Hence the smooth group extension ${\mathrm {Sym}}_G$ contains all information on equivariance.

3.3 Description via parallel transport

The extension ${\mathrm {Sym}}_G(P)$ can be described more explicitly using the parallel transport of a connection on P, as we will now explain. In Sect. 6 we apply this to the description of magnetic translations in quantum mechanics. We consider a principal H-bundle $P \longrightarrow M$. Let $P_0 G$ denote the diffeological space of smooth paths in G with sitting instants based at $e\in G$, ${\mathrm {ev}}_1:P_0G \longrightarrow G$ the evaluation at the end point, $(P_0G)^{[2]}$ the fibre product $P_0G\times _{G} P_0G$ with respect to ${\mathrm {ev}}_1$, and LM the space of smooth loops in M. We denote by $\star$ the concatenation of paths. For a path $\gamma :[0,1] \longrightarrow G$ we denote by ${\overline{\gamma }}$ the precomposition of $\gamma$ with

$$\begin{aligned}{}[0,1]&\longrightarrow [0,1] \\ t&\longmapsto 1-t \ . \end{aligned}$$

For a path $\gamma \in P_0 G$ and a point $x \in M$, set

$$\begin{aligned} \gamma _x :[0,1]&\longrightarrow M \\ t&\longmapsto \varPhi _{\gamma (t)} (x) \ . \end{aligned}$$

Endow P with an arbitrary connection A. The H-bundle P with connection then induces a principal ${\mathrm {Gau}}(P)$-bundle on G as follows: we set

$$\begin{aligned} {\mathcal {L}}_G :=\big ( P_0 G \times {\mathrm {Gau}}(P) \big ) \big /{\sim } \ , \end{aligned}$$

where we define the equivalence relation

$$\begin{aligned}&(\gamma , \phi ) \sim \big ( \alpha , {\text {hol}}(P, \alpha , \gamma )\circ \phi \big ) \nonumber \\&\qquad \text {with} \quad {\text {hol}}(P, \alpha , \gamma ) (x) :={\text {hol}}\big ( P, ( {\overline{\alpha }}\star \gamma )_x \big ) \ \in \ \mathsf {End}(P_x) \end{aligned}$$

for all $(\gamma ,\alpha )\in (P_0G)^{[2]}$ and $x\in M$, and we interpret the holonomy of P along a loop starting and ending at x as an endomorphism of the fibre $P_x$. Note that, with this notation, we have defined a smooth map ${\text {hol}}(P,-) :(P_0 G)^{[2]} \longrightarrow {\mathrm {Gau}}(P)$. We endow ${\mathcal {L}}_G$ with the quotient diffeology.

Then the ${\mathrm {Gau}}(P)$-bundle ${\mathcal {L}}_G \longrightarrow G$ can be defined in terms of descent data as follows: the action $\varPhi$ of G on M induces a smooth map

$$\begin{aligned} L\varPhi :(P_0 G)^{[2]} \times M&\longrightarrow LM \nonumber \\ (\gamma , \alpha , x)&\longmapsto ({\overline{\alpha }} \star \gamma )_x \ . \end{aligned}$$

(3.8)

Explicitly,

$$\begin{aligned} ( {\overline{\alpha }} \star \gamma )_x(t) = \varPhi _{({\overline{\alpha }} \star \gamma ) (t)}(x) \ \in \ M \end{aligned}$$

for all $t \in [0,1]$ and $x \in M$. The descent data for the bundle ${\mathcal {L}}_G$ consists of the subduction $P_0G\longrightarrow G$, the trivial bundle $P_0G\times {\mathrm {Gau}}(P)\longrightarrow P_0G$, and the smooth map

$$\begin{aligned} {{\mathsf {g}}}:(P_0 G)^{[2]}&\longrightarrow {\mathrm {Gau}}(P) \\ (\gamma ,\alpha )&\longmapsto {{\mathsf {g}}}(\gamma ,\alpha ) = {\text {hol}}( P, {\overline{\alpha }} \star \gamma ) \ . \end{aligned}$$

Proposition 3.9

The total space ${\mathcal {L}}_G$ is a smooth group extension

Proof

Let $\gamma$ and $\gamma '$ be two paths in G. The evaluation ${\mathrm {ev}}_1 :P_0 G \longrightarrow G$ is a group homomorphism with respect to the pointwise product of paths.

Let $x \in M$ be an arbitrary point. To any triple $(x, \gamma , \gamma ')$, we can associate a map

$$\begin{aligned} \Delta ^2(x,\gamma ,\gamma ') :|\Delta ^2|&\longrightarrow M \\ (t_1,t_2)&\longmapsto \varPhi _{\gamma (t_1)}\big (\gamma '_x(t_2)\big ) \ , \end{aligned}$$

where $|\Delta ^2|$ is the standard topological 2-simplex with $|\Delta ^2| \cong \{ (t_1, t_2) \in {\mathbb {R}}^2\, | \, 0 \le t_2 \le t_1 \le 1 \}$. Diagrammatically, this is a homotopy

between the product path $\gamma \, \gamma ' \in P_0 G$ and the concatenated path $(\gamma \, \gamma '(1)) \star \gamma ' \in P_0 G$.

For $\gamma , \gamma ' \in P_0G$ and $\phi , \phi ' \in {\mathrm {Gau}}(P)$, we define

$$\begin{aligned} \mu \big ( (\gamma , \phi ), (\gamma ', \phi ') \big ) :=\big ( \gamma \, \gamma ',\, {\mathtt {pt}}_{\gamma \, \gamma '}^{-1} \circ {\mathtt {pt}}_{\gamma \, \left( \gamma '(1)\right) } \circ (\varPhi _{\gamma '(1)}^*\phi )\, \circ {\mathtt {pt}}_{\gamma '} \circ \phi ' \big ) , \end{aligned}$$

(3.10)

where we denote by ${\mathtt {pt}}_\gamma$ the isomorphism $P\longrightarrow \varPhi _{\gamma (1)}^*P$ defined at a point $x\in M$ by the parallel transport along the path $\gamma _x$. This is well-defined: let $\alpha , \alpha ' \in P_0 G$ with $\gamma (1) = \alpha (1)$ and $\gamma '(1) = \alpha '(1)$. Then

$$\begin{aligned}&\mu \big ( (\alpha , {\text {hol}}(P, \alpha , \gamma ) \circ \phi ), (\alpha ', {\text {hol}}(P, \alpha ', \gamma ')\circ \phi ') \big ) \\&\quad = \big ( \alpha \, \alpha ',\, {\mathtt {pt}}_{\alpha \, \alpha '}^{-1} \circ \varPhi _{\alpha '(1)}^*({\mathtt {pt}}_{\alpha } \circ {\text {hol}}(P, \alpha , \gamma ) \circ \phi ')\, \circ {\mathtt {pt}}_{\alpha '} \circ {\text {hol}}(P, \alpha ', \gamma ')\circ \phi ' \big ) \\&\quad = \big ( \alpha \, \alpha ',\, {\text {hol}}(P, \alpha \, \alpha ', \gamma \, \gamma ') \circ {\mathtt {pt}}_{\gamma \, \gamma '}^{-1} \circ \varPhi _{\gamma '(1)}^*({\mathtt {pt}}_{\gamma } \circ \phi ')\, \circ {\mathtt {pt}}_{\gamma '}\circ \phi ' \big ) \\&\quad = \big ( \gamma \, \gamma ',\, {\mathtt {pt}}_{\gamma \, \gamma '}^{-1} \circ \varPhi _{\gamma '(1)}^*({\mathtt {pt}}_{\gamma } \circ \phi ')\, \circ {\mathtt {pt}}_{\gamma '}\circ \phi ' \big ) \\&\quad = \mu \big ( (\gamma , \phi ), (\gamma ', \phi ') \big ) \ , \end{aligned}$$

where we used $\varPhi _{\gamma '(1)}^*{\mathtt {pt}}_{\gamma }= {\mathtt {pt}}_{\gamma \, (\gamma '(1))}$. Associativity then follows immediately from the associativity of the products in $P_0 G$ and ${\mathrm {Gau}}(P)$, together with associativity of taking pullbacks. Smoothness follows from the definition of the quotient diffeology and the smooth dependence of parallel transport on the path. $\square$

Remark 3.11

For abelian structure group H, we can use the fact that parallel transport commutes with gauge transformations to get the simplified expression

$$\begin{aligned} \mu \big ( (\gamma , \phi ), (\gamma ', \phi ') \big ) = \big ( \gamma \, \gamma ',\, {\text {hol}}(P, \partial |\Delta ^2|) \, (\varPhi _{\gamma '(1)}^*\phi ) \circ \phi ' \big ) \end{aligned}$$

for the multiplication (3.10). $\square$

Remark 3.12

If G is abelian, then the multiplicative structure yields isomorphisms

$$\begin{aligned} {\mathcal {L}}_{G|g} \times {\mathcal {L}}_{G|g'} \longrightarrow {\mathcal {L}}_{G|g\,g'} = {\mathcal {L}}_{G|g'\,g} \longrightarrow {\mathcal {L}}_{G|g'} \times {\mathcal {L}}_{G|g} \end{aligned}$$

for all $g,g' \in G$. That is, the group extension ${\mathcal {L}}_G$ spoils the commutativity of G, since its fibres multiply commutatively only up to coherent isomorphism. $\square$

We summarise the connection to the construction from Sect. 3.1 in

Proposition 3.13

Let G be a connected Lie group, and let $P\longrightarrow M$ be a principal H-bundle on a manifold M with smooth G-action. The map

$$\begin{aligned} \Gamma :{\mathcal {L}}_{G}&\longrightarrow {\mathrm {Sym}}_G(P) \\ \big [(\gamma ,\phi )\big ]&\longmapsto \big ({\mathtt {pt}}_{\gamma } \circ \phi :P \longrightarrow \varPhi _{\gamma (1)}^*P\big ) \end{aligned}$$

is an isomorphism of diffeological group extensions of G.

Proof

The map is well-defined: consider two representatives $(\gamma , \phi )$ and $(\alpha , {\text {hol}}(P,\alpha ,\gamma )\circ \phi )$ of the same equivalence class in ${\mathcal {L}}_G$, and calculate

$$\begin{aligned} {\mathtt {pt}}_\alpha \circ {\text {hol}}(P,\alpha ,\gamma )\circ \phi = {\mathtt {pt}}_\alpha \circ {\mathtt {pt}}_{{\overline{\alpha }}}\circ {\mathtt {pt}}_\gamma \circ \phi ={\mathtt {pt}}_\gamma \circ \phi \ . \end{aligned}$$

The map is bijective, because two gauge transformations $P\longrightarrow \varPhi _{g}^*P$ differ by exactly one gauge transformation of P. It also follows directly from the definition that $\Gamma$ is a morphism of extensions. We check that $\Gamma$ is a group homomorphism: for $[(\gamma ,\phi )], \, [(\gamma ',\phi ')]\in {\mathcal {L}}_G$ we compute

$$\begin{aligned} \mu \big (\Gamma (\gamma ,\phi ), \Gamma (\gamma ',\phi ')\big )&= \mu ({\mathtt {pt}}_{\gamma } \circ \phi ,\, {\mathtt {pt}}_{\gamma '} \circ \phi ') \\&= \varPhi _{\gamma '(1)}^*({\mathtt {pt}}_{\gamma } \circ \phi ) \circ {\mathtt {pt}}_{\gamma '} \circ \phi ' \\&= \Gamma \big (\gamma \, \gamma ',\, {\mathtt {pt}}_{\gamma \, \gamma '}^{-1} \circ {\mathtt {pt}}_{\gamma \, (\gamma '(1))} \circ (\varPhi _{\gamma '(1)}^*\phi )\, \circ {\mathtt {pt}}_{\gamma '} \circ \phi ' \big ) \\&= \Gamma \Big (\mu \big ((\gamma ,\phi ), (\gamma ',\phi )\big )\Big ) \ . \end{aligned}$$

Finally, we verify that $\Gamma$ is smooth. Let $f:c \longrightarrow {\mathcal {L}}_G$ be a plot admitting a lift ${\widehat{f}}:c \longrightarrow P_0 G\times {\mathrm {Gau}}(P)$. We denote the components of ${\widehat{f}}$ by ${\widehat{f}}_\gamma$ and ${\widehat{f}}_{{\mathrm {Gau}}(P)}$. It is enough to show that

is a gauge transformation. This follows from the smoothness of parallel transport (recalled in Sect. 4.1 below). $\square$

Corollary 3.14

The action $\varPhi :G \times M \longrightarrow M$ lifts to an action

which covers the action of G on M.

4 A Global Approach to Parallel Transport for Bundle Gerbes

In Sect. 3 we have constructed two diffeological groups, ${\mathrm {Sym}}_G(P)$ and ${\mathcal {L}}_G$, which extend G and control the existence of G-equivariant structures on a principal bundle P over M. The key to constructing ${\mathcal {L}}_G$, as well as to comparing the groups ${\mathrm {Sym}}_G(P)$ and ${\mathcal {L}}_G$ (see Sect. 3.3), was the parallel transport on the principal bundle P.

If one replaces the principal bundle P by a bundle gerbe ${\mathcal {G}}$ on M, there exist categorified versions of both these constructions which will be given in Sect. 5. However, in order to write down the categorification of ${\mathcal {L}}_G$ we need a notion of parallel transport for ${\mathcal {G}}$. In this section we give a definition of parallel transport for ${\mathcal {G}}$ suited for our purposes and explicitly construct such a parallel transport from any connection on ${\mathcal {G}}$. Our construction relies heavily on Waldorf’s transgression-regression machine [Wal16].

There is a different approach to the parallel transport on a bundle gerbe developed by Schreiber and Waldorf [SW09, SW11, SW17]. It relies on their technology of transport functors and is based on local constructions, which are then glued to global objects. In [Wal18], this has been extended to a canonical assignment of a parallel transport (in terms of a transport 2-functor) to any principal 2-bundle with connection whose structure group is a Lie 2-group.

Here, in contrast, we directly define and construct a global version of parallel transport suitable for our purposes. As our main goal in this paper is the construction of categorified smooth group extensions, we leave it for future work to prove in detail that our notion of parallel transport for ${\mathcal {G}}$ agrees with that of Schreiber and Waldorf, and instead focus on building the necessary input for the constructions in Sect. 5.

4.1 A path space approach to parallel transport on line bundles

Before we give our definition and construction of the parallel transport for bundle gerbes, we recast the parallel transport on line bundles from a global perspective. Our notion of parallel transport for bundle gerbes will then be a categorification of this picture. Let M be a connected smooth manifold, and fix a base point $x\in M$; if M is not connected, we restrict to its connected components individually. We denote by PM the diffeological space of smooth paths with sitting instants in M and by $P_0M$ the subspace of paths starting at x. Let L be a line bundle on M with connection. The smoothness of the parallel transport on L can be encoded as follows: for $t \in [0,1]$, denote by ${\mathrm {ev}}_t :PM \longrightarrow M$, $\gamma \longmapsto \gamma (t)$, the evaluation at t. Parallel transport on L is in particular an isomorphism

$$\begin{aligned} {\mathtt {pt}}^L:{\mathrm {ev}}_0^*L&\longrightarrow {\mathrm {ev}}_1^*L \\ L_{\gamma (0)} = {\mathrm {ev}}_0^*L_\gamma \ni \ell&\longmapsto {\mathtt {pt}}^L_\gamma (\ell ) \in L_{\gamma (1)} = {\mathrm {ev}}_1^*L_\gamma \end{aligned}$$

of line bundles over PM.

There is a different way to construct this isomorphism using descent. Via transgression and regression [Wal12b] we can construct a bundle ${\mathcal {R}}{\mathcal {T}}(L)$, which is isomorphic to L, from the descent data

with respect to the path fibration. Here f is constructed as in Sect. 3.3 from the holonomy of L. The total space of the line bundle ${\mathcal {R}}{\mathcal {T}}(L)$ consists of equivalence classes of pairs $(\gamma ,\zeta )\in P_0 M\times {\mathbb {C}}$, where the equivalence relation reads as $(\gamma _1,\zeta )\sim (\gamma _2,f(\gamma _1,\gamma _2)\,\zeta )$ for $(\gamma _1,\gamma _2)\in (P_0{M})^{[2]}$ and $\zeta \in {\mathbb {C}}$. An isomorphism $g_\chi :{\mathcal {R}}{\mathcal {T}}(L) \longrightarrow L$ can be constructed by picking a trivialisation $\chi :{\mathbb {C}}\longrightarrow L_{x}$ of the fibre of L over the base point $x \in M$ and defining

$$\begin{aligned} g_\chi \big ([\gamma ,\zeta ]\big ) :={\mathtt {pt}}^L_\gamma \big (\chi (\zeta )\big ) \ . \end{aligned}$$

The pullbacks ${\mathrm {ev}}_0^* {\mathcal {R}}{\mathcal {T}}(L)$ and ${\mathrm {ev}}_1^* {\mathcal {R}}{\mathcal {T}}(L)$ are thus described in terms of descent data with respect to the covers ${\mathrm {ev}}_0^*P_0 M\cong P_0M \times _M PM \longrightarrow M$ and ${\mathrm {ev}}_1^*P_0 M \cong PM\times _M P_0M \longrightarrow M$, respectively. In order to construct the isomorphism ${\mathtt {pt}}^{{\mathcal {R}}{\mathcal {T}}(L)}$ explicitly we use the space (see Fig. 1)

$$\begin{aligned} P_{\partial \Delta ^2} M :={\mathrm {ev}}_0^*P_0 M \times _{PM} {\mathrm {ev}}_1^*P_0M \cong P_0 M \times _M PM \times _M P_0 M \ , \end{aligned}$$

which fits into the diagram

Fig. 1

Elements in the spaces $P_{\partial \Delta ^2}M$, ${\mathrm {ev}}_0^*P_0M$ and ${\mathrm {ev}}_1^*P_0M$

An isomorphism from ${\mathrm {ev}}_0^*{\mathcal {R}}{\mathcal {T}}(L)$ to ${\mathrm {ev}}_1^*{\mathcal {R}}{\mathcal {T}}(L)$ can be described by a function $P_{\partial \Delta ^2} M \longrightarrow {{\text {U}}}(1)$ which is compatible with the descent data. There is a canonical choice for such a function given by

$$\begin{aligned} P_{\partial \Delta ^2} M \longrightarrow LM \xrightarrow { \ {\text {hol}}\ } {{\text {U}}}(1) \ . \end{aligned}$$

Concretely, the induced map is

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {R}}{\mathcal {T}}(L)} :{\mathrm {ev}}_0^*{\mathcal {R}}{\mathcal {T}}(L)&\longrightarrow {\mathrm {ev}}_1^*{\mathcal {R}}{\mathcal {T}}(L) \\ [\gamma _{xy},\zeta ]&\longmapsto {\mathtt {pt}}^{{\mathcal {R}}{\mathcal {T}}(L)}_{(\gamma _{xy}, \gamma _{yz}, \gamma _{xz})} [\gamma _{xy},\zeta ] = \big [ \gamma _{xz},{\text {hol}}\big (L,\overline{\gamma _{xz}}\star ( \gamma _{yz}\star \gamma _{xy})\big )\, \zeta \big ] \ , \end{aligned}$$

where x is the fixed base point of M while $y,z \in M$ are arbitrary points, and $\gamma _{ab}$ denotes a path from a to b for $a,b \in \{x,y,z\}$. The holonomy appearing here agrees with ${\text {hol}}(L,(\overline{\gamma _{xz}}\star \gamma _{yz})\star \gamma _{xy})$. The construction is independent of all choices involved. Now a straightforward computation shows that the diagram

commutes. This shows that we can construct the parallel transport on L completely in terms of the descent data with respect to the path fibration. For bundle gerbes, the analogue of ${\mathtt {pt}}^L$ is difficult to define directly, but an analogous approach via descent data on $P_0M$ allows us to solve this problem.

4.2 Global definition of parallel transport on bundle gerbes

As before, let M be a manifold, and let ${\mathcal {G}}\in \mathrm {BGrb}(M)$ be a bundle gerbe on M. A parallel transport on ${\mathcal {G}}$ should in particular be a 1-isomorphism

$$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_1 :{\mathrm {ev}}_0^*{\mathcal {G}}\longrightarrow {\mathrm {ev}}_1^*{\mathcal {G}}\end{aligned}$$

in $\mathrm {BGrb}(PM)$ with a 2-isomorphism

$$\begin{aligned} {{\mathsf {c}}}^* {\mathtt {pt}}^{\mathcal {G}}_1 \cong 1_{\mathcal {G}}\ , \end{aligned}$$

where ${{\mathsf {c}}}:M \longrightarrow PM$ is the embedding of M into PM as constant paths. Note that the parallel transport is, in general, an isomorphism of gerbes without connections. The same is true for bundles: the parallel transport on a vector bundle with connection respects the connection if and only if the connection is flat.

To proceed further, we need some definitions. Let $i,n \in {\mathbb {N}}$ with $1 \le i \le n$. For each $s = (s_1, \ldots , s_{n-1}) \in [0,1]^{n-1}$, define a smooth map

$$\begin{aligned} \iota ^n_{i;s} :[0,1]&\longrightarrow [0,1]^n\\ t&\longmapsto (s_1, \ldots , s_{i-1}, t, s_i, \ldots , s_{n-1}) \ . \end{aligned}$$

Consider the diffeological spaces $P^nM$ which are defined by the sets of all maps

$$\begin{aligned} \varSigma :[0,1]^n \longrightarrow M \end{aligned}$$

satisfying the following property: for all $i = 1, \ldots , n$, there exists $\epsilon _i > 0$ such the map $\varSigma \circ \iota ^n_{i;s}:[0,1]\longrightarrow M$ is locally constant on $[0,\epsilon _i) \sqcup (1-\epsilon _i,1]$. Note that in a plot of $P^nM$, the $\epsilon _i$ do not have to be constant over the domain of the plot. The space $P^n M$ describes n-cubes in M with sitting instants in all directions perpendicular to the faces of $[0,1]^n$; that is, $P^nM$ describes iterated smooth homotopies of paths with sitting instants in M.

We also consider the subspaces $P^n_*M$ of the diffeological spaces $P^nM$ consisting of maps $\varSigma \in P^nM$ satisfying the following property: for all $s \in [0,1]^{n-1}$, and for each $j = 1, \ldots , n-1$ such that $s_j \in \{0,1\}$, the map $\varSigma \circ \iota ^n_{i;s}$ is constant for all $i>j$. The space $P^n_*M$ describes iterated smooth homotopies with fixed endpoints in M. For example, $P_*M = PM$ is the space of paths with sitting instants, $P^2_*M$ consists of maps $\varSigma \in P^2M$ such that

$$\begin{aligned} \varSigma (0,t) = \varSigma (0,0) \qquad \text{ and } \qquad \varSigma (1,t) = \varSigma (1,0) \end{aligned}$$

for all $t \in [0,1]$ and so is the space of homotopies of paths with fixed endpoints in M, and an element in $P^3_*M$ is a family of fixed-ends homotopies between two fixed paths in M. We say that an element $\varSigma$ in $P^n_*M$ or in $P^n M$ is thin if its differential $\varSigma _*$ has non-maximal ranks $\mathrm {rk}(\varSigma _{*|s}) < n$ for all $s \in [0,1]^n$.

Let $s = (s_1, \ldots , s_k) \in [0,1]^k$ and $n = k+l$. For $0 \le i_1< \cdots < i_l \le n$, we define a map

$$\begin{aligned} \iota ^n_{i_1, \ldots , i_l; s} :[0,1]^l \longrightarrow [0,1]^n \end{aligned}$$

which inserts the coordinates of $t = (t_1, \ldots , t_l) \in [0,1]^l$ into the k-tuple s such that

$$\begin{aligned} \big ( \iota ^n_{i_1, \ldots , i_l; s}(t) \big )_j = t_j \end{aligned}$$

for every $j \in \{i_1, \ldots , i_l\}$. The maps $\iota ^n_{i_1, \ldots , i_l; s} :[0,1]^l \longrightarrow [0,1]^n$ induce maps

$$\begin{aligned} \iota ^{n*}_{i_1, \ldots , i_l; s} :P^n M \longrightarrow P^l M \end{aligned}$$

which map $P_*^n M$ to $P^l_* M$.

For the parallel transport of a bundle gerbe, there should also be a 2-isomorphism

$$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_2 :(\iota ^{2*}_{1;0})^* {\mathtt {pt}}^{\mathcal {G}}_1 \longrightarrow (\iota ^{2*}_{1;1})^* {\mathtt {pt}}^{\mathcal {G}}_1 \end{aligned}$$

in $\mathrm {BGrb}(P^2_*M)$. In other words, any map $\varSigma \in P^2_*M$ is in particular a smooth map $[0,1]^2 \longrightarrow M$ from the square to M. This map is constant on the vertical edges of the square. Pulling back the isomorphism ${\mathtt {pt}}^{\mathcal {G}}_1$ to the horizontal edges of the square gives two 1-morphisms ${\mathcal {G}}_{\varSigma (0,0)} \longrightarrow {\mathcal {G}}_{\varSigma (1,0)}$, and the 2-morphism ${\mathtt {pt}}^{\mathcal {G}}_2$ relates these. The data $({\mathtt {pt}}^{\mathcal {G}}_1, {\mathtt {pt}}^{\mathcal {G}}_2)$ are required to satisfy the following two properties, which are motivated by [BW19, BW18, Wal16]:

• (1) For any two thin maps $\varSigma , \varSigma ' \in P^2_*M$ with $\varSigma \circ \iota ^2_{1;s} = \varSigma ' \circ \iota ^2_{1;s}$ for $s = 0,1$, there is an equality

  $$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_{2|\varSigma } = {\mathtt {pt}}^{\mathcal {G}}_{2|\varSigma '} \ . \end{aligned}$$

  (4.1)

  That is, the 2-morphism ${\mathtt {pt}}^{\mathcal {G}}_2$ evaluated on any pair of fixed-ends thin homotopies between any two given paths in M gives the same result.

• (2) We further demand that for any thin map $h \in P^3_*M$, there is an equality

  $$\begin{aligned} (\iota ^{3*}_{1,2;0})^*{\mathtt {pt}}^{\mathcal {G}}_2{}_{|h} = (\iota ^{3*}_{1,2;1})^*{\mathtt {pt}}^{\mathcal {G}}_2{}_{|h} \ . \end{aligned}$$

  (4.2)

As we will be using $P^n_* M$ mostly for $n = 0,1,2$, we adopt the convention to write $\gamma _2 \star \gamma _1$ for the concatenation of smooth paths in M, and if $\varSigma , \varSigma ' \in P_*^2 M$ are homotopies $\varSigma :\gamma \longrightarrow \gamma '$ and $\varSigma ' :\gamma ' \longrightarrow \gamma ''$, we write $\varSigma ' \star _2 \varSigma :\gamma \longrightarrow \gamma ''$ for their vertical concatenation. If $\Xi :\alpha \longrightarrow \alpha '$ is a further homotopy in $P_*^2 M$ such that the starting point of $\alpha$ is the endpoint of $\gamma$, then we write $\Xi \star \varSigma :\alpha \star \gamma \longrightarrow \alpha ' \star \gamma '$ for the horizontal concatenation of the homotopies. We will also often use the term ‘composition’ instead of ‘concatenation’.

Definition 4.3

Let M be a smooth manifold. A parallel transport on a bundle gerbe ${\mathcal {G}}\in \mathrm {BGrb}(M)$ is a quadruple ${\mathtt {pt}}^{\mathcal {G}}= ({\mathtt {pt}}^{\mathcal {G}}_1, {\mathtt {pt}}^{\mathcal {G}}_2, {\mathtt {pt}}^{\mathcal {G}}_\star , \varepsilon ^{\mathcal {G}})$ of

• (1) a 1-isomorphism

  $$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_1 :{\mathrm {ev}}_0^*{\mathcal {G}}\longrightarrow {\mathrm {ev}}_1^*{\mathcal {G}}\end{aligned}$$

  of bundle gerbes over PM,

• (2) a 2-isomorphism

  $$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_2 :(\iota ^{2*}_{1;0})^* {\mathtt {pt}}^{\mathcal {G}}_1 \longrightarrow (\iota ^{2*}_{1;1})^* {\mathtt {pt}}^{\mathcal {G}}_1 \end{aligned}$$

  in $\mathrm {BGrb}(P^2_*M)$,

• (3) a 2-isomorphism

  $$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_\star :{\text {pr}}_1^* {\mathtt {pt}}^{\mathcal {G}}_1 \circ {\text {pr}}_2^* {\mathtt {pt}}^{\mathcal {G}}_1 \longrightarrow (\,\varvec{\cdot }\, \star \,\varvec{\cdot }\,)^* {\mathtt {pt}}^{\mathcal {G}}_1 \end{aligned}$$

  over $PM \times _M PM$, where ${\text {pr}}_1$ and ${\text {pr}}_2$ are the respective projections of $PM\times _MPM$ to the first and second factors, and

• (4) a 2-isomorphism

  $$\begin{aligned} \varepsilon ^{\mathcal {G}}:{{\mathsf {c}}}^* {\mathtt {pt}}^{\mathcal {G}}_1 \longrightarrow 1_{\mathcal {G}}\end{aligned}$$

  over M, where ${{\mathsf {c}}}:M \longrightarrow PM$ is the inclusion of M as the space of constant paths.

These data are required to satisfy properties (4.1) and (4.2). Due to property (4.1), there is a canonical 2-isomorphism

$$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_{1|(\gamma _3 \star \gamma _2) \star \gamma _1} \cong {\mathtt {pt}}^{\mathcal {G}}_{1|\gamma _3 \star (\gamma _2 \star \gamma _1)} \end{aligned}$$

for every $(\gamma _1, \gamma _2, \gamma _3) \in PM \times _M PM \times _M PM$, and we demand that ${\mathtt {pt}}^{\mathcal {G}}_\star$ is coherently associative with respect to this isomorphism. The morphism ${\mathtt {pt}}^{\mathcal {G}}_\star$ also needs to be compatible with the unitors in $\mathrm {BGrb}(PM)$ and sit in a commutative diagram

for all $x,y,z \in M$, all paths $\gamma _1, \alpha _1$ from x to y, all paths $\gamma _2, \alpha _2$ from y to z in M, and for all fixed-ends homotopies $\varSigma _i :\gamma _i \longrightarrow \alpha _i$. Furthermore, ${\mathtt {pt}}^{\mathcal {G}}_2$ has to respect vertical composition and satisfy the interchange law

$$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}_{2|\varSigma '_1 \star \varSigma '_0} \circ {\mathtt {pt}}^{\mathcal {G}}_{2|\varSigma '_1 \star \varSigma '_0} = {\mathtt {pt}}^{\mathcal {G}}_{2|\varSigma '_1 \star _2 \varSigma _1} \circ _2 {\mathtt {pt}}^{\mathcal {G}}_{2|\varSigma '_0 \star _2 \varSigma _0} \end{aligned}$$

(4.5)

for all points $x_0,x_1,x_2 \in M$, all paths $\alpha _i, \beta _i, \gamma _i$ from $x_i$ to $x_{i+1}$, and for all fixed-ends homotopies $\varSigma _i :\alpha _i \longrightarrow \beta _i$ and $\varSigma '_i :\beta _i \longrightarrow \gamma _i$ with $i = 0,1$.

Remark 4.6

The associativity condition in detail reads as follows: for every concatenable triple $(\gamma _1, \gamma _2, \gamma _3)$ of paths in M there is a commutative diagram

in $\mathrm {BGrb}(PM\times _MPM)$, where the bottom arrow is the canonical 2-isomorphism obtained via (4.1) from any reparameterisation of [0, 1] that yields a homotopy $\gamma _3 \star (\gamma _2 \star \gamma _1) \sim (\gamma _3 \star \gamma _2) \star \gamma _1$. $\square$

Remark 4.7

By property (4.2), our definition factors through the path 2-groupoid of M as defined by Schreiber and Waldorf [SW11, SW17]. Given a manifold M, they construct a 2-groupoid internal to diffeological spaces, whose level sets are essentially M, PM and the quotient $P^2_* M/{\sim }$ of $P_*^2 M$ by thin homotopies. Note that in this quotient they also implement condition (4.1). $\square$

In contrast to the case of parallel transport on vector bundles, we can define morphisms between parallel transports on a given bundle gerbe.

Definition 4.8

Let ${\mathcal {G}}\in \mathrm {BGrb}(M)$ be a bundle gerbe on M. Let ${\mathtt {pt}}^{\mathcal {G}}= ({\mathtt {pt}}^{\mathcal {G}}_1, {\mathtt {pt}}^{\mathcal {G}}_2, {\mathtt {pt}}^{\mathcal {G}}_\star , \varepsilon ^{\mathcal {G}})$ and ${\mathtt {pt}}'{}^{\mathcal {G}}= ({\mathtt {pt}}'_1{}^{\mathcal {G}}, {\mathtt {pt}}'_2{}^{\mathcal {G}}, {\mathtt {pt}}'_\star {}^{\mathcal {G}}, \varepsilon '{}^{\mathcal {G}})$ be two choices of parallel transport on ${\mathcal {G}}$. A morphism ${\mathtt {pt}}^{\mathcal {G}}\longrightarrow {\mathtt {pt}}'{}^{\mathcal {G}}$ of parallel transports on ${\mathcal {G}}$ is a 2-isomorphism $\psi :{\mathtt {pt}}^{\mathcal {G}}_1 \longrightarrow {\mathtt {pt}}'_1{}^{\mathcal {G}}$ in $\mathrm {BGrb}(PM)$ that intertwines the 2-isomorphism ${\mathtt {pt}}^{\mathcal {G}}_2$ with ${\mathtt {pt}}'_2{}^{\mathcal {G}}$, the 2-isomorphism ${\mathtt {pt}}^{\mathcal {G}}_\star$ with ${\mathtt {pt}}'_\star {}^{\mathcal {G}}$, and the 2-isomorphism $\varepsilon ^{\mathcal {G}}$ with $\varepsilon '{}^{\mathcal {G}}$. This defines a groupoid ${\mathtt {PT}}({\mathcal {G}})$ of parallel transports on ${\mathcal {G}}$.

This notion of morphism of parallel transports is not an analogue of a gauge transformation, since it does not necessarily come from an automorphism of the bundle gerbe ${\mathcal {G}}$.

4.3 Construction of the parallel transport

We now proceed to show that every bundle gerbe with connection on a manifold M has a canonical parallel transport. Let M be a connected manifold, and fix a base point $x \in M$; otherwise, if M is not connected, we treat the connected components of M separately. By results of Waldorf [Wal16], any bundle gerbe ${\mathcal {G}}\in \mathrm {BGrb}^\nabla (M)$ is isomorphic to a bundle gerbe ${\mathcal {G}}' \in \mathrm {BGrb}^\nabla (M)$ that is defined over the diffeological path fibration $P_0 M \longrightarrow M$. Given a choice of base point $x \in M$, Waldorf constructs a bundle gerbe ${\mathcal {G}}' = {\mathcal {R}}{\mathcal {T}}({\mathcal {G}})$ as the regression of the transgression line bundle of ${\mathcal {G}}$, together with a natural 1-isomorphism ${{\mathcal {A}}}_{\mathcal {G}}:{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ in the homotopy category of $\mathrm {BGrb}^\nabla (M)$; that is, ${{\mathcal {A}}}_{\mathcal {G}}$ is determined only up to 2-isomorphism. (We remark, however, that the natural 1-isomorphism ${{\mathcal {A}}}_{\mathcal {G}}$ from [Wal16] is determined canonically once we fix a preimage of the base point $x \in M$ under the surjective submersion $\pi :Y \longrightarrow M$ underlying the bundle gerbe ${\mathcal {G}}$.)

Consider the bundle gerbe ${\mathcal {G}}' = {\mathcal {R}}{\mathcal {T}}({\mathcal {G}}) \in \mathrm {BGrb}^\nabla (M)$ with connection on M, defined with respect to the path fibration $\pi :P_0 M \longrightarrow M$. Its line bundle L is the pullback of the transgression line bundle ${\mathcal {T}}{\mathcal {G}}\longrightarrow LM$ along the map

$$\begin{aligned} (P_0 M)^{[2]}&\longrightarrow LM \\ (\alpha , \alpha ')&\longmapsto \overline{\alpha '} \star \alpha \ . \end{aligned}$$

By a slight abuse of notation, we also denote this pullback by ${\mathcal {T}}{\mathcal {G}}\longrightarrow (P_0 M)^{[2]}$.

4.3.1 Construction of ${\mathtt {pt}}^{{\mathcal {G}}'}_1$

We would like to construct a 1-isomorphism

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}}'}_1 :{\mathrm {ev}}_0^*{\mathcal {G}}' \longrightarrow {\mathrm {ev}}_1^*{\mathcal {G}}' \end{aligned}$$

(4.9)

in $\mathrm {BGrb}(PM)$. For $t = 0,1$, the bundle gerbe ${\mathrm {ev}}_t^*{\mathcal {G}}'$ is defined over the subduction ${\mathrm {ev}}_t^*P_0 M \longrightarrow PM$. There are canonical isomorphisms of diffeological spaces

$$\begin{aligned} {\mathrm {ev}}_0^*P_0 M \cong P_0 M \times _M PM \qquad \text {and} \qquad {\mathrm {ev}}_1^*P_0 M \cong PM \times _M P_0 M \ . \end{aligned}$$

Recall from Sect. 4.1 the space

$$\begin{aligned} P_{\partial \Delta ^2} M :={\mathrm {ev}}_0^*P_0 M \times _{PM} {\mathrm {ev}}_1^*P_0M \cong P_0 M \times _M PM \times _M P_0 M \ . \end{aligned}$$

A point in the total space $P_{\partial \Delta ^2} M$ is a triple $(\alpha _0, \gamma , \alpha _1)$ of a path $\gamma \in PM$ and based paths $\alpha _t \in P_0 M$ such that $\gamma (t) = \alpha _t(1)$ for $t = 0,1$. Any 1-morphism ${\mathrm {ev}}_0^*{\mathcal {G}}' \longrightarrow {\mathrm {ev}}_1^*{\mathcal {G}}'$ is defined over (possibly a refinement of) the subduction $\xi :P_{\partial \Delta ^2} M \longrightarrow PM$.

There is a smooth map, i.e. a morphism of diffeological spaces

$$\begin{aligned} {{\mathsf {s}}}:P_{\partial \Delta ^2} M&\longrightarrow LM \nonumber \\ (\alpha _0, \gamma , \alpha _1)&\longmapsto \overline{\alpha _1} \star (\gamma \star \alpha _0) \ . \end{aligned}$$

(4.10)

There is also the smooth map

$$\begin{aligned} {\tilde{{{\mathsf {s}}}}} :P_{\partial \Delta ^2} M&\longrightarrow LM \\ (\alpha _0, \gamma , \alpha _1)&\longmapsto (\overline{\alpha _1} \star \gamma ) \star \alpha _0 \ . \end{aligned}$$

The maps ${{\mathsf {s}}}$ and ${\tilde{{{\mathsf {s}}}}}$ are smoothly homotopic via precomposition by a homotopy h of piecewise smooth homeomorphisms $[0,1] \longrightarrow [0,1]$; these fail to be smooth exactly at those points of the interval where the concatenations happen, but at these points all three paths have sitting instants, so that at each time the homotopy maps to LM, as desired. For each triple of paths $(\alpha _0, \gamma , \alpha _1)$, this results in a thin homotopy in LM from $\overline{\alpha _1} \star (\gamma \star \alpha _0)$ to $(\overline{\alpha _1} \star \gamma ) \star \alpha _0$. By the superficiality of the parallel transport ${\mathtt {pt}}^{{\mathcal {T}}{\mathcal {G}}}$ on the transgression line bundle [Wal16, Definition 2.2.1] (see also the end of Sect. 2.2), we thus obtain a canonical isomorphism

$$\begin{aligned} r :{{\mathsf {s}}}^*{\mathcal {T}}{\mathcal {G}}\longrightarrow {\tilde{{{\mathsf {s}}}}}^*{\mathcal {T}}{\mathcal {G}}\end{aligned}$$

in $\mathrm {HLBdl}^\nabla (P_{\partial \Delta ^2} M)$. The fact that this isomorphism preserves connections is a direct consequence of [Wal16, Lemma 2.3.3]. Since ${\mathtt {pt}}^{{\mathcal {T}}{\mathcal {G}}}$ is thin-invariant, it follows that the morphism r is defined independently of the choice of homotopy h.

We define a morphism ${\mathtt {pt}}^{{\mathcal {G}}'}_1:{\mathrm {ev}}_0^* {\mathcal {G}}' \longrightarrow {\mathrm {ev}}_1^*{\mathcal {G}}'$ as follows: its underlying line bundle is the line bundle ${{\mathsf {s}}}^* {\mathcal {T}}{\mathcal {G}}\longrightarrow P_{\partial \Delta ^2} M$. To turn this into a morphism of bundle gerbes, we need to provide an isomorphism of line bundles

$$\begin{aligned} \beta :{\text {pr}}_0^*{\mathcal {T}}{\mathcal {G}}\otimes \xi _1^* {{\mathsf {s}}}^*{\mathcal {T}}{\mathcal {G}}\longrightarrow \xi _0^*{{\mathsf {s}}}^*{\mathcal {T}}{\mathcal {G}}\otimes {\text {pr}}_1^*{\mathcal {T}}{\mathcal {G}}\end{aligned}$$

over $(P_{\partial \Delta ^2} M)^{[2]}$. Let us unravel this: the fibre product $(P_{\partial \Delta ^2} M)^{[2]} = P_{\partial \Delta ^2} M \times _{PM} P_{\partial \Delta ^2} M$ consists of pairs $((\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1))$ where $(\alpha _0, \gamma , \alpha _1)$ and $(\alpha '_0, \gamma , \alpha '_1)$ are elements of $P_{\partial \Delta ^2} M$. For $t = 0,1$, there are the projection maps

$$\begin{aligned} {\text {pr}}_t :(P_{\partial \Delta ^2} M)^{[2]}&\longrightarrow (P_0 M)^{[2]} \\ \big ((\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1)\big )&\longmapsto (\alpha _t, \alpha '_t) \ . \end{aligned}$$

Thus

$$\begin{aligned} ({\text {pr}}_0^*{\mathcal {T}}{\mathcal {G}}\otimes \xi _1^* {{\mathsf {s}}}^*{\mathcal {T}}{\mathcal {G}})_{((\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1))}&= {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha '_0} \star \alpha _0} \otimes {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha '_1} \star (\gamma \star \alpha '_0)} \ , \\ (\xi _0^* {{\mathsf {s}}}^*{\mathcal {T}}{\mathcal {G}}\otimes {\text {pr}}_1^*{\mathcal {T}}{\mathcal {G}})_{((\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1))}&= {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\gamma \star \alpha _0)} \otimes {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha '_1} \star \alpha _1} \ . \end{aligned}$$

Let $\lambda :\pi _{0,1}^*{\mathcal {T}}{\mathcal {G}}\otimes \pi _{1,2}^*{\mathcal {T}}{\mathcal {G}}\longrightarrow \pi _{0,2}^*{\mathcal {T}}{\mathcal {G}}$ denote the fusion product of the transgression line bundle ${\mathcal {T}}{\mathcal {G}}$ over $(P_0 M)^{[3]}$ (see [Wal16, Section 4.2]), which provides the bundle gerbe multiplication on ${\mathcal {G}}'$. At a point $(\alpha _0,\alpha _1,\alpha _2)\in (P_0M)^{[3]}$ the fusion product consists of unitary isomorphisms

$$\begin{aligned} \lambda _{\alpha _0,\alpha _1,\alpha _2} :{\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1}\star \alpha _0}\otimes {\mathcal {T}}{\mathcal {G}}_{ \overline{\alpha _2} \star \alpha _1} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _2} \star \alpha _0} \ . \end{aligned}$$

The diffeological space $(P_{\partial \Delta ^2} M)^{[2]}$ comes with smooth maps

$$\begin{aligned} p_0 :(P_{\partial \Delta ^2} M)^{[2]}&\longrightarrow (P_0 M)^{[3]} \\ \big ((\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1)\big )&\longmapsto (\alpha _0, \alpha '_0, \overline{\gamma } \star \alpha '_1) \end{aligned}$$

and

$$\begin{aligned} p_1 :(P_{\partial \Delta ^2} M)^{[2]}&\longrightarrow (P_0 M)^{[3]} \\ \big ((\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1)\big )&\longmapsto (\gamma \star \alpha _0, \alpha '_1, \alpha _1) \ . \end{aligned}$$

We set

$$\begin{aligned} \beta :=p_1^*\lambda ^{-1} \circ r^{-1} \circ p_0^*\lambda \circ (1 \otimes r) \ . \end{aligned}$$

Explicitly, at a point $((\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1)) \in (P_{\partial \Delta ^2} M)^{[2]}$, this is the isomorphism defined by the diagram

This morphism is compatible with the bundle gerbe multiplication on ${\mathcal {G}}'$: consider an arbitrary point

$$\begin{aligned} \big ( (\alpha _0, \gamma , \alpha _1),(\alpha '_0, \gamma , \alpha '_1), (\alpha ''_0, \gamma , \alpha ''_1) \big ) \ \in \ (P_{\partial \Delta ^2} M)^{[3]} \ . \end{aligned}$$

Then there is a commutative diagram

The commutativity follows from the associativity of the fusion product $\lambda$ and the fact that it respects the connection on ${\mathcal {T}}{\mathcal {G}}$ [Wal16] so that, in particular, $\lambda$ is compatible with the morphism r.

4.3.2 Construction of ${\mathtt {pt}}^{{\mathcal {G}}'}_2$

Next we construct the 2-isomorphism

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}}'}_2:(\iota ^{2*}_{1;0})^* {\mathtt {pt}}_1^{{\mathcal {G}}'} \longrightarrow (\iota ^{2*}_{1,1})^* {\mathtt {pt}}_1^{{\mathcal {G}}'} \end{aligned}$$

in $\mathrm {BGrb}(P_*^2M)$ that is part of the parallel transport data for ${\mathcal {G}}'$. For this, we recall that the fibre of the hermitean line bundle ${\mathcal {T}}{\mathcal {G}}$ at a loop $\gamma$ is constructed from pairs $([{\mathcal {S}}], z)$ of a 2-isomorphism class $[{\mathcal {S}}]$ of trivialisations ${\mathcal {S}}:\gamma ^*{\mathcal {G}}\longrightarrow {\mathcal {I}}_0$ in $\mathrm {BGrb}^\nabla ({{\mathbb {S}}}^1)$ and a complex number $z \in {\mathbb {C}}$. The complex line ${\mathcal {T}}{\mathcal {G}}_{\gamma }$ is the set of equivalence classes of such pairs under the equivalence relation

$$\begin{aligned} \big ( [{\mathcal {S}}], z \big ) \sim \big ( [{\mathcal {S}}'], {\text {hol}}({{\mathbb {S}}}^1, {{\mathsf {R}}}( {\mathcal {S}}' \circ {\mathcal {S}}^{-1}))\, z \big ) \ , \end{aligned}$$

where for a manifold M, the functor ${{\mathsf {R}}}:\mathrm {BGrb}^\nabla (M)({\mathcal {I}}_B , {\mathcal {I}}_{B'}) \longrightarrow \mathrm {HLBdl}^\nabla (M)$ for $B,B'\in \Omega ^2(M)$ is essentially descent for line bundles; for details, see [Bun17, BSS18, Wal07b] (see also Sect. 2.2).

Let $M^{{{\mathbb {D}}}^2}$ be the diffeological space of smooth maps from the unit disk ${{\mathbb {D}}}^2$ to M. Let

$$\begin{aligned} \partial :M^{{{\mathbb {D}}}^2}&\longrightarrow LM \\ f&\longmapsto f_{|{{\mathbb {S}}}^1} \end{aligned}$$

denote the smooth map induced by restriction to the boundary of the unit disk. The hermitean line bundle $\partial ^*{\mathcal {T}}{\mathcal {G}}$ on $M^{{{\mathbb {D}}}^2}$ has a canonical trivialisation which is defined as follows: for a smooth map $f :{{\mathbb {D}}}^2 \longrightarrow M$, choose a trivialisation ${\mathcal {S}}:f^*{\mathcal {G}}\longrightarrow {\mathcal {I}}_B$ for some $B \in \Omega ^2({{\mathbb {D}}}^2)$. Define a unitary isomorphism of hermitean complex lines

$$\begin{aligned} \sigma _{f} :{\mathbb {C}}&\longrightarrow (\partial ^*{\mathcal {T}}{\mathcal {G}})_{f} \nonumber \\ z&\longmapsto \sigma _{f}(z) :=\Big [ [{\mathcal {S}}_{|{{\mathbb {S}}}^1}], \exp \Big ( - \mathrm {i}\, \int _{{{\mathbb {D}}}^2}\, B \Big )\, z \Big ] \ . \end{aligned}$$

(4.12)

This isomorphism is defined independently of the choice of ${\mathcal {S}}$: let ${\mathcal {S}}' :f^*{\mathcal {G}}\longrightarrow {\mathcal {I}}_{B '}$ be another trivialisation. Then the line bundle ${{\mathsf {R}}}({\mathcal {S}}' \circ {\mathcal {S}}^{-1})$ has curvature $B ' - B$, which implies that

$$\begin{aligned} \sigma _{f}(z)&:=\Big [ [{\mathcal {S}}_{|{{\mathbb {S}}}^1}], \exp \Big ( - \mathrm {i}\, \int _{{{\mathbb {D}}}^2}\, B \Big )\, z \Big ] \\&= \Big [ [{\mathcal {S}}_{|{{\mathbb {S}}}^1}], \exp \Big ( - \mathrm {i}\, \int _{{{\mathbb {D}}}^2}\, B '\Big )\, {\text {hol}}\big ({{\mathbb {S}}}^1, {{\mathsf {R}}}({\mathcal {S}}' \circ {\mathcal {S}}^{-1})\big )\, z \Big ] \\&= \Big [ [{\mathcal {S}}'_{|{{\mathbb {S}}}^1}], \exp \Big ( - \mathrm {i}\, \int _{{{\mathbb {D}}}^2}\, B '\Big )\, z \Big ] \ . \end{aligned}$$

This construction works equally well if we replace the ‘round’ unit disk ${{\mathbb {D}}}^2$ by the unit square $[0,1]^2$, as long as we consider maps $f :[0,1]^2 \longrightarrow M$ whose restrictions to $\partial [0,1]^2$ have sitting instants at the corners. By the construction of the fusion product $\lambda$ on ${\mathcal {T}}{\mathcal {G}}$, the section $\sigma$ is compatible with fusion,

$$\begin{aligned} \sigma _{f' \star _2 f} = \lambda (\sigma _{f'}, \sigma _f) \end{aligned}$$

for all disks $f,f' :[0,1]^2 \longrightarrow M$ that can be concatenated vertically. (This is merely the statement that the integral over $[0,1]^2$ decomposes as the sum $\int _{[0,1]^2} = \int _{[0,1] \times [0,\frac{1}{2}]} +\int _{[0,1] \times [\frac{1}{2},1]}$.)

Now consider the following setup: let $\varSigma :[0,1]^2 \longrightarrow M$ be an element in $P_*^2M$, presenting a fixed-end homotopy from a path $\gamma$ to a path $\gamma '$ in M. We want to compare the 1-isomorphisms $(\iota ^{2*}_{1;0})^* {\mathtt {pt}}^{{\mathcal {G}}'}_1$ and $(\iota ^{2*}_{1;1})^* {\mathtt {pt}}^{{\mathcal {G}}'}_1$ of bundle gerbes over $P_*^2M$. The source bundle gerbes of both these morphisms have subductions

$$\begin{aligned} Y_0 :=(\iota ^{2*}_{1;0})^* {\mathrm {ev}}_0^* P_0 M = {\mathrm {ev}}_{(0,0)}^* P_0 M = {\mathrm {ev}}_{(1,0)}^* P_0 M \longrightarrow P_*^2 M \ , \end{aligned}$$

while the target bundle gerbes live over

$$\begin{aligned} Y_1 :=(\iota ^{2*}_{1;0})^* {\mathrm {ev}}_1^* P_0 M = {\mathrm {ev}}_{(0,1)}^* P_0 M = {\mathrm {ev}}_{(1,1)}^* P_0 M \longrightarrow P_*^2 M \ . \end{aligned}$$

The fibre product ${\widehat{Y}} :=Y_0 \times _{P_*^2 M} Y_1$ is the space of triples $(\alpha _0, \varSigma , \alpha _1)$ of based paths $\alpha _0, \alpha _1 \in P_0 M$ and fixed-ends homotopies $\varSigma \in P_*^2M$ between arbitrary paths in M such that $\alpha _t(1) = \varSigma (0,t)$ for $t = 0,1$ (see Fig. 2).

Fig. 2

An element of the space ${\widehat{Y}}$

The 1-isomorphism $(\iota ^{2*}_{1;i})^* {\mathtt {pt}}^{{\mathcal {G}}'}_1$, for $i = 0,1$, is defined over the subduction

$$\begin{aligned} Z_i :=(\iota ^{2*}_{1;i})^* P_{\partial \Delta ^2}M \longrightarrow {\widehat{Y}} \ , \end{aligned}$$

which is actually an isomorphism. Consequently, the 2-isomorphism ${\mathtt {pt}}^{{\mathcal {G}}'}_2$ should be defined with respect to the subduction

$$\begin{aligned} {\widehat{Z}} :=Z_0 \times _{{\widehat{Y}}} Z_1 \longrightarrow {\widehat{Y}} \ , \end{aligned}$$

which again is an isomorphism. Its elements are triples $(\alpha _0, \varSigma , \alpha _1)$ as above. Set $\gamma _t :=\varSigma \circ \iota ^2_{1;t}$ for $t = 0,1$, and let $x = \gamma _t(0)$ and $y = \gamma _s(1)$ for $t,s = 0,1$.

At a point $(\alpha _0, \varSigma , \alpha _1)$, the morphism of hermitean line bundles over ${\widehat{Z}}$ that defines ${\mathtt {pt}}^{{\mathcal {G}}'}_2$ is given by the morphism

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}}'}_{2|(\alpha _0, \varSigma , \alpha _1)} :{\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\gamma _0 \star \alpha _0)} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\gamma _1 \star \alpha _0)} \end{aligned}$$

of complex lines obtained as follows:

• (1) Using a smooth family of rotations of ${{\mathbb {S}}}^1$, apply parallel transport on ${\mathcal {T}}{\mathcal {G}}$ to obtain an isomorphism

  $$\begin{aligned} \psi _1 :{\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\gamma _0 \star \alpha _0)} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{(\gamma _0 \star \alpha _0) \star \overline{\alpha _1}} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\gamma _0 \star (\alpha _0 \star \overline{\alpha _1})} \ . \end{aligned}$$

  This is achieved by parallel transport along a thin path in LM. Hence, since the parallel transport on ${\mathcal {T}}{\mathcal {G}}$ is superficial, this isomorphism is independent of the choice of a smooth family of rotations.

• (2) Use the canonical section $\sigma _{\varSigma }(1) \in {\mathcal {T}}{\mathcal {G}}_{\partial \varSigma }$ from (4.12) to obtain an isomorphism

  $$\begin{aligned} \psi _2 :{\mathcal {T}}{\mathcal {G}}_{\gamma _0 \star (\alpha _0 \star \overline{\alpha _1})} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\gamma _0 \star (\alpha _0 \star \overline{\alpha _1})} \otimes {\mathcal {T}}{\mathcal {G}}_{\partial \varSigma } \ . \end{aligned}$$

• (3) The boundary loop $\partial \varSigma$ is smoothly and thinly homotopic (via reparameterisations) to $((\text {id}_y \star \gamma _1) \star \text {id}_x) \star \overline{\gamma _0}$, where $\text {id}_x$ is the constant path at the point $x \in M$. This loop is, in turn, thinly homotopic to $\gamma _1 \star \overline{\gamma _0}$. We thus obtain a canonical isomorphism

  $$\begin{aligned} \psi _3 :{\mathcal {T}}{\mathcal {G}}_{\gamma _0 \star (\alpha _0 \star \overline{\alpha _1})} \otimes {\mathcal {T}}{\mathcal {G}}_{\partial \varSigma } \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\gamma _0 \star (\alpha _0 \star \overline{\alpha _1})} \otimes {\mathcal {T}}{\mathcal {G}}_{\gamma _1 \star \overline{\gamma _0}} \ . \end{aligned}$$

• (4) The fusion product on ${\mathcal {T}}{\mathcal {G}}$ yields an isomorphism

  $$\begin{aligned} \psi _4 :{\mathcal {T}}{\mathcal {G}}_{\gamma _0 \star (\alpha _0 \star \overline{\alpha _1})} \otimes {\mathcal {T}}{\mathcal {G}}_{\gamma _1 \star \overline{\gamma _0}} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\gamma _1 \star (\alpha _0 \star \overline{\alpha _1})} \ . \end{aligned}$$

• (5) Finally, we again use parallel transport along a path in LM that arises from a smooth family of rotations to obtain a canonical isomorphism

  $$\begin{aligned} \psi _5 :{\mathcal {T}}{\mathcal {G}}_{\gamma _1 \star (\alpha _0 \star \overline{\alpha _1})} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\gamma _1 \star \alpha _0)} \ . \end{aligned}$$

We then define

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}}'}_{2|(\alpha _0,\varSigma ,\alpha _1)} :=\psi _5 \circ \psi _4\circ \psi _3\circ \psi _2 \circ \psi _1 \ . \end{aligned}$$

This is compatible with vertical composition in $P_*^2M$: let $\varSigma , \varSigma ' \in P_*^2M$ be two maps $[0,1]^2 \longrightarrow M$ that can be concatenated vertically. Since the connection on ${\mathcal {T}}{\mathcal {G}}$ is superficial and compatible with the fusion product, we can replace the morphism $\psi _1$ by

$$\begin{aligned} {\tilde{\psi }}_1 :{\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\iota ^{2*}_{1;0}\varSigma \star \alpha _0)} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\iota ^{2*}_{1;0}\varSigma \star (\alpha _0 \star \overline{\alpha _1})} \ . \end{aligned}$$

Applying the fusion product with $\partial (\varSigma ' \star _2 \varSigma )$ yields an isomorphism

$$\begin{aligned} \varphi :{\mathcal {T}}{\mathcal {G}}_{\iota ^{2*}_{1;0}\varSigma \star (\alpha _0 \star \overline{\alpha _1})} \longrightarrow {\mathcal {T}}{\mathcal {G}}_{\iota ^{2*}_{1;1}\varSigma ' \star (\alpha _0 \star \overline{\alpha _1})} \ . \end{aligned}$$

Combining the fact that the fusion product $\lambda$ is associative and compatible with the parallel transport on ${\mathcal {T}}{\mathcal {G}}$, that the parallel transport on ${\mathcal {T}}{\mathcal {G}}$ is superficial (in particular, parallel transport along thin paths is independent of the choice of thin path), and that the section $\sigma$ from (4.12) is compatible with $\lambda$, it follows that ${\mathtt {pt}}^{{\mathcal {G}}'}_2$ respects vertical concatenation.

Since all morphisms involved in the construction of ${\mathtt {pt}}^{{\mathcal {G}}'}_2$ are smooth, it follows that ${\mathtt {pt}}^{{\mathcal {G}}'}_2$ is in fact a smooth morphism of bundle gerbes as desired.

4.3.3 Construction of ${\mathtt {pt}}^{{\mathcal {G}}'}_\star$

The 2-isomorphism

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}}'}_\star :{\text {pr}}_1^* {\mathtt {pt}}_1^{{\mathcal {G}}'} \circ {\text {pr}}_2^* {\mathtt {pt}}_1^{{\mathcal {G}}'} \longrightarrow (\,\varvec{\cdot }\, \star \,\varvec{\cdot }\,)^*{\mathtt {pt}}_1^{{\mathcal {G}}'} \end{aligned}$$

is directly constructed from the fusion product $\lambda$ on the transgression line bundle ${\mathcal {T}}{\mathcal {G}}$. Define $q :PM \times _M PM \longrightarrow M$ by $(\gamma , \gamma ') \longmapsto \gamma (0) = \gamma '(1)$. The morphism ${\mathtt {pt}}^{{\mathcal {G}}'}_\star$ is defined over the subduction

$$\begin{aligned} Q_1 :={\text {pr}}_1^* P_{\partial \Delta ^2}M \times _{q^* P_0M} {\text {pr}}_2^* P_{\partial \Delta ^2}M \longrightarrow PM \times _M PM \ . \end{aligned}$$

Given a point $\big ((\alpha _0, \gamma , \alpha _1), (\alpha _1, \gamma ', \alpha _2)\big ) \in Q_1$, the morphism ${\mathtt {pt}}^{{\mathcal {G}}'}_\star$ is given by the diagram

where the horizontal morphisms are induced by smooth families of reparameterisations. The compatibility of this morphism with the morphism $\beta$ from (4.11) follows again from the superficiality of the connection on ${\mathcal {T}}{\mathcal {G}}$ and the associativity of the fusion product $\lambda$.

The compatibility of ${\mathtt {pt}}^{{\mathcal {G}}'}_\star$ with ${\mathtt {pt}}^{{\mathcal {G}}'}_2$ as in (4.4) is seen analogously to how we proved the compatibility of ${\mathtt {pt}}^{{\mathcal {G}}'}_2$ with vertical concatenation of homotopies. The interchange law (4.5) is satisfied by the associativity of $\lambda$, its compatibility with the parallel transport on ${\mathcal {T}}{\mathcal {G}}$ and with the section $\sigma$ from (4.12), as well as the superficiality of the connection on ${\mathcal {T}}{\mathcal {G}}$.

4.3.4 Construction of $\varepsilon ^{{\mathcal {G}}'}$

Finally, the 2-isomorphism

$$\begin{aligned} \varepsilon ^{{\mathcal {G}}'}:{{\mathsf {c}}}^*{\mathtt {pt}}_1^{{\mathcal {G}}'} \longrightarrow 1_{{\mathcal {G}}'} \end{aligned}$$

is obtained directly from the superficial connection on ${\mathcal {T}}{\mathcal {G}}$: it is defined over the space of triples $(\alpha , \text {id}_x, \alpha ) \in P_{\partial \Delta ^2}M$, and all paths of the form $\overline{\alpha }\star \alpha$ are canonically contractible by thin homotopies.

All necessary coherences in Definition 4.3 then follow from the superficiality of the parallel transport on ${\mathcal {T}}{\mathcal {G}}$, the associativity of the fusion product $\lambda$ and its compatibility with the section $\sigma$, and the fact that the parallel transport on ${\mathcal {T}}{\mathcal {G}}$ is compatible with the fusion product. Thus we have

Theorem 4.13

Let ${\mathcal {G}}\in \mathrm {BGrb}^\nabla (M)$ be a bundle gerbe with connection on M, and let ${\mathcal {G}}' :={\mathcal {R}}{\mathcal {T}}({\mathcal {G}}) \in \mathrm {BGrb}^\nabla (M)$ be the regression of the transgression of ${\mathcal {G}}$. Then the quadruple ${\mathtt {pt}}^{{\mathcal {G}}'} = ({\mathtt {pt}}^{{\mathcal {G}}'}_1, {\mathtt {pt}}^{{\mathcal {G}}'}_2, {\mathtt {pt}}^{{\mathcal {G}}'}_\star , \varepsilon ^{{\mathcal {G}}'})$ defines a parallel transport on the bundle gerbe ${\mathcal {G}}'$.

4.3.5 Transfer to arbitrary bundle gerbes

In [Wal16], Waldorf shows that the functors ${\mathcal {T}}$ and ${\mathcal {R}}$ come with a canonical natural isomorphism

$$\begin{aligned} {{\mathcal {A}}}:1 \longrightarrow {\mathcal {R}}\circ {\mathcal {T}}\end{aligned}$$

as endofunctors of the homotopy 1-category $\mathtt {h}\mathrm {BGrb}^\nabla (M)$. Given a bundle gerbe ${\mathcal {G}}\in \mathrm {BGrb}^\nabla (M)$, we thus get a 2-isomorphism class of 1-isomorphisms ${\mathcal {G}}\longrightarrow {\mathcal {G}}' = {\mathcal {R}}{\mathcal {T}}({\mathcal {G}})$. Let ${{\mathcal {A}}}_{\mathcal {G}}:{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ be a representative for this class.

Let ${{\mathcal {B}}}:{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ be a 1-isomorphism with adjoint inverse ${{\mathcal {B}}}^{-1}$, i.e. a weak inverse ${{\mathcal {B}}}^{-1}$ together with 2-isomorphisms $\epsilon _{{\mathcal {B}}}:1_{\mathcal {G}}\longrightarrow {{\mathcal {B}}}^{-1} \circ {{\mathcal {B}}}$ and $\delta _{{\mathcal {B}}}:{{\mathcal {B}}}\circ {{\mathcal {B}}}^{-1} \longrightarrow 1_{{\mathcal {G}}'}$ that satisfy the triangle identities. We can use it to define a 1-isomorphism ${\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}}_1$ as the composition

We define 2-isomorphisms

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}}_2&:=1_{{{\mathcal {B}}}^{-1}} \circ {\mathtt {pt}}^{{\mathcal {G}}'}_2 \circ 1_{{\mathcal {B}}}\ , \\ {\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}}_\star&:=1_{{{\mathcal {B}}}^{-1}} \circ \big ( {\mathtt {pt}}^{{\mathcal {G}}'}_\star \circ _2 (1_{{\mathtt {pt}}^{{\mathcal {G}}'}_1} \circ \delta _{{\mathcal {B}}}\circ 1_{{\mathtt {pt}}^{{\mathcal {G}}'}_1}) \big ) \circ 1_{{\mathcal {B}}}\ , \\ \varepsilon ^{{\mathcal {G}},{{\mathcal {B}}}}&:=\epsilon _{{\mathcal {B}}}\circ _2 (1_{{{\mathcal {B}}}^{-1}} \circ \varepsilon ^{{\mathcal {G}}'} \circ 1_{{\mathcal {B}}}) \ , \end{aligned}$$

where we have omitted pullbacks. From these definitions we readily see

Proposition 4.14

The quadruple ${\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}} = ({\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}}_1, {\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}}_2, {\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}}_\star , \varepsilon ^{{\mathcal {G}},{{\mathcal {B}}}})$ defines an object in ${\mathtt {PT}}({\mathcal {G}})$.

For $\psi :{{\mathcal {B}}}\longrightarrow {{\mathcal {B}}}'$ a 2-isomorphism of 1-isomorphisms ${{\mathcal {B}}}, {{\mathcal {B}}}' :{\mathcal {G}}' \longrightarrow {\mathcal {G}}$, we obtain a 2-isomorphism

$$\begin{aligned} \psi ^{(-1)} \circ 1_{{\mathtt {pt}}^{{\mathcal {G}}'}_1} \circ \psi :{\mathtt {pt}}_1^{{\mathcal {G}},{{\mathcal {B}}}} \longrightarrow {\mathtt {pt}}_1^{{\mathcal {G}},{{\mathcal {B}}}'} \ . \end{aligned}$$

(4.15)

Here $\psi ^{(-1)}$ denotes the 2-isomorphism obtained from $\psi$ by taking the inverse with respect to horizontal composition. Again it follows from the definitions that this defines an isomorphism

$$\begin{aligned} {\widehat{\psi }} :{\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}} \longrightarrow {\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}'} \end{aligned}$$

in the category ${\mathtt {PT}}({\mathcal {G}})$. If $\psi ' :{{\mathcal {B}}}\longrightarrow {{\mathcal {B}}}'$ is another (parallel unitary) 2-isomorphism, then $\psi$ and $\psi '$ differ by multiplication with a locally constant ${{\text {U}}}(1)$-valued function $f_{\psi , \psi '}$ on M. Since horizontal inverses of 2-isomorphisms have dual underlying line bundles [Wal07b], the morphisms $\psi ^{(-1)}$ and $\psi '{}^{(-1)}$ differ by the locally constant ${{\text {U}}}(1)$-valued function $f_{\psi ^{(-1)}, \psi '{}^{(-1)}} = (f_{\psi , \psi '})^{-1}$. Consequently, we deduce from (4.15) that

$$\begin{aligned} \widehat{\psi '} = {\widehat{\psi }} \ . \end{aligned}$$

That is, for any pair of parallel unitary 1-isomorphisms ${{\mathcal {B}}}, {{\mathcal {B}}}' :{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ for which there exists some parallel unitary 2-isomorphism ${{\mathcal {B}}}\longrightarrow {{\mathcal {B}}}'$, we obtain a unique isomorphism ${\mathtt {pt}}^{{\mathcal {G}}, {{\mathcal {B}}}} \longrightarrow {\mathtt {pt}}^{{\mathcal {G}},{{\mathcal {B}}}'}$.

Let $[[{{\mathcal {A}}}_{\mathcal {G}}]]$ denote the full subgroupoid of $\mathrm {BGrb}^\nabla (M)({\mathcal {G}},{\mathcal {G}}')$ on those 1-isomorphisms ${\mathcal {G}}\longrightarrow {\mathcal {G}}'$ that are isomorphic to Waldorf’s 1-isomorphism ${{\mathcal {A}}}_{\mathcal {G}}$. Our constructions define a functor

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}}, (\,\varvec{\cdot }\,)} :[[{{\mathcal {A}}}_{\mathcal {G}}]] \longrightarrow {\mathtt {PT}}({\mathcal {G}}) \ . \end{aligned}$$

This functor factors through a groupoid $[[{{\mathcal {A}}}_{\mathcal {G}}]]_*$ with the same objects as $[[{{\mathcal {A}}}_{\mathcal {G}}]]$ and a unique isomorphism between any two objects. In particular, every object in $[[{{\mathcal {A}}}_{\mathcal {G}}]]_*$ is final and the canonical functor $[[{{\mathcal {A}}}_{\mathcal {G}}]] \longrightarrow [[{{\mathcal {A}}}_{\mathcal {G}}]]_*$ is a final functor. It follows that, for any category ${\mathscr {C}}$, any functor ${\mathscr {F}}:[[{{\mathcal {A}}}_{\mathcal {G}}]] \longrightarrow {\mathscr {C}}$ that factors through $[[{{\mathcal {A}}}_{\mathcal {G}}]]_*$ has a colimit, which is represented by ${\mathscr {F}}({{\mathcal {B}}})$ for any object ${{\mathcal {B}}}\in [[{{\mathcal {A}}}_{\mathcal {G}}]]$.

Definition 4.16

Let ${\mathcal {G}}\in \mathrm {BGrb}^\nabla (M)$ be a bundle gerbe with connection on M. The parallel transport of ${\mathcal {G}}$ is

$$\begin{aligned} {\mathtt {pt}}^{\mathcal {G}}:={\text {colim}}\big ( {\mathtt {pt}}^{{\mathcal {G}}, (\,\varvec{\cdot }\,)} :[[{{\mathcal {A}}}_{\mathcal {G}}]] \longrightarrow {\mathtt {PT}}({\mathcal {G}}) \big ) \ . \end{aligned}$$

4.4 The transgression line bundle as a holonomy

Let ${\mathcal {G}}\in \mathrm {BGrb}^\nabla (M)$ be a bundle gerbe with connection on M and write ${\mathcal {G}}' = {\mathcal {R}}{\mathcal {T}}({\mathcal {G}})$. We will now determine the holonomy of the parallel transport on ${\mathcal {G}}'$. For this, consider the diffeological space $L_*M$ of smooth maps ${{\mathbb {S}}}^1 \longrightarrow M$ that have a sitting instant at $1 \in {{\mathbb {S}}}^1$. In other words, $L_*M$ is the pullback

in ${\mathscr {D}}\mathrm{fg}$, where $\iota$ denotes the inclusion map and ${\varDelta }$ is the diagonal embedding. The pullback $\iota ^* {\mathtt {pt}}^{{\mathcal {G}}'}_1$ is an automorphism of ${\mathrm {ev}}_1^*{\mathcal {G}}'$, which we understand as the holonomy of ${\mathtt {pt}}^{{\mathcal {G}}'}$. It is defined over the subduction $\iota ^* P_{\partial \Delta ^2} M \longrightarrow L_*M$. Recall from Sect. 2.2 that a 1-automorphism of a bundle gerbe defines a line bundle via descent. Thus the holonomy $\iota ^*{\mathtt {pt}}^{{\mathcal {G}}'}_1$ gives rise to a descended line bundle ${\text {hol}}({\mathcal {G}}) \in \mathrm {HLBdl}(L_*M)$. Our goal is to understand this descended line bundle more explicitly.

Let $\widehat{{\mathrm {ev}}_1} :{\mathrm {ev}}_1^*P_0M \longrightarrow P_0M$ be the morphism induced by the pullback

in ${\mathscr {D}}\mathrm{fg}$. The hermitean line bundle (with connection) underlying the bundle gerbe ${\mathrm {ev}}_1^*{\mathcal {G}}'$ is the pullback bundle

$$\begin{aligned} L:=\widehat{{\mathrm {ev}}_1}^{[2]*}{\mathcal {T}}{\mathcal {G}}\longrightarrow ({\mathrm {ev}}_1^*P_0M)^{[2]} \cong \iota ^* P_{\partial \Delta ^2} M \ . \end{aligned}$$

We now apply the construction from the diagram (2.18) that produces a line bundle ${{\mathsf {R}}}({{\mathcal {A}}})$ from an automorphism ${{\mathcal {A}}}$ of a bundle gerbe: the tensor product bundle $L^\vee \otimes {\mathtt {pt}}^{{\mathcal {G}}'}_1$ on $\iota ^* P_{\partial \Delta ^2}M$ has fibres

$$\begin{aligned} \big ( L^\vee \otimes {\mathtt {pt}}^{{\mathcal {G}}'}_1 \big )_{(\alpha _0, \gamma , \alpha _1)} = {\mathcal {T}}{\mathcal {G}}^\vee _{\overline{\alpha _1} \star \alpha _0} \otimes {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\gamma \star \alpha _0)} \cong {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _0} \star \alpha _1} \otimes {\mathcal {T}}{\mathcal {G}}_{\overline{\alpha _1} \star (\gamma \star \alpha _0)} \ . \end{aligned}$$

Now the thin-invariant parallel transport and the fusion product on ${\mathcal {T}}{\mathcal {G}}$ yield an isomorphism

By the associativity of $\lambda$, this is an isomorphism of descent data for line bundles on $L_*M$. This shows

Proposition 4.18

The morphism (4.17) yields an isomorphism of hermitean line bundles

$$\begin{aligned} {\text {hol}}({\mathcal {G}}) :={{\mathsf {R}}}\big ( \iota ^*{\mathtt {pt}}^{{\mathcal {G}}'}_1 \big ) \overset{\cong }{\longrightarrow } {\mathcal {T}}{\mathcal {G}}_{|L_*M} \end{aligned}$$

over $L_*M$.

Thus the parallel transport ${\mathtt {pt}}^{{\mathcal {G}}'}$ reproduces the transgression line bundle ${\mathcal {T}}{\mathcal {G}}$ as its holonomy.

Remark 4.19

For a generic bundle gerbe ${\mathcal {G}}$ with parallel transport ${\mathtt {pt}}^{\mathcal {G}}$, the morphism ${\mathtt {pt}}^{\mathcal {G}}_2$ induces a parallel transport on ${\text {hol}}({\mathcal {G}})$. It should be possible to construct from this a fusion line bundle with connection on LM in the sense of [Wal16], which then regresses to a bundle gerbe with connection on M. Its underlying bundle gerbe should be canonically isomorphic to ${\mathcal {G}}$ (up to 2-isomorphism), and that should allow the reconstruction of the connection on ${\mathcal {G}}$ from its parallel transport in our sense. However, this would go beyond the scope of this paper, and since for our applications in Sects. 5 and 6 having an explicit construction for ${\mathtt {pt}}^{{\mathcal {G}}'}$ is sufficient, we leave this reconstruction of the connection on ${\mathcal {G}}$ for future work. $\square$

5 2-Group Extensions from Bundle Gerbes

Let G be a connected Lie group with a smooth group action on a manifold M. In Sect. 3 we saw how a principal bundle $P \longrightarrow M$ gives rise to a group extension ${\mathrm {Sym}}_G(P) \longrightarrow G$ which encodes all information about equivariant structures on P. We were able to give two equivalent constructions for ${\mathrm {Sym}}_G(P)$, one as a subgroup of $\mathrm {Diff}(P)$, and one as descent data associated to the path fibration $P_0 G \longrightarrow G$ and a parallel transport on P.

In this section we study the analogous situation for a bundle gerbe ${\mathcal {G}}\in \mathrm {BGrb}(M)$ instead of a principal bundle $P\in {\mathrm {Bun}}_H(M)$. There are two main differences to the situation in Sect. 3: equivariant structures on ${\mathcal {G}}$ form a groupoid rather than a set, and they do not assemble into a topological or smooth space. We thus cannot expect a universal extension ${\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow G$ as diffeological groups. A good framework to describe this extension is that of group objects in categories fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$, where the fibration encodes the smooth structure. After carefully setting up this framework, we give two constructions of ${\mathrm {Sym}}_G({\mathcal {G}})$, in analogy to the two constructions of ${\mathrm {Sym}}_G(P)$ in Sect. 3. We conclude this section by showing that, again, the extension ${\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow G$ encodes all information about equivariant structures on ${\mathcal {G}}$.

5.1 Smooth groupoids and symmetries of gerbes

Let ${\mathcal {G}}\in \mathrm {BGrb}(M)$ be a bundle gerbe on M. Let $\varPhi :G \times M \longrightarrow M$ be an action of a connected Lie (or diffeological) group G on M. Let ${{\mathscr {C}}\mathrm{art}}$ denote the category of smooth manifolds that are diffeomorphic to ${\mathbb {R}}^n$ for some $n \in {\mathbb {N}}_0$. The morphisms in ${{\mathscr {C}}\mathrm{art}}$ are the smooth maps between these manifolds.

We can view M and G as presheaves on ${{\mathscr {C}}\mathrm{art}}$ by setting

$$\begin{aligned} M(c) = C^\infty (c,M) \qquad \text {and} \qquad G(c) = C^\infty (c,G) \ . \end{aligned}$$

By adding identity morphisms, we can canonically enhance the presheaf G to a (pre)stack on ${{\mathscr {C}}\mathrm{art}}$, i.e. a (pre)sheaf of groupoids, which we still denote by G. Given a section $f \in G(c)$, i.e. a smooth map $f :c \longrightarrow G$, we can define a map

We can then assign to f the groupoid

$$\begin{aligned} {\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f) :=\mathrm {BGrb}(c \times M) ({\text {pr}}_M^*{\mathcal {G}}, \varPhi _f^*{\mathcal {G}}) \ , \end{aligned}$$

where ${\text {pr}}_M :c \times M \longrightarrow M$ is the projection. The groupoid ${\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f)$ is non-empty: since the map $f :c \longrightarrow G$ is homotopic to the constant map at the identity in G, it follows that ${\text {pr}}_M^*{\mathcal {G}}$ and $\varPhi _f^*{\mathcal {G}}$ have the same Dixmier–Douady class as gerbes on $c \times M$, so that there exists an isomorphism ${\text {pr}}_M^*{\mathcal {G}}\longrightarrow \varPhi _f^*{\mathcal {G}}$.

The assignment $f \longmapsto {\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f)$ is evidently not a presheaf of groupoids on ${{\mathscr {C}}\mathrm{art}}$ since it depends not only on the object c, but also on a choice of a smooth map $f :c \longrightarrow G$. We can reformulate this in the following way: let $\underline{G}$ denote the category with objects the smooth maps $f :c \longrightarrow G$, where $c \in {{\mathscr {C}}\mathrm{art}}$ is any Cartesian space. The morphisms

$$\begin{aligned} \varphi :(f :c \longrightarrow G) \longrightarrow (f' :c' \longrightarrow G) \end{aligned}$$

in $\underline{G}$ are commutative triangles of smooth maps

Then ${\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})$ is a presheaf of groupoids on $\underline{G}\,$: to an object $f :c \longrightarrow G$ in $\underline{G}$ we assign the groupoid ${\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f)$, while to a morphism $\varphi :f \longrightarrow f'$ we assign the pullback functor

$$\begin{aligned} {\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(\varphi ) :=(\varphi \times 1_M)^* :{\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f') \longrightarrow {\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f) \ . \end{aligned}$$

By a slight abuse of notation, we will denote the functor ${\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(\varphi )$ by $\varphi ^*$. Explicitly, given a 1-isomorphism $A :{\text {pr}}_M^*{\mathcal {G}}\longrightarrow \varPhi _{f'}^*{\mathcal {G}}$ over $c'$, it is defined by the commutative diagram

By construction of the 2-category of bundle gerbes, this defines a pseudofunctor

$$\begin{aligned} {\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}}) :\underline{G}^\text {op}\longrightarrow {{\mathscr {G}}\mathrm {rpd}}\ , \end{aligned}$$

where ${{\mathscr {G}}\mathrm {rpd}}$ is the 2-category of groupoids, functors, and natural transformations.

Remark 5.1

The assignment $f \longmapsto {\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f)$ is not a strict presheaf of groupoids on $\underline{G}\,$, as it is only pseudofunctorial [Moe02]. There are several ways to technically treat such pseudo-presheaves of groupoids:

• (1) Encode the coherence morphisms by viewing pseudo-presheaves of groupoids as coherent simplicial presheaves, i.e. as simplicial functors ${\mathfrak {C}} \circ \mathrm{N}_\Delta (\underline{G})^\text {op}\longrightarrow {\mathscr {S}}\mathrm{et}_\Delta$ in the notation of [Lur09].

• (2) Use a strictification procedure to translate pseudo-presheaves of groupoids into presheaves of groupoids [Hol08].

• (3) Use the Grothendieck construction, or straightening, to translate pseudo-presheaves of groupoids into categories fibred in groupoids over $\underline{G}$ [Vis05, Lur09].

We will follow the third approach here because the transition between the parameterising categories $\underline{G}$ and ${{\mathscr {C}}\mathrm{art}}$ becomes particularly easy in that framework. $\square$

We will frequently make use of the Grothendieck construction to pass from ${{\mathscr {G}}\mathrm {rpd}}$-valued pseudo-functors to categories fibred in groupoids; for background on the Grothendieck construction and fibred categories we refer to [Vis05, Lur09]. We will, however, describe the resulting fibred categories explicitly. For example, the canonical projection functor ${\text {pr}}:\underline{G} \longrightarrow {{\mathscr {C}}\mathrm{art}}$ is the category fibred in groupoids obtained by applying the Grothendieck construction to the (pseudo)functor $c \longmapsto G(c)$, where G(c) is regarded as a groupoid with only identity arrows.

Definition 5.2

A functor $\pi :{\mathscr {D}}\longrightarrow {\mathscr {C}}$ between categories is a Grothendieck fibration in groupoids, or makes ${\mathscr {D}}$ into a category fibred in groupoids over ${\mathscr {C}}$, if it satisfies the properties:

• (1) For every object $d \in {\mathscr {D}}$ and for every morphism $f :c \longrightarrow \pi (d)$ in ${\mathscr {C}}$, there exists a morphism ${\widehat{f}} :{\widehat{c}} \longrightarrow d$ in ${\mathscr {D}}$ with $\pi ({\widehat{f}}\ ) = f$.

• (2) For every pair of diagrams

  

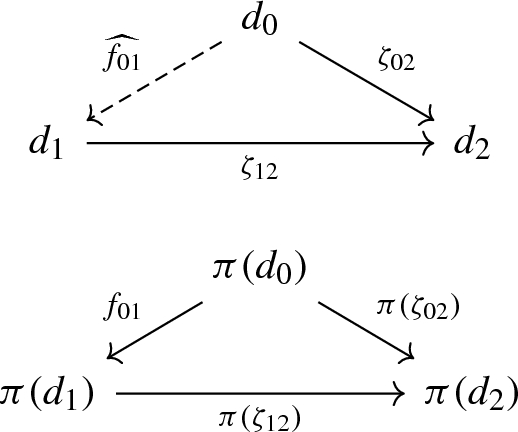
  in ${\mathscr {D}}$ and ${\mathscr {C}}$, respectively, there exists a unique lift $\widehat{f_{01}}$ of $f_{01}$ that makes the upper triangle commute.

The first requirement resembles a path-lifting condition. The second requirement can be viewed as a relative horn-filling property: given any $\Lambda ^2_2$-horn $\sigma$ in ${\mathscr {D}}$ and a filling of $\pi (\sigma )$ in ${\mathscr {C}}$ to a 2-simplex, there exists a unique filling of $\sigma$ to a 2-simplex in ${\mathscr {D}}$ that lifts the 2-simplex in ${\mathscr {C}}$. Alternatively, consider an arbitrary functor $\pi :{\mathscr {D}}\longrightarrow {\mathscr {C}}$ between categories and a morphism $\zeta _{12} :d_1 \longrightarrow d_2$ in ${\mathscr {D}}$. If for every pair of solid arrow diagrams as in (5.3) the dashed arrow exists such that the upper triangle commutes and such that $\pi (\widehat{f_{01}}) = f_{01}$, one says that $\zeta _{12}$ is $\pi$-Cartesian. In particular, if $\pi$ is a Grothendieck fibration in groupoids, then property (2) of Definition 5.2 is equivalent to saying that every morphism in ${\mathscr {D}}$ is $\pi$-Cartesian. If $\pi :{\mathscr {D}}\longrightarrow {\mathscr {C}}$ is a Grothendieck fibration in groupoids and $c \in {\mathscr {C}}$, we denote by ${\mathscr {D}}_{|c} = \pi ^{-1}(c)$ the fibre over c, which is the groupoid with objects $d \in {\mathscr {D}}$ such that $\pi (d) = c$ and morphisms ${\widehat{f}} :d \longrightarrow d'$ such that $\pi ({\widehat{f}}\ ) = 1_c$.

Definition 5.4

A category fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$ is a smooth groupoid. Let ${\mathscr {H}}$ denote the strict 2-category of smooth groupoids. Its objects are smooth groupoids, its morphisms are (strictly) commutative diagrams of functors

and its 2-morphisms are natural transformations that project to the identity. We denote by $\underline{{\mathscr {H}}}({{\mathsf {X}}},{{\mathsf {Z}}})$ the groupoid of functors ${{\mathsf {X}}}\longrightarrow {{\mathsf {Z}}}$ that project to the identity on ${{\mathscr {C}}\mathrm{art}}$.

Example 5.5

Let M be a smooth manifold. An important example of a smooth groupoid is given by the Grothendieck fibration $\mathrm {HLBdl}^M \longrightarrow {{\mathscr {C}}\mathrm{art}}$, whose objects are pairs (c, L) of a Cartesian space $c \in {{\mathscr {C}}\mathrm{art}}$ and a hermitean line bundle $L \longrightarrow c \times M$, and whose morphisms $(c,L) \longrightarrow (c',L')$ are pairs $(\varphi , \psi )$ of a smooth map $\varphi :c \longrightarrow c'$ and an isomorphism $\psi :L \longrightarrow (\varphi \times 1_M)^*L'$ of hermitean line bundles on $c \times M$. One can interpret $\mathrm {HLBdl}^M$ as describing smooth families of hermitean line bundles on M. For $M = *$, we write $\mathrm {HLBdl}^* =:\mathrm {HLBdl}$. $\square$

Definition 5.6

Let $p:{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}$ denote the category fibred in groupoids obtained by applying the Grothendieck construction to the pseudofunctor ${\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}}) :\underline{G}^\text {op}\longrightarrow {{\mathscr {G}}\mathrm {rpd}}$. Explicitly, the category ${\mathrm {Sym}}_G({\mathcal {G}})$ consists of:

• $\underline{\mathrm{Objects:}}$ pairs (f, A), where $f \in \underline{G}$ is a smooth map $f :c \longrightarrow G$ and $A :{\text {pr}}_M^*{\mathcal {G}}\longrightarrow \varPhi _f^*{\mathcal {G}}$ is a 1-isomorphism of bundle gerbes over $c \times M$.

• $\underline{\mathrm{Morphisms:}}$ a morphism $(f_0,A_0) \longrightarrow (f_1, A_1)$ is a pair $(\varphi , \psi )$ of a morphism $\varphi :f_0 \longrightarrow f_1$ in $\underline{G}$ and a 2-isomorphism $\psi :A_0 \longrightarrow \varphi ^*A_1$ in ${\mathrm {Sym}}_G^{{\mathtt {PSh}}}({\mathcal {G}})(f_0)$.

The functor $p:{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}$ is automatically a fibration in groupoids, since it arises as the Grothendieck construction of a pseudo-presheaf of groupoids. Since Grothendieck fibrations are stable under composition [Vis05], the composite functor

makes ${\mathrm {Sym}}_G({\mathcal {G}})$ into a smooth groupoid.

5.2 Smooth 2-groups

We would now like to establish that ${\mathrm {Sym}}_G({\mathcal {G}})$ is not just a smooth groupoid, but can also be regarded as a higher group in some sense. That is, we would like to find on ${\mathrm {Sym}}_G({\mathcal {G}})$ the same type of structure as we found on the bundle ${\mathrm {Sym}}_G(P) \longrightarrow G$ in Sect. 3.1. Here, however, we are working inside the ambient 2-category ${\mathscr {H}}$, and so we will need to make precise what we mean by a group in ${\mathscr {H}}$. The notion of a group object in a 2-category goes back to [BL04]. The following definitions are taken from [SP11] which are strongly based on [BL04]. Let ${\mathscr {C}}$ be a 2-category with finite products; in particular, it has a terminal object $*$. Examples are the 2-categories ${{\mathscr {G}}\mathrm {rpd}}$ and ${\mathscr {H}}$.

Definition 5.7

([BL04]) A monoid object in ${\mathscr {C}}$ is a sextuple $({{\mathsf {H}}}, {{\mathsf {u}}}, \otimes , {{\mathsf {a}}}, {{\mathsf {l}}}, {{\mathsf {r}}})$ of

• an object ${{\mathsf {H}}}\in {\mathscr {C}}$,

• 1-morphisms ${{\mathsf {u}}}:* \longrightarrow {{\mathsf {H}}}$ and $\otimes :{{\mathsf {H}}}\times {{\mathsf {H}}}\longrightarrow {{\mathsf {H}}}$, and

• 2-isomorphisms

  $$\begin{aligned} {{\mathsf {a}}}:\otimes \circ \, (\otimes \times 1_{{\mathsf {H}}})&\longrightarrow \otimes \circ (1_{{\mathsf {H}}}\times \otimes ) \ , \\ {{\mathsf {l}}}:\otimes \circ \, ({{\mathsf {u}}}\times 1_{{\mathsf {H}}})&\longrightarrow 1_{{\mathsf {H}}}\ , \\ {{\mathsf {r}}}:\otimes \circ \, (1_{{\mathsf {H}}}\times {{\mathsf {u}}})&\longrightarrow 1_{{\mathsf {H}}}\ . \end{aligned}$$

These data are required to satisfy a pentagon and a triangle identity; see [SP11, Definition 41].

An abelian monoid object comes with an additional 2-isomorphism $\beta :\otimes \circ \, \tau \longrightarrow \otimes$ satisfying the coherence conditions in [SP11, Definition 47], where $\tau :{{\mathsf {H}}}\times {{\mathsf {H}}}\longrightarrow {{\mathsf {H}}}\times {{\mathsf {H}}}$ is the interchange of factors.

Definition 5.8

A 1-morphism of monoid objects $({{\mathsf {H}}}, {{\mathsf {u}}}, \otimes , {{\mathsf {a}}}, {{\mathsf {l}}}, {{\mathsf {r}}}) \longrightarrow ({{\mathsf {H}}}', {{\mathsf {u}}}', \otimes ', {{\mathsf {a}}}', {{\mathsf {l}}}', {{\mathsf {r}}}')$ in ${\mathscr {C}}$ consists of a triple $(F_1, F_\otimes , F_{{\mathsf {u}}})$ of

• a 1-morphism $F_1 :{{\mathsf {H}}}\longrightarrow {{\mathsf {H}}}'$ and

• 2-isomorphisms $F_\otimes :\otimes ' \circ \, (F_1 \times F_1) \longrightarrow F_1 \circ \otimes$ and $F_{{\mathsf {u}}}:{{\mathsf {u}}}' \longrightarrow F_1 \circ {{\mathsf {u}}}$.

These are required to satisfy the coherence conditions in [SP11, Definition 42].

Morphisms of abelian monoid objects satisfy an additional compatibility condition for the symmetries $\beta$ and $\beta '$, which can be found in [SP11, Definition 48].

Definition 5.9

([SP11, Definition 43]) A 2-morphism $(F_1, F_\otimes , F_{{\mathsf {u}}}) \longrightarrow (E_1, E_\otimes , E_{{\mathsf {u}}})$ of monoid objects in ${\mathscr {C}}$ is a 2-morphism $\theta :F_1 \longrightarrow E_1$ such that the diagrams

commute. 2-morphisms of abelian monoid objects are 2-morphisms of the underlying monoid objects.

Example 5.10

A monoid object in the 2-category ${\mathscr {C}}\mathrm{at}$ of categories is precisely a monoidal category. Similarly, 1-morphisms and 2-morphisms between monoid objects in ${\mathscr {C}}\mathrm{at}$ are precisely the monoidal functors and the monoidal natural transformations, respectively. The abelian monoids in ${\mathscr {C}}\mathrm{at}$ are precisely the symmetric monoidal categories. $\square$

Definition 5.11

[[SP11, Definition 41]]. A group object in ${\mathscr {C}}$ is a monoid object $({{\mathsf {H}}}, {{\mathsf {u}}}, \otimes , {{\mathsf {a}}}, {{\mathsf {l}}}, {{\mathsf {r}}})$ in ${\mathscr {C}}$ such that the 1-morphism

$$\begin{aligned} (\otimes , {\text {pr}}_1) :{{\mathsf {H}}}\times {{\mathsf {H}}}\longrightarrow {{\mathsf {H}}}\times {{\mathsf {H}}}\end{aligned}$$

is (weakly) invertible. An abelian group object in ${\mathscr {C}}$ is an abelian monoid object whose underlying monoid object is a group object.

For ${\mathscr {C}}$ a 2-category with finite products, we denote the 2-category of group objects in ${\mathscr {C}}$ by $2{{\mathscr {G}}\mathrm {rp}}({\mathscr {C}})$.

Definition 5.12

The 2-category of 2-groups is $2{{\mathscr {G}}\mathrm {rp}}({{\mathscr {G}}\mathrm {rpd}})$. The 2-category of smooth 2-groups is $2{{\mathscr {G}}\mathrm {rp}}({\mathscr {H}})$.

Both these 2-categories are enriched in groupoids. Let us examine Definition 5.12 a little more closely. Consider two objects $\pi _{{\mathsf {C}}}:{{\mathsf {C}}}\longrightarrow {{\mathscr {C}}\mathrm{art}}$ and $\pi _{{\mathsf {D}}}:{{\mathsf {D}}}\longrightarrow {{\mathscr {C}}\mathrm{art}}$ in ${\mathscr {H}}$. The product in ${\mathscr {H}}$ is given by the pullback in ${\mathscr {C}}\mathrm{at}$:

$$\begin{aligned} \big ({{\mathsf {C}}}\xrightarrow { \ \pi _{{\mathsf {C}}}\ } {{\mathscr {C}}\mathrm{art}}\big ) \times \big ({{\mathsf {D}}}\xrightarrow { \ \pi _{{\mathsf {D}}}\ } {{\mathscr {C}}\mathrm{art}}\big ) = \big ( {{\mathsf {C}}}\times _{{\mathscr {C}}\mathrm{art}}{{\mathsf {D}}}\longrightarrow {{\mathscr {C}}\mathrm{art}}\big ) \ . \end{aligned}$$

Explicitly, the category ${{\mathsf {C}}}\times _{{\mathscr {C}}\mathrm{art}}{{\mathsf {D}}}$ has

• $\underline{\mathrm{Objects:}}$ pairs $(c \in {{\mathsf {C}}}, d \in {{\mathsf {D}}})$ such that $\pi _{{\mathsf {C}}}(c) = \pi _{{\mathsf {D}}}(d)$.

• $\underline{\mathrm{Morphisms:}}$ pairs $(\phi , \psi )$ of morphisms $\phi$ in ${{\mathsf {C}}}$ and $\psi$ in ${{\mathsf {D}}}$ such that $\pi _{{\mathsf {C}}}(\phi ) = \pi _{{\mathsf {D}}}(\psi )$.

A monoid structure on ${{\mathsf {C}}}\in {\mathscr {H}}$ thus allows us to multiply pairs of objects in the same fibre and pairs of morphisms that lie over the same morphism in ${{\mathscr {C}}\mathrm{art}}$.

Example 5.13

The tensor product of line bundles turns the presheaf of groupoids of hermitean line bundles with connection $\mathrm {HLBdl}^{\nabla } \longrightarrow {{\mathscr {C}}\mathrm{art}}$ into an abelian group object in ${\mathscr {H}}$. Similarly, for any manifold M it also turns the internal hom $\big (\mathrm {HLBdl}^{\nabla }\big )^M$ into an abelian group object in ${\mathscr {H}}$. $\square$

5.3 Smooth principal 2-bundles

We shall now establish our precise notion of an extension of smooth 2-groups.

Definition 5.14

Let ${\mathscr {C}}$ be a 2-category with finite products, let $({{\mathsf {H}}}, {{\mathsf {u}}}, \otimes _{{\mathsf {H}}}, {{\mathsf {a}}}, {{\mathsf {l}}}, {{\mathsf {r}}})$ be a monoid object in ${\mathscr {C}}$, and let ${{\mathsf {C}}}\in {\mathscr {C}}$. A right action of ${{\mathsf {H}}}$ on ${{\mathsf {C}}}$ is a morphism $\otimes :{{\mathsf {C}}}\times {{\mathsf {H}}}\longrightarrow {{\mathsf {C}}}$ in ${\mathscr {C}}$, together with 2-morphisms $\alpha$ and u in ${\mathscr {C}}$ that witness the commutativity of the diagrams

and that are coherent with respect to the 2-isomorphism ${{\mathsf {a}}}$, ${{\mathsf {l}}}$ and ${{\mathsf {r}}}$. Left actions are defined analogously.

Example 5.15

The standard example for an action of a monoid object is that of a module category ${{\mathsf {C}}}$ over a monoidal category ${{\mathsf {H}}}$ in ${\mathscr {C}}= {\mathscr {C}}\mathrm{at}$. $\square$

Definition 5.16

Let ${\mathscr {C}}$ be a category. Suppose there are categories fibred in groupoids $\pi _i :{{\mathsf {D}}}_i \longrightarrow {\mathscr {C}}$, for $i=0,1$, and $\pi _{{\mathsf {E}}}:{{\mathsf {E}}}\longrightarrow {\mathscr {C}}$ over ${\mathscr {C}}$, and suppose there is a diagram

of categories fibred in groupoids over ${\mathscr {C}}$. The homotopy pullback ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^{\mathtt {h}} {{\mathsf {D}}}_1$ is the category with

• $\underline{\mathrm{Objects:}}$ triples $(d_0,\eta , d_1)$, where $d_i \in {{\mathsf {D}}}_i$ and $\eta :F_0(d_0) \longrightarrow F_1(d_1)$ is an isomorphism in ${{\mathsf {E}}}$ that projects to the identity under $\pi _{{\mathsf {E}}}$.

• $\underline{\mathrm{Morphisms:}}$ a morphism $(d_0,\eta ,d_1) \longrightarrow (d'_0, \eta ', d'_1)$ is a pair $(\psi _0, \psi _1)$ of morphisms $\psi _i :d_i \longrightarrow d'_i$ such that the diagram

  

  commutes in ${{\mathsf {E}}}$.

This comes with a canonical functor

$$\begin{aligned} \pi _{\mathtt {h}} :{{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^{\mathtt {h}} {{\mathsf {D}}}_1&\longrightarrow {\mathscr {C}}\\ (d_0,\eta ,d_1)&\longmapsto \pi _0(d_0)=\pi _1(d_1) \\ (\psi _0,\psi _1)&\longmapsto \pi _0(\psi _0)=\pi _1(\psi _1) \ , \end{aligned}$$

which, as we show in Appendix A, is a Grothendieck fibration in groupoids.

Definition 5.17

Let ${{\mathsf {H}}}$ be a smooth 2-group, and let ${{\mathsf {X}}}\in {\mathscr {H}}$ be any smooth groupoid. An ${{\mathsf {H}}}$-principal 2-bundle on ${{\mathsf {X}}}$ is an object ${{\mathsf {P}}}\in {\mathscr {H}}$ with a morphism $\pi :{{\mathsf {P}}}\longrightarrow {{\mathsf {X}}}$, a right action $(\otimes , \alpha )$ of ${{\mathsf {H}}}$ on ${{\mathsf {P}}}$ and a 2-isomorphism

such that

• (1) the functor $\pi :{{\mathsf {P}}}\longrightarrow {{\mathsf {X}}}$ is an essentially surjective Grothendieck fibration,

• (2) the action $(\otimes , \alpha )$ of ${{\mathsf {H}}}$ on ${{\mathsf {P}}}$ and the 2-isomorphism $\eta$ are compatible in the sense that the diagram

  

  is coherent, where the front face carries the 2-isomorphism $\alpha$ that is part of the action of ${{\mathsf {H}}}$ on ${{\mathsf {P}}}$, the back, right-hand, and bottom faces carry the 2-isomorphism $\eta$, and the left-hand face commutes strictly,

• (3) the composition ${{\mathsf {P}}}\times {{\mathsf {H}}}\longrightarrow {{\mathsf {P}}}\times _{{\mathsf {X}}}{{\mathsf {P}}}\times {{\mathsf {H}}}\longrightarrow {{\mathsf {P}}}\times _{{\mathsf {X}}}^{\mathtt {h}} {{\mathsf {P}}}$ is an equivalence, where the first functor is induced by the diagonal functor ${{\mathsf {P}}}\longrightarrow {{\mathsf {P}}}\times _{{\mathsf {X}}}{{\mathsf {P}}}$.

The first condition can be understood as demanding that ${{\mathsf {P}}}\longrightarrow {{\mathsf {X}}}$ has local sections (see Lemma A.1 from Appendix A). The second condition implements the property that the ${{\mathsf {H}}}$-action preserves the projection to ${{\mathsf {X}}}$ up to coherent homotopy. The third condition says that the ${{\mathsf {H}}}$-action is principal. Note that upon choosing an inverse to the equivalence ${{\mathsf {P}}}\times _{{\mathsf {X}}}{{\mathsf {P}}}\hookrightarrow {{\mathsf {P}}}\times _{{\mathsf {X}}}^{\mathtt {h}} {{\mathsf {P}}}$, one could equivalently formulate condition (3) using strict pullbacks alone (again by Lemma A.1 from Appendix A).

In order to understand the notion of an extension of smooth 2-groups, we first need to define the kernel of a morphism of smooth 2-groups. Naively, the kernel could easily be defined as a fibre over ${{\mathsf {u}}}$, but the resulting category will not generally be fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$. As it turns out, the homotopy pullback does satisfy this property.

Definition 5.18

Let $p :{{\mathsf {H}}}\longrightarrow {{\mathsf {G}}}$ be a morphism of smooth 2-groups in ${\mathscr {H}}$. Its kernel $\ker ^{\mathtt {h}}(p)$ is the homotopy pullback

Explicitly, $\ker ^{\mathtt {h}}(p)$ is given by

$$\begin{aligned} \ker ^{\mathtt {h}}(p) :=*_{\mathscr {H}}\times _{{\mathsf {G}}}^{\mathtt {h}} {{\mathsf {H}}}\ . \end{aligned}$$

Using Definition 5.16 we can equivalently describe it as the category with objects given by pairs $(h,\eta )$ of an object $h \in {{\mathsf {H}}}$ and an isomorphism $\eta :p(h) \longrightarrow {{\mathsf {u}}}_{{\mathsf {G}}}(\pi _{{\mathsf {H}}}(h))$ in ${{\mathsf {G}}}$. Its morphisms $(h_0,\eta _0) \longrightarrow (h_1,\eta _1)$ are given by morphisms $\zeta :h_0 \longrightarrow h_1$ such that $\eta _1 \circ p(\zeta ) = u_{{\mathsf {G}}}(\pi _{{\mathsf {H}}}(\zeta ))\circ \eta _0$. We readily observe that the restrictions of the structure morphisms $\otimes _{{\mathsf {H}}}$, ${{\mathsf {a}}}_{{\mathsf {H}}}$, ${{\mathsf {l}}}_{{\mathsf {H}}}$ and ${{\mathsf {r}}}_{{\mathsf {H}}}$, together with the morphism ${{\mathsf {u}}}_{{\mathsf {H}}}$, turn $\ker ^{\mathtt {h}}(p)$ into a smooth 2-group. It should also be possible to turn the strict kernel $\ker (p)$ into a smooth 2-group in this case, using an inverse to the equivalence $\ker (p) \hookrightarrow \ker ^{\mathtt {h}}(p)$ (compare Lemma A.2 from Appendix A), but the homotopy-kernel $\ker ^{\mathtt {h}}(p)$ carries a canonical 2-group structure, and using $\ker (p)$ instead of $\ker ^{\mathtt {h}}(p)$ would make Construction 5.21 below rather cumbersome.

Lemma 5.19

In the setting of Definition 5.18, the functor $\kappa$ is a Grothendieck fibration in groupoids.

Proof

This follows directly by Lemma A.2 (1) from Appendix A. $\square$

Let $\ker (p)$ denote the strict pullback of the diagram ${{\mathscr {C}}\mathrm{art}}\overset{{{\mathsf {u}}}_{{\mathsf {G}}}}{\longrightarrow } {{\mathsf {G}}}\overset{p}{\longleftarrow } {{\mathsf {H}}}$. Explicitly, it is the category with objects $h \in {{\mathsf {H}}}$ such that $p(h) = {{\mathsf {u}}}_{{\mathsf {G}}}(\pi _{{\mathsf {H}}}(h))$ and morphisms $\zeta :h_0 \longrightarrow h_1$ such that $p(\zeta ) = {{\mathsf {u}}}_{{\mathsf {G}}}(\pi _{{\mathsf {H}}}(\zeta ))$. The functor $\ker (p) \longrightarrow {{\mathscr {C}}\mathrm{art}}$ is not a Grothendieck fibration in groupoids in general. However, if $p :{{\mathsf {H}}}\longrightarrow {{\mathsf {G}}}$ is a Grothendieck fibration in groupoids, then so are the functors $\ker ^{\mathtt {h}}(p) \longrightarrow {{\mathscr {C}}\mathrm{art}}$ and $\ker (p) \longrightarrow {{\mathscr {C}}\mathrm{art}}$, and the canonical inclusion $\ker (p) \hookrightarrow \ker ^{\mathtt {h}}(p)$ is an equivalence. The next definition is loosely modelled on [SP11, Definition 75].

Definition 5.20

Let ${{\mathsf {A}}}$ and ${{\mathsf {G}}}$ be smooth 2-groups. An extension of ${{\mathsf {G}}}$ by ${{\mathsf {A}}}$ is a pair (F, p) of a morphism of smooth 2-groups $p :{{\mathsf {H}}}\longrightarrow {{\mathsf {G}}}$ that turns ${{\mathsf {H}}}$ into a $\ker ^{\mathtt {h}}(p)$-principal 2-bundle over ${{\mathsf {G}}}$, and an equivalence of smooth 2-groups $F :{{\mathsf {A}}}\longrightarrow \ker ^{\mathtt {h}}(p)$.

By Lemma A.2 from Appendix A, we could equivalently require p to turn ${{\mathsf {H}}}$ into a $\ker (p)$-principal 2-bundle, but then we would need to use the non-canonical 2-group structure on $\ker (p)$. This essentially amounts to choosing an inverse for the equivalence $\ker (p) \hookrightarrow \ker ^{\mathtt {h}}(p)$.

Our goal now is to define when an extension of smooth 2-groups is central. Again, we follow the ideas of [SP11], where the criterion for an extension of ${{\mathsf {G}}}$ by ${{\mathsf {A}}}$ to be central is formulated using a functor ${{\mathsf {G}}}\longrightarrow \mathsf {Aut}({{\mathsf {A}}})$ from ${{\mathsf {G}}}$ into the automorphisms of ${{\mathsf {A}}}$ as a 2-group; the smooth structure does not matter here. In [SP11], this functor is obtained from abstract arguments.

Construction 5.21

In our formalism, we can understand this construction as follows: consider smooth 2-groups ${{\mathsf {G}}}$ and ${{\mathsf {A}}}$, where ${{\mathsf {A}}}$ is abelian, and let (F, p) be a smooth 2-group extension of ${{\mathsf {G}}}$ by ${{\mathsf {A}}}$, with morphism $p :{{\mathsf {H}}}\longrightarrow {{\mathsf {G}}}$. Then ${{\mathsf {A}}}$ is abelian if and only if $\ker ^{\mathtt {h}}(p)$ is abelian, which is true if and only if $\ker (p)$ is abelian (since the 2-group structure induces Picard groupoid structures on the fibres of these smooth 2-groups, where F induces monoidal equivalences). Fix an arbitrary Cartesian space $c \in {{\mathscr {C}}\mathrm{art}}$. Let $\mathsf {Aut}(\ker ^{\mathtt {h}}(p)_{|c})$ denote the Picard groupoid of monoidal autoequivalences of the fibre $\ker ^{\mathtt {h}}(p)_{|c}$ of $\ker ^{\mathtt {h}}(p)$ over c. Note that we do not claim that the Picard groupoids $\mathsf {Aut}(\ker ^{\mathtt {h}}(p)_{|c})$ assemble into a smooth 2-group (though it might be possible to achieve this). We claim that there is a functor ${{\mathsf {G}}}_{|c} \longrightarrow \mathsf {Aut}(\ker ^{\mathtt {h}}(p)_{|c})$ which is canonical up to unique natural isomorphism.

Let $(\,\varvec{\cdot }\,)^\vee :{{\mathsf {H}}}_{|c} \longrightarrow {{\mathsf {H}}}_{|c}$ denote a choice of functorial inverse in ${{\mathsf {H}}}_{|c}$. This can always be enhanced to a functorial choice of adjoint inverse, i.e. a functor $k \longmapsto (k^\vee , {\mathrm {ev}}_k, {\mathrm {coev}}_k)$ that maps k to a triple of a dual object $k^\vee$, and duality morphisms (which are isomorphisms in this case) ${\mathrm {ev}}_k :k \otimes _{{\mathsf {H}}}k^\vee \longrightarrow {{\mathsf {u}}}_{{\mathsf {H}}}(c)$ and ${\mathrm {coev}}_k :{{\mathsf {u}}}_{{\mathsf {H}}}(c) \longrightarrow k^\vee \otimes _{{\mathsf {H}}}k$ which satisfy the triangle identities. The functor $(\,\varvec{\cdot }\,)^\vee$ acts on morphisms $\psi :k \longrightarrow k'$ by taking the dual of $\psi ^{-1}$ with respect to the chosen duality data on k and $k^\vee$. This enhancement can be achieved by choosing an adjoint inverse for the equivalence of categories $(\otimes _{{\mathsf {H}}}, {\text {pr}}_1)_{|c} :{{\mathsf {H}}}_{|c} \times {{\mathsf {H}}}_{|c} \longrightarrow {{\mathsf {H}}}_{|c} \times {{\mathsf {H}}}_{|c}$ (which is always possible).

To an object $k \in {{\mathsf {H}}}_{|c}$ we associate the functor

$$\begin{aligned} {\mathrm {Ad}}_k :\ker ^{\mathtt {h}}(p)_{|c}&\longrightarrow \ker ^{\mathtt {h}}(p)_{|c} \\ (h,\varphi )&\longmapsto (k \otimes _{{\mathsf {H}}}h \otimes _{{\mathsf {H}}}k^\vee , \varphi _k) \\ \big ( \zeta :(h_0, \varphi _0) \longrightarrow (h_1, \varphi _1) \big )&\longmapsto 1_k \otimes _{{\mathsf {H}}}\zeta \otimes _{{\mathsf {H}}}1_{k^\vee } \ , \end{aligned}$$

where the morphism $\varphi _k$ is the composition

Given another object $k' \in {{\mathsf {H}}}_{|c}$ such that $p(k) = p(k')$ in ${{\mathsf {G}}}$, the principality condition implies that there exists an object $(b, \beta ) \in \ker ^{\mathtt {h}}(p)$ and an isomorphism $\psi :k' \longrightarrow k \otimes _{{\mathsf {H}}}b$. Since $\ker ^{\mathtt {h}}(p)$ is abelian, this induces an isomorphism

$$\begin{aligned} \alpha _{k,k'} :(1_k \times {\mathrm {ev}}_b \times 1_{k^\vee }) \circ (\psi \times 1_h \times \psi ^\vee ) :{\mathrm {Ad}}_{k'}(h) \longrightarrow {\mathrm {Ad}}_k(h). \end{aligned}$$

By the functoriality of $(\,\varvec{\cdot }\,)^\vee$, any other choice of $(b,\beta )$ and $\psi$ yields the same isomorphism ${\mathrm {Ad}}_{k'}(h) \longrightarrow {\mathrm {Ad}}_k(h)$ in this way. Furthermore, this isomorphism is natural in k and h by the functoriality of $\otimes _{{\mathsf {H}}}$ and $(\,\varvec{\cdot }\,)^\vee$. That is, the pair $({\mathrm {Ad}},\alpha )$ defines an object

$$\begin{aligned} ({\mathrm {Ad}},\alpha )_c \in {\text {holim}}^{{{\mathscr {G}}\mathrm {rpd}}} \underline{2{{\mathscr {G}}\mathrm {rp}}} \big ( {{\mathsf {H}}}_{|c}^{[\bullet ]}, \mathsf {Aut}(\ker ^{\mathtt {h}}(p)_{|c}) \big ) \ , \end{aligned}$$

where ${{\mathsf {H}}}_{|c}^{[\bullet ]} \longrightarrow {{\mathsf {G}}}_{|c}$ denotes the Čech nerve of the functor $p_{|c}$. As we show in the proof of Proposition A.3 in Appendix A, any choice of preimages of the objects $g \in {{\mathsf {G}}}_{|c}$ under $p_{|c}$ now induces a functor ${{\mathsf {G}}}_{|c} \longrightarrow \mathsf {Aut}(\ker ^{\mathtt {h}}(p)_{|c})$ from these data. Moreover, any other choice of such preimages will induce a canonical natural isomorphism of functors. Hence we obtain a well-defined isomorphism class of functors, which we denote by

$$\begin{aligned}{}[{\mathrm {Ad}},\alpha ]_c \in \pi _0 \Big ( \underline{2{{\mathscr {G}}\mathrm {rp}}} \big ( {{\mathsf {G}}}_{|c}, \mathsf {Aut}(\ker ^{\mathtt {h}}(p)_{|c}) \big ) \Big ) \ . \end{aligned}$$

This class allows us to state when a smooth 2-group extension is central. $\square$

Definition 5.22

Let (F, p) be an extension of a smooth 2-group ${{\mathsf {G}}}$ by a smooth 2-group ${{\mathsf {A}}}$. Then (F, p) is central if ${{\mathsf {A}}}$ is abelian, and for every $c \in {{\mathscr {C}}\mathrm{art}}$ the isomorphism class $[{\mathrm {Ad}},\alpha ]_c$ agrees with the isomorphism class of the trivial 2-group morphism ${{\mathsf {G}}}_{|c} \longrightarrow \mathsf {Aut}(\ker ^{\mathtt {h}}(p)_{|c})$.

5.4 Global description of the 2-group extension

We shall now apply the general considerations of Sects. 5.2 and 5.3 to the smooth groupoid ${\mathrm {Sym}}_G({\mathcal {G}})$ constructed in Sect. 5.1.

Theorem 5.23

The functor $\pi :{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow {{\mathscr {C}}\mathrm{art}}$ is a smooth 2-group.

Proof

First we show that ${\mathrm {Sym}}_G({\mathcal {G}})$ carries the structure of a monoid object in ${\mathscr {H}}$. The terminal object $*_{\mathscr {H}}\in {\mathscr {H}}$ is the identity functor $1_{{\mathscr {C}}\mathrm{art}}:{{\mathscr {C}}\mathrm{art}}\longrightarrow {{\mathscr {C}}\mathrm{art}}$. We start by defining the 1-morphism ${{\mathsf {u}}}:*_{\mathscr {H}}\longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$; it is the functor that assigns to every object $c \in {{\mathscr {C}}\mathrm{art}}$ the object $(e_c, {\text {pr}}_M^*1_{\mathcal {G}}) \in {\mathrm {Sym}}_G({\mathcal {G}})$, where $e_c :c \longrightarrow G$ is the constant map at the identity object $e \in G$.

Next we define the 1-morphism

$$\begin{aligned} \otimes :{\mathrm {Sym}}_G({\mathcal {G}}) \times _{{\mathscr {C}}\mathrm{art}}{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}}) \end{aligned}$$

in the following way: consider two arbitrary objects $(f_0,A_0), (f_1,A_1) \in {\mathrm {Sym}}_G({\mathcal {G}})$ in the same fibre of $\pi :{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow {{\mathscr {C}}\mathrm{art}}$, i.e. $f_0,f_1$ are defined over the same object $c \in {{\mathscr {C}}\mathrm{art}}$. We define the map $(1,\varPhi _{f_0})$ as the composition

Observe that

$$\begin{aligned}&{\text {pr}}_M \circ (1,\varPhi _{f_0}) = \varPhi _{f_0} \ , \quad \varPhi _{f_1} \circ (1,\varPhi _{f_0}) = \varPhi _{f_1 \, f_0}\nonumber \\&\qquad \text {and} \qquad (1,\varPhi _{f_1}) \circ (1,\varPhi _{f_0}) = (1, \varPhi _{f_1 \, f_0}) \ , \end{aligned}$$

(5.24)

where the second and third identities use the fact that $\varPhi$ is a group action. Thus we can form the 1-morphism

The solid unlabelled arrows are canonical isomorphisms that stem from the fact that $\mathrm {BGrb}$ is a (pre)sheaf of 2-categories on the category of manifolds ${\mathscr {M}}\mathrm{fd}$ [Wal07b, NS11]. By a slight abuse of notation, we denote the composite morphism by $(1,\varPhi _{f_0})^*A_1 \circ A_0$. Then we set

$$\begin{aligned} (f_1,A_1) \otimes (f_0,A_0) :=\big ( f_1 \, f_0,\, (1,\varPhi _{f_0})^*A_1 \circ A_0 \big ) \ , \end{aligned}$$

(5.25)

and analogously on 2-isomorphisms. The associator and unitors are readily obtained from those in the sheaf of 2-categories $\mathrm {BGrb}$. The coherence conditions in $\mathrm {BGrb}$ imply that ${\mathrm {Sym}}_G({\mathcal {G}})$, endowed with the multiplication and coherence morphisms defined here, is a monoid object in ${\mathscr {H}}$.

Now we show that ${\mathrm {Sym}}_G({\mathcal {G}})$ is in fact a group object in ${\mathscr {H}}$. Set

$$\begin{aligned} (f,A)^{-1} :=\big ( f^{-1},\, (1, \varPhi _{f^{-1}})^* A^{-1} \big ) \end{aligned}$$

(5.26)

and analogously on morphisms, where $f^{-1}$ denotes the composition of the map $f :c \longrightarrow G$ with the inversion map in the group G. It follows from the properties (5.24) of $\varPhi _{(\,\varvec{\cdot }\,)}$ that this provides a functorial (two-sided) inverse object with respect to the 1-morphism $\otimes$, and hence shows that the morphism

$$\begin{aligned} (\otimes ,{\text {pr}}_1) :{\mathrm {Sym}}_G({\mathcal {G}}) \times _{{\mathscr {C}}\mathrm{art}}{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}}) \times _{{\mathscr {C}}\mathrm{art}}{\mathrm {Sym}}_G({\mathcal {G}}) \end{aligned}$$

is an equivalence in ${\mathscr {H}}$ (where the product is taken in ${\mathscr {H}}$). Thus ${\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow {{\mathscr {C}}\mathrm{art}}$ is indeed a group object in ${\mathscr {H}}$. $\square$

Theorem 5.27

There is a smooth 2-group extension

where we abbreviate $*_{\mathscr {H}}={{\mathscr {C}}\mathrm{art}}$ by 1.

Proof

The projection functor ${\text {pr}}:\underline{G} \longrightarrow {{\mathscr {C}}\mathrm{art}}$ is a smooth 2-group via $\otimes _G :\underline{G} \times _{{\mathscr {C}}\mathrm{art}}\underline{G} \longrightarrow \underline{G}$ defined by

$$\begin{aligned} (f_1 :c \longrightarrow G) \otimes _G (f_0 :c \longrightarrow G) = (f_1 \, f_0 :c \longrightarrow G) \ . \end{aligned}$$

It is evident from (5.25) that $p :{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}$ is a morphism of smooth 2-groups. It is a Grothendieck fibration in groupoids by construction, and it is surjective on objects since G is connected (as we have argued at the beginning of this section).

Next we define the morphism $\iota :\mathrm {HLBdl}^M \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$ in ${\mathscr {H}}$. Over a Cartesian space $c\in {{\mathscr {C}}\mathrm{art}}$, it is simply the canonical inclusion

$$\begin{aligned} \mathrm {HLBdl}(c \times M)&\longrightarrow \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, \varPhi _{e_c}^*{\mathcal {G}}) = \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, {\text {pr}}_M^*{\mathcal {G}}) \ . \end{aligned}$$

Here $e_c :c \longrightarrow G$ is the constant map at the unit element of G. Since the inclusion of line bundles into morphisms of bundle gerbes strictly maps the tensor product to the composition [Wal07b, Bun17], we readily find that $\iota$ is a morphism of smooth 2-groups.

To see that (5.28) is an extension of smooth 2-groups, we first show that the inclusion $\iota$ is an equivalence $\mathrm {HLBdl}^M \longrightarrow \ker ^{\mathtt {h}}(p)$. By Lemma A.2 from Appendix A and the fact that $p :{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}$ is a Grothendieck fibration in groupoids, it follows that the canonical inclusion $\ker (p) \hookrightarrow \ker ^{\mathtt {h}}(p)$ is an equivalence. Consequently, it suffices to show that $\iota$ induces an equivalence $\mathrm {HLBdl}^M \longrightarrow \ker (p)$. Over an object $c \in {{\mathscr {C}}\mathrm{art}}$, the fibre of $\ker (p)$ consists of the automorphism groupoid of ${\text {pr}}_M^* {\mathcal {G}}\in \mathrm {BGrb}(c \times M)$. It is well-known [Wal07b] that the inclusion $\mathrm {HLBdl}(c \times M) \longrightarrow \mathrm {BGrb}(c \times M)$ given by $L \longmapsto L \otimes 1_{{\text {pr}}_M^*{\mathcal {G}}}$ is an equivalence of groupoids.

To see that the functor $p :{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}$ is an $\mathrm {HLBdl}^M$-principal 2-bundle (see Definition 5.17), it now suffices to show that the functor

$$\begin{aligned} (1, \alpha ) :{\mathrm {Sym}}_G({\mathcal {G}}) \times _{{\mathscr {C}}\mathrm{art}}\mathrm {HLBdl}^M&\longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})\times _{\underline{G}} {\mathrm {Sym}}_G({\mathcal {G}})\\ \big ( (f,A), L \big )&\longmapsto \big ( (f,A), (f, A \otimes L) \big ) \end{aligned}$$

is an equivalence in ${\mathscr {H}}$, where we have written out the product in ${\mathscr {H}}$ as the fibre product over ${{\mathscr {C}}\mathrm{art}}$. Observe that by the equivalence $\mathrm {HLBdl}^M \longrightarrow \ker ^{\mathtt {h}}(p)$, it is enough to consider the action of $\mathrm {HLBdl}^M$, and since $\underline{G}$ has discrete fibres, i.e. the fibres have no non-identity morphisms, there is an identity ${\mathrm {Sym}}_G({\mathcal {G}})\times _{\underline{G}}^{\mathtt {h}} {\mathrm {Sym}}_G({\mathcal {G}}) = {\mathrm {Sym}}_G({\mathcal {G}})\times _{\underline{G}} {\mathrm {Sym}}_G({\mathcal {G}})$, and hence we can work with the strict pullback instead of the homotopy pullback.

Since both sides are fibred over ${{\mathscr {C}}\mathrm{art}}$, it suffices to show that this functor is an equivalence on all fibres [Vis05, Proposition 3.36]. Thus we fix an object $c \in {{\mathscr {C}}\mathrm{art}}$. We need to check that the functor

$$\begin{aligned} (1, \alpha )_{|c} :{\mathrm {Sym}}_G({\mathcal {G}})_{|c} \times \mathrm {HLBdl}(c \times M)&\longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})_{|c} \times _{\underline{G}_{\,|c}} {\mathrm {Sym}}_G({\mathcal {G}})_{|c} \nonumber \\ \big ( (f,A), L \big )&\longmapsto \big ( (f,A), (f, A \otimes L) \big ) \end{aligned}$$

is an equivalence. By construction, both sides decompose into coproducts

$$\begin{aligned}&{\mathrm {Sym}}_G({\mathcal {G}})_{|c} \times \mathrm {HLBdl}(c \times M) \\&\quad = \coprod _{f :c \longrightarrow G}\, \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, \varPhi _f^*{\mathcal {G}}) \times \mathrm {HLBdl}(c \times M) \end{aligned}$$

and

$$\begin{aligned}&{\mathrm {Sym}}_G({\mathcal {G}})_{|c} \times _{\underline{G}_{\,|c}} {\mathrm {Sym}}_G({\mathcal {G}})_{|c} \\&\quad = \coprod _{f :c \longrightarrow G}\, \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, \varPhi _f^*{\mathcal {G}}) \times \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, \varPhi _f^*{\mathcal {G}}) \ , \end{aligned}$$

so the functor $(1, \alpha )_{|c}$ decomposes into functors

$$\begin{aligned} (1, \alpha )_{|f} :\mathrm {BGrb}(c \times M)&({\text {pr}}_M^*{\mathcal {G}}, \varPhi _f^*{\mathcal {G}}) \times \mathrm {HLBdl}(c \times M) \\&\longrightarrow \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, \varPhi _f^*{\mathcal {G}}) \times \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, \varPhi _f^*{\mathcal {G}}) \ . \end{aligned}$$

This functor acts as the identity on the first factor and as the standard action of line bundles on isomorphisms of bundle gerbes in the second factor. Thus $(1, \alpha )_{|f}$ is an equivalence since on any manifold X, the category of 1-isomorphisms between any given bundle gerbes is a torsor category over $\mathrm {HLBdl}(X)$ with respect to this action [Wal07b]. $\square$

Proposition 5.29

If G acts non-trivially on M, then the extension (5.28) is not central.

Proof

This follows readily from the explicit forms (5.25) and (5.26) of the product and the inverse in ${\mathrm {Sym}}_G({\mathcal {G}})$, together with the fact that composition of morphisms of bundle gerbes is compatible with tensoring by line bundles. Explicitly, given $(f,A) \in {\mathrm {Sym}}_G({\mathcal {G}})_{|c}$ and $L \in \mathrm {HLBdl}(c\times M)$ we find

$$\begin{aligned} (f,A) \otimes \iota (L) \otimes (f,A)^{-1} \cong (e_c, \varPhi _f^*L) = \iota (\varPhi _f^*L) \ . \end{aligned}$$

Hence $({\mathrm {Ad}}, \alpha )_c(f)(L) \cong \varPhi _f^* L$. Observe that since $\underline{G}$ has discrete fibres, we have $\ker ^{\mathtt {h}}(p) = \ker (p)$, and by the equivalence $\mathrm {HLBdl}^M \longrightarrow \ker (p)$ it is sufficient to consider the adjoint action on the smooth 2-group $\mathrm {HLBdl}^M$ here.

Let $c = *$, so that the data f corresponds to an element $g \in G$. Assume that the extension (5.28) is central. Then, by Construction 5.21 and Definition 5.22, there is an isomorphism $\varphi :({\mathrm {Ad}}, \alpha )_{*} \longrightarrow 1_{\mathrm {HLBdl}(M)}$ of morphisms of 2-groups $G \longrightarrow \mathsf {Aut}(\mathrm {HLBdl}(M))$. Let $I \in \mathrm {HLBdl}(M)$ denote the trivial line bundle, and let $\psi :I \longrightarrow I$ be any automorphism, i.e. any ${{\text {U}}}(1)$-valued function on M. The naturality of $\varphi$ then implies, in particular, that the diagram

commutes. But this is equivalent to the identity $\psi = g^*\psi$ for any $g \in G$ and $\psi :M \longrightarrow {{\text {U}}}(1)$, which is a contradiction if the G-action on M is non-trivial. $\square$

We now obtain an action of ${\mathrm {Sym}}_G({\mathcal {G}})$ on ${\mathcal {G}}$ in the following sense: let ${\widehat{{\mathcal {G}}}} \in {\mathscr {H}}$ denote the category fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$ which is defined as follows. Consider the presheaf of groupoids on $\underline{M}$ that assigns to $f :c \longrightarrow M$ the category $\mathrm {BGrb}(c)({\mathcal {I}}, f^*{\mathcal {G}})$. Then $q:{\widehat{{\mathcal {G}}}}\longrightarrow \underline{M}$ is obtained by applying the Grothendieck construction to this presheaf. The action of ${\mathrm {Sym}}_G({\mathcal {G}})$ on ${\mathcal {G}}$ is then the morphism of categories over $\underline{G \times M} \cong \underline{G} \times \underline{M}$ obtained through the diagram

where we suppress pullbacks and denote by ${\text {pr}}_M , \varPhi :\underline{G} \times \underline{M} \longrightarrow \underline{M}$ the functors induced from the smooth maps ${\text {pr}}_M, \varPhi$ via postcomposition. The functor ${\widehat{\varPhi }}$ sends an object $({{\mathcal {A}}},{\mathcal {J}}) \in {\mathrm {Sym}}_G({\mathcal {G}})_{|c} \times {\widehat{{\mathcal {G}}}}_{|f}$ to the composition ${\varDelta }^*(1_c \times f)^*(\AA , {\mathcal {J}})$, where ${\varDelta } :c \longrightarrow c \times c$ is the diagonal map.

The construction ${\mathrm {Sym}}_G$ is 2-functorial: let $E :{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ be a 1-isomorphism of bundle gerbes. Pick an adjoint inverse $E^{\vee }$. The 1-isomorphism E induces a 1-isomorphism of smooth 2-groups

$$\begin{aligned} {\widehat{E}} :{\mathrm {Sym}}_G({\mathcal {G}})&\longrightarrow {\mathrm {Sym}}_G({\mathcal {G}}') \\ \big (f:c \longrightarrow G ,A :{\text {pr}}_M^*{\mathcal {G}}\longrightarrow \varPhi _f^*{\mathcal {G}}\big )&\longmapsto \Big (f, {\text {pr}}_M^*\mathcal {G'} \xrightarrow {{\text {pr}}_M^*E^{\vee }}{\text {pr}}_M^*{\mathcal {G}}\overset{A}{\longrightarrow } \varPhi _f^* {\mathcal {G}} \xrightarrow {\varPhi _f^* E} \varPhi _f^* {\mathcal {G}}'\Big ) \ . \end{aligned}$$

Let $E, E' :{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ be 1-isomorphisms and $\eta :E \longrightarrow E'$ a 2-isomorphism. We construct a smooth 2-isomorphism ${\widehat{\eta }}:{\widehat{E}} \longrightarrow \widehat{E'}$ whose component at an object (f, A) of ${\mathrm {Sym}}_G({\mathcal {G}})$ is given by

5.5 Descent description of the 2-group extension

We can describe the smooth 2-group ${\mathrm {Sym}}_G({\mathcal {G}})$ in a way analogously to Sect. 3.3; that is, we can construct ${\mathrm {Sym}}_G({\mathcal {G}})$ in terms of descent data for the path fibration $P_0 G \longrightarrow G$ and the parallel transport on ${\mathcal {G}}$ introduced in Sect. 4. However, for a bundle gerbe ${\mathcal {G}}$ this construction is more involved compared to the case of a principal bundle P. In particular, we need to replace the associated bundle construction $(P_0 G \times {\mathrm {Gau}}(P))/{\sim }$ of ${\mathcal {L}}_G$ (cf. Section 3.3) by a homotopy-coherent version. Once established, the descent presentation of ${\mathrm {Sym}}_G({\mathcal {G}})$ allows us to study and compute this smooth 2-group very explicitly in certain situations, as we demonstrate in Sect. 6.

Recalling the notation of Sect. 3.3, let ${\mathcal {G}}\in \mathrm {BGrb}^\nabla (M)$ be a bundle gerbe with connection on M. Using the smooth map (3.8) we obtain a diffeological hermitean line bundle

$$\begin{aligned} {{\mathsf {L}}}^\dashv :=(L\varPhi )^*({\mathcal {T}}{\mathcal {G}}) \longrightarrow (P_0 G)^{[2]} \times M \ . \end{aligned}$$

(5.30)

This object is completely analogous to (3.8) when one views the holonomy of a line bundle L on M as the transgression of L to the loop space LM, and subsequently the transgression line bundle ${\mathcal {T}}{\mathcal {G}}$ as the holonomy of the bundle gerbe ${\mathcal {G}}$ on M (cf. Section 4.4). In the adjoint picture, we can interpret ${{\mathsf {L}}}^\dashv$ as a smooth assignment of a line bundle with connection ${{\mathsf {L}}}_{(\gamma ,\alpha )}$ on M to each pair of based paths $(\gamma , \alpha ) \in (P_0G)^{[2]}$.

Consider the simplicial diffeological space $(P_0 G)^{[\bullet ]} \times M$ with face maps

$$\begin{aligned} d_i:(P_0 G)^{[n]} \times M\longrightarrow (P_0 G)^{[n-1]} \times M \end{aligned}$$

for $0\le i\le n-1$ defined by deleting the ith entry of $(P_0G)^{[n]}$. The fusion product $\lambda$ on the transgression line bundle ${\mathcal {T}}{\mathcal {G}}$ over the loop space LM induces an isomorphism

$$\begin{aligned} (L\varPhi )^*\lambda :d_0^*{{\mathsf {L}}}^\dashv \otimes d_2^*{{\mathsf {L}}}^\dashv \longrightarrow d_1^*{{\mathsf {L}}}^\dashv \end{aligned}$$

(5.31)

of hermitean line bundles over $(P_0 G)^{[3]} \times M$, which is coherent over $(P_0 G)^{[4]} \times M$.

Remark 5.32

In an adjoint fashion, the hermitean line bundle ${{\mathsf {L}}}^\dashv$ on $(P_0 G)^{[2]} \times M$ from (5.30) can be seen as a morphism of smooth groupoids ${{\mathsf {L}}}:(P_0 G)^{[2]} \longrightarrow \mathrm {HLBdl}^M$ (under the equivalence of diffeological vector bundles and morphisms to $\mathrm {HLBdl}$ following from [Bun20a, Thm. 4.8]). In this picture, the coherent isomorphism $(L\varPhi )^*\lambda$ from (5.31) corresponds to a coherent isomorphism $d_0^* {{\mathsf {L}}}\otimes d_2^* {{\mathsf {L}}}\longrightarrow d_1^*{{\mathsf {L}}}$ of morphisms $(P_0 G)^{[3]} \longrightarrow \mathrm {HLBdl}^M$. In this sense, $({{\mathsf {L}}}^\dashv , (L\varPhi )^*\lambda )$ represent a smooth $\mathrm {HLBdl}^M$-valued Čech 1-cocycle on G with respect to the Čech nerve of the subduction $P_0 G \longrightarrow G$. Note that this nicely fits the formalism for higher principal bundles with not-necessarily strict structure groups—such as $\mathrm {HLBdl}^M$—from [NSS15]. $\square$

Definition 5.33

Let $c\in {{\mathscr {C}}\mathrm{art}}$ be a Cartesian space and $f :c \longrightarrow G$ a smooth map. We define a category ${\mathfrak {Des}}^{\mathtt {PSh}}_{{\mathsf {L}}}(f)$ with

• $\underline{\mathrm{Objects:}}$ pairs $(J, \jmath )$, where $J \in \mathrm {HLBdl}(f^*P_0 G \times M)$ and where $\jmath$ is an isomorphism of hermitean line bundles

  $$\begin{aligned} \jmath :d_1^*J \longrightarrow \big ({\widehat{f}}^{\,[2]} \times 1\big )^*{{\mathsf {L}}}^\dashv \otimes d_0^*J \end{aligned}$$

  over $(f^*P_0G)^{[2]}\times M$, where ${\widehat{f}}^{\,[n]} :(f^*P_0 G)^{[n]} \longrightarrow P_0 G^{[n]}$ is the canonical map induced by the pullback of the subduction $P_0 G \longrightarrow G$ along f. These data are required to satisfy the compatibility condition that

  

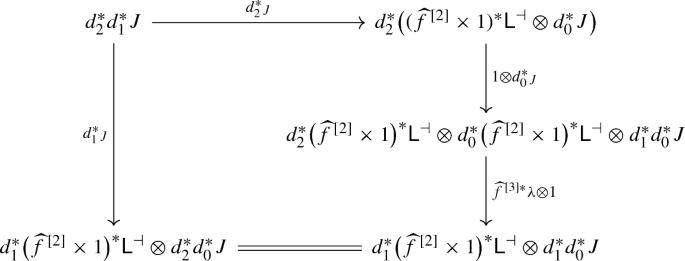
  is a commutative diagram in $\mathrm {HLBdl}((f^*P_0 G)^{[3]} \times M)$, where we use the simplicial relations.

• $\underline{\mathrm{Morphisms:}}$ a morphism $(J,\jmath ) \longrightarrow (J',\jmath ')$ is an isomorphism $\psi :J \longrightarrow J'$ such that

  

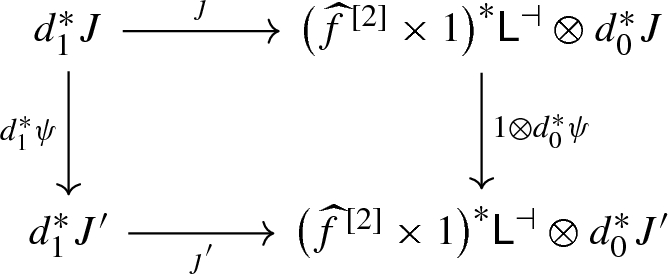
  is a commutative diagram in $\mathrm {HLBdl}((f^*P_0 G)^{[2]} \times M)$.

Pullbacks of morphisms of bundle gerbes turns the assignment $(f :c \longrightarrow G) \longmapsto {\mathfrak {Des}}^{\mathtt {PSh}}_{{\mathsf {L}}}(f)$ into a presheaf of groupoids on $\underline{G}\,$. (This is actually even a sheaf of groupoids, but we will not need this fact here.) Applying the Grothendieck construction, we obtain a category fibred in groupoids over $\underline{G}\,$, $p_{{\mathsf {L}}}:{\mathfrak {Des}}_{{\mathsf {L}}}\longrightarrow \underline{G}\,$, and composing with the canonical projection functor ${\text {pr}}:\underline{G} \longrightarrow {{\mathscr {C}}\mathrm{art}}$ we obtain a category fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$

which defines a smooth groupoid ${\mathfrak {Des}}_{{\mathsf {L}}}$.

Proposition 5.35

The functor $\pi _{{\mathsf {L}}}:{\mathfrak {Des}}_{{\mathsf {L}}}\longrightarrow {{\mathscr {C}}\mathrm{art}}$ is a smooth 2-group.

Proof

Let $(f_0,J_0,\jmath _0), (f_1,J_1,\jmath _1) \in {\mathfrak {Des}}_{{\mathsf {L}}}$ be two objects, where $(J_i,\jmath _i)$ lies in the fibre over a smooth map $f_i :c \longrightarrow G$ for $i = 0,1$. The product $(f_1,J_1,\jmath _1) \otimes (f_0,J_0,\jmath _0)$ is defined as follows. First, observe that it should lie in the fibre of ${\mathfrak {Des}}_{{\mathsf {L}}}$ over the pointwise product map $f_1 \, f_0 :c \longrightarrow G$, $u \longmapsto f_1(u) \, f_0(u)$. Consider the smooth map

$$\begin{aligned} F :m^*P_0G \times _{G\times G} {\text {pr}}_1^*P_0G \times _{G\times G} {\text {pr}}_2^*P_0G&\longrightarrow P_{\partial \Delta ^2} G \\ (\gamma _{10},\gamma _1,\gamma _0)&\longmapsto F(\gamma _{10},\gamma _1,\gamma _0) = \big ( \gamma _{10}, \gamma _1 \, \gamma _0(1),\, \gamma _0 \big ) \ , \end{aligned}$$

where $m :G\times G\longrightarrow G$ is the multiplication of G, and ${\text {pr}}_1$ and ${\text {pr}}_2$ are the projections to the first and second factors of $G\times G$. Let us denote by $\varPhi _{{\mathrm {ev}}_1}$ the composition $P_0G \times M \longrightarrow G \times M \longrightarrow M$, where the first map evaluates a based path at its end point and the second map is the action $\varPhi$ of G on M. The pair $(f_1,f_0)$ defines a map $c \longrightarrow G\times G$. Let ${{\mathsf {s}}}:P_{\partial \Delta ^2}G \longrightarrow LG$ be the map defined in (4.10), and let (by a slight abuse of notation) $L\varPhi :LG \times M \longrightarrow LM$ denote the map $(\gamma , x) \longmapsto \gamma _x$, with $\gamma _x(t) = \varPhi _{\gamma (t)}(x)$. Consider the hermitean line bundle

$$\begin{aligned} K :=F^*{{\mathsf {s}}}^*L\varPhi ^*{\mathcal {T}}{\mathcal {G}}\otimes (1_{P_0 G} \times \varPhi _{{\mathrm {ev}}_1})^*J_1 \otimes J_0 \end{aligned}$$

on the diffeological space

$$\begin{aligned} Y_{f_1,f_0} :=\big ((f_1 \, f_0)^*P_0G \times _c f_1^*P_0G \times _c f_0^*P_0G\big ) \times M \ . \end{aligned}$$

We claim that the bundle K descends along the projection $p_1 :Y_{f_1,f_0} \longrightarrow (f_1 \, f_0)^*P_0G \times M$. The descended bundle is the hermitean line bundle underlying the product $(f_1,J_1,\jmath _1) \otimes (f_0,J_0, \jmath _0)$.

We thus endow the bundle K with an isomorphism $\kappa :(p_1)_0^*K \longrightarrow (p_1)_1^*K$ over $Y_{f_1,f_0}^{[2]}$, which is required to satisfy a cocycle relation over $Y_{f_1,f_0}^{[3]}$. An element of $Y_{f_1,f_0}^{[2]}$ can be identified with a pair of triples $((\gamma _{10},\gamma _1,\gamma _0), (\gamma _{10}, \gamma '_1, \gamma '_0))$, where $(\gamma _i, \gamma '_i) \in (P_0G)^{[2]}$ for $i = 0,1$. We define the isomorphism $\kappa$ as the composition of the fusion product $\lambda$ on ${\mathcal {T}}{\mathcal {G}}$ with $(1 \times \varPhi _{{\mathrm {ev}}_1})^*\jmath _1 \otimes \jmath _0$. Then the cocycle condition simply follows from the compatibility condition (5.34) and the associativity of the fusion product. (We also need to use thin reparameterisations, but these are implemented in a completely coherent way by the thin-homotopy invariant connection on ${\mathcal {T}}{\mathcal {G}}$.)

Thus we obtain a descended hermitean line bundle ${\mathfrak {Des}}(K,\kappa )$ on $(f_1 \, f_0)^*P_0G \times M$ (for descent properties of diffeological vector bundles, see [Bun20a]). Applying the fusion product in the first tensor factor of K, we obtain an isomorphism which (by the associativity of $\lambda$) descends to an isomorphism

$$\begin{aligned} \jmath _K :d_1^*{\mathfrak {Des}}(K,\kappa ) \longrightarrow \big (\,\widehat{f_1 \, f_0}{}^{[2]} \times 1 \big )^*{{\mathsf {L}}}^\dashv \otimes d_0^*{\mathfrak {Des}}(K,\kappa ) \end{aligned}$$

over $((f_1 \, f_0)^*P_0G)^{[2]} \times M$. Again by the associativity of $\lambda$ and thin-homotopy invariance, the pair $({\mathfrak {Des}}(K,\kappa ),\jmath _K)$ satisfies the relation (5.34), and hence it makes sense to set

$$\begin{aligned} (f_1,J_1,\jmath _1) \otimes (f_0,J_0,\jmath _0) :=\big (f_1\,f_0, {\mathfrak {Des}}(K,\kappa ),\jmath _K \big ) \ . \end{aligned}$$

The action of the product $\otimes$ in ${\mathfrak {Des}}_{{\mathsf {L}}}$ on morphisms simply sends $(\psi _1,\psi _0)$ to the descent along $p_1$ of the isomorphism $1_{{\mathcal {T}}{\mathcal {G}}} \otimes (1 \times \varPhi _{{\mathrm {ev}}_1})^*\psi _1 \otimes \psi _0$. The unitors of $\otimes$ are readily obtained from the construction, and the associator is defined from the fusion product; its coherence is yet another application of the associativity of $\lambda$ and the superficiality of the parallel transport on ${\mathcal {T}}{\mathcal {G}}$. Inverses are constructed analogously to (5.26). Finally, all constructions are compatible with pullbacks along maps $\varphi :c' \longrightarrow c$ of Cartesian spaces, so that we obtain the structure of a smooth 2-group on ${\mathfrak {Des}}_{{\mathsf {L}}}$. $\square$

Theorem 5.36

There is a weakly commutative diagram of smooth 2-groups

where the functor $\varPsi$ is an equivalence.

Proof

By the functoriality of ${\mathcal {G}}\longmapsto {\mathrm {Sym}}_G({\mathcal {G}})$ (see Sect. 5.4) we can assume that we are in the case where ${\mathcal {G}}' = {\mathcal {R}}{\mathcal {T}}({\mathcal {G}})$ is the regression of a transgression, so that we have direct access to our construction of a parallel transport on ${\mathcal {G}}'$ from Sect. 4.4. We start by constructing the functor $\varPsi$. For this, we construct a diagram in the 2-category ${\mathscr {H}}$ of the form

and the functor $\varPsi$ is the composition from left to right. Each of the functors in (5.38) is an equivalence of categories fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$, and hence so is $\varPsi$.

For a smooth map $f :c \longrightarrow G$, let $\varpi _f :f^*P_0 G \times M \longrightarrow c \times M$ denote the canonical projection. First we define the category ${\mathfrak {Des}}({\mathrm {Sym}}_G({\mathcal {G}}'))$. It is obtained via the Grothendieck construction applied to the presheaf ${\mathfrak {Des}}^{\mathtt {PSh}}({\mathrm {Sym}}_G({\mathcal {G}}'))$ of groupoids on $\underline{G}\,$, which assigns to a smooth map $f :c \longrightarrow G$ the groupoid ${\mathfrak {Des}}^{\mathtt {PSh}}({\mathrm {Sym}}_G({\mathcal {G}}'))(f)$ where

• objects are pairs $(A,\alpha )$ of a 1-isomorphism $A:\varpi _f^*{\mathcal {G}}' \longrightarrow \varpi _f^*\varPhi _f^*{\mathcal {G}}'$ over $f^*P_0G \times M$ and a 2-isomorphism $\alpha :d_1^*A\longrightarrow d_0^*A$ over $(f^*P_0 G)^{[2]} \times M$, which is coherent over $(f^*P_0 G)^{[3]} \times M$, and

• morphisms $(A, \alpha ) \longrightarrow (A', \alpha ')$ are given by 2-isomorphisms $\psi :A \longrightarrow A'$ satisfying $\alpha ' \circ d_1^*\psi = d_0^*\psi \circ \alpha$.

The functor $\varpi ^*$ simply pulls back 1-morphisms $A :{\text {pr}}_M^*{\mathcal {G}}' \longrightarrow \varPhi _f^*{\mathcal {G}}'$ along the subductions $\varpi _f$. This functor is an equivalence since morphisms of bundle gerbes satisfy descent³ [Bun17, Theorem A.19].

Next we introduce some notation: we define the map

$$\begin{aligned} P_0 \varPhi :P_0 G \times M&\longrightarrow PM \\ (\gamma ,x)&\longmapsto \gamma _x \ , \end{aligned}$$

where

$$\begin{aligned} \gamma _x(t) = \varPhi _{\gamma (t)}(x) =: P_0 \varPhi (\gamma ,x)(t) \end{aligned}$$

for all $t\in [0,1]$. Observe that

$$\begin{aligned} {\mathrm {ev}}_0 \circ P_0 \varPhi = {\text {pr}}_M \qquad \text{ and } \qquad {\mathrm {ev}}_1 \circ P_0 \varPhi = \varPhi \circ ({\mathrm {ev}}_1 \times 1_M) \ . \end{aligned}$$

Thus the pullback of the parallel transport 1-isomorphism (4.9) by the map $P_0\varPhi$ is a morphism

$$\begin{aligned} (P_0 \varPhi )^* {\mathtt {pt}}^{{\mathcal {G}}'}_1 :{\text {pr}}_M^*{\mathcal {G}}' \longrightarrow ({\mathrm {ev}}_1 \times 1_M)^* \varPhi ^*{\mathcal {G}}' \end{aligned}$$

in $\mathrm {BGrb}(P_0G\times M)$. Given a smooth map $f :c \longrightarrow G$, we obtain a smooth map

$$\begin{aligned} P_0 \varPhi \circ \big ({\widehat{f}} \times 1_M\big ) :f^*P_0 G \times M \longrightarrow PM \ . \end{aligned}$$

It satisfies

$$\begin{aligned} {\mathrm {ev}}_0 \circ P_0 \varPhi \circ \big ({\widehat{f}} \times 1_M\big ) = {\text {pr}}_M \qquad \text{ and } \qquad {\mathrm {ev}}_1 \circ P_0 \varPhi \circ \big ({\widehat{f}} \times 1_M\big ) = \varPhi _f \circ \varpi _f \ , \end{aligned}$$

where $\varpi _f :f^*P_0 G \times M \longrightarrow c \times M$ is the projection. Hence we obtain a morphism

$$\begin{aligned} {\mathtt {pt}}^{{\mathcal {G}}'}_f :=\big ( P_0 \varPhi \circ ({\widehat{f}} \times 1) \big )^* {\mathtt {pt}}^{{\mathcal {G}}'}_1 :\varpi _f^* {\text {pr}}_M^*{\mathcal {G}}' \longrightarrow \varpi _f^* \varPhi _f^*{\mathcal {G}}' \ , \end{aligned}$$

which is defined over $f^*P_0 G \times M$. By Proposition 4.18 there is a canonical 2-isomorphism

$$\begin{aligned} \big (d_0^* {\mathtt {pt}}^{{\mathcal {G}}'}_f\big )^{-1} \circ d_1^* {\mathtt {pt}}^{{\mathcal {G}}'}_f \xrightarrow { \ \cong \ } \big ( L\varPhi \circ (\tau \times 1_M) \circ ({\widehat{f}}^{\,[2]} \times 1_M) \big )^*{\mathcal {T}}{\mathcal {G}}\cong \big ({\widehat{f}}^{\,[2]} \times 1_M)^* {{\mathsf {L}}}^{\dashv \, \vee } \end{aligned}$$

of 1-automorphisms of the pullback of ${\text {pr}}_M^*{\mathcal {G}}'$ to $(f^*P_0 G)^{[2]} \times M$, where $\tau (\gamma _0, \gamma _1) = (\gamma _1, \gamma _0)$. Equivalently, this is a 2-isomorphism

$$\begin{aligned} \beta _f :d_0^* {\mathtt {pt}}^{{\mathcal {G}}'}_f \xrightarrow { \ \cong \ } \big ({\widehat{f}}^{\,[2]} \times 1_M\big )^* {{\mathsf {L}}}^\dashv \otimes d_1^* {\mathtt {pt}}^{{\mathcal {G}}'}_f \end{aligned}$$

(5.39)

of 1-isomorphisms $\varpi _f^* {\text {pr}}_M^* {\mathcal {G}}' \longrightarrow \varpi _f^*\varPhi _f^*{\mathcal {G}}'$ over $(f^*P_0 G)^{[2]} \times M$.

Now we come to the definition of the functor $(\,\varvec{\cdot }\,) \otimes {\mathtt {pt}}_1^{{\mathcal {G}}'}$. Given an object $(f,J,\jmath ) \in {\mathfrak {Des}}_{{\mathsf {L}}}$, define a morphism of bundle gerbes over $f^*P_0 G \times M$ via

$$\begin{aligned} J \otimes {\mathtt {pt}}^{{\mathcal {G}}'}_f :\varpi _f^* {\text {pr}}_M^*{\mathcal {G}}' \longrightarrow \varpi _f^* \varPhi _f^*{\mathcal {G}}' \ . \end{aligned}$$

Using the 2-isomorphism (5.39), we obtain a 2-isomorphism

over $(f^*P_0 G) ^{[2]} \times M$. By construction, the 2-isomorphism ${\widehat{\jmath }}\,$ is coherent over $(f^*P_0 G)^{[3]} \times M$, and thus the pair $(J \otimes {\mathtt {pt}}^{{\mathcal {G}}'}_f, {\widehat{\jmath }}\,)$ defines a descent datum (with respect to the subduction $f^*P_0 G \times M \longrightarrow c \times M$) for a 1-isomorphism of bundle gerbes ${\text {pr}}_M^* {\mathcal {G}}' \longrightarrow \varPhi _f^*{\mathcal {G}}'$. Analogously, morphisms in ${\mathfrak {Des}}_{{\mathsf {L}}}$ give rise to morphisms of descent data as constructed above. This defines the functor

$$\begin{aligned} (\,\varvec{\cdot }\,) \otimes {\mathtt {pt}}^{{\mathcal {G}}'}_1 :{\mathfrak {Des}}_{{\mathsf {L}}}\longrightarrow {\mathfrak {Des}}\big ( {\mathrm {Sym}}_G({\mathcal {G}}') \big ) \ . \end{aligned}$$

This is a functor of categories fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$ by the compatibility of pullbacks of bundles and their morphisms with the tensor product.

Finally, we introduce an inverse functor $\mathsf {Hom}_1\big ({\mathtt {pt}}^{{\mathcal {G}}'}_1,\,\varvec{\cdot }\,\big )$ for $(\,\varvec{\cdot }\,) \otimes {\mathtt {pt}}^{{\mathcal {G}}'}_1$. An object $(f, A, \alpha ) \in {\mathfrak {Des}}({\mathrm {Sym}}_G({\mathcal {G}}'))$ consists, in particular, of a 1-isomorphism $A :\varpi _f^* {\text {pr}}_M^*{\mathcal {G}}' \longrightarrow \varpi _f^* \varPhi _f^* {\mathcal {G}}'$ of bundle gerbes over $f^*P_0 G \times M$. Another such morphism is given by ${\mathtt {pt}}^{{\mathcal {G}}'}_f$. We can hence use the internal hom-functor $\mathsf {Hom}_1$ in the 2-category $\mathrm {BGrb}(f^*P_0G \times M)$ (see [Bun17, Section 3.2] and also [BW18, Section 2.1]) to produce a hermitean line bundle

$$\begin{aligned} \mathsf {Hom}_1\big ({\mathtt {pt}}^{{\mathcal {G}}'}_f, A\big ) \in \mathrm {HLBdl}(f^*P_0 G \times M) \ . \end{aligned}$$

This comes with an isomorphism over $(f^*P_0 G)^{[2]} \times M$ defined by the diagram

where the 2-isomorphism $\beta _f$ stems from (5.39) and where the lower horizontal isomorphism of line bundles stems from the (categorified) linearity of $\mathsf {Hom}_1$ [Bun17, Theorem 3.63]. It follows from the properties of $\alpha$ and $\beta _f$ that $\mathsf {Hom}_1\big ({\mathtt {pt}}^{{\mathcal {G}}'}_f, A\big )$ defines an object in $({\mathfrak {Des}}_{{\mathsf {L}}})_{|f}$. By mapping a morphism $\psi$ in ${\mathfrak {Des}}\big ({\mathrm {Sym}}_G({\mathcal {G}}')\big )_{|f}$ to $\mathsf {Hom}_1\big ({\mathtt {pt}}^{{\mathcal {G}}'}_f, \psi \big )$, we obtain a functor

$$\begin{aligned} \mathsf {Hom}_1\big ({\mathtt {pt}}_1^{{\mathcal {G}}'}, \,\varvec{\cdot }\, \big ) :{\mathfrak {Des}}\big ( {\mathrm {Sym}}_G({\mathcal {G}}') \big ) \longrightarrow {\mathfrak {Des}}_{{\mathsf {L}}}\end{aligned}$$

of categories fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$. Again by the linearity of $\mathsf {Hom}_1$, it follows straightforwardly that $(\,\varvec{\cdot }\,) \otimes {\mathtt {pt}}^{{\mathcal {G}}'}_1$ and $\mathsf {Hom}_1\big ({\mathtt {pt}}^{{\mathcal {G}}'}_1,\,\varvec{\cdot }\,\big )$ are mutually inverse functors.

To conclude the proof, we need to check that $\varPsi$ is compatible with the monoid structures on ${\mathrm {Sym}}_G({\mathcal {G}}')$ and on ${\mathfrak {Des}}_{{\mathsf {L}}}$. For $i = 0,1$, let $f_i :c \longrightarrow G$ be smooth maps from $c \in {{\mathscr {C}}\mathrm{art}}$ to G, and consider objects $A_i \in {\mathrm {Sym}}_G({\mathcal {G}}')_{|f_i}$ in the fibres over $f_i$. By the explicit construction of the 2-group structure on ${\mathfrak {Des}}_{{\mathsf {L}}}$ in the proof of Proposition 5.35 it follows that the hermitean line bundle underlying the object $\varPsi (f_1,A_1) \otimes \varPsi (f_0,A_0)$ of ${\mathfrak {Des}}_{{\mathsf {L}}}$ is given as the descent of the bundle

$$\begin{aligned}&{{\mathsf {L}}}^\dashv \otimes (1 \times \varPhi _{{\mathrm {ev}}_1})^* \big ( \mathsf {Hom}_1({\mathtt {pt}}^{{\mathcal {G}}'}_{f_1}, \varpi _{f_1}^* A_1) \big ) \otimes \mathsf {Hom}_1({\mathtt {pt}}^{{\mathcal {G}}'}_{f_0}, \varpi _{f_0}^* A_0) \nonumber \\&\quad \cong {{\mathsf {L}}}^\dashv \otimes \mathsf {Hom}_1 \big ( (1 \times \varPhi _{{\mathrm {ev}}_1})^* {\widehat{f}}_1^{\,*} {\mathtt {pt}}^{{\mathcal {G}}'}_1, (1 \times \varPhi _{{\mathrm {ev}}_1})^* \varpi _{f_1}^* A_1 \big ) \otimes \mathsf {Hom}_1({\widehat{f}}_0^{\,*} {\mathtt {pt}}^{{\mathcal {G}}'}_1, \varpi _{f_0}^* A_0) \nonumber \\&\quad \cong {{\mathsf {L}}}^\dashv \otimes \mathsf {Hom}_1 \big ( (1 \times \varPhi _{{\mathrm {ev}}_1})^* {\widehat{f}}_1^{\,*} {\mathtt {pt}}^{{\mathcal {G}}'}_1 \circ {\widehat{f}}_0^{\,*} {\mathtt {pt}}^{{\mathcal {G}}'}_1,\, (1 \times \varPhi _{{\mathrm {ev}}_1})^* \varpi _{f_1}^* A_1 \circ \varpi _{f_0}^* A_0 \big ) \nonumber \\&\quad \cong \mathsf {Hom}_1 \big ( (\widehat{f_1 \, f_0})^* {\mathtt {pt}}^{{\mathcal {G}}'}_1,\, \varpi _{f_1 \, f_0}^* (\varPhi _{f_0}^* A_1 \circ A_0) \big ) \ . \end{aligned}$$

(5.40)

The first and second isomorphisms follow from the properties of the internal hom-functor $\mathsf {Hom}_1$. The third isomorphism is a direct application of Proposition 4.18. The bundle in the last line is the line bundle underlying the object $\varPsi \big ((f_1,A_1) \otimes (f_0,A_0)\big )$ of ${\mathfrak {Des}}_{{\mathsf {L}}}$ (see (5.25)). Hence the canonical isomorphism (5.40) establishes the compatibility of $\varPsi$. Its coherence again follows from the properties of the transgression line bundle ${\mathcal {T}}{\mathcal {G}}$. The proofs that $\varPsi$ respects unitors as well as the weak commutativity of the diagram (5.37) are straightforward. $\square$

5.6 Equivariant bundle gerbes

We shall now investigate the relation between sections of the smooth 2-group extension ${\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}$ and equivariant structures on ${\mathcal {G}}$. We first recall an explicit definition of an equivariant bundle gerbe from [GSW11] (see also [M+17]), which can be understood very nicely from the perspective of the formalism developed in [NS11].

Let G be a connected Lie group, M a manifold with G-action $\varPhi :G\times M \longrightarrow M$, and ${\mathcal {G}}$ a hermitean bundle gerbe over M. Corresponding to the action groupoid $G\times M\rightrightarrows M$ there is a simplicial manifold

with face maps $d_i:G^{\times n}\times M\longrightarrow G^{\times n-1}\times M$ for $0\le i\le n$ given by

$$\begin{aligned} d_i(g_{0},g_1, \ldots , g_{n-1},x)= {\left\{ \begin{array}{ll} \big (g_{0},g_1, \ldots , g_{n-2},\varPhi _{g_{n-1}}(x)\big ) &{} \text {for }i=n \\ (g_{0},g_1, \ldots ,g_{i-1}\, g_{i}, \ldots , g_{n-1},x) &{} \text {for } 0< i < n \\ (g_{1}, \ldots , g_{n-1},x) &{} \text {for } i=0 \end{array}\right. } \ . \end{aligned}$$

On $G\times M$, the face maps $d_0={\text {pr}}_M$ and $d_1=\varPhi$ are the source and target maps of the action groupoid.

Definition 5.41

Let G be a connected Lie group, M a manifold with G-action $\varPhi :G\times M \longrightarrow M$, and ${\mathcal {G}}$ a hermitean bundle gerbe over M. A G-equivariant structure on ${\mathcal {G}}$ consists of a 1-isomorphism $A:{\text {pr}}_M^*{\mathcal {G}}\longrightarrow \varPhi ^*{\mathcal {G}}$ over $G\times M$ and a 2-isomorphism $\chi :d_2^*A \circ d_0^*A \longrightarrow d_1^*A$ over $G^{\times 2}\times M$ such that

$$\begin{aligned} d_2^*\chi \circ \big ( 1_{(d_3 \circ d_2)^*A} \circ d_0^*\chi \big )= d_1^*\chi \circ \big ( 1_{(d_0\circ d_0)^* A} \circ d_3^*\chi \big ) \end{aligned}$$

over $G^{\times 3}\times M$. A morphism $(A,\chi ) \longrightarrow (A',\chi ')$ between equivariant structures on ${\mathcal {G}}$ consists of a 2-isomorphism $\vartheta :A \longrightarrow A'$ such that the diagram

commutes. We denote by ${\mathcal {E}}({\mathcal {G}})$ the groupoid of equivariant structures on ${\mathcal {G}}$.

A splitting of $p :{\mathrm {Sym}}_G({\mathcal {G}})\longrightarrow {\underline{G}}$ is a smooth 2-group homomorphism $s:{\underline{G}} \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$ such that $p\circ s = 1_{{\underline{G}}}$. We assume here for simplicity and without loss of generality that unitors are strictly preserved. We denote by ${\mathcal {S}}(\underline{G}\,;{\mathrm {Sym}}_G({\mathcal {G}}))$ the groupoid of splittings of $p :{\mathrm {Sym}}_G({\mathcal {G}})\longrightarrow {\underline{G}}\,$. Concretely, a splitting consists of

• a 1-isomorphism $s(f) :{\text {pr}}_M^*{\mathcal {G}}\longrightarrow \varPhi _f^*{\mathcal {G}}$ of bundle gerbes on $c\times M$ for every Cartesian space $c\in {{\mathscr {C}}\mathrm{art}}$ and sections $f\in G(c)$,

• a 2-isomorphism $s(\varphi ):s(f)\longrightarrow \varphi ^* s(f')$ for every morphism $\varphi :f \longrightarrow f'$ in ${\underline{G}}$ , and

• a 2-isomorphism $s(f)\otimes s(f') \longrightarrow s(f\, f')$ in ${\mathrm {Sym}}_G({\mathcal {G}})$ for every $f,f'\in G(c)$,

such that $\varphi ^*s(\varphi ') \circ s(\varphi )= s(\varphi ' \circ \varphi )$ and the diagram

commutes. A morphism $\omega :s \longrightarrow s'$ of splittings consists of 2-isomorphisms $\omega (f): s(f)\longrightarrow s'(f)$ in $\mathrm {BGrb}(c\times M)$ for all $f\in G(c)$ such that the diagrams

commute.

In what follows we construct an equivalence

$$\begin{aligned} \Xi :{\mathcal {E}}({\mathcal {G}}) \longrightarrow {\mathcal {S}} \big ( {\underline{G}}\,;{\mathrm {Sym}}_G({\mathcal {G}}) \big ) \end{aligned}$$

of categories. Let $(A,\chi )$ be an equivariant structure on ${\mathcal {G}}$ and $(f:c\longrightarrow G) \in G(c)$. Pulling back A along $\varPhi _f$ gives rise to a 1-isomorphism $\varPhi _f^*A :{\text {pr}}_M^* {\mathcal {G}}\longrightarrow \varPhi _f^* {\mathcal {G}}$ over $c\times M$. We can define the section $\Xi (A,\chi ) :\underline{G} \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$ by $\Xi (A,\chi )(f)= \varPhi _f^*A :{\text {pr}}_M^*{\mathcal {G}}\longrightarrow \varPhi _f^* {\mathcal {G}}$. The 2-isomorphisms $\Xi (A,\chi )(\varphi )$ are induced by general properties of pullbacks and the 2-isomorphism $\chi$ induces the 2-isomorphism encoding the compatibility with multiplication. The action of $\Xi$ on morphisms of equivariant structures is again by pullback along $\varPhi _f$.

Theorem 5.42

The functor $\Xi :{\mathcal {E}}({\mathcal {G}}) \longrightarrow {\mathcal {S}}({\underline{G}}\,;{\mathrm {Sym}}_G({\mathcal {G}}))$ is an equivalence of categories.

Proof

We start by showing that $\Xi$ is essentially surjective. Let $s:\underline{G} \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$ be a splitting. We pick a good open cover $\{c_i\}_{i \in \Lambda }$ of G. This induces good open covers of $G^{\times 2}$ and $G^{\times 3}$ given by $\{c_i\times c_j\}_{i,j \in \Lambda }$ and $\{ c_i \times c_j \times c_k \}_{i,j,k \in \Lambda }$, respectively. Every $c_i$ comes with an embedding $f_i:c_i \longrightarrow G$ and hence can be regarded as an object of ${\underline{G}}\,$. Applying the section $s:{\underline{G}} \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$ to all elements of the open cover provides a collection of compatible 1-isomorphisms

$$\begin{aligned} s(c_i ):=s(f_i:c_i\longrightarrow G) :{\text {pr}}_M^* {\mathcal {G}}\longrightarrow \varPhi _{f_i}^* {\mathcal {G}}\ . \end{aligned}$$

On double intersections $c_{ij}:=c_i \cap c_j$ we get coherent 2-isomorphisms⁴

$$\begin{aligned} s(c_{ij}):s(c_i)_{|c_{ij}}\longrightarrow s(f_i{}_{|c_{ij}})= s(f_j{}_{|c_{ij}}) \longrightarrow s(c_j)_{|c_{ij}} \ , \end{aligned}$$

since ${\mathrm {Sym}}_G({\mathcal {G}})\longrightarrow {{\mathscr {C}}\mathrm{art}}$ is a Grothendieck fibration. Hence the 1-isomorphisms $s(c_i)$ glue together to a 1-isomorphism $A_s :{\text {pr}}_M^* {\mathcal {G}}\longrightarrow \varPhi ^* {\mathcal {G}}$ over $G\times M$.

Let ${\text {pr}}_1,{\text {pr}}_2:G^{\times 2}\longrightarrow G$ be the projections to the first and second factors, and $m:G^{\times 2}\longrightarrow G$ the multiplication in G. From $A_s$ we can construct three 1-morphisms ${\text {pr}}_1^* A_s$, ${\text {pr}}_2^*A_s$, and $m^* A_s$ over $G^{\times 2}\times M$. We would like to show that these 1-morphisms are canonically isomorphic to the 1-morphisms constructed from the good open cover $\{ c_i\times c_j \}_{i,j\in \Lambda }$ by applying s to the morphisms ${\text {pr}}_{1|c_i \times c_j}$, ${\text {pr}}_{2|c_i \times c_j}$, and $m_{|c_i \times c_j}$ on ${c_i \times c_j} \longrightarrow G$, respectively. For this, consider the commutative diagram

which implies that

$$\begin{aligned} {\text {pr}}_{1|c_i\times c_j}^*A_s= {\text {pr}}_{1|c_i\times c_j}^*s(c_i \hookrightarrow G) \xrightarrow { \ \cong \ } s\big (c_i \times c_j \xrightarrow {{\text {pr}}_1} c_i \hookrightarrow G\big ) \ , \end{aligned}$$

where the 2-isomorphism is part of the data of the section s. The same argument shows the claim for ${\text {pr}}_2$. To show the corresponding statement for m we need to pick a refinement $\{ {\widetilde{c}}_a\}_{a \in {\widetilde{\Lambda }}}$ of the cover $\{c_i\times c_j\}_{i,j \in \Lambda }$ such that the diagram

commutes. The cover $\{ {\widetilde{c}}_a\}_{a \in {\widetilde{\Lambda }}}$ can be constructed by choosing a common refinement of the covers $\{c_i \times c_j\}_{i,j\in \Lambda }$ and $\{ m^{-1}(c_i)\}_{i\in \Lambda }$ of $G^{\times 2}$.

The multiplication of $c_i \times c_j \xrightarrow {{\text {pr}}_1} G$ with $c_i \times c_j \xrightarrow {{\text {pr}}_2} G$ in ${\underline{G}}$ is $c_i \times c_j \xrightarrow { \ m \ } G$. The structure of a smooth 2-group homomorphism on s now provides natural 2-isomorphisms

$$\begin{aligned} s\big (c_i \times c_j \xrightarrow { \ {\text {pr}}_1 \ } G\big ) \otimes s\big (c_i \times c_j \xrightarrow { \ {\text {pr}}_2 \ } G\big )\longrightarrow s\big (c_i \times c_j \xrightarrow { \ m \ } G\big ) \end{aligned}$$

(5.43)

which glue together to a 2-isomorphism $\chi _s :\varPhi ^*({\text {pr}}_1^*A_s)\circ ({\text {pr}}_2^* A_s)\longrightarrow m^* A_s$ over $G^{\times 2}\times M$ because (5.43) is a 2-isomorphism of smooth 1-isomorphisms. The coherence condition for $\chi _s$ over $G^{\times 3}\times M$ follows from the observation that the various pullbacks to $G^{\times 3}\times M$ can be constructed by applying s to different functions from $c_i\times c_j \times c_k$ to G and the coherence condition for s. This shows that $\Xi$ is essentially surjective.

We next show that the functor $\Xi$ is faithful: let $\vartheta ,\vartheta ' :(A,\chi ) \longrightarrow (A',\chi ')$ be isomorphisms of equivariant structures on ${\mathcal {G}}$ such that $\Xi (\vartheta ')=\Xi (\vartheta )$, and let $g\in G$. We can take $c={\mathbb {R}}^0$ and $f:c \longrightarrow G$ to be the constant map at g to conclude that $\varphi _{|\{g\}\times M}=\Xi (A,\chi )(\varphi )(f)$ and $\varphi _{|\{g\}\times M}=\Xi (A',\chi ')(\varphi )(f)$ agree. Hence the two isomorphisms agree pointwise and the statement follows.

Finally, we show that the functor $\Xi$ is full: let $(A,\chi )$ and $(A',\chi ')$ be equivariant structures on ${\mathcal {G}}$ and $\omega :\Xi (A,\chi ) \longrightarrow \Xi (A',\chi ')$ a morphism of splittings. Evaluating $\omega$ on the good open cover $\{ c_i\}_{i \in \Lambda }$ from above provides isomorphisms $\omega :A_{|c_i\times M} \longrightarrow A'_{|c_i\times M}$. Since $\omega$ is a morphism of splittings, these morphisms glue together to a 2-isomorphism $\vartheta _\omega :A\longrightarrow A'$. That this is an isomorphism of equivariant structures follows from the coherence conditions for $\omega$ and the observation that it suffices to check the conditions locally. $\square$

Corollary 5.44

A bundle gerbe ${\mathcal {G}}$ on a manifold M admits an equivariant structure if and only if the 2-group extension

$$\begin{aligned} 1\longrightarrow \mathrm {HLBdl}^M \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})\longrightarrow \underline{G}\longrightarrow 1 \end{aligned}$$

admits a splitting.

Definition 5.45

Let $({\mathcal {G}},A,\chi )$ and $({\mathcal {G}}',A', \chi ')$ be G-equivariant bundle gerbes on M. An equivariant 1-isomorphism ${\mathcal {G}}\longrightarrow {\mathcal {G}}'$ consists of a 1-morphism of bundle gerbes $E :{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ together with a 2-morphism $\gamma :\varPhi ^*E\longrightarrow {\text {pr}}_M^*E$ defined by the diagram

in $\mathrm {BGrb}(G\times M)$, such that for every $g,g' \in G$ there is an equality of diagrams

Being an equivariant 1-isomorphism is a structure and not a property: given a 1-morphism $E:{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ of bundle gerbes there is a set ${\mathcal {E}}(E)$ of equivariant structures on E. According to Theorem 5.42 we can describe the equivariant structures on ${\mathcal {G}}$ and ${\mathcal {G}}'$ by splittings $s:{\underline{G}}\longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$ and $s':{\underline{G}} \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}}')$. We shall now give a description of an equivariant structure on E using these homomorphisms of 2-groups. For this, recall from the end of Sect. 5.4 that any 1-isomorphism $E :{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ in $\mathrm {BGrb}(M)$ gives rise to a morphism of smooth 2-groups ${\widehat{E}} :{\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}}')$: choose an adjoint inverse $E^{\vee }$ for E and define ${\widehat{E}}$ via

$$\begin{aligned} (f,A) \longmapsto \varPhi _f^*E \circ (f,A) \circ E^{\vee } \ . \end{aligned}$$

Proposition 5.46

There is a natural bijection $\Xi _E$ between the set ${\mathcal {E}}(E)$ of equivariant structures on E and the set of 2-isomorphisms ${\widehat{\gamma }}:{\widehat{E}} \circ s \longrightarrow s'$ of smooth morphisms of 2-groups.

Proof

Let ${\mathcal {G}}$ and ${\mathcal {G}}'$ be G-equivariant bundle gerbes on a manifold M with a smooth G-action $\varPhi :G\times M \longrightarrow M$, and let $(E,\gamma ) :{\mathcal {G}}\longrightarrow {\mathcal {G}}'$ be a 1-isomorphism of equivariant bundle gerbes. Fix an adjoint inverse $E^{\vee }$ to E. We construct the 2-isomorphism $\Xi _E(\gamma ) :{\widehat{E}} \circ s \longrightarrow s'$ as follows: let $f:c \longrightarrow G$ be an element of ${\underline{G}}\,$. The natural transformation $\Xi _E(\gamma )$ consists of a 2-isomorphism $\Xi _E(\gamma )_f :{\widehat{E}} \circ s(f) \longrightarrow s'(f)$ which we construct by the diagram

Using the same methods as in the proof of Theorem 5.42 one can show that $\Xi _E$ is a bijection. $\square$

Definition 5.47

An equivariant 2-isomorphism of G-equivariant bundle gerbes $(E,\gamma )\longrightarrow (E',\gamma ')$ consists of a 2-morphism $\eta :E \longrightarrow E'$ such that there is an equality of diagrams

Being an equivariant 2-morphism is a property.

The 2-group extension ${\mathrm {Sym}}_G({\mathcal {G}})\longrightarrow {\underline{G}}$ can also be used to study the existence of equivariant structures on 1-morphisms. A condition for 2-isomorphisms of bundle gerbes to be equivariant is

Proposition 5.48

Let $(E,\gamma )$ and $(E',\gamma ')$ be equivariant 1-isomorphisms. A 2-isomorphism $\eta :E \longrightarrow E'$ is equivariant if and only if $\Xi _{E'}(\gamma ') \circ ({\widehat{\eta }}\circ 1_\gamma ) =\Xi _{E}(\gamma )$.

Proof

This follows from Definition 5.47 using the fact that the inverses $E^{\vee }$ and $E'{}^{\vee }$ are adjoints to E and $E'$. $\square$

6 Application I: Nonassociative Magnetic Translations

Nonassociativity in quantum mechanics has a long history dating back to foundational work on the theory in the 1930’s. Its interest was revived in the 1980’s with the realisation that the magnetic translation operators on the states of a charged particle moving in a magnetic monopole background generally form a nonassociative algebra [Jac85, GZ86]; see [Sza19a] for a mathematical introduction to the subject together with a survey and comparison of the various approaches to the quantisation of the pertinent twisted Poisson structures. The recent revived interest in these models has come about from their conjectural relevance to the low-energy dynamics of closed strings in non-geometric backgrounds, which are based on arguments invoking T-duality applied to target spaces that are tori or more generally total spaces of torus bundles [Lüs10, MSS12, BL14, MSS14], and other compact Lie groups [BP11]. See e.g. [Sza19b] for a contemporary introduction to the subject with further references.

As a first application of the general framework presented in this paper, we reformulate the well-known theory of magnetic translations for source-free magnetic fields in the language of Sect. 3. We then use the results of Sect. 5 to describe nonassociative magnetic translations, which were first studied from a geometric perspective in [BMS19] on ${\mathbb {R}}^d$. They were subsequently studied from a quantum field theory perspective in [Mic19], where generalisations from ${\mathbb {R}}^d$ to connected Lie groups are also considered. Here we will show that they are induced by a natural section of ${\mathrm {Sym}}_G({\mathcal {G}})\longrightarrow {\underline{G}}$ constructed using the parallel transport of Sect. 4.

6.1 Magnetic translations on ${{\mathbb {T}}}^d$

Magnetic translations appear in the quantum mechanics of an electrically charged particle moving on a manifold M in the presence of a magnetic field, which is given by a 2-form $B\in \Omega ^2(M)$. In the semi-classical Maxwell theory of electromagnetism, the 2-form B is closed and has integer periods. The first requirement $H=\mathrm {d}B=0$ is the statement that there are no magnetic monopoles. The second requirement is the Dirac charge quantisation condition which states that B is the curvature of a connection on a hermitean line bundle L over M. In Bloch theory (see e.g. [Gru00]), the line bundle L is used in geometric quantisation of the shift of the canonical symplectic structure on the cotangent bundle $T^*M$ by the 2-form B, so that the quantum Hilbert space of wavefunctions for the particle is ${\mathcal {H}}= \mathrm{L}^2(M;L)$, the space of square-integrable sections of L. The (global) symmetry group G of the particle acts on M, and one would like to promote the G-action to an action on the Hilbert space by linear operators. In quantum mechanics, this action on ${\mathcal {H}}$ is only required to define a projective representation of G. If G acts via translations the resulting operators are called magnetic translations. The construction in Sect. 3 provides a universal mechanism to construct magnetic translations, which we will illustrate on the example of a d-dimensional torus $M={{\mathbb {T}}}^d$. Magnetic translations on ${{\mathbb {T}}}^d$ have been studied in e.g. [Fio13, DGTS20] (for constant magnetic fields B), but our treatment is more general and also fits in with expectations from string theory.

Instead of working on ${{\mathbb {T}}}^d$ directly, we work equivariantly on the universal cover ${\mathbb {R}}^d$ by viewing ${{\mathbb {T}}}^d={\mathbb {R}}^d/{\mathbb {Z}}^d$ as the quotient of the natural free action $\tau$ on ${\mathbb {R}}^d$ of the discrete subgroup ${\mathbb {Z}}^d\subset {\mathbb {R}}^d$ by translations. The corresponding projection $\pi :{\mathbb {R}}^d\longrightarrow {{\mathbb {T}}}^d$ is a surjective submersion. To describe line bundles on ${{\mathbb {T}}}^d$ we consider the diagram of manifolds

where we use the identification ${\mathbb {R}}^d\times {\mathbb {Z}}^d \ni (x,i) \longmapsto (x,x+i)\in {\mathbb {R}}^d \times _{{{\mathbb {T}}}^d} {\mathbb {R}}^d$; under this identification, $\pi _0={\text {pr}}_{{\mathbb {R}}^d}$ is the projection and $\pi _1=\tau$ is the ${\mathbb {Z}}^d$-action on ${\mathbb {R}}^d$. Any line bundle on ${{\mathbb {T}}}^d$ can be described by a smooth function $f:{\mathbb {R}}^d\times {\mathbb {Z}}^d\longrightarrow {{\text {U}}}(1)$ satisfying

$$\begin{aligned} f(x+i,j)\, f(x,i)=f(x,i+j) \end{aligned}$$

for all $x\in {\mathbb {R}}^d$ and $i,j\in {\mathbb {Z}}^d$. This means that f is a 1-cocycle on the group ${\mathbb {Z}}^d$ with values in the ${\mathbb {Z}}^d$-module $C^ \infty ({\mathbb {R}}^d;{{\text {U}}}(1))$. We will use the notation $f_i(\,\varvec{\cdot }\,):=f(\,\varvec{\cdot },i)\in C^\infty ({\mathbb {R}}^d;{{\text {U}}}(1))$ for $i\in {\mathbb {Z}}^d$. Concretely, the ${{\text {U}}}(1)$-bundle described by f is the quotient

$$\begin{aligned} P_f :=\big ( {\mathbb {R}}^d\times {{\text {U}}}(1) \big )\big /{\sim } \end{aligned}$$

by the equivalence relation

$$\begin{aligned} (x+i,1) \sim \big (x, f_i(x)\big ) \end{aligned}$$

for all $x\in {\mathbb {R}}^d$ and $i\in {\mathbb {Z}}^d$. Sections of the associated line bundle $L_f \longrightarrow {{\mathbb {T}}}^d$ are in one-to-one correspondence with equivariant functions on the universal covering space, which are functions $\psi \in C^\infty ({\mathbb {R}}^d;{\mathbb {C}})$ satisfying quasi-periodic boundary conditions

$$\begin{aligned} \psi (x+i)= f_i(x)\,\psi (x) \ . \end{aligned}$$

The action of the translation group $G={\mathbb {R}}^d_{\mathtt {t}}$ on ${\mathbb {R}}^d$, $x\longmapsto x+v$, induces an action $\tau$ of ${\mathbb {R}}^d_{\mathtt {t}}$ on ${{\mathbb {T}}}^d$. For $v\in {\mathbb {R}}^d_{\mathtt t}$, the bundle $\tau _v^*P_f$ is described by the functions $\tau _v^*f_i=f_i(\,\varvec{\cdot }\, -v)$.⁵ This allows us to give a concrete description for the fibres of the principal bundle ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt t}}(P_f)\longrightarrow {\mathbb {R}}^d_{\mathtt {t}}$ as

$$\begin{aligned} {\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}(P_f)_{|v}= & {} {\mathrm {Bun}}_{{{\text {U}}}(1)}(M)(P_f, P_{\tau _v^*f})\\= & {} \big \{g\in C^\infty ({\mathbb {R}}^d, {{\text {U}}}(1)) \ \big | \ g(x+i)=f_i(x)\,f_i(x-v)^{-1}\, g(x) \big \} \ . \end{aligned}$$

The group⁶$C^\infty ({{\mathbb {T}}}^d;{{\text {U}}}(1))=C^\infty ({\mathbb {R}}^d;{{\text {U}}}(1))^{{\mathbb {Z}}^d}$ acts freely and transitively on ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}(P_f)_{|v}$ by pointwise multiplication. The multiplicative structure from Proposition 3.4 on ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}(P_f)$ takes the concrete form

$$\begin{aligned} \mu \big ((g,v),(g',v')\big ):=\big ((\tau _{v'}^*g) \, g',v+v'\big ) \ . \end{aligned}$$

A smooth section of the short exact sequence

$$\begin{aligned} 1\longrightarrow C^\infty ({{\mathbb {T}}}^d, {{\text {U}}}(1))\longrightarrow {\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt t}}(P_f)\longrightarrow {\mathbb {R}}^d_{\mathtt {t}} \longrightarrow 1 \end{aligned}$$

induces a twisted action of ${\mathbb {R}}^d_{\mathtt {t}}$ on the quantum Hilbert space ${\mathcal {H}}=\mathrm{L}^2({{\mathbb {T}}}^d;L_f)$; here we do not require this section to be a group homomorphism, and the 2-cocycle twisting this action takes values in $C^\infty ({{\mathbb {T}}}^d; {{\text {U}}}(1))$. We can construct such a section from the choice of a connection on $P_f$, which reproduces the usual expression for magnetic translations. A connection on $P_f$ can be described by a 1-form $A\in \Omega ^1({\mathbb {R}}^d)$ satisfying

$$\begin{aligned} -\mathrm {i}\, \mathrm {d}\log f = \pi _0^*A - \pi _1^* A \ . \end{aligned}$$

This condition implies that the closed 2-form $\mathrm {d}A=\pi ^*B$ descends to a well-defined magnetic field B on ${{\mathbb {T}}}^d$. The section corresponding to A is given by parallel transport:

$$\begin{aligned} s_A :{\mathbb {R}}^d_{\mathtt {t}}&\longrightarrow {\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}(P_f) \\ v&\longmapsto s_A(v)= \exp \Big ( - \mathrm {i}\, \int _{\Delta ^1(\,\varvec{\cdot }\,;v)}\, A \Big ) \ , \end{aligned}$$

where

$$\begin{aligned} \Delta ^1(x;v)= \{ x-v +t\, v \in {\mathbb {R}}^d \mid 0\le t \le 1 \} \ . \end{aligned}$$

We check that this is indeed an element of ${\mathrm {Sym}}_{{\mathbb {R}}^d_\mathtt{t}}(P_f)_{|v}$:

$$\begin{aligned} \big (s_A(v)\big )(x+i)&= \exp \Big (-\mathrm {i}\,\int _{\Delta ^1(x+i;v)}\,A+\mathrm {i}\,\int _{\Delta ^1(x;v)}\,A\Big ) \ \big (s_A(v) \big ) (x) \\&=\exp \Big (\int _{\Delta ^1(x;v)}\,\mathrm {d}\log f_i\Big ) \ \big (s_A(v) \big ) (x) \\&= f_i(x)\, f_i(x-v)^{-1} \ \big (s_A(v) \big ) (x) \ . \end{aligned}$$

The corresponding 2-cocycle describing the extension agrees with the 2-cocycle constructed in e.g. [Sol18, BMS19].

By Proposition 3.5 the extension ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}(P_f)$ acts on the total space of the line bundle $L_f$ and hence on the quantum state space ${\mathcal {H}}$. The section $s_A$ realises translations $v\in {\mathbb {R}}^d_{\mathtt {t}}$ as linear operators ${\mathcal {P}}(v):{\mathcal {H}}\longrightarrow {\mathcal {H}}$ on this Hilbert space via

$$\begin{aligned} {\mathcal {P}}(v)\psi =s_A(v)\,\tau _v^*\psi \ . \end{aligned}$$

One easily checks that ${\mathcal {P}}(v)\psi \in {\mathcal {H}}$ for $\psi \in {\mathcal {H}}$, i.e. $\big ({\mathcal {P}}(v)\psi \big )(x+i) = f_i(x)\, \big ({\mathcal {P}}(v)\psi \big )(x)$. However, they only provide a projective representation of the translation group ${\mathbb {R}}^d_{\mathtt {t}}$ since $s_A$ is not a group homomorphism. Explicitly, using Stokes’ Theorem we find that the magnetic translations satisfy the relations of the twisted group algebra

$$\begin{aligned} {\mathcal {P}}(v)\,{\mathcal {P}}(v')= \exp \Big ( -\mathrm {i}\,\int _{\Delta ^2(\,\varvec{\cdot }\,; v',v) } \, \pi ^*B\Big ) \ {\mathcal {P}}(v+v') \ , \end{aligned}$$

where

$$\begin{aligned} \Delta ^2(x;v',v) = \{ x-v-v'+t_1 \, v' + t_2\, v\in {\mathbb {R}}^d \mid 0 \le t_2 \le t_1 \le 1 \} \ , \end{aligned}$$

and we used the relation

$$\begin{aligned} \partial \Delta ^2(x;v',v) = \Delta ^1(x;v)-\Delta ^1(x;v+v')+\Delta ^1(x+v;x+v+v') \end{aligned}$$

in the simplicial complex in ${\mathbb {R}}^d$.

Remark 6.1

By dropping the (quasi-)periodicity conditions everywhere one gets back the description of magnetic translations corresponding to (necessarily trivialisable) line bundles over ${\mathbb {R}}^d$ (cf. [BMS19]). $\square$

6.2 Nonassociative magnetic translations from parallel transport

Dirac’s extension of the classical Maxwell theory assumes a singular magnetic field B whose 3-form curvature $H=\mathrm {d}B$ is distributional, with zero-dimensional support consisting of the locations of magnetic monopoles on the configuration manifold M. However, in applications to string theory the closed 3-form H corresponds to an NS–NS flux and is typically smooth, as we now assume. The framework described in Sect. 6.1 is not capable of encoding magnetic fields with non-vanishing magnetic charge $H=\mathrm {d}B$, since in this case B can never be realised as the curvature of a line bundle. The quantisation problem now concerns an H-twisted Poisson structure on the cotangent bundle $T^*M$ [Sza19a], with twisting of the canonical Poisson structure which spoils the Jacobi identity for functions in $C^\infty (T^*M;{\mathbb {C}})$ that vary along the vertical directions. The corresponding quantum operators do not associate; it is not possible to realise a nonassociative algebra by linear operators acting on a Hilbert space. Different approaches to describing the nonassociative quantum mechanics of charged particles moving in the background of a magnetic field with smooth monopole sources are described in [MSS14, BBBS15, KS18].

Fluxes in string theory obey a generalised version of Dirac charge quantisation (see e.g. [Sza13]); in particular, the closed 3-form H has integer periods and hence is the curvature of a connection on a hermitean bundle gerbe over M. Based on this observation, in [BMS19] we suggested the following approach: geometrically the magnetic field B can be interpreted as the curving on a trivial gerbe ${\mathcal {I}}_B$ with curvature H. We proposed to use the 2-Hilbert space of sections of ${\mathcal {I}}_B$ as a replacement for the usual Hilbert space of quantum mechanics. The category of sections of a gerbe ${\mathcal {G}}$ on a manifold M is the morphism category $\Gamma (M;{\mathcal {G}}):=\mathrm {BGrb}({\mathcal {I}}, {\mathcal {G}})$; for details on the 2-Hilbert space structure on this category we refer to [BSS18, BS17, Bun17]. As evidence for our approach we constructed a projective action of nonassociative magnetic translation operators on this 2-Hilbert space, which naturally encodes the relations of the H-twisted Poisson algebra on $T^*M$. However, the drawback of this approach is that it does not work for topologically non-trivial fluxes H, or equivalently for gerbes ${\mathcal {G}}$ with non-torsion Dixmier–Douady class. Extending our geometric approach to nonassociative quantum mechanics along these lines was in fact one of our original motivations behind the present paper.

Let us first explain how the action of nonassociative magnetic translations for magnetic fields with sources on $M={\mathbb {R}}^d$, which was described in [BMS19], can be constructed via the 2-group extensions from Sect. 5. Every gerbe on ${\mathbb {R}}^d$ is isomorphic to a trivial gerbe ${\mathcal {I}}_B$ represented by the diagram

with trivial connection $A=0$ and curving $B\in \Omega ^2({\mathbb {R}}^d)$. The connection on ${\mathcal {I}}_B$ induces a section⁷

$$\begin{aligned} s_{B}:{\mathbb {R}}^d_{\mathtt {t}}\longrightarrow \text {Sym}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {I}}) \end{aligned}$$

via parallel transport:

$$\begin{aligned} s_{B}(v):=\big ({\mathtt {pt}}_{1}^{{\mathcal {I}}_B}\big )_{|\Delta ^1(\,\varvec{\cdot }\,;v)}:{\mathcal {I}}_B \longrightarrow \tau _v^* {\mathcal {I}}_B \ . \end{aligned}$$

Combining $s_B$ with the action of ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {I}})$ on ${\mathcal {I}}$ induces a higher projective action of ${\mathbb {R}}^d_{\mathtt {t}}$ on $\Gamma ({\mathbb {R}}^d;{\mathcal {I}})$. We refer to [BMS19, Section 4] for precise definitions.

Since all line bundles over ${\mathbb {R}}^d$ are isomorphic to a trivial line bundle, the category $\text {Sym}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {I}})_{|v}$ at $v\in {\mathbb {R}}^d_{\mathtt {t}}$ is equivalent to the category with one object and morphisms described by smooth functions ${\mathbb {R}}^d\longrightarrow {{\text {U}}}(1)$. Thus

$$\begin{aligned} {\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {I}}) \cong \big (*\big /\big /C^\infty ({\mathbb {R}}^d;{{\text {U}}}(1))\big ) \rtimes {\mathbb {R}}^d_{\mathtt {t}} \ . \end{aligned}$$

The 2-group structure on ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {I}})$ is given by

$$\begin{aligned} v\otimes v'&:=v+v' \ , \\ (h,v)\otimes (h',v')&:=\big ((\tau _{v'}^*h) \, h',v+v'\big ) \ . \end{aligned}$$

However, under this equivalence the action of the magnetic translation operators becomes elusive. In [BMS19] we equipped the 1-morphisms with a connection to circumvent this problem. We did not require the 2-morphisms to preserve these connections leading to equivalent categories. The parallel transport 1-morphisms ${\mathtt {pt}}_1^{{\mathcal {I}}_B}$ can be equipped with such a connection in a canonical way. This reproduces the constructions from [BMS19].

For this, let ${\mathcal {I}}_B$ be a trivial bundle gerbe on a smooth manifold M with curving $B\in \Omega ^2(M)$ and curvature $H=\mathrm {d}B$. We fix a base point $x\in M$. Via transgression and regression we get a bundle gerbe ${\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B)$ defined over the diffeological path fibration $P_0M\longrightarrow M$. The corresponding line bundle over $(P_0M)^{[2]}$ admits a canonical trivialisation. It comes equipped with a connection 1-form given as the pullback of the transgression of B to the loop space LM along the embedding $l:(P_0M)^{[2]} \longrightarrow LM$. To describe the curving of ${\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B)$ we note that a tangent vector to a based path $\gamma \in P_0M$ is a smooth section ${\mathcal {V}} \in \Gamma ([0,1];\gamma ^*TM)$ which is zero in a neighbourhood of 0 and constant in a neighbourhood of 1. The 2-form ${\mathcal {R}}{\mathcal {T}}(B)\in \Omega ^2(P_0M)$ is defined by the transgression formula

$$\begin{aligned} {\mathcal {R}}{\mathcal {T}}(B)({\mathcal {V}},{\mathcal {V}}') = \int _\gamma \, \imath _{{\mathcal {V}}'} \imath _{\mathcal {V}} H \ , \end{aligned}$$

where $\imath$ denotes the interior multiplication between a vector and a form. There is a natural 1-isomorphism [Wal16, Section 6.1] $W :{\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B) \longrightarrow {\mathcal {I}}_B$ with underlying diagram

of diffeological spaces. The line bundle which is part of this 1-morphism has a canonical trivialisation for trivial bundle gerbes ${\mathcal {I}}_B$ and has the connection 1-form $A_W\in \Omega ^1(P_0M)$ defined by the transgression formula

$$\begin{aligned} A_W({\mathcal {V}})= \int _\gamma \, \imath _{\mathcal {V}} B \ . \end{aligned}$$

In order to describe the parallel transport, we pull everything back to the path space PM along the two evaluation maps ${\mathrm {ev}}_0,{\mathrm {ev}}_1 :PM \longrightarrow M$. The parallel transport defined in Sect. 4 is a 1-morphism

$$\begin{aligned} {\mathtt {pt}}_1^{{\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B)}:{\mathrm {ev}}_0^*{\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B) \longrightarrow {\mathrm {ev}}_1^* {\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B) \end{aligned}$$

given by a line bundle with connection over the space $P_{\partial \Delta ^2}M$. An element of $P_{\partial \Delta ^2}M$ is a triple of paths $(\gamma _{xy},\gamma _{yz},\gamma _{xz})$, where $\gamma _{xy}$ is a path from the base point x to some other point $y\in M$, $\gamma _{yz}$ is a path from y to a third point $z\in M$, and $\gamma _{xz}$ is a path from x to z. Again, the line bundle for the parallel transport is trivial since we work with a trivial bundle gerbe. Its connection is given by

$$\begin{aligned} \int _{ \overline{\gamma _{xz}} \star \gamma _{yz} \star \gamma _{xy}} \, \imath _\bullet B \ , \end{aligned}$$

where the notation means that the evaluation on a tangent vector ${\mathcal {V}}$ is given by

$$\begin{aligned} \int _{ \overline{\gamma _{xz}} \star \gamma _{yz} \star \gamma _{xy}} \, \imath _{\mathcal {V}} B \ . \end{aligned}$$

We obtain a 1-morphism

$$\begin{aligned} {\mathtt {pt}}_1^{{\mathcal {I}}_B}:{\mathrm {ev}}_0^* {\mathcal {I}}_B \xrightarrow {{\mathrm {ev}}_0^* W^{-1}} {\mathrm {ev}}_0^* {\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B) \xrightarrow {{\mathtt {pt}}_1^{{\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B)}}{\mathrm {ev}}_1^* {\mathcal {R}}{\mathcal {T}}({\mathcal {I}}_B) \xrightarrow {{\mathrm {ev}}_1^*W} {\mathrm {ev}}_1^* {\mathcal {I}}_B \ , \end{aligned}$$

representing the colimit from Definition 4.16. Concretely, this is a trivial line bundle over PM with connection

$$\begin{aligned} \int _{\gamma _{yz}} \, \imath _\bullet B \ . \end{aligned}$$

This is exactly the formula used for the magnetic translations in [BMS19] in the case $M={\mathbb {R}}^d$, hence it provides a conceptual underpinning of the constructions in [BMS19], and moreover generalises them to trivial bundle gerbes on arbitrary manifolds M.

6.3 Nonassociative magnetic translations on ${{\mathbb {T}}}^d$

Now we generalise the description of nonassociative magnetic translations to the d-dimensional torus ${{\mathbb {T}}}^d$, see also [Mic19] for a discussion from a quantum field theory point of view. A problem in this context is that for topologically non-trivial gerbes on ${{\mathbb {T}}}^d$, there are no non-trivial sections. This makes the 2-Hilbert space of sections an uninteresting object to study.⁸ However, our 2-group extension still exists and should encode the geometry of nonassociative magnetic translations in this context, regardless of whether or not sections exist. Non-trivial gerbes over ${{\mathbb {T}}}^d$ are similarly treated as coming from ${\mathbb {Z}}^d$-equivariant (topologically trivial) gerbes over ${\mathbb {R}}^d$, as in e.g. [MW16, Section 7.1].

Bundle gerbes on ${{\mathbb {T}}}^d$ can be described using the surjective submersion $\pi :{\mathbb {R}}^d\longrightarrow {{\mathbb {T}}}^d$ and the corresponding diagram

Here we used the identification $(x,i,j)\in {\mathbb {R}}^d\times {\mathbb {Z}}^d \times {\mathbb {Z}}^d \longmapsto (x,x+i,x+i+j)\in ({\mathbb {R}}^d)^{[3]}$. Concretely, a bundle gerbe consists of a line bundle L over ${\mathbb {R}}^d\times {\mathbb {Z}}^d$, which we can assume to be trivial without loss of generality, and an isomorphism $f:\pi _{0,1}^*L\otimes \pi _{1,2}^*L \longrightarrow \pi _{0,2}^*L$ of line bundles over ${\mathbb {R}}^d\times {\mathbb {Z}}^d\times {\mathbb {Z}}^d$ satisfying a coherence condition over ${\mathbb {R}}^d\times ({\mathbb {Z}}^d)^{\times 3}$. We can describe this isomorphism by a collection of smooth maps $f_{i,j}:{\mathbb {R}}^d\longrightarrow {{\text {U}}}(1)$ for all $i,j\in {\mathbb {Z}}^d$, and the coherence condition translates to

$$\begin{aligned} f_{i,j}(x)\,f_{i+j,k}(x) = f_{i,j+k}(x)\,f_{j,k}(x+i) \end{aligned}$$

for all $x\in {\mathbb {R}}^d$ and $i,j,k\in {\mathbb {Z}}^d$, which is the 2-cocycle condition for

$$\begin{aligned} f_{\,\varvec{\cdot },\,\varvec{\cdot }\,}\in \mathrm{C}^2\big ({\mathbb {Z}}^d; C^\infty ({\mathbb {R}}^d;{{\text {U}}}(1))\big ) \ . \end{aligned}$$

We denote the gerbe described by f as ${\mathcal {G}}_f$.

For $v\in {\mathbb {R}}^d_{\mathtt {t}}$, the pullback of ${\mathcal {G}}_f$ along the translation $\tau _v$ can be described by the 2-cocycle $\tau _v^*f_{i,j}= f_{i,j}(\,\varvec{\cdot }\, - v)$. Using [Bun17, Proposition A.31] we can describe the category ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {G}}_f)_{|v}$ at $v\in {\mathbb {R}}^d_\mathtt{t}$ up to equivalence in the following way: its objects are functions $g:{\mathbb {R}}^d\times {\mathbb {Z}}^d \longrightarrow {{\text {U}}}(1)$ satisfying

$$\begin{aligned} f_{i,j}(x -v)\,g_{i}(x)\,g_{j}(x+i)=g_{i+j}(x)\, f_{i,j}(x) \ , \end{aligned}$$

for all $x\in {\mathbb {R}}^d$ and $i,j \in {\mathbb {Z}}^d$. It is straightforward to deduce the morphisms in ${\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {G}}_f)$ from [Bun17, Proposition A.31]; we find that a morphism from g to $g'$ is described by a function $h:{\mathbb {R}}^d \longrightarrow {{\text {U}}}(1)$ satisfying

$$\begin{aligned} h(x)\,g_i(x)= g_i'(x)\,h(x+i) \end{aligned}$$

for all $x\in {\mathbb {R}}^d$ and $i\in {\mathbb {Z}}^d$. Note that for the trivial 2-cocycle $f_{i,j}=1$ this describes the category of line bundles over ${{\mathbb {T}}}^d$ with arbitrary gauge transformations as morphisms. The 2-group structure on

$$\begin{aligned} {\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {G}}_f) = \coprod _{v\in {\mathbb {R}}^d_{\mathtt {t}}} \, {\mathrm {Sym}}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {G}}_f)_{|v} \end{aligned}$$

from Theorem 5.23 takes the form

$$\begin{aligned} (g_i,v)\otimes (g'_i,v')&:=\big ((\tau _{v'}^*g_i)\, g_i',v+v'\big ) \ , \\ (h,v)\otimes (h',v')&:=\big ((\tau _{v'}^*h)\, h',v+v'\big ) \ , \end{aligned}$$

fitting into the 2-group extension from Theorem 5.27:

$$\begin{aligned} 1 \longrightarrow \mathrm {HLBdl}({{\mathbb {T}}}^d) \longrightarrow \text {Sym}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {G}}_f) \longrightarrow {\mathbb {R}}^d_{\mathtt {t}} \longrightarrow 1 \ . \end{aligned}$$

(6.2)

As in the case of line bundles from Sect. 6.1, a connection (A, B) on ${\mathcal {G}}_f$ induces a section of the extension (6.2). A connection on ${\mathcal {G}}_f$ is described by a 2-form $B\in \Omega ^2({\mathbb {R}}^d)$ and a 1-form $A\in \Omega ^1({\mathbb {R}}^d\times {\mathbb {Z}}^d)$ satisfying

$$\begin{aligned} -\mathrm {i}\, \mathrm {d}\log f_{i,j}(x)&= A_{i+j}(x)-A_i(x) -A_j(x+i) \ , \\ \mathrm {d}A&= \pi _1^*B-\pi _0^*B \ , \end{aligned}$$

for all $x\in {\mathbb {R}}^d$ and $i,j \in {\mathbb {Z}}^d$. The second condition implies that the closed 3-form $\mathrm {d}B=\pi ^*H$ descends to a well-defined flux H on ${{\mathbb {T}}}^d$. Using the connection we can construct a section

$$\begin{aligned} s_{A,B}:{\mathbb {R}}^d_{\mathtt {t}}\longrightarrow \text {Sym}_{{\mathbb {R}}^d_{\mathtt t}}({\mathcal {G}}_f) \end{aligned}$$

by

$$\begin{aligned} s_{A,B}(v):=(g_i, v) \qquad \text{ with } \quad g_i=\exp \Big ( \mathrm {i}\, \int _{\Delta ^1(\,\varvec{\cdot }\,;v)}\, A_i \Big ) \ . \end{aligned}$$

We check that this is indeed an element of $\text {Sym}_{{\mathbb {R}}^d_{\mathtt {t}}}({\mathcal {G}}_f)_{|v}$:

$$\begin{aligned} g_i(x)\,g_j(x+i)\,g_{i+j}(x)^{-1}&= \exp \Big ( \mathrm {i}\, \int _{\Delta ^1(x;v)}\, A_i +\mathrm {i}\, \int _{\Delta ^1(x+i;v)}\, A_j - \mathrm {i}\, \int _{\Delta ^1(x;v)}\, A_{i+j} \Big ) \\&= \exp \Big ( -\int _{\Delta ^1(x;v)}\, \mathrm {d}\log f_{i,j} \Big ) \\&= f_{i,j}(x-v)^{-1}\,f_{i,j}(x) \ . \end{aligned}$$

For the multiplication we find

$$\begin{aligned} s_{A,B}(v)\otimes s_{A,B}(v')&= \bigg (\exp \Big ( \mathrm {i}\, \int _{\Delta ^1(\,\varvec{\cdot }\,-v';v)}\, A_i +\mathrm {i}\, \int _{\Delta ^1(\,\varvec{\cdot }\,;v')}\, A_i \Big ) ,\, v+v'\bigg ) \\&=\bigg (\exp \Big ( \mathrm {i}\, \int _{\Delta ^1(\,\varvec{\cdot }\,;v+v')}\, A_i-\mathrm {i}\, \int _{\Delta ^2(\,\varvec{\cdot }\,;v',v)}\, \big (B-\tau _i^*B\big )\Big ) ,\,v+v'\bigg ) \\&=s_{A,B}(v+v')\otimes \bigg (\exp \Big (-\mathrm {i}\, \int _{\Delta ^2(\,\varvec{\cdot }\,;v',v)}\big (B-\tau _i^*B\big ) \Big ) ,\,0\bigg ) \ . \end{aligned}$$

This particular product is associative on the nose. However, the line bundle on ${{\mathbb {T}}}^d$ described by the transition functions $\exp \big (-\mathrm {i}\,\int _{\Delta ^2(\,\varvec{\cdot }\,;v',v)}\, (B-\tau _i^*B)\big )$ is non-trivial. We can use the decomposition

$$\begin{aligned} \int _{\Delta ^2(\,\varvec{\cdot }\,;v',v)}\, \mathrm {d}\imath _\bullet B = \pounds _{\bullet }\int _{\Delta ^2(\,\varvec{\cdot }\,;v',v)} \, B -\int _{\Delta ^2(\,\varvec{\cdot }\,;v',v)}\, \imath _{\bullet } \pi ^*H \ , \end{aligned}$$

where $\pounds$ is the Lie derivative, to construct a 2-isomorphism

$$\begin{aligned} \varPi _{v,v'}:=\exp \Big (-\mathrm {i}\, \int _{\Delta ^2(\,\varvec{\cdot }\,;v',v)}\, B \Big ) :s_{A,B}(v)\otimes s_{A,B}(v') \longrightarrow s_{A,B}(v+v') \ , \end{aligned}$$

which has the advantage that the line bundle on the right-hand side is trivial.

Remark 6.3

In this last representation the nonassociativity of the higher magnetic translations is realised by the composition property

$$\begin{aligned} \varPi _{u,v+w} \circ \tau _{-u}^*\varPi _{v,w} = \omega _{u,v,w} \ \varPi _{u+v,w} \circ \varPi _{u,v} \ , \end{aligned}$$

where

$$\begin{aligned} \omega _{u,v,w} = \exp \Big (\mathrm {i}\, \int _{\Delta ^3(\,\varvec{\cdot }\,;w,v,u)}\, \pi ^*H \Big ) \end{aligned}$$

and

$$\begin{aligned} \Delta ^3(x;w,v,u) = \{x-u-v-w+t_1\,w+t_2\,v+t_3\,u \in {\mathbb {R}}^d \mid 0\le t_3\le t_2\le t_1\le 1\} \ . \end{aligned}$$

Concretely this means that there are two different ways to go from the triple product $s_{A,B}(u)\otimes s_{A,B}(v)\otimes s_{A,B}(w)$ to $s_{A,B}(u+v+w)$. Their difference is controlled by the 3-cocycle $\omega _{\,\varvec{\cdot },\,\varvec{\cdot },\,\varvec{\cdot }\,}$ on the translation group ${\mathbb {R}}^d_{\mathtt {t}}$ with values in $C^\infty ({{\mathbb {T}}}^d;{{\text {U}}}(1))$, as depicted in the commutative diagram

This is the implementation of nonassociativity in the higher categorical framework. $\square$

7 Application II: Anomalies in Quantum Field Theory

In this section we begin by using the group extensions ${\mathrm {Sym}}_G(P)$ from Sect. 3 to study the existence of equivariant trivialisations of line bundles. This has direct applications to the path integral description of the chiral anomaly in quantum field theory on even-dimensional spacetime manifolds. Then using the 2-group extension ${\mathrm {Sym}}_G({\mathcal {G}})$ from Sect. 5, we study the analogous questions for gerbes and apply our findings to the Hamiltonian description of the chiral anomaly on odd-dimensional time-slices.

7.1 Even dimensions: chiral anomalies

Let G be a connected Lie group, M a manifold with smooth G-action $\varPhi :G\times M \longrightarrow M$, and $(P,\chi )$ a G-equivariant ${{\text {U}}}(1)$-bundle on M. The equivariant structure on P can be described by a splitting $s_{P} :G \longrightarrow {\mathrm {Sym}}_G(P)$. Assume furthermore that P is trivial as a line bundle, i.e. there exists a 1-isomorphism $\psi :I \longrightarrow P$. The trivial bundle carries a canonical equivariant structure with corresponding splitting $s_I :G \longrightarrow {\mathrm {Sym}}_G(I)$.

Rewriting the result of Sect. 3.2 slightly, we see that $\psi$ is equivariant if and only if the smooth 1-cocycle

$$\begin{aligned} G&\longrightarrow C^\infty (M;{{\text {U}}}(1)) \\ g&\longmapsto s_{P}(g)\, {\widehat{\psi }}\big (s_I(g)\big )^{-1} \end{aligned}$$

is trivial. Every other isomorphism $I \longrightarrow P$ differs from $\psi$ by a uniquely determined element of $C^\infty (M;{{\text {U}}}(1))$. Their corresponding 1-cocycles differ by the coboundary defined by this element. Hence the obstruction for an equivariant bundle which is trivial as a line bundle to be also trivial as an equivariant bundle is an element of the degree one group cohomology $\mathrm{H}^1\big (G;C^\infty (M;{{\text {U}}}(1))\big )$. This has also been observed in [CM95] from a different perspective.

The question of whether a bundle is equivariantly trivial is important in the path integral perspective on chiral anomalies in quantum field theory. Let M be a based even-dimensional compact Riemannian spin manifold, G a Lie group, Q a principal G-bundle on M, and $\rho :G \longrightarrow \mathsf {End}(V)$ a unitary representation of G on a finite-dimensional vector space V which encodes the matter content of the field theory. Denote by $S^+$ and $S^-$ the positive and negative chirality spinor bundles on M, respectively, by $\varGamma$ the group of based gauge transformations of Q and by ${\mathscr {A}}$ the affine space of connections on Q. The field content of the theory are chiral spinors, which are smooth sections of the vector bundle $S^+\otimes V$, where here V is the hermitean vector bundle associated to Q via the representation $\rho$. There is a family of (twisted) Dirac operators

parameterised by gauge fields $A \in {\mathscr {A}}$, which are first order elliptic differential operators acting on chiral spinors. These data together define the content of a chiral gauge theory.

The formal path integral over the chiral spinor fields is the determinant of the Dirac operator . However, the determinant of is in general not a number but an element of a complex line, and it can be defined only after suitable regularisation as an element of the fibre of the determinant line bundle $\det \longrightarrow {\mathscr {A}}$ [AS84]. This defines the (exponentiated) effective action functional which is a section

$$\begin{aligned} Z=\exp (-S):{{\mathscr {A}}}\longrightarrow \det \ , \end{aligned}$$

with . The action of $\varGamma$ on ${\mathscr {A}}$ via gauge transformations can be lifted to the determinant line bundle, which hence descends to a line bundle over the moduli space of gauge connections ${\mathscr {A}}/ {\varGamma }$.

Being an affine space, ${{\mathscr {A}}}$ is contractible, so over ${\mathscr {A}}$ we can trivialise the determinant line bundle and hence identify the effective action functional Z with a complex function. However, this might not be possible over the orbit space ${\mathscr {A}}/ {\varGamma }$: if the descended line bundle is non-trivial then we cannot identify the effective action functional with a complex function in a gauge-invariant way, i.e. the gauge symmetry is anomalous. The line bundle over ${\mathscr {A}}/ {\varGamma }$ is trivial if and only if we can choose a ${\varGamma }$-equivariant trivialisation of the line . By our general discussion above, the obstruction to this is an element of $\mathrm{H}^1\big ({\varGamma }; {{\text {U}}}(1)^{{\mathscr {A}}}\big )$, where ${{\text {U}}}(1)^{{\mathscr {A}}}$ is the diffeological space of maps from ${{\mathscr {A}}}$ to ${{\text {U}}}(1)$. An explicit formula for this smooth 1-cocycle is obtained in [CM95].

7.2 Odd dimensions: the Faddeev–Mickelsson–Shatashvili anomaly

We shall now generalise the construction from the Sect. 7.1 to bundle gerbes. For this, we need to introduce a categorification of the first group cohomology which takes values in a smooth abelian 2-group. We use a definition along the lines of [BMS19], adjusted to the smooth setting.

Definition 7.1

Let G be a Lie group and ${{\mathsf {A}}}$ a smooth abelian 2-group equipped with a left action $\rho$ of $\underline{G}\,$. A smooth higher 1-cocycle on G with values in ${{\mathsf {A}}}$ consists of

• a morphism $\lambda :{\underline{G}}\longrightarrow {{\mathsf {A}}}$, $g\longmapsto \lambda _g$, in ${\mathscr {H}}$, and

• a smooth natural isomorphism $\chi _{g,g'}:\lambda _g \otimes \rho _g(\lambda _{g'})\longrightarrow \lambda _{g\,g'}$ of smooth functors ${\underline{G}}\times _{{\mathscr {C}}\mathrm{art}}\underline{G}\longrightarrow {{\mathsf {A}}}$,

such that for every $c \in {{\mathscr {C}}\mathrm{art}}$:

• $\lambda _{e_c} = I_c$ where $I_c$ is the monoidal identity object of the fibre ${{\mathsf {A}}}_{|c}$ of ${{\mathsf {A}}}$ over $c \in {{\mathscr {C}}\mathrm{art}}$, and where $e_c :c \longrightarrow G$ is the constant map at the identity element of G,

• $\chi _{e_c,\,\varvec{\cdot }\,}$ and $\chi _{\,\varvec{\cdot },e_c}$ agree with the left and right unitor morphisms in ${{\mathsf {A}}}_{|c}$, and

• the diagram

  

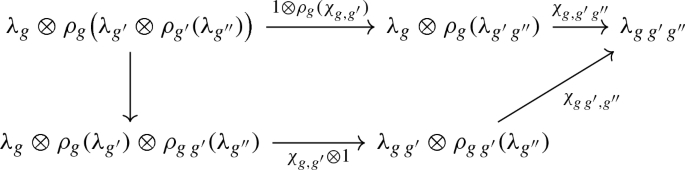
  commutes for all $g,g',g'' \in G(c)$.

We will also need the concept of a higher coboundary.

Definition 7.2

Let $(\lambda ,\chi )$ and $(\lambda ',\chi ')$ be higher 1-cocycles on a Lie group G valued in a smooth abelian 2-group ${{\mathsf {A}}}$. A higher coboundary between $(\lambda ,\chi )$ and $(\lambda ',\chi ')$ consists of

• a morphism $\theta :* \longrightarrow {{\mathsf {A}}}$, and

• smooth isomorphisms $\omega _g :\lambda _g\otimes \rho _g(\theta )\longrightarrow \theta \otimes \lambda '_{g}$ for every $g \in \underline{G}\,$,

such that $\omega _{e_c}$ agrees with the symmetry isomorphism $\beta _{{\mathsf {A}}}$, and the diagram

commutes for all $c \in {{\mathscr {C}}\mathrm{art}}$ and $g,g',g'' \in G(c)$.

Remark 7.3

There is a natural definition of morphisms between higher coboundaries, but these are not relevant for our purposes. $\square$

Let G be a connected Lie group, M a manifold with smooth G-action $\varPhi :G\times M \longrightarrow M$, and $({\mathcal {G}},A,\chi )$ a G-equivariant bundle gerbe on M. The equivariant structure on ${\mathcal {G}}$ can be described by a splitting $s_{{\mathcal {G}}} :{\underline{G}} \longrightarrow {\mathrm {Sym}}_G({\mathcal {G}})$, as explained in Sect. 5.6. Assume furthermore that ${\mathcal {G}}$ is trivial as bundle gerbe, i.e. there exists a 1-isomorphism $E :{\mathcal {I}}\longrightarrow {\mathcal {G}}$. From the results in Sect. 5.6 we can deduce that the obstruction to the existence of an equivariant structure on E is the higher 1-cocycle

$$\begin{aligned} ( f:c \longrightarrow G) \longmapsto s_{\mathcal {G}}(f)^{-1}\circ {\widehat{E}}\big (s_{\mathcal {I}}(f)\big ) \ \in \ \mathrm {BGrb}(c \times M)({\text {pr}}_M^*{\mathcal {G}}, {\text {pr}}_M^*{\mathcal {G}}) \cong \mathrm {HLBdl}(c\times M) \ . \end{aligned}$$

This 1-cocycle is trivial precisely if there exists a natural isomorphism to the constant 1-cocycle at the trivial line bundle I. The choice of such an isomorphism corresponds to the equivariant structure on E. The isomorphisms $\chi$ in Definition 7.1 use the smooth 2-group structure on $\mathrm {HLBdl}^M$, and the isomorphisms which are part of the splittings $s_{\mathcal {G}}$ and $s_{\mathcal {I}}$, and ${\widehat{E}}$. Generally, two 1-isomorphisms ${\mathcal {G}}\longrightarrow {\mathcal {G}}'$ of bundle gerbes differ by the action of a 1-automorphism of $\mathcal {G'}$. Hence the obstruction to the existence of an equivariant isomorphism is an element of the first higher group cohomology of G with coefficients in the smooth abelian 2-group $\mathrm {HLBdl}^M$.

Let us now explain the relation to the Hamiltonian description of chiral anomalies in terms of bundle gerbes, which was worked out in [Mic85, CM95, CM96, CMM97, CMM00]. Let M be a based odd-dimensional compact Riemannian spin manifold,⁹P a principal G-bundle on M, and $\rho :G \longrightarrow \mathsf {End}(V)$ a representation of G describing the matter content of the gauge theory. Again we denote by ${\mathscr {A}}$ the affine space of connections on P and by $\varGamma$ the pointed group of gauge transformations. For every $A\in {\mathscr {A}}$ we can construct a massless Dirac operator

where $S\longrightarrow M$ is the spinor bundle. The Dirac operator is a first order self-adjoint elliptic differential operator, which serves as the first quantised Hamiltonian acting on the one-particle Hilbert space ${\mathcal {H}}=\Gamma (M;S\otimes V)$.

To define the fermionic Fock space ${\mathcal {F}}_A({\mathcal {H}})$ of the quantum field theory in the presence of a gauge field $A \in {\mathscr {A}}$, one has to pick a polarisation ${\mathcal {H}}={\mathcal {H}}_+(A)\oplus {\mathcal {H}}_-(A)$. In general there are gauge fields $A\in {\mathscr {A}}$ for which the Dirac operator has zero modes; for these fields there is no universal and natural way of choosing such a polarisation. Denote by ${\mathscr {A}}_0\subset {\mathscr {A}}\times {\mathbb {R}}$ the subset of pairs (A, r) such that the real number r is not contained in the spectrum of . To equip this space with a diffeology we use the discrete diffeology on ${\mathbb {R}}$. For every point $(A,r)\in {\mathscr {A}}_0$ we get a decomposition of the one-particle Hilbert space

$$\begin{aligned} {\mathcal {H}}={\mathcal {H}}_+(A,r)\oplus {\mathcal {H}}_-(A,r) \end{aligned}$$

into the positive and negative eigenstates of the operator . The corresponding Fock bundle ${\mathcal {F}}({\mathcal {H}})\longrightarrow {{\mathscr {A}}}_0$ has fibres

$$\begin{aligned} {\mathcal {F}}({\mathcal {H}})_{|(A,r)} = {\wedge }\, {\mathcal {H}}_+(A,r) \otimes {\wedge }\, {\mathcal {H}}_-(A,r)^\vee \ . \end{aligned}$$

It is shown in [CM96] that the corresponding projective Hilbert bundle descends to a bundle over ${\mathscr {A}}$, and hence it induces a bundle gerbe ${\mathcal {G}}$ on ${\mathscr {A}}$. The bundle gerbe can be explicitly described in terms of determinant lines associated to families of Dirac operators, see [CM96, Section 5] for details. Since ${{\mathscr {A}}}$ is contractible, over ${{\mathscr {A}}}$ the projective Hilbert bundle is trivial and hence is associated to a bundle of Hilbert spaces. Again the action of $\varGamma$ on ${{\mathscr {A}}}$ lifts to an equivariant structure on ${\mathcal {G}}$. Therefore ${\mathcal {G}}$ as well as the projective Hilbert bundle descends to the orbit space ${{\mathscr {A}}}/{\varGamma }$. The Faddeev–Mickelsson–Shatashvili anomaly is the obstruction to the existence of a well-defined bundle of Hilbert spaces over ${{\mathscr {A}}}/{\varGamma }$, i.e. to the existence of a trivialisation of the descended projective Hilbert bundle. Equivalently, the anomaly vanishes if and only if ${\mathcal {G}}$ descends to a trivial bundle gerbe on ${{\mathscr {A}}}/{\varGamma }$. This in turn is the case if and only if ${\mathcal {G}}$ is trivial as a $\varGamma$-equivariant bundle gerbe on ${{\mathscr {A}}}$.

From the general discussion above it follows that the obstruction to the equivariant triviality of ${\mathcal {G}}$ is a smooth higher 1-cocycle on $\varGamma$ with values in $\mathrm {HLBdl}^{{\mathscr {A}}}$. Because ${{\mathscr {A}}}$ is contractible, there is an equivalence

$$\begin{aligned} \mathrm {HLBdl}^{{\mathscr {A}}}\cong * \big /\big /{{\text {U}}}(1)^{{\mathscr {A}}}\end{aligned}$$

with the smooth category with one object and the diffeological mapping space ${{\text {U}}}(1)^{{\mathscr {A}}}$ as morphisms. Since this is a smooth 2-group with one object, Definition 7.1 in this instance is equivalent to the definition of an ordinary group 2-cocycle on $\varGamma$ with values in ${{\text {U}}}(1)^{{\mathscr {A}}}$. That the obstruction to the vanishing of the anomaly is a 2-cocycle of this form is well-known, see e.g. [CM96]; this cocycle reproduces the usual Schwinger terms in the commutator anomaly for the gauge group action. What is new here is the construction of a smooth higher 1-cocycle, which only reduces to an ordinary 2-cocycle because the space ${\mathscr {A}}$ is contractible, as well as a rigorous incorporation of the smooth structures. Computing this cocycle explicitly and comparing it to the Faddeev–Mickelsson–Shatashvili cocycle is beyond the scope of this paper. We expect this to be possible using index theory following [CMM97].

8 Application III: The String Group

Any compact simple Lie group G has homotopy groups $\pi _3(G) \cong \mathrm {H}^3(G;{\mathbb {Z}}) \cong {\mathbb {Z}}$ and $\pi _i(G) \cong \mathrm {H}^i(G;{\mathbb {Z}}) \cong 0$ for $i = 0,1,2$; that is, G is 2-connected. It is of interest in topology and geometry (see e.g. [DHH11, Sto96, ST04]), as well as in string theory (see e.g. [SS20]), to study 3-connected approximations to G that arise as group extensions of G. We denote such approximating objects by ${\mathrm {String}}(G)$ and call them models for the string group of G. There is a variety of interpretations of what this means, based on different choices of ambient higher categories in which one considers G to be a group object. The general theme, however, is that one needs a way to realise a generator of $\pi _3(G) \cong {\mathbb {Z}}$ geometrically in the chosen framework, and a string group model for G will generally be a choice of such a generator.

In this final section we recall the definition and construction of a topological string group model, and show that our extensions ${\mathrm {Sym}}_G(P)$ from Sect. 3 provide a smooth enhancement thereof. We then propose the smooth 2-groups ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ from Sect. 5 as new string group models, for the specific choices of $M = G$ and of a gerbe ${\mathcal {G}}$ on G whose Dixmier–Douady class generates $\mathrm {H}^3(G;{\mathbb {Z}}) \cong {\mathbb {Z}}$. A model for ${\mathrm {String}}(G)$ which is very similar in spirit to our model ${\mathrm {Sym}}_G({\mathcal {G}})$ was found in [FRS16]. However, that construction relies on the choice of connection on ${\mathcal {G}}$ and considers connection-preserving symmetries of ${\mathcal {G}}$. Here, in contrast, we exhibit a construction of string group models for G from symmetries of gerbes on G without connections, and thus from representatives of the third integer cohomology of G rather than its differential cohomology. We defer further details and comments to Sect. 8.2.

8.1 A smooth string group model

The simplest and original framework for considering string group models is that of topological spaces.

Definition 8.1

Let G be a compact simple simply-connected Lie group. A topological model for the string group ${\mathrm {String}}(G)$ of G is a topological 3-connected group ${\mathrm {String}}_{\mathtt {t}}(G)$ along with a fibration ${\mathrm {String}}_{\mathtt {t}}(G) \longrightarrow G$ whose typical fibre is an Eilenberg-MacLane space $K({\mathbb {Z}};2)$.

Using homotopy and cohomology groups one shows that ${\mathrm {String}}_{\mathtt t}(G)$ cannot be a finite-dimen-sional Lie group [NSW13]. If a topological string group model can be enhanced to consist of smooth spaces (such as Fréchet manifolds or diffeological spaces), we denote it by ${\mathrm {String}}(G)$ and refer to it as a smooth model for the string group of G.

We recall Stolz’ model as a topological group [Sto96]: let ${{\mathbb {P}}\mathrm {U}}$ denote the projective unitary group of an infinite-dimensional separable Hilbert space. As a consequence of Kuiper’s Theorem, ${{\mathbb {P}}\mathrm {U}}$ has homotopy type $K({\mathbb {Z}};2)$. Hence the classifying space ${{\mathsf {B}}}{{\mathbb {P}}\mathrm {U}}$ has homotopy type $K({\mathbb {Z}};3)$, while at the same time it classifies topological principal ${{\mathbb {P}}\mathrm {U}}$-bundles. In particular, isomorphism classes of ${{\mathbb {P}}\mathrm {U}}$-bundles on a space X are in one-to-one correspondence with elements of the set $\mathrm {H}^3(X;{\mathbb {Z}})$.

Let $P \longrightarrow G$ be a principal ${{\mathbb {P}}\mathrm {U}}$-bundle on G such that P corresponds to a generator of $\mathrm {H}^3(G;{\mathbb {Z}}) \cong {\mathbb {Z}}$; such ${\mathbb {P}}{{\text {U}}}$-bundles on G are called basic. Let ${\widehat{G}}$ denote the group of ${{\mathbb {P}}\mathrm {U}}$-equivariant homeomorphisms of P to itself which act on G as left multiplication by some element of G. We can topologise ${\widehat{G}}$ as a subgroup of the topological group of homeomorphisms $P \longrightarrow P$. Thus ${\widehat{G}}$ comes with a continuous surjective group homomorphism ${\widehat{G}} \longrightarrow G$. The gauge group ${\mathrm {Gau}}(P)$ is the subgroup of ${\widehat{G}}$ of those elements whose projection to G is the identity element $e \in G$.

Theorem 8.2

[[Sto96, Section 5] and [NSW13]]. The extension of topological groups

exhibits ${\widehat{G}}$ as a topological model for ${\mathrm {String}}(G)$.

The crux of the proof of this theorem is showing that ${\mathrm {Gau}}(P)$ is homotopy equivalent to ${{\mathbb {P}}\mathrm {U}}$, i.e. that it is an Eilenberg-MacLane space $K({\mathbb {Z}};2)$. Part of the content in [NSW13] is to enhance this topological string group model to a smooth model in the sense that the groups appearing are Fréchet Lie groups.

The group extension ${\widehat{G}}\longrightarrow G$ agrees with the extension ${\mathrm {Sym}}_G(P) \longrightarrow G$ constructed in Sect. 3 when we set $M=G$ and $H={{\mathbb {P}}\mathrm {U}}$, and let G act on itself by left multiplication. Thus we immediately obtain

Corollary 8.3

Let $P \longrightarrow G$ be a basic ${\mathbb {P}}{{\text {U}}}$-bundle. The extension of diffeological groups

exhibits ${\mathrm {Sym}}_G(P)$ as a smooth model for ${\mathrm {String}}(G)$.

8.2 Smooth string 2-group models

Let G be a compact simply-connected Lie group, and let ${\mathcal {G}}$ be a bundle gerbe on G whose Dixmier–Douady class generates $\mathrm {H}^3(G;{\mathbb {Z}})$; such a bundle gerbe is said to be basic. Let $\varPhi :G \times G \longrightarrow G$ denote the left action of G on itself by left multiplication. In the spirit of Sect. 5, it is reasonable to expect that we should also be able to interpret the smooth 2-groups ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ as models for ${\mathrm {String}}(G)$. The idea of constructing ${\mathrm {String}}(G)$ as a smooth 2-group has also been considered in e.g. [BCSS07, SP11, Wal12a, NSW13, FRS16]. In the remainder of this section we will describe how ${\mathrm {Sym}}_G({\mathcal {G}})$ can be seen as a string 2-group model. By Theorem 5.36 it then follows that ${\mathfrak {Des}}_{{\mathsf {L}}}$ is also a model for ${\mathrm {String}}(G)$.

Smooth string 2-group models usually consist of extensions of G by the smooth 2-group ${{\mathsf {B}}}{{\text {U}}}(1)$, the delooping of the smooth abelian group ${{\text {U}}}(1)$. However, recall that in Theorem 5.27 we established ${\mathrm {Sym}}_G({\mathcal {G}})$ as an extension of $\underline{G}$ by the smooth abelian 2-group $\mathrm {HLBdl}^G$. Our point here is that what matters for string group models is only the homotopy type of the fibre and the total space of the map ${\mathrm {String}}(G) \longrightarrow G$, so that there is a lot of flexibility in choosing the smooth 2-group ${{\mathsf {A}}}$ that extends G. Observe that this ambiguity is inherent already in Definition 8.1. This forces us to state which smooth 2-groups ${{\mathsf {A}}}$ are admissible in order to obtain smooth 2-group extensions of G that deserve to be called string group models. Our proposed definition for smooth string 2-group models emphasises the structure of ${{\mathsf {A}}}$ as a smooth analogue of an Eilenberg-MacLane space $K({\mathbb {Z}};2)$. Note that for every smooth abelian 2-group ${{\mathsf {A}}}$ and any manifold M, we can define Čech cohomology of M with coefficients in ${{\mathsf {A}}}$ by evaluating (a delooping of ${{\mathsf {A}}}$) on the Čech nerve of good open coverings of M.

The definition of a smooth string 2-group model is thus a two-step process: we first fix the homotopy type of the extending 2-group ${{\mathsf {A}}}$ in a geometric way, and then we have to make precise when an ${{\mathsf {A}}}$-extension of G has the correct homotopy type.

Definition 8.4

Let H be a diffeological group. The delooping ${{\mathsf {B}}}\underline{H} \in {\mathscr {H}}$ is the category fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$ whose objects are the Cartesian spaces $c \in {{\mathscr {C}}\mathrm{art}}$, and whose morphisms $c_0 \longrightarrow c_1$ are pairs $(f_{01},h_{01})$ of smooth maps $f_{01} :c_0 \longrightarrow c_1$ and $h_{01} :c_0 \longrightarrow H$. Composition of morphisms is given by $(f_{12},h_{12}) \circ (f_{01},h_{01}) = \big (f_{12} \circ f_{01}, h_{01} \, (h_{12} \circ f_{01})\big )$.

If H is abelian, then ${{\mathsf {B}}}\underline{H}$ naturally becomes a smooth abelian 2-group.

Definition 8.5

A smooth 2-group ${{\mathsf {A}}}$ is string-admissible if it is abelian and equivalent (as a smooth 2-group) to the delooping ${{\mathsf {B}}}\underline{H}$ of a diffeological abelian group H whose underlying topological space is an Eilenberg-MacLane space $K({\mathbb {Z}};2)$.

From the equivalence ${{\mathsf {A}}}\simeq {{\mathsf {B}}}\underline{H}\,$ it follows that Čech cohomology with coefficients in ${{\mathsf {A}}}$ is equivalent to Čech cohomology with coefficients in H, shifted by one degree. Then since H has homotopy type $K({\mathbb {Z}};2)$, it follows that there are isomorphisms

$$\begin{aligned} {\check{\mathrm {H}}}{}^k(M; {{\mathsf {A}}}) \cong {\check{\mathrm {H}}}{}^k(M; {{\mathsf {B}}}\underline{H}) \cong \big [M, {{\mathsf {B}}}^{k+1}H\big ] \cong \big [M, K({\mathbb {Z}};k+2)\big ] \cong \mathrm {H}{}^{k+2}(M;{\mathbb {Z}}) \end{aligned}$$

for all $k \in {\mathbb {N}}$. (For the notion of Čech cohomology with coefficients in higher smooth groups, we refer the reader to [Sch13, NSS15].)

From any smooth principal 2-bundle ${{\mathsf {P}}}\longrightarrow \underline{M}$ over a manifold M with structure 2-group ${{\mathsf {A}}}$, we can distil a Čech cohomology class as follows: let ${{\mathcal {U}}}= \{U_i\}_{i \in I}$ be a good open covering of M. Denote intersections by $U_{i_1\cdots i_n}:=U_{i_1}\cap \cdots \cap U_{i_n}$. Viewing the (intersections of) open patches $U_{i_1 \cdots i_n} \hookrightarrow M$ as objects in $\underline{M}\,$, we denote by ${{\mathsf {P}}}_{|U_{i_1 \cdots i_n}}$ the fibres of ${{\mathsf {P}}}$ over these objects. By Definition 5.17, we can choose an object $\psi _i \in {{\mathsf {P}}}_{|U_i}$ for every $i \in I$. We can further choose an object ${{\mathsf {a}}}_{ij} \in {{\mathsf {A}}}_{|U_{ij}}$ for every $i,j \in I$ and an isomorphism $g_{ij} :\psi _{i|U_{ij}} \otimes {{\mathsf {a}}}_{ij} \longrightarrow \psi _{j|U_{ij}}$ in ${{\mathsf {P}}}_{|U_{ij}}$ (where we have chosen pullbacks of $\psi _i$ and $\psi _j$ to ${{\mathsf {P}}}_{|U_{ij}}$). Over the triple overlaps $U_{ijk}$ we obtain isomorphisms

$$\begin{aligned} \beta _{ijk} :\psi _{i|U_{ijk}} \otimes {{\mathsf {a}}}_{ij|U_{ijk}} \otimes {{\mathsf {a}}}_{jk|U_{ijk}} \longrightarrow \psi _{i|U_{ijk}} \otimes {{\mathsf {a}}}_{ik|U_{ijk}} \ , \end{aligned}$$

which are uniquely determined by the properties of the Grothendieck fibration ${{\mathsf {P}}}\longrightarrow \underline{M}\,$ (as previously, since $\underline{M}$ has discrete fibres, it follows that ${{\mathsf {P}}}\times _{\underline{M}}^{\mathtt {h}} {{\mathsf {P}}}= {{\mathsf {P}}}\times _{\underline{M}} {{\mathsf {P}}}$). Since the morphisms $(1_{\psi _{i|U_{ijk}}}, \beta _{ijk})$ lie in the image of the action functor ${{\mathsf {P}}}\times {{\mathsf {A}}}\longrightarrow {{\mathsf {P}}}\times _{\underline{M}} {{\mathsf {P}}}$, there are unique isomorphisms

$$\begin{aligned} \alpha _{ijk} :{{\mathsf {a}}}_{ij|U_{ijk}} \otimes _{{\mathsf {A}}}{{\mathsf {a}}}_{jk|U_{ijk}} \longrightarrow {{\mathsf {a}}}_{ik|U_{ijk}} \end{aligned}$$

in ${{\mathsf {A}}}_{|U_{ijk}}$, which satisfy the required coherence condition over quadruple overlaps by the fact that they are constructed as Cartesian lifts of identity morphisms. Hence these data assemble into an ${{\mathsf {A}}}$-valued Čech 1-cocycle on M with respect to the open covering ${{\mathcal {U}}}$. One can check that other choices of coverings and sections lead to 1-cocycles that become equivalent to $({{\mathsf {a}}}_{ij}, \alpha _{ijk})$ when passing to a common refinement of good open coverings.

Definition 8.6

Let G be a compact simply-connected Lie group, and let ${{\mathsf {A}}}$ be a string-admissible smooth 2-group. A smooth 2-group model for ${\mathrm {String}}(G)$ is a smooth 2-group extension

such that the principal 2-bundle ${\mathrm {String}}(G) \longrightarrow \underline{G}$ represents a generator of $\mathrm {H}^3(G;{\mathbb {Z}}) \cong {\mathbb {Z}}$ under the isomorphism ${\check{\mathrm {H}}}{}^1(G;{{\mathsf {A}}}) \cong \mathrm {H}^3(G;{\mathbb {Z}})$.

With these definitions we have

Theorem 8.7

For any 2-connected manifold M, the smooth 2-group $\mathrm {HLBdl}^M$ is string-admissible.

Theorem 8.8

Let G be a compact simply-connected Lie group, and let ${\mathcal {G}}\in \mathrm {BGrb}(G)$ be a basic bundle gerbe. Let ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ be the smooth 2-group extensions of $\underline{G}$ by $\mathrm {HLBdl}^G$ constructed from ${\mathcal {G}}$ with respect to the left action of G on itself by left multiplication. Then both ${\mathrm {Sym}}_G({\mathcal {G}})$ and ${\mathfrak {Des}}_{{\mathsf {L}}}$ are smooth 2-group models for ${\mathrm {String}}(G)$ in the sense of Definition 8.6.

Remark 8.9

Note that there is a model for ${\mathrm {String}}(G)$ based on regression and transgression of the basic gerbe on G [Wal12a]. Similarly, our model for ${\mathrm {String}}(G)$ which we obtain from ${\mathfrak {Des}}_{{\mathsf {L}}}$ also heavily relies on the transgression-regression formalism. However, the resulting models are very different: Waldorf’s model in [Wal12a] is the regression of the transgression of the basic gerbe. Waldorf observes that this gerbe picks up a multiplicative structure upon application of ${\mathcal {R}}\circ {\mathcal {T}}$. Since any gerbe on a manifold can be seen as an extension of M by ${\mathrm {B}}{{\text {U}}}(1)$ as Lie groupoids, the resulting gerbe provides a string group model in the sense of [SP11]. Our construction differs from this significantly not only in the fact that we work with smooth 2-groups instead of Lie 2-groups; most notably, we obtain an extension of G by the much larger smooth 2-group ${\mathrm {B}}(\underline{{{\text {U}}}(1)^H})$, which is not equivalent to ${\mathrm {B}}\underline{{{\text {U}}}(1)}$ as a smooth 2-group, but only on the level of their underlying homotopy types (see Theorem 8.7 as well as [Bun20b]). $\square$

The rest of this section is devoted to the proofs of Theorems 8.7 and 8.8. We begin with a few results that will combine to prove that $\mathrm {HLBdl}^M$ is string-admissible. Then we will prove Theorem 8.8 by observing that the $\mathrm {HLBdl}^G$-valued Čech 1-cocycles we obtain from the 2-bundle ${\mathrm {Sym}}_G({\mathcal {G}})$ agree with those obtained from local trivialisations of the bundle gerbe ${\mathcal {G}}$.

Lemma 8.10

Let M be a simply-connected manifold and $x\in M$ a fixed base point. Then the evaluation map ${\mathrm {ev}}_x :{{\text {U}}}(1)^M \longrightarrow {{\text {U}}}(1)$, $g \longmapsto g(x)$ and the inclusion ${{\mathsf {c}}}:{{\text {U}}}(1) \longrightarrow {{\text {U}}}(1)^M$ as constant maps form a homotopy equivalence of diffeological spaces.¹⁰

Proof

Since ${\mathrm {ev}}_x \circ {{\mathsf {c}}}= 1_{{{\text {U}}}(1)}$, it is enough to construct a smooth homotopy ${{\mathsf {c}}}\circ {\mathrm {ev}}_x\cong 1_{{{\text {U}}}(1)^M}$. Let $\pi :{\mathbb {R}}\longrightarrow {{\text {U}}}(1)$, $r \longmapsto \exp (2\pi \, \mathrm {i}\, r)$ be the universal cover of ${{\text {U}}}(1)$. The assumption that M is simply-connected implies (see e.g. [Bre93, Theorem 4.1]) that the diagram

admits a unique continuous lift ${\widehat{f}}:M \longrightarrow {\mathbb {R}}$ for arbitrary $f\in {{\text {U}}}(1)^M$ after fixing the lift at one point. We verify that the map ${\widehat{f}}$ is smooth. Fix a point $y \in M$ and a sufficiently small open neighbourhood $U_y$ of y which we identify with an open subset of ${\mathbb {R}}^d$, where $d=\dim (M)$. The restriction of f to $U_y$ is a plot of ${{\text {U}}}(1)$. Hence by Proposition 2.9 it admits a smooth lift ${\widehat{f}}_y:U_y\longrightarrow {\mathbb {R}}$ for sufficiently small $U_y$. From the uniqueness statement for lifts we obtain ${\widehat{f}}_{|U_y} = {\widehat{f}}_y +r_y$ for a fixed integer $r_y\in {\mathbb {Z}}$. This implies that ${\widehat{f}}$ is smooth and hence shows that the map $\pi ^M:{\mathbb {R}}^M \longrightarrow {{\text {U}}}(1)^M$ is surjective.

Consider the commutative diagram

where ${\widehat{{{\mathsf {c}}}}}\,(r)(y) = r$ for all $y \in M$, and where $\widehat{{\mathrm {ev}}_x}(g') = g'(x)$ for all $g'\in {\mathbb {R}}^M$. We define a homotopy ${\widehat{h}} :1_{{\mathbb {R}}^M}\longrightarrow {\widehat{{{\mathsf {c}}}}} \circ \widehat{{\mathrm {ev}}_x}$ by setting ${\widehat{h}}_t(g')(y) = g'(y) \,(1-t) + g'(x)\, t$. This homotopy descends to the desired homotopy $h:1_{{{\text {U}}}(1)^M} \longrightarrow {{\mathsf {c}}}\circ {\mathrm {ev}}_x$.

We verify that the homotopy h is smooth: let n be a natural number, $c \cong {\mathbb {R}}^n$ a Cartesian space and $f:c \longrightarrow {{\text {U}}}(1)^M\times [0,1]$ a plot; that is, the maps ${\text {pr}}_{[0,1]} \circ f:c \longrightarrow [0,1]$ and $({\text {pr}}_{{{\text {U}}}(1)^M}\circ f)^{\dashv }:c \times M \longrightarrow {{\text {U}}}(1)$ are smooth. We have to show that $h\circ f :c \longrightarrow {{\text {U}}}(1)^M$ is a plot. By the arguments above we can lift $({\text {pr}}_{{{\text {U}}}(1)^M}\circ f)^{\dashv }$ to a smooth map $c \times M \longrightarrow {\mathbb {R}}$ because $c\times M$ is simply-connected. This implies that we can lift f to a smooth map ${\widehat{f}}:c \longrightarrow {\mathbb {R}}^M\times [0,1]$ making the diagram

commute. The result now follows since ${\widehat{h}}$ and the projection $\pi ^M:{\mathbb {R}}^M\longrightarrow {{\text {U}}}(1)^M$ are smooth. $\square$

Lemma 8.11

There is an inclusion ${{\mathsf {B}}}(\underline{{{\text {U}}}(1)^M}) \hookrightarrow \mathrm {HLBdl}^M$ of smooth 2-groups which is given by sending $c \in {{\mathsf {B}}}(\underline{{{\text {U}}}(1)^M})$ (cf. Definition 8.4) to the trivial line bundle on $c \times M$. If $\mathrm {H}^2(M;{\mathbb {Z}}) = 0$, then this inclusion is an equivalence.

Proof

We readily see that the inclusion respects the group structures, and that it is fully faithful. If $\mathrm {H}^2(M;{\mathbb {Z}}) = 0$, then $\mathrm {HLBdl}^M{}_{|c} \cong \mathrm {HLBdl}(c \times M)$ is connected, so that in this case the inclusion is also fully faithful on all fibres. Thus it is an equivalence on every fibre and hence an equivalence in the 2-category ${\mathscr {H}}$ by [Vis05, Proposition 3.36].

$\square$

Combining Lemmas 8.10 and 8.11, we conclude that $\mathrm {HLBdl}^M$ is string-admissible for any 2-connected manifold M; that is, we have proven Theorem 8.7.

For the diffeological group $H = {{\text {U}}}(1)^M$ and a 2-connected manifold M, there is an explicit isomorphism ${\check{\mathrm {H}}}{}^k(X;{{\text {U}}}(1)^M) \cong {\check{\mathrm {H}}}{}^k(X;{{\text {U}}}(1))$ for $k>0$, for any manifold X, given by

Proposition 8.12

Let M be a 2-connected manifold with a fixed base point $x \in M$. For any manifold X, evaluation at $x \in M$ induces an isomorphism ${\check{\mathrm {H}}}{}^k(X; {{\text {U}}}(1)^M) \cong {\check{\mathrm {H}}}{}^k(X; {{\text {U}}}(1))$ for $k>0$ of Čech cohomology groups with coefficients in the sheaves of smooth ${{\text {U}}}(1)^M$-valued and ${{\text {U}}}(1)$-valued functions, respectively.

Proof

Consider the sequence of diffeological groups

$$\begin{aligned} 1 \longrightarrow {\mathbb {Z}}\longrightarrow {\mathbb {R}}^M \longrightarrow {{\text {U}}}(1)^M \longrightarrow 1 \ , \end{aligned}$$

which is exact by the argument from the proof of Lemma 8.10. The sheaf ${\mathbb {R}}^M$ admits a partition of unity by picking a partition of unity for the sheaf of smooth ${\mathbb {R}}$-valued functions and a constant extension to ${\mathbb {R}}^M$-valued functions; hence ${\check{\mathrm {H}}}{}^k(X; {\mathbb {R}}^M)=0$ for any manifold X and for any $k\ge 1$. Now the statement follows from applying the five lemma to the diagram

induced by the long exact sequence in sheaf cohomology and the evaluation at $x \in M$.

$\square$

It remains to determine the Čech cohomology class in ${\check{\mathrm {H}}}{}^1(G;\mathrm {HLBdl}^G) \cong \mathrm {H}^3(G;{\mathbb {Z}}) \cong {\mathbb {Z}}$ determined by the extension ${\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}\,$. The isomorphisms from Lemma 8.11 and Proposition 8.12 are useful in achieving this. From the smooth 2-group extension ${\mathrm {Sym}}_G({\mathcal {G}}) \longrightarrow \underline{G}$ we can extract a Čech 2-cocycle on G with values in the sheaf of smooth ${{\text {U}}}(1)^G$-valued functions. To construct it, we first follow the procedure of the paragraph preceding Definition 8.6 to extract $\mathrm {HLBdl}^G$-valued cocycle data and then choose local trivialisations of the line bundles which comprise it (which amounts to choosing an inverse for the equivalence from Lemma 8.11).

Let ${{\mathcal {U}}}= \{ U_i\}_{i \in I}$ be a good open cover of G, let $\pi _i :U_i \times G \longrightarrow G$ denote the projection onto the second factor, and let $m_i:U_i \times G \longrightarrow G$ be the multiplication map restricted to $U_i \times G$. We choose and fix 1-isomorphisms $\psi _i :m_i^* {\mathcal {G}} \longrightarrow \pi _i^* {\mathcal {G}}$ along with adjoint inverses $\psi _i^{-1}$, which induce equivalences ${\mathrm {Sym}}_G ({\mathcal {G}})_{|U_i}\cong \mathrm {HLBdl}(U_i\times G)$ of groupoids.

On double intersections $U_{ij}$ we can form the automorphism $\psi _{ij}:=\psi ^{-1}_{j|U_{ij}} \circ \psi _{i|U_{ij}}$ of $m_{ij}^*{\mathcal {G}}$. The isomorphism $\psi _{ij}$ can be identified with a line bundle $L_{ij}$ on $U_{ij}\times G$. Since $\mathrm {H}^2(G;{\mathbb {Z}})=0$, we can choose and fix a trivialisation of $L_{ij}$ for each $i,j \in I$.

On triple intersections $U_{ijk}$ we get a 2-isomorphism $\psi _{ijk}:\psi _{jk|U_{ijk}} \circ \psi _{ij|U_{ijk}} \longrightarrow \psi _{ik|U_{ijk}}$ inducing an isomorphism $L_{jk} \otimes L_{ij}\longrightarrow L_{ik}$ of line bundles over ${U_{ijk}}\times G$. (In contrast to the construction in the paragraph above Definition 8.6, here the isomorphisms $\psi _{ijk}$ can be obtained directly from the choice of $\psi _{ij}$.) Using the trivialisations of these line bundles we obtain a smooth map ${U_{ijk}}\times G \longrightarrow {{\text {U}}}(1)$ or equivalently a map $c_{ijk}:U_{ijk} \longrightarrow {{\text {U}}}(1)^G$. The collection $c_{ijk}$ form a smooth ${{\text {U}}}(1)^G$-valued Čech 2-cocycle.

The corresponding cohomology class is independent of all choices involved: let $\psi _i' :m_i^* {\mathcal {G}} \longrightarrow \pi _i^* {\mathcal {G}}$ be a different set of 1-isomorphisms. The automorphism $\psi _i^{-1} \circ \psi _i'$ of $m_i^* {\mathcal {G}}$ can be identified with a line bundle ${\varLambda }_i$ over $U_i \times G$. The definition of $L_{ij}$ implies $L_{ij}\otimes {\varLambda }_i \cong {\varLambda }_j \otimes L'_{ij}$. We can pick once and for all trivialisations of all bundles involved to identify this morphism with a function $A_{ij}:U_{ij}\times G \longrightarrow {{\text {U}}}(1)$. The diagram

commutes over $U_{ijk}$, which follows from the fact that all inverses were chosen to be adjoint so that the corresponding diagram involving $\psi _i$ and $\psi _i'$ commutes. Applying the trivialisations we get

$$\begin{aligned} c_{ijk}\, A_{ik}= c'_{ijk}\, A_{ij}\, A_{jk} \ . \end{aligned}$$

This argument also shows that the cocycles define the same cohomology class if $\psi _i'=\psi _i$ and only the trivialisations of $L_{ij}$ differ.

The image of $c_{ijk}$ in ${\check{\mathrm {H}}}{}^2(G; {{\text {U}}}(1)^G)$ under the isomorphism ${\check{\mathrm {H}}}{}^2(G; {{\text {U}}}(1)^G) \cong {\check{\mathrm {H}}}{}^2(G; {{\text {U}}}(1))$ of Proposition 8.12 can be computed by restricting each $\psi _i$ to $U_i\times \{ e\} \subset U_i\times G$; the restriction $\psi _{|U_i\times \{ e\}}$ is a 1-isomorphism ${\mathcal {G}}_{|U_i} \longrightarrow {\mathcal {G}}|_e$. After fixing once and for all a trivialisation of ${\mathcal {G}}_{|e}$, this is just a trivialisation of ${\mathcal {G}}_{|U_i}$. This shows that the image of $c_{ijk}$ in ${\check{\mathrm {H}}}{}^2(G; {{\text {U}}}(1))\cong \mathrm {H}^3(G;{\mathbb {Z}})$ agrees with the cocycle $c_{\mathcal {G}}$ classifying the bundle gerbe ${\mathcal {G}}$, which proves Theorem 8.8.

Remark 8.13

The arguments involving cocycles can be adjusted to the simpler case of principal bundles over the Lie group G. In that case, starting from a principal ${{\text {U}}}(1)$-bundle P on G we get a principal ${{\text {U}}}(1)^G$-bundle ${\mathrm {Sym}}_G(P)$ on G which is homotopy equivalent to P. The homotopy equivalence is induced by the maps ${\mathrm {ev}}_x$ and ${{\mathsf {c}}}$ from Lemma 8.10. We can iterate the procedure to get larger and larger groups ${\mathrm {Sym}}_G( \cdots {\mathrm {Sym}}_G({\mathrm {Sym}}_G(P))\cdots )$. However, these groups are all topologically equivalent, so that iterating the procedure does not produce anything that is topologically novel. $\square$

Properties of Smooth Principal 2-Bundles

1.1 Surjectivity on objects and homotopy pullbacks

Here we provide some technical background on smooth groupoids, as introduced in Definition 5.4.

Lemma A.1

Let $\pi :{{\mathsf {X}}}\longrightarrow {{\mathscr {C}}\mathrm{art}}$ and $\pi ' :{{\mathsf {P}}}\longrightarrow {{\mathscr {C}}\mathrm{art}}$ be objects in ${\mathscr {H}}$.

• (1) Either ${{\mathsf {X}}}= \varnothing$ or $\pi$ is surjective on objects.

• (2) Let $p :{{\mathsf {P}}}\longrightarrow {{\mathsf {X}}}$ be a morphism in ${\mathscr {H}}$ whose underlying functor is an essentially surjective Grothendieck fibration. Then p is surjective on objects.

Proof

To see (1), observe that ${{\mathscr {C}}\mathrm{art}}$ has a terminal object $* \in {{\mathscr {C}}\mathrm{art}}$. Thus since $\pi$ is a Grothendieck fibration, if ${{\mathsf {X}}}_{|*} = \pi ^{-1}(*)$ is non-empty then so is ${{\mathsf {X}}}_{|c}$ for any $c \in {{\mathscr {C}}\mathrm{art}}$. For any $c \in {{\mathscr {C}}\mathrm{art}}$ there exists a morphism $x :* \longrightarrow c$ in ${{\mathscr {C}}\mathrm{art}}$ given by choosing any point $x \in c$. It follows that as soon as ${{\mathsf {X}}}\ne \varnothing$, it has only non-empty fibres over ${{\mathscr {C}}\mathrm{art}}$.

Claim (2) follows from the general observation that a Grothendieck fibration is essentially surjective if and only if it is surjective on objects. $\square$

We now consider the setup of Definition 5.16.

Lemma A.2

Let ${\mathscr {C}}$ be a category, let $\pi _i :{{\mathsf {D}}}_i \longrightarrow {\mathscr {C}}$, for $i = 0,1$, and $\pi _{{\mathsf {E}}}:{{\mathsf {E}}}\longrightarrow {\mathscr {C}}$ be Grothendieck fibrations in groupoids, and let $F_i :{{\mathsf {D}}}_i \longrightarrow {{\mathsf {E}}}$, for $i=0,1$, be morphisms of categories fibred in groupoids over ${\mathscr {C}}$.

• (1) $({{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1, \pi _\mathtt{h}) \in {\mathscr {H}}$, i.e. $\pi _\mathtt{h}$ is a Grothendieck fibration in groupoids.

• (2) Any morphism $G = (G_0, G_{{\mathsf {E}}}, G_1)$ of diagrams

  

  in ${\mathscr {H}}$, where all vertical morphisms are equivalences, induces an equivalence ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1 \longrightarrow {{\mathsf {D}}}'_0 \times _{{{\mathsf {E}}}'}^\mathtt{h} {{\mathsf {D}}}'_1$.

• (3) If $F_1$ (resp. $F_0$) is a Grothendieck fibration in groupoids, then the inclusion ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}} {{\mathsf {D}}}_1 \hookrightarrow {{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ is an equivalence, and the projections ${\text {pr}}_0^\mathtt{h} :{{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1 \longrightarrow {{\mathsf {D}}}_0$ and ${\text {pr}}_0 :{{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}} {{\mathsf {D}}}_1 \longrightarrow {{\mathsf {D}}}_0$ (resp. the projections ${\text {pr}}_1^\mathtt{h}$ and ${\text {pr}}_1$ to ${{\mathsf {D}}}_1$) are Grothendieck fibrations in groupoids.

Proof

To prove (1), we first show that every morphism in ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ is $\pi _\mathtt{h}$-Cartesian. Consider morphisms $(\psi _0,\psi _1) :(d'_0,\eta ',d'_1) \longrightarrow (d''_0,\eta '',d''_1)$ and $(\varphi _0, \varphi _1) :(d_0, \eta , d_1) \longrightarrow (d''_0, \eta '', d''_1)$ in ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$. By assumption $\pi _0 (d_0) = \pi _1(d_1)$ in ${\mathscr {C}}$ (and analogously for $d'_i, d''_i$), and $\pi _0(\psi _0) = \pi _1(\psi _1)$ (and analogously for $\varphi _i$). Let $\chi :\pi _0(d_0) \longrightarrow \pi _0(d'_0)$ be a morphism in ${\mathscr {C}}$ such that $\pi _0(\psi _0) \circ \chi = \pi _0(\varphi _0)$. Since $\pi _{{\mathsf {E}}}$ is a Grothendieck fibration in groupoids, there exists a unique lift $\chi _{{{\mathsf {E}}},i} :F_i(d_i) \longrightarrow F_i(d'_i)$ induced by each of the pairs $(F_i(\psi _i), F_i(\varphi _i))$ of morphisms in ${{\mathsf {E}}}$. Similarly, the pairs $(\psi _i,\varphi _i)$ induce unique lifts $\chi _i:d_i\longrightarrow d_i'$ of $\chi$ to ${{\mathsf {D}}}_i$ along $\pi _i$. The uniqueness of lifts (along $\pi _{{\mathsf {E}}}$) implies that $F_i(\chi _i) = \chi _{{{\mathsf {E}}},i}$ for $i = 0,1$. It remains to show that $(\chi _0, \chi _1)$ defines a morphism $(d_0, \eta , d_1) \longrightarrow (d'_0, \eta ', d'_1)$. That is, we need to prove that $F_1(\chi _1) \circ \eta = \eta ' \circ F_0(\chi _0)$ in ${{\mathsf {E}}}$. So far we have a diagram

in ${{\mathsf {E}}}$, where each face of this diagram commutes, apart from the back left square. The commutativity of that square is what we need to prove. For this, observe that both $\eta ' \circ F_0(\chi _0)$ and $\eta \circ F_1(\chi _1)$ provide lifts of $\chi$ to ${{\mathsf {E}}}$ with respect to the morphisms $\eta '' \circ F_0(\varphi _0) :F_0(d_0) \longrightarrow F_1(d''_1)$ and $F_1(\psi _1) :F_1(d'_1) \longrightarrow F_1(d''_1)$. The desired identity now follows from the uniqueness of such lifts along the functor $\pi _{{\mathsf {E}}}$.

Next we need to show that for any morphism $f :c \longrightarrow c'$ in ${\mathscr {C}}$ and any object $(d'_0, \eta ', d'_1)$ in ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ over $c'$, there exists a lift ${\widehat{f}} = (f_0,f_1)$ of f to ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ with codomain $(d'_0, \eta ', d'_1)$. Such a lift is obtained by lifting f to morphisms $f_i :d_i \longrightarrow d'_i$ in ${{\mathsf {D}}}_i$ using the fact that $\pi _i$ is a Grothendieck fibration in groupoids, for $i = 0,1$. An isomorphism $\eta :F_0(d_0) \longrightarrow F_1(d_1)$ compatible with $f_0, f_1$ is obtained by filling the horn given by the morphisms $\eta '\circ F_0(f_0)$ and $F_1(f_1)$ over the identity morphism $1_c$ in ${\mathscr {C}}$. The filler is an isomorphism since the fibre ${{\mathsf {E}}}_{|c}$ is a groupoid.

To prove (2), we note that by [Vis05, Proposition 3.36] the induced morphism $G_0 \times _{G_{{\mathsf {E}}}}^\mathtt{h} G_1$ is an equivalence in ${\mathscr {H}}$ if and only if it restricts to an equivalence of groupoids between all fibres of $\pi _\mathtt{h}$ and $\pi '_\mathtt{h}$. A direct inspection on any $c\in {\mathscr {C}}$ reveals that

$$\begin{aligned} \pi _\mathtt{h}^{-1}(c) = \pi _0^{-1}(c) \times _{\pi _{{\mathsf {E}}}^{-1}(c)}^\mathtt{h} \pi _1^{-1}(c) \end{aligned}$$

as groupoids, and it is well-known that equivalences of spans of groupoids induce equivalences on homotopy pullbacks of groupoids.

To prove (3), we first show that ${\text {pr}}_0^\mathtt{h}$ is a Grothendieck fibration in groupoids. Consider a span

in ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$, and a morphism $\chi _0 :d_0 \longrightarrow d'_0$ in ${{\mathsf {D}}}_0$ such that $\psi _0 \circ \chi _0 = \varphi _0$. We obtain a commutative triangle in ${{\mathsf {E}}}$ formed by the morphisms $F_1(\psi _1)$, $F_1(\varphi _1)$, and $\eta ' \circ F_0(\chi _0) \circ \eta ^{-1}$. Since $F_1$ is a Grothendieck fibration in groupoids, this gives rise to a unique lift $\chi _1:d_1\longrightarrow d_1'$ of the latter morphism to ${{\mathsf {D}}}_1$. The pair $(\chi _0, \chi _1)$ is automatically a morphism in ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ which projects to $\chi _0$. If $(\chi '_0, \chi '_1)$ were any other such filling over $\chi _0$ of the horn given by $(\psi _0, \psi _1)$ and $(\varphi _0, \varphi _1)$, it would immediately follow that $\chi _0' = \chi _0$, and the uniqueness of fillings of $\psi _1, \varphi _1$ over $\eta ' \circ F_0(\chi _0) \circ \eta ^{-1}$ would imply that $\chi _1' = \chi _1$.

Let $\varphi _0 :d_0 \longrightarrow d'_0$ be a morphism in ${{\mathsf {D}}}_0$, and let $(d'_0, \eta ', d'_1)$ be an object in ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ which projects to $d'_0$. Let $\varphi _1$ be a lift along $\pi _1$ of $f :=\pi _0(\varphi _0)$ with codomain $d'_1$. The pair of morphisms $(\eta ' \circ F_0(\psi _0), F_1(\psi _1))$ then gives rise to a cospan in ${{\mathsf {E}}}$. Both morphisms project to f in ${\mathscr {C}}$ and hence, since $\pi _{{\mathsf {E}}}$ is a Grothendieck fibration in groupoids, there exists a unique isomorphism $\eta :F_0(d_0) \longrightarrow F_1(d_1)$ such that $(d_0, \eta , d_1) \in {{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ and such that $(\psi _0, \psi _1)$ is a lift of $\psi _0$ to ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$ with codomain $(d'_0, \eta ', d'_1)$. The claim for ${\text {pr}}_0$ is proven in an entirely analogous way by restricting $\eta$, $\eta '$ and $\eta ''$ to be identity morphisms.

Finally, consider the inclusion functor ${{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}} {{\mathsf {D}}}_1 \hookrightarrow {{\mathsf {D}}}_0 \times _{{{\mathsf {E}}}}^\mathtt{h} {{\mathsf {D}}}_1$. Since ${\text {pr}}_0^\mathtt{h}$ is a Grothendieck fibration in groupoids, so is its restriction to each fibre over ${\mathscr {C}}$. It is well-known that the inclusion of a pullback of groupoids into the homotopy pullback is an equivalence in case one of the functors in the diagram is a Grothendieck fibration. Thus our inclusion functor is an equivalence on each fibre over ${\mathscr {C}}$, whence the result follows by [Vis05, Proposition 3.36]. $\square$

1.2 Relation to principal $\infty$-bundles

Our notion of smooth principal 2-bundle does not have any notion of ‘local triviality’ built into it. This differs from the version of a principal 2-bundle defined in [SP11], but is very much in the spirit of the definition of a principal $\infty$-bundle from [NSS15]. The fact that we require essential surjectivity is our version of saying that the (homotopy) fibres of the bundle should be non-empty. In contrast to [NSS15] we have to require fibration properties because we do not work purely in an $\infty$-categorical framework. We shall now show that an ${{\mathsf {H}}}$-principal 2-bundle in ${\mathscr {H}}$ in the sense of Definition 5.17 gives rise to a principal 2-bundle in the sense of [NSS15, Definition 3.4], adapted from a general $\infty$-topos (described e.g. by presheaves of $\infty$-groupoids) to our situation involving presheaves of groupoids. Let $p :{{\mathsf {P}}}\longrightarrow {{\mathsf {X}}}$ be a morphism in ${\mathscr {H}}$, and let ${{\mathsf {P}}}^{[\bullet ]}$ be the Čech nerve of p. We write ${\text {hocolim}}^{\mathscr {C}}$ (resp. ${\text {holim}}^{\mathscr {C}}$) for a homotopy colimit (resp. limit) taken in a simplicial model category ${\mathscr {C}}$.

Proposition A.3

Every morphism $p :{{\mathsf {P}}}\longrightarrow {{\mathsf {X}}}$ in ${\mathscr {H}}$ whose underlying functor is an essentially surjective Grothendieck fibration in groupoids gives rise to an effective epimorphism: the morphism

$$\begin{aligned} \underset{\Delta ^\mathrm{op}}{{\text {hocolim}}}^{\mathscr {H}}\, {{\mathsf {P}}}^{[\bullet ]} \longrightarrow {{\mathsf {X}}}\end{aligned}$$

from its Čech nerve to ${{\mathsf {X}}}$ is an equivalence.

Because of Lemma A.2 and the assumption that p is a Grothendieck fibration in groupoids, it does not matter here if one uses the coherent Čech nerve, formed using ${{\mathsf {P}}}\times _{{\mathsf {X}}}^\mathtt{h} \cdots \times _{{\mathsf {X}}}^\mathtt{h} {{\mathsf {P}}}$, or the strict Čech nerve, formed using ${{\mathsf {P}}}\times _{{\mathsf {X}}}\cdots \times _{{\mathsf {X}}}{{\mathsf {P}}}$.

Proof

We work with Hollander’s model structure on ${\mathscr {H}}$ [Hol08]. In this picture, ${\mathscr {H}}$ is a model category enriched, tensored and cotensored in the model category ${{\mathscr {G}}\mathrm {rpd}}$ (seen as a strict category). In both ${\mathscr {H}}$ and ${{\mathscr {G}}\mathrm {rpd}}$ all objects are fibrant, and the functor $\underline{{\mathscr {H}}} :{\mathscr {H}}^\text {op}\times {\mathscr {H}}\longrightarrow {{\mathscr {G}}\mathrm {rpd}}$ is homotopical by [Vis05, Proposition 3.35], i.e. it preserves weak equivalences in each argument. The enrichment of ${\mathscr {H}}$ in ${{\mathscr {G}}\mathrm {rpd}}$ even enhances to an enrichment over ${{\mathscr {S}}\mathrm {et}_{\Delta }}$, the category of simplicial sets with the Kan-Quillen model structure. Thus homotopy (co)limits in ${\mathscr {H}}$ can be computed using (co)bar constructions [Rie14]. Let Q denote a cofibrant replacement functor in ${\mathscr {H}}$, and let ${{\mathsf {Z}}}\in {\mathscr {H}}$ be an arbitrary object. Then

$$\begin{aligned} \underline{{\mathscr {H}}} \Big ( \underset{\Delta ^\mathrm{op}}{{\text {hocolim}}}^{\mathscr {H}}\, {{\mathsf {P}}}^{[\bullet ]} ,\, {{\mathsf {Z}}}\Big ) \cong \underset{\Delta }{{\text {holim}}}^{{\mathscr {G}}\mathrm {rpd}}\ \underline{{\mathscr {H}}} \big ( Q({{\mathsf {P}}}^{[\bullet ]}),\, {{\mathsf {Z}}}\big ) \cong \underset{\Delta }{{\text {holim}}}^{{\mathscr {G}}\mathrm {rpd}}\ \underline{{\mathscr {H}}} \big ( {{\mathsf {P}}}^{[\bullet ]},\, {{\mathsf {Z}}}\big ) \ , \end{aligned}$$

where the first equivalence stems from the fact that ${{\mathsf {Z}}}$ is fibrant and ${\mathscr {H}}$ is a ${{\mathscr {G}}\mathrm {rpd}}$-enriched model category, and the second equivalence stems from the fact that $\underline{{\mathscr {H}}}$ is homotopical. It thus suffices to prove that the functor

$$\begin{aligned} p^* :\underline{{\mathscr {H}}}({{\mathsf {X}}}, {{\mathsf {Z}}}) \longrightarrow \underset{\Delta }{{\text {holim}}}^{{\mathscr {G}}\mathrm {rpd}}\ \underline{{\mathscr {H}}} \big ( {{\mathsf {P}}}^{[\bullet ]},\, {{\mathsf {Z}}}\big ) =:{\mathfrak {Des}}_p({{\mathsf {Z}}}) \end{aligned}$$

is an equivalence of groupoids.

An object in ${\mathfrak {Des}}_p({{\mathsf {Z}}})$ is a pair $(G,\eta )$ of a functor $G :{{\mathsf {P}}}\longrightarrow {{\mathsf {Z}}}$ of categories fibred in groupoids over ${{\mathscr {C}}\mathrm{art}}$, together with a natural isomorphism $\eta _{|(p_0,p_1)} :G(p_0) \longrightarrow G(p_1)$ from $d_1^*G$ to $d_0^*G$ of functors over ${{\mathscr {C}}\mathrm{art}}$, where $d_i$ are the face maps in the simplicial object ${{\mathsf {P}}}^{[\bullet ]}$. This natural isomorphism is subject to the conditions $d_2^*\eta \circ d_0^*\eta = d_1^*\eta$ over ${{\mathsf {P}}}^{[3]}$ and ${\varDelta }^*\eta =1_G$ over ${{\mathsf {P}}}$, where ${\varDelta }:{{\mathsf {P}}}\longrightarrow {{\mathsf {P}}}^{[2]}$ is the diagonal map. A morphism $(G,\eta ) \longrightarrow (G',\eta ')$ in ${\mathfrak {Des}}_p({{\mathsf {Z}}})$ is a natural isomorphism $\gamma :G \longrightarrow G'$ in ${\mathscr {H}}$ such that $\eta ' \circ d_1^*\gamma = d_0^*\gamma \circ \eta$.

We first show that $p^*$ is essentially surjective: let $(G,\eta ) \in {\mathfrak {Des}}_p({{\mathsf {Z}}})$ be any object. We define a functor $F :{{\mathsf {X}}}\longrightarrow {{\mathsf {Z}}}$ as follows: first, recalling that p is surjective on objects by Lemma A.1, we choose a section $s :\mathtt{ob}({{\mathsf {X}}}) \longrightarrow \mathtt{ob}({{\mathsf {P}}})$ of the map of objects defined by p. Then we set $F(x) :=G(s(x)) \in {{\mathsf {Z}}}$ for $x\in {{\mathsf {X}}}$. Now consider a morphism $\psi :x \longrightarrow y$ in ${{\mathsf {X}}}$. Since p is a Grothendieck fibration, $\psi$ has a lift ${\widehat{\psi }} :{\widehat{x}} \longrightarrow s(y)$ to a morphism in ${{\mathsf {P}}}$ with codomain s(y), where $p({\widehat{x}})=x$. Define $F(\psi ) :F(x) \longrightarrow F(y)$ via the diagram

The naturality of $\eta$, together with the two conditions it satisfies and the fact that p is a Grothendieck fibration in groupoids, imply that F is a well-defined functor. Furthermore, $\eta$ establishes an isomorphism $p^*F = (F,1_F) \longrightarrow (G,\eta )$ in ${\mathfrak {Des}}_p({{\mathsf {Z}}})$. Thus $p^*$ is essentially surjective.

That $p^*$ is fully faithful follows from its explicit construction and the fact that p is essentially surjective. $\square$