Symplectic resolutions of quiver varieties

Abstract

In this article, we consider Nakajima quiver varieties from the point of view of symplectic algebraic geometry. We prove that they are all symplectic singularities in the sense of Beauville and completely classify which admit symplectic resolutions. Moreover we show that the smooth locus coincides with the locus of canonically $\theta$-polystable points, generalizing a result of Le Bruyn; we study their étale local structure and find their symplectic leaves. An interesting consequence of our results is that not all symplectic resolutions of quiver varieties appear to come from variation of GIT.

1 Introduction

Nakajima’s quiver varieties [46, 48], have become ubiquitous throughout representation theory. For instance, they play a key role in the categorification of representations of Kac-Moody Lie algebras and the corresponding theory of canonical bases. They provide étale-local models of singularities appearing in important moduli spaces, together with, in most cases, a canonical symplectic resolution given by varying the stability parameter. They give global constructions of certain moduli spaces, such as resolutions of du Val singularities [46], Hilbert schemes of points on them [36], and Uhlenbeck and Gieseker instanton moduli spaces [35, 47, 49].

Surprisingly, there seems to be no explicit criterion in the literature for when a quiver variety admits a symplectic resolution; often, in applications, suitable sufficient conditions for their existence are provided, but they do not appear always to be necessary. The main motivation of this article is to give such an explicit criterion. Following arguments of Kaledin, Lehn and Sorger (who consider the related case of moduli spaces of semistable sheaves on a K3 or abelian surface), our classification applies Drezet’s criteria to show that certain GIT quotients are locally factorial. To do so we undertake a careful study of the local and global algebraic symplectic geometry of quiver varieties.

Our classification begins by generalizing Crawley-Boevey’s decomposition theorem [16] of affine quiver varieties into products of such varieties, which we will call indecomposable, to the non-affine case; i.e., to quiver varieties with nonzero stability condition (Theorem 1.4). Along the way, we also generalize Le Bruyn’s theorem, [38, Theorem 3.2], which computes the smooth locus of these varieties, again from the affine to nonaffine setting (Theorem 1.15).

Then, our main result, Theorem 1.5, states that those quiver varieties admitting resolutions are exactly those whose indecomposable factors, as above, are one of the following types of varieties:

• (a) Varieties whose dimension vectors are indivisible roots;

• (b) Symmetric powers of deformations or partial resolutions of du Val singularities ($\mathbb {C}^2/\Gamma$ for $\Gamma < {{\,\mathrm{\mathrm {SL}}\,}}_2(\mathbb {C})$);

• (c) Varieties whose dimension vector are twice a root whose Cartan pairing with itself is $-2$ (i.e., the variety has dimension ten).

Here, a dimension vector $\alpha \in \mathbb {N}^{I}$ is called indivisible if $\gcd (\alpha _i) = 1$ for $i \in I$. The last type (c) is perhaps surprising: it is closely related to O’Grady’s examples [31, 39, 55, 56]. In this case, one cannot fully resolve or smoothly deform via a quiver variety, but after maximally smoothing in this way, the remaining singularities are étale-equivalent to the product of $V=\mathbb {C}^4$ with the locus of square-zero matrices in $\mathfrak {sp}(V)$ (as considered in preceding articles). Via the partial Springer resolution [10], the latter is resolved by the cotangent bundle of the Lagrangian Grassmannian of V. As explained in [31, Remark 4.6], [39], this resolution can also be obtained by blowing up the reduced singular locus (once), which makes sense globally on the quiver variety.

In the case of type (a), one can resolve or deform by varying the quiver (GIT) parameters. In fact, (for $\lambda = 0$) it is shown in [5] that all symplectic resolutions can be realised in this way. On the other hand, for quiver varieties of type (b), one cannot resolve in this way, but the variety is well-known to be isomorphic to another quiver variety (whose quiver is obtained by adding an additional vertex, usually called a framing, and arrows from it to the other vertices), which does admit a resolution via varying the parameters. Moreover, in this case, if the stability parameter is chosen to lie in the appropriate chamber, then the resulting resolution is a punctual Hilbert scheme of the minimal resolution of the original du Val singularity; see [36]. The other chambers give in general different resolutions: in fact, thanks to [4], they again produce all symplectic resolutions of symmetric powers of du Val singularities.

1.1 Symplectic resolutions

In order to state precisely our main results, we will require some notation, which we will restate in more detail in Sect. 2. Let $Q = (Q_0,Q_1)$ be a quiver with finitely many vertices and arrows. We fix a dimension vector $\alpha \in \mathbb {N}^{Q_0}$, deformation parameter $\lambda \in \mathbb {C}^{Q_0}$, and stability parameter $\theta \in \mathbb {Z}^{Q_0}$, such that $\lambda \cdot \alpha = \theta \cdot \alpha = 0$. Unless otherwise stated, we make the following assumption throughout the paper:

$$\begin{aligned} \mathrm{If} \ \theta \ne 0 \ \mathrm{then} \ \lambda \in \mathbb {R}^{Q_0}. \end{aligned}$$

(1)

Nakajima associated to this data the (generally singular) variety, called a “quiver variety.” We briefly recall the definition; see Sect. 2 for more details. Let ${{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )$ be the vector space of representations of Q of dimension $\alpha$. The group $\mathrm {G}(\alpha ) := \prod _{i \in Q_0} {{\,\mathrm{\mathrm {GL}}\,}}_{\alpha _i}(\mathbb {C})$ acts on ${{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )$; write $\mathfrak {g}(\alpha ) = {{\,\mathrm{\mathrm {Lie}}\,}}\mathrm {G}(\alpha )$. Then $\mathrm {G}(\alpha )$ also acts on $T^*{{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha ) \cong {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )$ with a moment map $\mu : T^* {{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha ) \rightarrow \mathfrak {g}(\alpha )^* \cong \mathfrak {g}(\alpha )$; here $\overline{Q}$ is the doubled quiver, obtained by adding reverse arrows to Q. To $\lambda \in \mathbb {C}^{Q_0}$ we can associate $(\lambda {\text {Id}}_i)_{i \in Q_0} \in \mathfrak {g}(\alpha )$. By abuse of notation we will consider $\mathbb {C}^{Q_0}$ to be a subset of $\mathfrak {g}(\alpha )$ in this way and write $\mu ^{-1}(\lambda )$ for the fiber over $(\lambda {\text {Id}}_i)_{i \in Q_0}$. Let $\mu ^{-1}(\lambda )^{\theta } \subseteq \mu ^{-1}(\lambda )$ be the $\theta$-semistable locus; this is the locus corresponding to representations of $\overline{Q}$ such that the dimension vector $\beta$ of every subrepresentation satisfies $\theta \cdot \beta \le 0$. Then Nakajima defined the variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ as:

$$\begin{aligned} \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) := \mu ^{-1}(\lambda )^{\theta } /\!\!/\!\, \mathrm {G}({\alpha }). \end{aligned}$$

It does not seem to be known whether $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, equipped with its natural scheme structure, is reduced (though we expect it is the case). Therefore, following Crawley-Boevey [17], we will consider throughout the paper all quiver varieties as reduced schemes.

Remark 1.1

The construction in [46, 48] is apparently more general, depending on an additional dimension vector, called the framing. However, as observed by Crawley-Boevey [15], every framed variety can be identified with an unframed one. In more detail, for the variety as in [46, 48] with framing $\beta \in \mathbb {N}^{Q_0}$, it is observed in [15, Section 1] that the resulting variety can alternatively be constructed by replacing Q by the new quiver $(Q_0\cup \{\infty \}, \widetilde{Q_1})$, where $\widetilde{Q_1}$ consists of $Q_1$ together with, for every $i \in Q_0$, $\beta _i$ new arrows from $\infty$ to i; then Nakajima’s $\beta$-framed variety is the same as $\mathfrak {M}_{{(\lambda ,0)}} ({(\alpha ,1)},{(\theta ,-\alpha \cdot \theta )})$. Thus, for the purposes of the questions addressed in this article, it is sufficient to consider the unframed varieties.

Let $R_{\lambda ,\theta }^+$ denote those positive roots of Q that pair to zero with both $\lambda$ and $\theta$. If $\alpha \notin \mathbb {N}R^+_{\lambda ,\theta }$ then $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) = \emptyset$, therefore we assume $\alpha \in \mathbb {N}R^+_{\lambda ,\theta }$. As defined by Beauville [2], a normal variety X is said to be a symplectic singularity if there exists an (algebraic) symplectic 2-form $\omega$ on the smooth locus of X such that $\pi ^* \omega$ extends to a regular 2-form on the whole of Y, for any resolution of singularities $\pi : Y \rightarrow X$. We say that $\pi$ is a symplectic resolution if $\pi ^* \omega$ extends to a non-degenerate 2-form on Y. Note that a symplectic resolution does not always exist, and when it does exist, it is not always unique.

Theorem 1.2

The variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is an irreducible symplectic singularity.

This theorem is important because symplectic singularities have become important in representation theory: on the one hand they include many of the most important examples (aside from quiver varieties, they include linear quotient singularities, nilpotent cones, orbit closures, Slodowy slices, hypertoric varieties, and so on), and on the other hand they exhibit important properties, at least in the conical case, such as the existence of a nice universal family of deformations [33, 51, 52] and of quantizations [8, 11, 40].

From both the representation theoretic and the geometric point of view, it is important to know when the variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ admits a symplectic resolution. In this article, we address this question, giving a complete answer. The first step is to reduce to the case where $\alpha$ is a root for which there exists a $\theta$-stable point in $\mu ^{-1}(\lambda )$. This is done via the canonical decomposition of $\alpha$, as described by Crawley-Boevey; it is analogous to Kac’s canonical decomposition. In this article, the term canonical decomposition will only refer to the former, which we now recall. Associated to $\lambda ,\theta$ is a combinatorially defined set $\Sigma _{\lambda ,\theta } \subset R_{\lambda ,\theta }^+$; see Sect. 2 below. Then $\alpha$ admits a canonical decomposition

$$\begin{aligned} \alpha = n_1 \sigma ^{(1)} + \cdots + n_k \sigma ^{(k)} \end{aligned}$$

(2)

with $\sigma ^{(i)} \in \Sigma _{\lambda ,\theta }$ pairwise distinct, such that any other decomposition of $\alpha$ into a sum of roots belonging to $\Sigma _{\lambda ,\theta }$ is a refinement of the decomposition (2). Closed points in $\mu ^{-1}(\lambda )$ correspond to representations of the so-called deformed preprojective algebra $\Pi ^{\lambda }(Q)$; see Sect. 2.1 for details. Then points of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ are in bijection with isomorphism classes of $\theta$-polystable representations of $\Pi ^{\lambda }(Q)$ (equivalently, representations of the doubled quiver of moment $\lambda$ which decompose as direct sums of $\theta$-stable representations) of dimension $\alpha$. Generalizing [15, Theorem 1.2], Proposition 3.18 implies

Theorem 1.3

There exists a $\theta$-stable representation of the deformed preprojective algebra $\Pi ^{\lambda }(Q)$ of dimension $\alpha$ if and only if $\alpha \in \Sigma _{\lambda ,\theta }$.

Crawley-Boevey’s Decomposition Theorem [16], which we will show holds in somewhat greater generality, then implies that the canonical decomposition gives a decomposition of the quiver variety as a product of varieties for each of the summands (the first statement of the next theorem). We show that the question of existence of symplectic resolutions of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ can be reduced to the analogous question for each factor.

Theorem 1.4

With respect to the canonical decomposition (2):

• (a) The symplectic variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is isomorphic to $S^{n_1} \mathfrak {M}_{{\lambda }} ({\sigma ^{(1)}},{\theta }) \times \cdots \times S^{n_k} \mathfrak {M}_{{\lambda }} ({\sigma ^{(k)}},{\theta })$.

• (b) $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ admits a projective symplectic resolution if and only if each $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admits a projective symplectic resolution.

Here $S^n X$ denotes the nth symmetric product of X.

To finish the classification, it suffices to describe the case $\alpha \in \Sigma _{\lambda ,\theta }$. Write $\gcd (\alpha )$ for the greatest common divisor of the integers $\{ \alpha _i \}_{i \in Q_0}$; it is divisible if $gcd(\alpha )> 1$, and otherwise indivisible. Let $p(\alpha ) := 1-\frac{1}{2}(\alpha ,\alpha )$ where $(-,-)$ is the Cartan pairing associated to the undirected graph underlying the quiver, i.e., $(e_i, e_j) = 2 - |\{a \in Q_1\, | \, a :i \rightarrow j \text { or } a:j \rightarrow i\} |$, for elementary vectors $e_i, e_j$. As we will show below (in Corollary 3.24), $2 p(\alpha ) = \dim \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. Finally, as we will recall in Sect. 2, elements $\alpha \in \Sigma _{\lambda ,\theta }$ are divided into real roots (when $p(\alpha ) = 0$) and imaginary roots (when $p(\alpha ) > 0$). The case $p(\alpha )=1$ is particularly important and called isotropic, since it means $(\alpha ,\alpha )=0$. When $p(\alpha ) > 0$ we say that $\alpha$ is anisotropic. Note that, when $\sigma ^{(i)}$ is anisotropic in the canonical decomposition (2), then $n_i=1$ (see Corollary 2.3 below).

Our main theorem is then:

Theorem 1.5

Let $\alpha \in \Sigma _{\lambda ,\theta }$. Then $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ admits a projective symplectic resolution if and only if $\alpha$ is indivisible or $\left( \gcd (\alpha ),p\left( \gcd (\alpha )^{-1} \alpha \right) \right) = (2,2)$.

The latter case in the theorem will be referred to as “the (2, 2) case”.

If $\alpha \in \Sigma _{\lambda ,\theta }$ is indivisible and anisotropic, then a projective symplectic resolution of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is given by moving $\theta$ to a generic stability parameter. However, this fails in the (2, 2) case. It seems unlikely that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ can be resolved by another quiver variety in this case. Instead, we show that the 10-dimensional symplectic singularity $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ can be resolved by blowing up the singular locus. We will need the partial ordering $\ge$ on stability conditions, where $\theta ' \ge \theta$ if every $\theta '$-semistable representation is $\theta$-semistable; see Sect. 2.4 below.

Theorem 1.6

Let $\alpha \in \Sigma _{\lambda ,\theta }$, and suppose $\left( \gcd (\alpha ),p\left( \gcd (\alpha )^{-1} \alpha \right) \right) = (2,2)$. Let $\theta '$ be a generic stability parameter such that $\theta ' \ge \theta$.

If $\widetilde{\mathfrak {M}}_{\lambda }(\alpha ,\theta ')$ is the blowup of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '})$ along the reduced singular locus, then the canonical morphism $\pi : \widetilde{\mathfrak {M}}_{\lambda }(\alpha ,\theta ') \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is a projective symplectic resolution of singularities.

In most cases where a projective symplectic resolution does not exist, we can prove that neither does a proper one exist (note that every projective resolution is proper but not conversely). We say that $\alpha \in \Sigma _{\lambda ,\theta }$ is “$\Sigma$-divisible” if $\alpha = m\beta$ for $m \ge 2$ and $\beta \in \Sigma _{\lambda ,\theta }$. This is a slightly stronger condition than being divisible, although they coincide in most cases: see Theorem 2.2 below.

Theorem 1.7

If $\alpha \in \Sigma _{\lambda ,\theta }$ is $\Sigma$-divisible, and $\left( \gcd (\alpha ),p\left( \gcd (\alpha )^{-1} \alpha \right) \right) \ne (2,2)$, then $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ does not admit a proper symplectic resolution.

Moreover, for general $\alpha \in \mathbb {N}^{Q_0}$, if there exists a $\Sigma$-divisible factor $\sigma ^{(i)}$ in the decomposition (2) that satisfies $\left( \gcd (\sigma ^{(i)}),p\left( \gcd (\sigma ^{(i)})^{-1} \sigma ^{(i)} \right) \right) \ne (2,2)$, then $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ does not admit a proper symplectic resolution.

Remark 1.8

Most of the literature deals with projective rather than proper resolutions. However, there are interesting examples of proper symplectic resolutions that are not projective. For example, in [1] such examples are constructed admitting Hamiltonian torus actions of maximal dimension (this condition is called hypertoric there, which generalizes the usual definition of hypertoric variety).

It seems to be an interesting question if, whenever a proper symplectic resolution exists, also a projective symplectic resolution exists. More generally, it seems reasonable to ask whether, if a proper symplectic resolution exists, then every proper $\mathbb {Q}$-factorial terminalization is symplectic; if we restrict to projective resolutions and terminalizations, then the proof of [52, Theorem 5.5] shows that this holds at least when the singularity is conical with homogeneous generic symplectic form.

1.2 Symplectic leaves and the étale local structure

As Hamiltonian reductions, quiver varieties have a natural Poisson structure. The symplectic leaves of this Poisson structure are the maximal connected (analytic immersed) submanifolds on which the Poisson bracket is non-degenerate. Put differently, the reduction naturally is foliated by symplectic submanifolds. For example, the locus of stable representations of the doubled quiver inside $\mu ^{-1}(\lambda )$ consists of free closed orbits under the group $\mathrm {PG}(\alpha ):=\mathrm {G}(\alpha )/\mathbb {C}^{\times }$, hence its Hamiltonian reduction here is well known to be symplectic. If nonempty, this forms an open dense symplectic leaf of the quiver variety.

Since we have shown that quiver varieties have symplectic singularities, thanks to [30, Theorem 2.3], they must necessarily be a finite union of symplectic leaves and the latter are algebraic. It has long been assumed that the leaves are precisely the strata $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ given by the representation-type stratification. Here $\tau$ is a decomposition of $\alpha$ in $\Sigma _{\lambda ,\theta }$. Since this explicit identification of the symplectic leaves is crucial later in the article, we provide a complete proof that this is indeed the case.

Theorem 1.9

The symplectic leaves of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ are the representation-type strata $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$.

This result follows from Proposition 3.15 and Corollary 3.25. The classification of symplectic leaves already appears in [43], however there seems to be a gap in the proof given there; see remark 3.26.

Theorem 1.9 allows us to give a combinatorial classification, in Corollary 1.17 below, of those quiver varieties that are smooth.

An important tool in both the proof of Theorem 1.9 and later results on the factoriality of quiver varieties is an étale local description of the varieties. In the case of trivial stability parameter $\theta = 0$, this étale local picture was described by Crawley-Boevey in [17], where it was used to prove that those quiver varieties are normal. In Sect. 3.2 we show that this étale local description holds for all stability parameters. See Theorem 3.3 for the precise statement.

A relative version of Theorem 3.3, proving an étale local description of the morphism $\mathfrak {M}(\alpha ,\theta ) \rightarrow \mathfrak {M}(\alpha ,\theta ')$ is given in [4]. This result allows the authors to completely classify (in the case of a framed affine Dynkin quiver) those walls in the space of stability parameters that are flops; resp. are divisorial contractions. This is a key step in showing (as mentioned above) that all symplectic resolutions of symmetric powers of du Val singularities are given by variation of GIT.

1.3 Factoriality of quiver varieties

The real difficulty in the proof of Theorem 1.5 is in showing that if $\alpha \in \Sigma _{\lambda ,\theta }$ is divisible and anisotropic,

$$\begin{aligned} \left( \gcd (\alpha ),p\left( \gcd (\alpha )^{-1} \alpha \right) \right) \ne (2,2), \end{aligned}$$

(3)

then $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ does not admit a projective symplectic resolution. Based upon a result of Drezet [19], who considered instead the moduli space of semistable sheaves on a rational surface, we show in Corollary 6.9 the following result. Recall that a variety is locally factorial if all of its local rings are unique factorization domains.

Theorem 1.10

Assume that $\alpha \in \Sigma _{\lambda ,\theta }$ is an anisotropic root satisfying condition (3), and that $\theta$ is generic. Then the quiver variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is locally factorial.

Observe that we did not require $\alpha$ to be divisible, although if were indivisible then we already noted that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is smooth for generic $\theta$. On the other hand, in the divisible case, we will see that, for $\theta$ generic, the variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ has terminal singularities, using that, by [50], this is equivalent to having singularities in codimension at least four. Therefore, by a well-known fact, the above theorem implies that it cannot admit a proper symplectic resolution.

In fact, we prove in Corollary 6.9 a more precise statement than Theorem 1.10 which does not require that $\theta$ be generic. By the argument given in the proof of Theorem 6.13, we see that the corollary implies that this statement holds for open subsets of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. Therefore we conclude the following strengthening of the nonexistence direction of Theorem 1.5:

Corollary 1.11

Assume that $\alpha \in \Sigma _{\lambda ,\theta }$ is divisible, it satisfies condition (3), and $\theta$ is generic. Under the assumptions of Theorem 1.10, if $U \subseteq \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is any singular Zariski open subset, then U does not admit a proper symplectic resolution.

In fact, by Corollary 6.9 below, we can drop in Corollary 1.11 the assumption that $\theta$ is generic, at the price of replacing $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ by a certain canonical open set: the locus of direct sums of stable representations of dimension vector proportional to $\alpha$.

In particular, in many cases, there are open subsets $U \subseteq \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ which formally locally admit symplectic resolutions everywhere, but do not admit one globally. For example, if $\alpha = 2\beta$ for some $\beta \in \Sigma _{\lambda ,\theta }$ with $p(\beta ) \ge 3$ (cf. the definition of p above Theorem 1.5), then we can let U be the locus of representations which are either stable or decompose as $X = Y \oplus Y'$ for $Y,Y'$ nonisomorphic $\theta$-stable representations of dimension vectors equal to $\beta$.

There is one quiver variety in particular that captures the “unresolvable” singularities of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. This variety, which we denote $\mathfrak {X}(g,n)$ with $g,n \in \mathbb {N}$, has been studied in the works of Lehn, Kaledin and Sorger. Concretely,

$$\begin{aligned} \mathfrak {X}(g,n) := \left\{ (X_1,Y_1, \dots , X_g,Y_g) \in {{\,\mathrm{\mathrm {End}}\,}}_{\mathbb {C}}(\mathbb {C}^n) \ \left| \ \sum _{i = 1}^d [X_i,Y_i] = 0 \right. \right\} /\!\!/\!{{\,\mathrm{\mathrm {GL}}\,}}(n,\mathbb {C}), \end{aligned}$$

Viewed as a special case of Corollary 6.9, we see that $\mathfrak {X}(g,n)$ does not admit a proper symplectic resolution if $g, n \ge 2$ and $(g,n) \ne (2,2)$.

When $g = 1$, the Hilbert scheme of n points in the plane provides a symplectic resolution of $\mathfrak {X}(g,n) \simeq S^n \mathbb {C}^2$; see [23, Theorem 1.2.1, Lemma 2.8.3]. When $n = 1$, one has $\mathfrak {X}(g,n) \simeq \mathbb {C}^{2g}$.

Remark 1.12

It is interesting to note that [15, Theorem 1.1] implies that the moment map

$$\begin{aligned} (X_1,Y_1, \dots , X_g,Y_g) \mapsto \sum _{i = 1}^g [X_i,Y_i] \end{aligned}$$

is flat when $g > 1$, in contrast to the case $g = 1$, which is easily seen not to be flat.

Remark 1.13

Generalizing the Geiseker moduli spaces that arise from framings of the Jordan quiver, it seems likely that the framed versions of $\mathfrak {X}(g,n)$, which are smooth for generic stability parameters, should have interesting combinatorial and representation theoretic properties.

Remark 1.14

One does not need the full strength of Theorem 1.10 to prove that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ does not admit a symplectic resolution: it suffices to show that a formal neighborhood of some point does not admit a symplectic resolution. This reduces the problem to the one-vertex case, i.e., to $\mathfrak {X}(g,n)$. However, the techniques (following [32]) do not actually simplify in this case. Moreover, this would not be enough to imply Corollary 1.11.

1.4 Smooth versus canonically polystable points

In order to decide when the variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is smooth, we describe the smooth locus in terms of $\theta$-stable representations. Write the canonical decomposition $n_1 \sigma ^{(1)} + \cdots + n_k \sigma ^{(k)}$ of $\alpha \in \mathbb {N}R^+_{\lambda ,\theta }$ as $\beta ^{(1)} + \cdots + \beta ^{(\ell )}$, where a given $\beta \in \Sigma _{\lambda ,\theta }$ may appear multiple times. Recall that a representation is said to be $\theta$-polystable if it is a direct sum of $\theta$-stable representations. We say that a representation x is canonically $\theta$-polystable if $x = x_1 \oplus \cdots \oplus x_{\ell }$ where each $x_i$ is $\theta$-stable, $\dim x_i = \beta ^{(i)}$ and $x_i \not \simeq x_j$ for $i \ne j$, unless $\beta ^{(i)} = \beta ^{(j)}$ is a real root, i.e., $p(\beta ^{(i)}) = 0$. Observe that the notion of canonical $\theta$-polystability reduces to $\theta$-stability precisely in the case that $\alpha \in \Sigma _{\lambda ,\theta }$. In general, the set of points of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ which are the image of canonically $\theta$-polystable representations is a dense open subset. When $\theta = 0$, the result below is due to Le Bruyn [38, Theorem 3.2] (whose arguments we generalize).

Theorem 1.15

A point $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ belongs to the smooth locus if and only if it is canonically $\theta$-polystable.

Remark 1.16

Theorem 1.15 confirms the expectation stated after Lemma 4.4 of [25].

An element $\sigma \in \Sigma _{\lambda ,\theta }$ is said to be minimal if there are no $\beta ^{(1)}, \dots , \beta ^{(r)} \in \Sigma _{\lambda ,\theta }$, with $r \ge 2$, such that $\sigma = \beta ^{(1)} + \cdots + \beta ^{(r)}$.

Corollary 1.17

The variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is smooth if, and only if, in the canonical decomposition $\alpha = n_1 \sigma ^{(1)} + \cdots + n_k \sigma ^{(k)}$ of $\alpha$, each $\sigma ^{(i)}$ is minimal, and the multiplicity $n_i$ is one if $\sigma ^{(i)}$ is isotropic.

Since, as recalled in Corollary 2.3 below, $n_i$ is always one if $\sigma ^{(i)}$ is aniostropic, we could equivalently drop the assumption “is isotropic” at the end of the corollary.

Corollary 1.17 is a crucial ingredient in the proof of the main result of [4], where a key step is the classification of stability parameters for which the corresponding quiver variety (associate to a framed affine Dynkin quiver) is smooth.

1.5 Namikawa’s Weyl group

When both $\lambda$ and $\theta$ are zero, $\mathfrak {M}_{{0}} ({\alpha },{0})$ is an affine conic symplectic singularity. Associated to $\mathfrak {M}_{{0}} ({\alpha },{0})$ is Namikawa’s Weyl group W [51], a finite reflection group. In order to compute W, one needs to describe the codimension two symplectic leaves of $\mathfrak {M}_{{0}} ({\alpha },{0})$. More generally, we consider the codimension two leaves in a general quiver variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. It is enough by Crawley–Boevey’s canonical decomposition to consider the case $\alpha \in \Sigma _{\lambda ,\theta }$. We show that the codimension two symplectic leaves are parameterized by isotropic decompositions of $\alpha$.

Definition 6.15

The decomposition $\alpha = \beta ^{(1)} + \cdots + \beta ^{(s)} + m_1 \gamma ^{(1)} + \cdots m_t \gamma ^{(t)}$ is said to be an isotropic decomposition if

• (a) $\beta ^{(i)}, \gamma ^{(j)} \in \Sigma _{\lambda ,\theta }$.

• (b) The $\beta ^{(i)}$ are imaginary roots.

• (c) The $\gamma ^{(i)}$ are pairwise distinct real roots.

• (d) If $\overline{Q}''$ is the quiver with $s + t$ vertices without loops and $-(\alpha ^{(i)}, \alpha ^{(j)})$ arrows from vertex i to vertex $j \ne i$, where $\alpha ^{(i)},\alpha ^{(j)} \in \{ \beta ^{(1)}, \dots , \beta ^{(s)}, \gamma ^{(1)} , \dots , \gamma ^{(t)} \}$, then $Q''$ is an affine Dynkin quiver.

• (e) The dimension vector $(1,\dots , 1, m_1, \dots , m_t)$ of $Q''$ (where there are s ones) equals $\delta$, the minimal imaginary root.

Remark 1.19

In fact, as we will show in Lemma 7.2 below, in an isotropic decomposition of $\alpha \in \Sigma _{\lambda ,\theta }$, all of the anisotropic $\beta ^{(i)}$ are pairwise distinct. This may help in finding these decompositions.

However, the isotropic $\beta ^{(i)}$ need not be distinct. As an example, when Q is the quiver with two vertices 1, 2 and two arrows, one loop at 1 and one arrow from 1 to 2, then we can take $\alpha =(4,2)$, $\beta ^{(1)}=(1,0)=\beta ^{(2)}=\beta ^{(3)}=\beta ^{(4)}$, and $\gamma ^{(1)}=(0,1)$. Then $p(\alpha )=5$ and $\alpha \in \Sigma _{0,0}$, and the quiver $\overline{Q}''$ is of affine $D_4$ type with central vertex corresponding to $\gamma ^{(1)}$ and external vertices corresponding to the $\beta ^{(i)}$. This example is also interesting since $\alpha \in \Sigma _{0,0}$ is divisible, but not $\Sigma$-divisible (as $\frac{1}{2} \alpha \notin \Sigma _{0,0}$).

Given an isotropic decomposition with affine Dynkin quiver $Q''$, let $Q''_f$ be the finite part, which is a Dynkin diagram.

Theorem 1.20

Let $\alpha \in \Sigma _{\lambda ,\theta }$ be imaginary. Then the codimension two strata of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ are in bijection with the isotropic decompositions of $\alpha$. The singularity along each such stratum is étale-equivalent to the du Val singularity of the type $A_n, D_n, E_n$ corresponding to $Q''_f$.

As a consequence, for $\lambda =0=\theta$, by [51, Theorem 1.1] the Namikawa Weyl group is a product over all isotropic decompositions B of a group $W_B$. This group $W_B$ is either the Weyl group of the corresponding Dynkin diagram $Q''_f$, or else the centralizer therein of an automorphism of this diagram, corresponding to the monodromy around the fiber over a point of the stratum under a crepant resolution of the complement of the codimension $>2$ strata.

1.6 Character varieties

The methods we use seem to be applicable to many other situations. Indeed, as we have noted previously, they were first developed by Kaledin–Lehn–Sorger in the context of semistable sheaves on a K3 or abelian surface. Any situation where the symplectic singularity is constructed as a Hamiltonian reduction with respect to a reductive group of type A is amenable to this sort of analysis. One such situation, which is of crucial importance throughout geometry, topology, and group theory, is that of character varieties of a Riemannian surface.

Let $\Sigma$ be a compact Riemannian surface of genus $g > 0$ and $\pi$ its fundamental group. The ${{\,\mathrm{\mathrm {SL}}\,}}$-character variety of $\Sigma$ is the affine quotient

$$\begin{aligned} \mathscr {Y}(g,n) := {{\,\mathrm{\mathrm {Hom}}\,}}(\pi ,{{\,\mathrm{\mathrm {SL}}\,}}(n,\mathbb {C})) /\!\!/\!{{\,\mathrm{\mathrm {SL}}\,}}(n,\mathbb {C}). \end{aligned}$$

Similarly, the ${{\,\mathrm{\mathrm {GL}}\,}}$-character variety is

$$\begin{aligned} \mathscr {X}(g,n) = {{\,\mathrm{\mathrm {Hom}}\,}}(\pi ,{{\,\mathrm{\mathrm {GL}}\,}}(n,\mathbb {C})) /\!\!/\!{{\,\mathrm{\mathrm {GL}}\,}}(n,\mathbb {C}). \end{aligned}$$

In the article [7] we show that $\mathscr {X}(g,n)$ and $\mathscr {Y}(g,n)$ are irreducible symplectic singularities. Moreover, we show:

Theorem 1.21

[7] Assume that $g > 1$ and $(g,n) \ne (2,2)$. Then the varieties $\mathscr {X}(g,n)$ and $\mathscr {Y}(g,n)$ are locally factorial with terminal singularities and hence do not admit proper symplectic resolutions. The same holds for any singular open subset.

Another very similar situation is that of moduli spaces of Higgs bundles on a genus g curve. The symplectic singularities of these moduli spaces are considered by A. Tirelli in [60].

1.7 Applications

In joint work with A. Craw, the first author studies the symplectic resolutions of the symplectic quotient singularities $\mathbb {C}^{2n} / (\mathfrak {S}_n \wr \Gamma )$, where $\Gamma \subset \mathrm {SL}(2,\mathbb {C})$ is a finite group and $\mathfrak {S}_n \wr \Gamma = \Gamma ^n \rtimes \mathfrak {S}_n$ is the associated wreath product. It is well-known that $\mathbb {C}^{2n} / (\mathfrak {S}_n \wr \Gamma )$ is a quiver variety and symplectic resolutions of the quotient singularity can be realised using variation of GIT for quiver varieties. Using the results from this article, it is shown in [4] that in fact all projective symplectic resolutions of the quotient singularity can be realised using quiver varieties. Moreover, one can say when stability parameters lying in different chambers give rise to the same symplectic resolutions. To prove these statements, it is crucial to have (a) the characterization of smooth quiver varieties given by Corollary 1.17 (b) the classification of symplectic leaves given in Corollary 3.25; and (c) the local normal form given by Theorem 3.3.

More generally, in joint work [5] with A. Craw, we use results of this paper to give a complete classification of $\mathbb {Q}$-factorial terminalizations of quiver varieties.

In [13], the authors prove that symmetric powers of minimal resolutions of du Val singularities are also quiver varieties, for non-generic stability parameters on affine Dynkin quivers. By Theorem 1.2, this implies that they are symplectic singularities. Our results in Sect. 3.4 are also employed in the proof of their main result.

1.8 Other related work

In joint work [58] with Tirelli, the second author has used similar methods to give a classification of those multiplicative quiver varieties and character varieties of open Riemann surfaces that admit symplectic resolutions. Though the methods are similar, the situation considered in [58] is considerably more complex that the additive case considered here (owing, for example, to the fact that it is unknown there when the varieties in question are nonempty).

Our classification explains which quiver varieties fall under the general framework of Springer theory as recently developed by McGerty–Nevins [44]. Additionally, similar questions to ours are analyzed there in greater detail for the Dynkin cases.

1.9 Notation and proof of the main results

Throughout, a variety will mean a reduced, quasi-projective scheme of finite type over $\mathbb {C}$. If X is a (quasi-projective) variety equipped with the action of a reductive algebraic group G, then $X /\!\!/\!\, G$ will denote the good quotient (when it exists). In this case, let $\xi : X \rightarrow X /\!\!/\!\, G$ denote the quotient map. Then each fibre $\xi ^{-1}(x)$ contains a unique closed G-orbit. Following Luna, this closed orbit is denoted T(x).

The proof of the theorems and corollaries stated in the introduction can be found in the following sections.

Theorem 1.2	:	Section 6.3
Theorem 1.4	:	Section 6.4
Theorem 1.5	:	Section 6.4
Theorem 1.6	:	Section 5.2
Theorem 1.10	:	Section 6.2
Corollary 1.11	:	Section 6.4
Theorem 1.15	:	Section 4.2
Corollary 1.17	:	Section 4.3
Theorem 1.20	:	Section 7.1

2 Quiver varieties

In this section we fix notation.

2.1 Notation

Let $\mathbb {N}:= \mathbb {Z}_{\ge 0}$. We work over $\mathbb {C}$ throughout. All quivers considered will have a finite number of vertices and arrows. We allow Q to have loops at vertices. Let $Q = (Q_0,Q_1)$ be a quiver, where $Q_0$ denotes the set of vertices and $Q_1$ denotes the set of arrows. Given $a \in Q_1$, let $a_s, a_t \in Q_0$ be the source and target, so $a: a_s \rightarrow a_t$. For a dimension vector $\alpha \in \mathbb {N}^{Q_0}$, ${{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha ) := \prod _{a \in Q_1} {{\,\mathrm{\mathrm {Hom}}\,}}(\mathbb {C}^{\alpha _{a_s}}, \mathbb {C}^{\alpha _{a_t}})$ denotes the vector space of representations of Q of dimension $\alpha$. The group $\mathrm {G}(\alpha ) := \prod _{i \in Q_0} GL_{\alpha _i}(\mathbb {C})$ acts on ${{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )$; write $\mathfrak {g}(\alpha ) = {{\,\mathrm{\mathrm {Lie}}\,}}\mathrm {G}(\alpha )$. The torus $\mathbb {C}^{\times }$ in $\mathrm {G}(\alpha )$ of diagonal matrices acts trivially on ${{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )$. Thus, the action factors through $\mathrm {PG}(\alpha ) := \mathrm {G}(\alpha ) / \mathbb {C}^{\times }$. Let $\mathfrak {pg}(\alpha ) := {{\,\mathrm{\mathrm {Lie}}\,}}\mathrm {PG}(\alpha ) = \mathfrak {g}(\alpha )/\mathbb {C}$.

Let $\overline{Q}$ be the doubled quiver of Q, where for each arrow $a :i \rightarrow j$ of Q we add a reverse arrow $a^* :j \rightarrow i$ to form $\overline{Q}$. There is a natural identification $T^* {{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha ) = {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q}, \alpha )$. The group $\mathrm {G}(\alpha )$ acts symplectically on ${{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q}, \alpha )$ and the corresponding moment map is $\mu : {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q}, \alpha ) \rightarrow \mathfrak {g}(\alpha )$, where we have identified $\mathfrak {g}(\alpha )$ with its dual using the trace form. An element $\lambda \in \mathbb {C}^{Q_0}$ is identified with the tuple of scalar matrices $( \lambda _i \mathrm {Id}_{V_i})_{i \in Q_0} \in \mathfrak {g}(\alpha )$. The affine quotient $\mu ^{-1}(\lambda ) / \! / \mathrm {G}(\alpha )$ parameterizes semi-simple representations of the deformed preprojective algebra $\Pi ^{\lambda }(Q) := \mathbb {C}\overline{Q}/ (\sum _{a \in Q_1} (a a^* - a^* a) - \sum _{i \in Q_0} \lambda _i p_i)$, where $p_i$ is the length-zero path at the vertex i. See [15] for details.

If M is a finite dimensional $\Pi ^{\lambda }(Q)$-module, then $\dim M$ will always denote the dimension vector of M, and not just its total dimension.

2.2 Root systems

The coordinate vector at vertex i is denoted $e_i$. The set $\mathbb {N}^{Q_0}$ of dimension vectors is partially ordered by $\alpha \ge \beta$ if $\alpha _i \ge \beta _i$ for all i and we say that $\alpha > \beta$ if $\alpha \ge \beta$ with $\alpha \ne \beta$. The support of the vector $\alpha$ is the subquiver of Q obtained by deleting all vertices $i \in Q_0$ where $\alpha _i = 0$. Following [17, Section 8], $\alpha$ is called sincere if $\alpha _i > 0$ for all i i.e. the support of $\alpha$ equals Q. The Ringel form on $\mathbb {Z}^{Q_0}$ is defined by

$$\begin{aligned} \langle \alpha , \beta \rangle = \sum _{i \in Q_0} \alpha _i \beta _i - \sum _{a \in Q_1} \alpha _{t(a)} \beta _{h(a)}. \end{aligned}$$

Let $(\alpha ,\beta ) = \langle \alpha , \beta \rangle + \langle \beta , \alpha \rangle$ denote the corresponding Euler form and set $p(\alpha ) = 1 - \langle \alpha , \alpha \rangle$. The fundamental region $\mathcal {F}(Q)$ is the set of $0 \ne \alpha \in \mathbb {N}^{Q_0}$ with connected support and with $(\alpha , e_i) \le 0$ for all i.

If i is a loopfree vertex, so $p(e_i) = 0$, there is a reflection $s_i : \mathbb {Z}^{Q_0} \rightarrow \mathbb {Z}^{Q_0}$ defined by $s_i \alpha = \alpha - (\alpha ,e_i)e_i$. There is also the dual reflection, $r_i: \mathbb {Z}^{Q_0} \rightarrow \mathbb {Z}^{Q_0}, (r_i \lambda )_j = \lambda _j - (e_i, e_j) \lambda _i$. The real roots (respectively with imaginary roots) are the elements of $\mathbb {Z}^{Q_0}$ which can be obtained from the coordinate vector at a loopfree vertex (respectively ± an element of the fundamental region) by applying some sequence of reflections at loopfree vertices. Let $R^+$ denote the set of positive roots. Recall that a root $\beta$ is isotropic imaginary if $p(\beta ) = 1$ (i.e., $(\beta ,\beta )=0$) and anisotropic imaginary if $p(\beta ) > 1$. Abusing terminology slightly, we will simply say that a root $\alpha$ is (a) real if $p(\alpha ) = 0$, (b) isotropic if $p(\alpha ) = 1$, and (c) anisotropic if $p(\alpha ) > 1$.

2.3 The canonical decomposition

In this section we recall the canonical decomposition defined by Crawley-Boevey (not to be confused with Kac’s canonical decomposition). Fix $\lambda \in \mathbb {C}^{Q_0}$ and $\theta \in \mathbb {Z}^{Q_0}$. Then $R_{\lambda ,\theta }^+ := \{ \alpha \in R^+ \ | \ \lambda \cdot \alpha = \theta \cdot \alpha = 0 \}$. Following [15], we define

$$\begin{aligned}&\Sigma _{\lambda ,\theta } = \left\{ \alpha \in R_{\lambda ,\theta }^+ \ \left| \ p(\alpha ) > \sum _{i = 1}^r p \left( \beta ^{(i)} \right) \text { for any decomposition } \right. \right. \\&\left. \alpha = \beta ^{(1)} + \dots + \beta ^{(r)} \text { with } r \ge 2, \ \beta ^{(i)} \in R_{\lambda ,\theta }^+ \right\} . \end{aligned}$$

Example 1

Suppose that $\lambda =0=\theta$ and $\alpha \in \Sigma _{\lambda ,\theta }$ is real, i.e., $p(\alpha )=0$. Then $\alpha$ is a coordinate vector. Indeed, if not, by definition there is a vertex $i \in Q_0$ such that $\alpha = s_i \alpha + ke_i$ with $k \ge 1$. Then $0 = p(\alpha ) = p(s_i\alpha ) + kp(e_i)$ contradicts the fact that $\alpha \in \Sigma _{0,0}$.

Example 2

Again suppose that $\lambda =0=\theta$, and now assume that $\alpha \in \Sigma _{\lambda ,\theta }$ is isotropic i.e., $p(\alpha )=1$. Then as observed in the proof of [16, Proposition 1.2.(2)], $\alpha$ is supported on an affine Dynkin subquiver and there is the minimal imaginary root. We repeat the argument for the reader’s convenience. First, $\alpha$ is indivisible, since $\alpha =k\beta$ would imply $p(\alpha ) < kp(\beta )$, and as $\beta$ is also a root, this contradicts the assumption $\alpha \in \Sigma _{0,0}$. Next, $\alpha$ is in the fundamental region, since otherwise $\alpha = s_i \alpha + k e_i$ for some $i \in Q_0$ and $k \ge 1$, which implies $1=p(\alpha ) = p(s_i \alpha ) + kp(e_i)$, again contradicting the assumption that $\alpha \in \Sigma _{0,0}$. Now the support of $\alpha$ is connected. Letting $Q'$ be its supporting quiver (i.e., the result of discarding all vertices not in the support and all incident arrows), we obtain a connected quiver for which $\alpha$ is in the kernel of the Cartan pairing. By [28, Lemma 1.9.(d)], $Q'$ is affine (ADE) Dynkin and $\alpha$ is an imaginary root. Since it is also indivisible, it is the minimal imaginary root $\delta$ of $Q'$.

In several places below, we choose a parameter $\nu \in \mathbb {C}^{Q_0}$ such that $R_{\lambda ,\theta }^+ = R_{\nu }^+$ so that we can apply results of [16], where the case $\theta = 0$ is considered. This is only for convenience, since the arguments of [16] can also be generalized directly to the context of the pair $(\theta ,\lambda )$. Then [16, Theorem 1.1] implies that

Proposition 3.1

Let $\alpha \in \mathbb {N}R_{\lambda ,\theta }^+$. Then $\alpha$ admits a unique decomposition $\alpha = n_1 \sigma ^{(1)} + \cdots + n_k \sigma ^{(k)}$ as a sum of element $\sigma ^{(i)} \in \Sigma _{\lambda ,\theta }$ such that any other decomposition of $\alpha$ as a sum of elements from $\Sigma _{\lambda ,\theta }$ is a refinement of this decomposition.

As is apparent from the results stated in the introduction, indivisible roots in $\Sigma _{\lambda ,\theta }$ play an important role in this paper. Occasionally it is useful to compare this with the condition of being $\Sigma$-indivisible, i.e., being indivisible in $\Sigma _{\lambda ,\theta }$:

Theorem 2.2

If $\alpha \in \Sigma _{\lambda ,\theta }$ is imaginary, with $\alpha = m \beta$ for some indivisible root $\beta$, then one of the following hold:

• (a) $\beta$ is isotropic and $m = 1$,

• (b) $\beta$ is anisotropic and $\beta \in \Sigma _{\lambda ,\theta }$; or

• (c) $\beta$ is anisotropic, $\beta \notin \Sigma _{\lambda ,\theta }$ and $m > 1$ can be chosen arbitrarily.

The following converse to (b) holds: if $\beta \in \Sigma _{\lambda ,\theta }$ is anisotropic, then $m\beta \in \Sigma _{\lambda ,\theta }$ for all $m \ge 1$.

Proof

Once again, choose once again $\nu \in \mathbb {C}^{Q_0}$ such that $R_{\lambda ,\theta }^+ = R_{\nu }^+$ and let $\mathcal {F}_{\nu }$ be the “relative fundamental domain”, as defined in [15, §7]. Then Theorem 2.2 follows from [15, Theorem 8.1] provided that $\alpha \in \mathcal {F}_{\lambda ,\theta }$. Namely, there it is described precisely the set $\mathcal {F}_{\nu } \setminus \Sigma _{\nu }$, which has a very special form, called types (I), (II), and (III). Type (I) is the isotropic case: namely the multiples by positive integers $m \ge 2$ of the imaginary root of an affine Dynkin subquiver. They are divisible. Types (II) and (III) are indivisible, and anisotropic.

If $\alpha$ is not in $\mathcal {F}_{\nu }$ then, by definition, there is a sequence of admissible reflections (whose product is w say) mapping $\alpha$ to $w(\alpha ) \in \mathcal {F}_{w(\nu )}$ (where $w(\nu )$ uses the action of dual reflections rather than reflections). Moreover, by [15, Lemma 5.2], $w(\alpha )$ also belongs to $\Sigma _{w(\nu )}$. Thus, it suffices to note that if trichotomy of the theorem holds for $w(\alpha )$, then it also holds for the root $\alpha$.

The final statement follows from [16, Proposition 1.2 (3)]. For the convenience of the reader we recall the proof, since it is closely related to the above.

As we mentioned, the anisotropic cases (II) and (III) mentioned above are both indivisible. Thus every divisible anisotropic element of $\mathcal {F}_{\nu }$ is in $\Sigma _{\nu }$. So the above reductions imply the statement. $\square$

Corollary 2.3

In the canonical decomposition (2), $n_i = 1$ if $\sigma ^{(i)}$ is anisotropic.

Proof

This follows immediately from the final statement of Theorem 2.2, by the definition of the canonical decomposition. $\square$

Notice that Theorem 2.2 says that if $\beta$ is an indivisible anisotropic root such that some multiple of $\beta$ belongs to $\Sigma _{\lambda ,\theta }$, then every proper multiple of $\beta$ belongs to $\Sigma _{\lambda ,\theta }$. However, in some cases $\beta$ itself need not belong to $\Sigma _{\lambda ,\theta }$.

2.4 Stability

Let $\theta \in \mathbb {Z}^{Q_0}$ be a stability condition. Given a representation M of $\overline{Q}$ (e.g., a module over $\Pi ^{\lambda }(Q)$), let $\theta (M) := \theta \cdot \dim M$. Note that a representation M of $\Pi ^\lambda (Q)$ is the same as a point in the zero fiber $\mu ^{-1}(\lambda )$. Recall that a $\Pi ^{\lambda }(Q)$-representation M (hence also a point in $\mu ^{-1}(\lambda )$) such that $\theta (M) = 0$, is said to be $\theta$-stable, respectively $\theta$-semistable, if $\theta (M') < 0$, respectively $\theta (M') \le 0$, for all proper nonzero subrepresentations $M'$ of M. A representation M is said to be $\theta$-polystable if $M = M_1 \oplus \cdots \oplus M_k$ with $\theta (M_i) = 0$, such that each $M_i$ is $\theta$-stable. The set of $\theta$-semistable points in $\mu ^{-1}(\lambda )$ is denoted $\mu ^{-1}(\lambda )^{\theta }$. We define a partial order on $\mathbb {Z}^{Q_0}$ by setting $\theta ' \ge \theta$ if M $\theta '$-semistable implies that M is $\theta$-semistable, i.e.,

$$\begin{aligned} \theta ' \ge \theta \, \Longleftrightarrow \, \mu ^{-1}(\lambda )^{\theta '} \subset \mu ^{-1}(\lambda )^{\theta }. \end{aligned}$$

The space ${{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q}, \alpha )$ has a natural Poisson structure. Since the action of $\mathrm {G}(\alpha )$ on ${{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q}, \alpha )$ is Hamiltonian,

$$\begin{aligned} \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) = \mu ^{-1}(\lambda )^{\theta } /\!\!/\!\mathrm {G}(\alpha ) := \mathrm {Proj} \ \bigoplus _{k \ge 0} \mathbb {C}\left[ \mu ^{-1}(\lambda )\right] ^{k \theta } \end{aligned}$$

is a Poisson variety.

Lemma 2.4

If $\theta ' \ge \theta$, then there is a projective Poisson morphism $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

Proof

By definition, we have a $\mathrm {G}(\alpha )$-equivariant embedding $\mu ^{-1}(\lambda )^{\theta '} \hookrightarrow \mu ^{-1}(\lambda )^{\theta }$. This induces a morphism

$$\begin{aligned} \mathfrak {M}_{{\lambda }} ({\alpha },{\theta '}) = \mu ^{-1}(\lambda )^{\theta '} /\!\!/\!\mathrm {G}(\alpha ) \longrightarrow \mu ^{-1}(\lambda )^{\theta } /\!\!/\!\, \mathrm {G}(\alpha ) =\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) , \end{aligned}$$

between geometric quotients. We need to show that this morphism is projective. This is local on $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. Therefore we may choose $n \gg 0$ and a $n \theta$-semi-invariant f and consider the open subsets $U \cap \mu ^{-1}(\lambda )^{\theta '}$ and $U \cap \mu ^{-1}(\lambda )^{\theta }$, where $U = (f \ne 0) \subset {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )$. Then $\left( U \cap \mu ^{-1}(\lambda )^{\theta }\right) /\!\!/\!\, \mathrm {G}(\alpha ) = {{\,\mathrm{\mathrm {Spec}}\,}}\mathbb {C}\left[ U \cap \mu ^{-1}(\lambda )\right] ^{\mathrm {G}(\alpha )}$ is an open subset of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ and

$$\begin{aligned} \left( U \cap \mu ^{-1}(\lambda )^{\theta '}\right) /\!\!/\!\, \mathrm {G}(\alpha ) = \mathrm {Proj} \ \bigoplus _{k \ge 0} \mathbb {C}\left[ U \cap \mu ^{-1}(\lambda )\right] ^{k \theta '} \end{aligned}$$

such that $\left( U \cap \mu ^{-1}(\lambda )^{\theta '}\right) /\!\!/\!\, \mathrm {G}(\alpha ) \rightarrow \left( U \cap \mu ^{-1}(\lambda )\right) /\!\!/\!\mathrm {G}(\alpha )$ is the projective morphism

$$\begin{aligned} \mathrm {Proj} \ \bigoplus _{k \ge 0} \mathbb {C}\left[ U \cap \mu ^{-1}(\lambda )\right] ^{k \theta '} \longrightarrow {{\,\mathrm{\mathrm {Spec}}\,}}\mathbb {C}\left[ U \cap \mu ^{-1}(\lambda )\right] ^{\mathrm {G}(\alpha )}. \end{aligned}$$

It is clear that this morphism is Poisson. $\square$

It follows from the proof of Lemma 2.4 that if $\theta '' \ge \theta ' \ge \theta$ then the projective morphism $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta ''}) \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ factors through $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '})$.

We will frequently use the fact that for each point $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, there is a unique closed $\mathrm {G}(\alpha )$-orbit in the fibre over x of the quotient map $\xi : \mu ^{-1}(\lambda )^{\theta } \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. Recall that this closed orbit is denoted T(x).

3 Canonical decompositions of the quiver variety

In this section we recall the canonical decomposition of quiver varieties described in [16], and show that it holds in slightly greater generality than stated there.

3.1 A stratification

Let $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ be a closed point and $y \in T(x)$. Recall the following basic fact:

Proposition 3.9

[34, Proposition 3.2 (i)] A point of a closed $\mathrm {G}(\alpha )$-orbit in $\mu ^{-1}(\lambda )^{\theta }$ is a $\theta$-polystable representation.

In more detail, [34, Proposition 3.2 (ii)] states that two points of $\mu ^{-1}(\lambda )^{\theta }$ determine the same point of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ if and only if the corresponding representations admit filtrations whose associated graded subquotients are isomorphic $\theta$-polystable representations.

Therefore y decomposes into a direct sum $y_1^{e_1} \oplus \cdots \oplus y_k^{e_k}$ of $\theta$-stable representations, with multiplicity. Let $\beta ^{(i)} = \dim y_i$. The point x is said to have representation type $\tau = (e_1, \beta ^{(1)}; \dots ; e_k, \beta ^{(k)})$. Associated to this is the stabilizer group $G_{\tau }=\mathrm {G}(\alpha )_y$, which is independent of the choice of y up to conjugation in $\mathrm {G}(\alpha )$. Even though $\mu ^{-1}(\lambda )^{\theta }$ is not generally affine, the fact that a nonzero morphism between $\theta$-stable representations is an isomorphism implies:

Lemma 3.2

The group $G_{\tau }$ is reductive.

In fact, it is isomorphic to $\prod _{i = 1}^k GL_{e_i}(\mathbb {C})$. We denote the conjugacy class of a closed subgroup H of $\mathrm {G}(\alpha )$ by (H). Given a reductive subgroup H of $\mathrm {G}(\alpha )$, let $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(H)}$ denote the set of points x such that the stabilizer of any $y \in T(x)$ belongs to (H). We order the conjugacy classes of reductive subgroups of $\mathrm {G}(\alpha )$ by $(H) \le (L)$ if and only if L is conjugate to a subgroup of H.

3.2 Étale local structure

In this section, we recall the étale local structure of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, as described in [17, Section 4]. Since it is assumed in op. cit. that $\theta = 0$, we provide some details to ensure the results are still applicable in this more general setting. Let $x, y, y_1,\ldots ,y_k, \beta ^{(1)},\ldots ,\beta ^{(k)}$, and $\tau$ be as in Sect. 3.1. Let $Q'$ be the quiver with k vertices whose double has $2 p(\beta ^{(i)})$ loops at vertex i and $- (\beta ^{(i)},\beta ^{(j)})$ arrows from vertex i to j. The k-tuple $\mathbf{e} = (e_1, \dots , e_k)$ defines a dimension vector for the quiver $Q'$.

If X and Y are Poisson varieties, then we say that there is a étale Poisson isomorphism between a neighborhood of $x \in X$ and $y \in Y$ if there exists a Poisson variety Z and Poisson morphisms $Y {\mathop {\longleftarrow }\limits ^{\psi }} Z {\mathop {\longrightarrow }\limits ^{\phi }} X$ and $z \in Z$ such that $\phi (z) = x$, $\psi (z) = y$ and both $\phi$ and $\psi$ are étale at z.

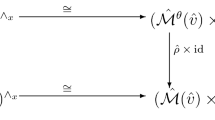
Theorem 3.3

There is an étale Poisson isomorphism between a neighborhood of 0 in $\mu _{Q'}^{-1}(0) /\!\!/\!\, \mathrm {G}(\mathbf{e} )$ and a neighborhood of $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

The proof of Theorem 3.3 is given in Sect. 3.3 below. By taking the completion $\widehat{\mathfrak {M}}_{\lambda }(\alpha ,\theta )_{x}$ of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ at x and the completion $\widehat{\mathfrak {M}}_{0}(\mathbf{e} ,0)_0$ of $\mathfrak {M}_{{0}} (\mathbf{e },{0})$ at 0, the formal analogue of Theorem 3.3 is:

Corollary 3.4

There is an isomorphism of formal Poisson schemes $\widehat{\mathfrak {M}}_{\lambda }(\alpha ,\theta )_{x} \simeq \widehat{\mathfrak {M}}_{0}(\mathbf{e} ,0)_0$.

Remark 3.5

An easy calculation shows that $p(\alpha ) =p(\mathbf{e} )$. It can also be deduced from the fact that $\dim \widehat{\mathfrak {M}}_{\lambda }(\alpha ,\theta )_{x} = \dim \widehat{\mathfrak {M}}_{0}(\mathbf{e} ,0)_0$. This fact will be useful later.

3.3 The proof of Theorem 3.3

Fix $M = {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )$ and $G = \mathrm {G}(\alpha )$. Recall that M has a canonical G-invariant symplectic form $\omega$. Since $y \in M^{\theta }$, there exists some $n > 0$ and $n \theta$-semi-invariant function $\gamma$ such that $\gamma (y) \ne 0$. We fix such a $\gamma$, and let $M_{\gamma } \subset M^{\theta }$ be the affine open subset of M defined by the non-vanishing of $\gamma$. Let $H := \mathrm {G}(\alpha )_y$ be the stabilizer of y in $\mathrm {G}(\alpha )$ and $\mathfrak {h}$ the Lie algebra of H. Since $\mathfrak {h}$ is reductive we can fix a $\mathfrak {h}$-stable complement L to $\mathfrak {h}$ in $\mathfrak {g}$. By [17, Lemma 4.1], the H-submodule $\mathfrak {g} \cdot y \subset M$ is isotropic, and by [17, Corollary 2.3], there exists a coisotropic H-module complement C to $\mathfrak {g} \cdot y$ in M. Let $W = (\mathfrak {g} \cdot y)^{\perp } \cap C$. The composition of $\mu : M \rightarrow \mathfrak {g}^*$ with the restriction map $\mathfrak {g}^* \rightarrow \mathfrak {h}^*$ is denoted $\mu _H$. Notice that $\mu _H$ is simply the moment map for the action of H on M. The restriction of $\mu _H$ to W is denoted $\hat{\mu }$. There is a natural identification of W with ${{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q}',\mathbf{e} )$ such that $\hat{\mu } = \mu _{Q'}$.

Lemma 3.6

The group H is isomorphic to $\mathrm {G}(\mathbf{e} )$ and $\theta |_{H}$ is the trivial character.

Proof

The isomorphism $H \simeq \mathrm {G}(\mathbf{e} )$ follows from the fact that ${{\,\mathrm{\mathrm {Hom}}\,}}_{\Pi ^{\lambda }(Q)}(M_1,M_2) = 0$ if $M_1$ and $M_2$ are non-isomorphic $\theta$-stable representations and ${{\,\mathrm{\mathrm {End}}\,}}_{\Pi ^{\lambda }(Q)}(M_i,M_i) = \mathbb {C}$. Under this identification,

$$\begin{aligned} \theta |_{\mathrm {G}(\mathbf{e} )} = (\theta \cdot \beta ^{(1)}, \dots , \theta \cdot \beta ^{(k)}) = (0,\dots ,0) \in \mathbb {Z}^{Q_0'} \end{aligned}$$

is the trivial stability condition. $\square$

As in [17], define $\nu : C \rightarrow L^*$ by

$$\begin{aligned} \nu (c) (l) = \omega (c,l \cdot y) + \omega (c,l \cdot c) + \omega (y,l \cdot c). \end{aligned}$$

Theorem 3.3 follows from the following more precise result.

Theorem 3.7

There exists a G-saturated affine open set $V \subset M^{\theta }$, and H-saturated affine open sets $Z \subset C$ and $U \subset {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q}',\mathbf{e} )$ such that

• (a) there are étale Poisson morphisms

  $$\begin{aligned} \phi : G \times _H Z \rightarrow V, \quad \psi : Z \cap \nu ^{-1}(0) \rightarrow U; \end{aligned}$$

• (b) the morphisms $\phi$ and $\psi$ induce étale Poisson maps

  $$\begin{aligned} (Z \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)) /\!\!/\!H&\rightarrow (U \cap \hat{\mu }^{-1}(0))/\!\!/\!H, \\ (\phi ^* \mu )^{-1}(\lambda )^{\theta } /\!\!/\!\, G&\rightarrow (V \cap \mu ^{-1}(\lambda )) /\!\!/\!\, G. \end{aligned}$$

• (c) There is an isomorphism of Poisson varieties,

  $$\begin{aligned} \Phi : (Z \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)) /\!\!/\!H {\mathop {\longrightarrow }\limits ^{\sim }} (\phi ^* \mu )^{-1}(\lambda )^{\theta } /\!\!/\!\, G. \end{aligned}$$

If we assume that $y \in \mu ^{-1}(\lambda )$ then for $k \in \mathfrak {h}$ and $l \in L$,

$$\begin{aligned} \mu (y + c) (k+l)&= \lambda (k+l) + \nu (c)(l) + \mu _H(c)(k) + \omega (y,k \cdot c) - \omega (k \cdot y, c) \\&= \lambda (k+l) + \nu (c)(l) + \mu _H(c)(k) \end{aligned}$$

because $k \cdot y = 0$. We define $\delta : C \rightarrow \mathbb {C}$ by $\delta (c) = \gamma (c + y)$. Then $\delta$ is H-invariant. We let $C_{\delta }$ denote the non-vanishing locus of $\delta$. Then

$$\begin{aligned} \{ c \in C \ | \ c + y \in M_{\gamma } \cap \mu ^{-1}(\lambda ) \} = C_{\delta } \cap \mu _H^{-1}(0) \cap \nu ^{-1}(0). \end{aligned}$$

(4)

Let $X = G \times _{H} C_{\delta }$. Since $M = C \oplus \mathfrak {g} \cdot y$, the map $\phi : X \rightarrow M_{\gamma }$, $\phi (g,c) = g \cdot (c + y)$ is étale at (1, 0). We recall that a G-morphism $\phi : X \rightarrow Y$ is said to be excellent if

• (a) $\phi$ is étale.

• (b) The induced map $\phi /G : X/\!\!/\!\, G \rightarrow Y/\!\!/\!\, G$ is étale.

• (c) The morphism $X \rightarrow Y \times _{Y /\!\!/\!\, G} X/\!\!/\!\, G$ is an isomorphism.

Lemma 3.8

There exists an affine, H-saturated open neighbourhood Z of 0 in $C_{\delta }$, such that $\phi$ restricts to an excellent Poisson morphism

$$\begin{aligned} \phi : G \times _H Z \rightarrow V := \mathrm {Im} \ \phi \subset M_{\gamma }, \end{aligned}$$

inducing a étale Poisson morphism

$$\begin{aligned} (\phi ^* \mu )^{-1}(\lambda ) /\!\!/\!\, G \rightarrow (\mu ^{-1}(\lambda ) \cap V) /\!\!/\!\, G. \end{aligned}$$

Proof

This is a direct consequence of Luna’s Fundamental Lemma [41], together with the fact that every G-saturated affine open subset of X is of the form $G \times _H Z$ for some H-saturated open subset of $C_{\delta }$. Since $\phi : G \times _H Z \rightarrow V$ is excellent, the form $\phi ^* \omega$ on X is symplectic, with moment map $\phi ^* \mu$. In particular, [27, Lemma 3.7] says that the corresponding étale morphism of Hamiltonian reductions $(\phi ^* \mu )^{-1}(\lambda ) /\!\!/\!\, G \rightarrow (\mu ^{-1}(\lambda ) \cap V) /\!\!/\!\, G$ is Poisson. $\square$

Proposition 3.15

There exist H-saturated open subsets Z of $\nu ^{-1}(0)$ and U of W such that the morphism

$$\begin{aligned} (\mu _H^{-1}(0) \cap Z) /\!\!/\!H \rightarrow (\hat{\mu }^{-1}(0) \cap U) /\!\!/\!H \end{aligned}$$

is Poisson and étale.

Proof

Let $\hat{\omega } = \omega |_W$. As in [17, Lemma 4.3], $\hat{\omega }$ is a H-invariant symplectic form on W, with corresponding moment map $\hat{\mu }$. Write $p : C \rightarrow W$ for the projection map along $C^{\perp }$ and $\overline{p} : \nu ^{-1}(0) \rightarrow W$ for the restriction of p to $\nu ^{-1}(0)$. We claim that $\overline{p}^* \hat{\omega } = \omega |_{\nu ^{-1}(0)}$ and $\overline{p}^* \hat{\mu } = \mu _H |_{\nu ^{-1}(0)}$. This follows, by definition, from $p^* \hat{\omega } = \omega |_{C}$ and $p^* \hat{\mu } = \mu _H |_{C}$. The latter two equalities can be checked by a direct computation.

By [17, Lemma 4.5], the map $\nu$ is smooth at 0 and $\omega |_{\nu ^{-1}(0)}$ is non-degenerate at 0 with moment map $\mu _H |_{\nu ^{-1}(0)}$. Moreover, loc. cit. shows that the kernel of $d_0 \nu$ is W, thus $d_0 p : T_0 \nu ^{-1}(0) \rightarrow T_0 W$ is the identity map. This implies that $\overline{p} : \nu ^{-1}(0) \rightarrow W$ is étale at 0. Applying Luna’s Fundamental Lemma once again, we deduce that there are H-saturated affine open subset $Z \subset \nu ^{-1}(0)$ and $U = \overline{p}(Z)$ such that $\overline{p} : Z \rightarrow U$ and $\overline{p}/H : Z /\!\!/\!H \rightarrow U /\!\!/\!H$ are étale. Since $\overline{p}^* \hat{\mu } = \mu _H |_{\nu ^{-1}(0)}$, pulling back $\overline{p}/H$ along the closed embedding $\hat{\mu }^{-1}(0) /\!\!/\!H \rightarrow W /\!\!/\!H$ gives an étale morphism $(Z \cap \mu _H^{-1}(0)) /\!\!/\!H \rightarrow (U \cap \hat{\mu }^{-1}(0)) /\!\!/\!H$.

Shrinking Z if necessary, we may assume that $\overline{p}^* \hat{\omega } = \omega |_{\nu ^{-1}(0)}$ is non-degenerate on Z. Since $\overline{p}^* \hat{\mu } = \mu _H |_{\nu ^{-1}(0)}$, it follows from [27, Lemma 3.7] that the map $(Z \cap \mu _H^{-1}(0)) /\!\!/\!H \rightarrow (U \cap \hat{\mu }^{-1}(0)) /\!\!/\!H$ is Poisson. $\square$

The H-equivariant closed embedding $j : \nu ^{-1}(0) \cap C_{\delta } \hookrightarrow G \times _H C_{\delta }$ given by $j(c) = (1,c)$ induces an isomorphism

$$\begin{aligned} \Psi : (\mu ^{-1}_H(0) \cap \nu ^{-1}(0) \cap Z) /\!\!/\!H {\;{\mathop {\rightarrow }\limits ^{_\sim }}\;}(\phi ^* \mu )^{-1}(\lambda ) /\!\!/\!\, G. \end{aligned}$$

(5)

We will show later that this isomorphism is Poisson. Let $M_{(H)}$ be the set of points m in $M^{\theta }$ such that

• (a) $G \cdot m$ is closed in $M^{\theta }$; and

• (b) $G_m$ is conjugate to H.

If V is a G-module, then $V_G$ denotes the complement to $V^G$.

Lemma 3.10

The set $M_{(H)}$ is a smooth locally closed subset of $M^{\theta }$ with

$$\begin{aligned} T_m M_{(H)} = T_m M^H \oplus (\mathfrak {g} / \mathfrak {h})_H, \quad \forall \ m \in \left( M_{(H)} \right) ^H. \end{aligned}$$

(6)

Proof

To show that $M_{(H)}$ is locally closed, it suffices to prove that, for each $m \in M_{(H)}$, there exists some G-stable affine open neighbourhood U of m in $M^{\theta }$ such that $U \cap M_{(H)}$ is closed in U. By a result of Richardson, [57, Proposition 3.3], the fact that all stabilizers are connected implies that there is a G-stable open set U such that the stabilizer $G_u$ of each $u \in U$ is conjugate to a subgroup of H. In particular, we see that if $n = \dim H$ then $\dim G_u < n$ for all $u \in U \smallsetminus M_{(H)}$. Therefore, $U \cap M_{(H)} = \{ u \in U \ | \ \dim G_u \ge n \}$. This is closed by [9, Lemma 2.2]. It will follow that $M_{(H)}$ is smooth if we can prove identity (6), since $M^H$ is smooth by [61, Corollary 6.5].

In order to prove identity (6), we apply Luna’s slice theorem [41]. There exists an excellent map $\phi : G \times _H S \rightarrow U$, where S is a slice to the G-orbit at m. Then, $\phi ^{-1}(M_{(H)}) = G \times _H S_{(H)} = G / H \times S^H$. Thus,

$$\begin{aligned} d_{(1,m)} \phi : T_{(1,m)} \left( G / H \times S^H\right) {\mathop {\longrightarrow }\limits ^{\sim }} T_p M_{(H)} \end{aligned}$$

has image $T_m S^H \oplus \mathfrak {g} \cdot m$ in $T_m M$, hence $T_m M_{(H)} = T_m S^H \oplus \mathfrak {g} \cdot m$. Since $S^H \subset M^H \subset M_{(H)}$, we have $T_m S^H \subset T_m M^H \subset T_m M_{(H)}$ and hence

$$\begin{aligned} T_m M^H = (T_m M)^H = (T_p M_{(H)})^H = T_m S^H \oplus (\mathfrak {g} \cdot m)^H. \end{aligned}$$

Thus,

$$\begin{aligned} T_p M_{(H)} = T_m S^H \oplus (\mathfrak {g} \cdot m)^H \oplus (\mathfrak {g} \cdot m)_H = T_m M^H \oplus (\mathfrak {g} / \mathfrak {h})_H \end{aligned}$$

as required. $\square$

Lemma 3.11

The variety $\mu ^{-1}(\lambda )^{\theta } \cap M_{(H)}$ is smooth, with

$$\begin{aligned} T_y \left( \mu ^{-1}(\lambda )^{\theta } \cap M_{(H)}\right) = (M^H \cap (\mathfrak {g} \cdot y)^{\perp }) \oplus (\mathfrak {g} \cdot y)_H, \end{aligned}$$

for all $y \in \mu ^{-1}(\lambda )^{\theta } \cap (M_{(H)})^H$.

Proof

Note that every point of $\mu ^{-1}(\lambda )^{\theta } \cap M_{(H)}$ is conjugate by G to some point in $\mu ^{-1}(\lambda )^{\theta } \cap (M_{(H)})^H$. By Lemma 3.10, we have

$$\begin{aligned} T_y \left( \mu ^{-1}(\lambda )^{\theta } \cap M_{(H)}\right)&= T_y M_{(H)} \cap {{\,\mathrm{\mathrm {Ker}}\,}}d_y \mu , \\&= (M^H \oplus \mathfrak {g} \cdot y ) \cap (\mathfrak {g} \cdot y)^{\perp } \\&= (M^H \cap (\mathfrak {g} \cdot y)^{\perp }) \oplus (\mathfrak {g} \cdot y)_H \end{aligned}$$

since $\mathfrak {g} \cdot y \subset (\mathfrak {g} \cdot y)^{\perp }$ is isotropic. Therefore, we just need to show that the dimension of $\mu ^{-1}(\lambda )^{\theta } \cap M_{(H)}$, as a reduced variety, is also equal to $\dim ((M^H \cap (\mathfrak {g} \cdot y)^{\perp }) \oplus (\mathfrak {g} \cdot y)_H)$. We have

$$\begin{aligned} (\phi ^* \mu )^{-1}(\lambda ) \cap (G \times _H C)_{(H)} = G \times _H (\nu ^{-1}(0) \cap \mu _H^{-1}(0))_{(H)}. \end{aligned}$$

Set-theoretically, this equals $G / H \times \nu ^{-1}(0)^H$ (which is smooth) and there is an étale map from this space to $G / H \times W^H$. Thus, we just need to show that

$$\begin{aligned} \dim ((M^H \cap (\mathfrak {g} \cdot y)^{\perp }) \oplus (\mathfrak {g} \cdot y)_H) = \dim G / H \times \nu ^{-1}(0)^H. \end{aligned}$$

If $M = C \oplus (\mathfrak {g} \cdot y)$, then $M^H = C^H \oplus (\mathfrak {g} \cdot y)^H$. The fact that $W = C \cap (\mathfrak {g} \cdot y)^{\perp }$ implies that

$$\begin{aligned} C^H \cap (\mathfrak {g} \cdot y)^{\perp } = \left( C \cap (\mathfrak {g} \cdot y)^{\perp } \right) ^H =W^H. \end{aligned}$$

Thus,

$$\begin{aligned} \dim ((M^H \cap (\mathfrak {g} \cdot y)^{\perp }) \oplus (\mathfrak {g} \cdot y)_H)&= \dim C^H \cap (\mathfrak {g} \cdot y)^{\perp } + \dim (\mathfrak {g} \cdot y)^H + \dim (\mathfrak {g} \cdot y)_H \\&= \dim W^H + \dim (\mathfrak {g} \cdot y) \\&= \dim G / H \times \nu ^{-1}(0)^H \end{aligned}$$

as required. $\square$

Theorem 3.12

There exists a unique symplectic form $\omega _H$ on $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(H)}$ such that

$$\begin{aligned} \pi ^* \omega _H = \omega |_{\mu ^{-1}(\lambda )^{\theta } \cap M_{(H)}}, \end{aligned}$$

where $\pi : \mu ^{-1}(\lambda )^{\theta } \cap M_{(H)} \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(H)}$ is the quotient map.

Proof

For brevity, let $Y =\mu ^{-1}(\lambda )^{\theta } \cap M_{(H)} \cap V$, where V is the affine open set of Lemma 3.8, and set $\mathfrak {M} = \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. Abusing notation, we will also write $\mathfrak {M} \cap V$ for the affine open subset $(V \cap \mu ^{-1}(\lambda )) /\!\!/\!\, G$ of $\mathfrak {M}$. We claim that we have a commutative diagram of linear maps

where the vertical map on the left is just projection.

Since $\phi$ is excellent, we have an identification

$$\begin{aligned} \phi ^{-1}(Y) = G / H \times (\nu ^{-1}(0)^H \cap U), \end{aligned}$$

which means that the diagram

commutes, with $\phi$ and $\phi /G$ being étale. Under the identification $T_0 \nu ^{-1}(0)^H = W^H$, the differential map $d \eta : T_0 \nu ^{-1}(0)^H \oplus \mathfrak {g} / \mathfrak {h} \rightarrow T_0 \nu ^{-1}(0)^H$ is the projection map $W^H \oplus \mathfrak {g}/\mathfrak {h} \rightarrow W^H$, as required.

We deduce that $\pi$ is a smooth morphism on Y. Hence $\pi ^* : \Omega ^2_{(\mathfrak {M} \cap V)_{(H)}} \rightarrow \Omega ^2_{Y}$ is an embedding, with image $\left( \Omega ^2_{Y} \right) ^G$. Thus, there is a unique (closed) 2-form $\omega _H$ on $(\mathfrak {M} \cap V)_{(H)}$, whose pull-back along $\pi$ equals $\omega |_{Y}$.

Finally, to prove that $\omega _H$ is symplectic it suffices to prove that the radical of $\omega |_{Y}$ at m equals $\mathfrak {g}/ \mathfrak {h}$. Clearly the latter is contained in the former. Since $T_m Y = W^H \oplus (\mathfrak {g} / \mathfrak {h})$, it suffices to show that $\omega |_{W^H}$ is non-degenerate. Recall that $\hat{\omega } = \omega |_W$ is non-degenerate. Then $W^H$ is a symplectic subspace since $\hat{\omega }$ is H-invariant. $\square$

Next, we show that the symplectic forms $\omega _H$ come from the Poisson structure on $\mu ^{-1}(\lambda )^{\theta }/\!/G$.

Lemma 3.13

For each $f \in \mathbb {C}[V]^G$, the Hamiltonian vector field $\zeta _f$ is tangent to $M_{(H)}$.

Proof

By Lemma 3.10, $M_{(H)}$ is smooth, therefore it suffices to show that $(\zeta _f)_y \in T_y M_{(H)}$ for all $y \in (M_{(H)})^H$. Recall from Lemma 3.10 that $T_y M_{(H)} = M^H \oplus (\mathfrak {g}/ \mathfrak {h})_H$. The canonical map $\mathrm {Der}(V) \rightarrow T_y M_{(H)}$ is H-equivariant. Since $\{ - , - \}$ is G-invariant, and $f \in \mathbb {C}[V]^G$, the Hamiltonian vector field $\zeta _f$ belongs to $\mathrm {Der}(V)^G \subset \mathrm {Der}(V)^H$. Hence $(\zeta _f)_y \in (T_y M)^H = M^H \subset T_y M_{(H)}$, as required. $\square$

Theorem 3.14

The space $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(H)}$ is a locally closed Poisson subvariety, such that the restriction $\{ - , - \} |_{\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(H)}}$ of the Poisson bracket on $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ equals the Poisson structure induced by $\omega _H$. In particular, it is non-degenerate.

Proof

Again, let $\mathfrak {M} = \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. First we show that it is a Poisson subvariety. It suffices to show that each Hamiltonian vector field $\zeta _{\bar{f}}$ on $\mathfrak {M} \cap V$ is tangent to $(\mathfrak {M} \cap V)_{(H)}$. Let $f \in \mathbb {C}[V]^G$ be a lift of $\bar{f}$. Then, by Lemma 3.13, $\zeta _f$ is tangent to $M_{(H)} \cap \mu ^{-1}(\lambda )^{\theta }$. By definition of Hamiltonian reduction, $\zeta _f$ is also tangent to $V \cap \mu ^{-1}(\lambda )^{\theta }$. Therefore, it descends to the vector field $\zeta _{\bar{f}}$ on $\mathfrak {M}$, which is tangent to $(M_{(H)} \cap V \cap \mu ^{-1}(\lambda )^{\theta }) /\!\!/\!\, G$. But, by Theorem 3.12,

$$\begin{aligned} (M_{(H)} \cap V \cap \mu ^{-1}(\lambda )^{\theta }) /\!\!/\!\, G = (\mathfrak {M} \cap V)_{(H)}, \end{aligned}$$

as required.

Next, we show that the two Poisson structures agree. Once again, we let $Y = V \cap M_{(H)} \cap \mu ^{-1}(\lambda )^{\theta }$, and let $\pi : Y \rightarrow (V \cap \mathfrak {M})_{(H)}$ be the quotient map.

Choose a function $\bar{f}$ defined on $(V \cap \mathfrak {M})_{(H)}$ and denote by the same symbol an arbitrary lift to $V \cap \mathfrak {M}$. Since the form $\omega _H$ is non-degenerate on $(V \cap \mathfrak {M})_{(H)}$ there exists a Hamiltonian vector field $\zeta _{\bar{f}}'$ on $(V \cap \mathfrak {M})_{(H)}$ satisfying the defining equation $\omega _H(\zeta _{\bar{f}}',\eta ) = - \eta (\bar{f})$ for all vector fields $\eta$. The non-degeneracy of $\omega _H$ implies that it suffices to prove that $\omega _H(\zeta _{\bar{f}},\eta ) = \omega _H(\zeta _{\bar{f}}',\eta )$ for all $\eta$, since $\zeta _{\bar{f}} =\zeta _{\bar{f}}'$ implies that $\{ \bar{f}, g\} = \{ \bar{f},g\}'$ for all functions g on $(V \cap \mathfrak {M})_{(H)}$. Thus, we must show that $\omega _H(\zeta _{\bar{f}},\eta ) = - \eta (\bar{f})$.

Since the quotient map $\pi : Y \rightarrow (V \cap \mathfrak {M})_{(H)}$ is smooth, we can choose a lift of $\eta$. In fact, if we ask that the lift be G-invariant, it is unique, and so we will denote it by $\eta$ too. If f is a lift of $\bar{f}$ to $\mathbb {C}[V]^G$, then $\zeta _f$ is tangent to Y, and $\zeta _f |_{Y}$ is a lift of $\zeta _{\bar{f}}$. Therefore,

$$\begin{aligned} \omega _H(\zeta _{\bar{f}},\eta ) = \pi ^* \omega _H( \zeta _f |_{Y}, \eta ) = \omega |_Y(\zeta _f |_Y, \eta ). \end{aligned}$$

Finally, if we choose an arbitrary lift $\eta '$ of $\eta$ to V, then

$$\begin{aligned} \omega |_Y(\zeta _f |_Y, \eta ) = \omega (\zeta _f, \eta ') |_Y = - \eta '(f)|_Y = - \eta (f |_Y) = - \eta (\bar{f}).\quad \quad \quad \quad \square \end{aligned}$$

Finally, we complete the proof of Theorem 3.7.

Proof of Theorem 3.7

All claims, except for the final one, follow from Lemma 3.8 and Proposition 3.9. Thus, it suffices to note that the isomorphism $\Psi$ of (5) is Poisson. Choose a generic point n in

$$\begin{aligned} (Z \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)) /\!\!/\!H \simeq (\phi ^* \mu )^{-1}(\lambda )^{\theta } /\!\!/\!\, G. \end{aligned}$$

Then there exists some $K \subset H$ such that $n \in ((Z \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)) /\!\!/\!H)_{(K)}$. Both Poisson structures on this open stratum are non-degenerate. Therefore, it suffices to show that the corresponding symplectic 2-forms agree via $\Psi$. Recall that the symplectic form on $((Z \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)) /\!\!/\!H)_{(K)}$ is the unique form such that its pull-back to $Z_{(K)} \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)$ agrees with $\omega |_{Z_{(K)} \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)}$. Similarly, the symplectic form on $((\phi ^* \mu )^{-1}(\lambda )^{\theta } /\!\!/\!\, G)_{(K)}$ is the unique symplectic form whose pull-back to $D := (G \times _H Z_{(K)}) \cap (\phi ^* \mu )^{-1}(\lambda )^{\theta }$ equals $(\phi ^* \omega ) |_{D}$. Therefore, since the map $\Psi$ is induced by the closed embedding j, it suffices to show that

$$\begin{aligned} j^* ((\phi ^* \omega ) |_{D}) = \omega |_{Z_{(K)} \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0)}. \end{aligned}$$

But this follows from the fact that

$$\begin{aligned} D = \phi ^{-1}(V_{(K)} \cap \mu ^{-1}(\lambda )^{\theta }), \quad j^{-1}(D) = Z_{(K)} \cap \nu ^{-1}(0) \cap \mu _H^{-1}(0), \end{aligned}$$

and $\phi \circ j$ is the map $c \mapsto c + m$, so that $j^* \phi ^* \omega = \omega |_{\nu ^{-1} (0) \cap C_{\delta }}$, since $\omega$ is invariant under translation. $\square$

The following result is an important consequence of Theorem 3.14.

Proposition 3.18

The strata $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau } := \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(G_\tau )}$ define a finite stratification of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ into locally closed subsets such that

$$\begin{aligned} \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(H)} \subset \overline{\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(L)}} \quad \Leftrightarrow \quad (H) \le (L). \end{aligned}$$

Moreover, the connected components of the strata are precisely the symplectic leaves of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, with respect to its natural Poisson bracket.

Proof

It is well-known that the stratification of ${{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )^{\theta }/\!\!/\!\, \mathrm {G}(\alpha )$ by stabilizer type is finite, with smooth locally closed strata. Therefore the stratification $\{ \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau } \}$ of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is finite with locally closed strata. Thus it suffices to show that (a) each stratum is smooth, and (b) the Poisson structure is non-degenerate on each stratum. In fact, (b) implies (a), and both statements are implied by Theorem 3.14. $\square$

We will show in Corollary 3.25 that each stratum $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ is connected.

3.4 Hyperkähler twisting

Let $\alpha = m_1 \nu ^{(1)} + \cdots + m_t \nu ^{(t)}$ be the canonical decomposition of $\alpha$ with respect to $\Sigma _{\lambda }$. It is shown in [16] that

Theorem 3.16

[16] There is an isomorphism of varieties $\prod _i S^{m_i} \left( \mathfrak {M}_{{\lambda }} ({\nu ^{(i)}},{0}) \right) \simeq \mathfrak {M}_{{\lambda }} ({\alpha },{0})$.

Moreover, if $\nu ^{(i)}$ is real then $S^{m_i} \left( \mathfrak {M}_{{\nu ^{(i)}}} ({\lambda },{0}) \right) = \{ \mathrm {pt} \}$ and if $\nu ^{(i)}$ is anisotropic then $m_i = 1$. We now adapt Crawley-Boevey’s result to the case where $\theta \ne 0$:

Theorem 3.17

Let $\alpha = n_1 \sigma ^{(1)} + \cdots + n_k \sigma ^{(k)}$ be the canonical decomposition of $\alpha$ with respect to $\Sigma _{\lambda ,\theta }$. Then, there is an isomorphism of Poisson varieties

$$\begin{aligned} \phi : \ \prod _i S^{n_i} \left( \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta }) \right) {\mathop {\longrightarrow }\limits ^{\sim }} \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) . \end{aligned}$$

The proof of Theorem 3.17 is given at the end of Sect. 3.5. In order to deduce Theorem 3.17 from [16, Theorem 1.1], we use hyperkähler twists. By our main assumption (1), $\lambda \in \mathbb {R}^{Q_0}$.

Proposition 3.21

Let $\nu = -\lambda - \mathbf{i} \theta$ and consider $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, $\mathfrak {M}_{{\nu }} ({\alpha },{0})$ as complex analytic spaces. Hyperkähler twisting defines a homeomorphism of stratified spaces

$$\begin{aligned} \Psi : \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) {\mathop {\longrightarrow }\limits ^{\sim }} \mathfrak {M}_{{\nu }} ({\alpha },{0}) , \end{aligned}$$

i.e. $\Psi$ restricts to a homeomorphism $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(H)} {\mathop {\longrightarrow }\limits ^{\sim }} \mathfrak {M}_{{\nu }} ({\alpha },{0}) _{(H)}$ for all classes (H). In particular, the homeomorphism maps stable representations to stable ($=$ simple) representations.

Proof

We follow the setup described in the proof of [14, Lemma 3]. We have moment maps

$$\begin{aligned} \mu _{\mathbb {C}}(x) = \sum _{a \in Q_1} [x_a,x_{a^*}], \quad \mu _{\mathbb {R}}(x) = \frac{\sqrt{-1}}{2} \sum _{a \in Q_1} [x_a,x_{a}^{\dagger }] + [x_{a^*},x_{a^*}^{\dagger }]. \end{aligned}$$

As shown in [34, Corollary 6.2], the Kempf-Ness Theorem says that the embedding $\mu _{\mathbb {C}}^{-1}( \lambda ) \cap \mu ^{-1}_{\mathbb {R}}( \mathbf{i} \theta ) \hookrightarrow \mu _{\mathbb {C}}^{-1}( \lambda )$ induces a bijection

$$\begin{aligned} \mu _{\mathbb {C}}^{-1}( \lambda ) \cap \mu ^{-1}_{\mathbb {R}}( \mathbf{i} \theta ) / U(\alpha ) {\mathop {\longrightarrow }\limits ^{\sim }} \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) . \end{aligned}$$

(7)

Since the embedding is clearly continuous and the topology on the quotients $\mu _{\mathbb {C}}^{-1}( \lambda ) \cap \mu ^{-1}_{\mathbb {R}}( i \theta ) / U(\alpha )$ and $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is the quotient topology (for the latter space, see [54, Corollary 1.6 and Remark 1.7]), the bijection (7) is continuous.

Define a stratification $\mu _{\mathbb {C}}^{-1}( \lambda ) \cap \mu ^{-1}_{\mathbb {R}}( \mathbf{i} \theta ) / U(\alpha )$ analogous to the stratification of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ described in Sect. 3.1. Let $y \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, and $x = x_1^{e_1} \oplus \cdots \oplus x_k^{e_k} \in T(y)$ a $\theta$-polystable lift in $\mu _{\mathbb {C}}^{-1}(\lambda ) \cap \mu ^{-1}_{\mathbb {R}}( i \theta )$ (which exists by Proposition 3.1). Then Lemma 3.6 says that $G_x = \mathrm {G}(\mathbf{e} )$ and [34, Proposition 6.5] implies that $U(\alpha )_{x} = U(\mathbf{e} )$. Hence $\mathrm {G}(\alpha )_x = U(\alpha )_x^{\mathbb {C}}$. Therefore the homeomorphism (7) restricts to a bijection

$$\begin{aligned} (\mu _{\mathbb {C}}^{-1}( \lambda ) \cap \mu ^{-1}_{\mathbb {R}}( \mathbf{i} \theta ) / U(\alpha ))_{(K)} \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(K^{\mathbb {C}})} \end{aligned}$$

for each (K).

Let the quaternions $\mathbb {H} = \mathbb {R}\oplus \mathbb {R}\mathbf{i} \oplus \mathbb {R}\mathbf{j} \oplus \mathbb {R}\mathbf{k}$ act on ${{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )$ by extending the usual complex structure so that $\mathbf{j} \cdot (x_{a},x_{a^*}) = (- x_{a^*}^{\dagger }, x_a^{\dagger })$ and $\mathbf{k} \cdot (x_{a},x_{a^*}) = ( -\mathbf{i} x_{a^*}^{\dagger }, \mathbf{i} x_a^{\dagger })$. Here the dagger denotes the Hermitian adjoint. In general,

$$\begin{aligned} (z_1 + z_2 \mathbf{j} ) \cdot (x_a,x_{a^*}) = (z_1 x_a - z_2 x_{a^*}^{\dagger }, z_1 x_{a^*} + z_2 x_a^{\dagger }). \end{aligned}$$

This action commutes with the action of $U(\alpha )$ and satisfies

$$\begin{aligned} \mu _{\mathbb {R}}(z \cdot x)&= ( ||z_1||^2 - || z_2||^2) \mu _{\mathbb {R}}(x) - \mathbf{i} z_1 \overline{z}_2 \mu _{\mathbb {C}}(x) - \mathbf{i} z_2 \overline{z}_1 \mu _{\mathbb {C}}(x)^{\dagger }, \end{aligned}$$

(8)

$$\begin{aligned} \mu _{\mathbb {C}}(z \cdot x)&= z_1^2 \mu _{\mathbb {C}}(x) - z_2^2 \mu _{\mathbb {C}}(x)^{\dagger } - 2 \mathbf{i} z_1 z_2 \mu _{\mathbb {R}}(x), \quad \forall \ z \in \mathbb {H}. \end{aligned}$$

(9)

Let $h = (\mathbf{i} - \mathbf{j} ) / \sqrt{2}$. Then multiplication by h defines a homeomorphism

$$\begin{aligned} \mu _{\mathbb {C}}^{-1}( \lambda ) \cap \mu ^{-1}_{\mathbb {R}}( \mathbf{i} \theta ) {\mathop {\longrightarrow }\limits ^{\sim }} \mu _{\mathbb {C}}^{-1}(- \lambda - \mathbf{i} \theta ) \cap \mu ^{-1}_{\mathbb {R}}( 0) \end{aligned}$$

Since multiplication by h commutes with the action of $U(\alpha )$, this homeomorphism descends to a homeomorphism

$$\begin{aligned} \left( \mu _{\mathbb {C}}^{-1}( \lambda ) \cap \mu ^{-1}_{\mathbb {R}}( \mathbf{i} \theta ) \right) /U(\alpha ) {\mathop {\longrightarrow }\limits ^{\sim }} \left( \mu _{\mathbb {C}}^{-1}(- \lambda - \mathbf{i} \theta ) \cap \mu ^{-1}_{\mathbb {R}}( 0) \right) / U(\alpha ) \end{aligned}$$

which preserves the stratification by stabilizer type.

Thus, the map $\Psi$ is the composition of three homeomorphisms, each of which preserves the stratification. $\square$

Remark 3.19

Our general assumption that $\lambda \in \mathbb {R}^{Q_0}$ if $\theta \ne 0$ is required in the proof of Proposition 3.18 to ensure that multiplication by h lands in $\mu _{\mathbb {R}}^{-1}(0)$. Equation (8) implies that it would suffice to assume more generally that there exists $z \in \mathbb {C}$ such that $|z| = 1$ and $z \lambda \in \mathbb {R}^{Q_0}$. It is natural to expect that Theorem 3.17 holds without the assumption $\lambda \in \mathbb {R}^{Q_0}$.

Remark 3.20

Using the notion of smooth structures on stratified symplectic spaces, as defined in [59], one can presumably strengthen Proposition 3.18 to the statement that there is a diffeomorphism of stratified symplectic spaces $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) {\mathop {\longrightarrow }\limits ^{\sim }} \mathfrak {M}_{{\nu }} ({\alpha },{0})$.

Proposition 3.28

The variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is irreducible and normal.

Proof

We begin by showing that the variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is connected. Proposition 3.18 implies that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is connected if and only if $\mathfrak {M}_{{\nu }} ({\alpha },{0})$ is connected. The latter is known to be connected (and nonempty) by [16, Corollary 1.4].

Next, we show that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is irreducible. Since $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is connected, it suffices to show that, for each $\mathbb {C}$-point $x\in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, the local ring $\mathcal {O}_{\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) ,x}$ is a domain. This ring embeds into the complete local ring of x in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. By Corollary 3.4, the complete local ring of x in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is isomorphic to the complete local ring of 0 in $\mathfrak {M}_{{0}} ({e},{0})$. By [16, Corollary 1.4], this is a domain. Finally, normality is an étale local property, [45, Remark 2.24 and Proposition 3.17]. Therefore, as in the previous paragraph this follows from Theorem 3.3 and [17, Theorem 1.1]. $\square$

We can now prove Theorem 1.3.

Proof of Theorem 1.3

Let $\nu = -\lambda - \mathbf{i} \theta$. By the last statement of Proposition 3.18, there exists a $\theta$-stable representation of $\Pi ^{\lambda }(Q)$ of dimension $\alpha$ if and only if there exists a simple representation of $\Pi ^{\nu }(Q)$ of dimension $\alpha$. By [15, Theorem 1.3], the latter happens if and only if $\alpha \in \Sigma _{\nu }$. Since $\lambda \in \mathbb {R}^{Q_0}$, the sets $\Sigma _{\nu }$ and $\Sigma _{\lambda ,\theta }$ are equal. Thus, we deduce that there exists a $\theta$-stable representation of $\Pi ^{\lambda }(Q)$ of dimension $\alpha$ if and only if $\alpha \in \Sigma _{\lambda ,\theta }$. $\square$

As a consequence of Theorem 1.3 and Proposition 3.21, we obtain:

Corollary 3.22

For $\alpha \in \Sigma _{\lambda ,\theta }$, the locus of $\theta$-stable representations is dense in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

3.5 The proof of Theorem 3.17

Recall that $\alpha = n_1 \sigma ^{(1)} + \cdots + n_k \sigma ^{(k)}$ is the canonical decomposition of $\alpha$ in $R^+_{\lambda ,\theta }$. The map $\phi$ is defined as follows. Let $H(\alpha )$ be the product $\mathrm {G}(\sigma ^{(1)})^{n_1} \times \cdots \times \mathrm {G}(\sigma ^{(k)})^{n_k}$, thought of as a subgroup of $\mathrm {G}(\alpha )$. There is a natural $H(\alpha )$-equivariant inclusion $\prod _i T^* {{\,\mathrm{\mathrm {Rep}}\,}}(Q,\sigma ^{(i)})^{n_i} \hookrightarrow T^* {{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )$. This is an inclusion of symplectic vector spaces. Since the moment map for the action of $H(\alpha )$ on $T^* {{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )$ is the composition of the moment map for $\mathrm {G}(\alpha )$ followed by projection from the Lie algebra of $\mathrm {G}(\alpha )$ to the Lie algebra of $H(\alpha )$, the above inclusion restricts to an inclusion $\prod _i (\mu _{\sigma ^{(i)}}^{-1}(\lambda )^{\theta })^{n_i} \hookrightarrow \mu ^{-1}_{\alpha }(\lambda )^{\theta }$, inducing a map of GIT quotients

$$\begin{aligned} \prod _i \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta }) ^{n_i} \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) . \end{aligned}$$

This map, which sends a tuple of representations $(M_{i,j})$ to the direct sum $\bigoplus _{i,j} M_{i,j}$ clearly factors through $\prod _i S^{n_i} \left( \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta }) \right)$. It is this map that we call $\phi$.

Passing to the analytic topology, Proposition 3.18 implies that we get a commutative diagram

(10)

where both vertical arrows are homeomorphisms and the bottom horizontal arrow is an isomorphism by Theorem 3.16. Therefore, we conclude that $\phi$ is bijective. Since we are working over the complex numbers, and we have shown in Proposition 3.21 that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is normal, we conclude by Zariski’s main theorem that $\phi$ is an isomorphism.

As a consequence, we can compute the dimension of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, which in the case $\theta \ne 0$ is [15, Corollary 1.4]. We begin with the following basic lemma:

Lemma 3.23

If $\alpha \in \Sigma _{\lambda ,\theta }$, then $\dim \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) = 2p(\alpha )$. Moreover $\dim \mu ^{-1}(\lambda )^\theta \ge \alpha \cdot \alpha + 2p(\alpha )-1$.

Proof

Let U be the subset of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ consisting of $\theta$-stable representations. Since $\alpha$ is assumed to be in $\Sigma _{\lambda ,\theta }$, Corollary 3.22 implies that U is a dense open subset of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. Let V be the open subset of ${{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )$ consisting of $\theta$-stable representations. Then U is the image of $\mu ^{-1}(\lambda ) \cap V$ under the quotient map and hence V is non-empty. The group $\mathrm {PG}(\alpha )$ acts freely on V and $\mu$ is smooth when restricted to V. Thus,

$$\begin{aligned} \dim U = \dim {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha ) - 2 (\dim \mathrm {G}(\alpha ) - 1) = 2 p(\alpha ), \end{aligned}$$

as required. For the second statement, observe that $\dim (V \cap \mu ^{-1}(\lambda )) = \dim U + \dim \mathrm {PG}(\alpha )$ since $\mathrm {PG}(\alpha )$ acts freely on V. $\square$

Then we immediately conclude

Corollary 3.24

For $\alpha \in R^+_{\lambda ,\theta }$ with canonical decomposition $\alpha = n_1 \sigma ^{(1)} + \cdots + n_k \sigma ^{(k)}$, the variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ has dimension $2 \sum _{i = 1}^k n_i p(\sigma ^{(i)})$.

Finally, we need to check that the morphism $\phi$ is Poisson. Since both varieties are normal by Proposition 3.21, it suffices to show that $\phi$ induces an isomorphism of smooth symplectic varieties between the open leaf of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ and the open leaf of $\prod _i S^{n_i} \left( \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta }) \right)$. By Proposition 3.15, the symplectic leaves of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ are connected components of the strata given by stabilizer type. The explicit description of $\phi$ given at the start of this section shows that $\phi$ restricts to an isomorphism between strata. In particular, $\phi$ restricts to an isomorphism between the open leaves.

The symplectic structure on the open leaf of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ comes from the symplectic structure on $T^* {{\,\mathrm{\mathrm {Rep}}\,}}(Q,\alpha )$. More specifically, the non-degenerate closed form on the latter space restricts to a degenerate $\mathrm {G}(\alpha )$-invariant two-form on $\mu ^{-1}(\lambda )^{\theta }$. Hence it descends to a closed two-form on $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. The restriction of this two-form to the open leaf is non-degenerate. The two-form on the open leaf of $\prod _i S^{n_i} \left( \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta }) \right)$ is defined similarly. Now the point is that under the embedding $\prod _i (\mu _{\sigma ^{(i)}}^{-1}(\lambda )^{\theta })^{n_i} \hookrightarrow \mu ^{-1}_{\alpha }(\lambda )^{\theta }$, the $H(\alpha )$-invariant closed two-form on $\prod _i (\mu _{\sigma ^{(i)}}^{-1}(\lambda )^{\theta })^{n_i}$ is simply the pull-back of the $\mathrm {G}(\alpha )$-invariant closed two-form on $\mu ^{-1}_{\alpha }(\lambda )^{\theta }$. This implies that the two-form on the open leaf of $\prod _i S^{n_i} \left( \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta }) \right)$ is the pull-back, under $\phi$, of the symplectic two-form on the open leaf of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

Using Proposition 3.21, we can now show that each stratum $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ is connected.

Corollary 3.25

Each stratum $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is irreducible (and thus connected) and nonempty. In particular, the strata $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ are precisely the symplectic leaves of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

Proof

Writing $\tau = (e_1, \beta ^{(1)}; \dots ; e_k, \beta ^{(k)})$, we can repeat the construction of $\phi$ given above (even though $\tau$ is not the canonical decomposition of $\alpha$) to get a morphism

$$\begin{aligned} \phi : \prod _i S^{e_i} \mathfrak {M}_{{\lambda }} ({\beta ^{(i)}},{\theta }) \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) . \end{aligned}$$

The stratum $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ is contained in the image of $\phi$ and $\phi ^{-1}(\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau })$ is dense in the domain of $\phi$ by Corollary 3.22. Since the domain is irreducible and nonempty by Proposition 3.21, we deduce that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ is irreducible. $\square$

Remark 3.26

The statement of Corollary 3.25 (at least in the case $\theta = 0$) appears as Theorem 1.3 of [43]. However, it is falsely claimed in Proposition 4.5 of that paper that the irreducibility of the stratum $\mathfrak {M}_{{\lambda }} ({\alpha },{0}) _{\tau }$ follows from a result of G. Schwarz.

3.6 Flatness of the moment map

We need an additional result which follows from [17]. Let $\xi : \mu ^{-1}(\lambda )^\theta \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ be the quotient map.

Theorem 3.27

[17, Corollary 6.4] For $\tau = (e_1, \beta ^{(1)}; \dots ; e_k, \beta ^{(k)})$ a representation type,

$$\begin{aligned} \dim \xi ^{-1}(\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _\tau ) \le \alpha \cdot \alpha - 1 +p(\alpha ) + \sum _{i = 1}^k p(\beta ^{(i)}). \end{aligned}$$

(11)

Proof

The proof follows verbatim as in [17, Corollary 6.4], substituting $\theta$-stable representations for simple representations. Alternatively, [17, Corollary 6.4] as written together with Theorem 3.3 yields the result. $\square$

Proposition 4.2

The restricted moment map $\overline{\mu }: {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )^\theta \rightarrow \mathfrak {pg}(\alpha )$ is flat over an open subset U containing $B_{\alpha ,\theta } := \{\lambda \in \mathbb {R}^{Q_0} \mid \alpha \in \Sigma _{\lambda ,\theta }\} \subseteq \mathbb {R}^{Q_0}$, with all fibers of dimension $\alpha \cdot \alpha + 2p(\alpha )-1$. In particular, if $\alpha \in \Sigma _{\lambda ,\theta }$, then the variety $\mu ^{-1}(\lambda )^\theta$ is a complete intersection in the open subset $\overline{\mu }^{-1}(U)^\theta \subseteq {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )^\theta$.

Proof

By Lemma 3.23 and Theorem 3.27, all of the fibers $\mu ^{-1}(\lambda )$ for $\lambda \in B_{\alpha ,\theta }$ have the same dimension, $\alpha \cdot \alpha + 2p(\alpha )-1$. Since this equals the difference of dimensions $\dim {{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha ) - \dim \mathfrak {pg}(\alpha )$, it follows that the subset of the base where the fiber has this dimension is open, call it U. Then, since $B_{\alpha ,\theta }$ is smooth, and $\mu ^{-1}(U)$ is open (hence smooth and therefore Cohen–Macaulay), it follows that the moment map is flat as stated, and therefore that every fiber is a complete intersection. $\square$

4 Smooth versus stable points

As usual, choose a deformation parameter $\lambda \in \mathbb {R}^{Q_0}$, a stability parameter $\theta \in \mathbb {Z}^{Q_0}$, and a dimension vector $\alpha \in \mathbb {N}R^+_{\lambda ,\theta }$. The main goal of this section is to prove Theorem 1.15, which says that $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is canonically $\theta$-polystable if and only if it is in the smooth locus of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

4.1 Isotropic roots

In this section, we briefly consider quiver varieties associated to isotropic roots. The subgroup of $\mathrm {GL}(\mathbb {Z}^{Q_0})$ generated by the reflection at loop free vertices is denoted W(Q).

Lemma 4.1

Let $\alpha \in \Sigma _{\lambda ,\theta }$ be an isotropic root. Then there exists $w \in W(Q)$ such that $\delta = w \alpha$ is in the fundamental domain, $Q' = \mathrm {Supp}\ \delta$ is an affine Dynkin quiver, $\delta |_{Q'}$ is the minimal imaginary root and $\mathfrak {M}_{\lambda }(\alpha ,\theta ) \simeq \mathfrak {M}_{w \lambda }(\delta , w \theta )$.

Proof

As the name implies, the fundamental domain $\mathcal {F}(Q)$ is a fundamental domain for the action of the reflection group W(Q) of Q on the set of imaginary roots. Therefore there exists w such that $w \alpha \in \mathcal {F}(Q)$. The fact that $Q'$ is affine Dynkin and $\delta |_{Q'}$ is the minimal imaginary root follows from [28, Lemma 1.9 (d)].

Thus, we show that $\delta \in \Sigma _{w \lambda ,w \theta }$ and $\mathfrak {M}_{\lambda }(\alpha ,\theta ) \simeq \mathfrak {M}_{w \lambda }(\delta , w \theta )$. The Lusztig-Maffei-Nakajima reflection isomorphisms of quiver varieties (see in particular [42, Theorem 26]) shows that if either $\lambda _i$ or $\theta _i$ is non-zero (equivalently, as explained in example 1, if $e_i \notin \Sigma _{\lambda ,\theta }$) then $\mathfrak {M}_{\lambda }(\alpha ,\theta ) \simeq \mathfrak {M}_{s_i \lambda }(s_i \alpha , s_i \theta )$. It is easily checked that if $e_i \in \Sigma _{\lambda ,\theta }$ then $(\alpha ,e_i) \le 0$ (otherwise $\alpha = (\alpha - e_i) + e_i$ with $p(\alpha ) = p(\alpha - e_i)$). Moreover, the fact that $s_i$ permutes the set $R^+ \smallsetminus \{ e_i \}$ implies that $s_i \alpha \in \Sigma _{s_i \lambda , s_i \theta }$ if $e_i \notin \Sigma _{\lambda ,\theta }$. Hence, we need to show that $w = s_{i_r} \cdots s_{i_1}$ can be chosen so that $(s_{i_l} \cdots s_{i_1} \lambda )_{i_{l+1}} \ne 0$ or $(s_{i_l} \cdots s_{i_1} \theta )_{i_{l+1}} \ne 0$ for all $l = 1, \dots , r-1$. Recall that every positive root $\beta = \sum _{i \in Q_0} k_i e_i$ has height $\mathrm {ht}(\beta ) := \sum _{i \in Q_0} k_i \ge 1$. As in the proof of [12, Proposition 16.10], the key thing to note is that $\delta$ is specified by the fact that it is the unique element of minimal height in the orbit $W(Q) \cdot \alpha$. Thus, if $\alpha \notin \mathcal {F}(Q)$, then there exists $i \in Q_0$ such that $(\alpha ,e_i) > 0$. This implies that $e_i \notin \Sigma _{\lambda ,\theta }$ and $\mathrm {ht}(s_i \alpha ) < \mathrm {ht}(\alpha )$. Since every element in the orbit $W(Q) \cdot \alpha$ is a positive root (and hence has positive height) this cannot continue forever, and the result follows. $\square$

In particular, we note that Lemma 4.1 implies that if $\alpha \in \Sigma _{\lambda ,\theta }$ is an isotropic root, then $\mathfrak {M}_{\lambda }(\alpha ,\theta )$ is the partial resolution of a partial deformation of a Kleinian singularity. Moreover, the type of the Kleinian singularity is specified by the support of $w \alpha \in \mathcal {F}$.

4.2 The proof of Theorem 1.15

The proof of Theorem 1.15 follows closely the arguments given in [38, Theorem 3.2]. We provide the necessary details that show that the arguments of loc. cit. are valid in our setting. First, notice that, under the isomorphism of Theorem 3.17, the open subset of canonically $\theta$-polystable points in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is the product of the canonically $\theta$-polystable points in the spaces $S^{n_i} \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$. Therefore it suffices to show that the set of canonically $\theta$-polystable points in $S^{n_i} \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ is precisely the smooth locus. If $\sigma ^{(i)}$ is real then $S^{n_i} \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ is a point. If $\sigma ^{(i)}$ is an isotropic root then by Lemma 4.1, $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ is a partial resolution of a du Val singularity. In particular, it is a 2-dimensional (quasi-projective) variety. This implies that the smooth locus of $S^{n_i} \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ equals

$$\begin{aligned}&S^{n_i, \circ } \ \mathfrak {M}_{\lambda }(\sigma ^{(i)},\theta )_{\mathrm {sm}}\\&:= \left\{ (p_j) \ \left| \ p_j \in \mathfrak {M}_{\lambda }(\sigma ^{(i)},\theta )_{\mathrm {sm}}, \ p_j \ne p_k \text { for }j \ne k \right. \right\} . \end{aligned}$$

On the other hand, the set of canonically $\theta$-polystable points in $S^{n_i} \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ equals $S^{n_i, \circ } U$, where $U \subset \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ is the set of canonically $\theta$-polystable points. Therefore, in this case it suffices to show that $\mathfrak {M}_{\lambda }(\sigma ^{(i)},\theta )_{\mathrm {sm}}$ equals U. Finally, in the case where $\sigma ^{(i)}$ is an anisotropic root, we have $n_i = 1$.

Thus, we are reduced to considering the situation where $\alpha \in \Sigma _{\lambda ,\theta }$ is an imaginary root. In this case, a point x is canonically $\theta$-polystable if and only if it is $\theta$-stable. As in the proof of Corollary 3.24, it is clear from the definition of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ that the set of $\theta$-stable points is contained in the smooth locus. Therefore it suffices to show that if x is not $\theta$-stable then it is a singular point. As in Sect. 3.2, let x be the image of a $\theta$-polystable representation $y = y_1^{e_1} \oplus \cdots \oplus y_{\ell }^{e_{\ell }}$ (with the $y_i$ $\theta$-stable). Let $\beta ^{(i)} = \dim y_i$. Let $Q'$ be the quiver with $\ell$ vertices whose double has $2 p(\beta ^{(i)})$ loops at vertex i and $- (\beta ^{(i)},\beta ^{(j)})$ arrows between vertex i and j. The $\ell$-tuple $\mathbf{e} = (e_1, \dots , e_{\ell })$ defines a dimension vector for the quiver $Q'$. By Theorem 3.3, it suffices to show that 0 is contained in the singular locus of $\mathfrak {M}_{0}(\mathbf{e} ,0)$.

In order to proceed, we require [37, Proposition 1.1], stated in our generality. The proof is identical to the proof given in loc. cit., this time using Theorem 3.3.

Proposition 6.5

Assume that $\alpha \in \Sigma _{\lambda ,\theta }$ and let x be a geometric point of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, of representation type $\tau = (e_1, \beta _1; \dots ; e_k, \beta _k)$. Then $\mathbf{e}$ is the dimension vector of a simple $\Pi ^0(Q')$-module, i.e., $\mathbf{e} \in \Sigma _0(Q')$.

Returning to the proof of Theorem 1.15, with Proposition 4.2 in hand, the argument given in the proof of [38, Theorem 3.2] goes through verbatim. This completes the proof of Theorem 1.15.

4.3 The proof of Corollary 1.17

By Theorem 1.15, $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is smooth if and only if every point is canonically $\theta$-polystable. As in the reduction argument given at the start of the proof of Theorem 1.15, this means that $n_i$ must be 1 when $\sigma ^{(i)}$ is an isotropic root. Moreover, it is clear that $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ consists only of $\theta$-stable points if and only if $\sigma ^{(i)}$ is minimal.

5 The (2, 2) case

In this section we will prove Theorem 1.6. First we restrict to the one vertex case.

5.1 The variety $\mathfrak {X}(2,2)$

Recall that $\mathfrak {X}(g,n)$ denotes the quiver variety

$$\begin{aligned} \left\{ (X_1,Y_1, \dots , X_g,Y_g) \in {{\,\mathrm{\mathrm {End}}\,}}_{\mathbb {C}}(\mathbb {C}^n) \ \left| \ \sum _{i = 1}^d [X_i,Y_i] = 0 \right. \right\} /\!\!/\!{{\,\mathrm{\mathrm {GL}}\,}}(n,\mathbb {C}). \end{aligned}$$

We note that $\mathfrak {X}(g,n)$ is an irreducible, normal affine variety of dimension $2 (n^2 (g - 1) + 1)$.

Set $(g,n)=(2,2)$, so $\dim \mathfrak {X}(g,n) = 10$. We recall results of Kaledin–Lehn [31], see also [39], which explain that $\mathfrak {X}(2,2)$ admits a projective symplectic resolution.

Let $W = \mathfrak {sl}_2$ and $(V,\omega )$ a 4-dimensional symplectic vector space. Let $\kappa$ denote the Killing form on W. Then $\kappa \otimes \omega$ is a symplectic form on $W \otimes V$. We identify $\mathfrak {sp}(V)^*$ with $\mathfrak {sp}(V)$ via its Killing form. There is an action of $\mathrm {PGL}(2)$ on W by conjugation and hence on $W \otimes V$. This action is Hamiltonian and commutes with the natural action of $\mathrm {Sp}(V)$ on $W \otimes V$. The moment map for the action of $\mathrm {PGL}(2)$ is given by

$$\begin{aligned} \mu \left( \sum _i A_i \otimes v_i \right)&= \sum _{i,j} A_i A_j \omega (v_i,v_j) \\&= \sum _{i < j} [A_i,A_j] \omega (v_i,v_j). \end{aligned}$$

The moment map for the action of $\mathrm {Sp}(V)$ is given by $\sum _i A_i \otimes v_i \mapsto \nu ( \sum _i A_i \otimes v_i )$, where

$$\begin{aligned} \nu \left( \sum _i A_i \otimes v_i \right) (u) = \sum _{i,j} \kappa (A_i,A_j) \omega (v_i,u) v_j. \end{aligned}$$

Since the actions of $\mathrm {PGL}(2)$ and $\mathrm {Sp}(V)$ on $\mu ^{-1}(0)$ commute, the map $\nu$ descends to a map $\mu ^{-1}(0) /\!\!/\!\mathrm {PGL}(2) \rightarrow \mathfrak {sp}(V)$, which we also denote by $\nu$. Let $\mathcal {N}_2^2 \subset \mathfrak {sp}(V)$ be the set $\{ B \ | \ B^2 = 0, \ \mathrm {rk} B = 2 \}$. The set $\mathcal {N}^2_2$ is a 6-dimensional adjoint $\mathrm {Sp}(V)$-orbit. Its closure $\mathcal {N} := \overline{\mathcal {N}}^2_2 = \mathcal {N}^2_2 \cup \mathcal {N}^2_1 \cup \{ 0\}$ consists of three $\mathrm {Sp}(V)$-orbits and one can check that $\overline{\mathcal {N}}^2_1 \simeq \mathbb {C}^4 / \mathbb {Z}_2$, where $\mathbb {Z}_2$ acts on $\mathbb {C}^4$ with weights $(-1,-1,-1,-1)$. The following result is proven in [31].

Theorem 5.1

[31] The map $\nu$ defines an isomorphism $\mu ^{-1}(0) /\!\!/\!\mathrm {PGL}(2) {\mathop {\longrightarrow }\limits ^{\sim }} \mathcal {N}$ of Poisson varieties. In particular, $\mu ^{-1}(0) /\!\!/\!\mathrm {PGL}(2)$ is a symplectic singularity.

Taking trace of the matrices $(X_1,X_2,Y_1,Y_2) \in \mathfrak {X}(2,2)$ defines an isomorphism of symplectic singularities $\mathfrak {X}(2,2) \simeq \mu ^{-1}(0)/\!\!/\!\mathrm {PGL}(2) \times \mathbb {C}^4$, where $\mathbb {C}^4$ is given the usual symplectic structure. Thus, $\mathfrak {X}(2,2) \simeq \mathcal {N} \times \mathbb {C}^4$.

5.2 Proof of Theorem 1.6

We now prove Theorem 1.6, following the arguments of [31, Remark 4.6]; see also [39].

Since $\alpha$ is anisotropic, $2 \alpha$ is also an anisotropic root. Choose a generic stability parameter $\theta ' \ge \theta$ with $\theta ' \cdot \beta \ne 0$ for all nonzero $\beta \le 2 \alpha$, $\beta \ne \alpha$. Then the projective Poisson morphism $\mathfrak {M}_{{\lambda }} ({2\alpha },{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({2 \alpha },{\theta })$ of Lemma 2.4 is a partial projective resolution. It is in fact birational, as explained in the proof of Theorem 6.13 below. Thus, if $Y \rightarrow \mathfrak {M}_{{\lambda }} ({2\alpha },{\theta '})$ is a projective symplectic resolution, then so is the composite $Y \rightarrow \mathfrak {M}_{{\lambda }} ({2\alpha },{\theta })$, i.e., it is enough to show that we can resolve $\mathfrak {M}_{{\lambda }} ({2\alpha },{\theta '})$ symplectically. Fix $X = \mathfrak {M}_{{\lambda }} ({2\alpha },{\theta '})$. Then $X = X_2 \sqcup X_1 \sqcup X_0$, where, by Theorem 1.15, $X_0$ is the smooth locus consisting of $\theta '$-stable representations, $X_1$ parameterizes representations $M = M_1 \oplus M_2$ with $\dim M_1 = \dim M_2 = \alpha$, $M_1 \not \simeq M_2$ are $\theta '$-stable representations and $X_2$ consists of all points $M^2$, with $\dim M = \alpha$. By Proposition 3.15, $X_2$ and $X_2 \cup X_1$ are closed in X.

Let $\widetilde{X}$ denote the blowup of X the along the sheaf of ideals of the reduced singular locus $X_1 \sqcup X_0$. The corollary will follow from the following claim: $\widetilde{X} \rightarrow X$ is a projective symplectic resolution.

Clearly, $\widetilde{X} \rightarrow X$ is a projective birational morphism, therefore we just need to show that $\widetilde{X}$ is smooth and the symplectic 2-form on $X_0$ extends to a symplectic 2-form on $\widetilde{X}$. We check this in a neighborhood of $x \in X_2$ and of $y \in X_1$. First consider $x \in X_2$. Replacing X by some affine open neighborhood of x, Theorem 3.3 says that there is an affine Z with

where $\pi$ and $\rho$ are étale. Let $\widetilde{\mathfrak {X}}(2,2) \rightarrow \mathfrak {X}(2,2)$, resp. $\widetilde{Z} \rightarrow Z$, denote the blowup along the reduced singular locus. Then

$$\begin{aligned} \widetilde{Z} \simeq \widetilde{X} \times _X Z \simeq \widetilde{\mathfrak {X}}(2,2) \times _{\mathfrak {X}(2,2)} Z. \end{aligned}$$

(12)

As noted in [31, Remark 4.6], $\widetilde{\mathfrak {X}}(2,2) \rightarrow \mathfrak {X}(2,2)$ is a projective symplectic resolution. Now Lemma 5.2 below and (12) imply that $\widetilde{X} \rightarrow X$ is a projective symplectic resolution.

For $y \in X_1$, Theorem 3.3 shows that there is an étale equivalence between a neighborhood of y and a neighborhood of the origin in a certain quiver variety, independent of the choice of $y \in X_1$. In particular such a neighborhood is also étale equivalent to a neighborhood of a point of $X_1$ inside the neighborhood of $x \in X_2$ used above, so the result follows from the previous statement. (One can also compute explicitly: the quiver needed is the one with two vertices, one arrow in each direction between the two vertices, and also two loops at each vertex, so the quiver variety is isomorphic to $\mathbb {C}^8 \times \mathbb {C}^2/\mathbb {Z}_2$, which is an $A_1$ singularity and hence blowing up the reduced ideal sheaf of the singular locus gives a projective symplectic resolution).

It remains to prove the following standard lemma:

Lemma 5.2

Let X be a symplectic singularity and $\pi : \widetilde{X} \rightarrow X$ a proper morphism. Then $\pi$ is a symplectic resolution if and only if it is so after a surjective étale base change i.e. being a symplectic resolution is an étale local property.

Notice that we are not making the (false) claim that X admits a symplectic resolution if and only if it does so étale locally.

Proof

Passing to the generic points of $\widetilde{X}$ and X, the fact that a surjective étale morphism is faithfully flat implies that $\pi$ is birational if and only if it is so after base change. Therefore it suffices to check that the extension $\omega '$ of the pullback $\pi ^* \omega$ is non-degenerate. If $b: Z \rightarrow X$ is a surjective étale morphism, then so too is $\widetilde{b} : \widetilde{Z} = \widetilde{X} \times _X Z \rightarrow \widetilde{X}$. The form $\omega '$ will be non-degenerate if and only if $\widetilde{b}^* \omega '$ is non-degenerate. $\square$

6 Factoriality of quiver varieties

In this section, which is the technical heart of the paper, we consider the case of a divisible anisotropic root. Fix $\alpha \in \Sigma _{\lambda ,\theta }$ to be an indivisible anisotropic root, and let $n \ge 2$ such that such that $(p(\alpha ),n) \ne (2,2)$. We prove the key result, Corollary 6.9, which says that if $\theta$ is generic then $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ is a locally factorial variety.

6.1 Weighted partitions

A weighted partition $\nu$ of n is a sequence $(\ell _1, \nu _1; \dots ; \ell _k,\nu _k)$, where $\nu _1 \ge \nu _2 \ge \cdots$ and $\sum _{i = 1}^k \ell _i \nu _i = n$. Recall from Proposition 3.15 that the quiver variety $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ has a finite stratification by representation type. Given a weighted partition $\nu$ of n we can associate naturally a representation type of $n\alpha$:

$$\begin{aligned} \nu \alpha := (\ell _1, \nu _1 \alpha ; \dots ; \ell _k, \nu _k \alpha ). \end{aligned}$$

(13)

By the last statement of Theorem 2.2, if $\alpha \in \Sigma _{\lambda ,\theta }$ is anisotropic, then $\nu \alpha$ is indeed a representation type for all partitions $\nu$.

Lemma 6.1

Let $\alpha \in \Sigma _{\lambda ,\theta }$ be an indivisible anisotropic root. Let $n \ge 2$.

• (1) We have the formula

  $$\begin{aligned} \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu \alpha } = 2 \left( k + (p(\alpha )-1) \sum _{i = 1}^k \nu _i^2 \right) . \end{aligned}$$

• (2) For $(p(\alpha ),n) \ne (2,2)$, we have $\dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) - \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu \alpha } \ge 4$ for all $\nu \ne (1,n)$.

• (3) For $(p(\alpha ),n) \ne (2,2)$ and $\nu \ne (1,n)$, we furthermore have

  $$\begin{aligned} \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) - \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu \alpha } \ge 8 \end{aligned}$$

  unless one of the following holds:

  • (i) $(p(\alpha ),n)=(2,3)$ and $\nu =(1,2;1,1)$; or

  • (ii) $(p(\alpha ),n)=(3,2)$ and $\nu =(1,1;1,1)$.

• (4) In the case that $\theta \cdot \beta \ne 0$ for all $\beta \le n \alpha$ not a multiple of $\alpha$, all strata of $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ are of the form $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu }$, and they are parameterized by weighted partitions of n. (It suffices to make the weaker assumption that $\Sigma _{\lambda ,\theta } \cap \{\beta \mid \beta \le n \alpha \} \subseteq \{m \alpha \mid m \le n\}$.)

Proof

We begin with the first claim. Set $d := p(\alpha )$. Then $p(n \alpha ) = n^2 (d - 1) + 1$. We have a finite surjective map $\prod _i \mathfrak {M}_{{\lambda }} ({\nu _i \alpha },{\theta }) \rightarrow \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu \alpha }$, so the dimension formula follows from Corollary 3.24.

For the second part, notice that

$$\begin{aligned} \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) - \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu }&= 2 (n^2 (d - 1) +1) - 2 \sum _{i = 1}^k (\nu _i^2 (d-1 ) + 1) \nonumber \\&= 2 (d-1) \sum _{i,j = 1}^k (\ell _i \ell _i - \delta _{i,j}) \nu _i \nu _j - 2 (k-1). \end{aligned}$$

(14)

Since $\sum _{i,j = 1}^k (\ell _i \ell _j - \delta _{i,j}) \nu _i \nu _j - (k-1) \ge 1$, we clearly have $\dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) - \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu } \ge 4$ when $d > 2$. When $d = 2$, a simple computation shows that $\dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) - \dim \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu } = 2$ if and only if $n = 2$ and $\nu = (1,1;1,1)$.

For the third part, we use again (14), noticing the following points: the RHS of (14) is increasing in d; the RHS is increased if we replace $(\ell _i,n_i)$ by $(\ell _i-1,n_i);(1,n_i)$; the RHS is increased if we replace (1, a) and (1, b) by $(1,a+b)$ (when $a+b < n$); and for $a> b > 1$, the RHS is increased if we replace (1, a) and (1, b) by $(1,a+1)$ and $(1,b-1)$. Since it suffices to prove the inequality after performing operations that increase the RHS, the result follows once we observe that the inequality holds in the following cases: (i) $\nu =(1,n-1;1,1)$ whenever $n \ge 4$ as well as (1, 1; 1, 1; 1, 1); (ii) for $\nu =(1,1;1,1)$ whenever $p(\alpha ) \ge 4$, as well as $\nu =(2,1)$ for $p(\alpha )=3$.

For the final claim, observe that each stratum of $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ consists of representations of the form $x= x_1^{\oplus \ell _1} \oplus \cdots \oplus x_k^{\oplus \ell _k}$, where the $x_i$ are pairwise non-isomorphic $\theta$-stable representations of fixed dimension vectors $\alpha _i \in \Sigma _{\lambda ,\theta }$. Under the assumptions given, each $\alpha _i$ must be a multiple of $\alpha$. Therefore the representation type is of the form $\nu \alpha$ for some weighted partition $\nu$ of n. $\square$

Since $p(\alpha ) > 1$, there exist infinitely many non-isomorphic $\theta$-stable $\Pi ^{\lambda }(Q)$-modules of dimension $\alpha$. Therefore, for all representation types $\nu \alpha = (\ell _1,\nu _1 \alpha ; \dots ; \ell _k , \nu _k \alpha )$ with $\sum _i \ell _i \nu _i = n$, the stratum $\mathfrak {M}_{{\lambda }} ({n \alpha },{\theta }) _{\nu \alpha }$ is non-empty. Let U be the union of all strata of “type $\nu \alpha$”.

Lemma 6.2

The subset U is open in $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$.

Proof

Since the stratum of representation type $\rho = (n,\alpha )$ is contained in the closure of all the other strata of type $\nu \alpha$, it suffices to show that there is no stratum $\beta = (e_1,\beta ^{(1)};\dots ; e_l, \beta ^{(l)})$ of any other type such that $\mathfrak {M}_{{\lambda }} ({n \alpha },{\theta }) _{\rho } \subset \overline{\mathfrak {M}_{{\lambda }} ({n \alpha },{\theta }) }_{\beta }$. Assume otherwise. If $G_{\rho } \simeq GL_n(\mathbb {C})$ is the stabilizer of some $x \in \mathfrak {M}_{{\lambda }} ({n \alpha },{\theta }) _{\rho }$, then the Hilbert–Mumford criterion implies that there exists some $y \in \mathfrak {M}_{{\lambda }} ({n \alpha },{\theta }) _{\beta }$ whose stabilizer $G_{\beta }$ is contained in $G_{\rho }$. Let $V_i$ be the $n \alpha _i$-dimensional vector space at the vertex i on which $\mathrm {G}(n \alpha )$ acts. Then, for each $g \in \mathrm {G}(n \alpha )$ and $u \in \mathbb {C}^{\times }$, the u-eigenspace of g is the direct sum over the u-eigenspaces $g |_{V_i}$. In particular, it has a well-defined dimension vector. Now the elements g of $G_{\rho }$ all have the property that the dimension vector of the u-eigenspace of g is of the form $r \alpha$ for some $r\in \mathbb {Z}_{\ge 0}$. On the other hand, since $\beta$ is not “of type $\nu \alpha$”, there is some i such that $e_i \beta ^{(i)} \ne r \alpha$ for any r. Take $u \ne 1$ and $g \in G_{\beta }$ that rescales the summand of y of dimension $e_i \beta ^{(i)}$ by u and is the identity on all other summands. Then the u-eigenspace of g has dimension vector $e_i \beta ^{(i)}$ which implies that $G_{\beta } \not \subset G_{\rho }$ - a contradiction. Thus, U is open. $\square$

The open subset of $\mu ^{-1}(\lambda )^\theta$ consisting of stable representations is denoted $\mu ^{-1}(\lambda )_{s}^{\theta }$, and its image in $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ is denoted $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) ^s$. Note that $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) ^s$ is an open subset of U, and the quotient map $\mu ^{-1}(\lambda )_{s}^{\theta } \rightarrow \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) ^s$ is a principal $\mathrm {PG}(n\alpha )$-bundle.

6.2 Factoriality of $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$

A closed point $x \in X$ is said to be factorial if the local ring $\mathcal {O}_{X,x}$ is a unique factorization domain. We say that X is locally factorial if every closed point of X is factorial. If $\xi : \mu ^{-1}(\lambda )^{\theta } \rightarrow \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ is the quotient map, then let $V = \xi ^{-1}(U)$, where U is the open subset of Lemma 6.2. We will need the following result from [17]:

Theorem 6.3

[17, Theorem 6.3, Corollary 6.4] Consider a stratum Z in $\mathfrak {M}_{{\lambda }} ({\beta },{\theta })$ of representation type $(k_1,\beta ^{(1)}; \ldots ; k_r,\beta ^{(r)})$. Then for all $z \in Z$, $\xi ^{-1}(z) \subseteq \mu ^{-1}(\lambda )^\theta$ has dimension at most $\beta \cdot \beta - 1 + p(\beta ) - \sum _t p(\beta ^{(t)})$, so the dimension of $\xi ^{-1}(Z)$ is at most $\beta \cdot \beta - 1 + p(\beta ) + \sum _t p(\beta ^{(t)})$.

We note that in [17], this is stated and proved for $\lambda$ and $\theta$ equal to zero, but the proof and result extends verbatim to the general case, replacing simple modules by $\theta$-stable modules. In the case that $\beta \in \Sigma _{\lambda ,\theta }$, applying Proposition 3.28 immediately yields

Corollary 6.4

The codimension of the preimage $\xi ^{-1}(Z)$ is at least $\frac{1}{2} {{\,\mathrm{\mathrm {codim}}\,}}(Z)= p(\beta )-\sum _t p(\beta ^{(t)})$.

Proposition 1.62 V is a local complete intersection, locally factorial and normal.

Proof

Since $\alpha \in \Sigma _{\lambda ,\theta }$, Proposition 3.28 implies that $\mu ^{-1}(\lambda )^\theta$ and hence V is a local complete intersection of dimension $n^2\alpha \cdot \alpha - 1 + 2p(n\alpha )$.

The main step is the second assertion. For this we will show that V is smooth outside a subset of codimension four, i.e., it satisfies the $R_3$ property. For any $\mathrm {G}(n\alpha )$-stable subset X of $\mu ^{-1}(\lambda )^{\theta }$, we write $X_{\mathrm {free}}$ for the subset of all points where $\mathrm {PG}(n\alpha )$ acts freely. The assertion will follow from estimating the codimension of the complement to $V_{\mathrm {free}}$ in V. Note that the free locus is the same as the locus of representations whose endomorphism algebra has dimension one, i.e., the “bricks”. We represent $\mu ^{-1}(\lambda )^\theta$ as the union of preimages of the (finitely many) strata, and consider over each such preimage the non-free locus.

If the preimage of the stratum has codimension at least four, it can be ignored. Thus, we just need to show that the complement to $\xi ^{-1}(Z)_{\mathrm {free}}$ has codimension at least four for those strata Z with $\mathrm {codim} \ \overline{\xi ^{-1}(Z)} \le 3$. Since we are explicitly excluding the case $(p(\alpha ),n) = (2,2)$, Corollary 6.4, together with Lemma 6.1 (3), imply that we are reduced to considering the cases $(p(\alpha ),n) = (2,3)$ and $\nu = (1,2;1,1)$, or $(p(\alpha ),n) = (3,2)$ and $\nu = (1,1;1,1)$.

Observe first that if Z is a stratum, then the polystable part of the preimage $\xi ^{-1}(Z)$ has codimension (in $\mu ^{-1}(\lambda )^{\theta }$) at least the codimension of Z itself (in $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$), since the fiber over a polystable representation M has dimension $\alpha \cdot \alpha - \dim {{\,\mathrm{\mathrm {End}}\,}}(M)$, which is maximized when M is stable. Thus if Z has codimension at least four (which is the case for us), then we can ignore the polystable part of $\xi ^{-1}(Z)$.

Next, if we consider a stratum Z of type (1, a; 1, b), note that every representation in this stratum is either polystable or an indecomposable extension of two non-isomorphic representations. The latter type is a brick, since there is a unique stable quotient and a unique stable subrepresentation and the two are nonisomorphic. Therefore applying the previous paragraph together with Lemma 6.1 (2) shows that we can ignore $\xi ^{-1}(Z)$ (the non-free locus has overall codimension at least four). This proves the final assertion.

Since $\mu$ is regular on the locus where $\mathrm {PG}(n\alpha )$ acts freely, $\mu ^{-1}(\lambda )_{\mathrm {free}}^{\theta }$ lies in the smooth locus of V. We conclude from the last assertion of the proposition that the singular locus of V has codimension at least 4 (i.e., property $R_3$ holds). Since V is a local complete intersection, and hence Cohen–Macaulay, it satisfies Serre’s condition $S_2$, so it is normal.

Finally, it follows from a theorem of Grothendieck, [32, Theorem 3.12], that since V is a complete intersection and satisfies $R_3$, the local ring $\mathcal {O}_{V,x}$ of any point $x \in V$ is a unique factorization domain. $\square$

The result that allows us to descend local factoriality from V to the quotient U is the following theorem by Drezet. Since the version given in [19] concerns the moduli space of semistable sheaves on a smooth surface, we provide full details to ensure the arguments are applicable in our situation. Let G be a connected reductive group.

Lemma 6.6

Let V be a locally factorial normal affine G-variety and $V_s \subset V$ a dense open subset of V, whose complement has codimension at least two in V. Then every G-equivariant line bundle on $V_s$ extends to a G-equivariant line bundle on V.

Proof

The fact that V is normal and locally factorial implies that

$$\begin{aligned} \mathrm {Pic} (V) = \mathrm {Div}(V) = \mathrm {Div} \left( V_s \right) = \mathrm {Pic} \left( V_s \right) . \end{aligned}$$

Hence if $L_0$ is a G-equivariant line bundle on $V_s$, forgetting the equivariant structure, there is an extension L to V. To show that the extension L has a G-equivariant structure, one repeats the argument of [20, Lemme 5.2], which uses the fact that the codimension of $V \smallsetminus V_s$ is at least two. $\square$

Theorem 6.7

[19, Theorem A] Let V be a locally factorial, normal G-variety, with good quotient $\xi : V \rightarrow U := V /\!\!/\!\, G$. Assume that there exists an open subset $U_s \subset U$ such that

• (a) the complement to $U_s$ has codimension at least two in U,

• (b) $V_s := \xi ^{-1}(U_s) \rightarrow U_s$ is a principal G-bundle; and

• (c) the complement to $V_s$ has codimension at least two in V.

Let $x \in U$ and $y \in T(x)$ a lift in V (so that $G \cdot y$ is closed in V). The following are equivalent:

• (i) The local ring $\mathcal {O}_{U,x}$ is a unique factorization domain.

• (ii) For every line bundle $M_0$ on $U_s$, there exists an open subset $U_0 \subset U$ containing both x and $U_s$ such that $M_0$ extends to a line bundle M on $U_0$.

• (iii) For every G-equivariant line bundle L on V, the stabilizer of y acts trivially on the fiber $L_y$.

Proof

Recall that $\mathcal {O}_{U,x}$ is a unique factorization domain if and only if every height one prime is principal. Geometrically, this means that for every hypersurface Y of U, the sheaf of ideals $\mathcal {I}_Y$ is free at x.

(i) implies (ii). It suffices to assume that $M_0 = \mathcal {I}_Y$, where Y is a hypersurface in $U_s$. If $\overline{Y}$ is the closure of Y in U, then $M = \mathcal {I}_{\overline{Y} \cap U_0}$ is the required extension.

(ii) implies (i). Let Y be a hypersurface in U. We wish to show that $\mathcal {I}_Y$ is free at x. Let M be the extension of $\mathcal {I}_Y|_{U_s}$ to $U_0$. The line bundle M corresponds to a Cartier divisor D on $U_0$; $M= \mathcal {O}_{U_0}(D)$. Then,

$$\begin{aligned} \mathcal {I}_{Y} |_{U_s} = \mathcal {O}_{U_s}(D \cap U_s), \end{aligned}$$

and the divisors Y and $-D \cap U_s$ are linearly equivalent. Since, by assumption, the codimension of the complement to $U_s$ in U has codimension at least two and U is normal, $\overline{Y} \simeq - D$. Hence $M = \mathcal {I}_{\overline{Y}}$ is free at x.

(ii) implies (iii). Suppose that L is a G-equivariant line bundle on V. Since G acts freely on $V_s$, the restriction $L |_{V_s}$ descends to the line bundle $M_0 = (L |_{V_s}) / G$ on $U_s$. Let M be the extension of $M_0$ to $U_0$. Then the G-equivariant line bundle $\xi ^* M$ agrees with L on $V_s$. This implies, as in the previous paragraph, that $\xi ^* M = L$ on $\xi ^{-1}(U_0)$. In particular, since $y \in \xi ^{-1}(U_0)$, the stabilizer of y acts trivially on $L_y$.

(iii) implies (ii). Let $M_0$ be a line bundle on $U_s$. By Lemma 6.6, $\xi ^* M_0$ extends to a G-equivariant line bundle L on V. Recall by definition of lift that $G \cdot y$ is closed in V. Therefore Lemma 6.8 below says that there is an affine open neighborhood $U'$ of x such that $G_{y'}$ acts trivially on $L_{y'}$ for all $y' \in \xi ^{-1}(U')$ such that $G \cdot y'$ is closed in V. Let $U_0 = U' \cup U_s$. Then, by descent [19, Theorem 1.1], there exists a line bundle M on $U_0$ such that $\xi ^* M \simeq L$. In particular, M extends $M_0$. $\square$

Let Y be a variety admitting an algebraic action of a reductive group G. Assume that there exists a good quotient $\xi : Y \rightarrow X = Y /\!\!/\!\, G$. The following result, which says that the descent locus of an equivariant line bundle is open, is presumably well-known, but we were unable to find it in the literature.

Lemma 6.8

Let L be a G-equivariant line bundle on Y and $y \in Y$ a closed point such that the orbit $\mathcal {O} = G \cdot y$ is closed and the stabilizer $G_y$ of y acts trivially on the fiber $L_y$. Then there exists an affine open neighborhood U of $\xi (y)$ such that the stabilizer $G_{y'}$ acts trivially on $L_{y'}$ for all $y' \in \xi ^{-1}(U)$ such that $G \cdot y'$ is closed.

Proof

The proof of the lemma can be easily deduced from the proof of [20, Theorem 2.3]. It is shown there that one can find a G-invariant section $s' : \mathcal {O} \rightarrow L |_{\mathcal {O}}$, which trivializes $L |_{\mathcal {O}}$. As explained in loc. cit., the fact that $\mathcal {O}$ is closed in Y implies that one can lift $s'$ to a G-invariant section $s \in \Gamma (\xi ^{-1}(U'), L)$, where $U'$ is some affine open neighborhood of $\xi (y)$. Let W be the (non-empty) open subset of $\xi ^{-1}(U')$ consisting of all points $y'$ such that $s(y') \ne 0$ i.e. s trivializes L over W. Then it suffices to show that there is some affine neighborhood U of $\xi (y)$ such that $\xi ^{-1}(U) \subset W$. Again, following [20, Theorem 2.3], the sets $\xi ^{-1}(U') \smallsetminus W$ and $\mathcal {O}$ are G-stable closed subsets of $\xi ^{-1}(U')$. Therefore the fact that $\xi$ is a good quotient implies that $\xi (\xi ^{-1}(U') \smallsetminus W)$ and $\xi (\mathcal {O}) =\{ \xi (y) \}$ are closed, disjoint subsets of $U'$. Thus, there exists an affine neighborhood U of $\xi (y)$ such that $U \cap \xi (\xi ^{-1}(U') \smallsetminus W) = \emptyset$, as required. $\square$

Corollary 6.9

Assume that $(p(\alpha ),n) \ne (2,2)$. Then the variety U is locally factorial.

Proof

Let $G = \mathrm {PG}(\alpha )$ and $U_s = \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _s$. Proposition 6.5 implies that V is normal and locally factorial. This implies that U is normal. Moreover, by Lemma 6.1, the codimension of the complement to $U_s$ in U has codimension at least two. Thus, assumptions (a) and (b) of Theorem 6.7 are satisfied. By Lemma 6.1 (2) and Corollary 6.4, the complement to $\mu ^{-1}(\lambda )_{s}^{\theta }$ in V has codimension at least 4. In particular, assumption (c) of Theorem 6.7 is also satisfied.

Next, recall from the proof of Lemma 6.2, the stratum of type $\rho = (n,\alpha )$ is contained in the closure of all other strata in U. If y is a lift in $\mu ^{-1}(\lambda )^{\theta }$ of a point of $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\rho }$ then y corresponds to a representation $M_0^{\oplus n}$, where $M_0 \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is a stable $\Pi ^{\lambda }(Q)$-module. Therefore $\mathrm {PG}(n\alpha )_y = PGL_n$ has no non-trivial characters. In particular, $\mathrm {PG}(n\alpha )_y$ will act trivially on $L_y$ for any $\mathrm {PG}(n\alpha )$-equivariant line bundle on V. Hence, we deduce from Theorem 6.7 that $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ is factorial at every point of $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\rho }$.

Now consider an arbitrary stratum $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) _{\nu \alpha }$ in U. If $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ is factorial at one point of the stratum then it will be factorial at every point in the stratum (for a rigorous proof of this fact, repeat the argument given in the proof of [32, Theorem 5.3]). On the other hand, a theorem of Boissière, Gabber and Serman [22] says that the subset of factorial points of U is an open subset. Since this open subset is a union of strata and contains the unique closed stratum, it must be the whole of U. $\square$

Remark 6.10

Notice that if $\theta$ is generic then $U = \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$. Hence Corollary 6.9 says that $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ is a locally factorial variety. This is precisely the statement of Theorem 1.10. In the special case where Q has a single vertex, g loops and $\alpha = e_1$, the parameters $\lambda = \theta = 0$ are generic. Then $\mathfrak {M}_{{0}} ({n},{0})$ is an affine cone and thus has trivial Picard group. Corollary 6.9 implies that when $(g,n) \ne (2,2)$, $\mathfrak {M}_{{0}} ({n},{0})$ is actually factorial. That is, $\mathbb {C}[\mathfrak {M}_{{0}} ({n},{0}) ]$ is a unique factorization domain.

6.3 The proof of Theorem 1.2

By Proposition 3.21, we know that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is irreducible and normal. Therefore, it suffices to show that it admits symplectic singularities. Since the isomorphism of Theorem 3.17 is Poisson, it suffices to show that the varieties $S^{n_i} \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admit symplectic singularities. If $\sigma ^{(i)}$ is real there is nothing to check.

Lemma 6.11

Let X be a smooth irreducible Poisson variety and Y a smooth symplectic variety. If $\pi : Y \rightarrow X$ is a birational, surjective Poisson morphism, then it is an isomorphism.

Proof

Since the morphism is birational, there is a dense open subset $U \subset X$ over which it is an isomorphism. By [26, I, Corollary 6.12], the complement of U has codimension at least two. On the other hand, since X is smooth, the locus where the Poisson structure on X is degenerate has codimension one. Therefore, X is symplectic too. This implies that $d_y \pi$ is an isomorphism for all $y \in Y$. Thus, by Zariski’s Main Theorem, $\pi$ is an isomorphism. $\square$

Lemma 6.12

Let X be a normal irreducible Poisson variety and assume that $\pi : Y \rightarrow X$ is a proper birational Poisson morphism from a variety Y with symplectic singularities. Then X has symplectic singularities.

Observe that one can drop the assumption of the lemma that X is Poisson and $\pi$ is a Poisson morphism: since $R^0 \pi _* \mathcal {O}_Y = \mathcal {O}_X$, Y endows X with a unique Poisson structure making $\pi$ Poisson.

Proof

Let $\rho : Z \rightarrow Y$ be a resolution of singularities. If $\varpi$ is the symplectic 2-form on the smooth locus of Y then $\rho ^* \varpi$ extends to a regular form on Z. Let $U = \pi ^{-1}(X_{\mathrm {sm}})$. Then, since $\pi : U \rightarrow X_{\mathrm {sm}}$ is proper and birational and $X_{\mathrm {sm}}$ is irreducible, $\pi$ is surjective. Lemma 6.11 implies that it is an isomorphism. In particular, there is a symplectic 2-form $\omega$ on $X_{\mathrm {sm}}$ such that the Poisson structure on $X_{\mathrm {sm}}$ is non-degenerate and induced from $\omega$. Moreover, $\pi ^* \omega = \varpi$. Thus, $(\pi \circ \rho )^* \omega = \rho ^* \varpi$ extends to a regular form, and hence X has symplectic singularities. $\square$

If $\sigma ^{(i)}$ is an indivisible anisotropic root then $n_i = 1$ by Corollary 2.3. Choosing a generic stability parameter $\theta ' \ge \theta$ defines a projective, Poisson resolution $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ with $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '})$ a smooth symplectic variety; see [17, Section 8]. Similarly, if $\sigma ^{(i)}$ is isotropic imaginary then it is well-known that one can frame the quiver so that there exists a projective, Poisson resolution of singularities from a quiver variety that is a smooth symplectic variety. Thus, Lemma 6.12 implies that $S^{n_i} \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admits symplectic singularities in these two cases.

Therefore we may assume that there exists an indivisible anisotropic root $\beta$ such that $\alpha = n \beta$, for some $n > 1$. Let $g = p(\beta )$. If $(g,n) = (2,2)$, then Theorem 1.6 and Lemma 6.12 imply that $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ has symplectic singularities. Therefore, it suffices to show that $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ has symplectic singularities when $(g,n) \ne (2,2)$. Again, choose a generic stability parameter $\theta ' \ge \theta$. Then $\pi :\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ is projective and Poisson by Lemma 2.4. Moreover, since both $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '})$ and $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ are irreducible by Proposition 3.21, and a generic element of $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ is $\theta$-stable, the map $\pi$ is birational. (see the proof of Theorem 6.13 below for more details). Thus, by Lemma 6.12, it suffices to show that $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '})$ admits symplectic singularities. This follows from Flenner’s Theorem [21], once we show that the singular locus of $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '})$ has codimension at least four. By Theorem 1.15, the singular locus of $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '})$ is the union of all strata except the open stratum. By Lemma 6.1 (2) each of these strata has codimension at least 4 in $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '})$.

6.4 The proof of Theorems 1.4, 1.5, and 1.7

We begin by considering the case of a divisible anisotropic root. Recall that $\alpha$ is $\Sigma$-divisible if $\alpha = m\beta$ for some $\beta \in \Sigma _{\lambda ,\theta }$ and $m \ge 2$.

Recall that a normal variety X with $\mathbb {Q}$-Cartier canonical divisor $K_X$ is said to have terminal singularities if $K_Y = f^*(K_X) + \sum _i a_i E_i$ with $a_i > 0$, where $f : Y \rightarrow X$ is any resolution of singularities, and the sum is over all exceptional divisors of f.

Theorem 6.13

Let $\alpha \in \Sigma _{\lambda ,\theta }$ be a divisible anisotropic root which is not of the form $\alpha =2\beta$ for $p(\beta )=2$.

Then the symplectic singularity $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ does not admit a projective symplectic resolution. If, moreover, $\alpha$ is $\Sigma$-divisible, then it does not admit a proper symplectic resolution.

Proof

Write $\alpha =n\beta$ for $n \ge 2$. First suppose that $\beta \in \Sigma _{\lambda ,\theta }$. If $\mathfrak {M}_{{\lambda }} ({n \beta },{\theta })$ admits a proper symplectic resolution then so too by restriction does the open subset U of Lemma 6.2. Recall from Theorem 1.15 that the singular locus of U is the complement of the open stratum. The singular locus is also nonempty since the stratum $(n,\beta )$ is nonempty. By Lemma 6.1, it has codimension at least four in U. Therefore, since U has symplectic singularities by Theorem 1.2, [50] says that U has terminal singularities. This implies that if $f : Y \rightarrow U$ is a proper symplectic resolution then the exceptional locus of f has codimension at least two in Y. On the other hand, we have shown in Corollary 6.9 that U is locally factorial. This implies by van der Waerden purity, see [18, Section 1.40], that the exceptional locus of f is a divisor. This is a contradiction.

Finally suppose that $\beta \notin \Sigma _{\lambda ,\theta }$. Since it is indivisible, it is clear that for generic $\theta '$, we have $\beta \in \Sigma _{\lambda ,\theta '}$. It follows from the previous paragraph that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '})$ does not admit a proper symplectic resolution, hence not a projective symplectic resolution.

We claim that, for generic $\theta ' > \theta$, $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is a projective birational Poisson morphism. For generic $\theta '$, note that every $\theta$-stable representation is also $\theta '$-stable: this is because we can assume that for $\beta < \alpha$ such that $\theta \cdot \beta < 0$, we also have $\theta ' \cdot \beta < 0$. Now, since every $\theta '$-semistable representation is also $\theta$-semistable, and the $\theta$-stable representations are dense in the $\theta$-semistable ones (by Corollary 3.22), it follows that the $\theta$-stable locus is dense in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '})$. Since stable orbits in $\mu ^{-1}(\lambda )$ are closed, in this case the locus of $\theta$-stable representations in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '})$ maps isomorphically onto the stable locus in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. The latter being dense as well, and stability being an open condition, we conclude that the map $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is birational. The other conditions follow from Lemma 2.4.

Now, suppose that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ admitted a projective symplectic resolution. If $\lambda =\theta =0$, then $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is conical. By [6, Theorem 2.2] (which is based on [52]), it would then follow that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '})$ also admitted a projective symplectic resolution, which is a contradiction.

For the general case, if $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ admitted a projective symplectic resolution, it would also do so étale-locally. By first decomposing $\beta$ into elements of $\Sigma _{\lambda ,\theta }$, we could find a representation type $\tau = (ne_1, \beta ^{(1)}; \dots ; ne_k, \beta ^{(k)})$ for $\alpha$ with coefficients multiples of n. Then, the étale-local quiver $(Q',\alpha ')$ at this stratum would have $n \mid \gcd (\alpha ')$. Moreover, the anisotropic root $\alpha '$ belongs to $\Sigma _{0,0}$, as the generic representation remains stable (one can also prove this directly). It would follow that $\mathfrak {M}_{{0}} ({\alpha '},{0})$ admits a projective resolution, contradicting the previous paragraph. $\square$

The proof also shows, more generally, that any singular open subset of U in Lemma 6.2 (in the $\Sigma$-divisible case) does not admit a symplectic resolution. If $\theta$ is generic, then $U = \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$. This implies Corollary 1.11 (as well as the stronger result discussed afterwards).

Corollary 6.14

Let $\alpha \in \Sigma _{\lambda ,\theta }$ be indivisible and $n \ge 1$. Then $\mathfrak {M}_{{\lambda }} ({n \alpha },{\theta })$ admits a projective symplectic resolution if one of the following conditions hold:

• (o) $\alpha$ is a real root ($p(\alpha )=0$);

• (i) $n=1$;

• (ii) $p(\alpha )=1$; or

• (iii) $(n,p(\alpha )) = (2,2)$.

If none of these conditions hold, then $\mathfrak {M}_{{\lambda }} ({n \alpha },{\theta })$ does not admit a proper symplectic resolution. In particular, existence of projective and proper symplectic resolutions is equivalent for $\mathfrak {M}_{{\lambda }} ({n \alpha },{\theta })$.

Proof

In case (o), $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$ is a point, so there is nothing to show. In case (i), let D be the open subset of $\{ \theta ' \in \mathbb {Q}^{Q_0} \ | \ \theta '(\alpha ) = 0\}$ consisting of all stability conditions vanishing on $\alpha$, but not on any other $\beta < \alpha$ with $\beta \in \Sigma _{\lambda ,\theta }$. Since $\alpha$ is indivisible, the set D is non-empty. Its closure is the whole space, thus there exists a connected component C such that $\theta \in \overline{C}$. Choose $\theta ' \in C$ (rescaling if necessary, we may assume that $\theta ' \in \mathbb {Z}^{Q_0}$). Then, just as shown in [17, Section 8], the morphism $\mathfrak {M}_{{\lambda }} ({ \alpha },{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({ \alpha },{\theta })$ is a projective symplectic resolution. For case (ii), first note that case (i) implies that $X:=\mathfrak {M}_{{\lambda }} ({\alpha },{\theta '}) \rightarrow \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is a projective symplectic resolution of (du Val) singularities for some $\theta ' \ge \theta$. In particular, X is a smooth symplectic surface. Next, $\mathfrak {M}_{{\lambda }} ({n\alpha },{\theta }) \cong S^n \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ by Theorem 3.16 because the canonical decomposition of $n\alpha$ is $\alpha + \cdots + \alpha$. We therefore obtain a partial resolution $S^n X \rightarrow \mathfrak {M}_{{\lambda }} ({n\alpha },{\theta })$. Now recall that the natural map ${{\,\mathrm{{\mathrm {Hilb}}}\,}}^n \mathfrak {M}_{{\lambda }} ({\alpha },{\theta '}) \rightarrow S^n \mathfrak {M}_{{\lambda }} ({\alpha },{\theta '})$ is a projective symplectic resolution; see [47, Theorem 1.8, Theorem 1.10]. Finally in case (iii) the resolution is given in Theorem 1.6. If none of the conditions hold, then $\alpha$ is an anisotropic root and the non-existence of a proper symplectic resolution is a consequence of Theorem 6.13. $\square$

We now proceed to the proof of Theorem 1.4. The isomorphism of Theorem 1.4 follows directly from Theorem 3.17. Therefore, it suffices to show that $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ admits a projective symplectic resolution if and only if each $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admits a projective symplectic resolution.

First note that if $\sigma ^{(i)}$ is a real root or an isotropic root, then $\sigma ^{(i)}$ is indivisible (for the latter property, a divisible isotropic root is not in $\Sigma _{\lambda ,\theta }$). In these cases, as recalled in Corollary 6.14, $S^{n_i}\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admits a projective symplectic resolution, as does $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$.

On the other hand, if $\sigma ^{(i)}$ is an anisotropic root, then $n_i = 1$, by Corollary 2.3. Moreover, by Corollary 6.14, $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admits a projective symplectic resolution if $\sigma ^{(i)}$ is indivisible or if $\sigma ^{(i)}$ is twice a root $\beta \in \Sigma _{\lambda ,\theta }$ satisfying $p(\beta )=2$, and otherwise it does not.

Therefore, if $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admits a projective symplectic resolution for all i, it follows that each $S^{n_i}\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ admits a projective symplectic resolution, and hence so does $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

If, on the other hand, some $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ did not admit a projective symplectic resolution, then Corollary 6.14 implies that $\sigma ^{(i)}$ is a divisible anisotropic root which is not twice a root $\beta \in \Sigma _{\lambda ,\theta }$ satisfying $p(\beta )=2$. In this case, by the proof of Theorem 6.13, étale-locally $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta })$ is a cone which admits a partial projective Poisson resolution $\mathfrak {M}_{{\lambda }} ({\sigma ^{(i)}},{\theta '})$ which itself is terminal, locally factorial, and singular. Taking products with the other factors, we see that étale-locally $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is itself a cone with a partial crepant resolution by a terminal, locally factorial, and singular variety. Such a variety does not admit a symplectic resolution, as explained in the proof of Theorem 6.13. By [6, Theorem 2.2], $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ itself does not admit a projective symplectic resolution. This completes the proof.

Notice that Theorems 1.5 and 1.7 also follow from the above argument.

6.5 Formal resolutions

Let $\alpha$ be a divisible anisotropic root, and assume that $\alpha$ is not of the form $\alpha =2\beta$ with $p(\beta )=2$. Though it might not be obvious from Corollary 1.11, the nature of the obstructions to the existence of a symplectic resolution of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is quite subtle. We have shown that Zariski locally no resolution exists. But then one can ask if a resolution exists étale locally, or in the formal neighborhood of a point? In this section we give a precise answer to this question.

Definition 1.72 The closed point $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is said to be formally resolvable if the formal neighborhood $\widehat{\mathfrak {M}}_{\lambda }(\alpha ,\theta )_x$ of x in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ admits a projective symplectic resolution.

Lemma 6.16

If $0 \in \mathfrak {M}_0(\alpha ,0)$ is formally resolvable, then $\mathfrak {M}_0(\alpha ,0)$ also admits a projective symplectic resolution, and conversely.

Proof

Let $\mathbb {C}^{\times }$ act on ${{\,\mathrm{\mathrm {Rep}}\,}}(\overline{Q},\alpha )$ by dilations. Then the moment map $\mu$ is homogeneous of degree two and the action of $\mathrm {G}(\alpha )$ commutes with the action of $\mathbb {C}^{\times }$. This implies that $\mathbb {C}[\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) ]$ is an $\mathbb {N}$-graded, connected algebra. Note also that the Poisson bracket on $\mathbb {C}[\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) ]$ has degree $-2$. The lemma follows from standard arguments; see [24, Proposition 5.2], [29, Theorem 1.4], and the references therein. The idea is that: 1) The induced action of $\mathbb {C}^{\times }$ on $\widehat{\mathfrak {M}}_{0}(\alpha ,0)_0$ lifts to the resolution. 2) The $\mathbb {C}^{\times }$-action allows one to globalize the resolution of the formal neighborhood of 0 to a resolution of the whole of $\mathfrak {M}_0(\alpha ,0)$. For the converse statement, we restrict a symplectic resolution of $\mathfrak {M}_0(\alpha ,0)$ to the formal neighborhood of zero. $\square$

By Corollary 3.4, if one point in a stratum $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau } \subset \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is formally resolvable, then so too is every other point in the stratum. If $\tau = (e_1, \beta ^{(1)}; \dots ; e_k, \beta ^{(k)})$, then define the greatest common divisor $\gcd (\tau )$ of $\tau$ to be the greatest common divisor of the $e_i$. If the greatest common divisor of $\tau$ is k, then each point in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ corresponds to a representation of the form $Y^{\oplus k}$ for some $\theta$-polystable representation Y. Let $U_{\text {fr}} \subset \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ be the union of all strata $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ such that $\gcd (\tau ) = 1$.

Lemma 6.17

Let $\alpha \in \Sigma _{\lambda ,\theta }$. Then $U_{\text {fr}}$ is a dense open subset of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$.

Proof

The set $U_{\text {fr}}$ is dense because it contains the open stratum $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{(1,\alpha )}$, consisting of stable representations. We will show that the complement to $U_{\text {fr}}$ is closed in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. It suffices to show that if the greatest common divisor of $\rho$ is greater than one and $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau } \subset \overline{\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) }_{\rho }$ then $\gcd (\tau ) > 1$ too. The argument is similar to the proof of Lemma 6.2. Let $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\rho }$ and $G_{\rho } \subset \mathrm {G}(\alpha )$ its stabilizer. By Proposition 3.15, there exists $x' \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau }$ such that its stabilizer $G_{\tau }$ contains $G_{\rho }$. Let $\gcd (\rho ) = k$, so that x corresponds to a representation $Y \otimes V$ for some $\theta$-polystable representation Y, and k-dimensional vector space V. Notice that $\alpha = k \dim Y$. Then GL(V) is a subgroup of $G_{\rho }$, and hence of $G_{\tau }$ too. An elementary argument shows that this implies that $x'$ corresponds to a representation $Y' \otimes V$ for some $\theta$-polystable representation $Y'$. Thus, $\gcd (\tau ) > 1$. In fact, we have shown that if $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau } \subset \overline{\mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) }_{\rho }$, then $\gcd (\rho )$ divides $\gcd (\tau )$. Thus, $U_{\text {fr}}$ is open in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$. $\square$

Theorem 6.18

Let $\alpha \in \Sigma _{\lambda ,\theta }$ be an anisotropic root, $\alpha = n \beta$ for some indivisible root $\beta$ and some $n > 1$. Assume that $(n,p(\beta )) \ne (2,2)$. Then a point x is formally resolvable if and only if $x \in U_{\text {fr}}$.

Proof

Let $x \in \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ have representation type $\tau = (e_1, \beta ^{(1)}; \dots ; e_k, \beta ^{(k)})$, where $m := \gcd (\tau )$. By Corollary 3.4, $\widehat{\mathfrak {M}}_{\lambda }(\alpha ,\theta )_x \simeq \widehat{\mathfrak {M}}_{0}(\mathbf{e} ,0)_0$ and hence Lemma 6.16 says that x is formally resolvable if and only if $\mathfrak {M}_{0}(\mathbf{e} ,0)$ admits a projective symplectic resolution. By definition, the greatest common divisor of $\mathbf{e}$ is m. Proposition 4.2 says that $\mathbf{e}$ belongs to $\Sigma _{0,0}$ for the quiver underlying $\mathfrak {M}_{0}(\mathbf{e} ,0)$. Moreover, by remark 3.5, we have $p(\alpha ) = p(\mathbf{e} )$ which implies that $\mathbf{e} = m \mathbf{f}$ with both $\mathbf{e}$ and $\mathbf{f}$ anisotropic. If $m = 1$ then Corollary 6.14 (i) implies that x is formally resolvable. Thus, we just need to show that if $m > 1$ then x is not formally resolvable.

First, we show:

$$\begin{aligned} \left( m, p(\mathbf{f} ) \right) = (2,2) \quad \Leftrightarrow \quad \left( n,p\left( \beta \right) \right) = (2,2). \end{aligned}$$

(15)

Assume that the left hand side of (15) holds. Then $p(\alpha ) = n^2 (p(\beta ) -1) + 1$ implies that

$$\begin{aligned} n^2 (p(\beta ) -1) + 1 = p(\alpha ) = p(\mathbf{e} ) = 5 \end{aligned}$$

and hence $n^2 (p(\beta ) -1) = 4$. But $p(\beta ) > 1$ since $\beta$ is anisotropic, and 2 divides n. Thus, $n = 2$ and $p(\beta ) = 2$. Conversely, assume that the right hand side of (15) holds. Then $5 = p(\alpha ) = p(\mathbf{e} )$ implies that $m^2 (p(\mathbf{f} ) - 1) = 4$. Since $\mathbf{f}$ is anisotropic and we have assumed that $m > 1$, we deduce that $\left( m, p(\mathbf{f} ) \right) = (2,2)$.

Notice that we have assumed in the statement of the theorem that $\left( n,p\left( \beta \right) \right) \ne (2,2)$. Thus, $\left( m,p(\mathbf{f} )\right)$ cannot equal (2, 2). Then Theorem 6.13 says that $\mathfrak {M}_{0}(\mathbf{e} ,0)$ does not admit a projective symplectic resolution because $m > 1$. $\square$

In the case where $\alpha \in \Sigma _{\lambda ,\theta }$ equals $2 \beta$ for some root $\beta \in \Sigma _{\lambda ,\theta }$ with $p(\beta ) = 2$, every point in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is formally resolvable. Similarly, if $\alpha$ is indivisible (or a multiple of an isotropic root), then every point in $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is formally resolvable.

Remark 6.19

If $U_{\text {fr}} \subsetneq \mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ then Corollary 1.11 implies that any open subset of $U_{\text {fr}}$ not contained in the smooth locus of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ does not admit a symplectic resolution, i.e. the singular locus of $U_{\text {fr}}$ consists of points that cannot be resolved Zariski locally, but do admit a resolution in a formal neighborhood (in fact étale locally).

7 Namikawa’s Weyl group

In the paper [51], Namikawa defined a finite group W associated to any conic affine symplectic singularity X such that the symplectic form on X has weight $\ell > 0$ with respect to the torus action. The group W acts as a reflection group on $H^2(Y,\mathbb {R})$, where $Y \rightarrow X$ is any $\mathbb {Q}$-factorial terminalization of X, whose existence is guaranteed by the minimal model program. The group W plays a key role in the birational geometry of X; see [53] and [3].

One computes W as follows: let $\mathcal {L}$ be a codimension 2 leaf of X and $x \in \mathcal {L}$. Then the formal neighborhood of x in X is isomorphic to the formal neighborhood of 0 in $\mathbb {C}^{2(n-1)} \times \mathbb {C}^2 / \Gamma$, where $2 n = \dim X$ and $\Gamma \subset SL_2(\mathbb {C})$ is a finite group; see [52, Lemma 1.3]. Associated to $\Gamma$, via the McKay correspondence, is a Weyl group $W_{\mathcal {L}}$ of type A, D or E. The fundamental group $\pi _1(\mathcal {L})$ acts on $W_{\mathcal {L}}$ via Dynkin automorphisms. Let $W_{\mathcal {L}}'$ denote the centralizer of $\pi _1(\mathcal {L})$ in $W_{\mathcal {L}}$. Then

$$\begin{aligned} W := \prod _{\mathcal {L}} W_{\mathcal {L}}'. \end{aligned}$$

Thus, in order to compute W, it is essential to classify the codimension 2 leaves of X, and describe $\pi _{1} (\mathcal {L})$. This is the goal of this section.

7.1 The proof of Theorem 1.20

We assume throughout that $\alpha \in \Sigma _{\lambda ,\theta }$, hence it is a root. Therefore the support of $\alpha$ on the quiver is connected. We can assume, up to replacing the quiver by the subquiver whose vertices are the support of $\alpha$, and whose arrows are the ones with endpoints in the support, that $\alpha$ is sincere. Then, the quiver is connected. We may assume that $\alpha$ is imaginary, otherwise the statement is vacuous.

Our goal is to compute the codimension two leaves of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$, proving Theorem 1.20. Recall from Definition 1.18 that $\alpha = \beta ^{(1)} + \cdots + \beta ^{(s)} + m_1 \gamma ^{(1)} + \cdots m_t \gamma ^{(t)}$ is an isotropic decomposition if

• (a) $\beta ^{(i)}, \gamma ^{(j)} \in \Sigma _{\lambda ,\theta }$.

• (b) The $\beta ^{(i)}$ are imaginary roots.

• (c) The $\gamma ^{(i)}$ are pairwise distinct real roots.

• (d) If $\overline{Q}''$ is the quiver with $s + t$ vertices without loops and $-(\alpha ^{(i)}, \alpha ^{(j)})$ arrows from vertex i to vertex $j \ne i$, where $\alpha ^{(i)},\alpha ^{(j)} \in \{ \beta ^{(1)}, \dots , \beta ^{(s)}, \gamma ^{(1)} , \dots , \gamma ^{(t)} \}$, then $Q''$ is an affine Dynkin quiver.

• (e) The dimension vector $(1,\dots , 1, m_1, \dots , m_t)$ of $Q''$ (where there are s ones) equals $\delta$, the minimal imaginary root.

To prove this, first let us consider a general stratum $\tau$ of $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$,

$$\begin{aligned}&\tau = \left( n_1, \beta ^{(1)}; \dots ; n_s, \beta ^{(s)}; m_1, \gamma ^{(1)}; \dots ; m_t, \gamma ^{(t)} \right) ,\nonumber \\&\quad \beta ^{(i)} \text { are imaginary, and }\gamma ^{(i)} \text {are real}. \end{aligned}$$

(16)

Since there is only one $\theta$-stable representation of dimension equal to each real root in $\Sigma _{\lambda ,\theta }$, it follows that the $\gamma ^{(i)}$ are all distinct.

Let us now set $\alpha ^{(i)} := \beta ^{(i)}$ for $1 \le i \le s$ and $\alpha ^{(i)} = \gamma ^{(i-s)}$ for $s+1 \le i \le s+t$. Let $k_i := n_i$ for $1 \le i \le s$ and $k_{i} = m_{i-s}$ for $s+1 \le i \le s+t$; let $\mathbf{k} = (k_1,\dots , k_{s+t})$. By Theorem 3.3, at a point of this stratum, $\mathfrak {M}_{{\lambda }} ({\alpha },{\theta })$ is étale-equivalent to $\mathfrak {M}_{{Q'}} ({0},\mathbf{k }) _{0}$, where the notation means we use the quiver $Q'$ instead of Q. Recall that $\overline{Q}'$ is the quiver with $s+t$ vertices, $2 p(\alpha ^{(i)})$ loops at the ith vertex and $-(\alpha ^{(i)},\alpha ^{(j)})$ arrows between i and j.

Note that $Q''$ is obtained from $Q'$ by discarding all loops at vertices. We will prove that, in the case that the stratum has codimension two, $\mathfrak {M}_{{Q''}} ({0},\mathbf{k }) _{0}$ étale-locally describes a transverse slice to the stratum.

Lemma 7.1

Suppose that $\tau$ is as in (16) and moreover $n_i=1$ for all i.

Then at every point of the stratum there is an étale-local transverse slice isomorphic to a neighborhood of zero in $\mathfrak {M}_{{Q''}} ({0},\mathbf{k })$.

Proof

A neighborhood of a point of the stratum is étale-equivalent to a neighborhood of zero in $\mathfrak {M}_{{Q''}} ({0},\mathbf{k })$. Inside the latter, the stratum containing zero consists of the representations which are a direct sum of simple representations, one at each vertex. At the vertices $1,\ldots ,s$, this representation has dimension one; at the other vertices there are no loops and hence the simple representations are the standard ones. The stratum has dimension $2 \sum _{i=1}^s p(\beta ^{(i)})$, where $p(\beta ^{(i)})$ equals the number of loops at the vertex i. A transverse slice is thus given by the representations which assign zero to all of the loops, which obviously identifies with $\mathfrak {M}_{{Q''}} ({0},\mathbf{k })$. $\square$

Lemma 7.2

Suppose that $\tau$ has codimension two. Then $n_i = 1$ for all i.

Moreover, the anisotropic $\beta ^{(i)}$ are pairwise distinct.

Proof

The codimension two condition can be written as:

$$\begin{aligned} 1=p(\alpha ) - \sum _i p \left( \beta ^{(i)} \right) - \sum _i p \left( \gamma ^{(i)}\right) = p(\alpha ) - \sum _i p\left( \beta ^{(i)}\right) , \end{aligned}$$

(17)

since $\dim \mathfrak {M}_{{\lambda }} ({\alpha },{\theta }) _{\tau } = 2\sum _i p \left( \beta ^{(i)} \right) + 2\sum _i p \left( \gamma ^{(i)}\right)$. Note that the $n_i \beta ^{(i)}$ are themselves imaginary roots. Let $I_{\text {ani}} \subseteq I := \{1,\ldots ,s\}$ be the set of indices such that $\beta ^{(i)}$ is anisotropic, and let $I_{\text {iso}}:=I\setminus I_{\text {ani}}$; so $p(\beta ^{(i)})=1$ if and only if $i \in I_{\text {iso}}$. Note the identity

$$\begin{aligned} p(m\alpha ) = m^2(p(\alpha ) - 1) + 1. \end{aligned}$$

Since $\alpha \in \Sigma _{\lambda ,\theta }$,

$$\begin{aligned} p(\alpha )\ge & {} \sum _{i \in I_{\text {ani}}} p\left( n_i\beta ^{(i)}\right) + \sum _{i \in I_{\text {iso}}} n_i p\left( \beta ^{(i)} \right) + \sum _i p\left( \gamma ^{(i)}\right) \\= & {} \sum _{i \in I_{\text {ani}}} (n_i^2 p\left( \beta ^{(i)}\right) + (1-n_i^2)) + \sum _{i \in I_{\text {iso}}} n_i, \end{aligned}$$

with equality holding only if $s=1$ and $\beta ^{(1)}$ is anisotropic. Therefore, the RHS of (17) is greater than or equal to

$$\begin{aligned} \sum _{i \in I_{\text {ani}}} (n_i^2-1) (p\left( \beta ^{(i)}\right) -1) + \sum _{i \in I_{\text {iso}}} (n_i-1), \end{aligned}$$

again with equality only if $s=1$ and $\beta ^{(1)}$ is anisotropic. Therefore, if $n_i > 1$ for any i, then the RHS of (17) is strictly greater than one, a contradiction.

To see that the anisotropic $\beta ^{(i)}$ are all distinct, suppose not. Group the ones that are not distinct together: let $I'$ be the index set so that $\beta ^{(i)}, i \in I$ gives all of the distinct roots once each, and let $\ell _i := |\{j: \beta _j = \beta '_i\}|$. Then, we obtain the inequality

$$\begin{aligned} p(\alpha ) - \sum _i p\left( \beta ^{(i)}\right) \ge p(\alpha ) - \sum _{i \in I'} \ell _i p\left( \beta ^{(i)}\right) > \sum _{i \in I} (\ell _i^2-\ell _i) (p\left( \beta ^{(i)}\right) -1), \end{aligned}$$

which is greater than one if any $\ell _i > 1$ with $i \in I_{\text {ani}}$.

Thus $n_i = 1$ for all i and the anisotropic $\beta ^{(i)}$ are pairwise distinct. $\square$

We can now proceed with the proof of the theorem:

Proof of Theorem 1.20

Consider a general stratum $\tau$ as in (16). By Lemmas 7.1 and 7.2, we know that $\tau$ has codimension two if and only if $n_i = 1$ for all i and $\dim \mathfrak {M}_{{Q''}} ({0},\mathbf{k }) = 2$. The latter is certainly true if $\tau$ is given by an isotropic decomposition. Moreover, in this case $\mathfrak {M}_{{Q''}} ({0},\mathbf{k })$ is a du Val singularity of type given by the quiver $Q''$.

It remains only to show that, if $\tau$ has codimension two, then $Q''$ is affine Dynkin (ADE), with $\mathbf{k}$ the minimal imaginary root. Consider the canonical decomposition of $\mathbf{k}$, say $\mathbf{k} = \mathbf{k} ^{(1)} + \cdots + \mathbf{k} ^{(r)}$. Then $\mathfrak {M}_{{Q''}} ({0},\mathbf{k }) \cong \prod _{i=1}^r \mathfrak {M}_{{Q''}} ({0},\mathbf{k ^{(i)}})$. The dimension of the latter is $2\sum _{i=1}^r p(\mathbf{k} ^{(i)})$. Hence exactly one of the $\mathbf{k} ^{(i)}$ is isotropic, i.e., $p(\mathbf{k} ^{(i_0)})=1$ for some $i_0$, and the others are real, i.e., $p(\mathbf{k} ^{(i)}) = 0$ for $i \ne i_0$. Let $\mathbf{k} ' := \mathbf{k} ^{(i_0)}$. Since $\mathbf{k} ' \in \Sigma _{0,0}(Q'')$, it follows that it is the minimal imaginary root of some affine Dynkin subquiver of $Q''$ (by the argument of the proof of [16, Proposition 1.2.(2)]).

We claim that $\mathbf{k} =\mathbf{k} '$. Given this, since every component of $\mathbf{k}$ is nonzero, $Q''$ is indeed affine Dynkin, which completes the proof.

To prove the claim, write $\mathbf{k} ' = (k'_1, \ldots , k'_{s+t})$ with $k'_i \le k_i$ for all i. Let $\alpha ' := \sum _{i=1}^{s+t} k'_i \alpha ^{(i)}$. Then Lemmas 7.1 and 7.2 applied to $\alpha '$ show also that the stratum $\tau '$ corresponding to $\mathbf{k} '$ in $\mathfrak {M}_{{\lambda }} ({\alpha '},{\theta })$ has codimension two. That is:

$$\begin{aligned} 2\sum _{i: k'_i \ne 0} p(\alpha ^{(i)}) = \dim \mathfrak {M}_{{\lambda }} ({\alpha '},{\theta }) - 2. \end{aligned}$$

(18)

By Lemma 7.3 below, the RHS of (18) is at most $2p(\alpha ')-2$. Now adding $\sum _{i: k'_i=0} p(\alpha ^{(i)})$ to both sides, we obtain:

$$\begin{aligned} \sum _i p(\alpha ^{(i)}) \le p(\alpha ') + \sum _{i: k'_i = 0} p(\alpha ^{(i)}) - 1. \end{aligned}$$

(19)

The LHS of (19) equals $p(\alpha )-1$ by assumption. Therefore we obtain:

$$\begin{aligned} p(\alpha ) \le p(\alpha ') + \sum _{i: k'_i = 0} p(\alpha ^{(i)}). \end{aligned}$$

(20)

Now, replace $\alpha '$ and each of the $\alpha ^{(i)}$ in the RHS of (20) by their canonical decompositions and let $\eta _1, \ldots , \eta _q$ be the resulting elements of $\Sigma _{\lambda ,\theta }$ with multiplicity. By Lemma 7.3 again, we obtain that $p(\alpha ) \le \sum _{i=1}^q p(\eta _i)$. Since $\alpha \in \Sigma _{\lambda ,\theta }$, this can only happen if $q=1$, i.e., $\alpha =\alpha '=\eta _1$. This is true if and only if $\mathbf{k} =\mathbf{k} '$. $\square$

Lemma 7.3

Suppose $\alpha \in \mathbb {N}R^+_{\lambda ,\theta }$ has canonical decomposition $\alpha = \sum _i n_i \sigma ^{(i)}$ with respect to $\lambda$ and $\theta$. Then $p(\alpha ) \le \sum _i n_i p(\sigma ^{(i)})$.

Proof

Let $\lambda '$ be such that $R^+_{\lambda '} = R^+_{\lambda ,\theta }$. As $\alpha \in \mathbb {N}R^+_{\lambda ,\theta }=\mathbb {N}R^+_{\lambda '}$, we know that $\mu ^{-1}_\alpha (\lambda ')$ is nonempty. The latter is a fiber of a map $\bigoplus _{a \in Q_1} {{\,\mathrm{\mathrm {Hom}}\,}}(\mathbb {C}^{\alpha _{t(a)}}, \mathbb {C}^{\alpha _{h(a)}}) \rightarrow \mathfrak {pg}(\alpha )$, where $\mathfrak {pg}(\alpha )$ is the Lie algebra of $\mathrm {PG}(\alpha )$. All of the irreducible components of the latter must have dimension at least $\sum _{a \in \overline{Q_1}} \alpha _{t(a)} \alpha _{h(a)} - \sum _{i \in Q_0} \alpha _i^2 +1 = \alpha \cdot \alpha - 2\langle \alpha , \alpha \rangle +1 = \alpha \cdot \alpha +2p(\alpha ) - 1$.

On the other hand, by [15, Theorem 4.4], $\dim \mu ^{-1}_{\alpha }(\lambda ') = \alpha \cdot \alpha - \langle \alpha , \alpha \rangle + m= \alpha \cdot \alpha + p(\alpha ) + (m-1)$ where m is the maximum value of $\sum _{i} p(\alpha ^{(i)})$ with $\alpha ^{(i)} \in R^+_{\lambda '}$ and $\alpha = \sum \alpha ^{(i)}$; as remarked at the top of page 3 in [16], we have $m = \sum _i n_i p(\sigma ^{(i)})$ (it is a direct consequence of [16, Theorem 1.1] which we discussed before Theorem 3.17).¹ We conclude that $\alpha \cdot \alpha + p(\alpha ) + (m-1) \ge \alpha \cdot \alpha + 2p(\alpha ) - 1$. Therefore, $m \ge p(\alpha )$, as desired.

$\square$

Remark 7.4

The lemma can be strengthened to prove: for any decomposition $\alpha = \sum _j \alpha ^{(j)}$ with $\alpha ^{(j)} \in \mathbb {N}R^+_{\lambda ,\theta }$, we have $\sum _j p(\alpha ^{(j)}) \le \sum _i n_i p(\sigma ^{(i)})$. This generalizes an observation on [16, p. 3] (dealing with the case where the $\alpha ^{(j)}$ are roots). To prove this, for arbitrary $\alpha ^{(j)}$, we can apply the lemma to each of the $\alpha ^{(j)}$, and then we get that $\sum _j p(\alpha ^{(j)}) \le \sum _j p(\beta ^{(j)})$ for some roots $\beta ^{(j)} \in R^+_{\lambda ,\theta }$ with $\alpha =\beta ^{(j)}$; then we are back in the case of roots so that $\sum _j n_i p(\sigma ^{(i)}) \ge \sum _j p(\beta ^{(j)})$.

Remark 7.5

The arguments of [15, 16] can be generalized to the context of the pair $(\lambda ,\theta )$, which as we pointed out in Sect. 2.3 would eliminate the need of picking a $\lambda '$ as in the proof of the lemma above.