Experimental Study on Effect of Tunnel Slope on Heat Release Rate with Heat Feedback Mechanism

Abstract

Heat release rate (HRR) is most important factor in the tunnel fire. Therefore, an accurate understanding of the relationship between tunnel fire and HRR is required. The HRR of a pool fire is related to the heat feedback mechanism. Heat feedback is mainly affected by the flow around the fire source. However, considering the flow characteristics that depend on the tunnel slope is insufficient. Therefore, in this study, the effect of flow with respect to the tunnel slope on the heat feedback was analyzed with an experimental method. The experiment was conducted with a reduced-scale shallow underground tunnel. The slope of the tunnel was limited to 0° to 7°, which corresponds to the construction standard. The ceiling jet and entrained-air flow were affected by the pool diameter and tunnel slope. Owing to the effect of the air entrainment, the ratio of the re-radiation heat flux incident on the fuel surface decreased linearly with increasing tunnel slope. Moreover, the re-radiation and re-convection ratios of the tunnel slope and pool pan size showed linear trends. Based on the analysis of the heat feedback mechanism, the empirical correlation for the effect of the tunnel slope on the HRR can be presented in terms of the re-radiation/re-convection fraction.

1 Introduction

1.1 Temperature and Velocity of Tunnel

During a fire in a tunnel, a ceiling jet is formed owing to buoyancy; the smoke propagates rapidly along the ceiling jet, which can cause many casualties. Therefore, many researchers have investigated ceiling jet flows. Alpert [1] presented the temperature and velocity distributions of the ceiling jet on an unconfined flat plate in terms of the ceiling height and heat release rate (HRR) of the fire source. In addition, Heskestad [2] presented the correlation of the maximal velocity and temperature of a ceiling jet based on energy conservation. Based on a dimensionless analysis, Lee and Ryou [3, 4] studied the average temperature of the ceiling jet according to the aspect ratio of a tunnel. Furthermore, Oka et al. [5,6,7,8,9,10] presented a cubic empirical equation for the temperature and velocity distributions of the ceiling jet based on the tunnel slope and HRR; they considered the cooling effect of the tunnel wall and variation in the smoke layer thickness due to the cooling effect. Chow et al. [11, 12] conducted series of experiments and proposed an empirical correlation for the temperature and velocity distributions of a ceiling jet in an inclined tunnel (0° to 30°). Ji et al. [13] determined the maximal temperature decrease of the ceiling jet from the centerline of the tunnel to the wall with respect to the tunnel aspect ratio. In addition, Kim et al. [14] analyzed the flow field in a shallow underground tunnel according to the tunnel slope with a natural exhaust system and presented the relationship between the tunnel slope and plug-holing phenomena. The previous research studies have revealed that the velocity and temperature distributions of the flow in tunnels is affected by the geometric characteristics of tunnels, particularly the tunnel slope. When the slope of a tunnel increases, the flow of the ceiling jet deflects off the lower part of the tunnel to the upper part, and fresh air enters from the lower part. In addition, the velocity and temperature distributions of the ceiling jet have been expressed based on the geometry factors aspect ratio of the tunnel, tunnel slope, and HRR. Therefore, estimating and applying the correct HRR value is crucial for determining the flow in a tunnel.

1.2 Effect of Flow on Heat Feedback Mechanism

The variation in the HRR due to external flow can be explained based on the heat feedback mechanism. Spalding [15] presented a dimensionless transfer number that represents the ratio of the energy released from the flame to the energy needed to vaporize the fuel. In addition, the researcher showed that the heat feedback mechanism is important for predicting the mass loss rate of fuel. Quintiere [16] suggested that the mass loss rate of fuel can be expressed in terms of factors:

$$ \dot{m}^{\prime\prime}c_{p} \delta /k = f\left( {{\text{Re}} ,Gr,\Pr ,B,r,\tau ,c_{p} ,T_{\infty } ,L} \right). $$

(1)

Moreover, Hu et al. [17] measured the conduction, convection, and radiation heat feedback in a rectangular Heptane pool fire (10 cm to 25 cm) at cross winds of 0 m/s to 3 m/s. By using the stagnant layer theory solution, the mass loss rate of the fuel was presented with the modified Spalding transfer number for a Froude number of Fr > 1. The combustion layer thickness ${\text{Re}}^{1/2}$ was dominated by the strong wind. The heat feedback mechanism, which considers the effects of flow, is presented in Eq. 2:

$$ \dot{m}^{\prime\prime}\sim (u/D)^{1/2} \left( {\frac{{\rho_{g}^{1/2} k_{g} }}{{\mu_{g}^{1/2} c_{p,g} }}} \right)\ln \left( {1 + B/\chi_{conv} } \right). $$

(2)

This equations are limited to a relatively high flow rate (Fr > 1). However, the flow velocity, which can affect the flame under the ceiling jet, shows a relatively slow velocity distribution compared to the ceiling jet [9, 13, 14]. Therefore, the Fr number in the tunnel fire should be less than one depending on the fire size or tunnel geometry.

In addition, Hu et al. [18, 19] showed that as the wind speed increases, the conduction-to-convection ratio increases and becomes constant over a certain Froude number. By contrast, radiation decreases with increasing wind speed.

Yao et al. [24] analyzed the heat feedback according to the flow rate in a large pool diameter of 1.5 m, 3.0 m, and 6 m with theoretical and numerical methods. The results showed that the amount of radiation heat feedback increased from 0.4 and stabilized at 1.5. Because the pool was relatively large, the ratio of radiation to heat feedback was dominant, the ratio of convection was relatively small, and the area of the pool rim where conduction occurred was relatively small. Therefore, conduction was considered negligible in this case.

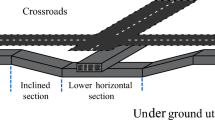
Previous studies of heat feedback have shown that the conduction, convection, and radiation heat feedback ratio vary with the forced ventilation speed. Therefore, the relationship between the heat feedback and flow characteristics is important. However, the flow in the tunnel has different flow characteristics, as shown in Fig. 1a and b. According to Fig. 1b, the ceiling jet is formed in the upper part of the tunnel, whereas air is entrained in the lower part. Furthermore, the ceiling jet and entrained-air flow should be affected by the tunnel slope. However, considering the effect of the flow characteristics in the tunnel on the heat feedback is insufficient.

Figure 1

Flow characteristics: (a) open space (forced ventilation), (b) tunnel fire (natural ventilation)

Moreover, research on existing heat feedback is focused on fast flow velocity or relative large diameter pools. However, the flow rate in tunnels using natural ventilation is relatively slow than previous researches as wind effect. In addition, road tunnels are exclusively for small cars such as sedans, and hybrid electric vehicles that have recently become eco-friendly are smaller heat release rate than gasoline car. Therefore, the researches on the heat feedback mechanism at a relatively small and slow flow rate is needed.

In this study, the effect of the tunnel slope on the HRR was analyzed based on the heat feedback mechanism with an experimental method.

2 Experimental Setup

2.1 Heat Feedback Measurement

To analyze the heat feedback mechanism, a Schmidt–Boelter heat flux meter was used, as shown in Fig. 2. To isolate the radiation and convection components from the Schmidt–Boelter heat flux meter, a ceramic insulator with a thickness of 6 mm and thermal conductivity of 0.07 W/mK was installed around the Schmidt–Boelter heat flux meter; in addition, a quartz shield of 2 mm thickness was installed on the top. The total diameter (including that of the insulator) is 32 mm. The radiation components from the flame and environment hit and pass the quartz shield; consequently, the convection component increases the temperature of the quartz shield. The heated quartz shield re-emits, and the sensor measures by combining the components emitted from the flame and quartz shield. The radiation emitted by the quartz shield can be obtained by measuring its temperature; thus, the radiation incident on the sensor ($\dot{q}_{in,sh}$) can be expressed as follows:

$$ \tau \cdot \dot{q}_{in} - \varepsilon_{q} \sigma \left( {T_{sh}^{4} - T_{w}^{4} } \right) = \dot{q}_{in,sh} , $$

(3)

Figure 2

Schematic of calibration of shielded Schmidt–Boelter heat flux meter

where $\dot{q}_{in}$ is the total radiation heat flux going through the quartz shield, $\varepsilon_{q}$ the emissivity of the quartz shield (0.92), $\sigma$ the Boltzmann constant, $T_{sh}^{{}}$ the temperature of the quartz shield, and $T_{w}^{{}}$ the outlet temperature of the cooling water. The sensor was cooled with water, and the water inlet and outlet temperatures were maintained at 20 °C ± 1.24 °C. It should be noted that $\dot{q}_{in,sh}$ is the radiation component originating from the flame that enters the sensor (not from the fuel); it differs from the re-radiation component $\dot{q}_{re,rad}$. The re-radiation component should consider the re-emitted component from the fuel.

Figure 3 presents the transmittance $\tau$ of the quartz-shield. When radiation passes through the quartz shield, a part of the incident radiation is reflected or absorbed. The transmittance is the fraction of incident radiation that is transmitted through a material. The transmittance was measured three times with a spectrophotometer. To consider the reflected and absorbed radiation components from the quartz shield, the measured value from the Schmidt–Boelter sensor was divided by the transmittance. The wavelength emitted by the flame was approximately in the infrared range. Therefore, the average value of 0.796 (79%) was used for the transmittance.

Figure 3

Transmittance of quartz shield

The calibration was performed with a hot air blower at a blow speed of 0 m/s (radiator only) and at blow speeds of 1 m/s and 3 m/s. The data were averaged over 5 s when the quartz shield temperature was in the quasi-steady state. Figure 4 shows the calibration results. The x-axis presents the shielded Schmidt–Boelter (which was calculated with Eq. 3), and the y-axis presents the output of the radiator. The maximal errors at 0 m/s, 1 m/s, and 3 m/s are 3%, 6%, and 12%, respectively. As discussed in detail in the later result section, the maximal flow velocity measured in this study is lower than 1 m/s. Therefore, the maximal error was properly calibrated (error of approximately 6%).

Figure 4

Calibration results of shielded Schmidt–Boelter heat flux meter

2.2 Tunnel Model and Installation

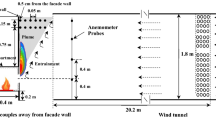
Figure 5 presents a schematic of the reduced-scale tunnel (1/13) and experimental equipment. The vertical shaft was installed at a distance of 2.7 m from the fire source. Under the shaft, a triangular compensator was inserted to make the shaft always perpendicular to the ground. The length of the tunnel is 7.8(W) m, and the tunnel cross section is 0.6(D) × 0.6(H) m. The vertical shaft is 0.25(W) × 0.25(D) × 0.5(H) m and perpendicular to the floor. In addition, the tunnel wall is made from ceramic insulation material with a thickness of 25 mm and thermal conductivity of 0.06 W/mK. For shallow underground tunnels, the construction standard proposes a maximal tunnel slope of 7°. Therefore, the slope of the tunnel was varied from 0°, 2°, 4°, and 6° to 7°. To obtain an image of the flame, one side of the tunnel can be opened, whereas the wall includes double-insulation glass with a thickness of 12 mm. Moreover, a load cell (BCA-HT, CAS) was used to measure the mass loss rate of the fuel; the load cell always maintain level. According to the previous research, the effect of conduction through the rim of the pool pan on the burning rate is negligible when the tunnel pool diameter is 7 cm to 30 cm [20]. The pool pan was insulated with ceramic insulation material with a thickness of 10 mm and thermal conductivity of 0.07 W/mK. Furthermore, n-Heptane was used as fuel, and 10 mm water was added to the pool pan to maintain the fuel at a constant level. The diameter of the pool pan was varied from 10 cm, 12 cm, 14 cm, and 16 cm to 18 cm. The slope of the tunnel was measured with a laser protractor (GLM 80, Bosch), and a data acquisition system (GL240, Graphtec) was used. The shape of the flame was determined by taking 20 images per second with a camera (EOS 5D, Canon); the images were superimposed for 3 s in a quasi-steady state. The camera was installed 2 m away from the side of the tunnel where the side of the flame could be seen. In addition, a hot wire anemometer was used to measure the flow velocity of the entrained air in the pool; the hot wire anemometer was installed at x = − 0.9 m and x = 1.35 m from the fire source. The experiment was conducted indoors space, which is much larger than the model tunnel. Indoor environment temperature is 26° and humidity is maintained at 25%. The temperature in the tunnel were measured using a k-type thermocouple at a location x = − 0.9 m away from the fire source.

Figure 5

Schematic of reduced-scale tunnel and experimental equipment

2.3 Uncertainty Analysis

Based on [21], the acceptable uncertainty of a heat flux meter in a pool pan is less than 20% for a turbulent flame. The uncertainty analysis was performed based on Eq. 4 [22]:

$$ U = \sqrt {\frac{1}{N - 1}\sum\limits_{n - 1}^{N} {\left[ {\left( {\frac{{\Delta \dot{m}^{\prime\prime}_{n} }}{{\dot{m}^{\prime\prime}_{n} }}} \right)^{2} + \left( {\frac{\Delta T}{T}} \right)^{2} + \left( {\frac{\Delta \tau }{\tau }} \right)^{2} + \left( {\frac{{\Delta \dot{q}}}{{\dot{q}}}} \right)^{2} + \left( {\frac{\Delta \theta }{\theta }} \right)^{2} + \left( {\frac{\Delta u}{u}} \right)^{2} } \right]} } , $$

(4)

where $\dot{m}^{\prime\prime}$ is the mass loss rate of the fuel, $T$ the temperature, $\tau$ the transmittance, $\dot{q}$ the heat flux, $\theta$ the tunnel slope, and $u$ the horizontal velocity.

The representative uncertainty values are listed in Table 1. The experiment was repeated at least 4 times. In the repeated experiment, the result of one time with maximum error of data was excluded. The uncertainty of the heat flux meter is relatively great compared to those of the other factors; nevertheless, it is acceptable; the total uncertainty (approximately 3%, which is acceptable) is lower than in previous studies.

Table 1 Uncertainty Percentage

2.4 Scaling Similarity

In many fire engineering researches, reduced-scale experiments are performed due to several limitations. Froude scaling method can be used to model the behavior of fires using reduced-scale experiments. The Froude number is the ratio of inertia force to gravity force. Preservation of the Froude number is important because the behavior of smoke by fire is dominated by buoyancy force which caused by gravity. Quntiere [25] presented a theoretical basic for applying Froude scaling to fire engineering. Hottel [26] and Heskestad [27] conducted a study to apply these Froude scaling models to fire engineering through series of experiments.

The Froude number is as Eq. 5.

$$ Fr = \frac{{V_{m}^{2} }}{{gl_{m} }} = \frac{{V_{f}^{2} }}{{gl_{f} }} $$

(5)

where subscript m and f are model scale and full scale. $l$ is characteristics length and in this study is the pool diameter.

The similarity to speed is as follows.

$$ V_{m} = V_{f} \sqrt {\frac{{l_{m} }}{{l_{f} }}} $$

(6)

Volumetric flow can be obtained by multiplying the velocity by the area and is as follows.

$$ \dot{V}_{m} = \dot{V}_{f} \left( {\frac{{l_{m} }}{{l_{f} }}} \right)^{5/2} $$

(7)

The mass flow rate can be obtained by multiplying the volume flow rate by the density.

$$ \dot{m}_{m} = \dot{m}_{f} \left( {\frac{{l_{m} }}{{l_{f} }}} \right)^{5/2} $$

(8)

The correlation for the heat release rate is as follows by substituting $Q = m \cdot C_{p} \cdot \Delta {\text{T}}$ as Eq. 9

$$ \dot{Q}_{m} = \dot{Q}_{f} \left( {\frac{{l_{m} }}{{l_{f} }}} \right)^{5/2} $$

(9)

According to this Froude scaling, the rate of mass loss rate of fuel depends on the pool diameter.

However, this study is available when the flow due to buoyancy force is dominant, and when there is an slope in the tunnel, the scaling for the case where pool fire is affected by flow such as wind effect is inadequate.

Recently, several experimental studies have been conducted on scaling of heat feedback. Yao et al. studied heat feedback in various pool fires and flow rates by numerical analysis, and showed that radiative heat transfer dominates as the pool diameter increases and the wind velocity decreases. [24]

De Ris et al. [28], proposed a radiation scaling model in fire. The fire radiation scaling model can be used under the assumption that the heat flux is coming from the flame and soot formation in diffusion flame is second order in pressure. In addition, the radiation emitted from the flame was calculated as the temperature at which the flame is cooled at the location where the soot is concentrated. Due to this limitation, there is a problem that it is difficult to apply when the flame is affected by the flow or is a turbulence flame.

Thus, re-convection and re-radiation are heat transfer phenomena affected by flow, and scaling to consider both heat transfer and flow is required. Therefore, the content presented in this study is useful only at 1/13 reduced-scale of pool diameter 10 cm to 18 cm and tunnel slope of 0° to 7°. Despite these limitations, it is considered that HRR and fuel mas loss rate in most fire engineering studies will be helpful in understanding the phenomenon.

3 Results and Discussion

Figure 6 shows the flow velocity distributions with respect to the tunnel slope at x = − 0.9 m. The diameters of the pool in Fig. 6a–e are 10 cm, 12 cm, 14 cm, 16 cm, and 18 cm, respectively. Flow velocity measurement was performed using a hot wire anemometer and the maximum error is 3.46%. The ceiling jet occurs in the upper part of the tunnel owing to buoyancy; it originates from the fire source, impinges on the ceiling, and spreads to the outside. In the lower part of the tunnel, a flow of entrained air is introduced from the outside. For every pool diameter, the velocity of the ceiling jet decreases with increasing slope of the tunnel. This is due to buoyancy caused by the height difference based on the tunnel slope. In addition, the tunnel angle affects the velocity of the entrained-air flow. When the region of entrained air has a velocity of more than 0 m/s, the velocity increases from 60% to 90% as the tunnel slope increases from 0° to 7°. The velocity of the upper part of entrained air decreases because the influence of the ceiling jet decreases with increasing tunnel slope. Moreover, the velocity of the lower part of entrained air increases with increasing tunnel slope; this increase is weaker than that of the upper part.

Figure 6

Velocity distributions with respect to tunnel slope at X = − 0.9 m, (a) to (e) are pool diameter of 10 cm, 12 cm, 14 cm, 16 cm and 18 cm respectively

Figure 7 shows the temperature distribution at the same location as the velocity measurement location at x = − 0.9 m. The diameters of the pool in Fig. 6a–e are 10 cm, 12 cm, 14 cm, 16 cm, and 18 cm, respectively. As the slope of the tunnel increases, the maximum temperature tends to decrease. Also, as the slope of the tunnel increases, the flow near the boundary between the ceiling jet and fresh air and the lower part temperature increase. This is because the entrained air mixes with the ceiling jet more as the slope of the tunnel increases.

Figure 7

Temperature distributions with respect to tunnel slope, (a) to (e) are pool diameter of 10 cm, 12 cm, 14 cm, 16 cm and 18 cm respectively

The flame is blown out and tilted by the entrained-air flow. It is well known that the radiation of the hydrocarbon fuel flame is emitted at the flame tip (sooty region). If the flame is tilted, the radiation component emitted by the flame and amount of radiation feedback is determined by the flame tilt angle; this phenomenon is often described with the concept of the view factor. Figure 8 shows the flame tilt with respect to the tunnel angle for a pool diameter of 14 cm. The correct flame tilt angle was not determined owing to the limitations of the measurement equipment and technique for dealing with fluctuation caused by turbulent flow in the tilted-flame state. However, the approximate trend of the flame tilt can be determined with a multiple picture overlay over time. As the tunnel slope increases, the flame is tilted in the direction of the entrained-air flow. More specifically, the flame is tilted by the tunnel slope by more than 4° because the variation in the velocity at the lower part of the tunnel decreases by more than 4°.

Figure 8

Images of tilted flame with respect to tunnel slope (images of intervals of 3 s are superimposed)

Figure 9 presents the re-radiation fraction of each tunnel slope. The re-radiation fraction is defined as the ratio of the net re heat flux over the re-radiation heat flux incident on the fuel. The shielded Schmidt–Boelter heat flux meter measured all radiation components from the surrounding environment to the fuel surface. Moreover, the average value of the pool surface was used for every heat flux component. To determine the re-radiation component that participates in the vaporization of the fuel, the component that is emitted by the incident radiation must be subtracted, as shown in Eq. 10. In case of the tunnel slope is 0°, Hu et al. [17], research results were compared for the radiation heat feedback part. As a result, it shows a similar trend, and it can be estimate that the measurement was performed properly.

$$ \dot{q}_{re,rad} = \dot{q}_{in,sh} - \dot{q}_{e} $$

(10)

Figure 9

Re-radiation fraction with respect to tunnel slope

The radiation component emitted by the fuel surface is as follow Eq. 11.

$$ \dot{q}_{e} = \varepsilon \sigma \left( {T_{s}^{4} - T_{\infty }^{4} } \right), $$

(11)

where $T_{s}$ is the temperature of the fuel surface, and $T_{\infty }$ is the ambient temperature.

The re-total heat flux can be determined based on the mass loss rate of the fuel multiplied by the evaporation heat of Heptane:

$$ \dot{q}_{re,t} = \dot{m}^{\prime\prime}_{f} L. $$

(12)

When the tunnel slope is 0°, the re-radiation fraction increases with increasing size of the pool pan (from 0.3 to 0.45).

In addition, the re-radiation fraction decreases linearly with increasing tunnel slope (from 0° to 7°). The linear reduction of this radiation fraction should be related to the tilt angle of the flame.

The variation in the flow in the tunnel with respect to the tunnel slope also affects the convective heat transfer. If the horizontal velocity around the flame is sufficiently fast, the main factors such as the boundary layers and Reynolds number affecting the heat feedback constitute the re-convection fraction. However, in case of fire with natural ventilation, the flow velocity of the entrained-air flow in the tunnel is not sufficiently fast compared to that of the mechanical ventilation. Thus, re-radiation and re-convection must be considered for the heat feedback mechanism.

Figure 10 shows the ratio of re-radiation to re-convection with respect to the tunnel slope. The ratio decreases with increasing tunnel slope. In addition, the re-radiation rate increases with increasing pool diameter. As previously mentioned, re-radiation is related to the shape of the flame. When the diameter of the pool pan increases, the buoyancy flow in the vertical direction around the flame becomes more dominant than the flow in the horizontal direction. Therefore, as the pool pan diameter increases, the tilt angle of the flame decreases, and the effect on the re-convection of the entrained fresh air decreases.

Figure 10

Ratio of re-radiation to re-convection

The ratio of re-radiation to re-convection can be fitted as follows:

$$ \chi_{re,rad} /\chi_{re,conv} = a\theta + b, $$

(13)

where $a$ is the slope (− 0.0383), and $b$ is the intercept. The latter is determined by the diameter $D$ of the pool pan:

$$ b = 5.1963D - 0.1186. $$

(14)

Equations 13 and 14 are only valid for the investigated tunnel type and tunnel slope. Equation 13 fitted the ratio of re-radiation to re-convection to the tunnel slope and pool diameter. However, it is assumed that the ratio of re-radiation to re-convection should be generalized by considering that the factors are related to the flow characteristics such as the Froude number. Therefore, further studies are needed.

The HRR of the pool fire can be derived by multiplying the mass loss rate of the fuel by the combustion heat. The effect of the tunnel slope on the mass loss rate was obtained based on the correlation of the re-radiation and re-convection ratios, which is based on the transfer number B proposed by Spalding [19]:

$$ \dot{m}^{^{\prime\prime}} \sim \left[ {\frac{{k_{g} }}{{c_{pg} \delta_{s} }}} \right]\ln \left( {1 + B \cdot \left( {\frac{{\chi_{re,rad} }}{{\chi_{re,conv} }}} \right)} \right). $$

(15)

The transfer number $B$ is presented in Eq. 16. The value of n-Heptane is 6.2 [23].

$$ B \equiv \frac{{Y_{{o_{2,\infty } }} \Delta H_{c} }}{rL} - \frac{{c_{p} (T_{v} - T_{\infty } )}}{L}, $$

(16)

where $Y_{{o_{2} ,\infty }}$, $\Delta H_{c}$, $r$, and $L$ are the oxygen mass fraction, heat of combustion, stoichiometric oxygen-to-fuel mass ratio, and heat of gasification, respectively; $c_{p}$ is the specific heat at a constant pressure, $T_{v}$ the vaporization temperature of the fuel, and $T_{\infty }$ the ambient temperature.

Spalding’s analogy suggests the existence of a thin fuel surface on which mass and heat transfers occur owing to vaporization. The mixture fraction of the fuel is zero at the thickness of $\delta_{s}$ where the outside of the thin layer and unit at the surface of the fuel. In addition, in this thin layer, the variation of the mixture fraction is similar to that of the temperature. De Ris and Orloff [24] defined a thin fuel layer at which the temperature rapidly decreases in a pool fire:

$$ \delta_{s} = \left[ {0.15\left( {\frac{{g(\rho_{\infty } - \rho_{f} }}{{\nu_{g} d_{g} \rho_{g} }}} \right)^{1/3} } \right]^{ \, - 1} , $$

(17)

where $\nu_{g}$ and $d_{g}$ are the kinematic viscosity and thermal diffusivity of the gas phase, respectively.

The mass loss rate per unit area denoted by $\dot{m}^{^{\prime\prime}}_{\exp }$ was measured by the load cell, and Eq. 15 is plotted in Fig. 11. Based on this process, the mass loss rate per unit area with respect to the tunnel slope can be determined with Eq. 18:

$$ \dot{m}^{^{\prime\prime}} = 1.67\left( {\frac{{k_{g} }}{{c_{pg} \delta_{s} }}} \right)\ln \left[ {1 + B \cdot \left( {\frac{{\chi_{re,rad} }}{{\chi_{re,conv} }}} \right)} \right] + 1.13. $$

(18)

Figure 11

Empirical correlation for mass loss rate of n-Heptane pool fire with respect to tunnel slope

This empirical correlation for the mass loss rate is valid for the flow caused by the tunnel conditions that were investigated in this study. The uncertainty of each term used to derive Eq. 18 is a maximum of 3.81%, as suggested in Chapter 2.3. Also, the R-square of the fitted equation is 0.973. Since the equation presented in this study is derived from reduce-scale, it is necessary to check the applicability of scaling. In general, the flow velocity of the ceiling jet of a tunnel increases as the size of the fire source increases, and can be similar to that of Froude scaling. However, even though re-radiation is affected by flow, it is necessary to confirm the applicability of the scaling method in the size of a fire source that is very large compared to the size of the tunnel. Even if the wind-velocity increases in pool with a diameter over the 1.5 m (about 4 MW), re-radiation is relatively dominant more than 80%. It is known that this is because in the pool diameter is large, the inside of the pool is less affected by the outside entrainment [24]. Therefore, the current approach is effective where re-radiation is sufficiently influenced by external flow, and the effective limit of scale needs further consideration.

Nevertheless, the equation for the mass loss rate presented in this study is considered to be effective in predicting the flow velocity and temperature in the tunnel through the Froude scaling method. To evaluate the effectiveness of the results presented in this study, we compared and analyzed the results of existing studies.

Froude number is defined as in Eq. 5. In order to calculate Froude number, the ceiling jet flow velocity distribution according to the tunnel slope is measured as shown in Fig. 12. The flow velocity of the ceiling jet was measured at x = 1.35 m from the fire source using a hot wire anemometer.

Figure 12

Velocity distributions with respect to tunnel slope, (a) to (e) are pool diameter of 10 cm, 12 cm, 14 cm, 16 cm and 18 cm respectively

Figure 13 shows the result of the Froude number. The maximum ceiling jet flow velocity was used to calculate the Froude number. Previous research of Ji et al. [13], is about 1/6 scale which real scale are 0.6 MW to 4.7 MW. The relatively large pool size also shows a similar trend, showing that Froude scaling is effective. However, it shows a large difference from the result of Oka et al. [7, 8], which has a tunnel slope of 10°, but this is thought to be due to the difference in the flow velocity measurement location.

Figure 13

Froude number comparison

The results of Chow et al. [12], are similar to the results of this study, but show slightly lower values. It is analyzed that this is because the mass loss rate of fuel is relatively low and the tunnel is wide, so the flow velocity of the ceiling jet is relatively slow.

In particular, comparing the chow et al., with this study, the maximum difference in mass loss rate is 26.56%. Also, Froude number also seems to be affected by this mass loss rate. it is indicating that accurate mass loss rate prediction is important for the flow of the smoke layer in the tunnel.

4 Conclusion

The effect of the tunnel slope on the mass loss rate of fuel was analyzed with an experimental method. In addition, the heat feedback mechanism was analyzed with respect to the tunnel slope. Note that, the current approach is valid in phenomena where re-radiation is sufficiently affected by flow. The presented equation is useful for understanding the HRR according to the tunnel slope, and can contribute understanding of the smoke layer flow in the tunnel by Froude scaling method.

The main conclusions are as follows:

• 1. The re-radiation, which is the incident radiation to the fuel surface, decreases linearly with increasing tunnel slope.

• 2. The ratio of re-radiation to re-convection could be presented as a function of the tunnel slope.

• 3. An empirical correlation for the mass loss rate with respect to the tunnel slope was fitted.

$$ \dot{m}^{^{\prime\prime}} = 1.67\left( {\frac{{k_{g} }}{{c_{pg} \delta_{s} }}} \right)\ln \left[ {1 + B \cdot \left( {\frac{{\chi_{re,rad} }}{{\chi_{re,conv} }}} \right)} \right] + 1.13 $$