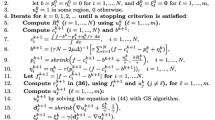Learning discontinuous piecewise affine fitting functions using mixed integer programming over lattice

Abstract

Piecewise affine functions are widely used to approximate nonlinear and discontinuous functions. However, most, if not all existing models, only deal with fitting a continuous function. In this paper, we investigate the problem of fitting a discontinuous piecewise affine function to a given function defined on an arbitrary subset of an integer lattice, where no restriction on the partition of the domain is enforced (i.e., its geometric shape can be nonconvex). This is useful for segmentation and denoising when the given function corresponds to a mapping from pixels of a bitmap image to their color depth values. We propose a novel Mixed Integer Program (MIP) formulation for the piecewise affine fitting problem, where binary edge variables determine the boundary between two partitions of the function domain. To obtain a consistent partitioning (e.g., image segmentation), we include multicut constraints in the formulation. The resulting problem is $\mathcal {NP}$-hard, and two techniques are introduced to improve the computation. One is to adopt a cutting plane method to add the exponentially many multicut inequalities on-the-fly. The other is to provide initial feasible solutions using a tailored heuristic algorithm. We show that the MIP formulation on grid graphs is approximate, while on king’s graph, it is exact under certain circumstances. We conduct initial experiments on synthetic images as well as real depth images, and discuss the advantages and drawbacks of the two models.

1 Introduction

Consider a function F defined on D, where D is a discrete subset of the integer lattice in the plane. In this paper, we seek to find (or approximate) a discontinuous piecewise affine function f that best fits F. Our target application is one where F represents the color depth associated to the pixels of a bitmap image. In statistics, regression is a widely used approach to model the relationship between the range and the domain of F, whenever F is either unknown, or too complicated to represent. If $y=F(z)$ for every $z\in D$, one postulates that F(z) is approximated by a function $f(\beta ,z)$ where $\beta$ is a vector of parameters. One then estimates the values of the parameters $\beta$ so that a certain function norm $||F(\cdot ) - f(\beta ,\cdot )||$ is minimized, i.e.,

$$\begin{aligned} \min \limits _\beta \sum \limits _{z\in D} \Vert F(z) - f(\beta , z) \Vert . \end{aligned}$$

An alternative approach consists in using non-parametric models, which do not assume the exact knowledge of parameter $\beta$. Function f is then not specified by a model but rather determined by its range, and, typically, some assumptions are made [20].

We call a function f piecewise affine (possibly discontinuous) over D if there is a partition of D into disjoint subsets $D_1, \ldots , D_k$ such that f is affine when restricted to each $D_i$ (we denote the function f restricted to $D_i$ as $f^i$). Let $\mathcal{D}$ be the set of all partitions of D, and $\mathcal{F}$ be the set of all piecewise affine functions over D, then any choice of $f \in \mathcal{F}$ defines a valid partition $\mathcal{D}'\in \mathcal{D}$. Moreover, once the partition $\mathcal{D}'$ is fixed, the corresponding $f \in \mathcal{F}$ can be easily identified by computing the affine parameters $\beta$ within each region $D_i$ under some objectives (e.g., mean square error).

The problem of piecewise affine fitting has been studied for decades. Numerous clustering based algorithms [5, 6, 30] are designed for different variants of the problem, but only suffice to find local optimal solutions. Exact formulations of the problem via MIP are also proposed, but often with restrictions. Examples include the continuous piecewise linear fitting models [29], where the domain partition is in a sense pre-defined, and the fitting function f is restricted to be continuous over D. A general n-dimensional piecewise linear fitting problem has been studied in [1], and formulated as a parametric model using MIP. However, the assumption that the partitions are linearly separable does not hold in many practical applications.

In this paper, we focus on the non-parametric model that finds a discontinuous piecewise affine function $f \in \mathcal{F}$ to approximate F, where the affine regions are unknown and the affine parameters within each $D_i$ are not explicitly computed. Our problem can be mathematically represented as follows:

$$\begin{aligned} \min _{\mathcal{D'}\in \mathcal{D}} \;\;&\sum _{i=1}^n \left( \int _{D_i} |~f^i(z)-F(z)~|~ dz + \lambda \mathbf {Per}(D_i)\right) \end{aligned}$$

(1a)

$$\begin{aligned}&(D_1 \cup D_2 \ldots \cup D_n) = D' \; \text {and} \; D_i\cap D_j = \emptyset , \;\; \forall i\ne j, \;i,j\le n , \end{aligned}$$

(1b)

$$\begin{aligned}&f^i \text { is affine on } D_i, \;\forall i=1, \ldots , n , \end{aligned}$$

(1c)

where $\mathbf {Per}(D_i)$ denotes the perimeter of each affine region $D_i$ and $\lambda$ is a regularization parameter [18] that penalizes over-partitioning. The first term of the objective function measures the quality of data fitting, and the second regularization term is used to balance the former with the number and boundary length of affine regions, to prevent from over-fitting. Note that an absolute fitting term is adopted here to enable a Mixed Integer Linear Programming (MILP) formulation of the model. Further constraints will be introduced to model the linearity within $D_i$, in Sects. 2 and 3.

Since we are mostly interested in the 2 dimensional (2D) case, and Fig. 1 shows a synthetic image with noise that has linear trends and its 3D view, where the horizontal axes $z(z_1, z_2)$ represent the coordinates of the image pixels. Upon finding a piecewise affine function $f\in \mathcal{F}$, we obtain a segmentation (to be introduced in next section) of the image into background and three partitions (segments), and a denoised image (with fitted value f(z)) as a by-product.

Fig. 1

A synthetic 2D image with noise that has linear trend and its 3D view

1.1 Related work on image processing

For denoising (fitting) 2D images, the total variation (TV) model [19] is widely used

$$\begin{aligned} \min _{f} \;\; \int _{D} (f(z)-F(z))^2 dz + \lambda \mathrm {TV}(f), \end{aligned}$$

(2)

where the first part is the squared data fitting term (f is the fitting function) and the second part is the regularization term. The $\mathrm {TV}$ regularizers can be either isotropic or anisotropic. The latter can be mathematically described as follows:

$$\begin{aligned} \mathrm {TV}_{\mathsf {ani}}(f) = \int _{D} \left( |\partial _{z_1} f |+ |\partial _{z_2} f |\right) dz, \end{aligned}$$

where $\partial _{z_i}$ represents the partial derivative of f with respect to $z_i$, for $i=1,2$. Lysaker and Tai [14] provide a second-order regularizer

$$\begin{aligned} R_2(f) = \int _{D} \left( |\partial _{z_1z_1}f |+ |\partial _{z_2z_2}f |\right) dz, \end{aligned}$$

which better fits the scenarios of this paper.

Let [n] denote the discrete set $\{1,2,\ldots , n\}$, and $\mathbf {y}\in \mathbb {R}^n$ be a vector of real values, where $y_i = F(i), \forall i\in Z$. Further denote $\mathbf {w}\in \mathbb {R}^n$ be a vector of unknown real variables, where $w_i = f(i), \forall i\in Z$. Then, the classical (discrete) piecewise constant Potts model [17, 26] has the form

$$\begin{aligned} \min _{\mathbf {w}} \;\Vert \mathbf {w}-\mathbf {y}\Vert _2 + \lambda \Vert \nabla ^1 \mathbf {w}\Vert _0, \end{aligned}$$

(3)

where $\Vert \cdot \Vert _2$ denotes the $\ell _2$ norm, and $\Vert \cdot \Vert _0$ the $\ell _0$ norm. The discrete first derivative $\nabla ^1 \mathbf {w}$ is the $n-1$ dimensional vector

$$\begin{aligned} \nabla ^1 \mathbf {w}= (w_2-w_1,w_3-w_2,\ldots ,w_n-w_{n-1}), \end{aligned}$$

and the $\ell _0$ norm of a vector is its number of nonzero entries. The case of F mapping from 2D lattice (corresponds to 2D images) can be easily generalized [23].

Fig. 2

Left: two representations of an image segmentation: node labeling (by colors) and edge labeling via multicuts (dashed edges). Right: example of a 9-pixel segment

Compared to the $\mathrm {TV}$ regularization term which over-penalizes the sharp discontinuities between two regions in an image, the $\ell _0$ term in the Potts model is more desirable, but also more computationally costly. The discrete Potts model is in general $\mathcal {NP}$-hard to solve. The work [7] was one of the first to utilize the Potts model, and recently [6, 27] formulate it as a MIP that could find global optimum.

Apart from image denoising, we also look into the image segmentation problem. In graph based models, one first builds a square grid graph G(V, E) to represent an image, where V corresponds to pixels of an image grid and E represents the 4 or 8 neighboring relations between pixels [25].

A graph partitioning $\mathcal {V}$ is a partition of V into disjoint node sets $\{V_1, V_2, \ldots , V_k\}$. Note that in graph-theoretical terms, the problem of image segmentation corresponds to graph partitioning. The multicut induced by $\mathcal V$ is the edge set $\delta (V_1, V_2, \ldots , V_k) = \{uv \in E \mid \exists i \ne j \text { with } u\in V_i \text { and } v \in V_j\}$. Hence, an image segmentation problem can be represented either by node labeling, i.e., assigning a label to each node $v\in V$, or by edge labeling, i.e., a multicut defined by a subset of edges $E^\prime \subseteq E$, see the left image of Fig. 2 as an example, where the multicut of 8 dashed edges uniquely defines a partition of the $4\times 4$-grid graph into 3 segments.

In machine learning, one often distinguishes between supervised and unsupervised learning. In the former case, the labels of classes (e.g., person, grass, sky, etc) are pre-defined, and annotated data is needed to train the model. Among many existing supervised models, the classical Markov Random Field (MRF) is well studied, and interested readers may refer to [28] for an overview of this field. Recently, Convolutional Neural Networks [13] have become increasingly important in many computer vision tasks, such as semantics and instance segmentation [8, 22, 24]. However, huge amount of annotation effort (in terms of pixel level annotated data) and computational budget (in terms of number of GPUs and training time) are needed.

In the unsupervised case, the labels’ class information is missing, or only partially provided (called weakly or semi-supervised learning). This introduces ambiguities when node labeling is used. See, for example, the node labeling in Fig. 2. If we permute the labels (colors), it will result in the same segmentation. On the contrary, edge labeling (e.g., by multicuts) does not exhibit such symmetries and is therefore more appealing in this case. Recent notable approaches are the (lifted) multicut problems [9,10,11] based on Integer Linear Programming formulations, which label edges (0 or 1) instead of pixels. The multicut constraints [11] (introduced in Sect. 3.2) are used to enforce a valid segmentation. These methods do not require annotated data and can be run directly on CPUs.

In this work, we borrow ideas from the second derivative $\mathrm {TV}$ and Potts model, and propose a novel MILP formulation for the discontinuous piecewise affine fitting problem. The proposed method is an unsupervised approach.

1.2 Main contributions

The main contributions of this paper are as follows.

• We propose a non-parametric model for the general discontinuous piecewise affine fitting problem over lattice.

• The model is formulated as a MILP and multicut constraints are added using cutting plane method to ensure a valid partition (affine region).

• The model is approximate on grid graph, while it is exact on king’s graph under certain circumstances.

• We design a tailored region fusion based heuristic algorithm, which is used as initial solution to the MILP.

• We validate both models on synthetic and real images data.

2 MIP for the piecewise linear fitting model: 1D

We first restrict ourselves to the simple case where the domain $D\subseteq \mathbb {Z}^1$ and $z_i = i$ (could be easily generalized to $D\subseteq \mathbb {R}^1$). Our model is able to find the optimal piecewise linear function $f\in \mathcal {F}$ that best fits the original function $F: D\rightarrow \mathbb {R}^1$.

2.1 Modeling as a MIP

The problem over lattice in 1D could be naturally modeled as a chain graph, and we assume $z_i = i$. The associated graph G(V, E) is defined with $V=\{i\;| \;i\in [n]\}$ and $E=\{e_{i}= (i,i+1)\;|\; i\in [n-1]\}$. We introduce $n-1$ binary variables:

$$\begin{aligned} x_{e}=\left\{ \begin{aligned} 1,&\;\;\text {if two nodes of edge} \;e\; \text {are in different linear regions, }\\ 0,&\;\;\text {otherwise,} \end{aligned} \right. \end{aligned}$$

where an edge e is called active if $x_e=1$, otherwise it is dormant.

Our goal is to fit a piecewise linear function $f\in \mathcal {F}$ to F. We denote the fitting value f(i) as $w_i$, for $i\in [n]$, and $x_i := x_{e_i}$, for $i\in [n-1]$. We further denote the discrete second derivative of $w_i$

$$\begin{aligned} \nabla ^2w_i:= w_{i-1}-2w_i+w_{i+1}, \; \; i\in [2:n-1], \end{aligned}$$

where $[2:n-1]$ denotes the discrete set $\{2,3,\ldots ,n-1\}$.

We then define the following property:

$$\begin{aligned} \nabla ^2w_i= 0&\Leftrightarrow x_{i-1} = x_{i} = 0, \; \; i\in [2:n-1]. \end{aligned}$$

(4)

The rationale behind (4) is that a zero second derivative imposes the same linear region, while a nonzero one infers the boarders of two linear pieces, i.e., there exists an active edge.

The above property can be modeled via MIP using the “big M” technique, which leads to the formulation

$$\begin{aligned} \min \;\; \sum \nolimits _{i=1}^n&| w_i -y_i |+\lambda \sum \nolimits _{i=1}^{n-1} x_{i} \end{aligned}$$

(5a)

$$\begin{aligned} |\nabla ^2w_{i}|&\le M(x_{i-1}+x_i), \;\; i\in [2:n-1], \end{aligned}$$

(5b)

$$\begin{aligned} w_i&\in \mathbb {R},\;\; i\in [n], \end{aligned}$$

(5c)

$$\begin{aligned} x_{i}&\in \{0,1\},\;\;i\in [n-1], \end{aligned}$$

(5d)

where $\lambda >0$ is similar to the regularization term in the Potts model (3). It is worth to mention that there are common tricks to formulate (5a)–(5d) as a MILP. Namely, $|w|\le Mx$ is replaced by two constraints $w\le Mx$ and $-w\le Mx$, and the absolute term $|w-y|$ in the objective function is replaced by $\epsilon ^+ +\epsilon ^-$, plus an additional constraint $w-y = \epsilon ^+ -\epsilon ^-$, where $\epsilon ^+ \ge 0$, $\epsilon ^- \ge 0$.

It can be easily proved that the optimal solution $x^\star$ of problem (5a)–(5d) satisfies property (4). The direction that $x^\star _{i-1} = x^\star _{i} = 0 \Rightarrow \nabla ^2w_i= 0$ is directly enforced by constraint (5b). On the other hand, if $\nabla ^2w_i = 0$, the optimal solutions satisfy $x^\star _{i-1}+x^\star _{i} = 0$ (thus $x^\star _{i-1} = x^\star _{i} = 0$) since (5a)–(5d) is a minimization problem with positive weights on x.

Fig. 3

An example with 3 affine segments and 2 active edges

Figure 3 shows an example of 3 linear functions pieces and 2 active edges computed by formulation (5a)–(5d). We see that the optimal solution $w_i$ is the fitting value for node i, and $x_i=1$ acts as the boundary between two linear pieces. As a result, the nodes between two active edges define one linear region. Although being non-parametric, the parameters for each linear function can be easily computed afterwards, and the number of regions equals $\sum \nolimits _{i=1}^{n-1} x_{i}+1$. Hence, upon solving the MIP formulation (5a)–(5d) in 1D, a piecewise linear function $f\in \mathcal {F}$ can be easily constructed, and $f(i) = w_i$, $\forall i\in [n]$, i.e., (1c) holds.

Note in the above example of Fig. 3, the cases where $\nabla ^2 w_i\ne 0$ actually induces $x_{i-1}+x_i=1$. However, there exists instances where $x_{i-1}+x_i=2$ for $\nabla ^2 w_i\ne 0$. The image on the left of Fig. 4 depicts an example where the node 5 is an outlier (as an one node partition), and $x_{e_l}+x_{e_r}=2$. We also observe that problem (5a)–(5d) does not necessarily output unique optimal integer solution x. One extreme example is shown in the right image of Fig. 4, where either $x_{e_l}$ or $x_{e_r}$ can be active (but not both) in the optimal solution, and they yield the same optimal objective value. Furthermore, notice that any solution with $\nabla ^2 w_i\ne 0$ and $x_{i-1}+x_i>0$ that satisfies  (5b), is feasible, but may not be optimal to (5a)–(5d).

Fig. 4

Left: example where outlier exists (both $e_l$ and $e_r$ are active). Right: example with two segments where the optimal solution is not unique (either $e_l$ or $e_r$ is active)

3 MIP of the piecewise affine fitting model: 2D grid graph

We are more interested in the case where $D\subseteq \mathbb {Z}^2$ and we assume $z_{i,j}= (i, j)$, and F represents the color depth associated to the pixels of a bitmap image. We first focus on the simple grid graph representation of D. Our model is able to find the fitting value w and a valid graph partition. The optimal piecewise affine function can be approximated and constructed afterwards.

3.1 Modeling as a MIP

The domain of a 2D image with $m\times n$ pixels could be naturally modeled as a rectangular grid graph G(V, E), where $V=\{(i,j)| \;i\in [m], j\in [n]\}$, and E represents the relations between the center and its 4 neighboring pixels (see Fig. 2 for demonstration). Let $y_{i,j}=F(i,j)$ be either gray scale or RGB value of pixel (i, j), and in this paper, we restrict ourself to the former, i.e., $y_{i,j}\in \mathbb {R}^1$. We divide the edge set E of the grid graph into its horizontal (row) edge and vertical (column) edge sets. Let $x^r_{i,j}$ denote the binary edge variable for $((i,j),(i,j+1))$, and $x^c_{i,j}$ for edge $((i,j),(i+1,j))$, and they are illustrated in the left of Fig. 5. Hence, for any edge $e\in E$, it can be represented as either $x^r_{i,j}$ or $x^c_{i,j}$, for some $i\in [m]$ and $j\in [n]$.

Fig. 5

Left: image segmentation with two multicuts on 2D king’s graph. Right: example of a 9-pixel segment

The piecewise affine fitting model in grid graph is obtained by formulating (5b) per row and column, and using a similar objective function

$$\begin{aligned} \min \; \sum \nolimits _{i=1}^m&\sum \nolimits _{j=1}^n | w_{i,j} - y_{i,j} |+\lambda \sum \nolimits _{e\in E} x_{e} \end{aligned}$$

(6a)

$$\begin{aligned} |\nabla _r^2w_{i,j}|&\le M(x^r_{i,j-1} + x^r_{ij}), \;\; i \in [m],\; j\in [2:n-1], \end{aligned}$$

(6b)

$$\begin{aligned} |\nabla _c^2w_{i,j}|&\le M(x^c_{i-1,j} + x^c_{ij}), \;\; i\in [2:m-1],\; j\in [n], \end{aligned}$$

(6c)

$$\begin{aligned} w_{ij}&\in \mathbb {R}, \;\;\;\;\; i\in [m], \; j\in [n], \end{aligned}$$

(6d)

$$\begin{aligned} x^r_{ij}&= x_{((i,j),(i,j+1))}, \;\; i \in [m],\; j\in [n-1], \end{aligned}$$

(6e)

$$\begin{aligned} x^c_{ij}&= x_{((i,j),(i+1,j))}, \;\; i \in [m-1],\; j\in [n],\end{aligned}$$

(6f)

$$\begin{aligned} x^r_{ij}&\in \{0,1\}, \;\;i \in [m],\; j\in [n-1], \end{aligned}$$

(6g)

$$\begin{aligned} x^c_{ij}&\in \{0,1\}, \;\;i \in [m-1],\; j\in [n], \end{aligned}$$

(6h)

$$\begin{aligned} x_e&\in \{0,1\}, \;\;e\in E , \end{aligned}$$

(6i)

where M is again the big-M constant. Here, $\nabla _r^2w_{i,j}=w_{i,j-1}-2w_{i,j}+w_{i,j+1}$, and $\nabla _c^2w_{i,j}=w_{i-1,j}-2w_{i,j}+w_{i+1,j}$. That is, the discrete second derivative with respect to $z_1$ and $z_2$-axis. Upon solving (6a)–(6i), it serves for the purpose of denoising by computing w. But two questions still remain: does the binary solution x represent a valid graph partition (or image segmentation)? If so, is w aligned with any piecewise affine function $f\in \mathcal {F}$, i.e., is (1c) satisfied?

The answer to both questions is “no”, unfortunately. We will show in the next two sections that the first “no” could be fixed by enforcing the multicut constraints [11]. However, the second one is not guaranteed, thus making this model approximate.

3.2 Multicut constraints for valid partitioning

The multicut constraints introduced in [2] are inequalities that enforce valid graph partitioning (image segmentation) in terms of edge variables. It reads

$$\begin{aligned} \sum _{e\in C\setminus \{e'\}}x_e\ge x_{e'}, \;\; \forall \;\hbox {cycles} C\subseteq E \hbox {,} e'\in C, \end{aligned}$$

(7)

which basically says that, for any cycle, the number of active edges cannot be 1. Recall that an edge is called active if its two end nodes belong to different paritions. Otherwise, the two nodes of the active edge are again “linked” (hence belong to the same partition) by connecting the rest edges of the cycle, hence a contradiction.

We now prove the following lemma.

Lemma 1

The multicut constraints (7) are needed for the optimal solution $x^\star$ of (6a)–(6i) to form a valid segmentation.

Proof

We prove this lemma by constructing a counter-example as follows:

In the left image of Fig. 6, the input function F, where D contains 15 elements (nodes), is constructed to lie exactly on two affine planes with respect to their coordinates $z=(z_1,z_2)$. The optimal fitting affine function of the left plane is $w^\star =4-z_2$ and the right one is $w^\star =z_2$. We shall see that the 3 pixels with fitting data $w=2$ lie on both affine planes with respect to the coordinates z.

Fig. 6

A counter-example where model (6a)–(6i) does not form a valid segmentation. Left: 3D view of the input image y (and the fitting function $w^\star$). Right: the corresponding graph and active edges

Let the vertical axis be y, and, if we project the 3D plot into the $z_2,y$-space, for fixed $z_1$, i.e., $z_1 = 0$, the resulting F is exactly the same 1D case we studied in the right image of Fig. 4. We have showed that the optimal solution is not unique.

Hence, we can easily construct one optimal solution $x^\star$ (with 2 green and 1 red active edges) of (6a)–(6i) shown in the right image of Fig. 6, where the multicut constraints (7) is not satisfied. That is, there exists a cycle $e_0-e_1-e_2-e_3$ that violates it. $\square$

3.3 The MIP formulation: 2D grid graph

We thus add the multicut constraints (7) to the piecewise affine fitting model (6a)–(6i), to form a valid partition. This leads to the MIP formulation of 2D grid graph

$$\begin{aligned} \min \; \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n&| w_{i,j} - y_{i,j} |+\lambda \sum \nolimits _{e\in E} x_{e} \end{aligned}$$

(8a)

$$\begin{aligned} |\nabla _r^2w_{i,j}|&\le M(x^r_{i,j-1} + x^r_{ij}), \;\; i \in [m],\; j\in [2:n-1], \end{aligned}$$

(8b)

$$\begin{aligned} |\nabla _c^2w_{i,j}|&\le M(x^c_{i-1,j} + x^c_{ij}), \;\; i\in [2:m-1],\; j\in [n], \end{aligned}$$

(8c)

$$\begin{aligned} \sum \nolimits _{e\in C\setminus \{e'\}}x_e&\ge x_{e'}, \;\;\forall \;\text{ cycles } \; C\subseteq E, e'\in C, \end{aligned}$$

(8d)

$$\begin{aligned} w_{ij}&\in \mathbb {R}, \;\; i\in [m], \; j\in [n], \end{aligned}$$

(8e)

$$\begin{aligned} x^r_{ij}&= x_{((i,j),(i,j+1))}, \;\; i \in [m],\; j\in [n-1], \end{aligned}$$

(8f)

$$\begin{aligned} x^c_{ij}&= x_{((i,j),(i+1,j))}, \;\; i \in [m-1],\; j\in [n], \end{aligned}$$

(8g)

$$\begin{aligned} x^r_{ij}&\in \{0,1\}, \;\;i \in [m],\; j\in [n-1], \end{aligned}$$

(8h)

$$\begin{aligned} x^c_{ij}&\in \{0,1\}, \;\;i \in [m-1],\; j\in [n], \end{aligned}$$

(8i)

$$\begin{aligned} x_e&\in \{0,1\}, \;\;e\in E . \end{aligned}$$

(8j)

Note that the number of inequalities (8d) is exponentially large [2] with respect to $|E |$, where $|E |$ denotes the number of edges in G. Hence, in practice, it is not possible to include them into (8a)–(8j) at one time. We will discuss in details in Sect. 5.2 the cutting plane algorithm that handles (8d).

It is well known that, if a cycle $C\in G$ is chordless, then the corresponding multicut constraint (7) is facet-defining for the corresponding multicut polytope [10, 12]. Among all, the simplest ones of a grid graph are the 4 and 8-edge chordless cycle constraints (see the 4-edge cycle $e_0-e_1-e_2-e_3$ in Fig. 2 for an example), and the number of these constraints is linear to $|E |$.

In Sect. 6, we will test different strategies of adding the 4 and 8-edge chordless cycle constraints to (8a)–(8j) as initial constraints.

3.4 Approximate model for piecewise affine fitting: 2D grid graph

We then prove the following theorem.

Theorem 1

The solution of the MIP formulation (8a)–(8j) does not necessarily correspond to a piecewise affine fitting function $f \in \mathcal{F}$ that fits F, i.e., (1c) does not hold.

Proof

We prove this theorem by constructing a counter-example where one feasible solution $w^\star \subset (w^\star , x^\star )$ of (8a)–(8j) restricted on one parition does not lie in the same affine function.

Suppose $x^\star$ corresponds to the graph partition in the right image of Fig. 2, where the 9 nodes on the top left corner form a partition. For simplicity, we restrict ourselves to this partition where the integer coordinates of the pixels range from (0, 0) to (2, 2), i.e., the top left node is at position (0, 0).

By constraint (8b), the $w^\star$ of the 3 nodes on each row satisfy the same linear function. Assume the linear function in the first and second row of nodes satisfy $w=a_1z_2+b_1$ and $w=a_2z_2+b_2$, where (a, b) are the coefficients of the linear function and $z_2$ the discrete coordinates that range from 0 to 2 in this case. Then, the fitting value $w^\star$ of the 6 nodes on the first two rows are listed in the following matrix:

$$\begin{aligned} \begin{bmatrix} w_{00}&{} w_{01} &{} w_{02} \\ w_{10} &{} w_{11} &{} w_{12} \end{bmatrix}= \begin{bmatrix} b_1 &{} a_1+b_1 &{} 2a_1+b_1 \\ b_2 &{} a_2+b_2 &{} 2a_2+b_2 \end{bmatrix}. \end{aligned}$$

We can then compute $w_{22}$ by using constraint (6c), where $w_{22} = 2w_{12} - w_{02}=4a_2+2b_2-2a_1-b_1$. We note that, if $w^\star$ of the 9 nodes lies in any affine function $f^i$, then $w_{00}-2w_{11}+w_{22} = 0.$

However, we have $w_{00}-2w_{11}+w_{22} = 2(a_2-a_1),$ which is a contradiction when $a_1\ne a_2$. Thus, we complete the proof. $\square$

Notice that, however, the MILP formulation (8a)–(8j) guarantees a valid partitioning, thanks to the multicut constraints. Hence, one can then fit an affine function within each partition afterwards, thus obtaining a valid (without optimality guarantee) piecewise affine function $f\in \mathcal {F}$ as post-processing. Hence, this model is approximate.

Fig. 7

A counter-example where model (8a)–(8j) does not form a valid segmentation, i.e., cycle $e_0-e_1-e_2$. Left: 3D view of input image y. Right: the corresponding king’s graph and active edges

4 MIP of the piecewise affine fitting model: 2D King’s graph

We now investigate the king’s graph representation, see Fig. 7 as an example. Recall that a king’s graph represents all legal moves of the king chess piece on a chessboard [3]. We show that, compared to the grip graph representation, our model is able to find a feasible piecewise linear function $f\in \mathcal {F}$ (hence exact), under certain circumstances. In other cases, an approximate piecewise affine function can be easily found afterwards.

4.1 The MIP formulation: 2D King’s graph

In addition to the column and row edges in Sect. 3.1, we further define two sets of diagonal edges variables, where $x^{d_1}_{i,j}$ represents edge $((i,j), (i+1, j+1))$, and $x^{d_2}_{i,j}$ for edge $((i,j), (i+1, j-1))$, as illustrated in the left of Fig. 5. The MIP formulation on king’s graph is similar to that of (8a), by adding the extra second derivative constraints on the diagonal direction (see (9d)–(9e)).

The multicut constraints (7) are still needed to form a valid segmentation. One counter example is shown in Fig. 7, where the dashed edges are “active“, and cycle $e_0-e_1-e_2$ does not satisfy the constraint (7). Its proof is similar to that of Lemma 1, and is omitted here.

The piecewise affine fitting model in 2D king’s graph reads

$$\begin{aligned} \min \; \sum \nolimits _{i=1}^m&\sum \nolimits _{j=1}^n | w_{i,j} - y_{i,j} |+\lambda \sum \nolimits _{e\in E} x_{e} \end{aligned}$$

(9a)

$$\begin{aligned} |\nabla _r^2w_{i,j}|&\le M(x^r_{i,j-1} + x^r_{ij}), \;\; i \in [m],\; j\in [2:n-1], \end{aligned}$$

(9b)

$$\begin{aligned} |\nabla _c^2w_{i,j}|&\le M(x^c_{i-1,j} + x^c_{ij}), \;\; i\in [2:m-1],\; j\in [n], \end{aligned}$$

(9c)

$$\begin{aligned} |\nabla _{d_1}^2w_{i,j}|&\le M(x^{d_1}_{i-1,j-1} + x^{d_1}_{i,j}), \;\; i\in [2:m-1] ,\;j\in [2:n-1], \end{aligned}$$

(9d)

$$\begin{aligned} |\nabla _{d_2}^2w_{i,j}|&\le M(x^{d_2}_{i-1,j+1} + x^{d_2}_{i,j}), \;\; i\in [2:m-1] ,\; j\in [2:n-1], \end{aligned}$$

(9e)

$$\begin{aligned} \sum \nolimits _{e\in C\setminus \{e'\}}x_e&\ge x_{e'}, \;\;\forall \;\text{ cycles } \; C\subseteq E, e'\in C, \end{aligned}$$

(9f)

$$\begin{aligned} w_{ij}&\in \mathbb {R}, \;\;\;\;\; i\in [m], \; j\in [n], \end{aligned}$$

(9g)

$$\begin{aligned} x^r_{ij}&= x_{((i,j),(i,j+1))}, \;\; i \in [m],\; j\in [n-1], \end{aligned}$$

(9h)

$$\begin{aligned} x^c_{ij}&= x_{((i,j),(i+1,j))}, \;\; i \in [m-1],\; j\in [n], \end{aligned}$$

(9i)

$$\begin{aligned} x^{d_1}_{i,j}&= x_{((i,j), (i+1, j+1))}, \;\; i \in [m-1],\; j\in [n-1], \end{aligned}$$

(9j)

$$\begin{aligned} x^{d_2}_{i,j}&= x_{((i,j), (i+1, j-1))}, \;\; i \in [m-1],\; j\in [2:n], \end{aligned}$$

(9k)

$$\begin{aligned} x^r_{ij}&\in \{0,1\}, \;\;i \in [m],\; j\in [n-1], \end{aligned}$$

(9l)

$$\begin{aligned} x^c_{ij}&\in \{0,1\}, \;\;i \in [m-1],\; j\in [n], \end{aligned}$$

(9m)

$$\begin{aligned} x^{d_1}_{i,j}&\in \{0,1\}, \;\;i \in [m-1],\; j\in [n-1], \end{aligned}$$

(9n)

$$\begin{aligned} x^{d_2}_{i,j}&\in \{0,1\}, \;\;i \in [m-1],\; j\in [2:n], \end{aligned}$$

(9o)

$$\begin{aligned} x_e&\in \{0,1\}, \;\;e\in E , \end{aligned}$$

(9p)

where M is again the big-M constant. Here, $\nabla _{d_1}^2w_{i,j}=w_{i-1,j-1}-2w_{i,j}+w_{i+1,j+1}$, and $\nabla _{d_2}^2w_{i,j}=w_{i-1,j+1}-2w_{i,j}+w_{i+1,j-1}$, that is, the discrete second derivative with respect to two diagonal directions $d_1$ and $d_2$ . Note that compared to the grid graph, we also have 3-edge cycles in (9f) now, as shown in Fig. 5.

Fig. 8

A set of minimal subgraphs where the solution $w^\star$ of  (9a)–(9p) are affine, up to permutation by rotating them any integer multiplier of 90 degrees

4.2 Exact model for piecewise affine fitting on King’s graph

We finally prove the following theorem.

Theorem 2

The MIP formulation (9a)–(9p) is exact in finding a piecewise affine fitting function $f \in \mathcal{F}$ that fits F (i.e., (1c) holds), if each of the resulted partition contains at most 3 nodes, or contains any one of those connected subgraphs illustrated in Fig. 8, up to permutation by rotating them any integer multiplier of  90 degrees.

Proof

The first part of the proof is straightforward, since any subgraph with less than or equal to 3 nodes must lie on the same affine function.

We prove the second part by using a similar but more general example of Theorem 1. Let the subgraph of 9 blue nodes be any partition of a feasible solution $(x^\star , w^\star )$ of  (9a)–(9p), shown in the right image of Fig. 5, and let the top left node be (i, j). We first prove $w^\star$ restricted on the following subgraph of 7 nodes lie on the same affine function

$$\begin{aligned} \begin{bmatrix} (i,j)&{} (i,j+1) &{} (i,j+2) \\ \cdot &{} (i+1,j+1) &{}\cdot \\ (i+2,j) &{} (i+2,j+1)&{} (i+2,j+2) \end{bmatrix}, \end{aligned}$$

Similar to the proof of Theorem 1,

$$\begin{aligned} \begin{bmatrix} w_{ij}&{} w_{i,j+1} &{} w_{i,j+2} \\ w_{i+2,j} &{} w_{i+2,j+1} &{} w_{i+2,j+2} \end{bmatrix}= \begin{bmatrix} ja_1 + b_1, &{} (j+1)a_1+b_1, &{} (j+2)a_1+b_1 \\ ja_2 +b_2, &{} (j+1)a_2+b_2, &{} (j+2)a_2+b_2 \end{bmatrix}, \end{aligned}$$

and with respect to the second column,

$$\begin{aligned}&w_{i+1,j+1} \\ =&\;\; \dfrac{w_{i,j+1} + w_{i+2,j+1}}{2} \\ =&\;\;\dfrac{(j+1)(a_1+a_2) + b_1 + b_2}{2}, \end{aligned}$$

Moreover, if we look at the $d_1$ diagonal direction, we have

$$\begin{aligned}&w_{i,j}-2w_{i+1,j+1}+w_{i+2,j+2} \\ =&\;\;ja_1 + b_1 - ((j+1)(a_1+a_2) + b_1 + b_2) + (j+2)a_2+b_2 \\ =&\;\;a_2-a_1\\ =&\;\;0, \end{aligned}$$

which implies $a_1 = a_2$. Hence, $w^\star$ restricted on the above subgraph of 7 nodes lie on the same affine function.

We then prove the above condition also holds on the following subgraph of 6 nodes

$$\begin{aligned} \begin{bmatrix} (i,j)&{} (i,j+1) &{} (i,j+2) \\ \cdot &{} (i+1,j+1) &{} (i+1,j+2) \\ \cdot &{} \cdot &{} (i+2,j+2) \end{bmatrix} \end{aligned}$$

We first look at the first row, and we have

$$\begin{aligned} \begin{bmatrix} w_{ij}&{} w_{i,j+1} &{} w_{i,j+2} \\ \end{bmatrix}= \begin{bmatrix} ja_1 + b_1,&(j+1)a_1+b_1,&(j+2)a_1+b_1 \end{bmatrix}, \end{aligned}$$

For the third column, we have

$$\begin{aligned} \begin{bmatrix} w_{i,j+2}&{} w_{i+1,j+2} &{} w_{i+2,j+2} \\ \end{bmatrix}= \begin{bmatrix} ia_2+b2,&(i+1)a_2+b2,&(i+2)a_2+b_2 \end{bmatrix}, \end{aligned}$$

Since $w_{i,j+2} = ia_2+b2 = (j+2)a_1+b_1$, then $b_2 = (j+2)a_1 - ia_2 + b_1$. Hence,

$$\begin{aligned} \begin{bmatrix} w_{ij}&{} w_{i,j+1} &{} w_{i,j+2} \\ \cdot &{} w_{i+1,j+1} &{} w_{i+1,j+2} \\ \cdot &{}\cdot &{} w_{i+2,j+2} \end{bmatrix}= \begin{bmatrix} ja_1 + b_1, &{} (j+1)a_1+b_1, &{} (j+2)a_1+b_1 \\ \cdot &{} a_2 + (j+1)a_1+b_1, &{} a_2 + (j+2)a_1+b_1 \\ \cdot &{}\cdot &{} 2a_2 + (j+2)a_1+b_1 \\ \end{bmatrix}, \end{aligned}$$

where $w_{i+1,j+1} = \dfrac{w_{i,j} + w_{i+2,j+2}}{2}=a_2 + (j+1)a_1+b_1$, restricted on the $d_1$ diagonal. Hence, $w^\star$ restricted on the above subgraph of 6 nodes lie on the same affine plane.

Similar proof can be made on

$$\begin{aligned} \begin{bmatrix} (i,j)&{} (i,j+1) &{} (i,j+2) \\ (i+1,j)&{} (i+1,j+1) &{} \cdot \\ (i+2,j)&{} \cdot &{} \cdot \end{bmatrix} \text {and} \begin{bmatrix} \cdot &{} \cdot &{} (i,j+2) \\ \cdot &{} (i+1,j+1) &{} (i+1,j+2) \\ (i+2,j)&{} (i+2,j+1)&{} (i+2,j+2) \end{bmatrix}, \end{aligned}$$

just to list some, subject to rotating the shape by integer multiplier of 90 degrees.

Thus we complete the proof. $\square$

Note that, the following two scenarios cannot guarantee $w^\star$ to lie on the same affine function,

$$\begin{aligned} \begin{bmatrix} (i,j)&{} (i,j+1) &{} (i,j+2) \\ (i+1,j) &{} (i+1,j+1) &{} (i+1,j+2) \\ \cdot &{} (i+2,j+1) &{} \cdot \end{bmatrix} \text {and} \begin{bmatrix} (i,j)&{} (i,j+1) &{} (i,j+2) \\ (i+1,j) &{} \cdot &{} \cdot \\ (i+2,j)&{} (i+2,j+1)&{} (i+2,j+2) \end{bmatrix}, \end{aligned}$$

since no diagonal second derivative constraints (9d)–(9d) can be enforced. Hence, this theorem only provides a sufficient condition.

5 Solution techniques

We now introduce a heuristic and an exact algorithm to solve both models (8a)–(8j) and (9a)–(9p). In this section, we will focus on solving the first model on grid graph, and the methods can be easily adopted to the second model on king’s graph as well.

5.1 Region fusion based heuristic algorithm

The resulting problem (8a)–(8j) is a MILP, which is solved using any off-the-shelf commercial MIP solvers. The underlying sophisticated algorithms are based on the branch and cut algorithm [16], where a good global upper bound usually helps to improve the performance. In the following, we will introduce a fast heuristic algorithm that provides a valid partition. It was then given to (8a)–(8j) and upon solving a linear program, its solution is served as a global upper bound.

Our heuristic is based on the region fusion algorithm [15] which approximates the Potts model (3). We start by performing parametric affine fitting over the 4 groups ($2\times 2$ squared nodes) of each node, as shown in Fig. 9. We take the group that has the minimum fitting mean square error, and assign the affine parameters (a vector of 3 in 2D case) to that node. Note that nodes located on the boarders of the grid graph only have 2 such groups, while corner nodes only have 1 group.

Fig. 9

Each node (colored red) has 4 groups of $2\times 2$ squared nodes for affine fitting

Our algorithm then starts with every node i belonging to its own partition $V_i$, and for each pair of nodes, the following minimization problem is solved.

$$\begin{aligned} \min _{\mathbf {w}} \;\tau _i\left\| w_i - Y_i \right\| _2 + \tau _j\left\| w_j - Y_j \right\| _2+\kappa _t \gamma _{ij} \mathbb {1}( w_i \ne w_j ), \end{aligned}$$

(10)

where $\mathbb {1}(\cdot )$ denotes the indicator function, $\tau _i$ the number of nodes in segment $V_i\subseteq V$, and $\gamma _{ij}$ represents the number of neighboring nodes between two segments $V_i$ and $V_j$. Here, $Y_i$ indicates the affine parameter of segment $V_i$, and $w_i$ the unknown variables, and $\kappa _t$ express the regularization parameter at the $k_{th}$ round of iteration.

To speed up computation, instead of solving (10) exactly, the following criteria is checked instead (see [15] for more detailed description):

$$\begin{aligned} \tau _i\tau _j \Vert Y_i-Y_j \Vert _2\le \kappa \gamma _{i,j} \left( \tau _i + \tau _j \right) . \end{aligned}$$

If the above condition holds, we merge partition $V_i$ and $V_j$, and the updated affine parameter (also the values of $w_i$ and $w_j$) is obtained by conducting a parametric affine fitting over the new partition. If not, the two partition and their affine parameters stay the same.

The algorithm iterates over each pair of nodes for solving (10), and the regularization parameter $\kappa$ grows over every round of iteration, which increasingly encourages merging. The algorithm stops after t round of iteration, when $\kappa _t = \lambda$, where $\lambda$ is the pre-defined regularization parameter with respect to (3).

5.2 Exact branch and cut algorithm

Apart from the classical branch-and-cut algorithm inside the MIP solver, we describes below the cutting plane method that iteratively add lazy constraints from (8d).

Cutting plane method. Similar to the cutting planes method that solves the multicut problem [10], we start solving (8a)–(8j) by ignoring constraints (8d), or with few of them (e.g., the 4 or 8-edge cycle constraints).

We then check the feasibility of the resulting solution with respect to (8d). If it is already feasible, we are done. Otherwise, we identify the current separation problem and then add the corresponding violated constraints (cuts) to (8a)–(8j). We resolve the updated MILP, and this procedure repeats until either we get a feasible solution, or the user-defined limit is reached.

Separation problem. Given an integer solution, it is polynomial to either check the feasibility with respect to (8d), or to identify and separate the integer infeasible solutions by adding violated constraints.

Phase 1: Given the incumbent solution of the MILP (8a)–(8j), we extract its binary solutions and remove edges where $x_e=1$ from the grid graph G(V, E). We thus obtain a new graph $G^\prime (V^\prime ,E^\prime )$ where $V^\prime = V$, $E^\prime \subseteq E$ and we identify its connected components. We then check for each active edge to see if their two end nodes belong to the same component. If there exists any, the current solution is infeasible (and we call the corresponding active edges violated). Otherwise, a feasible and optimal solution is found.

Phase 2: If violated edges exist, we search for violated constraints by finding paths between the two nodes of the edge. We first conduct a depth-first search on the graph $G^\prime$, and multiple such paths could be found. We set the maximum depth to 10 to restrict the searching time. If the depth-first search does not return any path, we then switch to the breadth-first search to return only one shortest path.

Phase 3: For each violated edge, we add the corresponding multicut constraints (8d) (possibly many) to our MILP (8a)–(8j), where the left hand side corresponds to the paths found in phase 2 .

Facet-defining searching strategy. The above mentioned strategy that finds violated constraints does not guarantee facet-defining inequalities. Recall that the multicut constraint (8d) is facet-defining if and only if the corresponding cycle is chordless. In the facet-defining searching strategy, we in addition keep track of the non-parental ancestors set (denoted S) of the current node during searching. When we search for the next node, we make sure that the potential node does not form an edge (with respect to G) with any node in S.

6 Computational experiments

In this section, all the experiments are conducted on a desktop with Intel(R) Xeon(R) CPU E5-2620 v4 @ 2.10GHz CPU and 64 GB memory, using IBM ILOG Cplex V12.8.0 as the MIP optimization solver.

We develop and compare the following variants of (8a)–(8j) or  (9a)–(9p), and report their computational results. The experiments are based on synthetic images of different sizes, as well as real depth images. We normalize the intensity values of all images to [0, 1], and each experiment is conducted 3 times and only the median of the results is reported. We report the running time, nodes of the branch and bound tree, optimality gap, cuts added and the objective function of the MILP.

• MP: The MILP formulation of the piecewise affine fitting model (8a)–(8j) that adds the multicuts without the facet-defining searching strategy.

• MPH: MP where we adopt the solution of the heuristic in 5.1 as an initial input.

• MPH-F: MPH with the facet-defining searching strategy.

• MPH-4: MPH with the 4-edge cycle multicut constraints as initial inequalities.

• MPH-4&8: MPH with the 4 and 8-edge cycle multicut constraints.

• MP$_E$HF: The MILP formulation (9a)–(9p) where we adopt the solution of the heuristic as an initial input, and with the facet-defining searching strategy.

• MP$_E$HF-3: MP$_E$H-F with the 3-edge cycle multicut constraints as initial inequalities.

• MP$_E$HF-3&4: MP$_E$H-F with the 3 and 4-edge cycle multicut constraints.

Fig. 10

Top: synthetic images with affine pieces, 2D view. Bottom: their 3D views

6.1 Automatic computation of parameters

Parameter $\varvec{\lambda }$ is the regularization term employed to avoid over-fitting in problem MP (8a)–(8j). We set $\lambda$ independently for each row and column, denoted $\lambda _{i}^r$ and $\lambda _{j}^c$, since intuitively, this may help adapt to local features. $\lambda$ is computed in a way to avoid making an outlier a one-node segment. Let $\lambda ^r_i=\frac{1}{2}\xi \cdot \text {max}_i \;|\nabla ^2 y^r_i|$ and $\lambda ^c_j=\frac{1}{2}\xi \cdot \text {max}_j \;|\nabla ^2 y^c_j|$, where $\xi$ is the user-defined parameter. In this manner, if there exists an outlier (i, j), making a one-node segment will active all four edges of (i, j), thus incurring a penalty value of $2(\lambda ^r_i+\lambda ^c_j)$.

Parameter $\varvec{M}$ is for the “big M” constraint in MP (8a)–(8j). In principle, it should be big enough so that the constraints (6b,6c) are always valid, i.e., $M = 2$. On the other hand, it should be not too big, or it may harm the tightness of the LP relaxation. The value of big M could be computed automatically each on row and column, following the strategy above. However, we have tested different variants and found out the results only have slight fluctuations. Hence, we simply set $M=2$ globally.

6.2 Numerical experiments on synthetic images

In this section, we generate 3 synthetic images that has affine trends, as shown in Fig. 10. We then test different variants of our models on 3 sizes of the images, i.e., $20\times 30$, $40\times 60$, and $80\times 120$. In addition, we further experiments on scenarios that add Gaussian noise of level 0, 0.001 and 0.005. Thus, a total of 27 tests (81 experiments, as we run each test 3 times and only report the medium) are done for each model. We set the time limit of each experiment to 600 seconds.

Before starting these 81 experiment, we run additional experiments to select the “right” values of $\xi$. We found out all three images achieve optimal segmentation (with respect to the ground truth) results when $\xi =0.5$. Thus, we keep it fixed throughout this section to keep our comparison concise.

Fig. 11

Table on MP, MPH and MPH-F

6.2.1 MP versus MPH

We first conduct experiments on solving MP with and without the heuristic algorithms (introduced in Sect. 5.1) to the MIP solver. Our heuristic algorithm is fast to compute, takes 3 seconds on average to converge on the $40\times 60$ sized images. Note that we only provide the MIP solver with initial integer solutions x of problem (8a)–(8j), hence it takes time for the solver to compute w by solving a linear program.

As we can see in the MP column of Fig. 11, MIP alone suffices to find optimal solutions in all tests when the image is clean (without Gaussian noise), even in $80\times 120$ size. It also reaches optimality on the $20\times 30$ images, with 0.001 Gaussian noise added. However, without heuristic, no feasible solution are found in Test 26 and 27 within 600 seconds. The results in MPH column indicates that adding the result of the heuristic as initial solution to the MIP solver mostly improves the results. For instance, MPH helps reduce the optimality gap from $92.33\%$ to $9.17\%$ in Test 15. It sometimes also reduce the performance, i.e., increases the running time of finding optimal solution from 16.08 to 96.18 seconds in Test 4.

6.2.2 MPH versus MPH-F

Given an heuristic solution, we further test the performance of adopting the facet-defining searching strategy. Recall that although it takes more time to find a facet-defining multicut constraint (8d) (as described in the facet-defining searching strategy), it is tighter compared to non facet-defining ones. The results are shown in the MPH and MPH-F columns of Fig. 11, where we could see MPH-F performs better than MPH in most of the cases, with only a few exceptions. For instance, MPH-F helps reduce the running time from 169.28 to 149.81 seconds in Test 5. MPH-F also reduces the optimality gap from 88.61 to 15.33% in Test 17.

Fig. 12

Table on MPH, MPH-4 and MPH-4&8

6.2.3 MPH versus MPH-4 and MPH-4&8

We compare whether adding few facet-defining multicut constraints as initial constraints to MPH improves computation. We test the performance of adding only 4-cycle constraints (MPH-4) and adding both 4-cycle and 8-cycle (MPH-4&8). The results are shown in Fig. 12. We notice that after adding these cycle constraints, Cplex rarely (only 1 out of 27) add any additional cuts to MPH. We also note that in general, adding 4-cycle constraints helps on improving the performance. For instance, MPH-4 reduces the optimality gap significantly on test 14, test 17 and test 22. In addition, compared to MPH-4, the experiments shows that adding the 8-cycle constraints seems harmful in most cases.

Fig. 13

Top: images ($40\times 60$) with 0.005 Gaussian noise. Bottom: results from MPH-4

6.2.4 Results on image segmentation and denoising

Upon solving our MILP (8a)–(8j), the active edges ($x_e=1$) together with the multicut constraints (8d) form a valid segmentation, and the fitting variables (w) removes noise. Although only an approximate formulation, the segmentation results of most tests (except for Test 25–27) are already “optimal” in terms of image segmentation (compared to the ground truth). An illustration of the denoising results (as well as segmentation) can be seen in Fig. 13, where the first row are the $40\times 60$ images with 0.005 Gaussian noise, and second row the results from MPH-4.

6.2.5 MP$_E$HF versus MP$_E$HF-3 and MP$_E$HF-3&4

We now conduct similar experiments on different variants of model (9a)–(9p). We see from Fig. 14 that, for image size $20\times 30$ and $40\times 60$, MP$_E$HF-3 and MP$_E$HF-3&4 perform better than MP$_E$HF, not only on the objective function, but also on the optimality gap. Furthermore, we see that the number of cuts also reduces tremendously. But when the image size becomes $80\times 120$, MP$_E$HF performs best instead. We think it may be due to the extremely large number of 3 and 4-cycle constraints.

Fig. 14

Table on MP$_E$HF vs MP$_E$HF-3 and MP$_E$HF-3&4

6.2.6 Comparison between MP and MP$_E$

Although only an approximate model, our experiments show that MP performs “much better” numerically than the “exact” model MP$_E$ in most of cases, in terms of optimality gap, and segmentation result. Note that, due to their different objective functions, we cannot simply compare their object function values. We think the performance of MP is superior mainly because MP only has roughly half of the edge variables and hence way fewer multicut constraints (7) than MP$_E$. However, we show in Fig. 15 that MP$_E$ achieves valid and optimal fitting result (compared to ground truth) while MP not. Although not easily visualized in the image, we confirm this by randomly selecting a few points within one segment and conduct affine fitting.

Hence, we argue that MP$_E$ may be useful for small instances, while is MP is more practical for large scale data.

Fig. 15

Left: original image with 0.01 Gaussian noise, Middle: result of MP, Right: result of MP$_E$

6.3 Numerical experiments on real images

We further conduct experiments on two real depth images with 2 different sizes (600 pixels and 2400 pixels), which are generated from the disparity maps of the Middlebury data set [21] (shown in Fig. 16). We only apply the approximate model (8a)–(8j) on them.

Fig. 16

Top: two images from [21]. Bottom: their disparity maps

According to the performance of different variants in previous section, we choose to test MPH-4-F (MPH with the 4-edge cycle multicut constraints using the facet-defining searching strategy) with respect to the regularization parameter $\xi$ and time limit. Since real images already contain noise, we do not add extra one. We also run each experiment 3 times and only report the medium. All the results are shown in Fig. 17.

Fig. 17

Table of tests on MPH-4-F with different regularization parameters $\xi$ and time limits

6.3.1 Regularization parameter $\xi$

The regularization parameter $\xi$ is introduced to penalize the perimeter as well as the number of partitions. The larger $\xi$ is, the fewer the partitions are. In this section, we conduct experiments on using 3 different value of parameter $\xi$ (0.5, 1 and 2), and the time limit is set to 1200 seconds.

The computational results are shown in the left table of Fig. 17. However, since the objective functions contain both fitting and regularization terms, their absolute values is not comparable. Instead, we visualize the segmentation results in Fig. 18. It is obvious to see that the number of segments decreases as $\xi$ increases.

Fig. 18

Segmentation results as the $\xi$ increases from left to right

6.3.2 Time limit

In this section, we conduct experiments on adopting 4 time limits (50, 200, 600 and 1200 seconds), and we set $\xi =0.5$. The computational results are shown in the right table of Fig. 17. Since none of tests finds an optimal solution, the performance could possibly be further improved by extending the time limit. In addition, a shorter time limit is still possible to produce a solution with acceptable gap, especially for images witch smaller size. Figure 19 visualizes the optimality gap with respect to time limit. As can be predicted, when time limit increases, the optimality gap drops.

Fig. 19

Optimality gap decreases as time limit increases

7 Conclusions

In this paper, we have presented two unsupervised and non-parametric model that either finds or approximates a discontinuous piecewise affine function to fit the given data. We formulate them as MILP and solve them with a standard optimization solver. In both cases, the inclusion of multicut constraints enables a feasible partitioning (or segmentation of the image domain). Thus, a corresponding piecewise affine function can be easily reconstructed for the approximate model.

The computational complexity is the main bottleneck of our approach, especially the exact model. To tackle with it, we add different sets of inequalities as initial constraints to our MIP, and add the remaining multicut constraints using cutting planes method on the fly. We also implemented a special heuristic algorithm that finds a feasible segmentation, which is used as an initial integer solution to the MIP solver. We conducted numerical experiments on different variants of our models and study the effects of adjusting model parameters. We demonstrate the feasibility of our approach by its applications to segmentation and denoising on both synthetic and real depth images.

As for future work, its generalization to 3D images is worth investigating. Furthermore, we would like to extend this work beyond the scope of image processing, to deal with other applications, such as signal compression [4].